Theoretical advances in understanding and enhancing the thermostability of energetic materials

Abstract

The quest for thermally stable energetic materials is pivotal in advancing the safety of applications ranging from munitions to aerospace. This perspective delves into the role of theoretical methodologies in interpreting and advancing the thermal stability of energetic materials. Quantum chemical calculations offer an in-depth understanding of the molecular and electronic structure properties of energetic compounds related to thermal stability. It is also essential to incorporate the surrounding interactions and their impact on molecular stability. Ab initio molecular dynamics (AIMD) simulations provide detailed theoretical insights into the reaction pathways and the key intermediates during thermal decomposition in the condensed phase. Analyzing the kinetic barrier of rate-determining steps under various temperature and pressure conditions allows for a comprehensive assessment of thermal stability. Recent advances in machine learning have demonstrated their utility in constructing potential energy surfaces and predicting thermal stability for newly designed energetic materials. The machine learning-assisted high-throughput virtual screening (HTVS) methodology can accelerate the discovery of novel energetic materials with improved properties. As a result, the newly identified and synthesized energetic molecule ICM-104 revealed excellence in performance and thermostability. Theoretical approaches are pivotal in elucidating the mechanisms underlying thermal stability, enabling the prediction and design of enhanced thermal stability for emerging EMs. These insights are instrumental in accelerating the development of novel energetic materials that optimally balance performance and thermal stability.

---

1. Introduction

Energetic materials, generally encompassing a diverse array of explosives, propellants, and pyrotechnics, are extensively utilized in both military and industrial domains.¹ These substances can be thought as controllable storage systems for vast amount of chemical energy, which, when harnessed, can be directed to achieve high-powered outcomes. In the present day, there is a continuing need for new high energy density materials (HEDMs) with improved properties, such as superior detonation performance, reliably high stability, cost efficiency, ease of synthesis, environmentally benign, and safe for handling and transportation.² Basically, detonation performance and safety are the two most critical indicators in assessing energetic materials, directly determining their practical applicability.^3,4 A new energetic material will be discarded if it has inadequate energy or fails to meet the safety standards. Traditional HEDMs are typically molecular crystals of organic CHNO-based molecules (TNT, TATB, RDX, etc.). However, from TNT to the synthesis of ONC,⁵ spanning over a century, the energy density per unit mass only increased by a factor of 1.8.^6,7 The advancement of traditional CHNO energetic materials has encountered a significant obstacle in further improving their energy density.⁸ Nowadays, research trends for novel energetic materials have transitioned from the synthesis of relatively simple organic molecules to the creation of more complex molecular architectures.^9–11 Strategies such as constructing cage-like structures (CL-20, ONC, and TEX) or using nitrogen-rich heterocyclic scaffolds (DDF, DTTO, TKX-50, etc.) are utilized to enhance the density and performance.¹² In recent years, advancements in the development of nitrogen-rich compounds have propelled polynitrogen materials to the forefront of energetic materials research, positioning them as next-generation HEDMs.¹³ Although these novel HEDMs exceed the traditional energetic materials in terms of energy, most of them are not adequate for real applications due to high sensitivity or low thermal stability. Generally, high performance is accompanied by inferior stability.^14,15 Therefore, finding a proper equilibrium between superior detonation capability and good safety for an EM remains a huge challenge.

For HEDM development, experimental research studies are often associated with elevated level of risk, costs, and development timelines, as there are many unknowns at the molecular and electronic levels that are beyond the scope of the experimental capabilities. In contrast, computational approaches can provide microscopic insights that are often difficult or impossible to achieve experimentally, thereby accelerating the discovery, synthesis, and optimization of advanced HEDMs.¹⁶ Theoretical studies for detonation performance based on quantum mechanical¹⁷ and semi-empirical^18,19 methods have demonstrated their effectiveness in accurately characterizing key factors, including heat of formation (HOF), as well as detonation velocity and pressure. Although safety stands out as a crucial indicator for an EM, its inherent complexity presents significant challenges in theoretical understanding and predictive modeling. A multitude of factors can affect the safety of energetic materials. EMs can be accidentally triggered through mechanical, thermal, or electrical stimuli. Therefore, understanding the relationship between molecular structures and stability is essential for ensuring their safety. In many cases, the action of these stimuli causes internal heating of the EM. For example, shock or impact to the energetic material can induce the formation of localized hot spots,^20,21 which are pivotal in initiating decomposition reactions within the crystal structures. Thus, sensitivity to ignition is often correlated with the thermal decomposition processes, and thermostability is commonly used as a key indicator to assess the safety of EMs.^22,23 Typically, thermal stability (heat resistance) of EMs is vital for their safe storage and transportation, ensuring that the energetic materials can withstand decomposition, deflagration, or detonation induced by thermal stress.⁴ Although many thermal analysis techniques^24–28 can provide information on decomposition temperatures and thermolysis products of energetic materials,^29–32 these methods are incapable of directly exploring the intricate reaction mechanisms in EMs. In this context, theoretical investigation emerges as a compelling alternative, enabling systematic exploration of thermostability properties at the microscopic scale.

From a molecular perspective, energetic materials can be conceptualized as residing in metastable local minima on their potential energy surfaces, with multiple kinetic barriers that separate them from the product states. The kinetic stability of a given EM is a critical determinant of its thermostability: a material with robust kinetic stability typically exhibits enhanced thermostability. Over the past decade, significant progress has been made in applying quantum mechanical calculations, especially density functional theory (DFT) methods as well as other post-Hatree-Fock approaches (CCSDT, MPn, CBS, etc.) to accurately characterize the thermal decay mechanisms of unimolecular and bimolecular reactions in the gas phase.^33,34 These theoretical studies have yielded profound insights into the reaction energies, activation barriers, and reaction rates for the thermolysis pathways. At the molecular and electronic level, conducting ab initio calculations can also provide a host of important indicators for thermal stability, including HOF,¹⁹ bond dissociation energy (BDE),³⁵ electrostatic potential (ESP),³⁶ Mulliken charge distribution, HOMO–LUMO gap,³⁷etc. Furthermore, theoretical approaches are also essential to offer insights into molecular engineering to enhance the thermal stability of HEDMs.^38,39 Strategic modifications to molecular architectures or introducing specific substituents^40,41 can potentially elevate bond strengths and alter the overall electronic structure of the EM compounds, tailoring energetic materials for desired properties with enhanced stability.

However, energetic compounds with good molecular stability often suffer from undesirable detonation performance, which stems from the trade-off between thermostability and detonation performance. Despite this, there are high-performing energetic materials that while exhibiting less favorable unimolecular stability, demonstrate commendable thermal stability.^42–44 This is largely due to the fact that unimolecular stability does not necessarily correlate with the behavior of EMs in aggregated states.⁴⁵ Within crystalline structures, intricate intermolecular interactions can profoundly influence overall stability, diverging from the properties obtained under isolated molecular conditions. Zhang et al.^46–48 demonstrated a correlation between crystal packing and impact sensitivity. Designing hydrogen bonding,^49,50 and energetic cocrystals^51–53 can also exert influence on the thermal stability of the EMs. Therefore, quantitative analysis of intermolecular interactions, including Hirshfeld surface analysis,¹⁷ is essential for estimating the stability of EMs.

On the other hand, gaining mechanistic insight into the initial thermal decomposition reactions is pivotal for understanding and assessing the thermal stability of a specified EM. A thorough knowledge of initial bond ruptures, key intermediates, and pivotal exothermal reactions in the thermal decomposition process can help to better understand the thermal stability properties and could potentially aid in the development of newer and safer EMs. Theoretically, molecular dynamics simulation techniques, utilizing ReaxFF, semi-empirical or ab initio approaches for potential energy description, are widely utilized to explore the thermal decomposition mechanisms of EMs at the molecular level.⁵⁴ These simulations are capable of depicting the breaking and formation of chemical bonds in complex systems under extreme conditions (high temperature or pressure), as well as statistically analyzing intermediates, products, and reaction pathways with high temporal and spatial resolutions during thermal decompositions.

In recent years, the application of machine learning (ML) techniques in energetic materials has become a captivating field.⁵⁵ ML is utilized to predict the physical and chemical properties of energetic materials, such as density, performance, and thermal stability.^56,57 By training ML models on datasets comprised of known compounds and their properties, researchers can predict these properties for new, untested compounds. ML models also play an essential role in the design and discovery of new energetic materials. By learning from the structure–property relationships of known materials, ML algorithms can guide the design of new molecules with tailored properties.^58,59 Thus, machine learning techniques open up new avenues for predicting and enhancing the thermostability of novel energetic materials.

Nowadays, the advancements in computational techniques, especially high-throughput computing (HTC) and high-performance computing (HPC), enable cutting-edge first-principles calculations and machine learning approaches to theoretically investigate the thermal stability of energetic materials. In this perspective, we will highlight the recent theoretical advancements in the study of thermal stability of energetic materials, and summarize the theoretical insights and strategies for creating novel energetic materials with enhanced thermostability.

2. Theoretical insights for molecular stability

To comprehensively understand the stability of energetic materials, it is imperative to examine their molecular and electronic structures theoretically, analyzing the stability of these materials. Energetically, traditional EMs are nearing their theoretical limit. Recently, nitrogen-rich heterocycles, and even all-nitrogen compounds, have been developed at the current state of the art. Apart from higher energy density, the use of pure nitrogen and simple polynitrogen compounds as HEDMs results in the production of clean N₂ molecules upon decomposition. However, their intrinsic instability presents substantial challenges in their synthesis and manipulation. Many polynitrogen species are unstable under ambient conditions and can only exist in high pressure environments.^60,61 Thus, efforts are focused on stabilizing polynitrogens, like the promising pentazole, for use as building blocks for energetic materials. As the last member of the azole family, pentazole has a unique five-membered nitrogen ring structure. The synthesis of arylpentazoles (ArN₅) in the 1950s marked a milestone in pentazole chemistry,^62–66 yet these compounds can only exist at temperatures below −40 °C. This limited thermal stability is primarily attributed to the low kinetic barrier for the N₂-leaving process, which has impeded their practical use. Thus, discovering strategies to sufficiently increase the kinetic stability of the N₅-ring within ArN₅ is crucial for their utility in HEDM chemistry.

Though chemists have made numerous attempts to strengthen the N₅-ring through substituent engineering,^67,68 the reported stabilization effect for ArN₅ remains below expectations. From a theoretical perspective, Brinck et al.⁶⁹ conducted a DFT investigation into the decomposition barriers of various para-substituted ArN₅ compounds. Their calculations revealed that the decomposition energy barrier for the N₅-ring is less than 22 kcal mol⁻¹, and the introduction of electron-withdrawing substituents lowers the Gibbs free energy barriers. Comparable findings were also reported by Burke et al.⁷⁰ employing high-level computational methods of CCSDT and DFT for RN₅ and ArN₅, respectively. Gong et al.⁷¹ conducted an extensive DFT study examining the thermal stability of ArN₅ in the presence of various para- and meta-substituents. A recent theoretical investigation into the thermostability of ArN₅ in both gas and solvents was reported by Liu et al.⁷² (Fig. 1). These findings indicate that substituents that facilitate increased electron density on the N₅ ring would enhance its stabilization, which suggests a potential strategy for stabilizing these molecules.

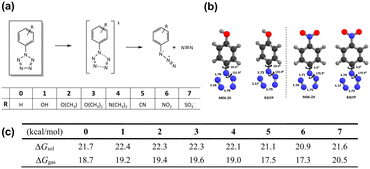Fig. 1 (a) Schematic view for the decomposition of arylpentazoles with substituents 0–7; (b) selected geometries of transition state structures; (c) reaction barriers of decomposition of para-substituted arylpentazoles 0–7. Reproduced with permission from ref. 72. Copyright 2019, The Royal Society of Chemistry.

From a theoretical standpoint, the limited kinetic stability of N₅ is attributed to the repulsion between the electron lone pairs (LP) of nitrogen atoms. Addressing this issue, Ding et al.⁷³ modeled the addition of a Lewis acid (LA) group to the ortho carbon of the benzene ring within ArN₅ compounds. This strategic introduction of LA sites is expected to interact with the proximate N atoms, effectively reducing LP repulsion and thus contributing to a significant co-stabilization effect. For the substitution of LA, two types of LA moieties, –BH₂ and –CH₂BH₂, were employed to modify one or both ortho positions on the benzene rings of ten parent arylpentazoles (see Fig. 2(a)). The energy barrier for the rate-determining step of ring decomposition was calculated using the CBS-QB3 method. As shown in Fig. 2(c), incorporating the LA groups into ArN₅ molecules significantly enhances their thermal stability. Notably, the highest kinetic barrier of 40.83 kcal mol⁻¹ was achieved for ArN₅ (06), doubling the value of 20.35 kcal mol⁻¹ for the parent ArN₅ molecule (see Fig. 2(c)). This theoretical design of novel functionalized ArN₅ compounds is ascribed to an innovative co-stabilization strategy, which entails attaching a Lewis acid moiety to the neighbouring nitrogen atoms of the N₅-ring. While this concept has not yet been realized experimentally, the predicted enhancement in thermal stability at the CBS-QB3 level provides a direction for the synthesis of more heat-resistant pentazole derivatives.

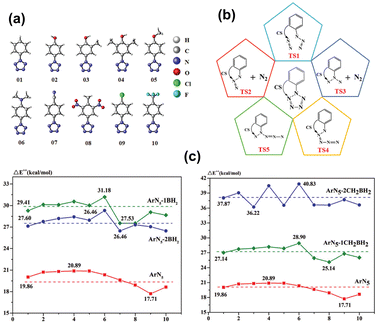Fig. 2 (a) Arylpentazoles as the parent models for co-stabilization (CS); (b) a schematic view of decomposition processes; (c) rate-determining energy barrier of ArN₅ without and with CS stabilization (CS = −nBH₂ and −nCH₂BH₂; n = 1, 2). Reproduced with permission from ref. 73. Copyright 2021, The Royal Society of Chemistry.

Compared to ArN₅, the pentazolate anion (cyclo-N₅⁻) is a much more prominent pentazole variant. Extensive theoretical research indicated that this all-nitrogen anion exhibits greater thermal stability than RN₅ compounds.^74–80 Theoretical investigations using a highly accurate CCSD(T)/CBS approach conducted by Dixon et al.⁷⁹ demonstrated that the ring decomposition of gas-phase cyclo-N₅⁻ has an energy barrier of 27.2 kcal mol⁻¹, suggesting that cyclo-N₅⁻ could potentially maintain stability in isolation under ambient conditions. Motivated by theoretical insights, there have been increased experimental efforts towards the synthesis of the pentazolate anion over the past two decades.^81–84 The breakthrough in first synthesizing a stable pentazolate crystal, PHAC ((N₅)₆(H₃O)₃(NH₄)₄Cl), was achieved by Hu et al.⁸⁵ in 2017. This pentazolate salt was synthesized from a mild acidic solution of arylpentazole with m-CPBA and [Fe(Gly)₂]. Since then, the experimental and computational research on cyclo-N₅⁻ was greatly enriched.^86–88 While Liu et al.⁸⁹ have theoretically clarified the generation mechanism of cyclo-N₅⁻ from ArN₅, intriguing questions persist regarding its stability: why the N₅⁻ anion remains unprotonated in acidic solutions and within the PHAC crystalline structure, even when in close proximity to ammonium ions.

To address this, Zhang et al.^90–93 delved into a series of in-depth theoretical analyses focused on the stabilization mechanism of cyclo-N₅⁻, and an interesting dual aromatic feature was identified within the compound. As shown in Fig. 3, the calculated LDOS surface for the minimum energy level of π Mos clearly indicates a pronounced π aromaticity. This is quantitively confirmed by the very negative nucleus-independent chemical shifts calculated at 1 Å above the ring centre in the z-axis (NICS(1)_π). Interestingly, unlike typical nitrogen lone pairs which tend to be localized, the LDOS for nitrogen LPs in cyclo-N₅⁻ is fully delocalized in the equatorial plane, forming a flower-like pattern (Fig. 3(c)). This indicates the presence of intriguing σ-aromaticity, as supported by the NICS(0)_σ value (−13.6). Thus, both π- and σ-electrons independently contribute to the overall aromaticity of cyclo-N₅⁻. This underscores the critical role of the net charge on the N₅-ring in establishing its dual aromaticity. Upon ionization to a neutral state, the redistribution of LP electrons significantly elevates the total energy of the system, making the neutral N₅ lose its stability.

Fig. 3 (A) Atomic orbital diagram of the cyclo-N₅⁻ anion; (B) top and side views of the LDOS isosurface at the lowest energy level of the aromatic π-system; (C) LDOS isosurface at the lowest energy level of the aromatic σ-system. Reproduced with permission from ref. 91. Copyright 2019, Wiley.

The stability and reactivity of cyclo-N₅⁻ under acidic conditions were further explored using theoretical models that examined cyclo-N₅⁻ in the presence of hydroniums and within the PHAC crystalline structures. As depicted in Fig. 4(A) and (B), cyclo-N₅⁻-hydronium cluster models with fewer than three binding hydronium ions (c = 1, 2) result in protonation of cyclo-N₅⁻, leading to reduction in dual aromaticity (Fig. 4(D)). For c = 3, the protonation of cyclo-N₅⁻ attains a critical threshold. As the number of surrounding protons increases to 4 and 5 (simulating the PHAC crystalline structure), cyclo-N₅⁻ relinquishes its proton affinity to restore the dual aromaticity. This shift renders cyclo-N₅⁻ resistant to the acid–base neutralization principle, resulting in its unprotonated state. Fig. 4(C) illustrates that an increase in the number of adjacent protons weakens the repulsion of LP within the σ-system, which in turn leads to a shortening of the N–N bond length within cyclo-N₅⁻. It is consistent with the bond strengths shown in Fig. 5, which indicates that the clustering of H₃O⁺ enhances the N–N bonds within cyclo-N₅⁻. Notably, the N₅⁻⋯4H₃O⁺ cluster, with reduced LP repulsion and intact dual aromaticity, offers optimal stability enhancement. This configuration strengthens all N–N bonds by approximately 57.16 kcal mol⁻¹, significantly surpassing the stability of its naked counterpart.

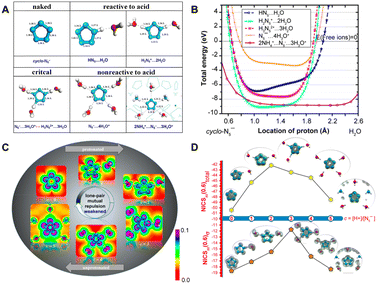Fig. 4 (A) Optimized structures of the cyclo-N₅⁻ complex/crystal at various acid concentrations; (B) energetic landscape of the cyclo-N₅⁻ complex/crystal as a function of the N–H distance; (C) LDOS at the antibonding energy level plotted in the equatorial plane of cyclo-N₅⁻ under varying acidities; (D) NICS_zz(0.6) total and NICS_zz(0.6) σ of the cyclo-N₅⁻ anion under varying acidities and the corresponding LDOS isosurfaces plotted for the lowest energy level (nonbonding) of the aromatic π- and σ-systems. Reproduced with permission from ref. 90. Copyright 2019, American Chemical Society.

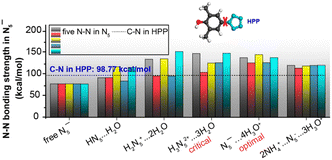Fig. 5 N–N bond strengths in the cyclo-N₅⁻ anion at various acid concentrations with respect to the C–N bond strength in HPP (dashed line). Reproduced with permission from ref. 90. Copyright 2019, American Chemical Society.

The theoretical insights demonstrated that cyclo-N₅⁻ can achieve enhanced stability in all of its N–N bonds only in a sufficiently acidic environment through the formation of a hydrogen-bonded complex with surrounding electrophiles. Without this, cyclo-N₅⁻ cannot be successfully isolated. To realize a high-yield synthesis of cyclo-N₅⁻, the proton concentration (H₃O⁺ or NH₄⁺) should be regulated for a high-yield synthesis of cyclo-N₅⁻. This dual aromaticity, as well as the acid stabilization mechanism discovered in the pentazolate anion, was also clarified in tetrazole and triazole-based anions (N₄C₁H₁⁻ and N₃C₂H₂⁻),⁹² exemplifying a general characteristic for the five-membered pnictogen ring systems. Recently, a theoretical exploration of the novel N₄²⁻ compound was also discovered to be acid stabilized by hydroniums,⁹³ revealing significant bond strength for N–N bonds within the N₄²⁻⋯4H₃O⁺ complex (Fig. 6). This mechanism should be applicable to other all-nitrogen aromatic compounds, which sheds light on the efficient isolation and stabilization of these compounds.

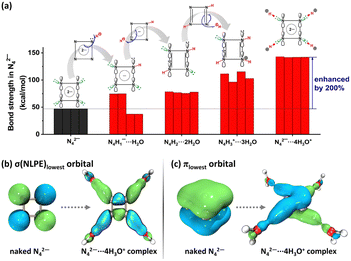Fig. 6 (a) Bond strength in N₄²⁻ shows that the firmness of N₄²⁻ continuously enhances as the acidity increases; (b) lowest σ orbital of nitrogen lone pairs indicates that nitrogen lone pairs are pulled by the proton in the N₄²⁻⋯4H₃O⁺ complex, which weakens the inter-lone-pair repulsion along the N₄²⁻ ring and facilitates N–N reinforcing; (c) lowest π orbital indicates that π electrons of N₄²⁻ can be delocalized in a much broader region when forming the N₄²⁻⋯4H₃O⁺ complex, facilitating energy reduction. Reproduced with permission from ref. 93. Copyright 2022, Elsevier.

In addition to the direct synthesis of pentazole compounds at ambient pressures, synthesizing a high-pressure stable pentazole compound and then recovering it under ambient conditions is an alternative and flexible approach to achieve stabilized pentazolate salts.^94–97 Theoretically, first-principles crystal structure prediction has been proven to be useful in searching for stable crystal structures.^98–100 This approach involves exploring a wide range of stoichiometries, symmetries, orientations, and spatial packings, at assumed pressures. Crystal structures are evaluated by calculating their total energies under these conditions and analyzing their energy landscapes. The most energetically favorable structures are then considered stable candidates. These candidates will undergo further stability checks through phonon calculations and molecular dynamics simulations. Alkali metals are capable of enhancing the stability of pentazolate in the solid phase: alkali elements promote the electron transfer to cyclo-N₅⁻, thus enabling both aromaticities in the isolated N₅⁻ and ionic bonding between them within the crystalline structure. Recent studies have conducted first-principles calculations using CALYPSO¹⁰¹ and USPEX¹⁰² to extensively explore stable alkali metal–cyclo-N₅⁻ crystal structures under various pressures. The crystal structures of CsN₅ and LiN₅ were theoretically predicted and synthesized using high-pressure techniques.^94,95,98 This suggests that crystal engineering based on theoretical approaches can potentially offer valuable insights prior to the experimental synthesis of energetic materials and accelerate the design and synthesis of novel HEDMs with superior performance and stability.

3. Thermal decomposition mechanisms in the condensed phase

Gaining mechanistic insight into the initial decomposition reactions is essential for understanding and assessing the thermal stability of a specified EM. The crystalline environment is important for the initial decomposition mechanisms of energetic molecules, which could result in reaction mechanisms that are significantly different from those under gas-phase conditions. A recent theoretical study by Liu et al.¹⁰³ has investigated the initial decomposition pathways and energy barriers of typical energetic materials, FOX-7 and RDX, under both gas phase conditions and crystalline environments. By constructing QM/MM models to describe decomposition within the crystalline environment, it has been shown that effects of the crystalline environment lead to higher kinetic barriers and reaction pathways that differ greatly from those observed under gas-phase conditions. Therefore, to correctly interpret the initial reaction mechanisms of energetic materials, it is crucial to consider the decomposition reactions within the crystalline environment in computational simulations. The thermal and kinetic aspects of condensed phase decomposition reactions can be extremely complex due to a large number of parameters, intermediates, and an overlap in thermal decomposition traces. Molecular dynamics simulation techniques, utilizing ReaxFF, semi-empirical or ab initio approaches for potential energy description, are capable of revealing thermal decomposition mechanisms of EMs under extreme conditions (high temperature or pressure).

Recently, using MD simulations combined with QM calculations, thermal decomposition mechanisms for a series of novel HEDMs as well as energetic cocrystals have been theoretically explored.^104–107 One such example is TKX-50 (5,5′-bistetrazole-1,1′-diolate), a recently developed nitrogen-rich energetic material with high energy content and performance.¹⁰⁸ As shown in Fig. 7, TKX-50 is an azole-based ionic crystal with high nitrogen content. The detonation performance of TKX-50¹⁰⁹ (D = 9.7 km s⁻¹, p_C–J = 42.4 GPa) was calculated to be close to CL-20, and its mechanical and thermal sensitivity was found to be lower than currently used explosives, such as RDX, HMX, and CL-20. TKX-50 also exhibited low toxicity, positioning it as a highly promising alternative to replace the more toxic RDX in practical applications.

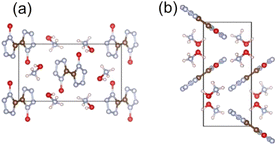Fig. 7 Crystal structure of TKX-50. Panel (a) is the view from the a direction, and panel (b) is the view from the c direction. Reproduced with permission from ref. 104. Copyright 2014, American Chemical Society.

Goddard et al.¹⁰⁴ conducted a theoretical simulation of the thermal decomposition dynamics of TKX-50 materials. To achieve computation efficiency with good accuracy, the semi-empirical SCC-DFTB was used to perform a temperature-programmed cook-off simulation with temperature increasing continuously from 300 K to 3000 K through heating. As illustrated in Fig. 8, a proton transfer to the anion group occurs when temperature is 491 K, leading to the formation of conjugated base hydroxylamine (NH₂OH) and acid H-diolate (H–C₂O₂N₈)⁻. With the temperature reaching 1700 K, N₂O appears, and at 1900 K, N₂ is observed. The presence of these products signifies the rupture of the (C(NO)N₃) ring. This ring-breaking reaction is regarded as pivotal in the initial reactions of TKX-50, as they release energy that promotes the subsequent decomposition reactions. Above 1900 K, secondary products of H₂O and NH₃ are observed, indicating the decomposition and recombination of NH₃OH⁺.

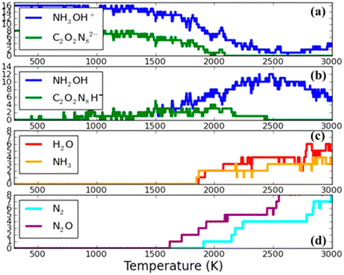Fig. 8 Fragment analysis during the cook-off simulation of TKX-50 as the temperature is ramped at a uniform rate of 180 K ps⁻¹ from 300 K to 3000 K. (a) The reactants: hydroxylammonium (NH₃OH)⁺ and diolate (C₂O₂N₈)2⁻. (b) The conjugate acid and base hydroxylamine (NH₂OH) and H-diolate (H–C₂O₂N8)⁻ that are produced by proton transfer reactions. (c) Two stable species (H₂O and NH₃) that are the products of the decomposition and recombination of (NH₃OH)⁺. (d) Two stable species (N₂ and N₂O), indicating ring breaking reactions in H-diolate. Reproduced with permission from ref. 104. Copyright 2014, American Chemical Society.

The MD simulations are limited in their ability to provide mechanistic insights such as reaction barriers and transition state information. To address this, reaction pathways were subsequently elucidated through QM calculations employing DFT methods, utilizing cluster models derived from the MD simulation results. Based on QM calculations, the protonation of the anion group within TKX-50 leads to kinetic barriers of 37.2 kcal mol⁻¹ and 59.5 kcal mol⁻¹ for the production of N₂ and N₂O, respectively. This indicates that the initial reaction preferentially cleaves that ring to yield N₂ over N₂O. Notably, these kinetic barriers are significantly lower than those associated with the direct decomposition of the anion (45.1 kcal mol⁻¹ and 72.2 kcal mol⁻¹), indicating that proton transfer decreases the reaction barriers for both releases of N₂ and N₂O by approximately 10 kcal mol⁻¹. These calculations suggest that the strategy to design more stable azole-based HEDMs is to prevent the proton transfer between the cation and anion.

Di-tetrazine-tetroxide (DTTO) is also a typical nitrogen-rich energetic material with high expected density and performance. The theoretical predicted molecular structures and crystal packing unit cell¹¹⁰ are displayed in Fig. 9. Recent research by Goddard et al.¹¹¹ has explored the condensed phase thermal decomposition mechanisms of DTTO using AIMD. Fig. 10 shows the dynamics of thermal decomposition for c1- and c2-DTTO crystals across a temperature range from 300 K to 3000 K. From the simulation results, it shows that no DTTO decomposes below 2000 K. For c1-DTTO, the initial decomposition occurs at 13.2 ps (T = 2100 K) through unimolecular fragmentation that yields two N₂O molecules. For c2-DTTO, the first reaction was found at 2672 K (17.5 ps), involving an intermolecular reaction between two c2 molecules, leading to the formation of a N₂ molecule at 17.9 ps (T = 2700 K) and a N₂O molecule shortly thereafter. Fig. 11 outlines the rate-determining reaction pathways, highlighting the initial bond-breaking and gas molecule generation process calculated using the DFT method. The results indicate that the initial decomposition reactions are influenced by crystal packing, as well as temperature and pressure. The thermal decay of c2-DTTO involves a bimolecular N₂ release with a higher kinetic energy than c1-DTTO, suggesting that c2-DTTO has a higher thermal stability. The reaction barriers of DTTOs (45.9 and 48.1 kcal mol⁻¹ for c1- and c2-DTTO, respectively) are found to be higher than the NO₂ dissociation barriers of RDX (39.0 kcal mol⁻¹), HMX (39.8 kcal mol⁻¹), and CL-20 (37.6 kcal mol⁻¹), all calculated at the same computational level. This comparison suggests that DTTO possesses superior thermal stability relative to these energetic materials.

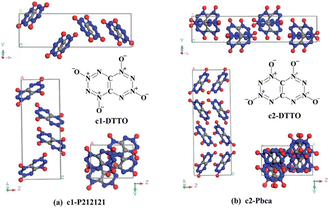Fig. 9 Most stable molecular isomers of DTTO (c1 and c2), and their predicted crystal structures predicted from DFT calculations. Reproduced with permission from ref. 110. Copyright 2015, The Royal Society of Chemistry.

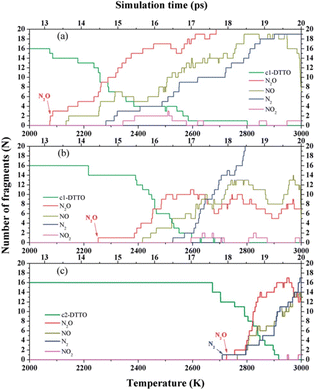Fig. 10 Species analyses for the decomposition of (a) c1-DTTO; (b) 30% uniaxial compressed c1-DTTO; and (c) c2-DTTO heated from 300 to 3000 K over 20 ps. Reproduced with permission from ref. 111. Copyright 2015, The Royal Society of Chemistry.

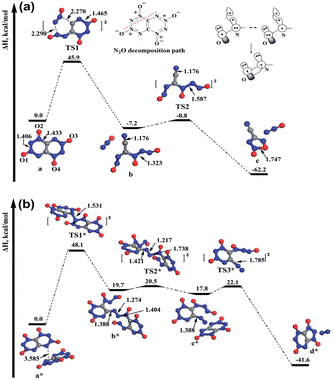Fig. 11 (a) Mechanism of c1-DTTO unimolecular decomposition starting from the reactive intermediate extracted from the AIMD trajectory; (b) mechanism from AIMD simulation by which two c2-DTTO molecules combine to release an N₂ molecule. Reproduced with permission from ref. 111. Copyright 2015, The Royal Society of Chemistry.

Combining AIMD simulations with high-level QM calculations offers a detailed, molecular-level understanding of the initial decomposition reactions in condensed phases. These approaches enable the extraction of intricate chemical information, encompassing both unimolecular and multimolecular reaction sequences, and facilitate the assessment of thermal stability based on these insights. However, for the mechanistic investigation of certain energetic material systems, such as cocrystals or systems with crystal defects, the necessity for large modeling systems renders AIMD simulations inefficient. While ReaxFF or semi-empirical methods are more computationally efficient, their parameters are system-specific and not universally applicable, limiting their utility in studying newly designed energetic materials (EMs). Machine learning-constructed force fields present a promising solution to this challenge, which will be further discussed in the subsequent part.

4. Machine learning methods for investigating the thermostability of energetic materials

In recent years, machine learning (ML) methods in the field of energetic materials have been a fascinating and rapidly evolving area.¹¹² Machine learning offers a powerful set of tools to enhance our understanding and capabilities in this field through the analysis of large datasets. One of the key applications of ML in this domain is the prediction of physical and chemical properties of energetic materials, such as density, performance, and thermal stability. By training ML models on datasets comprised of known compounds and their properties, researchers can predict these properties for new and untested compounds. ML models can also be used to design and discover new energetic materials. By learning from the structure–property relationships of known materials, ML algorithms can guide the design of new molecules that optimize desired properties. Techniques such as kernel ridge regression (KRR), support vector machines, neural networks, and genetic algorithms have shown potential in predicting and generating novel molecular structures with optimized performance characteristics.¹¹³ It should be noted that the quality and quantity of data available for training ML models are critical for their accuracy and generalizability. Advances in computational technology have enabled the use of high-throughput computing (HTC) for QM calculations, allowing the acquisition of extensive molecular level and crystal structure properties. These properties serve as essential descriptors in model training and substantially facilitate the application of machine learning in the field of energetic materials.

The main contributions of machine learning in predicting and enhancing the thermal stability of energetic materials are briefly summarized (Fig. 12). Through machine learning, thermal stability can be predicted based on training datasets of chemical structures and the thermostability of known energetic materials. By learning the relationships between molecular descriptors and thermal stability, ML algorithms can be utilized to predict the thermal stability of new compounds. In addition, feature selection is a crucial step in building ML models for thermal stability. It involves identifying the most relevant molecular descriptors that influence thermal stability.

Fig. 12 Scheme for machine learning methods in enhancing thermostability of energetic materials.

Accurate prediction of thermal decomposition temperature (T_d) is crucial for assessing the thermal stability of an EM. Machine learning technologies have become an area of heightened research interest for exploring quantitative relationships between the molecular structure and T_d, transcending the complex physical and chemical mechanisms inherent in the decomposition process. Qi et al.¹¹⁴ conducted an extensive machine learning study to construct a predictive model for T_d based on a dataset of 1022 selected experimental thermal decomposition temperatures. A set of molecular descriptors are used to quantitatively represent the properties of molecules as well as the transformed extended-connectivity fingerprints (ECFPs) (Fig. 13). For regression analyses, elastic net, support vector machine (SVM), multi-layered perceptron (MLP), gradient boost machine for regression (GBR), and K-nearest neighbours (KKN) were employed. The GBR model yielded the best prediction for T_d, with a mean absolute error (MAE) of 27.7 °C for the test set (Fig. 14). Furthermore, by analyzing the outlier structures, the researchers discovered that integrating features related to intermolecular interactions can further improve the model prediction accuracy.

Fig. 13 Transformation of molecules into ECFPs and descriptor matrices. Reproduced with permission from ref. 114. Copyright 2023, KeAi.

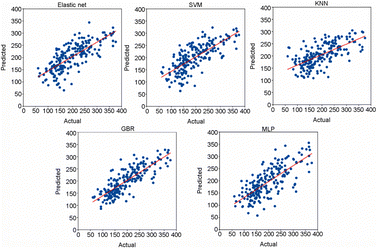Fig. 14 Regression plots of various models evaluated. Reproduced with permission from ref. 114. Copyright 2023, KeAi.

The selection of descriptors is crucial for the precise prediction of thermal decomposition temperatures. Different descriptors provide distinct insights into the thermostability of EMs. Liu et al.¹¹⁵ conducted a comprehensive investigation into a wide array of descriptors to evaluate and identify the limitations of the currently used descriptors in T_d prediction. A dataset of onset T_d of 1091 EMs was built for machine learning. Following the workflow shown in Fig. 15, the SMILES-generated data and wavefunctions calculated by quantum chemical approaches were utilized to generate five distinct sets of descriptors, which feature topological, geometric, and electronic structure properties of energetic materials. The descriptors were pre-screened and ranked by their relevance to the T_d value. These descriptors were then utilized to model T_d values using various algorithms (Fig. 15).

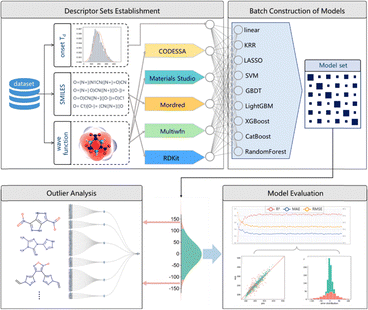Fig. 15 The workflow of T_d prediction. Four sections are involved, including descriptor set establishment, batch construction of models, model evaluation, and outlier analysis. Reproduced with permission from ref. 115. Copyright 2024, Elsevier.

The analysis revealed that the five descriptor sets exhibited similar trends in predicting T_d. The quantum chemical descriptors did not outperform those derived from SMILES codes. The best performance in T_d prediction is the model constructed using RDKit descriptors, with the mean absolute error (MAE) of 29.38 K. The current model successfully predicted the onset T_d for a set of 32 newly reported energetic materials, demonstrating consistency with experimental values. However, an in-depth analysis of the outlier predictions highlighted that descriptor sets emphasizing molecular properties were insufficient to enhance the prediction accuracy for certain compounds. To rectify this, it is crucial to explore descriptors at a more advanced level, focusing on crystal-level properties. Advances in computational techniques now allow for the quantum chemical analysis of periodic crystal structures and intermolecular interactions, including aspects like packing coefficients and intermolecular hydrogen bonds. Integrating crystal-level descriptors into machine learning models will enhance the precision and comprehension of thermal stability in energetic materials.

In terms of enhancing thermostability via molecular design, Zhang et al. reported a series of ML-assisted molecular designs for novel energetic materials with both high performance and thermal stability.^59,116 Followed by recent advancements where researchers design and synthesize new heat-resistant HEDMs using the materials genome approach,¹⁶ machine learning methods offer a more potent and efficient strategy for designing new energetic materials with tailored properties. Employing a high-throughput molecular generation technique enables a rapid and extensive generation of suitable molecular structures through heuristic enumeration. These structures were processed using machine learning models composed of property predictors and a graphite-like structure classifier. Through the high-throughput virtual screening approach, the promising energetic molecule ICM-104 was identified from a vast array of biheterocyclic molecular structures. The synthesis and testing of ICM-104 revealed excellent performance and thermal stability (onset at 326 °C). This highlights the potential of the ML-assisted method for efficiently designing new energetic materials with desired properties.

Recently, machine learning-based tools, especially neural networks (NNs), have been applied to construct PES models in an entirely data-driven manner, where the PES is abstracted from a well-selected training dataset using suitable functional expressions automatically.¹¹⁷ This enables the development of PES models with the efficiency of the empirical potentials and the accuracy of the DFT method. The construction of NN-based potentials (NNPs) is shown in Fig. 16. The process commenced with constructing an initial dataset through a brief ab initio molecular dynamics (AIMD) simulation, yielding essential structures, energies, and atomic forces. Subsequently, concurrent learning was implemented via neural network training for four distinct NNPs. A molecular dynamics (MD) simulation was then executed using the first NNP, generating snapshots that were scrutinized by the other three NNPs. Consistent predictions of atomic forces and energies across all four NNPs confirmed the accuracy of the training. Conversely, discrepancies prompted quantum mechanical (QM) recalculations for the respective snapshot, which were then integrated into the dataset, initiating another round of training. This iterative process persisted until no new data were generated, indicating a comprehensive dataset and a well-trained NNP force field derived from ab initio results.

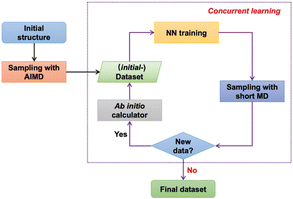Fig. 16 The workflow to construct the reference dataset. Reproduced with permission from ref. 118. Copyright 2022, The Royal Society of Chemistry.

Based on the NNP force field, Zhu et al.¹¹⁸ reported a reactive molecular dynamics simulation study to elucidate the thermal decomposition mechanisms of CL-20 and CL-20/TNT cocrystal systems. CL-20, as one of the most powerful synthesized explosives, has been hindered in its applications due to its low stability. Cocrystallization that combines two or more types of compounds in one crystal lattice through non-covalent interactions has proven to be an effective strategy to improve the stability of energetic materials. A direct DFT simulation for large cocrystal systems is challenging in terms of computational cost. By using the DeePMD-kit package,¹¹⁹ the NNP for the two systems was constructed (Fig. 17). Many important intermediate species and their associate reaction paths during the decomposition were identified in the simulations. As depicted in Fig. 18, from the simulation trajectories, detailed insights into the thermal decomposition process can be captured and analysed. The results reveal that the dissociation of CL-20 in the CL-20/TNT system is much slower compared to the pure CL-20 system. In the CL-20/TNT cocrystal, TNT molecules are relatively stable and can act as buffer fragments to prevent NO₂ and other small molecules from colliding with CL-20 molecules. The dynamic structures of CL-20/TNT reveal a higher number of intermolecular hydrogen bonds, which further stabilize the system.

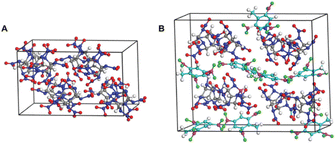Fig. 17 Initial models for the supercell of (A) pure CL-20 (288 atoms) and (B) CL-20/TNT cocrystal (456 atoms). Reproduced with permission from ref. 118. Copyright 2022, The Royal Society of Chemistry.

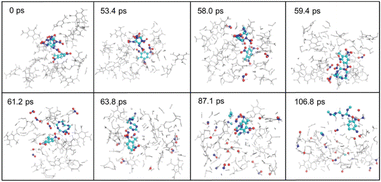Fig. 18 Decomposition snapshots of the CL-20/TNT cocrystal system. Reproduced with permission from ref. 118. Copyright 2022, The Royal Society of Chemistry.

From this, it is evident that neural network force fields have been successfully applied to simulate the thermal decomposition of large-scale energetic material systems, which has significant importance for uncovering the thermal decomposition mechanisms and the underlying thermal stability of energetic materials. Yet, the NNPs for energetic material systems currently lack generalizability and often require retraining from scratch for new systems. Recently, Zhang and colleagues have made significant strides in the development of a general reactive machine learning interatomic potential (MLIP) tailored for condensed-phase reactions with CHNO systems.¹²⁰ Utilizing a nanoreactor-based active learning technique to build the dataset combined with plane-wave DFT calculations, the reported general MLIP was successfully applied for a series of condensed-phase reactions. Inspired by these advancements, the development of general reactive force fields for energetic material systems has gained considerable momentum, which facilitates the researchers to analyze the behavior of various energetic compounds under different conditions.

To be brief, the integration of machine learning methods in the field of energetic materials represents a significant step forward in accelerating the design, discovery, and optimization of these critical compounds. By leveraging vast datasets and advanced algorithms, researchers can uncover new insights, predict material properties with greater accuracy, and design safer and more effective materials.

5. Summary and outlook

In this perspective, recent theoretical advancements in the study of thermostability of energetic materials have been extensively explored. Quantum chemical calculations can offer an in-depth understanding of the molecular and electronic structure properties of energetic compounds related to thermal stability. Additionally, it is also important to incorporate the surrounding interactions and their impact on molecular stability. Gaining insight into the initial decomposition mechanisms of energetic materials is vital for understanding and evaluating their thermal stability at the atomic level. Ab initio molecular dynamics simulations provide detailed theoretical insights into the reaction pathways and the key intermediates during thermal decomposition. The kinetic barrier of rate-determining steps under various temperatures and pressure conditions can be theoretically analyzed to have a comprehensive assessment for the thermal stability. Yet, implementing AIMD simulations for large molecular systems is highly inefficient due to the computational resources required. In contrast, machine learning techniques, particularly neural networks, offer a promising and innovative approach to address this limitation. Neural network potentials can be obtained through neural network training with datasets derived from first-principles calculations. The NNP simulations can achieve the efficiency of empirical potentials while maintaining the accuracy of DFT, paving the way for studying thermal decomposition reactions in large, complex systems like cocrystals and defected crystalline structures.

Leveraging machine learning, thermal decomposition temperatures can be predicted based on training datasets of molecular properties and T_d values of known energetic materials. Identifying the most relevant molecular descriptors that influence thermal stability is crucial for achieving accurate predictions, and incorporating crystal level descriptors, such as crystal packing and intermolecular HBs, can potentially improve the predictive accuracy. The machine learning-assisted high-throughput virtual screening (HTVS) methodology can accelerate the discovery of new energetic materials with improved properties. Based on this, the newly identified and synthesized energetic molecule ICM-104 revealed excellent performance and thermostability. Theoretical approaches for energetic materials play a pivotal role in elucidating the mechanisms underlying thermal stability, enabling the prediction and design of enhanced thermal stability for emerging EMs. These insights are essential in expediting the development of novel EMs that exhibit the desired balance of performance and thermal stability.

While machine learning excels in exploring quantitative relationships between descriptors and properties, the underlying intricate physical and chemical mechanisms are unveiled. Thus, it is essential to integrate first-principles calculations to gain a more comprehensive insight into these mechanisms. Further challenges include theoretical exploration of the role of electronically excited state species in thermal decomposition or detonation, as well as the enhancement of machine learning models to predict a broader range of properties with increased accuracy. With the advancement of computational power and methodologies, theoretical research will play an increasingly significant role in the field of energetic materials.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (22005177).

References

1. N. V. Muravyev, K. A. Monogarov, U. Schaller, I. V. Fomenkov and A. N. Pivkina, Propellants, Explos., Pyrotech., 2019, 44, 941–969.
2. Y. X. Tang, W. Huang, G. H. Imler, D. A. Parrish and J. M. Shreeve, J. Am. Chem. Soc., 2020, 142, 7153–7160.
3. R. P. Bu, Y. Xiong and C. Y. Zhang, Cryst. Growth Des., 2020, 20, 2824–2841.
4. Q. Sun, W. X. Chen, N. Ding, C. F. Zhao, Z. Y. Jiang, S. H. Li and S. P. Pang, Chem. Eng. J., 2022, 444, 136539.
5. M. X. Zhang, P. E. Eaton and R. Gilardi, Angew. Chem., Int. Ed., 2000, 39, 401.
6. P. C. Wang, Y. G. Xu, Q. H. Lin and M. Lu, Chem. Soc. Rev., 2018, 47, 7522–7538.
7. K. Zhong and C. Y. Zhang, Chem. Eng. J., 2024, 483, 149202.
8. W. Q. Zhang, J. H. Zhang, M. C. Deng, X. J. Qi, F. D. Nie and Q. H. Zhang, Nat. Commun., 2017, 8, 181–187.
9. Y. Du, H. Su, T. Fei, B. P. Hu, J. C. Zhang, S. H. Li, S. P. Pang and F. D. Nie, Cryst. Growth Des., 2018, 18, 5896–5903.
10. S. Y. Chen, Z. X. Yi, C. W. Jia, Y. Li, H. H. Chen, S. G. Zhu and L. Zhang, Small, 2023, 19, 2302631.
11. S. W. Song, Y. Wang, K. C. Wang, F. Chen and Q. H. Zhang, J. Mater. Chem. A, 2020, 8, 5975–5985.
12. C. Y. Zhang, Propellants, Explos., Pyrotech., 2018, 43, 855–856.
13. X. W. Wu, Q. Y. Yu, K. Wang, Y. Q. Li, J. H. Xu and J. G. Zhang, Langmuir, 2023, 39, 7221–7230.
14. S. Zeman and M. Jungová, Propellants, Explos., Pyrotech., 2016, 41, 426–451.
15. D. Mathieu, Ind. Eng. Chem. Res., 2017, 56, 8191–8201.
16. Y. Wang, Y. J. Liu, S. W. Song, Z. J. Yang, X. J. Qi, K. C. Wang, Y. Liu, Q. H. Zhang and Y. Tian, Nat. Commun., 2018, 9, 2444–2454.
17. L. Zhang, J. Z. Wu, S. L. Jiang, Y. Yu and J. Chen, Phys. Chem. Chem. Phys., 2016, 18, 26960–26969.
18. M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23.
19. D. D. Zhai, C. M. Ma, P. Ma, Y. Pan, L. N. Hao, X. Q. Liu and J. C. Jiang, Fuel, 2021, 294, 120497.
20. M. Akiki and S. Menon, Combust. Flame, 2015, 162, 1759–1771.
21. G. Langer and N. Eisenreich, Propellants, Explos., Pyrotech., 1999, 24, 113–118.
22. G. R. Liu, B. B. Tian, S. H. Wei and C. Y. Zhang, J. Phys. Chem. C, 2021, 125, 10057–10067.
23. A. K. Yadav, V. D. Ghule and S. Dharavath, ACS Appl. Mater. Interfaces, 2022, 14, 49898–49908.
24. J. Y. Zhang, X. Y. Guo, Q. J. Jiao, H. L. Zhang and H. Li, Cent. Eur. J. Energ. Mater., 2018, 15, 115–130.
25. P. Kumar, P. C. Joshi and R. Kumar, Cent. Eur. J. Energ. Mater., 2017, 14, 184–200.
26. A. Singh, G. Kaur, C. Sarkar and N. Mukherjee, Cent. Eur. J. Energ. Mater., 2018, 15, 258–282.
27. D. Badgujar and M. Talawar, Cent. Eur. J. Energ. Mater., 2017, 14, 296–303.
28. S. A. El-Sayed, J. Anal. Appl. Pyrolysis, 2022, 161, 105364.
29. J. Ehrhardt, L. Courty, P. Gillard and B. Baschung, Molecules, 2020, 25, 2276–2292.
30. L. P. Jiang, X. L. Fu, X. Z. Fan, J. Z. Li, W. X. Xie, G. F. Zhang, Z. Y. Zhou and W. Zhang, Combust. Flame, 2021, 229, 111406.
31. E. R. Yao, S. Y. Xu, F. Q. Zhao, T. H. Huang, H. J. Li, N. N. Zhao, J. H. Yi, Y. J. Yang and C. J. Wang, Catalysts, 2020, 10, 331–343.
32. A. Benhammada and D. Trache, Appl. Spectrosc. Rev., 2020, 55, 724–777.
33. Q. Wu, Q. N. Hu, M. Q. Li, Z. W. Zhang and W. H. Zhu, Mol. Syst. Des. Eng., 2020, 5, 1679–1690.
34. R. V. Tsyshevsky, P. Pagoria and M. M. Kuklje, J. Phys. Chem. C, 2015, 119, 8512–8521.
35. G. J. Bao, R. Y. Abe and Y. Akutsu, J. Therm. Anal. Calorim., 2021, 143, 3439–3445.
36. V. D. Ghule, Comput. Theor. Chem., 2012, 992, 92–96.
37. P. K. Adak, S. K. Singh, J. Singh, S. Mahesh, M. K. Jain, P. A. K. Sagar, S. Banerjee and A. S. Khan, J. Mol. Model., 2022, 28, 400–404.
38. H. Li, L. Zhang, N. Petrutik, K. C. Wang, Q. Ma, D. Shem-Tov, F. Q. Zhao and M. Gozin, ACS Cent. Sci., 2020, 6, 54–75.
39. C. Y. Zhang, F. B. Jiao and H. Z. Li, Cryst. Growth Des., 2018, 18, 5713–5726.
40. M. Rahm and T. Brinck, Chem. – Eur. J., 2010, 16, 6590–6600.
41. R. V. Tsyshevsky, P. Pagoria and M. M. Kuklja, AIP Conf. Proc., 2017, 1793.
42. A. K. Sikder and N. Sikder, J. Hazard. Mater., 2004, 112, 1–15.
43. R. S. Han, F. P. Lu, F. Zhang, Y. L. Wang, M. Zhou, G. S. Qin, J. H. Chen, H. F. Wang and E. Y. Chu, Def. Technol., 2023, 25, 166–173.
44. J. G. Xu, Y. F. Yan, X. Z. Li, F. K. Zheng and G. C. Guo, Chem. Eng. J., 2022, 429, 132451.
45. K. N. Zhang, L. Chen, D. S. Geng, J. Y. Lu and J. Y. Wu, Phys. Chem. Chem. Phys., 2020, 22, 13248–13260.
46. Y. Ma, A. B. Zhang, C. H. Zhang, D. J. Jiang, Y. Q. Zhu and C. Y. Zhang, Cryst. Growth Des., 2014, 14, 4703–4713.
47. B. B. Tian, Y. Xiong, L. Z. Chen and C. Y. Zhang, CrystEngComm, 2018, 20, 837–848.
48. C. Y. Zhang, X. C. Wang and H. Huang, J. Am. Chem. Soc., 2008, 130, 8359–8365.
49. D. S. Kretic, J. I. Radovanovic and D. Z. Veljkovic, Phys. Chem. Chem. Phys., 2021, 23, 7472–7479.
50. J. H. Zhang, Q. H. Zhang, T. T. Vo, D. A. Parrish and J. M. Shreeve, J. Am. Chem. Soc., 2015, 137, 1697–1704.
51. F. P. Wang, G. Y. Du, X. C. Liu, M. Y. Shao, C. G. Zhang and L. Chen, Nanotechnol. Rev., 2022, 11, 2141–2153.
52. R. Q. Ding, J. J. Xu, Y. T. Tao, J. Sun and M. Lei, J. Phys. Chem. A, 2020, 124, 6389–6398.
53. L. Zhang, S. L. Jiang, Y. Yu and J. Chen, Sci. Rep., 2019, 9, 1257–1263.
54. Y. S. Wen, C. Y. Zhang, X. G. Xue and X. P. Long, Phys. Chem. Chem. Phys., 2015, 17, 12013–12022.
55. N. V. Muravyev, L. Fershtat and Q. H. Zhang, Chem. Eng. J., 2024, 486, 150410.
56. A. D. Casey, S. F. Son, I. Bilionis and B. C. Barnes, J. Chem. Inf. Model., 2020, 60, 4457–4473.
57. P. Nguyen, D. Loveland, J. T. Kim, P. Karande, A. M. Hiszpanski and T. Y. J. Han, J. Chem. Inf. Model., 2021, 61, 2147–2158.
58. S. W. Song, Y. Wang, F. Chen, M. Yan and Q. H. Zhang, Engineering, 2022, 10, 99–109.
59. S. W. Song, F. Chen, Y. Wang, K. C. Wang, M. Yan and Q. H. Zhang, J. Mater. Chem. A, 2021, 9, 21723–21731.
60. Y. S. Yao and A. O. Adeniyi, Phys. Status Solidi B, 2021, 258, 2000588.
61. C. X. Qu, J. L. Li, K. W. Ding, S. S. Guo and Y. T. Jia, Molecules, 2024, 29, 504–516.
62. I. Ugi, Tetrahedron, 1963, 19, 1801.
63. I. Ugi, H. Perlinger and L. Behringer, Chem. Ber./Recl., 1959, 92, 186–1866.
64. I. Ugi and R. Huisgen, Chem. Ber./Recl., 1958, 91, 531–537.
65. I. Ugi, H. Perlinger and L. Behringer, Chem. Ber./Recl., 1958, 91, 2324–2329.
66. R. Huisgen and I. Ugi, Chem. Ber./Recl., 1957, 90, 2914–2927.
67. C. Zhang, C. G. Sun, B. C. Hu and M. Lu, J. Energ. Mater., 2016, 34, 103–111.
68. Y. Z. Yang, Y. C. Li, R. B. Zhang, C. H. Suna and S. P. Pang, RSC Adv., 2014, 4, 57629–57634.
69. P. Carlqvist, H. Östmark and T. Brinck, J. Phys. Chem. A, 2004, 108, 7463–7467.
70. L. A. Burke and P. J. Fazen, Int. J. Quantum Chem., 2009, 109, 3613–3618.
71. X. L. Zhang, J. Q. Yang, M. Lu and X. D. Gong, RSC Adv., 2014, 4, 56095–56101.
72. G. H. Ren, R. Z. Liu, P. W. Zhou, C. Y. Zhang, J. Y. Liu and K. L. Han, Chem. Commun., 2019, 55, 2628–2631.
73. X. X. Bo, Z. Y. Dong and Y. H. Ding, Chem. Commun., 2021, 57, 5310–5313.
74. A. Hammerl, T. M. Klapötke and P. Schwerdtfeger, Chem. – Eur. J., 2003, 9, 5511–5519.
75. H. F. Mull, J. M. Turney, G. E. Douberly and H. F. Schaefer, J. Phys. Chem. A, 2021, 125, 9092–9098.
76. M. T. Nguyen and T. K. Ha, Chem. Phys. Lett., 2000, 317, 135–141.
77. M. T. Nguyen and T. K. Ha, Chem. Phys. Lett., 2001, 335, 311–320.
78. L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079.
79. D. A. Dixon, D. Feller, K. O. Christe, W. W. Wilson, A. Vij, V. Vij, H. D. B. Jenkins, R. M. Olson and M. S. Gordon, J. Am. Chem. Soc., 2004, 126, 834–843.
80. G. Frison, G. Jacob and G. Ohanessian, New J. Chem., 2013, 37, 611–618.
81. A. Vij, J. G. Pavlovich, W. W. Wilson, V. Vij and K. O. Christe, Angew. Chem., Int. Ed., 2002, 41, 3051–3054.
82. R. N. Butler, J. C. Stephens and L. A. Burke, Chem. Commun., 2003, 1016–1017,  10.1039/b301491f.
83. S. A. Perera, A. Gregusová and R. J. Bartlett, J. Phys. Chem. A, 2009, 113, 3197–3201.
84. B. Bazanov, U. Geiger, R. Carmieli, D. Grinstein, S. Welner and Y. Haas, Angew. Chem., Int. Ed., 2016, 55, 13233–13235.
85. C. Zhang, C. Sun, B. Hu, C. Yu and M. Lu, Science, 2017, 355, 374–376.
86. Y. G. Xu, Q. H. Lin, P. C. Wang and M. Lu, Chem. – Asian J., 2018, 13, 1669–1673.
87. Y. G. Xu, Q. Wang, C. Shen, Q. H. Lin, P. C. Wang and M. Lu, Nature, 2017, 549, 78–81.
88. L. Chen, C. Yang, H. R. Hu, L. Shi, C. Zhang, C. G. Sun, C. Gao, Y. Du and B. C. Hu, CrystEngComm, 2022, 24, 8152–8159.
89. F. J. Shang, R. Z. Liu, J. Y. Liu, P. W. Zhou, C. Y. Zhang, S. H. Yin and K. L. Han, J. Phys. Chem. Lett., 2020, 11, 1030–1037.
90. L. Zhang, C. Yao, Y. Yu, S. L. Jiang, C. Q. Sun and J. Chen, J. Phys. Chem. Lett., 2019, 10, 2378–2385.
91. L. Zhang, C. Yao, Y. Yu, X. Wang, C. Q. Sun and J. Chen, Chem. Phys. Chem., 2019, 20, 2525–2530.
92. C. Y. Li, Y. L. Huang, C. Q. Sun and L. Zhang, Catalysts, 2021, 11, 766–777.
93. C. Y. Li, C. Yao, Q. G. Song, Y. L. Huang, C. Q. Sun and L. Zhang, J. Mol. Liq., 2022, 355, 18939–18947.
94. B. A. Steele, E. Stavrou, J. C. Crowhurst, J. M. Zaug, V. B. Prakapenka and I. I. Oleynik, Chem. Mater., 2017, 29, 735–741.
95. D. Laniel, G. Weck, G. Gaiffe, G. Garbarino and P. Loubeyre, J. Phys. Chem. Lett., 2018, 9, 1600–1604.
96. S. J. Liu, L. Zhao, M. G. Yao, M. S. Miao and B. B. Liu, Adv. Sci., 2020, 7, 1902320.
97. B. A. Steele and I. I. Oleynik, Chem. Phys. Lett., 2016, 643, 21–26.
98. F. Peng, Y. S. Yao, H. Y. Liu and Y. M. Ma, J. Phys. Chem. Lett., 2015, 6, 2363–2366.
99. C. Yao, K. L. Dou, Y. Z. Yang, C. Y. Li, C. Q. Sun, J. Sun, C. L. He, L. Zhang and S. P. Pang, J. Phys. Chem. Lett., 2024, 15, 1507–1514.
100. L. Zhang, S. L. Jiang, Y. Yu, Y. Long, H. Y. Zhao, L. J. Peng and J. Chen, J. Phys. Chem. B, 2016, 120, 11510–11522.
101. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
102. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
103. Y. H. Ma, M. H. Lv, F. J. Shang, C. Y. Zhang, J. Y. Liu and P. W. Zhou, J. Phys. Chem. A, 2022, 126, 1666–1673.
104. Q. An, W. G. Liu, W. A. Goddard, T. Cheng, S. V. Zybin and H. Xiao, J. Phys. Chem. C, 2014, 118, 27175–27181.
105. Z. W. Guo, X. H. Wang, G. Z. Hao, L. Xiao, X. J. Feng, J. Q. Yang and W. Jiang, Phys. Chem. Chem. Phys., 2024, 26, 9665–9674.
106. X. G. Xue, Y. Ma, Q. Zeng and C. Y. Zhang, J. Phys. Chem. C, 2017, 121, 4899–4908.
107. G. R. Liu, Y. Xiong, R. J. Gou and C. Y. Zhang, J. Phys. Chem. C, 2019, 123, 16565–16576.
108. N. Fischer, D. Fischer, T. M. Klapötke, D. G. Piercey and J. Stierstorfer, J. Mater. Chem., 2012, 22, 20418–20422.
109. Z. P. Lu, X. G. Xue, L. Y. Meng, Q. Zeng, Y. Chi, G. J. Fan, H. Z. Li, Z. M. Zhang, F. D. Nie and C. Y. Zhang, J. Phys. Chem. C, 2017, 121, 8262–8271.
110. X. L. Song, J. C. Li, H. Hou and B. S. Wang, J. Comput. Chem., 2009, 30, 1816–1820.
111. C. C. Ye, Q. An, W. A. Goddard, T. Cheng, W. G. Liu, S. V. Zybin and X. H. Ju, J. Mater. Chem. A, 2015, 3, 1972–1978.
112. X. N. Huang, C. Y. Li, K. Y. Tan, Y. S. Wen, F. Guo, M. Li, Y. L. Huang, C. Q. Sun, M. Gozin and L. Zhang, iScience, 2021, 24, 102240.
113. R. Wang, J. C. Jiang and Y. Pan, J. Energ. Mater., 2012, 30, 135–155.
114. J. N. Wu, S. W. Song, X. L. Tian, Y. Wang and X. J. Qi, Energ. Mater. Front., 2023, 4, 254–261.
115. Z. X. Zhang, C. Chen, Y. L. Cao, L. Y. Wen, X. K. He and Y. Z. Liu, Thermochim. Acta, 2024, 735, 179717.
116. S. W. Song, Y. Wang, F. Chen, M. Yan and Q. H. Zhang, Engineering, 2022, 10, 99–109.
117. Y. Z. Zhang, H. D. Wang, W. J. Chen, J. Z. Zeng, L. F. Zhang, H. Wang and E. Weinan, Comput. Phys. Commun., 2020, 253, 107206.
118. L. Q. Cao, J. Z. Zeng, B. Wang, T. Zhu and J. Z. H. Zhang, Phys. Chem. Chem. Phys., 2022, 24, 11801–11811.
119. Z. H. Wang, L. F. Zhang, J. Q. Han and W. N. E, Comput. Phys. Commun., 2018, 228, 178–184.
120. S. H. Zhang, M. Z. Makos, R. B. Jadrich, E. Kraka, K. Barros, B. T. Nebgen, S. Tretiak, O. Isayev, N. Lubbers, R. A. Messerly and J. S. Smith, Nat. Chem., 2024, 16, 727–734.

---