Open Access Article
Open Access ArticleActinide endohedral inter-metalloid clusters of the group 15 elements†
Nai-Xin
Zhang
ab,
Cong-Zhi
Wang
*a,
Jian-Hui
Lan
a,
Qun-Yan
Wu
 a and
Wei-Qun
Shi
a and
Wei-Qun
Shi
 *a
*a
aLaboratory of Nuclear Energy Chemistry, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China. E-mail: shiwq@ihep.ac.cn; wangcongzhi@ihep.ac.cn
bCollege of Nuclear Science and Technology, Harbin Engineering University, Harbin 150001, China
First published on 9th September 2024
Abstract
Inter-metalloid clusters in Zintl chemistry have been extensively studied due to their unique electronic structures and potential applications. In this work, we explored a series of actinide endohedral inter-metalloid clusters of the group 15 elements [An@Bi12]4− (An = Th–U) and [An@Sb12]4− using density functional theory (DFT). [Th@Bi12]4− and [U@Bi12]4− exhibit Cs symmetry, while [Pa@Bi12]4− and [An@Sb12]4− (An = Th–U) have C1 structures. Bonding analyses such as bond order, molecular orbitals (MO) and quantum theory of atoms in molecules (QTAIM) show covalent An–Bi/An–Sb bonding in the clusters. All these clusters are highly stable according to the studied formation reactions and may be accessible experimentally. Compared with [An@Bi12]4−, [An@Sb12]4− possesses stronger bonding interactions, mainly arising from the higher electrostatic interaction energy. For clusters with the same group 15 elements, the bonding interactions increase gradually from Th to U, which is mainly determined by the covalent interactions of An–Bi/An–Sb bonding. This work is expected to provide potential avenues for the construction of robust inter-metalloid clusters of the group 15 elements.
Introduction
Atomic clusters are intermediates between individual atoms and solids and often have special electronic, optical and catalytic properties that vary with cluster size.1–3 Among them, Zintl anions have been extensively studied since the 1930s.4 Zintl chemistry typically includes the Zintl phase and the Zintl anions. Zintl anions are groups of atoms that contain only main-group (semi) metal atoms in their structures. Zintl anions usually occur in clusters containing only main group element 14 or 15.5–8 For example, the pyramids Bi5+ and octahedral Bi62+ are isolated from ternary clusters,9 as well as Sb73− with C3 configuration and Ge94− with two crystal structures.10 When there is a central metal in the Zintl cluster, it is called an inter-metalloid cluster (which can be denoted by [Mx@Ey]q− or [Mx@EyMz]q−).11,12 Here, M stands for transition metal atoms or lanthanide and actinide atoms, and E denotes p-block (semi) metal atoms. Over the past few decades, inter-metalloid clusters [Mx@Ey]q− have attracted the research interest of chemists and physicists due to the large number of novel structures, bonding, and special chemical and physical properties they exhibit.5,13,14At present, the most reported inter-metalloid clusters are the transition metal atom-encapsulated clusters, which have rich structures and properties.5,15,16 For example, [M@Ge10]3− (M = Fe,17 Co18) is a pentagonal prismatic germanium cage with iron or cobalt atoms in the central cavity; [Ru@Ge12]3− is a non-decahedral cluster of 12 vertices;19 [Ir@Sn12]3− is a ligand-free icosahedral cluster with high symmetry;20 and [Co@Sn6Sb6]3− is an off-centre 12-vertex endohedral cluster.21 In addition to the embedding of transition metals in the Zintl anions,5,15 several lanthanide or actinide endohedral inter-metalloid clusters have been reported theoretically and experimentally. The [Eu@Sn6Bi8]4− cluster is a mini-fullerene-type anion containing lanthanide ions.22 [Ln@Sn7Bi7]4− and [Ln@Sn4Bi9]4− (Ln = La, Ce) are anionic cages of two lanthanides.23 Some clusters have also been confirmed by photoelectron spectroscopy (LnSin−(3 ≤ n ≤ 13; Ln = Ho, Gd, Pr, Sm, Eu, Yb)24). In addition, a series of actinide-centred main-group metal clusters such as [U@Tl2Bi11]3−, [U@Pb7Bi7]3− and [U@Pb4Bi9]3− have been successfully prepared,25 and several clusters have been predicted theoretically (e.g. Pu@Sn12 and Pu@Pb1226). For the binary inter-metalloid clusters of the group 15 elements, [La@Sb12]3− is stabilized by the interaction of three π-anti-aromatic units with the central lanthanide metal atom, representing the first localized π-antiaromatic all-metal system in the solid state.27 The anionic heavy-metal cluster [Th@Bi12]4− exhibits 2π-aromaticity, with a stronger ring current than benzene (6π) and close to that of porphyrin (26π), showing substantial all-metal π-aromaticity.28 Like Th, U can be encapsulated in Zintl clusters. The uranium-centred cluster [U@Bi12]3− has been isolated and characterized by quantum chemical calculations.25
Considering that the thorium-doped all-metal Bi cluster [Th@Bi12]4− has been synthesized,28 analogous clusters with other actinide atoms may be stable inter-metalloid clusters. In this work, we have systematically explored the structures and properties of [An@Bi12]4− (An = Th–U) using density functional theory (DFT). The antimony analogues [An@Sb12]4− (An = Th–U) were also studied for comparative analyses. This work provides an in-depth understanding of the binary inter-metalloid clusters of the group 15 elements and provides theoretical clues for the development of new materials for Zintl clusters.
Computational details
For the inter-metalloid clusters of [An@Bi12]4−/[An@Sb12]4−, geometrical optimization and vibrational frequency analysis were carried out using the Gaussian 16 package29 with a PBE30 pure density functional. The conductor-like screening model (COSMO) was used for charge compensation of the default parameters.31 The dispersion correction PBE-D3 was used to take into account the dispersion interactions between the actinides and the Bi/Sb atoms.32 Relativistic effects were considered with the relativistic effective core potentials (RECPs) replacing 60 core electrons (ECP60MWB) for actinides, and the corresponding basis set ECP60MWB_SEG33,34 was adopted. For Bi and Sb metals, ECP78MWB35 and ECP46MWB36 were used, respectively. For all of the clusters, geometry optimizations were performed at the PBE-D3/RECP level of theory. Harmonic vibrational analysis was carried out at the same theoretical level, and the optimized geometries were minimum structures on the potential energy surfaces with all real vibrational frequencies. Atomic dipole-corrected Hirshfeld atomic charge (ADCH)37 analysis was performed at the same theoretical level using the Multiwfn 3.8(dev) package.38 The Wiberg bond index (WBI) was also obtained at the PBE-D3/RECP theoretical level using the Multiwfn 3.8(dev) package. By using ADF 2022 software,39 VDD (Voronoi deformation density)40 charge analysis, the energy decomposition analysis (EDA) and quantum theory of atoms in molecules (QTAIM)41 topology analysis based on the optimized structures were performed using the PBE method and the TZP basis set without a frozen core, and scalar relativistic effects were taken into account by zero-order rule approximation (ZORA).42Results and discussion
Optimized structures of [An@Bi12]4−/[An@Sb12]4−
Structural optimization and frequency calculations of the [An@Bi12]4−/[An@Sb12]4− (An = Th–U) species were carried out at the PBE-D3/RECP level of theory. Similar to [Th@Bi12]4−,28 An4+ was considered as the central ion for each species. Given that the singlet, doublet, and triplet spin states were the highest for Th4+, Pa4+, and U4+, respectively, the singlet structures were calculated for [Th@Bi12]4−/[Th@Sb12]4−, and the doublet structures were considered for [Pa@Bi12]4−/[Pa@Sb12]4−. In the case of [U@Bi12]4−/[U@Sb12]4−, both the singlet and triplet states were considered, and the triplet structures were found to be more stable lying 12.6 ([U@Bi12]4−) and 6.8 ([U@Sb12]4−) kcal mol−1 below the corresponding singlet structures. In addition, for each cluster, other possible spin states were also considered, and the singlet, doublet, and triplet structures were more stable for [Th@Bi12]4−/[Th@Sb12]4−, [Pa@Bi12]4−/[Pa@Sb12]4−, and [U@Bi12]4−/[U@Sb12]4−, respectively (Table S1, ESI†).The optimized structures of [An@Bi12]4−/[An@Sb12]4− are displayed in Fig. 1. The geometry of each species shows an oblate structure.43 [Th@Bi12]4− and [U@Bi12]4− exhibit Cs symmetry, while [Pa@Bi12]4− and [An@Sb12]4− (An = Th–U) have no symmetry (C1). As for [An@Bi12]4−, since the An–Bi bond lengths (Table 1) vary considerably (0.3–0.5 Å), the An–Bi bonds in Bi12 rings can be divided into two types: one is the slightly longer bond from the central metal to the Bi ring (An–BiA), and the other is the relatively shorter An–BiB bond. Three butterfly-shaped Bi4 rings of [An@Bi12]4−, each perpendicular to the central metal, are connected by BiA–BiA′ bonds to form a closed Bi12 ring that encloses the actinide ion in the center. For each species of [An@Sb12]4−, Sb128− has a structure similar to that of Bi128−. The structure of [U@Bi12]4− is similar to that of the synthesized [U@Bi12]3−,25 with an average U–Bi bond distance difference of less than 0.14 Å (Table S2, ESI†), and the Bi–Bi bond distances of these two clusters are also very close to each other. For [Th@Bi12]4−, as tabulated in Table S3 (ESI†), the calculated Th–BiA and Th–BiB average bond lengths are 3.638 and 3.264 Å, respectively, which are very close to the experimental bond lengths,25 with the differences of only 0.02 and 0.01 Å, respectively. This indicates that the calculation method is reliable for the structural parameters of the studied inter-metalloid clusters.
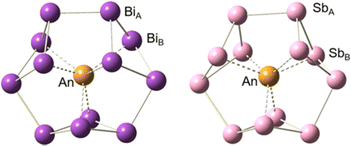 | ||
| Fig. 1 Optimized structures of [An@Bi12]4−/[An@Sb12]4− at the PBE-D3/RECP theoretical level. The purple, pink and yellow spheres represent Bi, Sb and An, respectively. | ||
| Species | Spin states | ρ An | An–Bi/Sb bond distances | |
|---|---|---|---|---|
| An–BiA/SbA | An–BiB/SbB | |||
| C s [Th@Bi12]4− | Singlet | — | 3.638 | 3.264 |
| C 1 [Pa@Bi12]4− | Doublet | 0.778 | 3.629 | 3.175 |
| C s [U@Bi12]4− | Triplet | 2.522 | 3.664 | 3.171 |
| C 1 [Th@Sb12]4− | Singlet | — | 3.548 | 3.234 |
| C 1 [Pa@Sb12]4− | Doublet | 0.730 | 3.527 | 3.155 |
| C 1 [U@Sb12]4− | Triplet | 2.342 | 3.528 | 3.148 |
As can be seen from Table 1, the Mulliken atomic spin densities of the Th, Pa and U atoms are consistent with the spin states of the clusters. Therefore, the unpaired electrons (An = Pa, U) are mainly located on the actinide atoms. As expected, the calculated An–Sb bonds are shorter than the corresponding An–Bi bonds. The average bond distances of the An–BiA bonds range from 3.629 to 3.664 Å, which are much longer than those of the An–BiB bonds (3.171–3.264 Å), and the differences are between 0.3 and 0.5 Å. As for [An@Sb12]4−, the average An–SbA bond lengths range from 3.527 to 3.548 Å, which are also much longer than those of the An–SbB bonds (3.148–3.234 Å). These results indicate the presence of stronger An–BiB/SbB bonds in these clusters. In addition, the relatively shorter U–BiB/SbB bonds suggest that [U@Bi12]4−/[U@Sb12]4− may have stronger U–BiB and U–SbB bonds than the other clusters.
Bond order and charge analysis
As listed in Table 2, at the PBE-D3/RECP level of theory, for each species, the WBIs values for the An–BiB/SbB bonds are significantly larger than those of An–BiA/SbA bonds, implying a higher covalency of the An–BiB/SbB bonds. For [An@Bi12]4−, the WBIs for An–BiB bonds vary from 0.756 to 1.018, which are slightly larger than those for An–SbB in [An@Sb12]4− (0.751–1.005). This indicates that the An–BiB bonding interaction is stronger than the An–SbB bonds. By contrast, the WBIs for the An–SbA bonds are 0.450–0.491, which are larger than those for the An–BiA bonds (0.430–0.469), indicating the higher covalent character of the An–SbA bonds. Besides, most of the WBIs for the An–BiA/SbA and An–BiB/SbB bonds increase from Th to U, suggesting stronger metal–ligand bonding in [U@Bi12]4−/[U@Sb12]4−.| Species | WBIs | Q An | ||
|---|---|---|---|---|
| An–BiA/SbA | An–BiB/SbB | ADCH | VDD | |
| C s [Th@Bi12]4− | 0.430 | 0.756 | 0.152 | 0.051 |
| C 1 [Pa@Bi12]4− | 0.466 | 0.925 | 0.230 | 0.096 |
| C s [U@Bi12]4− | 0.469 | 1.018 | 0.169 | 0.026 |
| C 1 [Th@Sb12]4− | 0.450 | 0.751 | 0.015 | 0.079 |
| C 1 [Pa@Sb12]4− | 0.510 | 0.889 | 0.112 | 0.135 |
| C 1 [U@Sb12]4− | 0.491 | 1.005 | 0.006 | 0.066 |
To evaluate the charge rearrangement of [An@Bi12]4−/[An@Sb12]4−, we performed the ADCH and VDD charge analyses based on the optimized structures. The calculated low ADCH and VDD charges on the actinide atoms (QAn) of [An@Bi12]4−/[An@Sb12]4− indicate that the charge flows from the central metal cations to the cages.
Molecular orbital (MO) analysis
In order to further understand the electronic structures of these actinide-doped all-metal clusters, we performed Kohn–Sham MO analysis with [An@Bi12]4− as a representative. The frontier-occupied MO diagram for [An@Bi12]4−is depicted in Fig. 2. Tables S4–S6 (ESI†) list the compositions of the MOs of [An@Bi12]4−. As shown in Tables S4–S6 (ESI†), the contribution of the Bi cages mainly comes from the Bi 6p orbitals. Fig. 2 shows a pictorial depiction of the main metal–ligand bonding orbitals for each cluster, along with the singly occupied molecular orbitals (SOMOs). The [Th@Bi12]4− species does not have a single electron because it is a closed-shell complex. The HOMO−1(a′′), HOMO−2(a′), HOMO−3(a′′), HOMO−5(a′), HOMO−6(a′) and HOMO−7(a′′) orbitals of [Th@Bi12]4− correspond to the Th–Bi bonding interactions, and these metal–ligand bonding orbitals mainly arise from the interactions between the 6d atomic orbitals of Th and 6p orbitals of Bi cages. For the [Pa@Bi12]4− species, SOMO(a) is mainly derived from the 5f atomic orbital of Pa, and HOMO−1(a), HOMO−2(a), HOMO−5(a), HOMO−6(a), and HOMO−7(a) stand for the interactions of Pa 5f and 6d atomic orbitals with 6p orbitals of Bi cages, while the main contribution of HOMO−3(a) comes from the 5f orbitals of Pa. The [U@Bi12]4− cluster has two single electrons, corresponding to SOMO(a′′) and SOMO−1(a′), and these orbitals mainly contribute to the 5f atomic orbitals of U. The HOMO−4(a′), HOMO−1(a′), HOMO−2(a′), HOMO−5(a′′), HOMO−6(a′′), and HOMO−9(a′′) orbitals of [U@Bi12]4− have U 5f orbitals and mixed 5f and 6d orbitals, respectively, along with the 6p orbitals of Bi cages, resulting in the metal–ligand bonding orbitals. Unlike [Th@Bi12]4−, the MOs of [Pa@Bi12]4− and [U@Bi12]4− show notable An 5f orbital contributions. Moreover, for the metal–ligand bonding orbitals, the atomic orbital compositions of Bi and Sb are obviously larger than those of the An atoms, which indicates that the An–Bi/An–Sb bonds are highly polarized. Hence, the results of the MO plots demonstrate the covalent interactions between the actinide metal cation and the Bi/Sb cage of the clusters, consistent with the bond order analysis discussed above. It should be noted that polarized An–Bi/An–Sb bonding is a secondary interaction in addition to ionic bonding.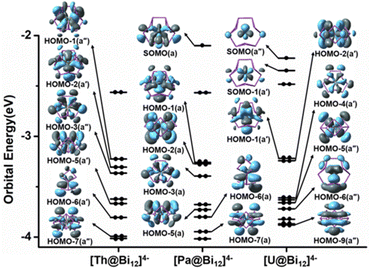 | ||
| Fig. 2 Energy levels of the frontier occupied Kohn–Sham molecular orbitals of [An@Bi12]4− at the PBE-D3/RECP theoretical level. | ||
To further understand the chemical bonding of [An@Bi12]4−/[An@Sb12]4−, an MO correlation diagram with [U@Bi12]4− as the representative cluster is shown in Fig. S2 (ESI†). The HOMO−1(a′), HOMO−2(a′), HOMO−4(a′), HOMO−5(a′′), HOMO−6(a′′), and HOMO−9(a′′) orbitals are the main metal–ligand bonding orbitals. The HOMO−1(a′), HOMO−2(a′), HOMO−4(a′), HOMO−5(a′′), and HOMO−6(a′′) orbitals are mainly derived from the interaction of the U 5f and 6d orbitals with contributions of more than 10%, respectively, and the Bi 6p orbitals of the Bi cages. The HOMO−9(a′′) orbital has comparable U 5f and 6d orbital contributions. Besides, the MO energy levels of these bonding orbitals are lower than those of the Bi cage, indicating that the insertion of the actinide atoms stabilizes the MOs of the cages.
QTAIM analysis
Topological analysis was performed at the theoretical level of the PBE-D3/RECP using the QTAIM method. In QTAIM analysis, the electron density (ρ(r)), Laplacian density (∇2ρ(r)), and energy density (H(r)) reflect the bonding properties of two atoms at the bond critical point (BCP). According to our calculations, for these all-metal clusters [An@Bi12]4−/[An@Sb12]4−, 8–11 BCPs are found between the actinide metal atoms and bismuth/antimony atoms (Fig. 3 and Fig. S1, ESI†), suggesting the presence of actinide–bismuth and actinide–antimony bonding interactions. As indicated in Table S7 (ESI†), the values of ρ are less than 0.1 and ∇2ρ(r) are all positive, indicating that the An–Sb and An–Bi bonds are mainly ionic. The negative H(r) values indicate covalent bonding interactions. Therefore, the interactions of the [An@Bi12]4− and [An@Sb12]4− species are primarily ionic with some covalent interactions. According to Table S7 (ESI†), for each cluster, the H(r) values of the An–BiB/SbB bonds are more negative than those of the An–BiA/SbA bonds. This indicates the stronger covalent interactions between the former bonds. Delocalization index (DI) analysis can be used to evaluate chemical bonding.44–49 As stated in Table S7 (ESI†), as expected, the higher DItotal values of the An–BiB/SbB bonds for each cluster also confirm that the covalent interactions of these bonds are stronger than those of the An–BiA/SbA bonds. In addition, for clusters with the same metal, the larger DItotal values for the An–BiB bonds suggest that the An–BiB bonds possess stronger covalent interactions than the An–SbB bonds. In contrast, the An–SbA bonds show higher covalency with larger DItotal values compared to the An–BiA bonds. These results are in agreement with the bond order analysis.EDA analysis
To quantitatively describe the bonding interactions between [An@Bi12]4− and [An@Sb12]4−, EDA analysis was performed at the PBE/TZP/ZORA level of theory. Each species was divided into two fragments: the actinide cation An4+ and the all-metal cage (Bi128−, Sb128−). In EDA analysis, the interaction energy between two fragments (ΔEint) is decomposed into three energy terms, as shown in the following equation:| ΔEint = ΔEelstat + ΔEPauli + ΔEorb |
The electrostatic and orbital interactions between the two fragments are denoted by ΔEelstat and ΔEorb, respectively, while the Pauli repulsive exchange interaction is denoted by ΔEPauli. The electrostatic and covalent contributions of these two fragments are expressed as percentages of ΔEelstat/(ΔEorb + ΔEelstat) and ΔEorb/(ΔEorb + ΔEelstat), respectively. The steric interaction is expressed as ΔEsteric, which is the sum of ΔEPauli and ΔEelstat. The EDA results for [An@Bi12]4− and [An@Sb12]4− are presented in Table 3. For each species, the contribution of electrostatic energy (62.7–66.1%) is higher than that of the orbital energy (33.9–37.3%), indicating that the An–Bi/Sb interactions are mainly ionic in the [An@Bi12]4− and [An@Sb12]4− clusters. For [An@Sb12]4−, the interaction energies ΔEint are between −2906 and −3001 kcal mol−1, which are more negative than those of the corresponding [An@Bi12]4− (−2841 to −2935 kcal mol−1), indicating a stronger interaction between An4+ and Sb128− of [An@Sb12]4−. Although the ΔEorb values of [An@Bi12]4− are more negative than those of the [An@Sb12]4− analogues, [An@Sb12]4− possesses higher interaction energies than [An@Bi12]4−. This is mainly due to the higher electrostatic interactions and lower Pauli repulsive exchange interactions, i.e. the higher steric interactions. The differences in ΔEPauli between [An@Bi12]4− and [An@Sb12]4− are smaller (17–24 kcal mol−1) than those in ΔEelstat (69–82 kcal mol−1), suggesting that the higher electrostatic interaction energy is responsible for the stronger bonding interactions of [An@Sb12]4−.
| Species | ΔEPauli | ΔEelstat (%) | ΔEsteric | ΔEorb (%) | ΔEint |
|---|---|---|---|---|---|
| C s [Th@Bi12]4− | 351.55 | −2059.83 (64.5) | −1708.28 | −1133.00 (35.5) | −2841.10 |
| C 1 [Pa@Bi12]4− | 405.65 | −2076.82 (62.9) | −1671.16 | −1224.03 (37.1) | −2895.23 |
| C s [U@Bi12]4− | 390.00 | −2085.28 (62.7) | −1695.28 | −1240.07 (37.3) | −2935.59 |
| C 1 [Th@Sb12]4− | 333.96 | −2142.36 (66.1) | −1808.41 | −1098.38 (33.9) | −2906.78 |
| C 1 [Pa@Sb12]4− | 386.26 | −2156.33 (64.3) | −1770.07 | −1195.17 (35.7) | −2965.08 |
| C 1 [U@Sb12]4− | 365.46 | −2154.50 (64.0) | −1789.04 | −1212.08 (36.0) | −3001.09 |
The interaction energies ΔEint of [U@Bi12]4− and [U@Sb12]4− are −2935.59 and −3001.09 kcal mol−1, respectively, both of which are the most negative ΔEint values in the [An@Bi12]4− and [An@Sb12]4− species, and [U@Sb12]4− shows the most negative ΔEint, indicating that [U@Sb12]4− possesses the strongest interactions. Except for [Pa@Sb12]4−, from Th to U, the electrostatic and orbital interactions gradually increase, which is similar to the trend of the interaction energy. Compared with [U@Sb12]4−, [Pa@Sb12]4− has a slightly higher ΔEelstat, while a larger ΔEPauli leads to a lower ΔEsteric for [Pa@Sb12]4−. It should be noted that the trend of the steric interaction energies ΔEsteric for [An@Bi12]4−/[An@Sb12]4− differs from the corresponding interaction energies ΔEint. Considering the similar trend of ΔEorb and ΔEint, the tendency of the bonding interactions of these clusters is mainly determined by the covalent interactions.
Energy analysis
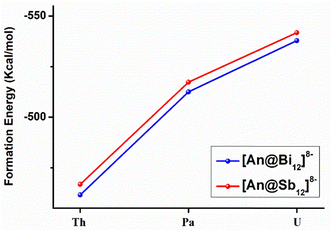
The formation energies (ΔE) were calculated by the reactions of An4+ + Bi128−→ [An@Bi12]4− and An4+ + Sb128− → [An@Sb12]4− at the theoretical level of the PBE-D3/RECP. The empty Sb128−/Bi128− cages were optimized (Fig. S3, ESI†), and the cages did not maintain the geometries in the clusters. Since the empty Sb128−/Bi128− cages are predicted to be stable, they should be able to serve as plausible reactants in the formation reactions. Therefore, at the same theoretical level, we optimized the structure of the side-attached isomer, represented by [U@Bi12]4− with U4+ attached externally to the cage, which may be an important precursor of the endohedral isomer. It was found that in the optimized side-attached isomer (Fig. S4, ESI†), the structures of the Bi128− cages changed considerably due to the coordination of U4+, and the structures lie 107.3 kcal mol−1 above the endohedral isomer.The formation energies are presented in Fig. 4 and Table S8 (ESI†). The calculated formation energies for [An@Bi12]4− vary between −461 and −538 kcal mol−1 (Table S8, ESI†), while those for [An@Sb12]4− range from −466.8 to −542.0 kcal mol−1. According to the studied formation reactions, it is shown that these all-metal clusters are highly stable in the gas phase at room temperature. For the [An@Sb12]4− clusters, [U@Sb12]4− has the most negative formation energy (−542.0 kcal mol−1), indicating that [U@Sb12]4− is more stable than [Th@Sb12]4− and [Pa@Sb12]4−. Similarly, the U-doped species of the [An@Bi12]4− metal cluster has the most negative formation energy of −538.0 kcal mol−1. Thus, among the metal clusters of [An@Bi12]4− and [An@Sb12]4−, the U-doped metal clusters are more stable, which is consistent with the trend of the covalent interactions of [An@Bi12]4− and [An@Sb12]4−. As shown in Fig. 4, the absolute values of ΔE display an upward trend from Th to U. Besides, the higher formation energies of [An@Sb12]4− indicate the stronger metal–ligand interactions in these clusters, in line with the stronger electrostatic interactions of [An@Sb12]4− than that of [An@Bi12]4−. Therefore, these trends in the formation energies are consistent with the results of the EDA analysis, which demonstrates that both the electrostatic interactions between the actinide cations and metal cages and the metal–ligand covalent interactions are crucial for the formation of these actinide-doped inter-metalloid clusters.
At the PBE-D3/RECP level of theory, we also performed dissociation energy (BDE, ΔH) analysis for [An@Bi12]4− and [An@Sb12]4− with core + shell products at room temperature, including the neutral metal atoms and the metal cations of An2+ and An4+. All of the empty Sb124−/Bi124−, Sb126−/Bi126− and Sb128−/Bi128− cages were optimized (Fig. S3, ESI†). As listed in Table S9 (ESI†), the high BDEs of these clusters indicate that they are all stable. As expected, the BDEs of these clusters gradually increased from Th to U, in line with the stronger covalent interactions of U–Bi/Sb bonding. For [An@Bi12]4− and [An@Sb12]4−, the BDEs with metal atoms An are the lowest, mainly due to the lower electrostatic interactions. For each cluster, the dissociation reaction shown in Table S9 (ESI†) involves the dissociation of 12 An–B bonds. According to the experimental formation energy (ΔH, −19.4 ± 0.5 kcal mol−1, 300 K) of ThBi,50 the dissociation energy of 12 Th–Bi bonds (probably 3.38 Å) is approximately 232.8 kcal mol−1, which is close to the calculated dissociation energy of [Th@Bi12]4− (238.9 kcal mol−1, 298.15 K) with an average Th–Bi bond distance of about 3.4 Å. These results further prove the reliability of the predictions for the studied clusters.
For the studied [An@Bi12]4−/[An@Sb12]4− clusters, the dissociation could occur along multiple channels other than those with core (An) + shell (cage) products. From the present cluster structure, dissociation into the core + shell would apparently require breaking six stronger and six weaker An–Bi/Sb bonds. The detachment of one (e.g., outermost) Bi/Sb requires only three Bi–Bi/Sb–Sb bonds and one An–Bi/Sb bond broken. Therefore, using [An@Bi12]4− as an example, we calculated the BDEs for the reactions of [An@Bi12]4− → Bi3+ + AnBi117− and [An@Bi12]4− → Bi + AnBi114−. As shown in Table S10 (ESI†), the calculated BDEs by the detachment of Bi3+ and Bi are between 78.5 and 100.6 kcal mol−1, which are lower than the corresponding reactions with core + shell products. As expected, the detachment of single Bi (Bi3+ and Bi) requires less energy than that of An. Thus, the actual system stability may be considerably lower with respect to the detachment of a single Bi/Sb. Based on the experimental results, the dissociation energy of Bi2 is 48.9 kcal mol−1 with the Bi–Bi bond distance of 2.66 Å,51,52 and the dissociation energy of one Th–Bi bond and three Bi–Bi bonds is approximately 166.7 kcal mol−1, which is higher than the calculated dissociation reaction energies of [Th@Bi12]4− (Table S10, ESI†). It should be noted that the average Bi–Bi and Th–Bi bond lengths of [Th@Bi12]4− are much longer than those of Bi2 and ThBi with a difference of about 0.4 Å and 0.2 Å, respectively. Therefore, the inconsistency in the dissociation energy is most likely due to the different bond lengths of the Bi–Bi and Th–Bi bonds. In addition, considering that [Th@Bi12]4− has been synthesized experimentally,28 the calculated BDEs of [Pa@Bi12]4− and [U@Bi12]4− are close to those of [Th@Bi12]4− (Table S10, ESI†); therefore, the Pa and U analogues may be accessible under suitable synthetic conditions.
Conclusions
In the present work, we explored a series of actinide endohedral inter-metalloid clusters of the group 15 elements [An@Bi12]4−/[An@Sb12]4− (An = Th–U) using DFT calculations. The predicted structures of these inter-metalloid clusters have similar geometries. The VDD and ADCH charge analyses showed that the central metal cations are electron donors to the metal cages. The bond order, QTAIM and MO analyses confirmed the covalent bonding interactions of the An–Bi and An–Sb bonds. The EDA analysis shows that electrostatic interactions play a major role in the stronger bonding interaction of [An@Sb12]4− than that of [An@Bi12]4−, which is consistent with the thermodynamic analysis. Among the [An@Bi12]4− and [An@Sb12]4− metal clusters, the U-doped metal cluster has the highest formation energy, which is consistent with the trend of covalent interactions of [An@Bi12]4− and [An@Sb12]4− in the EDA analysis. These results indicate that the covalent interactions determine the bonding tendencies of these clusters. Therefore, covalent and electrostatic interactions between actinide metal atoms and metal cages are essential for the formation of these actinide endohedral inter-metalloid clusters. This work predicts the feasibility of the actinide-doped inter-metalloid clusters of the group 15 elements and provides approaches for enriching bismuth and antimony clusters.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its supplementary materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 12175269 and U2067212).References
- Y. Li, Q. Zhang, L. Ren, Z. Li, X. Lin, Z. Ma, H. Yang, Z. Hu and J. Zou, Ind. Chem. Mater., 2023, 1, 282–298 RSC.
- R. S. McCoy, S. Choi, G. Collins, B. J. Ackerson and C. J. Ackerson, ACS Nano, 2013, 7, 2610–2616 CrossRef CAS PubMed.
- J. U. Reveles, P. A. Clayborne, A. C. Reber, S. N. Khanna, K. Pradhan, P. Sen and M. R. Pederson, Nat. Chem., 2009, 1, 310–315 CrossRef CAS PubMed.
- A. H. E. Zintl, Z. Phys. Chem., 1931, 154, 47 CrossRef.
- T. F. Fassler and S. D. Hoffmann, Angew. Chem., Int. Ed., 2004, 43, 6242–6247 CrossRef CAS PubMed.
- E. N. Esenturk, J. Fettinger and B. Eichhorn, J. Am. Chem. Soc., 2006, 128, 9178–9186 CrossRef CAS.
- L. F. Cui, X. Huang, L. M. Wang, J. Li and L. S. Wang, J. Phys. Chem. A, 2006, 110, 10169–10172 CrossRef CAS PubMed.
- L. G. Perla, A. G. Oliver and S. C. Sevov, Inorg. Chem., 2015, 54, 872–875 CrossRef CAS PubMed.
- M. Ruck, Z. Anorg. Allg. Chem., 1998, 624, 521–528 CrossRef CAS.
- H. G. vonSchnering, M. Baitinger, U. Bolle, W. CarrilloCabrera, J. Curda, Y. Grin, F. Heinemann, J. Llanos, K. Peters, A. Schmeding and M. Somer, Z. Anorg. Allg. Chem., 1997, 623, 1037–1039 CrossRef CAS.
- E. N. Esenturk, J. Fettinger, Y. F. Lam and B. Eichhorn, Angew. Chem., Int. Ed., 2004, 43, 2132–2134 CrossRef CAS PubMed.
- F. Lips and S. Dehnen, Angew. Chem., Int. Ed., 2009, 48, 6435–6438 CrossRef CAS PubMed.
- S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25, 5678–5692 CrossRef CAS.
- S. Scharfe and T. F. Fassler, Philos. Trans. R. Soc., A, 2010, 368, 1265–1284 CrossRef CAS.
- S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fassler, Angew. Chem., Int. Ed., 2011, 50, 3630–3670 CrossRef CAS PubMed.
- M. Ruck, Angew. Chem., Int. Ed., 2001, 40, 1182–1193 CrossRef CAS.
- B. B. Zhou, M. S. Denning, D. L. Kays and J. M. Goicoechea, J. Am. Chem. Soc., 2009, 131, 2802 CrossRef CAS.
- J. Q. Wang, S. Stegmaier and T. F. Fassler, Angew. Chem., Int. Ed., 2009, 48, 1998–2002 CrossRef CAS PubMed.
- G. Espinoza-Quintero, J. C. A. Duckworth, W. K. Myers, J. E. McGrady and J. M. Goicoechea, J. Am. Chem. Soc., 2014, 136, 1210–1213 CrossRef CAS PubMed.
- J. Q. Wang, S. Stegmaier, B. Wahl and T. F. Fassler, Chem. – Eur. J., 2010, 16, 1793–1798 CrossRef CAS.
- R. J. Wilson, F. Hastreiter, K. Reiter, P. Buschelberger, R. Wolf, R. M. Gschwind, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2018, 57, 15359–15363 CrossRef CAS PubMed.
- F. Lips, R. Clerac and S. Dehnen, Angew. Chem., Int. Ed., 2011, 50, 960–964 CrossRef CAS PubMed.
- F. Lips, M. Holynska, R. Clerac, U. Linne, I. Schellenberg, R. Pottgen, F. Weigend and S. Dehnen, J. Am. Chem. Soc., 2012, 134, 1181–1191 CrossRef CAS PubMed.
- A. Grubisic, Y. J. Ko, H. P. Wang and K. H. Bowen, J. Am. Chem. Soc., 2009, 131, 10783–10790 CrossRef CAS PubMed.
- N. Lichtenberger, R. J. Wilson, A. R. Eulenstein, W. Massa, R. Clerac, F. Weigend and S. Dehnen, J. Am. Chem. Soc., 2016, 138, 9033–9036 CrossRef CAS PubMed.
- J. P. Dognon, C. Clavaguera and P. Pyykko, C. R. Chim, 2010, 13, 884–888 CrossRef CAS.
- X. Min, I. A. Popov, F. X. Pan, L. J. Li, E. Matito, Z. M. Sun, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2016, 55, 5531–5535 CrossRef CAS PubMed.
- A. R. Eulenstein, Y. J. Franzke, N. Lichtenberger, R. J. Wilson, H. L. Deubner, F. Kraus, R. Clerac, F. Weigend and S. Dehnen, Nat. Chem., 2021, 13, 1755–4330 CrossRef PubMed.
- M. T. G. Frisch, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian Ict, Wallingford, CT, 2016 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Klamt and G. Schuurmann, J. Chem. Soc.-Perkin Trans. 2, 1993, 799–805 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- X. Y. Cao, M. Dolg and H. Stoll, J. Chem. Phys., 2003, 118, 487–496 CrossRef CAS.
- M. Dolg and X. Y. Cao, Chem. Rev., 2012, 112, 403–480 CrossRef CAS PubMed.
- W. Kuchle, M. Dolg, H. Stoll and H. Preuss, Mol. Phys., 1991, 74, 1245–1263 CrossRef.
- A. Bergner, M. Dolg, W. Kuchle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- T. Lu and F. W. Chen, J. Theor. Comput. Chem., 2012, 11, 163–183 CrossRef CAS.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. F. Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, New York, 1990 Search PubMed.
- E. Vanlenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- F. Lips, R. Clerac and S. Dehnen, J. Am. Chem. Soc., 2011, 133, 14168–14171 CrossRef CAS PubMed.
- R. F. W. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391–7399 CrossRef CAS.
- C. Foroutan-Nejad, Z. Badri and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 30670–30679 RSC.
- Z. Badri, C. Foroutan-Nejad, J. Kozelka and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 26183–26190 RSC.
- C. Foroutan-Nejad, S. Shahbazian and R. Marek, Chem. – Eur. J., 2014, 20, 10140–10152 CrossRef CAS PubMed.
- P. L. Bora, M. Novak, J. Novotny, C. Foroutan-Nejad and R. Marek, Chem. – Eur. J., 2017, 23, 7315–7323 CrossRef CAS PubMed.
- A. Jaros, Z. Badri, P. L. Bora, E. F. Bonab, R. Marek, M. Straka and C. Foroutan-Nejad, Chem. – Eur. J., 2018, 24, 4245–4249 CrossRef CAS PubMed.
- G. Borzone, A. Borsese and R. Ferro, J. Less-Common Met., 1982, 84, 165–172 CrossRef CAS.
- P. J. Linstrom and W. G. Mallard, J. Chem. Eng. Data, 2001, 46, 1059–1063 CrossRef CAS.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 97th edn, 2016 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: QTAIM analysis of [An@Bi12]4− (An = Th, Pa) and [An@Sb12]4− (An = Th–U), orbital interaction diagram of [U@Bi12]4−, the optimized structures of the empty cages, the optimized structures of the side-attached isomers of [U@Bi12]4−, relative energies for the [An@Bi12]4−/[An@Sb12]4− structures, An–Bi distances, the molecular orbital composition analysis of [An@Bi12]4−, formation energies and bond dissociation energies (BDEs) of [An@Bi12]4−/[An@Sb12]4−. See DOI: https://doi.org/10.1039/d4cp02546f |
| This journal is © the Owner Societies 2024 |