High-resolution infrared spectra and rovibrational analysis of the ν₁₂ band of propylene oxide

Abstract

The high-resolution infrared spectrum of the fundamental band ν₁₂ (ring breathing) of the chiral molecule propylene oxide (CH₃CHCH₂O) was recorded at room temperature and under jet-cooled conditions using a quantum cascade laser at 8 μm. The observed lines with quantum numbers J ≤ 55 and K_a ≤ 21 were assigned to strong b- and c-type bands, and some low J transitions were classified as weak a-type transitions. The lines were fitted using a Watsons A-reduced Hamiltonian in the I^r representation. From the rovibrational analysis the band origin as well as the rotational constants and four quartic centrifugal distortion constants were derived.

---

1 Introduction

Propylene oxide, CH₃CHCH₂O, also referred to as methyl oxirane, is a stable chiral molecule that has been extensively studied by means of spectroscopy and quantum chemical calculations.^1–4 Due to its conformational stability and commercial availability in enantiomerically pure samples, it has often been the subject of studies addressing molecular chirality. In particular, its chemical volatility at room temperature facilitates its investigation in gas phase experiments such as photo-electron circular dichroism (PECD),^5–7 cavity ring-down polarimetry (CRDP),⁸ Raman optical activity (ROA) spectroscopy,⁹ cold target recoil ion momentum spectroscopy (COLTRIMS),¹⁰ field-induced diastereomers¹¹ and chiral discrimination through bielliptical high-harmonic spectroscopy.¹² Propylene oxide is a closed-shell molecule consisting of ten light atoms whose molecular properties can be treated by accurate ab initio methods. It has been a subject of many high-level quantum chemical calculations, addressing the geometrical structure and electronic configuration, the vibrational dynamics and internal rotation, as well as chiral properties such as vibrational and photo-electron circular dichroism, optical rotation, and vibrational Raman optical activity.^13–15 Gas phase rotational resolved spectroscopy in the microwave and millimetre wavelength region has been used to derive the geometrical structure of propylene oxide and the internal dynamics of the methyl group, which possesses a hindered rotation of a symmetric top in a threefold potential of moderate barrier height. In the late 1950^th, Hershbach et al. reported the first microwave spectra of propylene oxide in the vibrational ground state and its first excited ν₂₄ torsional mode.^16,17 From the tunnelling splitting of transitions with A/E symmetry the torsional barrier height was experimentally derived. Later, accurate centrifugal distortion constants and several structural parameters were determined from microwave studies which also included spectra of some isotopologues.^18,19 In 2016, propylene oxide was detected as the first chiral molecule in a cold interstellar molecular cloud towards the galactic center.²⁰ Its relevance in astronomy has triggered several new laboratory and quantum chemical studies.^21,22 High-resolution laboratory spectra up to 1 THz led to significantly improved molecular parameters of the ground state and a refined value of the methyl torsional barrier height.²³ In a recent study, the rotational spectrum of the first excited torsional mode, ν₂₄, was revisited, and accurate molecular parameters were derived, including the A/E tunnelling splitting of the v₂₄ = 1 vibrationally excited state.²⁴ Compared to the ground state with a splitting on the order of 1 MHz or less, the splitting of the first excited torsional state is significantly larger and on the order of 100 MHz. The torsional potential barrier was also the subject of a recent study on doubly deuterated propylene oxide.²⁵

Several infrared (IR) spectroscopic studies have addressed the vibrational dynamics of propylene oxide. Most of the 24 fundamental modes were investigated using low-resolution liquid or gas phase spectroscopy whose band center positions are in good agreement with our recent ab initio calculations at the B3LYP/def2-TZVP level of theory. Nevertheless, rotationally resolved vibrational infrared data are rather sparse. Particularly, the unambiguous assignment to fundamental vibrational modes can be achieved only from high-resolution infrared spectra. Recently, first rotationally resolved spectra of adiabatically cooled propylene oxide at 3 μm were reported by Sunahori et al.²⁶ In their IR diode-laser spectra, the authors identified four of the six fundamental CH vibrational bands by comparison with ab initio calculations. Some of these band origins appeared to be significantly shifted due to vibrational couplings. Furthermore, the authors reported splittings of several rovibrational lines, which they attributed to Fermi-type and Coriolis-type interactions.

For future studies on the chiral properties of propylene oxide, e.g., high-resolution vibrational circular dichroism in the gas phase or cavity ring-down polarimetry,⁸ but also for the search for its infrared spectra in interstellar and circumstellar environments using the James Webb Space Telescope (JWST)²⁷ or the TEXES high-resolution mid-infrared spectrograph on Mauna Kea,²⁸ accurate infrared data at high spectral resolution are needed. In the presented study we report on rotationally resolved infrared spectra of propylene oxide using a tuneable continuous-wave (cw) quantum cascade laser (QCL) spectrometer. Accompanying calculations were carried out to facilitate the assignment of the vibrational modes.

2 Methodology

2.1 Experimental methods

High-resolution infrared absorption spectra of propylene oxide were obtained using two different experimental setups: one with a glass cell at room temperature and static pressure, the other with a pick-up source combined with a supersonic jet that expands in a vacuum chamber. In both experiments a racemic mixture of propylene oxide (CAS 75-56-9; Sigma Aldrich) of purity higher than 99.5% was used. An external-cavity quantum cascade laser (ec-QCL; daylight solutions) operating in the range of 1240 to 1380 cm⁻¹ (7.2 to 8.0 μm) with a laser power of 100 mW was used to record the room temperature spectrum of propylene oxide up to rotational transitions of J = 55. Furthermore, a 35 Kelvin cold supersonic jet spectrum was recorded with significantly reduced line widths up to quantum numbers J = 19.

The ec-QCL was operated in two different tuning modes. For the pulsed supersonic jet measurements, we used a fast-scanning current modulation mode of the laser to record 0.03 cm⁻¹ narrow spectra during the 10 μs transit time of molecules passing the laser beam.²⁹ For the room temperature measurements, a slow-scanning mode, utilizing a mechanically driven optical feedback grating, was used to record room temperature spectra in sections of roughly 0.1 cm⁻¹ spectral width. To calibrate the wavelength of the recorded spectra, a small fraction (5–10%) of the infrared radiation was used to simultaneously record the transmission of an etalon of 300 MHz free spectral range (FSR) and a reference gas spectrum of nitric acid (HNO₃). For the measurements at room temperature, propylene oxide was introduced into a glass cell (80 cm length) at a pressure of 3 mbar, and the intensity of the transmitted light was recorded using a liquid nitrogen cooled mercury cadmium telluride detector (lq-N₂ MCT Teledyne Judson Technology). For the supersonic jet measurements, we utilized a pick-up source filled with liquid propylene oxide. The evaporating sample was diluted in 5 bar of helium and pre-expanded through a pulsed valve into a slit nozzle source before being adiabatically expanded into a vacuum chamber at 10⁻² mbar background pressure. Perpendicularly oriented to the supersonic jet and 10 mm downstream from the slit nozzle exit, the infrared laser beam intersected the gas in a Herriott-type multi-pass configuration with 42 reflections to enhance the absorption signal recorded by a fast lq-N₂ cooled MCT detector (Vigo Photonics).

2.2 Computational methods

To support the data analysis of the recorded spectra, molecular parameters of ground and vibrationally excited states were derived from quantum chemical calculations at the B3LYP/def2-TZVP level of theory using the GAUSSIAN program suite.³⁰ After optimizing the geometry, harmonic and anharmonic vibrational frequencies, the alpha matrix with a correction of rotational constants in vibrationally excited states, and vibrational transition moments were derived. The initial prediction of the rovibrational spectra was done using the Picketts SPCAT³¹ program. Here we combined our calculated vibrational energy and rotational constants with experimentally obtained ground state rotational and centrifugal distortion constants from a previous study.²³ We used Pickett's SPFIT/SPCAT program and a home-made graphical tool for an iterative line by line analysis to derive the molecular parameters of a Watson's A-reduced semirigid Hamiltonian.^32,33 Finally, we utilized the PGOPHER program to estimate the rotational temperature of the supersonic jet spectrum and derive the relative band intensities of the a-type, b-type, and c-type spectra. We also used the PGOPHER program to plot the spectra shown in Fig. 1–3.³⁴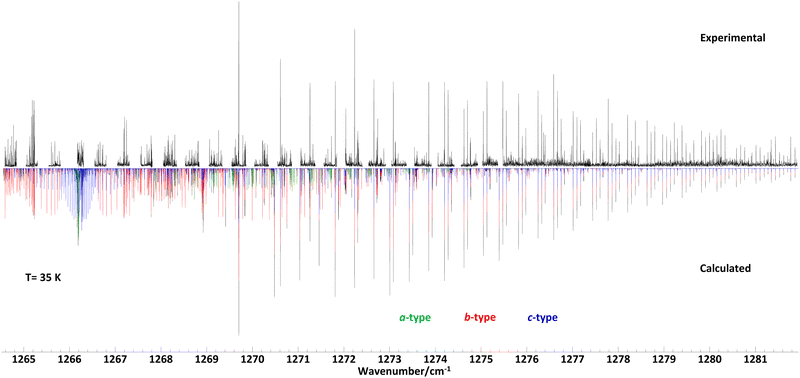

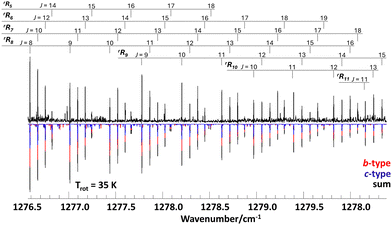
Fig. 1 High resolution infrared supersonic jet spectrum of propylene oxide (upper trace) and calculated spectrum based on molecular parameters from a least-squares fit data analysis assuming a rotational temperature of 35 K. The molecular parameters are given in Table 1. The band consists of a-type (green), b-type (red), and c-type (blue) transitions with intensity ratios given in Table 1. For overlapping lines of a-, b-, or c-type the resulting total intensities are shown in black.

Fig. 2 Measured ^rR_Ka branch transitions of propylene oxide (upper trace in black) and assigned b-type (red) and c-type (blue) transitions. The lower black spectrum shows the sum of b- and c-type transitions, calculated for a rotational temperature of 35 K.

Fig. 3 Band center of the ν₁₂ fundamental band of propylene oxide showing ^ΔK_aΔJ_Ka branches assigned to the a-type transitions of ^qQ_Ka with K_a = 1,2,3,… (green), b-type transitions of ^pQ₁ and ^rQ₀ (red) and c-type transitions of ^pQ₁ and ^rQ₀ (blue). The measured spectrum (black) shows two band gaps which are due to mode hops of the QCL.

3 Measurements

Room temperature spectra of propylene oxide in a glass cell were recorded in the range between 1264.5–1309.5 cm⁻¹ and spectra of adiabatically cooled propylene oxide in a supersonic jet expansion were measured between 1264.6–1281.9 cm⁻¹. An overview spectrum taken with the supersonic jet setup is displayed in Fig. 1, together with a calculated spectrum based on molecular constants from a least-squares fit data analysis. The measurements cover the band origin at 1266.2 cm⁻¹ and towards higher frequencies most of the ^rR and ^rQ branches (denoted ^ΔK_aΔJ with ΔK_a = +1). However, at lower frequencies most of the ^pP- and ^pQ-branches (ΔK_a = −1) were inaccessible due to the lack of frequency coverage by the laser. In addition, there are several gaps in the recorded spectrum below 1280 cm⁻¹, which are due to mode hops of the ec-QCL. Nevertheless, the recorded spectrum encompasses more than thousand lines which were sufficient to obtain the molecular parameters of the vibrational excited ν₁₂ = 1 state up to quartic order.

The supersonic jet spectrum shows narrow and well separated absorption lines of 40 MHz line width (FWHM). In comparison, the absorption lines at room temperature are three times as broad (120 MHz) and in most cases their line profiles overlap. A part of the measured line width can be attributed to the Doppler broadening. The Doppler line widths of propylene oxide at supersonic jet temperatures (35 K) and at room temperatures (300 K) are 21 MHz and 62 MHz (FWHM) respectively. We assume the additional line widths are due to pressure broadening, as the pressure in the glass cell was always a few mbar, which is also a realistic assumption for the pressure in a supersonic jet about 1–2 cm behind the exit of a two-dimensional slit nozzle.

4 Data analysis

We used the SPFIT/SPCAT program by Pickett³¹ for data analysis to derive molecular parameters of a Watsons A-reduced semi-rigid Hamiltonian in the I^r representation. The ground state molecular parameters were fixed to values obtained from millimetre wavelength spectra reported by Mesko et al. which show rotational lines split into E and A components.²³ The authors used the XIAM program suite to simultaneously fit E and A symmetry transitions to a Hamiltonian which includes parameters for the threefold potential barrier of the methyl group. To include the accurate ground state data of Mesko et al. into our infrared data analysis, we first fitted the E and A rotational transitions given in the ESI† of Mesko et al. to a Watson's A-reduced semi-rigid rotor Hamiltonian without internal motion. We derived one set of molecular parameters for E-state transitions and one set for A-state transitions, separately. Finally, we used the weighted averaged rotational parameters, e.g.,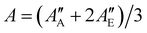 , and accordingly the weighted averaged higher order molecular parameters (see Table 1) for the ground state and kept these parameters fixed during the process of data analysis. For the vibrational excited ν₁₂ = 1 state, we used the ab initio calculated vibrational energy E_vib and the rotational–vibrational coupling constants α_A = A′′ − A′ = 30.2 MHz, α_B = B′′ − B′ − 4.2 MHz, and α_C = C′′ − C′ − 8.3 MHz, which were subtracted from the experimental ground state values A′′, B′′, C′′ to obtain good start parameters for the analysis of the ν₁₂ = 1 excited state (see calculated values in Table 1). From the least-squares fit analysis of more than thousand rovibrational transitions, we derived the molecular parameters of the ν₁₂ mode up to the quartic order. The sextic centrifugal constants could not be derived from the fit and were kept fixed to their ground state values. The final fit result is presented in Table 1. The output file from SPFIT³¹ reformatted by the PIFORM³⁵ program is provided in the ESI.†

Table 1 Rovibrational molecular parameters of propylene oxide

	G.S.^a	ν 12 = 1	ν 12 = 1
	Mesko et al.^23	Exp.	Calc.
Values in square parentheses have been set to zero or to the values of the ground state. 1σ uncertainties from the fit are given in round parentheses.a Watson's A-reduced molecular parameters for the ground state were derived from data published by Mesko et al.^23b The band intensities Ia, Ib, Ic were normalized to the total band intensity I = Ia + Ib + Ic. Experimental values were derived from the relative line intensities of measured a-, b-, and c-type transitions. Calculated values are the squared deperturbed dipole transition moments X(a)^2, Y(b)^2, Z(c)^2 of the ν12 fundamental mode derived from a B3LYP/def2-TZVP calculation in GAUSSIAN 16 and normalized to the total vibrational dipole moment X(a)^2 + Y(b)^2 + Z(c)^2.
E vib/cm^−1	[0]	1266.20143(9)	1267.3
A/MHz	18023.84821(84)	18 008.165(50)	17 993.6
B/MHz	6682.15013(32)	6685.117(43)	6686.3
C/MHz	5951.39761(32)	5959.310(30)	5959.7
Δ J/kHz	2.91500 (17)	2.9704(96)
Δ JK/kHz	3.46744 (69)	3.145(79)
Δ K/kHz	19.7360(13)	24.45(22)
δ J/kHz	0.192835(45)	0.1834(83)
δ K/kHz	2.5950(15)	[2.5950]
Φ J/Hz	0.001578(24)	[0.001578]
Φ JK/Hz	−0.00754(94)	[−0.00754]
Φ KJ/Hz	0.0309 (32)	[0.0309]
Φ K/Hz	0.0384 (23)	[0.0384]
φ J/Hz	0.0000897(84)	[0.0000897]
φ JK/Hz	[0]	[0]
φ K/Hz	0.116 (20)	[0.116]
Band intensities^b
I a /I		0.17(2)	0.19
I b /I		0.56(5)	0.57
I c /I		0.27(3)	0.24
J min/Jmax	0/82	1/55
K min/Kmax	0/49	0/21
rms	0.45881	0.66847

---

The supersonic jet spectrum shows rotationally resolved ^rR-branch transitions of a hybrid band with strong b/c-type transitions. Fig. 2 depicts a section of the measured spectrum (upper trace) encompassing the ^rR_Ka branches of K_a = 5,6,…,11. The relative intensities of b- and c-type transitions, which appear as overlapping red and blue lines in the calculated spectrum, were determined from lines near the band center, where the asymmetry splitting is large and b- and c-type transitions are well resolved (see Fig. 3). The rotational temperature of about 35 K was estimated from the measured total line intensities under the assumption of a Boltzmann thermal distribution. As expected for a rigid molecule close to the case of a symmetric prolate top, the B and C rotational constants are almost identical and close to the values of the ground state. The molecular rigidity is also reflected in the small values of the rotational–vibrational coupling constants and the centrifugal distortion constants, which despite the measured high rotational excitation of up to J′′ = 55 could only be determined up to quartic order.

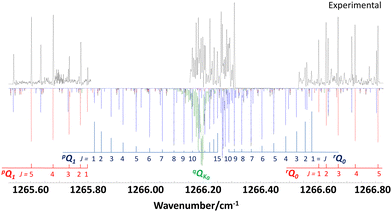
Fig. 3 shows the band center region with the prominent ^ΔK_aΔJ_Ka type branches ^pQ₁ and ^rQ₀ of the b-type spectrum (in red). Gaps in the spectral coverage of the infrared laser leaves strong lines of the ^pQ₁ and ^rQ₀ branches (in blue) of the c-type spectrum unobserved. Nevertheless, some higher J transitions of these branches near the band origin could be assigned and were used to determine the relative intensities of b- and c-type transitions. In addition, a spectral feature at 1266 cm⁻¹ was analyzed and assigned to a-type transitions of a series of ^qQ_Ka branches with K_a = 1,2,3,… (in green). In our PGOPHER simulations, we scaled the relative band intensities I_a, I_b and I_c, which are proportional to the squared vibrational transition moments I ∼ (∂μ/∂Q)², to match the intensity ratios of the measured a-, b- and c-type transitions. For better comparison with ab initio calculated results, we used normalized relative band intensities defined by I_a/I, I_b/I and I_c/I with I = I_a + I_b + I_c, which are dimensionless quantities. The Gaussian-16 output file of our DFT B3LYP/def2-TZVP calculation contains the derivatives of the vibrational dipole moment with respect to the molecular axis system, from which theoretical values for the normalized relative band intensities were calculated. The results listed in Table 1 show very good agreement between experimental and calculated results.

There is a noticeable shift in observed line positions with 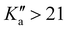and the degeneracy of the asymmetry components 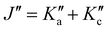and 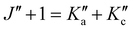is lifted. Since the supersonically cooled jet experiment only probes transitions of low J′′ and 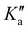quantum numbers (mostly < 10) the perturbation is only noticeable in the room temperature spectrum. We have also found regions in the spectrum where lines split into doublets of similar intensity that are separated by 60 to 360 MHz. Their origin is unclear, as the fundamental ν₁₂ mode has no tunnelling barrier that could possibly split the vibrational excited levels, and splittings in the ground state (about 1 MHz) are too small to be resolved in infrared line widths of 40 MHz and more. On the other hand, microwave spectra of the ν₂₄ torsional excited states ν₂₄ = 1,2 show splittings of E and A components of 100 and 240 MHz, respectively.²⁴ A possible rovibrational coupling with energetically nearby dark states, excited with at least one quantum in the ν₂₄ torsional vibrational mode, could cause the splitting of A/E levels in the ν₁₂ breathing mode, which otherwise remain unresolved. Similar splittings of lines were observed in the C–H stretching modes of propylene oxide at 3 μm.²⁶ The current lack of high-resolution infrared data of propylene oxide does not allow the analysis of A/E symmetry splitting as has been done for the torsional splitting of other molecules such as acetaldehyde.³⁶ Therefore, it is necessary to extend the current high resolution studies to other vibrational bands of propylene oxide.

5 Results and conclusions

5.1 Spectroscopic results

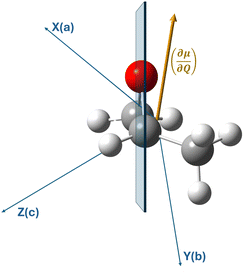
The measurements on the supersonic jet show well-resolved lines with a Doppler-limited frequency accuracy of better than 2 × 10⁻⁴ cm⁻¹. Over the entire measured frequency range, 60 non-degenerate, well-resolved lines could be assigned to their rovibrational energy states. In the ESI,† these lines, which are not superimposed by other lines, are marked with an asterisk. In contrast to the jet measurements, the spectra at room temperature are denser, with lines three times broader than those of the jet spectrum. Although in this case many lines overlap with neighboring lines, we were able to assign 1600 transitions of the room temperature spectrum with support from the results of the jet spectrum. Transitions with high J and K_a quantum numbers were particularly useful for determining the higher order centrifugal distortion constants.

As mentioned above, several lines of branches with high K_a quantum numbers are perturbed. The current data set is not sufficient for a robust treatment of the observed perturbations, but a second-order DFT perturbation analysis shows that Coriolis type interactions of the ring-breathing vibrational mode with several other modes are likely. This is also illustrated by Fig. 4, which shows the orientation of the vibrational dipole (∂μ/∂Q) of the ν₁₂ mode with respect to the molecular axis system. For simplicity, we do not show the displacement vectors associated with the ring-breathing mode, which have vibrational components along all three molecular axes. In contrast, Fermi and Darling–Dennison type resonances are almost negligible with respect to the ν₁₂ mode. Therefore, our preliminary conclusion regarding the observed perturbation is that the observed line shifts in high K_a branches are due to Coriolis coupling and not to Fermi or Darling–Dennison interactions. In particular, the observed splitting of some lines into well separated E and A components could indicate a Coriolis interaction between the ring breathing and the low-energy ν₂₄ torsional motion of the methyl group, a finding that needs to be discussed on the basis of extended measurements.

Fig. 4 Side view of propylene oxide, in which the plane of the oxirane ring (blue) is almost perpendicular to the plane of the figure. The vibrational dipole moment (∂μ/∂Q) of the ν₁₂ ring breathing mode is tilted with respect to the plane of the ring and has three non-zero components with respect to the molecular axis system of Cartesian coordinates X(a), Y(b) and Z(c). The methyl group's rotational axis is orientated outwards from the ring plane.

5.2 Spectroscopic implications

Low J and K_a rovibrational infrared transitions of propylene oxide may be of particular interest for future studies of molecular chirality. As Peterson et al. have shown, the enantiomeric excess of chiral molecules which have three non-zero permanent electric dipole components can be determined from three linearly polarized microwave signals of mutually perpendicular orientation.³⁷ This technique, known as microwave three-wave mixing (M3WM), is in principle not limited to the microwave range but can also be applied to rovibrational transitions using infrared radiation, as has been shown theoretically.³⁸ The availability of narrow-band tunable infrared radiation sources, in particular continuous-wave quantum cascade lasers (cw-QCL) and optical parametric oscillators (OPO) with line widths noticeably below the Doppler width of the rovibrational transitions, provide experimental access to 3 WM techniques for the mid-infrared (5–12 μm) range. Propylene oxide is a well-suited candidate molecule for this purpose, for which, in addition to the pure rotational transitions, high-resolution mid-infrared data are now available for the first time. There is a notable lack of high-resolution infrared data for chiral molecules, which can be addressed by new high-resolution spectrometers. Alternatively to the mentioned narrow-band radiation sources (QCLs and OPOs), modern Fourier transform spectrometers using synchrotron radiation, dual frequency combs as well as classical globars as radiation sources are promising instruments to improve the data situation.^39–46 Propylene oxide, the first chiral molecule that has been detected in space by microwave spectroscopy, could potentially also be detected in warm regions of star formation and planetary environments with infrared telescopes. In general, there is a growing interest in the astrochemistry of prebiotic molecules in interstellar clouds, protostellar disks and exoplanetary environments, which is strongly promoted by the current mission of the James Webb Space Telescope (JWST).^47,48 Although the spectral resolution of the JWST is too low to resolve the dense IR spectrum of propylene oxide, the high-resolution data and molecular parameters presented here will enable to model the spectral envelopes at various astrophysically relevant pressure and temperature conditions.

A pronounced homochirality is observed on earth and there is a debate whether this homochirality is already anticipated in low enantiomeric excesses in interstellar environments. In this context, it is interesting to note that different isomers of C₃H₆O were investigated in a quantum chemical study by Elango et al.¹³ It was shown that the C₃H₆O isomers propanal and allyl alcohol enable the chirality switching of propylene oxide between left- and right-handed enantiomers. Propylene oxide has also been discussed as a possible candidate for the detection of chiral asymmetry in the interstellar medium via the circular polarization contribution of microwave emission lines.⁴⁹ Although the authors concluded that the asymmetry effect is too small to be detected with current telescopes, it underlines the role of propylene oxide as a relevant object for chirality studies and the need for high-resolution data.

Author contributions

K. Vávra: measurement, analysis, software, writing and formatting. E. Döring: measurement, data curation, software. J. Jakob: measurement, data curation, software. F. Peterß and M. Kaufmann: contribution to experimental setups. P. Stahl: quantum chemical calculations. T. Giesen and G.W. Fuchs: planning and supervising of project, as well as working on manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) by the project 328961117 (SFB 1319 ELCH) and project 326572190 (FU 715/2-1).

References

1. V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, J. Chem. Phys., 2014, 141, 34107.
2. S. Luber, M. Iannuzzi and J. Hutter, J. Chem. Phys., 2014, 141, 094503.
3. M. C. Tam, N. J. Russ and T. D. Crawford, J. Chem. Phys., 2004, 121, 3550–3557.
4. M. Hodecker, M. Biczysko, A. Dreuw and V. Barone, J. Chem. Theory Comput., 2016, 12, 2820–2833.
5. M. Tia, M. Pitzer, G. Kastirke, J. Gatzke, H.-K. Kim, F. Trinter, J. Rist, A. Hartung, D. Trabert, J. Siebert, K. Henrichs, J. Becht, S. Zeller, H. Gassert, F. Wiegandt, R. Wallauer, A. Kuhlins, C. Schober, T. Bauer, N. Wechselberger, P. Burzynski, J. Neff, M. Weller, D. Metz, M. Kircher, M. Waitz, J. B. Williams, L. P. H. Schmidt, A. D. Müller, A. Knie, A. Hans, L. B. Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, R. Dörner, T. Jahnke, P. V. Demekhin and M. Schöffler, J. Phys. Chem. Lett., 2017, 8, 2780–2786.
6. K. Fehre, N. M. Novikovskiy, S. Grundmann, G. Kastirke, S. Eckart, F. Trinter, J. Rist, A. Hartung, D. Trabert, C. Janke, G. Nalin, M. Pitzer, S. Zeller, F. Wiegandt, M. Weller, M. Kircher, M. Hofmann, L. P. H. Schmidt, A. Knie, A. Hans, L. B. Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, J. B. Williams, T. Jahnke, R. Dörner, M. S. Schöffler and P. V. Demekhin, Phys. Rev. Lett., 2021, 127, 103201.
7. M. M. R. Fanood, I. Powis and M. H. M. Janssen, J. Phys. Chem. A, 2014, 118, 11541–11546.
8. T. Müller, K. B. Wiberg and P. H. Vaccaro, J. Phys. Chem. A, 2000, 104, 5959–5968.
9. J. Sebestik and P. Bour, J. Phys. Chem. Lett., 2011, 2, 498–502.
10. K. Fehre, N. M. Novikovskiy, S. Grundmann, G. Kastirke, S. Eckart, F. Trinter, J. Rist, A. Hartung, D. Trabert, C. Janke, M. Pitzer, S. Zeller, F. Wiegandt, M. Weller, M. Kircher, G. Nalin, M. Hofmann, L. P. H. Schmidt, A. Knie, A. Hans, L. B. Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, J. B. Williams, T. Jahnke, R. Dörner, P. V. Demekhin and M. S. Schöffler, Phys. Chem. Chem. Phys., 2022, 24, 26458–26465.
11. A. Yachmenev, J. Onvlee, E. Zak, A. Owens and J. Küpper, Phys. Rev. Lett., 2019, 123, 243202.
12. D. Baykusheva and H. J. Wörner, Phys. Rev. X, 2018, 8, 31060.
13. M. Elango, G. S. Maciel, F. Palazzetti, A. Lombardi and V. Aquilanti, J. Phys. Chem. A, 2010, 114, 9864–9874.
14. J. Kongsted, T. B. Pedersen, L. Jensen, A. E. Hansen and K. V. Mikkelsen, J. Am. Chem. Soc., 2006, 128, 976–982.
15. T. Crawford and K. Ruud, ChemPhysChem, 2011, 12, 3442–3448.
16. J. D. Swalen and D. R. Herschbach, J. Chem. Phys., 1957, 27, 100–108.
17. D. R. Herschbach and J. D. Swalen, J. Chem. Phys., 1958, 29, 761–776.
18. R. A. Creswell and R. H. Schwendeman, J. Mol. Spectrosc., 1977, 64, 295–301.
19. M. Imachi and R. L. Kuczkowski, J. Mol. Struct., 1983, 100, 223–234.
20. B. A. McGuire, P. B. Carroll, R. A. Loomis, I. A. Finneran, P. R. Jewell, A. J. Remijan and G. A. Blake, Science, 2016, 352, 1449–1452.
21. D. Ankan, G. Prasanta and C. S. K, J. Astrophys. Astron., 2019, 628, A73.
22. E. Bodo, G. Bovolenta, C. Simha and R. Spezia, Theor. Chem. Acc., 2019, 138, 97.
23. A. J. Mesko, L. Zou, P. B. Carroll and S. L. W. Weaver, J. Mol. Spectrosc., 2017, 335, 49–53.
24. P. Stahl, B. E. Arenas, O. Zingsheim, M. Schnell, L. Margulès, R. A. Motiyenko, G. W. Fuchs and T. F. Giesen, J. Mol. Spectrosc., 2021, 378, 111445.
25. P. Stahl, D. Kargin, R. Pietschnig, T. F. Giesen and G. W. Fuchs, J. Mol. Spectrosc., 2021, 380, 111498.
26. F. X. Sunahori, Z. Su, C. Kang and Y. Xu, Chem. Phys. Lett., 2010, 494, 14–20.
27. J. P. Gardner, J. C. Mather, M. Clampin, R. Doyon, M. A. Greenhouse, H. B. Hammel, J. B. Hutchings, P. Jakobsen, S. J. Lilly, K. S. Long, J. I. Lunine, M. J. Mccaughrean, M. Mountain, J. Nella, G. H. Rieke, M. J. Rieke, H.-W. Rix, E. P. Smith, G. Sonneborn, M. Stiavelli, H. S. Stockman, R. A. Windhorst and G. S. Wright, Space Sci. Rev., 2006, 123, 485–606.
28. J. H. Lacy, M. J. Richter, T. K. Greathouse, D. T. Jaffe and Q. Zhu, Astron. Soc. Pac., 2002, 114, 153.
29. D. Witsch, E. Döring, A. A. Breier, J. Gauss, T. F. Giesen and G. W. Fuchs, J. Phys. Chem. A, 2023, 127, 3824–3831.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. M. Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian Inc., 2016.
31. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377.
32. K. Vávra, K. Luková, P. Kania, J. Koucký and S. Urban, J. Mol. Struct., 2020, 1215, 128181.
33. K. Vávra, L. Kolesniková, A. Belloche, R. T. Garrod, J. Koucký, T. Uhlíková, K. Luková, J. C. Guillemin, P. Kania, H. S. P. Müller, K. M. Menten and S. Urban, J. Astrophys. Astron., 2022, 666, A50.
34. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242.
35. Z. Kisiel, in Spectroscopy from Space, ed. J. Demaison, K. Sarka and E. A. Cohen, Springer, Netherlands, Dordrecht, 2001, pp. 91–106.
36. A. M. Andrews, M. Y. Tretyakov, B. H. Pate, G. T. Fraser and I. Kleiner, Mol. Phys., 1995, 84, 201–210.
37. D. Patterson, M. Schnell and J. Doyle, Nature, 2013, 497, 475–477.
38. M. Leibscher, T. F. Giesen and C. P. Koch, J. Chem. Phys., 2019, 151, 014105.
39. B. Darquié, C. Stoeffler, A. Shelkovnikov, C. Daussy, A. Amy-Klein, C. Chardonnet, S. Zrig, L. Guy, J. Crassous, P. Soulard and P. Asselin, Chirality, 2010, 22, 870–884.
40. S. Albert, I. Bolotova, Z. Chen, C. Fábri, M. Quack, G. Seyfang and D. Zindel, Phys. Chem. Chem. Phys., 2017, 19, 11738–11743.
41. S. Albert, K. Keppler, V. Boudon, P. Lerch and M. Quack, J. Mol. Spectrosc., 2017, 337, 105–123.
42. A. Zehnacker and M. Suhm, Angew. Chem., Int. Ed., 2008, 47, 6970–6992.
43. K. Sung, G. Toon, B. Drouin, A. Mantz and M. Smith, J. Quant. Spectrosc. Radiat. Transfer, 2018, 213, 119–132.
44. B. Spaun, P. B. Changala, D. Patterson, B. J. Bjork, O. H. Heckl, J. M. Doyle and J. Ye, Nature, 2016, 533, 517–520.
45. M. Lepère, O. Browet, J. Clément, B. Vispoel, P. Allmendinger, J. Hayden, F. Eigenmann, A. Hugi and M. Mangold, J. Quant. Spectrosc. Radiat. Transfer, 2022, 287, 108239.
46. J. A. Agner, S. Albert, P. Allmendinger, U. Hollenstein, A. Hugi, P. Jouy, K. Keppler, M. Mangold, F. Merkt and M. Quack, Mol. Phys., 2022, 120, e2094297.
47. N. Madhusudhan, Annu. Rev. Astron. Astrophys., 2019, 57, 617–663.
48. J. Kalirai, Contemp. Phys., 2018, 59, 251–290.
49. B. Lankhaar, Astron. Astrophys., 2022, 666, A126.

---

Footnote

† Electronic supplementary information (ESI) available: The output file from SPFIT reformatted by the PIFORM program is provided in the supplementary materials (S1). See DOI: https://doi.org/10.1039/d4cp02943g

---