Open Access Article
Open Access ArticleFormation of complex organics by covalent and non-covalent interactions of the sequential reactions of 1–4 acrylonitrile molecules with the benzonitrile radical cation†
Paige
Sutton
 ,
John
Saunier
,
John
Saunier
 ,
Kyle A.
Mason
,
Kyle A.
Mason
 ,
Adam C.
Pearcy
,
Adam C.
Pearcy
 ,
Ka Un
Lao
,
Ka Un
Lao
 and
M.
Samy El-Shall
and
M.
Samy El-Shall
 *
*
Department of Chemistry, Virginia Commonwealth University, Richmond, VA 23284-2006, USA. E-mail: elshalls2@vcu.edu
First published on 21st November 2024
Abstract
Benzonitrile molecules are present in ionizing environments including interstellar clouds and solar nebulae, where their ions can form adducts with neutral molecules such as acrylonitrile leading to the formation of a variety of nitrogen-containing complex organics. Herein, we report on the formation of complex organics by the sequential reactions of 1–4 acrylonitrile (C3NH3) molecules with the benzonitrile radical cation (C7NH5+˙). The results reveal the formation of the covalently bonded N-acrylonitrile-benzonitrile radical cation (C10N2H8+˙) with a rate coefficient of 2.2 (±0.4) × 10−11 cm3 s−1 at 423 K and a calculated collision cross-section of 73.8 Å2 in good agreement with the measured cross-section of 70.7 Å2 of the C10N2H8+˙ adduct. Subsequent reversible association of 1–3 acrylonitrile molecules with the N-acrylonitrile-benzonitrile radical cation (C10N2H8+˙) at lower temperatures (250–200 K) results in the formation of the N-rich clusters (C10N2H8+˙)(C3NH3)1–3 which can be enhanced in the very cold cores of the interstellar medium (ISM) and could offer unique potential candidates for the substantial amount of nitrogen carriers detected in the emission spectra of the ISM. The observed N-acrylonitrile-benzonitrile covalent adduct and its associated acrylonitrile clusters could have significant implications in the formation of different types of complex organics in different regions of outer space. It is anticipated that the current results would have direct implications in the search for nitrogen-containing complex organics in space.
1 Introduction
The study of ion–molecule reactions and clustering offers a more detailed understanding of chemical reaction dynamics and thermodynamics and is of great importance in unravelling the mechanisms of key chemical and astrochemical processes such as the formation of complex organics in space.1–5 Because of the attractive interactions between charged and neutral species, ion–molecule reactions can provide efficient mechanisms for the formation of complex organics including polycyclic aromatic hydrocarbons (PAHs) and polycyclic aromatic nitrogen heterocyclics (PANHs) found in flames and combustion processes as well as in interstellar clouds and solar nebula.3–7The recent discovery of benzonitrile as the first aromatic molecule observed in the interstellar medium,8 and the subsequent detection of the PAHs 1- and 2-cyanonaphthalene in the cold molecular cloud Taurus molecular cloud 1 (TMC-1),9 have increased interest in the sequential reactions of small astrochemical relevant molecules with the benzonitrile radical cation since these reactions can act as potential precursors for the nitrogen-containing PAHs in space, thus providing a chemical link to the carriers of the unidentified infrared bands.10–14 Of particular interest are the interactions between the benzonitrile radical cation and other nitrogen-containing molecules such as acrylonitrile which can lead to the incorporation of a second nitrogen atom into a larger and more complex structure. Acrylonitrile is a small molecule bearing both a nitrogen atom and an olefin group. The molecule is found in a variety of astronomical environments in the ISM such as circumstellar envelopes and planetary atmospheres.15,16 The olefin group of acrylonitrile can greatly increase the possibility of a covalent interaction with the benzonitrile radical cation resulting in the addition of a second nitrogen atom to a larger ionized aromatic system. Herein, we report on the formation of a stable covalently-bonded adduct via the ion–molecule reaction between the benzonitrile radical cation and acrylonitrile resulting in linking of a second N-containing molecule to the N-atom of the benzonitrile structure. Subsequent reversible association of 1–3 acrylonitrile molecules onto the covalently-bonded adduct ion at low temperatures results in the formation of N-rich clusters which can offer unique potential candidates for the substantial amount of nitrogen carriers detected in the emission spectra of the ISM.17 The ability of a small molecule like acrylonitrile to form a covalent adduct with the benzonitrile radical cation is critical for the overall stability of large molecules and clusters forming complex organics in the interstellar medium. It is hoped that the present results would motivate the search for the benzonitrile-acrylonitrile covalent adduct as well as for a variety of its N-rich clusters in the cold-core TMC-1, which has long been known to possess a rich chemistry dominated by unsaturated molecules containing nitrile (R–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) groups.10–13
N) groups.10–13
2 Experimental and computational methods
The experiments were performed using the VCU mass-selected ion mobility system (MSIM) schematically illustrated in Fig. S1 (ESI†). Details of the instrument can be found in several publications18–20 and only a brief description of the experimental procedure is given here. The essential elements of the apparatus are jet and beam chambers coupled to an electron impact (EI) ionization source, a quadrupole mass filter, a drift cell, and a second quadrupole mass spectrometer. Benzonitrile radical cations (C6H5CN+˙) are formed by electron impact ionization (60 eV) of the neutral molecules generated using a supersonic beam expansion of 2.1 bar of ultra-high-pure helium seeded with 1–4% vapor of benzonitrile by passing the helium over liquid benzonitrile (99% purity, Sigma-Aldrich) and expansion through a pulsed supersonic nozzle (500 μm diameter) into a vacuum chamber maintained at a pressure of 10−6 mbar. The first quadrupole mass filter mass-selects the benzonitrile radical cations that are then injected into the drift cell in 30–50 μs pulses. The drift cell contains a vapor mixture of acrylonitrile obtained from liquid acrylonitrile (99% purity, Sigma-Aldrich) and a helium buffer gas. The liquid sample of acrylonitrile contains 35–45 ppm monomethyl hydroquinone as inhibitor but mass spectrometric analysis of the vapor above the liquid sample did not show any detectable signal of the inhibitor, most likely due to the low vapor pressure of the inhibitor. The injection energy (16–19 eV, laboratory frame) used in the experiments is slightly greater than the minimum energy required to introduce the benzonitrile ions into the drift cell against the outflow of helium/acrylonitrile escaping through the drift cell entrance but low enough to not cause fragmentation of the molecular ions. A majority of the ion thermalization takes place outside the cell entrance by collisions with helium atoms and acrylonitrile molecules escaping the cell entrance orifice. At a cell pressure of 1.4 Torr, the benzonitrile radical cation encounters nearly 104 collisions with helium atoms within the typical 1 ms residence time inside the cell resulting in full thermalization of the ions. Injected ions and products are separated via a second quadrupole mass filter that is coaxially positioned after the drift cell. After passing through the second quadrupole, an off-axis collision dynode and electron multiplier system detects the selected ions. Arrival time distributions (ATDs) of the mass-selected ions exiting the cell are measured by a multichannel scalar that is simultaneously triggered by the ion gate pulse.Density functional theory (DFT) calculations of the lowest energy structures of benzonitrile-acrylonitrile covalent adduct ion [(BN-AN)+˙, C10N2H8+˙] and the subsequent associated structures [(BN-AN)+˙(AN)n] with n = 1–3, were performed at the M06-2X/6-311++G** level using the Gaussian 16 program suite.21 Zero-point vibrational energies were obtained through frequency calculations on all optimized structures, confirming the absence of imaginary frequencies. This verification ensures that each structure is not at a saddle point but rather a true minimum. These structures were used to obtain average collision cross sections in helium using the Lennard-Jones scaled projection approximation (LJ-PA) method within the Sigma program for the covalent structures,22 and the exact hard sphere (EHS) model within the Mobcal program for the non-covalent structures.23 For the potential energy surface (PES) calculations, initial transition state structures were reliably and automatically generated using the freezing-string method.24,25 These structures were then optimized as transition states and subsequently confirmed via frequency calculations. All transition state calculations were performed at the M06-2X/6-311++G** level of theory using the developed version of Q-Chem.26
3 Results and discussion
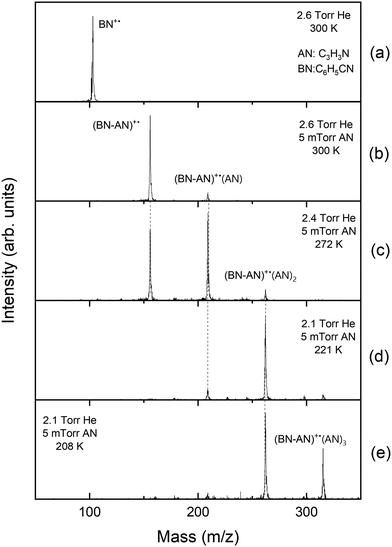
Fig. 1 displays the mass spectra obtained following the injection of the benzonitrile radical cation (BN+˙, C6H5CN, m/z 103) into the drift cell containing 2.6–3.3 Torr helium and 5 mTorr of acrylonitrile (AN, C2H3CN, m/z 53) at different temperatures. As shown in Fig. 1(a), in the presence of pure helium, only the molecular benzonitrile ion is observed with no fragmentation confirming the absence of excess ionization and injection energies which could lead to the fragmentation of the ion. At a very low pressure of C2H3CN (0.005 Torr), the adduct [(BN-AN)+˙, C10N2H8+˙, m/z 156] and the associated AN product [(BN-AN)+˙(AN), C13N3H11+˙, m/z 209] are readily formed at room temperature as shown in Fig. 1(b). Increasing the temperature of the drift cell results in the disappearance of the associated product [(BN-AN)+˙(AN)] and a small decrease in the ion intensity of the first adduct (BN-AN)+˙ accompanied with a corresponding increase in the intensity of the benzonitrile ion as shown in Fig. 1(c) and (d). However, at the highest temperature used (463 K), the adduct (BN-AN)+˙ still maintains most of the original ion intensity indicating that the adduct contain mostly covalent ions. As the temperature increases, the weakly bonded non-covalent ions dissociate by the loss of acrylonitrile molecules thus resulting in increasing the intensity of the benzonitrile ion. The ion intensity of the adduct (BN-AN)+˙ observed at 463 K (Fig. 1(d)) represents the covalently bonded ions that are thermally stable at this temperature.The arrival time distributions (ATDs) of the reactant (BN)+˙ and product (BN-AN)+˙ ions at 423.5 K shown in Fig. 2(a), are consistent with an irreversible reaction leading to the formation of covalently-bonded adduct ions. The formation of non-covalent cluster ions involves reversible association of neutral molecules into the parent ion which, under equilibrium conditions, typically results in identical ATDs of the reactant and product ions since they are coupled by reversible association–dissociation reactions as they travel across the drift cell.20,27,28 To measure the second order rate coefficient for the formation of the adduct [(BN-AN)+˙, C10N2H8+˙, m/z 156], the reactant benzonitrile ion (BN+˙, C7NH5+˙) is injected into the drift cell containing a very low pressure of acrylonitrile (AN), (0.005 Torr) in the presence of 2.3 Torr helium as a third body buffer gas at 423 K as shown in Fig. 2(b). A pseudo first-order rate constant is calculated from ln I/ΣI = −kt, where I is the integrated intensity of the ATD peak of the reactant ion, and ΣI is sum of the integrated intensities of the reactant and the product ion peaks, obtained from the areas of their ATD peaks, and t is the mean drift time taken as the center of the ATD peak of the reactant ion.18 The pseudo-first-order rate coefficient k1 is obtained from the slope of the plots of ln I/ΣI vs. t. The second-order rate constant k2 is then obtained from the equation k2 = k1/[N], where N is the number density of the acrylonitrile molecules in the drift cell (1–3 × 1014 molecules cm−3). The rate coefficients measured are reproduced at least three times, with an estimated error due to uncertainties in the neutral reactant partial pressure, drift cell temperature, fluctuations in ion signal and background noise.
The rate coefficient for the formation of the (BN-AN)+˙ adduct at 423 K is determined as 2.2 (±0.4) × 10−11 cm3 s−1, indicating a reaction efficiency (defined here as the ratio of the measured rate coefficient to the Langevin capture rate coefficient taken as 1.5 × 10−9 cm3 s−1) of 1.5% at 423 K for the formation of the covalent adduct. The measured rate coefficient at 423 K is similar to the rate coefficient (2.1 ± 0.4 × 10−11 cm3 s−1) recently measured for the reaction of acetylene with the benzonitrile radical cation which resulted in the formation of N-acetylene benzonitrile radical cation at 334.5 K.29 However, the measured rate coefficient for the acrylonitrile reaction at 423 K is lower than the rate coefficient of 6.2 (±0.3) × 10−11 cm3 s−1 recently reported by Rap et al. for the acetylene reaction with the benzonitrile radical cation at 150 K.14 The increased rate coefficient at the lower temperature could be attributed to the negative temperature dependence of ion–molecule reactions,1 and therefore, the rate of the reaction of acrylonitrile with the benzonitrile radical cation is expected to increase significantly at the very low temperatures of the ISM.17
The reaction efficiency of acrylonitrile with the benzonitrile radical cation at 423 K (1.5%) is significantly higher than the very low reaction efficiency of ≃0.0001 previously determined for the covalent addition of acetylene onto the benzene radical cation at 623 K.30 The efficiency of the acrylonitrile reaction with the benzonitrile radical cation is also higher than the efficiency of 0.001 measured for the acetylene reaction with the phenylacetylene radical cation at 302 K.18 The current results therefore, confirm the assumption that the barrier to the cation ring growth can be significantly reduced or overcome by the formation of N–C bonds.14,18,31,32
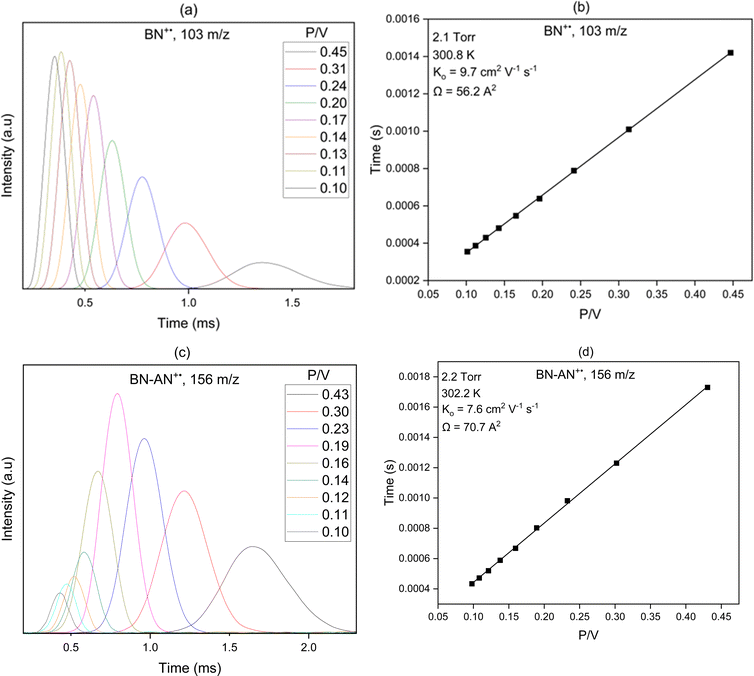
Structural information on gas phase ions can be obtained from mobility measurements, where the drift velocity of an ion is a function of its collision cross-section (Ω) with the buffer gas,19,33 which depends on the geometrical structure and shape of the ion. To identify the most plausible ion structure, theoretical calculations are performed on the geometry of several isomeric configurations, and the angle-averaged collision cross-sections are computed for the lowest energy isomers using the Lennard-Jones scaled projection approximation (LJ-PA) method for the covalent structures,22 and the exact hard spheres (EHS) model for the non-covalent structures.23 The theoretical Ω's are then compared to the experimentally measured values to identify the most likely structures.
The mobility K of an ion is defined by eqn (1) as:19,33
 | (1) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) d is the drift velocity and
d is the drift velocity and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) the field across the drift region. The reduced mobility K0 (scaled to the number density at standard temperature and pressure STP) is defined by eqn (2) as:
the field across the drift region. The reduced mobility K0 (scaled to the number density at standard temperature and pressure STP) is defined by eqn (2) as: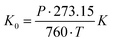 | (2) |
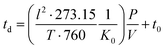 | (3) |
According to the kinetic theory of gases,33eqn (4) relates the mobility of an ion to the average collision cross-section (CCS) of the ion with the buffer gas according to:
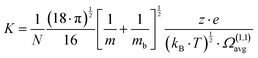 | (4) |
N is the buffer gas number density, m is the mass of the ion, mb is the mass of a buffer gas atom, z is the number of charges, e is the electron charge, kB is Boltzmann's constant and 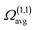 is the average collision integral (collision-cross section). The measured reduced mobility of the radical cations of benzonitrile and benzonitrile-acrylonitrile adduct (9.7 ± 0.3 cm2 V−1 s−1 and 7.6 ± 0.3 cm2 V−1 s−1, respectively) results in CCS values of 56.2 Å2 and 70.7 Å2, respectively at 301–302 K. The measured CCS (56.2 Å2) of the benzonitrile radical cation agrees very well (within 1%) with the CCS of 55.6 Å2 calculated using the Lennard-Jones scaled projection approximation (LJ-PA) method,22 and the DFT-M06-2X/6-311++G** optimized structure of the radical cation. To obtain structural information on the benzonitrile-acrylonitrile adduct (C10N2H8+˙), we compare the measured CCS with the calculated cross-sections for the lowest energy covalent and non-covalent structures of the C10N2H8+˙ ions that can be formed by the direct addition of acrylonitrile onto the benzonitrile radical cation without any H-shifts or rearrangements. Fig. 4 presents the structures of the four lowest energy ions (a), (b), (c), and (d) formed by the direct addition of acrylonitrile onto the benzonitrile cation, with geometries optimized at the M06-2X/6-311++G** level of theory.21 Notably, the lowest energy isomer (a) corresponds to the frustrated covalent adduct involving the formation of a N–C bond between the N atom of the nitrile group of the benzonitrile radical cation and CH2 group of acrylonitrile. The binding energy of this isomer (37.6 kcal mol−1) is clearly weaker than a typical N–C bond energy as a result of inefficient orbitals’ overlap between the N and the C atoms.34 However, the binding energy of the covalent adduct (a) is still significantly stronger than the non-covalent interactions represented by structures (b), (c) and (d). Structure (a) is used to obtain an average CCS using the LJ-PA method which results in a calculated Ω value of 73.8 Å2 as shown in Fig. 4(a).22 The calculated CCS of structure (a) is in good agreement with the measured CCS (70.7 Å2) of the benzonitrile-acrylonitrile adduct (C10N2H8+˙) as shown in Fig. 3(d).
is the average collision integral (collision-cross section). The measured reduced mobility of the radical cations of benzonitrile and benzonitrile-acrylonitrile adduct (9.7 ± 0.3 cm2 V−1 s−1 and 7.6 ± 0.3 cm2 V−1 s−1, respectively) results in CCS values of 56.2 Å2 and 70.7 Å2, respectively at 301–302 K. The measured CCS (56.2 Å2) of the benzonitrile radical cation agrees very well (within 1%) with the CCS of 55.6 Å2 calculated using the Lennard-Jones scaled projection approximation (LJ-PA) method,22 and the DFT-M06-2X/6-311++G** optimized structure of the radical cation. To obtain structural information on the benzonitrile-acrylonitrile adduct (C10N2H8+˙), we compare the measured CCS with the calculated cross-sections for the lowest energy covalent and non-covalent structures of the C10N2H8+˙ ions that can be formed by the direct addition of acrylonitrile onto the benzonitrile radical cation without any H-shifts or rearrangements. Fig. 4 presents the structures of the four lowest energy ions (a), (b), (c), and (d) formed by the direct addition of acrylonitrile onto the benzonitrile cation, with geometries optimized at the M06-2X/6-311++G** level of theory.21 Notably, the lowest energy isomer (a) corresponds to the frustrated covalent adduct involving the formation of a N–C bond between the N atom of the nitrile group of the benzonitrile radical cation and CH2 group of acrylonitrile. The binding energy of this isomer (37.6 kcal mol−1) is clearly weaker than a typical N–C bond energy as a result of inefficient orbitals’ overlap between the N and the C atoms.34 However, the binding energy of the covalent adduct (a) is still significantly stronger than the non-covalent interactions represented by structures (b), (c) and (d). Structure (a) is used to obtain an average CCS using the LJ-PA method which results in a calculated Ω value of 73.8 Å2 as shown in Fig. 4(a).22 The calculated CCS of structure (a) is in good agreement with the measured CCS (70.7 Å2) of the benzonitrile-acrylonitrile adduct (C10N2H8+˙) as shown in Fig. 3(d).
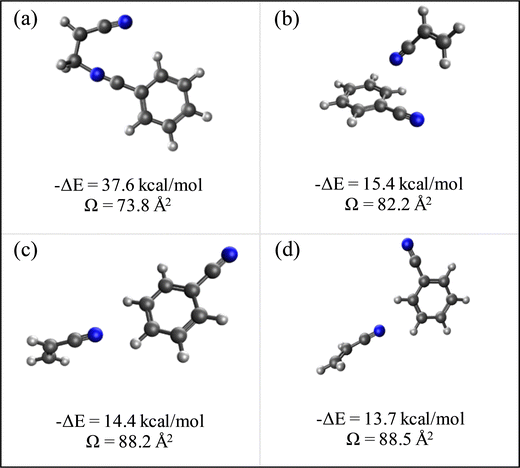 | ||
| Fig. 4 Lowest energy covalent (a) and non-covalent (b)–(d) structures of the benzonitrile-acrylonitrile adduct with their corresponding interaction energies (ΔE) and collision cross sections (Ω). | ||
The non-covalent structures are dominated by parallel and displaced extended orientations that maximize the electrostatic interactions between the N lone pair of acrylonitrile and the CHδ+ sites of the benzonitrile radical cation leading to the formation of unconventional CHδ+⋯N ionic hydrogen bonds.35 The non-covalent structures (b), (c) and (d) in Fig. 4 are used to obtain average collision cross sections using the EHS model within the Mobcal program.23 It is clear that the calculated CCSs of 82.2 Å2, 88.2 Å2 and 88.5 Å2 corresponding to the non-covalent structures (b), (c) and (d), respectively are significantly larger (16%–24%) than the measured value of 70.7 Å2 for the benzonitrile-acrylonitrile adduct. This indicates that the non-covalent structures have no contributions to the measured CCS of the benzonitrile-acrylonitrile adduct. The covalent nature of the C10N2H8+˙ adduct confirmed by the measured CCS is also supported by the thermal stability of the adduct with no significant dissociation at temperatures as high as 463 K (Fig. 1(d)) and the irreversible reaction kinetics observed at 423 K (Fig. 2).
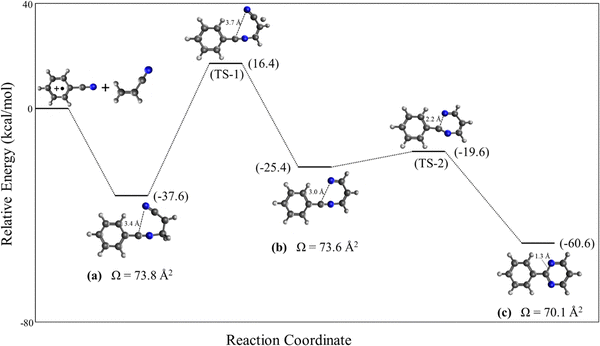
The benzonitrile-acrylonitrile covalent adduct C10N2H8+˙ (a) could undergo a 1,3 H-shift to form structure (b) which can efficiently cyclize in an exothermic transformation to form the bicyclic structure 2-phenylpyrimidine (c) as shown in Scheme 1 below.
To investigate the energetics of the transformation shown in Scheme 1, we calculated the reaction pathway's PES (potential energy surface) for the formation of the most stable bicyclic 2-phenylpyrimidine structure (c) from the covalently bound N-acrylonitrile-benzonitrile radical cation structure (a). Fig. 5 shows the reaction pathway starting from the exothermic formation of the covalently bound N-acrylonitrile-benzonitrile radical cation (a) (−37.6 kcal mol−1). This is followed by the first transition state (TS-1), with a barrier of 54.0 kcal mol−1 relative to (a), corresponding to a 1,3-hydrogen shift that yields intermediate (b), positioned 12.2 kcal mol−1 above (a) in energy. The second transition state (TS-2), with a barrier of 5.8 kcal mol−1 relative to (b), leads to a ring-closing reaction resulting in the most stable bicyclic structure 2-phenylpyrimidine (c) in an overall exothermic process of 60.6 kcal mol−1. Notably, the 2-phenylpyrimidine structure (c) exhibits a collision cross-section of 70.1 Å2, closely matching the experimental collision cross-section (70.7 Å2) of the benzonitrile-acrylonitrile adduct. However, the high energy barrier for the 1,3-hydrogen shift (54.0 kcal mol−1) compared to the binding energy of the N-acrylonitrile-benzonitrile adduct (a) (37.6 kcal mol−1) suggests that the formation of the intermediate (b) and its subsequent transformation to the 2-phenylpyrimidine structure (c) are highly unlikely under the current experimental conditions. It should be noted that the calculated CCS of the N-acrylonitrile-benzonitrile radical cation (a) (73.8 Å2) is in good agreement with the measured value of 70.7 Å2 within the typical margin of error of the mobility measurements of our system (5%).29
The reversible association of acrylonitrile molecules with the covalent adduct (BN-AN)+˙ is significantly enhanced at lower temperatures resulting in the formation of the cluster ion series (BN-AN)+˙(AN)n, with n = 1–3 as shown in mass spectra displayed in Fig. 6. The first associated product (BN-AN)+˙(AN) appears at 300 K (Fig. 6(b)) and becomes the major ion with the appearance of the second associated product (BN-AN)+˙(AN)2 at 272 K (Fig. 6(c)). At 221 K, the cluster distribution is dominated by the (BN-AN)+˙(AN)2 ion, and at 208 K both the (BN-AN)+˙(AN)2 and (BN-AN)+˙(AN)3 are the major species present. It is clear that at lower temperatures the cluster population shifts to higher clusters consistent with the population patterns typically observed for cluster ions present in equilibrium at different temperatures.20,27,28 Therefore, it should be clear that the (BN-AN)+˙ adduct is not absent at lower temperatures but is associated with several acrylonitrile molecules depending on the temperature. For example, at 208 K, the (BN-AN)+˙ adduct is associated with 2 and 3 acrylonitrile molecules and there is no free (BN-AN)+˙ adduct present at this temperature as shown in Fig. 6(e). Since the clustering association is reversible, higher order clusters dissociate at higher temperatures and thus the free (BN-AN)+˙ adduct can be observed as shown in Fig. 6(c) at 272 K.
The equilibria between the (BN-AN)+˙ adduct and AN molecules to form the cluster series (BN-AN)+˙(AN)n, with n = 1–3 can be verified by ensuring the following conditions:34 (i) the ATDs of the reactant and product ions are identical, indicating that the product and reactant ions are coupled in association–dissociation reactions faster than their movement through the cell as shown in Fig. S2 (ESI†), and (ii) a constant ratio of the abundance of the product to the reactant ions obtained during the residence time of the ions in the drift cell as shown in Fig. S2 (ESI†).
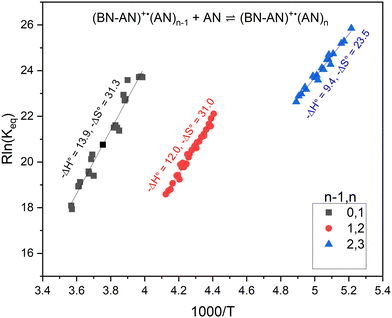
The association reactions of acrylonitrile (C3H3N) with the adduct ion C10N2H8+˙ is represented by eqn (5):
| C10H8N2+˙(C3H3N)n−1 + C3H3N ⇌ C10H8N2+˙(C3H3N)n | (5) |
When equilibrium is achieved, the equilibrium constant (Keq) is calculated from eqn (6):
| Keq = [I(C10H8N2+˙(C3H3N)n)/I(C10H8N2+˙(C3H3N)n−1) P(C3H3N)] | (6) |
| n − 1, n | −ΔH° (kcal mol−1) | −ΔS° (cal mol−1 K−1) | −ΔH°, (DFT calc) (kcal mol−1) |
|---|---|---|---|
| 0, 1 | 13.9 | 31.3 | 14.1 |
| 1, 2 | 12.0 | 31.0 | 13.1 |
| 2, 3 | 9.4 | 23.5 | 9.8 |
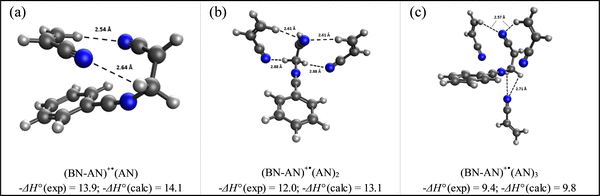
Fig. 8 displays the structures of the lowest energy non-covalent isomers of the (BN-AN)+˙(AN)n clusters with n = 1–3 along with the calculated bonding enthalpy (−ΔH°) values of 14.1, 13.1 and 9.8 kcal mol−1, respectively. These values are in very good agreement with the measured −ΔH° values of 13.9, 12.0 and 9.4 kcal mol−1, respectively, which indicates that the theory level used in the DFT calculations (M06-2X/6-311++G**) can describe the interactions between the benzonitrile radical cation and the acrylonitrile molecules accurately. The calculated structures clearly show the propensity of acrylonitrile to form a double H-bond dimer as a result of the interaction between the N atom lone pair of one molecule and the H atom of the CH2 group of the second molecule, thus leading to the formation of two unconventional N⋯HC hydrogen bonds.35 The measured entropy loss for the formation of the acrylonitrile double H-bond dimer (31.3 cal mol−1 K−1) is consistent with the relatively strong bonding and closely interacting acrylonitrile molecule with the (BN-AN)+˙ adduct. It is interesting that the formation of a second double H-bond dimer is observed in the structure of the (BN-AN)+˙(AN)2 cluster (Fig. 8(b)) which exhibits a similar −ΔS° value (31 cal mol−1 K−1) to the (BN-AN)+˙(AN) cluster. The inability of the (BN-AN)+˙(AN)3 cluster (Fig. 8(c)) to form a double H-bond dimer of acrylonitrile is clearly reflected in the significant drop in both the bonding enthalpy (9.4 kcal mol−1) and the entropy loss (23.5 cal mol−1 K−1).
4 Conclusions
In conclusion, benzonitrile molecules are present in ionizing environments including interstellar clouds and solar nebulae, where their ions can form adducts with neutral molecules such as acrylonitrile leading to the formation of a variety of N-rich complex organics. The present work establishes, for the first time, the formation of the covalently bonded N-acrylonitrile-benzonitrile radical cation (C10N2H8+˙) by the gas phase addition reaction of acrylonitrile on the benzonitrile radical cation. The rate coefficient of the reaction (2.2 (±0.4) × 10−11 cm3 s−1) indicates a reaction efficiency of 1.5% at 423 K for the formation of the covalent adduct. The direct addition of acrylonitrile onto the N atom of the benzonitrile cation results in the formation of an extended structure with a calculated collision cross-section of 73.8 Å2 in good agreement with the measured cross-section of 70.7 Å2 of the C10N2H8+˙ adduct. Potential energy surface calculations show that the energy barrier for the 1,3-hydrogen shift in the N-acrylonitrile-benzonitrile radical cation adduct is significantly larger than the binding energy of the adduct, and therefore the transformation to the 2-phenylpyrimidine structure is highly unlikely under the current thermal reaction conditions. At lower temperatures, subsequent additions of 1–3 acrylonitrile molecules onto the N-acrylonitrile-benzonitrile radical cation (C10N2H8+˙) results in the formation of N-rich clusters which can be enhanced in the cold cores of the ISM and could offer unique potential candidates for the substantial amount of nitrogen carriers detected in the emission spectra of the ISM. The observed N-acrylonitrile-benzonitrile covalently bound adduct and its associated acrylonitrile clusters could have significant implications to the formation of complex organics in different regions of outer space. The current results would have direct implications to the search for nitrogen-containing complex organics in space.Author contributions
M. S. E. conceived and designed the experiments. P. S., J. S., K. A. M., and A. C. P. performed the experiments and computations. K. U. L. performed the potential energy surface calculations. The results were interpreted and the manuscript was drafted and finalized by M. S. E., P. S. and J. S.Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank the National Science Foundation (CHE-1463989 and CHE-1900094) for the support of this work. High Performance Computing resources provided by the High-Performance Research Computing (HPRC) Core Facility at Virginia Commonwealth University (https://chipc.vcu.edu) were used for conducting the research reported in this work.Notes and references
- T. P. Snow and V. M. Bierbaum, Annu. Rev. Anal. Chem., 2008, 1, 229–259 CrossRef CAS PubMed.
- M. Frenklach, Phys. Chem. Chem. Phys., 2002, 4, 2028–2037 RSC.
- Y. M. Rhee, J. T. Lee, M. S. Gudipati, L. J. Allamandola and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5274–5278 CrossRef CAS PubMed.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- E. Herbst and E. F. van Dishoeck, Annu. Rev. Astron. Astrophys., 2009, 47, 427–480 CrossRef CAS.
- D. Ascenzi, J. Aysina, P. Tosi, A. Maranza and G. Tonachini, J. Chem. Phys., 2010, 133, 184308 CrossRef PubMed.
- M. L. Cable, S. M. Hoerst, R. Hodyss, P. M. Beauchamp, M. A. Smoth and P. A. Willis, Chem. Rev., 2011, 112, 1882 CrossRef PubMed.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS PubMed.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Science, 2021, 371, 1265–1269 CrossRef CAS PubMed.
- M. C. McCarthy and B. A. McGuire, J. Phys. Chem. A, 2021, 125, 3231–3243 CrossRef CAS PubMed.
- D. B. Rap, J. G. M. Schrauwen, A. N. Marimuthu, B. Redlich and S. Brünken, Nat. Astron, 2022, 6, 1059–1067 CrossRef.
- D. B. Rap, J. G. M. Schrauwen, B. Redlich and S. Brunken, Phys. Chem. Chem. Phys., 2024, 26, 7296–7307 RSC.
- R. A. Loomis, C. N. Shingledecker, G. Langston, B. A. McGuire, N. M. Dollhopf, A. M. Burkhardt, J. Corby, S. T. Booth, P. B. Carroll, B. Turner and A. J. Remijan, Mon. Not. R. Astron. Soc., 2016, 463, 4175–4183 CrossRef CAS.
- D. B. Rap, J. G. M. Schrauwen, A. N. Marimuthu, B. Redlich and S. Brünken, J. Am. Chem. Soc., 2024, 146, 23022–23033 CrossRef CAS PubMed.
- M. Agúndez, J. Cernicharo, J. R. Pardo, J. P. Fonfría Expósito, M. Guélin, E. D. Tenenbaum, L. M. Ziurys and A. J. Apponi, Astrophys. Space Sci., 2007, 313, 229–233 CrossRef.
- M. Y. Palmer, M. A. Cordiner, C. A. Nixon, S. B. Charnley, N. A. Teanby, Z. Kisiel, P. G. M. Irwin and M. J. Mumma, Sci. Adv., 2017, 3, e1700022 CrossRef PubMed.
- D. M. Hudgins, C. W. Bauschlicher, Jr. and L. J. Allamandola, Astrophys. J., 2005, 632, 316–332 CrossRef CAS.
- A. Soliman, I. K. Attah, A. M. Hamid and M. S. El-Shall, Int. J. Mass Spectrom., 2015, 377, 139–151 CrossRef CAS.
- K. A. Mason, A. C. Pearcy, A. M. Hamid and M. S. El-Shall, J. Chem. Phys., 2019, 150, 124303 CrossRef PubMed.
- K. A. Mason, A. C. Pearcy, Z. A. Christensen, I. K. Attah, M. Meot-Ner (Mautner) and M. S. El-Shall, J. Am. Chem. Soc., 2022, 144, 9684–9694 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- C. Bleiholder, T. Wyttenbach and M. T. Bowers, Int. J. Mass. Spetrom., 2011, 308, 1–10 CrossRef CAS.
- A. A. Shvartsburg and M. F. Jarrold, Chem. Phys. Lett., 1996, 261, 86–91 CrossRef CAS.
- A. Behn, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2011, 135, 224108 CrossRef PubMed.
- S. M. Sharada, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Theory Comput., 2012, 8(12), 5166 CrossRef PubMed.
- E. Epifanovsky, et al. , J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- A. R. Soliman, A. M. Hamid, S. A. Abrash and M. S. El-Shall, Chem. Phys. Lett., 2012, 523, 25–33 CrossRef CAS.
- S. P. Platt, I. K. Attah, M. S. El-Shall, R. Hilal, S. A. Elroby and S. G. Aziz, Phys. Chem. Chem. Phys., 2016, 18, 2580–2590 RSC.
- P. Sutton, J. Saunier, K. U. Lao and M. S. El-Shall, J. Phys. Chem. Lett., 2024, 15, 11067–11076 CrossRef CAS PubMed.
- P. O. Momoh, A.-R. Soliman, M. Meot-Ner, A. Ricca and M. S. El-Shall, J. Am. Chem. Soc., 2008, 130, 12848–12849 CrossRef CAS PubMed.
- A. R. Soliman, A. H. Hamid, I. Attah, P. Momoh and M. S. El-Shall, J. Am. Chem. Soc., 2013, 135, 155–166 CrossRef CAS PubMed.
- A. M. Hamid, P. P. Bera, T. J. Lee, S. G. Aziz, A. O. Alyoubi and M. S. El-Shall, J. Phys. Chem. Lett., 2014, 5, 3392–3398 CrossRef CAS PubMed.
- E. A. Mason and E. W. McDaniel, Transport Properties of Ions in Gases, New York, John Wiley & Sons, New York, 1988 Search PubMed.
- R. Peverati, S. P. Platt, I. K. Attah, S. Aziz, M. S. El-Shall and M. Head-Gordon, J. Am. Chem. Soc., 2017, 139, 11923–11932 CrossRef CAS PubMed.
- S. P. Platt, I. K. Attah, M. S. El-Shall, R. Hilal, S. A. Elroby and S. G. Aziz, Phys. Chem. Chem. Phys., 2016, 18, 2580–2590 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03594a |
| This journal is © the Owner Societies 2024 |