Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unveiling distinct bonding patterns in noble gas hydrides via interference energy analysis†
Lucas Araujo ab,
Marco A. C. Nascimento
ab,
Marco A. C. Nascimento a,
Thiago M. Cardozo
a,
Thiago M. Cardozo *a and
Felipe Fantuzzi
*a and
Felipe Fantuzzi *c
*c
aInstituto de Química, Universidade Federal do Rio de Janeiro, Av. Athos da Silveira Ramos, 149, CT, A-622, Cid. Univ., Rio de Janeiro, RJ 21941-909, Brazil. E-mail: thiago@iq.ufrj.br
bCenter for Theoretical Chemistry, Faculty of Chemistry and Biochemistry, Ruhr University Bochum, Universitätsstraße 150, 44801 Bochum, Germany
cSchool of Chemistry and Forensic Science, University of Kent, Park Wood Rd, Canterbury CT2 7NH, UK. E-mail: f.fantuzzi@kent.ac.uk
First published on 4th November 2024
Abstract
Despite their apparent simplicity, the helium hydride ion (HeH+) and its analogues with heavier noble gas (Ng) atoms present intriguing challenges due to their unusual electronic structures and distinct ground-state heterolytic bond dissociation profiles. In this work, we employ modern valence bond calculations and the interference energy analysis to investigate the nature of the chemical bond in NgH+ (Ng = He, Ne, Ar). Our findings reveal that the energy well formation in their ground-state potential energy curves is driven by a reduction in kinetic energy caused by quantum interference, identical to cases of homolytic bond dissociation. However, clear differences in bonding situation emerge: in HeH+ and ArH+, electron charge transfer leads to Ng+–H covalent bonds, while in NeH+, a preferred Ne + H+ valence bond structure suggests the formation of a dative bond. This study highlights the distinct bonding mechanisms within the NgH+ series, showcasing the interplay between quantum interference and quasi-classical effects in molecules featuring noble gases.
1. Introduction
Noble gas hydride ions (NgH+) belong to a fascinating class of molecular species in which traditionally inert noble gases are involved in chemical bonding. Though seemingly simple and featuring their lightest congener, HeH+, as isoelectronic to H2, NgH+ systems exhibit unique electronic structural features that have attracted the interest of various groups for almost 100 years.1 In contrast to typical diatomic molecules, which dissociate homolytically into neutral atoms, these hydrides are dissociated heterolytically into a neutral noble gas atom and a proton (Ng + H+), aligning with the Lewis acid–base model. This distinctive dissociation pattern suggests fundamental differences in their bonding compared to conventional covalent bonds. Despite this, the potential energy curve profiles associated with heterolytic dissociation in these systems remain largely unexplored, especially regarding the role of kinetic energy as the primary stabilising factor in bond formation and the systematic differences in bonding behaviour across the NgH+ series.Historically, HeH+ was first tentatively identified by Hogness and Lunn in 19251 through electron impact experiments in mixtures of helium and hydrogen. The observed mass-to-charge peak of 5, attributed to HeH+, was further confirmed by Bainbridge in 19332 and M’Ewen and Arnot in 1939.3 The latter study also revealed that its formation mechanism could be attributed to the reaction of H2+ with He. The discovery of HeH+ marked a pivotal moment in the exploration of noble gas chemistry, showcasing the potential for noble gases to form bonded systems under specific conditions.
The astrophysical significance of NgH+ systems adds another layer of interest to these species. HeH+ is regarded as the first molecule formed in the universe.4–10 Despite its early origins, HeH+ was only recently observed in interstellar space, specifically within the planetary nebula NGC 7027.7,9 It is known that HeH+ plays a crucial role in the formation of H2+ and subsequently H3+,5,6,11 which are fundamental molecules for the growth of chemical complexity in the universe. Meanwhile, although the detection of NeH+ and other neon-containing molecules remain elusive, ArH+ plays a prominent role in the interstellar chemistry, serving as an effective tracer of pure H2.12
HeH+ also received significant attention from the theoretical point of view since the early days. The first electronic structure investigations of the system were carried out by Glockler and Fuller in 1933.13 They considered two possible electronic structures for the system: the interaction (i) of an excited helium atom with a proton and (ii) of a helium ion with a hydrogen atom. In both cases, they found a stable minimum in the potential energy curve of HeH+, supporting the experimental evidence of its formation. Beach, in turn, used a variational method that combined the first two wave functions and included the interaction of a normal helium atom with a proton. This approach also yielded a stable molecule, with an improved treatment of the dissociation energy.
Theoretical investigations have also been conducted to explore the nature of the HeH+ chemical bond. Beach,14 for example, stated that two-thirds of the stabilisation of HeH+ comes from the formation of a He–H covalent bond, while the remaining part is due to the polarisation of the helium atom. This conclusion was independently supported by Coulson and Duncanson15 using both molecular orbital theory and classical valence bond (VB) methods. Notice that, to form a covalent bond, charge transfer from helium to the proton must occur. The covalent character of the HeH+ bond is further supported by studies such as those by Chandra and Sebastian in 197616 and, more recently, by Hendzel, Fidrysiak, and Spałek in 2022.17 In turn, Butscher and Schmidtke18 employed a self-consistent-field (SCF) calculation with near Hartree–Fock (HF) quality19 to investigate the roles of promotion, charge transfer, and quantum interference in HeH+. Similar investigations have not been yet conducted for its heavier congeners.
So far, modern valence bond (VB) wave functions, which are particularly well-suited to depict bonding effects and covalent character, have not yet been applied to NgH+ systems. The absence of a systematic study on the NgH+ series has left unexplained the observed variations in stability. VB methods provide a robust qualitative framework for understanding chemical bonds, offering both a physically accurate description and a clear basis for chemically intuitive reasoning.
Among the various approaches in the literature for investigating the nature of chemical bonds, Ruedenberg's density partitioning stands out as one of the most chemically intuitive and physically consistent methods.20–23 In this scheme, the electron density is separated into quasi-classical and interference contributions, with bond formation driven by the interference of one-electron states, which lowers the kinetic energy through inter-atomic electron delocalisation.21,22,24 Ruedenberg and co-workers demonstrated that near-equilibrium total, potential, and kinetic energy components arise primarily from intra-atomic orbital contractions, seen as side effects rather than driving forces of bond formation.25 These works underscore the central role of quantum interference in shaping chemical structures. Numerous studies have shown that covalent bond formation is driven by the quantum mechanical attenuation of kinetic energy due to inter-atomic electron delocalisation. This principle is general for most chemical bonds,26 including main-group22,27–31 and transition metal32 diatomics, alkenes and olefins,33–36 aromatic systems37 and one-electron bonds.32,38
The goal of this work is to describe the nature of the chemical bond in NgH+ (Ng = He, Ne, Ar) using modern VB wave functions, particularly the spin-coupled generalised valence bond (SCGVB)39 approach as implemented in the VB2000 program package,40 and the generalised product function energy partitioning (GPF-EP)41,42 method. We analyse how these bonds vary during the heterolytic dissociation of the ground state of these molecules and investigate whether the premise that quantum interference dictates the formation of chemical bonds through a reduction in interference kinetic energy—the part of kinetic energy associated with the interference effect—holds true even for such exotic species.
2. Computational methods
2.1. The GPF-EP approach
A concise overview of the GPF-EP method is provided, with additional details available elsewhere.41,42 Briefly, the GPF-EP approach applies Ruedenberg's partitioning scheme20 to a generalised product function (GPF),43 which offers an approximated solution to the many-electron problem. In a system comprising N electrons, these electrons are categorised and separated into groups, each exhibiting an average dependence akin to the SCF equations of the HF method. The GPF wave function is defined as follows:
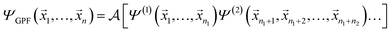 | (1) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i represents the spatial and spin coordinates of the i-th electron. The superscripts (1), (2), …, (N) denote the anti-symmetrised wave functions of the electron groups with n1, n2, …, nN electrons. The anti-symmetrising operator
i represents the spatial and spin coordinates of the i-th electron. The superscripts (1), (2), …, (N) denote the anti-symmetrised wave functions of the electron groups with n1, n2, …, nN electrons. The anti-symmetrising operator 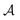 involves permutations of one electron from each group. Each group is strongly orthogonal to the others and can be described using methods such as HF, classical VB, SCGVB, or complete active space valence bond (CASVB).44
involves permutations of one electron from each group. Each group is strongly orthogonal to the others and can be described using methods such as HF, classical VB, SCGVB, or complete active space valence bond (CASVB).44
The GPF-EP method uses a GPF to express first and second-order reduced density matrices as reference (quasi-classical) and interference densities. For a single group, the quasi-classical and interference densities are defined as follows:
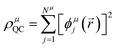 | (2) |
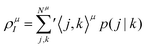 | (3) |
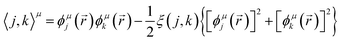 | (4) |
| E[TOT] = E[REF] + E[X] + E[I] + E[II] | (5) |
To accurately describe all possible spin couplings and resonance structures involved in the bonding of the NgH+ systems, we described the two valence electrons with a SCGVB group consisting of two electrons and three orbitals. This approach is based on the spin-coupled theory for N electrons in M orbitals developed by Karadakov and co-authors.45 The SC(N,M), or SCGVB(N,M), as recently recommended by the VB community, generalises the SCGVB function for varying numbers of orbitals and active space sizes. In our study, the two electrons are distributed over three orbitals, leading therefore to a SCGVB(2,3) group function and allowing for three distinct spin structures (see Fig. 1C for further details). An adaptation of the GPF-EP equations to accommodate SCGVB(N,M) wave functions was developed by de Sousa and Nascimento.46
The SCGVB orbitals are simultaneously optimised with the coefficients during the valence bond SCF (VBSCF)47,48 procedure. Since the VB structures are usually non-orthogonal, their weights are evaluated by the Chirgwin–Coulson coefficients,49 that can be calculated as:
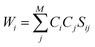 | (6) |
2.2. Computational details
Geometry optimisations, Hessian calculations and potential energy curves (PECs) for NgH+ (Ng = He, Ne, Ar) were obtained using ORCA 4.250 at the coupled-cluster CCSD(T)/aug-cc-pVTZ level considering the frozen core approximation.51–54 ChelpG (charges from electrostatic potentials using a grid-based method) charges55 were obtained from the orbital-optimised coupled-cluster doubles (OOCCD) method based on natural orbitals, which closely resembles the fully-relaxed CCSD density.56,57 The associated density matrices were generated using ORCA and processed with the Multiwfn 3.8 software.58 Spin-coupled generalised valence bond (SCGVB) calculations were done with aug-cc-pVTZ basis sets and performed using the VB2000 software as implemented in GAMESS (version September 30, 2022 R2).59 These computations were carried out on the NgH+ optimised geometries and their corresponding PECs to elucidate their chemical structures. For HeH+, the two electrons were treated using a SCGVB group with three orbitals. In contrast, for NeH+ and ArH+, the two valence electrons directly involved in the bonding were treated in a SCGVB group with three orbitals, while the remaining valence electrons, along with the core electrons, were placed in an HF group. This methodology is consistent with the approach we used in our previous work on Ng32+ systems.60 PECs were conducted at the SCGVB(2,3)/aug-cc-pVTZ level, continuously monitoring the Chirgwin–Coulson coefficients49 throughout the entire process. The interference energy analysis (IEA)42 of the distinct NgH+ systems was obtained by applying the GPF-EP method to the SCGVB(2,3)/aug-cc-pVTZ calculations throughout the PECs.3. Results and discussion
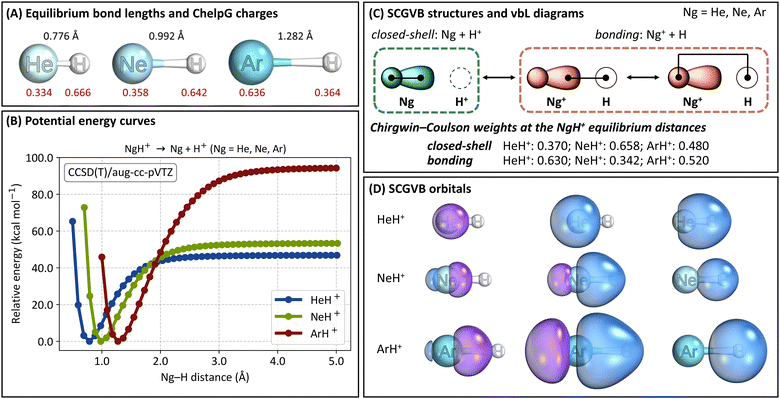
We begin by discussing the optimised structures, ChelpG charges, and dissociation energies of the NgH+ systems (Ng = He, Ne, Ar) obtained at the CCSD(T)/aug-cc-pVTZ level, as shown in Fig. 1A and B. Additional details are given in Tables S1 and S2 in the ESI.† For HeH+, we found an optimised bond distance of 0.776 Å. This value is in excellent agreement with the reference value of 1.463283 a.u. (0.774336 Å) reported by Pachucki, who used explicitly correlated asymptotic (ECA) functions with analytic formulas for two-centre two-electron systems.61 Our value is also consistent with CCSD calculations by Chołuj, Lipkowski, and Bartkowiak,62 who recently demonstrated in their basis-set dependence analysis that the aug-cc-pVTZ basis set yields errors well below 1% for HeH+. For NeH+, our optimised bond length is 0.992 Å, which is slightly longer than those calculated by Peyerimhoff at the near HF limit (1.83 a.u.; 0.968 Å)19 and by Pendergast, Heck, and Hayes at the CCSD(T) level (1.87 a.u.; 0.990 Å).63 Finally, for ArH+, our computed bond length of 1.282 Å is less than 1% different from the experimental value listed in the NIST Chemistry WebBook database (1.292 Å).64 These findings confirm the accuracy and reliability of our computational approach in predicting bond lengths for NgH+.Regarding the ChelpG charges, we observe that the charges on the Ng atom range from 0.334 to 0.636 as we move down the periodic table, from He to Ar. These values align with expectations: as the atomic volume increases, the ionisation potential decreases, and the polarizability increases, leading to a higher positive charge on the Ng atom.65
Next, from the potential energy curves shown in Fig. 1B, we observe that the three systems possess well-defined energy minima. The dissociation energies (without zero-point-energy correction, ZPE) at the CCSD(T)/aug-cc-pVTZ level of theory are 46.9 kcal mol−1 for HeH+, 53.4 kcal mol−1 for NeH+, and 94.7 kcal mol−1 for ArH+. Similar values were obtained at the SCGVB(2,3)/aug-cc-pVTZ level, with dissociation energies of 51.6 kcal mol−1 for HeH+, 56.6 kcal mol−1 for NeH+, and 96.8 kcal mol−1 for ArH+. Our values are also in good agreement with the literature. For example, Peyerimhoff19 reported dissociation energy values of 40.1 kcal mol−1 and 46.8 kcal mol−1 for HeH+ and NeH+, respectively, while Alekseyev, Liebermann and Buenker66 computed a value of 98.9 kcal mol−1 for ArH+. The calculated proton affinities at 0 K, including ZPE corrections at the CCSD(T)/aug-cc-pVTZ level, are 42.3 kcal mol−1 for HeH+, 49.2 kcal mol−1 for NeH+ and 90.8 kcal mol−1 for ArH+, all in excellent agreement with both theoretical and experimental reference values.67
The dissociation energies increase from HeH+ to ArH+, following the expected inverted trend compared to the ionisation potentials of these noble gases, which decrease from He to Ar. Furthermore, the fact that the dissociation energy, bond length, ionisation potential, and ChelpG charges of NeH+ are not that different from those of HeH+ suggests a reduced stability of Ne-containing molecules. This observation aligns not only with our previous findings60 but also with additional studies by others.65,68–70
In Fig. 1C, we present the three SCGVB structures considered in our wave functions, along with their corresponding valence-bond-Lewis (vbL) diagrams, as termed by Kalemos and Mavridis,71 or GVB diagrams, following Goddard's nomenclature.72 These structures are categorised into two distinct contributions. The closed-shell structure features the two one-electron orbitals of the Ng atoms being singly occupied. This structure involves only the internal coupling of the two ns-like electrons in He (and, analogously, the two npz-like electrons in Ne and Ar) and is the configuration that becomes dominant at larger interatomic distances in all NgH+ systems investigated herein.
The other two structures represent the inter-atomic electron coupling when a charge transfer from Ng to H+ is considered, therefore leading to the Ng+ + H configuration. The only difference between these two structures is that one involves a more diffuse and polarised orbital of the noble gas in the singlet coupling, while the other uses a more contracted orbital. It is worth noting that in SCGVB wave functions, valence lone pairs are typically represented by a pair of self-consistently optimised one-electron orbitals, one more diffuse than the other. This is precisely the description obtained in our case. The contributions of these two structures are considered collectively and are represented by the bonding representation in Fig. 1C.
Taking the three structures into consideration, HeH+ at equilibrium distances, for example, is described by:
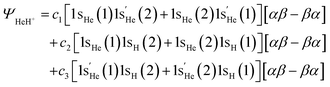 | (7) |
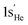 highlights that this one-electron orbital is different than 1sHe. Here, α and β represent the electron spins, with [αβ–βα] being the perfect pairing spin eigenfunction.
highlights that this one-electron orbital is different than 1sHe. Here, α and β represent the electron spins, with [αβ–βα] being the perfect pairing spin eigenfunction.
Fig. 1C also shows the Chirgwin–Coulson coefficients of the closed-shell and the bonding representations of the NgH+ systems at their corresponding equilibrium distances. The results indicate that while the bonding representation is the main contributor to HeH+ and ArH+, the equilibrium structure of NeH+ is dominated by the closed-shell structure. These values suggest a reduced propensity of Ne to form covalently bound compounds, which will be discussed in further detail later.
Fig. 1D shows the optimised one-electron SCGVB orbitals at the minimum energy structure of the three NgH+ systems investigated herein, calculated at the SCGVB(2,3)/aug-cc-pVTZ level of theory. Additional plots of the orbitals along the corresponding potential energy curves are shown in Fig. S1–S3 (ESI†). It is evident that in all cases, the 1s-like orbital from hydrogen overlaps with the lobe orbital of the corresponding Ng atom. In the case of HeH+, a more contracted hydrogen 1s-like orbital is observed, reflecting the smaller polarisation effect due to helium's lower nuclear charge compared to its heavier analogues. For NeH+ and ArH+, the bonding involves p-like orbitals from the noble gases, with the orbitals being more diffuse in the case of ArH+.
Fig. 2 presents distinct energy partitioning schemes at the SCGVB(2,3)/aug-cc-pVTZ level of theory for HeH+ along its ground state potential energy curve. These results, shown in the right plots of Fig. 2, are compared with the corresponding H2 curves, which provide a reference for the behaviour of the distinct energy terms of the interference energy analysis for a typical 2-centre 2-electron bond, displayed in the left part of the figure.
 | ||
| Fig. 2 Energy partitioning curves following the interference energy analysis of H2 (left panels) and HeH+ (right panels) at the SCGVB(2,3)/aug-cc-pVTZ level of theory. Energy terms are relative to their corresponding values at 4.0 Å. First row: total electronic energy (E[TOT]) partitioning into interference (E[INT]) and quasi-classical (E[QC]) contributions. Second row: E[TOT] partitioning into total kinetic (T[TOT]) and total potential (V[TOT]) contributions. Third row: first-order interference energy (E[I]) partitioning into its kinetic (T[I]) and potential (V[I]) terms. Fourth row: quasi-classical energy (E[QC]) partitioning into its kinetic (T[QC]) and potential (V[QC]) parts. For additional data, see Table S3 in the ESI.† | ||
The first two plots compare the energy partitioning of the total electronic energy, E[TOT], into the E[INT] and E[QC] components. For H2, it is observed that the depth of the potential well is dominated by the interference contribution, with the quasi-classical part displaying a shallow minimum energy contribution in the vicinity of the equilibrium distance. This is a typical feature found for a regular covalent bond across all systems investigated so far.42,73
A similar profile is observed for HeH+, where the minimum energy structure arises solely from contributions of the interference terms. Additionally, from the dissociation region up to distances of around 1.5 Å, both E[INT] and E[QC] terms remain relatively untouched, indicating that no significant changes in electron density have occurred up to this point. This contrasts with the profile observed for H2, where at 1.5 Å, interference is already contributing to a drop in total energy by around 50 kcal mol−1, nearly half of the bond dissociation energy of H2. These results suggest that the bonding structures shown in Fig. 1C are not yet playing a major role in HeH+, which will be further discussed in more detail. For distances below 1.5 Å, a significant change occurs in the bonding profile of HeH+, leading to a substantial drop in the E[INT] term to more negative values, which ultimately forms the system's potential energy well.
The second row of Fig. 2 shows the partitioning of E[TOT] of H2 (left) and HeH+ (right) into total kinetic (T[TOT]) and potential (V[TOT]) contributions. Both curves exhibit the general features typical of any diatomic in a bound state.74 As the atoms approach, the potential energy rises and the kinetic energy drops, with these trends reversing before reaching the equilibrium distance. From these curves, it can be observed that the virial theorem, which states that for atoms and molecules at their equilibrium geometries, the V/T ratio always equals −2, is successfully achieved in both cases (for H2: |2T/V| = 1.0011 for an H–H distance of 0.75 Å; for HeH+, |2T/V| = 0.9987 for a He–H distance of 0.77 Å). Although it is known that the virial theorem does not explain the mechanism of formation of chemical bonds,25 we show that it is respected in both PECs obtained at this level of theory.
The third row of Fig. 2 shows the partitioning of E[I] into T[I] and o V[I] for H2 (left) and HeH+ (right). The H2 picture shows the general trend observed for covalent bonds: the drop in the interference term is caused by a reduction in kinetic energy, despite an increase in potential energy, thus driving the formation of covalent bonding.42,73 For HeH+, the same trend is observed but more abruptly, which we attribute to the charge rearrangement within the system.
Finally, the fourth row of Fig. 2 compares the quasi-classical energy partitioning into kinetic (T[QC]) and potential (V[QC]) components. For H2 (left panel), V[QC] drops significantly in energy as the atoms approach, leading to the correct virial relation, whereas the kinetic energy increases. Again, this profile is consistent with all chemical bonds investigated thus far, and also holds for HeH+ (right panel). In summary, the bond formation in HeH+ also results from a reduction in kinetic energy due to quantum interference.
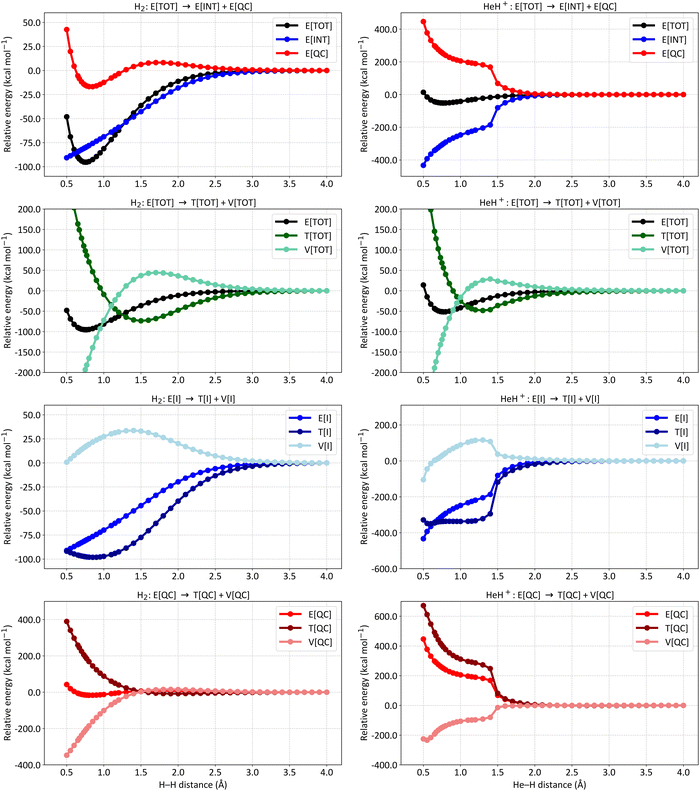
Fig. 3 presents the energy partitioning of NeH+ (left panels) and ArH+ (right panels) at the SCGVB(2,3)/aug-cc-pVTZ level of theory. The energy profiles observed for both cases are consistent with the overall picture observed for covalent bonds: the E[INT] term drops due to a reduction in kinetic energy caused by interference. Nevertheless, slight differences in the energy partitioning profile can be observed between the hydrides. For instance, the E[INT] term for NeH+ only starts to drop at smaller interatomic distances, while for ArH+, a drop of around −100.0 kcal mol−1 is already observed at an interatomic distance of approximately 2.0 Å.
 | ||
| Fig. 3 Energy partitioning curves following the interference energy analysis of NeH+ (left panels) and ArH+ (right panels) at the SCGVB(2,3)/aug-cc-pVTZ level of theory. Energy terms are relative to their corresponding values at 4.0 Å. First row: total electronic energy (E[TOT]) partitioning into interference (E[INT]) and quasi-classical (E[QC]) contributions. Second row: first-order interference energy (E[I]) partitioning into its kinetic (T[I]) and potential (V[I]) terms. Third row: quasi-classical energy (E[QC]) partitioning into its kinetic (T[QC]) and potential (V[QC]) parts. For additional data, see Tables S4 and S5 in the ESI.† | ||
Similarly, the analysis of the E[I] partitioning into T[I] and V[I] (second row of Fig. 3) shows that a more pronounced energy drop in the ArH+ system begins around 2.8 Å, whereas for NeH+, this occurs at about 1.2 Å, close to the equilibrium bond length. These results suggest that as the atoms are brought together, the bonding spin structures become relevant for ArH+ considerably sooner than for the other two cases (for HeH+, see Fig. 2 for comparison).
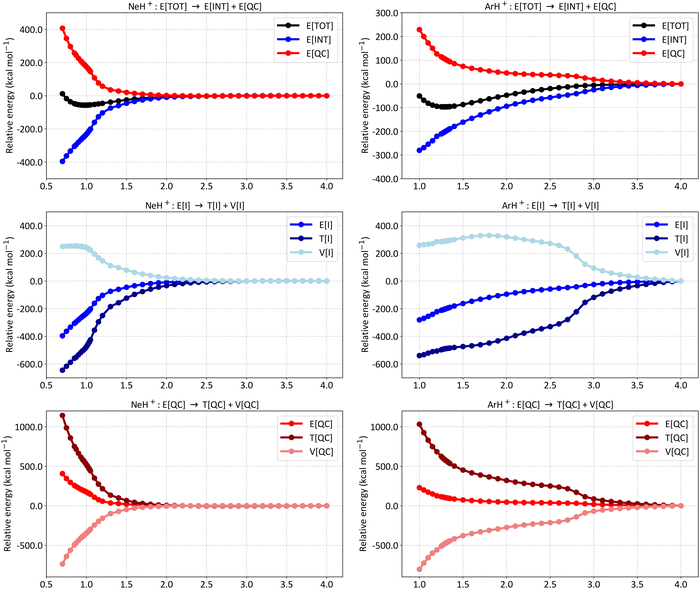
To better capture the differences in the bonding situations of the hydrides, Fig. 4 presents the absolute values of E[I] for the two distinct representations (closed-shell and bonding, see Fig. 1C for further details), along with their corresponding Chirgwin–Coulson coefficients. The E[I] terms are displayed in the left panels (A for HeH+, C for NeH+, and E for ArH+), while the Chirgwin–Coulson coefficients are shown in the right panels (B for HeH+, D for NeH+, and F for ArH+).
 | ||
| Fig. 4 Absolute values of the first-order interference energy (E[I]) and the Chirgwin–Coulson coefficients of the closed-shell (Ng + H+) and bonding (Ng+ + H) representations for (A) and (B) HeH+, (C) and (D) NeH+, and (E) and (F) ArH+. The calculations were performed at the SCGVB(2,3)/aug-cc-pVTZ level. The red vertical dashed lines indicate the equilibrium bond lengths. For additional data, see Table S6 in the ESI.† | ||
As anticipated, the dissociation products for all three systems are the neutral Ng atom and H+. This is evident from the decreasing significance of the Chirgwin–Coulson coefficient of the bonding representation (Ng+ + H) as the atoms separate, leading to a closed-shell structure contribution of 1.0 at around 4.0 Å in all cases. Correspondingly, the E[I] contribution of the bonding representation approaches zero at these larger distances, with the absolute E[I] term being dominated by the interference of the one-electron states involving the two Ng orbitals, reflecting Ng internal coupling.
As the atoms approach, the bonding representation becomes increasingly significant for all three systems, eventually dominating in HeH+ and ArH+. For HeH+, the bonding representation is negligible up to 2.0 Å, then rises exponentially until around 1.5 Å, where a clear change occurs, and its significance increases linearly with decreasing interatomic distance. Similarly, the E[I] value of the bonding representation drops sharply around 1.5 Å, where the E[I] terms of the two representations intersect. This intersection coincides with the change in the Chirgwin–Coulson coefficient profile. The crossing point of the coefficients occurs at a He–H distance of 1.15 Å, which is longer than the equilibrium distance of 0.776 Å. These results indicate that at the equilibrium distance, the bonding situation is primarily dominated by the bonding representation (0.630 versus 0.370), fitting well with the covalent nature of the He–H bond in HeH+.
For ArH+, the E[I] representation intersection occurs at 2.75 Å, considerably longer than the equilibrium bond length. In the Chirgwin–Coulson coefficient plot, the crossing occurs at 1.70 Å, approximately 0.42 Å longer than the equilibrium distance. These results show that the bonding representation is dominant in ArH+ as well, though by a small margin (0.520 versus 0.480 at the equilibrium distance).
In contrast, for NeH+, the Chirgwin–Coulson coefficient for the closed-shell form (0.658) is larger than the sum of the bonding structures (0.342). This suggests that NeH+ features a dative bond, or a donor–acceptor Lewis acid–base bond as used in some contexts,75,76 with the internal electron configuration of Ne remaining largely intact throughout the whole potential energy curve. To the best of our knowledge, this is the first time such a distinction in the bonding profile of noble gas hydrides has been reported. A simple rationale can explain Ne's deviation from the other cases: although Ne has an ionisation potential similar to that of He, its orbitals are larger and lie at much higher energy levels than the 1s orbital of H. As a result, typical covalent bonding is less favourable due to weaker orbital interactions between Ne and H. In turn, for HeH+, both electrons are involved in the 1s level of each atom, enhancing orbital interaction and leading to the predominance of bonding structures over the closed-shell form at the equilibrium geometry. In ArH+, the Ar valence orbitals, despite being at higher energy levels, are less contracted by the nucleus compared to Ne. The 3p orbitals are significantly polarised towards the H atom, allowing for greater interaction and facilitating the formation of covalent bonds. Therefore, although both Ne and Ar are noble gases with filled p orbitals, the larger atomic radius, lower ionisation potential, and higher polarisability of Ar, compared to Ne, lead to greater orbital interactions and charge transfer with H+. While the internal coupling in Ne is comparable to that in He, the interference between bonding orbitals is relatively low. In contrast, the internal coupling in Ar is not as strong, allowing for an enhanced covalent character in the bonding of ArH+ compared to NeH+. As a result, the closed-shell configuration for NeH+ predominates, resulting in a dative Ne → H+ bond, as also indicated by the Chirgwin–Coulson coefficients. Our results thus illustrate the differences in the bonding situations of the NgH+ systems, highlighting the lesser electron-sharing bonding effects in NeH+, consistent with the smaller tendency of Ne to form covalently bound compounds.
4. Conclusions
In summary, herein we investigate the nature of the chemical bond in noble-gas hydride ions (NgH+, where Ng = He, Ne, Ar) using modern VB-type wave functions, providing insights into the bonding mechanisms of these systems. Our results demonstrate that the formation of energy wells in their corresponding ground-state potential energy curves are caused by a reduction in kinetic energy caused by quantum interference, as typically observed in molecular systems. The analysis of the Chirgwin–Coulson coefficient allows us to distinguish two cases. Firstly, the bonding in HeH+ and ArH+ is primarily driven by electron charge transfer that facilitates the formation of typical covalent bonds. This charge rearrangement leads to a more delocalised electron state, significantly lowering the kinetic energy and stabilising the molecules. In contrast, for NeH+, interference also plays an essential role in the formation of an energy well in its ground-state potential energy curve, but the closed-shell structure, where the internal coupling of Ne remains intact, is the dominant structure throughout the entire potential energy curve. This suggests that the bonding situation in NeH+ is better described as a dative bond. This finding also aligns with the notion that neon is the most noble of the noble gases, exhibiting a lesser tendency to form typical covalent compounds and electron-sharing 2-centre 2-electron bonds, and underscoring its unique chemical inertness. It is noteworthy that the studied molecules exhibit the same mechanism for typical covalent bond formation, i.e. the lowering of the kinetic energy due to quantum interference, despite their dissociation curves leading to heterolytic cleavage.Author contributions
L. A. conducted all the calculations. All authors contributed to the discussions regarding the interpretation of the results and collaboratively worked on the manuscript's refinement.Data availability
The codes for VB2000 and the GPF-EP method can be found at https://vb2000.iq.ufrj.br/vb2000.html with DOI: https://doi.org/10.1002/qua.10293 [VB2000] and DOI: https://doi.org/10.1063/1.3085953 [GPF-EP]. The version of the code employed for this study is VB2000 version 3.0 (J. Li, B. Duke, D. W. O. de Sousa, R. S. Bitzer, R. McWeeny. VB2000 Version 3.0, ChemXAI Inc., Syosset, NY, 2021).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors express their gratitude to the Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) for the financial support through an MSc fellowship granted to L. A. (grant E-26/201.542/2023). T. M. C. acknowledges the financial support from CNPq for the project National Institute of Science and Technology on Molecular Sciences (INCT-CiMol), grant CNPq 406804/2022-2. M. A. C. N. acknowledges the financial support from CNPq (307924/2019-0) and FAPERJ (E-26/201.046/2021). F. F. is grateful to the University of Kent for their additional financial support.Notes and references
- T. R. Hogness and E. G. Lunn, Phys. Rev., 1925, 26, 44–55 CrossRef CAS.
- K. T. Bainbridge, Phys. Rev., 1933, 44, 57 CrossRef CAS.
- M. B. M’Ewen and F. L. Arnot, Proc. R. Soc. London, Ser. A, 1939, 172, 107–115 Search PubMed.
- S. Lepp and P. C. Stancil, The Molecular Astrophysics of Stars and Galaxies, Oxford University Press, Oxford, 1998, pp. 37–52 Search PubMed.
- S. Bovino, M. Tacconi, F. A. Gianturco and D. Galli, Astron. Astrophys., 2011, 529, A140 CrossRef.
- D. Galli and F. Palla, Annu. Rev. Astron. Astrophys., 2013, 51, 163–206 CrossRef CAS.
- R. Güsten, H. Wiesemeyer, D. Neufeld, K. M. Menten, U. U. Graf, K. Jacobs, B. Klein, O. Ricken, C. Risacher and J. Stutzki, Nature, 2019, 568, 357–359 CrossRef PubMed.
- O. Novotný, P. Wilhelm, D. Paul, Á. Kálosi, S. Saurabh, A. Becker, K. Blaum, S. George, J. Göck, M. Grieser, F. Grussie, R. von Hahn, C. Krantz, H. Kreckel, C. Meyer, P. M. Mishra, D. Muell, F. Nuesslein, D. A. Orlov, M. Rimmler, V. C. Schmidt, A. Shornikov, A. S. Terekhov, S. Vogel, D. Zajfman and A. Wolf, Science, 2019, 365, 676–679 CrossRef PubMed.
- R. C. Forrey, J. F. Babb, E. D. S. Courtney, R. T. McArdle and P. C. Stancil, Astrophys. J., 2020, 898, 86 CrossRef CAS.
- R. C. Fortenberry, Chem, 2019, 5, 1028–1030 CAS.
- S. R. Dash, T. Das and K. Vanka, Front. Chem., 2021, 9, 679750 CrossRef CAS PubMed.
- P. Schilke, D. A. Neufeld, H. S. P. Müller, C. Comito, E. A. Bergin, D. C. Lis, M. Gerin, J. H. Black, M. Wolfire, N. Indriolo, J. C. Pearson, K. M. Menten, B. Winkel, Á. Sánchez-Monge, T. Möller, B. Godard and E. Falgarone, Astron. Astrophys., 2014, 566, A29 CrossRef.
- G. Glockler and D. L. Fuller, J. Chem. Phys., 1933, 1, 886–887 CrossRef CAS.
- J. Y. Beach, J. Chem. Phys., 1936, 4, 353–357 CrossRef CAS.
- C. A. Coulson and W. E. Duncanson, Proc. R. Soc. London, Ser. A, 1938, 165, 90–115 CAS.
- A. K. Chandra and K. L. Sebastian, Mol. Phys., 1976, 31, 1489–1504 CrossRef CAS.
- M. Hendzel, M. Fidrysiak and J. Spałek, J. Phys. B: At., Mol. Opt. Phys., 2022, 55, 185101 CrossRef CAS.
- W. Butscher and H.-H. Schmidtke, Chem. Phys., 1978, 30, 41–51 CrossRef CAS.
- S. Peyerimhoff, J. Chem. Phys., 1965, 43, 998–1010 CrossRef CAS.
- K. Ruedenberg, Rev. Mod. Phys., 1962, 34, 326–376 CrossRef CAS.
- K. Ruedenberg and M. W. Schmidt, J. Comput. Chem., 2007, 28, 391–410 CrossRef CAS PubMed.
- K. Ruedenberg and M. W. Schmidt, J. Phys. Chem. A, 2009, 113, 1954–1968 CrossRef CAS PubMed.
- K. Ruedenberg, J. Chem. Phys., 2022, 157, 024111 CrossRef CAS PubMed.
- M. W. Schmidt, J. Ivanic and K. Ruedenberg, J. Chem. Phys., 2014, 140, 204104 CrossRef PubMed.
- G. B. Bacskay, S. Nordholm and K. Ruedenberg, J. Phys. Chem. A, 2018, 122, 7880–7893 CrossRef CAS PubMed.
- W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1973, 12, 546–562 CrossRef.
- T. M. Cardozo and M. A. C. Nascimento, J. Phys. Chem. A, 2009, 113, 12541–12548 CrossRef CAS PubMed.
- F. Fantuzzi and M. A. C. Nascimento, J. Chem. Theory Comput., 2014, 10, 2322–2332 CrossRef CAS PubMed.
- F. Fantuzzi, T. M. Cardozo and M. A. C. Nascimento, J. Phys. Chem. A, 2015, 119, 5335–5343 CrossRef CAS PubMed.
- D. W. O. de Sousa and M. A. C. Nascimento, J. Chem. Theory Comput., 2016, 12, 2234–2241 CrossRef CAS PubMed.
- F. Fantuzzi, D. W. O. de Sousa and M. A. Chaer Nascimento, Comput. Theor. Chem., 2017, 1116, 225–233 CrossRef CAS.
- D. W. O. de Sousa and M. A. C. Nascimento, Acc. Chem. Res., 2017, 50, 2264–2272 CrossRef PubMed.
- T. M. Cardozo, G. Nascimento Freitas and M. A. C. Nascimento, J. Phys. Chem. A, 2010, 114, 8798–8805 CrossRef CAS PubMed.
- F. Fantuzzi, T. M. Cardozo and M. A. C. Nascimento, Phys. Chem. Chem. Phys., 2012, 14, 5479–5488 RSC.
- F. S. Vieira, F. Fantuzzi, T. M. Cardozo and M. A. C. Nascimento, J. Phys. Chem. A, 2013, 117, 4025–4034 CrossRef CAS PubMed.
- D. S. Levine and M. Head-Gordon, Nat. Commun., 2020, 11, 4893 CrossRef CAS PubMed.
- T. M. Cardozo, F. Fantuzzi and M. A. C. Nascimento, Phys. Chem. Chem. Phys., 2014, 16, 11024–11030 RSC.
- D. W. O. de Sousa and M. A. C. Nascimento, Phys. Chem. Chem. Phys., 2019, 21, 13319–13336 RSC.
- T. H. Dunning, L. T. Xu, D. L. Cooper and P. B. Karadakov, J. Phys. Chem. A, 2021, 125, 2021–2050 CrossRef PubMed.
- J. Li and R. McWeeny, Int. J. Quantum Chem., 2002, 89, 208–216 CrossRef CAS.
- T. M. Cardozo and M. A. C. Nascimento, J. Chem. Phys., 2009, 130, 104102 CrossRef PubMed.
- T. M. Cardozo, D. W. O. De Sousa, F. Fantuzzi and M. A. C. Nascimento, Comprehensive Computational Chemistry, Elsevier, 2024, pp. 552–588 Search PubMed.
- R. McWeeny, Proc. R. Soc. London, Ser. A, 1959, 253, 242–259 CAS.
- K. Hirao, H. Nakano, K. Nakayama and M. Dupuis, J. Chem. Phys., 1996, 105, 9227–9239 CrossRef CAS.
- P. B. Karadakov, D. L. Cooper, B. J. Duke and J. Li, J. Phys. Chem. A, 2012, 116, 7238–7244 CrossRef CAS PubMed.
- D. W. O. de Sousa and M. A. C. Nascimento, J. Phys. Chem. A, 2021, 125, 4558–4564 CrossRef CAS PubMed.
- J. H. Van Lenthe and G. G. Balint-Kurti, Chem. Phys. Lett., 1980, 76, 138–142 CrossRef CAS.
- J. H. van Lenthe and G. G. Balint-Kurti, J. Chem. Phys., 1983, 78, 5699–5713 CrossRef CAS.
- B. H. Chirgwin and C. A. Coulson, Proc. R. Soc. London, Ser. A, 1950, 201, 196–209 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- U. Bozkaya, J. M. Turney, Y. Yamaguchi, H. F. Schaefer and C. D. Sherrill, J. Chem. Phys., 2011, 135, 104103 CrossRef PubMed.
- U. Bozkaya, A. Ünal and Y. Alagöz, J. Chem. Phys., 2020, 153, 244115 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- F. Zahariev, P. Xu, B. M. Westheimer, S. Webb, J. Galvez Vallejo, A. Tiwari, V. Sundriyal, M. Sosonkina, J. Shen, G. Schoendorff, M. Schlinsog, T. Sattasathuchana, K. Ruedenberg, L. B. Roskop, A. P. Rendell, D. Poole, P. Piecuch, B. Q. Pham, V. Mironov, J. Mato, S. Leonard, S. S. Leang, J. Ivanic, J. Hayes, T. Harville, K. Gururangan, E. Guidez, I. S. Gerasimov, C. Friedl, K. N. Ferreras, G. Elliott, D. Datta, D. D. A. Cruz, L. Carrington, C. Bertoni, G. M. J. Barca, M. Alkan and M. S. Gordon, J. Chem. Theory Comput., 2023, 19, 7031–7055 CrossRef CAS PubMed.
- L. Araujo, F. Fantuzzi and T. M. Cardozo, J. Phys. Chem. Lett., 2024, 15, 3757–3763 CrossRef CAS PubMed.
- K. Pachucki, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 042511 CrossRef.
- M. Chołuj, P. Lipkowski and W. Bartkowiak, Molecules, 2022, 27, 8997 CrossRef PubMed.
- P. Pendergast, J. M. Heck and E. F. Hayes, Int. J. Quantum Chem., 1994, 49, 495–509 CrossRef CAS.
- P. J. Linstrom and W. G. Mallard, J. Chem. Eng. Data, 2001, 46, 1059–1063 CrossRef CAS.
- G. Frenking, W. Koch, F. Reichel and D. Cremer, J. Am. Chem. Soc., 1990, 112, 4240–4256 CrossRef CAS.
- A. B. Alekseyev, H. Liebermann and R. J. Buenker, Phys. Chem. Chem. Phys., 2007, 9, 5088–5095 RSC.
- D. A. Dixon, W. A. de Jong, K. A. Peterson and T. B. McMahon, J. Phys. Chem. A, 2005, 109, 4073–4080 CrossRef CAS PubMed.
- M. W. Wong, J. Am. Chem. Soc., 2000, 122, 6289–6290 CrossRef CAS.
- E. G. Lewars, Modeling Marvels, Springer Netherlands, Dordrecht, 2008, pp. 67–80 Search PubMed.
- W. Grochala, Found. Chem., 2018, 20, 191–207 CrossRef CAS.
- A. Kalemos and A. Mavridis, J. Phys. Chem. A, 1998, 102, 5982–5992 CrossRef CAS.
- W. R. Wadt and W. A. Goddard, J. Am. Chem. Soc., 1975, 97, 3004–3021 CrossRef CAS.
- F. Fantuzzi, D. W. O. de Sousa and M. A. C. Nascimento, ChemistrySelect, 2017, 2, 604–619 CrossRef CAS.
- J. S. Winn, J. Chem. Phys., 1981, 74, 608–611 CrossRef CAS.
- J. Ren, D. B. Workman and R. R. Squires, J. Am. Chem. Soc., 1998, 120, 10511–10522 CrossRef CAS.
- Q. L. Almas and J. K. Pearson, ACS Omega, 2018, 3, 608–614 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional data for the CCSD(T) and SCGVB calculations. See DOI: https://doi.org/10.1039/d4cp04028g |
| This journal is © the Owner Societies 2024 |