Revolutionizing the structural design and determination of covalent–organic frameworks: principles, methods, and techniques
Yikuan
Liu†
 a,
Xiaona
Liu†
b,
An
Su†
a,
Xiaona
Liu†
b,
An
Su†
 a,
Chengtao
Gong†
a,
Shenwei
Chen
a,
Liwei
Xia
a,
Chengwei
Zhang
a,
Xiaohuan
Tao
a,
Yue
Li
f,
Yonghe
Li
a,
Tulai
Sun
a,
Mengru
Bu
a,
Wei
Shao
a,
Jia
Zhao
a,
Chengtao
Gong†
a,
Shenwei
Chen
a,
Liwei
Xia
a,
Chengwei
Zhang
a,
Xiaohuan
Tao
a,
Yue
Li
f,
Yonghe
Li
a,
Tulai
Sun
a,
Mengru
Bu
a,
Wei
Shao
a,
Jia
Zhao
 a,
Xiaonian
Li
a,
Yongwu
Peng
a,
Xiaonian
Li
a,
Yongwu
Peng
 *a,
Peng
Guo
*a,
Peng
Guo
 *bc,
Yu
Han
*bc,
Yu
Han
 *de and
Yihan
Zhu
*de and
Yihan
Zhu
 *a
*a
aCenter for Electron Microscopy, Institute for Frontier and Interdisciplinary Sciences, State Key Laboratory Breeding Base of Green Chemistry Synthesis Technology, College of Materials Science and Engineering and College of Chemical Engineering, Zhejiang University of Technology, Hangzhou 310014, Zhejiang, China. E-mail: yihanzhu@zjut.edu.cn; ywpeng@zjut.edu.cn
bNational Engineering Research Center of Lower-Carbon Catalysis Technology, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China. E-mail: pguo@dicp.ac.cn
cUniversity of Chinese Academy of Sciences, Beijing 100049, China. E-mail: pguo@dicp.ac.cn
dSchool of Emergent Soft Matter, South China University of Technology, Guangzhou, China. E-mail: hanyu@scut.edu.cn
eKing Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia. E-mail: yu.han@kaust.edu.sa
fInstitute of Intelligent Computing, Zhejiang Lab, Hangzhou 311121, China
First published on 15th December 2023
Abstract
Covalent organic frameworks (COFs) represent an important class of crystalline porous materials with designable structures and functions. The interconnected organic monomers, featuring pre-designed symmetries and connectivities, dictate the structures of COFs, endowing them with high thermal and chemical stability, large surface area, and tunable micropores. Furthermore, by utilizing pre-functionalization or post-synthetic functionalization strategies, COFs can acquire multifunctionalities, leading to their versatile applications in gas separation/storage, catalysis, and optoelectronic devices. Our review provides a comprehensive account of the latest advancements in the principles, methods, and techniques for structural design and determination of COFs. These cutting-edge approaches enable the rational design and precise elucidation of COF structures, addressing fundamental physicochemical challenges associated with host–guest interactions, topological transformations, network interpenetration, and defect-mediated catalysis.
1. Introduction
Covalent organic frameworks (COFs) constitute a fascinating class of porous materials, first developed in 2005 by O. Yaghi and colleagues as a novel type of crystalline covalent organic polymer.1 Since then, COFs have rapidly gained attention and spurred the emergence of an interdisciplinary research field focused on their design, synthesis, and application. Unlike metal–organic frameworks (MOFs) that rely on metal–ligand coordination to form the porous framework,2,3 COFs are based on the strong and stable covalent linkages between molecular building blocks, resulting in remarkable thermal and chemical stability.4 This provides unprecedented opportunities for the design and creation of pre-determined porous structures with desired sizes, densities, and interconnectivity of pores.5–8The architecture of COFs is fully pre-designable, based on reticular chemistry that involves the symmetries and connectivities of molecular monomers linked by covalent bonds. This results in polymeric networks beyond zero-dimensional (0D) supramolecules and ranging from one-dimensional (1D) to two-dimensional (2D) and even three-dimensional (3D) spaces, depending on the kind of molecular linkage.9–12 Of particular interest are 3D COFs, which are constructed using high-valence molecular monomers such as 4-connected Td-symmetric building blocks and 8-connected D4h-symmetric ones.13–15 These frameworks possess exceptional surface area, low density, and abundant functional sites accessible to guest molecules, making them highly desirable for practical applications such as catalysis and gas adsorption/separation. However, their crystallization poses significant challenges and often requires rigorous synthesis protocols, especially for those monomers with functional groups.16,17
In order to fully unlock the potential of COFs, it is crucial to address the key challenges facing this field. The challenges include (i) precisely designing polymer networks with targeted architectures, porosities, and topologies based on the symmetries and connectivities of molecular building blocks, (ii) exploring the structural design rationale and underlying logic behind polymer network construction to achieve target functionalities, and (iii) explicitly elucidating the structure of COFs and retrieving multi-dimensional correlated structural, chemical, and electronic information across spatial, time, energy, and momentum dimensions.18–20 Achieving this level of understanding is not without technical hurdles. For instance, COFs are highly fragile and subject to electron beam irradiation damage, making it challenging to achieve high spatial resolution characterization using modern electron microscopy techniques.21–23 However, by overcoming these obstacles, we can unravel the physical origin of fascinating phenomena taking place on the surfaces/interfaces, as well as within the bulk porosities and defects of COFs, including topological transformations, host–guest interactions, network interpenetration, and defect-mediated catalysis.24,25
In the realm of open framework materials, such as MOFs, zeolites, and COFs, designing structures with desired porosity and functionality is a critical task. This task is guided by the principles of reticular chemistry, which involves building open frameworks through the linkage of molecular building blocks via chemical bonding.26 While each type of material has its own unique building units with matched geometries (i.e. TO4 tetrahedra for zeolites, secondary building units (SBUs) for MOFs, and molecular monomers for COFs), the molecular design principle of COFs sets them apart from linear, hyperbranched, or cross-linked polymers. This design principle facilitates the pre-designing of primary and advanced COF structures to an unprecedented degree.26 Over the past decade, the discovery of new COF structures has evolved from scientific intuition and traditional trial-and-error experimental approaches to high-throughput predictive approaches from the viewpoint of materials genome initiative (MGI).27 These recently developed high-throughput approaches, assisted by advanced computational tools like machine learning (ML) and encoded multi-dimensional information spanning from topological to chemical spaces, are capable of predicting, screening, and optimizing hypothetic COF structures at an unparalleled scale and rate.24 This significantly expedites the innovation of new networks and allows the construction of large databases for COFs. These high-throughput approaches have been successful in predicting numerous unreported topologies and new structures that outperform widely recognized benchmark materials in various applications, including catalysis and gas storage.28
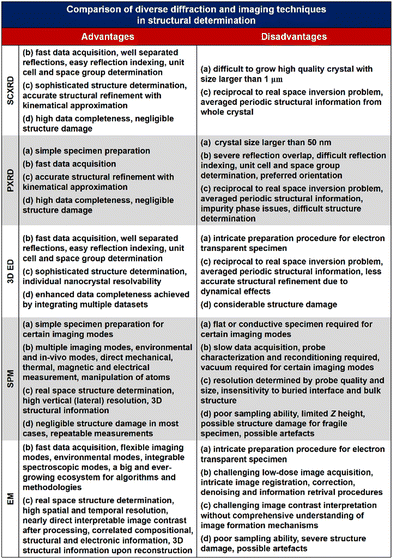
Structural determination of COFs is critical, and an ideal structural elucidation technique for COFs should be capable of determining their structures and dynamics across multiple scales and dimensions, with high spatial, temporal, and energy resolutions. Although spectroscopic techniques can deliver high-energy and temporal resolution to obtain fingerprint structural information on functional groups or species in COFs, their spatial resolution is limited. Diffraction-based techniques using X-ray or electron incidence can extract periodic structural information from Bragg scattering, providing high spatial resolution with sophisticated crystallographic strategies,29 while the different scattering abilities of elements allow the discrimination of chemical information within the frameworks. Electron diffraction techniques with nanofocusing capability enable the characterization of COF nanocrystals, circumventing their crystallization issues, though low-dose or cryogenic strategies are required to minimize electron beam damage to the organic frameworks.30 While diffraction-based crystallographic techniques can offer spatially averaged information over the periodic network, they cannot directly resolve local structural information such as surface, interface, defects, and partial disorder. Accordingly, they may have limitations in unraveling fundamental questions related to host–guest interactions, network interpenetration, and defect-mediated catalysis. Modern imaging techniques, such as scanning probe microscopy (SPM), allow direct molecular-level or even atomic-level imaging of conductive and/or low-dimensional structures like supramolecules, 1D COFs, and 2D COFs. Transmission electron microscopy (TEM) offers a more general solution to structural elucidation for most types of COFs, though inherent issues arising from the low electron scattering abilities and beam damage of these organic frameworks need to be tackled.31 TEM provides a powerful platform that integrates the capabilities of multi-dimensional correlated structural, chemical, and electronic information retrieval at high spatial resolution.32–35 Recent advances in the development of high-performance electron detectors enable various low-dose imaging techniques, such as direct detection cameras (DDC)-high resolution transmission electron microscopy (HRTEM),36 integrated-differential-phase-contrast (iDPC)-STEM and electron ptychography,37,38 providing unprecedented opportunities in direct imaging of beam-sensitive low-contrast crystalline and non-crystalline organic polymers.
This work reviews the fundamental concepts, principles and advanced techniques for the structural design and determination of COFs. It aims to unravel the rationale and underlying logic behind polymer network construction towards target functionalities and structure–property relationships for diverse applications.
2. Structural design
2.1. General principles for structural design
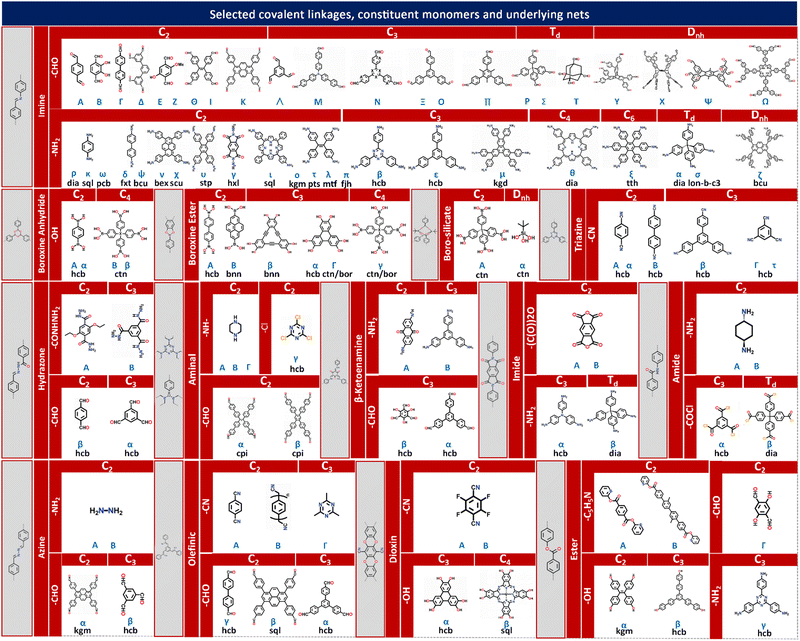
The theory and methods of reticular chemistry originated in the 1950s,39 but their renaissance came at the very beginning of this century right after the explosive growth of MOF chemistry.40 In the last century, the understanding of covalent bonding in organic molecules led to the development of a fully rational field of research in organic synthesis. However, covalently linked organic macromolecules, with the exception of linear 1D polymers, remained largely unexplored. The synthesis of the first COF that attains stacked 2D structures was achieved through reversible formation of boroxine and boronate ester bonds.1 Subsequently, Yaghi et al. synthesized the first 3D COF, 3D COF with interpenetrated networks, and 3D COF woven by organic threads in 2007, 2013, and 2016, respectively.41–43 In the 15 years since the discovery of 2D and 3D COFs, a plethora of novel COF structures have been reported, featuring diverse linkage chemistries, structure types, and pore metrics.Most COFs can be rationally designed and synthesized based on the basic principles of reticular chemistry. Reticular chemistry is fundamentally topological science, specifically with periodic nets that provide a blueprint for constructing crystal networks using multi-connected molecular building blocks under the stoichiometric condition. These nets are essential for designing crystals with specific properties.40 Such periodic nets are called underlying nets as they characterize the architecture of the whole structure. The combinatorial topology of a periodic net for a COF network is actually an abstraction of the geometrical properties where the concept of continuity, without distortions such as bending, twisting or affine transformations, is decisive. The underlying topology of a net may be designated by the three-letter symbols from the reticular chemistry structure resource (RCSR)44 and realized by diverse embeddings.45 In this sense, similar to MOFs and zeolites, COF networks with different embeddings can be well deconstructed stepwise to faithfully determine their underlying net and associated topology (Fig. 1a),13via computer programs like Systre26 and TOPOS.46 The design of COF networks, from a bottom-up perspective, can be well predicted and constructed based on the symmetry and connectivity of polytonic molecular monomers towards the formation of topologies with a minimum number of kinds of vertices and links (Fig. 1b).21
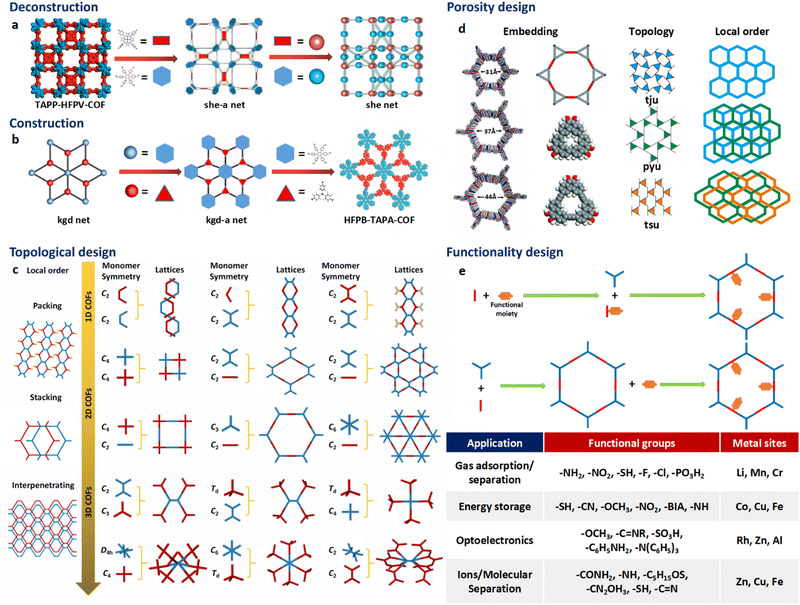 | ||
| Fig. 1 Fundamental construction and design principles of COFs. (a) and (b) Construction and deconstruction schemes of model COF networks. (a),13 (b)21 Modified with permission. Copyright 2022, 2023, American Chemical Society. (c) Topology design principles from monomers with diverse symmetries to COF lattices with different network dimensionalities. (d) Porosity design principles based on the effects from embedding, topology and local order. Reproduced with permission.17,47–49 Copyright 2022, 2019, 2015, 2017, American Chemical Society, Elsevier, Royal Society of Chemistry. (e) Functionalization-based synthesis strategies. | ||
The structural design rationale of COFs may be categorized into three different levels: (i) the network dimensionality (associated with monomer symmetry and connectivity), (ii) the network porosity (associated with the embeddings, topology, local order) and (iii) the network functionality (associated with both functional groups and metal sites). Beyond the 0D supramolecules, the COF networks span from 1D to 3D spaces when choosing different organic molecular monomers as building blocks, which are dictated by either linear, planar or stereoscopic shapes and different node-valency (Fig. 1c).
Specifically, 1D COFs consist of (quasi-)linear covalent linkages with two or more reactive sites that are confined in the one-dimensional direction and may exhibit noncovalent interactions, such as π–π interactions and hydrogen bonding, spanning the rest two dimensions. However, the high structural anisotropy and entropy-driven random packing of organic units pose major challenges in synthesizing molecular crystals of 1D COFs.10 Nonetheless, upgrading the structural dimensionality is possible through the packing of 1D COF molecular chains to induce local structural order as shown in Fig. 1c. For the construction of 2D COFs, the utilization of linear and/or planar monomers (e.g. triangle, square, and rectangle shaped molecular nodes) limits the expansion of the organic linkages within the 2D plane, and thus creating 2D frameworks that adopt diverse topologies.50 In general, stiff monomers may lead to more rigid 2D COFs with better crystallinity and higher surface area, arising from improved alignment and packing of the monomers within the framework.51 There is a wide availability of organic monomers with stiff backbones that meet these criteria, and they often constitute π-systems within the polymeric framework that may adopt 2D topologies including hcb, sql, hxl, kgm and kgd.52 These 2D organic layers may also upgrade the structural dimensionality through stacking and introduce local structural order (Fig. 1c). For instance, the AA stacking mode with the eclipsed configuration of the 2D polymeric framework that adopts hcb topology leads to local structural order along the third dimension and the formation of bnn topology. On the other side, the AB stacking mode with the staggered configuration leads to local structural order along the third dimension and the formation of gra topology.53 The construction of 3D COFs usually involves the stereoscopic molecular monomers with high valency, such as 4-, 6- and 8-connected stereoscopic nodes with Td, D3h, D3d, C3 and D4h symmetries.54–57 The combination of these stereoscopic molecular nodes (e.g. tetrahedron, cube, triangular prism and quadrangular prism shaped molecular nodes) along with other types of planar or linear nodes creates COFs that adopt dia, bcu, bor, ctn, and pts topology.58 Furthermore, the major challenge in designing and synthesizing 3D COFs is very limited choices of multiply connected stereoscopic molecular monomers as building blocks, especially for those with high-valency, which imposes severe constraints in evoking structural diversity compared with other open framework materials like MOFs. The recent development of high-valency molecular nodes, such as 8-connected stereoscopic nodes, has greatly enriched the 3D COF repertoire.59 Many 3D COF frameworks inevitably adopt entangled configurations that exhibit local structural order beyond the 3D structure and involve multiple interpenetrated networks displaced from each other (Fig. 1c).
The above-mentioned underlying framework topologies can be realized by diverse embeddings and allow the design of porosity (i.e. the size and shape of the micropores) that plays a critical role in determining the performance of COFs in various important applications such as gas adsorption/separation and catalysis. There are generally three major strategies in the porosity design of COFs:
(i) The choice of embeddings. Even by adopting an identical net with a specific topology, the porosity of a COF structure can be well tailored by employing molecular nodes with different sizes. Alternatively, molecular nodes in the framework can be replaced by different types of augmented building blocks that possess inherent porosity to introduce multimodal porosity (Fig. 1d).47,48
(ii) The choice of topologies. Depending on the kind of molecular linkage, identical molecular nodes may lead to different types of topologies and thus porosities. As a typical example, the in-plane linkage of K-shaped molecular nodes may lead to the formation of 2D frameworks dictated by either tju, pyu or tsu topologies as schematically illustrated in Fig. 1d. The porosities of these diverse COF types are markedly distinct, both in size and in shape.17
(iii) The effects of stacking and entanglement. The stacking and entanglement of existing COF networks upgrade the structural dimensionality of these networks from 2D or 3D spaces, and thus modulate the porosities. For 2D networks, the eclipsed-type (AA) stacking mode usually leads to straight micropores, while the staggered-type (AB) stacking mode leads to segmented micropores (Fig. 1d).49 On the other side, the entanglement of 3D COFs entails the interpenetration of networks and significantly reduces the pore size.22
The introduction of functional groups and metal sites endows the COFs with diverse functionalities (Fig. 1e). From either the bottom-up or peer-to-peer perspective, these two strategies can be generally achieved through pre-synthetic modification (pre-SM) or post-synthetic modification (post-SM).60 In pre-SM, functional groups or metal sites can be introduced into the molecular monomers before molecular linkages are formed through condensation. However, this approach may not be suitable for all the cases due to the incompatibility of the functionalized molecular monomers with the synthetic conditions of COFs. In contrast, post-SM introduces functionalities into the frameworks of pre-synthesized COFs through diverse bond formation reactions, such as azide–alkyne cycloaddition, Williamson ether synthesis reaction, esterification of the hydroxyl group and amidation of the carboxyl group.61–63 This approach allows the introduction of application-oriented and site-specific functionalities that cannot be simply integrated by pre-SM strategies. However, due to the extremely slow solid–liquid reactions and diffusion restrictions of molecular precursors, complete functionalization of the whole COF framework is usually challenging, especially for those precursor molecules exceeding the pore size of the COFs.64,65
2.2. Structural design based on reticular chemistry
Following the above-mentioned three levels of design rationale for COFs, achieving optimal porosity and functionality within the target dimensions should be the primary focus of structural design. Enormous insights into the structural design and synthesis guided by reticular chemistry and topological science can be gained from the fundamental principles and rich experience of other open framework materials like MOFs and zeolites. As summarized in Fig. 2, engaging a specific topology, diverse embeddings are realized by pre-designable molecular monomers dictated by different shapes and interconnected via various types of covalent linkages.48The linear, planar and stereoscopic multiply connected molecular monomers that adopt linear, polygonal or polyhedral shapes are endowed with multiple symmetrically distributed reactive sites. Many bond formation reactions allow the creation of diverse covalent linkages between these reactive sites and entail the targeted construction of COF networks guided by geometry alignment. Typical covalent linkages include:
(i) Boronate ester linkages that exhibit high thermal stability and are formed by the condensation reaction between a boronic acid and a diol or a hydroxyl group with a base or transition metal catalyst.66–68 (ii) Triazine linkages that exhibit high chemical stability and are formed by the self-condensation of nitrile with an acid or base catalyst.69–71 (iii) Imine linkages that are stable and formed by the condensation reaction between an amine and an aldehyde or ketone with an acid or base catalyst.72–74 (iv) Ketoenamine linkages that involve the formation of a double bond between a carbon atom in the keto (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) group of one monomer and a nitrogen atom in the enamine (C
O) group of one monomer and a nitrogen atom in the enamine (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) group of another monomer.75 (v) Imide linkages that are typically formed through the reaction of an amine and an acid anhydride with a base catalyst.76 (vi) Amide linkages that are typically difficult to obtain via the usual condensation reaction of an amine with a carboxylic acid, and are formed through the direct oxidation of the imine linkages.77 (vii) Olefinic linkages that are formed by the cross-coupling reaction between two alkenes with a base or transition metal catalyst, or by the aldol condensation of an aldehyde with an activated methyl group under a base.78 (viii) Ester linkages that are formed by the esterification reaction between an alcohol and a carboxylic acid with an acid catalyst, or by the condensation reaction between an alcohol and a reactive acid derivative, such as an acid chloride or anhydride.79,80
N) group of another monomer.75 (v) Imide linkages that are typically formed through the reaction of an amine and an acid anhydride with a base catalyst.76 (vi) Amide linkages that are typically difficult to obtain via the usual condensation reaction of an amine with a carboxylic acid, and are formed through the direct oxidation of the imine linkages.77 (vii) Olefinic linkages that are formed by the cross-coupling reaction between two alkenes with a base or transition metal catalyst, or by the aldol condensation of an aldehyde with an activated methyl group under a base.78 (viii) Ester linkages that are formed by the esterification reaction between an alcohol and a carboxylic acid with an acid catalyst, or by the condensation reaction between an alcohol and a reactive acid derivative, such as an acid chloride or anhydride.79,80
COF networks are constructed through the covalent bonding of molecular monomers that possess symmetrically distributed functional groups as reactive sites. These functional groups facilitate the formation of various covalent linkages between the monomers. Based on the reported types of covalent linkages (such as imine, boroxine anhydride, boroxine ester, boro-silicate, triazine, hydrazone, aminal), functional groups (such as –CHO, –NH2, –OH, –CONHNH2, –CN, –COCl, –NH–, –Cl, –(CO)2O, –COCl, –C5H5N), and point symmetries of the monomers (such as C2, C3, C4, Td, Dnh), a multi-element construction diagram of COF network topologies can be generated using the design principles of reticular chemistry. This figure, as shown in Fig. 2, provides direct guidance for the chemical synthesis of COF networks with desired underlying topologies through the corresponding chemical reactions between functional groups.
Integrating the symmetry and connectivity of monomers, common types of covalent linkages as well as the network topologies of the target COFs, a full construction diagram of COFs based on the concept of reticular chemistry can be generated as clearly illustrated in Fig. 2. Specifically, the 1D COFs for 2,2,4C3 topology can be constructed by covalent linkages in the [C2 + C2] (Fig. 1c), possibly through either imine, triazine, aminal or boroxine anhydride linkages as in Fig. 2.1,81–83
These 1D COFs possess a high degree of freedom in molecular packing, and act as candidates to construct non-centrosymmetric crystals.84 Meanwhile, the 1D COFs may further act as basic units to construct 2D COFs through the formation of interchain covalent linkages.84,85 2D COFs can also be constructed based on the topology diagrams with molecular monomers dictated by C2, C3, C4 and C6 symmetries. For example, hexagonal 2D COFs for hcb topology can be created in either [C3 + C2],86 [C2 + C2 + C2] or [C3 + C3] manner with different pore sizes and π-orderings.87,88 These networks are constructed based on covalent linkages including imine linkages between 1,1,2,2-tetrakis(4-aminophenyl)ethene (ETTA) and 1,3,5-triformylbenzene (TFB), and β-ketoenamine linkages between 1,3,5-tris(4′-aminophenyl)benzene (TAPB) and 1,3,5-triformylphloroglucinol (TFP) monomers.83,89 Tetragonal 2D COFs for sql topology can be created through the combinations of [C4 + C2] and [C4 + C4].90,91 Unlike 2D COFs, the involvement of stereoscopic nodes with Td point symmetries has greatly diversified the monomer combinations, thus enriching the networks for 3D COFs.22 The [Td + C3] and [Td + Td] diagrams can be used to create the ctn or bor networks, characterized by non-interpenetrating structures.41,92 These networks are constructed by covalent linkages including imine and boroxine ester linkages between hexahydroxytriphenylene (HHTP) and tetra(4-dihydroxyborylphenyl)silane (TBPS), tetra-(4-anilyl)methane (TAM) and tetra(4-formylphenyl)silane (TFS).93 The dia network can be constructed by the [Td + C2] diagram and belongs to the largest family of 3D COFs.92 This network is constructed by covalent linkages including imine linkages between pyromellitic dianhydride (PMDA) and tetra(4-aminophenyl)methane (TAPM).94 Moreover, the srs net is formed using the [Td + C3] diagram, with SiCOF-5 being an example that attains a two-fold interpenetrated network.95 The pts network can be constructed via the [Td + C2] and [Td + C4] diagrams, characterized by a multi-fold interpenetrated structure.96 Quite rarely, the [C2 + C3] diagram may also lead to the formation of 3D COFs with the underlying topology of ffc.27 Additionally, the involvement of high-valency stereoscopic nodes in the construction of 3D COFs may further lead to an outburst of new 3D COF topologies. By integrating 6-connected stereoscopic nodes, the stp, ceq, and hea networks can be constructed through the [D3h + C4], [D3h + C3], and [D3h + Td] combinations respectively, including imine linkages between 2,3,6,7,14,15-hexakis(4′-formylphenyl)triptycene (HFPTP) and 1,3,6,8-tetrakis(4-aminophenyl)pyrene (TAPPy),97 imine linkages between HFPTP and 1,3,5-tris(4-aminophenyl)triazine (TAPT),98 as well as imine linkages between HFPTP and tetrakis(4-amino biphenyl)methane (TABPM).97,99–102 More recently, by introducing a new type of high-valency quadrangular prism (D4h) stereoscopic node with a connectivity of eight, a two-fold interpenetrating 3D COF network with bcu topology can be derived.22 Moreover, the tty network can be readily constructed via the [D4h + C4] combination, including imine linkages between ((3,6-difluorobenzene-1,2,4,5-tetrayl)tetrakis(azanetriyl))octakis([1,1′-biphenyl]-4-carbaldehyde) (FBTA-8CHO) and TAPPy (Fig. 1c).54 The comprehensive topological information for COF structures spanning 1D to 3D spaces is encoded in the RCSR database, which provides important guidance for both the deconstruction and topological analysis of existing COF networks as well as the construction and structural prediction of unknown networks.58
The porosities of a COF with a given topology are well tunable through embeddings from the following perspective: (i) the pore size modulation of COFs can be achieved by manipulating the molecular size or chain length of the organic molecular monomers. Tri(4-formacylphenoxy)-1,3,5-triazine (TRIF) was subject to Schiff base condensation with different types of amine building blocks towards the formation of –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bonds and construction of three different 2D COFs, namely COF-SDU1, COF-SDU2 and COF-SDU3, by using TRIF as a N-rich aldehyde building block, and p-phenylenediamine (PA), hydrazine hydrate, and terephthalic dihydrazide (TPDH) as amine building blocks with pore sizes of 37 Å, 31 Å, and 44 Å respectively.47 (ii) Introducing augmented molecular nodes further allows the creation of the multimodal pore structure of COFs. For example, Yang et al. reported the synthesis of 2D COFs by upgrading each node in the unimodal hcb net to triangular augmented units towards the formation of the bimodal hcb-a net. Specifically, two types of arylene-ethynylene macrocycles (AEMs) are used as augmented units to replace the HHTP monomer and create secondary micropores in addition to the 32 and 38 Å primary mesopores respectively (Fig. 1d).48 Similarly, McGrier et al. reported the incorporation of two types of C3-symmetric and π-conjugated dehydrobenzoannulenes (DBAs) as augmented nodes with inherent pore sizes of 3.9 Å and 5.4 Å, respectively, into the 2D COF networks that adopt hexagonal mesopores with a size of 39 Å and 54 Å.103
N– bonds and construction of three different 2D COFs, namely COF-SDU1, COF-SDU2 and COF-SDU3, by using TRIF as a N-rich aldehyde building block, and p-phenylenediamine (PA), hydrazine hydrate, and terephthalic dihydrazide (TPDH) as amine building blocks with pore sizes of 37 Å, 31 Å, and 44 Å respectively.47 (ii) Introducing augmented molecular nodes further allows the creation of the multimodal pore structure of COFs. For example, Yang et al. reported the synthesis of 2D COFs by upgrading each node in the unimodal hcb net to triangular augmented units towards the formation of the bimodal hcb-a net. Specifically, two types of arylene-ethynylene macrocycles (AEMs) are used as augmented units to replace the HHTP monomer and create secondary micropores in addition to the 32 and 38 Å primary mesopores respectively (Fig. 1d).48 Similarly, McGrier et al. reported the incorporation of two types of C3-symmetric and π-conjugated dehydrobenzoannulenes (DBAs) as augmented nodes with inherent pore sizes of 3.9 Å and 5.4 Å, respectively, into the 2D COF networks that adopt hexagonal mesopores with a size of 39 Å and 54 Å.103
Even with identical combinations of molecular monomers, diverse types of interconnectivities of these monomers lead to different topologies of COFs that attain distinct pore size and shape. Based on three types of pre-synthesized metallosalphen-based monomers, self-polycondensation of these M-Salphen “two-in-one” monomers under solvothermal conditions creates the corresponding M-Salphen-COFs (M = Ni, Cu, Zn). Depending on the kind of interconnection, these K-type monomers have yielded three distinct pore size distribution 2D COF topologies in both theoretical design and practical synthesis (Fig. 1d).17 In 2020, Zhang et al. have shown that the topology of 2D COFs can be regulated by switching their linkage conformations. This can be achieved by introducing or eliminating intramolecular hydrogen bonding in the substituents of an identical molecular monomer. Through this approach, two highly crystalline 2D COFs with either kgm or monoclinic sql topology with different porosities of 12 and 27 Å were synthesized.104
The local stacking order of 2D COFs also affects the porosity design. Cui et al. have achieved synthetic control over the stacking of layers and chemical stability of 2D COFs by implementing a multivariate approach to manage interlayer steric hindrance. Through the co-condensation of triamines with or without alkyl substituents (ethyl and isopropyl) and a di- or tri-aldehyde, 2D COFs were created, with AA, AB, or ABC stacking order. The pore sizes in these 2D COFs are greatly influenced by their stacking order, ranging from 10 to 8.1 Å based upon diverse types of stacking order.105 The impact of network interpenetration of COFs on their porosity lies in the redistribution of pore size and pore volume. With the introduction of a high-valency quadrangular prism (D4h) stereoscopic node possessing a connectivity of eight, Peng et al. proposed two 3D COFs with interpenetrating structures, namely ZJUT-2 and ZJUT-3. This approach has been utilized to create two isoreticular 3D imine-linked COFs, with pore sizes of 12 and 18 Å for ZJUT-2 and 12 and 16 Å for ZJUT-3 respectively (Fig. 1d).22
Grafting diverse functional groups into COF networks as active sites serves as an effective functionalization strategy, endowing COF networks with enhanced performance in various applications such as gas adsorption/separation, energy storage, optoelectronics, and catalysis (as shown in Fig. 1e). For instance, –NO2 groups increase the charge density and oxidizability of COFs, thereby enhancing the host–guest interactions and gas storage capacity.106–108 Similarly, –SH groups enhance the thermal stability and reduce the electrical resistance of COFs, making them well-suited for use in supercapacitors.109–112 Additionally, –C6H4NH2 groups promote charge transfer and light absorption in COFs, facilitating photoelectric conversion and photocatalytic reactions.113,114 The –CONH2 group, when grafted into COF networks, exhibits superior heavy metal uptake capacity in terms of saturation adsorption (Fig. 1e).115–119 Another functionalization strategy involves metal site docking to COF networks. In addition to providing active sites, metal sites in COFs can significantly alter the electronic structure, catalytic activity, chemical stability, and optical properties. For example, positively charged metal cations have a strong affinity for CO2 molecules, with Li+ sites in COFs attaining the strongest binding energy with CO2 molecules. This enhances CO2 adsorption capacity and selectivity towards improved CO2 capture and storage performance.120,121 The introduction of Fe sites may increase the electrical conductivity of the network, thereby enhancing the energy storage capacity of COFs.111,120,122 Metal sites not only serve as adsorption sites but also integrate adsorption ability into COF networks through charge transfer effects. For instance, Cu sites in COF-506-Cu impart positive charges to organic polymeric backbones, enabling the combination of adsorption and anion exchange functionalities for the uptake of anionic dyes.123–125
The structural design of COFs holds immense significance, as the interplay between structure and properties is intricately intertwined, governed by the fundamental principle of the “structure–property relationship.” In pursuit of specific applications, it becomes imperative to elucidate the essential structural features exclusively relevant to the desired functionality. This knowledge serves as a guiding framework for the precise molecular- or atomic-level design of COFs. When focusing on applications involving the catalytic conversion of small molecules, the pore size and functional groups assume paramount importance as key structural features. These features can be intentionally manipulated through precise selection of molecular monomers, strategic construction of covalent linkages, and deliberate modifications of functional groups. For example, 3D microporous BF-COF-2 features a rectangular pore with dimensions of 7.7 × 10.5 Å2, enabling it to efficiently catalyze the conversion of benzaldehyde (with a molecular size of 6.1 × 8.7 Å2) into 2-benzylidenemalononitrile with a high conversion rate of 98%. In contrast, for 4-phenylbenzaldehyde (with a molecular size of 6.1 × 13.3 Å2), the conversion rate is only 2–4%. This discrepancy is attributed to the selective diffusion of molecules through the channels of COFs, facilitated by the deliberate manipulation of pore size and its distribution that dictate the mismatch between molecular size and pore aperture.126 Moreover, the effects of functional groups in COFs are also significant. Three isostructural COFs were synthesized by incorporating various functional groups, namely 2,2′-dimethoxyl-3,3′,5,5′-tetrakis(4-aminophenyl)biphenyl (OMe-TPBP)-COF (methoxy group), OMe-OH-TPBP-COF (methoxy and hydroxy groups), and OH-TPBP-COF (hydroxyl group). These tailored modifications of COFs were introduced to create specific docking sites inside their micropores, which entails great impact on the catalytic conversion of small molecules. The reaction yields for the three types of COFs towards the CO2 cycloaddition with epoxides were 91%, 89%, and 48%.127
On the other side, the metal site is usually regarded as an essential structural feature when targeting gas adsorption applications. The types and locations of metal sites anchored onto the COF network are well tunable by either pre-SM or post-SM approach from the bottom-up and peer-to-peer perspectives (Fig. 1e). For instance, the introduction of Li metal sites by post-SM into nanoporous COFs has yielded impressive results, enhancing the CO2 adsorption capacity of COF-102 to 409 mg g−1 and that of COF-105 to 344 mg g−1 under standard conditions (298 K and 1 bar).121 Similarly, the incorporation of Eu(III) into COOH-3D-COF by post-SM has significantly improved its adsorption capabilities, with an increased adsorption capacity of up to 211.4 mg g−1 for 9,10-phenanthrenequinone (PQ) and a notably higher PQ recovery rate (∼97% compared to ∼60% for metal-free COOH-3D-COF).128
For energy applications, such as supercapacitors, batteries, fuel cells, and photo- and electro-catalysis, extended π-conjugation of the COF network becomes an essential structural feature because it is closely related with fast charge transport and collection properties required to couple with not only the fast migration or insertion/extraction of metal ions during fast charging and discharging processes but also rapid chemical reactions at active sites. For example, Singh et al. harnessed the chemical stability and extended π-conjugation of thiazole-linked COFs, enabling the thiazole-linked COF electrode to undergo more than 5000 cycles in Li-organic batteries.129 In addition, compared to imine- or arylhydrazone-linked COFs, which exhibit relatively low stability and poor π-delocalization, olefin-linked COFs demonstrate excellent stability and photo-electrochemical performance.78
In most cases, the identification of crucial structural features dictating the properties of COFs has heavily relied on experience or scientific intuition. However, this approach proves to be inefficient and time-consuming, as the underlying structure–property relationship can only be revealed and validated afterwards using more robust experimental or theoretical tools such as QM/MM calculations. To overcome these limitations, emerging techniques empowered by flourishing ML methods offer a promising avenue as introduced in the following section. By leveraging diverse ML-enhanced high throughput methods and techniques, these structural features can be effectively utilized as descriptors, enabling more accurate, efficient, and targeted structural design and screening of high-performance COF materials tailored for specific applications.
2.3. Structural design enhanced by machine-learning
In addition to the design rationale of reticular chemistry for COF networks, which is based on the symmetry and connectivity of polytonic molecular monomers, there are pioneering works that enable the screening and prediction of COF materials for specific applications using ML methods.130–132 ML can be defined as a branch of artificial intelligence (AI) that develops algorithms and models capable of learning from data to make predictions or decisions without being explicitly programmed. At its core, ML relies on the analysis of large datasets to uncover patterns, correlations, and underlying structures. By iteratively adjusting model parameters based on training data, ML algorithms optimize their predictive performance, allowing them to generalize well to unseen data.In the field of materials science, ML provides a versatile toolbox for tackling the challenges of material discovery, design, and characterization.133–136 By utilizing a variety of algorithms, researchers can extract valuable insights from large amounts of experimental and computational data. The development of accurate predictive models can identify novel materials with desirable properties and accelerate the design and optimization process. One of these is represented by the afore-mentioned MGI, which was first proposed in 2011 and focuses its research on developing high-throughput computational tools and using ML to predict the properties and behaviors of materials faster and more accurately to accelerate innovation in advanced materials.137,138 MGI is a pioneering effort aimed at expediting the development of advanced materials. By harnessing the power of ML, MGI enables the extraction of valuable insights from vast volumes of experimental and computational data, thereby driving accelerated progress in materials research and innovation. The development of accurate predictive models can identify novel materials with desirable properties and accelerate the design and optimization process.
The general research process of ML encompasses several key steps, including data collection, preprocessing, selection of data description methods, selection of ML models, model interpretation, and application. These steps collectively determine the prediction accuracy, interpretability, and generalization ability of the ML model as schematically illustrated in Fig. 3.139–141
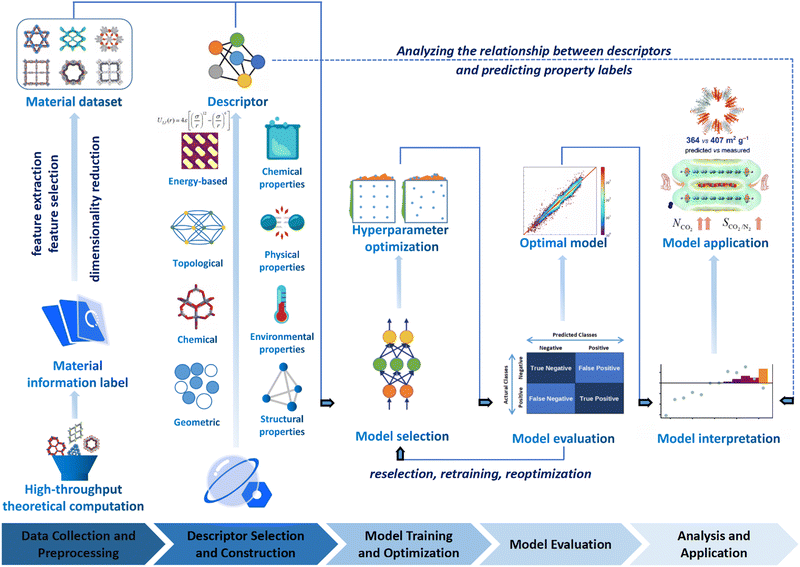 | ||
| Fig. 3 The flowchart of ML enhanced structural design for COFs, which involves data collection and preprocessing, selection of data description methods, and model interpretation and application. Modified with permission.141–144 Copyright 2021, 2022, 2022, 2019, American Chemical Society, Royal Society of Chemistry. | ||
(i) Data collection and preprocessing. The effectiveness of ML heavily relies on the quality of data used for training. For research focused on COFs, obtaining high-quality COF datasets is crucial for achieving better training results. However, acquiring such data can be challenging, and it may be necessary to perform preprocessing steps such as data cleaning, normalization, and feature engineering to ensure that the data are suitable for effective ML model training. Specifically, data cleaning entails identifying and rectifying inaccurate, incomplete, irrelevant, duplicated, or improperly formatted data. Normalization comes into play when the features of ML models have different ranges, and it involves scaling the dataset to ensure uniformity. On the other hand, feature engineering is the process of leveraging domain knowledge to restructure the data and create “features” that optimize ML algorithms.
(ii) Selection of data description methods. How COFs are described is an important factor that influences the performance of the ML models. In the process of ML, the descriptor usually plays a crucial role in establishing a meaningful correlation between the input and output data. This correlation is necessary to ensure that the COF materials are accurately described and that the resulting models can effectively deduce their target topologies, geometries, and properties. The more accurately and comprehensively the COFs are described, the better the prediction effects can be achieved. In addition to the cases of descriptors that can be calculated rapidly to determine the properties of COFs, abstract material representation without actual structural information may also be used through a representation scheme considering essential constituents and structural features of COF networks (i.e. molecular monomers and topologies of COFs).
(iii) Selection of ML models. Selecting suitable ML algorithms is essential for building high-performance models. Researchers need to carefully consider various ML algorithms such as decision trees (DT), random forests (RF), support vector machines (SVM), or deep learning methods like deep neural networks, depending on the specific objectives and characteristics of the COF dataset. Furthermore, hyperparameter optimization is necessary to fine-tune the models and achieve optimal performance.145
(iv) Model interpretation. Interpreting the ML models is crucial for gaining insights into the structure–property relationships of materials. Models with high interpretability can provide valuable information to researchers, helping them understand the underlying factors and mechanisms that contribute to the properties of COFs. Interpretation techniques such as feature importance analysis (FIA), shapley additive explanation (SHAP) values, or local interpretability methods (LIM) can be employed to gain a deeper understanding of the model's decision-making process.
In summary, the performance and capabilities of an excellent ML model are determined by the quality of training data, suitable data description methods, and appropriate selection of ML algorithms. In practical research and applications, researchers need to consider these three aspects comprehensively, make informed choices, and optimize accordingly to obtain high-quality predictive results and a deeper understanding of the problem.
Fortunately, despite these difficulties, a number of open-source COFs databases have emerged to advance ML in the materials domain. In 2018, Smit et al. first introduced an open-source COF structure database called the hypothetical covalent organic framework (hypoCOF), which has been updated to its third edition as of today.146 A collection of 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 COFs generated in silico from 666 different organic linkers were presented, forming both 2D layered and 3D configurations. The researchers investigated the potential use of these frameworks for methane storage by employing grand-canonical Monte Carlo (GCMC) simulations to calculate their deliverable capacities (DCs).147 The genomic covalent organic framework (GCOF) is a database that encompasses a library of genetic structural units (GSUs) and a collection of COFs obtained through materials genomics methods.27 The GSU library comprises 130 units categorized as center, linker, and functional group, offering diverse geometries and chemical compositions for building COFs. The GCOF database contains a total of 471
840 COFs generated in silico from 666 different organic linkers were presented, forming both 2D layered and 3D configurations. The researchers investigated the potential use of these frameworks for methane storage by employing grand-canonical Monte Carlo (GCMC) simulations to calculate their deliverable capacities (DCs).147 The genomic covalent organic framework (GCOF) is a database that encompasses a library of genetic structural units (GSUs) and a collection of COFs obtained through materials genomics methods.27 The GSU library comprises 130 units categorized as center, linker, and functional group, offering diverse geometries and chemical compositions for building COFs. The GCOF database contains a total of 471![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 structures, including 166
990 structures, including 166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 684 2D-COFs in various net topologies (e.g., hcb, sql, kgm) and 305
684 2D-COFs in various net topologies (e.g., hcb, sql, kgm) and 305![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306 3D-COFs in different frameworks (e.g., srs, bor, ctn). Researchers can leverage this database for high-throughput construction of COFs and targeted synthesis, finding applications in materials science and chemistry.
306 3D-COFs in different frameworks (e.g., srs, bor, ctn). Researchers can leverage this database for high-throughput construction of COFs and targeted synthesis, finding applications in materials science and chemistry.
Both hypoCOFs and GCOFs are based on high-throughput density functional theory (DFT) calculations, providing optimized structures and computed properties. Currently, they represent almost the only way to obtain large-scale COF property data. In terms of data quantity, computational properties obtained through quantum mechanics (QM) or molecular mechanics (MM) calculations, under a unified methodology, are more suitable for COF databases used in ML research compared to experimental material data. However, the process of constructing databases for COFs poses an inherent challenge. The feasibility of the calculations used in theoretical computations heavily relies on the methods and basis sets employed, but verifying every data point experimentally is not always possible for material scientists. Hence, it becomes essential to construct open-source databases using COFs collected from the literature as well.
The CoRe COF database, introduced by Tong et al. in 2017, has collected a total of 613 experimental COFs with solvent-free and disorder-free structure files. This database has served as a valuable resource for studying the structure–property relationships of COFs, particularly for Kr/Ar, Xe/Kr, and Rn/Xe separations.148 The database enables researchers to investigate the performance and capabilities of COFs in gas separation applications, specifically focusing on the aforementioned gas pairs. By utilizing the CoRe COF database, researchers can gain insights into the potential of COFs for gas separation processes and advance their understanding of the underlying structure–property relationships in COFs.
The CURATE database is designed to offer users access to high-quality, refined data from experimental sources. Currently, the database contains detailed information on 417 COFs, a subset of which have undergone structure optimization using DFT calculations.146 296 porous COFs were evaluated for carbon capture and storage (CCS) through the simulation of CO2 and N2 isotherms.
While the COF databases discussed earlier provide experimental data from the literature with higher feasibility and richer information compared to theoretical calculations, a few hundred data points are often insufficient to support large-scale ML training. Moreover, experimental data from different sources may involve complex environmental factors that make it challenging to compare the data. Ideally, a high-throughput MGI platform for COF material synthesis and characterization would enable the feasible acquisition of a large volume of experimental results under unified experimental conditions. However, a more practical and realistic approach would be to explore strategies for “augmenting” the limited data further. To address the challenge of data scarcity, several approaches can be considered.
(i) Data augmentation. Techniques such as data interpolation, extrapolation, or generation of synthetic data can be employed to increase the size of the existing dataset. This can help to enhance the diversity and coverage of the data.149
(ii) Transfer learning. Knowledge and models trained on related open-framework materials (e.g. zeolites or MOFs) or larger datasets can be leveraged and transferred to COFs. This approach can help to overcome data limitations by utilizing pre-existing knowledge and models.149,150
(iii) Active learning. By intelligently selecting a subset of samples for experimental characterization and validations based on model predictions, researchers can iteratively update and refine their models. This approach optimizes the use of limited experimental resources.151
(iv) Collaboration and data sharing. Encouraging collaboration among researchers and sharing of experimental data can lead to the accumulation of a larger and more diverse dataset, which can subsequently support more extensive ML studies. While the ideal scenario of a high-throughput experimental platform is desirable, these alternative approaches can help expand and utilize the existing limited data to drive advancements in COF research and enable more robust ML studies.
Descriptors that satisfy the above characteristics are not rare, and both structural information and some property information of the material can be used as descriptors. In general, from the perspective of the object being described, descriptors can be categorized into material structure descriptors and material property descriptors according to the recorded material information, and environmental descriptors, i.e., descriptors that do not describe the material itself, can also be added in some special studies. In practice, a mixture of these types of descriptors is often used to more fully characterize COFs. From the perspective of descriptor forms, they can be divided into geometric, topological, chemical, and energy-based descriptors.
(i) Geometric descriptors. These descriptors are fundamental metrics that relate to the target properties of COFs, such as pore size/volume, surface area, and density.
(ii) Topological descriptors. In addition to these basic metric descriptions, topological descriptors provide a more comprehensive representation of complex structural features of COFs. Topological data analysis (TDA) methods have been developed to effectively describe and deduce topological information associated with the intricate micropore environments in porous materials, including micropore typology, morphology, and connectivity.157,158
(iii) Chemical descriptors. Chemical descriptors can be compiled concurrently with the aforementioned descriptors to jointly consider both the compositional properties (e.g. atomic number) and the physicochemical properties of COFs (e.g. electronegativity, polarizability, ionization energy, dipole, quadrupole, and higher moments).
(iv) Energy-based descriptors. These descriptors enable the direct representation of crucial interactions that are closely linked to COF properties. For instance, the energy histogram of the potential energy landscape upon grid sampling is widely utilized to describe host–guest interactions between adsorbates and porous materials, facilitating the successful prediction of high-performance porous structures in gas adsorption and separation applications.141
In 2020, Li et al. reported a study utilizing ML methods to screen COFs for application in heating, cooling, and ice making. They selected descriptors including largest cavity diameter (LCD), accessible surface area (ASA), available pore volume (Va), helium void fraction (VF), Henry's law constant (KH), and adsorbent density (ρ). Using a RF model, they successfully predicted various high-performing COFs and MOFs for use in adsorption-driven heat pumps (AHPs). Among these descriptors, KH describes the solubility property of COFs, while the remaining descriptors, such as LCD, ASA, Va, VF, and ρ, are structural descriptors that capture various aspects of the material's structure.156
In 2021, Kumar et al. reported a study on the synthesis of COFs using sustainable solvents. In this study, they employed ML approaches for the first time to predict the surface area of COFs based on solvent and amine precursor descriptors. The researchers constructed a dataset consisting of 43 measured surface area data points and 2639 calculated descriptors. They utilized partial least squares regression and principal component analysis (PCA) to analyze the dataset and reduce the dimensionality of the correlated features.
A study on predicting the adsorption capacity of COFs was published by Yang et al. in 2021.142 The researchers selected a set of descriptors, including LCD, ASA, Va, percent elemental composition, and other structural or property descriptors, and trained multiple ML models using these descriptors. Another study conducted by Zhou et al. focused on using ML to design COFs for efficient catalytic hydrogen evolution reaction (HER). The researchers used a set of 23 features, including the ionic radii, electronegativity, electron affinity energy, and first ionization energy of the metal, to describe the COFs. After applying the gradient boosting regression (GBR) algorithm for feature selection, they identified 12 most important features for further analysis. The GBR model was then trained on these calculated features to predict 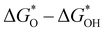 , which represents the difference in free energy between adsorbed oxygen and adsorbed hydroxyl species.159
, which represents the difference in free energy between adsorbed oxygen and adsorbed hydroxyl species.159
(i) Decision tree (DT). A DT is a commonly used ML algorithm for classification and regression problems. It constructs a tree by selecting the best splitting criterion to partition the dataset into different subsets. DTs are easy to understand and interpret, and they can handle various types of data, while also being robust to missing values and outliers. However, DTs are prone to overfitting, especially with larger depths. Overfitting occurs when the model performs well on the training set but poorly on unseen data.160,161
(ii) Random forest (RF). An RF or random decision forest (RDF) is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of DTs at the training time. Each DT is trained using a random subset of the training data and a random subset of the features. It repeats the process of building multiple independent DTs and obtains the final output through voting or averaging of predictions, which reduces the overfitting of datasets and improves the performance. RF can handle high-dimensional and large-scale data, exhibits robustness against missing values and outliers, and allows for the assessment of feature importance.162 However, it has poor interpretability and may not perform well with time series data that have temporal dependencies.163
(iii) Support vector machine (SVM). SVM is an algorithm for linear classification and regression in high-dimensional spaces, and with the addition of a kernel function, it is possible to carry out classification and regression tasks on nonlinearities. SVM is a powerful classifier that possesses the ability to handle nonlinear classification, robustness, and interpretability. However, it comes with higher computational complexity for large datasets, sensitivity to parameter selection, and requires additional handling for multi-class problems. In practical applications, it is important to consider the advantages and disadvantages of SVM, and perform appropriate parameter tuning and extensions based on specific circumstances to achieve optimal performance.
(iv) Artificial neural networks (ANN). An ANN is an algorithm that simulates the functioning of nerve cells in living organisms, and which constructs artificial neurons into a neuronal network according to certain relationships, and uses the algorithm to simulate signaling between neurons. Theoretically, a suitable ANN can fit any nonlinear function. An ANN can have multiple hidden layers, allowing for the abstraction and representation of input data through sequential computation and information propagation.164 It possesses powerful learning capabilities, adaptability, and parallel processing capabilities. However, it requires a large amount of training data and computational resources, as well as careful structural design and parameter tuning.
(v) Boosting. In ML, boosting is an ensemble meta-algorithm for primarily reducing bias, and also variance in supervised learning, and it is a family of ML algorithms that convert weak learners to strong ones. Boosting is a powerful ensemble learning algorithm that enhances predictive performance and robustness, while offering flexibility and feature selection capability. However, it is sensitive to noise, requires longer training time, and necessitates careful parameter tuning. When applying the Boosting algorithm, it is important to consider its strengths and weaknesses, and make appropriate adjustments and optimizations based on specific circumstances.
(vi) Partial least squares (PLS). PLS regression is a statistical method that bears some relationship to principal components regression (PCR); instead of finding hyperplanes of maximum variance between the response and independent variables, it finds a linear regression model by projecting the predicted variables and the observable variables to a new space. Because both the X and Y data are projected to new spaces, the PLS family of methods are known as bilinear factor models.
Deep learning. Deep learning is a ML algorithm based on multi-layer ANNs that are able to analyze complex patterns and relationships in data, and it is inspired by the structure and function of the human brain and turns out to be the most promising and efficient ML research method.
(i) Graphical neural network (GNN). GNNs are neural networks that can efficiently extract information from graph structures, in which the convolutional layer is able to extract the potential information in the graph structure, which is widely used in the direction of computer vision. The strength of a GNN lies in its ability to effectively handle unstructured graph data and perform complex reasoning and learning based on node and edge relationships.165 It can capture local structural patterns and global topological features among nodes, enabling more precise graph analysis and prediction.166 However, for large-scale graph data, the GNN exhibits high computational complexity, necessitating considerations for algorithm optimization and computational resources.
(ii) Transformer. The transformer model is a deep learning model based on the attention mechanism,167 which is commonly used in natural language processing tasks such as semantic recognition and translation. In recent years, the transformer model has emerged as a high-performance model such as for bidirectional encoder representations from transformers (BERT) and Graphormer after development.168,169
(iii) Generative deep learning model. Generative modeling is a ML model used to generate new samples similar to training data or to generate new data. The goal of a generative model is to learn the probability distribution of the data and generate new data points by sampling from that distribution. Common generative models are variational auto-encoder (VAE), generative adversarial network (GAN), and generative pre-trained transformer (GPT).
Practically, these deep learning ML models have enabled the efficient exploration of high-performance gas adsorption porous materials.170–173 As the state-of-the-art ML model, deep learning achieves excellent prediction results while reading only the structural information of the material as much as possible, which further reduces the computational cost for the material design. Notably, a deep learning based GNN modelling platform for materials chemistry has been well established recently,174 which would greatly facilitate the development of application-oriented high-performance COF materials in the near future. The characteristics, advantages and disadvantages of the ML model mentioned above as well as the problems to be paid attention to when applying in the field of COFs are listed in Fig. 5.
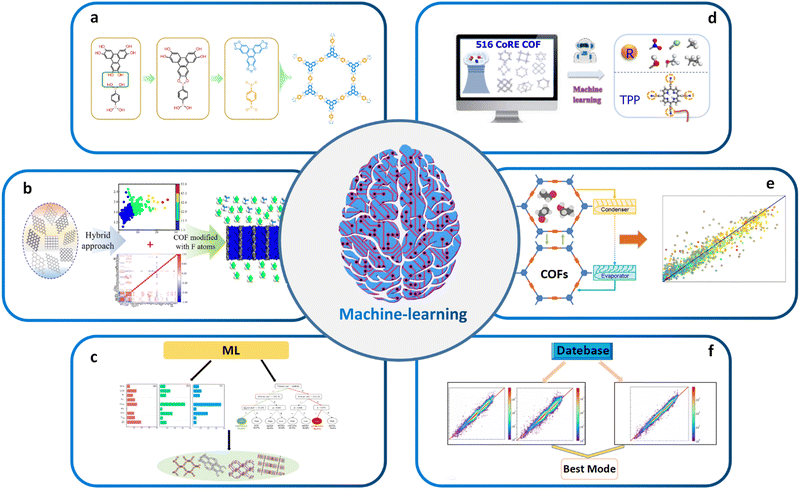 | ||
| Fig. 4 (a) High-throughput topology design and construction of COFs achieved using materials genomics methods. Modified with permission.27 Copyright 2018, Springer Nature. (b) Combining ML and molecular simulations for screening optimal COF structures tailored for gas separation applications. Modified with permission.143 Copyright 2022, American Chemical Society. (c) Using high-throughput molecular simulations to calculate the gas storage and deliverable capacities of COFs. Modified with permission.154 Copyright 2021, Elsevier. (d) ML aided computational screening of COFs to identify superior COF structures for gas capture. Modified with permission.155 Copyright 2022, American Chemical Society. (e) High-performance COFs for heating, cooling and ice-making were identified through high-throughput computational screening based on large classical Monte Carlo simulations in ML. Modified with permission.156 Copyright 2020, American Chemical Society. (f) Enabling intelligent ML: automated feature engineering, pipeline matching, parameter tuning, and model selection for building accurate ML prediction models. Modified with permission.142 Copyright 2021, American Chemical Society. | ||
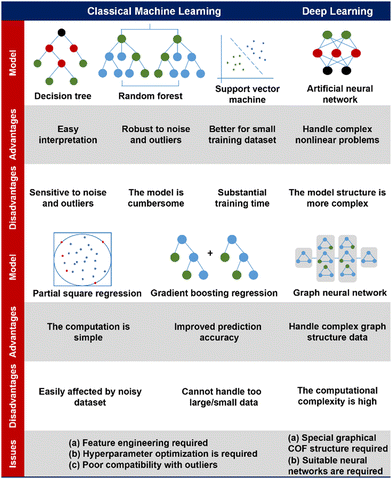 | ||
| Fig. 5 A comparison of diverse machine learning models, addressing their advantages, disadvantages, and issues for application in the field of COFs.142–144,151–154 | ||
Up to now, most studies that deploy ML algorithms for the structural design of open-framework materials are supervised, which involves training a ML model using labeled data. In contrast, allowing ML input–output pairs to autonomously cluster materials and search common characteristics among materials in a high-dimensional material space from different perspectives can help researchers understand their conformational relationships from a new perspective. While unsupervised ML studies have been applied in organic chemistry, particularly with pharmaceutical small molecules, this approach remains relatively uncommon in the field of COF structural design.175–177
In addition, the rapid development of generative modeling has enabled the computational design of novel compliant materials for COFs, which already has a rich application in organic chemistry and is emerging in the materials field.178,179 The available generative models, such as VAE, GAN, GPT, etc., already have sufficient capability to learn the structure and nature features and generate the corresponding new COF structures according to the desired properties or applications. However, it is worth noting that the application of these models requires large amounts of data and high computational power, as well as validation and experimental verification of the model results to ensure their accuracy and reliability.
Another important application of ML in materials science is the screening of high-performance structures and topologies for various applications. By training ML models based on vast amounts of properties or performance data, researchers can predict the properties or performance of millions of hypothetical structures for effective material screening, among which optimal ones can be further experimentally synthesized and tested to validate their properties and performance. For example, Cao et al. combined ML and molecular simulation to design optimal COFs for reversed C2H6/C2H4 separation before experimental resources are devoted (Fig. 4b).143 The results of this work can provide molecular-level insights for the structural design and synthesis of new COFs that can directly eliminate low concentrations of ethane from C2H4/C2H6 mixtures. Zhang et al. began with high-throughput molecular simulations to calculate the methane storage (6.5 MPa) and deliverable (6.5–0.58 MPa) capacities of 404![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 COFs at 298 K. The complete dataset with 23 features was then randomly divided into a training set and a test set in the ratio of 20
460 COFs at 298 K. The complete dataset with 23 features was then randomly divided into a training set and a test set in the ratio of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 for evaluating the predictive capabilities of several ML algorithms. The transportable capacities of the best COF structures were found to be superior to those of various adsorbents reported so far (Fig. 4c).154 Yang et al. conducted computational screening on 516 experimental COFs to identify the superior SBUs for wet flue gas separation by ML (Fig. 4d).155 ML also plays a critical role in screening high-performance COF-based catalysts and other functional materials. By training ML models on large datasets of known catalysts, researchers can predict the properties of hypothetical catalysts and identify those with desirable properties for specific chemical reactions. For example, Deng et al. utilized a combination of comprehensive DFT calculations and ML techniques to systematically investigate the OER activity of a range of simplified model catalysts. Interestingly, their findings revealed that certain Fe–N3O and Co–N2O2 model catalysts, which had not been previously explored experimentally, exhibited superior catalytic performance for OER. On the other side, Li et al. reported an approach to identify the high-performing structures of COFs for heating, cooling, and ice-making by high-throughput computational screening based on GCMC simulations and ML (Fig. 4e).156
80 for evaluating the predictive capabilities of several ML algorithms. The transportable capacities of the best COF structures were found to be superior to those of various adsorbents reported so far (Fig. 4c).154 Yang et al. conducted computational screening on 516 experimental COFs to identify the superior SBUs for wet flue gas separation by ML (Fig. 4d).155 ML also plays a critical role in screening high-performance COF-based catalysts and other functional materials. By training ML models on large datasets of known catalysts, researchers can predict the properties of hypothetical catalysts and identify those with desirable properties for specific chemical reactions. For example, Deng et al. utilized a combination of comprehensive DFT calculations and ML techniques to systematically investigate the OER activity of a range of simplified model catalysts. Interestingly, their findings revealed that certain Fe–N3O and Co–N2O2 model catalysts, which had not been previously explored experimentally, exhibited superior catalytic performance for OER. On the other side, Li et al. reported an approach to identify the high-performing structures of COFs for heating, cooling, and ice-making by high-throughput computational screening based on GCMC simulations and ML (Fig. 4e).156
Traditional ML models have been successfully used to predict essential synthetic descriptors from high-throughput ones that impact the structure and properties of target materials, providing guidance for the design of COFs. For example, the PLS ML model was used to explore green, sustainable solvents for COF synthesis. The first step was to predict the specific surface area of COFs using ML. Then, 43 COFs were synthesized in different green solvent environments, and their specific surface areas were measured. High-throughput theoretical calculations were used to obtain 2639 descriptors for ML training. After performing PCA and PLS regression, a trained ML model was obtained with an R2 value of 0.83.144 Additionally, a binary classification model was used to predict whether COFs are crystalline or amorphous, achieving a classification accuracy of 0.87. Feature analysis revealed that descriptors related to the solvent and amine precursor were the most important in predicting these two features. These results are significant in understanding the effect of solvent on COF performance and advancing the use of green solvents in COF synthesis. Generally, instead of the very labor-intensive and time-consuming trail-and-error material design and screening processes based on experimental validations or conventional computational algorithms, ML models allow the highly accurate and cost-effective application-oriented screening of COF materials. However, building robust prediction models is critical to analyze the test datasets. The selection of appropriate model architecture, training process, regularization method, and hyperparameters would have significant impact on the final performance of the ML algorithm, which is quite difficult and requires advanced data processing and analysis skills.139
Recently, automated machine learning (Auto ML) that effectively integrates the data preprocessing, feature engineering, algorithm selection, and model parameter optimization steps has become a research hotspot.180 It allows the automated selection of best combination of model parameters, which thus entails automatic feature engineering, pipeline matching, parameter adjustment, and model selection towards the construction of an accurate ML prediction model.142 In this sense, Auto ML significantly facilitates the application of ML and outperforms traditional ML algorithms. Yang et al. used Auto ML to analyze the working capacity of CH4 based on 403![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959 COFs. They found that the tree-based pipeline optimization tool not only eliminates complex data preprocessing and model parameter tuning but also outperforms traditional maximum likelihood models. Auto ML provides an extremely time efficient approach for screening COFs compared with traditional GCMC simulations (Fig. 4f).142
959 COFs. They found that the tree-based pipeline optimization tool not only eliminates complex data preprocessing and model parameter tuning but also outperforms traditional maximum likelihood models. Auto ML provides an extremely time efficient approach for screening COFs compared with traditional GCMC simulations (Fig. 4f).142
2.4. Challenges and opportunities
The relationship between the key characteristics of COFs and their specific application performance is crucial for the design and utilization of COF materials. The pore structure of COFs, including pore size, pore volume, and pore distribution, directly influences their performance in applications such as gas adsorption, separation, and energy storage.181 Surface area has a direct impact on gas adsorption, catalytic reactions, and electrochemical properties. Additionally, chemical functional groups can be adjusted to tailor the affinity of COFs for specific applications such as gas adsorption, catalytic reactions, or molecular recognition. The electronic structure of COFs affects their conductivity, light absorption, and electrochemical performance, which are critical for applications like photovoltaics, photocatalysis, and electrochemistry.182 Furthermore, the thermal stability and environmental adaptability of COFs play a crucial role in applications under high-temperature conditions or in diverse humidity and atmospheric environments. The design of COFs has undergone significant advances, particularly from the aspects of topologies, porosities, and functionalities. However, the constantly evolving requirements for application-oriented COF synthesis pose major challenges in transforming the structural design approach towards more targeted, comprehensive, and accurate construction of COF networks. These challenges can be broadly classified into three aspects.First, the current structural design approach for COFs, based on reticular chemistry and topological science, has limitations in scenarios involving geometry-mismatched or sub-stoichiometric construction of COF networks. Classical reticular chemistry theory predicts the COF network construction based on the hypothesis of geometry-matched and stoichiometric covalent linkage formation between the symmetrically distributed reactive sites of molecular monomers (Fig. 6a).183 However, insufficient (sub-stoichiometric) interconnections during the construction of COF networks give rise to exposed dangling reaction sites, thereby violating the predictions of classical reticular chemistry theory and causing a significant surge in structural diversity and complexity. Accordingly, the structural design and prediction of COFs confront major obstacles in scenarios associated with sub-stoichiometric or defective COF networks. In 2019, COF-340 was reported as the first crystalline, porous COF with a defective tth topology, demonstrating the need for more flexible and innovative methods to design and predict new topologies and properties of sub-stoichiometric or defective COF networks.184 Similarly, V. Lotsch demonstrated the unexpected formation of imine-linked [C4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3] sub-stoichiometric 2D COFs with a unique bex topology through the combination of tri- and tetratopic linkers.185 The discovery of sub-stoichiometric 2D COFs has greatly enriched the 2D COF repertoire and diversified the 2D topologies that have been long restricted to hcb, sql, hxl, kgm and kgd.52
C3] sub-stoichiometric 2D COFs with a unique bex topology through the combination of tri- and tetratopic linkers.185 The discovery of sub-stoichiometric 2D COFs has greatly enriched the 2D COF repertoire and diversified the 2D topologies that have been long restricted to hcb, sql, hxl, kgm and kgd.52
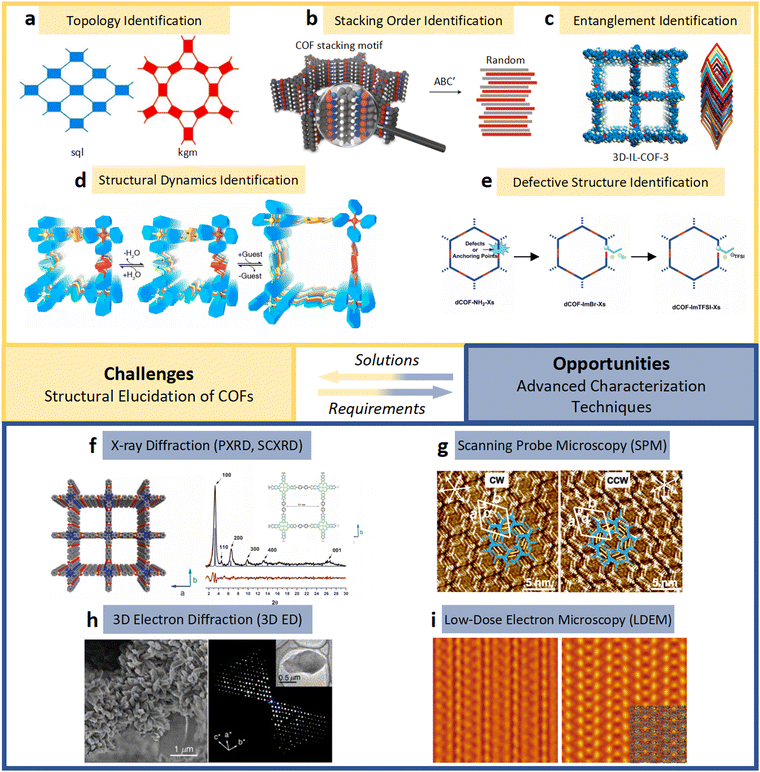 | ||
| Fig. 6 (a)–(e) The essential challenges and requirements in the structural elucidation of COFs for identifying topology, stacking order, entanglement, dynamics and defects. (a)–(e)183,191–194 Reproduced with permission. Copyright 2022, 2020, 2021, 2019, 2020, Springer Nature, Wiley-VCH. (f)–(i) The opportunities that arise from the development of advanced structural elucidation techniques such as X-ray diffraction, 3D electron diffraction, scanning probe microscopy and low-dose electron microscopy. (f)–(i)195–198 Reproduced with permission. Copyright 2013, 2021, 2017, 2023, Royal Society of Chemistry, Elsevier, American Association for the Advancement of Science. | ||
In addition, the ML based structural design of COFs faces major challenges as well as opportunities in rationally designing high-performance COF materials, including data collection and management, design bias, and featurization of material properties.
(i) Data collection and management. Experimental metadata include both instrumental and non-instrumental data as well as data of successful and failed experiments, all of which can be used to train and validate ML models, depending on the specific problem being addressed and the type of data available. Collection of complete experimental data is challenging and extremely time-consuming, and there is lack of a fully integrated solution to experimental data collection and an ecosystem with standards for data management. An electronic lab notebook provides a solution to the non-instrumental data collection, which gathers protocols, post-processing scripts, and measurement parameters, either successful or failed ones, with minimal effort from researchers.186,187 However, the major challenge of experimental data collection is to enable real-time instrumental data collection and to publish all data in a standard format.
(ii) Design bias. Quantifying the uncertainty of ML models in predicting new systems is challenging and costly,188,189 as these models do not rely on physical laws. In the field of chemistry, methods such as measuring the distance of new samples to training data or using ensemble models have been proposed to quantify uncertainty.190 Nevertheless, further research is needed to develop more reliable and cost-effective methods and provide guidance on selecting the appropriate method. Additionally, optimizing ML models based on a single performance metric can limit the discovery of new materials if the metric does not represent the actual application.
(iii) Featurization of material properties. Developing effective featurization schemes for describing material features, such as general purpose featurization methods including composition, simplified molecular-input line-entry system (SMILES) strings and Coulomb matrices,199 to predict target properties is a crucial step for ML. Challenges remain in generating featurization schemes for crystalline porous materials like COFs by considering both the representation of organic molecular monomers and periodicity/symmetry of the crystalline framework. In addition, material properties that require tensorial representations200 (e.g. stiffness, heat conduction and susceptibility tensors used for predicting mechanical, heat transport and magnetic/electronic properties) as well as subtle features associated with structural dynamics and framework flexibilities of COFs cannot be easily parameterized and implemented in ML.
Furthermore, the unambiguous validation of structural design and prediction of COFs remains challenging, especially for those with poor crystallinity or local structural features like defects, interfaces, stacking order, and entanglement.183,201,202 Traditional guidelines for the structural identification of other highly crystalline open-framework materials (e.g. MOFs and zeolites) may not be suitable for COFs that are usually subject to poor crystallinity due to the strong covalent linkages.203 The restricted coherent lengths of crystalline domains in COF materials pose a significant challenge to probe their atomistic structures by traditional crystallographic approaches. Moreover, the crystallization process of COFs gives rise to diverse types of local structural features, such as stacking order, interface, defects, and entanglement. These structures may emerge as a result of critical events such as mis-attachment,204 mis-stacking,105,205 intergrowth,206 and network interpenetration.22,207 The formation of these local structures during COF crystallization can be attributed to the interplay between the thermodynamic and kinetic aspects of the crystallization process,203,208 which usually have critical impact on the physicochemical properties of COFs and thus dramatically determine their performance in diverse applications. Thorough validation of COF structural design necessitates explicit and comprehensive elucidation of both periodic and local atomistic structures as well as their dynamics (Fig. 6a–e).183,191–194 However, this task remains arduous and demands advanced multiscale structural characterization tools and methodologies, potentially incorporating advanced diffraction and imaging characterization techniques. In the following section, advanced diffraction and imaging techniques dedicated to the multiscale structural elucidation of COFs, including X-ray and 3D electron diffraction, SPM as well as low-dose EM, are introduced (Fig. 6f–i).195–198
3. Structural determination by diffraction
3.1. Basic principles
The impact and role of diffraction in the structural elucidation of COFs can be summarized into three aspects. Firstly, diffraction can be used to determine the structure, lattice constant, and pore size of COFs. Secondly, it can be employed to check the synthesis of COFs, ensuring their purity and absence of impurities. Lastly, diffraction is beneficial to optimize the properties and performance of COFs by modifying their structure, such as gas adsorption and catalytic reaction. Overall, diffraction is an indispensable tool for investigating the structures and properties of COFs. Different diffraction techniques, including single crystal X-ray diffraction, powder X-ray diffraction, and electron diffraction, can be employed to determine the structures of COFs depending on the nature of the sample and the required level of structural information.When the incident beam and crystalline sample satisfy the following Bragg's law (eqn (I)), the constructive interference will occur and diffracted beams containing the structural information from the sample of interest will be recorded by detectors, producing diffracted spots or diffracted spectrum (Fig. 7a).209–211
2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ θ = nλ | (I) |
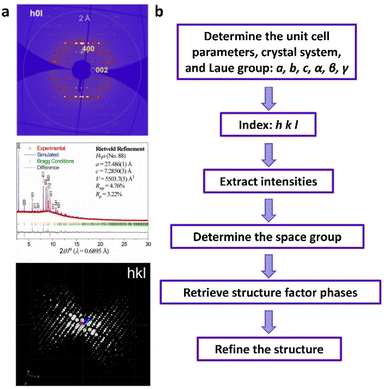 | ||
| Fig. 7 (a) Single crystal X-ray diffracted spots (upper), powder X-ray diffraction spectrum (middle), and 3D electron diffraction data (bottom). (a)209–211 Reproduced with permission. Copyright 2020, 2019, 2022 John Wiley and Sons, American Chemical Society. (b) Schematic illustration of structure determination using diffraction information. | ||
The intensity of each Miller index hkl is proportional to the square of its structure factor amplitude (|Fhkl|). Unfortunately, its structure factor phase (αhkl) is lost during the diffraction; however, it can be retrieved by using strong reflections in reciprocal space through a series of algorithms.213,214 It is called the “phase problem”, which has been considered as a challenging topic in crystallography. If αhkl of each Miller index is known, electron density or electrostatic potential density in real space can be calculated based on the following equation:
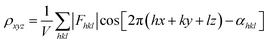 | (II) |
Thus, retrieving αhkl is the crucial step to obtain the electron densities (or electrostatic potential densities) that correspond with atomic positions. As shown in Fig. 7b, structure determination using diffraction methods (diffracted spots and diffracted spectrum) can generally be divided into six steps: (1) determine the unit cell parameters, crystal system, and Laue group; (2) index the diffracted spots or diffracted peaks; (3) extract intensities of hkl; (4) determine the space group based on the reflection conditions; (5) retrieve structure factor phases by using phasing algorithms such as direct method, Patterson methods, and charge-flipping algorithm. The initial structural model could be obtained after solving the phase problem. (6) Perform structure refinement to obtain all atomic coordinates, occupancy of atoms, atomic displacement parameters, host–guest interactions, etc.
3.2. Single crystal X-ray diffraction (SCXRD)
Among all diffraction methods for structure determination, SCXRD is the most mature technology, which is widely used in the structure determination of crystalline samples. In the successful structural analysis, processing of the single crystal selected for data collection is one of the key steps. The SCXRD technique has the strict requirement of crystal size which should be larger than 20 µm at least. However, a larger crystal size doesn't necessarily lead to superior data quality. The optimized crystal size depends on the crystal's diffraction capability and degree of absorption, the intensity of the selected radiation, and the sensitivity of the diffractometer's detector. The crystal's diffraction capability and absorption degree are determined by the type and quantity of elements it contains. Meanwhile, the intensity of the X-ray and the detector's sensitivity are both contingent upon the configuration of the diffractometer. It is generally observed that crystals composed predominantly of heavier atomic constituents necessitate smaller dimensions, whereas those comprising lighter atomic elements benefit from a larger size for optimal diffraction results.217 For COF materials, the formation of bonds between the building blocks is irreversible. This will lead to the presence of many defects and rapid termination of crystal growth, resulting in the formation of nanocrystals. Therefore, there are few studies on structural investigations of COFs by utilizing SCXRD due to the small crystal size of COFs.93,218,219 One of the key factors to synthesize single crystals is slowing down the crystallization rate and permitting the self-correction of defects during the growth of COFs. In 2018, Yaghi et al. reported a method for growing large single crystals of 3D imine-based COFs by introducing a large excess of anilines as modulators. Large crystals of COF-300, COF-303, LZU-79, and LZU-11 were synthesized by this synthetic approach and their structural features such as the degree of interpenetration, the arrangement of guest species, and reversed imine connectivity were investigated by SCXRD. For instance, the structural transformation of COF-300 in the hydrating process was explored by SCXRD. It turned out that water clusters are identified, and guest waters also interact with the imine functional group in the COF-300 framework, resulting in its framework shrinkage (Fig. 8a, b and 11d). It is also worth noting that COF-300 and COF-303 have almost identical structures except for the connectivity of imine and such fine structural features can also be detected by SCXRD (Fig. 8c–e).93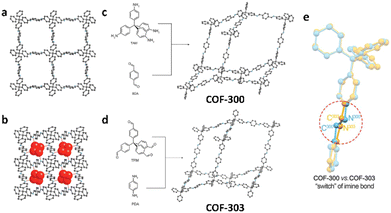 | ||
| Fig. 8 Crystal structure of (a) COF-300 and (b) hydrated COF-300. (c) COF-300 produced by TAM and BDA. (d) COF-303 produced by TFM and PDA. (e) Comparison of COF-300 (blue) and COF-303 (yellow). (a)–(e)93 Reproduced with permission. Copyright 2018, American Association for the Advancement of Science. | ||
3.3. Powder X-ray diffraction
As mentioned before, most COFs are prone to crystallize in nanosize. Thus, powder X-ray diffraction (PXRD) is the most commonly used method for structural characterization of COFs. Specimen preparation for PXRD is simpler than that for SCXRD. However, a true PXRD pattern requires a specimen with numerous particles showing diverse orientations. Essentially, particles must have a random distribution of crystallographic orientations relative to each other. Spinning the specimen continuously during data collection is an effective method to enhance the number of particles in the irradiated volume and ensure their random orientations. However, the intrinsic overlap of diffracted peaks makes it more challenging for structure determination using PXRD data. Besides the aforementioned “phase problem”, addressing the overlapped intensities is another significant issue in PXRD structure determination. Typically, two approaches are employed for this problem: (i) discard the reflections with completely or nearly overlapped peaks and (ii) distribute the total intensity of the overlapped peaks equally among the individual reflections. The former approach is most effective with the utilization of direct methods, while the latter proves to be favorable in the implementation of Patterson methods.220Due to large unit cell parameters and low crystallinity of COFs, PXRD is usually used to check whether the manually built structural models are correct or not through Le Bail fitting or Pawley refinement.221–225 There are a few reports regarding COF structures solved by PXRD.202 For example, COF-432 reported by Yaghi's group was partially solved by PXRD due to its high crystallinity. The unit cell parameters, space group, and even electron density map of fragments of ETTA were deduced from PXRD data (Fig. 9a).216 The complete initial structural model was finalized by manually linking ETTA fragments with TFB building blocks.216 Meanwhile, PXRD data are utilized not only for determining the stacking sequences of COFs (Fig. 11a),216 but also for monitoring structural transformation in their stacking sequences (Fig. 11b).226,227 For instance, Zhao et al. revealed the solvent-induced structural transformation of 2D COFs based on the PXRD data and computational modeling. In the dry form, 2D COFs experience AA-stacking structures. After adding solvent, the PXRD patterns of 2D COFs change and different quasi-AB-stacking structures were obtained (Fig. 11b).227 Moreover, guest-dependent dynamics of COFs can also be revealed by Rietveld refinements against PXRD data if pure phase COFs have high crystallinity and uniform morphologies. For instance, COF-300 reported in 2009 shows a step and hysteresis gas adsorption behavior.81 However, this dynamic structural feature was totally uncovered until 2019.202 Zhang and Zhou et al. found, based on PXRD, that COF-300 adopts a contracted structure in a moist atmosphere. Interestingly, COF-300 shows a large amplitude expansion when exposed to organic solvents such as tetrahydrofuran (THF) and this structure change is reversible (Fig. 9b). This expansion is attributed to the deformation of the tetrahedral building block, the displacement between frameworks, and the conformation changes of the imine bonds.
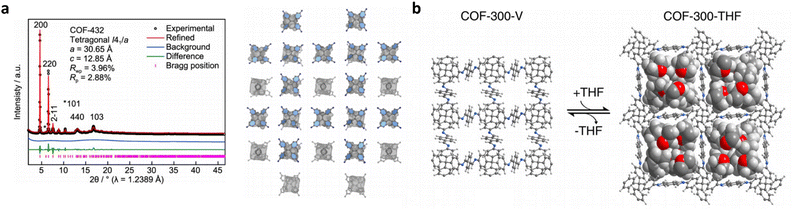 | ||
| Fig. 9 (a) Le Bail fitting (left) and electron density map (right) of COF-432. Reproduced with permission.216 Copyright 2020, American Chemical Society. (b) Structural dynamics of COF-303 in the presence/absence of THF guest species. Reproduced with permission.202 Copyright 2019, American Chemical Society. | ||
3.4. 3D electron diffraction
In 1924, De Broglie proposed that electrons should possess the wave–particle duality, which was proved by Davisson and Thomson in 1927 through diffraction experiments between electrons and metal.228,229 On the one hand, compared with X-rays, electrons with the wave nature have shorter wavelength and much stronger interactions with matter. Thus, electron diffraction (ED) can investigate single crystals down to nanometers. On the other hand, electrons are negatively charged particles and they can not only interact with outer electrons but also with the nucleus of atoms. Thus, ED of samples is associated with their distribution of electrostatic potentials. Recently, a series of 3D ED techniques such as electron diffraction tomography (EDT), rotation electron diffraction (RED), microcrystal electron diffraction (MicroED), serial electron diffraction (SerialED) and precession-assisted electron diffraction tomography (PEDT) have emerged for determining the crystallographic structures of novel functional materials and biomacromolecules that crystallize in nanosize.230–239 For example, Zou et al. proposed a method called RED for automatic collection of 3D ED in 2009, which combines the goniometer tilt and beam tilt. Unit cell parameters, space group, and even atomic coordinates can be obtained based on 3D ED data.239 Recently, the continuous RED (cRED) technique, an updated version of RED, has been developed and the quality of 3D ED data collected by cRED has been greatly improved. Moreover, in order to decrease the beam damage, a cryogenic sample holder or cryo-TEM combined with 3D ED techniques was employed.233Since most COFs crystallize in nano-size with low crystallinity, 3D ED techniques are combined with other characterization techniques to elucidate their structures. For instance, Ma et al. deduced the unit cell parameters and possible space groups of COF-505 from its 3D EDT data. Combined with the information of PXRD, HRTEM, and chemical composition, a 3D structural model of COF-505 was built.43 In another study, Liu et al. utilized 3D EDT and PXRD data to construct 3D structures of COF-506-Cu. They further investigated the demetallized form of COF-506-Cu, known as COF-506, and discovered its ability to accommodate guest molecules larger than the pores of COF-506-Cu, demonstrating the adaptive dynamics of COF-506 (Fig. 11c).123 If the crystallinity of COFs is higher, partial or total structural models can be obtained using 3D ED techniques. Zou et al. reported that the initial building block arrangement of COF-320 could be found from RED data collected at 89 K using FOX software (Fig. 10a and b) and only central carbon atoms of building blocks could be located from RED data collected at 298 K.240 Even more remarkably, Wang et al. utilized the cRED technique to uncover the intricate seven-fold interpenetrated pts structure of 3D-TPE-COF, which has potential applications in producing white light-emitting diodes (Fig. 11e).241 In addition to the structure of COFs composed of rigid building blocks, the atomic structure of FCOF-5, which contains flexible C–O single bonds, was determined by combining cRED and PXRD techniques (Fig. 11f).243 For 3D-TPB-COF with –H, –Me, or –F substituents, the resolution of its cRED datasets can reach 0.9–1.0 Å, enabling the location of all non-hydrogen atoms, including the functional groups, for the first time (Fig. 11g).244 More importantly, the host–guest interactions and dynamic features can also be resolved by 3D ED.242,245 The breathing behavior of FCOF-5 was uncovered by Sun et al. using enhanced cryo-cRED. The resolution and completeness of data are improved by merging the optimal datasets selected by hierarchical cluster analysis (HCA). As shown in Fig. 10c, the precise structure of the guest ethanol molecule and the pore size of expanded FCOF-5 were determined. In the contracted FCOF-5, 1,2,4,5-tetrakis[(4-formyphenoxy)methyl]benzene (TFMB) is twisted and its phenyl ring block the pores, resulting in the pore width reduced to 1.7 Å (Fig. 10d). This explains why contracted FCOF-5 has no N2 and Ar adsorption.242 Furthermore, the verification of topological transformations can be accomplished using 3D ED. For instance, the cRED technique has demonstrated that the topology of 3D COFs can be tuned through steric control. Wang et al. successfully altered the topology of a 3D COF from a pts net to a ljh net by increasing the steric hindrance of the substituents on the building blocks (Fig. 11h).246 This discovery presents a novel approach for the design and synthesis of COFs with new topologies.
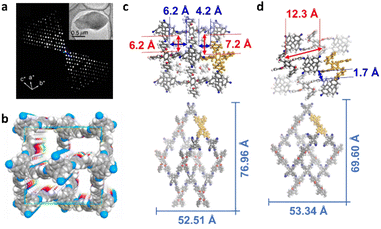 | ||
| Fig. 10 (a) Reconstructed 3D RED data of COF-320 collected at 89 K. (b) Corresponding structural model of COF-320 viewed along the [100] direction. The porous structure (upper) and single pts net (bottom) of (c) expanded FCOF-5 and (d) contracted FCOF-5. (a) and (b) Reproduced with permission.240 Copyright 2013, American Chemical Society. (c) and (d) Reproduced with permission.242 Copyright 2022, American Chemical Society. | ||
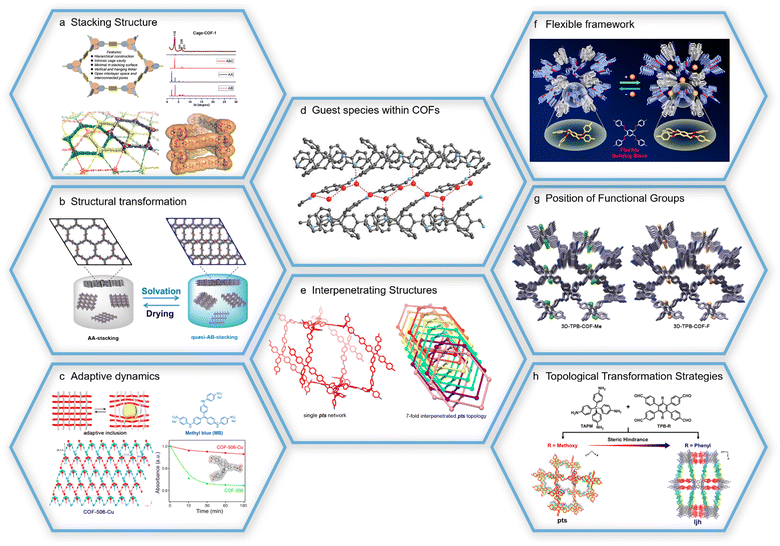 | ||
| Fig. 11 (a) PXRD patterns and structural representations of cage-COF-1 with ABC-stacking. Reproduced with permission.216 Copyright 2020, American Chemical Society. (b) Schematic representation of TAPB-TA COF structural transformation. Reproduced with permission.227 Copyright 2020, American Chemical Society. (c) Crystal structure of woven COF-506-Cu and its adaptive guest inclusion. Reproduced with permission.123 Copyright 2018, American Chemical Society. (d) Locations and interactions of water guest molecules in COF-300.93 Copyright 2018, American Association for the Advancement of Science. (e) Structures of 3D-TPE-COF with seven-fold interpenetration. Reproduced with permission.241 Copyright 2018, Springer Nature. (f) Structural representation of FCOF-5, which has flexible frameworks and breathing behavior. Reproduced with permission.243 Copyright 2021, American Chemical Society. (g) Atomic structures of 3D-TPB-COF-Me and 3D-TPB-COF-F showing the locations of functional groups. Reproduced with permission.244 Copyright 2019, John Wiley and Sons. (h) Schematic representation of topological transformation via steric hindrance. Reproduced with permission.246 Copyright 2021, American Chemical Society. | ||
Very recently, the combination of 3D ED and in situ PXRD has revealed that the tautomerization between symmetry and asymmetry, transitioning from diiminol to iminol/cis-ketoenamine, can be stabilized and toggled within a crystalline, porous, and dynamic 3D COF (dynaCOF-301). This stabilization and alteration occur through a coordinated structural transformation and host–guest interactions when various guest molecules are adaptively included or removed.247 The 3D ED technique was employed to ascertain the atomic structure of COF atropisomers, specifically COF-320 and COF-320A. It revealed a significant steric strain that prevents the interconversion between COF-320 and COF-320A. Notably, COF-320A displays unconventional stepwise isotherms at varying temperatures. Both 3D ED and in situ PXRD characterization indicates that the stepwise adsorption can be attributed to continuous and/or discontinuous internal pore expansion.248
3.5. Challenges and opportunities for structural determination
Diffraction techniques play a crucial role in the characterization of materials, and they have been extensively employed to address various important aspects in the study of COFs, including complex structures, host–guest interactions, and dynamic structures. However, it is important to note that not all COFs can have their atomic structures solved using diffraction methods. This limitation primarily arises from the low crystallinity of COFs, which leads to low-resolution diffraction data. In this case, there are two ways to solve this problem. First, modifying the synthetic method to improve the crystallinity of COFs. For example, Zhang et al. synthesized COF-300 with higher crystallinity and homogeneity through the ventilation-vial protocol.202 Second, developing new algorithms for solving the structures of COFs using the low-resolution diffraction data. For instance, Sun et al. found the initial positions of two building blocks of the zeolitic organic framework from cRED data with a resolution of 2 Å using the molecular replacement method.211 Ma et al. reported that using the direct-space genetic algorithm (GA) method, structure solution of COFs could be successfully achieved from 3D ED data with a resolution of 3.78 Å.249 Other methods such as ML and maximum-entropy might be applied on the low-resolution diffraction data for the structure determination of COFs.250,251Despite the advantages offered by 3D ED tools, achieving high-quality structural solutions through ED requires addressing limitations and artefacts introduced during specimen preparation and data collection. The former aspect will be discussed in Section 4.4, while the latter is directly associated with issues such as specimen damage, disorder, and dynamical diffraction effects. Lowering the specimen temperature significantly impacts the quality of ED data in two crucial ways, effectively mitigating artefacts. Firstly, it helps minimize sample damage caused by electron beam radiation, especially for beam-sensitive materials like COFs that are prone to radiolysis mechanisms. This reduction in damage during data collection improves specimen stability and enhances data quality (Fig. 16g).245 Secondly, lower temperatures decrease dynamic disorder within the specimen. The harmonic component resulting from thermal vibrations decreases linearly with temperature until reaching the Debye temperature, resulting in a more ordered structure and more accurate measurement of atomic positions. Simultaneously, thermal diffuse scattering is noticeably reduced as well.252 The structure determination through 3D ED can be achieved by utilizing well-established algorithms compatible with both SCXRD and PXRD with kinematical approximations, because the ranking of relative reflection intensities usually plays a more critical role in structure solutions.253 Dynamical effects on reflection intensities and conventional structure refinement procedures based on kinematical approximations often result in less well-defined difference electrostatic potentials and compromised accuracy of atomic coordinates (Fig. 16h).254 Recent advancements in dynamical structure refinement procedures, considering multiple scattering effects, have empowered 3D ED with powerful capabilities for the accurate and reliable determination of absolute structures.255
In addition to diffraction techniques that rely on reciprocal-space information to resolve structures, real-space imaging methods can also be utilized to determine the structures of COFs that have poor crystallinity.
4. Structural determination by imaging
4.1. Basic principles and strategies
Microstructural elucidation generally plays a crucial role in understanding the structure–property relationship of materials by extracting multi-dimensionally and spatiotemporally correlated structural information at high spatial resolution.256 However, the direct observation of intrinsic and dynamic properties of materials, such as their structure, chemical composition, electronic state, and spin, at multiple dimensions and atomic scales poses a major challenge in microstructure characterization. Unlike diverse diffraction-based techniques that achieve the high-resolution spatially averaged periodic structural information of COFs from the Bragg scattering in the reciprocal space, direct imaging techniques allow the real space visualization of not only periodic but also local structures of COFs with resolution up to atomic-level. These local structures of COFs, including surface, interface, defect and entanglement, play a significant role affecting the gas adsorption and separation, catalysis and ion exchange properties.257 Accordingly, there is an emerging requirement for the development of advanced techniques based on EM and SPM as powerful and compatible tools for the direct imaging of organic polymers such as COFs. Traditional imaging techniques confront major obstacles for the direct visualization of intrinsic crystal and local structures of these purely organic polymers. For example, these microporous materials are highly vulnerable to electron beam irradiation,258,259 which leads to inevitable structural degradation for traditional EM techniques and under a high accumulated electron dose.260 SPM also has limitations and challenges in characterizing COFs, including specimen preparation issues, poor electric conductivity, surface roughness, slow scanning speed and restricted field of view. Therefore, the ultimate target for the technological and methodological innovations in EM and SPM for imaging COFs is to pursue more correlated information at higher spatial resolution and with structural integrity.There are two basic imaging modes for EM: TEM and scanning transmission electron microscopy (STEM) (Fig. 12a).261 In general, under TEM mode the specimen is uniformly illuminated by a parallel electron beam that usually carries a low electron dose rate in the beam flux. In contrast, under STEM mode the specimen is raster-scanned by a focused and intensive electron probe that usually carries a high electron dose rate.262,263 Such marked difference between these two imaging modes in terms of beam illumination entails rather distinct beam damage behaviors of the specimen, arising from the complicated beam damage mechanisms including knock-on, radiolysis, charging, heating as well as diffusion.264 These damage mechanisms usually have different damage behaviors in response to the dose rate. For those specimens that experience greater structural damage or on the contrary less structural damage at higher dose rate, direct and inverse dose rate effects are attributed respectively. Accordingly, under a quite limited critical electron dose for beam-sensitive materials, TEM and STEM imaging modes achieve minimized beam damage for specimens with direct and inverse dose rate effects respectively.
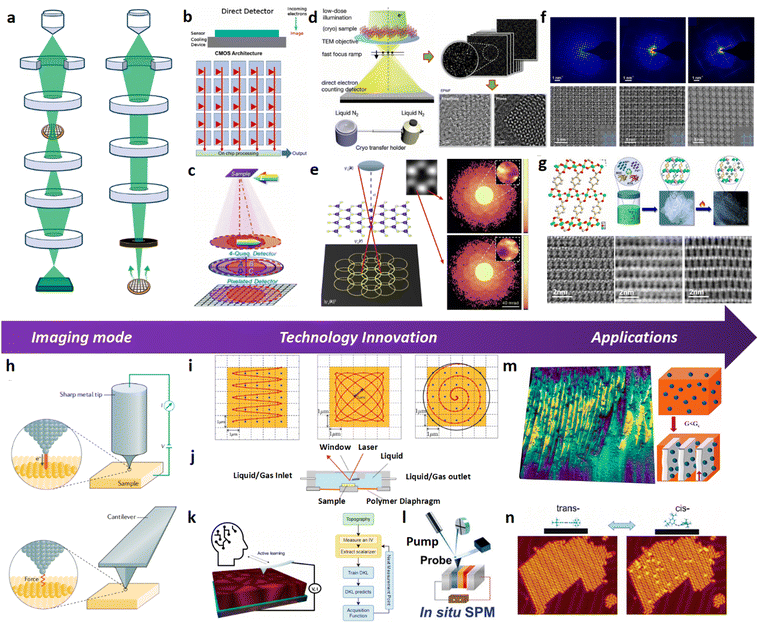 | ||
| Fig. 12 (a) Schematic drawing of the imaging optics of TEM and STEM modes. (b) Structure of the CMOS based electron direct detection device, with radiation hardened MAPS. Reproduced with permission.271 Copyright 2021, Journal of Physics: Materials. (c) Segmented and pixelated electron detectors, typically as hybrid pixel detectors (HPDs), endow diverse phase-contrast STEM imaging techniques. Reproduced with permission.272 Copyright 2022, Multidisciplinary Digital Publishing Institute. (d) Schematic illustration and workflow of the EPWF reconstruction technique and cryogenic transfer holder dedicated for cryo-EM imaging. Reproduced with permission.273 Copyright 2022, John Wiley and Sons. (e) 4D-STEM imaging and ptychography technique using pixelated detectors.274 Copyright 2018, Springer Nature. (f) Low-dose TEM images and SAED patterns of COF-2,3-Ph, COF-BPy and COF-BPh single-crystalline domains taken along the [001] direction. Reproduced with permission.275 Copyright 2022, American Chemical Society. (g) Characterization of multivariate MOFs with varying Fe and Ni contents using low-dose STEM. Reproduced with permission.276 Copyright 2022, John Wiley and Sons. (h) Schematic illustration of SPM (i.e. STM and AFM) structures and principles. Reproduced with permission.277 Copyright 1982, American Physical Society. (i) Comparison of different high-speed SPM scan geometries using sinusoidal scan, Lissajous scan and spiral scan modes. Reproduced with permission.278 Copyright 2023, Elsevier. (j) Schematic illustration of the liquid- and gas-cell accessories equipped in SPM for monitoring structural dynamics. (k) Workflow of the automated ML platform for in situ SPM probe tuning and conditioning. Reproduced with permission.279 Copyright 2023 American Chemical Society. (l) A general pump–probe geometry for diverse ultra-fast SPM techniques. Reproduced with permission.279 Copyright 2023, American Chemical Society. (m) Dynamics of NP migration and its impact on crystallization mechanisms monitored by in situ AFM. Reproduced with permission.280 Copyright 2022, American Chemical Society. (n) Monitoring reversible trans–cis isomerization and electric field-induced manipulation of azobenzene derivatives on the Au (111) surface using in situ STM. Reproduced with permission.281 Copyright 2006, American Chemical Society. | ||
Actually, despite the fact that alternative imaging mode can be selected to minimize the beam damage, most beam-sensitive materials suffer from restricted critical dose and thus limited spatial resolution for imaging, which ultimately originates from the effects of shot noise under low electron dose. Typically, beam-sensitive materials, such as zeolites, MOFs and COFs, have critical dose for marked structure degradation far below the accumulated dose for conventional EM imaging (i.e. 103–104 e− Å−2) and even ranging from a few to a few tens of electrons per Å2.265–267 These critical dose values are so low that under such an accumulated dose the EM image resolution is no longer determined by the electron optics but the electron dose used for imaging, due to the poor SNR. The dose-limited resolution (DLR, δ) can be defined by the following equation:264
A general goal for imaging beam-sensitive materials by EM is to maximize the spatial resolution under limited electron dose, which has led to recent developments in diverse low-dose EM imaging techniques for both TEM and STEM imaging modes.269 These technical and methodological innovations can be guided by the definition of the DLR equation itself, which is schematically illustrated in Fig. 12a–g. TEM and STEM-based phase-contrast imaging techniques, such as low-dose (bright-field) BF-HRTEM, (annular-bright-field) ABF-STEM, iDPC-STEM, and electron ptychography,270 are more dose-efficient than Z-contrast imaging techniques like ADF-STEM, due to much larger signal efficiency term F−1/2 arising from the greater fraction of scattered electrons collected by the electron detector.264 Actually, the electron detector records only the intensity of the electron wave and not its phase. The development of diverse advanced phase-retrieval techniques allows the recovery of phase images of specimens for phase-contrast (S)TEM imaging modes. For instance, the EPWF (exit-plane wave function) reconstruction technique allows the efficient phase retrieval and aberration correction of an object through image focal series acquisition under TEM mode (Fig. 12d).273 On the other side, either iterative or non-iterative electron ptychography techniques enable the recovery of the phase image of an object based on a series of probe position dependent convergent beam electron diffraction (CBED) patterns collected by a pixelated electron detector (Fig. 12e).274 Notwithstanding this, these phase-retrieval techniques require improvements to accommodate the critical low-dose EM imaging conditions for beam-sensitive COF materials. Furthermore, detectors with high DQE would also facilitate the low-dose EM imaging by minimizing the DQE−1/2 term of the DLR equation. Accordingly, the revolutionary invention of DDC has led to a significant breakthrough in the field of low-dose imaging by significantly improving the DQE of conventional scintillator-based CCD cameras (Fig. 12b).271 On the other side, modern segmented and pixelated electron detectors (e.g. EMPAD: electron microscope direct detection pixel-array detector) endow diverse phase-contrast STEM imaging techniques through 4D-STEM mode and with unprecedentedly high electron detection efficiency (Fig. 12c).282,283 These direct detection detectors are generally categorized as (i) monolithic active pixel sensors (MAPS) that adopt smaller but more abundant arrays of pixels with compromised dynamic range, which are suitable for collecting low fluence EM images, and (ii) hybrid pixel detectors (HPDs) that adopt small arrays of large pixels and high dynamic range, which are ideal to collect high fluence diffraction patterns.284 Moreover, the efficiency of contrast transfer spanning over all spatial frequency for these phase-contrast (S)TEM imaging techniques also imposes a marked impact on the DLR and can be evaluated by the phase-contrast-transfer-function (pCTF) and contributes to the term C−1 of the DLR equation. Generally, low-dose HRTEM suffers from contrast inversion problems of objective lens and the pCTF profiles usually exhibit poor contrast transfer at low spatial frequency and are significantly affected by aberrations.285 Correcting the contrast inversion effects in the HRTEM image usually results in more chemically interpretable images. Instead, diverse phase-contrast STEM imaging techniques eliminate the contrast inversion problem in pCTF profiles and exhibit better contrast transfer at low spatial frequency. Among these STEM imaging techniques, ptychography and its derivative techniques usually achieve more efficient contrast transfer.286 The contrast transfer efficiency of phase-contrast (S)TEM imaging techniques is more critical for imaging low-Z organic matters like COFs because they usually exhibit very weak contrast than other beam-sensitive materials such as MOFs and zeolites.259,287–289 Additionally, just as the δ term implies, the DLR is most closely related to the accumulated electron dose that is imparted onto the specimen, which should in principle be controlled below the critical dose (i.e. the 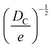 term) to maintain the structural integrity of beam-sensitive materials like COFs. There are two categories of strategies related with the
term) to maintain the structural integrity of beam-sensitive materials like COFs. There are two categories of strategies related with the 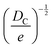 term to enhance the DLR for low-dose EM imaging: (i) to increase the Dc value by enhancing the beam durability of the specimen and (ii) to minimize the electron dose consumption during pre-imaging procedures. It has been widely reported that specimen coating and cooling significantly enhance the beam durability.290 It is thus sensible to integrate cryogenic and low-dose (S)TEM techniques for imaging COFs. On the other hand, the zone-axis alignment is critical for achieving structural information of crystalline matters like COFs, which is usually quite time and dose consuming. The implementation of the low-dose zone-axis alignment procedure allows the significant reduction of electron dose consumed in the pre-imaging procedures and improves the DLR by maximizing the “effective” electron dose used for image formation.23 In addition, the low-dose imaging of COFs encounters more critical issues arising from electron beam induced specimen motion and associated resolution degradation, due to their low image contrast and difficulties in properly registering the image series acquired during motion. To tackle these issues, the development and application of advanced low-dose motion correction algorithms are required.265,291 Recently, it has become more and more prevailing to unravel the atomic or molecular structures of beam sensitive open-framework materials including MOFs and COFs using low-dose (S)TEM techniques, which provides valuable insights into the structural design, crystal growth and catalytic properties of these materials (Fig. 12f and g).275,276
term to enhance the DLR for low-dose EM imaging: (i) to increase the Dc value by enhancing the beam durability of the specimen and (ii) to minimize the electron dose consumption during pre-imaging procedures. It has been widely reported that specimen coating and cooling significantly enhance the beam durability.290 It is thus sensible to integrate cryogenic and low-dose (S)TEM techniques for imaging COFs. On the other hand, the zone-axis alignment is critical for achieving structural information of crystalline matters like COFs, which is usually quite time and dose consuming. The implementation of the low-dose zone-axis alignment procedure allows the significant reduction of electron dose consumed in the pre-imaging procedures and improves the DLR by maximizing the “effective” electron dose used for image formation.23 In addition, the low-dose imaging of COFs encounters more critical issues arising from electron beam induced specimen motion and associated resolution degradation, due to their low image contrast and difficulties in properly registering the image series acquired during motion. To tackle these issues, the development and application of advanced low-dose motion correction algorithms are required.265,291 Recently, it has become more and more prevailing to unravel the atomic or molecular structures of beam sensitive open-framework materials including MOFs and COFs using low-dose (S)TEM techniques, which provides valuable insights into the structural design, crystal growth and catalytic properties of these materials (Fig. 12f and g).275,276
SPM is a powerful tool for characterizing material structures and properties at the nanoscale. One of the key features of SPM is its high spatial resolution, which enables the observation and manipulation of individual atoms and molecules. However, the theoretical limit of SPM resolution has been a topic of debate in the scientific community. According to the Rayleigh criterion, the resolution of an optical imaging system is inherently limited by the diffraction of light.292 SPM uses a physical probe to physically raster scan the surface of the specimen, the resolution of which is in principle determined by the scanning probe.293 Notwithstanding this, the resolution of SPM is also affected by several factors, including the size and shape of the probe, the interaction force between the probe and the sample, and the noise level in the measurement system.294 Theoretically, the resolution of SPM can reach atomic-scale or even subatomic-scale resolution, allowing researchers to observe individual atoms and molecules. However, achieving such high resolution requires careful calibration and control of the experimental parameters. For example, the probe must be sharp enough to provide a high spatial resolution.295 The interaction force between the probe and the sample must be carefully controlled to prevent sample deformation or damage. In addition, the noise level in the measurement system must be minimized to achieve high-quality images. This requires careful design and optimization of the SPM measurement system, as well as the use of advanced signal processing and image analysis techniques. In summary, the theoretical resolution limit of SPM is determined by the size and shape of the scanning probe and can practically reach atomic-scale or even subatomic-scale resolution under calibrated and optimized experimental conditions with advanced signal processing and image analysis techniques.
SPM technology has several advantages for imaging open framework materials, including high spatial resolution, multiple working modes, and environmental adaptability. By measuring material structures and properties through the interaction between the scanning probe and the sample surface, SPM allows the detection of fine surface features and properties such as atomic-scale surface morphology, surface chemical reactions, and surface charge distribution. SPM also permits imaging under different environmental conditions, providing dynamic behaviors and a better mechanistic understanding of chemical reactions involving target materials. Therefore, SPM has significant advantages for studying the surface features, properties and dynamics of COFs.296 However, there are some limitations and challenges that must be considered, including sample preparation, low conductivity of COF materials, complex surface geometry, and limitations in scanning speed and modes.
There are several different types of SPM, including atomic force microscopy (AFM) and scanning tunneling microscopy (STM). Each of these techniques has its own unique advantages and disadvantages, both of which can be used to investigate different properties of the sample. STM is a direct SPM technique used to measure the surface electron density of states of samples. The lateral resolution of STM is influenced by factors such as probe size, local surface morphology, and electron density of states. Typically, the basic principle formula of STM is297
| I ∝ exp(−2kd) |
This formula expresses that the tunneling current intensity is exponentially related to the distance between the probe and the sample. When the distance between the probe and the sample decreases, the tunneling current intensity increases. There are two scanning modes, constant-current, and constant-height mode. In the constant current mode, by using the measured tunneling current as the controlled object and establishing the equilibrium spacing between the tip and the sample by a feedback loop, the surface morphology can be obtained by scanning the tip along the equal-current xy plane. In the constant-height mode, the tip is held at a constant height and the tunnelling current is measured. The tunnelling current varies with the topographic and electronic characteristics of the sample.
AFM performs as a complementary SPM technique for STM because it eliminates the drawback that STM cannot directly image non-conductive samples. Instead of probing the tip–sample tunneling current in STM, AFM allows the measurement of interaction force between the tip and the sample (Fig. 12h).277 AFM operates under three different modes, contact, tapping and non-contact modes. In the traditional contact mode, the tip contacts the surface, and the tip–sample system falls into the repulsive force regime. Such force between the tip and the surface causes the cantilever to deflect and can be calculated using Hooke's law based on the following simple expression:298
| F = k(z − z0) |
The expression indicates that the repulsive force between the tip and the sample is proportional to their distance and the elastic constant of the tip. Accordingly, the variation in cantilever deflection is associated with the height of surface features and can be precisely probed by a laser beam focused onto and reflected by the backside of the cantilever that is usually coated with a reflective metal to enhance the reflected signal of the laser beam collected by the photodetector. When operating in constant force contact mode, AFM precisely measures the surface topography of the samples because the vertical displacement of the tip reflects topographic information. On the other hand, in constant height contact mode, the tip maintains a fixed height above the sample without any force feedback. Scanning the tip across the material surface while maintaining a constant tip–sample separation provides the basis for topographic imaging based on the deflection of the cantilever. The latter mode is faster but requires smoothness of the surface and is usually used for atomic resolution AFM. In the tapping mode, the tip–sample interaction falls within the transition region between the repulsive and the attractive force regime where the cantilever oscillates at or slightly below its resonant frequency. Topographic information can then be achieved by measuring the tip–sample interaction forces through the amplitude of cantilever oscillation. Additionally, the phase lag between drive and detected signals contains information associated with the mechanical properties of the sample. The tapping mode features higher lateral resolution and less sample damage but compromised scan speed. On the other hand, for non-contact mode, the tip–sample interaction is dominated by the attractive force regime. The cantilever oscillates near the surface without contact and at slightly above its resonant frequency. Compared with the tapping mode, the non-contact mode further minimizes the sample damage and enables atomic resolution imaging under ultra-high vacuum (UHV) conditions at the expense of even slower scan speed. As a result, non-contact mode AFM is suitable for imaging fragile biological and organic materials like COFs.299 Generally, similar to other SPM techniques, the lateral resolution of AFM is also influenced by various factors such as probe size, scanning speed and noise.300
SPM is generally faced with the crucial task of imaging not only static but also dynamic structural features in real space and under working conditions. This is essential because observing dynamic events on short timescales through in situ experiments can greatly enhance our understanding of critical biological, physical, and chemical processes, such as structural and topological transformation, molecular adsorption and desorption, and catalytic reactions. Therefore, technical advancements in SPM are primarily focused on achieving faster acquisition rates, automated tuning and tracking capabilities, and improved environmental compatibility.
To achieve a fast image acquisition rate, as typical SPM techniques, both AFM and STM share similar designs of the scanner unit and thus identical factors that limit the overall image acquisition speed but with different detection feedback loops. The general strategies to achieve high speed SPM imaging lie in optimizing data acquisition, scan geometry and electric feedback (Fig. 12i).278 A high data acquisition rate can be achieved by uniting fast digitizing units and real-time data processing and transfer. In addition, optimizing the scan geometry from conventional raster scan allows the faster image acquisition as well. The most frequently used scan geometry for high-speed SPM is sinusoidal raster scan that uses a sine wave in the fast scan direction instead of a triangle wave for conventional raster scan. Such scan geometry is easily implementable in existing SPM systems and enables high-speed and high-resolution SPM imaging with minimal effort in image reconstruction and distortion corrections. For SPM with a vertical feedback loop, sinusoidal raster scan performs well in terms of sampling frequency, probe velocity, and topography bandwidth. Without such feedback limitation, Lissajous and spiral scan geometries are considered to sample real space more efficiently, with higher sampling point density at the edge and center of the image respectively. Besides the scan geometry optimization, variable scan speed also facilitates the fast image acquisition and can be achieved by implementing a correlated SEM-AFM image acquisition scheme in a hybrid SEM-AFM system.301 Moreover, technical innovations in electric feedback systems also enhance the high-speed SPM imaging. For AFM, the acquisition rate is inherently restricted by the slow response of the Z-scanner and cantilever as the mechanical devices in contrast to other electronic ones. By integrating small cantilevers, fast scanners based on independent Z-piezo actuators and Q-control, fast amplitude detectors, as well as dynamic proportional-integral-derivative (PID) controllers, a high-speed AFM system can be constructed to eventually ensure a high frame rate of 10–16 fps.302 Similar to AFM, optimizing the limiting electric components of the electric feedback loop also increases the achievable frame rate for high-speed STM. Although the high bandwidth of the electronic feedback control system and the preamplifier improves the STM frame rate under the conventional constant current mode, the necessity to keep the tunneling current constant through real-time tip–sample distance control considerably retards the feedback loop. Instead, the constant height mode along with a dedicated tube piezo for fast scan is usually used for high-speed STM imaging. Generally, these strategies have achieved the temporal resolution of SPM imaging limited in the range of sub-second to micro-second. Introducing pump–probe configuration into the SPM systems further pushes forward the temporal resolution down to picoseconds or femtoseconds for probing ultrafast dynamics arising from the light–matter interactions.311,312 A case study that integrates a pump–probe configuration in STM and involves dispersion, polarization, and frequency modulation techniques for laser pulses entails ultrafast light-driven tunneling microscopy that allows the monitoring of photon-induced tunneling currents and tracking of electronic motion in molecules with simultaneous atomic-scale spatial resolution and sub-femtosecond temporal resolution.313 Similarly, constructing a pump–probe enhanced AFM system allows the precise measurement of electrostatic forces arising from nonlinear optical polarization with high temporal and spatial resolution.312 Ultrafast AFM also measures the local surface photovoltage (SPV) as the change in contact potential difference (CPD) between the tip and the sample upon pulsed illumination.314
To image structural dynamics in real space and under working conditions, real-time and automated SPM probe tuning is also necessary to ensure uncompromised spatial resolution during in situ experiments. This issue arises from the fact that standard ex situ tip preparation methods cannot accommodate in situ SPM experiments due to the loss of apex sharpness for SPM tips during imaging. Real-time detection of the tip condition and in situ tip treatments are critical to maintain the ideal condition of the SPM tip for high-resolution SPM imaging. Traditional tip reconditioning approaches include the repeated tip shaping using short voltage pulses and controlled tip indention into the sample, which are however extremely time-consuming. Developing automated real-time tip detection and reconditioning strategies, especially aided with ML algorithms, can greatly accelerate the tip reshaping and facilitate in situ high-resolution SPM imaging. For instance, Rashidi et al. presented automated methods based on ML algorithms for detecting and reconditioning the quality of the probe in a scanning tunneling microscope.315 Utilizing a convolutional neural network (CNN) trained to assess tip quality, a series of sequential operations are executed. These operations involve identifying a degraded probe, performing in situ tip reconditioning at a preselected spot on the sample surface, and repeating the tip reshaping process until the CNN detects a sharp probe. Such an automated ML platform for probe tuning has been effectively employed to recognize and assess isolated surface dangling bonds on a hydrogen-terminated Si(100) substrate with an accuracy of 97%. Furthermore, the accuracy that the platform achieves for tip quality classification surpasses 99%. Another critical issue for In situ SPM imaging lies in the efficient and accurate tracking of domains that exhibit multi-modal correlated structural features and properties so as to establish unambiguous structure–property relationships. In this sense, leveraging an active ML framework for driving an automated SPM allows the simultaneous achievements of structural and functional probing and thus the discovery of the explicit correlation between microstructures and target properties of materials. Liu et al. designed a workflow to implement an active deep kernel learning (DKL) on an operating SPM, which can actively learn the correlation between structural features (e.g. grains, grain boundaries (GBs) and defects) in the image data (e.g. STM, AFM or other SPM images) and functions (e.g. conductivity, hysteresis or other transport properties) in the spectroscopy data (e.g. IV curves, band gaps or density of states) (Fig. 12k).279 They implemented this approach in conductive AFM (cAFM) and successfully unraveled the relationship between microstructural elements (e.g. grains, different GBs and GB junctions) and conductivity in metal halide perovskite (MHP) thin films.
To enable the structural elucidation of COFs and their dynamics under various environmental and working conditions, it is critical to develop imaging techniques and build instruments that are compatible with these conditions. This requires the integration of extended setups into SPM instruments to allow imaging under variable pressures, temperatures ranging from ultralow to room temperature, and even in liquids via immersion in solutions. The development of diverse in situ SPM technologies allows researchers to characterize individual molecules on the substrate and in gas and liquid environments. When operated in a liquid environment, SPM techniques have been widely applied in studying dynamic processes or events in liquids, such as migration,280 aggregation316 and crystal growth.317 For instance, S. Schadler et al. utilized in situ AFM to track the migration of silica nanoparticles (NPs) from a poly(ethylene oxide) (PEO) melt into the interlamellar region. This study demonstrates that high-speed AFM served as an excellent tool for investigating NP migration and figuring out its impact on crystallization mechanisms (Fig. 12m).280 As another example, the tip of STM can desorb individual hydrogen atoms from a hydrogen-saturated silicon surface and induce synthesis steps of a biphenyl molecule in a liquid environment, indicating the capability of SPM in repairing or manipulating COF structures and studying their interactions with molecules in liquids.318 For measurements in a gas environment, Suzuki et al. devised an apparatus including STM and AFM to investigate highly oriented pyrolytic graphite (HOPG), revealing that STM captured atomic-resolution images across hydrogen, helium, neon, and argon atmospheres.319 Moreover, by applying an electric field between the STM tip and a metallic surface, Alemani et al. demonstrated the reversible trans–cis isomerization of individual azobenzene derivatives adsorbed on an Au(111) surface (Fig. 12n).281 These molecules have symmetrically distributed four tert-butyl groups, effectively isolating the azobenzene core from the metallic surface, thus promoting the formation of well-ordered islands. Such an approach allows the precise control and manipulation of the isomerization reactions of molecules on the surface and provides the capability for direct visualization of the dynamics at the nanoscale. Recent advances in developing in situ electrochemical atomic force microscopy (ECAFM) further allow the direct monitoring of electrochemical processes by combining the high-resolution interfacial analysis capability of AFM with the electrochemical instrumentation (Fig. 12l).320,321 It provides broad applications unraveling with high spatial resolution the critical interfacial phenomena occurring in individual electrochemical events. By integrating electrochemical control, ECAFM entails simultaneous investigation of electronic and mechanical properties of single molecules at the nanometer scale. As instrumentation, specially designed insulated conductive probes are used to simultaneously scan the surface and characterize sample properties. The hardware components of ECAFM include an atomic force microscopy module, consisting of an elastic cantilever with a sharp probe for scanning the sample surface and measuring topographical features; an electrochemical cell comprising a working electrode, reference electrode, and electrolyte, enabling electrochemical reactions during scanning; a potential control system for precise manipulation of the electrochemical cell's potential; a scanner for controlling the probe's position on the sample surface during scanning; and a data acquisition and analysis system for recording and analyzing both topographical and electrochemical data obtained from the scans. The integration of these components allows researchers to simultaneously study the topographical features and electrochemical properties of sample surfaces at the nanoscale, and thus gain deeper insights into material and process behaviors, enabling studies in electrochemical scenarios, such as corrosion and electrocatalysis. The advantages of ECAFM include not only the capability of topographic imaging regardless of sample conductivity but also the ability to image at high resolution in gaseous environments (e.g. inert gases like argon). Chen et al. investigated the surface structural changes during cathodic polarization of polycrystalline Pt electrodes and single crystalline Pt (111) electrodes in acid electrolytes, in the presence and absence of cations (Na+), using in situ ECAFM imaging in an argon gas environment.323 The presence of cations, such as Na+, was found essential for initiating cathodic etching of polycrystalline Pt surfaces.
4.2. Imaging COFs by SPM
SPM is an ideal tool to study the surface properties of nanoparticles, and thus is suitable for imaging low-dimensional materials. SPM provides detailed information on the size, shape, and surface roughness of nanoparticles. Specifically, AFM-based force spectroscopy allows the measurement of the mechanical properties of nanoparticles, such as stiffness, adhesion, and deformation, which are crucial for understanding their behavior in different environments.322 For example, Pratama et al. used STM and non-contact AFM (nc-AFM) to study different types of 0D molecules at the single-molecule level. By analyzing their STM and nc-AFM images, they provided a reliable description of amphetamine-type stimulant (ATS) drugs, which can be used for the classification and prediction of drug molecule activity (Fig. 13a).303 SPM techniques have been widely used to investigate the nanoscale properties of 1D materials, particularly nanowires. AFM can provide valuable information on the diameter, length, and surface roughness of nanowires, while STM can probe their electronic properties by measuring conductance and density of states. Additionally, AFM-based nanomanipulation techniques enable the fabrication and manipulation of nanowires for various applications. For instance, Lyu et al. used STM to explore the process of autonomous loading of 1D organometallic structures, demonstrating the formation of 1D sinusoidal chains or 2D molecular porous networks (Fig. 13c) composed of tris-pyridyl and carbonitrile monomers, creating covalent organic structures coordinated with Eu atoms.305 High-resolution surface topographic images obtained through STM can reveal the surface morphology and molecular structure of these metal complexes. Furthermore, STM can provide information about the electronic structure of the complexes, such as the local density of hole or electron states, thus enabling the study of the morphology and electronic properties of metal complexes. 2D COFs as a class of unique organic porous polymers have attracted significant interest in materials chemistry because of their signature topological structures as well as their important applications in catalysis. For 2D materials, SPM techniques such as AFM, STM, and Kelvin probe force microscopy (KPFM) have been widely used for the characterization of thin films, including graphene, transition metal dichalcogenides (TMDs), and other 2D materials. AFM can provide high-resolution imaging of the topography and morphology of thin films, while STM can probe their electronic properties, such as bandgap, carrier density, and mobility. KPFM can be used to measure the surface potential and work function of thin films, which are crucial for understanding their electrical and catalytic properties.328 Chen et al. have characterized the local electronic structure of a single-layer porphyrin-containing square-lattice COF on Au (111) by scanning tunneling spectroscopy (STS), an extension of STM (Fig. 13e).307 They found that the electron shifts in the frontier orbitals of the porphyrin core upon COF formation are due to the electron withdrawing nature of the imine linkages. The experimentally measured HOMO and LUMO wave functions of the COF show high intensity on the porphyrin cores, with an energy gap of 1.98 ± 0.04 eV. These findings provide insight into how electrons reorganize within the COF structure, highlighting the role of imine linkages and porphyrin cores in influencing the electronic properties of COFs.307 Lackinger et al. successfully synthesized regular and extended 2D COFs and investigated their self-assembly behavior on surfaces using STM.309 The structural versatility of the COFs was achieved by polycondensation of four different diboronic acids, each with varying organic backbones ranging from biphenyldiboronic acid, terphenyldiboronic acid, quaterphenyldiboronic acid, to pyrene-2,7-diboronic acid. This approach allows the creation of isoreticular 2D COF series with lattice parameters ranging from 1.5 nm to 3.8 nm, and corresponding pore sizes increasing from ∼1.0 to 3.2 nm (Fig. 13g).309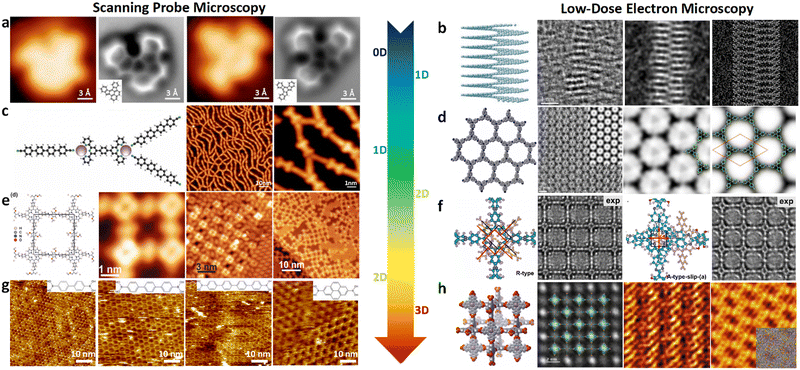 | ||
| Fig. 13 (a) Characterization and comparison of polycyclic aromatic hydrocarbon molecular structure models using STM and nc-AFM. Reproduced with permission.303 Copyright 2018, Easychair. (b) Observation of the 1D CNS structure using the low-dose STEM technique. Reproduced with permission.304 Copyright 2022, Springer Nature. (c) The atomistic model and STM imaging of mixture of 1D supramolecular chains. Reproduced with permission.305 Copyright 2016, Royal Society of Chemistry. (d) Low-dose HRTEM image of the 2D molecular network of an imine-linked TPA-COF with micropores and molecular nodes clearly visible. Reproduced with permission.306 Copyright 2017, American Chemical Society. (e) COF366-OMe network structure, DMA molecular deposition, and STM imaging of the Au(111) surface. Reproduced with permission.307 Copyright 2018, American Chemical Society. (f) HRTEM imaging of the 2D-PI-BPDA network and image simulations. Reproduced with permission.308 Copyright 2022, Springer Nature. (g) STM images of 2D COFs derived from polycondensation of the following monomers: biphenyldiboronic acid, terphenyldiboronic acid, quaterphenyldiboronic acid, and pyrene-2,7-diboronic acid. Reproduced with permission.309 Copyright 2012, American Chemical Society. (h) HRTEM image of the cubic crystal lattice of new 3D porous SPB-COF-DBA and MIM networks. Reproduced with permission.310 Copyright 2021, American Chemical Society. Reproduced with permission.198 Copyright 2023, American Association for the Advancement of Science. | ||
SPM techniques not only allow visualization of the microstructure of the samples, but also reveal the microscopic origin of their physicochemical properties and provide mechanistic insights into functionalities, such as heterogeneous catalysis, topological engineering, and polymer separation. For example, COF networks can be used as scaffolds for encapsulating enzymes to regulate their activity by modulating surface functional groups towards improved medical and catalytic applications.329–331 Moreover, intensive research has been devoted to materials with high carrier mobility and tunable bandgaps in nanoelectronics. 2D π-conjugated polymers have emerged as a promising subclass due to their ability to manipulate band structures by modulating molecular building blocks, while retaining key features such as Dirac cones and high carrier mobility. However, the main obstacle in the application of 2D π-conjugated polymers has been the small domain sizes and high defect densities achieved in synthesis. Galeotti et al. achieved the synthesis of highly ordered large-area honeycomb network monolayers by depositing tribromotrioxaazatriangulene (TBTANG) onto preheated Au surfaces and determining the dimensions between adjacent pores from STM images.332 This novel 2D π-conjugated polymer exhibits good thermal and environmental stability, suggesting its potential as a material in nanoelectronic devices. Xu et al. developed a simple and efficient method to prepare a COF called surface COFBTA–PDA at the interface between octanoic acid and graphene. They used STM to study the structure of surface COFBTA–PDA and observed “5+7” type defects on graphene. They also observed strong interaction between surface COFBTA–PDA and graphene by STM, which was further confirmed by computer simulations (Fig. 14e).325
 | ||
| Fig. 14 (a) Schematic illustrations present the [001] structural projection image of the HFPB-TAPT COF crystal with an ABC stacking sequence. Reproduced with permission.21 Copyright 2022, American Chemical Society. (b) Chemical structures of TBPBA and HTTP, along with high-resolution STM images visualizing the self-assembled TBPBA phase and boronate ester-based sCOFs-2. Modified with permission.323 Copyright 2020, American Chemical Society. (c) STM image revealing a grain boundary composed of pentagon and heptagon rings in COF-1, as well as the evolving adsorption of TCB within the grain boundary defects. Reproduced with permission.324 Copyright 2017, Royal Society of Chemistry. (d) Low-dose imaging and direct visualization of the 2-fold interpenetrated bcu 3D COF networks. Reproduced with permission.14 Copyright 2022, John Wiley and Sons. (e) Microstructural images of the hexagonal 2D surface COFBTA–PDA synthesized from benzene-1,3,5-tricarbaldehyde (BTA) and p-phenylenediamine (PDA) were obtained using SPM characterization techniques, revealing the mechanism of defect formation. Reproduced with permission.325 Copyright 2014, John Wiley and Sons. (f) The HR-TEM image and domain-mapped image, which depict the synthesis of boronate ester-linked COF films on graphene-coated TEM grids, revealing the structural defects. Reproduced with permission.326 Copyright 2021, American Chemical Society. (g) The structure diagram illustrates the topological regulation of 2D TPE-COFs and the transition between bimodal and unimodal porosities. Reproduced with permission.104 Copyright 2020, American Chemical Society. (h) Schematic illustration and HRTEM images for the morphological engineering of COF crystals between nanospheres (TPB-MeOTP-NS) and nanoparticles (TPB-MeOTP-NP). Reproduced with permission.327 Copyright 2022, American Chemical Society. | ||
Topological transformation of COFs has always been an important but challenging research topic, and progress in this field relies on the advances in structural characterization techniques. In case studies, TP-COF-DAB was obtained by heating TP-COF-BZ with 1,4-diaminobenzene and replacing the benzidine connector in TP-COF-BZ with 1,4-diaminobenzene under the reaction conditions, and the underlying COF to COF topological transformation was confirmed through PXRD.333 Using linker exchange as a medium, the exchange of building blocks with different symmetries can be achieved for 2D COFs, enabling the topological transformation between 2D COFs with different pore architectures. Zhan et al. achieved the topological transformation of COF structures, local reaction environment and reversible network switching (in response to the orientation of applied sample bias), through the application of an electric field, which was then visualized and confirmed by STM (Fig. 14b).323
There are also possibilities to explore the host–guest interactions in COFs, arising from the fact that many COFs attain unique separation capabilities through capturing and trapping guest molecules of variable sizes and shapes. Hu et al. introduced a novel surface-constrained host–guest chemistry approach, utilizing two-dimensional COFs as the host network, for separating arylenevinylene macrocycles (AVMs) from linear by-products. Owing to their stronger binding interactions, this method demonstrates effective selective immobilization of AVMs within the COF cavities, as directly observed through STM, while the linear by-products are washed away.334 Similarly, in 2015, Cui et al. showed by STM that COFs may act as a robust host for C60 fullerene guest molecules at the solution/solid interface.335 Subsequently, in 2017, they observed by STM that COF-1 forms well-defined ring boundary defects from pentagonal and heptagonal cyclic chains (Fig. 14c).324 STM images at the liquid/solid interface reveal the dynamic behaviors of trichlorobenzene (TCB) adsorption in the hexagonal pore of COF-1, with pore shape and size influencing the binding strength of the guest molecules. These examples highlight the unique capabilities of COFs in capturing molecules and show that surface-supported 2D porous COFs can selectively bind different molecules at specific sites via various types of interactions.
4.3. Imaging COFs by low-dose EM
SPM technology is more suitable for the characterization of low-dimensional COFs, such as 1D and 2D COFs. These low-dimensional materials usually feature extremely small thickness. SPM technology allows the observation of their surface morphology and structure at the atomic scale, providing high-resolution images and topological information that reveal their microstructure and pore architectures. Additionally, as a typical imaging rather than diffraction or spectroscopy technique, SPM also allows the direct observation and even quantitative analysis of local structural features like defects and active sites of low-dimensional COFs. Nevertheless, accurately elucidating the structures of a larger COF family with networks spanning from 1D to 3D spaces is still challenging, which is critical to correlate the structures with their properties in order to stimulate new structural designs. Traditional EM techniques provide a versatile tool for imaging diverse 1D, 2D and 3D nanostructures with atomic spatial resolution but confront major obstacles in imaging beam-sensitive materials like COFs. Therefore, there is an emerging need to develop and apply low-dose EM techniques to image beam-sensitive materials with structural integrity.336 The recent marked advances in both TEM and STEM based low-dose EM techniques provide unprecedented opportunities for the direct visualization of COFs in real space and with high resolution.337 By integrating diverse spectroscopy techniques in the EM platform (e.g. energy dispersive X-ray spectroscopy (EDS) and electron energy loss spectroscopy (EELS)),338,339 multimodal and correlated structural information, including the composition, atomistic structure, valence state, and coordination, can be readily achieved.Due to the nanoconfinement effect, 1D COFs usually have unique electronic properties that make them important for various applications, including electronics, energy storage, and catalysis. In recent years, low-dose EM has become an indispensable and powerful tool for imaging diverse 1D materials including COFs. In a recent study, a novel approach for synthesizing a metal-free carbon nanosolenoid (CNS) material in a bottom-up manner was proposed. The unique helical molecular structure of the CNS can be directly visualized with high spatial resolution by utilizing the low-dose phase-contrast iDPC-STEM imaging technique that provides contrast that closely resembles the projected electrostatic potential of the helical structure (Fig. 13b).304 The findings provide new insights into the structural characterization of CNS and offer a promising strategy for the controlled synthesis of nanoscale materials with intricate structures. For example, Xu et al. employed TEM with minimized electron dose to identify the different way leading to the assembly of 3D woven COFs or 1D metallo-COFs (MCOFs), where the mechanism is underpinned by the absence or presence of monomer exchange.340 Additionally, the authors used STEM to determine the position and distribution of metal ions in the MCOFs. Overall, low-dose TEM played a crucial role in characterizing the structure and properties of 1D COF materials without considerable beam damage.
2D COFs exhibit unique physical and chemical properties, making them attractive candidates for various applications such as electronics, optoelectronics, energy storage, and catalysis. Low-dose EM is particularly advantageous for 2D COFs because it provides the most critical in-plane structural information of 2D COFs with minimal radiation damage. EM imaging with high tension may further minimize the radiolytic beam damage of COFs due to the diminished fraction of inelastic scattering events, despite the compromised contrast of low-Z 2D COFs.341 The direct visualization of the 2D molecular network of an imine-linked TPA-COF can be achieved via low-dose TEM imaging under 300 kV with a DLR of ∼4 Å. In Fig. 13d, the structural details of 2D COFs including both 1D pore channels and contrast corresponding to the three benzene rings of tridentate tris(4-aminophenyl)amine (TAPA) or tris(4-formylphenyl)amine (TFPA) molecular building units can be clearly identified.306 Besides the 2D periodic molecular network, low-dose EM also reveals local structural features such as defects, stacking order and partial disorder in the material framework.336,342 For instance, Liang et al. observed defects in 2D polymers covalently linked by TEM imaging under 120 kV (Fig. 13f).308 Meanwhile, the enhanced contrast achieved at low tension allows the visualization of molecular interstitial defects and functional groups. A detailed and statistical comparison of image contrast for the linkers between 2D-PI-DhTPA and 2D-PI-BPDA COFs reveals that the main distinction lies in the linker widths. After contrast analysis averaged over 100 linker sites, the result shows that the FWHM of the DhTPA site was approximately 70% (0.9 Å) broader than that of BPDA, which can be attributed to the presence of hydroxyl groups. These observations could provide valuable insights into the basis of host–guest interactions.308 As another example, R. Dichtel et al. proposed a Fourier mapping method for TEM imaging of polycrystalline 2D COF films, which allows the explicit identification of individual crystalline nanodomains, their domain boundaries and point defects (Fig. 14f).326 This approach provides microscopic insights into the nanoscopic defective structures in COF-5 films with high accuracy and computational efficiency, with the conclusion that the defects in COF-5 films arise from broken B–O bonds formed during polymerization. The above observations also provide guidelines for developing defect-free 2D polymerization strategies that enable the fabrication of COF thin-film devices. In addition, from both the structural projection of 2D COFs and associated extinction rules based on the analysis of power spectrum or electron diffraction, the stacking order of 2D COF layers that originate from the displacement between each other can be unambiguously identified. Based on the extinction rules and image contrast from basal plane structural projections of the HFPB-TAPT 2D COF, the ABC stacking order that differs from those widely observed eclipsed (AA) and staggered (AB) stacking order modes for 2D COFs can be explicitly identified (Fig. 14a).21
3D COFs exhibit significantly greater structural diversity and complexity, which however are subject to severe crystallization issues. Accordingly, low-dose EM imaging plays an even more critical role in elucidating their structures even with compromised crystallinity. Wang et al. used reticular chemistry design principles to synthesize a new 3D porous COF with nbo topology and clearly visualize the cubic crystal lattice using HRTEM (Fig. 13h).310 As another example, Xiao et al. introduced a self-assembly strategy driven by boron–nitrogen bonds, successfully integrating mechanically interlocked molecules (MIM) into pure organic polyrotaxane crystals (Fig. 13h).198 This integration achieves new material properties that are unattainable by traditional methods and has been directly, clearly, and accurately confirmed through cryogenic low-dose TEM with a resolution of up to 2 Å. In comparison to the control group of non-rotaxane polymers, polyrotaxane crystals exhibit higher flexibility and elasticity, attributed to the coordinated micro-motion of the rotaxane subunits. This research highlights a novel approach to integrate MIM into pure organic crystal materials. Not only does real space TEM imaging provide a clue to the crystalline framework of 3D COFs, but it also offers a quantitative measurement of the lattice constants. Another important and frequently observed local structural feature that stabilizes 3D COFs is entanglement.343 The entanglement significantly alters their pore size and shape through network interpenetration and thus affects the gas adsorption properties of 3D COFs.98,344 For example, 3D COFs synthesized by Guan et al. adopt either 5-fold, 9-fold or 11-fold interpenetrating networks, which has high selectivity for the adsorption of CO2.201 Interpenetrated 3D COFs condensed by PMDA and TAPM monomers exhibit both high loadings and good release control in the application of drug delivery.345 In addition, entanglement in 3D COFs has also been reported to introduce site isolation and promote charge transport.346 Dogru et al. proposed that interpenetrated networks of semiconducting COFs with electron acceptor phases like PCBM offer a promising model for understanding and advancing efficient photovoltaic devices.347 However, the entanglement does not create additional long-range structural order beyond the periodic 3D COF network. EM imaging allows the direct visualization of such local structural features in real space. Conventional TEM imaging may contribute to the direct identification of general structural features like crystallinity and porosity of 3D COFs from lattice contrast, as demonstrated in studies of 3D COFs like SC-COF and NUST-5/6-COF.348,349 In another case, Zhang et al. designed, synthesized and imaged a 3D COF based on an 8-connected cubic node and created an interpenetrated network with pcb topology.349 Unfortunately, conventional TEM imaging cannot unravel fine structures and thus does not allow the explicit identification of network entanglement as typical fine local structural features in these studies. Instead, low-dose EM imaging achieves uncompromised spatial resolution in real space for beam-sensitive materials, which thus allows the direct visualization and identification of not only the interpenetrated 3D COF networks but also the multiplicity of entanglement. For example, low-dose EM imaging allows the direct visualization of the two-fold interpenetrated 3D imine-linked COFs that adopt bcu networks and comprise high-valency quadrangular prism (D4h) stereoscopic node with a connectivity of eight (Fig. 14d).14 Such an interpenetrated structure is formed by two identical bcu networks arranged in a staggered manner and displaced from each other by 15.3 Å, which can be directly visualized from the dark contrast of twin lattice fringes characteristic for the interpenetrated networks and validated by image simulations.
In addition, low-dose EM allows the direct visualization and validation of topological transformation of 2D COFs. For example, low-dose EM witnesses the topological regulation of 2D TPE-COFs by intramolecular hydrogen bonding, which allows the crossover between bimodal and unimodal porosities (Fig. 14g).104 Similarly, Chen et al. systematically controlled the topology of TetPB-COF by manipulating the ligand symmetry, and validated the regulation of kgm and sql topologies by low-dose EM imaging.350 These findings provide valuable insights into the relationship between monomer geometries, bonding characters and framework topology, which paves new routes to evoke the interplay of these structural factors to create the final COF framework that adopts the target topology.
EM imaging under relatively low-dose conditions also validates diverse multiscale structural engineering rationale of COFs towards energy-related catalysis and molecular separation applications.351,352 Yao et al. reported a morphological level structural engineering strategy of TPB-MeOTP COFs by controlling anisotropic versus isotropic crystal growth modes from the aspects of both nucleation behavior and growth kinetics of colloidal COFs.327 TEM imaging unambiguously confirms the covalent honeycomb networks of colloidal nanoplates that enable the preparation of smooth and homogeneous films with a controllable thickness towards efficient photoelectrochemical (PEC) solar-to-hydrogen conversion (Fig. 14h).327 Ying et al. provided an interfacial level structural engineering strategy to multilayer COF gas separation films for hydrogen separation by enabling layer-by-layer interfacial reaction of two COFs with different pore sizes to form narrowed apertures at the COF–COF interfaces, both of which had their crystalline networks identified by TEM imaging.353 On the other side, Vyas et al. proposed a molecular level structural engineering strategy of 2D azine-linked COFs from hydrazine and triphenylarene aldehydes with varying number of nitrogen atoms and validated the in-plane molecular network by TEM imaging.354 Through this strategy it is possible to precisely adjust the structural and optoelectronic properties of these azine-linked COFs towards enhanced photocatalytic hydrogen evolution activities under visible light.
4.4. Challenges and opportunities of imaging
SPM is a widely used technique for imaging material surfaces with atomic resolution and is suitable for low-dimensional COFs. However, the imaging performance of SPM is mainly limited by several factors: (i) the specimen requirements. The marked surface roughness of COF materials may significantly affect the SPM imaging quality and accuracy, especially for the STM mode.355 (ii) The specimen damage. The SPM tip may cause surface damage or property modification of the specimen during raster scanning, especially for soft or fragile specimens (e.g. biological samples and soft polymers). For example, both the contact and tapping mode AFM that operate in a repulsive tip–sample force regime may lead to considerable specimen damage or tip wear due to high forces exerted on the surface. Instead, non-contact (dynamic) mode AFM facilitates non-invasive surface imaging in a tip–sample attractive force regime, but usually with compromised lateral resolution and scan speed.356,357 (iii) Limited field of view and scan speed. SPM techniques, including STM, AFM, and others, have inherent limitations in scan speed, which arise from the sequential pixel-by-pixel mechanical displacements of the scanning probe (tip) controlled electronically and time restrictions of the associated feedback loop.357,358 Accordingly, the typical acquisition time per SPM image is usually within several seconds and several minutes, which limits the field of view (e.g. a few microns) and applications in tracking dynamic processes. High-speed AFM (HS-AFM) technology has been developed to overcome the limitations of SPM characterization of COFs, entailing fast scanning by rapidly oscillating the probe and producing high-speed and high-resolution images of COF materials.359 The high-speed imaging capability of HS-AFM will contribute to studies on conformational changes of biomolecules, such as protein folding and unfolding processes, and the interactions of biomolecules in different environments. HS-AFM allows the observations of molecular-scale dynamic structures and morphologies, such as intermolecular interactions and chemical reactions. These technological advances in HS-AFM provide critical insights into the in-depth understanding of molecular structures and biological functions (Fig. 15).The major challenge in low-dose EM imaging of COFs is to mitigate two critical issues, (i) beam irradiation damage and (ii) low contrast of a purely organic network,339 both of which pose a strong restriction onto the image resolution and achievable structural information limit. Such limitations can be straightforwardly interpreted by the critical dose and contrast terms (i.e. the 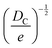 and C−1 terms) in the formulation of DLR for low-dose EM imaging.
and C−1 terms) in the formulation of DLR for low-dose EM imaging.
To address the beam damage issue, there are generally two strategies: (i) optimal imaging mode selection and (ii) specimen treatment. Depending on the underlying beam damage mechanisms of COFs, either TEM or STEM imaging mode may be selected as the optimal imaging mode to minimize beam damage, based on the investigation of their dose-rate effects (i.e. direct, inverse or linear effects).369 On the other side, specimen freezing or coating has been reported to greatly circumvent the radiolytic beam damage of open framework materials.370 Accordingly, cryo-EM provides unprecedented opportunities to enhance the DLR for low-dose imaging of COFs upon elevated critical dose.371 Alternatively, graphene coating has also been reported to enhance the beam durability of beam-sensitive materials and thus hold great promise for imaging COFs.
To further address the low contrast issue, there are mainly two strategies: (i) phase contrast transfer optimization and (ii) phase contrast information recovery. The contrast for low-dose phase contrast EM imaging of COFs largely depends on the efficiency of phase contrast transfer and associated function (pCTF). In TEM mode, the oscillating pCTF can be optimized to enhance the contrast of COFs based on the spatial frequency of target structural information by introducing aberrations such as defocus and spherical aberrations or phase shift by the phase plate.372 The contrast inversion effects arising from aberrations may then be corrected to obtain a chemically interpretable image that closely resembles the projected electrostatic potential of the structure.373 In STEM mode, the pCTF has a parabola shape and the phase contrast transfer at low spatial frequency is usually more effective than that in TEM mode and does not suffer from the contrast inversion issues of TEM. Diverse STEM based imaging techniques exhibit rather different pCTF, the efficiency of which has been reported to increase in the order ABF-STEM, iDPC-STEM and electron ptychography.374,375 Although introducing aberrations such as defocus and spherical aberrations further improves the low frequency phase contrast transfer in an oscillating manner, the deployment of the phase plate at the position of the probe-forming aperture combined with the matched illumination and detector interferometry (MIDI) approach (i.e. MIDI-STEM and ptychographic MIDI-STEM) allows efficient and flat contrast transfer spanning a full range of spatial frequencies.375,376 The recent proposal of a STEM holography configuration that involves a diffraction-grating beam splitter even allows more efficient and linear contrast transfer with nearly unity efficiency at zero spatial frequency.374 Experimental implementation and application of these leading EM techniques for enhanced phase contrast transfer may greatly circumvent the low-contrast issues for imaging the purely organic COF materials.
Low-dose EM imaging may also be subject to severe issues related with the phase contrast information recovery. Firstly, unlike the illumination condition of STEM imaging dictated by the pixel-by-pixel raster scanning of the electron probe with large instantaneous intensity, the continuous illumination under TEM condition inevitably introduces beam-induced motion of the specimen and significantly degrades the high-frequency structural information. The beam-induced motion has actually been regarded as one of the major obstacles in cryo-EM and low-dose EM imaging.258,259,377,378 Traditional image registration and motion correction algorithms widely adopted in biomedical imaging fields, such as algorithms based on cross-correlation, mutual information or multi-resolution pyramid approaches,379 fall short in scenarios involving low-dose EM due to the extremely high noise and low electron dose per image frame (ca. 10−2 e Å−2 frame−1). There are generally two approaches to accurately register noisy EM images, i.e. pre-registration image feature enhancement and noise model embedded registration. With the former approach, the amplitude-filtered cross-correlation algorithm has been proved to work in low-dose imaging of crystalline open framework materials like MOFs and zeolites.259,342,380,381 Recently, a geometric phase correction method was proposed and performs well in registering low-dose noisy HRTEM images.291 It selectively retrieves the unwrapped geometric phase shift of intensive and non-collinear Bragg spots in the spatial frequency domain of the HRTEM image with sub-pixel precision. This enhanced information from the image can be directly used to measure the relative drift of image frames. With the latter approach, specific statistical noise models can be incorporated into the image registration process to outperform traditional methods. S. Suhr et al. presented a general framework for registration of noisy images based on maximum a posteriori estimation.382 Secondly, information recovery from the noisy EM images by diverse denoising approaches is essential to uncover the chemically interpretable structural information of COFs. Besides the involvement of traditional denoising image filters, developing AI-enhanced high-performance denoising frameworks has attracted increasing attention recently. C. Ta et al. proposed a self-supervised Poisson2Sparse algorithm combined with a dictionary-learning approach, which greatly enhances the SNR of noisy images.383 J. Byun et al. implemented a PGE-net for the estimation of the Poisson noise level, which was subsequently subjected to a denoising FBI-net after generalized Anscombe transformation (GAT).384 J. M. Ede et al. employed an atrous convolutional encoder-decoder by ML to improve the signal-to-noise ratio (SNR) of electron micrographs.385
Consistently, selecting the most suitable characterization tool to unravel the molecular structure of COF materials has posed a formidable challenge in decision-making. By conducting a comprehensive comparison of both the strengths and limitations associated with various diffraction and imaging techniques (such as SCXRD, PXRD, 3D ED, SPM, and EM), it becomes possible to strategically select an appropriate structural elucidation technique for the specific objectives of the study, particularly in relation to crystalline COFs of varying types and sizes. This systematic approach ensures that the chosen technique aligns with the research goals, facilitating a more targeted and insightful investigation into the structural characteristics of COFs.
Nevertheless, it is crucial to acknowledge the numerous precautions, artefacts, and limitations associated with these structural elucidation techniques for characterizing materials including COFs. Specifically, it is important to recognize that specimen preparation can introduce artefacts that may impact the accuracy of structural elucidation. These artefacts can arise from various mechanical, chemical, physical, and ionic techniques utilized during specimen preparation, leading to a range of primary events such as deformation, cracking, defect formation, etching, segregation, amorphization, and phase transformation. Additionally, secondary events including redeposition and damage caused by secondary electrons, ions, and thermal effects can further contribute to the introduction of artificial morphological, compositional, structural, and electrical alterations. Careful discrimination is required to distinguish these artificially induced alterations from intrinsic features of the specimen. Several examples illustrating these effects are schematically depicted in Fig. 16a–f.360–363,386,387 Recent advancements in specimen preparation techniques have shown significant success in mitigating these artefacts in various structural elucidation methods. For instance, cryo-FIB techniques have gained popularity for fabricating delicate thin specimens, such as COFs, for ED and EM applications. This approach effectively minimizes ionic damage that can introduce artefacts. Similarly, cryo-ultramicrotomy has been reported as a method to prepare fragile organic specimens, avoiding surface effects and mechanical disturbances that may occur with conventional plunge freezing techniques.363
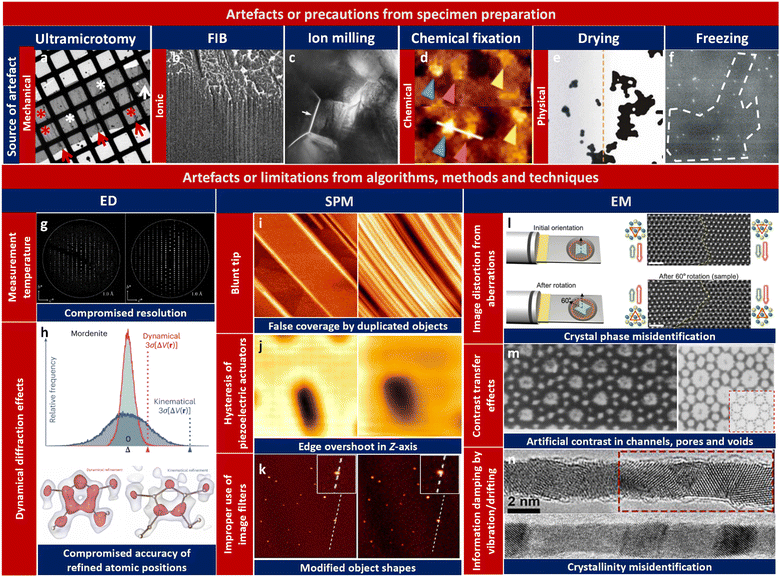 | ||
| Fig. 16 (a)–(f) Artefacts or precautions introduced by diverse specimen preparation techniques. (a) Artefacts in ultra-thin sections prepared by using an ultramicrotome. The ribbon consists of several sections separated by folded zones (red arrows). Cutting artefacts and deformations occurred when the ribbon was mounted on the grid, including folds (white asterisks), wrinkles (red asterisks), and tearing (white arrow). Reproduced with permission.360 Copyright 2005, Elsevier. (b) FIB curtaining artefacts induced by spatial variation of the sputter rate of the specimen. Modified with permission.360 Copyright 2009, SPIE. (c) Artificial intergranular crack (marked by a white arrow) of a polycrystalline ceramic introduced by ion milling. Reproduced with permission.361 Copyright 2022, Springer Nature. (d) Pseudo-clusters resulting from chemical fixation-induced artifacts. Modified with permission. Copyright 2015, Springer Nature. (e) The artifacts arising from particle aggregation due to liquid drying. Reproduced with permission.362 Copyright 2010, Springer. (f) The background's contrast variation corresponds to imperfections induced by cryo-ultramicrotomy. Modified with permission.363 Copyright 2018, Microscopy Society of America. (g) Comparison of ED data collection under different temperatures (room temperature vs liquid nitrogen temperature). Higher collection temperature results in degraded high frequency diffraction spots. Reproduced with permission.245 Copyright 2019, American Chemical Society. (h) Comparison of difference electrostatic potentials derived by structure refinement procedures based on kinematical and dynamical approximations. The former DESP is less well defined. Reproduced with permission.254 Copyright 2021, Springer Nature. (i) Image artifacts caused by a blunt tip (right) rather than a sharp one (left) in SPM. Reproduced with permission.364 Copyright 2019, Springer. (j) Edge overshoot (left) caused by scanner artefacts in contrast to a normal image (right). Reproduced with permission.365 Copyright 2021, Multidisciplinary Digital Publishing Institute. (k) Artificial object shape modification with (right) or without (left) a low-pass filter. Modified with permission.366 Copyright 2010, Oxford University Press. (l) Crystal phase misidentification due to image artifacts caused by the presence of threefold astigmatism aberration and proved by specimen rotation. Reproduced with permission.367 Copyright 2020, Science Advances. (m) Artificial in-channel contrast of an HRTEM image taken on a zeolite crystal referred from the structural projection. Modified with permission.368 Copyright 1990, Elsevier. (n) Anisotropic structural information degradation in a HRTEM image arising from specimen vibration (lower) compared with the original structure (upper). The polycrystalline nature of the crystal can hardly be identified. Modified with permission.306 Copyright 2014, American Chemical Society. | ||
It is important to exercise caution when working with SPM due to the presence of diverse types of artifacts including probe artefacts, scanner artefacts and image processing artefacts (Fig. 16i–k). Blunt, broken, contaminated, or double probes are common factors that can introduce artificial image features or distortions, potentially leading to incorrect feature sizes and shapes, spurious repeating patterns, and misrepresented side topology in SPM applications. Sharp asperities require equally sharp or sharper tips for accurate imaging. Blunt tips can yield incorrect estimates of thin film coverage, as shown in Fig. 16i,364 where a blunt tip creates the illusion of higher coverage due to multiple duplicated surface features. Additionally, issues related to scanner calibration, nonlinearity, scanner bow, creep problems, and hysteresis-induced edge overshoot can critically impact the acquired images. For instance, as the scanning speed increases in AFM near the edges, artefacts become more pronounced. This is attributed to the feedback controller's response to sudden changes in topography, leading to overshoot phenomena. These artefacts have the potential to impact the accurate characterization of the sample surface and can be mitigated through improvements in the feedback controller and similar approaches.365 It is important not to overlook the influence of image processing techniques, such as levelling and filtering processes. Levelling based on polynomial fitting, low-pass filters, and Fourier filters is commonly employed, but these approaches can easily introduce artificial or distorted features in SPM images (Fig. 16k).366
Similar to SPM imaging, caution must also be exercised when interpreting artefacts in TEM imaging. These artefacts can arise not only from image processing techniques but also from inherent issues in TEM imaging algorithms, methods, and techniques (Fig. 16l and m).306,367,368 For instance, image distortions resulting from aberrations, particularly those exhibiting rotational anisotropy, can introduce misleading or misinterpreted structural information. A specific example is the presence of threefold astigmatism (i.e., A2) with pronounced rotational anisotropy, which has been reported to cause critical challenges in correctly identifying crystal phases.367 Insufficient understanding of the underlying mechanisms of contrast transfer in a specific TEM imaging technique may overlook artefacts introduced by inadequate contrast transfer of structural information at different spatial frequencies. This lack of understanding can lead to misinterpretation of artificial contrast in empty channels, pores, and voids within various materials, significantly hindering the accurate determination of structural information for guest species inside. Moreover, it is important to acknowledge the potential challenges arising from anisotropic degradation of structural information, caused by factors such as vibration or drifting. These factors can introduce ambiguities and create confusion when distinguishing between the polycrystalline and single crystalline nature of nanowires (NWs) (Fig. 16n).388 The degradation selectively affects structural information along the direction of vibration or drifting, resulting in the presence of only one set of lattice fringes, even in polycrystalline NWs.
5. Outlook and perspective
In summary, the evolution of the structural design of COFs has been traced from its nascent beginnings in scientific intuition and empirical trial-and-error to its current state of sophistication, characterized by the deployment of diverse AI tools and high-throughput methods in an application-oriented approach. By harnessing the power of ML, researchers can transcend the limitations imposed by the underlying principles of reticular chemistry and topological science (e.g. stoichiometric network construction), and achieve feats that were once thought impossible. By developing AI-based algorithms for material design and discovery, the successful prediction of COFs can be significantly accelerated through search, reasoning, planning, and knowledge representation. These algorithms enable the prediction of new topologies, optimization of COF structures, and accurate evaluation of their properties. By overcoming the challenges in ML concerning the material data relevance, completeness, and standardization, this approach has the potential to greatly expedite the discovery and design of high-performance COF materials. To this end, the emerging demand for innovations in structural characterization tools stems from such rapid advances in the field of COFs, which require high-throughput, comprehensive, and nondestructive structural elucidations. Recent research outbursts in high-throughput serial rotation electron diffraction (SerialRED) and diverse low-dose 4D-STEM imaging techniques are instrumental in pioneering this cutting-edge field.389–391List of acronyms and abbreviations
| ABF | Annular-bright-field |
| AEMs | Arylene-ethynylene macrocycles |
| AFM | Atomic force microscopy |
| AHPs | Adsorption-driven heat pumps |
| AI | Artificial intelligence |
| ANN | Artificial neural networks |
| ASA | Accessible surface area |
| ATS | Amphetamine-type stimulants |
| Auto ML | Automated machine learning |
| AVMs | Arylenevinylene macrocycles |
| BERT | Bidirectional encoder representations from transformers |
| BF | Bright-field |
| BTA | Benzene-1,3,5-tricarbaldehyde |
| cAFM | Conductive atomic force microscopy |
| CBED | Convergent beam electron diffraction |
| CCS | Carbon capture and storage |
| CNN | Convolutional neural network |
| CNS | Carbon nanosolenoid |
| CPD | Contact potential difference |
| cRED | Continuous rotation electron diffraction |
| DBAs | Dehydrobenzoannulenes |
| DCs | Deliverable capacities |
| DDC | Direct detection cameras |
| DFT | Density functional theory |
| DKL | Deep kernel learning |
| DLR | Dose-limited resolution |
| DQE | Detective quantum efficiency |
| DT | Decision tree |
| ECAFM | Electrochemical atomic force microscopy |
| ED | Electron diffraction |
| EDS | Energy dispersive X-ray spectroscopy |
| EELS | Electron energy loss spectroscopy |
| ELN | Electronic lab notebook |
| EMPAD | Electron microscope pixel-array detector |
| EPWF | Exit-plane wave function |
| ETTA | 1,1,2,2-Tetrakis(4-aminophenyl) ethene |
| FIA | Feature importance analysis |
| FBTA-8CHO | ((3,6-Difluorobenzene-1,2,4,5-tetrayl)tetrakis(azanetriyl))octakis([1,1′-biphenyl]-4-carbaldehyde) |
| GA | Genetic algorithm |
| GAN | Generative adversarial network |
| GAT | Generalized Anscombe transformation |
| GBR | Gradient boosting regression |
| GBs | Grain boundaries |
| GCMC | Grand-canonical Monte Carlo |
| GCOFs | Genomic covalent organic frameworks |
| GNN | Graphical neural network |
| GPT | Generative pre-trained transformer |
| GSUs | Genetic structural units |
| HCA | Hierarchical cluster analysis |
| HFPTP | 2,3,6,7,14,15-Hexakis(4′-formylphenyl)triptycene |
| HHTP | Hexahydroxytriphenylene |
| HOPG | Highly oriented pyrolytic graphite |
| HPDs | Hybrid pixel detectors |
| HRTEM | High resolution transmission electron microscopy |
| HypoCOF | Hypothetical covalent organic framework |
| HS-AFM | High-speed atomic force microscopy |
| iDPC | Integrated-differential-phase-contrast |
| K H | Henry's law constant |
| KPFM | Kelvin probe force microscopy |
| LCD | Largest cavity diameter |
| LIM | Local interpretability methods |
| MAPS | Monolithic active pixel sensor |
| MCOFs | Metallo-COFs |
| MGI | Materials genome initiative |
| MHPs | Metal halide perovskites |
| MIDI | Matched illumination and detector interferometry |
| MIM | Mechanical interlocked molecules |
| ML | Machine learning |
| MM | Molecular mechanics |
| nc-AFM | Non-contact atomic force microscopy |
| NPs | Nanoparticles |
| OMe-TPBP | 2,2′-Dimethoxyl-3,3′,5,5′-tetrakis(4-aminophenyl)biphenyl |
| PA | p-Phenylenediamine |
| PBR | Peak-to-background ratio |
| PCA | Principal component analysis |
| PCR | Principal components regression |
| pCTF | Phase-contrast-transfer-function |
| PDA | p-Phenylenediamine |
| PEC | Photoelectrochemical |
| PEO | Poly(ethylene oxide) |
| PID | Proportional-integral-derivative |
| PLS | Partial least squares |
| post-SM | Post-synthetic modification |
| pre-SM | Pre-synthetic modification |
| PXRD | Powder X-ray diffraction |
| QM | Quantum mechanics |
| QReaxAA | Quasi-reactive assembly algorithms |
| RCSR | Reticular chemistry structure resource |
| RDF | Random decision forests |
| RED | Rotation electron diffraction |
| RF | Random forest |
| SBUs | Secondary building units |
| SCXRD | Single crystal X-ray diffraction |
| SHAP | Shapley additive explanations |
| SMILES | Simplified molecular-input line-entry system |
| SNR | Signal-to-noise ratio |
| SPM | Scanning probe microscopy |
| SPV | Surface photovoltage |
| STEM | Scanning transmission electron microscopy |
| STM | Scanning tunneling microscopy |
| STS | Scanning tunneling spectroscopy |
| SVM | Support vector machine |
| TABPM | Tetrakis(4-amino biphenyl)methane |
| TAM | Tetra-(4-anilyl)methane |
| TAPA | Tris(4-aminophenyl)amine |
| TAPB | 1,3,5-Tris(4′-aminophenyl)benzene |
| TAPPy | 1,3,6,8-Tetrakis(4-aminophenyl)pyrene |
| TAPT | 1,3,5-Tris(4-aminophenyl)triazine |
| TBPS | Tetra(4-dihydroxyborylphenyl)silane |
| TBTANG | Tribromotrioxaazatriangulene |
| TCB | Trichlorobenzene |
| TDA | Topological data analysis |
| TFB | 1,3,5-Triformylbenzene |
| TFMB | 1,2,4,5-Tetrakis[(4-formyphenoxy)methyl]benzene |
| TFP | 1,3,5-Triformylphloroglucinol |
| TFPA | Tris(4-formylphenyl) amine |
| TFS | Tetra(4-formylphenyl) silane |
| THF | Tetrahydrofuran |
| TMDs | Transition metal dichalcogenides |
| TPDH | Terephthalic dihydrazide |
| TRIF | Tri-(4-formacylphenoxy)-1,3,5-triazine |
| UHV | Ultra-high vacuum |
| V a | Available pore volume |
| VAE | Variational auto-encoder |
| V F | Helium void fraction |
| ρ | Adsorbent density |
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported in part by the National Key Research and Development Program of China (2022YFE0113800, 2021YFA1501801) and the National Natural Science Foundation of China (22075250, 22122505, 21771161, 22288101).Notes and references
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed.
- T. R. Cook, Y. R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734–777 CrossRef CAS PubMed.
- X. Li, J. Wang, X. Liu, L. Liu, D. Cha, X. Zheng, A. A. Yousef, K. Song, Y. Zhu, D. Zhang and Y. Han, J. Am. Chem. Soc., 2019, 141, 12021–12028 CrossRef CAS PubMed.
- S. Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568 RSC.
- P. Waller, S. Lyle, T. O. Popp, C. Diercks, J. Reimer and O. Yaghi, Abstr. Pap. Am. Chem. Soc., 2017, 253, 1 Search PubMed.
- N. Huang, P. Wang and D. L. Jiang, Nat. Rev. Mater., 2016, 1, 19 CrossRef.
- M. Dogru and T. Bein, Chem. Commun., 2014, 50, 5531–5546 RSC.
- R. P. Bisbey and W. R. Dichtel, ACS Cent. Sci., 2017, 3, 533–543 CrossRef CAS PubMed.
- X. Ni and J.-L. Brédas, Chem. Mater., 2022, 34, 1334–1341 CrossRef CAS.
- H. L. Nguyen, C. Gropp and O. M. Yaghi, J. Am. Chem. Soc., 2020, 142, 2771–2776 CrossRef CAS PubMed.
- X. Guan, F. Chen, Q. Fang and S. Qiu, Chem. Soc. Rev., 2020, 49, 1357–1384 RSC.
- A. M. Evans, L. R. Parent, N. C. Flanders, R. P. Bisbey, E. Vitaku, M. S. Kirschner, R. D. Schaller, L. X. Chen, N. C. Gianneschi and W. R. Dichtel, Science, 2018, 361, 52–57 CrossRef CAS PubMed.
- X. Xu, P. Cai, H. Chen, H.-C. Zhou and N. Huang, J. Am. Chem. Soc., 2022, 144, 18511–18517 CrossRef CAS PubMed.
- C. T. Gong, H. Wang, G. Sheng, X. K. Wang, X. Q. Xu, J. Wang, X. H. Miao, Y. K. Liu, Y. L. Zhang, F. N. Dai, L. J. Chen, N. J. Li, G. D. Xu, J. H. Jia, Y. H. Zhu and Y. W. Peng, Angew. Chem., Int. Ed., 2022, 61, 8 Search PubMed.
- F. Jin, E. Lin, T. Wang, S. Geng, T. Wang, W. Liu, F. Xiong, Z. Wang, Y. Chen, P. Cheng and Z. Zhang, J. Am. Chem. Soc., 2022, 144, 5643–5652 CrossRef CAS PubMed.
- S. Yan, X. Guan, H. Li, D. Li, M. Xue, Y. Yan, V. Valtchev, S. Qiu and Q. Fang, J. Am. Chem. Soc., 2019, 141, 2920–2924 CrossRef CAS PubMed.
- Z. Yang, W. Hao, X. Su, T. Zhang, W. Chen, G. Zhang and L. Chen, Chem. Mater., 2022, 34, 5888–5895 CrossRef CAS.
- D. Jiang, Chem, 2020, 6, 2461–2483 CAS.
- J. Guo and D. Jiang, ACS Cent. Sci., 2020, 6, 869–879 CrossRef CAS PubMed.
- T. F. Machado, M. E. S. Serra, D. Murtinho, A. J. M. Valente and M. Naushad, Polymers, 2021, 13 Search PubMed.
- L. Li, Q. Yun, C. Zhu, G. Sheng, J. Guo, B. Chen, M. Zhao, Z. Zhang, Z. Lai, X. Zhang, Y. Peng, Y. Zhu and H. Zhang, J. Am. Chem. Soc., 2022, 144, 6475–6482 CrossRef CAS PubMed.
- C. Gong, H. Wang, G. Sheng, X. Wang, X. Xu, J. Wang, X. Miao, Y. Liu, Y. Zhang, F. Dai, L. Chen, N. Li, G. Xu, J. Jia, Y. Zhu and Y. Peng, Angew. Chem., Int. Ed., 2022, 61, e202204899 CrossRef CAS PubMed.
- Q. Chen, C. Dwyer, G. Sheng, C. Zhu, X. Li, C. Zheng and Y. Zhu, Adv. Mater., 2020, 32, 1907619 CrossRef CAS PubMed.
- S. Aydin, C. Altintas and S. Keskin, ACS Appl. Mater. Interfaces, 2022, 14, 21738–21749 CrossRef CAS PubMed.
- W. Jiang, P. Wang, K.-i Otake, S. Kitagawa, Y. Noda, K. Takeda and K. Takegoshi, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv-2021-1drg9.
- M. O’Keeffe, Chem. Soc. Rev., 2009, 38, 1215–1217 RSC.
- Y. Lan, X. Han, M. Tong, H. Huang, Q. Yang, D. Liu, X. Zhao and C. Zhong, Nat. Commun., 2018, 9, 5274 CrossRef PubMed.
- L. Zhu and Y.-B. Zhang, Molecules, 2017, 22, 1149 CrossRef PubMed.
- J. Mahmood, I. Ahmad, M. Jung, J.-M. Seo, S.-Y. Yu, H.-J. Noh, Y. Kim, H.-J. Shin and J.-B. Baek, Commun. Chem., 2020, 3, 31 CrossRef CAS PubMed.
- T. Sun, W. Lei, Y. Ma and Y.-B. Zhang, Chin. J. Chem., 2020, 38, 1153–1166 CrossRef CAS.
- Z. J. W. A. Leijten, A. D. A. Keizer, G. de With and H. Friedrich, J. Phys. Chem. C, 2017, 121, 10552–10561 CrossRef CAS PubMed.
- N. Bilbao, D. Waghray, T. Janssen and S. Feyter, Microsc. Microanal., 2019, 25, 1478–1479 CrossRef.
- C. Wiktor, M. Meledina, S. Turner, O. I. Lebedev and R. A. Fischer, J. Mater. Chem. A, 2017, 5, 14969–14989 RSC.
- Y. Su, M. Nykanen, K. A. Jahn, R. Whan, L. Cantrill, L. L. Soon, K. R. Ratinac and F. Braet, Biophys. Rev., 2010, 2, 121–135 CrossRef PubMed.
- S. T. Skowron, T. W. Chamberlain, J. Biskupek, U. Kaiser, E. Besley and A. N. Khlobystov, Acc. Chem. Res., 2017, 50, 1797–1807 CrossRef CAS PubMed.
- Y. Li, K. Wang, W. Zhou, Y. Li, R. Vila, W. Huang, H. Wang, G. Chen, G.-H. Wu, Y. Tsao, H. Wang, R. Sinclair, W. Chiu and Y. Cui, Matter, 2020, 2, 1064 CrossRef.
- H. Wang, L. Liu, J. Wang, C. Li, J. Hou and K. Zheng, Molecules, 2022, 27, 3829 CrossRef CAS PubMed.
- H. Yang, R. N. Rutte, L. Jones, M. Simson, R. Sagawa, H. Ryll, M. Huth, T. J. Pennycook, M. L. H. Green, H. Soltau, Y. Kondo, B. G. Davis and P. D. Nellist, Nat. Commun., 2016, 7, 12532 CrossRef CAS PubMed.
- De Gruyter, Berlin, Boston, 2023.
- J. J. Oppenheim, G. Skorupskii and M. Dincă, Chem. Sci., 2020, 11, 11094–11103 RSC.
- H. M. El-Kaderi, J. R. Hunt, J. L. Mendoza-Cortés, A. P. Côté, R. E. Taylor, M. O'Keeffe and O. M. Yaghi, Science, 2007, 316, 268–272 CrossRef CAS PubMed.
- Y.-B. Zhang, J. Su, H. Furukawa, Y. Yun, F. Gándara, A. Duong, X. Zou and O. M. Yaghi, J. Am. Chem. Soc., 2013, 135, 16336–16339 CrossRef CAS PubMed.
- Y. Liu, Y. Ma, Y. Zhao, X. Sun, F. Gándara, H. Furukawa, Z. Liu, H. Zhu, C. Zhu, K. Suenaga, P. Oleynikov, A. S. Alshammari, X. Zhang, O. Terasaki and O. M. Yaghi, Science, 2016, 351, 365–369 CrossRef CAS PubMed.
- M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789 CrossRef PubMed.
- A. Schoedel, M. Li and D. Li, Chem. Rev., 2016, 116, 10–1021 CrossRef PubMed.
- V. A. Blatov and D. M. Proserpio, Acta Crystallogr. A, 2009, 65, 202–212 CrossRef CAS PubMed.
- M. Zhang, R. Zheng, Y. Ma, R. Chen, X. Sun and X. Sun, Microporous Mesoporous Mater., 2019, 285, 70–79 CrossRef CAS.
- H. Yang, Y. Du, S. Wan, G. D. Trahan, Y. Jin and W. Zhang, Chem. Sci., 2015, 6, 4049–4053 RSC.
- M.-X. Wu and Y.-W. Yang, Chin. Chem. Lett., 2017, 28, 1135–1143 CrossRef CAS.
- S. Dalapati, M. Addicoat, S. Jin, T. Sakurai, J. Gao, H. Xu, S. Irle, S. Seki and D. Jiang, Nat. Commun., 2015, 6, 7786 CrossRef CAS PubMed.
- P. H. J. Kouwer, M. Koepf, V. A. A. Le Sage, M. Jaspers, A. M. van Buul, Z. H. Eksteen-Akeroyd, T. Woltinge, E. Schwartz, H. J. Kitto, R. Hoogenboom, S. J. Picken, R. J. M. Nolte, E. Mendes and A. E. Rowan, Nature, 2013, 493, 651–655 CrossRef CAS PubMed.
- B. Zhang, H. Mao, R. Matheu, J. A. Reimer, S. A. Alshmimri, S. Alshihri and O. M. Yaghi, J. Am. Chem. Soc., 2019, 141, 11420–11424 CrossRef CAS PubMed.
- A. Trewin and A. I. Cooper, CrystEngComm, 2009, 11, 1819–1822 RSC.
- M. Wu, Z. Shan, J. Wang, T. Liu and G. Zhang, Chem. Eng. J., 2023, 454, 140121 CrossRef CAS.
- C. Wu, Y. Liu, H. Liu, C. Duan, Q. Pan, J. Zhu, F. Hu, X. Ma, T. Jiu, Z. Li and Y. Zhao, J. Am. Chem. Soc., 2018, 140, 10016–10024 CrossRef CAS PubMed.
- C. Qian, E.-C. Liu, Q.-Y. Qi, K. Xu, G.-F. Jiang and X. Zhao, Polym. Chem., 2018, 9, 279–283 RSC.
- C. Gropp, T. Ma, N. Hanikel and O. M. Yaghi, Science, 2020, 370, eabd6406 CrossRef CAS PubMed.
- C. S. Diercks and O. M. Yaghi, Science, 2017, 355, eaal1585 CrossRef PubMed.
- F. Jin, E. Lin, T. Wang, D. Yan, Y. Yang, Y. Chen, P. Cheng and Z. Zhang, Chem, 2022, 8, 3064–3080 CAS.
- J. Huang, X. Liu, W. Zhang, Z. Liu, H. Zhong, B. Shao, Q. Liang, Y. Liu, W. Zhang and Q. He, Chem. Eng. J., 2021, 404, 127136 CrossRef CAS.
- J. A. Martín-Illán, S. Royuela, M. Mar Ramos, J. L. Segura and F. Zamora, Chem. – Eur. J., 2020, 26, 6495–6498 CrossRef PubMed.
- N. Huang, X. Chen, R. Krishna and D. Jiang, Angew. Chem., Int. Ed., 2015, 54, 2986–2990 CrossRef CAS PubMed.
- Q. Guan, G.-B. Wang, L.-L. Zhou, W.-Y. Li and Y.-B. Dong, Nanoscale Adv., 2020, 2, 3656–3733 RSC.
- X. Shi, D. Ma, F. Xu, Z. Zhang and Y. Wang, Chem. Sci., 2020, 11, 989–996 RSC.
- Y. Li, M. Zhang, X. Guo, R. Wen, X. Li, X. Li, S. Li and L. Ma, Nanoscale Horiz., 2018, 3, 205–212 RSC.
- Y. Li, K. Zuo, T. Gao, J. Wu, X. Su, C. Zeng, H. Xu, H. Hu, X. Zhang and Y. Gao, RSC Adv., 2022, 12, 4874–4882 RSC.
- E. L. Spitler and W. R. Dichtel, Nat. Chem., 2010, 2, 672–677 CrossRef CAS PubMed.
- E. L. Spitler, M. R. Giovino, S. L. White and W. R. Dichtel, Chem. Sci., 2011, 2, 1588–1593 RSC.
- X. Hu, Z. Zhan, J. Zhang, I. Hussain and B. Tan, Nat. Commun., 2021, 12, 6596 CrossRef CAS PubMed.
- R. Sun, X. Wang, X. Wang and B. Tan, Angew. Chem., Int. Ed., 2022, 61, e202117668 CrossRef CAS PubMed.
- M. Liu, Q. Huang, S. Wang, Z. Li, B. Li, S. Jin and B. Tan, Angew. Chem., Int. Ed., 2018, 57, 11968–11972 CrossRef CAS PubMed.
- T.-Y. Zhou, S.-Q. Xu, Q. Wen, Z.-F. Pang and X. Zhao, J. Am. Chem. Soc., 2014, 136, 15885–15888 CrossRef CAS PubMed.
- G. Lin, H. Ding, R. Chen, Z. Peng, B. Wang and C. Wang, J. Am. Chem. Soc., 2017, 139, 8705–8709 CrossRef CAS PubMed.
- Y.-X. Ma, Z.-J. Li, L. Wei, S.-Y. Ding, Y.-B. Zhang and W. Wang, J. Am. Chem. Soc., 2017, 139, 4995–4998 CrossRef CAS PubMed.
- R. Wang, W. Kong, T. Zhou, C. Wang and J. Guo, Chem. Commun., 2021, 57, 331–334 RSC.
- Q. Fang, Z. Zhuang, S. Gu, R. B. Kaspar, J. Zheng, J. Wang, S. Qiu and Y. Yan, Nat. Commun., 2014, 5, 4503 CrossRef PubMed.
- P. J. Waller, S. J. Lyle, T. M. Osborn Popp, C. S. Diercks, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2016, 138, 15519–15522 CrossRef CAS PubMed.
- S. Wei, F. Zhang, W. Zhang, P. Qiang, K. Yu, X. Fu, D. Wu, S. Bi and F. Zhang, J. Am. Chem. Soc., 2019, 141, 14272–14279 CrossRef CAS PubMed.
- C. Zhao, H. Lyu, Z. Ji, C. Zhu and O. M. Yaghi, J. Am. Chem. Soc., 2020, 142, 14450–14454 CrossRef CAS PubMed.
- J. He, X. Jiang, F. Xu, C. Li, Z. Long, H. Chen and X. Hou, Angew. Chem., 2021, 133, 10072–10077 CrossRef.
- F. J. Uribe-Romo, J. R. Hunt, H. Furukawa, C. Klöck, M. O’Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 4570–4571 CrossRef CAS PubMed.
- P. Kuhn, M. Antonietti and A. Thomas, Angew. Chem., Int. Ed., 2008, 47, 3450–3453 CrossRef CAS PubMed.
- S.-Y. Jiang, S.-X. Gan, X. Zhang, H. Li, Q.-Y. Qi, F.-Z. Cui, J. Lu and X. Zhao, J. Am. Chem. Soc., 2019, 141, 14981–14986 CrossRef CAS PubMed.
- H.-S. Xu, Y. Luo, X. Li, P. Z. See, T. Ma, L. Liang, K. Leng, I. Abdelwahab, L. Wang, R. Li, X. Shi, Y. Zhou, X. Lu, X. Zhao, C. Liu, J. Sun and K. Loh, Nat. Commun., 2020, 11 Search PubMed.
- Z. Chen, K. Wang, X. Hu, P. Shi, Z. Guo and H. Zhan, ACS Appl. Mater. Interfaces, 2021, 13, 1145–1151 CrossRef CAS PubMed.
- S. Wan, J. Guo, J. Kim, H. Ihee and D. Jiang, Angew. Chem., Int. Ed., 2008, 47, 8826–8830 CrossRef CAS PubMed.
- A. P. Côté, H. M. El-Kaderi, H. Furukawa, J. R. Hunt and O. M. Yaghi, J. Am. Chem. Soc., 2007, 129, 12914–12915 CrossRef PubMed.
- Y.-F. Xie, S.-Y. Ding, J.-M. Liu, W. Wang and Q.-Y. Zheng, J. Mater. Chem. C, 2015, 3, 10066–10069 RSC.
- D. Kaleeswaran, P. Vishnoi and R. Murugavel, J. Mater. Chem. C, 2015, 3, 7159–7171 RSC.
- R. Chen, J.-L. Shi, Y. Ma, G. Lin, X. Lang and C. Wang, Angew. Chem., Int. Ed., 2019, 58, 6430–6434 CrossRef CAS PubMed.
- X. Ding, X. Feng, A. Saeki, S. Seki, A. Nagai and D. Jiang, Chem. Commun., 2012, 48, 8952–8954 RSC.
- L. A. Baldwin, J. W. Crowe, D. A. Pyles and P. L. McGrier, J. Am. Chem. Soc., 2016, 138, 15134–15137 CrossRef CAS PubMed.
- T. Ma, E. A. Kapustin, S. X. Yin, L. Liang, Z. Zhou, J. Niu, L.-H. Li, Y. Wang, J. Su, J. Li, X. Wang, W. D. Wang, W. Wang, J. Sun and O. M. Yaghi, Science, 2018, 361, 48–52 CrossRef CAS PubMed.
- Q. Fang, J. Wang, S. Gu, R. B. Kaspar, Z. Zhuang, J. Zheng, H. Guo, S. Qiu and Y. Yan, J. Am. Chem. Soc., 2015, 137, 8352–8355 CrossRef CAS PubMed.
- O. Yahiaoui, A. N. Fitch, F. Hoffmann, M. Fröba, A. Thomas and J. Roeser, J. Am. Chem. Soc., 2018, 140, 5330–5333 CrossRef CAS PubMed.
- G. Lin, H. Ding, D. Yuan, B. Wang and C. Wang, J. Am. Chem. Soc., 2016, 138, 3302–3305 CrossRef CAS PubMed.
- H. Li, J. Ding, X. Guan, F. Chen, C. Li, L. Zhu, M. Xue, D. Yuan, V. Valtchev, Y. Yan, S. Qiu and Q. Fang, J. Am. Chem. Soc., 2020, 142, 13334–13338 CrossRef CAS PubMed.
- Z. Li, L. Sheng, H. Wang, X. Wang, M. Li, Y. Xu, H. Cui, H. Zhang, H. Liang, H. Xu and X. He, J. Am. Chem. Soc., 2021, 143, 92–96 CrossRef CAS PubMed.
- L. Chen, C. Gong, X. Wang, F. Dai, M. Huang, X. Wu, C.-Z. Lu and Y. Peng, J. Am. Chem. Soc., 2021, 143, 10243–10249 CrossRef CAS PubMed.
- E. M. Carreira, J. Am. Chem. Soc., 2021, 143, 1–2 CrossRef CAS PubMed.
- Z. Li, L. Sheng, C. Hsueh, X. Wang, H. Cui, H. Gao, Y. Wu, J. Wang, Y. Tang, H. Xu and X. He, Chem. Mater., 2021, 33, 9618–9623 CrossRef CAS.
- S.-Y. Ding, J. Gao, Q. Wang, Y. Zhang, W.-G. Song, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2011, 133, 19816–19822 CrossRef CAS PubMed.
- L. A. Baldwin, J. W. Crowe, M. D. Shannon, C. P. Jaroniec and P. L. McGrier, Chem. Mater., 2015, 27, 6169–6172 CrossRef CAS.
- Y. Peng, L. Li, C. Zhu, B. Chen, M. Zhao, Z. Zhang, Z. Lai, X. Zhang, C. Tan, Y. Han, Y. Zhu and H. Zhang, J. Am. Chem. Soc., 2020, 142, 13162–13169 CrossRef CAS PubMed.
- X. Wu, X. Han, Y. Liu, Y. Liu and Y. Cui, J. Am. Chem. Soc., 2018, 140, 16124–16133 CrossRef CAS PubMed.
- E. Dautzenberg, F. W. Claassen and L. C. P. M. de Smet, Microporous Mesoporous Mater., 2023, 350, 112318 CrossRef CAS.
- G.-Y. Lee, J. Lee, H. T. Vo, S. Kim, H. Lee and T. Park, Sci. Rep., 2017, 7, 557 CrossRef PubMed.
- Z. Lei, L. J. Wayment, J. R. Cahn, H. Chen, S. Huang, X. Wang, Y. Jin, S. Sharma and W. Zhang, J. Am. Chem. Soc., 2022, 144, 17737–17742 CrossRef CAS PubMed.
- Y.-P. Zhu, Z.-Y. Yuan and H. N. Alshareef, ACS Mater. Lett., 2020, 2, 582–594 CrossRef CAS.
- D. Pakulski, V. Montes García, A. Gorczyński, W. Czepa, T. Chudziak, P. Samorì and A. Ciesielski, J. Mater. Chem. A, 2022, 10 Search PubMed.
- Y. An, S. Tan, Y. Liu, K. Zhu, L. Hu, Y. Rong and Q. An, Energy Storage Mater., 2021, 41, 354–379 CrossRef.
- A. K. Mandal, J. Mahmood and J.-B. Baek, ChemNanoMat., 2017, 3, 373–391 CrossRef CAS.
- N. Keller and T. Bein, Chem. Soc. Rev., 2021, 50, 1813–1845 RSC.
- X. Yan, H. Liu, Y. Li, W. Chen, T. Zhang, Z. Zhao, G. Xing and L. Chen, Macromolecules, 2019, 52, 7977–7983 CrossRef CAS.
- N. Huang, L. Zhai, H. Xu and D. Jiang, J. Am. Chem. Soc., 2017, 139, 2428–2434 CrossRef CAS PubMed.
- S.-Y. Ding, M. Dong, Y.-W. Wang, Y.-T. Chen, H.-Z. Wang, C.-Y. Su and W. Wang, J. Am. Chem. Soc., 2016, 138, 3031–3037 CrossRef CAS PubMed.
- E. A. Gendy, J. Ifthikar, J. Ali, D. T. Oyekunle, Z. Elkhlifia, I. I. Shahib, A. I. Khodair and Z. Chen, J. Environ. Chem. Eng., 2021, 9, 105687 CrossRef CAS.
- Q. Sun, B. Aguila, L. D. Earl, C. W. Abney, L. Wojtas, P. K. Thallapally and S. Ma, Adv. Mater., 2018, 30, 1705479 CrossRef PubMed.
- B. Zhang, M. Wei, H. Mao, X. Pei, S. A. Alshmimri, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2018, 140, 12715–12719 CrossRef CAS PubMed.
- J. Dong, X. Han, Y. Liu, H. Li and Y. Cui, Angew. Chem., Int. Ed., 2020, 59, 13722–13733 CrossRef CAS PubMed.
- J. Lan, D. Cao, W. Wang and B. Smit, ACS Nano, 2010, 4, 4225–4237 CrossRef CAS PubMed.
- Y. Cao, W. Peng, Y. Li, F. Zhang, Y. Zhu and X. Fan, Green Energy Environ., 2023, 8, 360–382 CrossRef CAS.
- Y. Liu, Y. Ma, J. Yang, C. S. Diercks, N. Tamura, F. Jin and O. M. Yaghi, J. Am. Chem. Soc., 2018, 140, 16015–16019 CrossRef CAS PubMed.
- J. Huang, X. Han, S. Yang, Y. Cao, C. Yuan, Y. Liu, J. Wang and Y. Cui, J. Am. Chem. Soc., 2019, 141, 8996–9003 CrossRef CAS PubMed.
- X. Liu, H. Xu, L. Wang, Z. Qu and N. Yan, Chem. Eng. J., 2020, 381, 122559 CrossRef CAS.
- Q. Fang, S. Gu, J. Zheng, Z. Zhuang, S. Qiu and Y. Yan, Angew. Chem., 2014, 126, 2922–2926 CrossRef.
- F. Yang, Y. Li, T. Zhang, Z. Zhao, G. Xing and L. Chen, Chem. – Eur. J., 2020, 26, 4510–4514 CrossRef CAS PubMed.
- W.-k Li, P. Ren, Y.-w Zhou, J.-t Feng and Z.-q Ma, J. Hazard. Mater., 2020, 388, 121740 CrossRef CAS PubMed.
- V. Singh, J. Kim, B. Kang, J. Moon, S. Kim, W. Y. Kim and H. R. Byon, Adv. Energy Mater., 2021, 11, 2003735 CrossRef CAS.
- H.-L. Jiang, F. Xue, J. Sun, J.-M. Lin, C. Zhang, X. Wang and R.-S. Zhao, Microchim. Acta, 2021, 188, 47 CrossRef CAS PubMed.
- R. Wang and Z. Chen, Microchim. Acta, 2017, 184, 3867–3874 CrossRef CAS.
- L. Guo, J. Liu, J. Li, L. Hao, W. Liu, C. Wang, Q. Wu and Z. Wang, J. Chromatogr. A, 2021, 1651, 462301 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- W. Sun, Y. Zheng, K. Yang, Q. Zhang, A. A. Shah, Z. Wu, Y. Sun, L. Feng, D. Chen, Z. Xiao, S. Lu, Y. Li and K. Sun, Sci. Adv., 2019, 5, eaay4275 CrossRef CAS PubMed.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, npj Comput. Mater., 2019, 5, 83 CrossRef.
- B. Kailkhura, B. Gallagher, S. Kim, A. Hiszpanski and T. Y.-J. Han, npj Comput. Mater., 2019, 5, 108 CrossRef.
- C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter, M. Haranczyk, D. S. Sholl, R. Q. Snurr and B. Smit, Energy Environ. Sci., 2015, 8, 1190–1199 RSC.
- Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. F. Stoddart, F. You, J. T. Hupp, O. K. Farha and R. Q. Snurr, Sci. Adv., 2016, 2, e1600909 CrossRef PubMed.
- J. G. Carbonell, R. S. Michalski and T. M. Mitchell, in Machine Learning, ed. R. S. Michalski, J. G. Carbonell and T. M. Mitchell, Morgan Kaufmann, San Francisco (CA), 1983, pp. 3–23 DOI:10.1016/B978-0-08-051054-5.50005-4.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Mol. Syst. Des. Eng., 2019, 4, 162–174 RSC.
- P. Yang, H. Zhang, X. Lai, K. Wang, Q. Yang and D. Yu, ACS Omega, 2021, 6, 17149–17161 CrossRef CAS PubMed.
- X. Cao, Z. Zhang, Y. He, W. Xue, H. Huang and C. Zhong, Ind. Eng. Chem. Res., 2022, 61, 11116–11123 CrossRef CAS.
- S. Kumar, G. Ignacz and G. Szekely, Green Chem., 2021, 23, 8932–8939 RSC.
- S.-W. Li, L.-C. Xu, C. Zhang, S.-Q. Zhang and X. Hong, Nat. Commun., 2023, 14, 3569 CrossRef CAS PubMed.
- D. Ongari, A. V. Yakutovich, L. Talirz and B. Smit, ACS Cent. Sci., 2019, 5, 1663–1675 CrossRef CAS PubMed.
- R. Mercado, R.-S. Fu, A. V. Yakutovich, L. Talirz, M. Haranczyk and B. Smit, Chem. Mater., 2018, 30, 5069–5086 CrossRef CAS.
- M. Tong, Y. Lan, Q. Yang and C. Zhong, Chem. Eng. Sci., 2017, 168, 456–464 CrossRef CAS.
- Z. Zhang, C. Zhang, Y. Zhang, S. Deng, Y.-F. Yang, A. Su and Y.-B. She, RSC Adv., 2023, 13, 16952–16962 RSC.
- H. Park, Y. Kang and J. Kim, PMTransformer: Universal Transfer Learning and Cross-material Few-shot Learning in Porous Materials, 2023.
- H. Tang and J. Jiang, AIChE J., 2022, 68, e17856 CrossRef CAS.
- L. M. Ghiringhelli, J. Vybiral, S. V. Levchenko, C. Draxl and M. Scheffler, Phys. Rev. Lett., 2015, 114, 105503 CrossRef PubMed.
- F. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Int. J. Quantum Chem., 2015, 115, 1094–1101 CrossRef CAS.
- H. Zhang, P. Yang, D. Yu, K. Wang and Q. Yang, Chin. J. Chem. Eng., 2021, 39, 286–296 CrossRef CAS.
- S. Yang, W. Zhu, L. Zhu, X. Ma, T. Yan, N. Gu, Y. Lan, Y. Huang, M. Yuan and M. Tong, ACS Appl. Mater. Interfaces, 2022, 14, 56353–56362 CrossRef CAS PubMed.
- W. Li, X. Xia and S. Li, ACS Appl. Mater. Interfaces, 2020, 12, 3265–3273 CrossRef CAS PubMed.
- Y. Lee, S. D. Barthel, P. Dłotko, S. M. Moosavi, K. Hess and B. Smit, Nat. Commun., 2017, 8, 15396 CrossRef CAS PubMed.
- X. Zhang, J. Cui, K. Zhang, J. Wu and Y. Lee, J. Chem. Inf. Model., 2019, 59, 4636–4644 CrossRef CAS PubMed.
- W. Zhou, L. Yang, X. Wang, W. Zhao, J. Yang, D. Zhai, L. Sun and W. Deng, JACS Au, 2021, 1, 1497–1505 CrossRef CAS PubMed.
- M. Garofalakis, D. Hyun, R. Rastogi and K. Shim, Data Min Knowl Discov, 2003, 7, 187–214 CrossRef.
- M. Carbon-Mangels and M. C. Hutter, Mol. Inform., 2011, 30, 885–895 CrossRef CAS PubMed.
- H. Kawakubo and H. Yoshida, Expert Syst. Appl., 2012, 40, 6241–6252 Search PubMed.
- M. Markiewicz and A. Wyłomańska, Int. J. Adv. Eng. Sci. Appl. Math., 2021, 13, 248–256 CrossRef.
- J. Wang, Y. Ma, L. Zhang, R. X. Gao and D. Wu, J. Manuf. Syst., 2018, 48, 144–156 CrossRef.
- H. Nakagawa, Y. Iwasawa and Y. Matsuo, IEEE/EIC/ACM International Conference on Web Intelligence, 2019, pp. 156–163.
- Y. Jin, G. Song and C. Shi, Proceedings of the AAAI Conference on Artificial Intelligence, 2020, vol. 34, pp. 4361–4368.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Adv. Neural Inf. Process, 2017, 30 Search PubMed.
- J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, arXiv, 2018, preprint arXiv:1810.04805.
- C. Ying, T. Cai, S. Luo, S. Zheng, G. Ke, D. He, Y. Shen and T.-Y. Liu, Adv. Neural Inf. Process, 2021, 34, 28877–28888 Search PubMed.
- Z. Zhang, J. A. Schott, M. Liu, H. Chen, X. Lu, B. G. Sumpter, J. Fu and S. Dai, Angew. Chem., Int. Ed., 2019, 58, 259–263 CrossRef CAS PubMed.
- R. Wang, Y. Zhong, L. Bi, M. Yang and D. Xu, ACS Appl. Mater. Interfaces, 2020, 12, 52797–52807 CrossRef CAS PubMed.
- A. S. Rosen, V. Fung, P. Huck, C. T. O’Donnell, M. K. Horton, D. G. Truhlar, K. A. Persson, J. M. Notestein and R. Q. Snurr, npj Comput. Mater., 2022, 8, 112 CrossRef CAS.
- A. E. Baumann, D. A. Burns, B. Liu and V. S. Thoi, Commun. Chem., 2019, 2, 86 CrossRef.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, npj Comput. Mater., 2021, 7, 84 CrossRef CAS.
- P. Schwaller, A. C. Vaucher, R. Laplaza, C. Bunne, A. Krause, C. Corminboeuf and T. Laino, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1604 CrossRef.
- A. Su and K. Rajan, Sci. Data, 2021, 8, 14 CrossRef PubMed.
- N. Fu, L. Wei, Y. Song, Q. Li, R. Xin, S. S. Omee, R. Dong, E. M. D. Siriwardane and J. Hu, 2022, preprint, arXiv:2206.13578.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- V. Bagal, R. Aggarwal, P. K. Vinod and U. D. Priyakumar, J. Chem. Inf. Model., 2022, 62, 2064–2076 CrossRef CAS PubMed.
- Y. Liu, T. Zhao, W. Ju and S. Shi, J. Mater., 2017, 3, 159–177 Search PubMed.
- Y. Song, Q. Sun, B. Aguila and S. Ma, Adv. Sci., 2019, 6, 1801410 CrossRef PubMed.
- X. Zhao, P. Pachfule and A. Thomas, Chem. Soc. Rev., 2021, 50, 6871–6913 RSC.
- X. Shi, L. Yi and H. Deng, Sci. China Chem., 2022, 65, 1315–1320 CrossRef CAS.
- L. Gong, X. Wang, T. Zheng, J. Liu, J. Wang, Y.-C. Yang, J. Zhang, X. Han, L. Zhang and Z. Xia, J. Mater. Chem. A, 2021, 9, 3555–3566 RSC.
- T. Banerjee, F. Haase, S. Trenker, B. P. Biswal, G. Savasci, V. Duppel, I. Moudrakovski, C. Ochsenfeld and B. V. Lotsch, Nat. Commun., 2019, 10, 2689 CrossRef PubMed.
- L. Patiny, M. Zasso, D. Kostro, A. Bernal, A. M. Castillo, A. Bolaños, M. A. Asencio, N. Pellet, M. Todd, N. Schloerer, S. Kuhn, E. Holmes, S. Javor and J. Wist, Magn. Reson. Chem., 2018, 56, 520–528 CrossRef CAS PubMed.
- P. Tremouilhac, A. Nguyen, Y.-C. Huang, S. Kotov, D. S. Lütjohann, F. Hübsch, N. Jung and S. Bräse, J. Cheminf., 2017, 9, 54 Search PubMed.
- S. Ryu, Y. Kwon and W. Y. Kim, Chem. Sci., 2019, 10, 8438–8446 RSC.
- Y. Zhang and A. A. Lee, Chem. Sci., 2019, 10, 8154–8163 RSC.
- D. Zhang, L. Lu, L. Guo and G. E. Karniadakis, J. Comput. Phys., 2019, 397, 108850 CrossRef.
- A. Mähringer and D. D. Medina, Nat. Chem., 2020, 12, 985–987 CrossRef PubMed.
- Y. Zhang, M.-X. Wu, G. Zhou, X.-H. Wang and X. Liu, Adv. Funct. Mater., 2021, 31, 2104996 CrossRef CAS.
- X.-F. Wang, Y. Chen, L.-P. Song, Z. Fang, J. Zhang, F. Shi, Y.-W. Lin, Y. Sun, Y.-B. Zhang and J. Rocha, Angew. Chem., Int. Ed., 2019, 58, 18808–18812 CrossRef CAS PubMed.
- Z. Li, Z. W. Liu, Z. Li, T. X. Wang, F. Zhao, X. Ding, W. Feng and B.-H. Han, Adv. Funct. Mater., 2020, 30, 1909267 CrossRef CAS.
- V. Neti, X. Wu, M. Hosseini, R. Bernal, S. Deng and L. Echegoyen, CrystEngComm, 2013, 15, 7157–7160 RSC.
- Z. Huang, E. S. Grape, J. Li, A. K. Inge and X. Zou, Coord. Chem. Rev., 2021, 427, 213583 CrossRef CAS.
- T. Chen, S.-Y. Li, D. Wang and L.-J. Wan, Sci. Adv., 2017, 3, e1701208 CrossRef PubMed.
- X. Xiao, D. Xiao, G. Sheng, T. Shan, J. Wang, X. Miao, Y. Liu, G. Li, Y. Zhu and J. L. Sessler, Sci. Adv., 2023, 9, eadi1169 CrossRef CAS PubMed.
- S. Raghunathan and U. D. Priyakumar, Int. J. Quantum Chem., 2022, 122, e26870 CrossRef CAS.
- A. E. A. Allen and A. Tkatchenko, Sci. Adv., 2022, 8, eabm7185 CrossRef CAS PubMed.
- X. Guan, Y. Ma, H. Li, Y. Yusran, M. Xue, Q. Fang, Y. Yan, V. Valtchev and S. Qiu, J. Am. Chem. Soc., 2018, 140, 4494–4498 CrossRef CAS PubMed.
- Y. Chen, Z.-L. Shi, L. Wei, B. Zhou, J. Tan, H.-L. Zhou and Y.-B. Zhang, J. Am. Chem. Soc., 2019, 141, 3298–3303 CrossRef CAS PubMed.
- C. Gropp, S. Canossa, S. Wuttke, F. Gándara, Q. Li, L. Gagliardi and O. M. Yaghi, ACS Cent. Sci., 2020, 6, 1255–1273 CrossRef CAS PubMed.
- H. Qi, B. Liang and U. Kaiser, SmartMat, 2021, 2, 131–138 CrossRef CAS.
- F. Auras, L. Ascherl, A. H. Hakimioun, J. T. Margraf, F. C. Hanusch, S. Reuter, D. Bessinger, M. Döblinger, C. Hettstedt, K. Karaghiosoff, S. Herbert, P. Knochel, T. Clark and T. Bein, J. Am. Chem. Soc., 2016, 138, 16703–16710 CrossRef CAS PubMed.
- H. Fan, A. Mundstock, A. Feldhoff, A. Knebel, J. Gu, H. Meng and J. Caro, J. Am. Chem. Soc., 2018, 140, 10094–10098 CrossRef CAS PubMed.
- T. Ma, J. Li, J. Niu, L. Zhang, A. S. Etman, C. Lin, D. Shi, P. Chen, L.-H. Li, X. Du, J. Sun and W. Wang, J. Am. Chem. Soc., 2018, 140, 6763–6766 CrossRef CAS PubMed.
- W. Wang, Y.-X. Ma, Z.-J. Li, T.-Q. Ma and Y.-B. Zhang, Acta Crystallogr. A, 2017, 73, C303 Search PubMed.
- L. Liang, Y. Qiu, W. D. Wang, J. Han, Y. Luo, W. Yu, G.-L. Yin, Z.-P. Wang, L. Zhang, J. Ni, J. Niu, J. Sun, T. Ma and W. Wang, Angew. Chem., Int. Ed., 2020, 59, 17991–17995 CrossRef CAS PubMed.
- Y. Chen, Z. L. Shi, L. Wei, B. Zhou, J. Tan, H. L. Zhou and Y. B. Zhang, J. Am. Chem. Soc., 2019, 141, 3298–3303 CrossRef CAS PubMed.
- Y. Liu, P. Chen, Y. Wang, J. Suo, J. Ding, L. Zhu, V. Valtchev, Y. Yan, S. Qiu, J. Sun and Q. Fang, Angew. Chem., Int. Ed., 2022, 61, e202203584 CrossRef CAS PubMed.
- A. A. Bunaciu, E. G. Udristioiu and H. Y. Aboul-Enein, Crit. Rev. Anal. Chem., 2015, 45, 289–299 CrossRef CAS PubMed.
- G. Oszlanyi and A. Suto, Acta Crystallogr. A, 2004, 60, 134–141 CrossRef PubMed.
- A. L. Patterson, Phys. Rev., 1934, 46, 372–376 CrossRef CAS.
- V. Pecharsky and P. Zavalij, Fundamentals of Powder Diffraction and Structural Characterization of Materials, Springer, US, 2005 Search PubMed.
- H. L. Nguyen, N. Hanikel, S. J. Lyle, C. Zhu, D. M. Proserpio and O. M. Yaghi, J. Am. Chem. Soc., 2020, 142, 2218–2221 CrossRef CAS PubMed.
- X. Chen and J. Cai, Principles and Practices of Single Crystal Structure Analysis, Science Press, 2003 Search PubMed.
- L. Liang, Y. Qiu, W. D. Wang, J. Han, Y. Luo, W. Yu, G. L. Yin, Z. P. Wang, L. Zhang, J. Ni, J. Niu, J. Sun, T. Ma and W. Wang, Angew. Chem., Int. Ed., 2020, 59, 17991–17995 CrossRef CAS PubMed.
- C. Gropp, T. Ma, N. Hanikel and O. M. Yaghi, Science, 2020, 370 Search PubMed.
- V. K. Pecharsky and P. Y. Zavalij, Fundamentals of Powder Diffraction and Structural Characterization of Materials, 2nd edn, 2009 Search PubMed.
- C. Gao, J. Li, S. Yin, J. Sun and C. Wang, J. Am. Chem. Soc., 2020, 142, 3718–3723 CrossRef CAS PubMed.
- R. R. Liang, S. Q. Xu, L. Zhang, R. H. A, P. Chen, F. Z. Cui, Q. Y. Qi, J. Sun and X. Zhao, Nat. Commun., 2019, 10, 4609 CrossRef PubMed.
- J. X. Ma, J. Li, Y. F. Chen, R. Ning, Y. F. Ao, J. M. Liu, J. Sun, D. X. Wang and Q. Q. Wang, J. Am. Chem. Soc., 2019, 141, 3843–3848 CrossRef CAS PubMed.
- Y. Meng, Y. Luo, J. L. Shi, H. Ding, X. Lang, W. Chen, A. Zheng, J. Sun and C. Wang, Angew. Chem., Int. Ed., 2020, 59, 3624–3629 CrossRef CAS PubMed.
- H. S. Xu, Y. Luo, P. Z. See, X. Li, Z. Chen, Y. Zhou, X. Zhao, K. Leng, I. H. Park, R. Li, C. Liu, F. Chen, S. Xi, J. Sun and K. P. Loh, Angew. Chem., Int. Ed., 2020, 59, 11527–11532 CrossRef CAS PubMed.
- J.-X. Ma, J. Li, Y.-F. Chen, R. Ning, Y.-F. Ao, J.-M. Liu, J. Sun, D.-X. Wang and Q.-Q. Wang, J. Am. Chem. Soc., 2019, 141, 3843–3848 CrossRef CAS PubMed.
- C. Kang, Z. Zhang, V. Wee, A. K. Usadi, D. C. Calabro, L. S. Baugh, S. Wang, Y. Wang and D. Zhao, J. Am. Chem. Soc., 2020, 142, 12995–13002 CrossRef CAS PubMed.
- C. Davisson and L. H. Germer, Nature, 1927, 119, 558–560 CrossRef CAS.
- G. P. Thomson, Nature, 1927, 120, 802 CrossRef CAS.
- M. T. B. Clabbers and H. Xu, Drug Discovery, 2020, 37, 93–105 Search PubMed.
- M. Gemmi, M. G. I. La Placa, A. S. Galanis, E. F. Rauch and S. Nicolopoulos, J. Appl. Crystallogr., 2015, 48, 718–727 CrossRef CAS.
- U. Kolb, T. Gorelik, C. Kubel, M. T. Otten and D. Hubert, Ultramicroscopy, 2007, 107, 507–513 CrossRef CAS PubMed.
- B. L. Nannenga, D. Shi, A. G. W. Leslie and T. Gonen, Nat. Methods, 2014, 11, 927–930 CrossRef CAS PubMed.
- L. Palatinus, V. Petricek and C. A. Correa, Acta Crystallogr. A, 2015, 71, 235–244 CrossRef CAS PubMed.
- S. Plana-Ruiz, Y. Krysiak, J. Portillo, E. Alig, S. Estrade, F. Peiro and U. Kolb, Ultramicroscopy, 2020, 211, 112951 CrossRef CAS PubMed.
- S. Smeets, X. Zou and W. Wan, J. Appl. Crystallogr., 2018, 51, 1262–1273 CrossRef CAS PubMed.
- W. Wan, J. Sun, J. Su, S. Hovmoller and X. Zou, J. Appl. Crystallogr., 2013, 46, 1863–1873 CrossRef CAS PubMed.
- T. Yang, T. Willhammar, H. Xu, X. Zou and Z. Huang, Nat. Protoc., 2022, 17, 2389–2413 CrossRef CAS PubMed.
- D. Zhang, P. Oleynikov, S. Hovmöller and X. Zou, Z. Kristallogr. Cryst. Mater., 2010, 225, 94–102 CrossRef CAS.
- Y. B. Zhang, J. Su, H. Furukawa, Y. Yun, F. Gandara, A. Duong, X. Zou and O. M. Yaghi, J. Am. Chem. Soc., 2013, 135, 16336–16339 CrossRef CAS PubMed.
- H. Ding, J. Li, G. Xie, G. Lin, R. Chen, Z. Peng, C. Yang, B. Wang, J. Sun and C. Wang, Nat. Commun., 2018, 9, 5234 CrossRef CAS PubMed.
- J. Li, C. Lin, T. Ma and J. Sun, Nat. Commun., 2022, 13, 4016 CrossRef CAS PubMed.
- X. Liu, J. Li, B. Gui, G. Lin, Q. Fu, S. Yin, X. Liu, J. Sun and C. Wang, J. Am. Chem. Soc., 2021, 143, 2123–2129 CrossRef CAS PubMed.
- C. Gao, J. Li, S. Yin, G. Lin, T. Ma, Y. Meng, J. Sun and C. Wang, Angew. Chem., Int. Ed., 2019, 58, 9770–9775 CrossRef CAS PubMed.
- T. Sun, L. Wei, Y. Chen, Y. Ma and Y. B. Zhang, J. Am. Chem. Soc., 2019, 141, 10962–10966 CrossRef CAS PubMed.
- Y. Xie, J. Li, C. Lin, B. Gui, C. Ji, D. Yuan, J. Sun and C. Wang, J. Am. Chem. Soc., 2021, 143, 7279–7284 CrossRef CAS PubMed.
- Y. Xu, T. Sun, T. Zeng, X. Zhang, X. Yao, S. Liu, Z. Shi, W. Wen, Y. Zhao and S. Jiang, Nat. Commun., 2023, 14, 4215 CrossRef CAS PubMed.
- C. Kang, Z. Zhang, S. Kusaka, K. Negita, A. K. Usadi, D. C. Calabro, L. S. Baugh, Y. Wang, X. Zou and Z. Huang, Nat. Mater., 2023, 1–8 Search PubMed.
- T. Sun, C. E. Hughes, L. Guo, L. Wei, K. D. M. Harris, Y. B. Zhang and Y. Ma, Angew. Chem., Int. Ed., 2020, 59, 22638–22644 CrossRef CAS PubMed.
- K. Kaufmann, C. Y. Zhu, A. S. Rosengarten, D. Maryanovsky, T. J. Harrington, E. Marin and K. S. Vecchio, Science, 2020, 367, 564–568 CrossRef CAS PubMed.
- C. J. Gilmore, Microsc. Res. Tech., 1999, 46, 117–129 CrossRef CAS PubMed.
- A. E. Goeta and J. A. K. Howard, Chem. Soc. Rev., 2004, 33, 490–500 RSC.
- S. Smeets and W. Wan, J. Appl. Crystallogr., 2017, 50, 885–892 CrossRef CAS.
- P. Klar, Y. Krysiak, H. Xu, G. Steciuk, J. Cho, X. Zou and L. Palatinus, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv-2021-4jh14.
- A. Saha, S. S. Nia and J. A. Rodríguez, Chem. Rev., 2022, 122, 13883–13914 CrossRef CAS PubMed.
- E. Holm, R. Cohn, N. Gao, A. Kitahara, T. Matson, B. Lei and S. R. Yarasi, Metall. Mater. Trans. A, 2020, 51, 1–15 Search PubMed.
- J. Tang, C. Su and Z. Shao, Small Methods, 2021, 5 Search PubMed.
- D. Zhang, Y. Zhu, L. Liu, X. Ying, C.-E. Hsiung, R. Sougrat, K. Li and Y. Han, Science, 2018, 359, 675–679 CrossRef CAS PubMed.
- Y. Zhu, J. Ciston, B. Zheng, X. Miao, C. Czarnik, Y. Pan, R. Sougrat, Z. Lai, C.-E. Hsiung, K. Yao, I. Pinnau, M. Pan and Y. Han, Nat. Mater., 2017, 16, 532–536 CrossRef CAS PubMed.
- B. Yang, O. Dyck, W. Ming, M.-H. Du, S. Das, C. M. Rouleau, G. Duscher, D. B. Geohegan and K. Xiao, ACS Appl. Mater. Interfaces, 2016, 8, 32333–32340 CrossRef CAS PubMed.
- Y. Lin, M. Zhou, X. Tai, H. Li, X. Han and J. Yu, Matter, 2021, 4, 2309–2339 CrossRef CAS.
- W. D. Pyrz and D. J. Buttrey, Langmuir, 2008, 24, 11350–11360 CrossRef CAS PubMed.
- H. Saka, in Carbon Alloys, ed. E.-i Yasuda, M. Inagaki, K. Kaneko, M. Endo, A. Oya and Y. Tanabe, Elsevier Science, Oxford, 2003, pp. 223–238 DOI:10.1016/B978-008044163-4/50014-0.
- R. F. Egerton, Microsc. Res. Tech., 2012, 75, 1550–1556 CrossRef CAS PubMed.
- J. Lv, H. Zhang, D. Zhang, L. Liu and Y. Han, Acc. Mater. Res., 2022, 3, 552–564 CrossRef CAS.
- X. Zhou, J. Dong, Y. Zhu, L. Liu, Y. Jiao, H. Li, Y. Han, K. Davey, Q. Xu, Y. Zheng and S.-Z. Qiao, J. Am. Chem. Soc., 2021, 143, 6681–6690 CrossRef CAS PubMed.
- B. Liu, J. Huang, Z. Liao, C. Zhu, Q. Chen, G. Sheng, Y. Zhu, Y. Huang and J. Dong, AIChE J., 2021, 67, e17177 CrossRef CAS.
- A. E. Burgess, J. Opt. Soc. Am. A, 1999, 16, 633–646 CrossRef CAS PubMed.
- Q. L. Chen, C. Dwyer, G. Sheng, C. Z. Zhu, X. N. Li, C. L. Zheng and Y. H. Zhu, Adv. Mater., 2020, 32, 42 Search PubMed.
- Z. Li, J. Biskupek, U. Kaiser and H. Rose, Microsc. Microanal., 2022, 28, 611–621 CrossRef CAS PubMed.
- B. D. A. Levin, J. Phys. Mater., 2021, 4, 15 Search PubMed.
- M. de la Mata and S. I. Molina, Nanomaterials, 2022, 12, 337 CrossRef CAS PubMed.
- I. Biran, L. Houben, H. Weissman, M. Hildebrand, L. Kronik and B. Rybtchinski, Adv. Mater., 2022, 34, 2202088 CrossRef CAS PubMed.
- Y. Jiang, Z. Chen, Y. Han, P. Deb, H. Gao, S. Xie, P. Purohit, M. W. Tate, J. Park, S. M. Gruner, V. Elser and D. A. Muller, Nature, 2018, 559, 343–349 CrossRef CAS PubMed.
- Z. Ou, B. Liang, Z. Liang, F. Tan, X. Dong, L. Gong, P. Zhao, H. Wang, Y. Zou, Y. Xia, X. Chen, W. Liu, H. Qi, U. Kaiser and Z. Zheng, J. Am. Chem. Soc., 2022, 144, 3233–3241 CrossRef CAS PubMed.
- D. Sun, L. W. Wong, H. Y. Wong, K. H. Lai, L. Ye, X. Xv, T. H. Ly, Q. Deng and J. Zhao, Angew. Chem., Int. Ed., 2023, 62, e202216008 CrossRef CAS PubMed.
- G. Binnig, H. Rohrer, C. Gerber and E. Weibel, Phys. Rev. Lett., 1982, 49, 57–61 CrossRef.
- L. Gura, Z. Yang, H. Junkes, M. Heyde and H.-J. Freund, in Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2023 DOI:10.1016/B978-0-323-85669-0.00069-6.
- Y. Liu, J. Yang, R. K. Vasudevan, K. P. Kelley, M. Ziatdinov, S. V. Kalinin and M. Ahmadi, J. Phys. Chem. Lett., 2023, 14, 3352–3359 CrossRef CAS PubMed.
- K. Bornani, N. F. Mendez, A. S. Altorbaq, A. J. Müller, Y. Lin, E. Z. Qu, K. Zhang, S. K. Kumar and L. S. Schadler, ACS Macro Lett., 2022, 11, 818–824 CrossRef CAS PubMed.
- M. Alemani, M. V. Peters, S. Hecht, K.-H. Rieder, F. Moresco and L. Grill, J. Am. Chem. Soc., 2006, 128, 14446–14447 CrossRef CAS PubMed.
- M. Krajnak, D. McGrouther, D. Maneuski, V. O'Shea and S. McVitie, Ultramicroscopy, 2016, 165, 42–50 CrossRef CAS PubMed.
- C. Z. Qilong Feng, Guan Sheng, Tulai Sun, Yonghe Li and Yihan Zhu, Acta Phys. Chim. Sin., 2023, 39, 2210017 Search PubMed.
- G. L. Mangan, G. Moldovan and A. Stewart, Microsc. Microanal., 2023, 29, 1380–1401 CrossRef PubMed.
- N. Ranson and P. Stockley, 2010, pp. 1–33 DOI:10.1142/9781848164666_0001.
- S. Cao, M. Chi and K. L. More, Microsc. Microanal., 2019, 25, 66–67 CrossRef.
- L. Liu, D. Zhang, Y. Zhu and Y. Han, Commun. Chem., 2020, 3, 99 CrossRef CAS PubMed.
- L. Liu, N. Wang, C. Zhu, X. Liu, Y. Zhu, P. Guo, L. Alfilfil, X. Dong, D. Zhang and Y. Han, Angew. Chem., Int. Ed., 2020, 59, 819–825 CrossRef CAS PubMed.
- L. Yu, X. Shang, H. Chen, L. Xiao, Y. Zhu and J. Fan, Nat. Commun., 2019, 10, 1932 CrossRef PubMed.
- T. Mullarkey, J. J. Peters, C. Downing and L. Jones, Microsc. Microanal., 2022, 28, 1428–1436 CrossRef CAS.
- Y. Yao, Y. Zhu and C. Zhu, Micron, 2023, 172, 103503 CrossRef PubMed.
- L. Alvarez and J. Siqueiros, 2010, pp. 1302–1319.
- G. H. Enevoldsen, H. P. Pinto, A. S. Foster, M. C. R. Jensen, A. Kühnle, M. Reichling, W. A. Hofer, J. V. Lauritsen and F. Besenbacher, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045416 CrossRef.
- M. V. Salapaka and S. M. Salapaka, IEEE Control Systems Magazine, 2008, 28, 65–83 Search PubMed.
- I. Notingher and A. Elfick, J. Phys. Chem. B, 2005, 109, 15699–15706 CrossRef CAS PubMed.
- D. P. Allison, N. P. Mortensen, C. J. Sullivan and M. J. Doktycz, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnology., 2010, 2, 618–634 Search PubMed.
- B. Voigtländer, Scanning probe microscopy: Atomic force microscopy and scanning tunneling microscopy, Springer, 2015 Search PubMed.
- H.-J. Güntherodt and R. Wiesendanger, Scanning tunneling microscopy I: general principles and applications to clean and adsorbate-covered surfaces, Springer, 1992 Search PubMed.
- T. Sulchek, R. Hsieh, J. Adams, G. Yaralioglu, S. Minne, C. Quate, J. Cleveland, A. Atalar and D. Adderton, Appl. Phys. Lett., 2000, 76, 1473–1475 CrossRef CAS.
- D. Tranchida, S. Piccarolo and R. A. C. Deblieck, Meas. Sci. Technol., 2006, 17, 2630 CrossRef CAS.
- J. Chen, J. Ge, B. K. Chen, Z. Gong, C. Zhou, C. Shi, C. Ru, H. Pu, Y. Peng and S. Xie, 2018.
- T. Ando, Biophys. Rev., 2017, 9, 421–429 CrossRef CAS PubMed.
- S. F. Pratama, A. K. Muda, C. Yun-Huoy, R. Carbo-Dorca and A. Abraham, Int. J. Comput. Inf. Syst. Ind. Manag. Appl., 2018, 10, 57–67 Search PubMed.
- J. Wang, Y. Zhu, G. Zhuang, Y. Wu, S. Wang, P. Huang, G. Sheng, M. Chen, S. Yang, T. Greber and P. Du, Nat. Commun., 2022, 13, 1239 CrossRef CAS PubMed.
- G. Q. Lyu, Q. S. Zhang, J. I. Urgel, G. W. Kuang, W. Auwarter, D. Ecija, J. V. Barth and N. Lin, Chem. Commun., 2016, 52, 1618–1621 RSC.
- Y. Peng, Y. Huang, Y. Zhu, B. Chen, L. Wang, Z. Lai, Z. Zhang, M. Zhao, C. Tan, N. Yang, F. Shao, Y. Han and H. Zhang, J. Am. Chem. Soc., 2017, 139, 8698–8704 CrossRef CAS PubMed.
- C. Chen, T. Joshi, H. Li, A. D. Chavez, Z. Pedramrazi, P.-N. Liu, H. Li, W. R. Dichtel, J.-L. Bredas and M. F. Crommie, ACS Nano, 2018, 12, 385–391 CrossRef CAS PubMed.
- B. Liang, Y. Zhang, C. Leist, Z. Ou, M. Položij, Z. Wang, D. Mücke, R. Dong, Z. Zheng, T. Heine, X. Feng, U. Kaiser and H. Qi, Nat. Commun., 2022, 13, 3948 CrossRef CAS PubMed.
- J. F. Dienstmaier, D. D. Medina, M. Dogru, P. Knochel, T. Bein, W. M. Heckl and M. Lackinger, ACS Nano, 2012, 6, 7234–7242 CrossRef CAS PubMed.
- X. Wang, M. Bahri, Z. Fu, M. A. Little, L. Liu, H. Niu, N. D. Browning, S. Y. Chong, L. Chen, J. W. Ward and A. I. Cooper, J. Am. Chem. Soc., 2021, 143, 15011–15016 CrossRef CAS PubMed.
- K. Liang, L. Bi, Q. Zhu, H. Zhou and S. Li, ACS Appl. Opt. Mater., 2023, 1, 924–938 CrossRef CAS PubMed.
- Z. Schumacher, R. Rejali, R. Pachlatko, A. Spielhofer, P. Nagler, Y. Miyahara, D. G. Cooke and P. Grütter, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 19773–19779 CrossRef CAS PubMed.
- M. Garg, A. Martin-Jimenez, Y. Luo and K. Kern, ACS Nano, 2021, 15, 18071–18084 CrossRef CAS PubMed.
- Z. Schumacher, Y. Miyahara, A. Spielhofer and P. Grutter, Phys. Rev. Appl., 2016, 5, 044018 CrossRef.
- M. Rashidi and R. A. Wolkow, ACS Nano, 2018, 12, 5185–5189 CrossRef CAS PubMed.
- T. Kowalewski and D. M. Holtzman, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3688–3693 CrossRef CAS PubMed.
- A. J. Malkin, T. A. Land, Y. G. Kuznetsov, A. McPherson and J. J. DeYoreo, Phys. Rev. Lett., 1995, 75, 2778–2781 CrossRef CAS PubMed.
- R. Xie, Y. Song, L. Wan, H. Yuan, P. Li, X. Xiao, L. Liu, S. Ye, S.-B. Lei and L. Wang, Anal. Sci., 2011, 27, 129–138 CrossRef CAS PubMed.
- Y. Suzuki, H. Enoki and E. Akiba, Ultramicroscopy, 2005, 104, 226–232 CrossRef CAS PubMed.
- Y. Ajay Kumar, M. Junhong and C. Jeong-Woo, in Modern Electrochemical Methods in Nano, Surface and Corrosion Science, ed. A. Mahmood, IntechOpen, Rijeka, 2014, ch. 3 DOI:10.5772/57236.
- J. Wan, H.-J. Yan, R. Wen and L.-J. Wan, ACS Energy Lett., 2022, 7, 2988–3002 CrossRef CAS.
- A. Viljoen, M. Mathelié-Guinlet, A. Ray, N. Strohmeyer, Y. J. Oh, P. Hinterdorfer, D. J. Müller, D. Alsteens and Y. F. Dufrêne, Nat. Rev. Methods Primers, 2021, 1, 63 CrossRef CAS.
- G. L. Zhan, Z. F. Cai, M. Martinez-Abadia, A. Mateo-Alonso and S. De Feyter, J. Am. Chem. Soc., 2020, 142, 5964–5968 CrossRef CAS PubMed.
- D. Cui, J. M. MacLeod, M. Ebrahimi and F. Rosei, CrystEngComm, 2017, 19, 4927–4932 RSC.
- L. Xu, X. Zhou, W. Q. Tian, T. Gao, Y. F. Zhang, S. Lei and Z. F. Liu, Angew. Chem., Int. Ed., 2014, 53, 9564–9568 CrossRef CAS PubMed.
- I. Castano, A. M. Evans, R. D. Reis, V. P. Dravid, N. C. Gianneschi and W. R. Dichtel, Chem. Mater., 2021, 33, 1341–1352 CrossRef CAS PubMed.
- L. Yao, A. Rodríguez-Camargo, M. Xia, D. Mücke, R. Guntermann, Y. Liu, L. Grunenberg, A. Jiménez-Solano, S. Emmerling, V. Duppel, K. Sivula, T. Bein, H. Qi, U. Kaiser, M. Grätzel and B. Lotsch, J. Am. Chem. Soc., 2022, 144 Search PubMed.
- M. Munz, B. R. Cuenya and C. S. Kley, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2023 DOI:10.1016/B978-0-323-85669-0.00058-1.
- M. M. Li, S. Qiao, Y. L. Zheng, Y. H. Andaloussi, X. Li, Z. J. Zhang, A. Li, P. Cheng, S. Q. Ma and Y. Chen, J. Am. Chem. Soc., 2020, 142, 6675–6681 CrossRef CAS PubMed.
- Q. Sun, C. W. Fu, B. Aguila, J. Perman, S. Wang, H. Y. Huang, F. S. Xiao and S. Q. Ma, J. Am. Chem. Soc., 2018, 140, 984–992 CrossRef CAS PubMed.
- L. Zhang, Z. W. Liu, Q. Q. Deng, Y. J. Sang, K. Dong, J. S. Ren and X. G. Qu, Angew. Chem., Int. Ed., 2021, 60, 3469–3474 CrossRef CAS PubMed.
- G. Galeotti, F. De Marchi, E. Hamzehpoor, O. MacLean, M. Rajeswara Rao, Y. Chen, L. V. Besteiro, D. Dettmann, L. Ferrari, F. Frezza, P. M. Sheverdyaeva, R. Liu, A. K. Kundu, P. Moras, M. Ebrahimi, M. C. Gallagher, F. Rosei, D. F. Perepichka and G. Contini, Nat. Mater., 2020, 19, 874–880 CrossRef CAS PubMed.
- C. Qian, Q. Y. Qi, G. F. Jiang, F. Z. Cui, Y. Tian and X. Zhao, J. Am. Chem. Soc., 2017, 139, 6736–6743 CrossRef CAS PubMed.
- C. H. Liu, E. Park, Y. H. Jin, J. Liu, Y. X. Yu, W. Zhang, S. B. Lei and W. P. Hu, Angew. Chem., Int. Ed., 2018, 57, 8984–8988 CrossRef CAS PubMed.
- D. Cui, J. M. MacLeod, M. Ebrahimi, D. F. Perepichka and F. Rosei, Chem. Commun., 2015, 51, 16510–16513 RSC.
- X. Gao, Y. Zhu, D. Yi, J. Zhou, S. Zhang, C. Yin, F. Ding, S. Zhang, X. Yi, J. Wang, L. Tong, Y. Han, Z. Liu and J. Zhang, Sci. Adv., 2018, 4, eaat6378 CrossRef PubMed.
- L. Zhang, Y. Zhou, M. Jia, Y. He, W. Hu, Q. Liu, J. Li, X. Xu, C. Wang, A. Carlsson, S. Lazar, A. Meingast, Y. Ma, J. Xu, W. Wen, Z. Liu, J. Cheng and H. Deng, Matter, 2020, 2, 1049–1063 CrossRef.
- Q. Zheng, X. Li, Q. Zhang, D. Lee, H. Mao, C. Yang, K. C. Bustillo, J. A. Reimer, Y. Liu, J. Jiang and H. Zheng, Mater. Today, 2022, 60, 98–105 CrossRef CAS.
- S. Wang, Y. Yang, P. Liu, Z. Zhang, C. Zhang, A. Chen, O. Ajao, B.-G. Li, P. Braunstein and W. Wang, Cell Rep. Phys. Sci., 2020, 1, 100062 CrossRef.
- H.-S. Xu, Y. Luo, X. Li, P. Z. See, Z. Chen, T. Ma, L. Liang, K. Leng, I. Abdelwahab, L. Wang, R. Li, X. Shi, Y. Zhou, X. F. Lu, X. Zhao, C. Liu, J. Sun and K. P. Loh, Nat. Commun., 2020, 11, 1434 CrossRef CAS PubMed.
- R. F. Egerton, Ultramicroscopy, 2014, 145, 85–93 CrossRef CAS PubMed.
- L. Liu, Z. Chen, J. Wang, D. Zhang, Y. Zhu, S. Ling, K.-W. Huang, Y. Belmabkhout, K. Adil, Y. Zhang, B. Slater, M. Eddaoudi and Y. Han, Nat. Chem., 2019, 11, 622–628 CrossRef CAS PubMed.
- R. Zhu, J. Ding, L. Jin and H. Pang, Coord. Chem. Rev., 2019, 389, 119–140 CrossRef CAS.
- G. Q. Lin, H. M. Ding, D. Q. Yuan, B. S. Wang and C. Wang, J. Am. Chem. Soc., 2016, 138, 3302–3305 CrossRef CAS PubMed.
- Q. R. Fang, J. H. Wang, S. Gu, R. B. Kaspar, Z. B. Zhuang, J. Zheng, H. X. Guo, S. L. Qiu and Y. S. Yan, J. Am. Chem. Soc., 2015, 137, 8352–8355 CrossRef CAS PubMed.
- M. Martínez-Abadía, K. Strutyński, B. Lerma-Berlanga, C. T. Stoppiello, A. N. Khlobystov, C. Martí-Gastaldo, A. Saeki, M. Melle-Franco and A. Mateo-Alonso, Angew. Chem., Int. Ed., 2021, 60, 9941–9946 CrossRef PubMed.
- M. Dogru, M. Handloser, F. Auras, T. Kunz, D. Medina, A. Hartschuh, P. Knochel and T. Bein, Angew. Chem., Int. Ed., 2013, 52, 2920–2924 CrossRef CAS PubMed.
- L. Peng, J. Sun, J. Huang, C. Song, Q. Wang, L. Wang, H. Yan, M. Ji, D. Wei, Y. Liu and D. Wei, Chem. Mater., 2022, 34, 2886–2895 CrossRef CAS.
- Z. Shan, M. Wu, D. Zhu, X. Wu, K. Zhang, R. Verduzco and G. Zhang, J. Am. Chem. Soc., 2022, 144, 5728–5733 CrossRef CAS PubMed.
- Y. Li, L. Guo, Y. Lv, Z. Zhao, Y. Ma, W. Chen, G. Xing, D. Jiang and L. Chen, Angew. Chem., Int. Ed., 2021, 60, 5363–5369 CrossRef CAS PubMed.
- S. Wan, F. Gandara, A. Asano, H. Furukawa, A. Saeki, S. K. Dey, L. Liao, M. W. Ambrogio, Y. Y. Botros, X. F. Duan, S. Seki, J. F. Stoddart and O. M. Yaghi, Chem. Mater., 2011, 23, 4094–4097 CrossRef CAS.
- G. L. Zhuang, Y. F. Gao, X. Zhou, X. Y. Tao, J. M. Luo, Y. J. Gao, Y. L. Yan, P. Y. Gao, X. Zhong and J. G. Wang, Chem. Eng. J., 2017, 330, 1255–1264 CrossRef CAS.
- Y. P. Ying, S. B. Peh, H. Yang, Z. Q. Yang and D. Zhao, Adv. Mater., 2022, 34, 9 Search PubMed.
- V. Vyas, F. Haase, L. Stegbauer, G. Savasci, F. Podjaski, C. Ochsenfeld and B. Lotsch, Nat. Commun., 2015, 6, 8508 CrossRef CAS PubMed.
- S. Yee, The Ohio State University, 2007 Search PubMed.
- M. Saadi, B. Uluutku, C. H. Parvini and S. D. Solares, Surf. Topogr.: Metrol. Prop., 2020, 8, 045004 CrossRef CAS.
- I. Casuso and S. Scheuring, Nanotechnology, 2009, 21, 035104 CrossRef PubMed.
- G. Schitter and M. Rost, Mater. Today, 2008, 11, 40–48 CrossRef.
- T. Ando, Biophys. Rev., 2018, 10, 285–292 CrossRef CAS PubMed.
- A. Al-Amoudi, D. Studer and J. Dubochet, J. Struct. Biol., 2005, 150, 109–121 CrossRef CAS PubMed.
- B. Michen, C. Geers, D. Vanhecke, C. Endes, B. Rothen-Rutishauser, S. Balog and A. Petri-Fink, Sci. Rep., 2015, 5, 9793 CrossRef CAS PubMed.
- J. Ayache, L. Beaunier, J. Boumendil, G. Ehret and D. Laub, in Sample Preparation Handbook for Transmission Electron Microscopy: Methodology, ed. J. Ayache, L. Beaunier, J. Boumendil, G. Ehret and D. Laub, Springer, New York, New York, NY, 2010, pp. 125–170 DOI:10.1007/978-0-387-98182-6_6.
- M. Gao, Microsc. Microanal., 2018, 21, 883–884 CrossRef.
- B. Voigtländer, in Atomic Force Microscopy, ed. B. Voigtländer, Springer International Publishing, Cham, 2019, pp. 137–147 DOI:10.1007/978-3-030-13654-3_8.
- L. O. Otieno, B. O. Alunda, J. Kim and Y. J. Lee, Sensors, 2021, 21, 362 CrossRef PubMed.
- P. Eaton and P. West, Atomic force microscopy, Oxford university press, 2010 Search PubMed.
- S. Lopatin, A. Aljarb, V. Roddatis, T. Meyer, Y. Wan, J.-H. Fu, M. Hedhili, Y. Han, L.-J. Li and V. Tung, Sci. Adv., 2020, 6, eabb8431 CrossRef CAS PubMed.
- V. Alfredsson, O. Terasaki and J.-O. Bovin, J. Solid State Chem., 1990, 84, 171–177 CrossRef CAS.
- A. Velazco, A. Béché, D. Jannis and J. Verbeeck, Ultramicroscopy, 2022, 232, 113398 CrossRef CAS PubMed.
- H. Xue, M. Zhang, J. Liu, J. Wang and G. Ren, Front. Chem., 2022, 10 Search PubMed.
- Y. Wang, Sci. China Mater., 2018, 61, 129–130 CrossRef.
- N. Tanaka, Sci. Technol. Adv. Mater., 2008, 9, 014111 CrossRef PubMed.
- K. Moore, U. Bangert and M. Conroy, APL Mater., 2021, 9, 020703 CrossRef CAS.
- T. R. Harvey, F. S. Yasin, J. J. Chess, J. S. Pierce, R. M. S. dos Reis, V. B. Özdöl, P. Ercius, J. Ciston, W. Feng, N. A. Kotov, B. J. McMorran and C. Ophus, Phys. Rev. Appl., 2018, 10, 061001 CrossRef CAS.
- H. Yang, P. Ercius, P. D. Nellist and C. Ophus, Ultramicroscopy, 2016, 171, 117–125 CrossRef CAS PubMed.
- C. Ophus, Microsc. Microanal., 2019, 25, 1–20 CrossRef.
- R. Cassetta, P. Piersimoni, M. Riboldi, V. Giacometti, V. Bashkirov, G. Baroni, C. Ordonez, G. Coutrakon and R. Schulte, J. Appl. Clin. Medical Phys., 2019, 20, 83–90 CrossRef PubMed.
- J. Ma, J. Huang, Q. Feng, H. Zhang, H. Lu, Z. Liang and W. Chen, Med. Phys., 2011, 38, 5713–5731 CrossRef PubMed.
- M. Strakowska, R. Strakowski, B. Wiecek and M. Strzelecki, Proceedings of the 11th International Conference on Quantitative InfraRed Thermography, Naples, Italy, 2012.
- B. Li, Z. Zhang, Y. Li, K. Yao, Y. Zhu, Z. Deng, F. Yang, X. Zhou, G. Li, H. Wu, N. Nijem, Y. J. Chabal, Z. Lai, Y. Han, Z. Shi, S. Feng and J. Li, Angew. Chem., Int. Ed., 2012, 51, 1412–1415 CrossRef CAS PubMed.
- J. Zhu, Y. Zhu, L. Zhu, M. Rigutto, A. van der Made, C. Yang, S. Pan, L. Wang, L. Zhu, Y. Jin, Q. Sun, Q. Wu, X. Meng, D. Zhang, Y. Han, J. Li, Y. Chu, A. Zheng, S. Qiu, X. Zheng and F.-S. Xiao, J. Am. Chem. Soc., 2014, 136, 2503–2510 CrossRef CAS PubMed.
- S. Suhr, D. Tenbrinck, M. Burger and J. Modersitzki, Cham, 2014.
- C.-K. Ta, A. Aich, A. Gupta and A. K. Roy-Chowdhury, presented in part at the Medical Image Computing and Computer Assisted Intervention – MICCAI 2022: 25th International Conference, Singapore, September 18–22, 2022, Proceedings, Part VIII, Singapore, Singapore, 2022.
- J. Byun, S. Cha and T. Moon, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 5768–5777.
- J. M. Ede and R. Beanland, Ultramicroscopy, 2019, 202, 18–25 CrossRef CAS PubMed.
- D. Stokes and M. Hayles, Proceedings of SPIE – The International Society for Optical Engineering, 2009, p. 7378.
- T. Ichikawa, D. Wang, K. Miyazawa, K. Miyata, M. Oshima and T. Fukuma, Commun. Biol., 2022, 5, 487 CrossRef CAS PubMed.
- Y. Zhu, J. He, C. Shang, X. Miao, J. Huang, Z. Liu, H. Chen and Y. Han, J. Am. Chem. Soc., 2014, 136, 12746–12752 CrossRef CAS PubMed.
- Y. Luo, B. Wang, S. Smeets, J. Sun, W. Yang and X. Zou, Nat. Chem., 2023, 15, 483–490 CrossRef CAS PubMed.
- J. Song, C. S. Allen, S. Gao, C. Huang, H. Sawada, X. Pan, J. Warner, P. Wang and A. I. Kirkland, Sci. Rep., 2019, 9, 3919 CrossRef PubMed.
- H. Zhang, G. Li, J. Zhang, D. Zhang, Z. Chen, X. Liu, P. Guo, Y. Zhu, C. Chen and L. Liu, Science, 2023, 380, 633–638 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |