Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The design and optimization of heterogeneous catalysts using computational methods
Shambhawi
a,
Ojus
Mohan
 b,
Tej S.
Choksi
b,
Tej S.
Choksi
 c and
Alexei A.
Lapkin
c and
Alexei A.
Lapkin
 *ad
*ad
aDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Cambridge CB3 0AS, UK. E-mail: aal35@cam.ac.uk
bChemical Engineering Department, Indian Institute of Technology Bombay, Powai, Mumbai, Maharashtra 400076, India
cSchool of Chemistry, Chemical Engineering and Biotechnology, Nanyang Technological University, 62 Nanyang Drive, 637459, Singapore
dCambridge Centre for Advanced Research and Education in Singapore Ltd, 1 Create Way, CREATE Tower #05-05, 138602, Singapore
First published on 1st December 2023
Abstract
The computational design of catalytic materials is a high dimensional structure optimization problem that is limited by the bottleneck of expensive quantum computation tools. Current implementations of first principles computational models for catalyst design are data-hungry, problem-specific and confirmatory in nature. However, they can be made less data-dependent, more transferable and exploratory by developing both forward and inverse catalyst mapping tools that are either inexpensive correlations, like scaling relations, or regression models that are based on relevant descriptors analysis. This work reviews the current application and the possible landscape for future advancements of such tools for developing generalized schemes for catalyst design and optimization.
1. Introduction
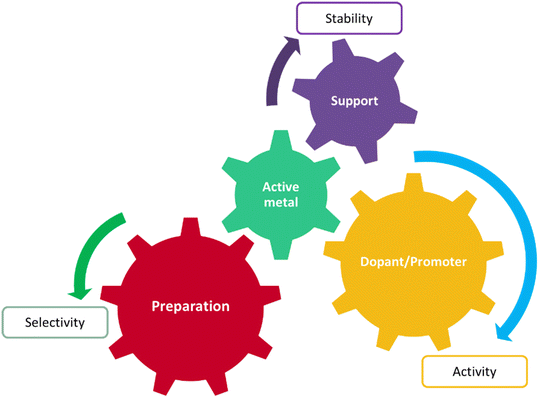
Today heterogeneous catalysis facilitates highly energy-efficient selective molecular transformations for over 90% of the chemical manufacturing processes and contributes towards 20% of all industrial products.1,2 Given the importance of heterogeneous catalysts in chemical processes, developing rational heterogeneous catalyst design rules is one of the most fundamental goals in reaction engineering and is the key towards developing future sustainable chemical technologies. However, catalyst design is a complex process, involving numerous interacting factors, such as active species (metal, oxide, etc.), promoter, support type, preparation method, and pre-treatment conditions, see Fig. 1. Any variation in these factors can cause significant changes in activity and selectivity of the catalyst. The same is true for the operating conditions: different combinations of reaction variables such as temperature, feed flow rate, and feed composition.3 Because of the multidimensional complexities, theoretical catalyst design has limited application in material exploration for catalyst development, whereas trial and error and repeated experiments are still the main strategies. Another major challenge associated with computational approaches is the disassociation of their performance evaluation metrics from real catalyst compositions, like obtaining a 3D structure of a synthesizable material as an output, from an inputted rate or selectivity.With the development of computer-aided data storage and processing techniques, vast amounts of accumulated knowledge on catalysts can be employed in analysis simultaneously.3 Additionally, the multidimensionality of the catalyst design problem can be represented in a machine readable format for developing prediction models. For example, ML algorithms have been trained on data corresponding to catalyst performance metrics (e.g. % reactant conversions,4,5 product yield or turnover frequency,4,6 key reaction energetics7–9), produced from high-throughput experimentation or computation coupled with a combinatorial algorithm, to predict catalyst materials with the best performance. They have also been used to construct inverse functions, i.e. mapping from properties to materials10/molecules.11 However, accuracy of predictions of these models is limited to the training set distribution, specifically, catalytic structures, composition variations and binding molecules. On the other hand, graph-based representations coupled with neural networks are used for a more generalized implementation, e.g. predicting energetics over a catalyst surface for subsequent micro-kinetic modelling.12 However, their data requirements can be two orders of magnitude higher than other simpler regression algorithms.13
Developing a generalized design scheme for heterogeneous gas-phase reactions that is computationally effective, accurate, and transferable (valid for different reaction systems and catalyst compositions), without relying on data-heavy techniques, is among the major research goals in catalysis. In this review, we discuss the implementation of popular theoretical tools, approaches and workflows used in materials investigation for catalyst screening and optimisation under the listed constraints. We compare their applicability for different problem systems while highlighting the recent advancements made in order to bypass the current computational bottleneck in catalyst design. We start with the tools used for computing reaction energetics over catalysts surfaces. These tools include first-principles methods, their semi-empirical/empirical adaptations and molecular dynamics. We compare different methods reported in the literature for developing reaction networks, catalyst optimization and screening. Lastly, we summarize state-of-the-art in theoretical catalyst design and discuss its potential future landscape based on the existing developments.
2. Reaction chemistry computation
The kinetics on a given catalyst surface are driven by the energetics of elementary steps occurring on active sites. In this section, we discuss the most common approaches for computating reaction energetics (adsorption energies, activation barriers) over catalyst surfaces. Density functional theory (DFT) is the most popular choice for quantum mechanical computations. Other tools are essentially semi-empirical/empirical implementations derived from or trained on DFT but are relatively less expensive. This also includes tools for molecular dynamics. We further compare them based on three key factors: transferability, accuracy, efficiency, applicable system size, and highlight their respective limitations, see Table 2.2.1 Quantum mechanical calculations and density functional theory (DFT)
In the realm of reaction chemistry computation, quantum mechanical calculations have emerged as indispensable tools.14–17 These calculations have revolutionized our understanding of the behavior of atoms, molecules and materials by providing insights into their electronic structure and properties at the microscopic level. Hartree–Fock (HF) calculations are one of the oldest quantum mechanical methods based on wavefunctions that is used to study electronic structure.18–20 They are based on a self-consistent field approach, where the electrons are treated as non-interacting particles within the mean field generated by the other electrons. While HF calculations provide a good starting point for understanding the electronic structure, they have limitations, particularly in accurately describing electron correlation effects.19 Several post-Hartree–Fock methods have been developed to account for electron correlation effects beyond the HF level. Examples include configuration interaction (CI),21 coupled cluster (CC),22 Møller–Plesset perturbation theory (MP2),23 and density functional theory (DFT).24,25 These methods offer improved accuracy by including electron correlation contributions, but some of them can be computationally demanding, especially for large systems. Among the post-Hartree–Fock methods, density functional theory (DFT) is the only method based on density function instead of wave functions. It has become a widely employed computational tool for studying the electronic structure and reaction energetics, especially for catalytic systems.26 It offers a versatile framework to investigate a wide range of systems and phenomena.DFT is a widely used method for electronic structure calculations. At the core of DFT calculations is the concept of electron density. Instead of solving Schrödinger equation for the system's wave function, DFT focuses on determining the electron density distribution, which is a more tractable quantity.24,25 This approach has proven to be highly effective in studying a wide range of catalytic systems.26 The most widely used form of DFT is Kohn–Sham density functional theory (KS-DFT). It was proposed by Walter Kohn and Pierre Hohenberg in 1964 and has become the cornerstone of modern DFT calculations.24,25
The Kohn–Sham approach introduces a set of auxiliary non-interacting electrons, represented by Kohn–Sham orbitals, to approximate the real system's electron density.24,25 These orbitals are derived from a fictitious system in which the electron–electron interactions are neglected. However, the electron density obtained from the Kohn–Sham orbitals should match the electron density of the real system. In KS-DFT, the electronic structure problem is mapped onto a set of non-interacting electrons moving in an effective potential. To solve the Kohn–Sham equations, a basis set is used to expand the Kohn–Sham orbitals. The choice of the basis set is critical in accurately representing the electronic structure of the system.27 The basis set represents a set of functions that span the space in which the electronic wave functions are defined. In KS-DFT calculations, the choice of a basis set and the package used to solve the equations depends on the nature of the system being studied: cluster/isolated system, bulk (periodic) system, or condensed media.
In cluster calculations, where a small group of atoms or molecules is isolated from its surroundings, the basis set is typically chosen to describe the electronic structure of the cluster accurately.28 The commonly used basis sets in cluster calculations include Gaussian-type orbitals (GTOs).29,30 Gaussian,31 ORCA,32 and GAMESS33 are widely used software packages for calculations involving cluster/isolated molecules.
In bulk or periodic system calculations, the electronic structure is determined for extended periodic structures such as crystals and surfaces. In these calculations, the basis set is expanded to include periodic boundary conditions.34–36 Plane-wave basis sets are commonly used in periodic system calculations, along with pseudopotentials or projector-augmented wave (PAW) potentials to efficiently treat the electron–ion interactions.36,37 Since the potential is periodic, the plane wave basis sets are well-suited for the description of periodicity in the crystal lattice. VASP,34,38 Quantum Espresso39,40 and CASTEP41 are popular packages for periodic DFT calculations.
Condensed media calculations involve studying systems where the electronic structure is influenced by the surrounding environment, such as liquids, solutions, or solids with embedded solvents. CPMD, which stands for Car–Parrinello molecular dynamics, is particularly useful for simulating condensed phase systems and exploring reaction mechanisms with atomistic detail.42 CPMD is a computational method that combines molecular dynamics simulations with DFT. CPMD utilizes plane wave basis sets to describe the electronic structure and employs the Born–Oppenheimer approximation to treat the nuclear motion.42 This approach allows for the study of dynamic processes, such as chemical reactions and materials transformations, at the quantum mechanical level. In short, the choice of basis set in DFT calculations significantly impacts the accuracy and computational cost of the calculations. Larger and more sophisticated basis sets can provide a more accurate description of the electronic structure but at the expense of increased computational resources and time.
In addition to the selection of an appropriate basis set, one of the other major challenges in DFT is choosing an appropriate exchange–correlation functional, which accounts for the electron–electron interactions.43,44 However, the exact form of the exchange–correlation functional is not known. Many approximations exist for the exchange–correlation functional, and selecting an appropriate functional is crucial to achieve reliable results. Generalized gradient approximation (GGA)45 functionals, such as PBE,46 PW91,47 and revPBE,48 are commonly employed in DFT calculations. Benchmarking of functionals is necessary to ensure their reliability in DFT-based catalyst design procedures. For instance, many studies employ GGA-based PBE and PW91 functionals for studying CO2 conversion reactions on solid catalysts. However, inconsistencies arise between the calculated values using these functionals and experimental data.49–51 Notably, the binding energies of CO2 on metal surfaces, often deviate significantly.52 Additionally, GGA functionals are inadequate for describing weakly bound systems, where dispersion interactions play a crucial role.53–55 Incorporating van der Waals (vdW) interactions through specific correlation functionals can improve the accuracy of dispersion-bonded systems.
The Hubbard U is yet another DFT parameter based on the Hubbard model (DFT+U method)56,57 that is crucial for accurately describing the electronic properties of transition metal oxides by employing DFT. Metal oxides, with their transition metal elements, exhibit strong electron–electron interactions and localized electron behaviour. Standard DFT functionals may not adequately capture these effects, leading to inaccurate predictions. The Hubbard U term represents the on-site Coulomb repulsion between electrons and helps describe the physical behaviour of transition metal oxides. Incorporating the Hubbard U parameter improves the agreement between DFT calculations and experimental observations, enabling accurate predictions of structural, electronic, and magnetic properties. Determining the appropriate Hubbard U value is challenging and often relies on empirical or theoretical approaches. By including Hubbard U, DFT calculations provide valuable insights into metal oxide properties, including bandgaps, energy levels, charge localization, and magnetic behaviour.58,59 The Hubbard U parameter is essential for understanding metal oxides' electronic structure and behaviour within the DFT framework. For further detailed overviews on DFT, its parameters and application we direct the readers to review articles in ref. 60 and 61.
Although DFT calculations are accurate and reliable for studying different reactions on a small set of catalysts, they cannot be directly applied to problems that require high throughput computations, particularly in catalyst design problems involving the calculations of potential energy surfaces (PES) for reaction chemistry. Although the computational cost of determining minima in the PES is reasonable, determining the maxima (saddle points) can increase the computation time significantly depending on the number of images used. For complex systems like nanoclusters, single atom alloys (SAAs) and single-atom catalysts (SACs), this increase can be even higher.
Given that the method is based on first principles, it is transferable, but the accuracy is highly affected by the choice of functional and other computational flags. The speed/efficiency of the method is also way below the requirement for a comprehensive analysis. This can be observed from Table 1 that highlights the computational resources needed for evaluating reaction energetics over three catalyst surfaces for performance comparison for the CO2 methanation reaction.
| Type of DFT calculation | No. of calculations | No. of cores | CPU time | Total core hours |
|---|---|---|---|---|
| Geometry optimization | 600 | 64 | 5 | 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Transition state searches (minimum energy path) | 135 | 96 | 15 | 194![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| Transition state optimization | 45 | 64 | 2 | 5760 |
| Transition state confirmation via vibrational frequency | 45 | 64 | 10 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| Adsorbate vibrational frequency | 24 | 64 | 10 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
| Grand total of core hours | 436![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 320 |
|||
| Number of catalyst surface investigated (Ni(111), Ru(0001), NiB(111)) | 3 | |||
| Total CPU (core years) | 145 | |||
2.2 Density functional based tight binding method (DFTB)
The density functional-based tight binding method or DFTB was initially based on a second-order expansion of the DFT total energy with respect to charge density fluctuations.62 However, the most common implementation, DFTB3,63 includes a third-order expansion of the DFT total energy.DFTB methods can be two-to-three orders of magnitude faster than ab initio and DFT.64 They are particularly attractive in applications to large molecules and condensed phase systems and have already been implemented for geometry optimization of inorganic solid structures,65 nanoclusters66 and SACs.67 DFTB has also been implemented for transition state searches for reactions involving large (bio) molecules.68
However, without proper benchmarking, the accuracy of the method can be heavily compromised,69 making the use of DFTB trade-off between speed vs. accuracy. Transferability of the model is also limited when heavy metal elements come into question.70
2.3 Unity bond index-quadratic energy potential (UBI-QEP)
UBI-QEP is a generalization of the BOC-MP (bond order conservation-Morse potential) method that is used for modelling chemisorption energetics and reaction mechanisms on metal surfaces. It has a fast and easy computational implementation and the UBI-QEP projections of reaction energetics are usually more accurate. It should be noted that the UBI-QEP modelling in particular is not competitive but complementary to quantum mechanical modelling.71 As input parameters, the method employs thermodynamic observables such as gas-phase bond energies and atomic chemisorption energies mostly obtained from DFT. Its output is the surface reaction energetics for all elementary steps in a mechanism thus improving the overall efficiency. Although these energies cannot be transferred to new adsorption systems without the initial DFT input.The BOC-MP and the UBI-QEP methods have been applied successfully to analyse mechanisms of many reactions of practical importance such as methanol synthesis,72 Fischer–Tropsch synthesis,73 and methane reforming chemistry on metal surfaces.74 There are also UBI-QEP analytical formalisms for bimetallic surfaces however, similar developments cannot be found for systems like single atom catalysts and nanoclusters.
2.4 Reactive force fields (ReaxFF)
The reactive force-fields (ReaxFF)75 are based on a bond-order formalism that implicitly describes chemical bonding without expensive quantum mechanical calculations. Its bond-order parameters are derived from computationally intensive DFT derived methods. Once these parameters are known, computing the energy matrix could be more than 100 times faster than DFT for gas-phase heterogeneous reaction systems. ReaxFF potential parameters have already been reported for hydrocarbons chemistry,76 H2 dissociation on transition metals,77,78 carbon interactions with transition metals79 and lastly hydrocarbon reactions catalysed on transition metals such as nickel80 and vanadium oxides.81,82In short, ReaxFF can model reactions at the gas–solid interface and assess the stability of SACs,83 nanoclusters84 and SAAs,85 which is pertinent to our problem of heterogeneous catalysts design. Moreover, the available parameters for elements in the literature are also transferable, as long as the aqueous phase reactions are not involved.75 However, proper benchmarking needs to be performed to determine the accuracy prior to any calculations and ReaxFF cannot be transferred to new systems without re-parameterizing the method.
The major drawback accompanying these force-field methods is the low accuracy of predictions which can be limited by proper parameterization of interatomic potentials. Recently there have been some developments in this area with the use of machine-learned (ML) force fields. These ML-corrected force fields have been found to be much more accurate. Further details on ML force fields can be found in section 5.1.4.
Table 2 summarizes the comparison of different quantum computational tools discussed here based on four the key factors: transferability, accuracy, efficiency and system size (number of atoms). There are additional methods in the literature that can be implemented to our problem of reaction chemistry computation but are not discussed here, e.g. MOPAC (Molecular Orbital PACkage) semi-empirical methods86 or group additivity87 used in automated reaction kinetics generation.88,89 For a comprehensive study, we refer our readers to other reviews that are focuses on these semi-empirical90 and empirical methods.91
| Method | Transferability | Accuracy | Efficiency | Approx. system size (# atoms) |
|---|---|---|---|---|
| DFT | Based on first principles hence more transferable than the semi-empirical/empirical methods | Relative comparison of catalysts can be performed accurately | Computational cost increases cubically with the increasing number of atoms in the system | 102 |
| Absolute catalyst predictions are also possible if the exchange correlation functionals are correctly identified using experimental data | ||||
| DFTB | Limited for heavy metal systems | Benchmarking is required to compute the accuracy | Computational cost increases cubically with the increasing number of atoms. However each single point computation is 2–3 three orders of magnitude faster than DFT | 103 |
| UBI-QEP | Needs re-calibration in case of a new adsorption system (e.g., in presence of a new bond or a new element) | Accuracy depends on the DFT data used for calibration | Computational cost increases linearly with the increasing number of atoms | 102 |
| Implementations limited to mono and bi-metallic catalyst systems | ||||
| ReaxFF | The ReaxFF potentials need to be evaluated and validated every time a new element and/or is added to the adsorption system | Benchmarking is required to compute the accuracy | Computational cost increases linearly with the increasing number of atoms | 105–106 |
| Not suitable for aqueous phase reactions |
3. Reaction mechanisms generation
A reaction mechanism describes a network of elementary reactions (reaction network) which corresponds to the reaction coordinate from reactants to products and byproducts. The hypotheses about possible reaction intermediates and elementary reaction steps are based on experimental observations, literature-based dissociation and association routes, and/or auto-reaction generators algorithms89 that employ reaction energy data,92–94 templates88,95 or heuristics. The methods for developing a reaction network can be broadly classified as:(1) Automated reaction mechanism generation that is based on reaction rates, and.
(2) User-defined reaction rules for mechanism generation that are based on literature and experiments.
This section discusses the tools for developing reaction mechanisms via these approaches.
3.1 Automated reaction mechanism generation
An automatic reaction-mechanism generation (ARMG) is based on an algorithm that can perform the following tasks:891. Recognize when two or more species in the mechanism are equivalent.
2. Predict all the possible elementary reactions for each species and pair of species.
3. Determine which of these possible reactions are important.
4. Estimate accurately all the necessary thermodynamic and kinetic parameters.
5. Ensure that the mechanism is thermodynamically consistent.
ARMG can be simultaneously used to update the reaction mechanism with catalyst surfaces during the optimisation of overall catalyst performance. This is particularly useful since reaction mechanism identification is based on the surface energetics over a catalyst. Therefore, surface energetics and by extension, the mechanism can vary from one catalyst to another.
A challenge with ARMG is determining the kinetically relevant reaction steps in the initial reaction network. A prior assumption about the list of intermediates and reactions can lead to biased results or limited solutions. If all possible intermediates and reactions are included, then the resulting reaction network quickly becomes unsolvable and, therefore, useless.
Gao et al.88 developed an algorithm to circumvent this problem. The algorithm uses reaction rates to determine which species and reactions to include in the model. Reaction rates higher than a given tolerance are included in the reaction network and its corresponding reaction species are categorised as core species. It employs a thermochemistry prediction algorithm for rate evaluation. It uses a database of thermochemistry for known gas-phase species and surface species with group additivity and scaling relations (see section 5.2) respectively to predict the thermochemistry for new species. Goldsmith and West et al.89 extended this tool for implementation in heterogeneous catalysis by adding an adsorption correction to the estimated gas-phase energy.
3.2 User-defined reaction rules to construct reaction mechanisms
Reaction networks can also be constructed using user-defined rules around a mechanism that is based on experimental evidence and literature. For example, Rangarajan et al.96 constructed a reaction network for glycerol conversion using rules based on experimental evidence. The rules allowed the algorithm to include reactions that perform C–C, C–H, C–O, and O–H scission, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O formation and further, C–H and C–O, and C–C formation. Several steps were not included because resulting intermediates were not reported in experimental studies.97,98
O formation and further, C–H and C–O, and C–C formation. Several steps were not included because resulting intermediates were not reported in experimental studies.97,98
This method can be categorized as reaction specific, partly intuitive and based on heuristics observed in the literature/experiments. The common framework is to look in the literature for elementary steps corresponding to reactant dissociation, product association and redox reaction steps in similar reactions with known mechanisms. For example, a study on methane reforming99 copies the mechanism for dry reforming of methane (DRM) directly from CH4 steam reforming with the addition of CO2 dissociation steps. It is found that for small molecules reaction systems like DRM, the literature and automated mechanism generators agree on the same reaction network.89,99 There are also approaches in literature that automate the rule based reaction network generation100 by including a language compiler that can convert an English-like reaction language into internal representations and instructions.
Designing a simple, yet representative reaction network is important for limiting the cost of evaluation and ensuring model solvability during mechanism identification and subsequent catalyst optimization. A way to achieve that would be via a partial reaction network made from relevant reaction species. A recent study101 outlines a workflow that can be used to create such partial reaction networks that are transferable across different catalyst surfaces and can be used for comparing catalyst activity performance.
4. Catalyst optimization
A reaction network and corresponding energetics observed over a catalyst surface are used for building kinetic models for evaluation of catalyst' performance and their subsequent optimization. There are top-down and bottom up approaches for building a kinetic model. The top-down kinetic model includes approaches based on power law expressions and Langmuir–Hinshelwood–Hougen–Watson (LHHW) mechanism. The assumptions in these approaches are more implicit. For example, assuming certain rate-determining elementary reactions, quasi-equilibrated elementary reactions, and the most abundant surface intermediates.102 Bottom-up approaches are theoretical models that do not make such initial assumptions about the nature of rate-determining elementary reactions but can be designed to enable different simplifications as per user requirements. This section discusses the theoretical bottom-up approaches used for quantifying catalyst performance.4.1 Micro-kinetic modelling for optimizing catalyst surfaces
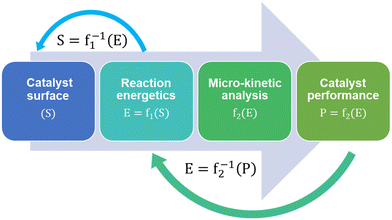
Micro-kinetic models (MKM) are a vital tool in catalyst research and design.102 Microkinetic models predict and compare the performances of different catalyst surfaces for a given reaction in terms of their reactivity, selectivity and stability against deactivation mechanisms like coking. MKMs are often designed and validated for a specific reaction system based on certain reaction conditions. As a result, complete MKMs are not adopted in subsequent studies, except for maybe certain model fragments, such as reaction networks and energy data. Different assumptions while creating an MKM also lead to different model predictions and the validity of these assumptions can vary. For example, using collision theory instead of transition state theory to model gas-phase adsorption, kinetic Monte Carlo instead of mean-field approximation to include the effect of surface coverage, and assuming quasi-equilibrium of certain reaction steps.Regardless of the assumptions, formulating MKMs are computationally expensive. Subsequent catalyst design using MKM is therefore described as an expensive head-on approach for performance optimization. Fig. 2 shows MKM-aided optimization of the catalyst surface for a reaction system in a step-wise manner:103
(1) An initial catalyst surface is fed into the micro-kinetic model.
(2) Reaction energetics are computed based on thermodynamics.
(3) The reaction kinetics are written followed by the reactor mass-balance equations.
(4) The model is then solved to predict the corresponding catalyst performance.
The MKM-aided catalyst optimization employs the model to develop a function mapping between the catalyst structure and its performance. It then maximises the performance by closely studying the inverse function and its derivative,103i.e. f1−1 and f2−1 in Fig. 2.
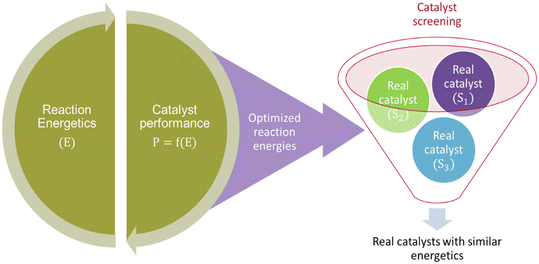
The literature also reports another study104 employing the MKM-aided catalyst optimization framework but in a less expensive inverse approach. The reaction energies are optimized independently, that is without subsequent optimisation of catalyst structure (see Fig. 3). Therefore, these energies correspond to a hypothetical catalyst that demonstrates improve catalytic performance and can be used for screening real catalyst materials. Although, the procedure for screening real catalysts is not elaborated.
The reaction energetics of a given reaction system can be very complex with interlinking energy values. A descriptor identification is important to make catalyst screening feasible. Herein, the descriptor would correspond to the energetics of the most relevant elementary reaction step (reader is directed to section 4.3 for further details).
4.2 Structure–activity/property mapping for screening catalyst materials
Contrary to the MKM-aided optimization approach, the quantitative structure–activity/property relationships (QSAR/QSPR) are based on developing a direct mapping between the microscopic (e.g. surface energies) and macroscopic properties (e.g. reactant conversions) of a catalyst. In the case of heterogeneous catalysis, artificial neural networks (ANNs) are most used to develop this mapping for a given range of catalyst materials. The database used for training the ANNs are generated via high-throughput experimentation/simulations. The QSAR/QSPR105 approach has already been implemented on different problems like materials screening, molecular design and synthesis. Their implementations for heterogeneous catalysis are also reported. Catalyst input features are usually the catalyst synthesis conditions and elemental compositions. However, depending on the adsorbate size, molecular descriptors can also be used to represent intermediates.Despite the straightforward implementations of QSAR/QSPR, they are often limited to a specific problem system due to the lack of a diverse database, limited data points and reproducibility issues during experiments. A robust and reliable property prediction model is not possible if either of the following is true:
(1) The experimental measurements have high uncertainties.
(2) The chemical diversity beyond training sets.
(3) The range of measured property values is too small.
4.3 Descriptor-based optimization of catalyst surfaces
The descriptor-based catalyst search is the most common approach towards theoretical catalyst optimization. It reduces the cost of exact model evaluation to descriptor evaluation and catalysts with descriptor values corresponding to maximum performance can be screened using the volcano plots106 (reader is directed to section 4.3.3 for further elaboration on volcano plots). The overall optimization will depend on the chosen catalyst descriptors and is limited by the volcano plot relation, thus identifying relevant catalyst descriptors is a very important step for catalyst design. We discuss methods used to identify reaction descriptors, i.e. sensitivity analysis and reaction pathway analysis followed by a small introduction to volcano plots.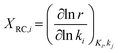 | (1) |
Although DRC is an extraordinarily useful concept for reaction mechanisms analysis, the energies of intermediates and transition states are linked through scaling relations (see section 5.2) and so are the rate constants. Thus, they cannot be changed independently during catalyst design. Therefore, instead of employing reaction energies with the highest DRC as catalyst descriptors, another metric is applied (eqn (2)), i.e. degree of catalyst control (DCC).108
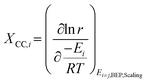 | (2) |
Based on the DCC, the activation/binding energy of the most sensitive reaction step/species is then chosen as the reaction descriptor. This descriptor is specific to the reaction investigated and can change if the reaction conditions are drastically changed.
Despite its popularity, volcano plots limit the maximum attainable catalytic performance corresponding to bulk catalytic structures and cannot be generalized to structures like single atom alloys (SAAs) that are known for breaking the scaling relations based on bulk materials.111,112 They are also prone to error depending upon the linear scaling relation (see section 5.2) used in their construction. Section 5.2 highlights a specific scenarios where a deviation from volcano plots and scaling relations in observed. The reader is referred to ref. 112 for further details.
5. Catalyst screening
The ability to solve either the forward or the reverse optimization problems essentially boils down to the catalyst screening method. An ideal catalyst screening tool should be capable of performing high-throughput computation for a range of catalyst structures and composition variations.In this section, we discuss the most common methods for inexpensive high-throughput screening of catalysts based on identified reaction descriptors, i.e. (1) machine learning for developing energy prediction models and (2) scaling relations as linear empirical relations for predicting reaction energies.
5.1 Machine learning (ML) models
Machine learning models can be employed to reduce the cost of reaction thermochemistry computation, thus enabling efficient catalyst screening. They can be trained on energies evaluated from DFT or other semi-empirical/empirical tools depending on the required accuracy and available data. ML models can be implemented at different stages in the overall computation. Implementations have been identified in the literature for predicting DFT wave functions or electronic density,113 predicting DFT energies114 and accelerating transition state searches.115,116 Further implementations include feature construction from relevant descriptors for initial catalyst screening117 and reactive force-fields parameters optimization for a more rigorous screening (see section 5.1.4).118Given the inherent complexity of catalytic reactions, these machine learning-based implementations are relevant tools to efficiently navigate through this high-dimensional catalyst optimization problem. Although their performances rely on the training algorithm and feature sets, their predictions are not transferable beyond the training set. In the following sections, we list common catalyst features, available catalyst databases and learning algorithms used for developing these models.
(1) The features must be unique in representing the electronic and geometric structures of an active site.
(2) They must be easily computed or readily available from databases to enable rapid screening.
(3) They should be physically intuitive to ensure model robustness and direct inference of chemical insights.
Table 3 lists some of the primary features observed in the literature that were either used in feature construction or directly employed for predicting properties such as adsorption energies.
| Class | Name | Abbreviations | References |
|---|---|---|---|
| a GCN corresponds to the generalized coordination number. b W mtod is the d band center computed from muffin-tin orbital theory. | |||
| Stoichiometry | L p | ‖xp‖ | 120, 121 |
| Atomic properties of components | Atomic number | Z | 114, 120, 121 |
| Atomic weight | A | 114, 120, 121 | |
| Group | G | 114, 120–122 | |
| Period | P | 114, 120–122 | |
| Mendeleev number | MN | 120, 123 | |
| Atomic radius | r X | 114, 117, 119, 121, 122 | |
| Covalent radius | r C, rC1, rC2, rC3 | 120–122 | |
| van der Waals radius | r vdW | — | |
| Pauling electronegativity | PE | 114, 117, 119–122, 124–127 | |
| Ionization potential | IP | 114, 117, 119, 122, 124, 125 | |
| Electron affinity | EA | 117, 119, 122, 124, 125 | |
| # s valence electrons | v s | 120, 121 | |
| # p valence electrons | v p | 120, 121 | |
| # d valence electrons | v d | 117, 120, 121 | |
| # f valence electrons | v f | 120, 121 | |
| Total # valance electrons | v | 120–122 | |
| Magnetic moment/atom at 0 K ground state | m | 120, 121 | |
| Bulk properties of components | fcc nearest neighbour distance | bulknnd | 124 |
| Partial radial distribution function | g αβ | 128 | |
| Radius of d-orbitals | r d | 117, 119, 124 | |
| Radius of p-orbitals | r p | 129 | |
| Coupling matrix element squared | V ad 2 | 117, 119, 124, 126 | |
| Specific volume | V s | 114, 120 | |
| Band gap energy of 0 K ground state | E BG | 120 | |
| Space group number of 0 K ground state | — | 120 | |
| Melting point | t MP | 114 | |
| Boiling point | t BP | 114 | |
| Enthalpy of fusion | ΔHfusion | 114 | |
| Surface | Work function | W | 117, 119, 124, 126 |
| Cohesive energy | E cohesive | 125 | |
| Surface energy | E surface | 114 | |
| Site | Number of atoms in ensemble | siteno | 124 |
| Coordination number | CN, GCNa | 124, 130 | |
| Orbital wise coordination number | CNα (α = s, d) | 131 | |
| Bond-energy-integrated orbital wise coordination number |
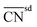
|
129 | |
| Nearest neighbour distance | sitennd | 122, 124 | |
| d-band centre | ε d | 117, 119, 124, 126 | |
| p-band centre | ε p | 132 | |
| d-bandwidth | W d, Wmtodb | 117, 119, 124, 127 | |
| d-band skewness | s d | 117, 119, 124 | |
| d-band kurtosis | k d | 117, 119, 124 | |
| d-band filling | f d | 117, 119, 124 | |
| sp-band filling | f sp | 124 | |
| Antibonding states (eg) filling | f eg | 133 | |
| Density of d-states at Fermi level | DOSd | 124 | |
| Upper d-band edge | ε u | 134 | |
| Density of sp-states at Fermi level | DOSsp | 124 | |
| Thermodynamic stability of active sites | BEM | 135 | |
| Crude estimate of the property being predicted | — | 136 | |
These primary features can be implemented directly or can be used to-handcraft secondary features using dimensionality reduction methods like LASSO, SISSO, etc. On-the-fly construction of these features has been a common approach for developing specific features for the set of catalysts relevant to the study. A generalized approach is to use a graphical representation of catalyst structures. Please refer to section 5.1.3 for more details.
From Table 3 it is noted that most of the site-specific features require an expensive ab initio calculation (e.g. bandwidth, band-filling, density of states, etc.). Moreover, these features are comparatively more important. Li et al.137 identified them as an important feature for his study on perovskites by performing a recursive feature elimination on a list of 66 features that included some of each atomic-specific, bulk-specific, surface and site-specific features. They also demonstrate a higher linear correlation with the binding energies of catalysts suggesting higher relevance.
Even so, these expensive ab initio features are not ideal features, given that one must perform a total energy DFT calculation to obtain them. To circumvent this, Andersen et al.124 proposed a solution. Instead of computing the site-specific properties of surface atoms in diverse structures/compositions, the authors computed the site-specific properties of each site atom in their bulk phase and then averaged them. This model had a reasonable accuracy for predicting the binding energies of some common intermediates. However, this study only included multi-metallic catalyst systems whose structures are similar to the bulk-phase structure of the host metal, i.e. only a handful of atoms are replaced by a different metal atom in the bulk structure. It is difficult to implement the same model for catalyst compositions leading to a new structure entirely different from their respective bulk phase structure.
Noh et al.127 and Li et al.138 proposed a more prevalent solution. They used the semi-empirical tight-binding LMTO formulation developed by Harrison and Froyen139 to the evaluate interatomic coupled matrix element which was further used to derive site-specific properties. Noh et al. used the formulation to compute LMTO d-bandwidth and Li. et al.138 used it to compute an orbital-based coordination number. Li. et al.138 further reported that the models based on LMTO features performed same as the model based on expensive ab initio features. Noh. et al.127 claimed that LMTO d-bandwidths are an even better feature than d-bandwidths computed from expensive DFT. Harrison and Froyen's formulation139 has been also extended to oxides and even f-block elements.7
The CatApp database140 includes reaction energies for approximately 3000 surface reactions on close-packed as well as stepped fcc and hcp on the following metal surfaces; Ag, Au, Co, Cu, Fe, Ir, Mo, Ni, Pd, Pt, Re, Rh, Ru, Sc, V. All values have been calculated with the same code (DACAPO), the same exchange–correlation energy functional (GGA-RPBE46). Therefore, one adsorption energy or reaction barrier can be compared to another with some confidence. The limitation of CatApp is that it does not store the atomic structures that are an output of the electronic structure calculations. Because of this data reproducibility is limited.
The Catalyst-Hub database141 contains more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 electronic structure geometries and results from more than 50 publications, including the ones present in the CatApp database. The datasets stem includes a direct link to their respective publications. The database contains a large variety of alloy surfaces and oxides. A large part of these reaction energies stems from the high-throughput study of chemical adsorption and hydrogenation on more than 2000 bimetallic alloy and pure metal surfaces.142 The calculations are performed using different tools and functionals and, hence, cannot be directly compared. However, the geometries could easily be used to re-compute the energies as per requirement.
000 electronic structure geometries and results from more than 50 publications, including the ones present in the CatApp database. The datasets stem includes a direct link to their respective publications. The database contains a large variety of alloy surfaces and oxides. A large part of these reaction energies stems from the high-throughput study of chemical adsorption and hydrogenation on more than 2000 bimetallic alloy and pure metal surfaces.142 The calculations are performed using different tools and functionals and, hence, cannot be directly compared. However, the geometries could easily be used to re-compute the energies as per requirement.
The Open Catalyst database (OC20)143 is the most recent and comprehensive database that is inclusive of previous databases and has further calculations based on the Materials Project database144 that are consistent in their computation parameters like the DFT functional. OC20 consists of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281
281![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121 density functional theory (DFT) relaxation calculations for 5243 different material compositions and 82 different adsorbates (small adsorbates, C1/C2 compounds, and N/O-containing intermediates). Although the adsorption energies most likely do not correspond to the lowest energy configuration.
121 density functional theory (DFT) relaxation calculations for 5243 different material compositions and 82 different adsorbates (small adsorbates, C1/C2 compounds, and N/O-containing intermediates). Although the adsorption energies most likely do not correspond to the lowest energy configuration.
It should be noted that despite the knowledge accumulation over the years for creating heterogeneous databases, they are far from being representative of the vast number of possible catalytic systems. Even the most recent OC20 database seems to include only 18.9% of the total systems and only 0.07% of the possible calculations.143 Databases are also biased in the sense that they mostly include systems that have been considered hot by the computational heterogeneous catalysis community.
Materials Project145 is another notable database that was constructed to accelerate material property investigation in general but also guides catalyst structure investigation. It has structural and ab initio data available for over 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 inorganic compounds that can be used to construct catalyst surfaces, define catalyst search spaces and also evaluate relevant features for machine-learning-based model predictions of intermediate binding energies.146
000 inorganic compounds that can be used to construct catalyst surfaces, define catalyst search spaces and also evaluate relevant features for machine-learning-based model predictions of intermediate binding energies.146
In addition to these databases, there are also several studies114,127,137,146 that have published data on intermediate binding energies, mostly CO* and H* adsorption energies. Although these data are mostly specific to their corresponding catalytic systems under consideration.
There are structural variations within the same catalyst composition and stable binding sites could also be different on the same surface depending on the adsorbate. To incorporate these variations, graph-based representations of catalyst surfaces have been developed.8,150 These representations do not require extensively handcrafted features (e.g. d-bandwidth) and can be generalized to different structures and compositions (beyond d-band elements). Although the learning algorithm is not limited to the ones compatible with graphical input data. Graphs can be vectorized to employ different regression algorithms, but the process eventually reduces the information present in a graphical representation, thus, forcing us back to some kind of handcrafted features.
Convolution neural networks (CCNs) and variants151 are the most common approaches for preserving this information along the different training layers of neural networks and are found to outperform other implementations.150 However, these models have a huge data requirement, more than 104 data points for a single adsorbate. These limitations bring us to the different training algorithms that have been specifically developed for these scenarios.
Active learning. Active learning is a user-interactive learning technique that is applied in cases where obtaining data labels is expensive. The algorithm identifies new training data dynamically based on a query strategy. The technique is helpful in the effective utilization of resources for data point evaluation and model training. It is found to increase the model prediction RMSE of binding energies from 0.18 eV to 0.05 eV and from 0.65 eV to 0.4 eV in bi-metallic systems127 and perovskites respectively.7 Active learning algorithms have also been employed on datasets consisting of in-house generated data coupled with the above-mentioned available databases.127,146 Although there is a drawback to this supervised learning technique, i.e. estimating the actual prediction accuracy of the model using batch sampling. Increasing the batch sampling size narrows the confidence interval for actual prediction accuracy but increases the data requirement simultaneously.7
Transfer learning. Transfer learning is a popular technique where a model trained on one task is re-purposed on a second task, i.e. the model hyper-parameters are constant when transferring from one task to another thus reducing the training data required for the new task. This is mostly implemented for deep learning models where data requirements can be significant, although, implementation for regression models like decision trees152 and Gaussian Process153 can also be found. Transfer learning is an effective tool when computing binding energies of related adsorbates (e.g. C* and
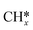 ) on catalyst surfaces. Although its applicability should be restricted to problems with limited data availability, else it could lead to the overfitting of output-layer hyper-parameters.
) on catalyst surfaces. Although its applicability should be restricted to problems with limited data availability, else it could lead to the overfitting of output-layer hyper-parameters.
An ML potential can be generated for a given material using a database of reference structures (see section 5.1.2), a mathematical representation of the atomic structure and a regression model.155 The representations are based on the local environment of the active site, centered on an atom and encoding information about its neighbors, ranging from simple two- or three-body terms all the way to complex “many-body” formalisms. The most commonly used representation is the “smooth overlap of atomic positions” (SOAP) as a many-body descriptor.156 The regression approaches, on the other hand, can be either artificial neural networks (NNs), kernel-based methods or linear regression.154,155
Recently ML-based interatomic potentials have been actively generated for elements in different bonding states157–159 including long range interactions.160 Studies have also been focusing on developing a training workflow for rapidly generating machine-learned force fields (MLFFs) for investigating reaction mechanisms over catalyst surfaces. These workflows are automated and iterative where the training set eventually expands using different adaptive sampling and/or query strategies.154,161 The accuracy of reaction energetics predicted via these MLFFs is claimed to be as low as 0.05 eV (ref. 161) of those obtained through density functional which is quite remarkable.
5.2 Scaling relations
Scaling relations are theoretical constructs derived from the d-band model162 that relates the binding energies of a wide variety of catalytic intermediates to atomic adsorption energies for a range of catalyst surfaces.163 There are two types of scaling relations in heterogeneous catalysis: thermodynamic scaling relations162,164 which describe correlations between adsorption properties of chemically related species (e.g. CHx and C) and Brønsted–Evans–Polanyi (BEP) relations165 that is a linear correlation between activation energies and reaction enthalpy.The development of scaling relationships has provided a rigorous theoretical basis for enabling automate reaction mechanism generation (see section 3.1), identifying independent catalyst descriptors (see section 4.3.1) and further developing volcano plots (see section 4.3.3) for catalyst screening based on DFT calculations. These relationships are extensively used for heterogeneous reactions on monometallics,106 bimetallics,166,167 oxides,168 and metal/support interfaces169 and have even been extended for application in nanocatalyst developments.135 Scaling relations only require a handful of data point evaluation (approx. 20–30 data points) and can thus be developed on the fly for screening catalysts or even assessing the formation of nanocatalysts and SAAs.
It should however be noted that scaling relations with prediction errors beyond 0.2 eV are not considered appropriate for facilitating predictions, especially when using scaling relations consecutively, e.g. employing BEP relations that were developed over thermodynamic scaling relations.
Adsorbing intermediates prefer to coordinate to a metal surface. Sometimes the need for higher coordination of adsorbate could lead to spillover to host metal, i.e. the minimum binding energy configuration occurs at the host site. This can lead to a deviation in the binding energy that breaks the scaling relation. This spillover phenomenon has been investigated in detail in ref. 111. It was observed that SAAs followed a unique linear BEP scaling relation (different from the bulk catalyst) when there is no spillover. However there is no discernible linear relations in the occurrence of a spillover onto the host.
There are also other factors reported in literature112 that could cause a deviation from volcano plots and scaling relation predictions. For example, intermediates adsorbed over high entropy alloys experience site-specific Pauli repulsion interactions that can lead to deviations from scaling relations.171 We refer readers to ref. 112 to further explore different factors causing deviation from volcano plots and scaling relation predictions.
5.3 Summary
The reviewed ML models and scaling relations are developed using data points generated from either DFT or DFT-based semi-empirical/empirical methods. They have been found to demonstrate reasonable accuracy and can be used for high-throughput screening of catalyst materials based on reaction energetics. They can also be developed for mapping material compositions that demonstrate the required activity, stability and selectivity for a given reaction system. However the corresponding property descriptor needs to be identified, for example using convex hulls to assess thermodynamic stability of catalyst materials.172 Their implementation can be both exploratory and confirmatory in nature, depending on the descriptor's applicability.6. Conclusions
This review discusses different state-of-the-art tools that allow to bypass the current challenges in catalyst design, screening and optimisation. Starting with the computational bottleneck, i.e. obtaining reaction energetics, semi-empirical/empirical quantum chemical and molecular dynamics tools, i.e. DFTB, UBI-QEP, and ReaxFF have been developed. They can provide two-three times faster execution than DFT depending on system size and have been implemented for different problem systems in the literature. Their implementations are decided based on the required computational efficiency, transferability, accuracy, and applicable system size. There is always a trade-off between efficiency on the one side and transferability and accuracy on the other side. For example, ReaxFF can be implemented in a catalytic system for faster evaluation of reaction energetics, however, it cannot be transferred to another system without undergoing DFT parameterization. Likewise, there are set approaches for developing reaction networks and identifying reaction mechanisms. The obtained reaction networks are most likely based on literature evidence and heuristics, however, recent advancements have been made to automate the entire process using network analysis and intermediate scaling relations.Once the reaction network is known, there are different approaches for theoretical catalyst optimization via micro-kinetic modelling, i.e. the direct and the inverse approaches. Most of the studies on catalyst optimisation focuses on identifying relevant descriptors that scale energetics with performance, circumventing the computational bottlenecks. Methods for such descriptor identification are based on sensitivity analysis, degree of rate control and degree of catalyst control, and reaction network/pathway analysis. Recent investigations have reported that descriptors identification over a given reaction system might not be transferable over different catalyst surfaces, due to significant variation in energetics. In such scenarios, descriptors are strictly identified for a set range of varying energetics, beyond which they are not applicable.
Identified descriptors can be used for quick screening of relevant catalysts materials. However, high-throughput computational screening of catalysts can be elusive because descriptor evaluation is expensive, especially when the descriptor corresponds to activation barriers rather than binding energies and the material search space is large. However, inexpensive screening tools based on machine learning, secondary descriptors and on-the-fly scaling relations can be developed to solve this problem. ML models in particular have a range of implementations in heterogeneous catalysis, e.g. wave-function prediction, energy prediction and transition state searches. The availability of databases like Open Catalyst 2020, further makes their implementation more feasible.
Although, it should be noted that these databases only represent 18.9% of the total possible compositions and the perfect universal catalyst database does not exist. This is where ML techniques like active learning and transfer learning become relevant. These techniques are implemented for minimizing the number of expensive data evaluations, whereas the later focuses on bridging the accuracy of ab initio methods and efficiency of molecular dynamics using minimum data points. Additionally, on-the-fly scaling relations are also a feasible option as they only require a handful of data point evaluations and can be implemented for fast screening. In short, current approaches for developing a generalised catalyst design scheme can circumvent the computational bottlenecks. However, individual heterogeneous catalytic studies should be more inclusive of the bigger problem, knowledge accumulation, database contributions and generalization of findings including those of prediction models. Conscious efforts should be made to make reaction data more accessible and reproducible. We hope this review promotes better practices in this regard.
Another challenge associated with catalyst design is the functional mapping between the required rate/selectivity and the material composition in 3D. Scaling relations and generative ML have been found to be relevant tools for screening materials and asses their synthesizability based on stability factors like convex hulls/machine-learned accelerated molecular dynamics. A potential future catalyst design approach, therefore, combines multiple ML models and provides a list of candidate 3D structures with their stability/rates/selectivity/synthesizability scores.
We are still some way away from this scenario as individual segments of such a workflow are in place, i.e. preliminary screening based on catalyst performance descriptor, further proof of concept, i.e. combining generative models with synthesizability checks are in development to further guide advancements in theoretical catalyst design and optimisation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Shambhawi acknowledges the research scholarship funding from Science and Engineering Research Board, India and Cambridge Trust. This work was in part supported by National Research Foundation (NRF), Prime Minister's Office, Singapore under its Campus for Research Excellence and Technological Enterprise (CREATE) program as a part of the Cambridge Centre for Advanced Research and Education in Singapore Ltd (CARES), and Engineering and Physical Sciences Research Council via project EP/S024220/1 EPSRC Centre for Doctoral Training in Automated Chemical Synthesis Enabled by Digital Molecular Technologies. OM acknowledges the new faculty seed grant from IIT Bombay. T. S. C. acknowledges support from the Ministry of Education Academic Research Fund Tier 1: RG5/22.References
- J. C. Védrine, Heterogeneous Catalysis on Metal Oxides, Catalysts, 2017, 7(11), 341 CrossRef.
- A. F. Lee, J. A. Bennett, J. C. Manayil and K. Wilson, Heterogeneous catalysis for sustainable biodiesel production via esterification and transesterification, Chem. Soc. Rev., 2014, 43(22), 7887–7916 RSC.
- M. E. Günay and R. Yildirim, Neural network Analysis of Selective CO Oxidation over Copper-Based Catalysts for Knowledge Extraction from Published Data in the Literature, Ind. Eng. Chem. Res., 2011, 50(22), 12488–12500 CrossRef.
- A. Corma, et al., Application of Artificial Neural Networks to Combinatorial Catalysis: Modeling and Predicting ODHE Catalysts, ChemPhysChem, 2002, 3(11), 939–945 CrossRef PubMed.
- L. Baumes, D. Farrusseng, M. Lengliz and C. Mirodatos, Using Artificial Neural Networks to Boost High-throughput Discovery in Heterogeneous Catalysis, QSAR Comb. Sci., 2004, 23(9), 767–778 CrossRef.
- M. Suvarna, T. P. Araújo and J. Pérez-Ramírez, A generalized machine learning framework to predict the space-time yield of methanol from thermocatalytic CO2 hydrogenation, Appl. Catal., B, 2022, 315, 121530 CrossRef.
- S. Shambhawi, G. Csányi and A. A. Lapkin, Active Learning Training Strategy for Predicting O Adsorption Free Energy on Perovskite Catalysts using Inexpensive Catalyst Features, Chem.: Methods, 2021, 1(10), 444–450 Search PubMed.
- G. H. Gu, et al., Practical Deep-Learning Representation for Fast Heterogeneous Catalyst Screening, J. Phys. Chem. Lett., 2020, 11(9), 3185–3191 CrossRef.
- A. J. Chowdhury, et al., Prediction of Adsorption Energies for Chemical Species on Metal Catalyst Surfaces Using Machine Learning, J. Phys. Chem. C, 2018, 122(49), 28142–28150 CrossRef.
- A. Zunger, Inverse design in search of materials with target functionalities, Nat. Rev. Chem., 2018, 2(4), 0121 CrossRef.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361(6400), 360–365 CrossRef.
- W. Xu and B. Yang, Microkinetic modeling with machine learning predicted binding energies of reaction intermediates of ethanol steam reforming: The limitations, Mol. Catal., 2023, 537, 112940 CrossRef.
- S. Back, et al., Convolutional Neural Network of Atomic Surface Structures To Predict Binding Energies for High-Throughput Screening of Catalysts, J. Phys. Chem. Lett., 2019, 10(15), 4401–4408 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1(1), 37–46 CrossRef.
- F. Studt, Grand Challenges in Computational Catalysis, Front. Catal., 2021, 1, 2673–7841 Search PubMed.
- O. Eisenstein and S. Shaik, Computational Catalysis: A Land of Opportunities, Top. Catal., 2022, 65(1), 1–5 CrossRef.
- K. D. Vogiatzis, et al., Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities, Chem. Rev., 2019, 119(4), 2453–2523 CrossRef.
- J. C. Slater, A Simplification of the Hartree-Fock Method, Phys. Rev., 1951, 81(3), 385–390 CrossRef.
- D. R. Hartree, The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part II. Some Results and Discussion, Math. Proc. Cambridge Philos. Soc., 1928, 24(1), 111–132 CrossRef.
- C. Froese Fischer, General Hartree-Fock program, Comput. Phys. Commun., 1987, 43(3), 355–365 CrossRef.
- C. David Sherrill and H. F. Schaefer, The Configuration Interaction Method: Advances in Highly Correlated Approaches, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, J. R. Sabin, M. C. Zerner and E. Brändas, 1999, Academic Press, pp. 143–269 Search PubMed.
- J. Paldus, Chapter 7 - The beginnings of coupled-cluster theory: An eyewitness account, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 115–147 Search PubMed.
- C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46(7), 618–622 CrossRef.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138 CrossRef.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Density functional theory in surface chemistry and catalysis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(3), 937–943 CrossRef PubMed.
- F. Jensen, Atomic orbital basis sets, WIREs Comput. Mol. Sci., 2013, 3(3), 273–295 CrossRef CAS.
- R. F. Stewart, Small Gaussian Expansions of Slater-Type Orbitals, J. Chem. Phys., 2003, 52(1), 431–438 CrossRef.
- W. J. Hehre, R. F. Stewart and J. A. Pople, Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals, J. Chem. Phys., 2003, 51(6), 2657–2664 CrossRef.
- T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023 CrossRef.
- M. J. Frisch, et al., Gaussian 16 Rev. C.01, 2016, Wallingford, CT Search PubMed.
- F. Neese, The ORCA program system, WIREs Comput. Mol. Sci., 2012, 2(1), 73–78 CrossRef.
- M. S. Gordon and M. W. Schmidt, Chapter 41 - Advances in electronic structure theory: GAMESS a decade later, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189 Search PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef PubMed.
- N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(3), 1993–2006 CrossRef.
- G. Makov and M. C. Payne, Periodic boundary conditions in ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(7), 4014–4022 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef.
- P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29(46), 465901 CrossRef CAS.
- S. J. Clark, et al., First principles methods using CASTEP, Z. Kristallogr., 2005, 220(5–6), 567–570 CAS.
- R. Car and M. Parrinello, Unified Approach for Molecular Dynamics and Density-Functional Theory, Phys. Rev. Lett., 1985, 55(22), 2471–2474 CrossRef PubMed.
- M. S. Tameh, A. K. Dearden and C. Huang, Accuracy of Density Functional Theory for Predicting Kinetics of Methanol Synthesis from CO and CO2 Hydrogenation on Copper, J. Phys. Chem. C, 2018, 122(31), 17942–17953 CrossRef.
- P. J. Feibelman, et al., The CO/Pt(111) Puzzle, J. Phys. Chem. B, 2001, 105(18), 4018–4025 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(11), 7413–7421 CrossRef.
- K. Burke, J. P. Perdew and Y. Wang, Derivation of a Generalized Gradient Approximation: The PW91 Density Functional, in Electronic Density Functional Theory: Recent Progress and New Directions, ed. J. F. Dobson, G. Vignale and M. P. Das, Springer US, Boston, MA, 1998, pp. 81–111 Search PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22(2), 022201 CrossRef.
- L. C. Grabow and M. Mavrikakis, Mechanism of Methanol Synthesis on Cu through CO2 and CO Hydrogenation, ACS Catal., 2011, 1(4), 365–384 CrossRef CAS.
- Y.-F. Zhao, et al., Insight into methanol synthesis from CO2 hydrogenation on Cu(111): Complex reaction network and the effects of H2O, J. Catal., 2011, 281(2), 199–211 CrossRef CAS.
- F. Muttaqien, et al., CO2 adsorption on the copper surfaces: van der Waals density functional and TPD studies, J. Chem. Phys., 2017, 147(9), 094702 CrossRef PubMed.
- O. Mohan, Q. T. Trinh, A. Banerjee and S. H. Mushrif, Predicting CO2 adsorption and reactivity on transition metal surfaces using popular density functional theory methods, Mol. Simul., 2019, 1–10 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS.
- A. Tkatchenko and M. Scheffler, Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102(7), 073005 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943–954 CrossRef PubMed.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA + U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(19), 195107 CrossRef.
- K. Bhola, et al., Influence of Hubbard U Parameter in Simulating Adsorption and Reactivity on CuO: Combined Theoretical and Experimental Study, J. Phys. Chem. C, 2017, 121(39), 21343–21353 CrossRef.
- Q. T. Trinh, et al., Synergistic Application of XPS and DFT to Investigate Metal Oxide Surface Catalysis, J. Phys. Chem. C, 2018, 122(39), 22397–22406 CrossRef.
- J. Kapil, P. Shukla and A. Pathak, Review Article on Density Functional Theory, Recent Trends in Materials and Devices, Springer Singapore, Singapore, 2020 Search PubMed.
- P. Makkar and N. N. Ghosh, A review on the use of DFT for the prediction of the properties of nanomaterials, RSC Adv., 2021, 11(45), 27897–27924 RSC.
- M. Elstner, et al., Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(11), 7260–7268 CrossRef.
- M. Gaus, Q. Cui and M. Elstner, DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB), J. Chem. Theory Comput., 2011, 7(4), 931–948 CrossRef CAS.
- M. Elstner, SCC-DFTB: What Is the Proper Degree of Self-Consistency?, J. Phys. Chem. A, 2007, 111(26), 5614–5621 CrossRef CAS.
- M. Van den Bossche, H. Grönbeck and B. Hammer, Tight-Binding Approximation-Enhanced Global Optimization, J. Chem. Theory Comput., 2018, 14(5), 2797–2807 CrossRef CAS PubMed.
- M. Van den Bossche, DFTB-Assisted Global Structure Optimization of 13- and 55-Atom Late Transition Metal Clusters, J. Phys. Chem. A, 2019, 123(13), 3038–3045 CrossRef CAS PubMed.
- Y. Zhou, et al., Multilayer stabilization for fabricating high-loading single-atom catalysts, Nat. Commun., 2020, 11(1), 5892 CrossRef CAS.
- M. Gruden, Benchmarking density functional tight binding models for barrier heights and reaction energetics of organic molecules, J. Comput. Chem., 2017, 38(25), 2171–2185 CrossRef CAS.
- G. Zheng, S. Irle and K. Morokuma, Performance of the DFTB method in comparison to DFT and semiempirical methods for geometries and energies of C20–C86 fullerene isomers, Chem. Phys. Lett., 2005, 412(1), 210–216 CrossRef CAS.
- F. Spiegelman, et al., Density-functional tight-binding: basic concepts and applications to molecules and clusters, Adv. Phys.: X, 2020, 5(1), 1710252 Search PubMed.
- E. Shustorovich and H. Sellers, The UBI-QEP method: A practical theoretical approach to understanding chemistry on transition metal surfaces, Surf. Sci. Rep., 1998, 31(1), 1–119 CrossRef.
- E. Shustorovich and A. T. Bell, An analysis of methanol synthesis from CO and CO2 on Cu and Pd surfaces by the bond-order-conservation-Morse-potential approach, Surf. Sci., 1991, 253(1), 386–394 CrossRef.
- E. Shustorovich and A. T. Bell, An analysis of Fischer-Tropsch synthesis by the bond-order-conservation-Morse-potential approach, Surf. Sci., 1991, 248(3), 359–368 CrossRef.
- K. H. Delgado, et al., Surface Reaction Kinetics of Steam- and CO2-Reforming as Well as Oxidation of Methane over Nickel-Based Catalysts, Catalysts, 2015, 5(2), 871–904 CrossRef.
- T. P. Senftle, et al., The ReaxFF reactive force-field: development, applications and future directions, npj Comput. Mater., 2016, 2(1), 15011 CrossRef.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105(41), 9396–9409 CrossRef.
- J. Ludwig, D. G. Vlachos, A. C. T. van Duin and W. A. Goddard, Dynamics of the Dissociation of Hydrogen on Stepped Platinum Surfaces Using the ReaxFF Reactive Force Field, J. Phys. Chem. B, 2006, 110(9), 4274–4282 CrossRef PubMed.
- C. Zou, A. C. T. van Duin and D. C. Sorescu, Theoretical investigation of Hydrogen Adsorption and dissociation on Iron and Iron Carbide Surfaces using the ReaxFF force Field Method, Top. Catal., 2012, 55(5), 391–401 CrossRef.
- K. D. Nielson, et al., Development of the ReaxFF Reactive Force Field for Describing Transition Metal Catalyzed Reactions, with Application to the Initial Stages of the Catalytic Formation of Carbon Nanotubes, J. Phys. Chem. A, 2005, 109(3), 493–499 CrossRef.
- J. E. Mueller, A. C. T. van Duin and W. A. Goddard, Development and Validation of ReaxFF Reactive Force Field for Hydrocarbon Chemistry Catalyzed by Nickel, J. Phys. Chem. C, 2010, 114(11), 4939–4949 CrossRef.
- K. Chenoweth, et al., Development and Application of a ReaxFF Reactive Force Field for Oxidative Dehydrogenation on Vanadium Oxide Catalysts, J. Phys. Chem. C, 2008, 112(37), 14645–14654 CrossRef.
- K. Chenoweth, A. C. T. van Duin and W. A. Goddard III, The ReaxFF Monte Carlo Reactive Dynamics Method for Predicting Atomistic Structures of Disordered Ceramics: Application to the Mo3VOx Catalyst, Angew. Chem., Int. Ed., 2009, 48(41), 7630–7634 CrossRef.
- L. Wu, et al., Stabilizing mechanism of single-atom catalysts on a defective carbon surface, npj Comput. Mater., 2020, 6(1), 23 CrossRef.
- X.-Q. Zhang, et al., Site Stability on Cobalt Nanoparticles: A Molecular Dynamics ReaxFF Reactive Force Field Study, J. Phys. Chem. C, 2014, 118(13), 6882–6886 CrossRef.
- W. Guichang, Y. Wenqi, W. Jie and Q. Yuanyuan, Reactive Force Field Model Molecular Dynamics Study on the Thermal Stability of Single Atom Alloy Catalysts, Xinyang Shifan Xueyuan Xuebao, Ziran Kexueban, 2020, 33(2), 191 Search PubMed.
- J. J. P. Stewart, MOPAC: A semiempirical molecular orbital program, J. Comput.-Aided Mol. Des., 1990, 4(1), 1–103 CrossRef PubMed.
- S. W. Benson and J. H. Buss, Additivity Rules for the Estimation of Molecular Properties. Thermodynamic Properties, J. Chem. Phys., 1958, 29(3), 546–572 CrossRef.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef.
- C. F. Goldsmith and R. H. West, Automatic Generation of Microkinetic Mechanisms for Heterogeneous Catalysis, J. Phys. Chem. C, 2017, 121(18), 9970–9981 CrossRef.
- W. Thiel, Semiempirical quantum–chemical methods, WIREs Comput. Mol. Sci., 2014, 4(2), 145–157 CrossRef.
- T. Liang, et al., Reactive Potentials for Advanced Atomistic Simulations, Annu. Rev. Mater. Res., 2013, 43(1), 109–129 CrossRef.
- S. Maeda, T. Taketsugu and K. Morokuma, Exploring transition state structures for intramolecular pathways by the artificial force induced reaction method, J. Comput. Chem., 2014, 35(2), 166–173 CrossRef CAS PubMed.
- P. M. Zimmerman, Automated discovery of chemically reasonable elementary reaction steps, J. Comput. Chem., 2013, 34(16), 1385–1392 CrossRef CAS PubMed.
- Q. Zhao and B. M. Savoie, Simultaneously improving reaction coverage and computational cost in automated reaction prediction tasks, Nat. Comput. Sci., 2021, 1(7), 479–490 CrossRef.
- M. Liu, et al., Reaction Mechanism Generator v3.0: Advances in Automatic Mechanism Generation, J. Chem. Inf. Model., 2021, 61(6), 2686–2696 CrossRef CAS PubMed.
- S. Rangarajan, R. R. O. Brydon, A. Bhan and P. Daoutidis, Automated identification of energetically feasible mechanisms of complex reaction networks in heterogeneous catalysis: application to glycerol conversion on transition metals, Green Chem., 2014, 16(2), 813–823 RSC.
- D. A. Simonetti, E. L. Kunkes and J. A. Dumesic, Gas-phase conversion of glycerol to synthesis gas over carbon-supported platinum and platinum–rhenium catalysts, J. Catal., 2007, 247(2), 298–306 CrossRef.
- E. P. Maris and R. J. Davis, Hydrogenolysis of glycerol over carbon-supported Ru and Pt catalysts, J. Catal., 2007, 249(2), 328–337 CrossRef.
- K. H. Delgado, Surface Reaction Kinetics of Steam- and CO2-Reforming as Well as Oxidation of Methane over Nickel-Based Catalysts, Catalysts, 2015, 5(2), 871–904 CrossRef.
- C. T. Campbell, The Degree of Rate Control: A Powerful Tool for Catalysis Research, ACS Catal., 2017, 7(4), 2770–2779 CrossRef.
- Shambhawi, J. M. Weber and A. A. Lapkin, Micro-kinetics analysis based on partial reaction networks to compare catalysts performances for methane dry reforming reaction, Chem. Eng. J., 2023, 143212 CrossRef.
- A. H. Motagamwala and J. A. Dumesic, Microkinetic Modeling: A Tool for Rational Catalyst Design, Chem. Rev., 2021, 121(2), 1049–1076 CrossRef.
- Z. Wang and P. Hu, Towards rational catalyst design: a general optimization framework, Philos. Trans. R. Soc., A, 2016, 374(2061), 20150078 CrossRef.
- S. Rangarajan, C. T. Maravelias and M. Mavrikakis, Sequential-Optimization-Based Framework for Robust Modeling and Design of Heterogeneous Catalytic Systems, J. Phys. Chem. C, 2017, 121(46), 25847–25863 CrossRef.
- T. Le, V. C. Epa, F. R. Burden and D. A. Winkler, Quantitative Structure–Property Relationship Modeling of Diverse Materials Properties, Chem. Rev., 2012, 112(5), 2889–2919 CrossRef PubMed.
- A. J. Medford, et al., CatMAP: A Software Package for Descriptor-Based Microkinetic Mapping of Catalytic Trends, Catal. Lett., 2015, 145(3), 794–807 CrossRef.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, Degree of rate control approach to computational catalyst screening, J. Catal., 2015, 330, 197–207 CrossRef.
- J. K. Nørskov, T. Bligaard and J. Kleis, Rate Control and Reaction Engineering, Science, 2009, 324(5935), 1655–1656 CrossRef PubMed.
- O. Mohan, et al., Investigating CO2 Methanation on Ni and Ru: DFT Assisted Microkinetic Analysis, ChemCatChem, 2021, 13(10), 2420–2433 CrossRef.
- P. Sabatier, La catalyse en chimie organique, 1920 Search PubMed.
- M. T. Darby, M. Stamatakis, A. Michaelides and E. C. H. Sykes, Lonely Atoms with Special Gifts: Breaking Linear Scaling Relationships in Heterogeneous Catalysis with Single-Atom Alloys, J. Phys. Chem. Lett., 2018, 9(18), 5636–5646 CrossRef.
- S. M. Stratton, S. Zhang and M. M. Montemore, Addressing complexity in catalyst design: From volcanos and scaling to more sophisticated design strategies, Surf. Sci. Rep., 2023, 78(3), 100597 CrossRef.
- A. Chandrasekaran, et al., Solving the electronic structure problem with machine learning, npj Comput. Mater., 2019, 5(1), 22 CrossRef.
- T. Toyao, et al., Toward Effective Utilization of Methane: Machine Learning Prediction of Adsorption Energies on Metal Alloys, J. Phys. Chem. C, 2018, 122(15), 8315–8326 CrossRef.
- A. A. Peterson, Acceleration of saddle-point searches with machine learning, J. Chem. Phys., 2016, 145(7), 074106 CrossRef.
- O.-P. Koistinen, Nudged elastic band calculations accelerated with Gaussian process regression, J. Chem. Phys., 2017, 147(15), 152720 CrossRef PubMed.
- X. Ma, Z. Li, L. E. K. Achenie and H. Xin, Machine-Learning-Augmented Chemisorption Model for CO2 Electroreduction Catalyst Screening, J. Phys. Chem. Lett., 2015, 6(18), 3528–3533 CrossRef.
- F. Guo, et al., Intelligent-ReaxFF: Evaluating the reactive force field parameters with machine learning, Comput. Mater. Sci., 2020, 172, 109393 CrossRef.
- Z. Li, et al., High-throughput screening of bimetallic catalysts enabled by machine learning, J. Mater. Chem. A, 2017, 5(46), 24131–24138 RSC.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2(1), 16028 CrossRef.
- B. Meredig, et al., Combinatorial screening for new materials in unconstrained composition space with machine learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(9), 094104 CrossRef.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef PubMed.
- P. Villars, et al., Data-driven atomic environment prediction for binaries using the Mendeleev number: Part 1. Composition AB, J. Alloys Compd., 2004, 367(1), 167–175 CrossRef.
- M. Andersen, S. V. Levchenko, M. Scheffler and K. Reuter, Beyond Scaling Relations for the Description of Catalytic Materials, ACS Catal., 2019, 9(4), 2752–2759 CrossRef.
- J. Dean, M. G. Taylor and G. Mpourmpakis, Unfolding adsorption on metal nanoparticles: Connecting stability with catalysis, Sci. Adv., 2019, 5(9), eaax5101 CrossRef.
- H. Xin, A. Holewinski and S. Linic, Predictive Structure–Reactivity Models for Rapid Screening of Pt-Based Multimetallic Electrocatalysts for the Oxygen Reduction Reaction, ACS Catal., 2012, 2(1), 12–16 CrossRef.
- J. Noh, S. Back, J. Kim and Y. Jung, Active learning with non-ab initio input features toward efficient CO2 reduction catalysts, Chem. Sci., 2018, 9(23), 5152–5159 RSC.
- K. T. Schütt, et al., How to represent crystal structures for machine learning: Towards fast prediction of electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(20), 205118 CrossRef.
- D. Wu, C. Dong, H. Zhan and X.-W. Du, Bond-Energy-Integrated Descriptor for Oxygen Electrocatalysis of Transition Metal Oxides, J. Phys. Chem. Lett., 2018, 9(12), 3387–3391 CrossRef CAS PubMed.
- F. Calle-Vallejo, et al., Fast Prediction of Adsorption Properties for Platinum Nanocatalysts with Generalized Coordination Numbers, Angew. Chem., Int. Ed., 2014, 53(32), 8316–8319 CrossRef CAS.
- X. Ma and H. Xin, Orbitalwise Coordination Number for Predicting Adsorption Properties of Metal Nanocatalysts, Phys. Rev. Lett., 2017, 118(3), 036101 CrossRef.
- Y.-L. Lee, et al., Prediction of solid oxide fuel cell cathode activity with first-principles descriptors, Energy Environ. Sci., 2011, 4(10), 3966–3970 RSC.
- J. Suntivich, et al., A Perovskite Oxide Optimized for Oxygen Evolution Catalysis from Molecular Orbital Principles, Science, 2011, 334(6061), 1383–1385 CrossRef CAS.
- H. Xin, et al., Effects of $d$-band shape on the surface reactivity of transition-metal alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(11), 115114 CrossRef.
- T. S. Choksi, L. T. Roling, V. Streibel and F. Abild-Pedersen, Predicting Adsorption Properties of Catalytic Descriptors on Bimetallic Nanoalloys with Site-Specific Precision, J. Phys. Chem. Lett., 2019, 10(8), 1852–1859 CrossRef CAS PubMed.
- Y. Zhang and C. Ling, A strategy to apply machine learning to small datasets in materials science, npj Comput. Mater., 2018, 4(1), 25 CrossRef.
- Z. Li, L. E. K. Achenie and H. Xin, An Adaptive Machine Learning Strategy for Accelerating Discovery of Perovskite Electrocatalysts, ACS Catal., 2020, 10(7), 4377–4384 CrossRef CAS.
- Z. Li, X. Ma and H. Xin, Feature engineering of machine-learning chemisorption models for catalyst design, Catal. Today, 2017, 280, 232–238 CrossRef CAS.
- W. A. Harrison and S. Froyen, Universal linear-combination-of-atomic-orbitals parameters for $d$-state solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21(8), 3214–3221 CrossRef CAS.
- J. S. Hummelshøj, et al., CatApp: A Web Application for Surface Chemistry and Heterogeneous Catalysis, Angew. Chem., 2012, 124(1), 278–280 CrossRef.
- K. T. Winther, et al., Catalysis-Hub.org, an open electronic structure database for surface reactions, Sci. Data, 2019, 6(1), 75 CrossRef.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, High-throughput calculations of catalytic properties of bimetallic alloy surfaces, Sci. Data, 2019, 6(1), 76 CrossRef PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, Open Catalyst 2020 (OC20) Dataset and Community Challenges, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS.
- A. Jain, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- A. Jain, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- K. Tran and Z. W. Ulissi, Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution, Nat. Catal., 2018, 1(9), 696–703 CrossRef CAS.
- R. A. Hoyt, et al., Machine Learning Prediction of H Adsorption Energies on Ag Alloys, J. Chem. Inf. Model., 2019, 59(4), 1357–1365 CrossRef CAS PubMed.
- M. M. Montemore and J. W. Medlin, Scaling relations between adsorption energies for computational screening and design of catalysts, Catal. Sci. Technol., 2014, 4(11), 3748–3761 RSC.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, A Bayesian framework for adsorption energy prediction on bimetallic alloy catalysts, npj Comput. Mater., 2020, 6(1), 177 CrossRef CAS.
- K. Tran, et al., Methods for comparing uncertainty quantifications for material property predictions, Mach. Learn.: Sci. Technol., 2020, 1(2), 025006 Search PubMed.
- L. Chanussot, et al., Open Catalyst 2020 (OC20) Dataset and Community Challenges, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS.
- J. W. Lee and C. Giraud-Carrier, Transfer Learning in Decision Trees in 2007 International Joint Conference on Neural Networks, 2007 Search PubMed.
- B. Zhang, et al., Transfer learning-based online multiperson tracking with Gaussian process regression, Concurr. Comput. Pract. Exp., 2018, 30(23), e4917 CrossRef.
- O. T. Unke, et al., Machine Learning Force Fields, Chem. Rev., 2021, 121(16), 10142–10186 CrossRef CAS.
- V. L. Deringer, M. A. Caro and G. Csányi, Machine Learning Interatomic Potentials as Emerging Tools for Materials Science, Adv. Mater., 2019, 1902765 CrossRef CAS.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(18), 184115 CrossRef.
- A. P. Bartók, J. Kermode, N. Bernstein and G. Csányi, Machine Learning a General-Purpose Interatomic Potential for Silicon, Phys. Rev. X, 2018, 8(4), 041048 Search PubMed.
- V. L. Deringer and G. Csányi, Machine learning based interatomic potential for amorphous carbon, Phys. Rev. B, 2017, 95(9), 094203 CrossRef.
- W. J. Szlachta, A. P. Bartók and G. Csányi, Accuracy and transferability of Gaussian approximation potential models for tungsten, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(10), 104108 CrossRef.
- H. Muhli, et al., Machine learning force fields based on local parametrization of dispersion interactions: Application to the phase diagram of C60, Phys. Rev. B, 2021, 104(5), 054106 CrossRef CAS.
- L. L. Schaaf, E. Fako and S. De, et al., Accurate energy barriers for catalytic reaction pathways: an automatic training protocol for machine learning force fields, npj Comput. Mater., 2023, 9(1), 180 CrossRef.
- F. Abild-Pedersen, et al., Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces, Phys. Rev. Lett., 2007, 99(1), 016105 CrossRef CAS.
- J. Greeley, Theoretical Heterogeneous Catalysis: Scaling Relationships and Computational Catalyst Design, Annu. Rev. Chem. Biomol. Eng., 2016, 7(1), 605–635 CrossRef.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Introducing structural sensitivity into adsorption–energy scaling relations by means of coordination numbers, Nat. Chem., 2015, 7(5), 403–410 CrossRef CAS PubMed.
- M. G. Evans and M. Polanyi, J. Chem. Soc., Faraday Trans., 1936, 32, 1333–1360 RSC.
- C. Fan, Origin of synergistic effect over Ni-based bimetallic surfaces: A density functional theory study, J. Chem. Phys., 2012, 137(1), 014703 CrossRef.
- Y. Huang, et al., Methane dehydrogenation on Au/Ni surface alloys – a first-principles study, Catal. Sci. Technol., 2013, 3(5), 1343–1354 RSC.
- J. Rossmeisl, et al., Electrolysis of water on oxide surfaces, J. Electroanal. Chem., 2007, 607(1), 83–89 CrossRef CAS.
- T. Choksi, P. Majumdar and J. P. Greeley, Electrostatic Origins of Linear Scaling Relationships at Bifunctional Metal/Oxide Interfaces: A Case Study of Au Nanoparticles on Doped MgO Substrates, Angew. Chem., Int. Ed., 2018, 57(47), 15410–15414 CrossRef CAS PubMed.
- A. Logadottir, et al., The Brønsted–Evans–Polanyi Relation and the Volcano Plot for Ammonia Synthesis over Transition Metal Catalysts, J. Catal., 2001, 197(2), 229–231 CrossRef CAS.
- Q. Gao, et al., Breaking adsorption-energy scaling limitations of electrocatalytic nitrate reduction on intermetallic CuPd nanocubes by machine-learned insights, Nat. Commun., 2022, 13(1), 2338 CrossRef CAS.
- C. J. Bartel, et al., A critical examination of compound stability predictions from machine-learned formation energies, npj Comput. Mater., 2020, 6(1), 97 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |