Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of temperatures and loadings on olefin diffusion in MFI-type zeolites in one- to three-dimensions†
Jiahuan
Tong
,
Takumi
Miyakage
,
Takashi
Toyao
 and
Ken-ichi
Shimizu
and
Ken-ichi
Shimizu
 *
*
Institute for Catalysis, Hokkaido University, Sapporo 001-0021, Japan. E-mail: kshimizu@cat.hokudai.ac.jp
First published on 16th February 2024
Abstract
A detailed understanding of the molecular diffusion in zeolite frameworks is crucial for analysing the factors controlling their catalytic performance in alkenes. In this work, we present a molecular dynamics study of propylene diffusion in acidic zeolite MFI in the temperature range of 453–653 K. Moreover, the effects of different temperatures and propylene loadings on olefin diffusion in the acidic zeolite MFI were considered. A detailed analysis of olefin deformation in one to three dimensions was performed to illustrate the anisotropy and influence of the olefin structure on its diffusion in zeolites. The propylene diffusion direction was elucidated by correlating the temperature with the diffusion coefficients of the straight and zigzag channels of the H-MFI zeolite. Furthermore, the analysis of the radial distribution function and Brønsted acid sites showed that the olefins interacted mainly with acidic protons and that the degree of clustering of olefin was higher at higher loadings. These results help understand the differences in the catalytic performance of zeolites in olefin reactions at different temperatures and loadings; are beneficial for understanding the catalytic activity, stability, and product distribution; and guide the design of catalysts with specific morphologies.
1. Introduction
Plastics are versatile materials with numerous applications in daily life. Their affordability, durability, and ease of manufacture have led to their widespread use in various industries.1,2 However, the environmental challenges associated with plastic pollution and limited conversion rates are significant concerns.3 Light olefins, such as ethylene, propylene, and butadiene, play key roles in the production, degradation, and conversion of plastics. They are original components of plastic preparation and can be produced or reused in plastic degradation and conversion, helping to reduce plastic pollution and resource waste and achieve resource conversion.4 Light olefins also play a pivotal role in the petroleum industry, as they constitute the fundamental components of various chemicals and products, ranging from fuels to chemicals derived from crude oil.5–10 Their production and applications have far-reaching implications for modern industry. These industrial processes are primarily based upon fluid catalytic cracking.11,12 Zeolite catalysts are vital for numerous of these catalytic conversion processes.13–18 The ongoing quest for adaptability adjustments to zeolite topological structures remains a long-term goal for fine-tuning the performance of these technologies.19 The three-dimensional (3D) zeolite structure is a network consisting of silicon–oxygen and aluminium–oxygen tetrahedra.20 The zeolite framework is formed by sharing oxygen atoms along the edges. The arrangement of silicon–oxygen and aluminium–oxygen tetrahedra and the silicon-to-aluminium ratio can alter the pore structure and properties of the zeolites. Currently, there are 255 known basic zeolite frameworks. In theory, by adjusting the silicon-to-aluminium ratio and introducing other elements, an infinite number of zeolite types can be synthesised to meet various application requirements.21–23 The diversity and tunability of zeolites make them vital materials in chemical engineering,24,25 petroleum industry,26,27 and environmental engineering,28,29 providing extensive versatility in processes such as adsorption,30–32 separation,33,34 and catalysis.35,36 In particular, H-MFI zeolite is highly favoured in crucial industrial processes such as cracking due to the presence of a combination of microporous and mesoporous structures and Brønsted acid sites.37–40 This is because they facilitate molecular transformations and product selectivity, thereby enhancing the efficiency and sustainability of industrial processes.41,42 For example, a comparative study of MFI, MEL, and TON zeolites from methanol to olefins conducted by Hunger et al. showed that under optimised conditions, the selectivity of the H-MFI zeolite to propylene reached 51%, whereas the selectivity of the TON zeolite to propylene was only 38%.43 García-Hurtado et al. systematically studied the influence of zeolite type on CO2 conversion over multifunctional catalysts combining K/Fe3O4 with different zeolites (BEA, MFI, and CHA). Based on their analysis, MFI efficiently increased the yield of C5 hydrocarbons.44 These studies showed that the microporous structure of H-MFI facilitated the production and conversion of small molecules, thereby accelerating the catalytic reaction rate. More importantly, high yields were positively correlated with the diffusion rate of molecules in the zeolite channels.45,46 Therefore, there is an urgent need to understand the diffusion behaviour of molecules in zeolite channels. To date, most experimental studies have been directed towards investigating the effects of external conditions such as temperature and pressure on the diffusion rate of olefins within H-MFI channels. For example, Botchway et al. conducted an in-depth investigation on the diffusion of methanol in all-silica and acidic zeolite MFI and Beta frameworks over the temperature range of 373–473 K. They found that the methanol diffusion increased with increasing temperature.47 Some studies on changing the zeolite topology to increase the olefin diffusion behaviour and thus affect the yield have been conducted. Wang et al. improved the morphology of MFI with a b-axis orientation length of 80–100 nm. The modified MFI improved the cracking of polypropylene and produced light hydrocarbon C1–C7 products with yields of up to 75%. Hydrogen participation in the cracking process hindered the formation of polycyclic species within the zeolite micropores, which also contributed to rapid molecular diffusion.48 Later, they found that the modified MFI catalyst Na-FeCx/MFI, synthesized by mixing iron carbide with MFI zeolite, exhibited 82.5% CO2 conversion and 72.0% olefin selectivity at a low temperature of 260 °C. Using DFT simulation, they found that the diffusion barriers for ethene were strongly related to the adsorption sites, and the diffusion efficiency in one zeolite crystal should be inversely proportional to the number of adsorption sites and the zeolite channel distance.49However, there have been no reports thus far that analyse the morphology of propylene molecules when they diffuse in zeolite, that is, (1) whether the propylene molecules remain straight or bent at a certain angle during the diffusion process (detailed analysis is described in section 4.3) and (2) the movement path of olefin molecules in different dimensions when diffusing in zeolites (detailed analysis is described in section 4.1 and 4.2) in this study, we investigated the sensitivity of the propylene diffusivity in H-MFI zeolites to temperature and propylene loading using molecular dynamics (MD) simulations, analysed the diffusion mechanism of propylene in the pores from one to three dimensions, and revealed the morphological changes in propylene molecules during the diffusion process and the effects of different morphologies on diffusion. Finally, we analysed the interaction between the H-MFI zeolite topology and propylene to reveal the importance of Brønsted acid sites in the zeolite structure and its impact on propylene diffusion. We believe that an in-depth understanding of the diffusion state of propylene in zeolite channels will considerably improve the design of zeolites with high olefin diffusivity and provide a strong theoretical basis for promoting catalytic cracking reactions.
2. Module
The MFI zeolite structure can be described as a 3D molecular sieve with a cross-channel architecture. The initial framework of pure MFI consisting of eight five-membered rings interconnected by edges, resulting in a network of channels was obtained from Zeolite database.50 These channels can be categorised into two types: zigzag and straight-through. The zigzag channels have an elliptical cross-section with dimensions of 0.51 nm × 0.55 nm on the [1 0 0] plane, whereas the straight-through channels exhibit nearly circular cross-sections measuring 0.53 nm × 0.56 nm on the [0 1 0] plane. The structure of the ZSM-5 zeolite used in this study was obtained from the Materials Studio database. It is characterised as an orthorhombic crystalline system with a space group of Pnma and has the following cell parameters: a = 20.022 Å, b = 19.899 Å, c = 13.383 Å, with all three angles (α, β, and γ) equal to 90°. To facilitate the Si/Al ratio adjustment and enhance the visualisation of the simulation, a 1 × 2 × 2 supercell was created by expanding the cell parameters to 20.07 × 39.798 × 26.766 Å3.The MFI structure was created by replacing Si atoms with Al atoms and subsequently introducing an equal number of protons (H+) to maintain charge neutrality. These protons were inserted into the oxygen atoms connected to the Al atoms following the Loewenstein rule while ensuring that there were no Al–O–Al structural arrangements.51 Notably, previous studies by Loewenstein et al. determined that the substitution of Si at the T12 site with Al required the least energy compared with other positions.52 Therefore, the T12 site was identified as the preferred location for the replacement of Si with Al. The resulting concrete structure is illustrated in Fig. 1.
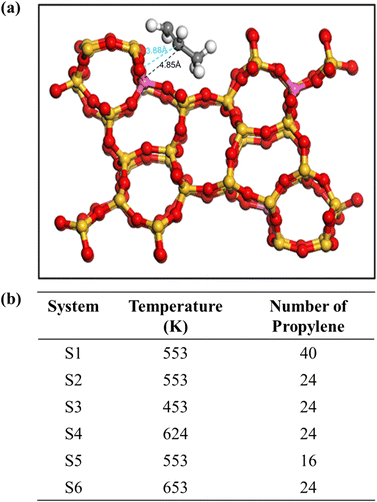 | ||
| Fig. 1 (a) MFI zeolite shows the substituted Al at T12. (b) Detailed composition of all simulation systems. | ||
3. Method
All simulations were performed using the DL-POLY4 package.53 Visualisations and plots were constructed using visual MD (VMD)54 and an open visualisation tool (OVITO).55 The force field for propylene was derived from a report by Oie et al., which has been previously shown to have good diffusion coefficients that are consistent with the experimental values.56 For zeolites, a flexible force field was used to capture the dynamic effects of the framework on diffusion.57,58 A cutoff of 9 Å was used for non-bonded interactions, and the Ewald summation was used to calculate the electrostatic forces.MD simulations were initiated by equilibration, which was first conducted under an NVT ensemble over 2 ns; subsequently, the production run of 5 ns was performed on an NVT ensemble. A time step of 0.25 fs was used in the simulation, and the atomic coordinates were recorded every 1 ps. Simulations were performed at the temperatures of 453, 553, 624 and 653 K. A Berendsen thermostat was used to regulate the temperature during equilibration with the NVT ensemble with a time constant of 1 ps. Three different loadings of olefin molecules were employed to analyse the effect of molecular concentration on diffusion. At the lower loading, 16 and 24 olefin molecules were adsorbed in the supercells of H-MFI, that is, 4 and approximately 6 molecules per unit cell (mpuc), respectively, whereas almost twice the number of olefin molecules was used for a higher concentration, that is, 40 molecules, resulting in 10 mpuc. All simulation systems are shown in Fig. 1(b). For each loading, the H-MFI zeolites had the same ratio between the number of molecules and the volume of the supercell. The multiple initial time method was employed to average the trajectory from 5 ns of the production run to 1 ns, shifting the initial time t0 every 30 ps. This reduced the statistical noise generated in the mean square displacement (MSD) plots. All simulation details are provided in ESI.†
4. Results and discussions
4.1. Diffusion analysis
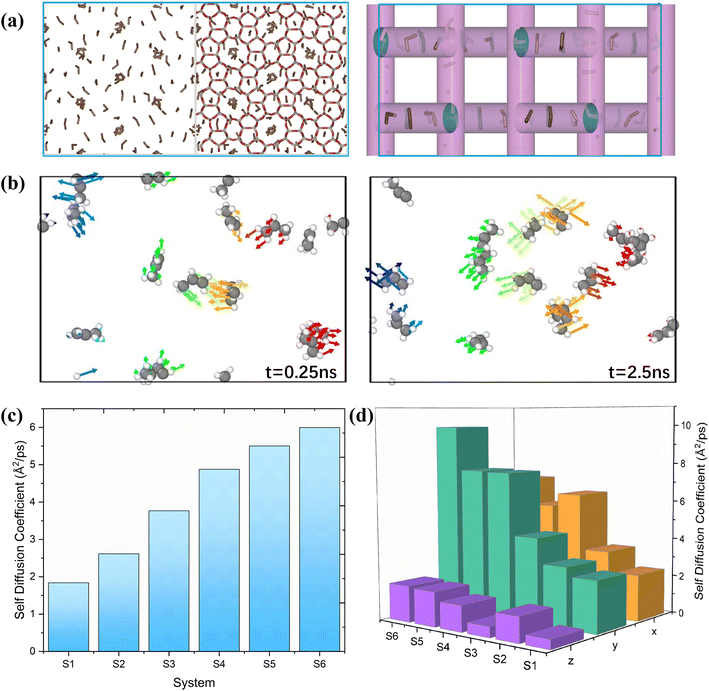
The study of diffusion plays a pivotal role in enhancing the understanding of olefin movement within pore systems. This movement is influenced by several factors, including interactions with the active sites, temperature fluctuations, and changes in the zeolite structure and micropore size. These factors collectively determine the catalytic efficiency of zeolites.In this study, the self-diffusion coefficient (Ds) was calculated by fitting the slope of the mean square displacement (MSD) as a function of time over long periods.59
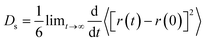 | (1) |
The MSD values for propylene in one, two, and three dimensions in this interval are shown in Fig. S1.† The corresponding self-diffusion coefficients of the ions are shown in Fig. 2(c). In this work, the Ds of propylene molecules at different temperatures and loadings were studied because they are key components for synthesising various organic compounds, including polymers, coatings, adhesives, solvents, and fragrances, and have been widely investigated in plastic manufacturing and petrochemical industries. The calculated Ds of propylene inside MFI agreed well with the value reported by Yuan et al. (in the order of 10−8 m2 s−1).60Fig. 2(c) and Table S1† show the detailed values of the simulated Ds of propylene for the six systems. The propylene diffusion also presents an Arrhenius-type response to temperature with an activation energy of 9.85 kJ mol−1, as shown in Fig. S2.† This result agrees with the value reported by Alaithan et al., which is 7.2 kJ mol−1, considering that they used different force fields and loadings of propylene.61 This further confirmed the validity of our calculations.
Furthermore, the simulation results show that the self-diffusion coefficient increases with increasing temperature. This result is consistent with that reported by Yuan et al.60 Moreover, by comparing systems 1, 2, and 5, it is obvious that the diffusion coefficient of propylene in MFI is inversely proportional to the number of loadings in the unit cell; that is, the low loading of propylene (four propylene per unit cell in system 5) corresponds to the highest diffusion coefficient. Similar results are reported by Alaithan et al.61 As shown in Fig. 2(a), the 3D channel of the H-MFI has a 10-ring zigzag channel with a window size of 5.1 Å × 5.5 Å along the X and Z directions, and a 10-ring straight channel (5.3 Å × 5.6 Å) is distributed in the Y direction. Diffusion analysis in each dimension reveals that propylene prefers to move in zigzag channels at 453 K and 553 K; that is, Dx > Dy. As shown in Fig. 2(b), the same results are obtained through a detailed analysis of the direction of motion of the propylene molecules. As indicated by the arrow, at 453 K, propylene diffuses in the zig-zag direction. (The 5 ns motion trajectory of propylene is shown as an animation in the ESI†). In contrast, as shown in Fig. 2(d), for systems 4 and 6, Dy is considerably larger than Dx, implying that propylene prefers linear channels at high temperatures. The explanation for these phenomena is that in the presence of Brønsted acid sites, considering that propylene first preferentially adsorbs onto the acidic sites in the acidic zeolite MFI at low temperatures, the molecule resides in the acidic sites during most of the simulation time (the analysis of the interaction between propylene and acidic protons is presented in detail in section 4.4.)
4.2. Root mean square deviation
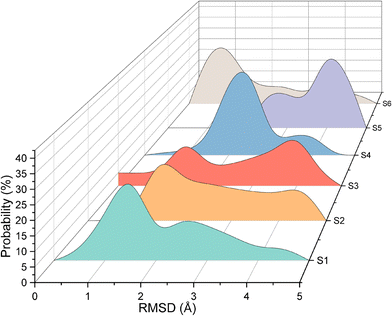
Quantitative analysis of the deformation of molecular structures at various temperatures is highly significant. In this context, the root mean square deviation (RMSD) of the Cartesian coordinates of equivalent atoms in two structures, namely, the reference and transient configurations, serves as a standard metric for measuring molecular deformation.62 Before the RMSD calculation, it is necessary to use a rigid body translation and rotation of one structure with respect to the other using a least-squares superposition procedure. The MD trajectories of propylene are analysed by comparing each molecule at each step at various temperatures with respect to the reference structure. Finally, the probabilities of each RMSD value at different temperatures are calculated. RMSD values were calculated using the VMD package. In this study, the root mean square deviation of propylene is defined by the following equation: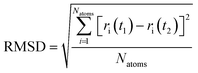 | (2) |
As shown in Fig. 3, for system 1, the RMSD is always less than 3 Å, indicating that propylene molecules can maintain linear diffusion for a long time at 553 K and a loading of 10 mpuc, and are not easily deformed. However, the RMSDs of systems 2–6 have a broad distribution, with an obvious peak appearing at approximately 4 Å. The linear structure of propylene is gradually destroyed and deformed, affecting its diffusion in the MFI channel.
4.3. The shape of the propylene molecule inside MFI
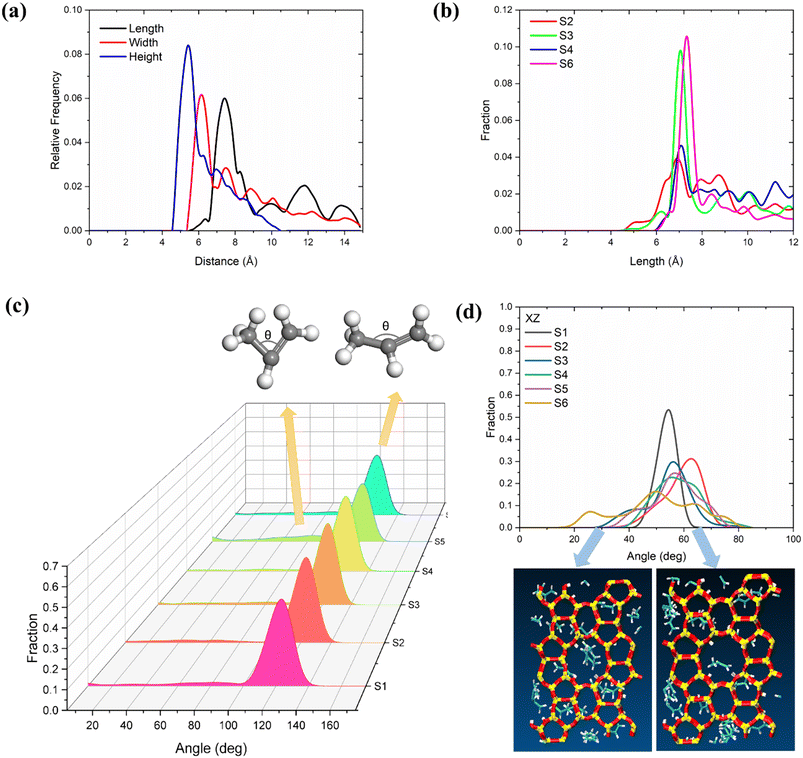
To further determine the effects of temperature and loading on propylene deformation, we conducted a detailed structural analysis of propylene in MFI zeolites according to the method reported by Yuan et al.60 first, the length, width, and height of the propylene molecules were quantified and calculated from the difference between the maximum and minimum coordinates of a molecule in each direction (x, y, and z) (the van der Waals radius was considered). In this study, the length, width, and height were defined by eqn (3).| a = xmax − xminb = ymax − yminc = zmax − zminLength = maximum (a, b, c) + 1.7 × 2Width = median (a, b, c) + 1.7 × 2Height = minimum (a, b, c) + 1.7 × 2 | (3) |
As shown in Fig. 4(a), the three dimensions of the propylene inside the MFI zeolite follow the order of length > width > height. The peak of the distribution of the length of propylene is at 7.05 Å at 453 K, and shifts to 7.56 Å at 653 K (Fig. 4(b)). The width and height distributions of propylene are shown in Fig. S2.† As the temperature increases, the width and height decrease simultaneously. According to the above analysis of the diffusion coefficient, we believe that for olefin molecules, the longer the length and the smaller the width and height, the faster the diffusion in the zeolite. This phenomenon is consistent with the findings of Zheng et al. Furthermore, we analysed the angle distribution of propylene in the 5 ns trajectory. As shown in Fig. 4(c), in most systems, the angle between the three carbon atoms in the propylene molecule remains at approximately 126°. However, we found another weak peak at 40–80°, the intensity of which increases with increasing temperature. This indicates that the higher the temperature, the greater the bending of the molecule and the thicker the molecule (consistent with the results for the width and height in Fig. S2†), causing increased diffusion. In particular, we analysed the angles of the propylene molecules on a two-dimensional plane to understand whether the propylene molecules in the zeolite channels are parallel or perpendicular to the channels. As shown in Fig. 4(d), at 453 and 553 K, the angle between the propylene and the xz plane is mainly distributed at 50–70°, that is, the olefins tend to be parallel to the channel. However, at 653 K, the angle distribution increases, and an obvious angle appears at 25°. The wider peak indicates that the propylene molecules transition from a parallel to a vertical state.
4.4. The radial distribution function
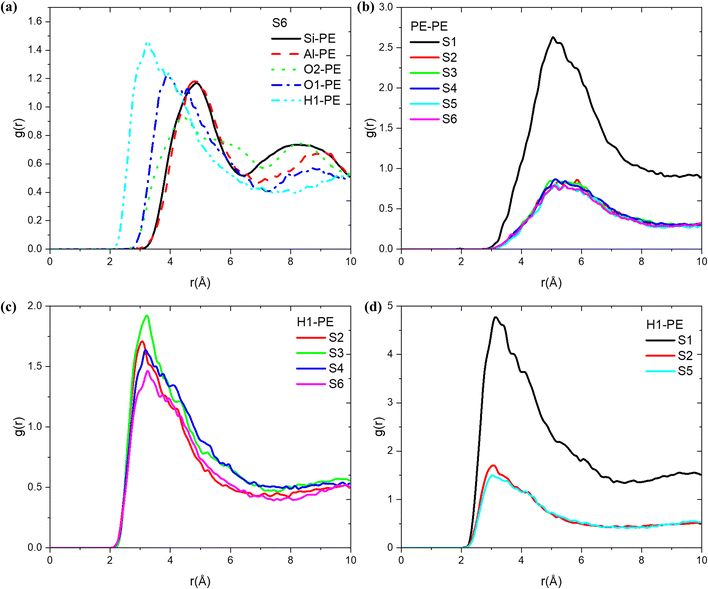
By examining the radial distribution function (RDF) of the atomic pairs formed by each atom of the olefin molecule, the structure–activity relationship of olefin diffusion in MFI was further analysed. As shown in Fig. 5, at 653 K, a strong peak is observed at a distance of 3.24 Å between propylene and the acidic protons (H1) in the MFI zeolite, indicating that during the diffusion of olefins in H-MFI, they mainly interact with acidic protons and affect the diffusion state. Furthermore, a second strong peak corresponding to O2 is observed at 3.88 Å. Since O2 is connected to H1, it can be shown that propylene mainly interacts with the Brønsted acid site to affect molecular diffusion. To illustrate the impact of temperature on the propylene-MFI interaction, we examined the variation of RDF (H1-propylene) with temperature. As shown in Fig. 5(c), the interaction between PE and Brønsted acid sites weakens as the temperature increases. Considering the earlier discussion on diffusion coefficients, we hypothesise that at lower temperatures, propylene molecules have a greater tendency to bind to acidic sites and adsorb onto H, resulting in lower diffusion rates. At higher temperatures, the preference of propylene for diffusion in the y-direction (straight channels) leads to lower peaks in the RDF results. Regarding the decrease in RDF peak values with increasing temperature, similar findings were reported by Keyvanloo et al.63 They observed that the RDF of methanol and ethanol in HZSM-5 decreased consistently with increasing temperature. In addition, we performed RDF analysis (Fig. S4†) of all atoms on the MFI and propylene, and the results showed that the interactions between all atoms (Al, H1, O1) on the Brønsted acidic site and propylene were sensitive to temperature changes. However, the interactions between the Si atoms and O2 on the original MFI skeleton and propylene remained almost unchanged with temperature. This demonstrated the importance of protonated zeolite structures in olefin catalysis. Similarly, we conducted an RDF analysis on systems 1, 2, and 5 (Fig. 5(d)), illustrating the trends in the interaction between the acid protons and propylene molecules under different loading conditions. The results indicated that the higher the loading of propylene, the stronger its interaction with MFI.The RDF for the atomic pair formed by the carbon atoms of two distinct olefin molecules offers valuable insights into the clustering of molecules within the micropore system, as shown in Fig. 5(b). The RDF curve for propylene in the MFI zeolite exhibits a strong peak at approximately 5.5 Å. As the loading increases, the peak corresponding to propylene–propylene interactions significantly intensifies, indicating a significant increase in C—C interactions. This indicates that the presence of a large number of adsorbed molecules in the system makes it easier to disrupt interactions with acid sites, and the olefin molecules come into contact with each other more frequently.
5. Conclusion
In this study, we investigated the effects of temperature and loading on the diffusion mechanism of propylene in H-MFI zeolites using MD simulations. The results showed that propylene diffusion in the H-MFI was positively correlated with temperature, inversely related with loading amount. We correlated the morphology of propylene with its diffusion behaviour in the zeolite channels. By calculating the anisotropy and shape of propylene and analysing its direction of motion, we determined that propylene tended to diffuse in a zigzag direction, showing a shape parallel to the horizontal plane at low temperatures. At high temperatures, propylene diffused along straight channels because of its tendency to adopt a vertical morphology, resulting in a higher diffusion rate. This work elucidates the light-olefin diffusion mechanisms in zeolite channels, presents valuable perspectives for improving zeolite models, and helps guide the design of zeolites.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by KAKENHI (21K18185, 21H04626, 22K14538, 23KF0129, and 23H01997) from the Japan Society for the Promotion of Science (JSPS) and the Joint Usage/Research Center for Catalysis. J. T. acknowledge support by Japan Society for the Promotion of Science (JSPS) under its postdoctoral fellowship (Project No. PE22033); and the Calculation Resource Supports from the Molecular Simulation Computing Platform in Kyoto University.References
- L. Li, H. Luo, Z. Shao, H. Zhou, J. Lu, J. Chen, C. Huang, S. Zhang, X. Liu, L. Xia, J. Li, H. Wang and Y. Sun, J. Am. Chem. Soc., 2023, 145, 1847–1854 CrossRef CAS PubMed.
- E. L. Bell, R. Smithson, S. Kilbride, J. Foster, F. J. Hardy, S. Ramachandran, A. A. Tedstone, S. J. Haigh, A. A. Garforth, P. J. R. Day, C. Levy, M. P. Shaver and A. P. Green, Nat. Catal., 2022, 5, 673–681 CrossRef CAS.
- I. Vollmer, M. J. F. Jenks, R. Mayorga González, F. Meirer and B. M. Weckhuysen, Angew. Chem., 2021, 60, 16101–16108 CrossRef CAS PubMed.
- W. Zhang, S. Kim, L. Wahl, R. Khare, L. Hale, J. Hu, D. M. Camaioni, O. Y. Gutiérrez, Y. Liu and J. A. Lercher, Science, 2023, 379, 807–811 CrossRef CAS PubMed.
- N. Netsch, J. Vogt, F. Richter, G. Straczewski, G. Mannebach, V. Fraaije, S. Tavakkol, S. Mihan and D. Stapf, Chem. Ing. Tech., 2023, 95, 1305–1313 CrossRef CAS.
- S. M. Sadrameli, Fuel, 2016, 173, 285–297 CrossRef CAS.
- Z. Gholami, F. Gholami, Z. Tišler and M. Vakili, Energies, 2021, 14, 8190 CrossRef CAS.
- J. Zhang, M. Ma, Z. Chen, X. Zhang, H. Yang, X. Wang, H. Feng, J. Yu and S. Gao, J. Energy Inst., 2023, 108, 101235 CrossRef CAS.
- M. Artetxe, G. Lopez, M. Amutio, G. Elordi, J. Bilbao and M. Olazar, J. Chem. Eng., 2012, 207–208, 27–34 CrossRef CAS.
- D. T. Sekyere, J. Zhang, Y. Chen, Y. Huang, M. Wang, J. Wang, N. Niwamanya, A. Barigye and Y. Tian, Fuel, 2023, 333, 126339 CrossRef CAS.
- Z. Gholami, F. Gholami, Z. Tišler, M. Tomas and M. Vakili, Energies, 2021, 14, 1089 CrossRef CAS.
- A. Akah, J. Williams and M. Ghrami, Catal. Surv. Jpn., 2019, 23, 265–276 CrossRef CAS.
- L. Du, Y. Han, Y. Zhu, Y. Xu, X. Bai, Y. Ouyang, Y. Luo and X. Shu, ACS Omega, 2023, 8, 7093–7101 CrossRef CAS PubMed.
- T. Mizuno, H. Yamazaki, Y. Takamiya, H. Hasegawa, C. Tanaka and T. Mitsui, Appl. Catal., A, 2023, 661, 119214 CrossRef CAS.
- H. X. Vu, M. Schneider, U. Bentrup, T. T. Dang, B. M. Q. Phan, D. A. Nguyen, U. Armbruster and A. Martin, Ind. Eng. Chem. Res., 2015, 54, 1773–1782 CrossRef CAS.
- E. D. da Silva Ferracine, K. T. G. Carvalho, D. S. A. Silva and E. A. Urquieta-Gonzalez, Catal. Lett., 2020, 150, 3481–3494 CrossRef CAS.
- K. A. Nadeina, O. V. Potapenko, M. O. Kazakov, V. P. Doronin, A. V. Saiko, T. P. Sorokina, A. V. Kleimenov, O. V. Klimov and A. S. Noskov, Catal. Today, 2021, 378, 2–9 CrossRef CAS.
- B. Jha and D. N. Singh, Basics of Zeolites. in Fly Ash Zeolites, Springer, Singapore, 2016, vol. 78, pp. 5–31 Search PubMed.
- Y. Chai, W. Dai, G. Wu, N. Guan and L. Li, Acc. Chem. Res., 2021, 54, 2894–2904 CrossRef CAS PubMed.
- J. Liu, L. Chen, H. Cui, J. Zhang, L. Zhang and C. Y. Su, Chem. Soc. Rev., 2014, 43, 6011–6061 RSC.
- A. Corma, J. Catal., 2003, 216, 298–312 CrossRef CAS.
- S. Wang and Y. Peng, J. Chem. Eng., 2010, 156, 11–24 CrossRef CAS.
- A. Phan, C. J. Doonan, F. J. Uribe-Romo, C. B. Knobler, M. Okeeffe and O. M. Yaghi, Acc. Chem. Res., 2010, 43, 58–67 CrossRef CAS PubMed.
- Z. Cao, N. D. Anjikar and S. Yang, Separations, 2022, 9, 47 CrossRef CAS.
- H. Serati-Nouri, A. Jafari, L. Roshangar, M. Dadashpour, Y. Pilehvar-Soltanahmadi and N. Zarghami, Mater. Sci. Eng., C, 2020, 116, 111225 CrossRef CAS PubMed.
- J. V. Milato, R. J. França and M. R. C. Marques, Environ. Technol., 2021, 42, 1013–1022 CrossRef CAS PubMed.
- W. Vermeiren and J. P. Gilson, Top. Catal., 2009, 52, 1131–1161 CrossRef CAS.
- L. F. De Magalhães, G. R. Da Silva and A. E. C. Peres, Adsorpt. Sci. Technol., 2022, 2022, 1–26 CrossRef.
- Y. Li, L. Li and J. Yu, Chem, 2017, 3, 928–949 CAS.
- N. Jiang, R. Shang, S. G. J. Heijman and L. C. Rietveld, Sep. Purif. Technol., 2020, 235, 116152 CrossRef CAS.
- T. D. Nguyen, T. M. P. Nguyen, H. T. Van, V. Q. Nguyen, L. H. Nguyen, T. D. Nguyen, T. H. V. Nguyen, T. H. H. Chu, T. H. Nguyen, L. T. Ha, N. D. Vinh, V. N. Thai, K. A. Nguyen and P. Q. Thang, Environ. Technol. Innovation, 2022, 25, 102244 CrossRef CAS.
- A. E. Burakov, E. V. Galunin, I. V. Burakova, A. E. Kucherova, S. Agarwal, A. G. Tkachev and V. K. Gupta, Ecotoxicol. Environ. Saf., 2018, 148, 702–712 CrossRef CAS PubMed.
- M. Sinaei Nobandegani, L. Yu and J. Hedlund, J. Chem. Eng., 2022, 446, 137223 CrossRef CAS.
- D. G. Boer, J. Langerak and P. P. Pescarmona, ACS Appl. Energy Mater., 2023, 6, 2634–2656 CrossRef CAS.
- M. M. Zagho, M. K. Hassan, M. Khraisheh, M. A. A. Al-Maadeed and S. Nazarenko, Chem. Eng. J. Adv., 2021, 6, 100091 CrossRef CAS.
- Y. Cui, B. Li, H. He, W. Zhou, B. Chen and G. Qian, Acc. Chem. Res., 2016, 49, 483–493 CrossRef CAS PubMed.
- Y. Zhang, R. Zhao, M. Sanchez-Sanchez, G. L. Haller, J. Hu, R. Bermejo-Deval, Y. Liu and J. A. Lercher, J. Catal., 2019, 370, 424–433 CrossRef CAS.
- H. Windeck, F. Berger and J. Sauer, Angew. Chem., 2023, 62, e202303204 CrossRef CAS PubMed.
- K. H. Chung and B. G. Park, J. Ind. Eng. Chem., 2009, 15, 388–392 CrossRef CAS.
- P. Ana and V. Valentin, Appl. Catal., A, 2020, 606, 117795 CrossRef.
- F. Berger, M. Rybicki and J. Sauer, J. Catal., 2021, 395, 117–128 CrossRef CAS.
- Z. Liu, J. Zhou, X. Tang, F. Liu, J. Yuan, G. Li, L. Huang, R. Krishna, K. Huang and A. Zheng, AIChE J., 2020, 66, e16269 CrossRef CAS.
- M. Dyballa, P. Becker, D. Trefz, E. Klemm, A. Fischer, H. Jakob and M. Hunger, Appl. Catal., A, 2016, 510, 233–243 CrossRef CAS.
- E. García-Hurtado, A. Rodríguez-Fernández, M. Moliner and C. Martínez, Catal. Sci. Technol., 2020, 10, 5648–5658 RSC.
- S. Gao, Z. Liu, S. Xu, A. Zheng, P. Wu, B. Li, X. Yuan, Y. Wei and Z. Liu, J. Catal., 2019, 377, 51–62 CrossRef CAS.
- J. Yuan, M. Gao, Z. Liu, X. Tang, Y. Tian, G. Ma, M. Ye and A. Zheng, Nat. Commun., 2023, 14, 1735 CrossRef CAS PubMed.
- C. H. Botchway, R. Tia, E. Adei, A. J. O'malley, N. Y. Dzade, C. Hernandez-Tamargo and N. H. de Leeuw, Catalysts, 2020, 10, 1342 CrossRef CAS.
- J. Duan, W. Chen, C. Wang, L. Wang, Z. Liu, X. Yi, W. Fang, H. Wang, H. Wei, S. Xu, Y. Yang, Q. Yang, Z. Bao, Z. Zhang, Q. Ren, H. Zhou, X. Qin, A. Zheng and F. S. Xiao, J. Am. Chem. Soc., 2022, 144, 14269–14277 CrossRef CAS PubMed.
- C. Wang, W. Fang, Z. Liu, L. Wang, Z. Liao, Y. Yang, H. Li, L. Liu, H. Zhou, X. Qin, S. Xu, X. Chu, Y. Wang, A. Zheng and F. S. Xiao, Nat. Nanotechnol., 2022, 17, 714–720 CrossRef CAS PubMed.
- L. B. McCusker, D. H. Olson and C. Baerlocher, Atlas of Zeolite Framework Types, Elsevier, Amsterdam, Netherlands, 2007 Search PubMed.
- J. Van Der Mynsbrugge, S. L. C. Moors, K. De Wispelaere and V. Van Speybroeck, ChemCatChem, 2014, 6, 1906–1918 CrossRef CAS.
- W. Loewenstein, Am. Mineral., 1954, 39, 92–96 CAS.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- T. Oie, G. M. Maggiora, R. E. Christoffersen and D. J. Duchamp, Int. J. Quantum Chem., 1981, 20, 1–47 CrossRef.
- A. Ghysels, S. L. C. Moors, K. Hemelsoet, K. De Wispelaere, M. Waroquier, G. Sastre and V. Van Speybroeck, J. Phys. Chem. C, 2015, 119, 23721–23734 CrossRef CAS.
- G. Sastre, Catal. Today, 2014, 226, 25–36 CrossRef CAS.
- K. Hahn, J. Kärger and V. Kukla, Phys. Rev. Lett., 1996, 76, 2762 CrossRef CAS PubMed.
- J. Yuan, Z. Liu, Y. Wu, J. Han, X. Tang, C. Li, W. Chen, X. Yi, J. Zhou, R. Krishna, G. Sastre and A. Zheng, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102097118 CrossRef CAS PubMed.
- Z. A. Alaithan, N. Harrison and G. Sastre, J. Phys. Chem. C, 2021, 125, 19200–19208 CrossRef CAS.
- K. Hahn and J. Kärger, J. Phys. Chem., 1996, 100, 316–326 CrossRef CAS.
- Z. Keyvanloo, A. Nakhaei Pour, F. Moosavi and S. M. Kamali Shahri, J. Mol. Graphics Modell., 2022, 110, 108048 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy01590d |
| This journal is © The Royal Society of Chemistry 2024 |