Diffusion mechanisms and preferential dynamics of promoter molecules in ZSM-5 zeolite

Abstract

The diffusion in ZSM-5 zeolite of methanol and of two series of promoters of the methanol to dimethyl ether reaction (linear methyl esters, benzaldehyde, 4-n-alkyl benzaldehydes) has been studied using classical molecular dynamics in the NVT ensemble. Whereas promoter diffusion coefficients decrease with increasing alkyl chain length in methyl esters, the aromatic aldehyde promoters all have similar diffusion coefficients. The lowest diffusion coefficient is that of benzaldehyde. All the promoters exhibit a preference for moving in the straight pore, a preference that is most pronounced for the 4-n-alkylbenzaldehydes and least for the longest aliphatic esters. A novel diffusion mechanism, a molecular ‘3-point turn’, is observed. This likely plays an important role in allowing the most potent promoters, with longer linear alkyl chains, to access all of the Brønsted acid reaction sites. The diffusion coefficient of methanol is larger than that of all the promoters. The more catalytically active aromatic aldehyde promoters limit methanol diffusion less than the aliphatic esters.

---

1 Introduction

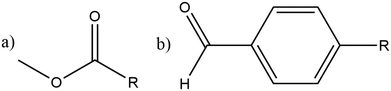
The utilisation of alternative feedstocks for everyday chemicals is of key industrial importance as we move towards net zero and beyond. Methanol derived from various carbon sources, such as CO₂, biomass, and biogas, is already of considerable economic interest.¹ The methanol-to-hydrocarbon (MTH) process is poised to offer a pathway to numerous commercially and industrially significant chemicals. The first step in the MTH process, the dehydration of methanol to dimethyl ether (DME), is of particular interest as DME is an important solvent and the starting material for many other products.

The methanol to DME reaction is promoted by the unique porous structure of zeolites, this provides a confinement effect that leads to transition state stabilisation.^2–6 This work focuses on the MFI framework type structure (commonly known as ZSM-5), shown in Fig. 1. This framework has orthorhombic symmetry (Pnma) within a large range of operating temperatures, and is composed of straight parallel pores (Fig. 1a) intersected by sinusoidal pores (Fig. 1b). These ordered pores provide large internal surface areas which leads to the transition state stabilising confinement effect. Addition of organic carbonyl compounds further promotes the methanol to DME reaction allowing for use of milder reaction conditions; this reduces the risk of catalyst deactivation and side reactions in the hydrocarbon pool mechanism.⁷ The aliphatic esters and aromatic aldehydes investigated here have shown significant promotional effects (increasing catalytic activity by well over an order of magnitude) down to concentrations as low as 1 ppm in methanol.^7–9

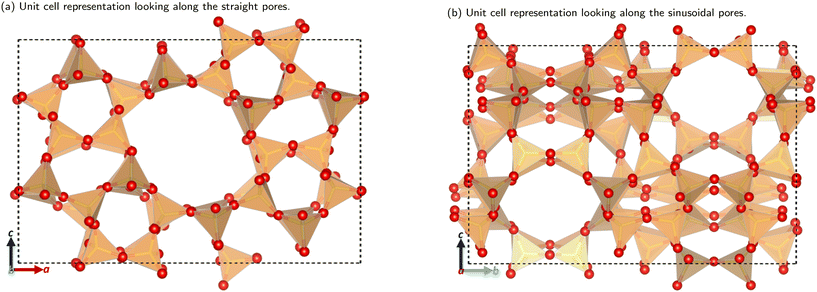Fig. 1 The unit cell structure of the MFI framework. Colour key: orange tetrahedra = SiO₄; red atom = O. Figures made using VESTA.¹⁰

Promoter potency was found to increase markedly with alkyl group chain length, for both linear aliphatic methyl esters, and 4-n-alkylbenzaldehydes. In situ FT-IR studies showed that the potent methyl n-hexanoate and very potent 4-n-pentylbenzaldedhyde promoters are able to fully titrate all the Brønsted acid (BA) sites in H-ZSM-5, indicating that they can readily navigate around the zeolite microporous network.^7,9 For the aliphatic ester promoters, kinetic, spectroscopic and molecular modelling studies are consistent with DME being formed via a bimolecular reaction between methanol and a methyl ester interacting with a Brønsted acid site. In the case of the aromatic aldehyde promoters the reaction was found to proceed via the formation of a methyl oxonium species formed from methanol and the aldehyde interacting with a Brønsted acid site, which reacts in a second step with another methanol to form DME.

Our previous work employed a set of multilevel quantum calculations to investigate the action of aliphatic ester promoters in DME formation from methanol dehydration within H-ZSM-5.¹¹ Our results showed how the promoters provide a more favourable route to DME formation. The promoters' adsorption to the reaction site is one crucial factor. Previously, we did not consider the role of diffusion; in the lead-up to the reaction, molecules must navigate the zeolite pores to access reaction sites and the reaction site becomes accessible for further reactions after product molecules diffuse away. At elevated temperatures the reaction potentially becomes diffusion limited, if the rate-limiting step shifts to diffusion of reactants in and products out of the reaction site. Many factors affect the diffusion of molecules in microporous solids, and molecular dynamics (MD) simulations have long been used to elucidate the dynamics of organic molecules in porous systems. Key to this is the flexibility of both the organic and inorganic components.¹² It is not possible to know a priori how zeolite flexibility will affect diffusion, so results with a fixed framework cannot be extrapolated to one which is flexible.¹³ Compounding this, recent work by Xu et al. has demonstrated flaws in the way some MD codes calculate temperatures and apply degrees of freedom for systems with rigid or frozen particles.¹⁴ For these reasons, in this paper we opt for simulations of flexible molecules within a flexible zeolite.

Molecules can follow different diffusion pathways in zeolites depending on their size and shape.^15–17 In the present work, we examine the diffusion through the different pores within ZSM-5 of methanol and the larger organic promoter molecules shown in Scheme 1. We investigate the spatial distribution of the promoter molecules. Diffusion coefficients are estimated and how these change when promoter and methanol are present together are examined. Novel behaviour, a molecular ‘3-point turn’, is observed which we suggest enhances the manoeuvrability of the promoters and their navigation through the three dimensional zeolite network, allowing greater access to reaction sites.

Scheme 1 a) Aliphatic esters, b) 4-n-alkylbenzaldehyde (R = H, C_nH_2n+1; n = 1–5).

2 Methodology

The MD simulations presented here were carried out with the open-source MD engine LAMMPS, utilising its Størmer–Verlet time integration algorithm.^18–21 The ZSM-5 unit cell was obtained from the Database of Disordered Zeolite Structures, and a 2 × 2 × 2 supercell was constructed, containing 768 Si atoms and 1536 O atoms.²² All simulations were performed with periodic boundary conditions in the canonical ensemble (NVT) at 423; lattice parameters can be found in the ESI.† No Brønsted acid sites were present in the zeolite simulated here. We used a Nosé–Hoover thermostat with a chain length of 3 and a damping parameter of 200 fs. Tests using the Langevin thermostat showed it was unsuitable; these results can be found in the ESI.† The well-known inter-atomic rigid-ion potentials for zeolites of Catlow et al. were combined with the OPLS force field.^23–25 Interactions between organic molecules and zeolites were modelled with Lennard-Jones potentials. The OPLS parameters were obtained from LigParGen.²⁶ This combination has been used successfully in previous work on adsorption of organic molecules on clay surfaces.²⁷ The set of force field parameters used here can be found in the ESI.†

2.1 Simulations without methanol

Promoter molecules were placed at the intersection of the straight and sinusoidal pores in the ZSM-5 structure. One promoter molecule was placed in each primitive unit cell, leading to 8 molecules in the simulation cell. Equilibration was then carried out at 10 K for 2 ns, the temperature was then increased to 423 K over the next 2 ns. A new set of velocities was assessed, and equilibration continued at 423 K for a further 2 ns. Placement of large molecules into the zeolite structure can lead to unphysically short interatomic separations with high potential energy and thus this careful equilibration process is required. A timestep of 0.5 fs was used for aliphatic ester promoters and 1 fs for aromatic aldehyde promoters; a 0.5 fs timestep was trialled for aromatic aldehydes but was found to be too computationally expensive and did not provide simulations long enough, in the time frame of this study, for appropriate diffusion statistics. Ten production runs were performed for each promoter, during which the atomic positions was recorded every 2000 steps. These production simulations were run for sufficient time to produce a linear dependence of the mean-squared displacement (MSD) on time; this was 10 ns for the linear aliphatic esters and 100 ns for the aromatic aldehydes, as shown in the ESI.†

2.2 Simulations with methanol and promoters

Taking well-equilibrated structures from the promoter simulations, two methanol molecules were added per promoter molecule, and the simulations were then equilibrated at 423 K for 2 ns. This loading was chosen to mimic the starting reaction conditions for the methanol to DME reaction.

2.3 Calculation of diffusion coefficients

Diffusion coefficients were computed from simulation trajectories using the Python package kinisi-1.0.0.²⁸ This package implements a Bayesian regression scheme that obtains a statistically efficient estimate of the diffusion coefficient and predicts associated uncertainties.²⁹ This approach parameterises multivariate normal distributions that describe the sets of MSDs obtained from the data. These sets average over all similar molecules across similar production runs: leading to 80 molecules in the promoter sets and 160 molecules in the methanol sets. Markov-chain Monte Carlo sampling is then used to sample the posterior distribution of the self-diffusion coefficient, D* from the Einstein relation:

〈r²〉 = 2nD*Δt, (1)

where 〈r²〉 is the ensemble mean-squared displacement, n is the dimensionality (1 for a, b, & c diffusion and 3 for combined abc diffusion), and Δt is the time interval. The ballistic regime at small values of Δt is unsuitable for calculating diffusion coefficients using the Einstein relation. Diffusion coefficients are therefore calculated from the linear region, where the MSD is in the diffusive regime. MSD plots can be found in the ESI.†

3 Results and discussion

3.1 Promoter diffusion

3.1.1 Aliphatic ester promoters. The calculated self-diffusion coefficients of the aliphatic ester promoters are shown in Fig. 2a. The diffusion coefficients decrease as the alkyl chain length increases. The activation enthalpies of diffusion increase with chain length (as do enthalpies of adsorption¹¹) due to increased dispersion interactions with the zeolite pore walls.

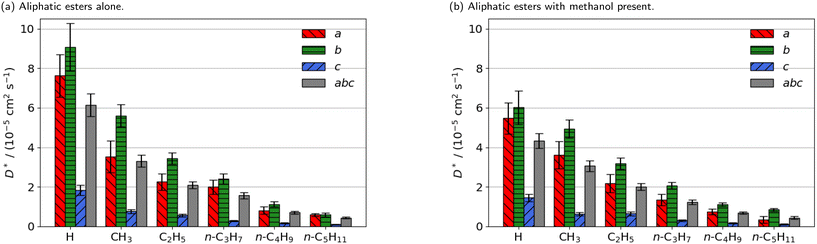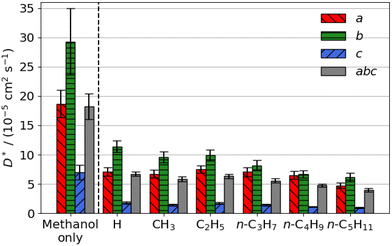
Fig. 2 Estimated self-diffusion coefficients (D*) of methyl aliphatic ester promoters (of the form RCO₂Me, where R is given on the x axis) along the a, b, c directions shown in Fig. 1. Error bars show the standard deviation in the diffusion coefficient. Diffusion coefficient of methanol alone is 18.2 × 10⁻⁵ cm² s⁻¹.

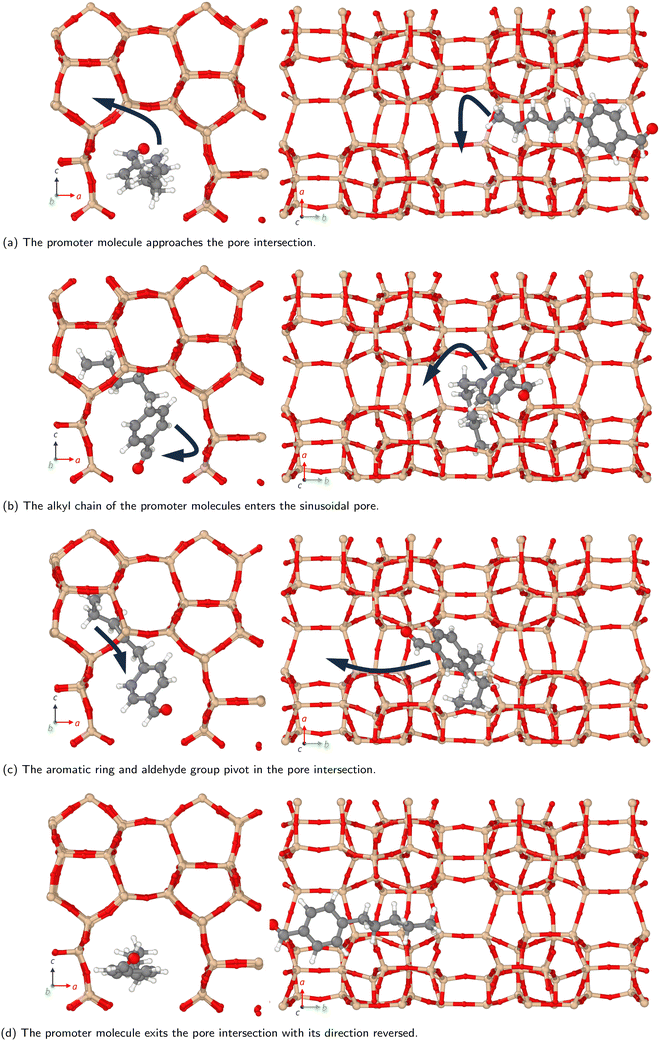
Smaller promoters exhibit a preference for diffusion through the straight pore, consistent with greater self-diffusion coefficients in the straight pores (b direction) than the sinusoidal pores (a direction) (Fig. 2a). This preference decreases as the alkyl chain length increases, and completely disappears for methyl n-hexanoate for which the diffusion coefficients through each type of pore are comparable.

Previous interactive molecular dynamics in virtual reality studies identified a diffusion bottleneck for methyl n-hexanoate in ZSM-5, created by a 10-membered ring in the straight pore.³¹ Furthermore, Cnudde et al.^32,33 demonstrated that diffusion of longer chain hydrocarbons through similar rings is more hindered than short chains, due to reduced conformational freedom. Consequently, this bottleneck hinders the diffusion of the longer alkyl chain promoters to a greater extent, reducing their preference for diffusion through the straight pore, and reducing their overall rate of diffusion within the 3D pore network.

The estimated self-diffusion coefficients of the aliphatic ester promoters with methanol present are depicted in Fig. 2b. These data show trends identical to those discussed above, in that longer chain lengths result in decreased self-diffusion coefficients. When the promoter is of comparable size to methanol, such as methyl formate, competitive diffusion reduces the total diffusion of both species. Where promoter and methanol differ substantially in size (e.g., methyl n-hexanoate), there is an increase in the preference for diffusion of the promoter in the straight pores (b direction). Methanol thus influences the diffusion pathways of the large aliphatic promoters, mitigating the effects of the bottleneck observed in the straight pore.

3.1.2 Aromatic aldehyde promoters. Unlike the aliphatic ester promoters above, the diffusion coefficients of the 4-n-alkylbenzaldehydes are broadly similar (Fig. 3a), allowing for the estimated uncertainties. Here, increasing alkyl chain length, in the 4 position of the benzene ring, does not lead to a significant change in the total diffusion coefficient. In contrast, smaller and lighter benzaldehyde has a lower diffusion coefficient of all the promoters studied. In all cases, the diffusion coefficient is greater along the straight pores (b direction).

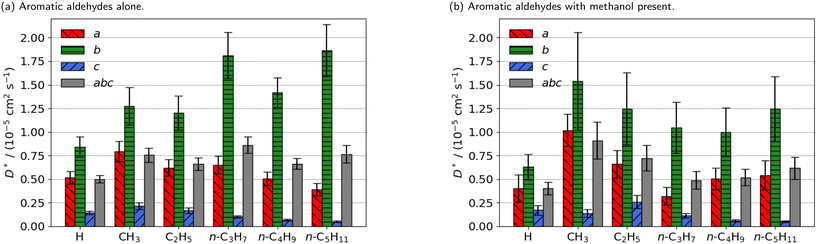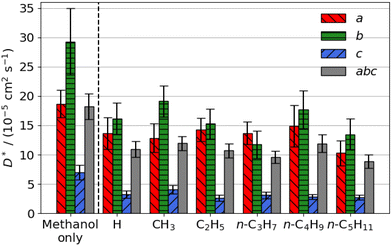
Fig. 3 Estimated self-diffusion coefficients (D*) of aromatic aldehyde promoters (of the form RC₆H₄CHO, where R is given on the x axis) along the a, b, c directions shown in Fig. 1. Error bars show the standard deviation in the diffusion coefficient. Diffusion coefficient of methanol alone is 18.2 × 10⁻⁵ cm² s⁻¹.

The free energy barrier of diffusion depends both on the enthalpy of the transition state and the probability that the molecules are in an appropriate location with an appropriate velocity towards the bottleneck (see above). Spatial probability distributions for the molecular centre of mass (COM) of benzaldehyde and 4-n-pentylbenzaldehyde can be seen in Fig. 4, probability distributions on the other axes are in the ESI.† In all cases the highest probability COM position is in the pore intersections. With increasing chain length in the 4-n-alkylbenzaldehydes, there is an increasing tendency to lie in the straight pore (b direction) and around the identified bottleneck. We suggest there is a smaller probability of benzaldehyde adopting the orientation need to pass through the bottleneck, in the straight pore, than for other aromatic aldehyde promoters, due to the greater rotational freedom it experiences in the intersection. The presence of the alkyl chains in the 4-n-alkylbenzaldehydes limits the promoters' ability to rotate in the intersection, analogous to toluene and p-xylene in ZSM-5.^34–36

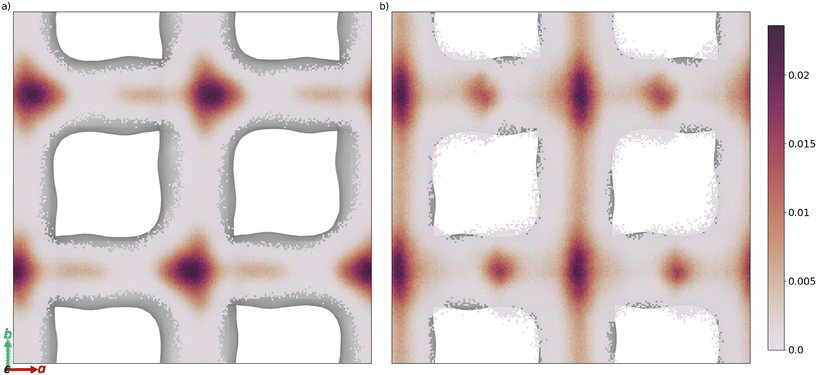Fig. 4 Spatial probability distribution of the molecular centre of mass, in a and b, of a) benzaldehyde and b) 4-n-pentylbenzaldehyde, overlaid on the internal surface of ZSM-5 (Ovito was used to produce this surface with the Gaussian density method³⁰).

There is no significant reduction in aromatic aldehyde promoter diffusion on addition of methanol (Fig. 3b). This trend aligns with the larger aliphatic ester promoters, where non-competitive diffusion is present. We observe that those promoters that have the highest catalytic efficiency exhibit non-competitive diffusion.

3.1.3 3-Point turn. An interesting feature we have seen when analysing our MD simulations is the occasional reversal of the direction of motion by the promoters performing a ‘3-point turn’ (a.k.a. ‘K-’, ‘Y-’ or ‘broken u-’ turn). Most often, this is precipitated at the pore intersection by the alkyl chain moving from the straight pore into the sinusoidal pore. This provides room for the ester group or aromatic ring to manoeuvre in the intersection and subsequently exit in the reverse direction. A representation of one of these events can be seen in Fig. 5. We have previously seen this behaviour in less thermodynamically rigorous interactive molecular dynamics simulations in virtual reality, in which the user applies an external force to the promoter molecule.³¹ This process takes many forms from partial turnarounds to much longer manoeuvres involving many steps; a video of one of these processes can be found in the ESI.† These changes of conformation and orientation allow the promoters to navigate around the zeolite and reach all the Brønsted acid reaction sites. These manoeuvres likely play an important role in the efficacy of the most potent promoters (those with long linear alkyl chains).

Fig. 5 Snapshots of a 4-n-pentylbenzaldehyde molecule performing a ‘3-point turn’ in a pore intersection.

3.2 Methanol diffusion

The estimated self-diffusion coefficients of methanol with an aliphatic ester or aromatic aldehyde promoter present are shown in Fig. 6 and 7. Methanol diffuses faster than any of the promoters; aliphatic ester and aromatic aldehyde promoters substantially reduce its diffusion coefficient by an average of 70% and 41%, respectively. Methanol diffusion is reduced in the straight pores (b direction) more than in the sinusoidal (a direction).

Fig. 6 Estimated self-diffusion coefficients (D*) of methanol with methyl aliphatic ester promoters (of the form RCO₂Me, where R is given on the x axis) present. Error bars show the standard deviation in the diffusion coefficient.

Fig. 7 Estimated self-diffusion coefficients (D*) of methanol with aromatic aldehyde promoters (of the form RC₆H₄CHO, where R is given on the x axis) present. Error bars show the standard deviation in the diffusion coefficient.

4 Conclusions

The diffusion of two series of promoters, linear methyl esters and 4-n-alkylbenzaldehydes, and of methanol in ZSM-5 have been studied using molecular dynamics. Promoter diffusion decreases with increasing alkyl chain length in methyl esters. The much slower diffusing aromatic aldehydes do not show this trend, instead having similar diffusion coefficients irrespective of alkyl chain length. Benzaldehyde itself has the lowest diffusion coefficient of any promoter studied. All studied promoters exhibit a preference for diffusion in the straight pore, which is more pronounced for 4-n-alkylbenzaldehydes. We observed a behaviour previously only seen in approximate sampling of rare events in interactive molecular dynamics in virtual reality – a molecular ‘3-point turn’. The diffusion coefficient of methanol is always greater than that of the promoters; the more catalytically active aromatic aldehyde promoters limit methanol diffusion less than the aliphatic ester promoters. This could be critical at low methanol partial pressure, where diffusion of methanol to reaction sites may start to become a limiting factor.

In future work it will be worthwhile to consider a wider range of promoters, and different loadings and clustering of methanol (see e.g., Woodward et al.³⁷) and promoters. Extension to simulations incorporating Brønsted acid sites, will require ab initio molecular dynamics.³⁸ We believe the methods here can be applied more widely to different reactions and different zeolites and it will be interesting to see what general principles and trends emerge.

Author contributions

J. D.: investigation; formal analysis; methodology; software; visualization; writing – original draft. J. C.-L.: investigation; formal analysis; writing – original draft. A. R. M.: software; methodology; supervision; writing – review & editing. F. J.: supervision; writing – review & editing. C. B.: conceptualization; funding acquisition; supervision; writing – review & editing. G. J. S.: conceptualization; funding acquisition; writing – review & editing. A. J. M.: conceptualization; funding acquisition; project administration; writing – review & editing. N. L. A.: conceptualization; funding acquisition; project administration; writing – review & editing.

Conflicts of interest

The promoters examined here are the subjects of a number of patent applications, some of which have been granted.^39–41

Acknowledgements

BP plc is thanked for the financial support of J. D. and J. C.-L. through industrial CASE (ICASE) studentships in partnership with the Engineering and Physical Sciences Research Council (EPSRC). ICASE grant reference EP/T51763X/1.

References

1. J. Xie and U. Olsbye, Chem. Rev., 2023, 123, 11775–11816.
2. E. G. Derouane, J. Mol. Catal. A: Chem., 1998, 134, 29–45.
3. A. Bhan and E. Iglesia, Acc. Chem. Res., 2008, 41, 559–567.
4. R. Gounder and E. Iglesia, Acc. Chem. Res., 2012, 45, 229–238.
5. A. J. Jones, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2014, 118, 17787–17800.
6. A. Bhan, A. D. Allian, G. J. Sunley, D. J. Law and E. Iglesia, J. Am. Chem. Soc., 2007, 129, 4919–4924.
7. Z. Yang, B. J. Dennis-Smither, C. Buda, A. Easey, F. Jackson, G. A. Price, N. Sainty, X. Tan, Z. Xu and G. J. Sunley, Catal. Sci. Technol., 2023, 13, 3590–3605.
8. B. J. Dennis-Smither, Z. Yang, C. Buda, X. Liu, N. Sainty, X. Tan and G. J. Sunley, Chem. Commun., 2019, 55, 13804–13807.
9. Z. Yang, B. J. Dennis-Smither, Z. Xu, Z. Zhao, M. Guo, N. Sainty, G. Hou, X. Liu and G. J. Sunley, Chemistry, 2023, 5, 511–525.
10. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
11. J. Crossley-Lewis, J. Dunn, I. F. Hickman, F. Jackson, G. Sunley, C. Buda, A. J. Mulholland and N. L. Allan, Phys. Chem. Chem. Phys., 2024 10.1039/D3CP05987A.
12. S. Ghojavand, E. Dib and S. Mintova, Chem. Sci., 2023, 14, 12430–12446.
13. J. Toda, A. Corma, R. H. Abudawoud, M. S. Elanany, I. M. Al-Zahrani and G. Sastre, Mol. Simul., 2015, 41, 1438–1448.
14. H. Xu, R. Cabriolu and B. Smit, J. Chem. Theory Comput., 2022, 18, 2826–2835.
15. L. A. Clark, T. Y. George and R. Q. Snurr, Phys. Rev. Lett., 2000, 84, 2893.
16. Z. Chen, L. Zhang, Y. Yu, D. Liu, N. Fang, Y. Liu and M. He, Microporous Mesoporous Mater., 2022, 332, 111715.
17. R. Harish, D. Karevski and G. Schütz, J. Catal., 2008, 253, 191–199.
18. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
19. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017.
20. M. E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford University Press, 2023.
21. D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, Inc., USA, 3rd edn, 2023.
22. H. G. Ch. Baerlocher, L. B. McCusker and B. Marler, Database of Disordered Zeolite Structures, http://www.iza-structure.org/databases/, 23-June-2022, Accessed: 23-November-23.
23. D. R. Collins and C. R. A. Catlow, Am. Mineral., 1992, 77, 1172–1181.
24. W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670.
25. L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870.
26. L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336.
27. M. R. Warne, N. L. Allan and T. Cosgrove, Phys. Chem. Chem. Phys., 2000, 2, 3663–3668.
28. A. R. McCluskey, A. G. Squires, J. Dunn, S. W. Coles and B. J. Morgan, J. Open Source Softw., 2024, 9, 5984.
29. A. R. McCluskey, S. W. Coles and B. J. Morgan, Accurate Estimation of Diffusion Coefficients and their Uncertainties from Computer Simulation, arXiv, 2023, preprint, arXiv:2305.18244 [cond-mat.stat-mech],  DOI:10.48550/arXiv.2305.18244.
30. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012.
31. J. Crossley-Lewis, J. Dunn, C. Buda, G. J. Sunley, A. M. Elena, I. T. Todorov, C. W. Yong, D. R. Glowacki, A. J. Mulholland and N. L. Allan, J. Mol. Graphics Modell., 2023, 125, 108606.
32. P. Cnudde, R. Demuynck, S. Vandenbrande, M. Waroquier, G. Sastre and V. V. Speybroeck, J. Am. Chem. Soc., 2020, 142, 6007–6017.
33. P. Cnudde, E. A. Redekop, W. Dai, N. G. Porcaro, M. Waroquier, S. Bordiga, M. Hunger, L. Li, U. Olsbye and V. Van Speybroeck, Angew. Chem., 2021, 133, 10104–10110.
34. O. Gobin, S. Reitmeier, A. Jentys and J. Lercher, Microporous Mesoporous Mater., 2009, 125, 3–10.
35. K. Margeta and A. Farkaš, Zeolites, IntechOpen, Rijeka, 2020.
36. C. R. A. Catlow, R. A. V. Santen and B. J. Smit, Computer Modelling of Microporous Materials, Elsevier, Amsterdam, 1st edn, 2004.
37. C.-L. M. Woodward, A. J. Porter, K. S. Morton and A. J. O'Malley, Catal. Commun., 2022, 164, 106415.
38. S. A. F. Nastase, P. Cnudde, L. Vanduyfhuys, K. De Wispelaere, V. Van Speybroeck, C. R. A. Catlow and A. J. Logsdail, ACS Catal., 2020, 10, 8904–8915.
39. B. J. Dennis-Smither, J. G. Sunley and Z. Yang, WO2019037764, 2019, BP P.L.C. and BP China Holding Ltd.
40. B. J. Dennis-Smither, N. Sainty and J. G. Sunley, WO2019037768, 2019, BP P.L.C. and BP China Holding Ltd.
41. B. J. Dennis-Smither, J. G. Sunley and Z. Yang, WO2020168539, 2020, BP P.L.C. and BP China Holding Ltd.

---

Footnote

† Electronic supplementary information (ESI) available: Zeolite lattice parameters, force field parameters, mean squared displacement plots, and spatial probability distribution. See DOI: https://doi.org/10.1039/d4cy00506f

---