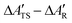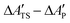Open Access Article
Open Access ArticleMachine learning thermodynamic perturbation theory offers accurate activation free energies at the RPA level for alkene isomerization in zeolites†
Jérôme
Rey
a,
Michael
Badawi
 *ab,
Dario
Rocca
a,
Céline
Chizallet
*ab,
Dario
Rocca
a,
Céline
Chizallet
 *c and
Tomáš
Bučko
*c and
Tomáš
Bučko
 *de
*de
aLaboratoire de Physique et Chimie Théoriques (LPCT), CNRS, Université de Lorraine, F-54000 Nancy, France
bLaboratoire Lorrain de Chimie Moléculaire (L2CM), CNRS, Université de Lorraine, F-54000 Nancy, France. E-mail: michael.badawi@univ-lorraine.fr
cIFP Energies Nouvelles, Rond-Point de l'Échangeur de Solaize, BP3, 69360 Solaize, France. E-mail: celine.chizallet@ifpen.fr
dDepartment of Physical and Theoretical Chemistry, Faculty of Natural Sciences, Comenius University Bratislava, Ilkovičova 6, SK-84215 Bratislava, Slovakia
eInstitute of Inorganic Chemistry, Slovak Academy of Sciences, Dúbravská Cesta 9, SK-84236 Bratislava, Slovakia. E-mail: tomas.bucko@uniba.sk
First published on 23rd July 2024
Abstract
The determination of accurate free energy barriers for reactions catalyzed by proton-exchanged zeolites by quantum chemistry approaches is a challenge. While ab initio molecular dynamics is often required to sample correctly the various states described by the system, the level of theory also has a crucial impact. In the present work, we report the determination of accurate barriers for a type B isomerization of a monobranched C7 alkene (4-methyl-hex-1-ene) into a dibranched tertiary cation inside a protonated chabazite zeolite. This is done by using the Machine Learning Thermodynamic Perturbation Theory (MLPT) at the Random Phase Approximation (RPA) level, on the basis of blue-moon sampling dynamic data obtained at the Generalized Gradient Approximation (GGA) level (PBE+D2). The comparison of PBE+D2 and RPA profiles shows that the former overstabilizes cationic intermediates with respect to neutral ones. The transition state of the isomerization is a non-classical edge protonated cyclopropane, the stabilization of which is lower than that of the π-complex when PBE+D2 is replaced by RPA, but higher than that of the classical tertiary carbenium. Consequently, the backward isomerization barrier is decreased. Applying the MLPT approach to recompute the free energy barriers with various dispersion correction schemes to the PBE energies shows that none of the schemes is sufficient to improve both the forward and backward barriers with respect to the RPA reference. These data complement previously determined alkene cracking barriers [Rey et al., Angew. Chem., Int. Ed., 2024, 63, e202312392], thanks to which it is possible to compare the presently determined barriers with reference experimental data [Schweitzer et al., ACS Catal., 2022, 12, 1068–1081]. The agreement with experiments is significantly improved at the RPA with respect to GGA. Chemical accuracy is approached (maximum deviation of 6.4 kJ mol−1), opening the door to predictive kinetic modelling starting from first principles approaches.
1 Introduction
The determination of accurate free energy barriers is a key challenge in computational catalysis. Indeed, as it can be deduced from the Eyring equation,1 errors made on free energy barriers translate exponentially on the rate constant, itself being directly linked to the rate of elementary steps through rate equations. Reaching chemical accuracy, i.e., predicting barriers with a deviation with respect to experiments lower than 4.2 kJ mol−1, is thus more than ever needed. For example, at a reaction temperature of 500 K, the chemical accuracy implies that the ratio of experimental versus computed rate constants must not exceed 2.8.Achieving this goal requires improving both the level of theory and the quality of the sampling of states to quantify the stability of reactants, transition states and products. In the current common practice, which is determined by the available computer power, performing ab initio molecular dynamics (AIMD) for simulation cells relevant for the modelling of heterogeneous catalysts at higher levels of theory than density functional theory (DFT) is not feasible. In the present study, our goal is to quantify accurate barriers making use of the Random Phase Approximation2,3 (RPA) level. RPA was indeed shown to perform remarkably well for a series of properties of solids such as lattice parameters,4,5 for adsorption energies of various molecules on surface (including metals6,7 and zeolites8,9), and for barriers of simple reactions.10–13 Very recently, we quantified free energy barriers for a set of zeolite catalyzed reactions14 at the RPA level combined to AIMD, thanks to Machine Learning Thermodynamic Perturbation Theory (MLPT).15–18 The breakthrough result of this study is that it demonstrated that it is possible to perform sampling of realistic systems at a very high level of theory in a reasonable time (a few weeks), which is just a small fraction of the estimated computational time that would be needed to perform AIMD at the RPA level of the same length in a naive way (a millennium). An unprecedented accuracy was reached when comparing the computed barriers with experimental ones, extracted from a complex reaction network thanks to kinetic modelling.19
Zeolite-catalyzed reactions play a major role in a large array of mature and developing catalytic processes, belonging to the fields of refining, petrochemistry, pollution abatement, biomass conversion and plastic recycling, among others.20–29 Understanding the mechanisms at play and being able to accurately predict the rate constants of important elementary steps for such reactions is thus highly important.30 For a large array of zeolite-catalyzed reactions, reliance on high levels of theory31–34 (beyond DFT) and explicit sampling of configuration space via AIMD35–41 has proven essential to properly capture the nature and stability of intermediates. As mentioned above, effective combination of these two requirements became achievable only very recently,14,42,43 thanks to development of machine learning approaches.
Many of the previously cited works address hydrocarbon transformation reactions on Brønsted acidic zeolite, in which main active sites are bridging Si–(OH)–Al groups. The reactions involve both neutral (adsorbed alkanes and alkenes) and ionic (carbonium or carbenium ions, obtained by protonation of the hydrocarbon molecules) species. The variation of the free energy estimate of these species as a function of the level of theory (GGA versus higher level methods) appeared to depend strongly on the charge state of these species.31,34,42,44–46 It is crucial to quantify the intensity of this effect, also accounting for the impact of the charge state on the dynamic behavior of the confined intermediates. This requirement holds true for the family of reactions that we have considered in our previous work,14 namely the isomerization and cracking of alkenes containing seven carbon atoms.
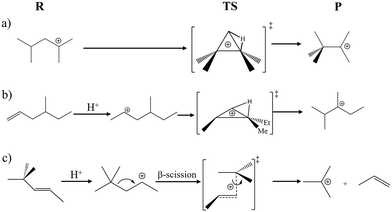
By the MLPT approach, we have previously addressed type B isomerization reactions (which induce a change in the branching degree of the hydrocarbon skeleton) linking di- and tri-branched tertiary carbenium ions, and a type B1 cracking reaction transforming a secondary cation into a tertiary carbenium plus propene (Fig. 1a and c). In the present work, we extend this analysis by considering a type B isomerization of a monobranched alkene (4-methyl-hex-1-ene) into a dibranched tertiary cation, passing through a secondary carbenium ion (Fig. 1b). Previous AIMD study conducted at the PBE+D2 level showed that the latter was only an elusive reaction intermediate.35 This additional case study is relevant in a practical context, as the bifunctional hydroisomerization and cracking of linear alkanes pass through the gradual increase of the degree of branching of intermediates (alkenes and carbenium ions, obtained after dehydrogenation of alkanes on a metallic phase).19,30,47 We show in the present work that MLPT at the RPA level is a precious tool to approach chemical accuracy, whereas adjusting the dispersion correction scheme brought to the PBE energies does not lead to substantial improvement. A fundamental interest can also be found in the combination of neutral and ionic intermediate states in a same isomerization reaction, whereas in our previous work,14 a neutral intermediate was invoked as the reactant of a cracking reaction. Thanks to MLPT, a better rationalization can be made between the level of theory and the stability of important species in the reaction network, taking into account their dynamic behavior.
2 Methods
All the simulations have been performed using the periodic DFT program VASP,48–50 utilizing the projector-augmented wave (PAW) method implemented by Blöchl and Kresse et al.51,52 The Kohn–Sham equations were solved self-consistently with a convergence criterion of 10−7 eV per cell. The basis set with plane waves with kinetic energy of up to 400 eV was used and the integrations over the Brillouin zone were realized using a single k-point at the position Γ. A Gaussian smearing with a smearing parameter of 0.05 eV was applied. The simulation cell used to represent the chabazite structure is shown in Fig. 2. The proton initially lies onto the framework oxygen atom O1, which is, according to experiment,53 one of the two most populated proton sittings in CHA.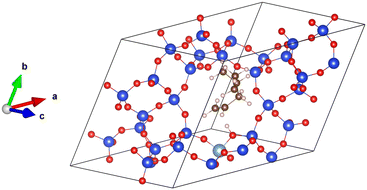 | ||
| Fig. 2 The supercell of acid chabazite with the π-complex, reactant for the isomerization reaction. Color code: Si in blue, O in red, Al in light blue, C in brown, H in white. | ||
The MLPT calculations were performed using the NVT Born–Oppenheimer AIMD free energy calculations at 500 K (Andersen thermostat, collision frequency per atom of 0.01 fs−1) at the PBE54 level with D2 (ref. 55) dispersion correction described in our previous work.36 In the following, we shall refer to the PBE+D2 method used to produce the AIMD data as the production method. The free energy of activation (ΔA‡) was determined thanks to simulations in the Blue Moon ensemble,56,57 as reported in ref. 35. A reaction coordinate based on distances between relevant atoms (C and H from the hydrocarbon moiety, H and O from the zeolite acid site) was chosen and shown to lead to reliable results. In the present work, using the computed free energy of activation and ensembles of reactant and transition state structures obtained with the production method, the free energies of activation at various target method levels (ΔÇ), involving PBE+D3(0) and PBE+D3(BJ),58,59 PBE+D4,60–62 PBE+dDsC,63 PBE+TS,64,65 PBE+TS/HI,66,67 PBE+MBD,68–70 PBE+MBD/FI,71 and RPA,2,3,72–74 were determined via
| ΔÇ = ΔA‡ + ΔATS − ΔAR, | (1) |
ΔATS = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp[−ΔV(q)/kBT]〉ξ* ln〈exp[−ΔV(q)/kBT]〉ξ* | (2) |
ΔAR = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp[−ΔV(q)/kBT]〉, ln〈exp[−ΔV(q)/kBT]〉, | (3) |
As an auxiliary quantity, the internal energy of activation can be defined as follows:15,57
| ΔŨ‡ = ŨTS − ŨR, | (4) |
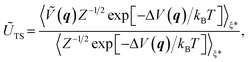 | (5) |
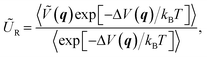 | (6) |
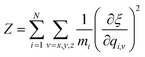 with N and mi being the number of atoms in the system and the mass of an atom i.
with N and mi being the number of atoms in the system and the mass of an atom i.
In order to compute the terms ΔAi and Ũi, up to 225 configurations from production method AIMD of the state i were selected and the target method potential energies were computed in single point calculations. The differences ΔV(q) were then determined using the production method energies available from AIMD and these data were employed to train a Δ-ML model that was subsequently used to predict ΔV(q) for a representative ensemble of configurations of a state i (every 10th point of the original production method trajectory). As in our previous work,14 the kernel ridge regression75 with the REMatch kernel76 and the SOAP (smooth overlap of atomic positions) descriptors77 were used for this purpose. Compared to other ML-based methods used to study chemical reactions, our approach has advantage that it does not require building a global model for whole reaction process but, instead, it uses two separate models specifically trained for R and TS.
The results for ΔATS and ΔAR obtained as described above can be affected by the systematic error due to imperfect Δ-ML model. As shown in ref. 16, this source of error can be significantly reduced by applying the correction:
| ΔAi ← ΔAi + Δε | (7) |
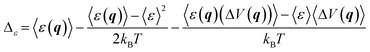 | (8) |
Finally, let us remark that if the ΔATS and ΔAR terms are determined using a Δ-ML model based on the same method and values of hyperparameters, which is the case in this study, the corresponding Δε values are likely to take very similar values and, consequently, their contribution to ΔÇ determined viaeqn (1) is likely to vanish. Indeed, ΔÇ was shown16,79 to converge much faster than the individual ΔATS and ΔAR terms.
3 Results and discussion
3.1 Convergence of the MLPT results
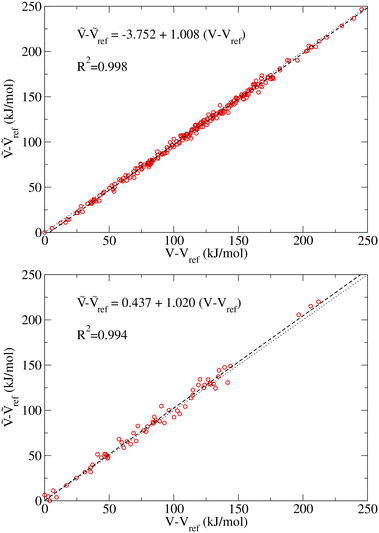
In this section we examine the convergence of the ΔAR, ΔATS, and ΔÇ − ΔA‡ = ΔATS − ΔAR terms for the forward reaction mode with respect to the training set size used in the MLPT calculations. As a demonstration example, PBE+dDsC target method is used but similar trends are observed also for other methods considered here. For both states, R and TS, 225 configurations were first selected from production parts of the MD-generated trajectories in such a way that their separation was 400 MD steps (i.e., more than assumed correlation time of ∼100 fs). Out of these configurations, Ntrain = 10, 25, 62, 113, and 225 structures were used as a training and remaining 225-Ntrain as a correction set for calculation of Δεviaeqn (8). Alternatively, the LOO strategy described in Sec. 2 was applied using the training set only.The numerical results obtained for the ΔAR, ΔATS, and ΔÇ terms are listed in Table 1. As evident from the data, the uncorrected values show very rapid convergence with respect to the training set size, and even the model prepared with Ntrain = 10 yields result for ΔÇ − ΔA‡ that is within 1 kJ mol−1 identical to our best estimate obtained with Ntrain = 225. Such an excellent convergence is possible because of the strong linear correlation between the potential energies of the target and production methods, which can be demonstrated for all target methods considered in this work (see Fig. 3).
| Quantity | Correction | N train | ||||
|---|---|---|---|---|---|---|
| 10 | 25 | 62 | 113 | 225 | ||
| ΔAR | None | −44.38 | −44.18 | −43.58 | −43.48 | −43.62 |
| 225-Ntrain | −43.62 | −43.53 | −43.66 | −43.72 | — | |
| LOO | −45.96 | −44.74 | −43.86 | −43.62 | −43.70 | |
| ΔATS | None | −39.52 | −39.17 | −39.57 | −39.70 | −39.74 |
| 225-Ntrain | −40.22 | −40.02 | −39.90 | −39.99 | — | |
| LOO | −40.36 | −39.69 | −39.84 | −39.87 | −39.81 | |
| ΔÇ − ΔA‡ | None | 4.86 | 5.01 | 4.01 | 3.77 | 3.88 |
| 225-Ntrain | 3.41 | 3.51 | 3.76 | 3.72 | — | |
| LOO | 5.60 | 5.05 | 4.02 | 3.75 | 3.89 | |
Despite this strong correlation, the variance in ΔV(q) is far from being negligible - if this were the case, the calculation of ΔÇ − ΔA‡ would be trivial, namely ΔÇ − ΔA‡ = ΔV(qi) for arbitrarily chosen qi. In the case of the 225 configurations reactant state, for instance, ΔV(q) varies between −46.88 and −34.61 kJ mol−1. Since a similar variance is observed also in the TS data (here ΔV(q) ranges between −48.84 and −27.98 kJ mol−1), the uncertainty in prediction of ΔÇ − ΔA‡ made using a randomly selected single R and TS configurations would be much greater than the ΔÇ − ΔA‡ itself (−3.86 kJ mol−1, see Table 1) and even the sign of the free energy difference would be a matter of chance.
The correction Δε obtained using 225-Ntrain data points basically eliminates any uncertainty resulting from systematic error of ML in predicted ΔAR, ΔATS, and ΔÇ (see Table 1). At first sight, the benefit of the present procedure might not be obvious since, after all, the same number of data points is used in all cases with different Ntrain, the difference being only in their partitioning between the training and correction set. Nevertheless, even this simple example shows that, since the systematic error can be eliminated a posteriori, one should actually demand convergence of corrected rather than uncorrected free energy values. This idea is particularly useful in context of our alternative computationally more effective simulation protocol in which the correction set is prepared using the LOO procedure (see Sec. 2) and hence the explicit target method calculations need to be performed only for Ntrain data points. In this case, as expected, the quality of correction for very small training sets is poor but systematically improves by increasing Ntrain (see Table 1) and the values obtained with 62 and 225 datapoints are virtually identical to the results corrected with independent training set (Table 1). Importantly, consistency in corrected and uncorrected results for ΔATS − ΔAR obtained using a certain value of Ntrain clearly indicates that the systematic error does not significantly affect predictions of free energy differences. As shown in Table 2, this indeed holds true for all methods discussed in this work when Ntrain = 62 was used. Discussion presented in remaining part of this work is therefore based on the results obtained with this setting and correction estimated from the LOO procedure.
Finally we note that a good overlap between the configuration spaces sampled by target and production methods must be achieved to get reliable MLPT results.80 This important requirement can conveniently be measured by the index Iw16,17 with the limiting values of 0.0 and 0.5, corresponding to zero and perfect overlap, respectively. This is achieved by computing the weighting factors wi = e−ΔV(qi)/kBT for all N configurations used in MLPT calculation, ordering them in an ascendant order, and identifying the lowest M fulfilling the condition 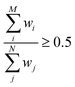 , which then defines Iw as follows:
, which then defines Iw as follows:
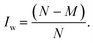 | (9) |
As shown by Herzog et al.,17 the MLPT procedure is reliable if Iw ≥ 005, which was fulfilled for all methods except of PBE+TS/HI applied to the TS structure, see Table 3.
| Target method | R | TS | P |
|---|---|---|---|
| PBE+D3(0) | 0.16 | 0.08 | 0.20 |
| PBE+D3(BJ) | 0.23 | 0.13 | 0.24 |
| PBE+D4 | 0.23 | 0.14 | 0.23 |
| PBE+TS | 0.17 | 0.17 | 0.18 |
| PBE+TS/HI | 0.06 | 0.02 | 0.13 |
| PBE+dDsC | 0.27 | 0.19 | 0.25 |
| PBE+MBD | 0.21 | 0.18 | 0.20 |
| PBE+MBD/FI | 0.23 | 0.16 | 0.28 |
| RPA | 0.12 | 0.07 | 0.13 |
3.2 MLPT results at various levels of theory
In the type B isomerization reaction investigated in this work, a π-complex (reactant) is first transformed into a monobranched secondary cation after proton is transferred from the zeolite. The very elusive secondary cation is subsequently isomerized into a tertiary dibranched cation via an edge protonated cyclopropane transition state (Fig. 1b). The corresponding free and internal energy barriers for the forward and backward steps determined by AIMD (PBE+D2) and MLPT (other levels of theory) are reported in Table 4. In addition, the free energy profiles computed at the PBE+D2 (AIMD) and RPA (MLPT) levels of theory are compared in Fig. 4.| Method | Forward | Backward | ||
|---|---|---|---|---|
| ΔA‡ | ΔU‡ | ΔA‡ | ΔU‡ | |
| PBE+D2 | 69.2 (−7.1) | 72.6 (−2.7) | 94.5 (2.0) | 60.6 (1.8) |
| PBE+D3(0) | 72.9 (−3.4) | 77.9 (2.6) | 102.0 (9.5) | 68.5 (9.7) |
| PBE+D3(BJ) | 75.4 (−0.9) | 82.4 (7.1) | 101.6 (9.1) | 68.4 (9.6) |
| PBE+D4 | 74.2 (−2.1) | 80.7 (5.4) | 100.9 (8.4) | 69.5 (9.7) |
| PBE+TS | 71.1 (−5.2) | 74.8 (−0.5) | 98.1 (5.6) | 58.6 (−0.2) |
| PBE+TS/HI | 66.4 (−9.9) | 69.0 (−6.3) | 100.4 (7.9) | 68.8 (10.0) |
| PBE+dDsC | 73.2 (−3.1) | 77.6 (2.3) | 98.0 (5.5) | 62.3 (3.5) |
| PBE+MBD | 70.7 (−5.6) | 76.1 (0.8) | 98.1 (5.6) | 67.6 (8.8) |
| PBE+MBD/FI | 68.4 (−7.9) | 75.3 (0.0) | 98.4 (5.9) | 65.6 (6.8) |
| RPA | 76.3 | 75.3 | 92.5 | 58.8 |
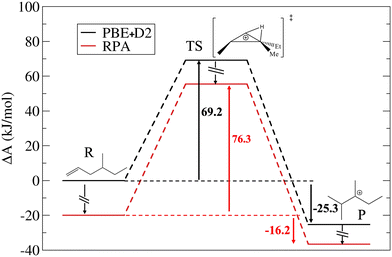 | ||
| Fig. 4 Comparison of free energy diagrams computed by AIMD PBE+D2 and MLPT RPA levels of theory for the isomerization reaction from the monobranched alkene to the tertiary dibranched cation. | ||
The forward step corresponds to the transition from the neutral π-complex to the cationic edge protonated cyclopropane (PCP) transition structure and the corresponding ΔA‡ obtained in Blue Moon ensemble AIMD simulations at the PBE+D2 level is 69.2 kJ mol−1.35 The MLPT calculation at the RPA target method level leads to increase of this barrier to 76.3 kJ mol−1, which is related to a relative stabilization of the π-complex reactant with respect to the cationic edge protonated transition state. For the backward reaction, which involves transformation from tertiary dibranched cation to PCP, the PBE+D2 free energy of activation is 94.5 kJ mol−1. Unlike for the forward reaction, RPA predicts decrease of ΔA‡ by 2.0 kJ mol−1 compared to the PBE+D2 result. Thus, in contrast to the type B isomerization linking tertiary cations considered in our previous work14 (Fig. 1a), the product (tertiary cation) is slightly less stabilized than the cationic PCP transition state by RPA. Computing the free energy of reaction as the difference between ΔA‡ determined for the forward and backward reaction modes, we find that both methods predict that the tertiary carbenium ion is more stable than the π-complex. Nevertheless, the relative stability of the former with respect to the latter is significantly reduced when PBE+D2 is replaced by RPA, whereby the free energy of reaction increases from −25.3 kJ mol−1 to −16.2 kJ mol−1.
Since the difference between the ΔA‡ and ΔU‡ terms determined for the R → TS transformation (see Table 4) is only 3.4 (PBE+D2) and −1.0 kJ mol−1 (RPA), one can deduce that the entropy change linked with this first part of reaction is only modest. In contrast, ΔA‡ − ΔU‡ for the P → TS transformation is much larger (33.9 and 33.7 kJ mol−1 for PBE+D2 and RPA, respectively), indicating that the entropy of product is significantly higher than that of reactant and transition states. As explained in our previous work,35 the entropy gain in the product state is due mainly to release of frustrated rotations and translations upon breaking relatively strong H-bonds present in reactant. Interestingly, this entropic effect predicted by RPA is about the same as that obtained in PBE+D2 calculations.
Combining the free energy results presented here with the data previously reported for the type B isomerization between tertiary cations and for type B1 cracking,14,37 we predict the general trend according to which all neutral intermediates are more stabilized with respect to ionic species at the RPA than at the PBE+D2 level of theory. The fact that PBE+D2 overestimates the stability of ionic species with respect to higher levels of theory is qualitatively compatible with previous reports made on short-chains alkenes.42,44 The isomerization PCP transition states do not follow strictly the trend of tertiary carbenium ions, so that the barriers linking tertiary cations to these TS are lower at the RPA level.
Equipped with the RPA high-level reference results, we can now proceed to evaluation of the quality of approximate methods based on various dispersion correction methods to the PBE functional, which belongs to most popular computationally inexpensive ab initio simulation methods used in theoretical catalysis. For the forward reaction mode, the approximate methods predict change in ΔA‡ by −2.8 (PBE+TS/HI) to 6.2 kJ mol−1 (PBE+D3(BJ)) with respect to the PBE+D2 method, whereby the closest agreement with the RPA reference is achieved by the PBE+D3(BJ) followed by the PBE+D4 and PBE+dDsC methods (ΔA‡ of 75.4, 74.2, and 73.2 kJ mol−1, respectively). In contrast, the PBE+TS/HI and PBE+MBD/FI methods predict a qualitatively different trend, i.e., a slight reduction in ΔA‡ (by −2.8 and −0.8 kJ mol−1, respectively). Disappointingly somewhat, all the dispersion correction methods predict incorrect trend for the free energy barrier of the backward reaction mode, whereby the predicted changes range between 3.5 (PBE+dDsC) to 7.5 kJ mol−1 (PBE+D3(0)). Importantly, the effect of dispersion correction on the forward and backward barrier is similar in most cases, leading to a very small effect on the free energy of reaction. Exceptions are the PBE+TS/HI and PBE+MBD/FI methods, which predict an increase in backward and a decrease in forward barriers, leading to a significant decrease in the free energy of reaction (−34.0 and −30.0 kJ mol−1, respectively) in comparison to the PBE+D2 method (−25.3 kJ mol−1), which is in striking contrast to the trend observed for the RPA method (increase to −16.2 kJ mol−1).
Furthermore, comparison of the ΔA‡ and ΔU‡ values presented in Table 4 reveals that although the general entropy trend along the R → TS → P sequence obtained by the different methods remain qualitatively the same as that predicted by the RPA and PBE+D2 methods, the quantitative differences are non-negligible. Hence, ΔA‡ − ΔU‡ for the R → TS step ranges between 2.6 (PBE+TS) and 7.0 kJ mol−1 (PBE+D3(BJ)), while that for the P → TS step is between 30.5 (PBE+MBD) and 39.5 (PBE+TS). These results show that a significant portion of the deviation between most levels of theory and RPA can be assigned to entropic factors.
All these results suggest that the improvement in the approximate results cannot be achieved via the choice of the method for description of the long-range dispersion interactions but rather through a careful selection of the density functional approximation. In particular, the use of hybrid functionals that incorporate a portion of Hartree–Fock exchange can be expected to reduce some of the errors of semi-local functionals, such as the self-interaction or delocalization errors, possibly leading to improvement of the description of ionic states and reaction barriers. Unfortunately, in line with our previous work,14,17 our attempted MLPT calculations with hybrid functionals (namely HSE06 (ref. 81–83) and B3LYP84,85) did not yield reliable results because of poor overlaps between the configuration spaces sampled by the production and target methods (Iw < 0.001). As proposed by Herzog et al.,17 this problem can be overcome by performing additional Monte Carlo calculations employing the Δ-ML model trained within MLPT (so called MLMC approach). However, these calculations would require performing additional tens of thousands of explicit calculations of the production method, and hence represent a significant additional computational cost to an already very high cost of the RPA simulations presented in this work. Nevertheless, our qualitative static calculations (see Sec. SI in the ESI†) suggest that hybrid functionals will not lead to reliable results with respect to the RPA reference level.
3.3 Comparison with experimental and kinetic modelling results
With these new data in hand, we can now compare the improvement brought by the RPA MLPT approach with the previous estimates, using as reference data extracted from the kinetic modelling of experimental data (bifunctional hydroisomerization of n-heptane) acquired thanks to a high-throughput setup, as reported in ref. 19. The comparison between computational and experimental results is not straightforward as the reaction network consists of forty type B isomerization steps, including the ones (forward and backward) investigated in the present work (termed TS5b in ref. 19). A single-event kinetic model was built on the basis of previous AIMD calculations for the cracking steps37 and on static calculations made on purpose for the whole set of type B isomerization steps.The agreement between experiments and the ab initio-based kinetic model was not optimal at the first try. The difference between the free energy barriers of the type B isomerization and B1 cracking needed to be adjusted to reproduce accurately the isomerization over cracking selectivity. The choice was made to keep the isomerization barrier unchanged, and to increase the cracking barrier by 15 kJ mol−1, but one may have chosen to decrease by 15 kJ mol−1 the isomerization barriers, keeping the cracking barrier unchanged. A similar improvement of the description of the isomerization versus cracking selectivity would have been modelled. The isomerization/cracking selectivity is indeed monitored by the free energy barrier difference between the two kinds of events, independently of their absolute value. Thus, we consider as “reference data” the free energy barrier differences between type B isomerization and B1 cracking, but not the absolute values themselves.
Table 5 reports the free energy barriers for the currently considered type B isomerization and for the B1 cracking step, by the various computational approaches undertaken (AIMD at the PBE+D2 level, RPA MLPT) and the one used in the optimal kinetic model. From these values, the difference between free energy barriers of type B isomerization and B1 cracking (kJ mol−1) was determined and reported in Table 6. It can be seen very clearly that the RPA level provides much better results when comparing to the available reference data than the PBE+D2 AIMD calculations. Chemical accuracy (deviation with respect to experiment within 4.2 kJ mol−1) is approached with RPA MLPT (remaining deviation from experimental data of 5.0 and 6.4 kJ mol−1 for the forward and backward isomerization steps, respectively). These results are consistent with those obtained in our previous work14 for the type B isomerization reaction involving tertiary cations only (Fig. 1a) showing that the improvement achieved by replacing the PBE+D2 by the RPA level of theory is significant regardless of the nature of the reactant under consideration (π-complex or cation).
| Step | PBE+D2 AIMD | RPA MLPT | Kinetic modelling |
|---|---|---|---|
| Isom. B, forward | 69.2 | 76.3 | 74.7 |
| Isom. B, backward | 94.5 | 92.5 | 89.5 |
| B1 cracking | 60.1 | 71.6 | 75.0 |
| Isomerization step | PBE+D2 AIMD | RPA MLPT | Kinetic modelling |
|---|---|---|---|
| Forward | 9.1 (9.4) | 4.7 (5.0) | −0.3 |
| Backward | 34.4 (19.9) | 20.9 (6.4) | 14.5 |
4 Conclusions
In the present work, an accurate quantification of the barrier of the Brønsted acidic zeolite-catalyzed type B isomerization of a monobranched C7 alkene (4-methyl-hex-1-ene) into a dibranched tertiary cation was reported at the RPA level and PBE method linked with various dispersion corrections. The combination of AIMD with RPA was made possible thanks to MLPT within a few weeks, whereas it is not feasible to date to perform full AIMD at the RPA level of theory.The isomerization reaction considered here is of interest because it links a neutral reactant (a π-complex) to a cationic species (a tertiary carbenium ions). Analyzing the respective stabilization of neutral and ionic species when shifting from PBE+D2 to RPA indicates that PBE+D2 overstabilizes cationic species with respect to neutral ones, in agreement with previous reports made on shorter-chain species. The transition state of the isomerization is a non-classical carbenium ion, called an edge protonated cyclopropane. Accordingly, its stabilization is weaker than that of the π-complex, but stronger than that of the classical tertiary carbenium ion, leading to a slight decrease of the backward isomerization barrier.
Using a level of theory as high as RPA appeared to be mandatory to approach chemical accuracy. Deviations with respect to reference experimental data, extracted thanks to kinetic modelling, were as low as 5.0 and 6.4 kJ mol−1 when considering the difference between the B1 cracking barrier and the forward/backward isomerization barrier respectively. This free energy barrier difference is indeed the relevant kinetic parameter to compare to, as absolute barriers of independent events cannot unambiguously be determined with the current experimental results. Applying the MLPT approach to a variety of dispersion correction schemes to the PBE energies, reveals that such changes are not sufficient to reduce the deviation with respect to reference data.
The use of MLPT has thus the potential of being instrumental in accessing high levels of theory while accounting for dynamic effects in heterogeneous catalysis, a first step toward the predictive kinetic modeling of catalytic reactions starting from ab initio calculations.
Data availability
Data for this article, including MLPT codes, production and target levels calculations, are available at Zenodo at https://doi.org/10.5281/zenodo.12597668.Author contributions
JR: investigation, formal analysis, writing – original draft, writing – review & editing, DR: conceptualization, writing – review & editing, MB: conceptualization, resources, supervision, project administration, writing – review & editing, CC: conceptualization, project administration, writing – original draft, writing – review & editing, TB: conceptualization, project administration, investigation, formal analysis, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was granted access to the HPC resources of TGCC under the allocation 2022-A0120810433 and 2023-A0140810433 made by GENCI. Part of the research was obtained using the computational resources procured in the national project National competence centre for high performance computing within the Operational programme Integrated infrastructure (project code: 311070AKF2). J. R., D. R. and M. B. are grateful for the financial support given by the COMETE project (COnception in silico de Matériaux pour l'EnvironnemenT et l'Energie), co-funded by the European Union as part of the “FEDER-FSE Lorraine et Massif des Vosges 2014-2020” program. C. C. and M. B. acknowledge the Agence Nationale de la Recherche under France 2030 (contract ANR-22-PEBB-0009), for support in the context of the MAMABIO project (B-BEST PEPR). T. B. acknowledges support from Slovak Research and Development Agency under the Contract No. APVV-20-0127 and the grant VEGA 1/0254/24 from the Ministry of Education Research, Development and Youth of the Slovak Republic.References
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. Bohm and D. Pines, Phys. Rev., 1953, 92, 609–625 CrossRef CAS.
- D. Langreth and J. Perdew, Solid State Commun., 1975, 17, 1425–1429 CrossRef.
- J. Harl and G. Kresse, Phys. Rev. Lett., 2009, 103, 056401 CrossRef PubMed.
- J. Harl, L. Schimka and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115126 CrossRef.
- X. Ren, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045402 CrossRef.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741–744 CrossRef CAS PubMed.
- F. Göltl, A. Grüneis, T. Bučko and J. Hafner, J. Chem. Phys., 2012, 137, 114111 CrossRef PubMed.
- D. Rocca, A. Dixit, M. Badawi, S. Lebègue, T. Gould and T. C. V. Bučko, Phys. Rev. Mater., 2019, 3, 040801 CrossRef CAS.
- J. Paier, X. Ren, P. Rinke, G. E. Scuseria, A. Grüneis, G. Kresse and M. Scheffler, New J. Phys., 2012, 14, 043002 CrossRef.
- J. E. Bates, P. D. Mezei, G. I. Csonka, J. Sun and A. Ruzsinszky, J. Chem. Theory Comput., 2017, 13, 100–109 CrossRef CAS PubMed.
- C. Waitt, N. M. Ferrara and H. Eshuis, J. Chem. Theory Comput., 2016, 12, 5350–5360 CrossRef CAS PubMed.
- J. Chedid, N. M. Ferrara and H. Eshuis, Theor. Chem. Acc., 2018, 137, 158 Search PubMed.
- J. Rey, C. Chizallet, D. Rocca, T. Bučko and M. Badawi, Angew. Chem., Int. Ed., 2024, 63, e202312392 CrossRef CAS PubMed.
- B. Chehaibou, M. Badawi, T. Bučko, T. Bazhirov and D. Rocca, J. Chem. Theory Comput., 2019, 15, 6333–6342 CrossRef CAS PubMed.
- T. Bučko, M. Gešvandtnerová and D. Rocca, J. Chem. Theory Comput., 2020, 16, 6049–6060 CrossRef PubMed.
- B. Herzog, M. Chagas da Silva, B. Casier, M. Badawi, F. Pascale, T. Bučko, S. Lebègue and D. Rocca, J. Chem. Theory Comput., 2022, 18, 1382–1394 CrossRef CAS.
- B. Herzog, A. Gallo, F. Hummel, M. Badawi, T. Bučko, S. Lebègue, A. Grüneis and D. Rocca, npj Comput. Mater., 2024, 10, 68 CrossRef.
- J.-M. Schweitzer, J. Rey, C. Bignaud, T. Bučko, P. Raybaud, M. Moscovici-Mirande, F. Portejoie, C. James, C. Bouchy and C. Chizallet, ACS Catal., 2022, 12, 1068–1081 CrossRef CAS.
- A. Corma, Chem. Rev., 1995, 95, 559–614 CrossRef CAS.
- G. Busca, Chem. Rev., 2007, 107, 5366–5410 CrossRef CAS PubMed.
- W. Vermeiren and J.-P. Gilson, Top. Catal., 2009, 52, 1131–1161 CrossRef CAS.
- E. T. C. Vogt and B. M. Weckhuysen, Chem. Soc. Rev., 2015, 44, 7342–7370 RSC.
- T. Ennaert, J. van Aelst, J. Dijkmans, R. de Clercq, W. Schutyser, M. Dusselier, D. Verboekend and B. F. Sels, Chem. Soc. Rev., 2016, 45, 584–611 RSC.
- A. J. Martín, C. Mondelli, S. D. Jaydev and J. Pérez-Ramírez, Chem, 2021, 7, 1487–1533 Search PubMed.
- A. T. Sandro Brandenberger, O. Kröcher and R. Althoff, Catal. Rev.: Sci. Eng., 2008, 50, 492–531 CrossRef.
- A. M. Beale, F. Gao, I. Lezcano-Gonzalez, C. H. F. Peden and J. Szanyi, Chem. Soc. Rev., 2015, 44, 7371–7405 RSC.
- C. Bornes, I. C. Santos-Vieira, R. Vieira, L. Mafra, M. M. SimÃμes and J. Rocha, Catal. Today, 2023, 419, 114159 CrossRef CAS.
- Z. Dong, W. Chen, K. Xu, Y. Liu, J. Wu and F. Zhang, ACS Catal., 2022, 12, 14882–14901 CrossRef CAS.
- C. Chizallet, C. Bouchy, K. Larmier and G. Pirngruber, Chem. Rev., 2023, 123, 6107–6196 CrossRef CAS PubMed.
- C. Tuma, T. Kerber and J. Sauer, Angew. Chem., Int. Ed., 2010, 49, 4678–4680 CrossRef CAS PubMed.
- G. Piccini, M. Alessio and J. Sauer, Angew. Chem., Int. Ed., 2016, 55, 5235–5237 CrossRef CAS PubMed.
- M. Rybicki and J. Sauer, J. Am. Chem. Soc., 2018, 140, 18151–18161 CrossRef CAS PubMed.
- F. Berger, M. Rybicki and J. Sauer, J. Catal., 2021, 395, 117–128 CrossRef CAS.
- J. Rey, P. Raybaud, C. Chizallet and T. Bučko, ACS Catal., 2019, 9, 9813–9828 CrossRef CAS.
- J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, J. Catal., 2019, 373, 361–373 CrossRef CAS.
- J. Rey, C. Bignaud, P. Raybaud, T. Bučko and C. Chizallet, Angew. Chem., 2020, 132, 19100–19104 CrossRef.
- V. Van Speybroeck, M. Bocus, P. Cnudde and L. Vanduyfhuys, ACS Catal., 2023, 13, 11455–11493 CrossRef PubMed.
- V. Van Speybroeck, K. De Wispelaere, J. Van der Mynsbrugge, M. Vandichel, K. Hemelsoet and M. Waroquier, Chem. Soc. Rev., 2014, 43, 7326–7357 RSC.
- G. Piccini, M.-S. Lee, S. F. Yuk, D. Zhang, G. Collinge, L. Kollias, M.-T. Nguyen, V.-A. Glezakou and R. Rousseau, Catal. Sci. Technol., 2022, 12, 12–37 RSC.
- C. Paolucci, I. Khurana, A. A. Parekh, S. Li, A. J. Shih, H. Li, J. R. D. Iorio, J. D. Albarracin-Caballero, A. Yezerets, J. T. Miller, W. N. Delgass, F. H. Ribeiro, W. F. Schneider and R. Gounder, Science, 2017, 357, 898–903 CrossRef CAS PubMed.
- K. De Wispelaere, P. N. Plessow and F. Studt, ACS Phys. Chem. Au, 2022, 2, 399–406 CrossRef CAS PubMed.
- F. Berger, M. Rybicki and J. Sauer, ACS Catal., 2023, 13, 2011–2024 CrossRef CAS.
- Q. Ren, M. Rybicki and J. Sauer, J. Phys. Chem. C, 2020, 124, 10067–10078 CrossRef CAS.
- T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376 CrossRef CAS.
- F. Berger and J. Sauer, Angew. Chem., 2021, 60, 3529–3533 CrossRef CAS PubMed.
- C. Bouchy, G. Hastoy, E. Guillon and J. A. Martens, Sci. Technol. Energy Transition, 2009, 64, 91–112 CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- L. Smith, A. Davidson and A. Cheetham, Catal. Lett., 1997, 49, 143–146 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744 CrossRef CAS.
- E. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472–477 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2011, 134, 044117 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- T. Bučko, S. Lebègue, J. Hafner and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064110 CrossRef.
- T. Bučko, S. Lebègue, J. Hafner and J. G. Ángyán, J. Chem. Theory Comput., 2013, 9, 4293–4299 CrossRef PubMed.
- T. Bučko, S. Lebègue, J. G. Ángyán and J. Hafner, J. Chem. Phys., 2014, 141, 034114 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, J. DiStasio, A. Robert and A. Tkatchenko, J. Chem. Phys., 2014, 140, 8 CrossRef PubMed.
- T. Bučko, S. Lebègue, T. Gould and J. G. Ángyán, J. Phys.: Condens. Matter, 2016, 28, 045201 CrossRef PubMed.
- T. Gould, S. Lebègue, J. G. Ángyán and T. Bučko, J. Chem. Theory Comput., 2016, 12, 5920–5930 CrossRef CAS PubMed.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035101 CrossRef.
- M. Kaltak, J. Klimeš and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054115 CrossRef CAS.
- M. Rupp, Int. J. Quantum Chem., 2015, 115, 1058–1073 CrossRef CAS.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769 RSC.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- M. Gešvandtnerová, D. Rocca and T. Bučko, J. Catal., 2021, 396, 166–178 CrossRef.
- A. Pohorille, C. Jarzynski and C. Chipot, J. Phys. Chem. B, 2010, 114, 10235–10253 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127, 024103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00548a |
| This journal is © The Royal Society of Chemistry 2024 |