Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiscale modelling of CO2 hydrogenation of TiO2-supported Ni8 clusters: on the influence of anatase and rutile polymorphs†
Lulu
Chen
,
Ying-Ying
Ye
 ,
Rozemarijn D. E.
Krösschell
,
Rozemarijn D. E.
Krösschell
 ,
Emiel J. M.
Hensen
,
Emiel J. M.
Hensen
 and
Ivo A. W.
Filot
and
Ivo A. W.
Filot
 *
*
Laboratory of Inorganic Materials and Catalysis, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: i.a.w.filot@tue.nl
First published on 16th September 2024
Abstract
The selection of TiO2 phase, whether anatase or rutile, for supporting small Ni clusters significantly influences the activity and selectivity in CO2 hydrogenation to methane. To model and understand these variances, we developed a hierarchical multiscale catalytic model. Utilizing a hybrid approach combining genetic algorithms and density functional theory, we identified the putative global minimum structures of Ni8 clusters supported on anatase (Ni8/TiO2-a) and rutile (Ni8/TiO2-r), which are morphologically distinct. Microkinetics simulations based on the energetics derived from DFT calculations over these distinct clusters reveal the mechanism of CO2 hydrogenation to CO, CH4 and CH3OH. On both Ni8/TiO2-a and Ni8/TiO2-r, CH4 is the main product at low temperature while a shift to CO occurs with increasing temperature. In comparison to Ni8/TiO2-r, Ni8/TiO2-a exhibits a higher activity and keeps a higher selectivity towards CH4 with increasing temperature. Using a sensitivity analysis, we identify the steps responsible for the observed selectivity difference and rationalize the observed barrier differences for these steps between the different clusters by means of detailed electronic structure analysis.
1. Introduction
In recent decades, the escalating levels of atmospheric carbon dioxide (CO2) contribute significantly to rising global temperatures, sea-level rise, altered weather patterns, and various ecological disruptions. To mitigate these adverse effects and transition towards a more sustainable and carbon-neutral future, innovative approaches and technologies capable of reducing CO2 emissions at scale are required.1–5 Sustainably produced hydrogen, for example from excess wind and solar power, can be utilized to convert CO2 to CH4 in the so-called power-to-gas concept.6–8 An important benefit of CH4 is that existing infrastructure for storage and transport can be repurposed.6,9For the practical implementation of CO2 hydrogenation to CH4, catalysts are essential to ensure both high reaction rates and selectivity towards the desired product. While methanation catalysts have been extensively studied, Ru stands out for its superior performance among investigated transition metals.10,11 However, the widespread industrial application of Ru catalysts is hindered by its relatively high cost. In contrast, Co and Ni also demonstrate high conversion rates in CO2 methanation, with Ni being the preferred choice for industrial applications, as it is the cheaper of the two metals.12–14
The activity of supported transition metal catalysts is affected by many factors, with the size of the nanoparticles being a dominant one, strongly affecting the abundance of specific surface atom arrangements relevant to dissociation and association reactions below 10 nm.15 The effect of nanoparticle size on the activity and selectivity of CO2 hydrogenation to CO and CH4 remains a topic of intense debate. Two dominant trends can be identified in the literature. Some studies show an increased surface-normalized CO2 conversion with increasing particle size,16–21 while others find an optimum.22–24 In a recent study of Simons et al., it was found that Ni-catalyzed CO2 methanation uses two different types of active sites, one for reverse-water-gas-shift (RWGS) reaction yielding intermediary CO and another type of site for CO conversion to methane. While RWGS is structure-independent, the activity of CO methanation shows strong structure-dependence caused by the particle size dictating the abundancy of this latter type of active site.25
In addition to nanoparticle size, the support material can influence the morphology of the nanoparticles. Apart from the wetting properties of the support affecting the nanoparticle, the surface structure of the support also has an epitaxial effect that influences nanoparticle morphology by favoring specific alignments at the support–nanoparticle interface.26–29 A notable example is found when using TiO2 as a support material, which exists in three primary crystalline forms, being anatase, rutile and brookite. CO2 methanation catalyzed by TiO2-supported nanoparticles show different activity and selectivity trends based on the phase of TiO2.30–33 Li et al. showed that for similarly sized Co nanoparticles (∼20 nm), the anatase-supported particles mainly produce CO under CO2 hydrogenation conditions, while the rutile-supported counterpart exhibits high methane selectivity.30 Wang et al. reported a similar effect for small Ru nanoparticles (∼2–3 nm), where the rutile phase is significantly more active and selective towards CH4 than the anatase phase. This enhanced selectivity is assigned to the formation of a favorable overlayer structure guided by the interfacial compatibility between the RuO2 precursor phase and rutile, prior to reduction. In contrast, on anatase only small nanoparticles are formed.32 Likewise, the works of Lin et al. and Messou et al. observe for similarly sized Ni nanoparticles (∼30 nm) an increased activity and selectivity towards CH4 for the rutile phase over the anatase phase in CO2 hydrogenation. The increased activity is assigned to the rutile phase giving rise to Ni nanoparticles that portray facile CO dissociation and H2 activation.31,33
Clearly, the choice of TiO2 phase, whether anatase or rutile, has a strong impact on the catalytic activity, even when the nanoparticles are roughly the same size. Different support materials, their phases and surface termination determine the metal–support interaction strength and thus modulate particle sizes invoking known structure sensitivity patterns. When nanoparticle sizes remain comparable between different support structures, yet a different kinetic response is observed, this is a strong indicator that the support influences the particle shape. Computational catalysis can aid in understanding these effects, yet the scale of these systems remains still prohibitively large for detailed electronic structure calculations. One way to tackle this is by means of DFT-based force fields, as performed earlier by us for both unsupported Co nanoparticles26 as well as Co nanoparticles on a model support material.34 In this work, rather than producing such a force field, the system is made computationally accessible by focusing on small Ni clusters. Small Ni clusters provide an excellent model system to study active site configurations that are guided by the alignment of the support substructure.
To understand and characterize how support effects can influence the activity and selectivity in CO2 hydrogenation to methane for small clusters, we construct a multiscale model for Ni8 clusters supported on rutile and anatase. Although experimentally always a range of particle size distributions is observed, these small Ni8 clusters are representative for particle sizes below 1 nm. By means of a DFT-based genetic algorithm in conjunction with machine learning, we explore the configuration space of TiO2-supported Ni8 clusters and identify the putative global minimum configuration. Next, the kinetic pathways for CO2 hydrogenation to CH4 are calculated. By means of microkinetics simulations, we found that Ni8/TiO2-anatase in comparison to Ni8/TiO2-rutile exhibits a much higher activity while also portraying a higher selectivity to CH4 with increasing temperature. Using a sensitivity analysis, we identified that the preferred manner of C–O bond scission – hydrogen-assisted pathway via HCO* for Ni8/TiO2-anatase, while in a direct fashion for Ni8/TiO2-rutile – dictates the observed activity and selectivity differences. These differences are caused by the specific topology of the active site dictated by the alignment of Ni atoms with the support structure. By means of a crystal orbital Hamilton population analysis, the difference in barrier for CO dissociation is rationalized. This study adds to our understanding by which mechanism the catalyst support can modulate the catalytic reaction.
2. Methods
2.1 DFT calculations
All density functional theory (DFT) calculations were performed using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional35 as implemented in the Vienna ab initio simulation package (VASP) software.36,37 All DFT calculations were conducted with spin-polarization taken into account. The interaction of the core-electrons and nucleus was described with the Projector Augmented Wave (PAW) method.38–40 The cut-off energy was set to 400 eV. The Brillouin zone was sampled using a 1 × 1 × 1 grid. Gaussian smearing with a width of 0.05 eV determined partial occupancies for each orbital. Ionic convergence was achieved when the forces were smaller than 0.05 eV Å−1 for each atom in each Cartesian direction. A Van-der-Waals correction was added to our calculation using the DFT-D3 method with the Becke–Johnson damping function.41,42 Climbing image nudged elastic band (CI-NEB) was employed to investigate the transition pathway.43,44 The transition state was optimized using a quasi-Newton algorithm and the optimized geometry was examined by vibrational mode analysis. It was verified that all transition states have a single imaginary mode in the direction of the reaction coordinate. We employed a finite difference approach to construct the Hessian matrix for frequency analysis by perturbing the atomic positions by 0.01 Å in each Cartesian direction. Furthermore, the vibrational mode analysis was used to construct zero-point energy corrections.2.2 Structural models
For anatase and rutile TiO2, the periodically repeated (101) and (110) surface terminations were employed as supports for Ni8 clusters, as these surfaces are known to be the most thermodynamically stable for their respective phases.45,46 Ni8 clusters deposited on (101) surface of TiO2 anatase and (110) surface of TiO2 rutile are denoted as Ni8/TiO2-a and Ni8/TiO2-r, respectively. We specifically selected Ni8 clusters because they are large enough to potentially support step-edge configurations, which are known to promote C–O bond scission.47 However, this does not guarantee that these active site patterns are thermodynamically favorable, as the support interface also plays a crucial role. Nevertheless, choosing smaller cluster sizes would a priori prevent studying such sites.The lattice parameters of TiO2-a and TiO2-r bulks were optimized and found to be 3.816 Å × 3.816 Å × 9.539 Å and 4.650 Å × 4.650 Å × 2.966 Å, respectively. These optimized lattice parameters are in good agreement with the values obtained from experimental results.48,49 For TiO2-a, a 1 × 3 (101) surface termination with dimensions of 10.42 Å × 11.46 Å was constructed. Its slab model hosts three O–Ti–O layers with the bottom layer fixed while the top two layers are allowed to relax.50 For Ni8/TiO2-r, a 5 × 2 (110) surface termination with dimensions of 14.85 Å × 13.18 Å was constructed. The corresponding slab model has four O–Ti–O layers. The bottom layer was fixed while the top three layers were allowed to perturb. To avoid the spurious interaction of neighboring supercells in the z-direction, the TiO2-a and TiO2-r super cells have a vacuum space of at least 15 Å. A depiction of the supercells is given in the ESI† in Fig. S1.
2.3 Genetic algorithm
In order to search for the putative global minimum structure of Ni8 clusters deposited on the anatase (101) and rutile (110) surface of TiO2, a GA-DFT algorithm based on the approach as described by Hammer et al. was employed.51 In this approach, an ensemble of cluster configurations is procedurally generated and the stability of these clusters on the surface is assessed by DFT calculations. To efficiently probe the configuration space of cluster configurations, a genetic algorithm method is used wherein new cluster configurations are generated by a sequence of operations including translations, rotations, atomic migrations and mixing of clusters. For each generation, at least 12 candidates are generated to form the next generation. To enhance the diversity of the population, approximately 30% to 50% of the structures are mutated. Each cluster is subjected to a geometry optimization in a conventional DFT simulation and based on the energies of the clusters they are ranked in terms of stability. New generations of clusters are derived from an older generation using stability and similarity metrics. This yields a strong (i.e. containing many stable structures) yet sufficiently diverse population between all iterations. The algorithm is considered to be converged when no new more stable configurations are found for a number of generations, typically between 5–10. Details of the GA-DFT procedure can be found in the earlier work of Chang et al.52To assess the similarity of the clusters and identify common shapes, an unsupervised non-linear dimensionality reduction was conducted via the t-distributed stochastic neighbor embedding (t-SNE) method as implemented in the sklearn Python library.53,54 The dimensionality reduction is applied to a N × N square distance metric matrix M with N being the number of clusters. Each element in M corresponds to the minimized Hilbert–Schmidt norm55 of the distance-difference matrix between two clusters. The minimized Hilbert–Schmidt norm is constructed by first constructing an atomic distance matrix R for each cluster.
 | (1) |
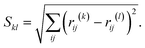 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 320 permutations were explicitly considered. The lowest value found, i.e. Skl,min, is then used as the elements to construct M. For the construction of M, we used the in-house developed program Bramble which employs a GPU-accelerated procedure to evaluate all permutations.56
320 permutations were explicitly considered. The lowest value found, i.e. Skl,min, is then used as the elements to construct M. For the construction of M, we used the in-house developed program Bramble which employs a GPU-accelerated procedure to evaluate all permutations.56
2.4 Microkinetics simulations
Microkinetics simulations based on DFT-derived reaction networks were conducted to determine the catalytic performance of Ni8/TiO2-a and Ni8/TiO2-r for CO2 hydrogenation. All microkinetics simulations were performed using the in-house developed MKMCXX program.57,58 For each elementary reaction step in the chemokinetic network as given by | (3) |
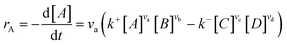 | (4) |
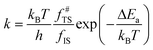 | (5) |
For the adsorption steps, it is assumed that the adsorbing molecule loses one of the translational degrees of freedom with respect to the initial state. The rate constant for adsorption is then determined by the rate of surface impingement of gas-phase molecules for non-activated molecular adsorption and is given by59
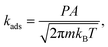 | (6) |
Considering the reversibility of the adsorption step, the molecule regains all its rotational degrees of freedom (i.e. three degrees of freedom for non-linear molecules and two degrees of freedom for linear molecules) and two translational degrees of freedom in the desorption step. Therefore, the desorption rate is given by
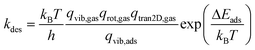 | (7) |
In our simulations, the initial gas phase contained a mixture of CO2 and H2 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratio at a total pressure of 1 atm, in line with the conditions used in the experiment.60 To identify the elementary reaction steps that control the overall rate of CO2 consumption, Campbell's degree of rate control analysis was employed.61
4 ratio at a total pressure of 1 atm, in line with the conditions used in the experiment.60 To identify the elementary reaction steps that control the overall rate of CO2 consumption, Campbell's degree of rate control analysis was employed.61
3. Results and discussions
3.1 Ni8 clusters supported on anatase and rutile TiO2
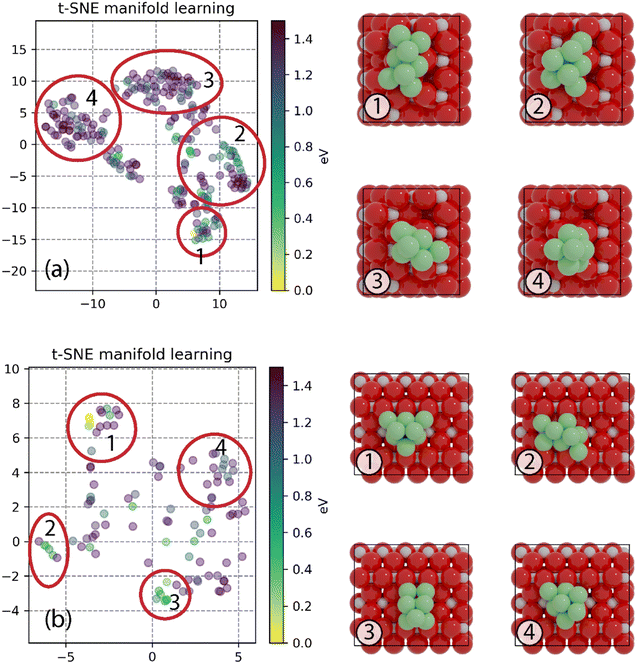
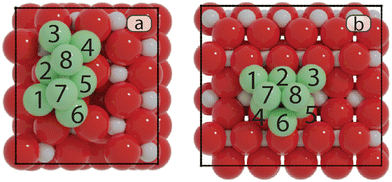
To find the most stable structures for Ni8 clusters supported on anatase and rutile TiO2, a GA-DFT algorithm was employed which produced 244 and 104 candidate structures for the anatase and rutile systems, respectively. The candidates were ranked based on the total energy of the system. The 10 most stable structures for anatase and rutile TiO2 are given in Fig. S2 and S4,† respectively. To investigate whether there are multiple cluster configurations that are topologically distinct yet portray a similar stability on the surface, a similarity analysis was conducted by calculating the minimized Hilbert–Schmidt norm between all clusters. Using a non-linear dimensionality reduction based on the t-SNE method, we could classify all clusters into distinct categories as shown in Fig. 1. Representative cluster configurations for each of these groups are shown in Fig. 1 as well.The most stable Ni cluster on the anatase TiO2 (101) surface, representative of group 1, adopts a bilayer configuration in which 6 Ni atoms are located in the bottom layer forming two fourfold type of adsorption sites on which the two atoms of the top layer are located. The clusters in groups 2–4 exhibit fewer Ni atoms binding to the O atoms of the support and are higher in energy. In Fig. S3,† the 9 most similar clusters with respect to the most stable cluster are shown. We can readily observe that these structures are related to the most stable structure either via a rotation or via a migration of one or two Ni atoms.
On the rutile TiO2 (110) surface, the most stable cluster of Ni8 also adopts a bilayer configuration. In contrast to the anatase system, the bottom layer has a triangular shape exposing four threefold adsorption sites. The top layer is constructed by the adsorption of two Ni atoms on two of these threefold adsorption sites. The t-SNE manifold learning shows that, for this system, also four distinct groups of clusters are found. The most stable configuration belongs to group 1, group 2 shows a different configuration yet similar to group 1 on anatase TiO2(101) with 6 atoms in the bottom layer and two atoms in the top layer. In contrast, groups 3 and 4 show a configuration with 5 atoms in the bottom layer and 3 in the top layer. Groups 2, 3 and 4 are, on average, higher in energy than group 1 as they either lack a strong interaction with the support (groups 3 and 4) or have more undercoordinated metal atoms (group 2).
Furthermore, due to known SMSI effects, we also investigated planar Ni8 clusters that optimize the contact area between the TiO2-support and the Ni8 cluster. The configurations are shown in Fig. S6 in the ESI.† It was found that on both TiO2 anatase and rutile, a planar Ni8 cluster is less stable than a non-planar cluster by 1.35 eV and 1.06 eV, respectively. As such, we proceeded with evaluating the elementary reaction steps for CO2 hydrogenation using non-planar cluster configurations.
3.2 Chemical reactivity of CO2 hydrogenation over Ni8/TiO2-a and Ni8/TiO2-r
• Ti: the top site of Nii.
• Bi–j: the bridge site located between Ni and Nij.
• Hi–j–k: the hollow site that comprises Nii, Nij, and Nik.
• Fi–j–k–l: the four-fold site formed by Nii, Nij, Nik, and Nil.
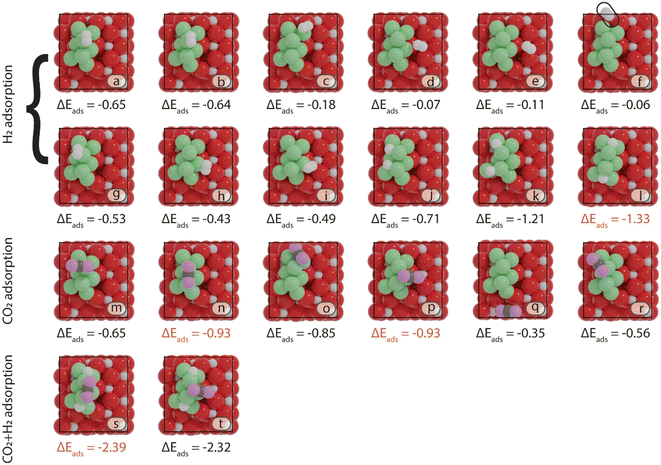
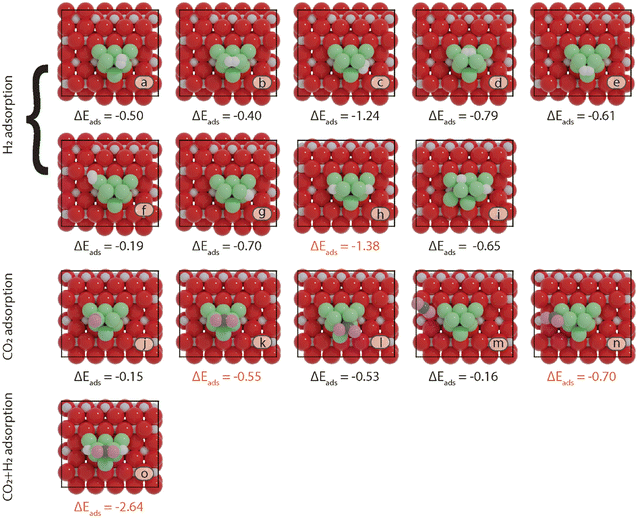
First, the preferred adsorption configurations of CO2 and H2 on the various active sites are explored. For H2, we considered both molecular as well as dissociative adsorption. In Fig. 3 and 4, an overview is given of the different adsorption modes and corresponding adsorption energies of CO2 and H2 on Ni8/TiO2-a and Ni8/TiO2-r, respectively. From the results in Fig. 3 and 4, it can be seen that dissociative H2 adsorption is more exothermic as compared to molecular adsorption and the H atoms preferentially reside at the metal–support interface. The most stable configurations for H2 adsorption correspond to adsorption energies of ΔEads = −1.23 eV and ΔEads = −1.37 eV for Ni8/TiO2-a and Ni8/TiO2-r, respectively. In these configurations, H2 is dissociatively adsorbed to form 2H*. This process is activated by 0.11 eV and 0.39 eV for Ni8/TiO2-a and Ni8/TiO2-r, respectively. These results are similar to H2 dissociation on a Ni13 cluster (ΔEact = 0.21 eV) and Ni/In2O3 (ΔEact = 0.22 eV).62,63 H spillover is commonly discussed experimentally.64 Therefore, H spillover is also considered on these two models. As shown in Fig. S7,† H spillover occurs with activation energies of ΔEact = 0.89 eV and ΔEact = 1.09 eV on Ni8/TiO2-a and Ni8/TiO2-r, respectively. This step is endothermic with reaction energies of ΔER = 0.67 eV and ΔER = 0.50 eV for Ni8/TiO2-a and Ni8/TiO2-r, respectively. Given the endothermic nature of the H spillover reaction and the fact that CO2 adsorption takes place on Ni clusters (vide infra), H spillover is not further considered in the evaluation of the reaction mechanism. On Ni8/TiO2-a, CO2 adsorption is preferred at the B7–8 or H5–7–8 sites, both sites yielding an adsorption energy of ΔEads = −0.93 eV. On Ni8/TiO2-r, the most stable site for CO2 adsorption is H1–4–7 with an adsorption energy of ΔEads = −0.70 eV. Based on the preferred adsorption sites of H2 and CO2, we also considered the co-adsorption of CO2 and H2. For Ni8/TiO2-a we find a total adsorption energy of ΔEads = −2.39 eV, which is more exothermic than the sum of the individual CO2 and H2 adsorption energies. In a similar fashion, we find for Ni8/TiO2-r that the co-adsorbed state is more exothermic (ΔEads = −2.64 eV) than the sum of the individual adsorption energies. As these co-adsorbed states represent favorable adsorption modes, we considered these in the further exploration of the reaction pathways.
 | ||
| Fig. 5 Reaction network for CO2 hydrogenation on Ni8/TiO2-a. The numbers correspond to the elementary reaction steps in Tables S1 and S2 and Fig. S8–S11.† The activation energy, adsorption energy, and desorption energy are reported in eV and include a zero-point energy correction (colors: brown: CHx-intermediates pathway; red: HxCO-intermediates pathway; and orange and blue: HxCOO-intermediates pathways). | ||
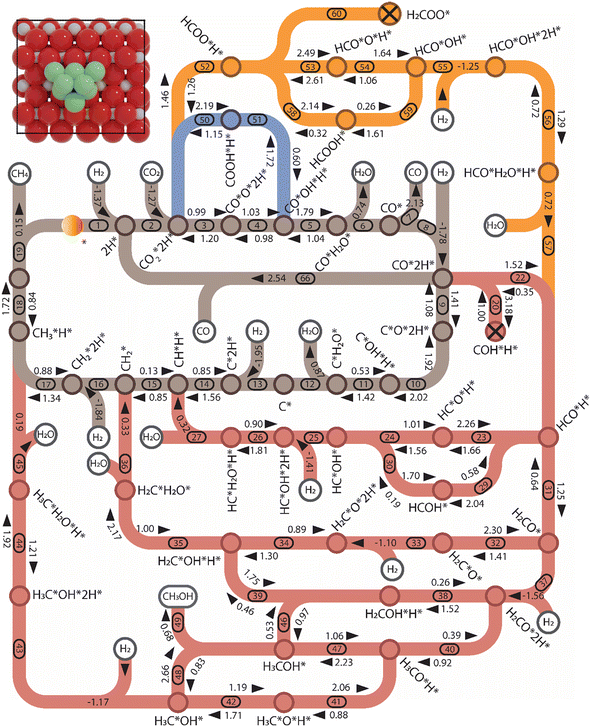 | ||
| Fig. 6 The forward and backward activation energies in the network of CO2 hydrogenation in C1 chemistry for Ni8-TiO2-r (colors: brown: CHx-intermediates pathway; red: HxCO-intermediates pathway; and orange and blue: HxCOO-intermediates pathways). The energy reported here is zero-energy corrected and given by eV. The cross on COH*H* and H2COO* signifies that their formation is impeded by high activation energies, leading to the exclusion of subsequent reactions. The numbers correspond to the elementary reaction steps in Table S1 and S2 and Fig. S12–S15.† The activation energy, adsorption energy, and desorption energy are reported in eV and include a zero-point energy correction. | ||
3.2.2.1 Ni8/TiO2-a.
Pathway involving CHx intermediates. We first discuss the elementary reaction steps among the CHx intermediates (R1 to R19; brown section in Fig. 5) with CH4 and CO as the main products. Initially, the reaction proceeds by adsorption and activation of H2 (R1) and CO2 (R2). Direct dissociation of
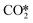 (R3) needs to overcome an activation energy of 0.99 eV and this step is exothermic by 0.81 eV. After
(R3) needs to overcome an activation energy of 0.99 eV and this step is exothermic by 0.81 eV. After 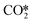 dissociation, the resulting O* is removed from the surface as H2O via two consecutive hydrogenation steps. The H* located at H1–6–7 site reacts with O*, leading to the formation of OH* (R4, ΔEact = 1.40 eV, ΔER = 0.26 eV). After a hydrogen migration step with a minor energy change (ΔER = 0.06 eV), the OH intermediate can be hydrogenated to H2O (R5). Including the migration step, this step has activation and reaction energies of 1.39 eV and 1.07 eV, respectively. Finally, the desorption of H2O (R6) is endothermic by ΔEdes = 0.94 eV, leaving an adsorbed CO* on Ni8/TiO2-a. This CO* species can either desorb from the surface (R7) with an energy of 1.93 eV or dissociate to form C* and O* (for H-assisted CO* dissociation, see below). It should be emphasized that CO desorption can also occur at the states CO*O*2H*, CO*OH*H* and CO*2H* with desorption energies of 2.18, 2.16 and 2.17 eV, respectively. These pathways are not explicitly shown in Fig. 5, though they are taken into account in the microkinetic modelling (vide infra).
dissociation, the resulting O* is removed from the surface as H2O via two consecutive hydrogenation steps. The H* located at H1–6–7 site reacts with O*, leading to the formation of OH* (R4, ΔEact = 1.40 eV, ΔER = 0.26 eV). After a hydrogen migration step with a minor energy change (ΔER = 0.06 eV), the OH intermediate can be hydrogenated to H2O (R5). Including the migration step, this step has activation and reaction energies of 1.39 eV and 1.07 eV, respectively. Finally, the desorption of H2O (R6) is endothermic by ΔEdes = 0.94 eV, leaving an adsorbed CO* on Ni8/TiO2-a. This CO* species can either desorb from the surface (R7) with an energy of 1.93 eV or dissociate to form C* and O* (for H-assisted CO* dissociation, see below). It should be emphasized that CO desorption can also occur at the states CO*O*2H*, CO*OH*H* and CO*2H* with desorption energies of 2.18, 2.16 and 2.17 eV, respectively. These pathways are not explicitly shown in Fig. 5, though they are taken into account in the microkinetic modelling (vide infra).
The adsorption of H2 on the surface containing CO* (R8) is exothermic by −1.46 eV. The direct dissociation of CO* (R9, ΔEact = 1.99 eV, ΔER = −0.24 eV) generates an adsorbed C* at F1–2–7–8 site and an adsorbed O* at H5–6–7 site, which can be hydrogenated to CH4 and H2O, respectively. Compared to the direct CO dissociation on Ni8/In2O3 (ΔEact = 3.24 eV),62 which shares a similar Ni8 cluster morphology as Ni8/TiO2 anatase, a lower activation energy is observed on Ni8/TiO2 anatase. This suggests that Ni/TiO2 is a more effective catalyst for CO2 methanation than Ni/In2O3, the latter mainly producing methanol. In contrast, the work of Sterk et al.65 shows that for the Ni(110) extended surface a relatively low barrier of ΔEact = 1.56 eV is found for CO dissociation. Hydrogenation of O* to OH* (R10) is endothermic by 0.60 eV with an activation energy of 1.52 eV. The OH* reacts with another H* to form an H2O molecule (R11, ΔEact = 1.46 eV, ΔER = 1.03 eV), which then desorbs from the surface (R12, ΔEdes = 0.74 eV) and leaves an adsorbed C* species. H2 adsorption (R13) provides two H* with an adsorption energy of −1.60 eV. C* is subsequently hydrogenated to CH* (R14, ΔEact = 0.88 eV, ΔER = 0.39 eV) and 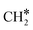 (R15, ΔEact = 0.97 eV, ΔER = 0.70 eV). In order to form CH4, one more H2 molecule adsorbs (R16, ΔEads = −1.86 eV). The reaction between
(R15, ΔEact = 0.97 eV, ΔER = 0.70 eV). In order to form CH4, one more H2 molecule adsorbs (R16, ΔEads = −1.86 eV). The reaction between 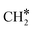 and H* results in the formation of
and H* results in the formation of 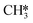 (R17, ΔEact = 1.31 eV, ΔER = 0.49 eV). Next, H* migrates from B6–7 to H1–6–7 resulting in a more stable configuration (ΔER = −0.31 eV). This H* reacts with
(R17, ΔEact = 1.31 eV, ΔER = 0.49 eV). Next, H* migrates from B6–7 to H1–6–7 resulting in a more stable configuration (ΔER = −0.31 eV). This H* reacts with 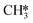 forming
forming 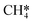 (R18) with an activation energy of 1.41 eV and this step is endothermic by 0.74 eV. The final step is CH4 desorption (R19) closing the catalytic cycle.
(R18) with an activation energy of 1.41 eV and this step is endothermic by 0.74 eV. The final step is CH4 desorption (R19) closing the catalytic cycle.
Pathway involving HxCO intermediates. For many transition metals, it has been observed that when direct C–O bond scission is associated with a prohibitively high barrier, CO dissociation will occur via COH* or HCO* intermediates.65 These steps correspond to the red section in Fig. 5. Starting at co-adsorbed CO and H2 (between R8 and R9), CO* can become hydrogenated to COH* (R20) with an activation energy of ΔEact = 2.27 eV (ΔER = 1.38 eV). Its subsequent dissociation (R21, ΔEact = 1.10 eV, ΔER = −1.05 eV) results in the same configuration of C*OH*H* as found in the direct CO* dissociation pathway. The overall activation energy for COH* dissociation is 2.48 eV, which is higher than the activation energy for the direct CO* dissociation. The alternative pathway proceeds via the hydrogenation of CO* to form HCO* (R22), which is endothermic by 1.06 eV and has an activation energy of 1.16 eV. Next, the H* located at H3–4–8 migrates to a more stable site (B6–7) with an exothermic reaction energy of 0.33 eV. HCO* dissociation generates an adsorbed CH* and O* (R23, ΔEact = 0.93 eV, ΔER = −0.79 eV). The overall activation energy for the HCO* formation and dissociation is 1.66 eV, lower than the overall barriers found for direct CO* dissociation and COH* pathways, corresponding to 1.99 and 2.48, respectively. The overall activation energy of 1.66 eV lies in between the values found for Ni8/In2O3 (1.80 eV)62 and for a stepped Ni(110)65 surface (1.21 eV).
After HCO* dissociation, the O* reacts with the remaining H* forming OH* (R24). The activation energy and reaction energy for OH* formation are ΔEact = 1.84 eV and ΔER = 0.67 eV, respectively, including the migration of H* and OH*. H2 adsorption provides two H* located at H1–6–7 and H3–4–8 (R25, ΔEads = −1.28 eV). The OH* then is hydrogenated to H2O* (R26, ΔEact = 1.05 eV, ΔER = 0.81 eV), which desorbs from the surface (R27) and generates the same configuration of CH*H* as found in the direct CO dissociation pathway.
Alternatively, HCO* can be hydrogenated to form HCOH* (R29, ΔEact = 2.28 eV, ΔER = 0.99 eV), which can alternatively be obtained through COH* hydrogenation (R28, ΔEact = 1.25 eV, ΔER = 0.64 eV). HCOH* dissociation yields HC* and OH* (R30) with an activation energy of 0.95 eV and a reaction energy of −1.43 eV. The overall activation energies of HCOH* dissociation via COH* and HCO* are 2.97 eV and 2.98 eV, respectively. Both these pathways are higher in energy than the overall activation energy of HCO* dissociation, implying that the HCOH* dissociation pathway is unlikely to occur.
Another mode of H-assisted CO dissociation proceeds via the hydrogenation of HCO* to form H2CO* which can subsequently dissociate (R31 and R32). These two steps require activation energies of 1.19 eV and 2.19 eV, respectively. The corresponding reaction energies are 0.63 eV and −0.60 eV. The overall activation energy from CO*2H* to H2C*O* is 3.52 eV, implying that this pathway is likely not the most favorable pathway. H2 adsorption (R33, ΔEads = −1.32 eV) provides two H* to remove the O* through the formation of H2O. The reaction starts with the interaction of O* and H* (R34, ΔEact = 1.10 eV, ΔER = 0.04 eV), leading to the formation of OH* which can be further hydrogenated to H2O* (R35, ΔEact = 1.99 eV, ΔER = 1.42 eV). Finally, H2O desorbs from the catalyst surface (R36, ΔEdes = 0.70 eV), leaving behind 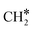 as an adsorbate on the catalyst surface and linking back to the CHx-intermediates section of the kinetic network.
as an adsorbate on the catalyst surface and linking back to the CHx-intermediates section of the kinetic network.
CH3OH formation can proceed via twofold hydrogenation of H2CO*. Two H* are supplied by the adsorption of H2 (R37, ΔEads = −1.23 eV) after which H2CO* can be hydrogenated to form H3CO* (R40, ΔEact = 0.91 eV, ΔER = 0.53 eV). The H3CO* intermediate can be further hydrogenated to form adsorbed CH3OH (R47, ΔEact = 1.80 eV, ΔER = 0.87 eV) or dissociate into H3C* and O* (R41, ΔEact = 0.75 eV, ΔER = −0.25 eV), the latter being clearly more favorable. The dissociated O* combines with the H* forming OH* (R42) with an activation energy of 0.34 eV. Alternatively, this state can also be obtained via H3COH* dissociation (R48, ΔEact = 0.55 eV, ΔER = −1.70 eV). H2 adsorption on the surface containing 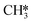 and OH* (R43) is exothermic by 1.34 eV. The resulting H* atoms can hydrogenate OH* forming H2O (R44, ΔEact = 1.66 eV, ΔER = 0.38 eV) which can desorb from the surface with a desorption energy of 1.05 eV (R45) leaving
and OH* (R43) is exothermic by 1.34 eV. The resulting H* atoms can hydrogenate OH* forming H2O (R44, ΔEact = 1.66 eV, ΔER = 0.38 eV) which can desorb from the surface with a desorption energy of 1.05 eV (R45) leaving 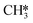 and H*.
and H*.
The last branch in the HxCO* section of the kinetic network involves the conversion of the O-terminated H2CO* intermediate. H2CO* can be hydrogenated to form H2COH* (R38, ΔEact = 1.58 eV, ΔER = 0.82 eV) which in turn can dissociate into H2C* and OH* (R39) with an activation energy of 0.52 eV. This step is exothermic by 1.46 eV. Alternatively, H2COH* is hydrogenated to H3COH* (R46), which is associated with an activation energy of 0.93 eV and an endothermic reaction energy of 0.58 eV.
3.2.2.2 Ni8/TiO2-r.
Pathway involving CHx intermediates. The brown section in Fig. 6 corresponds to the elementary reaction steps among the CHx intermediates over Ni8/TiO2-r. After adsorption of H2 (R1) and CO2 (R2), direct dissociation of
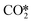 generates adsorbed CO* and O* (R3, ΔEact = 0.99 eV, ΔER = −0.21 eV). The dissociated O* atom is removed by H* through the formation and desorption of H2O. The formation of OH* (R4), including a migration of O* from H2–7–8 to H2–3–8, requires and activation energy of 1.03 eV and is endothermic by 0.25 eV. To facilitate the formation of H2O, the remaining H* needs to migrate to the H2–3–8 site to be close to the OH* (ΔER = 0.54 eV). The activation energy and reaction energy for H2O* formation (R5) are 1.25 eV and 0.21 eV, respectively. Finally, the desorption of H2O (R6) is endothermic by ΔEdes = 0.74 eV, leaving an adsorbed CO* on Ni8/TiO2-r. This remaining CO* species can either desorb from the surface (R7) with a desorption energy of ΔEdes = 2.13 eV or dissociate to form C* and O*. Similar to the Ni8/TiO2-a system, CO desorption can also occur at the states CO*O*2H*, CO*OH*H* and CO*2H* with desorption energies of 2.11, 2.23 and 2.54 eV, respectively. These pathways are not explicitly shown in Fig. 6, though they are taken into account in the microkinetic modelling (vide infra).
generates adsorbed CO* and O* (R3, ΔEact = 0.99 eV, ΔER = −0.21 eV). The dissociated O* atom is removed by H* through the formation and desorption of H2O. The formation of OH* (R4), including a migration of O* from H2–7–8 to H2–3–8, requires and activation energy of 1.03 eV and is endothermic by 0.25 eV. To facilitate the formation of H2O, the remaining H* needs to migrate to the H2–3–8 site to be close to the OH* (ΔER = 0.54 eV). The activation energy and reaction energy for H2O* formation (R5) are 1.25 eV and 0.21 eV, respectively. Finally, the desorption of H2O (R6) is endothermic by ΔEdes = 0.74 eV, leaving an adsorbed CO* on Ni8/TiO2-r. This remaining CO* species can either desorb from the surface (R7) with a desorption energy of ΔEdes = 2.13 eV or dissociate to form C* and O*. Similar to the Ni8/TiO2-a system, CO desorption can also occur at the states CO*O*2H*, CO*OH*H* and CO*2H* with desorption energies of 2.11, 2.23 and 2.54 eV, respectively. These pathways are not explicitly shown in Fig. 6, though they are taken into account in the microkinetic modelling (vide infra).
The adsorption of H2 on the surface containing CO* (R8) is exothermic by 1.78 eV. It is important to note that CO can desorb from CO*2H*, generating 2H* species (R66, ΔEdes = 2.54 eV), which should be considered as a part of the rWGS cycle. A relatively low activation energy of 1.41 eV is required for direct CO* dissociation (R9, ΔER = 0.33 eV). The dissociated O* fragment is two-fold hydrogenated to form H2O. After the formation of OH* (R10, ΔEact = 2.02 eV, ΔER = 0.80 eV), the OH* migrates from H2–7–8 to B7–8 (ΔER = −0.70 eV). Subsequently the OH* reacts with the remaining H* forming H2O* (R11, ΔEact = 1.42 eV, ΔER = 0.89 eV). After the desorption of H2O (R12, ΔEdes = 0.87 eV), the C* undergoes four consecutive hydrogenation steps yielding CH4. H2 adsorption (R13, ΔEads = −1.95 eV) provides two H* for the hydrogenation of C* to CH* (R14, ΔEact = 1.56 eV, ΔER = 0.71 eV) and 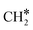 (R15, ΔEact = 0.85 eV, ΔER = 0.75 eV).
(R15, ΔEact = 0.85 eV, ΔER = 0.75 eV). 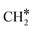 will be hydrogenated to
will be hydrogenated to 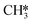 and
and 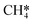 by the presence of two H* (R16, ΔEads = −1.84 eV).
by the presence of two H* (R16, ΔEads = −1.84 eV). 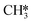 formation (R17) is endothermic by 0.47 eV overcoming an activation energy of 1.34 eV.
formation (R17) is endothermic by 0.47 eV overcoming an activation energy of 1.34 eV. 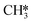 migration from T6–7–8 to B7–8 (ΔER = 0.02 eV) is followed by the formation of CH4. The activation energy and reaction energy for CH4 formation (R18) are 1.72 eV and 0.86 eV, respectively. Once CH4 is formed, it desorbs from the catalyst (R19, ΔEdes = 0.15 eV).
migration from T6–7–8 to B7–8 (ΔER = 0.02 eV) is followed by the formation of CH4. The activation energy and reaction energy for CH4 formation (R18) are 1.72 eV and 0.86 eV, respectively. Once CH4 is formed, it desorbs from the catalyst (R19, ΔEdes = 0.15 eV).
Pathway involving HxCO intermediates. In the red section of Fig. 6, the elementary reaction steps involving HxCO species are shown. Part of this network is comprised of the H-assisted CO dissociation. Due to the high activation energy required to form COH* formation (R20, ΔEact = 3.18 eV), we did not proceed with the calculation of the subsequent COH* dissociation or COH* hydrogenation to HCOH*. The alternative route for CO* hydrogenation by C–H bond formation leading to HCO* (R22) has an activation energy of 1.52 eV and is endothermic by 1.17 eV. Subsequent dissociation of HCO* (R23) results in the formation of CH* located at H6–7–8 and O* located at H1–4–7. The activation energy and reaction energy associated with the dissociation of HCO* are 1.66 eV and −0.60 eV, respectively. Due to the large distance between O* and H*, H* needs to migrate to H1–2–7 site first (ΔER = 0.35 eV). Formation of OH* (R24) requires an activation energy of 1.21 eV, accompanied by a reaction energy of 0.20 eV. H2 adsorption (R25) provides H* to hydrogenate the OH* to H2O* and is associated with an adsorption energy of −1.41 eV. OH* reacts with H* located at H2–7–8 forming H2O (R26, ΔEact = 1.81 eV, ΔER = 0.91 eV), which desorbs generating CH*H* (R27, ΔEdes = 0.32 eV), linking back to the CHx-intermediates section. HCO* can be hydrogenated to HCOH* (R29) by overcoming an activation energy of 2.04 eV. The formation of HCOH* is endothermic by 1.46 eV. HCOH* can be dissociated into CH* and OH* (R30) with an activation energy of ΔEact = 0.19 eV and a reaction energy of ΔER = −1.51 eV.
HCO* can undergo hydrogenation to form H2CO* (R31, ΔEact = 1.25 eV, ΔER = 0.61 eV), which then dissociates into H2C* and O* by overcoming an activation energy barrier of 1.41 eV (R32). The dissociation of H2CO* is exothermic by 0.89 eV. The O* species is subsequently hydrogenated to H2O*. The adsorption of H2 on the surface containing H2C* and O* is exothermic by 1.10 eV (R33). The initial hydrogenation of O* leads to the formation of OH* (R34), involving an activation energy of 1.30 eV and a reaction energy of 0.40 eV. The migration of H* occurs to react with OH* and form H2O (ΔER = 0.52 eV). Subsequently, the formation of H2O (R35) is endothermic by 0.65 eV, requiring an activation energy of 1.65 eV. Finally, H2O desorbs into the gas phase (R36) with a reaction energy of 0.33 eV and leaving an adsorbed 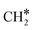 species on the surface. The subsequent hydrogenation of
species on the surface. The subsequent hydrogenation of 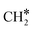 to CH4 has been discussed in the
to CH4 has been discussed in the  intermediates pathway (vide supra).
intermediates pathway (vide supra).
The adsorption of H2 on the surface containing H2CO* provides two H* species, which are subsequently utilized for the hydrogenation of H2CO*. This adsorption process is exothermic by 1.56 eV (R37). Hydrogenation of H2CO* can occur either via hydrogenation at the O-terminus or at the C-terminus, resulting in the formation of H2COH* (R38, ΔEact = 1.52 eV, ΔER = 1.27 eV) or H3CO* (R40, ΔEact = 0.92 eV, ΔER = 0.53 eV), respectively. The dissociation of H2COH* gives rise to H2C*OH*H* (R39, ΔEact = 0.46 eV, ΔER = −1.29 eV), which serves as an intermediate in the H2CO* dissociation pathway. H3CO* resulting from H2CO* hydrogenation can either undergo another hydrogenation step to form H3COH* (R47) or dissociate into H3C* and O* (R41). The dissociation of H3CO* is more favorable, exhibiting an activation energy of ΔEact = 0.88 eV and is exothermic by ΔER = −1.17 eV. In comparison, its hydrogenation has an activation energy of ΔEact = 2.23 eV and a reaction energy of ΔER = 1.18 eV. Upon the dissociation of H3CO*, the O* reacts with the remaining H* forming OH* (R42, ΔEact = 1.71 eV, ΔER = 0.52 eV). This configuration can alternatively be obtained through the dissociation of the C–O bond in H3COH* (R48, ΔEact = 0.83 eV, ΔER = −1.83 eV). The OH* is hydrogenated to H2O* in the presence of H* (R44, ΔEact = 1.92 eV, ΔER = 1.21 eV). The H* is provided by the adsorption of H2 (R43), which is exothermic by 1.17 eV. Finally, H2O desorbs from the surface with a desorption energy of 0.19 eV (R45). On the surface, there exist a 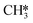 species along with a remaining H* species, and the reaction between these two entities has been previously described within the context of the
species along with a remaining H* species, and the reaction between these two entities has been previously described within the context of the  intermediates pathway. Finally, hydrogenation of H2COH* leads to the formation of H3COH* with an activation energy of 0.97 eV and a reaction energy of 0.44 eV (R46), which can desorb from the surface (R49, ΔEdes = 0.68 eV).
intermediates pathway. Finally, hydrogenation of H2COH* leads to the formation of H3COH* with an activation energy of 0.97 eV and a reaction energy of 0.44 eV (R46), which can desorb from the surface (R49, ΔEdes = 0.68 eV).
3.2.2.3 Comparison of reaction networks. Overall, our investigations on both Ni8/TiO2-a and Ni8/TiO2-r surfaces indicate that the direct dissociation of CO2 is favored over H-assisted CO2 dissociation. The corresponding reaction energy diagrams for this pathway is shown in Fig. S16.† This finding aligns with the observations made by Zhang et al., who conducted DFT calculations on Ni4/CeO2 (111) and reported activation energies of 2.55 eV for HCOO* formation, 2.80 eV for COOH* formation, and 1.60 eV for CO2 direct dissociation.66
The activation energy for the direct dissociation of CO* on Ni8/TiO2-a is 1.88 eV. In comparison, the overall activation energy for HCO* formation and dissociation is 1.66 eV whereas the overall activation energy for H2CO* formation via CO*2H* → HCO*H* → H2CO* is 1.92 eV. Based on these values, the H-assisted CO* dissociation via HCO* is energetically the most favorable pathway. For Ni8/TiO2-r, it was found that direct dissociation of CO* requires an activation energy of 1.41 eV. In comparison, the overall activation energy for HCO* formation and dissociation is 2.83 eV while the overall activation energy for H2CO* formation is 2.42 eV. Based on these numbers, direct CO* dissociation is energetically the most likely pathway over Ni8/TiO2-r.
Finally, comparing Ni8/TiO2-r to Ni8/TiO2-a, the former exhibits a lower activation energy for the direct dissociation of CO*, but the subsequent hydrogenation steps are associated with higher barriers. For example, the overall activation energy for 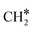 hydrogenation to CH4 on Ni8/TiO2-a and Ni8/TiO2-r are 1.59 eV and 2.18 eV, respectively. Nevertheless, assessment of the most facile pathways purely based on the DFT energetics remains in absence of the surface coverages limited and microkinetics simulations are conducted to further study the kinetic behavior of these systems.
hydrogenation to CH4 on Ni8/TiO2-a and Ni8/TiO2-r are 1.59 eV and 2.18 eV, respectively. Nevertheless, assessment of the most facile pathways purely based on the DFT energetics remains in absence of the surface coverages limited and microkinetics simulations are conducted to further study the kinetic behavior of these systems.
3.3 Microkinetics simulations
Microkinetics simulations are conducted to predict the catalytic performance of Ni8/TiO2-a and Ni8/TiO2-r for CO2 hydrogenation. The activation energies and pre-exponential factors as determined by DFT were employed for these microkinetics simulations.Fig. 7 depicts the reaction rate and product distribution for Ni8/TiO2-a and Ni8/TiO2-r. Ni8/TiO2-a exhibits a significantly higher CO2 conversion rate than Ni8/TiO2-r. These turn-over-frequencies are lower than those observed by Liu et al., who report a TOF = 2.14 × 10−3 for Ni nanoparticles of 2.2 nm at a temperature of T = 200 °C.67 Abir et al. reported a TOF = 2 × 10−2 for 2.9 nm particles at T = 350 °C.68 In both studies, a mixed anatase/rutile support was used. In contrast, Li et al. report a TOF = 5.1 × 101 s−1 for 1 nm particles supported on TiO2-anatase at T = 500 °C.69 These latter results align well to our results found for Ni8/TiO2-a. At low temperature, both surface models produce mainly CH4, while the selectivity to CO increases with temperature at the expensive of the CH4 selectivity. The selectivity towards CH3OH is negligible at all temperatures considered. At a temperature of 350 K, Ni8/TiO2-a only produces CH4, while the CH4 selectivity for Ni8/TiO2-r is 85%.
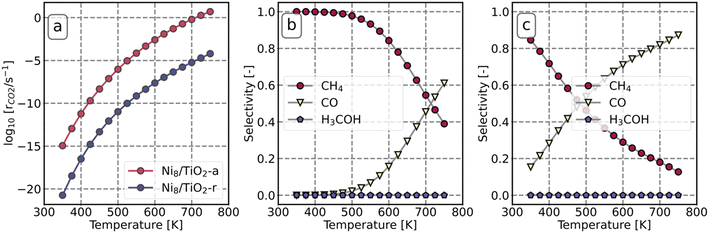 | ||
| Fig. 7 Reaction rate of CO2 as a function of temperature (a). The selectivity of CO, CH4 and H3COH as a function of temperature on Ni8/TiO2-a (b) and Ni8/TiO2-r (c). | ||
To determine the dominant pathway for CO2 hydrogenation within the chemokinetic network of Ni8/TiO2-a and Ni8/TiO2-r, a reaction pathway analysis is conducted. Fig. S17 and S18† provide the molar rate fluxes for Ni8/TiO2-a and Ni8/TiO2-r at T = 600 K. The dominant reaction pathways for product formation at this temperature are indicated in Fig. 8. For both models, direct dissociation of CO2 is preferred over H-assisted CO2 dissociation. The manner of CO dissociation differs between Ni8/TiO2-a and Ni8/TiO2-r. On Ni8/TiO2-a, the former favors H-assisted CO dissociation while the latter favors direct CO* dissociation.
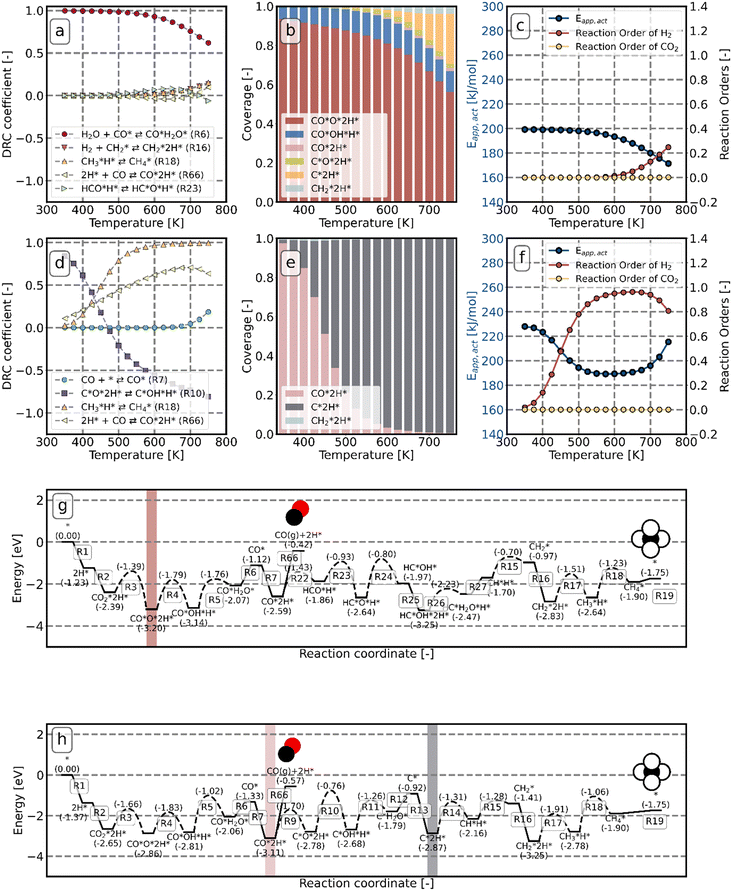
To determine which steps control the overall activity and selectivity, DRC and DSC analyses (with respect to CO2 consumption) are conducted. Fig. 9a shows that at low temperature, the desorption of H2O (R6 in Fig. 5) is the rate-determining step on Ni8/TiO2-a. The dominant species on the surface is CO*O*2H* (Fig. 9b). This observation can be attributed to the fact that the elementary reactions R4, R5, and R6 in Fig. 5 are endothermic. As such, CO*O*2H* is the state lowest in energy prior to the rate-determining step R6 which consequently becomes the most abundant state under these conditions. From Fig. 9c, we can see that the apparent activation energy is around 200 kJ mol−1 at low temperature and decreases with increasing temperature. This result can be rationalized from Fig. 9g which shows the potential energy diagram for CH4 formation via the HCO* dissociation pathway. The dominant intermediary state is highlighted in red and the overall barrier for H2O desorption (the rate-determining step) with respect to this state is determined to be 2.08 eV, which is in agreement with the apparent activation energy. The reaction orders are in line with this observation. Since the dominant CO*O*2H* state already has two hydrogen atoms present, no further hydrogen is necessary to proceed towards the rate-determining step and consequently the reaction order in H2 (Fig. 9c) is observed to be zero. Likewise, since the dominant state already represents the fragments of CO2 dissociation, a reaction order of 0 in CO2 is found.
At temperatures between T = 500 K and T = 650 K, H2O desorption becomes less rate-limiting to the rate of CO2 consumption while HCO*H* ⇄ HC*O*H* (R23) and 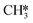 hydrogenation (R18) becomes more rate-limiting. Simultaneously, it is observed that CO desorption (R66) becomes rate-inhibiting. Due to the increase in temperature, there is more thermal energy available to overcome the H2O desorption barrier resulting in barriers further down the kinetic pathway to become rate-limiting. Since CO desorption (R66) prevents the formation of CH4 which is still the dominant product under these conditions, this step is rate-inhibiting. Further increasing the temperature above T = 650 K results in further decreasing the degree of rate control of the H2O desorption reaction. Simultaneously, HCO*H* ⇄ HC*O*H* (R23) becomes rate-inhibiting, whereas
hydrogenation (R18) becomes more rate-limiting. Simultaneously, it is observed that CO desorption (R66) becomes rate-inhibiting. Due to the increase in temperature, there is more thermal energy available to overcome the H2O desorption barrier resulting in barriers further down the kinetic pathway to become rate-limiting. Since CO desorption (R66) prevents the formation of CH4 which is still the dominant product under these conditions, this step is rate-inhibiting. Further increasing the temperature above T = 650 K results in further decreasing the degree of rate control of the H2O desorption reaction. Simultaneously, HCO*H* ⇄ HC*O*H* (R23) becomes rate-inhibiting, whereas 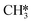 hydrogenation (R18) and CO desorption (R66) become rate-limiting. These changes reflect the change in selectivity from CH4 to CO. At elevated temperature, the dominant pathway switches from CH4 production via the HCO* intermediate to a rWGS pathway via R66. Since H2O desorption is a step in the kinetic network for both CO as well as CH4 production, this step remains rate-limiting to some extent.
hydrogenation (R18) and CO desorption (R66) become rate-limiting. These changes reflect the change in selectivity from CH4 to CO. At elevated temperature, the dominant pathway switches from CH4 production via the HCO* intermediate to a rWGS pathway via R66. Since H2O desorption is a step in the kinetic network for both CO as well as CH4 production, this step remains rate-limiting to some extent. 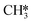 hydrogenation is also still a rate-limiting step as even at elevated temperature there remains a significant selectivity towards CH4. Nevertheless, the rate of CO2 consumption for CH4 production is lower than for CO and a change in selectivity towards CH4 by lowering the barrier for HCO*H* ⇄ HC*O*H* would result in a decreased overall activity, explaining why this step becomes rate-inhibiting at elevated temperature. The DSC analysis as shown in Fig. S19† further reflects upon this. From this figure, it can be seen that HCO*H* ⇄ HC*O*H* and CO* desorption control the selectivity between CH4 and CO. The apparent activation energy and reaction orders change accordingly as a function of temperature. With increasing temperature, the catalyst tends to reside in states further down the kinetic pathway with respect to CO*O*2H*, specifically CO*OH*H*, CO*2H*, C*O*2H*, C*2H* and
hydrogenation is also still a rate-limiting step as even at elevated temperature there remains a significant selectivity towards CH4. Nevertheless, the rate of CO2 consumption for CH4 production is lower than for CO and a change in selectivity towards CH4 by lowering the barrier for HCO*H* ⇄ HC*O*H* would result in a decreased overall activity, explaining why this step becomes rate-inhibiting at elevated temperature. The DSC analysis as shown in Fig. S19† further reflects upon this. From this figure, it can be seen that HCO*H* ⇄ HC*O*H* and CO* desorption control the selectivity between CH4 and CO. The apparent activation energy and reaction orders change accordingly as a function of temperature. With increasing temperature, the catalyst tends to reside in states further down the kinetic pathway with respect to CO*O*2H*, specifically CO*OH*H*, CO*2H*, C*O*2H*, C*2H* and 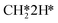 . From Fig. 9f it can be readily seen that these states are all higher in energy with respect to CO*O*2H*. With respect to the barrier of the dominant rate-limiting step for these intermediates, i.e. either
. From Fig. 9f it can be readily seen that these states are all higher in energy with respect to CO*O*2H*. With respect to the barrier of the dominant rate-limiting step for these intermediates, i.e. either 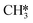 hydrogenation or CO* desorption, the energy difference is somewhat smaller than between CO*O*2H* and the barrier for H2O* desorption. Since all these intermediary species already contain fragments arising from
hydrogenation or CO* desorption, the energy difference is somewhat smaller than between CO*O*2H* and the barrier for H2O* desorption. Since all these intermediary species already contain fragments arising from 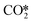 adsorption, the reaction order in CO2 remains zero. In contrast, with the exception of
adsorption, the reaction order in CO2 remains zero. In contrast, with the exception of 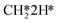 , all other abundant intermediary states require the adsorption of another H2 molecule in order to proceed to the rate-limiting step of
, all other abundant intermediary states require the adsorption of another H2 molecule in order to proceed to the rate-limiting step of 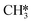 hydrogenation. Consequently, the increased reaction order in H2 reflects the decrease in surface abundance of CO*O*2H* in favor of a number of intermediates that are precursor species towards CH4 formation that requires the adsorption of H2 to produce CH4.
hydrogenation. Consequently, the increased reaction order in H2 reflects the decrease in surface abundance of CO*O*2H* in favor of a number of intermediates that are precursor species towards CH4 formation that requires the adsorption of H2 to produce CH4.
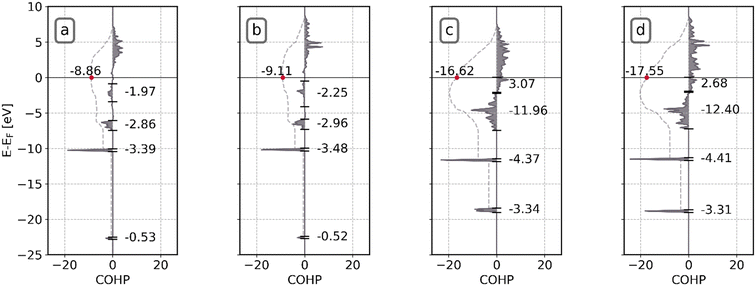
In Fig. 9d, the DRC analysis for Ni8/TiO2-r is shown. At low temperatures, the reaction is mainly controlled by the rate of C*O*2H* ⇄ C*OH*H* (R10) and CO*2H* is the most abundant cluster configuration. The desorption of CO requires 2.54 eV, whereas the activation energy between CO*2H* and R10 is 2.35 eV. At low temperature CH4 formation is preferred, yet the selectivity towards CH4 rapidly decreases in favor of CO with increasing temperature as desorption rates increase more rapidly with increasing temperature in comparison to surface reactions. With increasing temperature, the degree of rate-control of step R10 decreases in favor of CO* desorption (R66) and CH3 hydrogenation (R18) becoming rate-limiting steps. A further increase in temperature results in C*O*2H* ⇄ C*OH*H* becoming rate-inhibiting while the degree of rate-control for CO* desorption and CH3 hydrogenation increase further. From Fig. 9e, it is found that CO*2H is the dominant surface state at the low temperature regime whereas with increase in temperature C*2H* becomes the most abundant surface state. The change in surface coverage reflects the degree of rate control for C*O*2H* ⇄ C*OH*H*. When this step is rate-controlling, the state lowest in energy prior to the barrier of this step corresponds to CO*2H*. When this step is no longer rate-limiting due to the increase in temperature, the state C*2H* is the next state lowest in energy prior to one of the rate-limiting steps (i.e. R18 and R66).
The apparent activation energy and the reaction orders as shown in Fig. 9f are in line with these trends. At low temperature, a value of 230 kJ mol−1 is found, corresponding to the difference in energy between the CO*2H state (Fig. 9h, highlighted in pink) and the height of the transition state for C*O*2H hydrogenation. With increasing temperature, the system spends more time in the C*2H* state which lies higher in energy. Consequently, the apparent activation energy decreases. In contrast to the low temperature situation, a facile quantitative comparison between the energy levels of the states in the potential energy diagram and the apparent activation energy is not possible for the high temperature situation as no single elementary reaction step is predominantly rate-controlling. The increase in the apparent activation energy for T > 700 K is caused by the deposition of carbonaceous species leading to catalyst deactivation. The observation that C*O*2H* hydrogenation is strongly rate-inhibiting is in line with this observation. As this step becomes more facile, O* that could otherwise be used to recombine with C* to form CO* which can desorb from the surface, is now removed as H2O. In absence of O* and with C* + 2H* being very stable on the surface, further progression towards CH4 is prevented. The branch in the kinetic network via R9–R13 effectively leads to a dead state of the catalyst. Finally, Fig. 9f shows that the reaction order in CO2 remains close to zero, irrespective of temperature whereas the reaction order in H2 increases as a function of temperature. Since both the CO*2H* intermediate and the C*2H* intermediates already contain the dissociation fragments of CO2 necessary for the rate-limiting steps to proceed, an increase or decrease in the partial pressure of CO2 will not affect the overall rate. In contrast, in the high temperature regime the dominant state lacks 2H* species for the 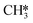 + H* reaction to proceed. The reaction order in H2 therefore reflects the extent to which this pathway controls the overall reaction rate. At temperatures T > 700 K, we however observe that the reaction order in H2 slightly decreases. Here, additional H* is detrimental to the activity of the catalyst as it leads to further O* removal and thus the formation of strongly bound C*.
+ H* reaction to proceed. The reaction order in H2 therefore reflects the extent to which this pathway controls the overall reaction rate. At temperatures T > 700 K, we however observe that the reaction order in H2 slightly decreases. Here, additional H* is detrimental to the activity of the catalyst as it leads to further O* removal and thus the formation of strongly bound C*.
Conclusively, the lower reactivity observed for the Ni8/TiO2-r system in comparison to Ni8/TiO2-a is caused by the presence of a relative facile direct CO dissociation. The low barrier for CO dissociation coincides with C* being strongly bound to the catalyst leading to catalyst deactivation. In contrast, for Ni8/TiO2-a, direct CO dissociation is difficult, and a H-assisted pathway is more facile. This is already indicative for C* being less strongly bound to the catalyst benefiting its activity. These results are according to the Sabatier principle which shows that although strong adsorption leads to facile activation of the adsorbates, it prevents the desorption of the products, poisoning the catalyst.
As the utilization of the PBE functional commonly leads to an overestimation of the binding energy of CO,70–72 we need to critically assess its effect. As such, additional microkinetic simulations were conducted wherein simultaneously the CO and CO2 adsorption energy were decreased in a range of 0.0 to 0.3 eV on both Ni8/TiO2-a and Ni8/TiO2-r models, ensuring that this modification does not affect the overall thermodynamics of the reaction. The resulting reaction rates of CO2 and selectivity were analyzed and summarized in Fig. S26 and S27.† Decreasing the CO adsorption energy on both Ni8/TiO2-a and Ni8/TiO2-r catalysts results in an increase in the CO selectivity. For these two surfaces, CO becomes the main product when the correction of CO adsorption energy was set to 0.3 eV at 600 K.
Although we established that H-spillover is associated with relatively high barriers, we nevertheless explored the effect of an enhanced H* coverage on the Ni8-clusters. This analysis was however limited to CO and HCO dissociation and HCO formation as these steps were found to affect the selectivity of the reaction (Fig. S19†). As we determined H-spillover to be difficult, thus assuming that accumulation of additional H* species on the clusters would proceed via adsorption from the gas phase, we furthermore calculated the adsorption energy of H2 as function of the H* coverage. The results are shown in Tables S3–S5 in the ESI.† From Tables S3 and S4,† it can be seen that on Ni8/TiO2-anatase, the overall activation energies for HCO* formation and dissociation are always higher than the activation energies for direct dissociation of CO*. Conversely, on the Ni8/TiO2 rutile surface, the direct CO* dissociation exhibits a lower activation energy as compared to the HCO* formation and dissociation. Therefore, the conclusion that Ni8/TiO2 anatase predominantly follows the HCO* pathway while Ni8/TiO2-rutile favors the direct CO* dissociation pathway remains valid, irrespective of the H* coverage. Furthermore, from Table S5† it can be observed that additional H* accumulation is associated with a significantly decreased adsorption energy. Given the loss of entropy of H2 upon adsorption, we estimate, especially at higher temperature, that the presence of more than two H* species, in addition to HxCO, on the Ni8 clusters is highly unlikely.
From these additional simulations we can conclude that the Ni8 clusters have a vastly lower activity as compared to experiment,67,68 even when taking potential effects of overbinding and H-accumulation into account. Despite that Ni8/TiO2-r allows for a direct CO dissociation, it results in the formation of a very stable C* species effectively poisoning the catalyst surface. This poisoning condition is less severe on Ni8/TiO2-a, yet compared to extended Ni surfaces, also here much higher adsorption energies are observed for the reaction intermediates. We assign the increased adsorption strength of CO* and C* to the presence of coordinatively undersaturated Ni atoms in these clusters, which due to the specific alignment of the Ni atoms with the support, lead to much stronger adsorption energies for Ni8/TiO2-rutile as compared to Ni8/TiO2-anatase.
3.4 Electronic structure analysis
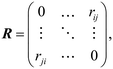
Microkinetic simulations show that for both Ni8/TiO2-a as well as Ni8/TiO2-r the initial C–O bond scission in CO2 proceeds in a direct fashion. After removal of the dissociated O* fragment as H2O, the remaining CO* fragment needs to dissociate as well for CH4 formation. For this step, the two models differ in the preferred pathway as shown in Fig. 8. For Ni8/TiO2-a, C–O bond scission proceeds in a H-assisted fashion via an HCO* intermediate, whereas for Ni8/TiO2-r it proceeds in a direct fashion. This observation can be readily explained based on the activation energies. The activation energy of CO direct dissociation for Ni8/TiO2-r is 1.41 eV, whereas for Ni8/TiO2-a a higher activation energy of 1.99 eV is found. The barriers for CO* hydrogenation to HCO* and its subsequent dissociation to CH* and O* are 1.16 eV and 0.93 eV. Despite the initial hydrogenation step being endothermic by 0.70 eV, the effective barrier for the H-assisted step is 1.66 eV, making the H-assisted pathway preferred over the direct pathway.To better understand the differences in the activation energies of CO* direct dissociation, we performed a density of states (DOS) and Crystal Orbital Hamilton Population (COHP) analysis on CO* and the transition state of its dissociation towards C* + O* for Ni8/TiO2-a and Ni8/TiO2-r. The results of this analysis are shown in Fig. 10 and S24.† In Fig. S21a and f,† the DOS and COHP for the C–O interaction of CO in the gas phase is shown. Note that a more negative COHP coefficient indicates that the Kohn–Sham states provide a bonding contribution to the pair of atoms, while a more positive COHP coefficient indicates that the Kohn–Sham state provides a more anti-bonding contribution. Fig. S21a† displays the canonical molecular orbitals of CO and their occupancies. These molecular orbitals are commonly divided among σ- and π-type orbitals based on the presence or absence of a nodal plane alongside the C–O bonding axis. It can be readily observed that the number of valence electrons of CO in the gas phase corresponds to 10. From Fig. S21f,† the bonding character for each of the orbitals is seen including the integrated COHP (iCOHP) at the Fermi level which is a quantitative measure of the C–O bond strength. Upon adsorption, we can see from Fig. S24a and c† that the 3σ and 4σ interactions are largely unchanged due to a limited mixing of these molecular orbitals with the d-orbitals on Ni. In contrast, the 1π and 5σ orbitals show pronounced mixing as evidenced by the broadening of the peaks. Furthermore, due to the mixing of the anti-bonding 2π* orbitals with the d-orbitals on Ni, the newly formed states derived from these orbitals descent below the Fermi level and become occupied. The integrated DOS (iDOS) at the Fermi level for adsorbed CO shows that the electron density around CO increases, in line with the higher electronegativity of CO as compared to Ni and resulting in the occupation of the anti-bonding orbitals. The occupation of these anti-bonding orbitals together with the reduction in bonding character of the 1π-type orbitals lead to an activation of the CO molecule, as evidenced by the reduced iCOHP value shown in Fig. S21† corresponding to −15.86 and −16.09 for Ni8/TiO2-a and Ni8/TiO2-r, respectively. These values are however sufficiently similar that we cannot attribute the difference in the dissociation barrier to a difference in the activation of the CO molecule upon adsorption. The C–O interaction in the transition state, as shown in Fig. S21,† are also substantially similar from which we infer that both clusters have the same propensity towards activating CO and we hypothesize that the difference in the CO dissociation barrier should therefore be caused by differences in the stabilization of the pre-dissociated fragments in the transition state. It should be noted that this result contrasts with CO activation patterns typically found for extended metals, as showcased in the work of Fariduddin et al.73
To test our hypothesis, in Fig. 10a–d, a COHP analysis is conducted for the Ni–CO interaction. Similar to the results found for the C–O interaction, here the COHP acts as a metric to assess the interaction strength between the cluster and the C* and O* fragments. The iCOHP values for adsorbed CO*, i.e. in the initial state, at the Fermi level are −8.86 and −9.11 for Ni8/TiO2-a and Ni8/TiO2-r. These values are in line with the observed adsorption heats of −2.14 eV and −2.54 eV for Ni8/TiO2-a and Ni8/TiO2-r, respectively. For the transition state, significantly lower iCOHP values of −16.62 and −17.55 are found for Ni8/TiO2-a and Ni8/TiO2-r, respectively. Clearly, Ni8/TiO2-r shows a significant increase in the Ni–CO interaction strength between the TS and IS in comparison to Ni8/TiO2-a, explaining the much lower reaction barrier observed. We attribute this enhanced bonding interaction of pre-dissociated C* and O* in the transition state on Ni8/TiO2-r to the presence of a very stable fivefold adsorption site for C, whereas for Ni8/TiO2-a a less favorable quasi-fourfold adsorption site is present (as shown in Fig. S25†). This five-fold site of Ni8/TiO2-r hosts a square-planar motif for which exceptional stability for C* has been identified earlier in the work of Nandula et al.74
Conclusively, a critical factor in the preferred kinetic pathway is assigned to the presence of a low CO dissociation barrier. In the absence of such a barrier, a H-assisted route is preferred as seen for Ni8/TiO2-a. In contrast, Ni8/TiO2-r allows for a direct CO dissociation due to the availability of an active motif for which the COHP analysis predicts enhanced stability for the dissociation fragments.
4. Conclusions
In this study, the effect of the TiO2 phase, anatase or rutile, on CO2 hydrogenation over small Ni8 cluster was investigated. Using a hybrid genetic algorithm/density functional theory approach, the putative global minimum structure for Ni8 clusters supported on the most stable anatase and rutile surface terminations were searched. Due to different metal–support interactions, the Ni8 clusters adopt different morphologies on anatase and rutile TiO2.By means of density functional theory calculations, all elementary reaction steps relevant to CO2 hydrogenation, i.e. direct and H-assisted CO2 and CO dissociation as well as subsequent hydrogenation steps to form CH4 and CH3OH were calculated. By means of microkinetic modelling, we observed that the anatase supported Ni8 clusters yielded a higher activity towards CO2 consumption as compared to the rutile equivalent. For both clusters, at the low temperature the selectivity is mainly towards CH4 whereas with increasing temperature, the selectivity switches to CO. The amount of CH3OH produced remains negligible.
Both catalysts exhibit direct CO2 dissociation. Ni8/TiO2-r shows direct dissociation whereas for Ni8/TiO2-a the H-assisted route via a HCO* intermediate is preferred. Analysis of the reaction energy diagram and the DFT calculations reveal that this difference can be assigned to the stronger adsorption for carbonaceous species on Ni8/TiO2-r as compared to Ni8-TiO2-a. Not only leads this to a lower barrier for direct dissociation for the former catalyst, it also leads to the reaction intermediates being too strongly bound to the catalyst, effectively deactivating the catalyst. This rationalizes the consistent lower activity observed for Ni8-TiO2-r.
Analysis of the kinetic network pinpoints the CO dissociation barrier playing a critical role in determining the overall activity and mechanistic route. To understand the underlying electronic effects leading to the difference in CO dissociation barrier between the anatase and rutile supported Ni8 clusters, a combined density of states and crystal orbital Hamilton population analysis was conducted. The integrated COHP value for the Ni–CO interaction at the Fermi level for the transition states for these two structures reveal that CO is more tightly bound to Ni8 supported on rutile as compared to a cluster supported on anatase. This is not caused by electronic metal support interactions but rather by the different morphology of the cluster. For Ni8/TiO2-r, the morphology allows for highly stable fivefold-coordinated CO whereas for Ni8/TiO2-a, only a fourfold-coordinated mode is available which leads to less strongly bound CO.
This study showcases the potential role the support has in affecting the preferred pathway, selectivity and activity of a catalyst by inducing a preferred morphology of adsorbed clusters.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Lulu Chen: conceptualization, data curation, formal analysis, investigation, validation, visualization, writing-original draft; Ying-Ying Ye: data curation, formal analysis, investigation, visualization; Rozemarijn D. E. Krösschell: data curation, formal analysis visualization; Emiel J. M. Hensen: conceptualization, supervision, writing-review & editing, funding acquisition; Ivo A. W. Filot: conceptualization, methodology, resource, visualization, supervision, writing-review & editing, funding acquisition.Conflicts of interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.Acknowledgements
We gratefully acknowledge the financial support provided by the China Scholarship Council. We also thank NWO and SurfSARA for granting the computational resources used to perform the DFT calculations.References
- C. Vogt, M. Monai, G. J. Kramer and B. M. Weckhuysen, Nat. Catal., 2019, 2 Search PubMed.
- J. C. Navarro, M. A. Centeno, O. H. Laguna and J. A. Odriozola, Catalysts, 2018, 8 Search PubMed.
- L. Guerra, S. Rossi, J. Rodrigues, J. Gomes, J. Puna and M. T. Santos, J. Environ. Chem. Eng., 2018, 6, 671–676 CrossRef CAS.
- K. Müller, M. Städter, F. Rachow, D. Hoffmannbeck and D. Schmeißer, Environ. Earth Sci., 2013, 70, 3771–3778 CrossRef.
- S. Chen and A. M. Abdel-Mageed, Int. J. Hydrogen Energy, 2013, 48, 24915–24935 CrossRef.
- M. Götz, J. Lefebvre, F. Mörs, A. McDaniel Koch, F. Graf, S. Bajohr, R. Reimert and T. Kolb, Renewable Energy, 2016, 85, 1371–1390 CrossRef.
- M. Lehner, R. Tichler, H. Steinmüller and M. Koppe, Power-to-Gas: Technology and Business Models, Springer Briefs in Energy, 2014 Search PubMed.
- F. Graf, Impact, 2018, 2018, 81–83 CrossRef.
- O. Mohan, S. Shambhawi, R. Xu, A. A. Lapkin and S. H. Mushrif, ChemCatChem, 2021, 13, 2420–2433 CrossRef CAS.
- P. Frontera, A. Macario, M. Ferraro and P. L. Antonucci, Catalysts, 2017, 7, 59 CrossRef.
- A. Quindimil, U. De-La-Torre, B. Pereda-Ayo, A. Davó-Quiñonero, E. Bailón-García, D. Lozano-Castelló, J. A. González-Marcos, A. Bueno-López and J. R. González-Velasco, Catal. Today, 2020, 356, 419–432 CrossRef CAS.
- A. Parastaev, V. Muravev, E. H. Osta, T. F. Kimpel, J. F. M. Simons, A. J. F. van Hoof, E. Uslamin, L. Zhang, J. J. C. Struijs, D. B. Burueva, E. V. Pokochueva, K. V. Kovtunov, I. V. Koptyug, I. J. Villar-Garcia, C. Escudero, T. Altantzis, P. Liu, A. Béché, S. Bals, N. Kosinov and E. J. M. Hensen, Nat. Catal., 2022, 5, 1051–1060 CrossRef CAS.
- Z. Liu, X. Gao, B. Liu, W. Song, Q. Ma, T. s. Zhao, X. Wang, J. W. Bae, X. Zhang and J. Zhang, Appl. Catal., B, 2022, 310, 121303 CrossRef CAS.
- S. Tada, T. Shimizu, H. Kameyama, T. Haneda and R. Kikuchi, Int. J. Hydrogen Energy, 2012, 37, 5527–5531 CrossRef CAS.
- R. van Hardeveld and A. van Montfoort, Surf. Sci., 1966, 4, 396–430 CrossRef CAS.
- G. Melaet, A. E. Lindeman and G. A. Somorjai, Top. Catal., 2014, 57, 500–507 CrossRef CAS.
- X. Wang, H. Shi, J. H. Kwak and J. Szanyi, ACS Catal., 2015, 5, 6337–6349 CrossRef CAS.
- V. Iablokov, S. K. Beaumont, S. Alayoglu, V. V. Pushkarev, C. Specht, J. Gao, A. Paul Alivisatos, N. Kruse and G. A. Somorjai, Nano Lett., 2012, 12, 3091–3096 CrossRef CAS PubMed.
- J. H. Kwak, L. Kovarik and J. Szanyi, ACS Catal., 2013, 3, 2449–2455 CrossRef CAS.
- P. Panagiotopoulou, Appl. Catal., A, 2017, 542, 63–70 CrossRef CAS.
- N. L. Visser, O. Daoura, P. N. Plessow, L. C. J. Smulders, J. W. de Rijk, J. A. Stewart, B. D. Vandegehuchte, F. Studt, J. E. S. van der Hoeven and P. E. de Jongh, ChemCatChem, 2022, 14, e202200665 CrossRef CAS.
- C. Vogt, E. Groeneveld, G. Kamsma, M. Nachtegaal, L. Lu, C. J. Kiely, P. H. Berben, F. Meirer and B. M. Weckhuysen, Nat. Catal., 2018, 1, 127–134 CrossRef CAS.
- C. Vogt, F. Meirer, M. Monai, E. Groeneveld, D. Ferri, R. A. van Santen, M. Nachtegaal, R. R. Unocic, A. I. Frenkel and B. M. Weckhuysen, Nat. Commun., 2021, 12, 7096 CrossRef CAS PubMed.
- Y. Guo, S. Mei, K. Yuan, D. J. Wang, H. C. Liu, C. H. Yan and Y. W. Zhang, ACS Catal., 2018, 8, 6203–6215 CrossRef CAS.
- E. J. M. H. Jérôme, F. M. Simons, T. J. de Heer, R. C. J. van de Poll, V. Muravev and N. Kosinov, J. Am. Chem. Soc., 2023, 145, 20289–20301 CrossRef PubMed.
- M. P. C. Van Etten, B. Zijlstra, E. J. M. Hensen and I. A. W. Filot, ACS Catal., 2021, 11, 8484–8492 CrossRef CAS PubMed.
- S. Liang, C. Hao and Y. Shi, ChemCatChem, 2015, 7, 2559–2567 CrossRef CAS.
- R. Zhou, N. Rui, Z. Fan and C. Liu, Int. J. Hydrogen Energy, 2016, 41, 22017–22025 CrossRef CAS.
- C.-J. Pan, M.-C. Tsai, W.-N. Su, J. Rick, N. G. Akalework, A. K. Agegnehu, S.-Y. Cheng and B.-J. Hwang, J. Taiwan Inst. Chem. Eng., 2017, 74, 154–186 CrossRef CAS.
- W. Li, G. Zhang, X. Jiang, Y. Liu, J. Zhu, F. Ding, Z. Liu, X. Guo and C. Song, ACS Catal., 2019, 9, 2739–2751 CrossRef CAS.
- Y. Lin, Y. Zhu, X. Pan and X. Bao, Catal. Sci. Technol., 2017, 7, 2813–2818 RSC.
- J. Zhou, Z. Gao, G. Xiang, T. Zhai, Z. Liu, W. Zhao, X. Liang and L. Wang, Nat. Commun., 2022, 13, 327 CrossRef CAS PubMed.
- D. Messou, V. Bernardin, F. Meunier, M. B. Ordoño, A. Urakawa, B. F. Machado, V. Collière, R. Philippe, P. Serp and C. Le Berre, J. Catal., 2021, 398, 14–28 CrossRef CAS.
- M. P. C. Van Etten, M. E. De Laat, E. J. M. Hensen and I. A. W. Filot, J. Phys. Chem. C, 2023, 127, 15148–15156 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- P. W. Fry, I. E. Itskevich, S. R. Parnell, J. J. Finley, L. R. Wilson, K. L. Schumacher, D. J. Mowbray, M. S. Skolnick, A. G. Cullis, M. Hopkinson, J. C. Clark and G. Hill, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 784–791 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- N. Martsinovich and A. Troisi, Phys. Chem. Chem. Phys., 2012, 14, 13392–13401 RSC.
- D. H. M. Azevedo, G. S. L. Fabris, J. R. Sambrano and J. M. M. Cordeiro, Comput. Mater. Sci., 2020, 171, 109222 CrossRef CAS.
- R. D. E. Krösschell, E. J. M. Hensen and I. A. W. Filot, J. Phys. Chem. C, 2024, 128, 8947–8960 CrossRef PubMed.
- C. J. Howard, T. M. Sabine and F. Dickson, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 462–468 CrossRef.
- S. Wu, X. Luo, Y. Long and B. Xu, IOP Conf. Ser.: Mater. Sci. Eng., 2019, 493, 012010 CrossRef CAS.
- S. Ma, W. Song, B. Liu, H. Zheng, J. Deng, W. Zhong, J. Liu, X. Q. Gong and Z. Zhao, Catal. Sci. Technol., 2016, 6, 6128–6136 RSC.
- L. B. Vilhelmsen and B. Hammer, J. Chem. Phys., 2014, 141, 044711 CrossRef PubMed.
- M. W. Chang, L. Zhang, M. Davids, I. A. W. Filot and E. J. M. Hensen, J. Catal., 2020, 392, 39–47 CrossRef CAS.
- L. Van Der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, A. Müller, J. Nothman, G. Louppe, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, D. Cournapeau, M. Brucher and M. Perrot, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- I. Gohberg, S. Goldberg and M. A. Kaashoek, Classes of Linear Operators, Birkhäuser Basel, Basel, 1990, vol. I, pp. 138–147 Search PubMed.
- I. A. W. Filot, M. P. C. van Etten, D. W. J. G. Trommelen and E. J. M. Hensen, J. Open Source Softw., 2023, 8, 5710 CrossRef.
- I. A. W. Filot, Introduction to microkinetic modeling, Technische Universiteit Eindhoven, 2018 Search PubMed.
- I. A. W. Filot, R. A. Van Santen and E. J. M. Hensen, Angew. Chem., Int. Ed., 2014, 53, 12746–12750 CrossRef CAS PubMed.
- P. Nitoń, A. Zywociński, M. Fiałkowski and R. Hołyst, Nanoscale, 2013, 5, 9732–9738 RSC.
- W. L. Vrijburg, E. Moioli, W. Chen, M. Zhang, B. J. P. Terlingen, B. Zijlstra, I. A. W. Filot, A. Züttel, E. A. Pidko and E. J. M. Hensen, ACS Catal., 2019, 9, 7823–7839 CrossRef CAS.
- C. T. Campbell, Top. Catal., 1994, 1, 353–366 CrossRef CAS.
- F. Cannizzaro, E. J. M. Hensen and I. A. W. Filot, ACS Catal., 2023, 13, 1875–1892 CrossRef CAS PubMed.
- Q. Ke, L. Kang, X. Chen and Y. Wu, Chem. Sci. J., 2020, 132, 1–11 CrossRef.
- A. Mahdavi-Shakib, T. N. Whittaker, T. Y. Yun, K. B. Sravan Kumar, L. C. Rich, S. Wang, R. M. Rioux, L. C. Grabow and B. D. Chandler, Nat. Catal., 2023, 6, 710–719 CrossRef CAS.
- E. B. Sterk, A. E. Nieuwelink, M. Monai, J. N. Louwen, E. T. C. Vogt, I. A. W. Filot and B. M. Weckhuysen, JACS Au, 2022, 2, 2714–2730 CrossRef CAS PubMed.
- J. Zhang, Y. Yang, J. Liu and B. Xiong, Appl. Surf. Sci., 2021, 558, 149866 CrossRef CAS.
- J. Liu, C. Li, F. Wang, S. He, H. Chen, Y. Zhao, M. Wei, D. G. Evans and X. Duan, Catal. Sci. Technol., 2013, 3, 2627–2633 RSC.
- M. A. Abir, R. E. Phillips, J. Z. M. Harrah and M. R. Ball, Catal. Sci. Technol., 2024, 14, 4506–4521 RSC.
- J.-Y. Li, X.-M. Lai, H. Gu, C.-X. Wang, X.-P. Fu, W.-W. Wang, Q. Fu, F. Ryan Wang, C. Ma and C.-J. Jia, ChemRxiv, 2023, preprint, DOI:10.26434/chemrxiv-2023-bm0gl.
- F. Abild-Pedersen and M. P. Andersson, Surf. Sci., 2007, 601, 1747–1753 CrossRef CAS.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- O. Mohan, Q. T. Trinh, A. Banerjee and S. H. Mushrif, Mol. Simul., 2019, 45, 1163–1172 CrossRef CAS.
- I. A. W. Filot, F. Fariduddin, R. J. P. Broos, B. Zijlstra and E. J. M. Hensen, Catal. Today, 2016, 275, 111–118 CrossRef CAS.
- A. Nandula, Q. T. Trinh, M. Saeys and A. N. Alexandrova, Angew. Chem., Int. Ed., 2015, 54, 5312–5316 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00586d |
| This journal is © The Royal Society of Chemistry 2024 |