Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory and microkinetics of ethylene chain growth and termination on silica grafted group 4 metal hydrides†
Neha
Mehra
 a and
William F.
Schneider
a and
William F.
Schneider
 *ab
*ab
aDepartment of Chemical and Biomolecular Engineering, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: wschneider@nd.edu
bDepartment of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN 46556, USA
First published on 19th July 2024
Abstract
The creation and ethylene oligomerization function of silica-anchored group 4 metal (M = Ti, Zr, Hf) hydrides as a function of the anchor site structure are explored using density functional theory models. Oligomerization potential energy surfaces are sensitive both to the metal ion and to the structure of the anchoring site. Microkinetic models predict the oligomerization rate and degree of polymerization as a function of the site, temperature, and reactant pressures. Intrinsic catalytic activity is predicted to vary as Ti < Zr > Hf down the group, irrespective of site model, while absolute rates and product distributions are strongly sensitive to the site model, temperature, and hydrogen pressure. Catalysts based on these sites are plausible candidates for high-temperature ethylene oligomerization of interest for generating fuels from ethylene, but selectivity is expected to require careful control over the site structure and reaction conditions.
1 Introduction
Group 4 metal (M = Ti, Zr, Hf) ions anchored to oxide supports are known to catalyze a wide variety of hydrocarbon transformations.1–4 Initially explored as heterogeneous catalysts for olefin polymerization,5,6 anchored heterogenized ions have also been shown to activate paraffinic C–H bonds and to depolymerize paraffins.7–12 Zakharov et al. demonstrated early on that group 4 tetraalkyl precursors dosed to silica and treated with hydrogen form catalysts active for ethylene polymerization at near ambient temperatures,5,6,11 as evidenced by the appearance of vibrational features characteristic of methylene and methyl groups.1,5,6 Depolymerization and hydrogenolysis is observed when the polymer/catalyst combination is treated in hydrogen at elevated temperatures.1,13 Similarly prepared Ti,7,14 Zr,8,9,11,12 and Hf1,10 catalysts are also observed to be active for hydrogenolysis of waxes and alkanes at 150–180 °C. These observations reflect the ability of anchored group 4 ions to form, rearrange and cleave C–C bonds, and thus their potential utility as oligomerization catalysts at elevated temperatures.Controlled coupling of ethylene into short-chain linear alpha olefins (LAOs) or transportation fuels is particularly timely and relevant.15 The development of shale gas reserves has created a rich new source of light hydrocarbons, including ethane.16 Ridha et al. have shown that the catalytic dehydrogenation of ethane to ethylene followed by oligomerization is a potentially efficient route to liquid fuel.17 A hydrogen-tolerant, high temperature, and selective oligomerization catalyst would obviate the need for hydrogen separation before oligomerization. In this light, hydrogen treated and supported group-4 metal catalysts are appealing candidates as potential oligomerization catalysts. As evidence of the potential, Szeto et al. have reported that anchored Zr is highly selective for 2-butene dimerization at an elevated pressure and temperature.18
The generation of anchored single-site catalysts typically takes advantage of the reaction of metal alkyl precursors with surface hydroxyls.2,19 The precise nature of the resultant site is observed to be a function of the hydroxyl coverage.20–22 Active catalysts are prepared by treatment in hydrogen to remove residual alkyls and form surface hydrides.7,14,21,23–25 These processes have been investigated spectroscopically using vibrational infrared (IR), 1H/29Si and 1H/13C solid state nuclear magnetic resonance (NMR) and 1H double-quantum (DQ) solid-state NMR, and extended X-ray absorption fine structure (EXAFS) spectroscopies, as well as chemical methods. When tetraalkyl group 4 precursors are dosed to silica, typical products after hydrogen treatment include mono-((![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH) and dihydrides ((
SiO)3MH) and dihydrides ((![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2MH2).1,8,12,24–26
SiO)2MH2).1,8,12,24–26
Guided by these observations, atomistic representations of silica-anchored group 4 ions have been attempted by cluster and periodic approaches that use silica models of different types and sizes.24,27–31 Cluster models capture local site structure and approximate the constraints imposed by the larger silica framework. Mono- and dihydrides of Zr or Ti have been grafted on clusters composed of two to three silicon atoms for evaluating energy profiles of methane activation, ethylene chain growth and hydrogenolysis of M-alkyl reactions.3,28,31–33 Kalhor et al. investigated the reactivity of similarly modeled Zr-hydrides towards N2O and CO2 probe molecules and found predicted IR and NMR signatures to be consistent with experimental observations.34 β-Cristobalite is a popular choice35,36 for describing a silica support, because it can be simply represented within a supercell, it incorporates the constraints of the bulk oxide, and its (111)- and (001)-facets have local order similar to amorphous silica, based on X-ray diffraction observations.37 Approximate models of amorphous silica have been constructed through molecular dynamics simulations starting from a fully hydroxylated β-cristobalite surface38,39 or other siliceous structures.36,40,41 The reactivity is reported to be sensitive to the details of the support model, whether represented as a cluster,42,43 a pseudo-amorphous structure,30,44–46 or an ordered β-cristobalite surface.27,36 The “right” balance of strain,44,45 topological orientation,43 and relative site abundance47–49 are all reported to have an impact on reactivity. In general, there is no agreement on the appropriate strategy or exact relationship between the representation of the anchoring site and reactivity.50
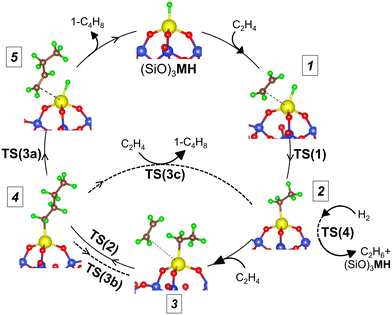
From the available experimental5,51,52 and computational3,33,53,54 evidence, supported metal hydrides catalyze olefin chain growth through olefin insertion into M–H bonds (reaction (1)) and into M–C bonds (reaction (2)):
| M–H + C2H4(g) → M–C2H5 | (1) |
| M–C2H5 + C2H4(g) → M–C4H9 | (2) |
| M–C4H9 → M–H + C4H8(g) | (3a) |
| M–C4H9 → M–C2H5 + C2H4(g) | (3b) |
| M–C4H9 + C2H4(g) → M–C2H5 + C4H8(g) | (3c) |
| M–C4H9 + C2H4(g) → M–C2H3 + C4H10(g) | (3d) |
Besedin et al. compared pathways relevant to ethylene polymerization (reactions (1) and (2)) on cluster models of Zr mono- and dihydrides.33 They reported activation energies for insertion of ethylene into M–C bonds (reaction (2)) to be greater than insertion into the M-hydride (reaction (1)), making the former rate limiting for chain growth. Similar models of Ti mono- and dihydrides predict M–C insertion barriers to be greater than that for Zr,3 suggesting a role of the metal ion in controlling chain growth. Their work did not comment upon the role of termination pathways (reactions (3a)–(3d)).
Kaminsky et al.,57 Hoffman et al.,58 and Kissin et al.59 reported that co-fed H2 reduces the polymer average molecular weight relative to a pure ethylene feed, suggesting that hydrogenolysis of the M–R bond competes with chain growth:1,13
| M–R + H2(g) → MH + RH | (4) |
To address this need, here we use supercell DFT models to compare ethylene chain growth and termination pathways (reactions (1) to (4)) on group 4 metal hydrides grafted on silica. We construct models to probe the sensitivity of energetics to metal ion identity and nature of the anchoring site. We find non-periodicity in kinetics with Zr sites having the lowest activation energies for all reaction steps, followed by Hf and Ti sites, irrespective of the hydrides considered. However, we observe that chain growth kinetics are sensitive to the host silica ring size. We use the DFT results as inputs to microkinetic models to predict turnover frequencies and degree of polymerization (![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n) as a function of the metal ion, site environment and hydrogen pressures at various temperatures. We show that the rate and
n) as a function of the metal ion, site environment and hydrogen pressures at various temperatures. We show that the rate and ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n are sensitive to both the metal ion and anchoring site. We conclude that these isolated ions are candidates to synthesize fuel range to polymeric products from ethylene, given that the control is exercised over synthesis protocols, reaction conditions and feed composition.
n are sensitive to both the metal ion and anchoring site. We conclude that these isolated ions are candidates to synthesize fuel range to polymeric products from ethylene, given that the control is exercised over synthesis protocols, reaction conditions and feed composition.
2 Methods
2.1 Computational details
Plane-wave, supercell DFT calculations are performed using the Vienna Ab initio simulation package (VASP),60–63 and projector augmented wave64 treatment of core-valence interactions. All systems studied are closed shell and were treated non-spin-polarized using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA).65,66 The Brillouin zone is sampled at the Γ point, plane waves are included to a cutoff of 400 eV, and self-consistent field electronic energies converged to 10−6 eV. Atomic forces are converged to less than 0.05 eV Å−1 using a conjugate gradient algorithm. Transition states are constructed using a climbing image nudged elastic band (CI-NEB)67,68 by linearly interpolating between initial and final structures. Final clean up of transition states was performed using a quasi-Newton (variable metric) optimization or the dimer method.69 Transition states are confirmed through harmonic frequencies and by visual inspection of imaginary modes in the graphical interface of the atomic simulation environment (ASE).70 Harmonic vibrational frequencies of the species are computed by finite difference with a step size of 0.01 Å including all adsorbate atoms, metal atom, and/or oxygens of the first coordination sphere. Free gas molecules are put in 15 × 15 × 15 Å3 cubic cells; energies are given in Table S1.† Electronic energies of reaction intermediates and transition states are reported in Tables S7, S13, S19† and reaction and activation energies for elementary steps in Tables S8, S14 and S20.† All energies reported in electron volts (eV) where 1 eV = 23.06 kcal mol−1 = 96.5 kJ mol−1. Molecular visualizations are created using VESTA.71We built baseline silica surface models starting from cubic (Fd3m) β-cristobalite (Fig. S1a†).72 Within the optimization parameters used here, the relaxed bulk lattice constant is 7.23 Å (experimental: 7.16 Å). The 1% overestimation is typical for gradient-corrected functionals.27,73 Silica surfaces having Si–OH groups are created by cleaving Si–O bonds of β-cristobalite along the (111) and (001) planes74 and saturating oxygen and silicon dangling bonds with H and OH, respectively. Fully relaxed slabs are shown in Fig. S1b and S1c.† The surface hydroxyl density of the (111) and (001) models are 3.8 and 7.6 OH per nm2, respectively. Metal complexes are anchored on these surface hydroxyls or silanols (Si–OH). We also reconstruct these surfaces to modify the support environment around the metal sites. Overall, we compare three distinct metal hydride site models (Fig. S2†). The first two models are of (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH situated on three Si–OH groups of isolated silanols (separated by –O–Si–O– bonds) and of vicinal silanols (separated by –O– bonds) on the (111) silica surface, while the third is of (
SiO)3MH situated on three Si–OH groups of isolated silanols (separated by –O–Si–O– bonds) and of vicinal silanols (separated by –O– bonds) on the (111) silica surface, while the third is of (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2MH2 anchored on a pair of vicinal Si–OHs of (001) silica. We refer to sites as a-bmr (
SiO)2MH2 anchored on a pair of vicinal Si–OHs of (001) silica. We refer to sites as a-bmr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)4−nMHn where a is the number of rings and b is the membered ring (mr) size formed by consecutive M–OSi bonds with the silica support. Further model details are provided below.
SiO)4−nMHn where a is the number of rings and b is the membered ring (mr) size formed by consecutive M–OSi bonds with the silica support. Further model details are provided below.
2.2 Microkinetic models
We use the DFT results to parameterize mean-field microkinetic models. The net rate of surface reaction j over time t is written as: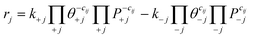 | (5) |
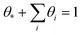 | (6) |
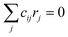 , giving linear algebraic equations that are solved symbolically with the SymPy75 library and then numerically in Python76 to obtain steady-state coverages at each temperature and pressure condition. Steady state rates (s−1) or turnover frequencies (TOFs) are obtained from these coverages.
, giving linear algebraic equations that are solved symbolically with the SymPy75 library and then numerically in Python76 to obtain steady-state coverages at each temperature and pressure condition. Steady state rates (s−1) or turnover frequencies (TOFs) are obtained from these coverages.
Rate constants for non-activated adsorption of species i are calculated using the Hertz–Knudsen equation (eqn (7)), where α′ is a sticking coefficient that we take as unity, mi is the molecular weight of the adsorbing species, kB is the Boltzmann constant, T is the temperature, and A is the area per free site, which we approximate as the surface area of the unit cell. This approximation likely exaggerates A, thus increasing absolute adsorption rates, but is unlikely to influence reactivity trends.
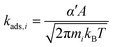 | (7) |
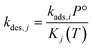 | (8) |
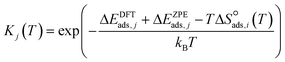 | (9) |
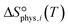 to be
to be 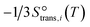 , where
, where 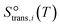 is the translational entropy of the gas-phase species i calculated by the Sackur–Tetrode equation.78,79
is the translational entropy of the gas-phase species i calculated by the Sackur–Tetrode equation.78,79
Surface reaction rate constants (k) are calculated using transition state theory, DFT-computed and ZPE corrected activation energies Ea,j and the entropy change ΔS‡j(T).
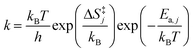 | (10) |
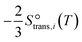 and that between a chemisorbed species and a transition state is zero. Test calculations show that the relative entropy changes are similar to those obtained from the harmonic oscillator and rigid rotor approximation for adsorbates. The free energy change of an elementary reaction
and that between a chemisorbed species and a transition state is zero. Test calculations show that the relative entropy changes are similar to those obtained from the harmonic oscillator and rigid rotor approximation for adsorbates. The free energy change of an elementary reaction 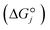 is approximated as
is approximated as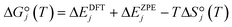 | (11) |
3 Results and discussion
3.1
3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) SiO)3MH site construction
SiO)3MH site construction
We compute the energies to graft model tetraalkyl M(CH3)4 precursors to the silica (111) surface shown in Fig. S1b,† whose adjacent Si–OH groups are separated by –O–Si–O– linkages. The choice of the precursor mimics the organometallic precursors typical for grafting metals. Grafting creates covalent M–O–Si linkages, resulting in (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)n–M(CH3)4−n species that vary in their degree of coordination to the support, n (details on page 5 in the ESI†). Fig. S3† shows the relaxed structures for n = 1, 2, 3 and Table S2† has their energies. The energies of successive grafting steps of the Zr(CH3)4 precursor on the (111) surface (Fig. S4a†) indicate that the Zr species tri-coordinated to the support (n = 3) is the most thermodynamically favored. A parity plot of integral grafting energies for all metal ions (values in Table S3†) against Zr as shown in Fig. S4b† highlights the exothermic trend to be Ti < Zr < Hf, in line with the reported M–O and M–C bond energies (Table S4†).80 Successive grafting energies decrease in magnitude with increasing degree of grafting, likely reflecting accumulated strain.
SiO)n–M(CH3)4−n species that vary in their degree of coordination to the support, n (details on page 5 in the ESI†). Fig. S3† shows the relaxed structures for n = 1, 2, 3 and Table S2† has their energies. The energies of successive grafting steps of the Zr(CH3)4 precursor on the (111) surface (Fig. S4a†) indicate that the Zr species tri-coordinated to the support (n = 3) is the most thermodynamically favored. A parity plot of integral grafting energies for all metal ions (values in Table S3†) against Zr as shown in Fig. S4b† highlights the exothermic trend to be Ti < Zr < Hf, in line with the reported M–O and M–C bond energies (Table S4†).80 Successive grafting energies decrease in magnitude with increasing degree of grafting, likely reflecting accumulated strain.
We next compute the energy to remove residual –CH3 ligands with hydrogen. Hydrogenolysis of each (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)nM(CH3)4−n to form the corresponding hydride (Table S2†) is exothermic (Table S3†). Relaxed (
SiO)nM(CH3)4−n to form the corresponding hydride (Table S2†) is exothermic (Table S3†). Relaxed (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)nM(H)4−n, M = Ti, Zr, Hf, structures are shown in Fig. S5.† M–O and M–H bond lengths in the tetrahedral M-hydride sites vary non-periodically as Ti < Hf ≤ Zr, following their ionic radii.81,82 The average O–M–H angle in (
SiO)nM(H)4−n, M = Ti, Zr, Hf, structures are shown in Fig. S5.† M–O and M–H bond lengths in the tetrahedral M-hydride sites vary non-periodically as Ti < Hf ≤ Zr, following their ionic radii.81,82 The average O–M–H angle in (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3M(H) also follows the same trend. Overall, Ti sites have the least negative formation energies, referenced to silica (111) and the precursor.
SiO)3M(H) also follows the same trend. Overall, Ti sites have the least negative formation energies, referenced to silica (111) and the precursor.
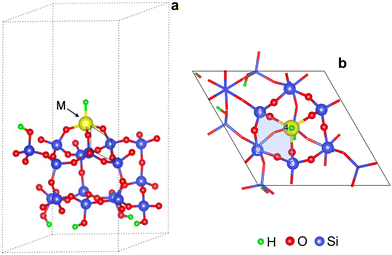
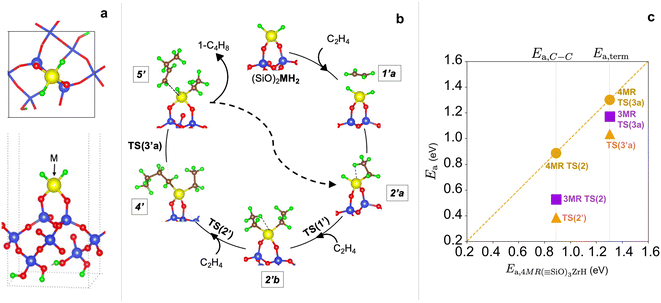
Fig. 1 shows a representative modeled metal monohydride, (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH on silica (111), obtained upon full relaxation. The metal ion forms three M–O–Si bonds to the support and thus, rests upon three 4-membered rings (3-4mr), each containing three Si and a metal ion (Si/Si/Si/M). Oxygen atoms are excluded while naming the ring. Adjacent M–O–Si bonds are separated by O–Si–O linkages. We name this model as 3-4mr (
SiO)3MH on silica (111), obtained upon full relaxation. The metal ion forms three M–O–Si bonds to the support and thus, rests upon three 4-membered rings (3-4mr), each containing three Si and a metal ion (Si/Si/Si/M). Oxygen atoms are excluded while naming the ring. Adjacent M–O–Si bonds are separated by O–Si–O linkages. We name this model as 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH, where 3 is for the number of rings it forms with silica and 4 refers to the size of each ring. Computed M–H stretch vibrations of 3-4mr (
SiO)3MH, where 3 is for the number of rings it forms with silica and 4 refers to the size of each ring. Computed M–H stretch vibrations of 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH in the harmonic limit agree well with experimentally reported frequencies (Table S5†). These results are consistent with the well-known ability of a hydroxyl covered silica surface to accommodate metal alkyl precursors and their further conversion to thermodynamically stable hydrides.
SiO)3MH in the harmonic limit agree well with experimentally reported frequencies (Table S5†). These results are consistent with the well-known ability of a hydroxyl covered silica surface to accommodate metal alkyl precursors and their further conversion to thermodynamically stable hydrides.
3.2 Oligomerization intermediates on 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) SiO)3MH sites
SiO)3MH sites
To evaluate the sensitivity of ethylene oligomerization to the metal ion, we computed reaction pathways for ethylene insertion and chain growth, steps 1 through 4 in Fig. 2, including the three competing chain termination routes, on the 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH models. Transition states (TSs) are labeled according to the corresponding reaction number. Multiple configurations of each intermediate were explored, and the lowest-energy structures and corresponding transition states are shown in Fig. S6.† CONTCARs are available in a Zenodo data repository. Based on geometry data in Table S6,† the Ti species have the widest O–M–O angle and the shortest M–H or M–C bonds. The Hf species have slightly shorter bond lengths than the Zr species. CI-NEB trajectories are shown in Fig. S7.† Electronic energies of the structures are given in Table S7† and the DFT-computed reaction and activation energies for elementary steps are in Table S8.†
SiO)3MH models. Transition states (TSs) are labeled according to the corresponding reaction number. Multiple configurations of each intermediate were explored, and the lowest-energy structures and corresponding transition states are shown in Fig. S6.† CONTCARs are available in a Zenodo data repository. Based on geometry data in Table S6,† the Ti species have the widest O–M–O angle and the shortest M–H or M–C bonds. The Hf species have slightly shorter bond lengths than the Zr species. CI-NEB trajectories are shown in Fig. S7.† Electronic energies of the structures are given in Table S7† and the DFT-computed reaction and activation energies for elementary steps are in Table S8.†
Potential energy surfaces (PESs) for ethylene insertion and chain growth are reported in Fig. 3a. The calculations reveal ethylene physisorbs on the hydride site (structure 1 in Fig. 2 and 3a) with some distortion of the O3MH tetrahedron. The binding energies are modestly negative. Ethylene inserts into the M–H bond through a four-membered-ring transition state, TS(1) (Fig. 3b), to generate M-ethyl (structure 2). TS(1) structures are relatively insensitive to metal ions, except for the noticeable difference in the Si–O–M angle that is widest for Ti. Activation energies relative to the hydride and ethylene range from −0.02 to 0.12 eV. Reaction energies from the hydride to the ethyl are slightly greater on Ti (by −0.14 eV) than those on Zr and Hf (1*, 1 in Table S8†). The results suggest that ethylene insertion into the hydride will be rapid and roughly insensitive to the metal.
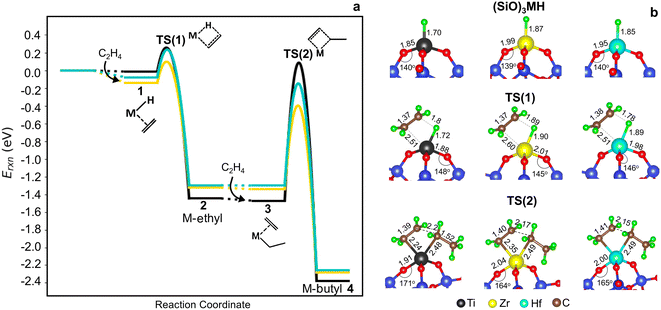 | ||
Fig. 3 (a) Cossee–Arlman potential energy surfaces computed and referenced to 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH sites and 2C2H4 gas molecules for M = Ti (black), Zr (yellow) and Hf (blue). Species numbers correspond to Fig. 2. (b) Structures of 3-4mr ( SiO)3MH sites and 2C2H4 gas molecules for M = Ti (black), Zr (yellow) and Hf (blue). Species numbers correspond to Fig. 2. (b) Structures of 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH, TS(1) and TS(2). Bond distances in Å and bond angles in °. SiO)3MH, TS(1) and TS(2). Bond distances in Å and bond angles in °. | ||
Ethylene adsorption at M-ethyl occurs with little distortion of the O3MC tetrahedron (structure 3 in Fig. 2) and ethylene sits away from and weakly bound to the metal center (Fig. S6† and 3a, 2* in Table S8†). A representative CI-NEB trajectory for migratory insertion of ethylene into the M–C bond of M-ethyl via the TS(2) on the Hf site forming the C–C bond is shown in Fig. S7b.† The initially bent butyl chain then rotates to an elongated, zig-zagged M-butyl that is lower in energy (structure 4 in Fig. 2). Migratory insertion into the M–C bond has a substantially greater barrier that decreases from Ti > Hf > Zr, in inverse variation to the M–C and M–O bond lengths. Ustynyuk et al.3 similarly report higher M–C insertion activation energies for Ti-monohydride than that for Zr on cluster models. Ethylene is closest to Ti in the TS(2) (shown in Fig. 3b) due to its smallest ionic radius. The Si–O–Ti angle increases to 171°, 6° more than the Si–O–Hf and Si–O–Zr angles. The average strain induced by stretching of the Si–O–M angles as the site passes through a TS is measured by 〈a〉 and is reported in Table S9.† For the TS(2), 〈a〉 varies with the barrier of migratory insertion into the M–C bond and decreases from Ti to Hf to Zr. Thus, a larger 〈a〉 indicates a greater structural distortion associated with a larger energy penalty for reaching the TS.
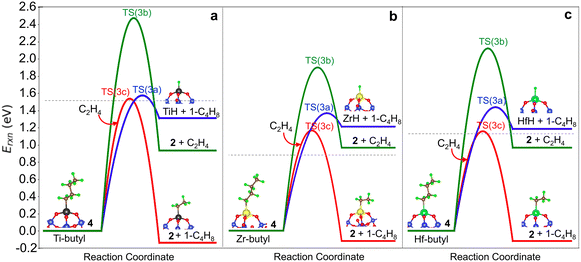
We compare the three termination pathways (reactions (3a)–(3c)) in Fig. 4a, b and c, respectively. Overall, the three termination routes have barriers comparable to or greater than chain growth (dashed line in Fig. 4a–c). Termination by reaction (3a) occurs via the TS(3a) (structure in Fig. S6†) and involves β-H transfer from M-butyl to the metal ion. Simultaneous loss of the M–C bond yields 1-butene adsorbed on (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH (structure 5 in Fig. 2). Ti has the highest activation energy for this step, followed by Hf and then Zr. Butene binds weakly to the metal ion (3a* in Table S8†). This pathway is the reverse of ethylene insertion into the M–H bond and there is an orientational resemblance between the TS(3a) and TS(1).
SiO)3MH (structure 5 in Fig. 2). Ti has the highest activation energy for this step, followed by Hf and then Zr. Butene binds weakly to the metal ion (3a* in Table S8†). This pathway is the reverse of ethylene insertion into the M–H bond and there is an orientational resemblance between the TS(3a) and TS(1).
Transfer of a β-alkyl fragment to M releases an ethylene molecule from the growing chain (reaction (3b)) and thus is the reverse of reaction (2). We replot the computed energy profile of the latter, referenced to M-butyl, 4, in Fig. 4a–c. Activation energies increase from Zr to Hf to Ti and are greater than β-H to M activation energies by at least 0.55 eV.
The TS(3c) for ethylene-assisted termination (reaction (3c)) is obtained by coordinating an ethylene to M-butyl and simulating a direct transfer of H from the β-C of the butyl chain to ethylene (CI-NEB in Fig. S7d†), yielding 1-butene and M-ethyl. TS(3c) is a 6-membered ring and is geometrically similar on Ti, Zr, and Hf (structures in Fig. S6†). Fig. 4a–c shows that reaction (3c) is slightly exothermic, unlike reactions (3a) and (3b). This route is kinetically favored over β-H transfer to M on Ti-, Zr- and Hf-butyl. However, the entropic cost to coordinate an ethylene to M-butyl also enters into the contribution of this route, as discussed further below.
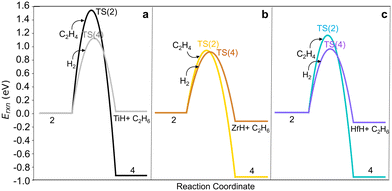
Hydrogenolysis of the M–C bond via reaction (4) would also terminate the growing chain. We computed H2 dissociation across the M–C bond of M-ethyl (2) to form ethane and restore (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH (reaction (4)) via the TS(4) (Fig. S7e†). Fig. 5 shows that C–C bond formation yielding M-butyl (4) is more exothermic than hydrogenolysis to ethane (reactions 2*, 2, 4*, 4 in Table S8†). Barriers are comparable on Zr-ethyl and lower for hydrogenolysis on Ti- and Hf-ethyl. The resultant ethylene hydrogenation (C2H4 + H2 → C2H6) is highly exothermic (−1.40 eV). Hydrogen will likely impact both overall chain growth and selectivity to olefinic products.
SiO)3MH (reaction (4)) via the TS(4) (Fig. S7e†). Fig. 5 shows that C–C bond formation yielding M-butyl (4) is more exothermic than hydrogenolysis to ethane (reactions 2*, 2, 4*, 4 in Table S8†). Barriers are comparable on Zr-ethyl and lower for hydrogenolysis on Ti- and Hf-ethyl. The resultant ethylene hydrogenation (C2H4 + H2 → C2H6) is highly exothermic (−1.40 eV). Hydrogen will likely impact both overall chain growth and selectivity to olefinic products.
These findings show that the key steps of chain growth and termination by chain transfer to the ethylene monomer are highly sensitive to the nature of the group-4 metal ion and will impact overall reaction chemistry. Differences in initiation steps and hydrogenolysis also exist, but are modest.
3.3 Oligomerization microkinetics on 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) SiO)3MH sites
SiO)3MH sites
We use DFT-computed reaction and activation energies to formulate a fully reversible microkinetic model. Adsorbates are assumed to lose all translational entropy and to retain all rotational and vibrational entropy; a harmonic oscillator and rigid rotor model yields nearly equivalent results (Fig. S8†). We include initiation, chain growth and β-H transfer to the metal with the model. Other termination pathways are kinetically uncompetitive at the temperatures probed here (Fig. S9†). Calculations on homogeneous Ti-alkoxide complexes similarly report a preference for the β-H to M termination pathway.83 As our goal is to compare ideal rates and selectivities to olefin vs. paraffin products vs. the metal, we neglect reinsertion reactions and chain-walking processes, which can lead to isomerized chains and secondary products. Thus, we focus on primary reaction channels, and assume that transport of products from active sites is more rapid than reinsertions.
Steady state rates are computed at zero conversion in pure ethylene feed at 17 bar pressure to capture the intrinsic activities. Computed turnover frequencies (TOFs) are shown as an Arrhenius plot in Fig. 6. TOFs vary as Zr > Hf > Ti, opposite apparent activation energy trends. Fig. S10† shows that Hf-ethyl and Ti-ethyl are the most abundant surface intermediate (MASI) at all temperatures, while the MASI evolves from Zr-butyl to Zr-ethyl with increasing T.
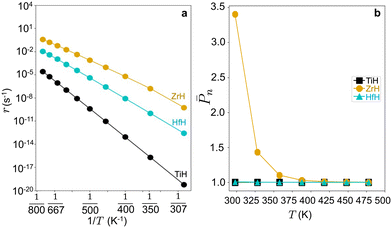 | ||
Fig. 6 (a) Oligomerization rates (r) at PC2H4 = 17 bar against reciprocal temperature (1/T) and (b) ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) nvs. temperature (T) on 3-4mr ( nvs. temperature (T) on 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH sites (M = Ti, Zr, Hf). SiO)3MH sites (M = Ti, Zr, Hf). | ||
To identify the elementary steps most responsible for controlling the dimerization rates, degree of rate control (DRC)84 analysis is performed. The rate sensitivity to specific reactions is calculated as XRC,j (eqn (12)) by changing the forward (k+j) and reverse (k−j) rate constants of step j simultaneously by 2%, and monitoring the change of the overall rate r with respect to the reference rate, r0. The rate constants of other steps and the equilibrium constant, Kj, are kept constant.
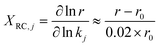 | (12) |
We employ DFT rate constants to first estimate the degree of polymerization (![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n) promoted by each metal site on the reaction with olefins and in the absence of H2. The
n) promoted by each metal site on the reaction with olefins and in the absence of H2. The ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n model assumes that chain growth occurs with a probability of propagation, α,85,86 calculated by steady state mole balance applied to an M-alkyl site assuming all reactions are irreversible and rate constants for chain growth, kcc and termination, kterm are independent of chain length (eqn (S11), details in the ESI,† page 21). The
n model assumes that chain growth occurs with a probability of propagation, α,85,86 calculated by steady state mole balance applied to an M-alkyl site assuming all reactions are irreversible and rate constants for chain growth, kcc and termination, kterm are independent of chain length (eqn (S11), details in the ESI,† page 21). The ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n value for ethylene only feed expresses the average number of oligomeric units86,87 in the olefinic product:
n value for ethylene only feed expresses the average number of oligomeric units86,87 in the olefinic product:
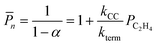 | (13a) |
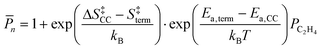 | (13b) |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n. The calculated
n. The calculated ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n values are shown in Fig. 6b and follow Ti ≤ Hf < Zr.
n values are shown in Fig. 6b and follow Ti ≤ Hf < Zr. ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n is a decreasing function of temperature and is greatest on Zr. Thus, within the 3-4mr site model, ZrH is expected to be a more effective catalyst than TiH or HfH, each of which would have little to any oligomerization activity. Such small
n is a decreasing function of temperature and is greatest on Zr. Thus, within the 3-4mr site model, ZrH is expected to be a more effective catalyst than TiH or HfH, each of which would have little to any oligomerization activity. Such small ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n stands in contrast to experimental observations of polymerization by group-4 metal hydrides on silica.1,5,6,11
n stands in contrast to experimental observations of polymerization by group-4 metal hydrides on silica.1,5,6,11![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n on a 3-4mr ZrH site at low ethylene pressure is approximately one (Fig. S12b†). This observation suggests that some feature of the model other than the metal itself is relevant to the catalysis.
n on a 3-4mr ZrH site at low ethylene pressure is approximately one (Fig. S12b†). This observation suggests that some feature of the model other than the metal itself is relevant to the catalysis.
Hydrogenolysis will compete with β-H elimination with co-fed H2(g). To incorporate this competition into the ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n, α is recast as αH2 (eqn (14a) and (S12)†). The contributions of olefin and paraffin to total
n, α is recast as αH2 (eqn (14a) and (S12)†). The contributions of olefin and paraffin to total ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n (computed with αH2) are obtained by multiplying this
n (computed with αH2) are obtained by multiplying this ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n by the ratio of individual fraction's production rate to the total rate of product formation:
n by the ratio of individual fraction's production rate to the total rate of product formation:
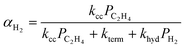 | (14a) |
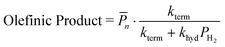 | (14b) |
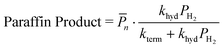 | (14c) |
![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n values at 298 K and 473 K. Rate constants are computed from entropy-corrected energy profiles (Fig. S13†). At 298 K, a decrease in
n values at 298 K and 473 K. Rate constants are computed from entropy-corrected energy profiles (Fig. S13†). At 298 K, a decrease in ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n can be seen for the 3-4mr (
n can be seen for the 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH site along with the increasing dominance of paraffinic products even when a small amount of hydrogen is added (0–0.1 molar ratio, Fig. 7). The same behavior is seen for Ti and Hf (Fig. S13†), but the decline in
SiO)3ZrH site along with the increasing dominance of paraffinic products even when a small amount of hydrogen is added (0–0.1 molar ratio, Fig. 7). The same behavior is seen for Ti and Hf (Fig. S13†), but the decline in ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n is not significant.
n is not significant. ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n at 473 K on the three 3-4mr (
n at 473 K on the three 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3MH sites shown in Fig. S13† is close to unity and the sites are inactive for ethylene hydrogenation.
SiO)3MH sites shown in Fig. S13† is close to unity and the sites are inactive for ethylene hydrogenation.
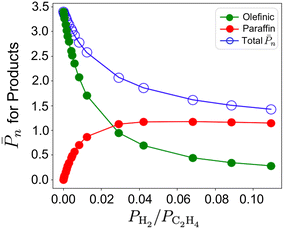 | ||
Fig. 7 Total ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n on the 3-4mr ( n on the 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH site and relative contributions of olefin (green) and paraffin (red) fractions to it against PH2/PC2H4 at T = 298 K and total pressure of 17 bar. SiO)3ZrH site and relative contributions of olefin (green) and paraffin (red) fractions to it against PH2/PC2H4 at T = 298 K and total pressure of 17 bar. | ||
3.4 Influence of the anchoring site
To explore the sensitivity of the results above to the silica anchoring site, we considered a model in which the M ion is anchored via three 3-membered-rings (3-3mr) to silica (Fig. 8a). We adopt the reconstructed silica (111) facet to represent the host site (Fig. S14†), yielding an environment similar to prior cluster models,3,33 and focus on M = Zr for the comparisons. Fig. S16† shows the structures and Tables S10 and S11† report the energies to form (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)n–Zr(CH3)4−n (n = 1–3) by Zr(CH3)4 grafting and hydrogenation to (
SiO)n–Zr(CH3)4−n (n = 1–3) by Zr(CH3)4 grafting and hydrogenation to (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)n–Zr(H)4−n (plot in Fig. S15a†). Grafting energies are less exothermic than on the more open 3-4mr site (parity plot in Fig. S15b†), as is hydrogenolysis. Bond distances are similar across the two models, but Zr–O–Si angles are less obtuse at the more constrained 3-3mr site. The M–H stretch frequency is red shifted 36 cm−1 relative to the corresponding 3-4mr (
SiO)n–Zr(H)4−n (plot in Fig. S15a†). Grafting energies are less exothermic than on the more open 3-4mr site (parity plot in Fig. S15b†), as is hydrogenolysis. Bond distances are similar across the two models, but Zr–O–Si angles are less obtuse at the more constrained 3-3mr site. The M–H stretch frequency is red shifted 36 cm−1 relative to the corresponding 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH.
SiO)3ZrH.
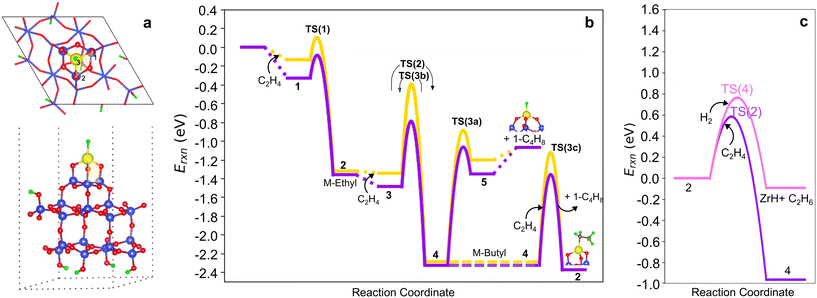 | ||
Fig. 8 (a) Top and side views of 3-3mr (SiO)3ZrH site. (b) Comparison of 3-4mr (yellow) and 3-3mr (purple) ZrH ethylene dimerization PESs computed and referenced to the site and number of C2H4 molecules reacting with it. Species numbers correspond to Fig. 2. (c) Migratory insertion into the M–C bond (purple) and hydrogenolysis (pink) pathways on 3-3mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH sites. SiO)3ZrH sites. | ||
We computed the same ethylene insertion and termination pathways on the 3-3mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH site. The structures are shown in Fig. S17,† bond distances and angles in Table S12,† energies in Table S13,† and reaction and activation energies in Table S14.†Fig. 8b compares the reaction profiles on the 3-3mr and 3-4mr sites. The energies of the intermediates are nearly the same in the two models, while olefin physisorption (points 1, 3, and 5) is somewhat more exothermic within the more strained 3-3mr model. Activation barriers for chain growth (TS(2)) and for the three termination routes TS(3a–c) are 0.2 eV less within the 3-3mr model as is the extent of 〈a〉 as the TSs are approached (Table S15†). The O–M–H angle increases 8° from the 3-4mr to the 3-3mr model, reflecting an increase in access of olefin to the metal site in the latter case. β-H transfer has the lowest activation barrier of all termination routes independent of the site model. In contrast, ethylene insertion has a lower activation energy than hydrogenolysis in the 3-3mr model (Fig. 8c), opposite that observed for the 3-4mr case.
SiO)3ZrH site. The structures are shown in Fig. S17,† bond distances and angles in Table S12,† energies in Table S13,† and reaction and activation energies in Table S14.†Fig. 8b compares the reaction profiles on the 3-3mr and 3-4mr sites. The energies of the intermediates are nearly the same in the two models, while olefin physisorption (points 1, 3, and 5) is somewhat more exothermic within the more strained 3-3mr model. Activation barriers for chain growth (TS(2)) and for the three termination routes TS(3a–c) are 0.2 eV less within the 3-3mr model as is the extent of 〈a〉 as the TSs are approached (Table S15†). The O–M–H angle increases 8° from the 3-4mr to the 3-3mr model, reflecting an increase in access of olefin to the metal site in the latter case. β-H transfer has the lowest activation barrier of all termination routes independent of the site model. In contrast, ethylene insertion has a lower activation energy than hydrogenolysis in the 3-3mr model (Fig. 8c), opposite that observed for the 3-4mr case.
To compute the oligomerization rates, we again took β-H transfer to M to be the dominant termination pathway based on a free energy analysis (Fig. S18a and b†) and computed rates using the same initiation, growth, and termination model. Fig. 9a compares the computed rates on the 3-3mr and 3-4mr sites at elevated ethylene pressure. The rates are two- to three-orders of magnitude greater on the 3-3mr site. DRC analysis reports the same shift from β-H termination to ethylene insertion with increasing temperature (Fig. S18d†), in correspondence with a shift of the MASI (Fig. S18c†) from Zr-butyl to Zr-ethyl. The ethylene-only ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n on the 3-3mr site (Fig. 9b) is similarly significantly increased than that on the 3-4mr site (Fig. 6c) at 17 bar. The performance is thus expected to be highly sensitive to the anchoring site. The high activity associated with the more constrained anchoring site is consistent with the observation that high temperature dehydroxylation of silica creates smaller and more active anchoring sites.21,22,38,88,89
n on the 3-3mr site (Fig. 9b) is similarly significantly increased than that on the 3-4mr site (Fig. 6c) at 17 bar. The performance is thus expected to be highly sensitive to the anchoring site. The high activity associated with the more constrained anchoring site is consistent with the observation that high temperature dehydroxylation of silica creates smaller and more active anchoring sites.21,22,38,88,89
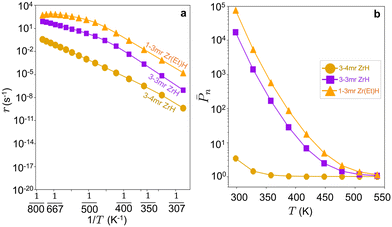 | ||
Fig. 9 (a) Oligomerization rate (r) vs. reciprocal temperature (1/T) and (b) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) nvs. temperature (T) on 3-4mr, 3-3mr ( nvs. temperature (T) on 3-4mr, 3-3mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH and 1-3mr (SiO)2Zr(Et)H sites at PC2H4 = 17 bar. SiO)3ZrH and 1-3mr (SiO)2Zr(Et)H sites at PC2H4 = 17 bar. | ||
Silica-anchored zirconium hydrides are reported to polymerize ethylene at near-ambient temperatures.6,11 The calculated ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n values at the 3-3mr ZrH site at 0.02 and 0.27 bar (Table S16 and Fig. S12b†) are consistent with these experimental observations. At higher ethylene pressures, bimolecular reactions (reactions (3c) and (3d)) as well as co-adsorbed ethylene intermediates90 could compete with the M–C insertion and unimolecular β-H transfer reactions, introducing errors into
n values at the 3-3mr ZrH site at 0.02 and 0.27 bar (Table S16 and Fig. S12b†) are consistent with these experimental observations. At higher ethylene pressures, bimolecular reactions (reactions (3c) and (3d)) as well as co-adsorbed ethylene intermediates90 could compete with the M–C insertion and unimolecular β-H transfer reactions, introducing errors into ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n.91,92 We re-computed the TS(3a) with co-adsorbed ethylene (bim-TS(3a), Fig. S17†) and found the activation energy to be comparable to that of chain transfer to monomer (TS(3c)). The activation energy for ethylene-mediated paraffin elimination (reaction (3d), Fig. S17†) is also similar to chain transfer to the monomer (Tables S13 and S14†). Relative activation energies are consistent with prior calculations.31,33 The activation free energies of all five termination routes at 298 and 473K are reported in Table S16† along with corresponding consequences for
n.91,92 We re-computed the TS(3a) with co-adsorbed ethylene (bim-TS(3a), Fig. S17†) and found the activation energy to be comparable to that of chain transfer to monomer (TS(3c)). The activation energy for ethylene-mediated paraffin elimination (reaction (3d), Fig. S17†) is also similar to chain transfer to the monomer (Tables S13 and S14†). Relative activation energies are consistent with prior calculations.31,33 The activation free energies of all five termination routes at 298 and 473K are reported in Table S16† along with corresponding consequences for ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n.
n. ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n is insensitive to the incorporation of these additional routes. We conclude that the unimolecular β-H transfer is the dominant termination route and the 3-3mr ZrH site can be tuned from a polymerization active site at room temperature to a selective oligomerization site at higher temperatures at appropriate pressures.
n is insensitive to the incorporation of these additional routes. We conclude that the unimolecular β-H transfer is the dominant termination route and the 3-3mr ZrH site can be tuned from a polymerization active site at room temperature to a selective oligomerization site at higher temperatures at appropriate pressures.
To evaluate the sensitivity of results to co-fed H2, we report the ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n and olefin/paraffin contributions on the 3-3mr site vs. PH2/PC2H4 at 17 bar total pressure and 298 and 473 K (Fig. 10). The corresponding entropy-corrected potential energy profiles for the chain growth and two competing termination reactions are shown in Fig. S19a and b.† At 298 K (Fig. 10a),
n and olefin/paraffin contributions on the 3-3mr site vs. PH2/PC2H4 at 17 bar total pressure and 298 and 473 K (Fig. 10). The corresponding entropy-corrected potential energy profiles for the chain growth and two competing termination reactions are shown in Fig. S19a and b.† At 298 K (Fig. 10a), ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n decreases and the contribution of paraffinic products increases even at low hydrogen compositions (0.1 molar ratio), as with the 3-4mr (
n decreases and the contribution of paraffinic products increases even at low hydrogen compositions (0.1 molar ratio), as with the 3-4mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH site (Fig. 7). However,
SiO)3ZrH site (Fig. 7). However, ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n on 3-3mr ZrH is approximately two orders of magnitude greater than on the 3-4mr ZrH site, even at PH2/PC2H4 = 1.
n on 3-3mr ZrH is approximately two orders of magnitude greater than on the 3-4mr ZrH site, even at PH2/PC2H4 = 1. ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n is much less sensitive to H2 at 473 K (Fig. 10b), and the short-chain products are primarily olefinic.
n is much less sensitive to H2 at 473 K (Fig. 10b), and the short-chain products are primarily olefinic.
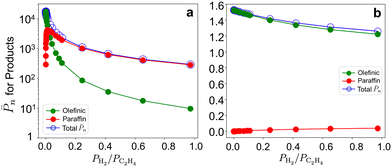 | ||
Fig. 10 Olefinic (green) and paraffinic (red) product contributions in total ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n (blue) on the 3-3mr ( n (blue) on the 3-3mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)3ZrH site vs. PH2/PC2H4 at 17 bar and (a) 298K and (b) 473K. SiO)3ZrH site vs. PH2/PC2H4 at 17 bar and (a) 298K and (b) 473K. | ||
We consider a third site model in which M is anchored to silica through only two oxygen linkages, constructed from a dehydroxylated (001) facet of silica (Fig. S20†). Zr(CH3)4 grafting energies forming (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2Zr(CH3)2 are intermediate between the 3-4mr and 3-3mr models (Fig. S21, Tables S17 and S18†) and subsequent hydrogenation is exothermic (structures in Fig. S22†). Hydrogenation to the dihydride (
SiO)2Zr(CH3)2 are intermediate between the 3-4mr and 3-3mr models (Fig. S21, Tables S17 and S18†) and subsequent hydrogenation is exothermic (structures in Fig. S22†). Hydrogenation to the dihydride (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2ZrH2 results in a site anchored via two Zr–O–Si bonds (Fig. 11a) forming a 1-3mr (
SiO)2ZrH2 results in a site anchored via two Zr–O–Si bonds (Fig. 11a) forming a 1-3mr (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2ZrH2 site.
SiO)2ZrH2 site.
The computed structures and PES for the Fig. 11b pathway are provided in Fig. S23 and S24,† respectively and the energies in Tables S19 and S20.† The availability of two Zr–H bonds offers the potential for growth of two chains. The computed barriers to insert ethylene sequentially into these two are both less than 0.1 eV. The more open coordination around Zr enables “agostic” interactions93,94 between ethyl hydrogen atoms and Zr, evidenced in the reduced distances and angles; test calculations indicate that these interactions stabilize the intermediates by approximately 0.1 eV and cost approximately the same amount at transition states (Fig. S25†).
We computed the PES for chain growth starting from (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2ZrEt2 (2′b, Et = ethyl) and termination to 1-butene and (
SiO)2ZrEt2 (2′b, Et = ethyl) and termination to 1-butene and (![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) SiO)2Zr(H)Et (2′a in Fig. 11b). As shown in Fig. 11c, both steps have activation energies less than those on the 3-4mr and 3-3mr models. Fig. 9a and b show that the predicted oligomerization rates and degree of polymerization are greater on the 1-3mr Zr-dihydride than either Zr-monohydride site. This remains true even at lower ethylene pressures and temperature where the site forms polymers (Fig. S12†).
SiO)2Zr(H)Et (2′a in Fig. 11b). As shown in Fig. 11c, both steps have activation energies less than those on the 3-4mr and 3-3mr models. Fig. 9a and b show that the predicted oligomerization rates and degree of polymerization are greater on the 1-3mr Zr-dihydride than either Zr-monohydride site. This remains true even at lower ethylene pressures and temperature where the site forms polymers (Fig. S12†).
The corresponding results for the Ti- and Hf-dihydrides are reported in the ESI† Fig. S23–S28, and Tables S19 and S20. Variations with the metal follow the same trend as found for the 3-4mr mono-hydride sites.
4 Conclusions
Ethylene oligomerization and polymerization performance of heterogenized metal ions are known to be influenced by the metal ion identity, support morphology, and reaction conditions. Here we compare the predicted performance across the three group 4 metal ions and three different silica anchoring site models. Microkinetic models based on DFT results show that Zr has the highest intrinsic activity of the three metals (Fig. 6), as measured by the oligomerization rate, in which activity is modulated significantly by the local support environment (Fig. 9), and further that both the degree of polymerization and fraction of olefinic vs. paraffinic products are sensitive to co-fed H2. Table S16 and Fig. S12† along with Fig. 9 lay out the selectivity change from polymerization to oligomerization on 3-3mr Zr-monohydride and 1-3mr Zr-dihydride sites going from low to high temperatures under different pressures. The results indicate that the anchored Zr ions are promising candidates for high-temperature oligomerization of ethylene, but that product selectivity will require uniformity in the anchoring site and control of temperature and hydrogen concentration.Data availability
The data that support the findings of this study (separate folders for CONTCARs of all structures, vibrational frequency output file, transition state trajectory calculations and python scripts to create potential energy plots, rates, coverages,![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) n and degree of rate control) are shared in the Zenodo data repository openly available at https://zenodo.org/doi/10.5281/zenodo.11251372.
n and degree of rate control) are shared in the Zenodo data repository openly available at https://zenodo.org/doi/10.5281/zenodo.11251372.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Engineering Research Centers Program of National Science Foundation (NSF) for the project named Center for Innovative and Strategic Transformation of Alkane Resources (CISTAR) under Cooperative Agreement no. EEC-1647722. The authors would like to thank their CISTAR collaborators, in particular Jason Hicks and Galiya Magazova from University of Notre Dame for providing experimental perspective. Computing resources and technical support for this work were provided by the Notre Dame Center for Research Computing.References
- G. Tosin, C. C. Santini and J.-M. Basset, Polymerization of α-olefins and Hydrogenolysis of the Resulting Polyolefins with Hafnium Hydrides Supported on Silica, Top. Catal., 2009, 52, 1203–1210 CrossRef CAS.
- J. D. Pelletier and J. M. Basset, Catalysis by Design: Well-Defined Single-Site Heterogeneous Catalysts, Acc. Chem. Res., 2016, 49, 664–677 CrossRef CAS PubMed.
- L. Y. Ustynyuk, D. V. Besedin, I. E. Nifant'ev, E. A. Fushman, Y. A. Ustynyuk and V. V. Lunin, Catalytic reactions of hydrocarbons promoted by coordination unsaturated Zr and Ti compounds: A density functional theory study, Moscow Univ. Chem. Bull., 2009, 64, 343–365 CrossRef.
- C. Copéret, M. Chabanas, R. Petroff Saint-Arroman and J. M. Basset, Surface organometallic chemistry: Homogeneous and heterogeneous catalysis: Bridging the gap through surface organometallic chemistry, Angew. Chem., Int. Ed., 2003, 42, 156–181 CrossRef PubMed.
- V. A. Zakharov, G. A. Nesterov, S. A. Vasnetsov and K. H. Thiele, Active Centers of the Supported Organic and Hydride Transition Metal Catalysts for Ethylene Polymerization, in Transition Metals and Organometallics as Catalysts for Olefin Polymerization, ed. W. Kaminsky and H. Sinn, Springer, Berlin, Heidelberg, 1988, pp. 91–100 Search PubMed.
- V. A. Zakharov, V. K. Dudchenko, L. G. Karakchiev and Y. I. Yermakov, Formation of Zirconium hydrides in Supported OrganoZirconium Catalysts and Their Role in Ethylene Polymerization, J. Mol. Catal., 1977, 2, 421–435 CrossRef CAS.
- C. Rosier, G. P. Niccolai and J.-M. Basset, Catalytic Hydrogenolysis and Isomerization of Light Alkanes over the Silica-Supported Titanium Hydride Complex (SiO)3TiH, J. Am. Chem. Soc., 1997, 119, 12408–12409 CrossRef CAS.
- J. Corker, F. Lefebvre, C. Lécuyer, V. Dufaud, F. Quignard, A. Choplin, J. Evans and J. M. Basset, Catalytic cleavage of the C-H and C-C bonds of alkanes by surface organometallic chemistry: An EXAFS and IR characterization of a Zr-H catalyst, Science, 1996, 271, 966–969 CrossRef CAS.
- C. Lecuyer, F. Quignard, A. Choplin, D. Olivier and J.-M. Basset, Surface Organometallic Chemistry on Oxides: Selective Catalytic Low-Temperature Hydrogenolysis of Alkanes by a Highly Electrophilic Zirconium Hydride Complex Supported on Silica, Angew. Chem., Int. Ed. Engl., 1991, 30, 1660–1661 CrossRef.
- L. d'Ornelas, S. Reyes, F. Quignard, A. Choplin and J.-M. Basset, Hafnium-Hydride Complexes Anchored to Silica. Catalysts of the Low Temperature Hydrogenolysis of Alkanes and Hydrogenation of Olefins, Chem. Lett., 1993, 22, 1931–1934 CrossRef.
- F. Quignard, C. Lécuyer, A. Choplin and J.-M. Basset, From synthesis to chemical reactivity of supported d0 complexes. Part 1. An in situ infrared spectroscopic study of silica-anchored zirconium hydrides, J. Chem. Soc., Dalton Trans., 1994, 1153–1158 RSC.
- F. Quignard, C. Lécuyer, A. Choplin, D. Olivier and J.-M. Basset, Surface organometallic chemistry of zirconium: Application to the stoichiometric activation of the CH bonds of alkanes and to the low-temperature catalytic hydrogenolysis of alkanes, J. Mol. Catal., 1992, 74, 353–363 CrossRef CAS.
- V. Dufaud and J.-M. Basset, Catalytic Hydrogenolysis at Low Temperature and Pressure of Polyethylene and Polypropylene to Diesels or Lower Alkanes by a Zirconium Hydride Supported on Silica-Alumina: A Step Toward Polyolefin Degradation by the Microscopic Reverse of Ziegler-Natta Polymerization, Angew. Chem., Int. Ed., 1998, 37, 806–810 CrossRef CAS PubMed.
- C. Larabi, N. Merle, S. Norsic, M. Taoufik, A. Baudouin, C. Lucas, J. Thivolle-Cazat, A. De Mallmann and J. M. Basset, Surface organometallic chemistry of titanium on silica-alumina and catalytic hydrogenolysis of waxes at low temperature, Organometallics, 2009, 28, 5647–5655 CrossRef CAS.
- C. P. Nicholas, Applications of light olefin oligomerization to the production of fuels and chemicals, Appl. Catal., A, 2017, 543, 82–97 CrossRef CAS.
- P.-A. R. Breuil, L. Magna and H. Olivier-Bourbigou, Role of Homogeneous Catalysis in Oligomerization of Olefins : Focus on Selected Examples Based on Group 4 to Group 10 Transition Metal Complexes, Catal. Lett., 2015, 145, 173–192 CrossRef CAS.
- T. Ridha, Y. Li, E. Gençer, J. J. Siirola, J. T. Miller, F. H. Ribeiro and R. Agrawal, Valorization of Shale Gas Condensate to Liquid Hydrocarbons through Catalytic Dehydrogenation and Oligomerization, Processes, 2018, 6, 1–21 CrossRef.
- K. C. Szeto, N. Merle, C. Rios, P. Rouge, J. L. Castelbou and M. Taoufik, Tailoring the selectivity in 2-butene conversion over supported d0 group 4, 5 and 6 metal hydrides: from dimerization to metathesis, Catal. Sci. Technol., 2015, 5, 4765–4771 RSC.
- M. Rimoldi and A. Mezzetti, Catalysis Science & Technology Perspective Site isolated complexes of late transition metals grafted on silica: challenges and chances for synthesis and catalysis, Catal. Sci. Technol., 2014, 4, 2724–2740 RSC.
- S. A. Holmes, F. Quignard, A. Choplin, R. Teissier and J. Kervennal, Tetraneopentyltitanium Derived Supported Catalysts Part 1. Synthesis and Catalytic Properties for the Epoxidation of Cyclohexene with Aqueous Hydrogen Peroxide, J. Catal., 1998, 176, 173–181 CrossRef CAS.
- G. Tosin, C. C. Santini, A. Baudouin, A. De Mallman, S. Fiddy, C. Dablemont and J.-M. Basset, Reactivity of Silica-Supported Hafnium Tris-neopentyl with Dihydrogen: Formation and Characterization of Silica Surface Hafnium Hydrides and Alkyl Hydride, Organometallics, 2007, 26, 4118–4127 CrossRef CAS.
- C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez Zarur and P. A. Zhizhko, Surface Organometallic and Coordination Chemistry toward Single-Site Heterogeneous Catalysts: Strategies, Methods, Structures, and Activities, Chem. Rev., 2016, 116, 323–421 CrossRef PubMed.
- F. Rataboul, A. Baudouin, C. Thieuleux, L. Veyre, C. Copéret, J. Thivolle-Cazat, J.-M. Basset, A. Lesage and L. Emsley, Molecular Understanding of the Formation of Surface Zirconium Hydrides upon Thermal Treatment under Hydrogen of [
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) (SiO)Zr(CH2tBu)3] by Using Advanced Solid-State NMR Techniques, J. Am. Chem. Soc., 2004, 126, 12541–12550 CrossRef CAS PubMed , PMID: 15453787.
(SiO)Zr(CH2tBu)3] by Using Advanced Solid-State NMR Techniques, J. Am. Chem. Soc., 2004, 126, 12541–12550 CrossRef CAS PubMed , PMID: 15453787. - C. Thieuleux, E. A. Quadrelli, J. M. Basset, J. Döbler and J. Sauer, Methane activation by silica-supported Zr(IV) hydrides: The dihydride [(
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SiO)2ZrH2] is much faster than the monohydride [(
SiO)2ZrH2] is much faster than the monohydride [(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SiO)3ZrH], Chem. Commun., 2004, 1729–1731 RSC.
SiO)3ZrH], Chem. Commun., 2004, 1729–1731 RSC. - G. Tosin, M. Delgado, A. Baudouin, C. C. Santini, F. Bayard and J. M. Basset, Surface organometallic chemistry of Hf(CH2tBu)4 on silica and silica-alumina: Reaction of the resulting grafted hafnium neopentyl with dihydrogen, Organometallics, 2010, 29, 1312–1322 CrossRef CAS.
- V. A. Zakharov and Y. A. Ryndin, Surface Hydride Complexes of Group IV Transition Metals as Active Sites for Polymerization and Hydrogenation reactions, J. Mol. Catal., 1989, 56, 183–193 CrossRef CAS.
- J. J. Mortensen and M. Parrinello, A Density Functional Theory Study of a Silica-Supported Zirconium Monohydride Catalyst for Depolymerization of Polyethylene, J. Phys. Chem. B, 2000, 104, 2901–2907 CrossRef CAS.
- L. Y. Ustynyuk, Y. A. Ustynyuk, D. N. Laikov and V. V. Lunin, DFT study of the mechanism of alkane hydrogenolysis by transition metal hydrides. 1. Interaction of silica-supported zirconium hydrides with methane, Russ. Chem. Bull., 2001, 50, 2050–2053 CrossRef CAS.
- C. Plascencia, L. A. Curtiss and C. Liu, Hydrogen Activation by Silica-Supported Metal Ion Catalysts: Catalytic Properties of Metals and Performance of DFT Functionals, J. Phys. Chem. A, 2019, 123, 171–186 CrossRef CAS PubMed.
- A. M. Jystad, A. Biancardi and M. Caricato, Simulations of Ammonia Adsorption for the Characterization of Acid Sites in Metal-Doped Amorphous Silicates, J. Phys. Chem. C, 2017, 121, 22258–22267 CrossRef CAS.
- A. Q. Kane, A. M. Esper, K. Searles, C. Ehm and A. S. Veige, Probing β-alkyl elimination and selectivity in polyolefin hydrogenolysis through DFT, Catal. Sci. Technol., 2021, 6155–6162 RSC.
- L. Y. Ustynyuk, I. A. Aleshkin, Y. V. Suleimanov, D. V. Besedin, Y. A. Ustynyuk and V. V. Lunin, The activation of C-H bonds in C1-C3 alkanes by zirconium(III,IV) and titanium(III,IV) hydrides immobilized on the surface of SiO2: a density functional theory study, Russ. J. Phys. Chem. A, 2007, 81, 752–758 CrossRef CAS.
- D. V. Besedin, L. Y. Ustynyuk, Y. A. Ustynyuk and V. V. Lunin, Hydrogenolysis of alkanes and olefin polymerization on the silica-supported zirconium hydrides: A comparative DFT study, Top. Catal., 2005, 32, 47–60 CrossRef CAS.
- M. P. Kalhor, R. Wischert, C. Copéret and H. Chermette, Reactivity of silica supported zirconium hydride towards N2O and CO2 probe molecules: a computational point of view, New J. Chem., 2014, 38, 3717–3721 RSC.
- F. Tielens, C. Gervais, J. F. Lambert, F. Mauri and D. Costa, Ab Initio Study of the Hydroxylated Surface of Amorphous Silica: A Representative Model, Chem. Mater., 2008, 20, 3336–3344 CrossRef CAS.
- F. Tielens, M. Gierada, J. Handzlik and M. Calatayud, Characterization of amorphous silica based catalysts using DFT computational methods, Catal. Today, 2020, 354, 3–18 CrossRef CAS.
- I. S. Chuang and G. E. Maciel, A detailed model of local structure and silanol hydrogen bonding of silica gel surfaces, J. Phys. Chem. B, 1997, 101, 3052–3064 CrossRef CAS.
- A. Comas-Vives, Amorphous SiO2 surface models: energetics of the dehydroxylation process, strain, ab initio atomistic thermodynamics and IR spectroscopic signatures, Phys. Chem. Chem. Phys., 2016, 18, 7475–7482 RSC.
- P. Ugliengo, M. Sodupe, F. Musso, I. J. Bush, R. Orlando and R. Dovesi, Realistic Models of Hydroxylated Amorphous Silica Surfaces and MCM-41 Mesoporous Material Simulated by Large-scale Periodic B3LYP Calculations, Adv. Mater., 2008, 20, 4579–4583 CrossRef CAS.
- C. S. Ewing, S. Bhavsar, G. Veser, J. J. McCarthy and J. K. Johnson, Accurate Amorphous Silica Surface Models from First-Principles Thermodynamics of Surface Dehydroxylation, Langmuir, 2014, 30, 5133–5141 CrossRef CAS PubMed.
- A. Rimola, D. Costa, M. Sodupe, J.-F. Lambert and P. Ugliengo, Silica Surface Features and Their Role in the Adsorption of Biomolecules: Computational Modeling and Experiments, Chem. Rev., 2013, 113, 4216–4313 CrossRef CAS PubMed.
- P. Patel, R. H. Wells, D. M. Kaphan, M. Delferro, R. T. Skodje and C. Liu, Computational Investigation of the Role of Active Site Heterogeneity for a Supported Organovanadium(III) Hydrogenation Catalyst, ACS Catal., 2021, 11, 7257–7269 CrossRef CAS.
- S. A. Khan, S. M. Godahewa, P. N. Wimalasiri, W. H. Thompson, S. L. Scott and B. Peters, Modeling the Structural Heterogeneity of Vicinal Silanols and Its Effects on TiCl4 Grafting onto Amorphous Silica, Chem. Mater., 2022, 34, 3920–3930 CrossRef CAS.
- C. S. Praveen, A. P. Borosy, C. Copéret and A. Comas-Vives, Strain in Silica-Supported Ga(III) Sites: Neither Too Much nor Too Little for Propane Dehydrogenation Catalytic Activity, Inorg. Chem., 2021, 60, 6865–6874 CrossRef CAS PubMed.
- L. Floryan, A. P. Borosy, F. Núñez-Zarur, A. Comas-Vives and C. Copéret, Strain effect and dual initiation pathway in CrIII/SiO2 polymerization catalysts from amorphous periodic models, J. Catal., 2017, 346, 50–56 CrossRef CAS.
- U. Das, G. Zhang, B. Hu, A. S. Hock, P. C. Redfern, J. T. Miller and L. A. Curtiss, Effect of Siloxane Ring Strain and Cation Charge Density on the Formation of Coordinately Unsaturated Metal Sites on Silica: Insights from Density Functional Theory (DFT) Studies, ACS Catal., 2015, 5, 7177–7185 CrossRef CAS.
- B. Peters, S. L. Scott, A. Fong, Y. Wang and A. E. Stiegman, Reexamining the evidence for proton transfers in ethylene polymerization, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E4160–E4161 CAS.
- A. Fong, C. Vandervelden, S. L. Scott and B. Peters, Computational Support for Phillips Catalyst Initiation via Cr–C Bond Homolysis in a Chromacyclopentane Site, ACS Catal., 2018, 8, 1728–1733 CrossRef CAS.
- C. Huang, Z. Liu, B. Liu, M. Terano and Y. Jin, Computational Insights into the Multisite Nature of the Phillips CrOx/SiO2 Catalyst for Ethylene Polymerization: The Perspective of Chromasiloxane Ring Size and F Modification, ACS Catal., 2022, 12, 3589–3603 CrossRef CAS.
- B. R. Goldsmith, B. Peters, J. K. Johnson, B. C. Gates and S. L. Scott, Beyond Ordered Materials: Understanding Catalytic Sites on Amorphous Solids, ACS Catal., 2017, 7, 7543–7557 CrossRef CAS.
- P. Cossee, Ziegler-Natta Catalysis I. Mechanism of Polymerization of α-Olefins with Ziegler-Natta Catalysts, J. Catal., 1964, 3, 80–88 CrossRef CAS.
- D. R. Burfield, Ziegler-Natta polymerization: The nature of the propagation step, Polymer, 1984, 25, 1645–1654 CrossRef CAS.
- V. I. Avdeev, I. I. Zakharov, V. A. Zakharov, G. D. Bukatov and Y. I. Ermakov, Quantum-chemical study of the mechanism of the growth reaction in the catalytic polymerization of alkenes, J. Struct. Chem., 1977, 18, 420–436 CrossRef.
- T. K. Woo, L. Fan and T. Ziegler, A Density Functional Study of Chain Growing and Chain Terminating Steps in Olefin Polymerization by Metallocene and Constrained Geometry Catalysts, Organometallics, 1994, 13, 2252–2261 CrossRef CAS.
- M. E. O'Reilly, S. Dutta and A. S. Veige, β-Alkyl Elimination: Fundamental Principles and Some Applications, Chem. Rev., 2016, 116, 8105–8145 CrossRef PubMed.
- L. Cavallo, G. Guerra and P. Corradini, Mechanisms of Propagation and Termination Reactions in Classical Heterogeneous Ziegler-Natta Catalytic Systems: A Nonlocal Density Functional Study, J. Am. Chem. Soc., 1998, 120, 2428–2436 CrossRef CAS.
- W. Kaminsky and H. Lüker, Influence of hydrogen on the polymerization of ethylene with the homogeneous ziegler system bis(cyclopentadienyl)zirconiumdichloride/aluminoxane, Makromol. Chem., Rapid Commun., 1984, 5, 225–228 CrossRef CAS.
- A. S. Hoffman, B. A. Fries and P. C. Condit, The role of hydrogen in ziegler-natta polymerizations, J. Polym. Sci., Part C: Polym. Symp., 1963, 4, 109–126 CrossRef.
- Y. V. Kissin, L. A. Rishina and E. I. Vizen, Hydrogen effects in propylene polymerization reactions with titanium-based Ziegler–Natta catalysts. II. Mechanism of the chaintransfer reaction, J. Polym. Sci., Part A: Polym. Chem., 2002, 40, 1899–1911 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B, 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 ( Phys. Rev. Lett. , 1997 , 78 , 1396–1396 ) CrossRef CAS PubMed.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, Climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jönsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. H. Larsen, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- K. Momma and F. Izumi, VESTA: a three-dimensional visualization system for electronic and structural analysis, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- R. W. G. Wyckoff, Crystal Structures, John Wiley & Sons, 2nd edn, 1963, ch. 4, vol. 1, pp. 239–444 Search PubMed.
- L. He, F. Liu, G. Hautier, M. J. T. Oliveira, M. A. L. Marques, F. D. Vila, J. J. Rehr, G.-M. Rignanese and A. Zhou, Accuracy of generalized gradient approximation functionals for density-functional perturbation theory calculations, Phys. Rev. B, 2014, 89, 064305 CrossRef.
- X. Rozanska, F. Delbecq and P. Sautet, Reconstruction and stability of β-cristobalite 001, 101, and 111 surfaces during dehydroxylation, Phys. Chem. Chem. Phys., 2010, 12, 14930–14940 RSC.
- A. Meurer, et al., SymPy: symbolic computing in Python, PeerJ Comput. Sci., 2017, 3, e103 CrossRef.
- G. Van Rossum and F. L. Drake, Python 3 Reference Manual, CreateSpace, Scotts Valley, CA, 2009 Search PubMed.
- K. Toch, J. Thybaut and G. Marin, Ethene oligomerization on Ni-SiO2-Al2O3: Experimental investigation and Single-Event MicroKinetic modeling, Appl. Catal., A, 2015, 489, 292–304 CrossRef CAS.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, John Wiley, 2nd edn, 2004, ch. 2, pp. 22–44 Search PubMed.
- C. T. Campbell and J. R. Sellers, The entropies of adsorbed molecules, J. Am. Chem. Soc., 2012, 134, 18109–18115 CrossRef CAS PubMed.
- P. J. Davidson, M. F. Lappert and R. Pearce, Metal σ-Hydrocarbyls, MRn Stoichiometry, Structures, Stabilities, and Thermal Decomposition Pathways, Chem. Rev., 1976, 76, 219–242 CrossRef CAS.
- N. Greenwood and A. Earnshaw, Chemistry of Elements, Pergamon Press, 2nd edn, 1989, ch. 4, pp. 220–329 Search PubMed.
- G. Tosin, C. C. Santini, M. Taoufik, A. De Mallmann and J. M. Basset, Reactivity of tetraneopentylhafnium, Hf(CH2tBu)4, with silica surfaces, Organometallics, 2006, 25, 3324–3335 CrossRef CAS.
- R. Robinson, D. S. McGuinness and B. F. Yates, The mechanism of ethylene dimerization with the Ti(OR)4/AlR3 catalytic system: DFT studies comparing metallacycle and Cossee proposals, ACS Catal., 2013, 3, 3006–3015 CrossRef CAS.
- L. C. Grabow, in Computational Catalysis, ed. A. Asthagiri and M. J. Janik, The Royal Society of Chemistry, 2013, pp. 1–58 Search PubMed.
- A. Fong, Y. Yuan, S. L. Ivry, S. L. Scott and B. Peters, Computational kinetic discrimination of ethylene polymerization mechanisms for the Phillips (Cr/SiO2) catalyst, ACS Catal., 2015, 5, 3360–3374 CrossRef CAS.
- G. J. Britovsek, R. Malinowski, D. S. McGuinness, J. D. Nobbs, A. K. Tomov, A. W. Wadsley and C. T. Young, Ethylene Oligomerization beyond Schulz-Flory Distributions, ACS Catal., 2015, 5, 6922–6925 CrossRef CAS.
- D. P. Lo and W. H. Ray, Kinetic modeling and prediction of polymer properties for ethylene polymerization over nickel diimine catalysts, Ind. Eng. Chem. Res., 2005, 44, 5932–5949 CrossRef CAS.
- L. Zhuravlev, The surface chemistry of amorphous silica. Zhuravlev model, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- J. H. Z. dos Santos, C. Krug, M. B. da Rosa, F. C. Stedile, J. Dupont and M. de Camargo Forte, The effect of silica dehydroxylation temperature on the activity of SiO2-supported zirconocene catalysts, J. Mol. Catal. A: Chem., 1999, 139, 199–207 CrossRef.
- L. Cavallo and G. Guerra, A Density Functional and Molecular Mechanics Study Of β-Hydrogen Transfer in Homogeneous Ziegler-Natta Catalysis, Macromolecules, 1996, 29, 2729–2737 CrossRef CAS.
- J. N. Harvey, F. Himo, F. Maseras and L. Perrin, Scope and Challenge of Computational Methods for Studying Mechanism and Reactivity in Homogeneous Catalysis, ACS Catal., 2019, 9, 6803–6813 CrossRef CAS.
- G. Talarico and P. H. M. Budzelaar, Variability of Chain Transfer to Monomer Step in Olefin Polymerization, Organometallics, 2008, 27, 4098–4107 CrossRef CAS.
- J. C. W. Lohrenz, T. K. Woo and T. Ziegler, A Density Functional Study on the Origin of the Propagation Barrier in the Homogeneous Ethylene Polymerization with Kaminsky-Type Catalysts, J. Am. Chem. Soc., 1995, 117, 12793–12800 CrossRef CAS.
- M. Brookhart, M. L. H. Green and G. Parkin, Agostic interactions in transition metal compounds, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00684d |
| This journal is © The Royal Society of Chemistry 2024 |