Vibrational frequencies utilized for the assessment of exchange–correlation functionals in the description of metal–adsorbate systems: C₂H₂ and C₂H₄ on transition-metal surfaces

Abstract

Describing the interaction between reactive species and surfaces is crucial for designing catalyst materials. Density-functional approximation is able to quantitatively model such interaction, but its accuracy strongly depends on the choice of exchange–correlation (XC) functional approximation. In this work, we assess the performance of XC functionals for describing the interaction of C₂H₂ and C₂H₄ with the (111) surfaces of Cu, Pt, Pd, and Rh by particularly focusing on RPBE and mBEEF functionals. We study the geometry and the vibrational frequencies associated with the adsorbed molecules as well as the adsorption energies and the reaction enthalpy of semi-hydrogenation of C₂H₂ in the gas phase. Crucially, experimental values for vibrational frequencies of molecules adsorbed on metal surfaces are available for more systems compared to physical quantities typically used to benchmark XC functionals, such as adsorption energies. Thus, vibrational frequencies can be utilized as a reference to assess the reliability of the exchange–correlation functionals. We find that the mean percentage errors (MPEs) of RPBE and mBEEF with respect to reported experimental values of vibrational frequencies are 0.64% and −3.88%, respectively (36 data points). For adsorption enthalpy, RPBE and mBEEF provide MPEs of 27.61% and −59.81%, respectively, with respect to reported experimental values (7 data points). Therefore, the performance of RPBE is superior to that of mBEEF for the considered systems.

---

1. Introduction

Transition metals are widely used as heterogeneous catalysts.^1–7 Thus, investigating the interaction of adsorbates with metal surfaces and their impact on the reaction mechanisms is important for the design of novel catalysts. Electronic-structure calculations can provide the needed detailed description.⁸ In particular, density functional theory (DFT)⁹ in the Kohn–Sham¹⁰ framework is a widely applied theoretical approach for catalytic systems.¹¹ However, in practice, we are bound to use approximated exchange–correlation (XC) functionals, and the accuracy of such density functional approximation (DFA) strongly depends on the XC functional. Consequently, many studies have been carried out (see ref. 12–15) to assess the performance and accuracy of XC functionals for, e.g., bulk band structures, structural properties, and surface properties of transition metals. According to benchmark studies on the adsorption of small molecules on metal surfaces, the alternative revision of the Perdew–Burke–Ernzerhof XC functional (RPBE)¹⁶ provides an accurate description of the most stable adsorption sites and adsorption energies.^13,14 Recently, a benchmark study by Kabalan et al.¹⁷ on the performance of XC functionals, specifically for transition metals, showed that meta-generalized gradient XC functional approximation based on Bayesian error estimation (mBEEF)¹⁸ provides good agreement with experimental data, such as surface energy and work function.¹⁷ Ref. 17 focused on pristine surfaces without adsorbates, and RPBE was not considered in the context of surface properties because its error for experimental bulk properties is larger than that of the other tested XC functionals.

Ethylene (C₂H₄) is one of the most important chemical building blocks for polymer production.^19–21 Ethylene is typically obtained by naphtha steam cracking. In this process, acetylene (C₂H₂) is formed as a by-product. However, the presence of acetylene is undesirable, as it deactivates the catalyst for C₂H₄ polymerization, which is one of the key processes where ethylene is utilized. Thus, C₂H₂ has to be removed before the polymerization process. This can be achieved by the catalytic selective hydrogenation of C₂H₂ to C₂H₄. The catalyst selectively hydrogenates C₂H₂ while suppressing the hydrogenation of C₂H₄ to ethane (C₂H₆). Pd and Pd-based alloys have been used as catalyst materials in this process.^6,7,22,23 Many DFA studies investigated the selective hydrogenation of acetylene.^24–28 In order to design new catalyst, the accurate description of both acetylene and ethylene adsorption is necessary.¹¹ All the benchmark studies proclaim the challenge of finding an optimal functional that could simultaneously capture both covalent and non-covalent interactions of adsorbates on metal surfaces, with no clear preference for a particular functional. Thus, the accuracy of the XC functional for these specific target systems still needs to be scrutinized. However, reliable experimental and/or higher-level theoretical reference data for assessing the performance of the XC functional for adsorption of molecules on surfaces are limited.

In this study, we assess the performance of RPBE and mBEEF by focusing on the vibrational frequencies associated to C₂H₄ and C₂H₂ molecules adsorbed on transition-metal (TM) surfaces. The vibrational frequencies of adsorbed molecules reflect the nature and strength of the molecules' interaction with the TM surfaces. Additionally, reliable and accurate experimental values for vibrational frequencies of molecules adsorbed on TM surfaces are available. The aim of this study is not to find the best XC functional for describing the adsorption of C₂H₄ and C₂H₂ molecules on TM surfaces among a wide range of functionals. Instead, we aim at demonstrating how the performance of XC functionals for describing surfaces and catalysis can be assessed via the experimental vibrational frequencies. The RPBE and mBEEF are widely used XC functionals and they provide good accuracy for the surface properties and adsorption energies of molecules on TM surfaces. Thus, these two XC functionals are adopted to showcase the concept. We would like to stress that the properties of adsorbed molecules, such as bond elongation, have been directly correlated to catalytic activity.²⁹ Additionally, the accuracy of XC functionals for the vibrational frequency is important in the context of calculating energy curvatures around equilibrium and transition states and the calculated properties of adsorbed molecules can be considered as potentially relevant parameters in artificial intelligence (AI) analysis that aim to identify intricate correlations between material properties and catalytic performance. These calculated parameters can be offered along with experimental parameters related to other underlying processes in the AI analysis.³⁰ The accuracy and reliability of the data employed in AI is crucial. Thus, proposing the proper way for assessment of the performance of XC functionals is also an urgent task for data-centric heterogeneous catalyst design.

We study adsorbed C₂H₂ and C₂H₄ on the surfaces of Pd, Pt, Cu, and Rh. These are transition metals widely used as catalysts for the selective hydrogenation of C₂H₂, and the vibrational frequencies of C₂H₂ and C₂H₄ on these metals have been determined experimentally.^31–39 We also assess the performance of the functionals based on adsorption energies of the molecules on Pt, for which experimental values are available. However, the available reference data are scarcer than in the case of the vibrational frequencies. Additionally, we investigate the performance for the reaction enthalpy of semi-hydrogenation of C₂H₂ to C₂H₄ in the gas phase. To demonstrate further application of our concept, we also investigate the C₂H₄ adsorption on Pt(111) by using other XC functionals (PBEsol⁴⁰ and TPSS⁴¹) and RPBE with the Tkatchenko–Scheffler van der Waals (vdW) interaction correction⁴² (RPBE + TS).

2. Computational details

2.1 DFA calculations

All the calculations were performed within the DFA framework as implemented in the all-electron full-potential electronic-structure package FHI-aims⁴³ (version 210226). RPBE is a generalized gradient approximation (GGA) functional, which only differs from the original PBE XC functional by the mathematical form of the exchange energy enhancement factor (see ref. 16). The functional was mainly proposed to improve the chemisorption energetics of atoms and molecules on TM surfaces. The mBEEF is a meta-GGA, which combines machine learning with Bayesian statistics to find the exchange model parameters (see ref. 18). It was designed to give reasonably accurate predictions of material properties, such as cohesive energies and lattice constants. The mBEEF calculations are done by interfacing FHI-aims with the LibXC⁴⁴ library. In all the calculations, scalar relativity is included via the atomic zero-order regular approximation (ZORA).⁴⁵ The calculations are done by employing a tight basis set and a converged Γ-centered k-grid of 20 × 20 × 20 and 12/n × 12/n × 1 (n is the supercell size) for the bulk and surfaces, respectively. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm⁴⁶ with a force convergence criterion of 10 meV Å⁻¹ along all directions is employed for the geometry optimizations. A dipole correction is applied along the surface normal (non-periodic direction, see the following section for more details) to eliminate any potential electrostatic dipole that could result from a non-symmetric slab relaxation and molecule adsorption.

2.2 Surface models

The (111) surface is the most stable facet of the TMs adopted in this study (i.e., Cu, Pt, Pd, Rh), which have the face-centered cubic (fcc, space group Fm̄3m) bulk structure,⁴⁷ and is the focus of experimental studies. To model the surfaces, firstly, the lattice parameters of the bulk structures were optimized by mBEEF or RPBE. Then, the equilibrium lattice parameters were used to model the (111) surfaces by a two-dimensional slab with the periodic boundary conditions. Unless otherwise stated, the surfaces are modeled by 2 × 2 and 3 × 3 surface supercells to account for the adsorption coverages observed in experiments. Each slab is separated by at least a 20 Å vacuum perpendicular to the (111) surface (z-direction) to decrease the interaction between slab periodic images so that it can be ignored. Each slab consists of seven atom layers with the three bottom layers kept fixed at their ideal bulk positions during the geometry optimization. The atomic simulation environment (ASE) Python package⁴⁸ is used to create surface slab models from the fully optimized bulk geometries.

2.3 Vibrational frequencies

Vibrational modes and frequencies of the C₂H₂ and C₂H₄ molecules in the gas phase and adsorbed on TM surfaces are computed by FHI-aims and Phonopy⁴⁹ using a finite-differences approach to calculate second derivatives of forces. The absolute displacement of each atom for the finite difference calculations is 0.01 Å. The forces are converged within 1 meV Å⁻¹ during the self-consistency cycle. To exclude the atomic displacements of the fixed layers in the slab models, we employ the modified version of the Phonopy–FHI-aims interface.⁵⁰

2.4 Adsorption energies

The adsorption energy (E_ads) is calculated using the following equation.

E_ads = E_mol+slab − E_slab − E_mol (1)

Here E_mol+slab, E_slab, and E_mol are the total energies of the slab model with the adsorbate, the pristine slab model, and the adsorbate in the gas phase, respectively.

The experimental adsorption energies (heat of adsorption) cited in the present study were measured by microcalorimetry. Thus, they should be compared to calculated adsorption enthalpy (H_ads).

H_ads = H_mol+slab − H_slab − H_mol (2)

Here, H_mol+slab, H_slab, and H_mol are the enthalpy of the slab model with the adsorbate, the pristine slab model, and the adsorbate in the gas phase, respectively. These values were calculated within the ideal-gas approximation implemented in ASE.⁴⁸ For H_mol, translational, rotational, and vibrational degrees of freedom are taken into account. For H_mol+slab, the rotational and translational degrees of freedom are excluded since those motions should be suppressed by the interaction with the surfaces. Rotational and translational degrees of freedom are also neglected for the evaluation of H_slab. As examined in a previous study,⁵¹ the vibrational enthalpy (and entropy) is converged by considering the vibrations of the metal atoms that are nearest neighbors of the adsorbate. Thus, only vibrations of the adsorbate and its nearest-neighbor metal atoms are considered in the present study.

The adsorption of C₂H₄/Pt(111) can be dissociative, resulting in adsorbed ethylidyne and hydrogen:

C₂H₄ + Pt(111) → (CCH₃ + H)/Pt(111) (3)

Therefore, we also include the dissociated configuration for the adsorption energy analysis.

3. Results and discussion

3.1 Geometry analysis

As a first step, we performed geometry optimizations for C₂H₂ and C₂H₄ in the gas phase and adsorbed on the TM surfaces, and the results were compared with the corresponding experimental data. The geometry optimizations are evaluated at 0 K without zero-point vibrational corrections. As shown in Table S1 in the ESI,† the calculated geometry parameters in the gas phase are in good agreement with the experimental results: the mean absolute errors in calculated bond lengths are 8 × 10⁻³ and 6 × 10⁻³ Å for the mBEEF and RPBE functionals, respectively. For bond angles, the MAE for both functionals is 0.23°.

As described in the computational details, the slab models of TM surfaces were prepared from bulk structures obtained by minimizing the total energy at T = 0 K as listed in Table S2 of the ESI.† The results of bulk calculations show that both functionals accurately represent the experimental lattice constant of each metal. The mean absolute percentage errors of RPBE and mBEEF are 1.342% and 0.589%, respectively. Although RPBE provides larger error in comparison with mBEEF, the difference is only 0.753% (the MAE of mBEEF and RPBE are 0.022 Å and 0.052 Å, respectively).

Thus, both RPBE and mBEEF provide accurate results for lattice constants of the metals in this study. We also investigated the thermal effects on the lattice constants by using the quasi-harmonic approximation (QHA) implemented in Phonopy.^49,52 As shown in Table S2,† at the experimental temperature for the measurements (291–298 K),^53,54 the change in the lattice constants induced by the thermal effects is rather small (the maximum difference from the value without the thermal effect is 0.067 Å).

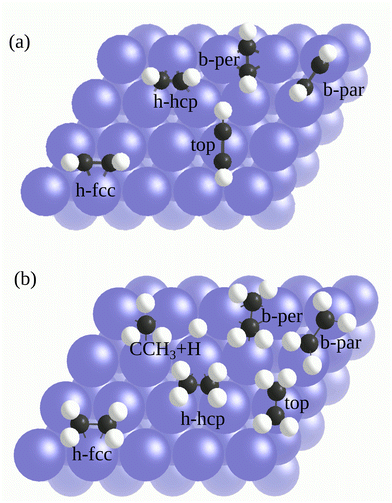
Several different adsorption configurations of the molecules on the surfaces are studied. Fig. 1a illustrates the possible adsorption structures for C₂H₂ on a fcc(111) metal surface. According to theoretical and experimental literature, the preferred C₂H₂ adsorption site on Pd(111),^55–57 Pt(111),⁵⁸ and Rh(111)⁵⁹ surfaces is the threefold fcc hollow site (h-fcc in Fig. 1a) with di-σ/π bonding (i.e., σ-bonding to two metal atoms along the C–C axis direction, and π-bonding to the remaining metal atom). However, the favorite site on Cu(111) is the bridge site (b-per in Fig. 1a) with the C–C axis perpendicular to the Cu–Cu bond.⁶⁰ We investigated all the shown adsorption sites and found that the preferred sites obtained from both functionals are in agreement with previous theoretical and experimental studies cited above. In addition to the most stable configuration, we also looked for metastable adsorption configurations.

Fig. 1 Different adsorption sites for (a) C₂H₂ and (b) C₂H₄ on a fcc(111) metal surface. The CCH₃ + H in (b) shows the adsorption structure of C₂H₄ in dissociative mode. Here, CCH₃ and H adsorb at neighbouring h-fcc sites. Metal, carbon, and hydrogen atoms are shown as purple, black, and white spheres, respectively.

According to available literature, the b-par (known as di-σ bonding) and top (known as π bonding) are the configurations for C₂H₂ on Pd(111) and Pt(111), which can be present at finite temperature and/or coverage. Based on our RPBE results shown in Table 1 and Table S6 of the ESI,† we obtain the following order of stability (starting from the most stable site with lowest adsorption energy): h-fcc, b-par, and top. This order is in agreement with other studies.^59,61–65 However, we find that geometry optimization with mBEEF misses some configurations that can be obtained by RPBE, such as the top configurations on Pd(111) and Cu(111).

Table 1 Comparison of our calculated E_ads (in eV) for C₂H₂ and C₂H₄ at Pt(111) with available experimental and theoretical data reported in the literature. H_ads values (in eV) are shown in brackets. θ is the coverage in monolayers (ML)

System	Site	θ (ML)	mBEEF	RPBE	Exp.	Other DFA studies
C2H2/Pt(111)	h-fcc	1/4	−2.67	−1.89		−2.37 (PW91),^59 −2.26 (PW91)^66
		1/9	−2.70	−1.83		−2.11 (BEEF-vdW)^67
		1/16	−2.87	−2.01	−2.18 (173 K)^68
			[−2.64 (173 K)]	[−1.79 (173 K)]
	b-par	1/4	−2.09	−1.47		−1.99 (PW91)^59
	Top	1/4	−0.68	−0.23		−0.73 (PW91)^59
C2H4/Pt(111)	Top	1/4	−0.80	−0.28	−0.41 ± 0.1 (112 K)^69	−0.76 (PW91),^61 −0.55 (PW)^62
			[−0.69 (112 K)]	[−0.18 (112 K)]
			[−0.70 (110 K)]	[−0.19 (110 K)]
					−0.22–−0.39 (110 K)^70
	b-par	1/4	−1.36	−0.74	−0.39–−0.74 (110 K)^70	−1.21 (PW91),^61 −1.26 (PW)^62
			[−1.23 (110 K)]	[−0.62 (110 K)]	−0.74 (100 K)^71
			[−1.23 (100 K)]	[−0.62 (100 K)]
	CCH3 + H	1/9	−1.78	−1.12	−1.36 (300 K)^72	−1.65 (PBE),^15 −1.74 (PBE),^72 −1.20 (RPBE),^15 −1.75 (optPBE),^72 −1.83 (optPBE-vdW),^15 −1.34 (BEEF-vdW),^15 −1.43 (BEEF),^72 −1.68 (MS2),^15 −2.21 (SCAN),^15 −2.33 (SCAN + rVV10),^15 −2.21 (HSE06),^15 −1.44 (PW91)^61
			[−1.40 (300 K)]	[−0.81 (300 K)]	−1.24 (300 K)^73

---

Finally, the adsorption of C₂H₄ was investigated. C₂H₄ can also adsorb dissociatively on TM surfaces: ethylidyne (CCH₃) and H. For the adsorption of C₂H₄/Pt(111), all the possible adsorption sites shown in Fig. 1b were examined. By employing both functionals, we find that the b-par site with a di-σ bonding is the global minimum for the adsorption of the C₂H₄ molecule for both functionals, which is in agreement with other theoretical and experimental studies.^31,66,71,74

3.2 Vibrational frequencies

The vibrational frequencies of C₂H₂ and C₂H₄ both in the gas phase and adsorbed on the TM surfaces are computed with mBEEF and RPBE functionals. For the molecules in the gas phase, the mBEEF functional tends to overestimate the vibrational frequencies, and the MPE of mBEEF (3.04%) is larger than that of RPBE (0.12%). In particular, the C–C and C–H stretching modes calculated by mBEEF show a large deviation from the experimental results. More details of the obtained results are discussed in Sections S3 and S4 of the ESI.†

For the molecules adsorbed on each metal, we used the adsorption site reported for the corresponding experiments. Except for ref. 38 and 39 where Fourier-transform reflection-adsorption infrared (FT-RAIR) spectroscopy was employed, the other experimental vibrational frequencies used in our study are obtained by high-resolution electron energy loss spectroscopy (HREELS). The calculated vibrational frequencies are summarized in Table S5 of the ESI.† Although experimental studies of vibrational spectroscopy report the configuration of the adsorbed molecule on the surface and the chamber exposure, the coverages are rarely mentioned. Therefore, in this study, the effect of the coverage on the calculated vibrational frequencies is investigated by comparing the results for two coverages: 1/4 and 1/9 monolayer (ML). These selected coverages are close to the C₂H₂ and C₂H₄ gas exposures reported in the experimental references (see Table S4 of the ESI†). As can be seen in Fig. 2, the obtained results are altogether only little affected by the change of coverage in the considered range. The MAE of mBEEF at both coverages is 66 cm⁻¹ and that of RPBE slightly increases from 42 cm⁻¹ to 43 cm⁻¹ with increasing coverage. Therefore, in the following, we only discuss the results of 1/9 ML.

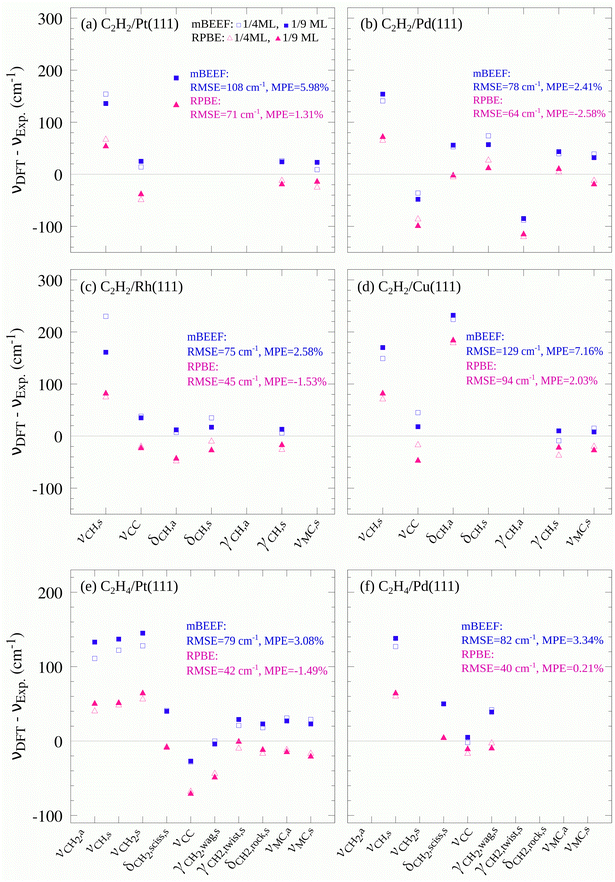Fig. 2 Deviations of calculated vibrational frequencies for C₂H₂ and C₂H₄ molecules adsorbed on fcc(111) TM surfaces from corresponding experimental values. ν, δ and γ denote stretching mode, in-plane bending mode, and out-of-plane bending mode, respectively. The blue squares and pink triangles indicate the deviations obtained with mBEEF and RPBE XC functionals, respectively (see Table S5 of the ESI† for the values of vibrations and experimental references). The mean percentage error is calculated by using the following formula: 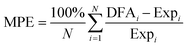. Some vibrations are absent either because of experimental method limitations or because only the most intense modes were listed in the references.

According to Table S5,† the values of all the experimental vibrational frequencies assigned to the C≡C stretching mode for chemisorbed C₂H₂ display a large shift from 1974 cm⁻¹ (in the gas phase) to 1260–1402 cm⁻¹ (adsorbed on TM surfaces). This frequency shift is a consequence of the partial rehybridization of the C≡C triple bond from sp to sp² or sp³ hybrid orbitals due to the formation of the covalent bond between carbon atoms of C₂H₂ and the metal surfaces. Our mBEEF and RPBE results also show such a large shift from 2082 and 2001 to 1295–1353 and 1238–1303 cm⁻¹, respectively, and the range of the shift depends on the adsorption configurations. For other modes, the shift in vibrational frequencies relative to the free molecules occurs as well, but it is not as strong as for the ν_CC mode. Similar results are obtained for the ν_CC mode of C₂H₄ adsorbed on Pt(111) and Pd(111). For this molecule, the absolute changes of the frequencies are 573 and 520 cm⁻¹ at Pt(111) and Pd(111), respectively. Both mBEEF and RPBE XC functionals reproduce this large drop in frequency. The absolute changes obtained with mBEEF are 674 and 595 cm⁻¹ at Pt(111) and Pd(111), respectively. The results from RPBE give absolute changes of 651 and 544 cm⁻¹ at Pt(111) and Pd(111), respectively. Thus, the absolute changes of the frequencies obtained from RPBE are closer to the experimental changes. Therefore, according to our results, the adsorbate–substrate bonding is described more accurately by RPBE.

Comparing the calculated vibrational frequencies with the corresponding experimental values illustrated in Fig. 2 shows that the calculated stretching modes display the largest deviations, and the mBEEF functional tends to overestimate the frequencies. These trends are similar to the results for free molecules as discussed in Section S4 in the ESI.† For each adsorbed system, the RMSE for both functionals is also calculated. As shown in Fig. 2, the RMSE of RPBE is smaller than that of mBEEF in all the TM systems studied here. For the adsorbed C₂H₂ at all the four fcc(111) surfaces, the values of RMSE obtained with mBEEF and RPBE are 98 and 70 cm⁻¹, respectively (see Fig. 2a–d). For the case of C₂H₄ over the Pt and Pd surfaces (see Fig. 2e and f), the RMSEs of mBEEF and RPBE are 80 and 41 cm⁻¹, respectively. Altogether, the overall RMSEs for the studied systems (i.e., 36 vibrational modes listed in Table S5†) are 118 cm⁻¹ and 61 cm⁻¹ for mBEEF and RPBE XC functionals, respectively. The highest achieved resolution of HREELS reported before 2010, when the reference values adopted in this study were measured, was 60–80 cm⁻¹.^31,75 Thus, the RPBE RMSE of 61 cm⁻¹ is within the range of the reported HREELS resolution.

3.3 Adsorption energies of C₂H₂ and C₂H₄

Let us now examine the performance of the two XC functionals for adsorption enthalpy by comparing with the experimental heat of adsorption measured by microcalorimetry. The H_ads values of C₂H₂ and C₂H₄ on Pt(111) are computed and summarized in Table 1 along with the available experimental data and those from other studies. Ideally, the performance of XCs for the heats of adsorption should be assessed for multiple systems, and the results should be compared with the performance for the vibrational frequencies. However, we only did it for Pt because the measured data of the heat of adsorption are not available for other systems to the best of our knowledge.

For C₂H₂ adsorbed at h-fcc site on Pt(111), the absolute adsorption energy differences (|H_DFT − H_Exp.|) obtained from mBEEF and RPBE with the experimental value (−2.18 eV)⁶⁸ are 0.46 and 0.39 eV, respectively. Thus, the adsorption enthalpy obtained with both functionals deviates from experiment, but the RPBE results are closer to experiment. Our RPBE results are also closer to those obtained by BEEF-vdW⁶⁷ and PW91.^59,66 According to the experimental and theoretical studies summarized in Table 1, for the adsorption of C₂H₄/Pt(111) without dissociation, the molecule can adsorb at top and b-par sites. The RPBE adsorption enthalpy is closer to the experimental values than mBEEF adsorption enthalpy. The absolute difference of adsorption enthalpy obtained with RPBE and mBEEF for the top configuration in comparison with the experimental value of −0.41 eV (ref. 69) is 0.23 and 0.28 eV, respectively. For the molecular adsorption of C₂H₄/Pt(111) on the b-par site, the obtained result from RPBE is in the range of the reported experimental values, while the value obtained from the mBEEF functional is largely overestimated (see Table 1). In the case of the dissociative adsorption of C₂H₄/Pt(111) to form ethylidyne (CCH₃) and hydrogen, the energy differences in the adsorption energies calculated with RPBE and mBEEF and available experimental results (−1.36 eV)⁷² are 0.55 and 0.04 eV, respectively. Thus, for the dissociative adsorption of C₂H₄/Pt(111), H_ads calculated by mBEEF is closer to the experimental value than that calculated by RPBE. Table 1 also summarizes other theoretical values reported in the literature: RPBE, BEEF-vdW, BEEF, and PW91 show good agreement with the reported experimental values. In order to analyze the general performance of the two functionals, we plot in Fig. 3 the computed values of H_adsversus the experimental ones. As can be seen in the figure, RPBE with RMSE of 0.32 eV for adsorption enthalpy displays a better agreement with the experimental results. mBEEF tends to overestimate H_ads. This systematic tendency towards the overestimation of the adsorption enthalpy is confirmed by the obtained MPE values, also shown in Fig. 3: MPE = −59.81% (mBEEF) and 27.61% (RPBE). The measurement error for the heat of adsorption cited in the present work is 0.085–0.175 eV. Thus, the RMSEs for H_ads of the RPBE and mBEEF XC functionals are larger than the experimental error.

Fig. 3 Calculated adsorption enthalpy (H_ads) at temperatures listed in Table 1 of acetylene and ethylene on the Pt(111) surface versus corresponding experimental values. Dotted lines show least-squares-fit for the mBEEF and RPBE results. The gray line shows the ideal match between theory and experiment. In cases when a range of experimental adsorption energies were given, the average value along with the error bars are included in the plot. The mean percentage error is calculated by using the following formula: .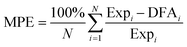

Finally, we also assessed the performance of two additional XC functionals and the influence of vdW corrections. In particular, we calculated vibrational frequencies and adsorption enthalpies for the C₂H₄/Pt(111) system with PBEsol and TPSS. The details of this analysis are discussed in Section S7 in the ESI.† TPSS is reported as the reliable functional for the bulk and surface properties of metals,¹⁷ and PBEsol is also a widely used functional for solid systems. Additionally, for the metal–adsorbate systems, the importance of adding the vdW correction to the GGA functionals has been discussed.^76–78 Thus, we also assess the performance of the RPBE functional with the Tkatchenko–Scheffler (TS) vdW correction. As shown in Fig. S3a and Table S7,† PBEsol shows the lowest RMSE for the vibrational frequency (30 cm⁻¹). TPSS shows a moderate performance among the adopted XC functionals (RMSE = 61 cm⁻¹), and there is no significant effect of the vdW correction on vibrational frequency in RPBE + TS (RMSE increased by 2 cm⁻¹). RPBE shows the second best RMSE for the vibrational frequencies (42 cm⁻¹), but mBEEF shows the highest RMSE among the considered XC functionals (83 cm⁻¹). On the other hand, as shown in Fig. S3b,† RPBE + TS overestimates the adsorption enthalpy by 0.47 eV. This overestimation is at least partly due to overestimation of long-range vdW interaction with metal surfaces by pairwise dispersion interaction models.⁷⁹ Additionally, PBEsol shows the highest error among the considered functionals (0.94 eV) while TPSS shows a moderate performance (error = 0.35 eV). For the adsorption enthalpy, RPBE shows the best performance (error = 0.05 eV), but mBEEF shows the second worst performance (error = 0.66 eV). The reaction enthalpy of the semi-hydrogenation of C₂H₂ to C₂H₄ in the gas phase was also calculated with all considered functionals. Interestingly, the accuracy trend across functionals is the same as the one for the adsorption enthalpy (Fig. S3c†).

Because RPBE shows high performance for all considered properties (assuming that the long-range vdW correction weakly depends on the specific functional among the considered ones), our study shows that RPBE is the most reliable functional for the considered system. On the other hand, PBEsol shows good accuracy for the vibrational frequency, but its accuracy for the adsorption and reaction enthalpy is lowest among the functionals. These results suggest that, if possible, the reliability of XC functionals should be assessed by investigating the accuracy for several physical quantities. However, in practice, we are limited by the scarcity of reliable experimental data, such as vibrational frequencies, for the metal–adsorbate systems.

We note that modelling the full catalytic progression by DFA and statistical mechanics is impractical, since catalysis is governed by an intricate interplay of several underlying processes, such as the surface reactions, the material restructuring under reaction conditions, and the transport of reactants and products. However, DFA can be used to obtain possibly relevant descriptive parameters correlated with atomistic processes. These parameters can be combined with experimental data in order to model catalysis via artificial intelligence (AI).³⁰ Indeed, we have recently considered such an AI approach for identifying the key descriptive parameters correlated to the experimental performance, out of many offered candidate descriptive parameters obtained from theory and/or experiment.^30,80–82 In analogy to genes in biology, these key parameters might be called “material genes” of catalysis,⁸⁰ as they correlate with the processes triggering, favouring or hindering the catalytic performance without providing the full understanding of the underlying processes.

Conclusions

In this study, we have evaluated the performance of mBEEF and RPBE functionals by mainly focusing on the vibrational frequencies of C₂H₂ and C₂H₄ both in the gas phase and adsorbed on TM surfaces. The experimentally measured frequencies are available for multiple systems such as the gas-phase molecules and the molecules adsorbed on Pt, Pd, Rh, and Cu surfaces (in total 36 data points). According to our vibrational frequency analysis for the molecules in the gas phase, the RMSEs obtained with RPBE are smaller than those obtained with mBEEF by 79 cm⁻¹ for C₂H₂ and 58 cm⁻¹ for C₂H₄. For the adsorbed molecules, we studied different adsorption structures at each TM surface. Our results show that the mBEEF functional misses some metastable adsorption structures. Moreover, we find that for vibrational frequencies, mBEEF, despite being in relatively good agreement with experimental data (RMSE = 118 cm⁻¹), performs worse than RPBE (RMSE = 61 cm⁻¹) for the considered systems. The accuracy of the functionals is also evaluated by studying the adsorption energy of the molecules on the Pt(111) surfaces. This study also shows that RPBE is more accurate than mBEEF. RMSEs of 0.41 eV and 0.32 eV are obtained for adsorption enthalpy with mBEEF and RPBE, respectively.

To demonstrate further application of our approach, the adsorption enthalpy and vibrational frequencies of the C₂H₄/Pt(111) system were also investigated with TPSS, PBEsol, and RPBE with the Tkatchenko–Scheffler pairwise long-range vdW correction. The performance of these functionals is worse than that of RPBE. Our results indicate that RPBE shows high reliability in describing the interaction between the metal surfaces and C₂H₂ or C₂H₄. Our study has demonstrated that the measured vibrational frequencies can be utilized for assessing the accuracy of the XC functionals. Such assessment is particularly important for the application of the DFA data to building an AI model for heterogeneous catalysis.

Data availability

Part of the data for this article is available at NOMAD (upload ID: oiPDzxLcTlClT6CAeiMsKg).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the discussion with our colleagues from the Max Planck-Cardiff Centre on the Fundamentals of Heterogeneous Catalysis (FUNCAT). This work received funding from the European Union's Horizon 2020 Research and Innovation Programme (grant agreement No. 951786), the NOMAD CoE. The work was partially supported by the Max-Planck Network on BigData-Driven Materials Science (BiGmax). We gratefully acknowledge the scientific support and HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) under the NHR project ID c100ba. NHR funding is provided by federal and Bavarian state authorities. NHR@FAU hardware is partially funded by the German Research Foundation (DFG) – 440719683. A part of the computation was also performed at the Research Center for Computational Science, Okazaki, Japan (project: 24-IMS-C002), and the Center for Computational Materials Science, Institute for Materials Research, Tohoku University is acknowledged for the use of MASAMUNE-IMR (project No. 202403-SCKXX-0026). R. M. acknowledges the support by the Joint Usage/Research Center for Catalysis (Proposal 22AY0053), the MEXT project “Integrating Research Consortium on Chemical Science”, and JSPS KAKENHI Grant Number JP24K17554. S. F. acknowledges the Alexander von Humboldt Foundation for financial support. S. V. L. is grateful for the support by RSCF grant 24-13-00317. Open Access funding provided by the Max Planck Society.

Notes and references

1. M. Niu, Y. Wang, W. Li, J. Jiang and Z. Jin, Catal. Commun., 2013, 38, 77–81.
2. K. K. Tanabe, M. S. Ferrandon, N. A. Siladke, S. J. Kraft, G. Zhang, J. Niklas, O. G. Poluektov, S. J. Lopykinski, E. E. Bunel, T. R. Krause, J. T. Miller, A. S. Hock and S. T. Nguyen, Angew. Chem., Int. Ed., 2014, 53, 12055–12058.
3. O. B. Ayodele, R. Cai, J. Wang, Y. Ziouani, Z. Liang, M. C. Spadaro, K. Kovnir, J. Arbiol, J. Akola, R. E. Palmer and Y. V. Kolen'ko, ACS Catal., 2020, 10, 451–457.
4. Z. Chen, C. Cai and T. Wang, J. Phys. Chem. C, 2022, 126, 3037–3042.
5. M. Bowker, S. DeBeer, N. F. Dummer, G. J. Hutchings, M. Scheffler, F. Schüth, S. H. Taylor and H. Tüysüz, Angew. Chem., Int. Ed., 2022, 61, e202209016.
6. K. S. Kley, J. De Bellis and F. Schüth, Catal. Sci. Technol., 2023, 13, 119–131.
7. I.-T. Trotuş, T. Zimmermann and F. Schüth, Chem. Rev., 2014, 114, 1761–1782.
8. F. Studt, F. Abild-Pedersen, T. Bligaard, R. Z. Sørensen, C. H. Christensen and J. K. Nørskov, Science, 2008, 320, 1320–1322.
9. P. Hohenberg and W. Kohn, Phys. Rev. A, 1964, 136, B864–B871.
10. W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, A1133–A1138.
11. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943.
12. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816.
13. B.-T. Teng, X.-D. Wen, M. Fan, F.-M. Wu and Y. Zhang, Phys. Chem. Chem. Phys., 2014, 16, 18563–18569.
14. J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44.
15. S. Mallikarjun Sharada, R. K. B. Karlsson, Y. Maimaiti, J. Voss and T. Bligaard, Phys. Rev. B, 2019, 100, 035439.
16. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
17. L. Kabalan, I. Kowalec, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2021, 23, 14649–14661.
18. J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen and T. Bligaard, J. Chem. Phys., 2014, 140, 144107.
19. E. Espí, A. Salmerón, A. Fontecha, Y. García and A. I. Real, J. Plast. Film Sheeting, 2006, 22, 85–102.
20. H. Yue, Y. Zhao, X. Ma and J. Gong, Chem. Soc. Rev., 2012, 41, 4218–4244.
21. J. Wu, Z. Wu, Y. Wei, H. Ding, W. Huang, X. Gui, W. Shi, Y. Shen, K. Tao and X. Xie, ACS Appl. Mater. Interfaces, 2020, 12, 19069–19079.
22. K. Xie, K. Xu, M. Liu, X. Song, S. Xu and H. Si, Materials Today Catalysis, 2023, 3, 100029.
23. X. Cao, B. W.-L. Jang, J. Hu, L. Wang and S. Zhang, Molecules, 2023, 28, 2572.
24. C. S. Spanjers, J. T. Held, M. J. Jones, D. D. Stanley, R. S. Sim, M. J. Janik and R. M. Rioux, J. Catal., 2014, 316, 164–173.
25. L. Ye, X. Duan, S. Wu, T.-S. Wu, Y. Zhao, A. W. Robertson, H.-L. Chou, J. Zheng, T. Ayvalı, S. Day, C. Tang, Y.-L. Soo, Y. Yuan and S. C. E. Tsang, Nat. Commun., 2019, 10, 914.
26. Y. Cao, H. Zhang, S. Ji, Z. Sui, Z. Jiang, D. Wang, F. Zaera, X. Zhou, X. Duan and Y. Li, Angew. Chem., Int. Ed., 2020, 59, 11647–11652.
27. Y. Wang, W. Zheng, B. Wang, L. Ling and R. Zhang, Chem. Eng. Sci., 2021, 229, 116131.
28. W. Zheng, Y. Wang, B. Wang, M. Fan, L. Ling and R. Zhang, J. Phys. Chem. C, 2021, 125, 15251–15261.
29. A. Mazheika, Y. G. Wang, R. Valero, F. Vines, F. Illas, L. M. Ghiringhelli, S. V. Levchenko and M. Scheffler, Nat. Commun., 2022, 13, 419.
30. R. Miyazaki, K. S. Belthle, H. Tüysüz, L. Foppa and M. Scheffler, J. Am. Chem. Soc., 2024, 146, 5433–5444.
31. H. Ibach and S. Lehwald, J. Vac. Sci. Technol., 1978, 15, 407–415.
32. P. Y. Timbrell, A. J. Gellman, R. M. Lambert and R. F. Willis, Surf. Sci., 1988, 206, 339–347.
33. J. A. Gates and L. L. Kesmodel, Surf. Sci., 1983, 124, 68–86.
34. C. M. Mate, C. T. Kao, B. E. Bent and G. A. Somorjai, Surf. Sci., 1988, 197, 183–207.
35. B. J. Bandy, M. A. Chesters, M. E. Pemble, G. S. McDougall and N. Sheppard, Surf. Sci., 1984, 139, 87–97.
36. M. A. Chesters and E. M. McCash, J. Electron Spectrosc. Relat. Phenom., 1987, 44, 99–108.
37. H. Steininger, H. Ibach and S. Lehwald, Surf. Sci., 1982, 117, 685–698.
38. D. Stacchiola, F. Calaza, T. Zheng and W. T. Tysoe, J. Mol. Catal. A: Chem., 2005, 228, 35–45.
39. M. Sock, A. Eichler, S. Surnev, J. N. Andersen, B. Klötzer, K. Hayek, M. G. Ramsey and F. P. Netzer, Surf. Sci., 2003, 545, 122–136.
40. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
41. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
42. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
43. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
44. S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, SoftwareX, 2018, 7, 1–5.
45. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
46. J. Nocedal and S. J. Wright, Numerical Optimization, Springer, New York, NY, 2th edn, 2006.
47. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
48. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
49. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
50. https://github.com/fidanyan/phonopy .
51. I. Kowalec, L. Kabalan, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2022, 24, 9360–9373.
52. A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174301.
53. K. Hellwege, A. Hellwege, B. Eisenmann and H. Schaefer, Structure data of elements and intermetallic phases, Springer, 1971.
54. G. Grube, A. Schneider and U. Esch, Heraeus Festschrift, 1951.
55. L. Lie-Quan and C. Pei-Lin, J. Phys.: Condens. Matter, 1996, 8, 3313.
56. J. C. Dunphy, M. Rose, S. Behler, D. F. Ogletree, M. Salmeron and P. Sautet, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R12705–R12708.
57. C. Matsumoto, Y. Kim, T. Okawa, Y. Sainoo and M. Kawai, Surf. Sci., 2005, 587, 19–24.
58. T. Okada, Y. Kim, M. Trenary and M. Kawai, J. Phys. Chem. C, 2012, 116, 18372–18381.
59. J. W. Medlin and M. D. Allendorf, J. Phys. Chem. B, 2003, 107, 217–223.
60. S. Bao, K. M. Schindler, P. Hofmann, V. Fritzsche, A. M. Bradshaw and D. P. Woodruff, Surf. Sci., 1993, 291, 295–308.
61. R. M. Watwe, R. D. Cortright, M. Mavrikakis, J. K. Nørskov and J. A. Dumesic, J. Chem. Phys., 2001, 114, 4663–4668.
62. Q. Ge and D. A. King, J. Chem. Phys., 1999, 110, 4699–4702.
63. R. M. Watwe, B. E. Spiewak, R. D. Cortright and J. A. Dumesic, J. Catal., 1998, 180, 184–193.
64. Y.-T. Wong and R. Hoffmann, J. Chem. Soc., Faraday Trans., 1990, 86, 4083–4094.
65. H. A. Aleksandrov, L. V. Moskaleva, Z. J. Zhao, D. Basaran, Z. X. Chen, D. H. Mei and N. Rösch, J. Catal., 2012, 285, 187–195.
66. F. Mittendorfer, C. Thomazeau, P. Raybaud and H. Toulhoat, J. Phys. Chem. B, 2003, 107, 12287–12295.
67. Z.-J. Zhao, J. Zhao, X. Chang, S. Zha, L. Zeng and J. Gong, AIChE J., 2019, 65, 1059–1066.
68. B. E. Spiewak, R. D. Cortright and J. A. Dumesic, J. Catal., 1998, 176, 405–414.
69. J. Kubota, S. Ichihara, J. N. Kondo, K. Domen and C. Hirose, Surf. Sci., 1996, 357-358, 634–638.
70. M. Salmeron and G. A. Somorjai, J. Phys. Chem., 1982, 86, 341–350.
71. J. M. Essen, J. Haubrich, C. Becker and K. Wandelt, Surf. Sci., 2007, 601, 3472–3480.
72. S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930.
73. W. A. Brown, R. Kose and D. A. King, Chem. Rev., 1998, 98, 797–832.
74. E. A. Carter and B. E. Koel, Surf. Sci., 1990, 226, 339–357.
75. O. L. Krivanek, N. Dellby, J. A. Hachtel, J. C. Idrobo, M. T. Hotz, B. Plotkin-Swing, N. J. Bacon, A. L. Bleloch, G. J. Corbin, M. V. Hoffman, C. E. Meyer and T. C. Lovejoy, Ultramicroscopy, 2019, 203, 60–67.
76. R. B. Araujo, G. L. S. Rodrigues, E. C. Dos Santos and L. G. M. Pettersson, Nat. Commun., 2022, 13, 6853.
77. J. B. Davis, F. Baletto and R. L. Johnston, J. Phys. Chem. A, 2015, 119, 9703–9709.
78. E. O. Bartaquim, R. C. Bezerra, A. F. B. Bittencourt and J. L. F. Da Silva, Phys. Chem. Chem. Phys., 2022, 24, 20294–20302.
79. W. Liu, A. Tkatchenko and M. Scheffler, Acc. Chem. Res., 2014, 47, 3369–3377.
80. L. Foppa, L. M. Ghiringhelli, F. Girgsdies, M. Hashagen, P. Kube, M. Hävecker, S. J. Carey, A. Tarasov, P. Kraus, F. Rosowski, R. Schlögl, A. Trunschke and M. Scheffler, MRS Bull., 2021, 46, 1016–1026.
81. L. Foppa, F. Rüther, M. Geske, G. Koch, F. Girgsdies, P. Kube, S. J. Carey, M. Hävecker, O. Timpe, A. V. Tarasov, M. Scheffler, F. Rosowski, R. Schlögl and A. Trunschke, J. Am. Chem. Soc., 2023, 145, 3427–3442.
82. L. Foppa, C. Sutton, L. M. Ghiringhelli, S. De, P. Löser, S. A. Schunk, A. Schäfer and M. Scheffler, ACS Catal., 2022, 12, 2223–2232.

---

Footnotes

† Electronic supplementary information (ESI) available: Geometry analysis for the C₂H₂ and C₂H₄ molecules in the gas phase, bulk lattice constants of each metal, vibrational frequencies of the molecules in the gas phase and adsorbed on the metal surfaces, adsorption energies on Pd(111), and comparison with other XC functionals for the C₂H₄/Pt(111) system. See DOI: https://doi.org/10.1039/d4cy00685b

‡ These authors contributed equally: Ray Miyazaki and Somayeh Faraji.

---