Open Access Article
Open Access ArticlePredicting the effect of framework and hydrocarbon structure on the zeolite-catalyzed beta-scission†
Yannick
Ureel
 a,
Konstantinos
Alexopoulos
a,
Konstantinos
Alexopoulos
 *b,
Kevin M.
Van Geem
*b,
Kevin M.
Van Geem
 a and
Maarten K.
Sabbe
a and
Maarten K.
Sabbe
 *a
*a
aLaboratory for Chemical Technology, Department of Materials, Textiles and Chemical Engineering, Ghent University, Technologiepark 125, 9052 Gent, Belgium. E-mail: Maarten.Sabbe@UGent.be
bDepartment of Chemical Engineering, Pennsylvania State University, University Park, Pennsylvania 16802-1503, USA. E-mail: kxa5325@psu.edu
First published on 15th October 2024
Abstract
Developing improved zeolites is essential in novel sustainable processes such as the catalytic pyrolysis of plastic waste. This study used density functional theory to investigate how alkyl chain length, unsaturated bonds, and branching affect β-scission kinetics in four zeolite frameworks, a key reaction in hydrocarbon cracking. The activation enthalpy was evaluated for a wide variety of 23 hydrocarbons, with 6 to 12 carbon atoms, in FAU, MFI, MOR, and TON. The consideration of both branched and linear olefin and diolefin reactants for the β-scission indicates how the reactant structure influences the intrinsic cracking kinetics, which is especially relevant for the catalytic cracking of plastic waste feedstocks. Intrinsic chemical effects, such as resonance stabilization, the inductive effect, and pore stabilization were found to provide an essential contribution to the activation enthalpy. Additionally, a predictive group additive model incorporating a novel so-called “pore confinement descriptor” was developed for fast prediction of the β-scission activation barrier of a wide range of molecules in the four zeolites. The obtained model can serve as an input for detailed kinetic models in zeolite-catalyzed cracking reactions. The acquired fundamental insights in the cracking of hydrocarbons, relevant for renewable feedstocks, correspond well with experimental observations and will facilitate an improved rational zeolite design.
1. Introduction
Zeolite-based catalysis has become an essential tool within the current chemical industry.1,2 Especially as highly acidic heterogeneous catalysts, they are indispensable in the current petrochemical industry. For example, in fluid catalytic cracking (FCC) and hydrocracking (HC) these zeolites are the cornerstone of the process. These cracking processes are some of the most important processes in the oil refining industry, as they convert heavy oil fractions into valuable lighter cuts.3,4 However, zeolites are not only important in today's industry but will also play a crucial role in facilitating the required shift towards a sustainable and climate-neutral chemical industry. To achieve this, the incorporation of plastic waste and biomass as a sustainable carbon source is an essential step to limit greenhouse gas emissions and move away from fossil fuels.5,6 Here, the goal is to produce base chemicals such as light olefins (ethylene, propylene) and BTX (benzene, toluene, xylene) from these recyclable carbon streams. Zeolites can convert the long-chain polymer hydrocarbons or lignin compounds into these valuable base chemicals via, for example, catalytic pyrolysis or hydrocracking followed by steam cracking.7–15 Also in other sustainable processes such as methanol-to-olefins (MTO), zeolites play a crucial role.16–18Many years of development have gone into designing the present-day fluid catalytic cracking and hydrocracking catalysts.19 Nevertheless, these zeolites are specifically designed for their task and are not necessarily optimal for the conversion of plastic waste or biomass feeds. For example with catalytic pyrolysis of plastic waste, much larger hydrocarbon chains have to be cracked compared to regular fluid catalytic cracking.7,20–24 Hence, a hierarchical mesoporous ZSM-5 catalyst was investigated by Eschenbacher et al. which resulted in much higher conversions to typical FCC or ZSM-5 catalysts.25,26 This work demonstrated the need for modified zeolites which are specifically optimized for their intended process, being the conversion of renewable carbon sources to valuable base chemicals.
To design improved zeolites, a proper mechanistic understanding of the occurring reactions is required. An important elementary reaction step in catalytic cracking is the β-scission.27–29 In this reaction, the carbon–carbon bond in β-position to the positively charged carbon atom breaks. Many experimental and quantum chemical investigations on the β-scission, both static and dynamic, have been performed in the past.30–32 The effect of zeolite confinement and shape selectivity is one of the effects that has been extensively studied.33,34 Shape selectivity describes how the reactant, transition state or formed products are (de-)stabilized by the zeolite pore shape, to promote or inhibit a reaction.35 This is also the power of zeolites and demonstrates the importance of zeolite topology. High-throughput experimental campaigns have been performed to find optimal zeolite frameworks for which ZSM-5 (MFI) proved a good zeolite to promote the β-scission of linear alkanes.36
In addition to the zeolite topology, its acidity and the location of acid sites in zeolites have been extensively investigated both experimentally and computationally.30,37–39 Variations in acid site location ZSM-5 have been shown to result in 44 kJ mol−1 difference in NH3 adsorption energy by DFT.40 Moreover, the proximity of acid sites to one another is also an important influence varying the NH3 adsorption energy by around 20 kJ mol−1.41 The zeolite acidity is a well-known parameter influencing the selectivity of the occurring β-scissions.42–45 The stronger the Brønsted acidity of the zeolite, the stronger it will promote all β-scissions resulting in a more active but less selective catalyst.37,46,47 On the other hand, weaker acid sites tend to promote β-scissions with lower activation energies hence resulting in more selective catalysts. Quantum chemical calculations and experiments have elucidated the effect of distribution, concentration and strength of the Brønsted acid sites on the cracking reactions, and how these are influenced by the zeolite composition.30,48,49 Recently, it was found by quantum chemical calculations that the type of heteroatom (Al, Ga, Fe, or B) influences the acid strength much stronger than the Si/Al-ratio or zeolite framework.50 This indicates that the product selectivity and activity of different zeolites is mostly dependent on the stabilization of the zeolite framework, making shape selectivity the determining factor for product yields.50,51
In addition to effects of the zeolite framework, the effect of hydrocarbon reactant on the β-scission kinetics have been investigated by both static and dynamic quantum chemical calculations. Cnudde et al. elucidated that carbenium ions are stable reaction intermediates at cracking process conditions and not alkoxides or physisorbed hydrocarbons.52 While alkoxides can be stable at lower temperatures due to their lower enthalpy and entropy, secondary and tertiary alkoxides were found to be less stable than their carbenium counterparts at temperatures relevant for catalytic cracking (400–600 °C).52 Weitkamp defined five cracking modes for the β-scission depending on the primary, secondary or tertiary nature of the carbenium reactant and product.53 It was found that the activation energy was strongly dependent on the scission mode, especially on the primary, secondary or tertiary nature of the reaction.54,55 Also experimentally, these scission trends were confirmed with tertiary reactants resulting in faster cracking kinetics.28,32,56 Experimentally, the reactant chain length has also been found to influence the intrinsic activation energy for hydrocarbons.57–59 Janda et al. investigated the effect of chain length by configurational-bias Monte Carlo simulations matching experimental data.57 Here, they investigated the cracking of linear C3–C6 alkanes and saw a dependency of the intrinsic activation energy with the chain length. However, at present mainly small hydrocarbons (≤C6) have been investigated making it impossible to estimate the effect of the hydrocarbon or framework on the intrinsic activation energy of the β-scission for the larger molecules relevant for the catalytic conversion of plastic waste or biomass.
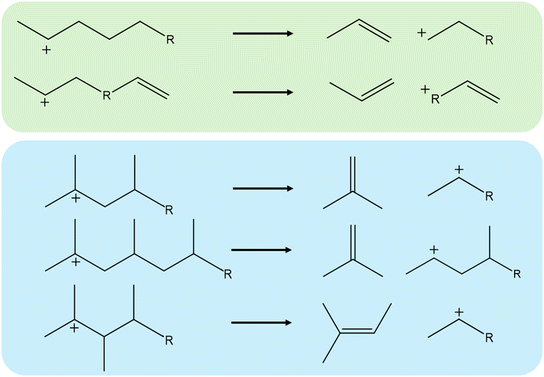
In this work, static density functional theory-based (DFT) calculations are performed to determine the intrinsic activation energy of the β-scission of various hydrocarbons in four different zeolites. The studied zeolite frameworks are FAU, MFI, MOR, and TON as these are industrially relevant and have widely differing pore structures.12,60 For every framework, 23 different carbenium ion reactants have been investigated with varying alkyl chain length, unsaturated bonds, and branches. The examined carbenium ions are depicted in Fig. 1, being relevant species for the catalytic cracking of polyethylene and polypropylene. The investigated carbenium ions have a carbon number ranging from 6–12 which is the relevant range for the catalytic cracking of plastic waste volatiles.7
This aids the elucidation of the effect of the hydrocarbon structure and zeolite framework on both the β-scission activation enthalpy and entropy. While molecular dynamics can scan a wide range of conformers in a zeolite, it is computationally intensive and difficult to interpretate.61 Because of the extensive range of hydrocarbons and frameworks studied, static DFT-calculations were preferred. Especially, as the purpose of this work is to investigate the relative change in activation energy of altering hydrocarbon structure in all frameworks. This relative change in activation energy can be properly predicted with static DFT-calculations, as opposed to absolute properties for which the deviation can be larger.62 A detailed qualitative and quantitative analysis has been performed to provide further insight in the obtained kinetic properties. Furthermore, a predictive model based on group-additivity and molecular mechanics calculations has been developed for each zeolite framework. In this way, improved kinetic models can be developed which can include the dependency of the reactant on the β-scission kinetics.
2. Materials and methodology
2.1. Zeolite models
A total of four common zeolite frameworks have been investigated i.e., FAU, MFI, MOR, and TON. In all frameworks one silicon atom was replaced by an aluminum atom and an acidic proton on the adjacent oxygen atom, to represent the highly-acidic catalytic cracking zeolite. The initial zeolite structures were taken from the International Zeolite Association.63 In all zeolites, the unit cell was extended to avoid any interaction of the hydrocarbons in the framework with itself because of the assumed periodicity in the DFT calculations. The reported dimensions of the empty zeolite are based on optimized structures.The FAU framework is a large pore zeolite with pore diameters of 1300 pm that are interconnected by 12-membered rings with dimensions of 740 × 740 pm.64 A 96T zeolite cluster was taken as unit cell with a Si/Al-ratio of 95. The acid site is located at the Al1O1 position as commonly assumed in literature.65–67 The dimensions of the empty zeolite framework were optimized, resulting in a unit cell lattice with a = 1740 pm, b = 1736 pm, c = 3484 pm, α = 59.9°, β = 59.8°, and γ = 59.9°. The MFI framework is a medium-pore zeolite with interconnecting straight and sinusoidal channels. The straight channels are 540 × 560 pm, while the 10-membered sinusoidal channels are 510 × 540 pm.64 A unit cell consisting of 96T-atoms was employed with a Si/Al-ratio of 95. The acid site within the MFI framework was taken at the Al12O24 intersecting position to represent ZSM-5.68–71 The dimensions of the optimized empty MFI-cell were a = 2039 pm, b = 2024 pm, c = 1362 pm, α = 90.0°, β = 90.0°, and γ = 90.0°. The MOR topology has a large 12-membered ring channel with dimensions 650 × 700 pm. These channels are interconnected by 8-membered 260 × 570 pm pockets.64 The unit cell is taken as a 144T zeolite cluster with a Si/Al-ratio of 143. The acid site is selected at the Al4O2H position.68 The optimized empty MOR framework had the following parameters: a = 1826 pm, b = 2053 pm, c = 2263 pm, α = 90.0°, β = 90.0°, and γ = 90.0°. The final considered framework was the TON topology. The one-dimensional small-pore zeolite has a straight channel with dimensionality 460 × 570 pm.64 A total of 96T-atoms are considered for the unit cell, resulting in a Si/Al ratio of 95. The acid site was located at the Al3O3 position to represent the ZSM-22 catalyst.66,67 Prior to all calculations, the empty unit cell was optimized which led to the following parameters: a = 1411 pm, b = 1784 pm, c = 2102 pm, α = 90.0°, β = 90.0°, and γ = 90.0°. The optimized zeolite topologies are visualized in Fig. S1–S4 of the ESI.†
2.2. Quantum chemical calculations
Transition state search was performed by nudged elastic band (NEB)79 and dimer calculations.80–82 The NEB was employed to find an initial guess of the transition state, starting from geometries taken from molecular dynamic calculations.55 For the NEB calculations, a softer preliminary convergence criterion of 0.15 eV Å−1 on the forces was considered. Subsequently, dimer calculations were performed to obtain the final transition state geometry. Here, the convergence criterion on the forces of 0.05 eV Å−1 was used with a stricter self-consistent field (SCF) convergence level of 10−7 eV.
The frustrated motions of adsorbed species can sometimes result in low frequencies which provide an unrealistic large contribution to the resulting entropy. Therefore, low frequencies (<50 cm−1) are replaced by a frequency of 50 cm−1. This approach was shown to improve the accuracy of the calculated entropy by De Moor et al.83 Furthermore, it was explicitly verified that transition states have one single imaginary frequency and stable compounds have none.
2.3. Data-analysis
The 92 calculated activation enthalpies were rigorously analyzed to provide further insights and develop a predictive model for the activation enthalpy. As shape selectivity is the main driver for the different selectivities of zeolites, structural or topological properties are required to link the zeolite properties with the obtained activation enthalpies. Many descriptors have been proposed in literature such as the void diameter, undulation parameter, collision diameter, non-sphericity index, and charge separation.50,85–87 However, a linear model comprising of these properties as variables failed to predict the activation enthalpy as it achieved a mean absolute error (MAE) by training on all data of 16.0 kJ mol−1 (results not shown) which is on the high end of DFT-accuracy (10–20 kJ mol−1).88,89 Therefore, a novel pore confinement descriptor is introduced to improve these predictions.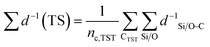 | (1) |
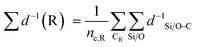 | (2) |
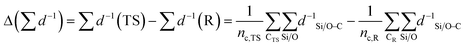 | (3) |
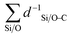 denotes the sum of reciprocal distances between a given carbon atom and all silicon and oxygen atoms considered in the unit cell. The reciprocal distance is commonly used when considering electrostatic interactions.90–92 The unit cell was replicated once along every dimension for the calculation. Next, the average of this sum for all carbon atoms is evaluated, after which the same calculation is repeated for the transition state
denotes the sum of reciprocal distances between a given carbon atom and all silicon and oxygen atoms considered in the unit cell. The reciprocal distance is commonly used when considering electrostatic interactions.90–92 The unit cell was replicated once along every dimension for the calculation. Next, the average of this sum for all carbon atoms is evaluated, after which the same calculation is repeated for the transition state 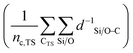 . The pore confinement descriptor is then defined as the difference between both values.
. The pore confinement descriptor is then defined as the difference between both values.
The obtained value is a measure for the confinement and stabilization energy of the pores and the carbon chain of the compound determined as an energy field. Similar to the electrostatic potential which scales with d−1, 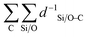 is a measure for the total pore stabilization energy of the compound. The smaller the distance of the alkyl chain to the zeolite framework, the higher the sum of d−1 and the higher the pore (de-)stabilization energy of the compound. It was found that averaging over the number of carbon atoms was meaningful for the description of the kinetic properties of the β-scission and correlated better with the activation energies. This makes the pore confinement descriptor more of an intensive property as it divides two extensive properties likewise to kinetic properties.
is a measure for the total pore stabilization energy of the compound. The smaller the distance of the alkyl chain to the zeolite framework, the higher the sum of d−1 and the higher the pore (de-)stabilization energy of the compound. It was found that averaging over the number of carbon atoms was meaningful for the description of the kinetic properties of the β-scission and correlated better with the activation energies. This makes the pore confinement descriptor more of an intensive property as it divides two extensive properties likewise to kinetic properties.
It should be noted that the pore confinement descriptor is a measure for the difference between the transition state and reactant in average distance between the carbon chain and the zeolite framework. A positive pore confinement descriptor denotes that the transition state is closer to the zeolite framework than the reactant, and a negative descriptor vice versa for the reactant. It is not a measure to determine the optimal location of a hydrocarbon in a zeolite, but describes the change in average distance of the carbon chain by altering the type of reactant for the same location of reactive center.
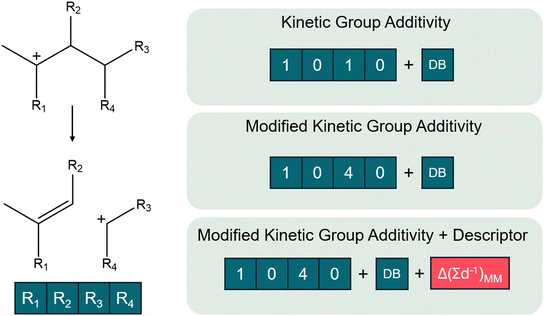
Within the unmodified kinetic group additive model, solely the carbon atoms neighboring the reactive center are accounted for. This corresponds to a carbon atom in the R1–4 position for the studied dataset. In this way, a β-scission is then represented by a five-dimensional one-hot encoded vector with a value of one when a chain is present or zero when it is absent in the respective R1–4 position and DB-value denoting whether a double bond is present in the hydrocarbon. As the position of the R3 and R4 are symmetrical, the R3 value has priority for the carbon atom. Consequently, it is impossible that the fourth position in the vector has a value of one while the third is still zero.
In addition to the kinetic group additivity, a modified group additive model is proposed. Here, a similar five-dimensional vector is constructed but the value of the ith element of the vector now corresponds to the number of carbon atoms on the respective branch Ri. The advantage of this approach is that it can differentiate between different chain lengths of branches while maintaining the same dimensionality of the representation.
Lastly, a predictive model combining the so-called pore confinement descriptor as defined before and the modified group additive model is evaluated. However, the pore confinement descriptor can only be determined, given an optimized reactant and transition state geometry. Therefore, pore confinement descriptors were determined based on the geometries obtained by fast and computationally cheap molecular mechanics calculations, which are defined below.
The molecular mechanics calculations were performed via Gaussian16 and the DREIDING force-fields as defined by Mayo et al.93,94 The geometry of the reactive center and the optimized zeolite cage were taken from the DFT-based calculations performed via VASP 6.2, as provided in ESI† (section S12). Subsequently, the geometry was modified by manually adding branches in arbitrary directions after which the optimized force-field geometry was determined both for the reactants and for the transition states. During optimization, the position of the reactive center was fixed, in this way the geometry of both the transition state and the reactant were determined. The geometry of the relevant reactive centers and frameworks are provided in ESI† (section S12) to allow further use of the developed models.
3. Results and discussion
The activation enthalpy of a wide variety of 23 hydrocarbons was obtained in four different zeolite frameworks. These carbenium ions are all relevant for the ex situ catalytic pyrolysis of plastic waste, and in addition serve as common reactants in other zeolite-catalyzed cracking processes. The studied carbenium ions varied in number of carbon atoms, methyl-branches, and number of double bonds. In this way, the effect of chain length, unsaturated bonds, and branches was investigated in FAU, MFI, MOR, and TON. The complete list of calculated activation enthalpies and entropies is provided in ESI† (Table S1). The activation entropy is not elaborately discussed in this work as these are typically less accurate for static calculations.833.1. Effect of chain length
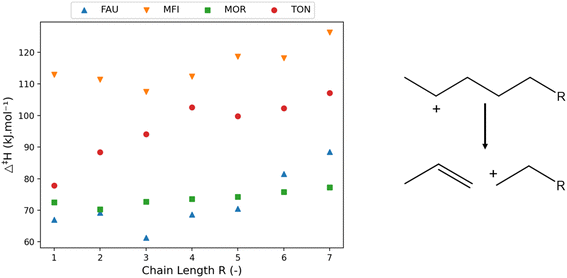 | ||
| Fig. 3 The variation of activation enthalpy (Δ‡H) with increasing chain length of linear components (left) investigated in FAU, MFI, MOR, and TON for the depicted reaction template (right). | ||
The activation enthalpy was clearly influenced by the chain length of the reactant, though less so in the case of MOR. The activation enthalpy is the difference in enthalpy between the β-scission transition state and the carbenium ion, hence it is influenced by the stability of both. The TON framework is a one-dimensional small-pore zeolite. The volume increase of the transition state is detrimental for the stability within the small pore resulting in a high molecular strain. Consequently, the longer the chain length becomes, the more of the alkyl chain is in the vicinity of the zeolite framework which increases the activation energy.
In addition to the effect of pore (de-)stabilization, pure chemical effects also play a role in the change in activation energies. Inductive stabilization is a well-known important effect in radical and carbenium ion chemistry.99,100 The unstable positive charge of the carbon atom in the carbenium ion and transition state will be stabilized by inductive stabilization of the connected alkyl-chain. The longer this alkyl-chain, the stronger the inductive stabilization and the better stabilized the respective molecule. As the β-scission transition state is a late transition state,54 it resembles closely the character of the products being primary carbenium ions in this case. These primary carbenium ions are more unstable than the secondary reactant making the effect of inductive stabilization more important in the transition state. Furthermore, the alkyl chain length of the transition state is shorter, enhancing the effect of increasing or decreasing alkyl chain length. The combination of the inductive stabilization and pore confinement determines the trends in activation enthalpy as can be seen in MFI. First, a decrease in activation enthalpy is found up to oct-2-ylium (R = 3) stemming from inductive stabilization after which pore confinement becomes more dominant. This initial decrease in activation energy in the MFI framework has also been observed computationally by Janda et al. who investigated the β-scission activation energy for C3–C6 linear species.57 There, a decreasing trend of activation energy was observed with increasing chain length while the difference in activation energy decreased with increasing chain length. These trends comply with the results of Fig. 3 up to R = 3, while an increase in activation energy is observed for even larger species.
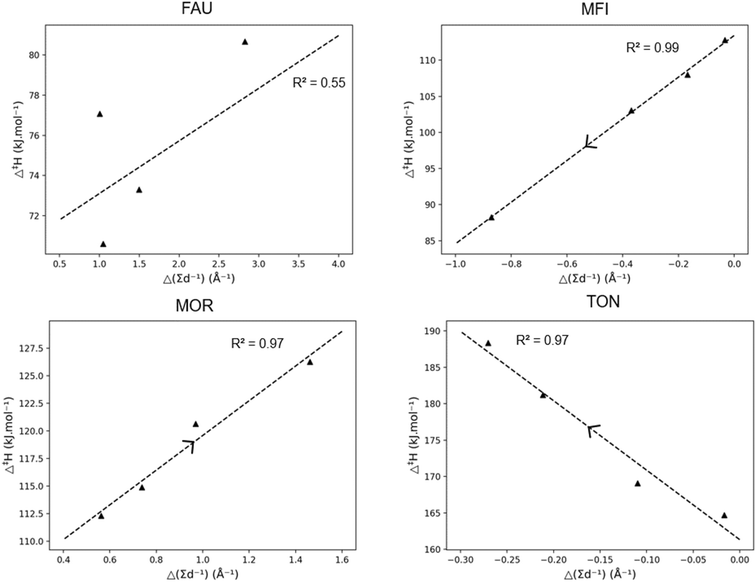
To provide further insight into the effects of pore confinement, the so-called “pore confinement descriptor” Δ(∑d−1) was determined to quantify the difference in location of the reactant and transition state in the zeolite pore. Throughout this work we use the term pore stabilization when a reactant or transition state moving closer to the zeolite framework is energetically favored and vice versa for pore destabilization. Fig. 4 displays the correlation between the obtained activation enthalpies and the pore confinement descriptor. The slopes and intercepts with corresponding 95%-confidence intervals are reported in ESI† in Table S2. A remarkably strong correlation is found between both properties, especially for the MFI and MOR frameworks. An increasing Δ(∑d−1) corresponds with a transition state which is closer to the zeolite pore wall and/or a reactant which is further away from the zeolite. Here, the pore confinement descriptor is positive in all four frameworks indicating that the transition state is more closely located to the zeolite framework than the reactant. The transition state is more closely located because of two reasons. First, the transition state is more voluminous making it be overall closer to the zeolite pore walls, especially within the medium and small pore zeolites. Second, since the positive charge of the primary carbenium ion at the transition state is more unstable, the TS and zeolite framework move closer to each other to stabilize the primary carbenium ion while balancing the strain caused by the relative deformation of the zeolite framework. For example in MOR, the distance between the positively charged carbon atom of the carbenium ion and the negatively charged oxygen atom of the zeolite framework is 2.96 Å at the hept-2-ylium reactant and 2.22 Å at the TS. This illustrates the carbenium ion and zeolite moving closer at the TS. Moreover, the Si–O–Al angle with the hept-2-ylium reactant is 135.4° where this is 131.7° for the transition state as the negatively charged oxygen atom moves towards the hydrocarbon transition state.
The trends in Fig. 4 allow to elucidate the reasons behind the change in activation enthalpy in the four different frameworks. For FAU, an increase in pore confinement descriptor results in a decreasing activation enthalpy. Consequently, the closer the transition state is to the FAU framework, the lower the activation enthalpy. As FAU is a large pore zeolite this is logical, as it offers little stabilization for the transition state. Moreover, the stabilization of the transition state was found to be the most important driver for the activation enthalpy as the ∑d−1(TS) offers a better correlation for FAU than Δ(∑d−1) with an R2 of 0.78 as shown in ESI† (S3). The longer the chain length of the carbenium ion, the further the transition state was from the pore and hence the higher the activation enthalpy in FAU due to the lack of pore confinement.
For MFI and MOR, a better correlation with Δ(∑d−1) was found, with pore destabilization leading to an increase in activation enthalpy the closer the transition state was to the zeolite pore. Notably for the larger MOR framework, only slight deviations in activation enthalpy were found for increasing chain length. With MFI, the trend was more profound and as the chain length became longer, the closer the transition state was to the zeolite pore, and the higher the activation enthalpy was. Similarly for TON, the volume increase of the transition was found to be detrimental for the activation enthalpy as previously discussed. Anderson et al. investigated the kinetics of the hydride transfer reactions for C6–C10 paraffins in TON, MFI, and MOR.101 Here, similar sterical effects were observed with a fast increase in activation energy for TON, a slighter increase for MFI, and nearly no effect of chain length in MOR.
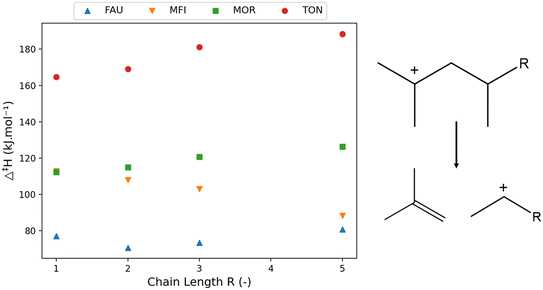 | ||
| Fig. 5 The variation of activation enthalpy (Δ‡H) with increasing chain length of branched components (left) for the depicted reaction template (right). | ||
Fig. 5 presents the activation enthalpy of the four hydrocarbons in the four zeolite cells. Within the large FAU framework, little change in activation enthalpy has been observed with an increasing carbon number. To discuss pore stabilization, the correlation between the “pore confinement descriptor” and the activation enthalpy in the four frameworks is presented in Fig. 6. It is important to note the difference in scale of the activation enthalpy depicted on the y-axis. This shows that the trend between Δ‡H and Δ(∑d−1) is minor for FAU because of the small change in activation enthalpy which lies within the margin of error for static transition state calculations. The slopes and intercepts with corresponding 95%-confidence intervals are reported in ESI† in Table S3.
The correlations for the other frameworks between Δ‡H and Δ(∑d−1) are remarkably high. In Fig. 5, for the MFI framework, a decrease in activation enthalpy has been found with increasing chain length. The increasing chain length resulted in a decrease of the pore confinement descriptor as found in Fig. 6. This is related to the loss of branches in the transition state offering more positional freedom. The double branched reactant is relatively close to the medium pore MFI framework and the more voluminous transition state fits properly in the MFI channel intersection. Moreover, the transition state is not constrained by the zeolite pore as the acid site in MFI is located in the spacious intersection of the straight and zigzag channel. Therefore, the decrease in activation enthalpy observed in MFI is very strongly correlated with a transition state which moves relatively further from the zeolite pore than its reactant.
The other medium-pore framework MOR has a reverse trend with increasing activation enthalpy with increasing chain length and increasing pore confinement descriptor. As the chain length of the reactant and transition state increases, the position of transition state is on average closer to the zeolite pore wall. This is caused by the larger straight channel of the MOR framework compared to the MFI framework, offering the branched compound adequate space but not enough for the larger transition state, especially as the channel intersections of MOR are smaller than the large MFI intersections. For MOR, the increasing chain length forces the transition state to move closer on average to the pore wall which results in pore destabilization for the TS and an increasing activation enthalpy. Lastly, the small-pore TON zeolite has a strongly increasing activation enthalpy with increasing carbon number. As more atoms are added to the transition state, the more spacious it becomes and the further away from the narrow pore wall it moves. This is the result of the dominating steric hindrance in the more voluminous transition state. For the TON zeolite, a negative Δ(∑d−1) is observed meaning that the reactant is more closely positioned to the zeolite framework than the transition state and as the chain length increases, the reactant moves closer to the pore wall and pore stabilization on the reactant leads to an increasing activation energy.
From previous discussions it is clear that the effect of chain length in zeolites is dependent on both the type of hydrocarbon being either linear or branched and the topology and size of the corresponding zeolite framework. Within the large pore zeolite FAU, the effect of chain length is generally limited aside for when the hydrocarbon becomes too big and is not properly stabilized by the pore. For the medium-pore MFI and MOR, the effect is more complex and the location of the acid site is found to be important. Within the medium-pore zeolites it is generally found (apart from branched hydrocarbons in MFI) that increasing chain length corresponds with increasing activation enthalpy as the voluminous transition state is closer to the zeolite pore. However, with the loss of branches and an acid site at the MFI intersection, a decrease in activation enthalpy is found with increasing chain length. Consequently, when the acid site at the MFI would move to be positioned in either the straight or sinusoidal channel one can expect an increasing activation enthalpy with increasing chain length similar to the MOR topology.
The magnitude of the slope of the correlation between the activation enthalpy and pore confinement descriptor (as displayed in Fig. 4 and 6) correlates with the size of the pore. If the slope is close to zero such as with FAU or MOR, the zeolite is well-suited to crack larger chains, while a steep slope denotes a high dependency of the activation enthalpy with the carbon chain length corresponding to a pore which is too small.
3.2. Effect of unsaturated bonds
Besides a larger chain length, renewable carbon sources tend to contain more unsaturated hydrocarbons than fossil sources. Upon cracking these give rise to the formation of diolefins or carbenium ion reactants with an unsaturated end-chain bond. Therefore, the β-scission activation enthalpy of seven unsaturated carbenium ions with end-chain double bonds were determined in the four different frameworks. The studied hydrocarbons ranged from hex-1-ene-5-ylium to dodec-1-ene-11-ylium, as depicted in Fig. 7, similar to the saturated linear carbenium ions previously studied. | ||
| Fig. 7 Reaction template of the β-scission of the studied unsaturated hydrocarbons with increasing chain length R (R = 1–7). | ||
Fig. 8 shows the calculated activation enthalpies for the four different frameworks together with the previously presented activation enthalpies for the corresponding saturated hydrocarbons, for an equal number of carbon atoms. These graphs clearly show the chain-length dependent effect of adding an unsaturated double bond. At 6 carbon atoms, corresponding to the cracking of hex-1-ene-5-ylium, a significant drop in activation enthalpy is found in all frameworks. The products of this cracking reaction are propylene and the strongly resonance stabilized allylium. The resonance stabilization is also present in the transition state making it much more stable (∼30 kJ mol−1) than the non-resonance stabilized structures.
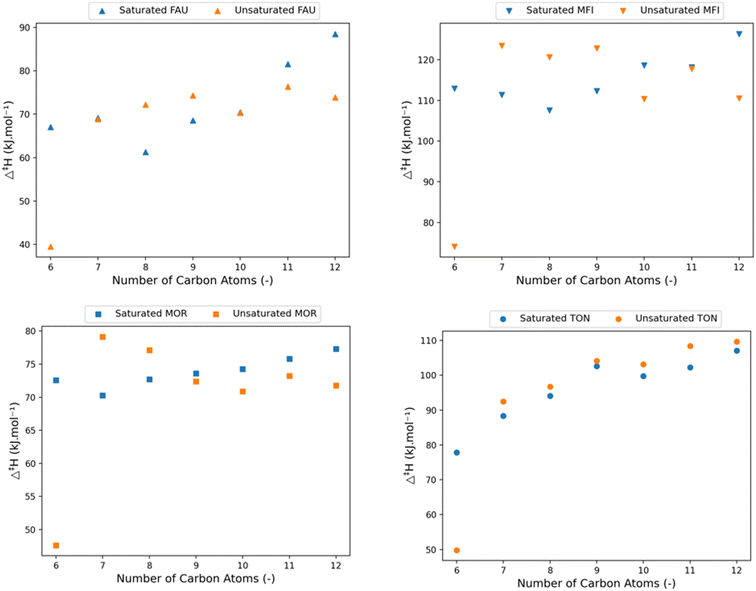 | ||
| Fig. 8 The variation of activation enthalpy (Δ‡H) with increasing chain length of saturated (blue) and unsaturated linear carbenium-ions (orange). | ||
A clear pattern in the effect of double bond is present for the larger pore FAU, MFI, and MOR frameworks. At smaller chain lengths, ranging from 7 to 9 carbon atoms, the presence of the unsaturated bonds seems to be destabilizing for the transition state, whereas for longer chains the unsaturated carbenium ion transition states are more stable than their saturated counterparts. The initial higher activation enthalpy for the cracking of unsaturated hydrocarbons is because of the negative inductive effect the double bond has on the positive charge.105 This destabilizing inductive effect is chain length dependent, and as the chain length of the transition state is shorter than the reactant it will increase the activation enthalpy. With increasing chain length this effect becomes less pronounced because of the distance between the unsaturated bond and the charged carbon atom and is compensated by a higher pore stabilization of the unsaturated end-chain, both for the reactant and transition state. The pore stabilization effect is more pronounced for the reactant as it is more optimally oriented in the zeolite pore than the transition state which has less conformational freedom. As a result, the reaction barrier decreases because of this. The interaction of the electron rich π-orbital with the zeolite cage results in a slightly better stabilization due to Van der Waals forces. Consequently, the unsaturated carbenium ions will have a lower activation enthalpy for longer alkyl chains.
The small-pore TON framework does not follow the same pattern of competing inductive and pore stabilization. In the TON framework a slightly higher β-scission activation enthalpy is obtained for all unsaturated carbenium ions compared to the saturated carbenium ions. Here, the inductive effect is less dominant than the larger pore destabilization effects on the reactants and transition states as the unsaturated hydrocarbons have a higher activation enthalpy independent of the number of carbon atoms. Within the small TON framework, the unsaturated end-chain is positioned closer to the zeolite framework than a saturated end-chain (see ESI† Fig. S7 and S8). The unsaturated C–C bond at the end-chain angles slightly towards the deprotonated zeolite framework which destabilizes the transition state and reactant. This effect is however more pronounced for the transition state as it is closer located to the zeolite framework. The correlation between the pore confinement descriptor and activation enthalpy is provided in the ESI† and again displays a strong correlation for all topologies (Fig. S10†).
To summarize, the presence of an end-chain double bond in the protonated hydrocarbon reactant above 6 carbon atoms is detrimental for the activation enthalpy for relatively smaller molecules but stabilizing for larger molecules. The effect is found to be independent of zeolite framework when comparing medium-pore (MFI, MOR) and large-pore (FAU) zeolites. For the small-pore TON cell, the activation enthalpy increases slightly because of the suboptimal chain orientation. This knowledge allows us to make predictions for the effect of internal double bonds on the β-scission kinetics. The inductive effect will decrease slightly, depending on the size of the alkyl chain between the end-chain and the double bond. The more bonds between the end-chain and double bond, the weaker the inductive effect will be. Unfortunately, this conclusion cannot be extrapolated for internal double bonds. The presence of an internal double bond limits the rotational freedom which alters the effect of the pore stabilization and as a result the activation enthalpy. Fig. S5† provides an overview of the activation enthalpy of the unsaturated hydrocarbons in all four frameworks.
3.3. Effect of branching
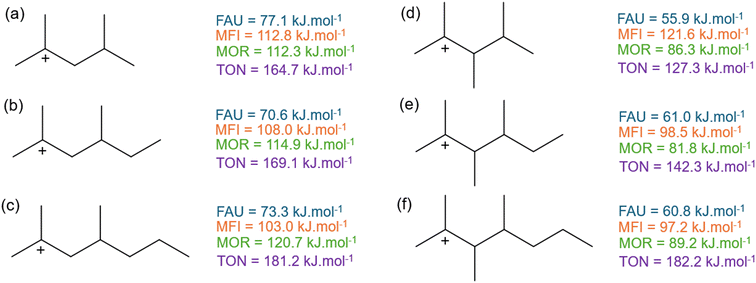
A last investigated effect is the addition of an extra branch on the β-scission activation enthalpy of branched hydrocarbons. A total of nine different hydrocarbons with a varying number of branches has been examined.Fig. 9 presents the activation enthalpy of six of these branched carbenium ion reactants. The activation enthalpies of the hydrocarbons on the left side (a–c) have been previously presented in Fig. 5 when discussing the effect of increasing chain length of branched compounds. The branched compounds on the right side (d–f) have an additional methyl-group in α-position to the positive charge. In this way, the reactant has become more spacious, especially because of the steric effects forcing the methyl-branches in antiperiplanar conformation. When looking at the larger FAU and MOR zeolites, it is clear that adding an extra branch decreases the activation enthalpy. The decrease in activation enthalpy is caused by a lower stability of the branched reactant in the zeolite pores. Upon cracking, 2-methylbut-2-ene (d–f) and a linear carbenium-ion are formed resulting in a much less spacious transition state. For MFI, the same trend is found as in FAU and MOR with regard to 2,3,4-trimethylhex-2-ylium and 2,3,4-trimethylhept-2-ylium (e and f). However, for 2,3,4-trimethylpent-2-ylium (d) an increase of 8.8 kJ mol−1 is observed instead of a decrease as with the other branched species. This is due to the specific topology of the MFI framework which “perfectly” fits the 2,3,4-trimethylpent-2-ylium in the intersection of the straight and zigzag channel as presented in Fig. S8.† The increased stability of the reactant (d) results in an elevated activation enthalpy compared to 2,4-dimethylpent-2-ylium (a). Lastly, in the TON framework the activation enthalpy increases as an extra branch is added but also a chain length dependency is observed as the activation enthalpy of 2,3,4-trimethylhept-2-ylium (f) is similar to 2,4-dimethylhept-2-ylium (c). In the previous section, it was demonstrated that increasing the chain length in the TON zeolite resulted in an increase in activation enthalpy. Likewise, the activation enthalpy increases for both branched series, but it increases faster for (d–f) than for (a–c).
Fig. 10 displays the activation enthalpy of four other branched hydrocarbons. Here, an additional methyl-branch is added to compound (c and g) in δ-position to the positively charged carbon atom resulting in species (h and i). In contrast to (c and g), the β-scission products of 2,4,6-trimethylhept-2-ylium (h) and 2,4,6-trimethylnon-2-ylium (i) are both branched products and hence also have a branched transition state. This differs from the hydrocarbons in Fig. 9 where only linear carbenium ions were formed. This alters the effects of additional branches to the carbenium reactants. For the large-pore FAU, a slight increase in activation energy of 3 kJ mol−1 is found when adding the branch in δ-position. The additional branch in the transition state slightly moves the transition state further away from the zeolite cage, destabilizing the corresponding transition state. Within MFI, this effect is less pronounced because of its intersecting channel topology. For the addition of the methyl-branch between 2,4-dimethylnon-2-ylium (g) and 2,4,6-trimethylnon-2-ylium (i) an increase in activation enthalpy is found similar to FAU. However, for 2,4-dimethylhept-2-ylium (c) and for 2,4,6-trimethylhept-2-ylium (h) the opposite effect is observed. Here, the transition state of 2,4,6-trimethylhept-2-ylium (h) moves relatively closer to the zeolite pore than the transition state of 2,4-dimethylhept-2-ylium (c). This is reflected in an increased pore confinement descriptor between (c) and (h) from −0.36 to −0.33 respectively, whereas for (g) and (i) the pore confinement descriptor decreases from −0.87 to −0.90. For MFI, these branched reactants and transition states are located in the spacious channel intersection which is not present in MOR. Here, the branched reactant can be partially located in a side-pocket but this is not possible for the transition state. This results in a high steric hindrance of the branched transition state leading to a markedly high activation enthalpy in MOR. Lastly within the TON cluster, a decrease in activation enthalpy is found by the addition of the methyl-branch. This a consequence of the additional branch destabilizing the reactant further in the small-pore zeolite. This is also reflected in the decrease in pore confinement descriptor by the addition of the branch between (c) and (h) from −0.21 to −0.25 and between (g) and (i) from −0.27 to −0.42. This displays that the reactant for (h) and (i) is forced to be closer to the TON framework which results in pore destabilization of the reactant as an extra branch is added. All pore confinement descriptors of the branched reactants can be found in ESI† (Fig. S11 and Table S1).
 | ||
| Fig. 10 The activation enthalpy of (c) 2,4-dimethylhept-2-ylium, (g) 2,4-dimethylnon-2-ylium, (h) 2,4,6-trimethylhept-2-ylium, (i) 2,4,6-trimethylnon-2-ylium in FAU, MFI, MOR, and TON. | ||
In summary, two separate cases of additional branches were examined in Fig. 9 and 10 with differing effects. When the branch was added to the reactant but still resulted in a linear carbenium ion transition state, a decrease in activation enthalpy was generally found as the reactant was less stable (apart from 2,3,4-trimethylpent-2-ylium in MFI). The decrease in activation energy for branched compared to linear reactants was also found by Mazar et al.54 When the added methyl-branch resulted in a branched carbenium-ion, the effect depended on the zeolite framework. In the spacious FAU and less so in MFI, this generally resulted in small increase in activation enthalpy. For MOR, the small side pocket could partially stabilize the reactant but not the transition state resulting in a high enthalpy barrier. The small-pore one-dimensional TON channel could not stabilize the reactant resulting in a relative decrease of activation enthalpy. It is clear that not only the size of the pores in the zeolite framework play a role in their effect on the β-scission kinetics but also their specific topology, with, for example, the presence of intersections and side-pockets.
3.4. Group-additive modeling
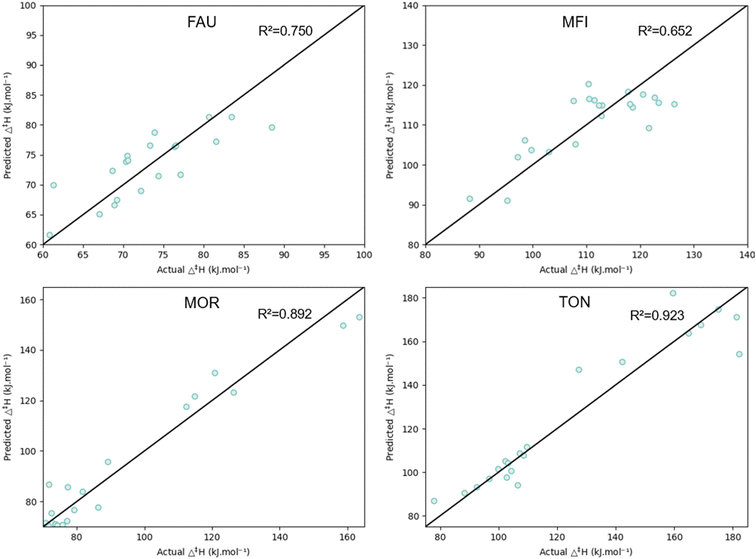
The effect of the alkyl chain length, presence of unsaturated bonds, and branches on the β-scission activation enthalpy in four vastly different zeolites has been qualitatively described in the previous sections. In addition to the qualitative description, a quantitative predictive model based on group additivity has been developed which allows for fast prediction of activation enthalpies for these reactions. Three different group additive-based approaches have been employed as described in the methodology, being a kinetic group additive model, a modified group additive model and a modified group additive model accounting for the pore confinement descriptor. The latter model incorporates the pore confinement descriptor determined based on the force-field geometry of the reactant and transition state, hence allowing still for a predictive model as no expensive quantum chemical calculations are needed. The group additive values were determined for every separate zeolite framework by training on all 23 β-scissions, excluding the scission of the resonance stabilized hex-1-ene-5-ylium. The mean absolute errors on the prediction of the activation enthalpy for the three different models in four zeolite frameworks are reported in Table 1.| MAE (Δ‡H) [kJ mol−1] | kGAV | mGAV | mGAV + Δ(∑d−1)MM |
|---|---|---|---|
| MFI | 6.1 | 5.8 | 4.9 |
| FAU | 4.2 | 3.1 | 3.0 |
| MOR | 6.7 | 7.2 | 5.3 |
| TON | 9.1 | 6.4 | 6.4 |
The kinetic group additive model is a one-hot encoding of the number of substituents on the reactive center and the presence of an end-chain double bond. The obtained model parameters are supplied in ESI† (Table S4). This reaction representation cannot capture the chain length dependence which clearly has an effect on the activation enthalpy. Therefore, a modified group additive model has been proposed which incorporates the chain length (Table S3†). This generally improves the predictions on the activation enthalpy as depicted in Table 1; especially in FAU and TON the chain length dependency of the modified group additive model improves the mean absolute error up to 30%. For MFI and MOR, the effect is less pronounced.
The pore confinement descriptor has been shown to correlate well with the activation enthalpy in the previous sections. To determine the pore confinement descriptor of a β-scission, an optimized geometry of the respective reactant and transition state is required. These cannot rely on expensive DFT-calculations as this limits the predictive character of the model. Therefore, force-field based geometries have been determined for the reactant and transition state as specified in the methods section 2.3.2. Consequently, a pore confinement descriptor could be determined and incorporated in the modified group additive model. The incorporation of Δ(∑d−1)MM improves the predictions for the MFI and MOR framework while it does not alter the accuracy for FAU and TON. The incorporation of the force-field pore confinement descriptor allows to describe the effect of the complex shaped zeolites (MFI and MOR) on the activation enthalpy. For the simpler FAU and TON frameworks, the pore confinement is properly incorporated by the modified group additive models. Fig. 11 illustrates the parity plots of the predicted and calculated activation enthalpy by the modified group additive model with pore confinement descriptor within the four zeolites. The group additive values of the four models can be found in Table 2. As R1 and R4 were linearly dependent in the employed dataset, the same model parameters were obtained for both. Every time a methyl substituent was present in the R1 position, a methyl substituent was also present in the R4 position. This because we are investigating (branched) hydrocarbons relevant to the cracking of plastic waste and polypropylene cracking products display this trend in R1 and R4. When regressing the parameters only R1 is considered and its value is halved to obtain the value for R1 and R4. The activation enthalpy can then be calculated via the common group additive approach as illustrated in eqn (4), with Ri, DB and Δ(∑d−1)MM being the values of the molecular representation as shown in the methodology.
| Δ‡H = a + R1CR1 + R2CR2 + R3CR3 + R4CR4 + DB CDB + Δ(∑d−1)MMCΔ∑(d−1)TS | (4) |
| Δ‡H (kJ mol−1) | a | C R1 | C R2 | C R3 | C R4 | C DB | C Δ∑(d−1)TS |
|---|---|---|---|---|---|---|---|
| FAU | 60.2 ± 7.0 | 4.5 ± 5.6 | −14.9 ± 6.7 | 2.4 ± 1.2 | 4.5 ± 5.6 | −0.9 ± 5.2 | 0 |
| MFI | 120.2 ± 11.0 | −2.8 ± 6.3 | −2.0 ± 11.5 | −2.0 ± 2.0 | −2.8 ± 6.3 | 1.8 ± 8.4 | 14.2 ± 12.5 |
| MOR | 56.3 ± 18.5 | 42.7 ± 12.5 | −46.7 ± 16.4 | 14.5 ± 11.9 | 42.7 ± 12.5 | −3.1 ± 12.8 | −56.1 ± 51 |
| TON | 77.2 ± 17.4 | 41.4 ± 7.0 | −17.5 ± 16.9 | 4.1 ± 3.0 | 41.4 ± 7.0 | 2.6 ± 13.0 | 0 |
To validate the obtained group additive values, leave-one-out cross-validation was performed. Every reaction was sequentially removed from the training set after which the group additive values were regressed, and their activation enthalpy was predicted. The mean absolute error of all predictions was determined, which are supplied in Table 3. This shows the consistency of the determined group additive models.
| MAE (Δ‡H) [kJ mol−1] | mGAV + Δ(∑d−1)MM |
|---|---|
| MFI | 6.6 |
| FAU | 3.7 |
| MOR | 7.3 |
| TON | 8.5 |
The developed group additivity-based models allow to predict the relative change in β-scission activation enthalpy in four vastly different zeolites. This is an important step towards reaching rational zeolite design and implementing accurate β-scission kinetics in first-principle microkinetic models. Nevertheless, the deduced relations in this work do not necessarily require the development of complex microkinetic models to improve zeolite design. The qualitative trends extracted in this work can offer guidance for zeolite design in cracking reactions. For example, in the catalytic pyrolysis of plastic waste it is found that FAU-based catalysts achieve high conversions with a selectivity towards larger carbon chains because of the large pore size,106 similar to what is found in this work. Whereas zeolites with a MOR framework crack predominantly linear chains and are less active for the cracking of branched components,107 confirming the results of this work. The MFI-based catalyst is very selective towards valuable lighter products,108 as also shown by the lower β-scission activation enthalpy for small chains and it was found by the pore confinement descriptor that the transition state was destabilized by the small pore (see Fig. 3). Therefore, modified mesoporous ZSM-5 are one of the best working catalysts for the conversion of plastic waste as they are both active and selective towards valuable light olefins.26 These results are of course a combination of both diffusion, adsorption and kinetics which are all influenced by the zeolite type but display similar trends with the observations in this work. Also, the dependency on the alkylation reaction (the reverse β-scission) has to be considered for the design of zeolites. These alkylation reactions will be avoided as much as possible in catalytic pyrolysis of plastic waste by tuning the space time and temperature. While we focus here on β-scission, this work provides also a start to the prediction of the alkylation kinetics as the provided β-scission transition states in ESI† are the same for the alkylation. The discussed qualitative trends offer valuable guidance for the development of improved zeolites. For example, a MOR-based zeolite might be valuable for the ex situ catalytic pyrolysis of PE-based waste as it can excellently crack linear chains almost independent of carbon chain length (see Fig. 3) and produces little aromatics which should enhance its stability.109
Here a pore confinement descriptor was introduced which can assist in the further development of zeolites. In future work, the predictive capabilities of the easy-to-determine pore confinement descriptor should be investigated. Potential applications are the prediction of the effect of different aluminum positions in a similar zeolite cage and the β-scission performance of different or modified frameworks.
4. Conclusions
The effect of hydrocarbon reactant and zeolite framework has been investigated on the β-scission activation enthalpy. Specifically, the effect of alkyl chain length, unsaturated bonds, and branching has been explicitly described. It was found that both intrinsic chemical effects such as the inductive effect and resonance stabilization, and pore (de-)stabilization play an important role on the activation enthalpy. An increasing alkyl chain length generally led to an increase in activation enthalpy for linear hydrocarbons, while for branched hydrocarbons there was a clear dependency on zeolite framework. The presence of an unsaturated bond in the hydrocarbon increased the β-scission reaction barrier for small hydrocarbons (6 < #C ≤ 9) while for larger species in MFI and MOR it was found to be stabilizing for the transition state because of pore stabilization. These results comply with experimental trends and demonstrate why mesoporous ZSM-5 zeolites are both active and selective towards lights olefins in catalytic pyrolysis of plastic waste. The presence of an additional branch results generally in a decreasing activation enthalpy when this produces a linear carbenium ion. However, when a branched reactant produced a branched transition state the effect was heavily dependent on the zeolite structure. Not only the pore size, but the presence of intersections and side-pockets played an important role here.A strong correlation between the pore confinement descriptor and activation enthalpy was found which facilitated the construction of a predictive group additive-based model. This model links the intrinsic chemistry of the β-scission with the framework topology to provide a fast estimation of the relative changes in activation energy in the four studied frameworks. The incorporation of this model will enable more accurate kinetic models as currently the intrinsic activation energy is often assumed constant. In this way, these models are an important step towards model-guided zeolite design. In addition, important fundamental insights into the intricate chemistry of zeolite cracking were acquired which can qualitatively aid the design of superior zeolites. The inclusion of the so-called pore confinement descriptor can provide a guideline for the construction of new improved zeolite models. Future studies can in this way predict the activation enthalpy of several reactions in new zeolites with a minimum of quantum chemical calculations, hereby enabling an improved model-guided zeolite design for novel sustainable processes.
Data availability
The data supporting this article including quantum chemical properties, calculated pore confinement descriptors, obtained model parameters, and optimized structure geometries are included in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Yannick Ureel acknowledges financial support from the Fund for Scientific Research Flanders (FWO Flanders) through the doctoral fellowship grant 1185822N and a personal travel grant. The authors acknowledge funding from the European Research Council under the European Union's Horizon 2020 research and innovation program/ERC grant agreement no 818607. The computational resources (Stevin Supercomputer Infrastructure) and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by Ghent University, FWO and the Flemish Government – department EWI. The authors also acknowledge the Institute for Computational and Data Sciences (ICDS) at Penn State for providing high-performing computation resources through the Roar Supercomputer.References
- J. Weitkamp, Solid State Ionics, 2000, 131, 175–188 CrossRef CAS.
- A. Corma, Chem. Rev., 1997, 97, 2373–2420 CrossRef CAS PubMed.
- T. F. Degnan Jr, Top. Catal., 2000, 13, 349–356 CrossRef.
- M. Stöcker, Microporous Mesoporous Mater., 2005, 82, 257–292 CrossRef.
- J.-P. Lange, Energy Environ. Sci., 2021, 14, 4358–4376 RSC.
- J.-P. Lange, Green Chem., 2002, 4, 546–550 RSC.
- M. S. Abbas-Abadi, Y. Ureel, A. Eschenbacher, F. H. Vermeire, R. J. Varghese, J. Oenema, G. D. Stefanidis and K. M. Van Geem, Prog. Energy Combust. Sci., 2023, 96, 101046 CrossRef.
- R. H. Venderbosch, ChemSusChem, 2015, 8, 1306–1316 CrossRef CAS PubMed.
- Y. Peng, Y. Wang, L. Ke, L. Dai, Q. Wu, K. Cobb, Y. Zeng, R. Zou, Y. Liu and R. Ruan, Energy Convers. Manage., 2022, 254, 115243 CrossRef CAS.
- M. M. Rahman, R. Liu and J. Cai, Fuel Process. Technol., 2018, 180, 32–46 CrossRef CAS.
- H. Yuan, C. Li, R. Shan, J. Zhang, Y. Wu and Y. Chen, Fuel Process. Technol., 2022, 238, 107531 CrossRef CAS.
- S. Tsubota, S. Kokuryo, K. Tamura, K. Miyake, Y. Uchida, A. Mizusawa, T. Kubo and N. Nishiyama, Catal. Sci. Technol., 2024, 14, 1369–1374 RSC.
- X. Xian, C. Ran, P. Yang, Y. Chu, S. Zhao and L. Dong, Catal. Sci. Technol., 2018, 8, 4241–4256 RSC.
- S. Kokuryo, K. Tamura, K. Miyake, Y. Uchida, A. Mizusawa, T. Kubo and N. Nishiyama, Catal. Sci. Technol., 2022, 12, 4138–4144 RSC.
- I. Vollmer, M. J. F. Jenks, S. Rejman, F. Meirer, A. Gurinov, M. Baldus and B. M. Weckhuysen, Catal. Sci. Technol., 2024, 14, 894–902 RSC.
- M. Yang, D. Fan, Y. Wei, P. Tian and Z. Liu, Adv. Mater., 2019, 31, 1902181 CrossRef CAS.
- P. Tian, Y. Wei, M. Ye and Z. Liu, ACS Catal., 2015, 5, 1922–1938 CrossRef CAS.
- G. F. Froment, W. J. H. Dehertog and A. J. Marchi, in Catalysis, ed. J. J. Spivey, The Royal Society of Chemistry, 1992, vol. 9, pp. 1–64 Search PubMed.
- T. Degnan, G. Chitnis and P. H. Schipper, Microporous Mesoporous Mater., 2000, 35, 245–252 CrossRef.
- S. M. Sadrameli, Fuel, 2015, 140, 102–115 CrossRef CAS.
- R. Miandad, M. A. Barakat, M. Rehan, A. S. Aburiazaiza, I. M. I. Ismail and A. S. Nizami, Waste Manage., 2017, 69, 66–78 CrossRef CAS.
- M. Artetxe, G. Lopez, M. Amutio, G. Elordi, J. Bilbao and M. Olazar, Chem. Eng. J., 2012, 207–208, 27–34 CrossRef CAS.
- S. Liu, Y. Tian, X. He, Y. Liu, C. Qiao and G. Liu, Catal. Sci. Technol., 2023, 13, 1119–1127 RSC.
- Y. Liu, B. Qin, H. Gao, W. Ning, L. Zhang, J. Zheng, Y. Du, Y. Wang, W. Li and R. Li, Catal. Sci. Technol., 2020, 10, 2303–2312 RSC.
- A. Eschenbacher, R. J. Varghese, M. S. Abbas-Abadi and K. M. Van Geem, Chem. Eng. J., 2022, 428, 132087 CrossRef CAS.
- A. Eschenbacher, R. J. Varghese, E. Delikonstantis, O. Mynko, F. Goodarzi, K. Enemark-Rasmussen, J. Oenema, M. S. Abbas-Abadi, G. D. Stefanidis and K. M. Van Geem, Appl. Catal., B, 2022, 121251 CrossRef CAS.
- A. Corma and A. V. Orchillés, Microporous Mesoporous Mater., 2000, 35, 21–30 CrossRef.
- J. S. Buchanan, J. G. Santiesteban and W. O. Haag, J. Catal., 1996, 158, 279–287 CrossRef CAS.
- W. O. Haag, R. M. Dessau and R. M. Lago, in Studies in Surface Science and Catalysis, Elsevier, 1991, vol. 60, pp. 255–265 Search PubMed.
- G. Li and E. A. Pidko, ChemCatChem, 2019, 11, 134–156 CrossRef CAS.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111 RSC.
- J. Weitkamp, ChemCatChem, 2012, 4, 292–306 CrossRef CAS.
- J. Van der Mynsbrugge, A. Janda, S. Mallikarjun Sharada, L.-C. Lin, V. Van Speybroeck, M. Head-Gordon and A. T. Bell, ACS Catal., 2017, 7, 2685–2697 CrossRef CAS.
- M. John, K. Alexopoulos, M.-F. Reyniers and G. B. Marin, ACS Catal., 2016, 6(7), 4081–4094 CrossRef CAS.
- B. Smit and T. L. M. Maesen, Nature, 2008, 451, 671–678 CrossRef CAS PubMed.
- S. M. Babitz, B. A. Williams, J. T. Miller, R. Q. Snurr, W. O. Haag and H. H. Kung, Appl. Catal., A, 1999, 179, 71–86 CrossRef CAS.
- L. Lin, C. Qiu, Z. Zhuo, D. Zhang, S. Zhao, H. Wu, Y. Liu and M. He, J. Catal., 2014, 309, 136–145 CrossRef CAS.
- L. F. Lin, S. F. Zhao, D. W. Zhang, H. Fan, Y. M. Liu and M. Y. He, ACS Catal., 2015, 5, 4048–4059 CrossRef CAS.
- A. J. Jones and E. Iglesia, ACS Catal., 2015, 5, 5741–5755 CrossRef CAS.
- A. Ghorbanpour, J. D. Rimer and L. C. Grabow, Catal. Commun., 2014, 52, 98–102 CrossRef CAS.
- A. T. Smith, P. N. Plessow and F. Studt, J. Phys. Chem. C, 2021, 125, 16508–16515 CrossRef CAS.
- J. W. Thybaut, G. B. Marin, G. V. Baron, P. A. Jacobs and J. A. Martens, J. Catal., 2001, 202, 324–339 CrossRef CAS.
- C. S. Laxmi Narasimhan, J. W. Thybaut, G. B. Marin, P. A. Jacobs, J. A. Martens, J. F. Denayer and G. V. Baron, J. Catal., 2003, 220, 399–413 CrossRef CAS.
- A. Corma, J. Planelles, J. Sanchez-Marin and F. Tomas, J. Catal., 1985, 93, 30–37 CrossRef CAS.
- K. Tarach, K. Góra-Marek, J. Tekla, K. Brylewska, J. Datka, K. Mlekodaj, W. Makowski, M. I. López, J. M. Triguero and F. Rey, J. Catal., 2014, 312, 46–57 CrossRef CAS.
- C.-M. Wang, R. Y. Brogaard, B. M. Weckhuysen, J. K. Nørskov and F. Studt, J. Phys. Chem. Lett., 2014, 5, 1516–1521 CrossRef CAS PubMed.
- Y. Chu, B. Han, A. Zheng and F. Deng, J. Phys. Chem. C, 2012, 116, 12687–12695 CrossRef CAS.
- S. Sklenak, J. Dědeček, C. Li, B. Wichterlova, V. Gabova, M. Sierka and J. Sauer, Phys. Chem. Chem. Phys., 2009, 11, 1237–1247 RSC.
- J. A. Van Bokhoven, T.-L. Lee, M. Drakopoulos, C. Lamberti, S. Thieß and J. Zegenhagen, Nat. Mater., 2008, 7, 551–555 CrossRef CAS PubMed.
- M. L. Sarazen, E. Doskocil and E. Iglesia, J. Catal., 2016, 344, 553–569 CrossRef CAS.
- J. Z. Tan, C. W. Hullfish, Y. Zheng, B. E. Koel and M. L. Sarazen, Appl. Catal., B, 2023, 338, 123028 CrossRef CAS.
- P. Cnudde, K. De Wispelaere, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, J. Catal., 2017, 345, 53–69 CrossRef CAS.
- J. Weitkamp, P. A. Jacobs and J. A. Martens, Appl. Catal., 1983, 8, 123–141 CrossRef CAS.
- M. N. Mazar, S. Al-Hashimi, M. Cococcioni and A. Bhan, J. Phys. Chem. C, 2013, 117, 23609–23620 CrossRef CAS.
- P. Cnudde, K. De Wispelaere, L. Vanduyfhuys, R. Demuynck, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, ACS Catal., 2018, 8, 9579–9595 CrossRef CAS PubMed.
- R. L. Schowen, Prog. Phys. Org. Chem., 1972, 275–332 CrossRef CAS.
- A. Janda, B. Vlaisavljevich, L.-C. Lin, S. Mallikarjun Sharada, B. Smit, M. Head-Gordon and A. T. Bell, J. Phys. Chem. C, 2015, 119, 10427–10438 CrossRef CAS.
- B. A. De Moor, M.-F. o. Reyniers, O. C. Gobin, J. A. Lercher and G. B. Marin, J. Phys. Chem. C, 2011, 115, 1204–1219 CrossRef CAS.
- F. Eder, M. Stockenhuber and J. A. Lercher, J. Phys. Chem. B, 1997, 101, 5414–5419 CrossRef CAS.
- V. Blay, P. J. Miguel and A. Corma, Catal. Sci. Technol., 2017, 7, 5847–5859 RSC.
- K. Alexopoulos, M.-S. Lee, Y. Liu, Y. Zhi, Y. Liu, M.-F. Reyniers, G. B. Marin, V.-A. Glezakou, R. Rousseau and J. A. Lercher, J. Phys. Chem. C, 2016, 120, 7172–7182 CrossRef CAS.
- G. Piccini, M. Alessio and J. Sauer, Angew. Chem., Int. Ed., 2016, 55, 5235–5237 CrossRef CAS PubMed.
- C. Baerlocher, D. Brouwer, B. Marler and L. B. McCusker, Database of Zeolite Structures, 2017, https://www.iza-structure.org/databases/ Search PubMed.
- C. Baerlocher, L. B. McCusker and D. H. Olson, Atlas of zeolite framework types, Elsevier, 2007 Search PubMed.
- M. Sierka and J. Sauer, Faraday Discuss., 1997, 106, 41–62 RSC.
- C. M. Nguyen, B. A. De Moor, M.-F. Reyniers and G. B. Marin, J. Phys. Chem. C, 2012, 116, 18236–18249 CrossRef CAS.
- C. M. Nguyen, M.-F. Reyniers and G. B. Marin, J. Catal., 2015, 322, 91–103 CrossRef CAS.
- M. Brändle and J. Sauer, J. Am. Chem. Soc., 1998, 120, 1556–1570 CrossRef.
- M. John, K. Alexopoulos, M.-F. Reyniers and G. B. Marin, J. Catal., 2015, 330, 28–45 CrossRef CAS.
- S. R. Lonsinger, A. K. Chakraborty, D. N. Theodorou and A. T. Bell, Catal. Lett., 1991, 11, 209–217 CrossRef CAS.
- B. F. Mentzen and M. Sacerdote-Peronnet, Mater. Res. Bull., 1994, 29, 1341–1348 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 48, 13115 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B, 1992, 46, 6671 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- A. De Vita and M. J. Gillan, J. Phys.: Condens. Matter, 1991, 3, 6225 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123(22), 224101 CrossRef PubMed.
- J. Kästner and P. Sherwood, J. Chem. Phys., 2008, 128(1), 014106 CrossRef PubMed.
- B. A. De Moor, M.-F. Reyniers and G. B. Marin, Phys. Chem. Chem. Phys., 2009, 11, 2939–2958 RSC.
- J. Lym, G. R. Wittreich and D. G. Vlachos, Comput. Phys. Commun., 2020, 247, 106864 CrossRef CAS.
- M. L. Sarazen, E. Doskocil and E. Iglesia, ACS Catal., 2016, 6, 7059–7070 CrossRef CAS.
- G. Noh, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2018, 122, 25475–25497 CrossRef CAS.
- G. Noh, Z. Shi, S. I. Zones and E. Iglesia, J. Catal., 2018, 368, 389–410 CrossRef CAS.
- P. N. Plessow and F. Studt, J. Phys. Chem. Lett., 2020, 11, 4305–4310 CrossRef CAS PubMed.
- T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376 CrossRef CAS.
- J. Macht, R. T. Carr and E. Iglesia, J. Am. Chem. Soc., 2009, 131, 6554–6565 CrossRef CAS PubMed.
- J. Macht, M. J. Janik, M. Neurock and E. Iglesia, J. Am. Chem. Soc., 2008, 130, 10369–10379 CrossRef CAS PubMed.
- P. Deshlahra and E. Iglesia, ACS Catal., 2016, 6, 5386–5392 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. von Aretin and O. Hinrichsen, Ind. Eng. Chem. Res., 2014, 53, 19460–19470 CrossRef CAS.
- T. von Aretin, S. Schallmoser, S. Standl, M. Tonigold, J. A. Lercher and O. Hinrichsen, Ind. Eng. Chem. Res., 2015, 54, 11792–11803 CrossRef CAS.
- S. Vernuccio, E. E. Bickel, R. Gounder and L. J. Broadbelt, ACS Catal., 2019, 9, 8996–9008 CrossRef CAS.
- S. Vernuccio, E. E. Bickel, R. Gounder and L. J. Broadbelt, J. Catal., 2021, 395, 302–314 CrossRef CAS.
- Y. Ureel, F. H. Vermeire, M. K. Sabbe and K. M. Van Geem, Chem. Eng. J., 2023, 472, 144874 CrossRef CAS.
- Y. Ureel, F. H. Vermeire, M. K. Sabbe and K. M. Van Geem, Ind. Eng. Chem. Res., 2022, 62(1), 223–237 CrossRef.
- B. G. Anderson, R. R. Schumacher, R. Van Duren, A. P. Singh and R. A. Van Santen, J. Mol. Catal. A: Chem., 2002, 181, 291–301 CrossRef CAS.
- M. Saunders, P. Vogel, E. L. Hagen and J. Rosenfeld, Acc. Chem. Res., 1973, 6, 53–59 CrossRef CAS.
- Z. M. George and H. W. Habgood, J. Phys. Chem., 1970, 74, 1502–1508 CrossRef CAS.
- M. Kusenberg, A. Zayoud, M. Roosen, H. D. Thi, M. S. Abbas-Abadi, A. Eschenbacher, U. Kresovic, S. De Meester and K. M. Van Geem, Fuel Process. Technol., 2022, 227, 107090 CrossRef CAS.
- C. K. Ingold, Chem. Rev., 1934, 15, 225–274 CrossRef CAS.
- B. P. S. Santos, D. Almeida, M. d. F. V. Marques and C. A. Henriques, Fuel, 2018, 215, 515–521 CrossRef CAS.
- J. Gancedo, H. Li, J. S. Walz, L. Faba, S. Ordoñez and G. W. Huber, Appl. Catal., A, 2024, 669, 119484 CrossRef CAS.
- B. Whajah, J. N. Heil, C. L. Roman, J. A. Dorman and K. M. Dooley, Ind. Eng. Chem. Res., 2023, 62, 8635–8643 CrossRef CAS PubMed.
- J. Aguado, D. P. Serrano, J. M. Escola and A. Peral, J. Anal. Appl. Pyrolysis, 2009, 85, 352–358 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: S1. Calculated activation enthalpy (Δ‡H) and activation entropy (Δ‡S) S2. zeolite frameworks S3. FAU correlation linear hydrocarbons S4. 95%-confidence interval slope and intercept of correlation with pore confinement descriptor S5. activation enthalpy unsaturated hydrocarbons S6. TON position unsaturated S7. MFI position 2,3,4-trimethylpent-2-ylium S8. correlation pore confinement descriptor unsaturated hydrocarbons S9. correlation pore confinement descriptor branched hydrocarbons S10. correlation pore confinement descriptor all hydrocarbons S11. group additive values S12. optimized reactant and transition state geometries. See DOI: https://doi.org/10.1039/d4cy00973h |
| This journal is © The Royal Society of Chemistry 2024 |