Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of noise on inverse design: the case of NMR spectra matching†
Dominik
Lemm
 ab,
Guido Falk
von Rudorff
ab,
Guido Falk
von Rudorff
 cd and
O.
Anatole von Lilienfeld
cd and
O.
Anatole von Lilienfeld
 efg
efg
aUniversity of Vienna, Faculty of Physics, Kolingasse 14-16, AT-1090 Vienna, Austria
bUniversity of Vienna, Vienna Doctoral School in Physics, Boltzmanngasse 5, AT-1090 Vienna, Austria
cUniversity Kassel, Department of Chemistry, Heinrich-Plett-Str.40, 34132 Kassel, Germany
dCenter for Interdisciplinary Nanostructure Science and Technology (CINSaT), Heinrich-Plett-Straße 40, 34132 Kassel, Germany
eDepartments of Chemistry, Materials Science and Engineering, and Physics, University of Toronto, St. George Campus, Toronto, ON, Canada. E-mail: anatole.vonlilienfeld@utoronto.ca
fVector Institute for Artificial Intelligence, Toronto, ON M5S 1M1, Canada
gMachine Learning Group, Technische Universität Berlin and Institute for the Foundations of Learning and Data, 10587 Berlin, Germany
First published on 17th October 2023
Abstract
Despite its fundamental importance and widespread use for assessing reaction success in organic chemistry, deducing chemical structures from nuclear magnetic resonance (NMR) measurements has remained largely manual and time consuming. To keep up with the accelerated pace of automated synthesis in self driving laboratory settings, robust computational algorithms are needed to rapidly perform structure elucidations. We analyse the effectiveness of solving the NMR spectra matching task encountered in this inverse structure elucidation problem by systematically constraining the chemical search space, and correspondingly reducing the ambiguity of the matching task. Numerical evidence collected for the twenty most common stoichiometries in the QM9-NMR database indicate systematic trends of more permissible machine learning prediction errors in constrained search spaces. Results suggest that compounds with multiple heteroatoms are harder to characterize than others. Extending QM9 by ∼10 times more constitutional isomers with 3D structures generated by Surge, ETKDG and CREST, we used ML models of chemical shifts trained on the QM9-NMR data to test the spectra matching algorithms. Combining both 13C and 1H shifts in the matching process suggests twice as permissible machine learning prediction errors than for matching based on 13C shifts alone. Performance curves demonstrate that reducing ambiguity and search space can decrease machine learning training data needs by orders of magnitude.
1. Introduction
Current development times of novel molecular materials can span several decades from discovery to commercialization. In order for humanity to react to global challenges, the digitization4–8 of molecular and materials discovery aims to accelerate the process to a few years. Long experiment times severely limit the coverage of the vastness of chemical space, making the development of self driving laboratories for autonomous robotics experimentation crucial for high throughput synthesis of novel compounds (Fig. 1a)).9–15 To keep the pace of automated synthesis, fast and reliable characterization of reaction products through spectroscopic methods is required, an often manual, time intense and possibly error prone task. One of the most common methods to elucidate the structure of reaction products are nuclear magnetic resonance (NMR) experiments.16 Through relaxation of nuclear spins after alignment in a magnetic field, an NMR spectrum, characteristic of local atomic environments of a compound, i.e. functional groups, can be recorded. In particular, 1H and 13C NMR experiments are routinely used by experimental chemists to identify the chemical structure or relevant groups just from the spectrum. For larger compounds, however, the inverse problem of mapping spectrum to structure becomes increasingly difficult, ultimately requiring NMR of additional nuclei, stronger magnets, or more advanced two-dimensional NMR experiments.17,18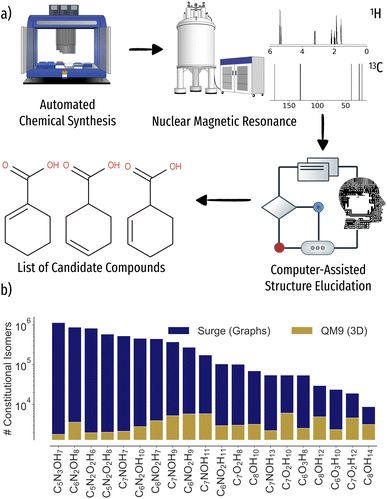 | ||
| Fig. 1 Schematic workflow for autonomous chemical discovery as well as scaling of constitutional isomer space versus data availability in the QM9 (ref. 1) database. (a) After the chemical synthesis of molecular compounds, reaction products are characterized using spectroscopic methods such as nuclear magnetic resonance (NMR). The measured 1H and 13C spectra are automatically processed and potential candidate structures suggested via machine learning. (b) Number of constitutional isomers for 20 stoichiometries considered. | ||
Computer-assisted structure elucidation algorithms aim to iteratively automatize the structure identification process.19–23 Current workflows include repeated predictions of chemical shifts for candidate structure inputs through empirical or ab initio methods.24–26 Albeit accurate even in condensed phase through use of plane-waves27 or QM/MM setup,28 the cost of density functional theory (DFT) calculations severely limits the number of candidate structures that can be tested, leaving the identification of unknown reaction products out of reach for all but the smallest search spaces. Data driven machine learning models leveraging experimental or theoretical NMR databases29–32 provide orders of magnitude of speedup over ab initio calculations, reaching 1–2 ppm 13C mean-absolute-error (MAE) w.r.t. experiment or theory, respectively.31,33–38 However, while the stoichiometry of the reaction product is usually known, e.g. through prior mass spectrometry experiments, the number of possible constitutional isomers exhibits NP hard scaling in number of atoms, quickly spanning millions of valid molecular graphs already for molecules of modest size (Fig. 1b)). As such, the inverse problem of inferring the molecular structure from an NMR spectrum still poses a major challenge even for rapid solvers.
Recent machine learning approaches tackle the inverse problem using a combination of graph generation and subsequent chemical shift predictions for candidate ranking.39–41 First explored by Jonas,39 a Top-1 ranking with 57% reconstruction success-rate was achieved using deep imitation learning to predict bonds of molecular graphs. Sridharan et al.41 used online Monte Carlo tree search to build molecular graphs resulting in a similar Top-1 ranking of 57.2%. Huang et al.40 relied on substructure predictions from which complete graphs can be constructed, reaching 67.4% top-1 accuracy by ranking substructure profiles instead of shifts. A commonality between all algorithms is the subsequent ranking of candidates using spectra matching or other heuristics. Consequently, even though the correct query compound could be detected early, similar candidates might be ranked higher, making the ranking process as critical as the candidate search itself.
In this work, we analyse the effectiveness of the NMR spectra matching task encountered in the inverse structure elucidation problem. As stagnating improvements26 in chemical shift predictions due to limited public NMR data aggravate candidate rankings, results suggest that both the prediction error of machine learning models and the number of possible candidates are crucial factors for elucidation success. By systematically controlling the size of chemical search space and accuracy of chemical shifts, we find that higher error levels become permissible in constrained search spaces. Moreover, results indicate that increasing the uniqueness through including both 13C and 1H shifts in the matching process, rather than relying on a single type of shift, significantly reduces ambiguity and enhances error tolerance. To evaluate the spectra matching task throughout chemical compound space, we systematically control the accuracy of 1D 13C and 1H chemical shifts of the 20 most common stoichiometries in QM9-NMR1,31 by applying distinct levels of Gaussian white noise. Note that while we focus on DFT based 1D NMR in this work, future studies could include experimental data and 2D NMR information. Comparisons amongst stoichiometries suggest that chemical spaces with increasing amounts of heteroatoms and number of constitutional isomers are harder to characterize than others. To test the spectra matching method on a large search space, we extended QM9-NMR to 56 k C7O2H10 constitutional isomers. Controlling the chemical shift accuracy through machine learning models trained at increasing training set sizes, performance curves again indicate a trade-off between search space and accuracy. Hence, as less accurate shift predictions become useful, results show that machine learning training data needs can be reduced by multiple orders of magnitude.
2. Theory & methods
2.1. NMR spectra matching
Consider a query 13C or 1H spectrum with a set of N possible candidate constitutional isomer spectra. We chose the squared euclidean distance as a metric to rank candidate spectra against the query spectrum (see ESI Fig. 3† for comparison against other metrics):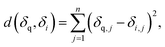 | (1) |
With δ being a sorted spectrum of n chemical shifts (13C or 1H), q being the query, i being the i-th of N candidates, and j being the j-th chemical shift in a spectrum, respectively. To use both 13C and 1H shifts simultaneously for spectra matching, a total distance can be calculated as follows:
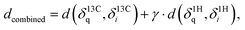 | (2) |
with γ = 64 being a scaling factor determined via cross-validation (see ESI Fig. 1†) to ensure similar weighting. Final rankings are obtained by sorting all candidates by distance. The top-1 accuracy is calculated as the proportion of queries correctly ranked as the closest spectrum, respectively.
2.2. Elucidation performance curves
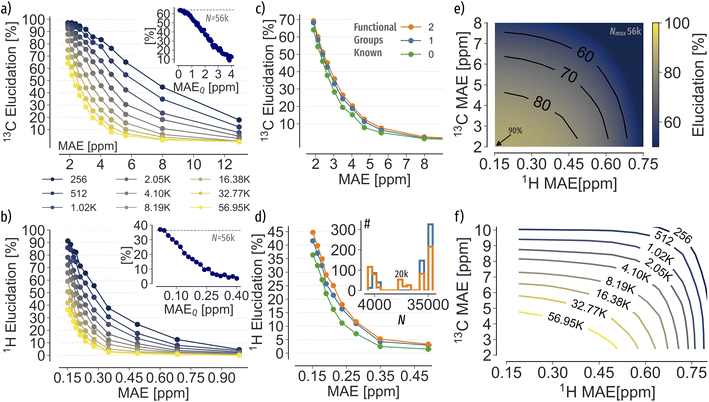
To analyse the spectra matching elucidation accuracy, we systematically control the number of possible candidates N and the accuracy of chemical shifts, respectively. For each constitutional isomer set, we choose 10% as queries and 90% as search pool, respectively. Next, we randomly sample N spectra from the search pool, including the query spectrum. Each sample size is drawn ten times and the top-1 accuracy averaged across all runs. To control the accuracy of chemical shifts, we apply Gaussian white noise (up to 1 or 10 σ for 1H and 13C, respectively) or use the machine learning error as a function of training set size (c.f. ESI Fig. 5† for learning curves). For each N and chemical shift accuracy, results are presented as elucidation performance curves, showing the elucidation success as a function of chemical shift accuracy in terms of mean absolute deviation (MAD) for Gaussian noise (c.f.Fig. 2a and b)) or mean absolute error (MAE) for machine learning predictions (c.f.Fig. 4).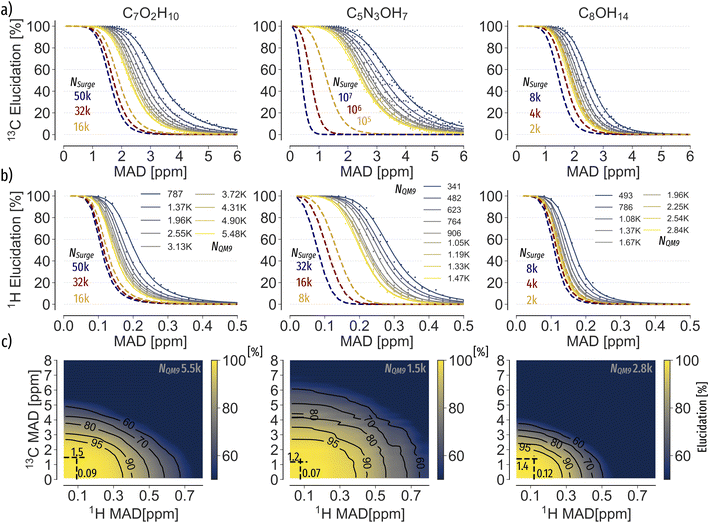 | ||
Fig. 2 Elucidation performance curves of C7O2H10, C5N3OH7, C8OH14 spectra using Gaussian noise to control chemical shift accuracy in terms of mean absolute deviation (MAD) corresponding to 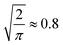 of the standard deviation.2 (a) and (b) 13C and 1H spectra matching. Individual points were obtained by calculating the percentage of queries where noisy and noise free query spectra have the lowest distance. All points have been fitted using eqn (3). Solid curves correspond to candidate numbers NQM9 from QM9.1 Dashed curves are an extrapolation to candidate numbers NSurge as obtained via graph enumeration.3 The legend corresponds to both (a) and (b), respectively. (c) Spectra matching using both 1H and 13C shifts. Dashed lines correspond to the accuracy required to correctly elucidate 95% of queries when only 1H or 13C spectra are being used, respectively. of the standard deviation.2 (a) and (b) 13C and 1H spectra matching. Individual points were obtained by calculating the percentage of queries where noisy and noise free query spectra have the lowest distance. All points have been fitted using eqn (3). Solid curves correspond to candidate numbers NQM9 from QM9.1 Dashed curves are an extrapolation to candidate numbers NSurge as obtained via graph enumeration.3 The legend corresponds to both (a) and (b), respectively. (c) Spectra matching using both 1H and 13C shifts. Dashed lines correspond to the accuracy required to correctly elucidate 95% of queries when only 1H or 13C spectra are being used, respectively. | ||
2.3. Chemical shift prediction
We relied on kernel ridge regression (KRR) for machine learning 13C and 1H chemical shifts as presented in ref. 31 and commonly being used in learning NMR properties from quantum chemical calculations.37,42–46 We use a Laplacian kernel and the local atomic Faber–Christensen–Huang–Lilienfeld (FCHL19 (ref. 47)) representation with a radial cutoff31 of 4 Å. The kernel width and regularization coefficient have been determined through 10-fold cross-validation on a subset of 10′000 chemical shifts of the training set. Note that while we relied on KRR within this work, other NMR shift estimation methods could have been used such as Hierarchically ordered spherical environment (HOSE) codes48,49 or neural network based approaches.50–532.4. Data
The QM9-NMR1,31 dataset was used in this work, containing 130′831 small molecules up to nine heavy atoms (CONF) with chemical shieldings at the mPW1PW91/6-311+G(2d,p)-level of theory. We used the 20 most common stoichiometries (Fig. 1b)), having a minimum of 1.7 k constitutional isomers available in the dataset.To extend the QM9-NMR C7O2H10 constitutional isomers space, we used the systematic graph enumeration software Surge3 to generate 54′641 SMILES. 3D geometries of all SMILES have been generated using the ETKDG54 method in RDKit. Lowest lying conformer structures were sampled using the CREST55 algorithm, using the GFN2-xTB/GFN-FF composite method in a meta-dynamics based sampling scheme, with a final relaxation at the GFN2-xTB level. Adding all successfully generated structures to QM9, a total pool size of 56.95 k C7O2H10 isomers was obtained.
For the training of chemical shift machine learning models, we selected C8OH12, C8OH10, C8OH14, C7O2H8 and C7O2H12 constitutional isomers, yielding a total of 143 k 13C and 214 k 1H training points, respectively.
3. Results & discussion
3.1. Spectra matching accuracy with synthetic noise
To analyse the influence of noise and number of candidates on the elucidation success, we applied Gaussian noise to 13C and 1H shifts of C7O2H10, C5N3OH7 and C8OH14 constitutional isomers, respectively. Fig. 2a and b) depicts a sigmoidal shaped trend of top-1 elucidation performances as a function of mean absolute deviation (MAD) corresponding to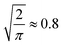 of the standard deviation2 caused by applying the Gaussian noise. Note that increasing the maximum candidate pool size NQM9 leads to an offset of the trend towards less permissible errors. A possible explanation is the correlation of the density of chemical space with increasing numbers of candidate spectra N.56 As shift predictions need to become more accurate, limiting N through prior knowledge of the chemical space could be beneficial. Similar findings have been reported by Sridharan et al.,41 noting that brute force enumerations of chemical space lead to worse rankings than constrained graph generation. Note that while the trends in 13C and 1H elucidation are similar, less error is permissible when using 1H shifts.
of the standard deviation2 caused by applying the Gaussian noise. Note that increasing the maximum candidate pool size NQM9 leads to an offset of the trend towards less permissible errors. A possible explanation is the correlation of the density of chemical space with increasing numbers of candidate spectra N.56 As shift predictions need to become more accurate, limiting N through prior knowledge of the chemical space could be beneficial. Similar findings have been reported by Sridharan et al.,41 noting that brute force enumerations of chemical space lead to worse rankings than constrained graph generation. Note that while the trends in 13C and 1H elucidation are similar, less error is permissible when using 1H shifts.
To further reduce the ambiguity, we include both 13C and 1H shifts into the matching problem as per eqn (2). Results suggest 50% and ∼150% more permissible 13C and 1H errors when both spectra are considered in the matching process (Fig. 2c)). Similar to how chemists solve the elucidation problem, the inclusion of more distinct properties increases the uniqueness and can improve the elucidation success.
3.2. Extrapolating the search space
Due to the limited amount of constitutional isomers in databases compared to the number of possible graphs faced during inverse design (Fig. 1b)), assessing the chemical shift accuracy for successful elucidation is severely limited. As such, we extrapolate elucidation performance curves to obtain estimates about chemical shift accuracies in candidate pool sizes larger than QM9. We fit each elucidation performance curve (Fig. 2a and b)), respectively, using a smoothly broken power law function: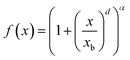 | (3) |
With xb controlling the upper bend and offset, d changing the curvature and α changing the tilt of the function (see ESI Fig. 2†), respectively. The parameters of eqn (3) as a function of N can again be fitted using a power law function (see ESI Fig. 2†) and extrapolated to the total number of graphs NSurge, respectively.
Results of the extrapolation (Fig. 2a and b) dashed) indicate significant differences in elucidation efficiency among stoichiometries. For instance, C8OH14 queries are potentially easier to elucidate than C5N3OH7 structures. Possible reasons are the limited number of C8OH14 graphs compared to millions of C5N3OH7 isomers. Moreover, the number of heteroatoms of the C5N3OH7 stoichiometry might hamper the characterization when only relying on 13C or 1H, respectively. Hence, to solve the inverse structure elucidation problem using experimental data of compounds larger than QM9, reducing ambiguities through including both 13C and 1H shifts as well as to reduce the candidate space is critical for elucidation success.
3.3. Trends in chemical space
To analyse the elucidation efficiency throughout chemical space, we applied the Gaussian noise and extrapolation procedure to the 20 most common stoichiometries in QM9 (Fig. 1b)). Fig. 3a) shows the MAD required for 95% elucidation success as a function of NSurge. Results suggest that less error is permissible for stoichiometries with large NSurge and fewer carbon atoms. As such, using only 13C shifts might not be sufficient to fully characterize the compound. Again, similar to how chemists use multiple NMR spectra to deduct chemical structures, additional information such as 1H shifts are beneficial to extend the information content.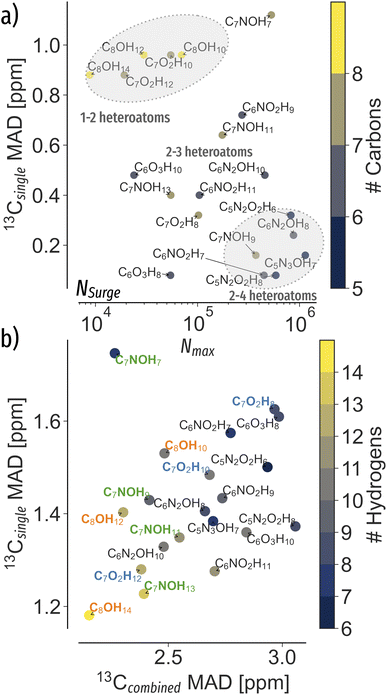 | ||
Fig. 3 Trends in QM9 (ref. 1) chemical compound space to correctly elucidate queries at 95% accuracy. The mean absolute deviation (MAD) 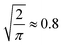 of the standard deviation.2 (a) Extrapolated MAD at candidate numbers NSurge of the 20 most common stoichiometries in QM9.1 (b) MAD using only 13C spectra (13Csingle) against 13C and noise-free 1H spectra combined (13Ccombined) at candidate numbers NQM9 from QM9.1 of the standard deviation.2 (a) Extrapolated MAD at candidate numbers NSurge of the 20 most common stoichiometries in QM9.1 (b) MAD using only 13C spectra (13Csingle) against 13C and noise-free 1H spectra combined (13Ccombined) at candidate numbers NQM9 from QM9.1 | ||
In Fig. 3b), the error permissiveness of spectra matching using only 13C (see ESI Fig. 4† for 1H) versus combining both 13C and 1H is being compared, revealing a linear trend between both. Note that the C7NOH7 stoichiometry shows the smallest benefit from adding additional 1H information. Interestingly, a hierarchy for C7NOHX stoichiometries of different degrees of unsaturation is visible, indicating an inverse correlation between number of hydrogens and 13Csingle MAD (Fig. 3b) green). Similar hierarchies are also observed for other stoichiometries such as C7O2HX and C8OHX (Fig. 3b) blue and orange). On average, the combination of 13C and 1H for spectra matching increases the error permissiveness of 13C and 1H by 85% and 261% (see ESI Fig. 4†), respectively.
3.4. Comparison to machine learned shift predictions
To test the elucidation performance using machine learning predictions, we trained 13C and 1H KRR models at increasing training set sizes (see ESI Fig. 5† for learning curves) and predicted chemical shifts of 56 k C7O2H10 constitutional isomers. Note that within this proof of concept application we rely on xTB-GFN2 relaxed geometries as queries, which on average are within 0.06 Å RMSD of C7O2H10 B3LYP level of theory structures.57 Results again show similar trends as observed with Gaussian noise (Fig. 4a and b)), however, indicate more permissive accuracy thresholds. For instance, KRR 13C predictions at 2 ppm MAE can identify 64% of queries rather than only 17% suggested by the Gaussian noise experiment. The difference could be explained due the systematic, non uniform nature of the QM9 (ref. 1) chemical space, influencing the shape and extrapolation of elucidation performance curves in Fig. 2. Moreover, Gaussian noise is applied to all shifts at random compared to possibly more systematic machine learning predictions. Note that the trade-off between error and N is consistent and that the exact parameters will depend on the machine learning model and the finite sampling of constitutional isomer space.To model possible experimental noise on query spectra, we apply Gaussian noise to query spectra and evaluate the elucidation performance of the best performing machine learning model (see insets in Fig. 4a and b)). Results indicate a halving of elucidation accuracy when the query spectrum contains up to 2 ppm MAEQ in 13C and 0.15 ppm MAE in 1H error, respectively. Thus, in the presence of experimental measurement noise even higher prediction accuracies might be necessary. Combining both 13C and 1H spectra for matching improves the elucidation performance up to 90% (Fig. 4e)). Again, the combination of spectra for elucidation highlights the effectiveness of reducing the ambiguity of the matching problem by including additional properties.
Investigating potential strategies to reduce the constitutional isomer search space, we constrained N based on functional groups (see ESI Table 1†). Randomly selecting functional groups present in each query, N can be reduced by 50% and 62% on average (see Fig. 4d) inset for distributions), respectively. Results in Fig. 4c and d) indicate an increase of the elucidation accuracy by 5% in 13C and up to 10% for 1H, respectively, in agreement with the elucidation performance in Fig. 4a and b). Note that the knowledge of two functional groups only led to marginal improvements. However, fragmentation could be more beneficial for larger compounds than present in QM9,1 as reported by Yao et al.58 Using both 13C and 1H shifts on the reduced search space only lead to marginal improvements of 0.5% over the results of the full search space.
3.5. Balancing search space and accuracy
We use performance curves to analyse the relationship between the elucidation performance of C7O2H10 queries, machine learning prediction errors and candidate pool sizes N. Similar to learning curves, showing the systematic decay of out-of-sample machine learning prediction errors as a function of training data, elucidation performance curves show for a specific elucidation threshold, e.g. 90%, the machine learning prediction error as a function of pool size. Note that while learning curves of chemical shift predictions only show the predictive accuracy, e.g. in terms of MAE, the addition of elucidation performance allow a multifaceted evaluation of new spectra estimation algorithms, considering data efficiency as well as pool size. The systematic decay of performance curves (Fig. 5 red and blue) again demonstrates that constraining N with prior knowledge allows for less accurate shift predictions to be applicable. Extrapolating the 13Csingle performance curves indicates a machine learning MAE of 0.93 ppm to correctly rank 90% of queries out of 56 k possible candidates (Fig. 5 red), 0.02 ppm lower than suggested by Gaussian noise. To reach an MAE of 0.93 ppm, four million training instances are required (Fig. 5 orange). Using both 13C and 1H shifts requires two orders of magnitude less training data (Fig. 5 blue). As such, facing expensive experimental measurements and ab initio calculations, more effective inverse structure elucidation could be achieved by balancing machine learning data needs through reduced search spaces and incorporation of additional properties.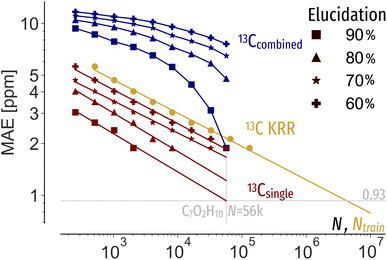 | ||
| Fig. 5 Performance curves (red, blue) of the MAE permissible to correctly identify 60, 70, 80, 90% of C7O2H10 query spectra at a given pool size N using machine learning shifts predictions, respectively. 13Csingle (red) only uses 13C shifts for elucidation, whereas 13Ccombined uses 13C and 1H spectra combined, assuming a 1H MAE of 0.15 ppm. The learning curve (orange) indicates the systematic improvement of QM9 (ref. 1) 13C chemical shift predictions as a function of training set size Ntrain using KRR with the FCHL19 (ref. 47) representation. | ||
4. Conclusion
We have presented an analysis of the effectiveness of the NMR spectra matching task encountered in the inverse structure elucidation problem. By systematically controlling the predictive accuracy of 13C and 1H chemical shifts, we found consistent trends throughout chemical compound space, suggesting that higher errors become permissible as the number of possible candidates decreases. Note that while we relied on 1D ab initio NMR data, similar analysis could be performed using 1D or 2D experimental spectra. Applications to the most common constitutional isomers in QM9 highlight that chemical spaces with many heteroatoms are harder to characterize when only relying on a single type of chemical shift. Using both 13C and 1H chemical shifts increases the error permissiveness by 85% and 261% on average, respectively. Machine learning predictions for 56 k C7O2H10 compounds showed that using both 13C or 1H shifts increased elucidation success to 90% compared to only 64% and 36% when used alone, respectively. The usefulness of the analysis is expressed via performance curves, showing that training demands can be reduced by orders of magnitude compared to relying on specific shifts alone.We believe that as the accuracy of machine learning models to distinguish spectra is limited, constrained search spaces or inclusion of more distinct properties are necessary to improve candidate rankings. Rather than solely relying on more accurate models, future approaches could deal with estimating the applicability of machine learning models to successfully elucidate unseen chemical spaces, as well as including explicit knowledge of chemical reactions, functional groups or data from mass spectrometry, infrared- or Raman spectroscopy,59–64 respectively.
Finally, explicitly accounting for atomic similarities and chemical shift uncertainties via the DP5 probability might further increase the confidence in structure assignments.23
Data availability
The QM9-NMR31 dataset is openly available at https://doi.org/10.17172/NOMAD/2021.10.16-1. The code and additional data used in this study are available at https://doi.org/10.5281/zenodo.8126379.Conflicts of interest
The authors have no conflict of interest.Acknowledgements
O.A.v.L. has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 772834). O.A.v.L. has received support as the Ed Clark Chair of Advanced Materials and as a Canada CIFAR AI Chair. This research is part of the University of Toronto's Acceleration Consortium, which receives funding from the Canada First Research Excellence Fund (CFREF). Icons in Fig. 1 are from DBCLS, Openclipart and Simon Dürr from http://bioicons.com under CC-BY 4.0 and CC0, respectively.References
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1(1), 1–7 CrossRef PubMed.
- R. C. Geary, The Ratio of the Mean Deviation to the Standard Deviation as a Test of Normality, Biometrika, 1935, 27(3/4), 310 CrossRef.
- B. D. McKay, M. A. Yirik and C. Steinbeck, Surge: a fast open-source chemical graph generator, J. Cheminf., 2022, 14(1), 24 Search PubMed.
- J. Bai, L. Cao, S. Mosbach, J. Akroyd, A. A. Lapkin and M. Kraft, From Platform to Knowledge Graph: Evolution of Laboratory Automation, JACS Au, 2022, 2(2), 292–309 CrossRef CAS PubMed.
- S. Herres-Pawlis, O. Koepler and C. Steinbeck, NFDI4Chem: Shaping a Digital and Cultural Change in Chemistry, Angew. Chem., Int. Ed., 2019, 58(32), 10766–10768 CrossRef CAS PubMed.
- P. S. Gromski, J. M. Granda and L. Cronin, Universal Chemical Synthesis and Discovery with ‘The Chemputer, Trends Chem., 2020, 2(1), 4–12 CrossRef CAS.
- I. W. Davies, The digitization of organic synthesis, Nature, 2019, 570(7760), 175–181 CrossRef CAS PubMed.
- B. Huang, G. F. von Rudorff and O. A. von Lilienfeld, The central role of density functional theory in the AI age, Science, 2023, 381(6654), 170–175 CrossRef CAS PubMed.
- R. J. Hickman, M. Aldeghi, F. Häse and A. Aspuru-Guzik, Bayesian optimization with known experimental and design constraints for chemistry applications, Digital Discovery, 2022, 1, 732–744 RSC.
- Y. Xie, K. Sattari, C. Zhang and J. Lin, Toward autonomous laboratories: Convergence of artificial intelligence and experimental automation, Prog. Mater. Sci., 2023, 132, 101043 CrossRef.
- Y. Jiang, D. Salley, A. Sharma, G. Keenan, M. Mullin and L. Cronin, An artificial intelligence enabled chemical synthesis robot for exploration and optimization of nanomaterials, Sci. Adv., 2022, 8(40), eabo2626 CrossRef CAS PubMed.
- R. D. King, K. E. Whelan, F. M. Jones, P. G. K. Reiser, C. H. Bryant and S. H. Muggleton, et al., Functional genomic hypothesis generation and experimentation by a robot scientist, Nature, 2004, 427(6971), 247–252 CrossRef CAS PubMed.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai and X. Wang, et al., A mobile robotic chemist, Nature, 2020, 583(7815), 237–241 CrossRef CAS PubMed.
- H. Fakhruldeen, G. Pizzuto, J. Glowacki and A. I. Cooper, ARChemist: Autonomous Robotic Chemistry System Architecture, arXiv, 2022, preprint, arXiv:2204.13571, DOI:10.48550/arXiv.2204.13571.
- N. H. Angello, V. Rathore, W. Beker, A. Wołos, E. R. Jira and R. Roszak, et al., Closed-loop optimization of general reaction conditions for heteroaryl Suzuki-Miyaura coupling, Science, 2022, 378(6618), 399–405 CrossRef CAS PubMed.
- M. Elyashberg, Identification and structure elucidation by NMR spectroscopy, TrAC, Trends Anal. Chem., 2015, 69, 88–97 CrossRef CAS.
- M. E. Elyashberg, K. A. Blinov, A. J. Williams, S. G. Molodtsov, G. E. Martin and E. R. Martirosian, Structure Elucidator: A Versatile Expert System for Molecular Structure Elucidation from 1D and 2D NMR Data and Molecular Fragments, J. Chem. Inf. Comput. Sci., 2004, 44(3), 771–792 CrossRef CAS PubMed.
- P. Giraudeau, Challenges and perspectives in quantitative NMR, Magn. Reson. Chem., 2017, 55(1), 61–69 CrossRef CAS PubMed.
- P. H. Willoughby, M. J. Jansma and T. R. Hoye, A guide to small-molecule structure assignment through computation of (1H and 13C) NMR chemical shifts, Nat. Protoc., 2014, 9(3), 643–660 CrossRef CAS PubMed.
- M. Elyashberg and D. Argyropoulos, Computer Assisted Structure Elucidation (CASE): Current and future perspectives, Magn. Reson. Chem., 2021, 59(7), 669–690 CrossRef CAS PubMed.
- C. S. Kim, J. Oh and T. H. Lee, Structure elucidation of small organic molecules by contemporary computational chemistry methods, Arch. Pharmacal Res., 2020, 43(11), 1114–1127 CrossRef CAS PubMed.
- A. Howarth, K. Ermanis and J. M. Goodman, DP4-AI automated NMR data analysis: straight from spectrometer to structure, Chem. Sci., 2020, 11(17), 4351–4359 RSC.
- A. Howarth and J. M. Goodman, The DP5 probability, quantification and visualisation of structural uncertainty in single molecules, Chem. Sci., 2022, 13(12), 3507–3518 RSC.
- W. Bremser, Hose — a novel substructure code, Anal. Chim. Acta, 1978, 103(4), 355–365 CrossRef CAS.
- M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Computational Prediction of 1H and 13C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry, Chem. Rev., 2012, 112(3), 1839–1862 CrossRef CAS PubMed.
- E. Jonas, S. Kuhn and N. Schlörer, Prediction of chemical shift in NMR: A review, Magn. Reson. Chem., 2022, 60(11), 1021–1031 CrossRef CAS PubMed.
- D. Sebastiani and M. Parrinello, A New ab-Initio Approach for NMR Chemical Shifts in Periodic Systems, J. Phys. Chem. A, 2001, 105(10), 1951–1958 CrossRef CAS.
- D. Sebastiani and U. Rothlisberger, Nuclear Magnetic Resonance Chemical Shifts from Hybrid DFT QM/MM Calculations, J. Phys. Chem. B, 2004, 108(9), 2807–2815 CrossRef CAS.
- S. Kuhn and N. E. Schlörer, Facilitating quality control for spectra assignments of small organic molecules: nmrshiftdb2–a free in-house NMR database with integrated LIMS for academic service laboratories, Magn. Reson. Chem., 2015, 53(8), 582–589 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72(Pt 2), 171–179 CrossRef CAS PubMed.
- A. Gupta, S. Chakraborty and R. Ramakrishnan, Revving up 13C NMR shielding predictions across chemical space: benchmarks for atoms-in-molecules kernel machine learning with new data for 134 kilo molecules, Mach. learn.: sci. technol., 2021, 2(3), 035010 Search PubMed.
- L. A. Bratholm, W. Gerrard, B. Anderson, S. Bai, S. Choi and L. Dang, et al., A community-powered search of machine learning strategy space to find NMR property prediction models, PLoS One, 2021, 16(7), e0253612 CrossRef CAS PubMed.
- M. Rupp, R. Ramakrishnan and O. A. von Lilienfeld, Machine learning for quantum mechanical properties of atoms in molecules, J. Phys. Chem. Lett., 2015, 6(16), 3309–3313 CrossRef CAS.
- Y. Kwon, D. Lee, Y. S. Choi, M. Kang and S. Kang, Neural Message Passing for NMR Chemical Shift Prediction, J. Chem. Inf. Model., 2020, 60(4), 2024–2030 CrossRef CAS PubMed.
- E. Jonas and S. Kuhn, Rapid prediction of NMR spectral properties with quantified uncertainty, J. Cheminf., 2019, 11(1), 50 Search PubMed.
- J. Han, H. Kang, S. Kang, Y. Kwon, D. Lee and Y. S. Choi, Scalable graph neural network for NMR chemical shift prediction, Phys. Chem. Chem. Phys., 2022, 24, 26870–26878 RSC.
- F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Chemical shifts in molecular solids by machine learning, Nat. Commun., 2018, 9(1), 4501 CrossRef PubMed.
- F. Musil, M. J. Willatt, M. A. Langovoy and M. Ceriotti, Fast and Accurate Uncertainty Estimation in Chemical Machine Learning, J. Chem. Theory Comput., 2019, 15(2), 906–915 CrossRef CAS PubMed.
- E. Jonas. Deep imitation learning for molecular inverse problems, in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2019, vol. 32 Search PubMed.
- Z. Huang, M. S. Chen, C. P. Woroch, T. E. Markland and M. W. Kanan, A framework for automated structure elucidation from routine NMR spectra, Chem. Sci., 2021, 12, 15329–15338 RSC.
- B. Sridharan, S. Mehta, Y. Pathak and U. D. Priyakumar, Deep Reinforcement Learning for Molecular Inverse Problem of Nuclear Magnetic Resonance Spectra to Molecular Structure, J. Phys. Chem. Lett., 2022, 13(22), 4924–4933 CrossRef CAS PubMed.
- W. Gerrard, L. A. Bratholm, M. J. Packer, A. J. Mulholland, D. R. Glowacki and C. P. Butts, IMPRESSION – prediction of NMR parameters for 3-dimensional chemical structures using machine learning with near quantum chemical accuracy, Chem. Sci., 2020, 11(2), 508–515 RSC.
- W. Gerrard, C. Yiu and C. P. Butts, Prediction of 15N chemical shifts by machine learning, Magn. Reson. Chem., 2021, 60(11), 1087–1092 CrossRef PubMed.
- R. Gaumard, D. Dragún, J. N. Pedroza-Montero, B. Alonso, H. Guesmi and I. Malkin Ondík, et al., Regression machine learning models used to predict DFT-computed NMR parameters of zeolites, Computation, 2022, 10(5), 74 CrossRef CAS.
- Y. H. Tsai, M. Amichetti, M. M. Zanardi, R. Grimson, A. H. Daranas and A. M. Sarotti, ML-J-DP4: An Integrated Quantum Mechanics-Machine Learning Approach for Ultrafast NMR Structural Elucidation, Org. Lett., 2022, 24(41), 7487–7491 CrossRef CAS PubMed.
- M. Cordova, E. A. Engel, A. Stefaniuk, F. Paruzzo, A. Hofstetter and M. Ceriotti, et al., A Machine Learning Model of Chemical Shifts for Chemically and Structurally Diverse Molecular Solids, J. Phys. Chem. C, 2022, 126(39), 16710–16720 CrossRef CAS PubMed.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole von Lilienfeld, FCHL revisited: Faster and more accurate quantum machine learning, J. Chem. Phys., 2020, 152(4), 044107 CrossRef CAS PubMed.
- W. Bremser, HOSE—a novel substructure code, Anal. Chim. Acta, 1978, 103(4), 355–365 CrossRef CAS.
- S. Kuhn and S. R. Johnson, Stereo-Aware Extension of HOSE Codes, ACS Omega, 2019, 4(4), 7323–7329 CrossRef CAS PubMed.
- P. A. Unzueta, C. S. Greenwell and G. J. O. Beran, Predicting Density Functional Theory-Quality Nuclear Magnetic Resonance Chemical Shifts via Δ-Machine Learning, J. Chem. Theory Comput., 2021, 17(2), 826–840 CrossRef CAS PubMed.
- H. Rull, M. Fischer and S. Kuhn, NMR shift prediction from small data quantities, J. Cheminform., 2023, 15, 114 CrossRef PubMed.
- H. Han and S. Choi, Transfer Learning from Simulation to Experimental Data: NMR Chemical Shift Predictions, J. Phys. Chem. Lett., 2021, 12(14), 3662–3668 CrossRef CAS PubMed.
- E. Jonas and S. Kuhn, Rapid prediction of NMR spectral properties with quantified uncertainty, J. Cheminf., 2019, 11(1), 1–7 CAS.
- S. Riniker and G. A. Landrum, Better Informed Distance Geometry: Using What We Know To Improve Conformation Generation, J. Chem. Inf. Model., 2015, 55(12), 2562–2574 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- D. Lemm, G. F. von Rudorff and O. A. von Lilienfeld, Improved decision making with similarity based machine learning, arXiv, 2022, preprint, arXiv:2205.05633, DOI:10.48550/arXiv.2205.05633.
- D. Lemm, G. F. von Rudorff and O. A. von Lilienfeld, Machine learning based energy-free structure predictions of molecules, transition states, and solids, Nat. Commun., 2021, 12(1), 4468 CrossRef CAS PubMed.
- L. Yao, M. Yang, J. Song, Z. Yang, H. Sun and H. Shi, et al., Conditional Molecular Generation Net Enables Automated Structure Elucidation Based on 13C NMR Spectra and Prior Knowledge, Anal. Chem., 2023, 95(12), 5393–5401 CrossRef CAS PubMed.
- M. Gastegger, K. T. Schütt and K. R. Müller, Machine learning of solvent effects on molecular spectra and reactions, Chem. Sci., 2021, 12(34), 11473–11483 RSC.
- C. McGill, M. Forsuelo, Y. Guan and W. H. Green, Predicting Infrared Spectra with Message Passing Neural Networks, J. Chem. Inf. Model., 2021, 61(6), 2594–2609 CrossRef CAS PubMed.
- S. Grimme, Towards First Principles Calculation of Electron Impact Mass Spectra of Molecules, Angew. Chem., Int. Ed., 2013, 52(24), 6306–6312 CrossRef CAS PubMed.
- A. D. Shrivastava, N. Swainston, S. Samanta, I. Roberts, M. W. Muelas and D. B. Kell, MassGenie: A Transformer-Based Deep Learning Method for Identifying Small Molecules from Their Mass Spectra, Biomolecules, 2021, 11(12), 1793 CrossRef CAS PubMed.
- G. Jung, S. G. Jung and J. M. Cole, Automatic materials characterization from infrared spectra using convolutional neural networks, Chem. Sci., 2023, 14(13), 3600–3609 RSC.
- P. Pracht, D. F. Grant and S. Grimme, Comprehensive Assessment of GFN Tight-Binding and Composite Density Functional Theory Methods for Calculating Gas-Phase Infrared Spectra, J. Chem. Theory Comput., 2020, 16(11), 7044–7060 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00132f |
| This journal is © The Royal Society of Chemistry 2024 |