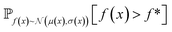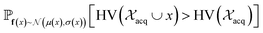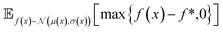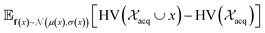Open Access Article
Open Access ArticlePareto optimization to accelerate multi-objective virtual screening†
Jenna C.
Fromer
 a,
David E.
Graff
a,
David E.
Graff
 ab and
Connor W.
Coley
ab and
Connor W.
Coley
 *ac
*ac
aDepartment of Chemical Engineering, MIT, Cambridge, MA 02139, USA. E-mail: ccoley@mit.edu
bDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA
cDepartment of Electrical Engineering and Computer Science, MIT, Cambridge, MA 02139, USA
First published on 15th January 2024
Abstract
The discovery of therapeutic molecules is fundamentally a multi-objective optimization problem. One formulation of the problem is to identify molecules that simultaneously exhibit strong binding affinity for a target protein, minimal off-target interactions, and suitable pharmacokinetic properties. Inspired by prior work that uses active learning to accelerate the identification of strong binders, we implement multi-objective Bayesian optimization to reduce the computational cost of multi-property virtual screening and apply it to the identification of ligands predicted to be selective based on docking scores to on- and off-targets. We demonstrate the superiority of Pareto optimization over scalarization across three case studies. Further, we use the developed optimization tool to search a virtual library of over 4M molecules for those predicted to be selective dual inhibitors of EGFR and IGF1R, acquiring 100% of the molecules that form the library's Pareto front after exploring only 8% of the library. This workflow and associated open source software can reduce the screening burden of molecular design projects and is complementary to research aiming to improve the accuracy of binding predictions and other molecular properties.
1 Introduction
Molecular discovery aims to identify molecules that balance multiple, often competing, properties. The need to simultaneously optimize multiple properties is especially notable in drug discovery workflows. Small molecule drugs operating through direct single-target binding interactions must exhibit not only strong binding affinity for the target protein but also minimal off-target interactions and suitable pharmacokinetic properties.1–3 One formulation of small molecule drug discovery is to identify compounds that bind strongly to a protein of interest and subsequently modify them to fulfill remaining property constraints.1,4,5 A candidate molecule with high activity but a poor pharmacokinetic profile may ultimately be abandoned, resulting in wasted time and resources.3,6Selectivity is one property that is often considered only after a hit with promising primary activity is identified.1 Selectivity may be measured with binding assays against off-targets that are structurally similar to the primary target or known to be associated with adverse side effects (e.g., cytochromes P450 and the hERG channel).3,7 Non-specific ligands that bind to many proteins in addition to the target may require additional optimization steps when compared to their selective counterparts.2,8 Consideration of promiscuity early in a drug discovery project may aid in deprioritizing chemical series that are inherently nonselective.9,10 In other settings, binding interactions with multiple targets can be advantageous.11 Therapeutics for Alzheimer's disease12,13 and thyroid cancer14,15 have exhibited improved efficacy through affinity for multiple protein targets. Optimizing affinity to multiple targets is another goal that can be brought into earlier stages of hit discovery.16,17
Anticipating protein–ligand interactions that contribute to potency and selectivity is possible, albeit imperfectly, with structure-based drug design techniques that employ scoring functions to estimate energetic favorability. Docking to off-targets has been applied to improve the selectivity profiles of identified compounds.18–20 These demonstrations have revealed that falsely predicted non-binders may incorrectly be categorized as selective because scoring functions designed for hit-finding typically aim to minimize the false positive rate (i.e., weak binders predicted to bind strongly), not the false negative rate (i.e., binders predicted not to bind).20,21 Although structure-based methods like docking are limited in their predictive accuracy,22–27 docking-based virtual screens can still effectively enrich a virtual library for molecules that are more likely to exhibit target activity.28–32
The computational cost of virtual screening33 has motivated the development of model-guided optimization methods that reduce the total number of docking calculations required to recover top-performing molecules.34–40 As one example, Graff et al.37 only require the docking scores of 2.4% of a 100M member virtual library to identify over 90% of the library's top-50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ligands. Similar principles apply when using more expensive evaluations such as relative binding free energy calculations,41 where a reduction of computational cost can be particularly beneficial. These methods are designed to optimize a single property and are inherently single-objective optimizations.
000 ligands. Similar principles apply when using more expensive evaluations such as relative binding free energy calculations,41 where a reduction of computational cost can be particularly beneficial. These methods are designed to optimize a single property and are inherently single-objective optimizations.
The need for model-guided optimization methods in virtual screening is heightened when multiple properties are screened. The resources required for a multi-objective virtual screen scale linearly with the number of screened properties (“objectives”) and library size. In some settings, exhaustive screens of large virtual libraries (millions to billions) may be infeasible. Model-guided multi-objective optimization has the potential to reduce the computational cost of a multi-objective virtual screen without sacrificing performance. Mehta et al.42 have previously applied Bayesian optimization to identify molecules that simultaneously optimize the docking score to Tau Tubulin Kinase 1, calculated octanol–water partition coefficient (clogP),43 and synthetic accessibility score (SA_Score).44 Their implemented acquisition function is a product of acquisition scores for individual objectives,42 leading to the recovery of over 90% of the most desirable molecules after scoring only 6% of the virtual library. Multi-objective virtual screens involve multiple design choices primarily related to the acquisition strategy, which have not yet been compared in the context of virtual screening. Further, existing methods for multi-objective virtual screening do not implement Pareto optimization. Pareto optimization aims to identify the molecules that form or are close to the Pareto front, for which an improvement in one objective necessitates a detriment to another. Molecules that form the Pareto front optimally balance multiple desired properties, illustrate which combinations of objective values are possible, and reveal trade-offs in the objective space; this is not possible with scalarization.
In this work, we extend the molecular pool-based active learning tool MolPAL37 to this setting of multi-objective virtual screening. MolPAL is publicly available, open source, and can be adopted for multi-objective virtual screening with any desired set of objective functions, including those beyond structure-based drug design. We demonstrate through three retrospective case studies that MolPAL can efficiently search a virtual library for putative selective binders. We compare optimization performance across multi-objective acquisition functions and demonstrate the superiority of Pareto-based acquisition functions over scalarization ones. We also implement a diversity-enhanced acquisition strategy that increases the number of acquired scaffolds by 33% with only a minor impact on optimization performance. Finally, we apply MolPAL to efficiently search the Enamine Screening Collection45 of over 4 million molecules for selective dual inhibitors of EGFR and IGF1R as an exemplary 3-objective optimization. After exploration of only 8% of the virtual library, 100% of the library's non-dominated points and over 60% of the library's top ∼0.1%, defined by non-dominated sorting, are identified by MolPAL.
2 Multi-objective virtual screening with MolPAL
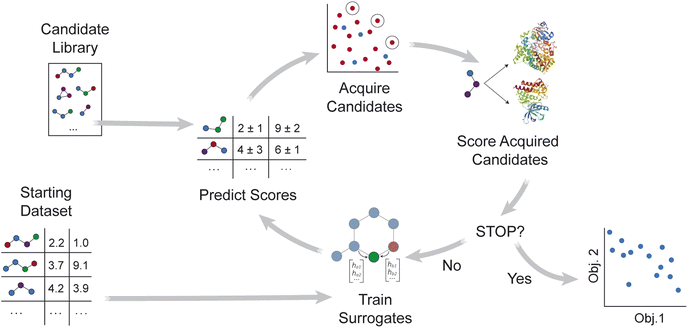
MolPAL applies the multi-objective pool-based workflow described in ref. 46, combining multi-objective Bayesian optimization and surrogate models to efficiently explore a virtual library for molecules that simultaneously optimize multiple properties (Fig. 1). Similar workflows have been demonstrated for the design of battery materials47–49 and other functional materials.50–52 As summarized in Algorithm S2,† objective values are first calculated for a subset of the library, and surrogate models that predict each objective are trained on these initial observations. After objective values are predicted for all candidate molecules, an acquisition function selects a set of promising molecules for objective function evaluation. The surrogate models are then retrained with new observations, and the iterative loop repeats until a stopping criterion is met.Relative to its initial release in ref. 37, MolPAL was extended primarily through modification of the acquisition strategy and handling of multiple surrogate models. The multi-objective extension of MolPAL allows users to select between Pareto optimization and scalarization strategies.
Scalarization reduces a multi-objective optimization problem into a single-objective problem, often through a weighted sum:
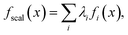 | (1) |
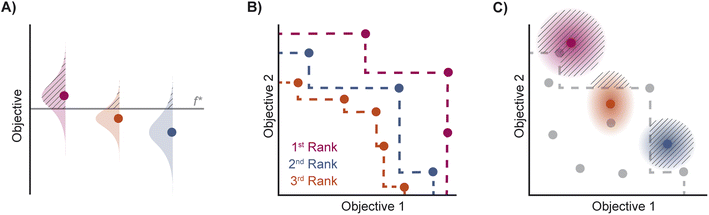 | ||
| Fig. 2 Depiction of acquisition functions in Bayesian optimization. (A) Probability of improvement (PI) estimates the likelihood that an as-yet unobserved objective function value exceeds the current maximum value f*. Expected improvement (EI) estimates the amount that f* would increase if an unobserved point is acquired.53 (B) Non-dominated sorting assigns integer “Pareto ranks” to each candidate. (C) Hypervolume-based acquisition functions53 extend the principles of PI and EI to multiple dimensions using the observed Pareto front (grey dashed line) rather than f*. Probability of hypervolume improvement (PHI) represents the likelihood that acquisition of an unobserved point would increase the hypervolume by any amount. Expected hypervolume improvement (EHI) estimates the increase in hypervolume if the objective function value of such a point is scored.53 Objectives are defined so that optimization corresponds to maximization. | ||
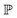 and
and 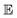 represent probability and expected value, respectively. f* is the current best objective value, HV is hypervolume, and rank is the Pareto rank. Surrogate models provide prediction means μ and standard deviations σ for the objective value f of candidate point x.
represent probability and expected value, respectively. f* is the current best objective value, HV is hypervolume, and rank is the Pareto rank. Surrogate models provide prediction means μ and standard deviations σ for the objective value f of candidate point x. 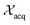 is the set of points acquired in previous iterations. Bold variables are vectors.
is the set of points acquired in previous iterations. Bold variables are vectors. 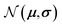 implies that the covariance matrix is treated as diagonal with entries σi2, i.e., uncertainty is uncorrelated across objective functions
implies that the covariance matrix is treated as diagonal with entries σi2, i.e., uncertainty is uncorrelated across objective functions
Pareto optimization is a multi-objective optimization strategy that reveals the trade-offs between objectives and does not require any measure of the relative importance of objectives. Further, Pareto optimization aims to identify the entire Pareto front, a feature not guaranteed by single-objective methods such as weighted sum scalarization.61,62 Common multi-objective acquisition functions include the probability of hypervolume improvement (PHI),53 expected hypervolume improvement (EHI),53 non-dominated sorting (NDS),63,64 and Pareto upper confidence bound (P-UCB).65 These are natural extensions of single-objective acquisition functions (Table 1) that instead aim to increase the region, or hypervolume, dominated by the acquired points (Fig. 2). P-UCB and its single-objective analog UCB are not considered in this work. For model-guided Pareto optimization, either a multi-task surrogate model, multiple single-task surrogate models, or a combination thereof is needed to predict the set of objective function values. As outlined in Algorithm S2,† MolPAL trains N single-task surrogate models to predict N objectives to circumvent the challenge of loss function weighting in multi-task learning.66
Acquiring a batch of k points in a single iteration may be more efficient than sequential acquisition when objectives functions can be calculated in parallel. “Top-k batching” naively selects the k points with the highest acquisition scores.67 More sophisticated batch acquisition strategies iteratively construct optimal batches one point at a time by hallucinating objective function values.68–73 Other strategies use heuristics to select batches that are diverse in the design space or objective space in order to improve the utility of a batch.74–79 MolPAL implements both naive top-k batching and diversity-enhanced acquisition strategies that apply clustering in both the design space and in the objective space (Section 5.5).
3 Results and discussion
3.1 Description of case studies
We test MolPAL with three retrospective case studies with an emphasis on docking-predicted binding selectivity to compare optimization performance across acquisition functions. The pairs of objectives used in these case studies are exclusively docking scores even though the framework of MolPAL is more general. For example, this workflow may be used to optimize docking scores to an ensemble of protein structures80 (“ensemble docking”) or optimize multiple docking scoring functions provided with a single target.81–83Each case explores a virtual library of approximately 260k molecules and optimizes two competing docking score objectives from the DOCKSTRING benchmark.84 Case 1's goal is modeled after identifying antagonists of dopamine receptor D3 (DRD3) that are selective over dopamine receptor D2 (DRD2), which may enable effective treatment of various conditions without the side effects triggered by DRD2 antagonists.85–87 Case 2 treats Janus Kinase 2 (JAK2), a lukemia target, as the on-target and lymphocyte-specific protein tyrosine kinase (LCK) as the off-target.88,89 Finally, case 3 aims to identify selective inhibitors of insulin-like growth factor 1 receptor (IGF1R)90,91 that do not bind to cytochrome P450 3A4 (CYP3A4),92,93 an off-target known to impact the pharmacokinetic properties of drugs though metabolism.94–96 The property trade-offs for each case are shown in Fig. 3. Because both positive docking scores and scores of 0 should be interpreted as non-binders, we clip docking scores to 0.
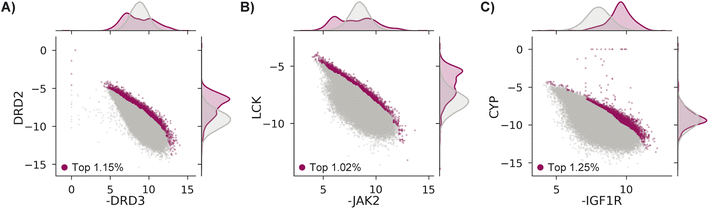 | ||
| Fig. 3 Docking scores in the DOCKSTRING dataset84 for (A) case 1, (B) case 2, and (C) case 3. All molecules considered in the top ∼1%, as determined by NDS rank (Section 5.6), are shown as magenta points, with the remaining data in grey. There are 2986 (1.15%), 2651 (1.02%), and 3261 (1.25%) molecules in the top ∼1% for cases 1, 2, and 3, respectively. | ||
We employ single-task directed message-passing neural networks97,98 for each objective as surrogate models (Section 5.4). An initial set of 2602 molecules is randomly sampled at the zeroth iteration, and 1% of the library (2602 molecules) is acquired in each subsequent iteration. Scalarization weighting factors (λ1 and λ2 in eqn (1)) were set to 0.5. Five trials with distinct initialization seeds were completed for each acquisition function. Section 5 contains full implementation details.
3.2 Pareto acquisition functions outperform scalarization
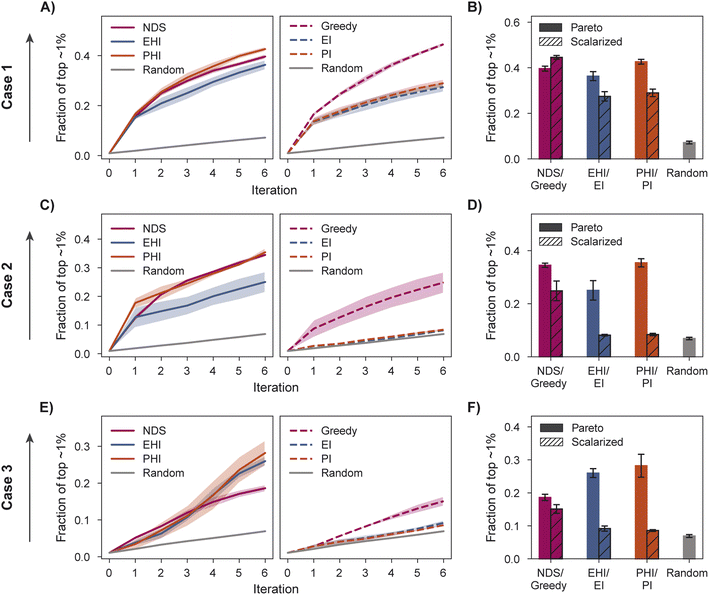
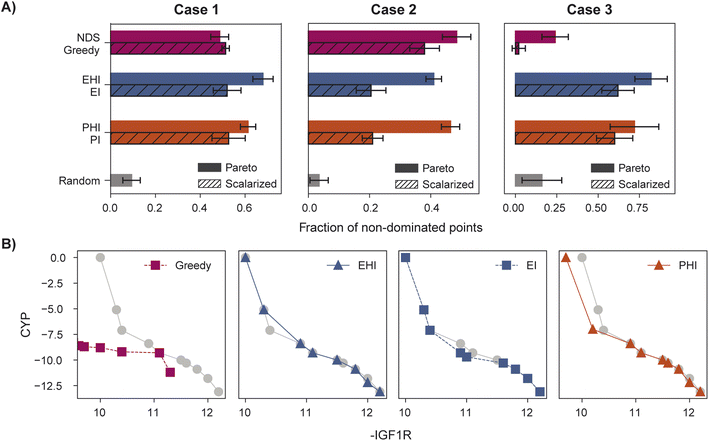
We characterize optimization performance with three metrics: fraction of the top ∼1% acquired, hypervolume (HV), and fraction of non-dominated points acquired. We motivate the selection of these metrics and describe their implementation in Section 5.6.All Pareto optimization acquisition functions show substantial improvement over random acquisition according to the top ∼1% metric, with PHI performing most consistently across cases (Fig. 4A–F). Analyzing the same metric, greedy is clearly the best scalarized acquisition function despite its poor performance in case 3 relative to PHI and EHI. Only in case 1 does the best scalarization acquisition function outperform the best Pareto acquisition function. Performance metrics using the acquisition function described by Mehta et al.42 (MO-MEMES) are included as an additional baseline in Tables S1–S3.† Pareto optimization acquisition functions consistently outperform MO-MEMES.
When performance is measured by the fraction of non-dominated points acquired, EHI and PHI outperform scalarization acquisition functions (Fig. 5) even though the degree of improvement varies across cases. The sensitivity of the hypervolume metric to outliers on the Pareto front leads to noisy hypervolume profiles (Fig. S2†). Similar trends are observed when measuring the inverted generational distance metric (Fig. S3†). Overall, Pareto optimization acquisition functions strongly outperform or match the performance of scalarization for the pairs of objectives and virtual library considered.
The variation in relative performance of different acquisition functions across evaluation metrics is noteworthy. For example, greedy scalarization performs quite well in the top ∼1% metric for all cases but worse than random acquisition according to hypervolume and fraction of non-dominated points in case 3. The results shown here highlight the importance of assessing the performance across different sets of objectives. Despite the variation across cases and metrics, EHI and PHI consistently perform as well as scalarization or substantially better than scalarization. These acquisition functions are suitable choices for new sets of objectives. Alternatively, when a previously unexplored set of objectives is to be optimized, a retrospective study on a scored subset of the library can inform the selection of a suitable acquisition strategy. Each reported metric corresponds to distinct optimization goals (Section 5.6); the primary application of a multi-objective virtual screen should inform which metric to use for acquisition function comparison and selection.
3.3 Clustering-based acquisition improves molecular diversity
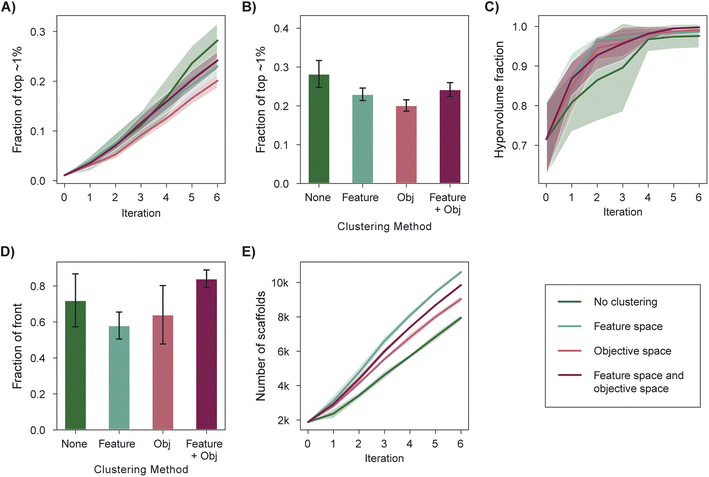
Scoring functions used in structure-based virtual screening can exhibit systematic errors that bias selection toward specific interactions.99 This poses a risk for experimental validation if specific scaffolds are overrepresented in the top-scoring molecules. Selecting a structurally diverse set of candidates is one strategy to mitigate this risk and can be achieved via a diversity-enhanced acquisition strategy (Section 5.5). First, a set of molecules larger than the target batch size is selected according to the acquisition function and is then partitioned into a number of clusters equal to the batch size in feature (e.g., molecular fingerprint) space. The molecule with the best acquisition score in each cluster is acquired. We analyzed the performance of diversity-enhanced acquisition for case 3, using PHI as the acquisition function. All hyperparameters were the same as those used for previous experiments (Section 5).Feature space clustering slightly hinders optimization performance according to all four performance metrics (Fig. 6A–E), but it also increases the number of graph-based Bemis–Murcko scaffolds100 acquired by 33% when compared to a naïve batch construction strategy. This degradation in measured performance is expected given that the performance metrics do not consider the overall diversity of the selected molecules. The increased structural diversity of the selected molecules can be qualitatively visualized via dimensionality reduction through UMAP101 (Fig. S4†).
Certain multi-objective optimization methods such as NSGA-II64 also incorporate objective space diversity, i.e., the selection of points better distributed along the Pareto front.46 We find that clustering in the objective space during acquisition (Section 5.5) mildly hinders performance in all optimization metrics (Fig. 6A–E). An acquisition strategy that considers diversity in both the objective space and feature space (Section 5.5) performs similarly to the standard acquisition strategy across most optimization metrics (Fig. 6A–D) while acquiring a more structurally diverse set of molecules when compared to standard acquisition (Fig. 6F and S4†). Overall, we recommend the use of feature space clustering if having structurally distinct candidates is a priority for experimental validation.
3.4 MolPAL scales to 3 objectives and larger libraries
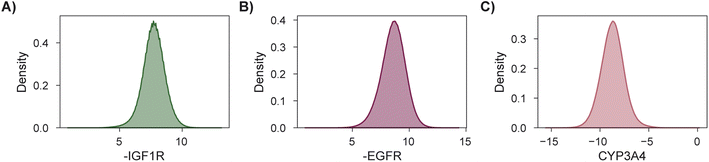
As a final demonstration, we show that MolPAL scales well to larger virtual libraries and more than two objectives by searching the Enamine Screening Collection45 of over 4 million molecules for those that optimize three docking objectives. The objectives were defined to identify putative dual inhibitors of IGF1R and EGFR102–104 with selectivity over CYP3A4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 94–96,105 which could in principle serve as starting points for esophageal cancer therapeutics. To analyze performance according to the four considered evaluation metrics, we perform this search retrospectively after docking the entire library using DOCKSTRING's protocol for each target84 (Section 5.1). The distributions of individual objectives for the entire library are shown in Fig. 7. We use PHI acquisition without clustering and acquire 1% of the library at each iteration, repeating each experiment three times.
94–96,105 which could in principle serve as starting points for esophageal cancer therapeutics. To analyze performance according to the four considered evaluation metrics, we perform this search retrospectively after docking the entire library using DOCKSTRING's protocol for each target84 (Section 5.1). The distributions of individual objectives for the entire library are shown in Fig. 7. We use PHI acquisition without clustering and acquire 1% of the library at each iteration, repeating each experiment three times.
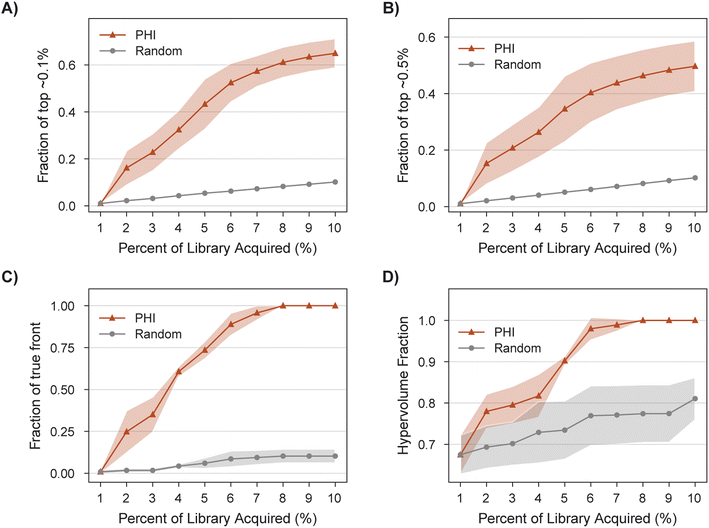
MolPAL succeeds in acquiring 100% of the library's non-dominated points in all three replicates after exploring only 8% of the search space (Fig. 8C), a 9X improvement of in the fraction of acquired non-dominated points over random acquisition. At this same degree of exploration (8% of the library), over 60% of the library's top ∼0.1% molecules have been identified (Fig. 8A). Improvements in IGD and hypervolume with MolPAL over random acquisition are also notable (Fig. 8 and Table 2). The results of this retrospective run indicate that MolPAL can substantially reduce the computational resources required to identify molecules that simultaneously optimize multiple properties from a virtual library of millions of molecules.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 molecules), and Pareto front points (39 molecules) acquired
015 molecules), and Pareto front points (39 molecules) acquired
| Acquisition function | Top ∼0.1% ↑ | Top ∼0.5% ↑ | HV ↑ | IGD ↓ | Fraction of true front ↑ |
|---|---|---|---|---|---|
| PHI | 0.65 ± 0.06 | 0.50 ± 0.09 | 1.00 ± 0.00 | 0.00 ± 0.00 | 1.00 ± 0.00 |
| Random | 0.10 ± 0.00 | 0.10 ± 0.00 | 0.81 ± 0.05 | 0.88 ± 0.04 | 0.10 ± 0.04 |
The virtual library's true Pareto front of 39 molecules, all of which were recovered by MolPAL, is visualized in Fig. 9. The structures of all non-dominated molecules are shown in Fig. S6–S8.† The structures of these molecules, several of which look more like dye molecules than drug-like molecules, expose some remaining challenges of docking for selectivity prediction. Molecules predicted to be non-binders to CYP3A4, such as M4 and M20 in Fig. 9, are relatively large molecules that do not fit inside the pocket of CYP3A4, leading to steric clashes and less favorable binding energetics. The ability for such molecules to score well against the IGF1R and EGFR but poorly against CYP3A4 is exemplified by the computed docking poses and protein–ligand interactions of M4 (Fig. S5†). Although steric clashes may be a valid reason for hypothetical selectivity towards EGFR/IGF1R over CYP3A4, the molecules predicted to be most selective (e.g., M4 and M20) are not attractive candidates for experimental validation. In practice, dominated molecules that are close to the identified Pareto front should also be considered for experimental validation or follow-up studies. Molecules that are obviously not suitable starting points for a drug discovery campaign, including those in Fig. 9, should be deprioritized for experimental testing. A ligand efficiency score may also be used as an objective function to penalize very large molecules.106 Nevertheless, given the imperfections of docking as an oracle function, MolPAL perfectly identifies the Pareto front at a reduced computational cost and scores well in terms of all evaluation metrics. We do not intend to nominate the visualized molecules as starting points for a drug discovery project but instead aim to demonstrate the ability for MolPAL to efficiently identify molecules that optimize any set of oracles such as those that predict binding affinity.
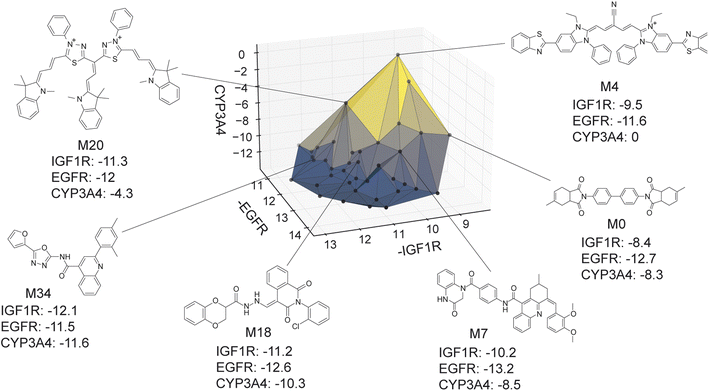 | ||
| Fig. 9 Visualization of the Pareto front for the 3-objective optimization for the identification of putative selective dual inhibitors. All non-dominated points depicted were acquired by MolPAL after scoring only 8% of the virtual library. Structures for some molecules on the Pareto front are shown. Many of these molecules (e.g., M4 and M20) would not be suitable starting points for a drug discovery campaign, highlighting the imperfections of docking as a sole oracle function. Docking scores to targets EGFR and IGF1R and off-target CYP3A4 were calculated with the AutoDock Vina wrapper DOCKSTRING.84 | ||
4 Conclusion
We have introduced an open source multi-objective extension of the pool-based optimization tool MolPAL37 and demonstrated its ability to accelerate docking-based multi-objective virtual screening. MolPAL provides a flexible Pareto optimization framework that allows users to systematically vary key design choices like acquisition strategy. MolPAL is most appropriate for optimizing objectives that are more expensive to calculate than surrogate molecular property prediction models. Beyond docking, these include objectives that require binding free energy calculations, quantum mechanical simulations, or experiments to measure. Objectives that are calculable in CPU milliseconds, such as SA_Score or clogP, can be screened exhaustively and do not warrant model-guided optimization tools. MolPAL could also be applied to consensus docking by optimizing multiple scoring functions that predict binding affinity to the same target.81–83 MolPAL is designed to flexibly accommodate custom objectives and facilitate the optimization of other property predictions relevant to molecular design.We first assessed MolPAL on three two-objective case studies that aim to identify putative selective binders. We found that expected hypervolume improvement and probability of hypervolume improvement, both Pareto optimization acquisition functions, consistently performed as well as or better than scalarization. A diversity-enhanced acquisition strategy that applies clustering in molecular fingerprint space was found to increase the number of Bemis–Murcko scaffolds observed by 33% when compared to standard acquisition. Finally, we demonstrated that MolPAL can efficiently search large virtual libraries and optimize three objectives simultaneously through a case study aiming to identify putative selective dual inhibitors from the Enamine Screening Collection of over 4 million molecules; MolPAL acquired all of the library's non-dominated molecules after exploring only 8% of the library in all three replicates.
Exploration of other multi-objective optimization approaches, such as random scalarization and Chebyshev scalarization, in the context of molecular optimization could expose benefits of strategies not explored in this work. Other published diversity-enhanced acquisition strategies79,107 may have the potential to improve both molecular diversity and optimization performance.
While the use of docking to off-targets as a proxy for selectivity is well precedented,18–20 the high false negative rates of docking screens (i.e., binders predicted to be nonbinding) pose a risk for experimental validation of molecules predicted to be selective.20,21,108 Pharmacophore models and scoring functions that are designed for off-target activity9,19,109 could be more appropriate for cross-docking for selectivity in the future. Because MolPAL is a general multi-objective optimization strategy that can be applied to any combination of oracle functions, it will maintain its relevance as these oracle functions improve in time. Future efforts applying MolPAL to hit discovery and early-stage molecular design are necessary to validate the benefits of considering multiple objectives at early stages of molecular discovery.
5 Methods
All code required to reproduce the reported results can be found in the branch of MolPAL at https://github.com/coleygroup/molpal/tree/multiobj.
branch of MolPAL at https://github.com/coleygroup/molpal/tree/multiobj.
5.1 Data collection
All docking scores used in Sections 3.2 and 3.3 were used without reprocessing from the DOCKSTRING benchmark84 (downloaded June 2023). For the larger scale study in Section 3.4, the Enamine Screening Collection of over 4 million compounds45 (downloaded May 2023) was docked against IGF1R, EGFR, and CYP3A4 using DOCKSTRING84 with default settings for each target. Before docking, molecules were stripped of salts using RDKit's SaltRemover module.110 Of the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032
032![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 in the library, 4
152 in the library, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010
010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199 were docked successfully to CYP3A4, 4
199 were docked successfully to CYP3A4, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010
010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 to IGF1R, and 4
191 to IGF1R, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010
010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 to EGFR. Unsuccessful docking calculations resulted primarily from failures during the ligand preparation process. The full set of docking scores are available at https://figshare.com/articles/dataset/Enamine_screen_CYP3A4_EGFR_IGF1R_zip/23978547.
187 to EGFR. Unsuccessful docking calculations resulted primarily from failures during the ligand preparation process. The full set of docking scores are available at https://figshare.com/articles/dataset/Enamine_screen_CYP3A4_EGFR_IGF1R_zip/23978547.
5.2 Objectives
Docking scores to on-targets were minimized objectives, and scores to off-targets were maximized objectives. A positive docking score is not meaningfully different from a docking score of zero. We therefore adjust docking objectives to be:| fdock(x) = min(0,f(x)) | (2) |
5.3 Acquisition functions
We modify PHYSBO's implementation111 of expected hypervolume improvement and probability of hypervolume improvement, which applies the algorithm proposed by Couckuyt et al.112 MolPAL uses the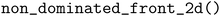 utility in pygmo113 for non-dominated sorting in two dimensions. In more than three dimensions, MolPAL iteratively identifies non-dominated points using the Pareto class in PHYSBO111 and removes those points from the unranked set until enough points have been ranked.
utility in pygmo113 for non-dominated sorting in two dimensions. In more than three dimensions, MolPAL iteratively identifies non-dominated points using the Pareto class in PHYSBO111 and removes those points from the unranked set until enough points have been ranked.
In the scalarization runs, f was calculated according to eqn (1) with λ1 = λ2 = 0.5. For prediction mean μ, prediction standard deviation σ, and current maximum value f*, expected improvement and probability of improvement in the scalarization runs were calculated as:
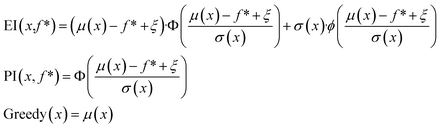 | (3) |
5.4 Surrogate model
Because the optimization campaigns explored in this study comprise batches of thousands of molecules, we elect to use a directed message-passing neural network architecture97 as the surrogate model for all runs. MolPAL contains a PyTorch114 implementation of ChemProp97,98 as in the original publication.37 We use an encoder depth of 3, directed edge messages only (no atom messages), a hidden size of 300, ReLU activation, and two layers in the feed-forward neural network as default parameters. The model was trained with an initial learning rate of 10−4 using a Noam learning rate scheduler and an Adam optimizer. In each iteration, the model is retrained from scratch, as this was found to provide a benefit over fine-tuning.37We use mean-variance estimation115,116 for surrogate model uncertainty quantification. The surrogate model is trained to predict both the mean f(x) and the variance of the estimation σ2(x) via a negative log likelihood loss function:
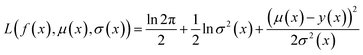 | (4) |
5.5 Clustering
We implement three diversity-enhancing acquisition strategies using clustering: in the feature space, in the objective space, and in both (Section 3.3). Feature space clustering is performed according to 2048-bit atom-pair fingerprints117 calculated using the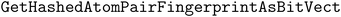 function in RDKit110 with the minimum length and maximum length of paths between pairs to 1 and 3, respectively. Atom pair fingerprints have been shown to outperform other extended connectivity fingerprints in recovering 3D-shape analogs118 and ranking close analogs by structural similarity.119 The predicted objective means were used for clustering in the objective space.
function in RDKit110 with the minimum length and maximum length of paths between pairs to 1 and 3, respectively. Atom pair fingerprints have been shown to outperform other extended connectivity fingerprints in recovering 3D-shape analogs118 and ranking close analogs by structural similarity.119 The predicted objective means were used for clustering in the objective space.
The acquisition strategy first selects a superset of molecules according to the acquisition scores as in a standard acquisition strategy. In our trials, the size of the superset is 10X the batch size, b. Then, the superset is clustered according to molecular fingerprints or predicted objective values. We use the implementation of 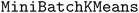 120 in scikit-learn121 with b clusters, 10 random initializations, an initialization size of 3b, and a reassignment ratio of 0 for batch size b. Although b clusters are specified, some clusters may be returned as empty in the case of a low-dimensional cluster basis. We ensure that b points are acquired by iteratively looping through all clusters, beginning with the largest clusters, and acquiring the molecule in the cluster with the highest acquisition score. This process is continued until b molecules are acquired.
120 in scikit-learn121 with b clusters, 10 random initializations, an initialization size of 3b, and a reassignment ratio of 0 for batch size b. Although b clusters are specified, some clusters may be returned as empty in the case of a low-dimensional cluster basis. We ensure that b points are acquired by iteratively looping through all clusters, beginning with the largest clusters, and acquiring the molecule in the cluster with the highest acquisition score. This process is continued until b molecules are acquired.
When clustering in both the feature and objective spaces, the superset is first clustered in the objective space into 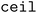 (b/2) clusters, and
(b/2) clusters, and 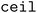 (b/2) points are acquired by iterating through the clusters and selecting the molecule with the highest acquisition score. The superset is then supplemented with the b/2 unacquired candidate points that have the highest acquisition scores. Then, the superset is clustered in the atom-pair fingerprint space into b −
(b/2) points are acquired by iterating through the clusters and selecting the molecule with the highest acquisition score. The superset is then supplemented with the b/2 unacquired candidate points that have the highest acquisition scores. Then, the superset is clustered in the atom-pair fingerprint space into b − 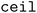 (b/2) clusters, and the point with the highest acquisition score in each cluster is acquired. Thus, when both forms of clustering are used, effectively b/2 points are selected to improve objective space diversity, and b/2 points are selected to improve feature space diversity.
(b/2) clusters, and the point with the highest acquisition score in each cluster is acquired. Thus, when both forms of clustering are used, effectively b/2 points are selected to improve objective space diversity, and b/2 points are selected to improve feature space diversity.
5.6 Performance metrics
Four performance metrics designed for Pareto optimization were measured to holistically assess the performance of MolPAL. The underlying goal of a multi-property virtual screen (e.g., understanding the trade-offs between objectives, identifying a set of potentially promising selective inhibitors) can guide which evaluation metric to be deemed most important. Reported metrics and the motivation for selecting each is described below.For multi-property virtual screening, the set of top-k molecules is not well-defined. We opt to define the top ∼k% through non-dominated sorting of the library (Fig. S1†). The non-dominated points in the library are iteratively selected and removed from the candidate pool until ≥k% of the library has been selected. These points then serve as the top ∼k%. Because multiple points are selected as part of the top ∼k% in each iteration (i.e., all points of a certain Pareto rank), the fraction is slightly larger than k%.
The top ∼k% metric best describes virtual screens aiming to identify many molecules roughly close to the Pareto front. Compared to other metrics that consider points on or much closer to the Pareto front, it best captures the expectation that not all top-performing molecules will validate experimentally.
5.7 Scaffold analysis
To quantify the improvement in molecular diversity using diversity-enhanced acquisition, we count the number of observed Bemis–Murcko scaffolds100 using RDKit's and
and  functions.
functions.
Data availability
The developed open source tool and all code required to reproduce the reported results can be found in the branch of MolPAL at https://github.com/coleygroup/molpal/tree/multiobj. Docking scores from the DOCKSTRING benchmark are available at https://figshare.com/articles/dataset/dockstring_dataset/16511577. Docking scores for IGF1R, EGFR, and CYP3A4 computed as a part of this work can be found at https://figshare.com/articles/dataset/Enamine_screen_CYP3A4_EGFR_IGF1R_zip/23978547.
branch of MolPAL at https://github.com/coleygroup/molpal/tree/multiobj. Docking scores from the DOCKSTRING benchmark are available at https://figshare.com/articles/dataset/dockstring_dataset/16511577. Docking scores for IGF1R, EGFR, and CYP3A4 computed as a part of this work can be found at https://figshare.com/articles/dataset/Enamine_screen_CYP3A4_EGFR_IGF1R_zip/23978547.
Author contributions
Conceptualization: J. C. F., D. E. G., C. W. C.; data curation: J. C. F., D. E. G.; formal analysis: J. C. F.; funding acquisition: C. W. C.; investigation: J. C. F., D. E. G., C. W. C.; methodology: J. C. F., D. E. G., C. W. C.; project administration: C. W. C.; resources: C. W. C.; software: J. C. F., D. E. G.; supervision: C. W. C.; validation: J. C. F.; visualization: J. C. F.; writing (original draft): J. C. F., C. W. C.; writing (review & editing): J. C. F., D. E. G., C. W. C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the DARPA Accelerated Molecular Discovery program under contract number HR00111920025. J. C. F. received additional support from the National Science Foundation Graduate Research Fellowship under Grant No. 2141064. The authors acknowledge the MIT SuperCloud,123 Lincoln Laboratory Supercomputing Center, and the MIT Engaging Cluster for providing HPC resources that have contributed to the research results reported within this paper. The authors thank Samuel Goldman for helpful discussions about the content of this manuscript.References
- J. Hughes, S. Rees, S. Kalindjian and K. Philpott, Principles of Early Drug Discovery, Br. J. Pharmacol., 2011, 162, 1239–1249 CrossRef CAS PubMed.
- J. G. Kettle and D. M. Wilson, Standing on the Shoulders of Giants: A Retrospective Analysis of Kinase Drug Discovery at Astrazeneca, Drug Discovery Today, 2016, 21, 1596–1608 CrossRef CAS PubMed.
- M. Beckers, N. Fechner and N. Stiefl, 25 Years of Small-Molecule Optimization at Novartis: A Retrospective Analysis of Chemical Series Evolution, J. Chem. Inf. Model., 2022, 62, 6002–6021 CrossRef CAS PubMed.
- G. M. Keserű and G. M. Makara, Hit Discovery and Hit-to-Lead Approaches, Drug Discovery Today, 2006, 11, 741–748 CrossRef PubMed.
- D. Sun, W. Gao, H. Hu and S. Zhou, Why 90% of Clinical Drug Development Fails and How to Improve It?, Acta Pharm. Sin. B, 2022, 12, 3049–3062 CrossRef CAS PubMed.
- M. D. Segall and C. Barber, Addressing Toxicity Risk When Designing and Selecting Compounds in Early Drug Discovery, Drug Discovery Today, 2014, 19, 688–693 CrossRef CAS PubMed.
- T. R. Van Vleet, M. J. Liguori, I. Lynch, J. James, M. Rao and S. Warder, Screening Strategies and Methods for Better Off-Target Liability Prediction and Identification of Small-Molecule Pharmaceuticals, SLAS Discovery, 2019, 24, 1–24 CrossRef CAS PubMed.
- K. H. Bleicher, H.-J. Böhm, K. Müller and A. I. Alanine, Hit and Lead Generation: Beyond High-Throughput Screening, Nat. Rev. Drug Discovery, 2003, 2, 369–378 CrossRef CAS PubMed.
- M. Recanatini, G. Bottegoni and A. Cavalli, Silico Antitarget Screening, Drug Discovery Today: Technol., 2004, 1, 209–215 CrossRef CAS PubMed.
- A. Macchiarulo, I. Nobeli and J. M. Thornton, Ligand Selectivity and Competition Between Enzymes in Silico, Nat. Biotechnol., 2004, 22, 1039–1045 CrossRef CAS PubMed.
- N. M. Raghavendra, D. Pingili, S. Kadasi, A. Mettu and S. V. U. M. Prasad, Dual or Multi-Targeting Inhibitors: The Next Generation Anticancer Agents, Eur. J. Med. Chem., 2018, 143, 1277–1300 CrossRef CAS PubMed.
- M. M. Ibrahim and M. T. Gabr, Multitarget Therapeutic Strategies for Alzheimer's Disease, Neural Regener. Res., 2019, 14, 437–440 CrossRef CAS PubMed.
- O. Benek, J. Korabecny and O. Soukup, A Perspective on Multi-target Drugs for Alzheimer's Disease, Trends Pharmacol. Sci., 2020, 41, 434–445 CrossRef CAS PubMed.
- M. Brassard and G. Rondeau, Role of Vandetanib in the Management of Medullary Thyroid Cancer, Biol.: Targets Ther., 2012, 6, 59–66 CAS.
- K. Okamoto, M. Ikemori-Kawada, A. Jestel, K. von König, Y. Funahashi, T. Matsushima, A. Tsuruoka, A. Inoue and J. Matsui, Distinct Binding Mode of Multikinase Inhibitor Lenvatinib Revealed by Biochemical Characterization, ACS Med. Chem. Lett., 2015, 6, 89–94 CrossRef CAS PubMed.
- X. H. Ma, Z. Shi, C. Tan, Y. Jiang, M. L. Go, B. C. Low and Y. Z. Chen, In-Silico Approaches to Multi-target Drug Discovery, Pharm. Res., 2010, 27, 739–749 CrossRef CAS PubMed.
- Z. Yousuf, K. Iman, N. Iftikhar and M. U. Mirza, Structure-Based Virtual Screening and Molecular Docking for the Identification of Potential Multi-Targeted Inhibitors Against Breast Cancer, Breast Cancer: Targets Ther., 2017, 9, 447–459 CAS.
- V. Chahal and R. Kakkar, A Combination Strategy of Structure-Based Virtual Screening, MM-GBSA, Cross Docking, Molecular Dynamics and Metadynamics Simulations Used to Investigate Natural Compounds as Potent and Specific Inhibitors of Tumor Linked Human Carbonic Anhydrase Ix, J. Biomol. Struct. Dyn., 2023, 41, 5465–5480 CrossRef CAS PubMed.
- S. Schieferdecker and E. Vock, Development of Pharmacophore Models for the Important Off-Target 5-HT2B Receptor, J. Med. Chem., 2023, 66, 1509–1521 CrossRef CAS PubMed.
- P. Matricon, A. T. Nguyen, D. D. Vo, J.-A. Baltos, M. Jaiteh, A. Luttens, S. Kampen, A. Christopoulos, J. Kihlberg, L. T. May and J. Carlsson, Structure-Based Virtual Screening Discovers Potent and Selective Adenosine A1 Receptor Antagonists, Eur. J. Med. Chem., 2023, 257, 115419 CrossRef CAS PubMed.
- D. R. Weiss, J. Karpiak, X.-P. Huang, M. F. Sassano, J. Lyu, B. L. Roth and B. K. Shoichet, Selectivity Challenges in Docking Screens for GPCR Targets and Antitargets, J. Med. Chem., 2018, 61, 6830–6845 CrossRef CAS PubMed.
- H. Chen, P. D. Lyne, F. Giordanetto, T. Lovell and J. Li, On Evaluating Molecular-Docking Methods for Pose Prediction and Enrichment Factors, J. Chem. Inf. Model., 2006, 46, 401–415 CrossRef CAS PubMed.
- A. N. Jain, Bias, Reporting, and Sharing: Computational Evaluations of Docking Methods, J. Comput.-Aided Mol. Des., 2008, 22, 201–212 CrossRef CAS PubMed.
- J. B. Cross, D. C. Thompson, B. K. Rai, J. C. Baber, K. Y. Fan, Y. Hu and C. Humblet, Comparison of Several Molecular Docking Programs: Pose Prediction and Virtual Screening Accuracy, J. Chem. Inf. Model., 2009, 49, 1455–1474 CrossRef CAS PubMed.
- J. J. Irwin and B. K. Shoichet, Docking Screens for Novel Ligands Conferring New Biology, J. Med. Chem., 2016, 59, 4103–4120 CrossRef CAS PubMed.
- E. D. Boittier, Y. Y. Tang, M. E. Buckley, Z. P. Schuurs, D. J. Richard and N. S. Gandhi, Assessing Molecular Docking Tools to Guide Targeted Drug Discovery of CD38 Inhibitors, Int. J. Mol. Sci., 2020, 21, 5183 CrossRef CAS PubMed.
- F. Stanzione, I. Giangreco and J. C. Cole, Progress in Medicinal Chemistry, ed. D. R. Witty and B. Cox, Elsevier, 2021, vol. 60, pp. 273–343 Search PubMed.
- L. E. Ling and et al., Transforming Growth Factor-β in Cancer Therapy, Volume II: Cancer Treatment and Therapy, ed. S. B. Jakowlew, Cancer Drug Discovery and Development, Humana Press, Totowa, NJ, 2008, pp. 685–696 Search PubMed.
- D. Bajusz, G. G. Ferenczy and G. M. Keserű, Discovery of Subtype Selective Janus Kinase (JAK) Inhibitors by Structure-Based Virtual Screening, J. Chem. Inf. Model., 2016, 56, 234–247 CrossRef CAS PubMed.
- J. Lyu, S. Wang, T. E. Balius, I. Singh, A. Levit, Y. S. Moroz, M. J. O'Meara, T. Che, E. Algaa, K. Tolmachova, A. A. Tolmachev, B. K. Shoichet, B. L. Roth and J. J. Irwin, Ultra-Large Library Docking for Discovering New Chemotypes, Nature, 2019, 566, 224–229 CrossRef CAS PubMed.
- F. Gentile, M. Fernandez, F. Ban, A.-T. Ton, H. Mslati, C. F. Perez, E. Leblanc, J. C. Yaacoub, J. Gleave, A. Stern, B. Wong, F. Jean, N. Strynadka and A. Cherkasov, Automated Discovery of Noncovalent Inhibitors of Sars-Cov-2 Main Protease by Consensus Deep Docking of 40 Billion Small Molecules, Chem. Sci., 2021, 12, 15960–15974 RSC.
- A. Alon, et al., Structures of the σ2 Receptor Enable Docking for Bioactive Ligand Discovery, Nature, 2021, 600, 759–764 CrossRef CAS PubMed.
- B. I. Tingle and J. J. Irwin, Large-Scale Docking in the Cloud, J. Chem. Inf. Model., 2023, 63, 2735–2741 CrossRef CAS PubMed.
- R. Garnett, T. Gärtner, M. Vogt and J. Bajorath, Introducing the ‘Active Search’ Method for Iterative Virtual Screening, J. Comput.-Aided Mol. Des., 2015, 29, 305–314 CrossRef CAS PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less Is More: Sampling Chemical Space with Active Learning, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- F. Gentile, V. Agrawal, M. Hsing, A.-T. Ton, F. Ban, U. Norinder, M. E. Gleave and A. Cherkasov, Deep Docking: A Deep Learning Platform for Augmentation of Structure Based Drug Discovery, ACS Cent. Sci., 2020, 6, 939–949 CrossRef CAS PubMed.
- D. E. Graff, E. I. Shakhnovich and C. W. Coley, Accelerating High-Throughput Virtual Screening Through Molecular Pool-Based Active Learning, Chem. Sci., 2021, 12, 7866–7881 RSC.
- Y. Yang, K. Yao, M. P. Repasky, K. Leswing, R. Abel, B. K. Shoichet and S. V. Jerome, Efficient Exploration of Chemical Space with Docking and Deep Learning, J. Chem. Theory Comput., 2021, 17, 7106–7119 CrossRef CAS PubMed.
- S. Mehta, S. Laghuvarapu, Y. Pathak, A. Sethi, M. Alvala and U. D. Priyakumar, MEMES: Machine Learning Framework for Enhanced Molecular Screening, Chem. Sci., 2021, 12, 11710–11721 RSC.
- D. E. Graff, M. Aldeghi, J. A. Morrone, K. E. Jordan, E. O. Pyzer-Knapp and C. W. Coley, Self-Focusing Virtual Screening with Active Design Space Pruning, J. Chem. Inf. Model., 2022, 62, 3854–3862 CrossRef CAS PubMed.
- J. Thompson, W. P. Walters, J. A. Feng, N. A. Pabon, H. Xu, M. Maser, B. B. Goldman, D. Moustakas, M. Schmidt and F. York, Optimizing Active Learning for Free Energy Calculations, Artif. Intell. Life Sci., 2022, 2, 100050 Search PubMed.
- S. Mehta, M. Goel and U. D. Priyakumar, MO-MEMES: A Method for Accelerating Virtual Screening Using Multi-Objective Bayesian Optimization, Front. Med., 2022, 9 DOI:10.3389/fmed.2022.916481.
- S. A. Wildman and G. M. Crippen, Prediction of Physicochemical Parameters by Atomic Contributions, J. Chem. Inf. Comput. Sci., 1999, 39, 868–873 CrossRef CAS.
- P. Ertl and A. Schuffenhauer, Estimation of Synthetic Accessibility Score of Drug-like Molecules Based on Molecular Complexity and Fragment Contributions, J. Cheminf., 2009, 1, 8 Search PubMed.
- Enamine Screening Collections, https://enamine.net/compound-collections/screening-collection, downloaded May 2023.
- J. C. Fromer and C. W. Coley, Computer-Aided Multi-Objective Optimization in Small Molecule Discovery, Patterns, 2023, 4, 100678 CrossRef CAS PubMed.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, Accurate Multiobjective Design in a Space of Millions of Transition Metal Complexes with Neural-Network-Driven Efficient Global Optimization, ACS Cent. Sci., 2020, 6, 513–524 CrossRef CAS PubMed.
- G. Agarwal, H. A. Doan, L. A. Robertson, L. Zhang and R. S. Assary, Discovery of Energy Storage Molecular Materials Using Quantum Chemistry-Guided Multiobjective Bayesian Optimization, Chem. Mater., 2021, 33, 8133–8144 CrossRef CAS.
- R. Jalem, Y. Tateyama, K. Takada and S.-H. Jang, Multiobjective Solid Electrolyte Design of Tetragonal and Cubic Inverse-Perovskites for All-Solid-State Lithium-Ion Batteries by High-Throughput Density Functional Theory Calculations and AI-Driven Methods, J. Phys. Chem. C, 2023, 127, 17307–17323 CrossRef CAS.
- A. M. Gopakumar, P. V. Balachandran, D. Xue, J. E. Gubernatis and T. Lookman, Multi-objective Optimization for Materials Discovery via Adaptive Design, Sci. Rep., 2018, 8, 3738 CrossRef PubMed.
- Z. del Rosario, M. Rupp, Y. Kim, E. Antono and J. Ling, Assessing the Frontier: Active Learning, Model Accuracy, and Multi-Objective Candidate Discovery and Optimization, J. Chem. Phys., 2020, 153, 024112 CrossRef PubMed.
- Y. Murakami, S. Ishida, Y. Demizu and K. Terayama, Design of Antimicrobial Peptides Containing Non-Proteinogenic Amino Acids Using Multi-Objective Bayesian Optimisation, Digital Discovery, 2023, 2, 1347–1353 RSC.
- A. J. S. Keane, Improvement Criteria for Use in Multiobjective Design Optimization, AIAA J., 2006, 44, 879–891 CrossRef.
- B. Paria, K. Kandasamy and B. Póczos, A Flexible Framework for Multi-Objective Bayesian Optimization using Random Scalarizations, Proceedings of The 35th Uncertainty in Artificial Intelligence Conference. 2020, pp. 766–776 Search PubMed.
- R. Zhang and D. Golovin, Random Hypervolume Scalarizations for Provable Multi-Objective Black Box Optimization, Proceedings of the 37th International Conference on Machine Learning, 2020, pp. 11096–11105 Search PubMed.
- R. E. Steuer and E.-U. Choo, An Interactive Weighted Tchebycheff Procedure for Multiple Objective Programming, Math. Program., 1983, 26, 326–344 CrossRef.
- I. Giagkiozis and P. J. Fleming, Methods for Multi-Objective Optimization: An Analysis, Inf. Sci., 2015, 293, 338–350 CrossRef.
- H. J. A. Kushner, New Method of Locating the Maximum Point of an Arbitrary Multipeak Curve in the Presence of Noise, J. Basic Eng., 1964, 86, 97–106 CrossRef.
- J. Močkus, On Bayesian Methods for Seeking the Extremum. Optimization Techniques IFIP Technical Conference Novosibirsk, July 1-7, 1974, Berlin, Heidelberg, 1975, pp. 400–404 Search PubMed.
- N. Srinivas, A. Krause, S. M. Kakade and M. W. Seeger, Information-Theoretic Regret Bounds for Gaussian Process Optimization in the Bandit Setting, IEEE Trans. Inf. Theory, 2012, 58, 3250–3265 Search PubMed.
- J. G. Lin, Directions in Large-Scale Systems: Many-Person Optimization and Decentralized Control, ed. Y. C. Ho and S. K. Mitter, Springer US, Boston, MA, 1976, pp. 117–138 Search PubMed.
- Y. Hu, R. Xian, Q. Wu, Q. Fan, L. Yin and H. Zhao, Revisiting Scalarization in Multi-Task Learning: A Theoretical Perspective, 2023, http://arxiv.org/abs/2308.13985 Search PubMed.
- N. Srinivas and K. Deb, Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms, Evol Comput., 1994, 2, 221–248 CrossRef.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef.
- M. M. Drugan and A. Nowe, Designing Multi-Objective Multi-Armed Bandits Algorithms: A Study. The 2013 International Joint Conference on Neural Networks, IJCNN, 2013, pp. 1–8 Search PubMed.
- T. Gong, T. Lee, C. Stephenson, V. Renduchintala, S. Padhy, A. Ndirango, G. Keskin and O. H. Elibol, A Comparison of Loss Weighting Strategies for Multi task Learning in Deep Neural Networks, IEEE Access, 2019, 7, 141627–141632 Search PubMed.
- H. Bellamy, A. A. Rehim, O. I. Orhobor and R. King, Batched Bayesian Optimization for Drug Design in Noisy Environments, J. Chem. Inf. Model., 2022, 62, 3970–3981 CrossRef CAS PubMed.
- D. Ginsbourger, R. Le Riche and L. Carraro, Computational Intelligence in Expensive Optimization Problems, ed. Y. Tenne and C.-K. Goh, Adaptation Learning and Optimization, Springer, Berlin, Heidelberg, 2010, pp. 131–162 Search PubMed.
- J. Snoek, H. Larochelle and R. P. Adams, Practical Bayesian Optimization of Machine Learning Algorithms, Advances in Neural Information Processing Systems, 2012 Search PubMed.
- J. Janusevskis, R. Le Riche, D. Ginsbourger and R. Girdziusas, Expected Improvements for the Asynchronous Parallel Global Optimization of Expensive Functions: Potentials and Challenges. Learning and Intelligent Optimization, Berlin, Heidelberg, 2012, pp. 413–418 Search PubMed.
- C. Chevalier and D. Ginsbourger, Fast Computation of the Multi-Points Expected Improvement with Applications in Batch Selection, Learning and Intelligent Optimization, Berlin, Heidelberg, 2013, pp. 59–69 Search PubMed.
- S. Jiang, G. Malkomes, G. Converse, A. Shofner, B. Moseley and R. Garnett, Efficient Nonmyopic Active Search, Proceedings of the 34th International Conference on Machine Learning, 2017, pp. 1714–1723 Search PubMed.
- A. Tran, J. Sun, J. M. Furlan, K. V. Pagalthivarthi, R. J. Visintainer and Y. Wang, pBO-2GP-3B: A Batch Parallel Known/Unknown Constrained Bayesian Optimization with Feasibility Classification and Its Applications in Computational Fluid Dynamics, Comput. Methods Appl. Mech. Eng., 2019, 347, 827–852 CrossRef.
- J. Azimi, A. Fern and X. Fern, Batch Bayesian Optimization via Simulation Matching, Advances in Neural Information Processing Systems, 2010 Search PubMed.
- J. Gonzalez, Z. Dai, P. Hennig and N. Lawrence, Batch Bayesian Optimization via Local Penalization, Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, 2016, pp. 648–657 Search PubMed.
- M. Konakovic Lukovic, Y. Tian and W. Matusik, Diversity-Guided Multi-Objective Bayesian Optimization With Batch Evaluations, Adv. Neural Inf. Process., 2020, 17708–17720 Search PubMed.
- G. Citovsky, G. DeSalvo, C. Gentile, L. Karydas, A. Rajagopalan, A. Rostamizadeh and S. Kumar, Batch Active Learning at Scale, Adv. Neural Inf. Process., 2021, 11933–11944 Search PubMed.
- N. Maus, K. Wu, D. Eriksson and J. Gardner, Discovering Many Diverse Solutions with Bayesian Optimization, Proceedings of the 26th International Conference on Artificial Intelligence and Statistics, AISTATS, Valencia, Spain, 2023 Search PubMed.
- L. D. González and V. M. Zavala, New Paradigms for Exploiting Parallel Experiments in Bayesian Optimization, Comput. Chem. Eng., 2023, 170, 108110 CrossRef.
- S.-Y. Huang and X. Zou, Ensemble Docking of Multiple Protein Structures: Considering Protein Structural Variations in Molecular Docking, Proteins: Struct., Funct., Bioinf., 2007, 66, 399–421 CrossRef CAS PubMed.
- H. Li, H. Zhang, M. Zheng, J. Luo, L. Kang, X. Liu, X. Wang and H. Jiang, An effective docking strategy for virtual screening based on multi-objective optimization algorithm, BMC Bioinf., 2009, 10, 58 CrossRef PubMed.
- D. R. Houston and M. D. Walkinshaw, Consensus Docking: Improving the Reliability of Docking in a Virtual Screening Context, J. Chem. Inf. Model., 2013, 53, 384–390 CrossRef CAS PubMed.
- J. Gu, X. Yang, L. Kang, J. Wu and X. Wang, Modock: A Multi-Objective Strategy Improves the Accuracy for Molecular Docking, Algorithms Mol. Biol., 2015, 10, 8 CrossRef PubMed.
- M. García-Ortegón, G. N. C. Simm, A. J. Tripp, J. M. Hernández-Lobato, A. Bender and S. Bacallado, DOCKSTRING: Easy Molecular Docking Yields Better Benchmarks for Ligand Design, J. Chem. Inf. Model., 2022, 62, 3486–3502 CrossRef PubMed.
- D. J. Watson, F. Loiseau, M. Ingallinesi, M. J. Millan, C. A. Marsden and K. C. Fone, Selective Blockade of Dopamine D3 Receptors Enhances while D2 Receptor Antagonism Impairs Social Novelty Discrimination and Novel Object Recognition in Rats: A Key Role for the Prefrontal Cortex, Neuropsychopharmacology, 2012, 37, 770–786 CrossRef CAS PubMed.
- S. E. Williford, C. J. Libby, A. Ayokanmbi, A. Otamias, J. J. Gordillo, E. R. Gordon, S. J. Cooper, M. Redmann, Y. Li, C. Griguer, J. Zhang, M. Napierala, S. Ananthan and A. B. Hjelmeland, Novel Dopamine Receptor 3 Antagonists Inhibit the Growth of Primary and Temozolomide Resistant Glioblastoma Cells, PLoS ONE, 2021, 16, e0250649 CrossRef CAS PubMed.
- A. Bonifazi, E. Saab, J. Sanchez, A. L. Nazarova, S. A. Zaidi, K. Jahan, V. Katritch, M. Canals, J. R. Lane and A. H. Newman, Pharmacological and Physicochemical Properties Optimization for Dual-Target Dopamine D3 (D3R) and μ-Opioid (MOR) Receptor Ligands as Potentially Safer Analgesics, J. Med. Chem., 2023, 66(15), 10304–10341 CrossRef CAS PubMed.
- J. S. Fridman, et al., Selective Inhibition of JAK1 and JAK2 Is Efficacious in Rodent Models of Arthritis: Preclinical Characterization of INCB028050, J. Immunol., 2010, 184, 5298–5307 CrossRef CAS PubMed.
- Q. Liu, D. G. Batt, J. S. Lippy, N. Surti, A. J. Tebben, J. K. Muckelbauer, L. Chen, Y. An, C. Chang, M. Pokross, Z. Yang, H. Wang, J. R. Burke, P. H. Carter and J. A. Tino, Design and Synthesis of Carbazole Carboxamides as Promising Inhibitors of Bruton's Tyrosine Kinase (BTK) and Janus Kinase 2 (JAK2), Bioorg. Med. Chem. Lett., 2015, 25, 4265–4269 CrossRef CAS PubMed.
- R. Li, A. Pourpak and S. W. Morris, Inhibition of the Insulin-like Growth Factor-1 Receptor (IGF1R) Tyrosine Kinase as a Novel Cancer Therapy Approach, J. Med. Chem., 2009, 52, 4981–5004 CrossRef CAS PubMed.
- M. K. Pasha, I. Jabeen and S. Samarasinghe, 3D QSAR and Pharmacophore Studies on Inhibitors of Insuline Like Growth Factor 1 Receptor (IGF-1R) and Insulin Receptor (IR) as Potential Anti-Cancer Agents, Curr. Res. Chem. Biol., 2022, 2, 100019 CrossRef CAS.
- U. Velaparthi, P. Liu, B. Balasubramanian, J. Carboni, R. Attar, M. Gottardis, A. Li, A. Greer, M. Zoeckler, M. D. Wittman and D. Vyas, Imidazole Moiety Replacements in the 3-(1H-Benzo[d]imidazol-2-Yl)pyridin-2(1H)-One Inhibitors of Insulin-Like Growth Factor Receptor-1 (IGF-1R) to Improve Cytochrome P450 Profile, Bioorg. Med. Chem. Lett., 2007, 17, 3072–3076 CrossRef CAS PubMed.
- K. Zimmermann, et al., Balancing Oral Exposure with CYP3A4 Inhibition in Benzimidazole-Based IGF-IR Inhibitors, Bioorg. Med. Chem. Lett., 2008, 18, 4075–4080 CrossRef CAS PubMed.
- J. H. Lin and A. Y. H. Lu, Inhibition and Induction of Cytochrome P450 and the Clinical Implications, Clin. Pharmacokinet., 1998, 35, 361–390 CrossRef CAS PubMed.
- T. Lynch and A. Price, The Effect of Cytochrome P450 Metabolism on Drug Response, Interactions, and Adverse Effects, Am. Fam. Physician, 2007, 76, 391–396 Search PubMed.
- F. Cheng, Y. Yu, Y. Zhou, Z. Shen, W. Xiao, G. Liu, W. Li, P. W. Lee and Y. Tang, Insights into Molecular Basis of Cytochrome P450 Inhibitory Promiscuity of Compounds, J. Chem. Inf. Model., 2011, 51, 2482–2495 CrossRef CAS PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, Analyzing Learned Molecular Representations for Property Prediction, J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS PubMed.
- E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green and C. J. McGill, Chemprop: A Machine Learning Package for Chemical Property Prediction, 2023, https://chemrxiv.org/engage/chemrxiv/article-details/64d1f13d4a3f7d0c0dcd836b Search PubMed.
- B. J. Bender, S. Gahbauer, A. Luttens, J. Lyu, C. M. Webb, R. M. Stein, E. A. Fink, T. E. Balius, J. Carlsson, J. J. Irwin and B. K. Shoichet, A Practical Guide to Large-Scale Docking, Nat. Protoc., 2021, 16, 4799–4832 CrossRef CAS PubMed.
- G. W. Bemis and M. A. Murcko, The Properties of Known Drugs. 1. Molecular Frameworks, J. Med. Chem., 1996, 39, 2887–2893 CrossRef CAS PubMed.
- L. McInnes, J. Healy, N. Saul and L. Großberger, UMAP: Uniform Manifold Approximation and Projection (version 0.5.4), J. Open Source Softw., 2018, 3, 861 CrossRef.
- R. Tandon, et al., RBx10080307, a Dual EGFR/IGF-1R Inhibitor for Anticancer Therapy, Eur. J. Pharmacol., 2013, 711, 19–26 CrossRef CAS PubMed.
- L. Hu, M. Fan, S. Shi, X. Song, F. Wang, H. He and B. Qi, Dual Target Inhibitors Based on EGFR: Promising Anticancer Agents for the Treatment of Cancers (2017-), Eur. J. Med. Chem., 2022, 227, 113963 CrossRef CAS PubMed.
- J. Kang, Z. Guo, H. Zhang, R. Guo, X. Zhu and X. Guo, Dual Inhibition of EGFR and IGF-1R Signaling Leads to Enhanced Antitumor Efficacy against Esophageal Squamous Cancer, Int. J. Mol. Sci., 2022, 23, 10382 CrossRef CAS PubMed.
- M. A. S. Abourehab, A. M. Alqahtani, B. G. M. Youssif and A. M. Gouda, Globally Approved EGFR Inhibitors: Insights into Their Syntheses, Target Kinases, Biological Activities, Receptor Interactions, and Metabolism, Molecules, 2021, 26, 6677 CrossRef CAS PubMed.
- Y. Pan, N. Huang, S. Cho and A. D. MacKerell, Consideration of molecular weight during compound selection in virtual target-based database screening, J. Chem. Inf. Comput. Sci., 2003, 43, 267–272 CrossRef CAS PubMed.
- A. Kirsch, J. van Amersfoort and Y. Gal, BatchBALD: Efficient and Diverse Batch Acquisition for Deep Bayesian Active Learning, Advances in Neural Information Processing Systems, 2019 Search PubMed.
- D. J. Huggins, W. Sherman and B. Tidor, Rational Approaches to Improving Selectivity in Drug Design, J. Med. Chem., 2012, 55, 1424–1444 CrossRef CAS PubMed.
- T. Klabunde and A. Evers, GPCR Antitarget Modeling: Pharmacophore Models for Biogenic Amine Binding GPCRs to Avoid GPCR-Mediated Side Effects, ChemBioChem, 2005, 6, 876–889 CrossRef CAS PubMed.
- RDKit, Open-Source Cheminformatics Software(version 2021.03.3), http://www.rdkit.org/ Search PubMed.
- Y. Motoyama, R. Tamura, K. Yoshimi, K. Terayama, T. Ueno and K. Tsuda, Bayesian Optimization Package: PHYSBO, Comput. Phys. Commun., 2022, 278, 108405 CrossRef CAS.
- I. Couckuyt, D. Deschrijver and T. Dhaene, Fast Calculation of Multiobjective Probability of Improvement and Expected Improvement Criteria for Pareto Optimization, J. Global Optim., 2014, 60, 575–594 CrossRef.
- F. Biscani and D. Izzo, A Parallel Global Multiobjective Framework for Optimization: Pagmo (version 2.19.5), J. Open Source Softw., 2020, 5, 2338 CrossRef.
- A. Paszke and et al., PyTorch: An Imperative Style, High-Performance Deep Learning Library (version 1.13.1), Advances in Neural Information Processing Systems, 2019 Search PubMed.
- D. Nix and A. Weigend, Estimating the Mean and Variance of the Target Probability Distribution, Proceedings of 1994 IEEE International Conference on Neural Networks, (ICNN'94), 1994, vol. 1, pp. 55–60 Search PubMed.
- L. Hirschfeld, K. Swanson, K. Yang, R. Barzilay and C. W. Coley, Uncertainty Quantification Using Neural Networks for Molecular Property Prediction, J. Chem. Inf. Model., 2020, 60, 3770–3780 CrossRef CAS PubMed.
- R. E. Carhart, D. H. Smith and R. Venkataraghavan, Atom Pairs as Molecular Features in Structure-Activity Studies: Definition and Applications, J. Chem. Inf. Comput. Sci., 1985, 25, 64–73 CrossRef CAS.
- M. Awale and J.-L. Reymond, Atom Pair 2D-Fingerprints Perceive 3D-Molecular Shape and Pharmacophores for Very Fast Virtual Screening of ZINC and GDB-17, J. Chem. Inf. Model., 2014, 54, 1892–1907 CrossRef CAS PubMed.
- N. M. O'Boyle and R. A. Sayle, Comparing structural fingerprints using a literature-based similarity benchmark, J. Cheminf., 2016, 8, 36 Search PubMed.
- D. Sculley, Web-Scale k-Means Clustering, Proceedings of the 19th international conference on World wide web, Raleigh North Carolina USA, 2010, pp. 1177–1178 Search PubMed.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python (version 1.3.2), J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- R. Tanabe and H. Ishibuchi, An Analysis of Quality Indicators Using Approximated Optimal Distributions in a 3-D Objective Space, IEEE Trans. Evol. Comput., 2020, 24, 853–867 Search PubMed.
- A. Reuther and et al., Interactive Supercomputing on 40,000 Cores for Machine Learning and Data Analysis, 2018 IEEE High Performance extreme Computing Conference (HPEC), 2018, pp. 1–6 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00227f |
| This journal is © The Royal Society of Chemistry 2024 |