Open Access Article
Open Access ArticleAn equivariant graph neural network for the elasticity tensors of all seven crystal systems†
Mingjian
Wen
 *a,
Matthew K.
Horton
*a,
Matthew K.
Horton
 bc,
Jason M.
Munro
b,
Patrick
Huck
bc,
Jason M.
Munro
b,
Patrick
Huck
 d and
Kristin A.
Persson
d and
Kristin A.
Persson
 ef
ef
aChemical and Biomolecular Engineering, University of Houston, Houston, 77204, TX, USA. E-mail: mjwen@uh.edu
bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, 94720, CA, USA
cMicrosoft Research, Redmond, 98052, WA, USA
dEnergy Technologies Area, Lawrence Berkeley National Laboratory, Berkeley, 94720, CA, USA
eMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, 94720, CA, USA
fDepartment of Materials Science and Engineering, University of California, Berkeley, Berkeley, 94720, CA, USA
First published on 5th February 2024
Abstract
The elasticity tensor is a fundamental material property that describes the elastic response of a material to external force. The availability of full elasticity tensors for inorganic crystalline compounds, however, is limited due to experimental and computational challenges. Here, we report the materials tensor (MatTen) model for rapid and accurate prediction of the full fourth-rank elasticity tensors of crystals. Based on equivariant graph neural networks, MatTen satisfies two essential requirements for elasticity tensors: independence of the frame of reference and preservation of material symmetry. Consequently, it provides a unified treatment of elasticity tensors for all seven crystal systems across diverse chemical spaces, without the need to deal with each separately. MatTen was trained on a dataset of first-principles elasticity tensors garnered by the Materials Project over the past several years (we are releasing the data herein) and has broad applications in predicting the isotropic elastic properties of polycrystalline materials, examining the anisotropic behavior of single crystals, and discovering materials with exceptional mechanical properties. Using MatTen, we have found a hundred crystals with extremely large maximum directional Young's modulus and eleven polymorphs of elemental cubic metals with unconventional spatial orientation of Young's modulus.
1 Introduction
All materials exhibit elastic behavior under small external loads and return to their original shape upon the release of these loads.1 The elasticity tensor provides a fundamental and complete description of a material's response to such loads. It offers a lens to examine the inherent strength of the bonding in a material and enables the understanding, analyzing, and designing of many macroscopic physical properties of materials. Commonly employed mechanical properties (for instance, Young's modulus and Poisson's ratio), thermal properties (for instance, thermal conductivity) and acoustic properties (for instance, sound velocity) can be mathematically derived from the elasticity tensor. These properties have long been leveraged, for example, by materials scientists to search for ultrahard materials2,3 and by geophysicists to interpret seismic data.4,5 More recently, the anisotropic elastic behavior of inorganic solid electrolytes has been found to play a decisive role in determining the stability of electrodeposition at the interfaces in solid-state batteries.6,7 Moreover, in solid-state synthesis, one would want to utilize the elasticity tensor to determine the local stability of a material, so as to avoid unsuccessful synthesis of materials that spontaneously transform into different structures.8,9In spite of the importance, elasticity tensor data from experimental measurement is limited to a small number of materials. For example, for inorganic crystalline compounds, experimental data is only on the order of a few hundred, considering entries both tabulated in handbooks and scattered in individual papers.10 The major difficulty lies in preparing large enough single crystals for accurate experimental measurement using current techniques such as resonant acoustic spectroscopy.11 In the past decade, efficient and reliable electronic structure calculation methods such as density functional theory (DFT)12 with automation frameworks13–15 have enabled high-throughput computational investigation of materials. Using this approach in the Materials Project,16 we produced an initial dataset of elasticity tensors for 1181 crystals in 2015,10 which has been expanded over time to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276, which we now release as a new dataset with this work. Nevertheless, this only accounts for 6.6% of the more than 154
276, which we now release as a new dataset with this work. Nevertheless, this only accounts for 6.6% of the more than 154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystals in the Materials Project, let alone the even greater number of crystals recorded in the Inorganic Crystal Structure Database (ICSD)17 and predicted by universal interatomic potentials.18
000 crystals in the Materials Project, let alone the even greater number of crystals recorded in the Inorganic Crystal Structure Database (ICSD)17 and predicted by universal interatomic potentials.18
It is therefore no surprise that machine learning (ML) has gathered substantial interest as a means to develop efficient surrogate models for the prediction of elastic properties. In a nutshell, state-of-the-art ML models for elastic properties encode compositional information19–21 and/or structural information20–23 in a material as feature vectors and then map them to a target using some regression algorithms. This approach is adopted in many existing works for learning elastic properties (e.g., for alloys24–27 and polycrystals28,29) and related atomic properties like stress and energy fields.30 They are, however, limited to derived scalar elastic properties such as bulk modulus and shear modulus, and separate models are built for each derived property. Ideally, one would hope to predict the full elasticity tensor, from which all other elastic properties can be derived. Along this direction, there have been attempts to predict individual tensor components.31,32 These models are great first steps, but essentially they still predict separate scalars in a specific coordinate system and thus unavoidably violate the transformation rules of tensors.
Geometric machine learning33 such as equivariant graph neural networks (GNNs)34–38 and equivariant kernel methods39,40 can directly operate in the space of high-rank tensors and adhere to their transformation rules. The main use case is still for scalar molecular and materials properties, but a couple of works have explored the application in predicting tensorial properties such as the molecular dipole moment,40,41 magnetic moment,42 and dielectric response.39 Other applications that do not directly predict final tensorial targets have also successfully taken advantage of internal tensorial representations to learn scalar fields such as molecular electron density.43,44 Although these efforts focus on scalars or low-rank tensors, they demonstrate the viability of direct machine learning of the full fourth-rank elasticity tensor.
In this work, we develop the Materials Tensor (MatTen) model for a rapid and accurate estimate of the fourth-rank elasticity tensors of inorganic compounds. Our model, based on equivariant GNNs, takes a crystal structure as input and outputs its full elasticity tensor with all symmetry-related transformation rules automatically satisfied. Other elastic properties such as bulk modulus and shear modulus can then be derived from the full elasticity tensor. The model satisfies two essential symmetry requirements for elasticity tensors: independence of the frame of reference, meaning that the choice of a specific coordinate system does not affect the model output, and preservation of material symmetry, meaning that the symmetry in a crystal is captured and reflected in the output elasticity tensor. The capabilities of MatTen are demonstrated via the study of both isotropic and anisotropic elastic properties. Using MatTen, we screened the Materials Project database for the identification of materials with a large maximum directional Young's modulus. On average, the values of the newly found materials are more than three times larger than existing data, as verified by first-principles calculations. In addition, we have identified 11 unconventional polymorphs of elemental cubic metals whose maximum directional Young's moduli are in the 〈100〉 directions.
2 Results and discussion
2.1 Symmetry and irreducible representation of the elasticity tensor
The elasticity tensor C is a fourth-rank tensor that fully characterizes the elastic behavior of a material. Given that it is the second derivative of the total elastic energy with respect to the strain tensor and that the strain tensor is symmetric,46,47 the elasticity tensor possesses major symmetry Cijkl = Cklij and minor symmetry Cijkl = Cjikl = Cijlk (in indicial notation, where i, j, k, l ∈ {1, 2, 3}). Consequently, only 21 of the 81 components of C are independent. It is convenient to write the elasticity tensor in a contracted matrix c (cαβ, where α, β ∈ {1, 2, …, 6}) with a pairs of indices ij in the tensor notation replaced with a single index α in the matrix notation: 11 → 1; 22 → 2; 33 → 3; 23, 32 → 4; 13, 31 → 5; and 12, 21 → 6. This Voigt matrix48 is a 6 × 6 matrix symmetric about the main diagonal, reflecting the fact that the elasticity tensor has 21 independent components.The intrinsic material symmetry of a crystal can further reduce the number of independent components.8,47 For example, copper is a cubic crystal with mirror planes and three-fold rotation axes (point group m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), and such symmetry results in a number of only three independent components. Formally, the material symmetry imposes the following constraints on the elasticity tensor:45,49
m), and such symmetry results in a number of only three independent components. Formally, the material symmetry imposes the following constraints on the elasticity tensor:45,49
| Cijkl = QipQjqQkrQlsCpqrs, | (1) |
It turns out that there exists only eight distinct classes (Fig. 1), proved via a purely algebraic approach by directly identifying the equivalence classes corresponding to eqn (1).49 Of the eight classes, one is for isotropic materials, and each of the other seven corresponds to a crystal system.45,50 In our opinion, there is still significant confusion on this topic. For example, the categorization by Wallace51 and populated by Nye,47 which incorrectly gives two unique classes for each of the tetragonal and trigonal cases (Fig. S1 in the ESI†), is still widely cited in recent works.52–54 We refer to Section 6.5 of ref. 45 for a historical note on the development of the categorization.
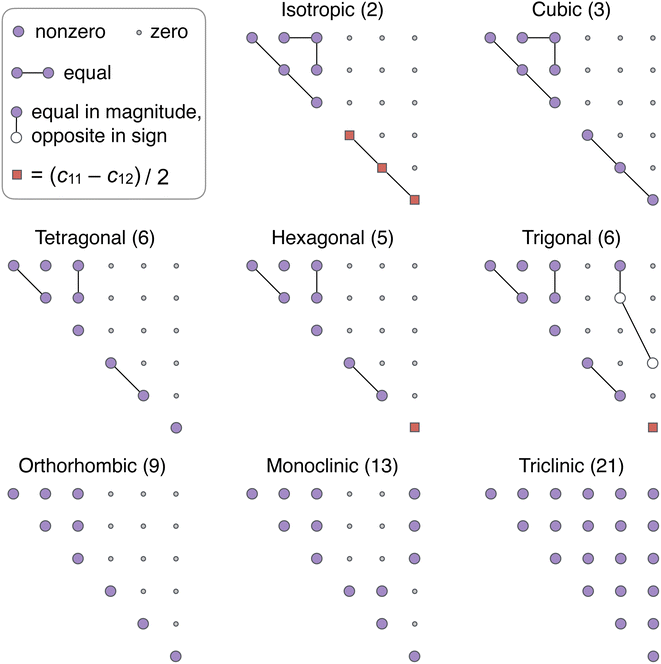 | ||
| Fig. 1 Symmetry classes and independent components of the elasticity tensor. The value in the parentheses after the name indicates the number of independent components. All matrices are symmetric about the main diagonal, with the lower triangular part omitted in the depiction. For single crystals considered in this work, the isotropic case does not apply. See ref. 45 for a detailed treatment of the classification. | ||
The Voigt matrix provides a visual way to observe the material symmetry of a crystal reflected in the elasticity tensor (Fig. 1). The values of the matrix components, however, depend on the choice of the coordinate system and do not show any systematic pattern upon coordinate transformation,55,56 making it difficult to build predictive models for elasticity tensors. This can be overcome by the harmonic decomposition,57 where the space of all elasticity tensors is factored into the direct sum of irreducible representations of SO(3). Consequently, any elasticity tensor can be written in the form,
| C = h1(λ) + h2(η) + h3(A) + h4(B) + h5(H), | (2) |
2.2 Equivariant graph neural networks for high-rank tensors
The MatTen model captures the structure–property relationship of crystalline materials. It takes a crystal structure as input, represents it as a three-dimensional crystal graph, performs feature updates on the crystal graph, and finally outputs a tensor property of the material built according to the reverse process of the harmonic decomposition in eqn (2).In the GNN model (Fig. 2), the input crystal is represented as a graph 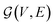 , with atoms as the nodes V and bonds as the edges E. The feature Fi ∈ V characterizes atom i, and the initial value of Fi is obtained by encoding the atomic number Zi using a one-hot scheme. A bond/edge between two atoms is created if the distance ‖
, with atoms as the nodes V and bonds as the edges E. The feature Fi ∈ V characterizes atom i, and the initial value of Fi is obtained by encoding the atomic number Zi using a one-hot scheme. A bond/edge between two atoms is created if the distance ‖![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0072_20d1.gif) ij‖ is smaller than a cutoff value, where
ij‖ is smaller than a cutoff value, where ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0072_20d1.gif) ij denotes the distance vector between atoms i and j. Periodic boundary conditions are considered when constructing the bonds, using super cell vectors. The distance vector
ij denotes the distance vector between atoms i and j. Periodic boundary conditions are considered when constructing the bonds, using super cell vectors. The distance vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0072_20d1.gif) ij is separated into two parts: the unit vector
ij is separated into two parts: the unit vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij from atom i to atom j and the scalar distance rij between them. The former is expanded on real spherical harmonics Yml, and the latter is expanded on the Bessel radial basis functions.58 In sum, these embedding modules extract structural information (coordinates of atoms, atomic numbers, and super cell vectors) from the crystal and provide them to the interaction blocks.
ij from atom i to atom j and the scalar distance rij between them. The former is expanded on real spherical harmonics Yml, and the latter is expanded on the Bessel radial basis functions.58 In sum, these embedding modules extract structural information (coordinates of atoms, atomic numbers, and super cell vectors) from the crystal and provide them to the interaction blocks.
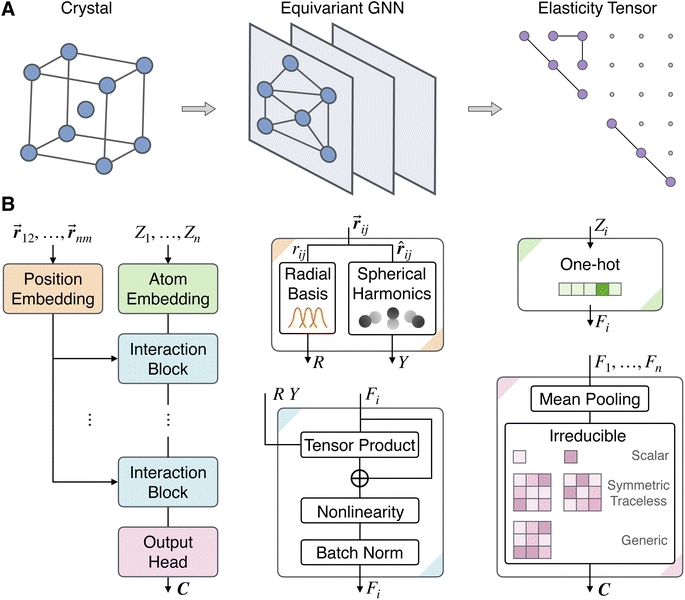 | ||
Fig. 2 Schematic overview of the MatTen graph neural network model. (A) The model takes a crystal structure as input, performs message passing with equivariant graph neural network (GNN) layers, and outputs the full elasticity tensor satisfying all symmetry requirements. (B) Architecture of the model. The model consists of four modules: the position embedding module converts an input displacement vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0072_20d1.gif) ij between atoms i and j to radial (R) and spherical (Y) expansions; the atom embedding module encodes the atomic number Zi as irreducible atom features Fi using a one-hot encoding; interaction blocks iteratively refine the features using convolutions based on tensor product; and the output head selects the appropriate irreducible features corresponding to the elasticity tensor and assembles them as the output tensor C. Following ref. 56, the fourth-rank harmonic part of the elasticity tensor is depicted as a generic matrix. The ⊕ symbol denotes addition. ij between atoms i and j to radial (R) and spherical (Y) expansions; the atom embedding module encodes the atomic number Zi as irreducible atom features Fi using a one-hot encoding; interaction blocks iteratively refine the features using convolutions based on tensor product; and the output head selects the appropriate irreducible features corresponding to the elasticity tensor and assembles them as the output tensor C. Following ref. 56, the fourth-rank harmonic part of the elasticity tensor is depicted as a generic matrix. The ⊕ symbol denotes addition. | ||
The interaction blocks iteratively refine the atom features via convolution operations. The architecture of the interaction block follows the design of Tensor Field Network34 and NequIP.36 Unlike many existing GNNs for molecules and crystals22,59–61 that utilize scalar features, here, the atom feature Fi is a set of scalars, vectors, and high-rank tensors. Formally, it is a geometric object consisting of a direct sum of irreducible representations of the SO(3) rotation group.34,36 There are two major benefits of using such geometric features. First, they are incorporated as inductive bias which can improve model accuracy and reduce the amount of training data. Second, from them, one can easily construct other physical tensors such as the elasticity tensor in this work.
The convolution on these geometric objects is an equivariant function, meaning that if the input atom feature F to the convolution is transformed under a rotation in SO(3), the output is transformed accordingly. This is achieved via the tensor product convolution by updating the atom feature in the (k + 1)th interaction block from that in the kth interaction block,
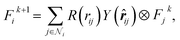 | (3) |
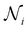 denotes the set of neighboring atoms for atom i, R indicates a multilayer perceptron (MLP) on the radial basis expansion of rij, and Y indicates the spherical harmonics expansion of
denotes the set of neighboring atoms for atom i, R indicates a multilayer perceptron (MLP) on the radial basis expansion of rij, and Y indicates the spherical harmonics expansion of ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij. The tensor product ⊗ between Y and Fjk is a bilinear map, which is a generalization of the outer product of two vectors. The product output is decomposed back onto the irreducible representations, and the entire operation is equivariant.34 The use of an MLP makes the convolution learnable. After a skip connection,62 the feature Fik+1 is passed through a nonlinear activation function and finally normalized using an equivariant normalization function.63
ij. The tensor product ⊗ between Y and Fjk is a bilinear map, which is a generalization of the outer product of two vectors. The product output is decomposed back onto the irreducible representations, and the entire operation is equivariant.34 The use of an MLP makes the convolution learnable. After a skip connection,62 the feature Fik+1 is passed through a nonlinear activation function and finally normalized using an equivariant normalization function.63
The output head maps the refined features from the interaction blocks to the target materials tensor of interest. First, the features of all atoms are aggregated to obtain a representation of the crystal. For intensive properties such as the elasticity tensor, meaning that the property value does not depend on the size of the system, we adopt the mean pooling by averaging the features such that the representation of the crystal is independent of the number of atoms. Next, an appropriate subset of the pooled irreducible representations that correspond to the target tensor of interest is selected and then assembled as the model output. For the elasticity tensor, the selected ones are two scalars, two second-rank traceless symmetric tensors, and a fourth-rank harmonic tensor. They are assembled to an elasticity tensor according to eqn (2).
Overall, MatTen is a function C = f(x) that maps a crystal structure x to its elasticity tensor C. The function f is equivariant to the SO(3) group transformation, that is, for any x and g ∈ SO(3), we have Dy(g)f(x) = f(Dx(g)x), where Dx(g) and Dy(g) are rotation matrices parameterized by g for the crystal structure and the elasticity tensor, respectively. This ensures that the model can produce an elasticity tensor C that respects the orientation of the input crystal structure. In other words, the choice of a specific coordinate system does not affect the model output; if the coordinate system is rotated, the output tensor rotates accordingly. This independence of the frame of reference characteristic is an indispensable property for models that predict tensors. In addition, any such model should also preserve the material symmetry of the crystal. By construction, MatTen guarantees the material symmetry reflected in the elasticity tensor. Concretely, if the predicted elasticity tensor is represented as a Voigt matrix, the symmetry and number of independent components in Fig. 1 are automatically maintained for all seven crystal systems (proof in the ESI†). For example, for a cubic crystal, the model guarantees that there are only three independent components c11 = c22 = c33, c12 = c13 = c23, and c44 = c55 = c66 and that all other components are zero.
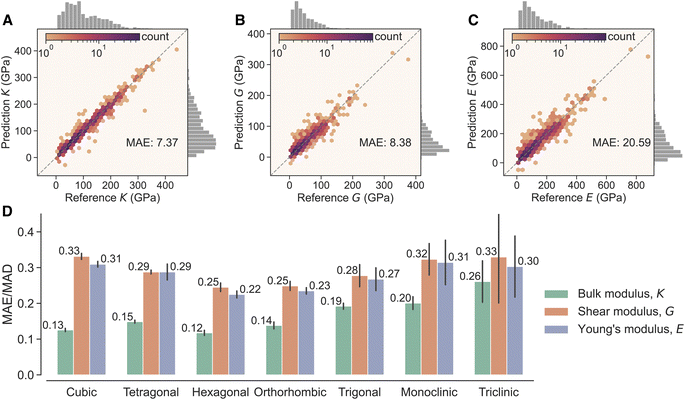
2.3 Elastic properties of polycrystals
The MatTen model directly outputs the full elasticity tensor. To assess its performance, we computed several commonly used elastic properties for polycrystals from the elasticity tensor. Fig. 3 illustrates the results on the moduli obtained using the Hill average scheme.64 The DFT reference values have a range of 4–442 GPa, 3–375 GPa, and 9–878 GPa for the bulk modulus K, shear modulus G, and Young's modulus E, respectively. The formulae to obtain the moduli are given in Section 4, and their statistics and distribution are given in Fig. S4–S7 in the ESI.† The predictions of MatTen closely align with the DFT reference values along the entire ranges, achieving mean absolute errors (MAEs) of 7.37 GPa, 8.38 GPa, and 20.59 GPa for K, G, and E, respectively. To connect the MAE values to practical applications, let's examine the error in strain caused by the MAE in Young's modulus. For example, at E = 128.4 GPa (the mean of DFT references), an error of 20.59 GPa will lead to a relative error of 19% in the strain (calculation given in the ESI†). While different applications necessitate varied accuracy, a relative error of 19% in the strain can be acceptable, given that noncontact experimental techniques for strain measurement such as the digital image correlation method65 have a typical error of ∼10%.For comparison, we trained two additional models. The first is a variant of MatTen, where the tensor output head of MatTen is replaced with a scalar output head, referred to as MatSca hereafter. The second is the AutoMatminer algorithm, an automated machine learning pipeline designed for predicting scalar materials properties.20 We evaluated their performance in predicting the elastic moduli, and the results are listed in Table 1. Both MatTen and MatSca have smaller MAEs than AutoMatminer across all three moduli, owning to the effectiveness of the underlying neural networks in learning materials properties from structures. The performance of MatTen and MatSca are comparable. However, it is worth highlighting that while an individual MatSca model was trained for each modulus, a single MatTen model successfully produced all the elastic moduli, demonstrating the versatility of the MatTen model.
| K (GPa) | G (GPa) | E (GPa) | ||||
|---|---|---|---|---|---|---|
| MAE | MAE/MAD | MAE | MAE/MAD | MAE | MAE/MAD | |
| MatTen | 7.37 (0.10) | 0.130 (0.002) | 8.38 (0.16) | 0.280 (0.005) | 20.59 (0.35) | 0.275 (0.005) |
| MatSca | 7.32 (0.09) | 0.129 (0.002) | 8.63 (0.07) | 0.288 (0.002) | 19.87 (0.43) | 0.265 (0.006) |
| AutoMatminer | 9.84 (0.34) | 0.174 (0.006) | 9.27 (0.32) | 0.309 (0.011) | 22.10 (0.77) | 0.295 (0.024) |
Upon closer examination of Fig. 3A–C, we have identified some inconsistencies in the predictions. All crystals in the DFT dataset have positive moduli, the predicted moduli by MatTen, however, occasionally yield negative values, indicating that the associated crystal is elastically unstable. This is an inherent challenge faced by machine learning regression models in general, albeit with physical inductive biases embedded in the model such as the symmetry requirements in MatTen. The number of crystals with negative predicted moduli remains minimal, accounting for only 3, 2, and 2 out of the 1021 test data for bulk, shear, and Young's moduli, respectively. The moduli alone, however, do not provide a comprehensive understanding. For a crystal to be elastically stable, the sufficient and necessary condition is that the Voigt matrix should be positive definite.8 We checked this and found that 25 crystals in the test set do not satisfy this condition. The majority of them are due to the incorrect prediction of the relative magnitudes of the diagonal and off-diagonal components of the Voigt matrix. A breakdown of the errors is provided in the ESI.† Nevertheless, this is not a concern in practical use; one can filter out the negative ones if desired.
To assess how MatTen performs for different elastic properties as well as for different crystal systems, we computed the scaled error, SE = MAE/MAD, in which MAE and MAD are the mean absolute error and mean absolute deviation, respectively (see Section 4). MAD quantifies the distance of reference values to their mean, and larger MAD means the reference values are more scattered. A model that makes accurate predictions for each data point will have an SE of 0, and a model that always predicts the mean of the dataset will have an SE of exactly 1. Comparing between properties, we see from Fig. 3D that the SE of bulk modulus is smaller than those of shear modulus and Young's modulus across all crystal systems. This suggests that bulk modulus is easier to predict, in agreement with existing observations.19–22 Next, we compare between crystal systems. The dataset used for model development has an uneven distribution in terms of the number of materials in each crystal system (Fig. S2 in the ESI†). For example, it contains 4217 cubic crystals, fewer than 800 trigonal and monoclinic crystals, and only 60 triclinic crystals. As a result, the SE and the error bar of the predicted moduli are larger for trigonal, monoclinic, and triclinic crystals in general (Fig. 3D). Despite the slightly higher errors, it is notable that the model can still perform well for the crystal systems with a low presence in the training data, particularly for triclinic crystals. This is primarily because MatTen internally treats all crystals the same, enabling crystal systems with fewer data to leverage the abundant data from other crystal systems and acquire enhanced representations. This type of transferability is not possible with models that are built separately for each crystal system.
The elastic moduli have values across different orders from near zero to hundreds (Fig. S4–S7 in the ESI†). To mitigate the challenge of learning values across a broad spectrum, some existing models19–22 adopt the approach of predicting the logarithm of the moduli. Unlike these models, MatTen directly predicts the full tensor without any data transformation, and all other elastic properties (including their logarithms) can be computed from it. The logarithms of the bulk, shear, and Young's moduli obtained from MatTen are comparable to those that learn in the logarithmic space (Table S1 in the ESI†). Further, the performance of MatTen can be further improved with additional training data. The MAE almost decreases linearly with the logarithm of the number of data used to train the model (Fig. S10 in the ESI†). Finally, it is also possible to predict the full elasticity tensor by separately modeling its non-zero independent components.31,32 MatTen performs much better than this approach thanks to its ability to deal with all crystal systems within a united framework (further discussion in the ESI†).
2.4 Anisotropic elastic properties
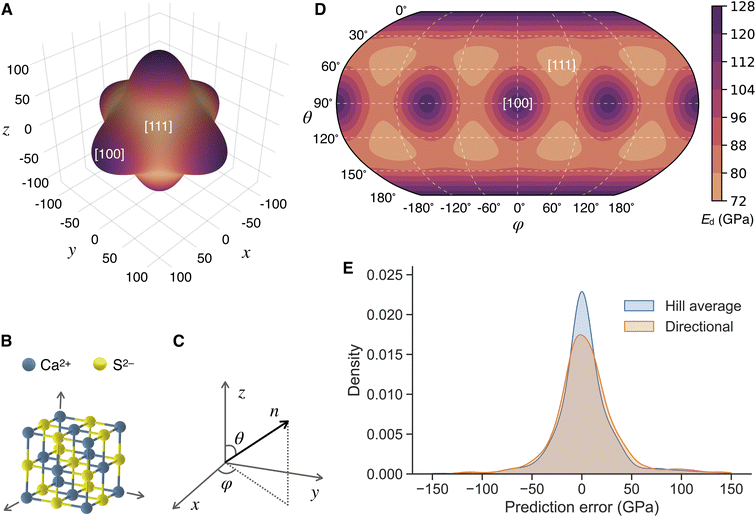
Crystals are inherently anisotropic, and thus their elastic properties can vary depending on the direction of measurement. This anisotropy arises from a crystal's structure, including the symmetry of the lattice and the arrangement of the atoms. MatTen predicts the full elasticity tensor, and, for the first time with a machine learning model, we are able to investigate the anisotropic elastic behavior of crystals. We focus our discussion on the directional dependence of Young's modulus (further results on shear modulus given in the ESI†).Young's modulus E discussed in Section 2.3 is an averaged property for isotropic polycrystals. But for single crystals, Young's modulus depends on the direction along which the strain/stress is applied and measured. Given the elasticity tensor Cijkl (equivalently, the compliance tensor Sijkl, see Section 4), the directional Young's modulus can be computed as47,54
| Ed(n) = (ninjnknlSijlk)−1, | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ·cos
θ·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ·sin
θ·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] (Fig. 4C), it can be represented in two dimensions (Fig. 4D, with a Robinson map projection67). Such plots make it easier to visually investigate the anisotropic characteristics of Young's modulus. For example, for the cubic rocksalt CaS crystal (Fig. 4B), the maximum directional Young's modulus Emaxd is along the 〈100〉 directions (for instance, θ = 90° and φ = 0°), while the minimum Emind is along the 〈111〉 directions (for instance, θ = 54.7° and φ = 45°). In fact, for cubic crystals such as CaS, the extreme values of Ed are guaranteed to occur in these two directions.47Eqn (4) can be simplified as Ed(n) = [S1111 − 2(S1111 − S1122 − 2S2323)(n12n22 + n22n32 + n32n12)]−1 for cubic crystals, expressed in terms of their three independent elasticity tensor components. It can be mathematically shown that, if
θ] (Fig. 4C), it can be represented in two dimensions (Fig. 4D, with a Robinson map projection67). Such plots make it easier to visually investigate the anisotropic characteristics of Young's modulus. For example, for the cubic rocksalt CaS crystal (Fig. 4B), the maximum directional Young's modulus Emaxd is along the 〈100〉 directions (for instance, θ = 90° and φ = 0°), while the minimum Emind is along the 〈111〉 directions (for instance, θ = 54.7° and φ = 45°). In fact, for cubic crystals such as CaS, the extreme values of Ed are guaranteed to occur in these two directions.47Eqn (4) can be simplified as Ed(n) = [S1111 − 2(S1111 − S1122 − 2S2323)(n12n22 + n22n32 + n32n12)]−1 for cubic crystals, expressed in terms of their three independent elasticity tensor components. It can be mathematically shown that, if| S1111 − S1122 − 2S2323 < 0, | (5) |
To quantitatively assess the ability of MatTen in predicting anisotropic elastic properties, we measured the error between the model predicted directional Young's modulus Epredd and the DFT reference Erefd. For CaS, MatTen prediction closely follows DFT reference, with a maximum under-prediction of 8.7 GPa along the 〈111〉 directions and a maximum over-prediction of 9.4 GPa along the 〈100〉 directions (Fig. S14 in the ESI†). In addition to this example crystal, we calculated the error for the entire test set, computed as D = Ds·Dv for each crystal. The value of the error is 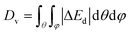 , where ΔEd(θ,φ) = Epredd(θ,φ) − Erefd(θ,φ) and |·| denotes the absolute value. The sign of the error is Ds = +1 if
, where ΔEd(θ,φ) = Epredd(θ,φ) − Erefd(θ,φ) and |·| denotes the absolute value. The sign of the error is Ds = +1 if 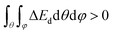 , and Ds = −1 otherwise. Put differently, the value Dv quantifies the average deviation from the DFT reference, while the sign Ds characterizes whether the overall prediction is larger than the DFT reference. The integration over θ and φ is performed using the Chebyshev quadratures, which uniformly distribute the integration points on the sphere and can avoid biasing specific points.68 The distribution of the prediction error D of Ed for the test set is plotted in Fig. 4E. It has a Gaussian-like shape, and it almost overlaps with that of isotropic Young's modulus obtained using the Hill average. Similar behaviors are observed for shear modulus and MAEs by crystal systems (Fig. S15 and S16 in the ESI†). These observations suggest that, on average, MatTen performs equally well for the anisotropic and averaged isotropic elastic properties. Accurate prediction of anisotropic properties offers a comprehensive understanding of the elastic characteristics exhibited by crystals, enabling the discovery of new materials through the utilization of these predictive capabilities.
, and Ds = −1 otherwise. Put differently, the value Dv quantifies the average deviation from the DFT reference, while the sign Ds characterizes whether the overall prediction is larger than the DFT reference. The integration over θ and φ is performed using the Chebyshev quadratures, which uniformly distribute the integration points on the sphere and can avoid biasing specific points.68 The distribution of the prediction error D of Ed for the test set is plotted in Fig. 4E. It has a Gaussian-like shape, and it almost overlaps with that of isotropic Young's modulus obtained using the Hill average. Similar behaviors are observed for shear modulus and MAEs by crystal systems (Fig. S15 and S16 in the ESI†). These observations suggest that, on average, MatTen performs equally well for the anisotropic and averaged isotropic elastic properties. Accurate prediction of anisotropic properties offers a comprehensive understanding of the elastic characteristics exhibited by crystals, enabling the discovery of new materials through the utilization of these predictive capabilities.
2.5 Screening of crystals with extreme properties
The maximum of the directional Young's modulus, Emaxd, characterizes the smallest possible deformation of a crystal under applied external loading. It helps in the selection and orientating of materials to minimize shape change to guarantee the reliability of precision devices such as micro-electromechanical systems.69We have also applied the MatTen model to screen for crystals with large Emaxd. We first filtered crystals from the Materials Project database based on their energy above the convex hull values, selecting those with a value of ≤50 meV per atom. This energy determines the thermodynamic stability of a crystal and has been shown to correlate with the synthesizability of crystals.70,71 We further narrowed down the selection to crystals with fewer than 50 atomic sites to reduce computational cost and remove crystals already present in the dataset used to develop the model. This resulted in 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 crystals for further analysis. Next, we employed MatTen to predict the full elasticity tensors for these crystals and compute their Emaxd. The top 100 crystals with the highest Emaxd were then supplied for DFT computation to obtain their elasticity tensors. Fig. 5 presents a histogram of Emaxd for the identified 100 crystals. Their Emaxd values all fall at the tail of the distribution of Emaxd from the training data. Quantitatively, the mean of Emaxd for the identified crystals is 606 GPa, while that for the training data is 174 GPa, corresponding to the expected value for a randomly selected material. This demonstrates the effectiveness of leveraging MatTen to screen for materials with extreme elastic properties. The newly identified crystals are provided in Data Availability.
480 crystals for further analysis. Next, we employed MatTen to predict the full elasticity tensors for these crystals and compute their Emaxd. The top 100 crystals with the highest Emaxd were then supplied for DFT computation to obtain their elasticity tensors. Fig. 5 presents a histogram of Emaxd for the identified 100 crystals. Their Emaxd values all fall at the tail of the distribution of Emaxd from the training data. Quantitatively, the mean of Emaxd for the identified crystals is 606 GPa, while that for the training data is 174 GPa, corresponding to the expected value for a randomly selected material. This demonstrates the effectiveness of leveraging MatTen to screen for materials with extreme elastic properties. The newly identified crystals are provided in Data Availability.
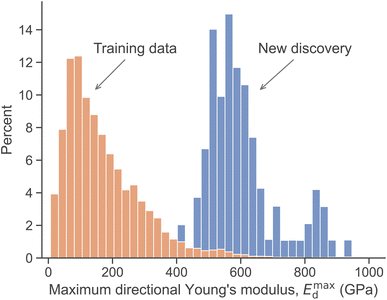 | ||
| Fig. 5 Screening of crystals with large maximum directional Young's modulus. The training data and new discoveries are separately normalized such that each sums to 100 percent. | ||
In addition, we have identified 11 unconventional polymorphs of elemental cubic metals regarding the direction of the extreme values of Young's modulus. Five of them have already been experimentally synthesized (four stable ground-state polymorphs and one metastable polymorph71), and the other six are metastable polymorphs that have not yet been experimentally observed. It is believed that Emaxd is along the 〈111〉 directions (meaning eqn (5) is not satisfied) for all cubic metals except Mo.47 We suspect that there exist other polymorphs of elemental cubic metals satisfying the criterion in eqn (5). To test this, we performed a screening of the Materials Project database. From the dataset used to develop MatTen, we have identified six such crystals. Mo is among them, and the other five are V (one polymorph), Cr (two polymorphs), and W (two polymorphs). For crystals not in the dataset, we first used MatTen to predict their elasticity tensors and then selected the 18 crystals that meet the verification criterion using DFT. DFT predicted 12 crystals satisfying the criterion; six are elastically unstable structures whose Voigt matrix has negative eigenvalues,8,9 and the other six successful ones are Mn, Na, K, Cs, Rh, and Tl (one polymorph for each). Among the 11 newly identified crystals, polymorphs of alkali metals Na, K, and Cs have DFT calculated S1111 − S1122 − 2S2323 values much more negative than that of Mo, but they are all hypothetical crystals that have not been experimentally synthesized yet. Five polymorphs are indeed experimentally observed, and they are all neighbors of Mo in the periodic table, namely V, Cr, Mn, and W. Among them, four are thermodynamically stable ground-state polymorphs, and one polymorph of Cr is metastable. Crystal structures, ground-state information, and elasticity tensors of the 11 unconventional polymorphs are provided in Data Availability and Table S3 in the ESI.†
3 Conclusions
A model such as MatTen that can predict the full elasticity tensors of inorganic crystalline compounds across crystal systems and chemical species brings new possibilities to probe and design materials with targeted mechanical properties. MatTen has several unique characteristics: (1) it learns the full elasticity tensor and automatically handles all symmetry requirements, without the need to build separate models for individual components of the tensor or for each crystal system; (2) any elastic properties such as the bulk, shear, and Young's moduli can be computed from the predicted elasticity tensor, leading to a unified framework for modeling elasticity; and (3) it allows for the exploration of anisotropic elastic behaviors (not possible with existing machine learning models), demonstrated by screening for crystals with extreme directional Young's modulus.It should be noted, however, that a crucial aspect regarding the practical use of the model relies on the robustness of the input structure. Given two structures of a crystal where the atomic coordinates are slightly different, we would expect the elastic properties to be similar. If, otherwise, the model is extremely sensitive to the input, then it is not ideal for practical application. Extra work such as highly accurate DFT structure relaxation is needed before applying the model for predictions. We tested MatTen by using structures directly queried from the Materials Project database and structures with tighter geometry optimization. The MAE of Emaxd between using the two types of structures is 6.55 GPa (Fig. S17 in the ESI†), more than three times smaller than the MAE (22.36 GPa) of Emaxd between model predictions and DFT references. This suggests that MatTen is robust enough to its input, and reasonably optimized structures (for example, from online databases) would not introduce extra error larger than the intrinsic error in the model.
The MatTen model is not limited to inorganic crystalline compounds and even elasticity tensors in general. The elastic behavior of other classes of materials such as two-dimensional layered materials and molecular crystals play a significant role in determining their functionality, and MatTen can be directly applied to model their elasticity tensors. Of course, a curated dataset of reference elasticity tensors is needed. Such data already exists, for example, in the Computational 2D Materials Database (C2DB).72 Moreover, besides elasticity tensor, MatTen can be applied to other tensorial properties of materials. These can be broadly categorized into two classes: material-level property and atom-level property. While the former means a single tensor for each crystal, the latter means a separate tensor for each atom in the crystal. Other material-level properties such as piezoelectric and dielectric tensors can be modeled by updating the output head as in Fig. 2 to use the corresponding irreducible representations of the tensor of interest (for example, a single second-rank symmetric matrix for the dielectric tensor). For atom-level properties such as the neutron magnet resonance (NMR) tensor, instead of using a mean pooling to aggregate atom features, one can directly map the features of an atom to a tensor for that atom. Using MatTen, we have conducted such an analysis for NMR tensors of silicon oxides and found that MatTen significantly outperforms both historic analytical models and other machine learning models by more than 50% for isotropic and anisotropic NMR chemical shift.73
One potential limitation of the proposed approach is the reliance on a relatively large dataset to develop the model. We have curated a dataset of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 elasticity tensors which took millions of CPU hours to obtain. Such large datasets for other tensorial properties may not be readily available, but they begin to emerge. For example, the Materials Project has about 3000 piezoelectric and 7000 dielectric tensors.74,75 This amount of data might still be a good start to training faithful models, given that piezoelectric and dielectric are third- and second-rank tensors, respectively, which are much simpler than the fourth-rank elasticity tensor. In fact, for the second-rank NMR tensor, we only used a dataset of 421 crystals to obtain the best-performing model.73 Another possibility is to apply a transfer learning approach, where the model is first trained on a different property with large data (for instance, elasticity tensor) and then finetuned on the target property of interest (for instance, piezoelectric tensor). A limitation of the trained model can come from the data. The data consists of DFT calculations of perfect single crystals with relatively small super cells at a temperature of 0 K. Given that the efficacy of the model is intrinsically tied to the scope of the training data, it is imperative to exercise caution when applying the model to scenarios that extend beyond these parameters. For example, the model is not appropriate for crystals with defects, such as vacancies, dislocations, and grain boundaries. Additionally, it is not advisable to directly employ the model for estimating the mechanical properties at finite temperate, especially for those materials, like metallic alloys, which exhibit a pronounced temperature dependency.
276 elasticity tensors which took millions of CPU hours to obtain. Such large datasets for other tensorial properties may not be readily available, but they begin to emerge. For example, the Materials Project has about 3000 piezoelectric and 7000 dielectric tensors.74,75 This amount of data might still be a good start to training faithful models, given that piezoelectric and dielectric are third- and second-rank tensors, respectively, which are much simpler than the fourth-rank elasticity tensor. In fact, for the second-rank NMR tensor, we only used a dataset of 421 crystals to obtain the best-performing model.73 Another possibility is to apply a transfer learning approach, where the model is first trained on a different property with large data (for instance, elasticity tensor) and then finetuned on the target property of interest (for instance, piezoelectric tensor). A limitation of the trained model can come from the data. The data consists of DFT calculations of perfect single crystals with relatively small super cells at a temperature of 0 K. Given that the efficacy of the model is intrinsically tied to the scope of the training data, it is imperative to exercise caution when applying the model to scenarios that extend beyond these parameters. For example, the model is not appropriate for crystals with defects, such as vacancies, dislocations, and grain boundaries. Additionally, it is not advisable to directly employ the model for estimating the mechanical properties at finite temperate, especially for those materials, like metallic alloys, which exhibit a pronounced temperature dependency.
4 Experimental
4.1 Data generation
The elasticity tensors were computed by a liner fitting of the stresses and strains obtained from DFT calculations using the Vienna Ab Initio Simulation Package (VASP).76 The calculations follow the same procedures discussed in ref. 10, using PREC = Accurate, a tight convergence criterion of EDIFF = 1 × 10−6, an energy cutoff of ENCUT = 700 eV, and a k-points density of 64 Å−3 in the reciprocal space to sample the Brillouin zone. Two additional improvements are made. First, to get more precise stresses for calculating the elasticity tensor, the projection operators in VASP are evaluated in the reciprocal space, that is, the setting LREAL = False was adopted. Second, to reduce numerical error in the calculations, the stresses are symmetrized according to the crystal symmetry. The entire workflow was implemented in the open-source atomate package.154.2 Model architecture
A crystal structure is converted to a graph using a distance-based approach, where an edge is created between a pair of atoms if their distance is smaller than a cutoff radius rcut. Periodic boundary conditions are considered in the graph construction.For atom a, its atomic number Za is embedded as a vector with c components using a one-hot encoding to obtain the initial atom feature Fa. The unit vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij from atom i to atom j is expanded using a spherical harmonics basis consisting up to a degree of l = 4. (Explicitly, this corresponds to the “0e + 1o + 2e + 3o + 4e” irreducible representations in e3nn notation63). The distance rij between atoms i and j is expanded into a vector R using the radial basis functions,58
ij from atom i to atom j is expanded using a spherical harmonics basis consisting up to a degree of l = 4. (Explicitly, this corresponds to the “0e + 1o + 2e + 3o + 4e” irreducible representations in e3nn notation63). The distance rij between atoms i and j is expanded into a vector R using the radial basis functions,58
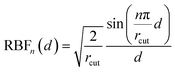 | (6) |
With the atom features F, the spherical harmonics expansion of ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij, and the radial basis expansion R of rij obtained from the embedding layers, the interaction block performs tensor product–based convolution to refine the atom features. This is achieved viaeqn (3), more specifically,34
ij, and the radial basis expansion R of rij obtained from the embedding layers, the interaction block performs tensor product–based convolution to refine the atom features. This is achieved viaeqn (3), more specifically,34
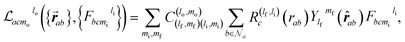 | (7) |
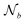 within the cutoff rcut; l is an integer indicating the degree of the spherical harmonic function, and m = −l, …, l; the subscripts i, o, and f indicate input, output, and filter, respectively; c is the channel index (for example, for the embedding layer, it indicates the components of the one-hot encoding); C denotes the Clebsch–Gordan coefficients; and finally, R(lcf,li) are learnable multilayer perceptrons (MLPs), which take the RBF expansion as the input and contain most of the parameters of the model. Essentially, this combines the atom features of neighbors b to be the new atom features of the center atom a, in the same spirit of a message-passing graph neural network. A major characteristic of eqn (7) is that the use of the spherical harmonics and the Clebsch–Gordan coefficients together imply that convolutions are equivariant.34
within the cutoff rcut; l is an integer indicating the degree of the spherical harmonic function, and m = −l, …, l; the subscripts i, o, and f indicate input, output, and filter, respectively; c is the channel index (for example, for the embedding layer, it indicates the components of the one-hot encoding); C denotes the Clebsch–Gordan coefficients; and finally, R(lcf,li) are learnable multilayer perceptrons (MLPs), which take the RBF expansion as the input and contain most of the parameters of the model. Essentially, this combines the atom features of neighbors b to be the new atom features of the center atom a, in the same spirit of a message-passing graph neural network. A major characteristic of eqn (7) is that the use of the spherical harmonics and the Clebsch–Gordan coefficients together imply that convolutions are equivariant.34
The atom features F is also passed through a self-interaction,
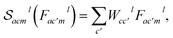 | (8) |
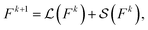 | (9) |
| SiLU(s) = σ(s)s, | (10) |
| G(t) = σ(x)t, | (11) |
The readout head aggregates the features of individual atoms to obtain a representation of the material via a mean pooling,
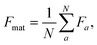 | (12) |
4.3 Model training
The dataset of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 elasticity tensors is split into three subsets for training, validation, and testing with a split ratio of 8
276 elasticity tensors is split into three subsets for training, validation, and testing with a split ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. A random split with stratification is adopted where each of the seven crystal systems is separately treated in the split. The model parameters are optimized using the training set, model hyperparameters are determined based on model performance on the validation set, and error analysis is performed using the test set unless otherwise stated. We train the model with the Adam optimizer to minimize a mean-squared-error loss function
1. A random split with stratification is adopted where each of the seven crystal systems is separately treated in the split. The model parameters are optimized using the training set, model hyperparameters are determined based on model performance on the validation set, and error analysis is performed using the test set unless otherwise stated. We train the model with the Adam optimizer to minimize a mean-squared-error loss function 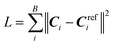 with a mini-batch size B of 32. Note, Ci denotes the irreducible representation of the model predicted elasticity tensor with 21 components (see eqn (2)), but not the Cartesian tensor with 81 components. Similarly, Crefi denotes the corresponding reference DFT values. The learning rate is set to 0.01, and a reduce-on-plateau learning rate scheduler is used, which decreases the learning rate by a factor of 0.5 if the validation error does not decrease for 50 epochs. The training stops when the validation error does not decrease for 150 consecutive epochs, and a maximum of 1000 epochs are allowed for the optimization. We performed a grid search to obtain model hyperparameters such as the rcut and c. Search ranges and their optimal values are listed in Table S4 in the ESI.†
with a mini-batch size B of 32. Note, Ci denotes the irreducible representation of the model predicted elasticity tensor with 21 components (see eqn (2)), but not the Cartesian tensor with 81 components. Similarly, Crefi denotes the corresponding reference DFT values. The learning rate is set to 0.01, and a reduce-on-plateau learning rate scheduler is used, which decreases the learning rate by a factor of 0.5 if the validation error does not decrease for 50 epochs. The training stops when the validation error does not decrease for 150 consecutive epochs, and a maximum of 1000 epochs are allowed for the optimization. We performed a grid search to obtain model hyperparameters such as the rcut and c. Search ranges and their optimal values are listed in Table S4 in the ESI.†
Ten-fold cross validation is also performed to test the effects of different data splits. Fig. S11 and S12 in the ESI† present the results, and MatTen is not sensitive to data splits. Detailed information on the training, validation, and test split, as well as the ten-fold split is given in the released dataset (see Data Availability).
4.4 AutoMatmainer training
AutoMatminer is a machine learning pipeline that automatically featurizes the crystals and selects the appropriate features to train a set of machine learning algorithms.20 The best-performing algorithm is used as the final model. For all the results reported in this work, the production preset is adopted. It was found that the gradient boost, random forest, and extra trees algorithms can all be selected as the best-performing model, depending on the target elastic property and the initialization of the parameters in the automatic pipeline. For each target elastic property, the reported results are obtained by averaging over multiple runs, each with a different initialization.4.5 Compliance tensor
The compliance tensor S is a fourth-rank tensor defined from the inverse stress–strain relation ε = Sσ, where ε and σ are the second-rank strain tensor and stress tensor, respectively. The compliance tensor in Voigt notation s can be obtained as the inverse of the elasticity tensor Voigt matrix,| s = c−1, | (13) |
 | (14) |
4.6 Averaged elastic moduli of polycrystals
Given the elasticity tensor of a single crystal, the averaged bulk, shear, and Young's moduli of polycrystalline materials can be computed using different average schemes. The Voigt average assumes that the strain is the same in each grain, equal to the macroscopically applied strain.48 The Voigt bulk modulus is| KV = [(c11 + c22 + c33) + 2(c12 + c23 + c31)]/9, | (15) |
| GV = [(c11 + c22 + c33) − (c12 + c23 + c31) + 3(c44 + c55 + c66)]/15. | (16) |
The Reuss average assumes that the stress is the same in each grain, equal to the macroscopically applied stress.79 The Reuss bulk modulus is
| KR = 1/[(s11 + s22 + s33) + 2(s12 + s23 + s31)], | (17) |
| GR = 15/[4(s11 + s22 + s33) − 4(s12 + s23 + s31) + 3(s44 + s55 + s66)]. | (18) |
The Voigt and Reuss averages are the two extreme cases. The Hill average takes their arithmetic mean and is considered the most accurate in a wide range of experimental conditions.64 The Hill bulk modulus is
| KH = (KV + KR)/2, | (19) |
| GH = (GV + GR)/2. | (20) |
Given the bulk modulus and the shear modulus (from any of the Voigt, Reuss, and Hill schemes), Young's modulus can be computed as80
| E = 9KG/(3K + G). | (21) |
In this work, we report the bulk modulus K = KH, shear modulus G = GH, and Young's modulus E = 9KHGH/(3KH + GH) from the Hill average scheme.
4.7 Scaled error
The mean absolute error (MAE) and mean absolute deviation (MAD) are defined as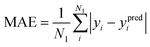 and
and 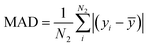 , in which yi is the reference value of data point i, ypredi is the model prediction for the data point, and ȳ is the average of all reference values. The numbers N1 and N2 do not necessarily need to be the same. This is the case in Fig. 3 and Table 1, where N1 is the number of crystals in a specific crystal system and N2 is the total size of the test set. The scaled error (SE) is then computed as SE = MAE/MAD.
, in which yi is the reference value of data point i, ypredi is the model prediction for the data point, and ȳ is the average of all reference values. The numbers N1 and N2 do not necessarily need to be the same. This is the case in Fig. 3 and Table 1, where N1 is the number of crystals in a specific crystal system and N2 is the total size of the test set. The scaled error (SE) is then computed as SE = MAE/MAD.
4.8 Software implementation
The MatTen model was implemented using the e3nn package63 built on top of PyTorch,81 and the training was performed using Pytorch-Lightning.82 The DFT calculations were performed using the atomate workflow15 and all crystal structure processing was performed using the Python Materials Genomics (pymatgen).13 Directional Young's modulus was obtained using the elate package.66Data availability
The elasticity tensors used for model development, the 100 new crystals with large maximum directional Young's modulus, and the elemental cubic metals are available at https://doi.org/10.5281/zenodo.8190849. The elasticity tensors are also available from the Materials Project database via the web interface at https://materialsproject.org or the API at https://api.materialsproject.org.Code availability
The MatTen model and training scripts are released as an open-source repository at https://github.com/wengroup/matten.Author contributions
Conceptualization, investigation, software, visualization, and writing – original draft: M. W.; data curation and formal analysis: M. W., M. K. H., J. M. M., and P. H.; writing – review & editing: M. W., M. K. H., J. M. M., P. H., and K. A. P.; project administration: M. W.; funding acquisition: M. W. and K. A. P.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The method development was supported by the National Science Foundation under Grant No. 2316667 and the startup funds from the Presidential Frontier Faculty Program at the University of Houston. Support for software and data infrastructure development was provided by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under contract No. DE-AC02-05-CH11231 (Materials Project program KC23MP). This work used computational resources provided by the Research Computing Data Core at the University of Houston, the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under contract No. DE-AC02-05CH11231, and the Lawrencium computational cluster resource provided by the IT Division at the Lawrence Berkeley National Laboratory (Supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under contract No. DE-AC02-05CH11231).References
- R. B. Hetnarski and J. Ignaczak, The mathematical theory of elasticity, CRC Press, 2016, DOI:10.1115/1.1849176.
- R. B. Kaner, J. J. Gilman and S. H. Tolbert, Designing superhard materials, Science, 2005, 308(5726), 1268–1269, DOI:10.1126/science.1109830.
- A. M. Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, Machine learning directed search for ultraincompressible, superhard materials, J. Am. Chem. Soc., 2018, 140(31), 9844–9853, DOI:10.1021/jacs.8b02717.
- O. L. Anderson, E. Schreiber, R. C. Liebermann and N. Soga, Some elastic constant data on minerals relevant to geophysics, Rev. Geophys., 1968, 6(4), 491–524, DOI:10.1029/SP026p0237.
- B. B. Karki, L. Stixrude and R. M. Wentzcovitch, High-pressure elastic properties of major materials of earth's mantle from first principles, Rev. Geophys., 2001, 39(4), 507–534, DOI:10.1029/2000RG000088.
- C. Monroe and J. Newman, The effect of interfacial deformation on electrodeposition kinetics, J. Electrochem. Soc., 2004, 151(6), A880, DOI:10.1149/1.1710893.
- Z. Ahmad and V. Viswanathan, Stability of electrodeposition at solid-solid interfaces and implications for metal anodes, Phys. Rev. Lett., 2017, 119(5), 056003, DOI:10.1103/PhysRevLett.119.056003.
- F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(22), 224104, DOI:10.1103/PhysRevB.90.224104.
- K. Tolborg, J. Klarbring, A. M. Ganose and A. Walsh, Free energy predictions for crystal stability and synthesisability, Digital Discovery, 2022, 1(5), 586–595, 10.1039/D2DD00050D.
- M. De Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. Krishna Ande, S. Van Der Zwaag and J. J. Plata, et al., Charting the complete elastic properties of inorganic crystalline compounds, Sci. Data, 2015, 2(1), 1–13, DOI:10.1038/sdata.2015.9.
- X. Du and J.-C. Zhao, Facile measurement of single-crystal elastic constants from polycrystalline samples, npj Comput. Mater., 2017, 3(1), 17, DOI:10.1038/s41524-017-0019-x.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark and A. Dal Corso, et al., Reproducibility in density functional theory calculations of solids, Science, 2016, 351(6280), aad3000, DOI:10.1126/science.aad3000.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python materials genomics (pymatgen): a robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319, DOI:10.1016/j.commatsci.2012.10.028.
- A. Jain, S. P. Ong, W. Chen, B. Medasani, X. Qu, M. Kocher, M. Brafman, P. Guido, G.-M. Rignanese and G. Hautier, et al., Fireworks: a dynamic workflow system designed for high-throughput applications, Concurrency Comput. Pract. Ex., 2015, 27(17), 5037–5059, DOI:10.1002/cpe.3505.
- K. Mathew, J. H. Montoya, A. Faghaninia, S. Dwarakanath, M. Aykol, H. Tang, I.-h. Chu, T. Smidt, B. Bocklund and M. Horton, et al., Atomate: a high-level interface to generate, execute, and analyze computational materials science workflows, Comput. Mater. Sci., 2017, 139, 140–152, DOI:10.1016/j.commatsci.2017.07.030.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al., Commentary: the materials project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002, DOI:10.1063/1.4812323.
- M. Hellenbrandt, The inorganic crystal structure database (icsd)—present and future, Crystallogr. Rev., 2004, 10(1), 17–22 CrossRef CAS.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2(11), 718–728, DOI:10.1038/s43588-022-00349-3.
- A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, Compositionally restricted attention-based network for materials property predictions, npj Comput. Mater., 2021, 7(1), 77, DOI:10.1038/s41524-021-00545-1.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking materials property prediction methods: the matbench test set and automatminer reference algorithm, npj Comput. Mater., 2020, 6(1), 138, DOI:10.1038/s41524-020-00406-3.
- P.-P. De Breuck, G. Hautier and G.-M. Rignanese, Materials property prediction for limited datasets enabled by feature selection and joint learning with modnet, npj Comput. Mater., 2021, 7(1), 83, DOI:10.1038/s41524-021-00552-2.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph networks as a universal machine learning framework for molecules and crystals, Chem. Mater., 2019, 31(9), 3564–3572, DOI:10.1021/acs.chemmater.9b01294.
- K. Choudhary and B. DeCost, Atomistic line graph neural network for improved materials property predictions, npj Comput. Mater., 2021, 7(1), 185, DOI:10.1038/s41524-021-00650-1.
- B. O. Mukhamedov, K. V. Karavaev and I. A. Abrikosov, Machine learning prediction of thermodynamic and mechanical properties of multicomponent fe-cr-based alloys, Phys. Rev. Mater., 2021, 5(10), 104407, DOI:10.1103/PhysRevMaterials.5.104407.
- G. Vazquez, P. Singh, D. Sauceda, R. Couperthwaite, N. Britt, K. Youssef, D. D. Johnson and R. Arróyave, Efficient machine-learning model for fast assessment of elastic properties of high-entropy alloys, Acta Mater., 2022, 232, 117924, DOI:10.1016/j.actamat.2022.117924.
- N. Linton and D. S. Aidhy, A machine learning framework for elastic constants predictions in multi-principal element alloys, APL Mach. Learn., 2023, 1(1), 016109, DOI:10.1063/5.0129928.
- M. Lupo Pasini, G. S. Jung and S. Irle, Graph neural networks predict energetic and mechanical properties for models of solid solution metal alloy phases, Comput. Mater. Sci., 2023, 224, 112141 CrossRef CAS.
- K. Karimi, H. Salmenjoki, K. Mulewska, L. Kurpaska, A. Kosińska, M. J. Alava and S. Papanikolaou, Prediction of steel nanohardness by using graph neural networks on surface polycrystallinity maps, Scr. Mater., 2023, 234, 115559, DOI:10.1016/j.scriptamat.2023.115559.
- J. M. Hestroffer, M.-A. Charpagne, M. I. Latypov and I. J. Beyerlein, Graph neural networks for efficient learning of mechanical properties of polycrystals, Comput. Mater. Sci., 2023, 217, 111894, DOI:10.1016/j.commatsci.2022.111894.
- Z. Yang and M. J. Buehler, Linking atomic structural defects to mesoscale properties in crystalline solids using graph neural networks, npj Comput. Mater., 2022, 8(1), 198, DOI:10.1038/s41524-022-00879-4.
- Z. Ahmad, T. Xie, C. Maheshwari, J. C. Grossman and V. Viswanathan, Machine learning enabled computational screening of inorganic solid electrolytes for suppression of dendrite formation in lithium metal anodes, ACS Cent. Sci., 2018, 4(8), 996–1006, DOI:10.1021/acscentsci.8b00229.
- V. Revi, S. Kasodariya, A. Talapatra, G. Pilania and A. Alankar, Machine learning elastic constants of multi-component alloys, Comput. Mater. Sci., 2021, 198, 110671, DOI:10.1016/j.commatsci.2021.110671.
- M. M. Bronstein, J. Bruna, T. Cohen and P. Veličković, Geometric deep learning: grids, groups, graphs, geodesics, and gauges, arXiv, 2021, preprint, arXiv:2104.13478, DOI:10.48550/arXiv.2104.13478.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, Tensor field networks: Rotation-and translation-equivariant neural networks for 3d point clouds, arXiv, 2018, preprint, arXiv:1802.08219, DOI:10.48550/arXiv.1802.08219.
- V. Garcia Satorras, E. Hoogeboom and M. Welling. E (n) equivariant graph neural networks, in International conference on machine learning, PMLR, 2021, pp. 9323–9332 Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E (3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13(1), 2453, DOI:10.1038/s41467-022-29939-5.
- S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi and Y. Asano, et al., Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements, Nat. Commun., 2022, 13(1), 2991, DOI:10.1038/s41467-022-30687-9.
- Y.-L. Liao, B. Wood, A. Das, T. Smidt, Equiformerv2: improved equivariant transformer for scaling to higher-degree representations, arXiv, 2023, preprint arxiv:2306.12059, DOI:10.48550/arXiv.2306.12059.
- A. Grisafi, D. M. Wilkins, G. Csányi and M. Ceriotti, Symmetry-adapted machine learning for tensorial properties of atomistic systems, Phys. Rev. Lett., 2018, 120(3), 036002, DOI:10.1103/PhysRevLett.120.036002.
- M. Veit, D. M. Wilkins, Y. Yang, R. A. DiStasio and M. Ceriotti, Predicting molecular dipole moments by combining atomic partial charges and atomic dipoles, J. Chem. Phys., 2020, 153(2), 024113, DOI:10.1063/5.0009106.
- K. Schütt, O. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, in Proceedings of the 38th International Conference on Machine Learning, ed. M. Meila and T. Zhang, Proceedings of Machine Learning Research, PMLR, 2021, vol. 139, pp. 9377–9388 Search PubMed.
- H. Li, Z. Tang, X. Gong, N. Zou, W. Duan and Y. Xu, Deep-learning electronic-structure calculation of magnetic superstructures, Nat. Comput. Sci., 2023, 3(4), 321–327, DOI:10.1038/s43588-023-00424-3.
- O. Unke, M. Bogojeski, M. Gastegger, M. Geiger, T. Smidt and K.-R. Müller, Se (3)-equivariant prediction of molecular wavefunctions and electronic densities, Adv. Neural Inf. Process. Syst., 2021, 34, 14434–14447 Search PubMed.
- J. A. Rackers, L. Tecot, M. Geiger and T. E Smidt, A recipe for cracking the quantum scaling limit with machine learned electron densities, Mach. Learn.: Sci. Technol., 2023, 4(1), 015027, DOI:10.1088/2632-2153/acb314.
- E. B. Tadmor, R. E. Miller and R. S. Elliott, Continuum mechanics and thermodynamics: from fundamental concepts to governing equations, Cambridge University Press, 2012, DOI:10.1017/CBO9781139017657.
- F. I. Fedorov, Theory of elastic waves in crystals, Springer, 1968, DOI:10.1007/978-1-4757-1275-9.
- J. Frederick Nye, Physical properties of crystals: their representation by tensors and matrices, Oxford University Press, 1985, DOI:10.1063/1.3060200.
- W. Voigt, Lehrbuch der kristallphysik (mit Ausschluss der Kristalloptik), Vieweg+Teubner Verlag Wiesbade, 1966, DOI:10.1007/978-3-663-15884-4.
- S. Forte and M. Vianello, Symmetry classes for elasticity tensors, J. Elasticity, 1996, 43, 81–108, DOI:10.1007/BF00042505.
- P. Chadwick, M. Vianello and S. C. Cowin, A new proof that the number of linear elastic symmetries is eight, J. Mech. Phys. Solids, 2001, 49(11), 2471–2492, DOI:10.1016/S0022-5096(01)00064-3.
- D. C. Wallace, Thermodynamics of Crystals, Wiley & Sons, 1972, DOI:10.1119/1.1987046.
- S. Singh, L. Lang, V. Dovale-Farelo, U. Herath, P. Tavadze, F.-X. Coudert and A. H. Romero, Mechelastic: a python library for analysis of mechanical and elastic properties of bulk and 2d materials, Comput. Phys. Commun., 2021, 267, 108068, DOI:10.1016/j.cpc.2021.108068.
- Y. Li, L. Vočadlo and J. P. Brodholt, Elast: a toolkit for thermoelastic calculations, Comput. Phys. Commun., 2022, 273, 108280, DOI:10.1016/j.cpc.2021.108280.
- Z. Ran, C. Zou, Z. Wei and H. Wang, Velas: an open-source toolbox for visualization and analysis of elastic anisotropy, Comput. Phys. Commun., 2023, 283, 108540, DOI:10.1016/j.cpc.2022.108540.
- Y. Itin and F. W. Hehl, The constitutive tensor of linear elasticity: its decompositions, cauchy relations, null lagrangians, and wave propagation, J. Math. Phys., 2013, 54(4), 042903, DOI:10.1063/1.4801859.
- Y. Itin, Irreducible matrix resolution for symmetry classes of elasticity tensors, Math. Mech. Solids, 2020, 25(10), 1873–1895, DOI:10.1177/1081286520913596.
- G. Backus, A geometrical picture of anisotropic elastic tensors, Rev. Geophys., 1970, 8(3), 633–671, DOI:10.1029/RG008i003p00633.
- J. Gasteiger, J. Groß and S. Günnemann, Directional message passing for molecular graphs, in International Conference on Learning Representations, ICLR, 2020 Search PubMed.
- T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120(14), 145301, DOI:10.1103/PhysRevLett.120.145301.
- M. Wen, S. M. Blau, E. W. C. Spotte-Smith, S. Dwaraknath and K. A. Persson, Bondnet: a graph neural network for the prediction of bond dissociation energies for charged molecules, Chem. Sci., 2020, 12(5), 1858–1868, 10.1039/D0SC05251E.
- M. Wen, S. M. Blau, X. Xie, S. Dwaraknath and K. A. Persson, Improving machine learning performance on small chemical reaction data with unsupervised contrastive pretraining, Chem. Sci., 2022, 13, 1446–1458, 10.1039/D1SC06515G.
- K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, in 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR, 2016, pp. 770–778, DOI:10.1109/CVPR.2016.90.
- M. Geiger and T. Smidt, e3nn: Euclidean neural networks, arXiv, 2022, preprint, arXiv:2207.09453, DOI:10.48550/arXiv.2207.09453.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., Sect. A, 1952, 65(5), 349, DOI:10.1088/0370-1298/65/5/307.
- P. L. Reu, E. Toussaint, E. Jones, H. A. Bruck, M. Iadicola, R. Balcaen, D. Z. Turner, T. Siebert, P. Lava and M. D. I. C. Simonsen, Dic challenge: developing images and guidelines for evaluating accuracy and resolution of 2d analyses, Exp. Mech., 2018, 58, 1067–1099, DOI:10.1007/s11340-021-00806-6.
- R. Gaillac, P. Pullumbi and F.-X. Coudert, Elate: an open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28(27), 275201, DOI:10.1088/0953-8984/28/27/275201.
- A. H. Robinson, A new map projection: its development and characteristics, International yearbook of cartography, 1974, vol. 14, pp. 145–155 Search PubMed.
- C. H. L. Beentjes, Quadrature on a spherical surface, Technical report, Mathematical Institute, University of Oxford, 2015, https://cbeentjes.github.io/files/Ramblings/QuadratureSphere.pdf Search PubMed.
- Y. Huang, A. Sai Sarathi Vasan, R. Doraiswami, M. Osterman and M. Pecht, Mems reliability review, IEEE Trans. Device Mater. Reliab., 2012, 12(2), 482–493, DOI:10.1109/TDMR.2012.2191291.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, The thermodynamic scale of inorganic crystalline metastability, Sci. Adv., 2016, 2(11), e1600225, DOI:10.1126/sciadv.1600225.
- C. J. Bartel, Review of computational approaches to predict the thermodynamic stability of inorganic solids, J. Mater. Sci., 2022, 57(23), 10475–10498, DOI:10.1007/s10853-022-06915-4.
- M. N. Gjerding, A. Taghizadeh, A. Rasmussen, S. Ali, F. Bertoldo, T. Deilmann, N. R. Knøsgaard, M. Kruse, A. H. Larsen and S. Manti, et al., Recent progress of the computational 2d materials database (c2db), 2D Mater., 2021, 8(4), 044002, DOI:10.1088/2053-1583/ac1059.
- M. C. Venetos, M. Wen and K. A. Persson, Machine learning full nmr chemical shift tensors of silicon oxides with equivariant graph neural networks, J. Phys. Chem. A, 2023, 127(10), 2388–2398, DOI:10.1021/acs.jpca.2c07530.
- M. De Jong, W. Chen, H. Geerlings, M. Asta and K. A. Persson, A database to enable discovery and design of piezoelectric materials, Sci. Data, 2015, 2(1), 1–13, DOI:10.1038/sdata.2015.53.
- I. Petousis, D. Mrdjenovich, E. Ballouz, M. Liu, D. Winston, W. Chen, T. Graf, T. D Schladt, K. A. Persson and F. B. Prinz, High-throughput screening of inorganic compounds for the discovery of novel dielectric and optical materials, Sci. Data, 2017, 4(1), 1–12, DOI:10.1038/sdata.2016.134.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558, DOI:10.1016/0022-3093(95)00355-X.
- D. Hendrycks and K. Gimpel, Gaussian error linear units (gelus), arXiv, 2016, preprint arXiv:1606.08415, DOI:10.48550/arXiv.1606.08415.
- M. Weiler, M. Geiger, M. Welling, W. Boomsma, T. S. Cohen, 3d steerable cnns: learning rotationally equivariant features in volumetric data, Adv. Neural Inf. Process. Syst., 2018, vol. 31 Search PubMed.
- A. Reuß, Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle, J. Appl. Math. Mech., 1929, 9(1), 49–58 Search PubMed.
- L. Anand, K. Kamrin and S. Govindjee, Introduction to mechanics of solid materials, Oxford University Press, 2022, DOI:10.1093/oso/9780192866073.002.0004.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, et al., Pytorch: an imperative style, high-performance deep learning library, Adv. Neural Inf. Process. Syst., 2019, vol. 32 Search PubMed.
- W. Falcon, Pytorch lightning, 2023, https://github.com/Lightning-AI/lightning, accessed 2023-06-11 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00233k |
| This journal is © The Royal Society of Chemistry 2024 |