Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A multiobjective closed-loop approach towards autonomous discovery of electrocatalysts for nitrogen reduction†
Lance
Kavalsky
 a,
Vinay I.
Hegde
a,
Vinay I.
Hegde
 b,
Bryce
Meredig
b,
Bryce
Meredig
 b and
Venkatasubramanian
Viswanathan
b and
Venkatasubramanian
Viswanathan
 *a
*a
aCarnegie Mellon University, Pittsburgh, PA 15213, USA. E-mail: venkvis@cmu.edu
bCitrine Informatics, Redwood City, CA 94063, USA
First published on 2nd April 2024
Abstract
Electrocatalyst discovery is an inherently multiobjective challenge that can benefit from closed-loop approaches towards acceleration. However, previous computational closed-loop efforts for electrocatalysis have often focused on a single objective to be optimized. Here, we propose a multiobjective closed-loop strategy driven by sequential learning (SL) that employs a product of normalized property metrics to score candidates. In each iteration, a candidate catalyst system is autonomously selected via the multiobjective score, as implemented in our AutoCat software, and evaluated using a high-throughput density functional theory (DFT) pipeline. As a demonstration, we apply this scheme towards a model problem of searching for single-atom alloy (SAA) electrocatalysts for nitrogen reduction, balancing three targets: activity, stability, and cost. We limit our search to dopants on close-packed surface facets of simple transition metals, resulting in a total of 441 SAA systems in our design space. We show that our proposed formulation of the multiobjective scoring system and the SL framework efficiently explore the SAA design space to find optimal candidates. We also propose a ranking scheme that quantifies the effectiveness of an identified candidate in balancing all the target objectives, taking into account the uncertainty in the preliminary evaluation method (DFT) itself. Based on this scheme, we identify a few top-performing SAA candidates—Zr1Cr, Hf1Cr, Ag1Re, Au1Re, and Ti1Fe—for further investigation.
1 Introduction
A rapid discovery of novel high-performing electrocatalysts is crucial to facilitate an electrochemical revolution in the chemicals and materials industry.1,2 However, identifying the most promising catalyst systems from a large number of possible design spaces represents a significant challenge.3 This challenge is exacerbated with increasing nuance in electrocatalyst design, expanding to novel materials classes, where identifying activity trends to find the optimum can be highly non-trivial. Not only does a newly-identified catalyst need to possess the optimum catalytic activity, it needs to satisfy several other performance constraints to be relevant at the industrial scale. For example, (1) any promising candidate system must be economically viable (e.g. able to be synthesized at scale at relatively low cost), (2) the candidate system must be thermodynamically and operationally stable, and so on. Thus, the discovery and design of an ideal high-performing catalyst needs to balance several criteria, not limited to catalytic performance, making the search inherently a multiobjective optimization problem.Closed-loop computational frameworks as a tool to address this challenge in particular, and accelerating materials discovery in general, have recently been gaining traction.4–6 Such frameworks typically employ a sequential learning (SL) approach using predictions from machine learning (ML) models trained on existing data to identify promising systems in an unexplored design space, and evaluate such candidates with physics-based simulations (e.g., density functional theory (DFT)) in an iterative feedback loop. This approach, when combined with end-to-end automation and optimized runtimes, has the potential to significantly (by up to 20×) accelerate materials discovery endeavors.7 Such closed-loop frameworks have been leveraged for electrocatalysis, e.g., for CO2 reduction8 and oxygen evolution.9 However, prior efforts in this space have focused almost exclusively on optimizing the single objective of catalysis activity within the loop, with relatively limited consideration for other criteria such as cost and catalyst stability which are equally important. It is therefore crucial to incorporate multiobjective optimization in closed-loop frameworks for electrocatalyst discovery, as seen elsewhere for molecular design.10–12
Such a closed-loop computational framework that can simultaneously optimize several properties of interest will allow us to tackle some of the biggest current challenges in electrocatalysis, e.g., electrochemical nitrogen reduction (NRR) towards sustainable ammonia production.13–15 Ammonia is critical for synthetic fertilizers, and forecasts predict its market size to reach between 220–402 million tons produced by 2050.16 Currently, almost all industrial synthesis of ammonia uses the environmentally-harsh Haber–Bosch process, which is single-handedly responsible for 2% of global energy consumption.13 Thus, finding a high-performing electrocatalyst for NRR that is cost-effective as well as stable in a timely manner is likely to have an outsized impact on the global energy landscape.
As an example design space, single-atom alloys (SAAs) are a novel class of materials with unique electronic and geometric properties and have shown much promise for catalytic applications.17–19 Transition metal atoms dispersed in the dilute limit on a host surface can exhibit free atom-like d-states.20 This unusual electronic character of these SAA systems can be leveraged by modulating their binding with reaction intermediates.21,22 In addition, approaching the dilute limit of dispersion of a transition metal species on a host surface can also be cost-beneficial, by maximizing the utility of expensive-yet-active species in a catalyst. However, the unique properties and behavior of SAA materials preclude choosing host and dopant combinations based purely off of their performance as separate bulk materials. Further, a search over this design space is inherently multiobjective, with the ideal system possessing several characteristics such as high activity, selectivity against parasitic hydrogen evolution, low material and synthesis costs, and stability towards dopant segregation and aggregation. Therefore, the use of an iterative closed-loop approach to guide the exploration of this promising SAA design space is particularly well-motivated.
In this work, we propose a scoring scheme to support multiobjective closed-loop searches consisting of a product of normalized property metrics. Demonstrating this approach we use AutoCat, an open-source python software package, to perform a multiobjective search over the SAA design space. This software provides tooling for both electrocatalyst structure generation to be fed into DFT calculations and generalizable interfaces for the multiobjective closed-loop search. Combined with scripts to automate the required DFT calculations for evaluation, we show a fully autonomous multiobjective closed-loop framework for discovering promising SAA NRR electrocatalysts. Here we consider a simplified definition of ideal NRR electrocatalysts defined by proxies for three key target metrics—catalytic activity, material cost, and thermodynamic stability—all of which are readily amenable to our scheme. Our search places equal importance on all three metrics, and the limitations and implications of this model problem will be discussed. As a complement to the results of this search, we propose and apply a multiobjective ranking system after candidate evaluation to highlight systems of potential value within the confines of our defined ideal for further investigation.
2 Results and discussion
2.1 Design space and initial training data
SAAs consist of a transition-metal (TM) host with highly-dispersed atoms of another TM species at dilute concentrations embedded on the host surface (Fig. 1a), and the entire design space can be enumerated via three variables: host species, host surface facet, and dopant species. The host and dopant species can be chosen from the transition metal block of the periodic table. To help reduce the dimensionality of the design space, for all potential host metals we consider only the close-packed surface facet (111 for face-centered cubic, 110 for body-centered cubic, and 0001 for hexagonal close-packed). Moreover, we consider only substitutional doping of a single TM atom at the surface, leading to one surface per host–dopant combination. Other viable doping configurations include dimer formation, supporting the TM as an adatom, and burying the TM into the subsurface;23 these are beyond the scope of the present study. Individual SAAs (i.e. a single dopant–host combination) with a dopant of species X into a host of species Y will be denoted as X1Y. In total we consider 22 TM species as dopants and 21 TM hosts (Fig. 1b). Thus, the total design space of SAAs we use for searching is 441. Even though the size of the design space is relatively limited, performing a successful DFT calculation of each candidate surface is non-trivial (e.g., relaxing a large supercell with vacuum, including converging unexpected spin states). Even when using informed initial structure guesses, a high-fidelity DFT relaxation calculation can take on the order of days per candidate SAA system.7 Thus, a brute force evaluation of the entire design space poses a challenge.As a closed-loop sequential learning (SL) approach iteratively trains a surrogate ML model for predicting the target properties, an ideal starting setup would be to acquire a training set of examples that sample uniformly from the full design space. For applications where new data generation is expensive or time-consuming, such as here with high-fidelity density functional theory (DFT) calculations, leveraging already existing data is desirable. However, existing data is usually not uniformly distributed throughout the design space and may further be constrained to a small local neighborhood in it. Here, we use the structures from Tsiverioti et al.21 as part of our initial training set. This data consists mostly of Au hosts with a variety of TM dopant species, and is relatively local compared to the full SAA design space. We complement this set by randomly selecting and evaluating additional systems from the 3d block. Thus, our initial dataset consists of 18 SAA systems. Fig. 1b and c illustrates the total design space, as well as the host and dopant species present within this initial set. We exclude Mn due the significantly higher computational expense associated with its complex ground state crystal structure with a large 29-atom primitive unit cell.24
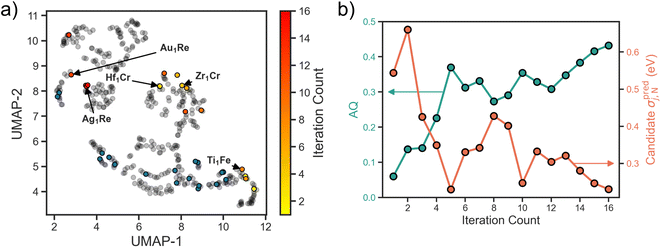
To visualize how this initial training set covers the design space, we use the uniform manifold approximation and projection (UMAP) method,25 a dimensionality reduction and visualization technique. Featurizing all of the design space compositions using the Magpie feature set,26 we apply UMAP to project onto a two-dimensional space (Fig. 1d). Blue circles represent SAA systems that are present within our initial training set and grey circles represent the full SAA design space considered here. Note that our training data is limited to a few clusters in the design space with large regions completely unexplored. This is fairly representative of real-world conditions where often previous data is leveraged as a springboard for materials design.
2.2 Electrocatalyst discovery as a multiobjective problem
Taking inspiration from existing approaches to closed-loop multiobjective design in general,10,11,27–29 here we define a framework specifically for treating electrocatalyst discovery as a quantifiable, multiobjective problem.Defining a multiobjective problem entails identifying all the objectives or target properties and their relative importances. In this work we will define the model ideal SAA NRR electrocatalyst using three properties: (1) NRR activity, (2) material cost, and (3) SAA stability. First, the ideal candidate must be active towards NRR. A common occurrence across the electrocatalysis space is the scaling of the adsorption energies which leads to an activity volcano and maximum predicted performance. From this activity volcano, an optimal adsorption energy window may be defined around the peak. Here, we will use a previously reported activity volcano with ΔGN as the descriptor.30 Second, the ideal electrocatalyst should avoid the use of any prohibitively expensive chemical species. As a proxy for the cost of elements, we use the previously-tabulated Herfindahl–Hirschman Index (HHI) for global reserves;31 the lower the HHI, the more abundant the element. While this neglects cost associated with materials synthesis, which may be a source of additional expenses, particularly at scale, HHI is applied here as a first approximation with a view towards added fidelity in future development. Third, by definition, an SAA must have the dopant atoms at the host surface to participate in the reaction. Thus, our ideal SAA must consist of a host–dopant pairing such that the dopant species thermodynamically segregate to the surface instead of the bulk of the host. This tendency can be estimated via the segregation energy, ΔEseg, a property that has been previously calculated for a number of TM species;32 a larger negative ΔEseg indicates higher tendency for a dopant to segregate to the host surface. A full description of stability would incorporate electrochemical stability, adsorbate-induced segregation, and aggregation energy (ability to avoid agglomeration into clusters on the surface). In this study, for the purposes of constraining our model problem to simple metrics, we rely solely on segregation energy.
It is worth emphasizing that our target system defined by these three metrics does not provide an exhaustive description of all properties possessed by an ideal SAA electrocatalyst for NRR. Aside from the limitations already described, selectivity represents another essential metric for a feasible NRR electrocatalyst. Moreover, tuning of the electrolyte to suppress HER is a design axis not currently considered by this model problem. These limitations highlight the trade-off between selecting metrics that provide a complete description of the ideal while remaining straightforward to calculate. Through definition of the ideal using these three manageable property metrics for activity, cost, and stability, we aim to demonstrate a scoring scheme that effectively balances targets relevant for electrocatalysis. Additionally, the formulation of each of these target metrics could serve as an example or foundation for future work that innovates towards both more realistic objectives while remaining compatible with closed-loop frameworks.
Having established this model problem and its ideal system defined by the three aforementioned target metrics, we can calculate “partial scores” of each candidate in the unexplored design space to help identify the most promising ones to evaluate. Associated with activity, cost, and stability we define Aj (eqn (1)), Cj (eqn (2)), and Sj (eqn (3)) of the j-th SAA system in the unexplored region of the design space, respectively. All three metrics are normalized with a target value of 1.
Before describing how each of these three terms are defined, it is worth reemphasizing that these partial scores are how we define the optimal candidate, and can be modified, extended, or replaced as appropriate for searches related to other electrocatalysis applications. Calculation of these partial scores has been implemented within AutoCat.
First, to quantify predicted catalytic performance of candidate system j we define Aj as follows:
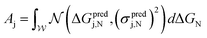 | (1) |
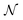 is the normal distribution,
is the normal distribution, 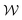 is the activity target window, ΔGpredj,N is the predicted adsorption energy of N on system j, and σpredj,N is the uncertainty in the adsorption energy prediction. In this work we define the target window to be ±0.3 eV from the volcano peak previously reported.30Aj is similar to a likelihood of improvement metric, whereby incorporating uncertainty allows for a balance of exploration and exploitation in the search for high-performers.
is the activity target window, ΔGpredj,N is the predicted adsorption energy of N on system j, and σpredj,N is the uncertainty in the adsorption energy prediction. In this work we define the target window to be ±0.3 eV from the volcano peak previously reported.30Aj is similar to a likelihood of improvement metric, whereby incorporating uncertainty allows for a balance of exploration and exploitation in the search for high-performers.
Second, as a proxy for material cost we define Cj for system j as follows:
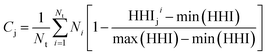 | (2) |
Third, to quantify the stability of the j-th host–dopant combination at stabilizing the dopant at the host surface we define Sj:
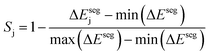 | (3) |
To autonomously select candidate systems in each iteration in the multiobjective closed-loop workflow, we need to collapse these partial scores for each target metric into a single overall score that can be used to rank candidates. There are various possible approaches towards combining these scores. For example, the previously proposed Chimera takes a lexicographic approach where metrics are ranked by importance and used to restrict the design space.27 Another approach uses distance from the Pareto frontier.28 Here, we make the choice that all three target properties are of equal importance. Since Aj, Cj, and Sj are all normalized, dimensionless, and with a target value of 1, we will formulate our acquisition function (AQ) for the j-th system as a product:
| AQj = Aj × Cj × Sj | (4) |
Formulating the AQ in this way has multiple implications. The first is in terms of candidates that are predicted to have poor performance in one of the metrics. For example, if the material cost of an SAA system was to be extremely high this will result in a Cj value close to 0 and thus a poor overall AQ score, automatically ruling it out as a promising candidate to evaluate. On the other hand, if a candidate were predicted to be highly performing in one of the metrics (e.g. Aj of 1), this is insufficient in itself and in turn places emphasis on the other metrics to determine the most promising candidate. Additionally, this score formulation assumes equal importance to activity, material cost, and stability. While to-date there have been substantial difficulties identifying suitably active NRR electrocatalysts, we argue that identification of an active material must still be cost-effective and thermodynamically stable to represent a commercially viable technology.
Alternatively, AQ can be formulated as a summation of weighted terms. Recent examples using this approach with Bayesian optimization are experimental electrochemical reactor protocols33 and electrocatalyst stoichiometry for fixed composition.34 A drawback of using a summation is the need for choosing appropriate weights for each term in the sum. Previous domain knowledge can guide this selection, but could be a barrier towards application in new domains.
Our approach here can also be contrasted with multiobjective filtering approaches where hard thresholds are defined for each metric based on prior knowledge to screen materials.35–38 When relevant large databases already exist, screening can be an attractive strategy for materials discovery. However, choosing such property thresholds can be ambiguous for some design problems. In addition, using hard thresholds can result in false negatives, e.g. when a candidate property is predicted to lie close to but not beyond a threshold, without accounting for any underlying uncertainty in the prediction and/or in the threshold itself. Our approach requires no such strict prior encoding, and allows for the full design space to be explored as determined by the AQ. Moreover, when large amounts of relevant data does not currently exist, the closed-loop SL-driven approach does not depend on the transferability of ML models and generates data on the fly as needed.
Another common approach to compare to is a closed-loop design where a single objective is optimized (e.g. activity) and then the most promising candidates further investigated and filtered based on the other properties.8,9 While this approach works well for data-scarce applications (and will generate data as needed), by optimizing for a single objective first, candidate systems that require a small compromise in one property for a better all-around performance may be missed. Incorporating the multiobjective nature of the problem directly into the AQ allows for this balance to be discovered autonomously in the loop. More explicit comparisons between closed-loop SL and thresholds-based filtering approaches are provided in Section 2.5 and ESI.†
2.3 Workflow topology
Our approach towards autonomous discovery is that of Forests with Uncertainty Estimation Learned Sequentially (FUELS).39 This approach combines high-throughput materials evaluation with candidate selection to autonomously explore a given design space and has been successfully applied in areas such as thermoelectrics39 and conducting organics.40 The core principle is that a random forest-based ML surrogate is trained on existing data and its predictions with uncertainty estimates are used to calculate AQ scores to identify promising candidate(s) to evaluate, retrain ML surrogates upon new evaluations, and so on, in an iterative manner. Such a closed-loop autonomous approach for materials discovery has the potential to accelerate the search for optimal candidates in a design space by a factor of 20× over the traditional approaches.7The FUELS approach adapted for SAA electrocatalyst search results in the workflow illustrated in Fig. 2. The process starts with training a random forest surrogate on the initial dataset (described in Section 2.1) to predict N adsorption energies with uncertainty. Using these predictions and uncertainties, the AQ scores, as defined in eqn (4), are then calculated for the entire unexplored design space. The candidate system with the highest score is selected and fed into an automated DFT pipeline. This pipeline conducts two DFT geometry optimizations: catalyst surface without any adsorbates as well as with N at the hollow site adjacent to the dopant. We choose to evaluate this single surface site for N adsorption as previous work has identified it to be the most thermodynamically favorable for single adatoms on SAAs.41 From these calculations along with the gas phase energy of N2 (which is a constant), the N adsorption energy, ΔGN, can be extracted and added to the dataset. With this newly acquired data point, the ML surrogate may be retrained and scores recalculated, thereby closing the loop. Additional details into the implementation of this workflow and the open-source software we have developed to support it, AutoCat, are provided in Section 3.3.
We note that our framework does not preclude the investigation of all unique surface sites for a candidate system, as is typically done in targeted catalyst studies, in each SL iteration. This would allow for a fully-general evaluation of the design space without the need for utilizing domain knowledge-based simplifications such as likely adsorption sites or scaling relations. However, this increased generalizability is at the cost of increased evaluation cost (i.e. number of DFT calculations per iteration), which we have previously identified as the most time-consuming task in a closed-loop computational workflow.7
2.4 Autonomous search for SAA NRR electrocatalysts
Applying the above workflow we conducted an autonomous search for SAA electrocatalysts for NRR. The full loop was allowed to iterate 16 times until signs of convergence in the design space was observed (i.e., multiple consecutive selections of candidates with a Re host). In Fig. 3a we show the search projected onto the UMAP space. For the first few iterations we observe an exploratory behavior, with candidates selected spanning the full design space. As the search progresses, the number of examples the surrogate is trained on increases, and there is a shift towards exploitative behavior. Specifically, we observe in the last few iterations an emphasis on the Re host region of the design space as evidenced by the clustering around the Ag1Re. We also observe a reluctance of the search to revisit the regions where the training data is concentrated. This could be an indication that the training data in these regions is both sufficient for the model to learn these parts of the design space and it is not where the optimum lies.The observed transition from exploration to exploitation is a reflection of our AQ. In the early iterations, uncertainty in the adsorption predictions are high as the underlying trends have yet to be learned. In Fig. 3b we visualize the uncertainty in the candidate property prediction as a function of SL iteration. We note that the highest uncertainties are mostly within the first few iterations and the lowest mostly in the last few iterations. However, a longer trajectory or multiple additional independent trajectories would be needed to claim an overall decreasing uncertainty.
In Fig. 3b we also visualize the AQ scores of the selected candidates for evaluation over the search. As desired, an overall increasing trend is observed. Since AQ embeds both the predicted value alongside its uncertainty estimate, this trend represents both the confidence of the model that the candidate is promising and its actual promise. In other words, low AQ values for the candidate in the early iterations does not necessarily mean that the model predicts poor performance for that system, but rather could imply high model uncertainty. Additionally, we highlight that while the optimal value of AQ is 1 and the trend is increasing, as our design space is discretized this value may not be achievable from the SAAs.
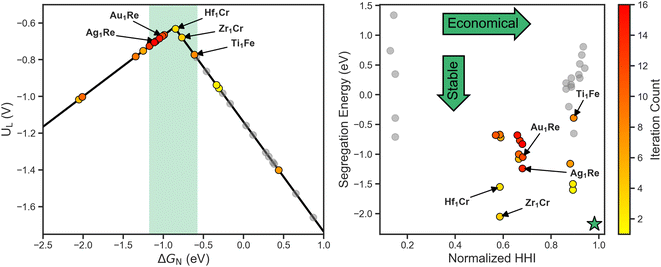
To get a better sense of the interplay between the three target metrics, we can decompose the AQ scores back into their respective quantities (Fig. 4). On the left the search trajectory on the activity volcano is shown with the target window in green. Initially, the search mainly focuses on the weak binding leg before exploring the strong binding leg. As the training set only consists of systems on the weak binding leg, this identification of systems on the strong binding leg demonstrates the exploratory nature of the search. In the latter stages, the search homes in on the strong binding leg near the peak and just inside the target window, showing the transition towards exploitation. Of the 16 candidates evaluated, 9 fall within the target activity window.
On the right of Fig. 4, the stability and cost axes of the search are visualized. The green star indicates the optimal zone of this objective space. Similarly to the activity and UMAP plots, we see an initial exploration along the HHI and segregation energy axes. This is then followed by a concentrated search, focusing on the systems with a Re host closer to the center of the space.
The concentration of the search in the latter stages implies that using Re as a host is among the most optimal region of the design space to balance all three target metrics. In terms of activity, this aligns with previous work that shows Re111 lies near the volcano peak,30 and illustrates SAAs as a method towards fine-tuning adsorption behavior to increase activity. Furthermore, this emergent design criteria demonstrates the utility of closed-loop frameworks beyond singling out individual systems, but also identifying trends and development methods.
2.5 Ranking candidate systems
Ranking of identified candidates is important for prioritizing systems to investigate experimentally. Within a single objective paradigm for discovery, ranking identified systems based on their promise can be done based upon their evaluated target values. For example, if one were to optimize solely for activity, one can rank promising systems based on their proximity to the activity volcano peak. Generalizing to multiobjective, however, ambiguity can arise from having multiple target criteria to consider based on relative performance for each axis.28Moreover, such a ranking should consider the uncertainty of the evaluation technique, here, DFT. As the exchange–correlation (XC) term within DFT is currently unknown, its approximation introduces an inherent fundamental uncertainty when evaluating our systems. Note that this is distinct from the uncertainty used in calculating Aj, which is the uncertainty in the ML-predicted value of the adsorption energy.
Bayesian error estimation (BEE) is an approach that enables quantification of this DFT uncertainty from XC approximation,42 and has been successfully applied for electrocatalysis previously.21,43–45 BEE generates an ensemble of XC functionals by sampling a previously fit posterior distribution, thereby generating an ensemble of energies for subsequent analysis. Incorporation of BEE within a ranking scheme provides an avenue for increased robustness through taking into account the underlying uncertainty in a DFT evaluation.
Formulating a score to allow such a ranking, we draw from our definition of AQ. While AQ uses activity predictions to quantify the promise of unlabelled systems, we can define an analogous quantity called the rank score (RS) to be used after the DFT evaluation is complete. This metric is similar to AQ in that it collapses the three properties into a single scalar. We define RS for the j-th system as follows:
| RSj = cactivej × Cj × Sj | (5) |
Note that, unlike AQ, RS is calculated using results from a DFT-based evaluation of a candidate (i.e., the cactivej term). Thus, RS cannot be used to guide an SL-based design space search, in contrast to AQ which is calculated for as-yet unevaluated candidates. Instead, RS aims to quantitatively rank or prioritize already-evaluated candidates for further investigation (e.g. experimental validation) based on how well they balance all the considered objectives.
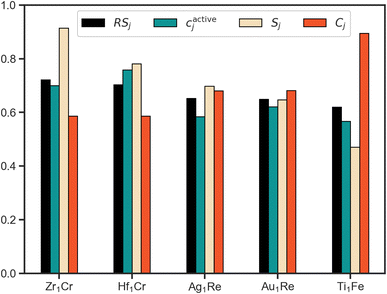
Using RS we rank the evaluated candidates with the scores of the top 5 systems shown in Fig. 5. Leveraging the fact that all of the partial scores are dimensionless and normalized with a target value of 1, we draw conclusions about the interplay of these three properties. To start, based upon this scheme Zr1Cr is identified as the system that most effectively balances our defined target metrics for activity, cost and stability. However, its cactivej is lower than Hf1Cr. As they both have identical Cj, the superior Sj of Zr1Cr is sufficient to overcome this relative deficiency. Thus, the multiobjective approach to ranking allows for emphasis on all-round performers by considering factors beyond solely activity.
Considering the top two ranked systems as defined by our multiobjective ranking scheme, Zr1Cr and Hf1Cr, it is interesting to note that while Zr and Cr have been proposed for NRR as mononitrides,46 and Hf complexes have been reported to cleave N2,47 to our knowledge these species have not been proposed for this application within SAAs. These findings point towards the ability of this closed-loop approach to discover interesting systems within feasible, yet unexplored regions of the SAA design space. However, as previously discussed, this comes with the caveat that our simplified property metrics do not provide a full description of the ideal NRR electrocatalyst.
Comparing the scores of the fourth and fifth ranked systems illustrates another example of the benefits of a quantitative multiobjective ranking scheme. While the activity and stability metrics of Au1Re are better than for Ti1Fe in direct comparison, the cost metric of Au1Re is noticeably worse than for Ti1Fe (higher Cj indicates a more cost effective material). Without a method to quantitatively compare, ambiguity could arise as to which system should be of higher priority. By introducing RS as a quantitative metric, any such ambiguity is removed.
In corroboration with the sequential learning trajectory, the platform homed in on Re-host systems, 2 of which are present in the top 5. Thus, reinforcing the autonomously unearthed design principle of Re-host SAAs. Discovery of design principles alongside individual systems is a desirable outcome towards accelerating discovery as it can highlight design space regions of importance.
As mentioned earlier, a viable alternate approach is to use pre-defined threshold values for the various target metrics (e.g., <0 eV segregation energy) to filter out candidates in the broader design space. Such an approach can require extensive domain knowledge to define threshold values, especially for objectives where the target values are not obvious, and otherwise-promising candidates may be excluded by one or more threshold-based filters. For example, using a filter of <0 eV for segregation energy and a filter of >0.8 for the normalized HHI value, would filter out 4 out of the top 5 candidates identified here (see ESI† for details).
In summary, we demonstrate a multiobjective approach for autonomous discovery of electrocatalysts and use it to identify several promising SAA candidates for NRR. Moreover, we propose a ranking scheme for identified candidates that considers multiple properties of interest. Looking ahead, we believe that coupling autonomous multiobjective searches with a multiobjective ranking scheme is useful to prioritize identified candidates for subsequent experimental studies.
3 Methods
3.1 Computational details
All spin-polarized DFT calculations were conducted using GPAW48,49via the Atomic Simulation Environment (ASE).50 A target grid spacing of 0.16 Å and a Monkhorst–Pack k-mesh of 4 × 4 × 1 were used for all systems. To approximate the electron–electron exchange–correlation, the BEEF-vdW XC functional was applied.42 For ion–electron interactions, the projector augmented wave method was used. Fermi–Dirac electron smearing with a width of 0.05 eV was applied to improve convergence.All host structures were represented as 3 × 3 supercells using the close-packed surface facet (111 for fcc, 110 for bcc, and 0001 for hcp). All slabs had four layers with the bottom two held fixed at their bulk locations. A single dopant was placed via substitution at the surface to generate the SAAs. The initial magnetic moments of the dopants were guessed based on their ground state magnetic moments, as tabulated in ASE.
For the adsorbate structures, the N was initially placed at the adjacent hollow site to the dopant. The initial guess for adsorbate height was made as per the AutoCat default. This is calculated by the following procedure:
(1) Fix the x–y coordinate of the adsorbate.
(2) Identify all surface nearest neighbors (NN) for that site.
(3) For each NN, estimate a pairwise height estimate via a right triangle where the hypotenuse is the sum of the covalent radii (as compiled in ASE) of the NN and adsorbate.
(4) Take the average of all pairwise height estimates to obtain a final height estimate.
The adsorption energy is calculated through the following expressions:
 | (6) |
| ΔGN = ΔEN + ΔZPE − TΔS | (7) |
3.2 Calculating ranking scores
When applying the BEE approach to calculating adsorption energies, we obtain an ensemble of adsorption energies by sampling from a previously fit posterior distribution.42 In this work, we take 2000 samples which yields an ensemble of XC functionals. Using each of these functionals within our energy functional, we then obtain an ensemble of 2000 adsorption energies. Analysis of this ensemble can provide insights into the sensitivity of our findings towards XC choice, and quantify the associated uncertainty.For each of our evaluated candidates, we leverage its resulting ensemble to calculate a confidence, cactivej, that its adsorption energy lies within the target activity window. We define this confidence for the for the j-th candidate as:
 | (8) |
3.3 Workflow implementation
The closed-loop workflow shown in Fig. 2 was automated using existing Python-based open-source packages as well as AutoCat, a new package specifically developed for catalyst materials design, with bespoke Python scripts implementing the interface between the various packages. The scripts and associated data files are made available via GitHub (see the “Code availability” section).• The clean SAA substrate crystal structure is generated using AutoCat.
• Input files for DFT (GPAW) calculations of the SAA substrate are automatically generated via the dftinputgen package (https://github.com/CitrineInformatics/dft-input-gen).
• All calculation management, including submission of the DFT job to high-performance compute (HPC) clusters, monitoring, restarting failed/interrupted jobs, and collection of successful job files, is performed using the FireWorks package.51
• Raw output files from successful DFT calculations are parsed into the Physical Information File (PIF) format,52 including images of the crystal structure and references to raw output files, using the dfttopif package (https://github.com/CitrineInformatics/pif-dft).
• Once the clean SAA substrate is fully relaxed, the N-adsorbed crystal structure is generated via AutoCat, and GPAW input files generated via dftinputgen, jobs handled by FireWorks, and data parsed by dfttopif into PIFs.
• The underlying ASE database with previously-calculated data is updated with the new calculation.
The design space of 441 SAA systems is represented within relevant interfaces implemented in AutoCat, and stored as an ASE database on disk. In each sequential learning (SL) iteration:
• The training set of SAA systems (i.e., all examples with a previously-calculated label, ΔGN, the N adsorption energy) is featurized into Magpie descriptors26 using the matminer package.54
• A random forest-based predictor is trained to predict ΔGN for unexplored systems in the design space. We used the implementation within the scikit-learn package,55 modified to estimate uncertainty in a given prediction as the standard deviation in the predictions of all individual tree-based estimators.
• A candidate from the unexplored design space with the highest acquisition score, incorporating the predicted adsorption energy and its uncertainty, cost, and stability targets (as described in Section 2.2), is selected for evaluation.
• The selected candidate is processed via the DFT calculation workflow as described in the previous section, to obtain the ΔGN.
• The design space is augmented with the results from the current iteration and the ASE database is updated with the modified design space. The above process is iterated upon, retraining the predictor with the new data and selecting a new candidate from the unexplored design space, until a certain number of iterations are complete or a certain number of potential high-performing candidates are identified. In other words, at the first iteration the training set consists of the 18 systems described in Section 2.1, and incrementally grows by one SAA system after each SL iteration. The interfaces implemented in AutoCat, such as DesignSpace, Predictor, CandidateSelector, SequentialLearner, and others fully automate the above-described workflow.
Code availability
AutoCat is an open-source python package and is available at https://github.com/aced-differentiate/auto_cat with tools for conducting multiobjective autonomous discovery of electrocatalyst materials.Data availability
All data and Python scripts required to perform the analysis presented in this work are made available via the GitHub repository at https://github.com/aced-differentiate/auto-electrocatalyst-discovery. Data shared includes DFT output data, BEE distributions for the candidate systems, parameters used to define the activity volcano, and serialized SequentialLearner and DesignSpace objects that contain search history statistics. Scripts shared include drivers for autonomous management of the DFT calculations and SL loop iteration, calculating AQ & RS scores, extracting partial scores, generating UMAP embeddings, and reproducing all figures from the paper. The open-source software used for this study, and their respective version numbers, are as follows: GPAW v20.1.0, ASE v3.19.1, AutoCat v2022.3.31, pymatgen v2022.11.1, fireworks v1.9.6, and scikit-learn v0.24.1.Author contributions
Conceptualization: B. M., L. K., V. H., V. V.; methodology: B. M., L. K., V. H., V. V.; software: L. K., V. H.; validation: L. K., V. H.; data curation: L. K.; writing – original draft: L. K., V. H.; writing – review & editing: all authors; visualization: L. K.; supervision: B. M., V. V.Conflicts of interest
V. V. is a co-founder at Aionics Inc.Acknowledgements
The work presented here was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001211. L. K. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC). The authors thank Lydia Tsiverioti for providing assistance in generating the initial training data.References
- D. S. Mallapragada, Y. Dvorkin, M. A. Modestino, D. V. Esposito, W. A. Smith and B. M. Hodge, et al., Decarbonization of the chemical industry through electrification: Barriers and opportunities, Joule, 2023, 7(1), 23–41 CrossRef CAS.
- Z. J. Schiffer and K. Manthiram, Electrification and decarbonization of the chemical industry, Joule, 2017, 1(1), 10–14 CrossRef.
- Y. Kim, E. Kim, E. Antono, B. Meredig and J. Ling, Machine-learned metrics for predicting the likelihood of success in materials discovery, npj Comput. Mater., 2020, 6(1), 1–9 CrossRef.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous discovery in the chemical sciences part I: Progress, Angew. Chem., Int. Ed., 2020, 59(51), 22858–22893 CrossRef CAS PubMed.
- E. Annevelink, R. Kurchin, E. Muckley, L. Kavalsky, V. I. Hegde and V. Sulzer, et al., AutoMat: Automated materials discovery for electrochemical systems, MRS Bull., 2022, 1–9 Search PubMed.
- J. H. Montoya, M. Aykol, A. Anapolsky, C. B. Gopal, P. K. Herring and J. S. Hummelshøj, et al., Toward autonomous materials research: Recent progress and future challenges, Appl. Phys. Rev., 2022, 9(1), 011405 CAS.
- L. Kavalsky, V. I. Hegde, E. Muckley, M. S. Johnson, B. Meredig and V. Viswanathan, By how much can closed-loop frameworks accelerate computational materials discovery?, Digital Discovery, 2023, 2(4), 1112–1125 RSC.
- K. Tran and Z. W. Ulissi, Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution, Nat. Catal., 2018, 1(9), 696–703 CrossRef CAS.
- R. A. Flores, C. Paolucci, K. T. Winther, A. Jain, J. A. G. Torres and M. Aykol, et al., Active learning accelerated discovery of stable iridium oxide polymorphs for the oxygen evolution reaction, Chem. Mater., 2020, 32(13), 5854–5863 CrossRef CAS.
- J. C. Fromer and C. W. Coley, Computer-aided multi-objective optimization in small molecule discovery, Patterns, 2023, 4(2), 100678 CrossRef CAS PubMed.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, Accurate multiobjective design in a space of millions of transition metal complexes with neural-network-driven efficient global optimization, ACS Cent. Sci., 2020, 6(4), 513–524 CrossRef CAS PubMed.
- C. Duan, A. Nandy, G. G. Terrones, D. W. Kastner and H. J. Kulik, Active Learning Exploration of Transition-Metal Complexes to Discover Method-Insensitive and Synthetically Accessible Chromophores, JACS Au, 2022, 3(2), 391–401 CrossRef PubMed.
- B. H. Suryanto, H. L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Challenges and prospects in the catalysis of electroreduction of nitrogen to ammonia, Nat. Catal., 2019, 2(4), 290–296 CrossRef CAS.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton and S. D. Minteer, et al., Catalysts for nitrogen reduction to ammonia, Nat. Catal., 2018, 1(7), 490–500 CrossRef.
- S. Zhang, X. Zhang, C. Liu, L. Pan, C. Shi and X. Zhang, et al., Theoretical and Experimental Progress of Metal Electrocatalysts for Nitrogen Reduction Reaction, Mater. Chem. Front., 2023, 7, 643–661 RSC.
- J. Lim, C. A. Fernández, S. W. Lee and M. C. Hatzell, Ammonia and nitric acid demands for fertilizer use in 2050, ACS Energy Lett., 2021, 6(10), 3676–3685 CrossRef CAS.
- R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Single-atom alloy catalysis, Chem. Rev., 2020, 120(21), 12044–12088 CrossRef CAS PubMed.
- R. T. Hannagan, G. Giannakakis, R. Réocreux, J. Schumann, J. Finzel and Y. Wang, et al., First-principles design of a single-atom–alloy propane dehydrogenation catalyst, Science, 2021, 372(6549), 1444–1447 CrossRef CAS.
- J. D. Lee, J. B. Miller, A. V. Shneidman, L. Sun, J. F. Weaver and J. Aizenberg, et al., Dilute Alloys Based on Au, Ag, or Cu for Efficient Catalysis: From Synthesis to Active Sites, Chem. Rev., 2022, 122(9), 8758–8808 CrossRef CAS PubMed.
- M. T. Greiner, T. Jones, S. Beeg, L. Zwiener, M. Scherzer and F. Girgsdies, et al., Free-atom-like d states in single-atom alloy catalysts, Nat. Chem., 2018, 10(10), 1008–1015 CrossRef CAS PubMed.
- L. M. Tsiverioti, L. Kavalsky and V. Viswanathan, Robust Analysis of 4e- vs 6e- reduction of Nitrogen on metal surfaces and single atom alloys, J. Phys. Chem. C, 2022, 126(31), 12994–13003 CrossRef CAS.
- H. Thirumalai and J. R. Kitchin, Investigating the reactivity of single atom alloys using density functional theory, Top. Catal., 2018, 61(5), 462–474 CrossRef CAS.
- K. K. Rao, Q. K. Do, K. Pham, D. Maiti and L. C. Grabow, Extendable machine learning model for the stability of single atom alloys, Top. Catal., 2020, 63(7–8), 728–741 CrossRef CAS.
- A. J. Bradley and J. Thewlis, The crystal structure of α-manganese, Proc. R. Soc. London, Ser. A, 1927, 115(771), 456–471 CAS.
- L. McInnes, J. Healy and J. Melville, Uniform manifold approximation and projection for dimension reduction, J. Open Source Softw. , 2018, 3, 29 Search PubMed.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, npj Comput. Mater., 2016, 2(1), 1–7 CrossRef.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Chimera: enabling hierarchy based multi-objective optimization for self-driving laboratories, Chem. Sci., 2018, 9(39), 7642–7655 RSC.
- Z. Del Rosario, M. Rupp, Y. Kim, E. Antono and J. Ling, Assessing the frontier: Active learning, model accuracy, and multi-objective candidate discovery and optimization, J. Chem. Phys., 2020, 153(2), 024112 CrossRef PubMed.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora and J. Li, et al., A Multi-Objective Active Learning Platform and Web App for Reaction Optimization, J. Am. Chem. Soc., 2022, 144(43), 19999–20007 CrossRef CAS PubMed.
- J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, The challenge of electrochemical ammonia synthesis: a new perspective on the role of nitrogen scaling relations, ChemSusChem, 2015, 8(13), 2180–2186 CrossRef CAS PubMed.
- M. W. Gaultois, T. D. Sparks, C. K. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Data-driven review of thermoelectric materials: performance and resource considerations, Chem. Mater., 2013, 25(15), 2911–2920 CrossRef CAS.
- A. Ruban, H. L. Skriver and J. K. Nørskov, Surface segregation energies in transition-metal alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(24), 15990 CrossRef.
- D. Frey, K. C. Neyerlin and M. A. Modestino, Bayesian optimization of electrochemical devices for electrons-to-molecules conversions: the case of pulsed CO 2 electroreduction, React. Chem. Eng., 2023, 8(2), 323–331 RSC.
- Y. Bai, Z. H. J. Khoo, R. I Made, H. Xie, C. Y. J. Lim and A. D. Handoko, et al., Closed-Loop Multi-Objective Optimization for Cu–Sb–S Photo-Electrocatalytic Materials' Discovery, Adv. Mater., 2024, 36(2), 2304269 CrossRef CAS PubMed.
- R. Tran, D. Wang, R. Kingsbury, A. Palizhati, K. A. Persson and A. Jain, et al., Screening of bimetallic electrocatalysts for water purification with machine learning, J. Chem. Phys., 2022, 157(7), 074102 CrossRef CAS PubMed.
- G. Zheng, Y. Li, X. Qian, G. Yao, Z. Tian and X. Zhang, et al., High-Throughput Screening of a Single-Atom Alloy for Electroreduction of Dinitrogen to Ammonia, ACS Appl. Mater. Interfaces, 2021, 13(14), 16336–16344 CrossRef CAS PubMed.
- G. K. K. Gunasooriya and J. K. Nørskov, Analysis of acid-stable and active oxides for the oxygen evolution reaction, ACS Energy Lett., 2020, 5(12), 3778–3787 CrossRef CAS.
- G. Hai, X. Xue, S. Feng, Y. Ma and X. Huang, High-Throughput Computational Screening of Metal–Organic Frameworks as High-Performance Electrocatalysts for CO2RR, ACS Catal., 2022, 12(24), 15271–15281 CrossRef CAS.
- J. Ling, M. Hutchinson, E. Antono, S. Paradiso and B. Meredig, High-dimensional materials and process optimization using data-driven experimental design with well-calibrated uncertainty estimates, Integr. Mater. Manuf. Innovation, 2017, 6, 207–217 CrossRef.
- E. Antono, N. N. Matsuzawa, J. Ling, J. E. Saal, H. Arai and M. Sasago, et al., Machine-learning guided quantum chemical and molecular dynamics calculations to design novel hole-conducting organic materials, J. Phys. Chem. A, 2020, 124(40), 8330–8340 CrossRef CAS PubMed.
- M. T. Darby, R. Réocreux, E. C. H. Sykes, A. Michaelides and M. Stamatakis, Elucidating the stability and reactivity of surface intermediates on single-atom alloy catalysts, ACS Catal., 2018, 8(6), 5038–5050 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis and J. K. Nørskov, et al., Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(23), 235149 CrossRef.
- L. Kavalsky and V. Viswanathan, Robust active site design of single-atom catalysts for electrochemical ammonia synthesis, J. Phys. Chem. C, 2020, 124(42), 23164–23176 CrossRef CAS.
- O. Vinogradova and V. Viswanathan, Distinguishing Among High Activity Electrocatalysts: Regression vs Classification, J. Phys. Chem. C, 2021, 125(8), 4468–4476 CrossRef CAS.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen and K. W. Jacobsen, et al., Assessing the reliability of calculated catalytic ammonia synthesis rates, Science, 2014, 345(6193), 197–200 CrossRef CAS PubMed.
- Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, Electroreduction of N2 to ammonia at ambient conditions on mononitrides of Zr, Nb, Cr, and V: A DFT guide for experiments, ACS Catal., 2016, 6(2), 635–646 CrossRef CAS.
- D. J. Knobloch, E. Lobkovsky and P. J. Chirik, Dinitrogen cleavage and functionalization by carbon monoxide promoted by a hafnium complex, Nat. Chem., 2010, 2(1), 30–35 CrossRef CAS PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-space grid implementation of the projector augmented wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109, DOI:10.1103/PhysRevB.71.035109.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak and L. Ferrighi, et al., Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method, J. Phys.: Condens. Matter, 2010, 22(25), 253202 CrossRef CAS PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen and M. Dułak, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002 CrossRef PubMed . Available from: http://stacks.iop.org/0953-8984/29/i=27/a=273002.
- A. Jain, S. P. Ong, W. Chen, B. Medasani, X. Qu and M. Kocher, et al., FireWorks: a dynamic workflow system designed for high-throughput applications, Concurrency Comput. Pract. Exper., 2015, 27, 5037–5059 CrossRef.
- K. Michel and B. Meredig, Beyond bulk single crystals: a data format for all materials structure–property–processing relationships, MRS Bull., 2016, 41, 617–623 CrossRef.
- C. K. Borg, E. S. Muckley, C. Nyby, J. E. Saal, L. Ward and A. Mehta, et al., Quantifying the performance of machine learning models in materials discovery, Digital Discovery, 2023, 2(2), 327–338 RSC.
- L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj and Q. Wang, et al., Matminer: An open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00244f |
| This journal is © The Royal Society of Chemistry 2024 |

![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif)