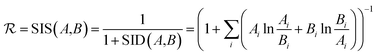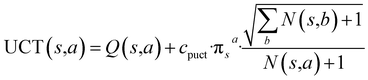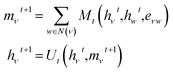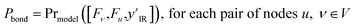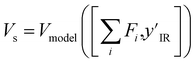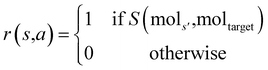DeepSPInN – deep reinforcement learning for molecular structure prediction from infrared and ¹³C NMR spectra

Abstract

Molecular spectroscopy studies the interaction of molecules with electromagnetic radiation, and interpreting the resultant spectra is invaluable for deducing the molecular structures. However, predicting the molecular structure from spectroscopic data is a strenuous task that requires highly specific domain knowledge. DeepSPInN is a deep reinforcement learning method that predicts the molecular structure when given infrared and ¹³C nuclear magnetic resonance spectra by formulating the molecular structure prediction problem as a Markov decision process (MDP) and employs Monte-Carlo tree search to explore and choose the actions in the formulated MDP. On the QM9 dataset, DeepSPInN is able to predict the correct molecular structure for 91.5% of the input spectra in an average time of 77 seconds for molecules with less than 10 heavy atoms. This study is the first of its kind that uses only infrared and ¹³C nuclear magnetic resonance spectra for molecular structure prediction without referring to any pre-existing spectral databases or molecular fragment knowledge bases, and is a leap forward in automated molecular spectral analysis.

---

Introduction

Molecular spectroscopy is the analysis of the electronic, vibrational, and rotational excitations of the nuclei of molecules as they interact with electromagnetic radiation. It is widely used as a tool to identify and characterize molecules for quantitative and qualitative analysis of materials. The spectrum of a molecule is the measured absorption or emission of the incident electromagnetic radiation. Each molecule produces a unique spectrum for a particular spectroscopic method, allowing the spectrum to be used as a fingerprint of the molecule.

Infrared (IR) spectroscopy is a spectroscopic technique that sheds light on the vibrational modes of a molecule that changes its dipole moment.¹ These vibrational modes cause the molecules to absorb electromagnetic radiation in the infrared spectral region, lying in the range of wavenumbers 4000–400 cm⁻¹. Functional groups have unique absorbances in the region of peaks beyond 1500 cm⁻¹ called the functional group region.² Peaks with wavenumbers <1500 cm⁻¹ are considered to be in the fingerprint region² since the elaborate patterns of peaks here are highly specific to a molecule and are often too complex to interpret.

Nuclear magnetic resonance (NMR) spectroscopy is another widely used spectroscopic technique to characterize the structure of molecules.³ In NMR spectroscopy, an external magnetic field is applied to a molecule and the nuclei of some isotopes (e.g.¹H, ¹³C) absorb radio waves of specific frequencies to change their nuclear spin. In ¹³C NMR for example, any small changes in the local environment of the atom in the molecule cause the ¹³C nuclei to absorb radio waves of different frequencies. The relative differences of these frequencies against a reference ¹³C NMR frequency of tetramethylsilane (TMS) are measured in parts per million (ppm)⁴ to give the chemical shifts of the nuclei. The spin–spin coupling of the adjacent protons of the ¹³C nuclei cause the splitting of the corresponding NMR signal and allows the calculation of the multiplicity of each peak. This chemical split of each ¹³C nuclei's chemical shift is indicative of the number of directly attached hydrogen atoms. Together, the chemical shift and chemical split values of a ¹³C NMR spectrum allow the deduction of the atom type and chemical environment of each carbon atom, and subsequently the complete structure of the molecule. The chemical split values however are difficult to obtain experimentally,⁵ and are not used by DeepSPInN.

For a structure to be elucidated from molecular spectra, all structural fragments are identified by interpreting the peaks in the spectra as the first step. These structural fragments are combined to list the possible molecular structures that can be made. These structures are then verified by cross-referencing the expected peaks of the functional groups in the input spectra, or by comparing their predicted spectra with the input spectra. CASE (Computer Aided Structure Elucidation) programs have evolved a lot since their introduction and have made good progress for structure elucidation from spectra, but they are still expected to have a degree of intervention from chemists and spectrometrists.⁶ These programs also typically require 2D spectra in addition to any 1D IR, NMR, and MS spectra as the input.⁷ Even today, most computational methods to identify a substance from its spectral data rely on matching against a database of already known spectra or by searching through knowledge bases of substructures.^8–16 Such methods restrict their applicability to the cases where the molecule's spectra is already stored in the database, or cases where the structural motifs are adequately represented in the dataset. These database methods are also sensitive to variations in the experimental conditions while collecting the spectra,¹⁴ and might fail if there are incorrect entries in the database.¹⁷

Recently, new methods have made use of machine learning (ML) algorithms to solve problems in computational chemistry such as predicting new drug molecules,^18–20 performing molecular dynamics simulations,^21–23 protein stability and binding site prediction,^24,25 and predicting physical molecular properties.^26–28 Efforts for finding correlations between the spectral features of molecules and their structural features using ML can be dated back to the 1990s.²⁹ Interpretation of spectra to understand the complex relationship between a spectrum and the molecular structure is a difficult task. Recent developments in deep learning open new avenues to explore the mapping between the molecular structure and the information-rich spectral data.

The forward problem for molecular structure elucidation can be defined as the prediction of the spectra of a given molecular structure, and the corresponding inverse problem is generating the molecular structure given the spectra (Fig. 1). Although they are computationally intensive, quantum mechanical methods can be used to obtain various molecular spectra. Many recent works made progress in solving the forward problem of predicting the spectra of a molecule where they utilize ML for predicting IR,^30–34 NMR,^35–37 UV-visible,³⁸ and photoionization^39,40 spectra.

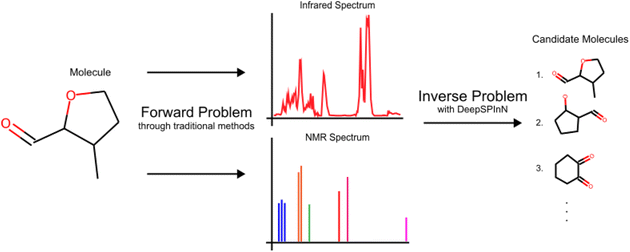Fig. 1 The IR and ¹³C NMR spectra of 3-methyloxane-2-carbaldehyde to highlight the definitions of a forward problem and its corresponding inverse problem.

There have been works demonstrating how deep learning can solve inverse problems⁴¹ in various domains. For the inverse problem in molecular structure elucidation, there have been works that aimed to automate the process of interpretation of IR spectra.^42,43 Many of them use only the functional group region of the spectra for their interpretation. Wang et al.⁴² use a support vector machine to do multi-class classification for spectra from the OMNIC FTIR spectral library. The trained support vector machine identified 16 functional groups with a prediction accuracy of 93.3%. Fine et al.⁴³ introduce a multi-label neural network to identify functional groups present in a sample using a combination of FTIR and MS spectra. Jonas⁴⁴ and Howarth et al.⁴⁵ used a deep neural network that works with proton-coupled ¹³C NMR to predict the molecular structure. Zhang et al.⁴⁶ use ChemTS⁴⁷ to identify a molecule from its NMR spectrum using Monte Carlo tree search (MCTS) guided by a recurrent neural network (RNN). Huang et al.⁵ propose an ML-based algorithm that takes ¹H and ¹³C NMR as input and predicts the correct molecule as the top scoring candidate molecule with an accuracy of 67.4%. Pesek et al.⁴⁸ introduce a rule based combinatorial approach in which the framework uses ¹H and ¹³C NMR, IR, and mass spectra to elucidate the structure of an unknown compound and emphasises that the approach does not depend on database searches. Although this method does not use any spectral databases, it involves a step to pick ¹H NMR peaks and their multiplicities, which is subject to user interpretation and is heavily dependent on the correctness of the peak-picking step.⁵ Such knowledge engineering and rule based approaches would limit the capability of the solution since they inherit the biases of the rules programmed,¹⁴ and might not contain the data for fragments that are appropriate for the given input spectra.⁴⁹ This highlights the need for molecular structure elucidation methods that do not depend on spectral databases, while also not requiring any knowledge engineering.

Elyashberg and Argyropoulos⁶ predict that using deep learning algorithms would improve the performance and robustness of CASE systems. They also highlight AlphaZero's success in mastering games⁵⁰ as a testament to how deep learning can learn to perform complicated tasks. A concurrent work⁵¹ proposes a transformer model that utilizes IR spectra to achieve a top-1 accuracy of ∼55% on molecules with less than 10 heavy atoms. Another similar concurrent work⁵² utilizes both ¹H and ¹³C NMR spectra to achieve a top-1 accuracy of ∼70% on molecules with less than 10 heavy atoms. It has recently been shown that a Monte-Carlo tree search (MCTS) algorithm can be used for the elucidation of molecular structure from ¹³C NMR chemical shifts and splits, achieving a top-1 accuracy of 57.2% (ref. 53) for molecules with less than 10 heavy atoms on the nmrshiftdb2 (ref. 54) dataset that contains experimentally calculated ¹³C NMR spectra of 2134 molecules.

In this paper, our main contribution is a framework that utilizes IR and ¹³C NMR spectra to accurately identify the molecular structure without any knowledge engineering or database searches. The proposed framework predicts the connectivity between the atoms, i.e. predicts the constitutional isomer of the molecular formula that corresponds to the input spectra. DeepSPInN formulates the molecular structure prediction problem as an MDP and employs MCTS to generate and traverse a search tree while using a set of pre-trained Graph Convolution Networks⁵⁵ to guide the tree search. DeepSPInN is able to achieve an accuracy of 91.5% on molecules with less than 10 heavy atoms, outperforming previous and concurrent works on structure elucidation from molecular spectra.

Methods

Dataset

The QM9 (ref. 56 and 57) dataset is a subset of the GDB-17 (ref. 58) chemical universe and consists of 134k stable small organic molecules with up to nine heavy atoms (CNOF). We first identified molecules in the QM9 dataset for which IR and ¹³C NMR spectra were calculated using the Gaussian 09 (ref. 59) suite of programs. We were able to calculate both IR and ¹³C NMR spectra for 119 062 molecules. We then chose molecules where the smallest ring (if any ring(s) exist(s)) in the molecule has at least 5 atoms to account for ring strain, and molecules where none of the atoms have any formal charge. This left us with about 50k molecules to use as the input data for this work. A train–val–test split of 80–10–20 was used to make the train, validation, and test dataset of molecules. We used the validation set to choose hyperparameters for DeepSPInN, which we used for evaluating DeepSPInN on the test set.

To calculate the IR absorbance spectra, the geometrical optimization and the subsequent calculation of the vibrational frequencies were done using the B3LYP density functional methods with a 6-31g(2df,p) basis set in the gas phase. The spectra from these DFT calculations for each molecule is a set of frequency–intensity pairs. These infinitely sharp stick spectra were broadened to mimic actual gas-phase spectra using a peak broadening function as described and trained by McGill et al.⁶⁰ This function is a two-layer fully connected neural network followed by an exponential transform, and takes frequency–intensity pairs to give a continuous spectrum. Following previous methods that predicted infrared spectra,⁶⁰ the intensities of the resulting spectra were binned with a bin-width of 2 cm⁻¹ in the spectral range from 400–4000 cm⁻¹ to accommodate the available datasets of experimental infrared spectra. This results in the gas-phase IR absorbance spectrum for each molecule being represented by a 1801-length vector.

To analyse the congruence of the simulated and experimental IR spectra, we compare the simulated and experimental IR spectra of the molecules from our dataset that are also in the NIST Quantitative Infrared Database⁶¹ and present this in the ESI.† Due to the shortcomings of the DFT calculations and the peak expansion, the simulated spectra are not sufficiently similar to the experimental spectra to be considered as replacements for the experimental spectra. However, they reflect the complexity of experimental spectra by being able to account for the signatures of functional groups and by containing realistic peak shapes.^60,62 If DeepSPInN performs well by learning to capture relevant characteristics of simulated infrared spectra, it could similarly interpret and learn from experimental infrared spectra.

To make a dataset of ¹³C NMR spectra, the peak positions (chemical shift) were obtained from the QM9-NMR dataset.⁶³ The QM9-NMR dataset has the gas phase mPW1PW91/6-311+G(2d,p)-level atom-wise isotropic shielding for the QM9 dataset. These ¹³C isotropic shielding (σ_iso) values were converted to ¹³C chemical shifts (δ_iso) through δ_iso = σ^reference_iso − σ_iso,⁶⁴ where σ^reference_iso is the reference value for tetramethylsilane (TMS), which is a standard reference compound. The root mean square error (RMSE) between the ¹³C NMR spectra obtained in this way against spectra from the experimental nmrshiftdb2 (ref. 54) database for the common molecules is 2.55 ppm per peak. As a reference, ¹³C NMR shift values are typically between 0–200 ppm. The state-of-the-art ML-based ¹³C NMR shift prediction methods achieve an RMSE of 1–5 ppm,^36,65,66 and DFT calculated ¹³C NMR shift values have RMSE values ranging between 2.5–8.0 ppm.⁶⁷ An RMSE of 2.5 ppm shows great congruence between experimental ¹³C NMR and the simulated ¹³C NMR spectra that we use.

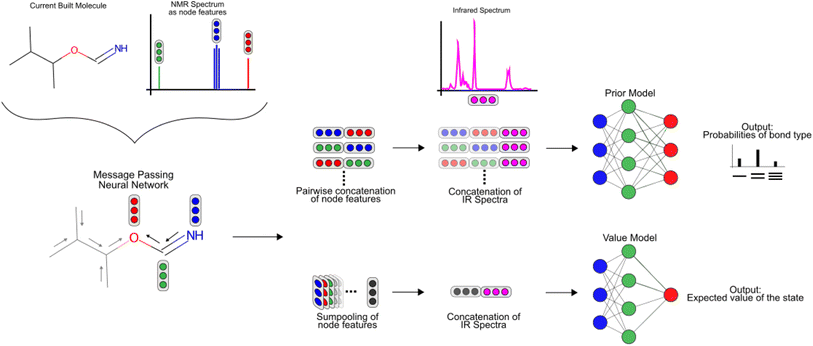
DeepSpInN framework

The methods section is divided into five parts to explain the proposed framework:

(i) Description of how molecular structure prediction can be modelled as a Markov decision process (MDP).

(ii) Description of how MCTS can be used to generate a search tree of molecules and refine the policy at each state.

(iii) Explanation of the architecture of the prior and value model used by DeepSPInN.

(iv) Explanation of how ¹³C NMR split values are used to prune the MCTS search tree.

(v) Description of the training methodology used to train the prior and value model.

MDP formulation

The problem of molecular structure prediction can be modelled as a finite Markov decision process (MDP)^68,69 in a way similar to the formulation in Sridharan et al.⁵³ An MDP is defined as a tuple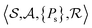 with states 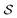, actions 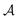, policy {P_s}, and reward function 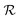.⁷⁰ The goal is to learn the policies P_s which gives the transition probabilities over the action space 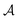at a particular state .

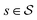Each state 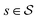consists of a molecular graph m and the target IR spectrum y_IR. A molecular graph represents a molecule where the atoms and bonds are mapped to nodes and edges in a graph. m also has the information about the target ¹³C NMR spectrum encoded as node-wise features. In the initial state, the molecular graph is a null graph with nodes representing each atom in the molecular formula and no edges. The molecule mol_s at a state s is the largest connected component in the molecular graph. The remaining individual nodes in m might join mol_s after taking an action 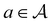. In the initial state, mol_s is just a single carbon atom corresponding to any of the nodes in m.

An action 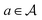adds an edge between two nodes in m, which is equivalent to the addition of a bond between two atoms. Since the QM9 dataset has molecules that have a maximum of 9 atoms (number of nodes) and since there are 3 types of bonds (edges), the action space 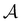has 9 × 9 × 3 = 243 actions. For the molecular graphs to represent chemically valid molecules, only a subset of these actions can be considered to be valid. If a state has no valid actions that can be taken to reach any children states, it is a terminal state. In the action space for a state s, the valid actions are those that satisfy these conditions:

• Out of the two nodes that the action adds an edge between, at least one of the nodes must belong to the largest connected component (mol_s) of the molecular graph, i.e. the current molecule of the state.

• The edge added by the action should satisfy the chemical valency rules of the two nodes. If all the edges of a node do not satisfy the octet of the corresponding atom type, it is implicitly assumed that hydrogen atoms contribute to the octet.

• The action should not create a self-loop since atoms do not form bonds with themselves.

• The action does not add an edge between two nodes that already belong to the same cycle.

• The action does not create a cycle whose length is less than 5, since rings with less than 5 atoms have high ring strain if they have double or triple bonds.

The reward function 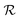returns a non-zero reward for all terminal states and a zero reward for all non-terminal states. For the terminal states, the reward is a function of the spectral distance between the input IR spectrum and the IR spectrum of mol_s as predicted by Chemprop-IR.⁶⁰ Chemprop-IR is an extension to the Chemprop⁷¹ architecture and uses a Directed Message Passing Neural Network⁷²(D-MPNN) to predict the IR spectrum of an input molecular graph. 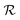is the Spectral Information Similarity⁶⁰ (SIS) metric which is calculated by rescaling the spectral divergence between two IR spectra found by their Spectral Information Divergence⁷³ (SID). The reward function 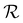is given by:

where A and B are two IR spectra.

Generating and exploring the search tree with MCTS

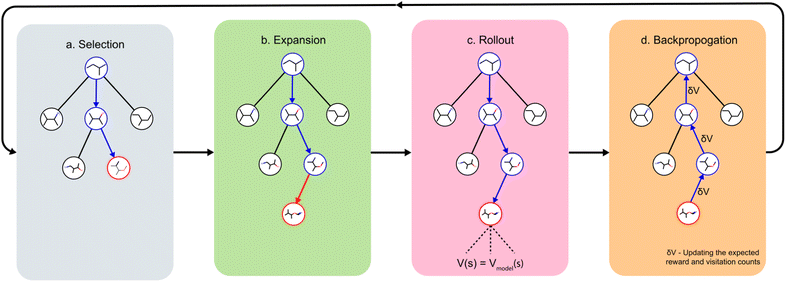
With this MDP formulation, we can use search algorithms to build a tree of state-labelled nodes.^74,75 We can build such a tree by repeatedly starting at the root state and reaching children states by taking any of the valid actions at each state. We use MCTS to estimate the optimal policy for the modelled reinforcement learning (RL) task.⁷⁶

Starting from a root node, MCTS has 4 stages – selection, expansion, roll-out, and back-propagation (see Fig. 2). In the selection stage, the algorithm chooses actions with probabilities proportional to their UCT⁷⁴ (Upper Confidence Bound applied to trees) values, until it reaches a leaf node. The UCT value of an action a at state s is given by

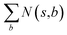where Q(s,a) is the expected reward of taking action a from state s, c_puct is a parameter to balance exploration and exploitation in the tree search, π_s^a is the probability of taking action a from state s according to the policy returned by a prior model, N(s,a) is the number of times action a has been taken from state s, and is the number of times state s has been reached.

Fig. 2 MCTS progresses in 4 stages to generate the search tree. (a) Selection: starting from the root node of the tree, choose actions based on the UCT values (b) expansion: when the tree search reaches a leaf node, add a new child state to the tree (c) rollout: calculate the expected reward of the new child state through a series of random roll-outs (d) backpropagation: update the UCT values of all ancestors of the new child state.

In the process of traversing the search tree according to the UCT values, the algorithm would reach a point where taking an action a from state s would lead to a state s′ that does not exist in the search tree. This leads to the expansion stage of MCTS where the new state s′ is added to the search tree.

Once a new child node s′ is added in the expansion stage, the rollout stage is used to evaluate the value of s′. An ideal way to calculate this value is to calculate the expected reward by a series of random rollouts. Due to the computational complexity of calculating the expected reward in the ideal way, we approximate the value using an offline-trained value model.^50,77 The value of s′ is recursively back-propagated through all its parent nodes till the root node to update the ancestors' values and visitation counts. If s is a terminal state that already exists in the tree, the reward of s is back-propagated to update the values of all ancestor nodes. A state s is considered to be terminal if it has no valid actions, or if its reward exceeds a particular threshold (explained in the ESI†). All 4 MCTS stages are repeated n_mcts number of times which is a hyper-parameter of DeepSPInN. After n_mcts repetitions of the above 4 MCTS stages, a true action is taken according to the final policy at this state.

Description of the prior and value model

To featurize the built molecule at each state, both the prior and value model use a Message Passing Neural Network^55,78 (MPNN) that run for three time steps (see Fig. 3). Consider a molecular graph G(V,E) where each node has initial node features x_v, ∀v ∈ V. Each x_v is a vector of length 88 and contains the chemical description of the atom and the ¹³C NMR peak of the atom corresponding to node v as listed in Table 1. Each node v also has hidden features h_v that are initialized to x_v, with the MPNN updating these hidden features in each time step of the forward pass. All edges in the molecular graph have edge features e_vw, ∀v, w ∈ V as listed in Table 1. The forward pass of an MPNN has T message passing time steps and a final gathering step. The message passing steps use a message function M_t to form messages from the hidden features of neighbouring nodes N(ν) and the features of their corresponding edges. An update function U_t updates the hidden features of a node based on its current hidden features and the messages it received from its neighbouring nodes.

Fig. 3 A prior model and a value model are used with the MCTS algorithm to get the probabilities over the action space and to predict the value of a particular state. An MPNN uses the initial node-wise features that contain the ¹³C NMR spectrum to give node-wise embeddings after three message passing steps. The prior model uses the pair-wise node embeddings and the IR spectrum to predict the probability of each pair of nodes having a single, double, or triple bond between them. The value model uses the sumpooled node-wise embeddings and the IR spectrum to predict the value of a particular state.

Table 1 Featurization of nodes and edges in the molecular graph

Node feature	Description
a Used only for the experiment with proton-coupled ^13C NMR spectra.
Element type	One-hot of [C, N, O, F]
Hybridization	One-hot of [sp, sp^2, sp^3]
Implicit valency	One-hot of [0, 1, 2, 3, 4]
Radical electrons	One-hot of [0, 1, 2]
Formal charge	One-hot of [−2, −1, 0, 1, 2]
^13C NMR split	One-hot of [0, 1, 2, 3]^a
^13C NMR shift	A Gaussian with σ = 2 centered at the chemical shift value discretized into 64 bins

---

Edge feature	Description
Bond type	One-hot of [single, double, triple, aromatic]
Bond conjugation	Boolean of whether the bond is conjugated
Presence in a ring	Boolean of whether the bond is in a ring

---

After T message passing steps, a gathering function G_T uses the initial node features x_v and the final hidden features h_v to give the node-wise features F_v.

F_v = G_T(x_v,h_v^t)

In DeepSPInN, M_t and U_t are fully connected neural networks, and G_T is an element-wise addition operation.

Using the node-wise features from the MPNN, the prior model generates all possible pairs of nodes and concatenates the node-wise features of all these pairs of nodes to get pair-wise features. y_IR is compressed into 100-length vectors by passing through a two-layer fully connected neural network to give 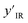and is appended to all these pair-wise features. The product of this concatenation is passed through another two-layer fully connected neural network Pr_model to predict the probabilities of a bond of each of the three types (single, double, triple) existing between the pair of nodes. The prior model works as follows

where, “[·]” represents a concatenation operation, Pr_model is the prior model, and P_bond is a 3-tuple giving the probabilities of nodes u and ν having a single, double, and triple bond respectively.

The value model first performs a sum-pooling operation on the node-wise features obtained from the MPNN. It then appends the compressed IR spectrum to the sum-pooled feature vector of the molecule and passes this through a two-layer fully connected neural network V_model to predict the value of this state. The value model works as follows

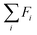where, is the result of the sum-pooling operation of all node-wise features in the molecular graph.

Training methodology

The prior and value model are trained on a set of experiences generated from a guided tree search on the molecules in the training dataset. These experiences are generated by building and exploring the search tree with MCTS, but with a modified reward function. Since the target molecule is known while training, the reward function is replaced with a binary function r that returns a value depending on whether the molecule built at the current state is subgraph isomorphic to the molecular graph of the target molecule. The reward for taking an action a from state s to reach state s′ is:
where mol_s′ is the molecular graph of the molecule at state s′, mol_target is the molecular graph of the target molecule, and S(mol_s′, mol_target) is RDKit's⁷⁹ substructure search that does a subgraph isomorphism check and returns a boolean value.

The policies and values of each state in the trees built during the training period are stored and are used to train the prior and value models. We use the Adam optimizer⁸⁰ with a learning rate of 1e − 5 to train the models. The entire training took about 45 hours on a system with a Intel Xeon E5-2640 v4 processor and a GeForce GTX 1080 Ti GPU.

Choosing the hyperparameters n_mcts and number of episodes

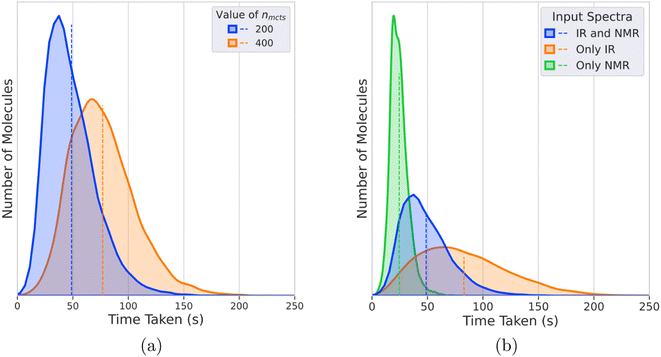
We test multiple values of the n_mcts hyperparameter and the number of episodes for each set of input spectra to choose the best values. Each episode builds the MCTS tree from scratch by going through all four phases of MCTS n_mcts times and returns a final molecule. All the unique candidate molecules from these episodes are then ranked using the reward function as a scoring function. To choose the best hyperparameters, we consider the top N metrics where each top N metric denotes whether the target molecule was present in the top N ranked candidate molecules.

For the n_mcts hyperparameter, we test the values 200, 400, and 800 on the validation set where each set of input spectra goes through a maximum of 40 episodes. The top N metrics for each value of n_mcts is shown in Table 2. Across the various n_mcts values, the top 1 (%) accuracy increases as n_mcts increases. There is a stark increase in the top 1 (%) accuracy between n_mcts = 200, 400, but there is only a marginal difference between n_mcts = 400, 800. This shows that increasing n_mcts further will result in diminishing increase in performance while taking a disproportionately greater amount of time as shown in Fig. 5b. We use n_mcts = 400 to show the best results of DeepSPInN, and n_mcts = 200 to run various experiments in a reasonable time. To choose the number of episodes, we analyse the number of episodes that are taken when a molecule is correctly predicted. For the correctly predicted molecules, the right molecule was found within 10 episodes 86% of the time. The right molecule was found 99.9% of the time when DeepSPInN is run for 32 episodes, which we found to be the ideal number of episodes for running further experiments. Further information regarding this is provided in the ESI.†

Table 2 Top N metrics for varying n_mcts values with 40 episodes on the validation set

n mcts	IR + ^13C NMR
	200	400	800
Top 1 (%)	86.47	91.42	91.56
Top 3 (%)	87.05	92.13	92.49
Top 5 (%)	87.20	92.19	95.57
Top 10 (%)	87.39	92.33	96.07

---

Results

To rigorously evaluate DeepSPInN, we present the results of a few experiments in the following subsections. The first subsection compares the performance of DeepSPInN for different n_mcts values. The next subsection compares the final rewards for correctly and incorrectly predicted molecules. In the following subsection, the time taken to predict the molecules for different n_mcts values is analyzed. In the subsequent subsection, performance of the model is discussed when only one of IR or ¹³C NMR spectrum is given as the input. The final subsection describes and presents the results of an experiment to check the generalizability of DeepSPInN.

Performance of DeepSPInN for varying n_mcts values

Table 3 compares the results for different values of n_mcts when given both IR and ¹³C NMR spectra. For n_mcts = 400, DeepSPInN correctly identifies the target molecule ∼91.5% of the time as the top candidate molecule. Even with n_mcts = 200, DeepSPInN is able to outperform the previous MCTS-based structure elucidation method⁵³ that has a best top 1 (%) accuracy of ∼60% compared to DeepSPInN's top 1 (%) accuracy of ∼86.9% for n_mcts = 200.

Table 3 Top N metrics for varying n_mcts on the test set

n mcts	IR + ^13C NMR
	200	400
Top 1 (%)	86.91	91.46
Top 3 (%)	87.54	92.16
Top 5 (%)	87.60	92.22
Top 10 (%)	87.62	92.24

---

Even within each n_mcts value, the top N (%) metrics increase marginally starting from top 1 (%) to top 10 (%). The increases across the top N (%) metrics are due to an imperfect scoring function being used to rank all the candidate molecules. If the correct target molecule is not ranked as the top candidate molecule, it would contribute to one of the top N (%) metrics. Still, we observe that the scoring function proposed in DeepSPInN is significantly better than the one used in Sridharan et al.⁵³ since they report great differences across the top N (%) metrics. DeepSPInN does not show such great differences in the top N metrics, illustrating that the scoring function used here performs better in ranking the candidate molecules. In DeepSPInN, if the correct molecule is found to be one of the candidate molecules, it is almost always ranked as the top candidate.

Comparison of rewards for correctly and incorrectly predicted molecules

Fig. 4 contains the histograms of the rewards for the cases when DeepSPInN was and was not able to predict the correct molecule as the top candidate. The histogram of the rewards for the correctly predicted molecules has a very narrow distribution and has an average reward of 0.975. It is also left-skewed with most of the correctly predicted molecules receiving a higher reward when compared to the incorrectly predicted molecules. The histogram of the rewards for the incorrectly predicted molecules has a broader distribution with an average reward of 0.808. 88.56% of the correctly predicted molecules had a reward ≥0.95 while only 8.9% of the incorrectly predicted molecules had a reward ≥0.95. DeepSPInN would allow researchers to use the final reward as a confidence measure of the correctness of the prediction. When DeepSPInN gives a final reward ≥0.95 for a set of input spectra, the top candidate is the target molecule 99.9% of the time. The top candidate molecules even for these incorrectly predicted molecules are structurally similar to the correct molecule, with the average Tanimoto similarity between the correct molecule and the top candidate molecule being 0.954 for the test set.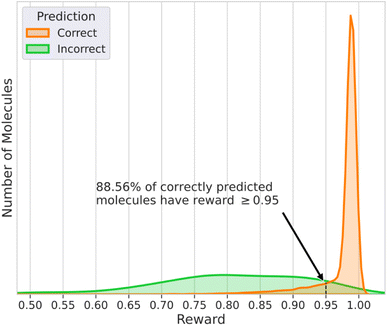

Fig. 4 Histogram of the rewards of molecules that had the correct and incorrect structure as the top ranked candidate molecule for n_mcts = 400.

Analysis of the time taken for the predictions

Fig. 5a shows the distribution of times taken for DeepSPInN to predict candidate molecules for input IR and ¹³C NMR spectra for different values of n_mcts. For n_mcts = 400, the average time taken is 77 seconds with 95% of the test molecules taking less than 130 seconds. Fig. 5b shows the distributions of times taken by IR-and-NMR-trained, IR-trained, and NMR-trained models to predict candidate molecules for n_mcts = 200. The NMR-trained model has the fastest average prediction time of 24 seconds, while the IR-trained model has the slowest average prediction time of 82 seconds. The IR-and-NMR-trained model has an average prediction time of 49 seconds. The NMR-trained model is the fastest because the model is smaller due to the IR spectrum compression neural networks being removed. The IR-trained model is the slowest since DeepSPInN has to explore more of the search tree in each episode, when compared to the IR-and-NMR-trained model that also has the ¹³C NMR shift values as the input.

Fig. 5 Histograms of time taken to predict each molecule when given both IR and ¹³C NMR spectra or either one spectrum. (a) Histograms of the time taken to predict each molecule when given both IR and ¹³C NMR spectra for varying n_mcts values, (b) histograms of the time taken to predict each molecule when given either IR or ¹³C NMR spectra for n_mcts = 200.

Importance of having both IR and ¹³C NMR spectra as input

To compare the distinguishing ability of IR and ¹³C NMR and to compare the utility of having both IR and ¹³C NMR spectra as the input, we performed ablation studies where we ran the model with either one of the spectra as the input for n_mcts = 200. Table 4 shows the top N metrics for the models that received both IR and NMR, only IR, and only NMR spectra as input. The IR-and-NMR-trained model has a top 1 accuracy of 86.9% while the IR-trained and NMR-trained models have a top 1 accuracy of 73.15% and 29.37% respectively. All top N metrics for the IR-and-NMR-trained model are greater than the models that work with either one of the spectra. This implies that the model is able to learn complementary information from both the spectra and subsequently performs better than the models with either one of the spectra as the input. Among the models that work on either one of the spectra, the IR-trained model performed significantly better than the NMR-trained model in all the top N metrics.

Table 4 Performance of IR-and-NMR-trained, IR-trained, and NMR-trained models for n_mcts = 200

	IR and NMR	Only IR	Only NMR
Top 1 (%)	86.91	73.15	29.37
Top 3 (%)	87.54	73.31	37.99
Top 5 (%)	87.60	73.32	39.76
Top 10 (%)	87.62	73.32	40.66

---

Generalizability of DeepSPInN in understanding the action space

To understand how well DeepSPInN generalizes learning about the actions, the prior and value models were first trained on all molecules with less than 8 heavy atoms. It was then tested on a subset of molecules with 8 or more heavy atoms using these prior and value models. Table 5 shows the top N metrics for this subset of test molecules, and the top N metric for 8-atom molecules and 9-atom molecules in this subset. DeepSPInN achieves a top 1 accuracy of 68.52% even when all the test molecules have more heavy atoms than the molecules that DeepSPInN was trained on. The top 1 accuracy on molecules with 8 and 9 heavy atoms is 89.88% and 64.63% respectively. The decreased accuracy when compared to the original model might be because there were very few molecules for training the prior and value models in this experiment. When DeepSPInN is trained on molecules with ≤7 atoms, it might perform worse on bigger molecules since they have more combinations of functional groups in each test molecule than it has seen in the molecules used for the training. We study whether DeepSPInN is able to predict some functional groups better than the others by calculating the top N for molecules that contain various functional groups. More details and results of both these experiments are available in the ESI.† In another experiment shown in the ESI,† the current DeepSPInN model trained on simulated spectra does not perform well on elucidating structures from experimental spectra. DeepSPInN is able to learn the complexity of spectra, as seen by its performance on simulated spectra, and can be generalized to perform well on unseen experimental spectra when it is also trained on experimental spectra.

Table 5 Training on molecules with ≤7 atoms and testing on molecules with ≥8 atoms for n_mcts = 200

	≥8 Atom molecules	8-Atom molecules	9-Atom molecules
Top 1 (%)	68.52	89.88	64.63
Top 3 (%)	68.92	90.14	65.05
Top 5 (%)	69.0	90.27	65.12
Top 10 (%)	69.06	90.27	65.19

---

Structural complexity of molecules resolved by DeepSPInN

To demonstrate the structural complexity addressed by DeepSPInN in elucidating molecular structures from infrared and ¹³C NMR spectra, we show 20 complex molecules that were the top candidate molecule as predicted by DeepSPInN in Fig. 6. We quantified the complexity of molecules using the Bertz complexity⁸¹ descriptor implemented in RDKit.⁷⁹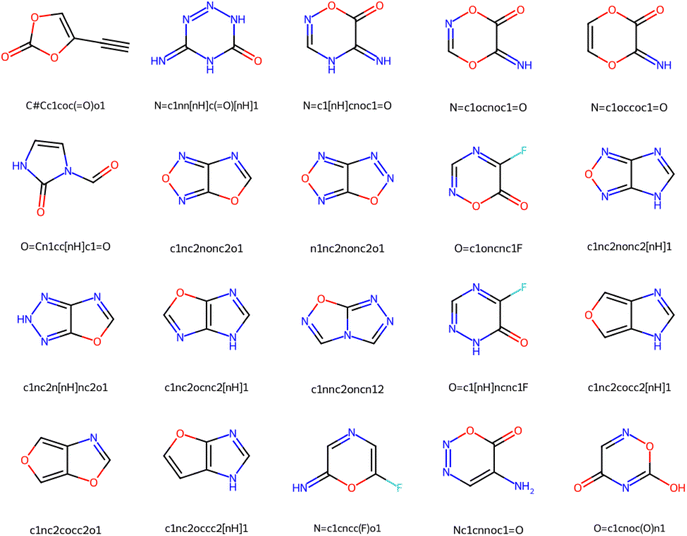

Fig. 6 20 complex molecules successfully predicted by DeepSPInN, demonstrating the structural complexity addressed by DeepSPInN.

Conclusions

DeepSPInN predicts the molecular structure when given an input IR and ¹³C NMR spectra without searching any pre-existing spectral databases or enumerating the possible structural motifs present in the input spectra. After formulating the molecular structure prediction problem as an MDP, DeepSPInN employs MCTS to explore and choose the actions in the MDP. After building a null molecular graph from the molecular formula, DeepSPInN builds the molecular graph by treating the addition of each edge as an action in the MDP with the help of offline-trained GCNs to featurize each state in the MDP. DeepSPInN is able to correctly predict the molecular structure for 91.5% of input IR and ¹³C NMR spectra in an average time of 77 seconds for molecules with <10 heavy atoms.

DeepSPInN currently works on molecules that have less than 10 heavy atoms and future work could extend DeepSPInN to work on bigger molecules, or perhaps introduce other approaches that can easily be extended to bigger molecules. Since the number of molecules increases exponentially as the number of heavy atoms increase, future work could try to have a subset of molecules for different number of heavy atoms rather than trying to exhaustively train on all possible molecules of greater sizes. DeepSPInN currently requires the molecular formula to be inferred from another chemical characterization technique apart from the input spectra. Removing this requirement is an aspect that can be explored in the future. We demonstrated the capability of our method to effectively learn to characterize simulated IR and ¹³C NMR spectra, which reflect the complexity of experimental spectra. This paves the way for future works to build datasets of experimental spectra and validate our method on them. Additionally, it will be interesting to see if DeepSPInN's accuracy improves with the addition of other spectral information such as UV-Vis spectra and mass spectra. We believe that DeepSPInN is a valuable demonstration of how machine learning can contribute to molecular structure prediction, and that it would help spur further research in the application of deep learning in high-throughput synthesis to enable faster and more efficient drug discovery pipelines.

Data availability

The data and code used in this work can be accessed through the GitHub repository.

Author contributions

S. D., B. S., and S. M. wrote the bulk of the code specific to this work. B. S., S. M., Y. P., and S. L. conceptualized the original approach. S. D. prepared the draft manuscript text and figures with input from B. S., S. M., G. V., and U. D. P. All co-authors were involved in editing and reviewing the final manuscript. U. D. P. defined the problem and supervised the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors have been partly or entirely supported by IHub-Data, DST-SERB (CRG/2021/008036), and IIIT Hyderabad’s Kohli Center on Intelligent Systems. The funders however did not have any role in the conceptualization, design, data collection, analysis, decision to publish, or preparation of the manuscript.

References

1. d. P. J. Atkins PW, Elements of physical chemistry, Oxford U.P,Oxford, 5th edn, 2009, p. 459.
2. J. G. Smith, Mass Spectrometry and Infrared Spectroscopy, Organic Chemistry, McGraw-Hill, 5th edn, 2016, ch. 13.
3. E. Brian and B. F. T. Mann, ¹³C NMR data for organometallic compounds, Academic Press, 1981.
4. The Theory of NMR – Chemical Shift, University of Colorado, Boulder, Chemistry and Biochemistry Department, 2011.
5. Z. Huang, M. S. Chen, C. P. Woroch, T. E. Markland and M. W. Kanan, A framework for automated structure elucidation from routine NMR spectra, Chem. Sci., 2021, 12, 15329–15338.
6. M. Elyashberg and D. Argyropoulos, Computer Assisted Structure Elucidation (CASE): Current and future perspectives, Magn. Reson. Chem., 2021, 59, 669–690.
7. D. C. Burns, E. P. Mazzola and W. F. Reynolds, The role of computer-assisted structure elucidation (CASE) programs in the structure elucidation of complex natural products, Nat. Prod. Rep., 2019, 36, 919–933.
8. C. Steinbeck, Recent developments in automated structure elucidation of natural products, Nat. Prod. Rep., 2004, 21, 512–518.
9. Y. Kwon, D. Lee, Y.-S. Choi and S. Kang, Molecular search by NMR spectrum based on evaluation of matching between spectrum and molecule, Sci. Rep., 2021, 11, 1–9.
10. K. Dührkop, H. Shen, M. Meusel, J. Rousu and S. Böcker, Searching molecular structure databases with tandem mass spectra using CSI: FingerID, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12580–12585.
11. M. E. Elyashberg, A. Williams and K. Blinov, Contemporary Computer-Assisted Approaches to Molecular Structure Elucidation, New Developments in NMR, The Royal Society of Chemistry, 2012, pp. P001–482.
12. M. C. Hemmer and J. Gasteiger, Prediction of three-dimensional molecular structures using information from infrared spectra, Anal. Chim. Acta, 2000, 420, 145–154.
13. M. Valli, H. M. Russo, A. C. Pilon, M. E. F. Pinto, N. B. Dias, R. T. Freire, I. Castro-Gamboa and V. da Silva Bolzani, Computational methods for NMR and MS for structure elucidation I: software for basic NMR, Phys. Sci. Rev., 2019, 4, 20180108.
14. M. Valli, H. M. Russo, A. C. Pilon, M. E. F. Pinto, N. B. Dias, R. T. Freire, I. Castro-Gamboa and V. da Silva Bolzani, Computational methods for NMR and MS for structure elucidation II: database resources and advanced methods, Phys. Sci. Rev., 2019, 4, 20180167.
15. G. T. M. Bitchagno and S. A. F. Tanemossu, Computational methods for NMR and MS for structure elucidation III: More advanced approaches, Phys. Sci. Rev., 2019, 4, 20180109.
16. M. Elyashberg, K. Blinov and E. Martirosian, A new approach to computer-aided molecular structure elucidation: the expert system Structure Elucidator, Lab. Autom. Inf. Manage., 1999, 34, 15–30.
17. L. M. G. Moreira and J. Junker, Sampling CASE Application for the Quality Control of Published Natural Product Structures, Molecules, 2021, 26, 7543.
18. J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Applications of machine learning in drug discovery and development, Nat. Rev. Drug Discovery, 2019, 18, 463–477.
19. S. Ekins, A. C. Puhl, K. M. Zorn, T. R. Lane, D. P. Russo, J. J. Klein, A. J. Hickey and A. M. Clark, Exploiting machine learning for end-to-end drug discovery and development, Nat. Mater., 2019, 18, 435–441.
20. S. Mehta, S. Laghuvarapu, Y. Pathak, A. Sethi, M. Alvala and U. D. Priyakumar, MEMES: Machine learning framework for Enhanced MolEcular Screening, Chem. Sci., 2021, 12, 11710–11721.
21. S. Manzhos and T. Carrington, Neural Network Potential Energy Surfaces for Small Molecules and Reactions, Chem. Rev., 2021, 121, 10187–10217.
22. P. Pattnaik, S. Raghunathan, T. Kalluri, P. Bhimalapuram, C. V. Jawahar and U. D. Priyakumar, Machine Learning for Accurate Force Calculations in Molecular Dynamics Simulations, J. Phys. Chem. A, 2020, 124, 6954–6967.
23. F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Machine Learning for Molecular Simulation, Annu. Rev. Phys. Chem., 2020, 71, 361–390 , PMID: 32092281..
24. Y. B. L. Samaga, S. Raghunathan and U. D. Priyakumar, SCONES: Self-Consistent Neural Network for Protein Stability Prediction Upon Mutation, J. Phys. Chem. B, 2021, 125, 10657–10671.
25. R. Aggarwal, A. Gupta, V. Chelur, C. V. Jawahar and U. D. Priyakumar, DeepPocket: Ligand Binding Site Detection and Segmentation using 3D Convolutional Neural Networks, J. Chem. Inf. Model., 2021, 62(21), 5069–5079.
26. Y. Pathak, S. Laghuvarapu, S. Mehta and U. D. Priyakumar, Chemically Interpretable Graph Interaction Network for Prediction of Pharmacokinetic Properties of Drug-Like Molecules, Proceedings of the AAAI Conference on Artificial Intelligence, 2020, vol. 34, pp. 873–880.
27. S. Laghuvarapu, Y. Pathak and U. D. Priyakumar, BAND NN: A Deep Learning Framework for Energy Prediction and Geometry Optimization of Organic Small Molecules, J. Comput. Chem., 2020, 41, 790–799.
28. M. Goel, S. Raghunathan, S. Laghuvarapu and U. D. Priyakumar, MoleGuLAR: Molecule Generation Using Reinforcement Learning with Alternating Rewards, J. Chem. Inf. Model., 2021, 61, 5815–5826.
29. D. Ricard, C. Cachet, D. Cabrol-Bass and T. P. Forrest, Neural network approach to structural feature recognition from infrared spectra, J. Chem. Inf. Comput. Sci., 1993, 33, 202–210.
30. H. Ren, H. Li, Q. Zhang, L. Liang, W. Guo, F. Huang, Y. Luo and J. Jiang, A machine learning vibrational spectroscopy protocol for spectrum prediction and spectrum-based structure recognition, Fundam. Res., 2021, 1, 488–494.
31. K. Yao, J. E. Herr, D. Toth, R. Mckintyre and J. Parkhill, The TensorMol-0.1 model chemistry: a neural network augmented with long-range physics, Chem. Sci., 2018, 9, 2261–2269.
32. A. A. Kananenka, K. Yao, S. A. Corcelli and J. L. Skinner, Machine Learning for Vibrational Spectroscopic Maps, J. Chem. Theory Comput., 2019, 15, 6850–6858.
33. M. Gastegger, J. Behler and P. Marquetand, Machine learning molecular dynamics for the simulation of infrared spectra, Chem. Sci., 2017, 8, 6924–6935.
34. K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. Müller, SchNetPack: A Deep Learning Toolbox For Atomistic Systems, J. Chem. Theory Comput., 2019, 15, 448–455.
35. F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Chemical shifts in molecular solids by machine learning, Nat. Commun., 2018, 9, 4501.
36. E. Jonas and S. Kuhn, Rapid prediction of NMR spectral properties with quantified uncertainty, J. Cheminf., 2019, 11, 50.
37. Z. Yang, M. Chakraborty and A. D. White, Predicting chemical shifts with graph neural networks, Chem. Sci., 2021, 12, 10802–10809.
38. S. Ye, W. Hu, X. Li, J. Zhang, K. Zhong, G. Zhang, Y. Luo, S. Mukamel and J. Jiang, A neural network protocol for electronic excitations of N-methylacetamide, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11612–11617.
39. K. Ghosh, A. Stuke, M. Todorović, P. B. Jørgensen, M. N. Schmidt, A. Vehtari and P. Rinke, Deep Learning Spectroscopy: Neural Networks for Molecular Excitation Spectra, Advanced Science, 2019, 6, 1801367.
40. S. Kumar Giri, U. Saalmann and J. M. Rost, Purifying Electron Spectra from Noisy Pulses with Machine Learning Using Synthetic Hamilton Matrices, Phys. Rev. Lett., 2020, 124(11), 113201.
41. G. Ongie, A. Jalal, C. A. Metzler, R. G. Baraniuk, A. G. Dimakis and R. Willett, Deep learning techniques for inverse problems in imaging, IEEE Journal on Selected Areas in Information Theory, 2020, 1(1), 39–56.
42. Z. Wang, X. Feng, J. Liu, M. Lu and M. Li, Functional groups prediction from infrared spectra based on computer-assist approaches, Microchem. J., 2020, 159, 105395.
43. J. A. Fine, A. A. Rajasekar, K. P. Jethava and G. Chopra, Spectral deep learning for prediction and prospective validation of functional groups, Chem. Sci., 2020, 11, 4618–4630.
44. E. Jonas, Deep imitation learning for molecular inverse problems, Advances in Neural Information Processing Systems, 2019, vol. 32.
45. A. Howarth, K. Ermanis and J. M. Goodman, DP4-AI automated NMR data analysis: straight from spectrometer to structure, Chem. Sci., 2020, 11, 4351–4359.
46. J. Zhang, K. Terayama, M. Sumita, K. Yoshizoe, K. Ito, J. Kikuchi and K. Tsuda, NMR-TS: de novo molecule identification from NMR spectra, Sci. Technol. Adv. Mater., 2020, 21, 552–561.
47. X. Yang, J. Zhang, K. Yoshizoe, K. Terayama and K. C. T. S. Tsuda, an efficient python library for de novo molecular generation, Sci. Technol. Adv. Mater., 2017, 18, 972–976.
48. M. Pesek, A. Juvan, J. Jakos, J. Kosmrlj, M. Marolt and M. Gazvoda, Database Independent Automated Structure Elucidation of Organic Molecules Based on IR, 1H NMR, 13C NMR, and MS Data, J. Chem. Inf. Model., 2020, 61, 756–763.
49. M. Elyashberg, K. Blinov, S. Molodtsov, Y. Smurnyy, A. J. Williams and T. Churanova, Computer-assisted methods for molecular structure elucidation: realizing a spectroscopist's dream, J. Cheminf., 2009, 1, 3.
50. D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepel and T. Lillicrap, Mastering chess and shogi by self-play with a general reinforcement learning algorithm, arXiv, 2017, preprint, arXiv:1712.01815,  DOI:10.48550/arXiv.1712.01815.
51. M. Alberts, T. Laino and A. C. Vaucher, Leveraging Infrared Spectroscopy for Automated Structure Elucidation, 2023.
52. M. Alberts, F. Zipoli and A. C. Vaucher, Learning the Language of NMR: Structure Elucidation from NMR spectra using Transformer Models, 2023.
53. B. Sridharan, S. Mehta, Y. Pathak and U. D. Priyakumar, Deep Reinforcement Learning for Molecular Inverse Problem of Nuclear Magnetic Resonance Spectra to Molecular Structure, J. Phys. Chem. Lett., 2022, 4924–4933.
54. S. Kuhn and N. E. Schlörer, Facilitating quality control for spectra assignments of small organic molecules: nmrshiftdb2 – a free in-house NMR database with integrated LIMS for academic service laboratories, Magn. Reson. Chem., 2015, 53, 582–589.
55. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural Message Passing for Quantum Chemistry, International Conference on Machine Learning, 2017, pp. 1263–1272.
56. L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52, 2864–2875 , PMID: 23088335..
57. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1, 140022.
58. L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52, 2864–2875.
59. M. J. Frisch et al. , Gaussian 09, Revision A.1., Gaussian Inc, Wallingford CT, 2016.
60. C. McGill, M. Forsuelo, Y. Guan and W. H. Green, Predicting Infrared Spectra with Message Passing Neural Networks, J. Chem. Inf. Model., 2021, 61, 2594–2609.
61. P. M. Chu, F. R. Guenther, G. C. Rhoderick and W. J. Lafferty, The NIST Quantitative Infrared Database, J. Res. Natl. Inst. Stand. Technol., 1999, 104, 59–81.
62. S. Wallace, S. G. Lambrakos, A. Shabaev and L. Massa, On using DFT to construct an IR spectrum database for PFAS molecules, Struct. Chem., 2022, 33, 247–256.
63. A. Gupta, S. Chakraborty and R. Ramakrishnan, Revving up 13C NMR shielding predictions across chemical space: benchmarks for atoms-in-molecules kernel machine learning with new data for 134 kilo molecules, Mach. Learn.: Sci. Technol., 2021, 2, 035010.
64. M. Mehring, High resolution NMR spectroscopy in solids, Springer Science & Business Media, 2012, vol. 11.
65. H. Rull, M. Fischer and S. Kuhn, NMR shift prediction from small data quantities, J. Cheminf., 2023, 15, 114.
66. Y. Guan, S. V. Shree Sowndarya, L. C. Gallegos, P. C. St. John and R. S. Paton, Real-time prediction of 1H and 13C chemical shifts with DFT accuracy using a 3D graph neural network, Chem. Sci., 2021, 12, 12012–12026.
67. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Computational prediction of 1H and 13C chemical shifts: a useful tool for natural product, mechanistic, and synthetic organic chemistry, Chem. Rev., 2011, 112, 1839–1862.
68. D. Silver, et al., Mastering the game of Go with deep neural networks and tree search, Nature, 2016, 529, 484–489.
69. S. James, G. Konidaris and B. Rosman, An Analysis of Monte Carlo Tree Search, Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, 2017, pp. 3576–3582.
70. R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, The MIT Press, 2nd edn, 2018.
71. K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, Analyzing Learned Molecular Representations for Property Prediction, J. Chem. Inf. Model., 2019, 59, 3370–3388.
72. H. Dai, B. Dai and L. Song, Discriminative embeddings of latent variable models for structured data, International Conference on Machine Learning, 2016, pp. 2702–2711.
73. C.-I. Chang, An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis, IEEE Trans. Inf. Theory, 2000, 46, 1927–1932.
74. L. Kocsis and C. Szepesvári, Bandit Based Monte-Carlo Planning. Machine Learning: ECML 2006, Berlin, Heidelberg, 2006, pp. 282–293.
75. M. H. S. Segler, M. Preuss and M. P. Waller, Planning chemical syntheses with deep neural networks and symbolic AI, Nature, 2018, 555, 604–610.
76. T. M. Moerland, J. Broekens, A. Plaat and C. M. Jonker, Monte Carlo tree search for asymmetric trees, arXiv, 2018, preprint, arXiv:1805.09218,  DOI:10.48550/arXiv.1805.09218.
77. D. Silver, et al., Mastering the game of Go without human knowledge, Nature, 2017, 550, 354–359.
78. D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Convolutional Networks on Graphs for Learning Molecular Fingerprints, Advances in Neural Information Processing Systems, 2015.
79. G. Landrum, RDKit: Open-Source Cheminformatics Software, 2016.
80. D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, 2017.
81. S. H. Bertz, The first general index of molecular complexity, J. Am. Chem. Soc., 1981, 103, 3599–3601.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00008k

‡ Contributed equally to this work.

---