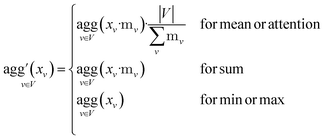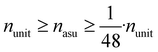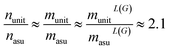Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Connectivity optimized nested line graph networks for crystal structures†
Robin
Ruff
 a,
Patrick
Reiser
a,
Patrick
Reiser
 ad,
Jan
Stühmer
bc and
Pascal
Friederich
ad,
Jan
Stühmer
bc and
Pascal
Friederich
 *ad
*ad
aInstitute of Theoretical Informatics, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany. E-mail: pascal.friederich@kit.edu
bInstitute for Anthropomatics and Robotics, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany
cHeidelberg Institute for Theoretical Studies, Schloß-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
dInstitute of Nanotechnology, Karlsruhe Institute of Technology, Kaiserstr. 12, 76131 Karlsruhe, Germany
First published on 20th February 2024
Abstract
Graph neural networks (GNNs) have been applied to a large variety of applications in materials science and chemistry. Here, we systematically investigate the graph construction for crystalline (periodic) materials and investigate its impact on the GNN model performance. We propose the asymmetric unit cell as a representation to reduce the number of nodes needed to represent periodic graphs by exploiting all symmetries of the system. Without any loss in accuracy, this substantially reduces the computational cost and thus time needed to train large graph neural networks. For architecture exploration we extend the original Graph Network framework (GN) of Battaglia et al., introducing nested line graphs (Nested Line Graph Network, NLGN) to include more recent architectures. Thereby, with a systematically built GNN architecture based on NLGN blocks, we improve the state-of-the-art results across all tasks within the MatBench benchmark. Further analysis shows that optimized connectivity and deeper message functions are responsible for the improvement. Asymmetric unit cells and connectivity optimization can be generally applied to (crystal) graph networks, while the suggested nested NLGN framework can be used as a template to compare and build more GNN architectures.
1 Introduction
Since the seminal work by Duvenaud et al.,2 graph neural networks (GNNs) have developed into one of the most versatile and accurate classes of machine learning models for the prediction of molecular and material properties.3 Consequently, GNNs find increasing application in materials sciences for structure–property predictions,4 materials screening5 and high-throughput simulations.6 Learning on experimental or simulated databases,7–9 GNNs show promising potential to develop new materials to tackle our society's growing demand for high-performance materials in the fields of catalysis, renewable energies, energy conversion or functional materials.10,11Graph convolutional neural networks operate on the (spatial) graph structure to transform node embeddings and have been suggested for semi-supervised node classification.12,13 With the focus on molecular graphs, the message passing framework (MPNN) was proposed by Gilmer et al.14 in order to group and generalize many GNN architectures that update node representations by iteratively exchanging information, or messages, across edges in the graph.15,16 Neural networks designed to predict the potential energy surface of molecules for molecular dynamics simulations,17 such as the continuous-filter convolutional network SchNet,18 can also be interpreted as MPNN graph networks. Significant progress was achieved by incorporating further geometric information such as bond39 and dihedral angles19 into the MPNN scheme. To compute explicit angle information, the graph network has to operate on higher order pathways or connect edge information in a so-called line graph, which sets up a graph on edges L(G), i.e. on top of the underlying graph G.20 A state-of-the-art model that makes use of this principle and reaches good performance for materials is ALIGNN.21 Recently, equivariant graph networks have been introduced,22 which build on irreducible representations of the Euclidean symmetry groups to achieve equivariance under e.g. rotation and translation.23
2 Related work
Although many of the previously mentioned GNNs can or have been applied to materials, fewer architectures have been developed with a primary focus on crystalline systems. The crystal-graph convolution neural network (CGCNN) first introduced a GNN architecture on a crystalline system by constructing a multi-graph that correctly represents the atomic neighbors in a periodic system.24 Its improved version iCGCNN incorporates information on the Voronoi tessellated crystal structure and explicit three-body correlations of neighboring constituent atoms.25 MEGNet further leverages global state information and added edge updates in the convolution process.26 With GeoCGNN a geometric GNN was introduced,27 which encodes the local geometrical information using an attention mask composed of Gaussian radial basis functions and plane waves from a k-point mesh of Monkhorst Pack special points.28 Although multiple GNN model architectures have been proposed in this context,21,24–27,29,30 there does not yet seem to be unanimous consent in the literature on which is the best method or the most decisive tool in geometric deep learning to process crystalline materials.In most cases, newly introduced GNNs make specific improvements over previous architectures and propose multiple reasonable new design decisions inspired by chemical domain knowledge. While this approach has so far led to a consistent improvement of model accuracy, we choose a more systematic approach inspired by the work of You et al.:31 first, we stake out a new design space based on a general extension of the original graph network (GN) framework,1 which we call nested line graph networks (NLGNs). Then we navigate through that design space to find suitable NLGN architectures.
In this work, we re-evaluate edge selection methods to build a multi-graph as suggested by Xie and Grossman24 and compare their performance on a wide set of parameters. In this context, we introduce the asymmetric unit cell as a representation to further exploit crystal symmetries and effectively reduce the number of edges. Next, we develop a connectivity-optimized crystal graph network (coGN/coNGN) from message passing and line-graph templates which are intentionally kept as general as possible. By optimizing within the generalized family of GNNs, we improve the state-of-the-art results on 6 out of 9 of the MatBench benchmark datasets32 and achieve parity results with the best models on the remaining 3 datasets, making our model the best general model on the entire set of diverse tasks in the benchmark.
3 Connectivity optimized nested line graph networks (coNGN)
3.1 Connectivity optimized crystal graph construction
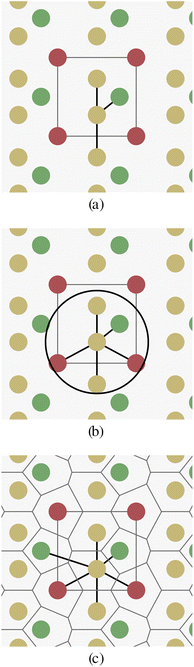
There are two main challenges when trying to build graph representations of crystal structures in contrast to organic molecules: (a) bonds between atoms in crystals have more diverse types (covalent, ionic, metallic bonds), or are often not well defined at all. (b) Crystal structures have no fixed finite size, as they are defined as periodic repetitions of a unit cell.Fig. 1 schematically shows a two-dimensional crystal pattern and three different methods for selecting edges between atoms. The k-nearest-neighbors approach (Fig. 1a) depends on the number of neighbors k, but can lead to largely different edge distances when the crystal density varies. The radius-based approach (Fig. 1b) limits the distance between two nodes by a hyperparameter r, but the number of neighbors is unbounded and the method can lead to either disconnected or overly dense graphs if r is chosen inappropriately. The parameter-free Voronoi-based approach (Fig. 1c) leads to an intuitive edge selection where edges are drawn between two atoms if there is a Voronoi cell ridge between them. However, at least in theory, the number of edges and their distances are also unbounded for this approach.
All three edge selection methods have been used previously in the context of crystals and GNNs.24–26,33 But to our knowledge, there is no detailed comparison between the methods and hyperparameters.
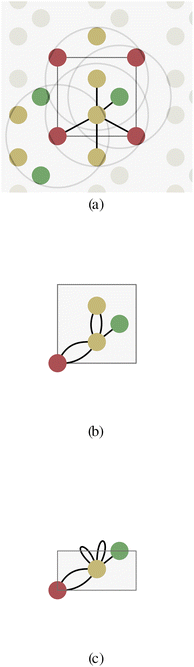
To solve this issue, Xie and Grossman24 proposed a multigraph crystal representation (Fig. 2b) introducing periodic/cyclic boundary conditions, which we will refer to as a unit cell graph. In this representation, one node represents all the shift-equivalent atoms of the crystal, which usually results in multiple edges with distance information matching their translated lattice positions. As a consequence, GNNs will always provide equivalent node embedding for periodic atoms, consistent with Bloch's theorem.
The periodicity of the unit cell graph represents translation symmetry. Since crystals often exhibit more symmetries, we propose the asymmetric unit graph representation for crystals, which considers all symmetries of a crystal structure.‡ For more information about the asymmetric unit (ASU) and space groups please see for example ref. 35–38. In this representation, all symmetry-equivalent atoms are represented by a single node in the graph. The example crystal in Fig. 2 exhibits a horizontal reflection symmetry. The two yellow atoms in the crystal unit cell are symmetry-equivalent and therefore merged into one node (with multiplicity two) for the asymmetric unit cell (Fig. 2c). Just like in unit cell graphs, self-loops and multi-edges can occur in asymmetric unit cell graphs.
Since physical target properties in ML tasks are often invariant under E(3) symmetry operations, many GNNs are designed to be E(3)-invariant, but as a consequence yield equal node embeddings for symmetrical atoms in the unit cell graph, leading to redundant computations in the message passing step. The asymmetric unit graph representation can further remove these redundancies and yet maintain the same node embeddings xv.§ However, global readout operations have to be adapted to handle asymmetric unit cells, since atoms can have different symmetry-related multiplicities 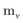 (the number of symmetry equivalent atoms for each equivalence class). A simple adaptation of the readout function can fix the issue and restore equal results for unit cell graphs and asymmetric unit graphs:
(the number of symmetry equivalent atoms for each equivalence class). A simple adaptation of the readout function can fix the issue and restore equal results for unit cell graphs and asymmetric unit graphs:
It should be noted that for the ASU representation the structure needs to remain in the same space group and its atoms in their original Wyckoff sites, which means that for inference during e.g. molecular dynamics simulations and structure changes, the ASU has to be reevaluated which is cumbersome and expensive. Nonetheless, GNNs can be trained on ASU structures, which requires one ASU evaluation of the training set, and then used on the normal unit cell representation for inference.
3.2 Nested line graph network framework
In addition to the choice of input representation, the GNN model architecture has a substantial impact on the quality of crystal graph property predictions.To find the best GNN architecture for a certain task, it is instructive to systematically explore (see e.g. ref. 31) the design space of GNN modules and building blocks. Moreover, a framework has to be chosen on how to define and process GNN modules. The Message Passing Framework by Gilmer et al.,14 for example, has shown that a framework can unify and accelerate the efforts of the scientific community.
For a combinatorial generalization of GNNs, we build upon the graph network (GN) framework of Battaglia et al.1 in this work. In this framework, one GNN layer is described by a GN block, which transforms a generic attributed graph with edge, node, and global graph features via three update functions ϕ and three aggregation functions ρ.
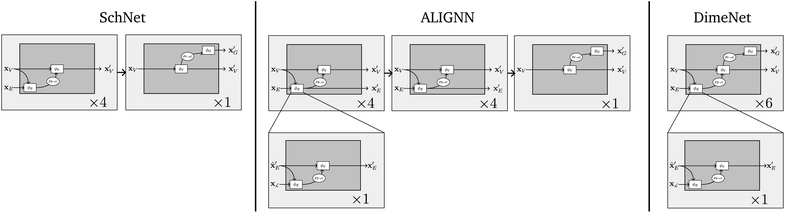
However, many state-of-the-art models such as DimeNet,39 GemNet,19 ALIGNN21 and M3GNet,30 which incorporate many-body interactions between atoms, are only indirectly captured by GNs. Therefore we propose an extension to the framework which we term nested line graph networks (NLGNs). In the following, we introduce NLGNs by first discussing how angle information is incorporated via the line graph concept21 and then explaining the flow of NLGN calculations, before we will show concrete examples of implementations of NLGNs in Section 4.1. Note that the term nested refers here to stacking GNs on the line graph, not to confuse with nesting as introduced by Zhang and Li,40 which describes nesting and pooling GNNs on sub-graphs.
To achieve rotation invariance, popular models such as SchNet18 or MEGNet26 only include scalar distances between two atoms as edge features. However, to incorporate more geometric information, models such as DimeNet39 or ALIGNN21 additionally use E(3)-invariant angle information, represented by combinations of edges (see Fig. 6). In the line graph L(G), which can be constructed uniquely based on G (see Fig. 3 and Harary and Norman41), there is an edge eeij,ejkL(G) for every two incident edges eij, ejk in G. This enables the assignment of angular information between three atoms to the edges of the line graph. The same applies to (generalized) dihedral angles (4-node or 3-edge objects) in the second-order line graph L(L(G)).
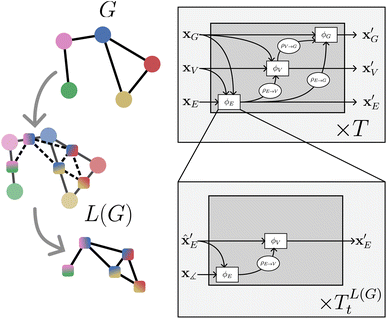 | ||
| Fig. 3 On the left: a graph G and the construction of its line graph L(G). On the right: nested line graph network architecture with GN blocks working on G and containing other GN blocks working on the line graph L(G) as an edge update function ϕE. The line graph is able to process multi-node geometric features, such as angles (see Table 1) | ||
NLGNs operate on the graph G as well as the line graph L(G) (potentially also L(L(G)) etc.), exploiting the one-to-one mapping of edges in G and nodes in L(G) (see Table 1). Each edge update function ϕE in GN blocks that operate on G can be instantiated as a nested GN (see Fig. 3). A more detailed description of the algorithm can be found in the ESI.† The NLGN framework extends the usual sequential compositionality of GN blocks with a hierarchical/nested compositionality, thereby increasing the expressiveness.42 The composition of simple and well-known building blocks facilitates the implementation and the ease of understanding of the framework. Furthermore, NLGNs generalize existing models such as SchNet,18 DimeNet39 and ALIGNN,21 making them more comparable and extensible (see Fig. 4).
| Entity in crystal | G | L(G) | L(L(G)) |
|---|---|---|---|
| Atoms | Nodes | ||
| Bonds | Edges | Nodes | |
| Angles | Edges | Nodes | |
| Dihedrals | Edges |
4 Experiments and evaluation
4.1 Datasets
To evaluate the preprocessing methods and GN architectures we relied on the MatBench benchmark,32 which can be considered to be the CIFAR43 dataset for machine learning models in materials science. The benchmark currently consists of 13 strictly standardized supervised crystal property prediction tasks curated from different data sources.44–47 Out of the 13 tasks, four provide only the crystal composition as input and the other nine incorporate the crystal structure with the geometric arrangement of atoms. Since this work focuses on crystal structures specifically, we only use the nine datasets that rely on structural information for property prediction. The size of the datasets ranges from 636 to 132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 752 crystal instances.
752 crystal instances.
4.2 Implementation
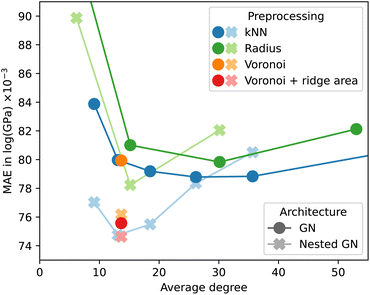
We used the Keras Graph Convolution Neural Networks (KGCNN) library48 to implement the GN and NLGNs used in the experiments of this work. The code for crystal preprocessing and GNN models is available online.¶Fig. 5 shows the effect of different preprocessing methods for a non-nested GN. Again, results were obtained before the final ordinal hyperparameter optimization, which explains the discrepancy with Table 2. The MAE is plotted as a function of the average degree over the resulting graphs of the log_gvrh dataset for different edge selection methods. The accuracy of GNN models tends to fall for increasing graph connectivity up to an average degree of approximately 30. For a higher average degree the accuracy either gets worse or quickly converges depending on the dataset. Interestingly, for the kNN edge selection the minimum corresponds to k = 24, whereas other works use a value of 12.21,24 The Voronoi-based edge selection results in graphs with an average degree of approximately 12. Adding the area of the Voronoi cell ridge to each edge as an additional edge feature can improve the predictive power of the GNN. We found, however, that this effect is much less pronounced after optimization of ordinal hyperparameters, making the k = 24 nearest-neighbor method the preferred choice for edge selection in our experiments.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (GPa)), log_gvrh (log
10 (GPa)), log_gvrh (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (GPa)), dielectric (unitless), phonons (1/cm) and jdft2d (meV per atom). Current benchmark holders on MatBench, namely, ALIGNN,21 MODNet49 and CGCNN,24 are listed. Additionally, recent models M3GNet30 and Matformer50 are added, which have been published during the preparation of this work. Since Matformer was not trained on the official benchmark, we retrained the original model. The best results are indicated in bold font, while other results within one standard deviation are underlined
10 (GPa)), dielectric (unitless), phonons (1/cm) and jdft2d (meV per atom). Current benchmark holders on MatBench, namely, ALIGNN,21 MODNet49 and CGCNN,24 are listed. Additionally, recent models M3GNet30 and Matformer50 are added, which have been published during the preparation of this work. Since Matformer was not trained on the official benchmark, we retrained the original model. The best results are indicated in bold font, while other results within one standard deviation are underlined
| Dataset | coGN (ours) | coNGN (ours) | ALIGNN | MODNet | CGCNN | M3GNet | Matformer |
|---|---|---|---|---|---|---|---|
| a For is_metal the classification metric is likely to change in future versions. | |||||||
| e_form ↓ | 17.0 ± 0.3 | 17.8 ± 0.4 | 21.5 ± 0.5 | 44.8 ± 3.9 | 33.7 ± 0.6 | 19.5 ± 0.2 | 21.232 ± 0.302 |
| is_metala ↑ | 0.9124 ± 0.0023 | 0.9089 ± 0.0019 | 0.9128 ± 0.0015 | 0.9038 ± 0.0106 | 0.9520 ± 0.0074 | 0.958 ± 0.001 | 0.812 ± 0.05 |
| Gap ↓ | 155.9 ± 1.7 | 169.7 ± 3.5 | 186.1 ± 3.0 | 219.9 ± 5.9 | 297.2 ± 3.5 | 183 ± 5 | 187.825 ± 3.817 |
| Perovskites ↓ | 26.9 ± 0.8 | 29.0 ± 1.1 | 28.8 ± 0.9 | 90.8 ± 2.8 | 45.2 ± 0.7 | 33 ± 1.0 | 31.514 ± 0.71 |
| log_kvrh ↓ | 0.0535 ± 0.0028 | 0.0491 ± 0.0026 | 0.0568 ± 0.0028 | 0.0548 ± 0.0025 | 0.0712 ± 0.0028 | 0.058 ± 0.003 | 0.063 ± 0.0027 |
| log_gvrh ↓ | 0.0689 ± 0.0009 | 0.0670 ± 0.0006 | 0.0715 ± 0.0006 | 0.0731 ± 0.0007 | 0.0895 ± 0.0016 | 0.086 ± 0.002 | 0.077 ± 0.0016 |
| Dielectric ↓ |
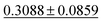
|
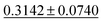
|
0.3449 ± 0.0871 | 0.2711 ± 0.0714 | 0.5988 ± 0.0833 | 0.312 ± 0.063 | 0.634 ± 0.131 |
| Phonons ↓ |
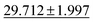
|
28.887 ± 3.284 |
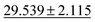
|
34.2751 ± 2.0781 | 57.7635 ± 12.311 | 34.1 ± 4.5 | 42.526 ± 11.886 |
| jdft2d ↓ |
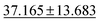
|
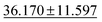
|
43.424 ± 8.949 | 33.192 ± 7.343 | 49.244 ± 11.587 | 50.1 ± 11.9 | 42.827 ± 12.281 |
The observations for non-nested GNs do not apply to NLGNs, when comparing their behavior in Fig. 5. For NLGNs, the minimum test error occurs at a lower average degree of approximately 12 edges per node and is followed by a steeper increase for higher connectivity. Higher-order nesting could potentially lead to further improvement at yet lower connectivity of the base graph, which should be systematically explored in the future.
At the same time, our observations raise the question of a trade-off between nesting and graph connectivity. This trade-off can also be explained from an analytical point of view. The reason for including angle information with NLGNs is shown in the example in Fig. 6. The two geometric graphs are not distinguishable for GNNs from relative distance information alone. Incorporating angles between edges into the GNN architecture increases expressiveness and allows for the distinction of the graphs. Yet, similar enhancements of expressiveness can also be achieved by increasing graph connectivity. In the example, adding the single dashed edge between two red nodes makes the graphs distinguishable for GNNs, without any angle information.
From our experiments, we cannot conclude that NLGNs offer a systematic advantage in accuracy over simple GNs when used on graphs with high connectivity. Inspired by the results of Fig. 5, we optimized an NLGN for less connected Voronoi (+ ridge area) preprocessed graphs and achieved the results displayed in Table 2. Although NLGNs showed the best performance on the specific dataset they have been (hyperparameter) optimized on, they cannot maintain their advantage consistently on all other datasets without re-optimizing. Unfortunately, NLGNs require the construction of line graphs and tend to have significantly more trainable parameters. Consequently, training is more than three times as computationally expensive as for non-nested GNs.
Finally, we were able to demonstrate the effectiveness of densely connected crystal graphs with the coGN model, by surpassing current state-of-the-art models on most of the MatBench datasets as shown in Table 2. The results also support that hyperparameters, which originate from the optimization on the log_gvrh dataset, generalize to other datasets and tasks.
Results of coGN/coNGN on other comparable materials benchmarks like JARVIS51 or OC22,9 which feature structure to property tasks, can be found in the ESI† and yield similar top ranking performance.
We found that for the MatBench datasets, the empirical average reduction factor for the number of nodes (n), edges (m = nL(G)) and line graph edges (mL(G)) is approximately 2.1:||
Approximately the same factor can be observed for the GPU memory footprint during training. Due to parallelization and batching the acceleration of the training runtimes is somewhat smaller and depends on the selected batch size. For batch sizes of 32, 64, and 128, for example, we observed a speedup of 1.2, 1.3, and 1.8, respectively.
5 Conclusions
This paper discusses fundamental aspects of crystal property prediction with GNNs: the incorporation of symmetries in GNN models, the interdependence of input graph generation from crystal structures (i.e. preprocessing) with the systematic exploration of a suitable GNN architecture, and the generalization of model architectures as nested line graph networks. We conclude that these aspects cannot be considered separately, which is done in many other studies.Our contribution to the first aspect includes the proposal of the asymmetric unit graph representation, which decreases training time and memory consumption without effects on predictive performance for E(3)-invariant GNNs. To use asymmetric unit graphs with equivariant GNNs some adaptations to message passing and readout operations are required, which will be addressed in future work. We furthermore compared different edge selection methods and discovered that graphs with higher connectivity (compared to previous works) can yield better performance. From this insight, we construct the coGN, which achieves state-of-the-art results on the MatBench benchmark.
To explore the space of GNN architectures, we introduced the nested line graph network (NLGN) framework, which subsumes state-of-the-art GNN models that incorporate angle information in line graph form. Although for the given dataset sizes in the MatBench benchmark we could not find an architecture for nested line graph networks that substantially outperforms graph networks without nesting, we still encourage further research in this direction, specifically into the scaling laws of accuracy as a function of data set size and complexity as well as the depth of line-graph nesting. Future work might overcome the mentioned trade-off between high connectivity and nesting and potentially explore specific nested line graph network architectures, which we did not consider due to hyperparameter space restrictions. Moreover, a practical but systematic comparison between recent equivariant GNs, which are more expressive than invariant GNs, and NLGNs could potentially offer further insight and gradual improvements.
Data availability
Training code and results can be found in the official benchmark submission (https://github.com/materialsproject/matbench/tree/main/benchmarks/matbench_v0.1_coGN, https://github.com/materialsproject/matbench/tree/main/benchmarks/matbench_v0.1_coNGN, https://github.com/usnistgov/jarvis_leaderboard/tree/main/jarvis_leaderboard/contributions/kgcnn_coGN, https://github.com/usnistgov/jarvis_leaderboard/tree/main/jarvis_leaderboard/contributions/kgcnn_coNGN). Additionally, the code for the crystal GNNs can be found on github: https://github.com/aimat-lab/gcnn_keras/tree/v3.0.1/kgcnn/literature/coGN. We provide a static Zenodo repository (https://doi.org/10.5281/zenodo.10557203) of the documented code and training scripts of all MatBench and Jarvis submissions in the folder training_scripts. Training was run on MatBench v0.1 and Jarvis 12-12-2022 version with the official train-test splits provided by the benchmarks. How to use the benchmark data and submit benchmarks can be found on the respective benchmark websites (https://matbench.materialsproject.org/HowToUse/2run/, https://pages.nist.gov/jarvis_leaderboard/guide/). Moreover, we provide a code capsule with the environment for training and example scripts for custom data at: https://doi.org/10.24433/CO.7659719.v1.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support by the state of Baden-Württemberg through bwHPC. P. F. acknowledges support by the Federal Ministry of Education and Research (BMBF) under Grant No. 01DM21001B (German-Canadian Materials Acceleration Center).Notes and references
- P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro, R. Faulkner, et al. Relational inductive biases, deep learning, and graph networks, arXiv, 2018, preprint, arXiv:1806.01261, DOI:10.48550/arXiv.1806.01261.
- D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Advances in Neural Information Processing Systems, 2015, vol. 28 Search PubMed.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans and T. Sommer, et al. , Commun. Mater., 2022, 3, 93 CrossRef CAS PubMed.
- M. Karamad, R. Magar, Y. Shi, S. Siahrostami, I. D. Gates and A. Barati Farimani, Phys. Rev. Mater., 2020, 4, 093801 CrossRef CAS.
- J. Schmidt, L. Pettersson, C. Verdozzi, S. Botti and M. A. L. Marques, Sci. Adv., 2021, 7, eabi7948 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11(10), 6059–6072 CrossRef CAS.
- R. Tran, J. Lan, M. Shuaibi, B. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, Z. Ulissi and C. L. Zitnick, arXiv, 2022, preprint, arXiv:2206.08917, DOI:10.1021/acscatal.2c05426.
- D. Gielen, F. Boshell and D. Saygin, Nat. Mater., 2016, 15(2), 117–120 CrossRef CAS PubMed.
- Y. Cui, B. Li, H. He, W. Zhou, B. Chen and G. Qian, Acc. Chem. Res., 2016, 49, 483–493 CrossRef CAS PubMed.
- T. N. Kipf and M. Welling, 5th International Conference on Learning Representations, ICLR 2017, Conference Track Proceedings, Toulon, France, April 24-26, 2017, 2017 Search PubMed.
- M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov and M. Welling, The Semantic Web, Cham, 2018, pp. 593–607 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, pp. 1263–1272 Search PubMed.
- P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Liò and Y. Bengio, International Conference on Learning Representations, 2018 Search PubMed.
- W. Hamilton, Z. Ying and J. Leskovec, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955 RSC.
- K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Advances in Neural Information Processing Systems, 2017, vol. 30 Search PubMed.
- J. Klicpera, F. Becker and S. Günnemann, Advances in Neural Information Processing Systems, 2021 Search PubMed.
- Z. Chen, L. Li and J. Bruna, International Conference on Learning Representations, 2019 Search PubMed.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, Tensor Field Networks: Rotation- and Translation-Equivariant Neural Networks for 3D Point Clouds, 2018, https://arxiv.org/abs/1802.08219 Search PubMed.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. W. Park and C. Wolverton, Phys. Rev. Mater., 2020, 4, 063801 CrossRef CAS.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- J. Cheng, C. Zhang and L. Dong, Commun. Mater., 2021, 2, 92 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- T. Yamamoto, Crystal graph neural networks for data mining in materials science, Research Institute for Mathematical and Computational Sciences, LLC, 2019 Search PubMed.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- J. You, R. Ying and J. Leskovec, NeurIPS, 2020 Search PubMed.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 138 CrossRef.
- O. Isayev, D. Fourches, E. N. Muratov, C. Oses, K. Rasch, A. Tropsha and S. Curtarolo, Chem. Mater., 2015, 27, 735–743 CrossRef CAS.
- A. Togo and I. Tanaka, arXiv, 2018, preprint, arXiv:1808.01590, DOI:10.48550/arXiv.1808.01590.
- R. W. Grosse-Kunstleve, B. Wong, M. Mustyakimov and P. D. Adams, Acta Crystallogr., Sect. A: Found. Crystallogr., 2011, 67, 269–275 CrossRef CAS PubMed.
- F. Hoffmann, Introduction to Crystallography, Springer International Publishing, 2020 Search PubMed.
- M. O'Keeffe and B. Hyde, Crystal Structures, Dover Publications, 2020 Search PubMed.
- T. Hahn, U. Shmueli, A. Wilson and I. U. of Crystallography, International Tables for Crystallography, D. Reidel Publishing Company, 1984 Search PubMed.
- J. Klicpera, J. Groß and S. Günnemann, arXiv, 2020, preprint, arXiv:2003.03123, DOI:10.48550/arXiv.2003.03123.
- M. Zhang and P. Li, Advances in Neural Information Processing Systems, 2021, pp. 15734–15747 Search PubMed.
- F. Harary and R. Z. Norman, Rend. Circ. Mat. Palermo, 1960, 9, 161–168 CrossRef.
- H. Maron, H. Ben-Hamu, H. Serviansky and Y. Lipman, Advances in Neural Information Processing Systems, 2019, vol. 32 Search PubMed.
- A. Krizhevsky, Learning Multiple Layers of Features From Tiny Images, Technical Report, 2009 Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- M. de Jong, W. Chen, T. Angsten, A. Jain, R. Notestine, A. Gamst, M. Sluiter, C. Krishna Ande, S. van der Zwaag, J. J. Plata, C. Toher, S. Curtarolo, G. Ceder, K. A. Persson and M. Asta, Sci. Data, 2015, 2, 150009 CrossRef CAS PubMed.
- K. Choudhary, I. Kalish, R. Beams and F. Tavazza, Sci. Rep., 2017, 7, 5179 CrossRef PubMed.
- I. E. Castelli, D. D. Landis, K. S. Thygesen, S. Dahl, I. Chorkendorff, T. F. Jaramillo and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 9034–9043 RSC.
- P. Reiser, A. Eberhard and P. Friederich, Software Impacts, 2021, 9, 100095 CrossRef.
- P.-P. De Breuck, G. Hautier and G.-M. Rignanese, npj Comput. Mater., 2021, 7, 83 CrossRef.
- K. Yan, Y. Liu, Y. Lin and S. Ji, arXiv, 2022, preprint, arXiv:2209.11807, DOI:10.48550/arXiv.2209.11807.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00018h |
| ‡ The set of symmetries for crystals and thus the asymmetric unit cell representation can be determined automatically based on the normal unit cell.34 |
| § It is in principle also possible to adapt E(3)-equivariant GNNs to asymmetric unit graph representations, by specifying equivariant convolutional layers on the asymmetric unit graph and adapting message passing accordingly. |
| ¶ https://github.com/aimat-lab/gcnn_keras/tree/v3.0.1/kgcnn/literature/coGN. |
| || The perovskite dataset is a special outlier, where asymmetric graphs are on average not significantly smaller than unit cell graphs. |
| This journal is © The Royal Society of Chemistry 2024 |