Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discovery of novel reticular materials for carbon dioxide capture using GFlowNets†
Flaviu
Cipcigan
 *a,
Jonathan
Booth
b,
Rodrigo Neumann
Barros Ferreira
c,
Carine
Ribeiro dos Santos
c and
Mathias
Steiner
c
*a,
Jonathan
Booth
b,
Rodrigo Neumann
Barros Ferreira
c,
Carine
Ribeiro dos Santos
c and
Mathias
Steiner
c
aIBM Research Europe, UK. E-mail: flaviu.cipcigan@ibm.com
bScience and Technologies Facilities Council, UK
cIBM Research, Brazil
First published on 16th February 2024
Abstract
Artificial intelligence holds promise to improve materials discovery. GFlowNets are an emerging deep learning algorithm with many applications in AI-assisted discovery. Using GFlowNets, we generate porous reticular materials, such as Metal Organic Frameworks and Covalent Organic Frameworks, for applications in carbon dioxide capture. We introduce a new Python package (matgfn) to train and sample GFlowNets. We use matgfn to generate the matgfn-rm dataset of novel and diverse reticular materials with gravimetric surface area above 5000 m2 g−1. We calculate single- and two-component gas adsorption isotherms for the top-100 candidates in matgfn-rm. These candidates are novel compared to the state-of-art ARC-MOF dataset and rank in the 90th percentile in terms of working capacity compared to the CoRE2019 dataset. We identify 13 materials with CO2 working capacity outperforming all materials in CoRE2019. After further analysis and structural relaxation, two outperforming materials remain.
1 Introduction
Artificial intelligence (AI) holds promise to improve the scientific method1,2 and to accelerate scientific discovery. Applied to materials,‡ AI unlocks vast search spaces and enables novel applications in pharmaceuticals,3–6 batteries or carbon capture.7Reticular materials8 such as Metal–Organic Frameworks (MOFs) and Covalent Organic Frameworks (COFs) are extended periodic structures connected via strong bonds.9 They are synthesized by connecting building blocks known as secondary building units to form three-dimensional periodic structures.10 By choosing the building blocks, the properties of a reticular material can be tuned to support many applications.8
Reticular materials with high gravimetric surface area are particularly useful for applications in carbon capture, since carbon dioxide molecules adsorb at the internal surface area.11 The larger the gravimetric surface area, the more gas molecules can be adsorbed per gram of material.
In this work, we use GFlowNets to generate reticular materials with high gravimetric surface area for applications in carbon capture. Our key contributions are:
(1) The matgfn Python library for training and sampling using GFlowNets.
(2) A workflow using matgfn to generate reticular materials using secondary building units.
(3) The matgfn-rm dataset of diverse and novel reticular materials with total internal surface area higher than 5000 m2 g−1. The top-100 candidates are novel compared to the reference ARC-MOF dataset, rank in the 90th percentile in terms of simulated working capacity compared to the CoRE2019 dataset. We identify 13 materials with CO2 working capacity outperforming all materials in CoRE2019. After further analysis and structural relaxation, 2 outperforming materials remain.
The code and dataset is available at http://github.com/flaviucipcigan/matgfn and archived on Zenodo.12
2 Background and related work
2.1 Generative flow networks
GFlowNets13,14 are an emerging machine learning algorithm with many applications in AI-assisted materials discovery.15 GFlowNets learn to generate composite objects![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) by sampling from an unnormalised distribution p(
by sampling from an unnormalised distribution p(![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) ) ∝ R(
) ∝ R(![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) ) where R(
) where R(![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) ) is a user-specified positive reward function. A composite object
) is a user-specified positive reward function. A composite object ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) consists of symbols drawn from a vocabulary and relationships between those symbols. For example,
consists of symbols drawn from a vocabulary and relationships between those symbols. For example, ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) can be a sequence
can be a sequence ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) =[x1,x2,…xn] or a graph. The object
=[x1,x2,…xn] or a graph. The object ![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) is built by through Markov decision process restricted to a directed acyclic graph. Transition probabilities p(xi + 1|
is built by through Markov decision process restricted to a directed acyclic graph. Transition probabilities p(xi + 1|![[x with combining low line]](https://www.rsc.org/images/entities/i_char_0078_0332.gif) ) are approximated by a neural network policy. GFlowNets need fewer evaluations of the reward function to generate samples with high reward, novelty and diversity when compared to alternatives such as Markov Chain Monte Carlo, Proximal Policy Optimisation or Bayesian Optimisation.13
) are approximated by a neural network policy. GFlowNets need fewer evaluations of the reward function to generate samples with high reward, novelty and diversity when compared to alternatives such as Markov Chain Monte Carlo, Proximal Policy Optimisation or Bayesian Optimisation.13
2.2 Building hypothetical reticular frameworks
Trillions of hypothetical frameworks such as MOFs or COFs can be generated by placing secondary building units10 into nodes and edges of a three dimensional topology.16 A secondary building unit is an organic molecule or a coordination compound (a metal linked to organic atoms). A topology is a three dimensional arrangement of nodes and edges. Replacing nodes and edges with secondary building units results in a three dimensional point cloud of atoms connected by covalent or metal–organic bonds. We use the pormake secondary building units17 and topology codes from the reticular chemistry structure resource.16 Previously, deep autoencoders18 and evolutionary methods17 have been used to generate frameworks using this approach.2.3 Reference datasets
We use two reference datasets in this work. These datasets are not used for training models, but as comparison once training is done, as GFlowNet generates candidates using just a reward function. The CoRE2019 dataset19 consists of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 metal–organic frameworks with carbon dioxide uptake properties calculated by Moosavi et al.20 using Grand Canonical Monte Carlo. ARC-MOF (reported in 2022)21 is a collection of MOFs from previous MOF datasets, containing both experimental and hypothetical MOFs. We used the 521
023 metal–organic frameworks with carbon dioxide uptake properties calculated by Moosavi et al.20 using Grand Canonical Monte Carlo. ARC-MOF (reported in 2022)21 is a collection of MOFs from previous MOF datasets, containing both experimental and hypothetical MOFs. We used the 521![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 structures that passed the structure checking protocol of Bruner et al. 2023,21 minus one structure which would give an error in our analysis.
380 structures that passed the structure checking protocol of Bruner et al. 2023,21 minus one structure which would give an error in our analysis.
3 Generating reticular frameworks with GFlowNets
3.1 Python package
We built a Python library called matgfn to train and sample GFlowNets. The library is built on top of PyTorch22 and Gymnasium23 and prioritises ease of use and code readability. We intend for matgfn to be a general Python package for generation of diverse types of materials from small molecules to framework materials. Architecturally, matgfn separates sampling, loss calculation, optimisation, and environment definition as modular Python classes. Each can be modified individually, to implement off-policy training or use improved losses, for example. We note similar architectural choices for torchgfn.243.2 Environment for reticular framework generation
We configure a GFlowNet environment to build string sequences made out of text tokens. Those text tokens start with either an N, representing a node building block, or an E, representing an edge building block. For example, one of the potential generated sequences is [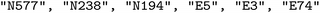 ]. We use building blocks in the pormake database. The string sequences are transformed to a Crystallographic Information File (*.cif) by pormake to create a reticular framework. Not all strings create valid materials. Thus, during generation, building blocks were restricted such that (a) each topology had the correct number of nodes and edges, (b) the building blocks were placed in the correct order and (c) each slot had a compatible building block.
]. We use building blocks in the pormake database. The string sequences are transformed to a Crystallographic Information File (*.cif) by pormake to create a reticular framework. Not all strings create valid materials. Thus, during generation, building blocks were restricted such that (a) each topology had the correct number of nodes and edges, (b) the building blocks were placed in the correct order and (c) each slot had a compatible building block.
Block compatibility was assessed as follows. For each slot in each topology, we pre-calculate a list of allowed building blocks. We allow only building blocks whose (a) number of attachment points is equal to the number of attachment points for the slot and (b) the RMSD between the block and the geometry is less than 0.3 Å. The RMSD is calculated using pormake's locator class by finding the best fit between a building block and a slot. At every generation step, the GFlowNet policy is set to zero for any block that is not allowed.
3.3 Reward
We calculate the Gravimetric Surface Area GSA in m2 g−1 with Zeo++25 during the training loop of the GFlowNet. We configure Zeo++ with a probe radius of 1.525 Å and 2000 samples. The GFlowNet is given the following reward: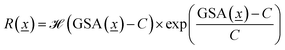 | (1) |
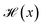 is the Heaviside step function
is the Heaviside step function 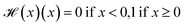 and C is a cutoff. Zeo++ and pormake sometimes raise errors due to large distances between atoms. The reward is zero when an error occurred to encourage the GFlowNet to avoid materials with unrealistic bond lengths.
and C is a cutoff. Zeo++ and pormake sometimes raise errors due to large distances between atoms. The reward is zero when an error occurred to encourage the GFlowNet to avoid materials with unrealistic bond lengths.
3.4 Relationship with CO2 capture
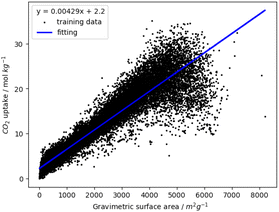
We demonstrate that the gravimetric surface area predicts CO2 uptake by analysing approximately 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MOFs from three databases: CoRE2019,19 ARABG26 and BW20K.27 We performed univariate linear regression of CO2 uptake at 16 bar using each of the geometric and chemical descriptors. The best performing descriptor was the gravimetric surface area with coefficient of determination is 0.88, RMSE is 2.41 mol kg−1 and Spearman's rank correlation coefficient of 0.97. Fig. 1 shows the CO2 uptake as a function of gravimetric surface area. We validated the regression using 50 rounds of 10-fold cross validation, with each cross-validation consisting of an 80–20 split between training and test data. The mean coefficient of determination is 0.88 ± 0.0002 and mean RMSE is 2.41 ± 0.022 mol kg−1. The training and test values of coefficient of determination and RMSE are the same to two decimal places and the standard deviation of these metrics during cross validation are very small which shows that the correlation is robust and stable.
000 MOFs from three databases: CoRE2019,19 ARABG26 and BW20K.27 We performed univariate linear regression of CO2 uptake at 16 bar using each of the geometric and chemical descriptors. The best performing descriptor was the gravimetric surface area with coefficient of determination is 0.88, RMSE is 2.41 mol kg−1 and Spearman's rank correlation coefficient of 0.97. Fig. 1 shows the CO2 uptake as a function of gravimetric surface area. We validated the regression using 50 rounds of 10-fold cross validation, with each cross-validation consisting of an 80–20 split between training and test data. The mean coefficient of determination is 0.88 ± 0.0002 and mean RMSE is 2.41 ± 0.022 mol kg−1. The training and test values of coefficient of determination and RMSE are the same to two decimal places and the standard deviation of these metrics during cross validation are very small which shows that the correlation is robust and stable.
4 The matgfn-rm dataset
4.1 Training
We trained a GFlowNet using trajectory balance loss28 and an LSTM policy. Each token was embedded using an embedding size of 32 and passed through an LSTM with two hidden layers of size 16. Finally, a MLP with one hidden layer of size 8 is used to compute the forward and backward policies as a single output vector. We use a learning rate of 5 × 10−3 for both the policy and the partition function. We train for a maximum of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 episodes and stop when the mean loss over 10
000 episodes and stop when the mean loss over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 episodes is lower than 1.8. We note that hyperparameter optimisation will likely improve the results.
000 episodes is lower than 1.8. We note that hyperparameter optimisation will likely improve the results.
The GFlowNet is trained from a reward rather than from x, y pairs (such as the case of supervised learning). Thus, data splitting methods are not relevant since there is no training set. An equivalent in sequential decision making is the exploration strategy, which in our case was on-policy.
Eleven topologies were chosen: CDZ-E, CLD-E, EFT, FFC, TSG, TFF, ASC, DMG, DNQ, FSO, URJ. These topologies were chosen because they were the fastest for which pormake can construct a MOF among the wider-known topologies. There is no limitation in using other topologies and thus further work can sample over a wider set of topologies or train a single, universal GFlowNet which chooses topology as one of its actions.
For each topology, two GFlowNets were trained, one with edges and one without. In pormake, each topology has two ways of constructing a MOF: with or without edges. To be comprehensive in our experiments, we trained a GFlowNet for each case. To avoid cherry-picking, we report all our results. For gravimetric surface area as a proxy, topologies with edges often outperform those without, as shown in ESI.†
Each trained GFlowNet (both with and without edges) was sampled between 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 120
000 and 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times. The number of samples varies depending on the time taken to calculate the reward, and the sampler was given a fixed wall-time. These samples were de-duplicated and combined with those seen during training with a non-zero reward, thus forming the matgfn-rm dataset containing 1
000 times. The number of samples varies depending on the time taken to calculate the reward, and the sampler was given a fixed wall-time. These samples were de-duplicated and combined with those seen during training with a non-zero reward, thus forming the matgfn-rm dataset containing 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709
709![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126 items. The dataset is reported in the dataset/dataset.json file of matgnfn.
126 items. The dataset is reported in the dataset/dataset.json file of matgnfn.
4.2 Diversity and novelty analysis
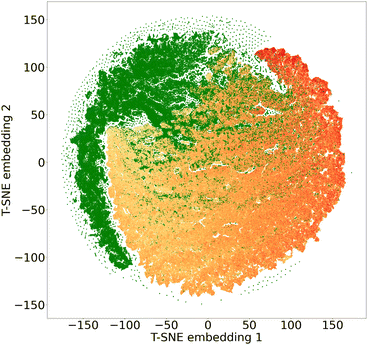
To assess diversity and novelty, we compare the whole matgfn-rm to the ARC-MOF dataset. We first compute the average minimum distance (AMD) descriptor29 of length 100 for each CIF file in both datasets. This descriptor uniquely identifies crystal structures and is a continuous metric, meaning that the distance (measured using the Chebyshev metric) is zero for similar crystals. We embed the AMD to two dimensions using t-SNE, implented in openTSNE,30 using the Chebyshev distance metric and nearest neighbour descent.31Fig. 2 shows the result. The matgfn-rm materials are separated from most materials from ARC-MOF. This indicates the generated materials are novel compared to existing datasets. To further assess novelty, we define the following distance metric given a dataset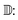
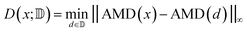 | (2) |
Intuitively, this metric is the distance to the closest point in the reference dataset. Using scikit-learn32's NearestNeighbor, we compute this metric for all materials in matgfn-rn with respect to ARC-MOF. Fig. 4 shows a histogram of D(x) and a violin plot of the gravimetric surface area in each bin. As the distance metric increases, the mean gravimetric surface area also increases, indicating that the “further” away a generated structure is from the reference dataset, the higher the gravimetric surface area. In ESI, Fig. S15† we present an similar analysis that only considers the top-100 structures in ARC-MOF and matgfn-rm. Given that the distribution of gravimetric surface area in the top-100 in those two datasets shows no overlap, the T-SNE embedding shows almost perfect separation, again indicating novelty of the generated top-100.
4.3 Simulated CO2 capture performance
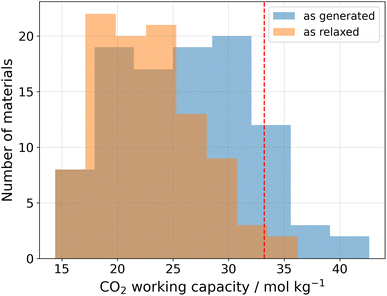
In order to confirm the expectation of efficient CO2 capture from an adsorption proxy (i.e., the gravimetric surface area), we run physics-based Grand Canonical Monte Carlo simulations for the top-100 generated materials in the matgfn-rm dataset.33,34 We simulated single-component adsorption isotherms for pure CO2, from which we extract the working capacity. All simulations were performed at 300 K, with pressures ranging from 0.15 to 16 bar. The working capacity was calculated as the difference in uptake of CO2 between the highest and lowest pressures. Fig. 3 shows (in blue) the distribution of working capacity for the top-100 matgfn-rm materials. All top-100 materials exhibit very high CO2 working capacities, corresponding to the 90th percentile of the experimentally-realised CoRE2019 dataset.20 They are (modestly) more selective towards CO2 than N2, achieving selectivity between 1 and 4 (not shown). Thirteen of the top-100 matgfn-rm materials have working capacities that are higher than all materials found in the CoRE2019 dataset. In particular, we highlight in Fig. 5 the covalent organic framework 005-ffc-10217 that achieved the highest CO2 working capacity of approximately 43 mol kg−1.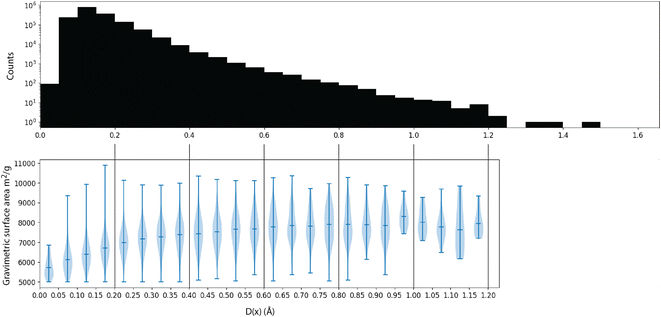 | ||
| Fig. 4 (Top) A histogram of the distance metric D(x) in eqn (2) with respect to the ARC-MOF dataset. (Bottom) For each bin in the histogram, a violin plot of the gravimetric surface area of elements in that bin, showing that materials with higher distance to the reference dataset have higher gravimetric surface areas. | ||
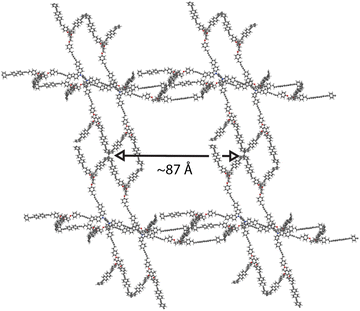 | ||
| Fig. 5 A render of the relaxed structure of 005-ffc-10217, the highest performing structure in the matgfn-rm dataset. We show here the 2 × 2 × 2 supercell. | ||
4.4 Relaxation and validity checks
Due to the hypothetical nature of the generated MOFs, the crystalline structures are not guaranteed to be perfect. We therefore used the mofchecker library35 to perform basic consistency checks on the generated CIFs. According to mofchecker, all of the top-100 matgfn-rm are porous (metal–) organic materials. However, due to the hypothetical interatomic distances sometimes being larger (or shorter) than the typical bond lengths, some atoms are flagged as either over- or under-coordinated. In order to obtain a more realistic structure, we performed atomic coordinate and unit cell relaxation using the CHGNet36 interatomic potential. Relaxing the structures solves most of the structural problems, with 98% presenting neither atomic overlaps nor over-coordination of C, N and H atoms, respectively. In particular, for the high-performing 005-ffc-10217 structure, relaxation led to a 23% reduction in the unit cell volume, bringing the CO2 working capacity down to 36.2 mol kg−1, which is still larger than those found in the CoRE2019 dataset. In Fig. 3, we show (in orange) the distribution of working capacity for the top-100 matgfn-rm materials after structural relaxation. Despite the overall reduction of the working capacity due to unit cell shrinkage, the subset remains in the 90th percentile of the CoRE2019 dataset. Two of the relaxed top-100 matgfn-rm materials have higher working capacities than any material found in the CoRE2019 dataset. The relaxed pore size of 005-ffc-10217 is approximately 87 Å. Structural relaxation changes the average minimum distance descriptors by a small amount and thus the diversity analysis still holds. See ESI, Fig. S14† for an illustration of the effect of relaxation on the t-SNE embeddings.5 Discussion
The ultimate goal of computer-aided discovery is materials with improved real-world performance. In carbon capture applications the choice of materials should consider figures-of-merit at the process level.37,38 Molecular-level metrics, such as the gravimetric surface area, working capacity, heat of adsorption and molecular selectivity, are useful, accessible proxies that help bridge the scale gap and provide an early prioritisation of candidates. Out of all the options, we chose the widely used working capacity as a representative metric, which was maximised despite not having been intentionally optimised for. Molecular selectivity is another key figure-of-merit in carbon dioxide capture. The realization that we have generated reticular structures with selectivity greater than one, even though selectivity was not explicitly included in the reward function, indicates the potential of GFlowNets for creating novel materials for application in chemical separations. To further improve the candidates, selectivity, working capacity or even process-level metrics can be included in the reward function, possibly using an active-learning approach.39Algorithmic approaches can also push the performance further. Key ones would be hyperparameter optimisation, improved exploration (e.g. using Thompson Sampling40), training a single GFlowNet for all topologies, improved losses41 and multi-objective reward functions42–44 that enable a more holistic evaluation of the material performance and usability, including stability and synthesisability dimensions.45 All these are possible using the framework presented here and thus our paper opens up all these possibilities for follow-up to obtain use-able, real-world materials.
6 Conclusion
In summary, we built a workflow using GFlowNets to generate diverse and novel reticular frameworks with gravimetric surface area greater than 5000 m2 g−1. As a key result, the top-100 candidates of the resulting matgfn-rm dataset have working capacities in the top 90th percentile of CoRE2019 reference dataset. Moreover, 2 of the top-100 matgfn-rm materials have working capacities that are higher than all materials found in the CoRE2019 dataset. After further analysis and structural relaxation, 2 outperforming materials remain. Further work is needed to confirm the stability and synthesizability of the materials generated in our study. Nevertheless, our results clearly demonstrate the potential of GFlowNets for materials discovery in carbon capture applications.Data availability
Matgfn is available at https://github.com/flaviucipcigan/matgfn and archived on Zenodo at https://zenodo.org/records/10246465. In the repository, the notebook to generate reticular materials is at notebooks/reticular_materials.ipynb, the training script at dataset/train_agent.py, the dataset in dataset/dataset.json and the analysis scripts in multiple python files in dataset/.Author contributions
Flaviu Cipcigan: project: conceptualisation, project administration. Paper: writing – coordination, writing – original draft, writing – review & editing. Software: main author of matgfn, contributor to MOF application code, results: methodology, experiments, formal analysis, validation, diversity analysis of matgfn-rm. Jonathan Booth: project: project administration, trained GFlowNets on MOF topologies paper: writing – MOF result section, writing – review & editing. Software: created reward function and other necessary code for MOF application of GFlownets results: methodology, experiments, formal analysis, validation. Rodrigo Neumann Barros Ferreira: paper: writing – original draft, writing – review & editing. Results: validation and simulations of matgfn-rm dataset. Carine Ribeiro dos Santos: results: validation and simulations of matgfn-rm dataset. Mathias Steiner: project: project administration. Paper: writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Dan Cunnington and Won Kyung Lee for valuable comments on the manuscript. Flaviu Cipcigan and Jonathan Booth were supported by the Hartree National Centre for Digital Innovation, a collaboration between STFC and IBM.Notes and references
-
T. Hey, S. Tansley and K. Tolle, The Fourth Paradigm: Data-Intensive Scientific Discovery, Microsoft Research, 2009 Search PubMed
.
- A. Agrawal and A. N. Choudhary, APL Mater., 2016, 4, 053208 CrossRef
.
- P. Das, T. Sercu, K. Wadhawan, I. Padhi, S. Gehrmann, F. Cipcigan, V. Chenthamarakshan, H. Strobelt, C. dos Santos, P.-Y. Chen, Y. Y. Yang, J. P. K. Tan, J. Hedrick, J. Crain and A. Mojsilovic, Nat. Biomed. Eng., 2021, 5, 613–623 CrossRef CAS PubMed
.
- D. Crusius, J. R. Schnell, F. Cipcigan and P. C. Biggin, Digital Discovery, 2023, 2, 1163–1177 RSC
.
- K. Hammond, F. Cipcigan, K. A. Nahas, V. Losasso, H. Lewis, J. Cama, F. Martelli, P. W. Simcock, M. Fletcher, J. Ravi, P. J. Stansfeld, S. Pagliara, B. W. Hoogenboom, U. F. Keyser, M. S. P. Sansom, J. Crain and M. G. Ryadnov, ACS Nano, 2021, 15, 9679–9689 CrossRef CAS PubMed
.
- F. Cipcigan, P. Smith, J. Crain, A. Hogner, L. D. Maria, A. Llinas and E. Ratkova, J. Chem. Inf. Model., 2020, 61, 263–269 CrossRef PubMed
.
- J. L. McDonagh, B. H. Wunsch, S. Zavitsanou, A. Harrison, B. Elmegreen, S. Gifford, T. van Kessel and F. Cipcigan, arXiv, 2023, preprint, arXiv:2303.14223, DOI:10.48550/arXiv.2303.14223.
-
O. M. Yaghi, M. J. Kalmutzki and C. S. Diercks, Introduction to reticular chemistry: metal-organic frameworks and covalent organic frameworks, John Wiley & Sons, 2019 Search PubMed
.
- R. Freund, S. Canossa, S. M. Cohen, W. Yan, H. Deng, V. Guillerm, M. Eddaoudi, D. G. Madden, D. Fairen-jimenez, H. Lyu, L. K. Macreadie, Z. Ji, Y. Zhang, B. Wang, F. Haase, C. Wöll, O. Zaremba, J. Andreo, S. Wuttke and C. S. Diercks, Angew. Chem., 2021, 60(45), 23946–23974 CrossRef CAS PubMed
.
- M. J. Kalmutzki, N. Hanikel and O. M. Yaghi, Sci. Adv., 2018, 4, eaat9180 CrossRef CAS PubMed
.
- O. K. Farha, I. Eryazici, N. C. Jeong, B. G. Hauser, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, S. T. Nguyen, A. Özgür Yazaydın and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 15016–15021 CrossRef CAS PubMed
.
-
F. Cipcigan, Zenodo archive for flaviucipcigan/matgfn, 2023, DOI:10.5281/zenodo.10246465
.
- E. Bengio, M. Jain, M. Korablyov, D. Precup and Y. Bengio, arXiv, 2021, preprint, arXiv:2106.04399v2, DOI:10.48550/arXiv.2106.04399.
- Y. Bengio, T. Deleu, E. J. Hu, S. Lahlou, M. Tiwari and E. Bengio, arXiv, 2021, preprint, arXiv:2111.09266, DOI:10.48550/arXiv.2111.09266.
- M. Jain, T. Deleu, J. S. Hartford, C.-H. Liu, A. Hernández-García and Y. Bengio, arXiv, 2023, preprint, arXiv:2302.00615, DOI:10.48550/arXiv.2302.00615.
- M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789 CrossRef PubMed
.
- S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, ACS Appl. Mater. Interfaces, 2021, 13, 23647–23654 CrossRef CAS PubMed
.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Nat. Mach. Intell., 2021, 3, 76–86 CrossRef
.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS
.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 4068 CrossRef CAS PubMed
.
- J. Burner, J. Luo, A. White, A. Mirmiran, O. Kwon, P. G. Boyd, S. Maley, M. Gibaldi, S. Simrod, V. Ogden and T. K. Woo, Chem. Mater., 2023, 35, 900–916 CrossRef CAS
.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Z. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, arXiv, 2019, preprint, arXiv:1912.01703, DOI:10.48550/arXiv.1912.01703.
-
M. Towers, J. K. Terry, A. Kwiatkowski, J. U. Balis, G. d. Cola, T. Deleu, M. Goulão, A. Kallinteris, K. G. Arjun, M. Krimmel, R. Perez-Vicente, A. Pierré, S. Schulhoff, J. J. Tai, A. T. J. Shen and O. G. Younis, Gymnasium, 2023, https://zenodo.org/record/8127025 Search PubMed
.
-
S. Lahlou, J. D. Viviano, V. Schmidt and Y. Bengio, torchgfn, A PyTorch GFlowNet library, 2023 Search PubMed
.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS
.
- R. Anderson, E. Argueta, A. Biong and D. Gomez-Gualdron, Chem. Mater., 2018, 30(18), 6325–6337 CrossRef CAS
.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Nature, 2019, 576, 253–256 CrossRef CAS PubMed
.
- N. Malkin, M. Jain, E. Bengio, C. Sun and Y. Bengio, Adv. Neural Inf. Process., 2022, 35, 5955–5967 Search PubMed
.
- D. Widdowson, M. M. Mosca, A. Pulido, A. I. Cooper and V. Kurlin, MATCH Commun. Math. Comput. Chem., 2021, 87, 529–559 CrossRef
.
- P. G. Poličar, M. Stražar and B. Zupan, bioRxiv, 2019, preprint, DOI:10.1101/731877.
-
W. Dong, C. Moses and K. Li, Proceedings of the 20th International Conference on World Wide Web, New York, NY, USA, 2011, pp. 577–586 Search PubMed
.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
-
R. Neumann Barros Ferreira, B. O Conchuir, T. Elengikal, B. Luan, R. L. Ohta, F. Lopes Oliveira, A. Mhadeshwar, J. Kalyanaraman, A. Sundaram, J. Falkowskiet al., Proceedings of the 16th Greenhouse Gas Control Technologies Conference, 2022 Search PubMed
.
- F. L. Oliveira, C. Cleeton, R. Neumann Barros Ferreira, B. Luan, A. H. Farmahini, L. Sarkisov and M. Steiner, Sci. Data, 2023, 10, 230 CrossRef CAS PubMed
.
- K. M. Jablonka, 2023, https://github.com/kjappelbaum/mofchecker.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 1–11 Search PubMed
.
- D. Yancy-Caballero, K. T. Leperi, B. J. Bucior, R. K. Richardson, T. Islamoglu, O. K. Farha, F. You and R. Q. Snurr, Mol. Syst. Des. Eng., 2020, 5, 1205–1218 RSC
.
- A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, Chem. Rev., 2021, 121, 10666–10741 CrossRef CAS PubMed
.
-
M. Jain, E. Bengio, A.-H. Garcia, J. Rector-Brooks, B. F. P. Dossou, C. Ekbote, J. Fu, T. Zhang, M. Kilgour, D. Zhang, L. Simine, P. Das and Y. Bengio, Biological Sequence Design with GFlowNets, 2022, https://arxiv.org/abs/2203.04115 Search PubMed
.
- J. Rector-Brooks, K. Madan, M. Jain, M. Korablyov, C.-H. Liu, S. Chandar, N. Malkin and Y. Bengio, arXiv, 2023, preprint, arXiv:2306.17693, DOI:10.48550/arXiv.2306.17693.
-
K. Madan, J. Rector-Brooks, M. Korablyov, E. Bengio, M. Jain, A. C. Nica, T. Bosc, Y. Bengio and N. Malkin, International Conference on Machine Learning, 2022 Search PubMed
.
-
M. Jain, S. C. Raparthy, A. Hernández-Garcıa, J. Rector-Brooks, Y. Bengio, S. Miret and E. Bengio, International Conference on Machine Learning, 2023, pp. 14631–14653 Search PubMed
.
- B. Liu, Y. Feng, P. Stone and Q. Liu, arXiv, 2023, preprint, arXiv.2306.03792, DOI:10.48550/arXiv.2306.03792.
-
Y. He, X. Feng, C. Cheng, G. Ji, Y. Guo and J. Caverlee, Proceedings of the ACM Web Conference, 2022, 2022, pp. 2205–2215 Search PubMed
.
- S. A. Mohamed, D. Zhao and J. Jiang, Commun. Mater., 2023, 4, 79 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00020j |
| ‡ Here, we conceptualise materials broadly to include molecules, proteins, crystals and complex materials. |
| This journal is © The Royal Society of Chemistry 2024 |