Open Access Article
Open Access ArticlePhysics-based reward driven image analysis in microscopy
K.
Barakati
 *a,
Hui
Yuan
c,
Amit
Goyal
d and
S. V.
Kalinin
*ab
*a,
Hui
Yuan
c,
Amit
Goyal
d and
S. V.
Kalinin
*ab
aDepartment of Materials Science and Engineering, University of Tennessee, Knoxville, TN 37996, USA. E-mail: K.barakati@vols.utk.edu; sergei2@utk.edu
bPacific Northwest National Laboratory, Richland, WA 99354, USA
cDepartment of Materials Science and Engineering, McMaster University, 1280 Main Street West, Hamilton, Ontario, L8S 4L7 Canada
dLaboratory for Heteroepitaxial Growth of Functional Materials & Devices, Department of Chemical & Biological Engineering, State University of New York, Buffalo, NY 14260, USA
First published on 12th September 2024
Abstract
The rise of electron microscopy has expanded our ability to acquire nanometer and atomically resolved images of complex materials. The resulting vast datasets are typically analyzed by human operators, an intrinsically challenging process due to the multiple possible analysis steps and the corresponding need to build and optimize complex analysis workflows. We present a methodology based on the concept of a Reward Function coupled with Bayesian Optimization, to optimize image analysis workflows dynamically. The Reward Function is engineered to closely align with the experimental objectives and broader context and is quantifiable upon completion of the analysis. Here, cross-section, high-angle annular dark field (HAADF) images of ion-irradiated (Y, Dy)Ba2Cu3O7−δ thin-films were used as a model system. The reward functions were formed based on the expected materials density and atomic spacings and used to drive multi-objective optimization of the classical Laplacian-of-Gaussian (LoG) method. These results can be benchmarked against the DCNN segmentation. This optimized LoG* compares favorably against DCNN in the presence of the additional noise. We further extend the reward function approach towards the identification of partially-disordered regions, creating a physics-driven reward function and action space of high-dimensional clustering. We pose that with correct definition, the reward function approach allows real-time optimization of complex analysis workflows at much higher speeds and lower computational costs than classical DCNN-based inference, ensuring the attainment of results that are both precise and aligned with the human-defined objectives.
Electron and scanning probe microscopy have emerged as a primary method to provide insights into the microstructure, composition, and properties of a wide range of materials, from metals and alloys to polymers and composites.1–4 These techniques generate large volumes of imaging data containing information on material structure that can be further connected to fundamental physics, chemistry, and and material processing.5 However, the large amount of imaging data requires consistent analysis methods.6–8 Traditionally, this has been accomplished using the collection of the standard image processing techniques including various forms of background subtraction,9,10 filtering,11 and peak finding,12–14 all applied by the human operator sequentially. The employment of machine learning methodologies, particularly DCNN (Deep Convolutional Neural Network) segmentation,15–19 has notably enhanced and expedited certain steps within this analytical framework; however, the overall progression of image analysis remains the same. This type of analysis is also computationally intensive20–23 and requires the ensemble networks to effectively manage deviations from anticipated data distributions.24–26 Most importantly, it is strongly biased by the operator's expertise and can potentially be steered towards anticipated answers via decisions made at each analysis step.
Here we present a method for image analysis that utilizes a reward function concept.27,28 This involves setting a measure(s) of success that can be quantitatively established by the end of the analysis. With the reward function defined, the analysis workflow including the sequence and hyper-parameters of individual operations can be optimized via one of the suitable stochastic optimization frameworks. The simple image analysis workflow is optimized by Bayesian Optimization29–32 which allows dynamic tuning of the parameters to achieve optimal performance. This concept can be further adapted to more complex, multi-stage workflows via reinforcement learning, Monte Carlo decision trees, or more complex algorithms.33,34
In proposing reward-driven workflows, we note that typically human-based image analysis is performed to optimize certain implicit measures of the analysis quality. For example, in atomic segmentation, this task is to identify and classify all the atoms of a certain type, or all defects within the image. Here we propose that analysis can be cast as an optimization problem if the reward function based on the analysis results can be formulated. Then the process becomes optimized in the parameter space of the simple analysis functions. Here, we consider two specific tasks, namely atom finding in atomically resolved images and identification of amorphized regions within the material.
As a model system, we chose a 1.2 μm thick YBa2Cu3O7−δ thick film, doped with Dy2O3 nanoparticles, fabricated using a metal–organic deposition process. The sample then was irradiated with an Au5+ ion beam oriented along the c-axis of the Yttrium Barium Copper Oxide (YBCO), and the cross-sectional and plan-view TEM specimens were prepared through standard mechanical polishing, followed by final thinning using Xe Plasma Focused Ion Beam (Xe PFIB).35
As a first model task, we consider the semantic segmentation,36–39 or “atom finding” of atomically resolved images.40 Traditionally this has been accomplished using the peak finding procedures, correlative filtering, Hough transforms,41,42 or versions of Laplacian of Gaussian (LoG) approaches.43,44 These approaches require extensive tuning of the parameters of the image analysis function with the human assessment of the results as feedback. The introduction of DCNNs has resulted in broad interest in deep learning segmentation of images,45–47 with multiple efforts utilizing versions of U-Nets,48,49 Mask R-CNNs,50 and other architectures recently reported such as SegNet,51 DeepLab,52 and Pyramid Scene Parsing Networks (PSPNet).53 The use of simple analysis methods requires careful manual tuning of parameters and tends to be very brittle – the contrast variations even within a single image can result in measurable differences of performance. Comparatively, DCNN methods are more robust, but require supervised training and can be sensitive to out-of-distribution drift effects.54–56
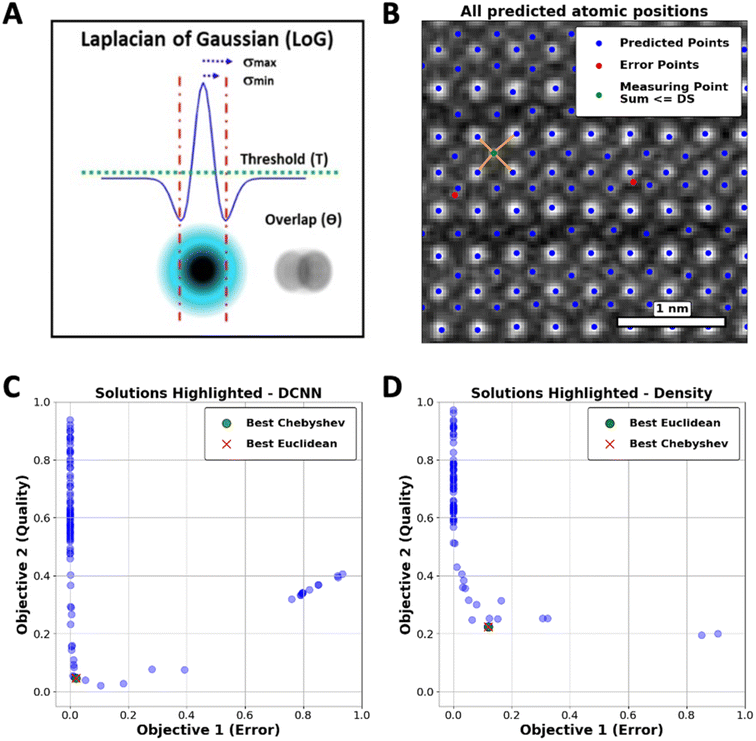
Taking atom detection as an initial instance of the reward-driven process, we demonstrate optimization of the conventional LoG algorithm. This approach is characterized by a set of control parameters, including min_sigma (σmin), which sets the smallest feature size that can be detected, max_sigma (σmax), which defines the largest detectable feature size, threshold (T), determining the minimum intensity required for a feature to be detected, and overlap (θ), controlling the degree of permissible overlap between detected features. These parameters collectively define the LoG algorithm's parameter space, as illustrated in Fig. 1(A).
To cast the image analysis as an optimization problem, we define possible physics-based reward (or objective) functions. One such function can be defined based on the expected number of atoms within the field of view, readily available from image size and lattice parameter of material. The LoG algorithm's effectiveness in relation to its hyper-parameters is determined by a metric we refer to as Quality Count (QC), which is defined as the normalized difference between the number of atoms found by LoG and the physics-based reward standard, formulated as:
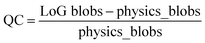 | (1) |
To avoid reward hacking in this context, we also recognize that the total count of atoms is an overarching characteristic, and for a segmentation algorithm to be effective, it should adhere to more specific requirements. The second constraint is that atoms need to be spaced at distances that are physically plausible. To incorporate this aspect, we introduce a second component to the reward function, which we call the error function.
The error function (ER) will be applied to measure the incidence of atoms in regions that are not aligned with the structural configuration of the YBCO lattice. As shown in Fig. 1(B), the ER calculates the sum of distances from each atom to its four nearest neighbors. If this sum, referred to as the Distance Sum (DS), falls below a certain threshold, the atom is considered incorrectly positioned and is classified as an error. This threshold is determined based on the expected inter-atomic distances within the ideal YBCO lattice parameters (lengths of the unit cell).
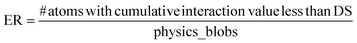 | (2) |
In this setting, the optimization of LoG analysis that we will further refer to as LoG*, becomes that of the multi-objective Bayesian Optimization in the image processing parameter space, where objectives QC and ER are minimized jointly.
In this case, we can further define a benchmark for accuracy, which we designate as “Oracle” in this context. A viable way to create an Oracle for the atomic segmentation task can be performed using the pre-trained DCNN, providing near-ideal identification of all atomic positions. These can be further classified (with human tuning) into specific types. We refer to the DCNN analysis as “Oracle” comparable to human-based analysis and use Oracle to verify the results of the reward-driven workflows accomplished with much simpler tools.
We employed the Skopt library57,58 to implement hyper-parameter optimization, specifically focusing on adjusting the threshold and overlap parameters of the LoG function. As represented in Fig. 1(C), a set of optimal solutions, or Pareto front, where no objective can be improved without degrading the other was obtained. Through this framework, a delicate balance between the dual objectives has been established, leading to the discovery of an optimal hyper-parameter configuration for the LoG function. Two common metrics to identify the “best” solutions within the Pareto Frontier are the Euclidean and Chebyshev distances.
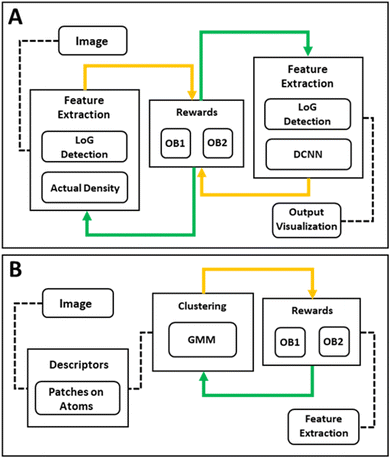
Displayed in Fig. 2(A) is the workflow development utilized for Multi Objective-Bayesian Optimization. This workflow outlines the order of steps throughout the analysis procedure. We note that this approach can be readily applied to the scenarios when the image quality or acquisition conditions vary across the image, e.g., due to the mis-tilt or presence of non-crystalline contaminates, etc. For these tasks, the algorithm can be implemented in the sliding window setting where the parameters are optimized for each. Further, this workflow can be customized to focus on different rewards such as the identification of the amorphous regions or other objectives of the study as presented in Fig. 2(B).
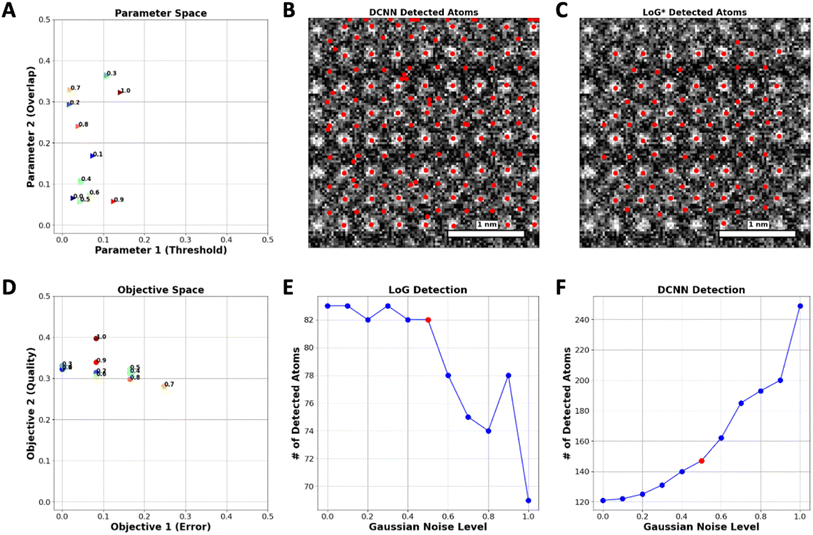
As a next step, we explore the robustness of the proposed approach with respect to the noise in the image. To accomplish this, Gaussian noise levels from 0 to 1, where 0 is the image without noise have been applied to a specific set of images. Upon noise addition, the number of atoms is identified both by DCNN and optimized LoG* algorithm. Fig. 3(A) depicts the variation in optimal hyperparameters of the LoG model in response to various levels of added noise. Correspondingly, Fig. 3(D) demonstrates that the best Pareto front solutions, which represent the objectives (QC and ER), adapt in a manner that fulfills the reward requirements.
In DCNN models, elevating the noise level leads to the introduction of artifacts that mimic the appearance of new atoms in the images, thereby generating false positives as depicted in Fig. 3(C). In contrast, the LoG function demonstrates resilience when subjected to comparable increases in noise, avoiding the misidentification of these artifacts as new atoms, as evidenced in Fig. 3(B). This stability can be attributed to the implementation of the ER function within the LoG framework, which effectively prevents the function from mistakenly identifying features caused by noise as real atomic points.
Fig. 3(F) illustrates the detection capability of the DCNN model regarding Gaussian noise levels. The number of detected atoms increases significantly with the Gaussian noise level after a certain point (Noise level of 0.6), which implies that the DCNN begins to mistakenly identify noise artifacts as atoms, thereby detecting false positives. Fig. 3(E) represents the detection results of the LoG method under the same conditions. In contrast to the DCNN, the LoG detection exhibits a much lower variability in the number of detected atoms across noise levels, maintaining a relatively consistent count. This implies that the LoG approach is more selective, mainly identifying actual atomic points and not creating false positives by noise-related distortions.
We have further explored the applicability of this approach towards more complex tasks of identification of the amorphous regions. Here, the complexity of analysis is that the damage introduces amorphization and change of observed image contrast on oxygen and copper lattices, whereas the bright atoms remain visible. Correspondingly, manual construction of the workflow combining segmentation, multiple possible clustering and dimensionality reduction algorithms can be a very time-consuming and operator-dependent step. Here, we illustrate that the use of the reward function approach enables us to address this problem through a comprehensive workflow. This workflow includes window-size selection and automated parameter tuning of the Gaussian Mixture Model (GMM) clustering method.59,60 We used GMM to model the data as a mixture of multiple Gaussian distributions, which provides a robust framework for clustering complex datasets, and offers a broad range of hyperparameters that enable fine-tuning of the model. In principle, other clustering models61 can also be used, which makes the selection of the model type a part of the optimization process.
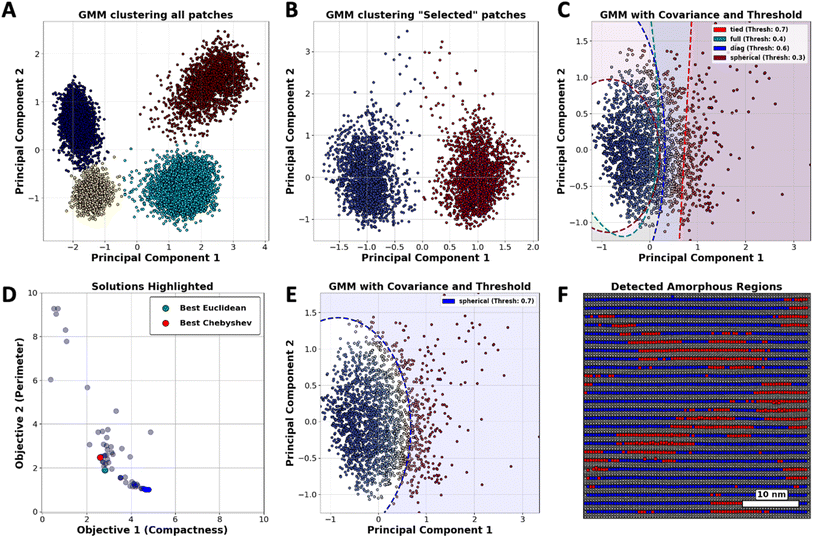
Considering the workflow in Fig. 2(B), we initially implemented GMM clustering techniques to identify the diverse atomic configurations within the YBCO structure. Fig. 4(A) displays the categorization of all atomic types present in the YBCO structure. We organized these into four distinct clusters corresponding to the CuO2 (planes), CuO (chains), Ba (barium), and Y (yttrium) components, respectively. Given that certain atomic varieties can dominate the clustering outcomes, we refined our approach by reducing the number of cluster types to specifically focus on barium (Ba) atoms. This was achieved by conducting two separate GMM clustering analyses on patches centered exclusively on Ba atoms. As illustrated in Fig. 4(B), two distinct clusters were identified, corresponding to the orientation of barium (Ba) atoms. These clusters are categorized based on their orientation: Ba1 is aligned along a principal axis, while Ba2 is configured to exhibit two-fold rotational symmetry with respect to Ba1. By concentrating solely on Ba1 or Ba2 atoms, GMM clustering enables us to detect the variations in Ba atoms.
In crystalline regions, atoms are generally well-ordered and maintain close alignment with their expected lattice positions, leading to the formation of tightly packed clusters with minimal deviations. However, any observed dispersity within these clusters serves as a clear indicator of deviations from the expected lattice positions, which is characteristic of atoms in amorphous areas. This distinction allows for the differentiation of crystalline and amorphous structures based on the spatial arrangement and variability of atomic positions.
Fig. 4(C) demonstrates that the clustering of atomic points can be controlled through the adjustment of two hyper-parameters of GMM: threshold and covariance type. According to our hypothesis, atomic points that surpass a predetermined threshold, when analyzed using a specific covariance type, should be classified as amorphous. This classification is substantiated by the observed dispersity of these points away from the core cluster, which is predominantly associated with crystalline regions. In this instance, the effectiveness of GMM clustering depends primarily on hyper-parameter selection and can be improved by devising a customized reward system that better aligns with desired outcomes.
To direct GMM clustering toward not only pinpointing the location but also assessing the area occupied by atoms deviating from their predicted positions, the compactness of these identified regions should be considered a valuable metric for rewards. Given that compactness is a critical characteristic, the second component of the reward should focus on regions with minimal perimeter. By integrating both compactness and perimeter as objectives in our analysis, we establish a workflow that is both practical and dependable.
To calculate these two objectives, we start by creating two binary masks to distinguish between crystalline and amorphous regions, where crystalline regions are labeled as “blue” based on provided data and everything else is considered amorphous. We then expand the boundaries of these masks slightly to ensure accurate measurements. Next, we calculate the area of each region by counting the pixels in the masks. For the amorphous regions, we label connected clusters of pixels and measure the length of their boundaries to get the total perimeter. These area and perimeter measurements are then normalized to account for the image size. Finally, we calculate the compactness of the amorphous regions using the formula. This helps in understanding how compact or spread out the amorphous regions are.
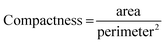 | (3) |
As depicted in Fig. 4(D), a set of optimal solutions was identified, demonstrating that no objective can be enhanced without adversely affecting another. By employing metrics to pinpoint the “best” solutions on the Pareto Frontier, the analysis effectively determined the optimal threshold and covariance type for GMM clustering, as presented in Fig. 4(E). The deployment of the clustering map on the image of the YBCO substrate, as demonstrated in Fig. 4(F), effectively reveals areas within the YBCO structure where there is a higher likelihood of atoms deviating from their predicted positions.
To summarize, here we introduce an approach for the development of complex image analysis workflows based on the introduction of a reward function aligned with experimental objectives. This reward function is a measure of the success of analysis, and can be built based on simple physical consideration, comparisons to the oracle functions, or any other approach imitating human perception. With the reward function being defined, the image analysis problem reduces to that of the optimization in the combinatorial space of image operations and corresponding hyper-parameters, taking advantage of the immense volume of knowledge in his field.
Here, this approach has proven to be effective in a case study involving in situ ion irradiated YBa2Cu3O7−δ layer images, where it facilitated the accurate identification of atomic positions and detection of amorphous regions. We propose the physics-based multi-objective reward functions for finding atom positions and classification of the amorphous regions and demonstrate the Bayesian optimization in the parameter space of multi-step simple image analysis functions to yield robust identification.
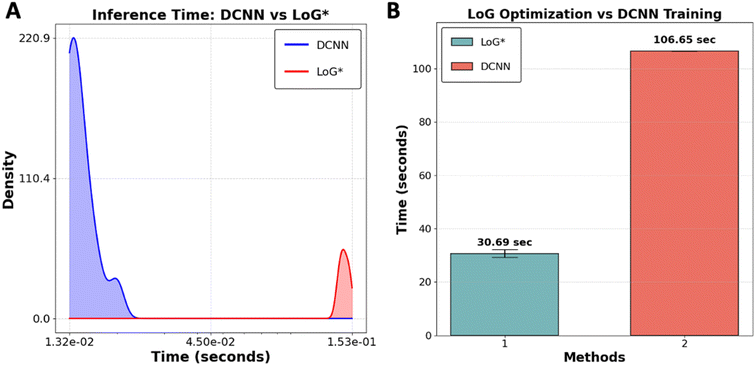
To evaluate the performance of the LoG* workflow as a suitable method for real-time analysis versus DCNN in case of time, we conducted a comparative study using 10 subimages of size 256 × 256 pixels extracted from YBCO sample. The comparison between DCNN and LoG* methods revealed distinct strengths and potential limitations for each, particularly regarding image processing speed and adaptability as presented in Fig. 5. DCNN exhibits a considerable speed advantage, processing images faster than LoG*. This efficiency is primarily due to the optimization of GPUs, which are engineered to manage the intensive computational demands of deep convolutional neural networks. Achieving this speed, however, requires an initial investment of time and resources to create and label the dataset for training the DCNN model. While this training process only needs to be done once, it can be particularly demanding for large datasets.
Although LoG* processes individual images at a slower pace, its key advantage is adaptability and explainability. This adaptability is particularly important when dealing with an out-of-distribution dataset. Additionally, the transparency of LoG* allows researchers to understand how specific features in the image contribute to the final output, making it easier to interpret results. In such cases, DCNN may struggle to provide accurate predictions because it heavily depends on the representativeness of its training data. If the new data deviates significantly from the training data, the DCNN model may fail, necessitating retraining, which diminishes its initial time efficiency. On the other hand, each time a new dataset is introduced, LoG* undergoes its optimization process, ensuring that it can accurately process data regardless of how different it is from previous datasets. This makes LoG* a more flexible, interpretable, and potentially more reliable choice in dynamic environments where the nature of the data can vary widely. The code utilized in this benchmarking analysis is available for public access on GitHub at [https://github.com/Kamyar-V2/RDW].
We believe that this approach has three significant impacts on microscopy. First, the introduction of a reward-function-based optimization approach makes the construction of analysis pipelines automated and unbiased, taking advantage of the powerful optimization approaches available today. Secondly, these analyses have the potential to be integrated into automated experiments and real-time data analytics workflows, enabling on-the-fly adjustments and decisions during data collection. Thirdly, the integration of reward functions across the domains offers a far more efficient approach for community integration than creation of disparate experimental data databases, contributing to the development of the open and FAIR experimental community.
Data availability
The code supporting the findings of this study is publicly accessible on GitHub at https://github.com/Kamyar-V2/RDW.Author contributions
Kamyar Barakati: conceptualization (equal), data curation (lead), formal analysis (equal), writing – original draft (equal); Sergei V. Kalinin: conceptualization (equal), formal analysis (equal), funding acquisition (equal), writing – review & editing (equal), supervision (equal). Hui Yuan: investigation (equal). Amit Goyal: investigation (equal).Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
This work (workflow development, reward-driven concept) was supported (K. B., S. V. K.) by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences as part of the Energy Frontier Research Centers program: CSSAS-The Center for the Science of Synthesis Across Scales under award number DE-SC0019288. The authors (A. G. and H. Y.) acknowledge support from the DOE/EERE under contract No. DE-EE0007870.References
- B. Layla Mehdi, M. Gu, L. R. Parent, W. Xu, E. N. Nasybulin, X. Chen, R. R. Unocic, P. Xu, D. A. Welch and P. Abellan, In situ electrochemical transmission electron microscopy for battery research, Microsc. Microanal., 2014, 20(2), 484–492 CrossRef CAS PubMed.
- M. Haider, S. Uhlemann, E. Schwan, H. Rose, B. Kabius and K. Urban, Electron microscopy image enhanced, Nature, 1998, 392(6678), 768–769 CrossRef CAS.
- M.-W. Chu, I. Szafraniak, D. Hesse, M. Alexe and U. Gösele, Elastic coupling between 90 twin walls and interfacial dislocations in epitaxial ferroelectric perovskites: a quantitative high-resolution transmission electron microscopy study, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(17), 174112 CrossRef.
- S. Jesse, P. Maksymovych and S. V. Kalinin, Rapid multidimensional data acquisition in scanning probe microscopy applied to local polarization dynamics and voltage dependent contact mechanics, Appl. Phys. Lett., 2008, 93(11), 112903 CrossRef.
- H.-C. Ni, R. Yuan, J. Zhang and J.-M. Zuo, Framework of compressive sensing and data compression for 4D-STEM, Ultramicroscopy, 2024, 259, 113938 CrossRef CAS PubMed.
- D. Bramich, A new algorithm for difference image analysis, Mon. Not. R. Astron. Soc.: Lett., 2008, 386(1), L77–L81 CrossRef.
- X. Xie, A review of recent advances in surface defect detection using texture analysis techniques, ELCVIA: electronic letters on computer vision and image analysis 2008, pp. 1–22 Search PubMed.
- R. De Borst, Challenges in computational materials science: multiple scales, multi-physics and evolving discontinuities, Comput. Mater. Sci., 2008, 43(1), 1–15 CrossRef CAS.
- S. Panahi, S. Sheikhi, S. Haddadan and N. Gheissari, Evaluation of background subtraction methods, in 2008 Digital Image Computing: Techniques and Applications, IEEE, 2008, pp. 357–364 Search PubMed.
- V. Cevher, A. Sankaranarayanan, M. F. Duarte, D. Reddy, R. G. Baraniuk and R. Chellappa, Compressive sensing for background subtraction, in Computer Vision–ECCV 2008: 10th European Conference on Computer Vision, Marseille, France, October 12-18, 2008, Proceedings, Part II 10, Springer, 2008, pp. 155–168 Search PubMed.
- P. Milanfar, A tour of modern image filtering: New insights and methods, both practical and theoretical, IEEE signal processing magazine, 2012, 30(1), 106–128 Search PubMed.
- M. Hadian-Jazi, M. Messerschmidt, C. Darmanin, K. Giewekemeyer, A. P. Mancuso and B. Abbey, A peak-finding algorithm based on robust statistical analysis in serial crystallography, J. Appl. Crystallogr., 2017, 50(6), 1705–1715 CrossRef CAS.
- P. Bayle, T. Deutsch, B. Gilles, F. Lançon, A. Marty and J. Thibault, Quantitative analysis of the deformation and chemical profiles of strained multilayers, Ultramicroscopy, 1994, 56(1–3), 94–107 CrossRef CAS.
- R. Bierwolf, M. Hohenstein, F. Phillipp, O. Brandt, G. Crook and K. Ploog, Direct measurement of local lattice distortions in strained layer structures by HREM, Ultramicroscopy, 1993, 49(1–4), 273–285 CrossRef CAS.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge, Recent advances and applications of deep learning methods in materials science, npj Comput. Mater., 2022, 8(1), 59 CrossRef.
- G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, Journal of Physics: Materials, 2019, 2(3), 032001 CAS.
- J. Schmidt, M. R. Marques, S. Botti and M. A. Marques, Recent advances and applications of machine learning in solid-state materials science, npj Comput. Mater., 2019, 5(1), 83 CrossRef.
- G. Pilania, Machine learning in materials science: from explainable predictions to autonomous design, Comput. Mater. Sci., 2021, 193, 110360 CrossRef CAS.
- L. Zhang and S. Shao, Image-based machine learning for materials science, J. Appl. Phys., 2022, 132(10) CrossRef.
- N. C. Thompson, K. Greenewald, K. Lee and G. F. Manso, The computational limits of deep learning, arXiv, 2020, preprint, arXiv:2007.05558, DOI:10.48550/arXiv.2007.05558.
- C. C. Aggarwal, Neural networks and deep learning, Springer, 2018, vol. 10, 978, p. 3 Search PubMed.
- I. Al Ridhawi, Y. Kotb, M. Aloqaily, Y. Jararweh and T. Baker, A profitable and energy-efficient cooperative fog solution for IoT services, IEEE Trans. Ind. Inf., 2019, 16(5), 3578–3586 Search PubMed.
- Z. Ali, L. Jiao, T. Baker, G. Abbas, Z. H. Abbas and S. Khaf, A deep learning approach for energy efficient computational offloading in mobile edge computing, IEEE Access, 2019, 7, 149623–149633 Search PubMed.
- T. G. Dietterich, Ensemble learning, The handbook of brain theory and neural networks, 2002, vol. 2, 1, pp. 110–125 Search PubMed.
- A. Ghosh, B. G. Sumpter, O. Dyck, S. V. Kalinin and M. Ziatdinov, Ensemble learning-iterative training machine learning for uncertainty quantification and automated experiment in atom-resolved microscopy, npj Comput. Mater., 2021, 7(1), 100 CrossRef.
- A. Ghosh, B. G. Sumpter, O. Dyck, S. V. Kalinin and M. Ziatdinov, Ensemble learning and iterative training (ELIT) machine learning: applications towards uncertainty quantification and automated experiment in atom-resolved microscopy, arXiv, preprint, arXiv:2101.08449, DOI:10.48550/arXiv.2101.08449.
- J. Eschmann, Reward function design in reinforcement learning. Reinforcement Learning Algorithms: Analysis and Applications, 2021, pp. 25–33 Search PubMed.
- N. Xu, H. Zhang, A.-A. Liu, W. Nie, Y. Su, J. Nie and Y. Zhang, Multi-level policy and reward-based deep reinforcement learning framework for image captioning, IEEE Trans. Multimed., 2019, 22(5), 1372–1383 Search PubMed.
- A. H. Victoria and G. Maragatham, Automatic tuning of hyperparameters using Bayesian optimization, Evol. Syst., 2021, 12, 217–223 CrossRef.
- M. A. Ziatdinov, A. Ghosh and S. V. Kalinin, Physics makes the difference: Bayesian optimization and active learning via augmented Gaussian process, Mach. Learn.: Sci. Technol., 2022, 3(1), 015003 Search PubMed.
- N. Creange, O. Dyck, R. K. Vasudevan, M. Ziatdinov and S. V. Kalinin, Towards automating structural discovery in scanning transmission electron microscopy, Mach. Learn.: Sci. Technol., 2022, 3(1), 015024 Search PubMed.
- B. N. Slautin, U. Pratiush, I. N. Ivanov, Y. Liu, R. Pant, X. Zhang, I. Takeuchi, M. A. Ziatdinov and S. V. Kalinin, Multimodal Co-orchestration for Exploring Structure-Property Relationships in Combinatorial Libraries via Multi-Task Bayesian Optimization, arXiv, 2024, preprint, arXiv:2402.02198, DOI:10.48550/arXiv.2402.02198.
- G. C. Critchfield and K. E. Willard, Probabilistic analysis of decision trees using Monte Carlo simulation, Med. Decis. Making, 1986, 6(2), 85–92 CrossRef CAS PubMed.
- Y. Li, Deep reinforcement learning: an overview, arXiv, 2017, preprint, arXiv:1701.07274, DOI:10.48550/arXiv.1701.07274.
- Y. Zhang, M. Rupich, V. Solovyov, Q. Li and A. Goyal, Dynamic behavior of reversible oxygen migration in irradiated-annealed high temperature superconducting wires, Sci. Rep., 2020, 10(1), 14848 CrossRef CAS PubMed.
- Y. Guo, Y. Liu, T. Georgiou and M. S. Lew, A review of semantic segmentation using deep neural networks, Int. J. Multimed. Inf. Retr., 2018, 7, 87–93 CrossRef.
- S. Hao, Y. Zhou and Y. Guo, A brief survey on semantic segmentation with deep learning, Neurocomputing, 2020, 406, 302–321 CrossRef.
- P. Wang, P. Chen, Y. Yuan, D. Liu, Z. Huang, X. Hou and G. Cottrell, Understanding convolution for semantic segmentation, in 2018 IEEE winter conference on applications of computer vision (WACV), IEEE, 2018, pp. 1451–1460 Search PubMed.
- Y. Mo, Y. Wu, X. Yang, F. Liu and Y. Liao, Review the state-of-the-art technologies of semantic segmentation based on deep learning, Neurocomputing, 2022, 493, 626–646 CrossRef.
- L. Vlcek, A. Maksov, M. Pan, R. K. Vasudevan and S. V. Kalinin, Knowledge extraction from atomically resolved images, ACS Nano, 2017, 11(10), 10313–10320 CrossRef CAS PubMed.
- J. Illingworth and J. Kittler, A survey of the Hough transform, Comput. Vis. Graph Image Process, 1988, 44(1), 87–116 CrossRef.
- J. R. Bergen and H. Shvaytser, A probabilistic algorithm for computing Hough transforms, J. Algorithm, 1991, 12(4), 639–656 CrossRef.
- P. P. Acharjya, R. Das and D. Ghoshal, Study and comparison of different edge detectors for image segmentation, Global J. Comput. Sci. Technol., 2012, 12(13), 28–32 Search PubMed.
- H. Kong, S. E. Sarma and F. Tang, Generalizing Laplacian of Gaussian filters for vanishing-point detection, IEEE Trans. Intell. Transport. Syst., 2012, 14(1), 408–418 Search PubMed.
- S. Wang, D. M. Yang, R. Rong, X. Zhan and G. Xiao, Pathology image analysis using segmentation deep learning algorithms, Am. J. Pathol., 2019, 189(9), 1686–1698 CrossRef PubMed.
- S. Minaee, Y. Boykov, F. Porikli, A. Plaza, N. Kehtarnavaz and D. Terzopoulos, Image segmentation using deep learning: a survey, IEEE Trans. Pattern Anal. Mach. Intell., 2021, 44(7), 3523–3542 Search PubMed.
- S. Ghosh, N. Das, I. Das and U. Maulik, Understanding deep learning techniques for image segmentation, ACM Comput. Surv., 2019, 52(4), 1–35 CrossRef.
- N. Siddique, S. Paheding, C. P. Elkin and V. Devabhaktuni, U-net and its variants for medical image segmentation: a review of theory and applications, IEEE Access, 2021, 9, 82031–82057 Search PubMed.
- O. Ronneberger, P. Fischer and T. Brox, U-net: convolutional networks for biomedical image segmentation, in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, October 5-9, 2015, Proceedings, Part III, Springer, Munich, Germany, 2015, vol. 18, pp. 234–241 Search PubMed.
- K. He, G. Gkioxari, P. Dollár and R. GirshickMask r-cnn, in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2961–2969 Search PubMed.
- V. Badrinarayanan, A. Kendall and R. Cipolla, Segnet: a deep convolutional encoder-decoder architecture for image segmentation, IEEE Trans. Pattern Anal. Mach. Intell., 2017, 39(12), 2481–2495 Search PubMed.
- L.-C. Chen, G. Papandreou, I. Kokkinos, K. Murphy and A. L. Yuille, Deeplab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs, IEEE Trans. Pattern Anal. Mach. Intell., 2017, 40(4), 834–848 Search PubMed.
- H. Zhao, J. Shi, X. Qi, X. Wang and J. JiaPyramid scene parsing network, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 2881–2890 Search PubMed.
- S. Disabato and M. RoveriLearning convolutional neural networks in presence of concept drift, in 2019 International Joint Conference on Neural Networks (IJCNN), IEEE, 2019, pp. 1–8 Search PubMed.
- A. De Silva, R. Ramesh, C. Priebe, P. Chaudhari and J. T. Vogelstein, The value of out-of-distribution data, in International Conference on Machine Learning, PMLR, 2023, pp. 7366–7389 Search PubMed.
- L. Yu, B. Twardowski, X. Liu, L. Herranz, K. Wang, Y. Cheng, S. Jui and J. v. d. Weijer, Semantic drift compensation for class-incremental learning, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 6982–6991 Search PubMed.
- skopt api documentation, https://scikit-optimize.github.io/stable/, accessed.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, Dropout: a simple way to prevent neural networks from overfitting, J. Mach. Learn. Res., 2014, 15(1), 1929–1958 Search PubMed.
- D. A. Reynolds, Gaussian mixture models, Encyclopedia of biometrics, 2009, vol. 741, pp. 659–663 Search PubMed.
- E. Patel and D. S. Kushwaha, Clustering cloud workloads: K-means vs. Gaussian mixture model, Proc. Comput. Sci., 2020, 171, 158–167 CrossRef.
- scikit-learn, scikit-learn, clustering, https://scikit-learn.org/stable/modules/clustering.html, accessed Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |