Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insight into ferromagnetic interactions in CuII–LnIII dimers with a compartmental ligand†
Anangamohan
Panja
 *ab,
Sagar
Paul
*ab,
Sagar
Paul
 *c,
Eufemio
Moreno-Pineda
*c,
Eufemio
Moreno-Pineda
 de,
Radovan
Herchel
de,
Radovan
Herchel
 f,
Narayan Ch.
Jana
f,
Narayan Ch.
Jana
 b,
Paula
Brandão
b,
Paula
Brandão
 g,
Ghenadie
Novitchi
h and
Wolfgang
Wernsdorfer
g,
Ghenadie
Novitchi
h and
Wolfgang
Wernsdorfer
 *ci
*ci
aDepartment of Chemistry, Gokhale Memorial Girls’ College, 1/1 Harish Mukherjee Road, Kolkata-700020, India. E-mail: ampanja@yahoo.co.in
bDepartment of Chemistry, Panskura Banamali College, Panskura RS, WB 721152, India
cPhysikalisches Institut, Karlsruhe Institute of Technology, D-76131 Karlsruhe, Germany. E-mail: wolfgang.wernsdorfer@kit.edu
dUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Depto. de Química-Física, 0824 Panamá, Panama
eUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Grupo de Investigación de Materiales, 0824 Panamá, Panama
fDepartment of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, 77146 Olomouc, Czech Republic
gDepartment of Chemistry, CICECO-Aveiro Institute of Materials, University of Aveiro, 3810-193 Aveiro, Portugal
hLaboratoire National des Champs Magnétiques Intenses, UPR CNRS 3228, Université Grenoble-Alpes, B.P. 166, 38042 Grenoble Cedex 9, France
iInstitute for Quantum Materials and Technology (IQMT), Karlsruhe Institute of Technology (KIT), Eggenstein-Leopoldshafen D-76344, Germany
First published on 27th December 2023
Abstract
In the last two decades, efforts have been devoted to obtaining insight into the magnetic interactions between CuII and LnIII utilizing experimental and theoretical means. Experimentally, it has been observed that the exchange coupling (J) in CuII–LnIII systems is often found to be ferromagnetic for ≥4f7 metal ions. However, exchange interactions at sub-Kelvin temperatures between CuII and the anisotropic/isotropic LnIII ions are not often explored. In this report, we have synthesized a series of heterobimetallic [CuLn(HL)(μ-piv)(piv)2] complexes (LnIII = Gd (1), Tb (2), Dy (3) and Er (4)) from a new compartmental Schiff base ligand, N,N’-bis(3-methoxy-5-methylsalicylidene)-1,3-diamino-2-propanol (H3L). X-ray crystallographic analysis reveals that all four complexes are isostructural and isomorphous. Magnetic susceptibility measurements reveal a ferromagnetic coupling between the CuII ion and its respective LnIII ion for all the complexes, as often observed. Moreover, μ-SQUID studies, at sub-Kelvin temperatures, show S-shaped hysteresis loops indicating the presence of antiferromagnetic coupling in complexes 1–3. The antiferromagnetic interaction is explained by considering the shortest Cu⋯Cu distance in the crystal structure. The nearly closed loops for 1–3 highlight their fast relaxation characteristics, while the opened loops for 4 might arise from intermolecular ordering. CASSCF calculations allow the quantitative assessment of the interactions, which are further supported by BS-DFT calculations.
Introduction
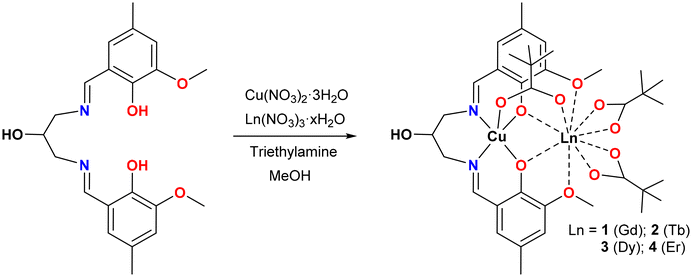
Heterometallic complexes with 3d and 4f metal ions have considerably attracted the interest of researchers due to their numerous advantages in the fields of catalysis,1 luminescence2,3 and molecular magnetism.4–6 In the field of molecular magnetism, their large magnetic moment and strong single-ion anisotropy make 4f ions appropriate candidates for the development of Single-Molecule Magnets (SMMs), a class of compounds usually characterized by their high-spin ground state, slow relaxation of magnetization and large axial anisotropy.7–11 A relatively strong magnetic exchange interaction between 3d and 4f metal ions, compared to those between 4f centres, yields further tunability of such magnetic characteristics in the 3d–4f cages. In several 3d–4f compounds, the exchange interaction between 3d and 4f ions has been found to effectively suppress the fast zero-field Quantum Tunnelling of Magnetization (QTM) of lanthanide ions, which in turn enhances the SMM behaviour.12–14 In general, the magnetic interaction between transition-metal and lanthanide ions plays a crucial role in defining the magnetic behaviour and applicability of such magnetic materials and hence needs to be evaluated. The pioneering work in the field of 3d–4f systems by Gatteschi et al. revealed a fairly strong Cu–Gd ferromagnetic exchange interaction,15 which was found to be an ideal model to study the magnetic exchange between transition metals and lanthanide ions owing to the isotropic nature of the GdIII ion.16,17 Subsequent studies in this field further ascertain the usual ferromagnetic coupling between CuII and GdIII ions in the synthesized compounds in which the degree of planarity of the bridging core plays a crucial role in the magnetic exchange coupling between the two metal ions.18–21 Furthermore, Matsumoto and co-workers successfully synthesized the first 3d–4f SMM complex [CuIITbIIIL1(hfac)2]2 (H3L1 = 1-(2-hydroxybenzamido)-2-(2-hydroxy-3-methoxy-benzylideneamino)-ethane), in which the magnetic interaction between CuII and TbIII ions has been proven to be critical for its SMM behaviour,22 and thereafter, the 3d–4f system is found to be increasingly important owing to its promising applications in quantum storage and spintronic devices.23–28The preparation of complexes containing only a limited number of 3d and 4f ions is crucial, particularly when the study is focused on gaining an in-depth understanding of the 3d–4f magnetic interactions. In such a case, the automatic choice is a simple heterobimetallic 3d–4f complex, well isolated from its congeners. Among several ligand systems, classical salen-type compartmental Schiff base ligands derived from o-vanillin and diamines are extensively utilized for the construction of heteronuclear 3d–4f complexes, because they offer two distinct preorganised coordination pockets to selectively accommodate 3d metal ions through a smaller and inner compartment with N2O2 donor sites and the lanthanide ions through a larger and outer compartment with O2O′2 donor sites.29–32 Several 3d–4f complex SMMs have also been reported to date using this class of compartmental ligands in which the ferromagnetic interaction between the metal ions is found to be significant.33–42 We have been working with new members of Schiff base ligands in the widespread family of salen-type compartmental Schiff base ligand systems derived from a methyl substituted o-vanillin to explore 4f or 3d–4f-based SMMs.43–46 As a follow-up, in the present work, we intend to develop Cu–Ln-based complexes with another new member of the salen-type compartmental ligand family, N,N’-bis(3-methoxy-5-methylsalicylidene)-1,3-diamino-2-propanol (H3L) (Scheme 1). Among the heavier LnIII ions, the obvious choice is the DyIII ion as the vast majority of reported SMMs are based on this oblate Kramer's ion together with the next most studied systems with oblate and non-Kramer's characteristics such as the TbIII ion and Kramer's ErIII ion with prolate electron distribution.47–50 Moreover, the isotropic GdIII ion has also been synthesized to obtain precise information regarding the magnetic exchange between the spin carriers in this system.51–53 Unlike NiII and CoII ions,54,55 the isotropic CuII ion does not contribute to the magnetic anisotropy at the molecular level, but the usual ferromagnetic coupling between CuII and heavier lanthanide ions (4f7 onwards), irrespective of the nature of binding and nuclearity of the systems, makes it useful in studying the magnetic behaviour in 3d–4f compounds.56–61 Keeping all these in mind, the ligand H3L was allowed to react with respective hydrated lanthanide nitrates, Ln(NO3)3·xH2O (x = 5 or 6), in the presence of pivalic acid and a triethylamine base to afford isostructural and isomorphous [CuLn(HL)(μ-piv)(piv)2] complexes (LnIII = Gd (1), Tb (2), Dy (3) and Er (4)). Herein, we report the synthesis, structures and low temperature and sub-Kelvin magnetic properties of the system via SQUID and μ-SQUID studies, and CASSCF and BS-DFT calculations were further performed to interpret the experimental results in these complexes.
Experimental section
Materials and methods
Reagent or analytical grade chemicals and solvents used in the present study were purchased from commercial sources and used without further purification. 2-Hydroxy-3-methoxy-5-methylbenzaldehyde (Me-val) was synthesized following a literature reported method.62 All reactions were carried out under aerobic conditions.Synthesis of complexes 1–4
All four binuclear [CuLn(HL)(μ-piv)(piv)2] complexes (LnIII = Gd (1), Tb (2), Dy (3) and Er(4)) have been synthesized by one-pot reactions and in a step-wise manner without the isolation of an intermediate CuII complex. The synthetic procedure consists of in situ formation of the Schiff-base ligand H3L by the condensation reaction of Me-val (0.50 mmol) and 1,3-diamino-2-propanol (0.25 mmol) in methanol under continuous stirring for about 30 minutes, followed by the addition of triethylamine (0.50 mmol) and Cu(NO3)2·3H2O (0.25 mmol), and the stirring was continued for another 1 hour. Then a methanolic solution (10 mL) of the corresponding hydrated lanthanide nitrate, Ln(NO3)3·6H2O (LnIII = Gd) or Ln(NO3)3·5H2O (LnIII = Tb, Dy and Er) (0.25 mmol), pivalic acid (piv, 0.75 mol) and triethylamine (0.75 mmol) were added to the reaction mixture. The mixture was continuously stirred for another 1 hour. The resulting dark green solution was then filtered and left undisturbed for slow evaporation at ambient temperature. After a week, X-ray quality dark green single crystals of complexes 1–4 were obtained. The crystals were collected by filtration, washed with methanol, and dried in air.Physical measurements
Elemental analyses (C, H, N) were conducted using a PerkinElmer 240C elemental analyser. FT-IR spectra were recorded using a Thermo Scientific Nicolet iS5 FTIR Spectrometer using a universal ATR sampling accessory from 4000 to 400 cm−1.X-ray crystallography
The single crystal X-ray diffraction study of complexes 1–4 was carried out on a Bruker Smart Apex-II CCD diffractometer with monochromated Mo-Kα radiation (λ = 0.71073 Å) at 150 K. Several scans were obtained in the φ and ω directions to increase the number of redundant reflections and were averaged during the refinement cycles. The intensity data were processed using the Bruker APEX-II suite (v2.0-2) program, then absorption correction and inter-frame scaling were performed and other systematic errors were fixed using the SADABS program.63 All structures were resolved by direct methods with SHELXT 2014/5 and then refined using the full matrix least-squares technique based on F2 using SHELXL2018/3.64 All non-hydrogen atoms were refined with anisotropic thermal displacement parameters. Hydrogen atoms connected to carbon atoms were placed at geometrically idealized positions with individual isotropic thermal parameters equal to 1.2 or 1.5 times the riding atoms, while the proton of the alcoholic–OH group was located in the difference Fourier map and refined freely. The molecular view and packing diagrams of the complexes were obtained using the Mercury-4.3.1 and POV-ray software. A summary of crystallographic data and refinement details is available in Table S1.†CASSCF calculations
The ab initio calculations for all complexes were performed employing the complete active space self-consistent field (CASSCF) method, specifically the CASSCF/SO-RASSI/SINGLE_ANISO approach implemented in the OpenMolcas package.65 For the calculations, the crystal structures were used as obtained from the single crystal X-ray analysis without further optimization. All atoms were described with the standard basis sets from the ANO-RCC library.66–68 For the anisotropic lanthanides, a basis set of VTZP quality was employed, while VDZP quality was employed for atoms in the first coordination sphere of the lanthanide. Basis sets of VDZ quality were used for the remaining atoms. Optimization of the molecular orbitals (MOs) was achieved by state averaged CASSCF calculations. The TbIII active space was defined by eight 4f electrons in the seven 4f orbitals. Four calculations were carried out (the RASSCF routine) with 7, 140, 588 and 490 states for S = 3, S = 2, S = 1 and S = 0, respectively. The CASSCF wavefunctions were subsequently mixed by spin–orbit coupling, employing the RASSI routine with all 7 states for S = 3 being included, while 106, 283 and 121 states were included for S = 2, S = 1 and S = 0, respectively. Lastly, the crystal field decomposition of the ground J = 6 multiplet of the 7F6 term was executed with the SINGLE_ANISO module. For DyIII, the active space was defined by the nine 4f electrons in the seven 4f orbitals. The RASSCF routine was carried out with 21, 224 and 490 states for S = 5/2, S = 3/2 and S = ½, respectively. The RASSI69 routine was executed for all 21 states for S = 5/2 being included, while 128 and 130 states were included for S = 3/2 and S = ½, respectively, and the crystal field decomposition of the ground J = 15/2 multiplet of the 6H15/2 term was executed with SINGLE_ANISO. The ErIII active space was defined by the eleven 4f electrons in the seven 4f orbitals. Two RASSCF calculations were conducted in this case with 35 and 112 states for S = 3/2 and S = ½, respectively. The RASSI routine was executed for all 35 states for S = 3/2 and 112 for the S = ½ state. The crystal field decomposition of the ground J = 15/2 multiplet of the 4I15/2 term was likewise executed with SINGLE_ANISO.70,71DFT calculations
Density Functional Theory (DFT) calculations were performed using ORCA 5.0 software.72 The ZORA relativistic approximation was used,73 together with ZORA-def2-TZVPP for Cu and Zn atoms, SARC2-ZORA-QZVP for lanthanide atoms, ZORA-def2-TZVP for N and O atoms, and ZORA-def2-SVP for C and H atoms.74,75 The calculations were sped up using the SARC/J Coulomb fitting basis set76 and the RIJCOSX approximation.77 The largest integration grid (DEFGrid3) and tightSCF convergence criteria were used in all calculations. The molecular structures were extracted from the X-ray data, and the atomic positions of the hydrogen atoms were optimized with the BP86 functional78 incorporating atom-pairwise dispersion correction (D4).79 The calculated data were visualized with the VESTA 3 program.80Magnetic measurements
The magnetic susceptibility studies for all the complexes were performed on a Quantum Design MPMS®3 SQUID magnetometer employing polycrystalline materials. The temperature range of the study was 2–300 K under an applied DC magnetic field of 1 kOe. AC data were collected using an oscillating magnetic field of 3.5 Oe and frequencies between 1 and 1.5 kHz. The DC data were corrected for diamagnetic contributions from the eicosane and core diamagnetism. The low-temperature magnetization measurements (0.03–5 K) were performed on single crystals via μ-SQUID apparatus at different sweep rates between 0.001 and 0.128 T s−1 with a time resolution of approximately 1 ms. The magnetic field can be applied in any direction of the μ-SQUID plane with a precision better than 0.1° by separately driving three orthogonal coils. The magnetic field was applied parallel to the easy axis of magnetization found using the transverse field method. To ensure good thermalization, each sample was fixed with apiezon grease.Results and discussion
Synthesis and characterization of Cu–Ln complexes
The salen-type compartmental Schiff base ligand derived from o-vanillin has been extensively utilized for the construction of heterometallic 3d–4f complexes with intriguing magnetic properties. In the present work, a new member of the salen-type compartmental Schiff base ligand H3L was prepared by the condensation reaction of Me-val and 1,3-diamino-2-propanol in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in methanol. This in situ generated ligand H3L thereafter was allowed to react with Cu(NO3)2·3H2O and the corresponding hydrated lanthanide nitrate, Ln(NO3)3·6H2O (LnIII = Gd) or Ln(NO3)3·5H2O (LnIII = Tb, Dy and Er), in 1
1 ratio in methanol. This in situ generated ligand H3L thereafter was allowed to react with Cu(NO3)2·3H2O and the corresponding hydrated lanthanide nitrate, Ln(NO3)3·6H2O (LnIII = Gd) or Ln(NO3)3·5H2O (LnIII = Tb, Dy and Er), in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio in the presence of 3 equivalents of pivalic acid to afford dark green crystals of [CuLn(HL)(μ-piv)(piv)2] (LnIII = Gd (1), Tb (2), Dy (3) and Er (4)) in high yield. The triethylamine base was added to deprotonate both ligand H3L and pivalic acid during the course of the reaction. In the IR spectra of the complexes (Fig. S1†), a broad band at ∼3280 cm−1 can be assigned to the ν(OH) vibration of the pendent hydroxyl group of the ligand, and a broad and bifurcated band at 1611–1629 cm−1 is consistent with the overlapping vibrations of the imine bond of the Schiff base and pivalate ion. Additionally, powder X-ray diffraction measurements were employed to confirm the phase purity of all the complexes (Fig. S2†).
1 molar ratio in the presence of 3 equivalents of pivalic acid to afford dark green crystals of [CuLn(HL)(μ-piv)(piv)2] (LnIII = Gd (1), Tb (2), Dy (3) and Er (4)) in high yield. The triethylamine base was added to deprotonate both ligand H3L and pivalic acid during the course of the reaction. In the IR spectra of the complexes (Fig. S1†), a broad band at ∼3280 cm−1 can be assigned to the ν(OH) vibration of the pendent hydroxyl group of the ligand, and a broad and bifurcated band at 1611–1629 cm−1 is consistent with the overlapping vibrations of the imine bond of the Schiff base and pivalate ion. Additionally, powder X-ray diffraction measurements were employed to confirm the phase purity of all the complexes (Fig. S2†).
Structural descriptions
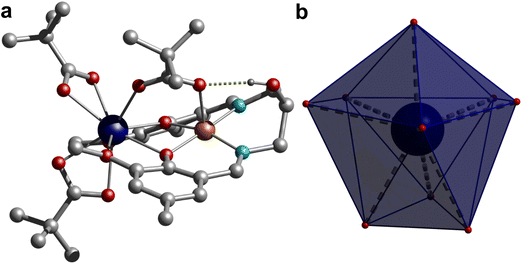
Single crystal structure analysis of the synthesized complexes reveals that all these heterobimetallic CuIILnIII complexes are isostructural and isomorphous, crystallized in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. The crystal structure of 3 is shown in Fig. 1, while the rest are displayed in Fig. S3,† and the selected bond distances are given in Table S2.† The asymmetric unit contains a neutral complex molecule with a general formula [CuLn(HL)(μ-piv)(piv)2], in which the CuII and LnIII ions occupy the inner N2O2 and outer O2O′2 compartments of the doubly deprotonated Schiff base ligand, respectively. Additionally, a pivalate ion bridges the metal centres in a κO:κO′ bridging fashion and two remaining pivalate ions bind the LnIII ions as a bidentate chelating ligand (κ2O,O′), resulting in CuN2O3 and LnO9 coordination environments around the CuII and LnIII ions, respectively, in these complexes. The CuII ion is invariably five-coordinated with a square-pyramidal geometry in all four complexes, in which the metal centre is slightly displaced (∼0.167 Å) from the N2O2 least squares plane towards the apically coordinated bridging pivalate-O atom, typical of a square pyramidal geometry, which is further supported by extracted continuous-shape measure (CShM) values on the basis crystallographic coordinates around the CuII ion using the Shape 2.1 software [Table S3†]. The Cu–O and Cu–N bond distances spanning the range 1.9373(10)–2.2164(16) Å are usual for CuII complexes.
space group. The crystal structure of 3 is shown in Fig. 1, while the rest are displayed in Fig. S3,† and the selected bond distances are given in Table S2.† The asymmetric unit contains a neutral complex molecule with a general formula [CuLn(HL)(μ-piv)(piv)2], in which the CuII and LnIII ions occupy the inner N2O2 and outer O2O′2 compartments of the doubly deprotonated Schiff base ligand, respectively. Additionally, a pivalate ion bridges the metal centres in a κO:κO′ bridging fashion and two remaining pivalate ions bind the LnIII ions as a bidentate chelating ligand (κ2O,O′), resulting in CuN2O3 and LnO9 coordination environments around the CuII and LnIII ions, respectively, in these complexes. The CuII ion is invariably five-coordinated with a square-pyramidal geometry in all four complexes, in which the metal centre is slightly displaced (∼0.167 Å) from the N2O2 least squares plane towards the apically coordinated bridging pivalate-O atom, typical of a square pyramidal geometry, which is further supported by extracted continuous-shape measure (CShM) values on the basis crystallographic coordinates around the CuII ion using the Shape 2.1 software [Table S3†]. The Cu–O and Cu–N bond distances spanning the range 1.9373(10)–2.2164(16) Å are usual for CuII complexes.
The geometry of the nona-coordinated LnIII ions in these complexes was also analysed using CShMs implemented in the Shape 2.1 software using the crystallographic coordinates, which reveals that the geometry of the LnIII ions is in-between a muffin-like geometry with Cs symmetry and a spherical capped square antiprism geometry with C4v symmetry as suggested by the CShM values given in Table S4.† The Ln–O bond distances with the phenolate–O atom and the bridging pivalate ion are shorter and span the range 2.2929(10)–2.4021(15) Å, while the Ln–O bond distances of the methoxy group are significantly longer and vary in the range 2.4745(10)–2.6525(15) Å. The Ln–O bond distances of the chelating pivalate groups fall in the intermediate range, spanning between 2.3502(10) and 2.4720(16) Å. Moreover, a typical consequence of the LnIII contraction has been observed as the respective Ln–O bond distances in these systems follow the order Gd > Tb > Dy > Er. Careful inspection of crystal packing reveals that the adjacent complex molecules interact with each other by the π⋯π interaction (Fig. S4†). Moreover, the pendent hydroxyl group of the ligand establishes an intramolecular hydrogen bond with the bridging pivalate ion. The CuO2Ln core is not planar as suggested by the dihedral angle of about 24.45° between the CuO2 and GdO2 planes in these complexes. The bridging pivalate ligand together with the aforesaid hydrogen bonding interaction involving the aliphatic hydroxyl group of the ligand and the bridging pivalate group is mainly responsible for the deviation of the CuO2Ln core from planarity. The Ln–O–Cu bridging angles vary in the narrow range of 103.29(14)–105.88(10)° with intermolecular Cu⋯Ln separations of 3.3758(3)–3.4206(3) Å, while the closest intermolecular Ln⋯Ln, Cu⋯Ln and Cu⋯Cu separations vary in the range 7.589–7.646, 7.206–7.321 and 6.109–6.343 Å, respectively, in these complexes.
Magnetic studies
High-temperature SQUID measurements were conducted on powdered samples. The observed χMT values were found to be 8.34, 12.34, 14.59 and 11.76 cm3 K mol−1 for 1, 2, 3 and 4, respectively (Fig. 2). All room temperature χMT values are found to be in agreement with the expected values for the isolated ions (cf., 8.25 cm3 K mol−1 for 1 with S = ½ and g = 2.0 for one CuII and S = 7/2 and g = 2 for one GdIII; 12.19 cm3 K mol−1 for 2 with S = ½ and g = 2.0 for one CuII and J = 6 and gJ = 3/2 for one TbIII; 14.54 cm3 K mol−1 for 3 with S = ½ and g = 2.0 for one CuII and J = 15/2 and gJ = 4/3 for one DyIII and 11.85 cm3 K mol−1 for 4 with S = ½ and g = 2.0 for one CuII and J = 15/2 and gJ = 6/5 for one ErIII). Upon cooling, χMT(T) is contingent on the lanthanide ion. For 1, however, below 200 K, χMT increases smoothly down to ∼50 K, and it sharply increases to a maximum value of 9.78 cm3 K mol−1 at 7 K. For 2, χMT(T) stays nearly constant down to 25 K, and it increases up to 12.31 cm3 K mol−1 at 10 K. For 3, χMT(T) decreases smoothly down to around 50 K, and it drops faster before increasing slightly between 12 and 6 K. The upsurge renders a χMT(T) value of 13.50 cm3 K mol−1 at 10 K, before decreasing again down to a minimum value of 12.01 cm3 K mol−1 at 2.0 K. Finally, the χMT(T) profile for 4 decreases smoothly down to ∼50 K, and it drops faster reaching a minimum value of 8.35 cm3 K mol−1 at 2.0 K. The observed upsurge in complexes 1–3 is characteristic of ferromagnetic interactions, often observed in 3d/4f complexes.33,37,81,82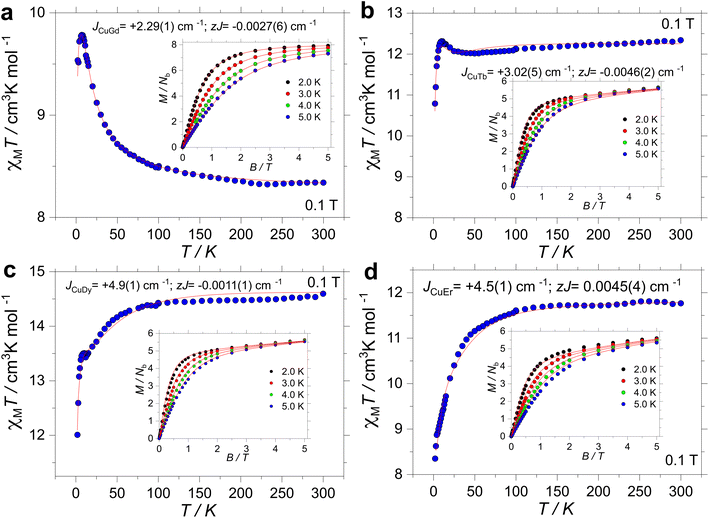 | ||
| Fig. 2 Experimental χMT(T) and M(B, T) (insets) for complex 1 (a), 2 (b), 3 (c) and 4 (d) under an applied field of 1 kOe. The red lines are the fits as described in the text. | ||
Magnetization versus field studies were likewise conducted for all complexes, leading to values of 7.92, 5.65, 5.63 and 5.60Nβ for 1, 2, 3 and 4, respectively. Note that saturation of M(B, T) was observed only for 1, while for 2–4, M(B, T) highlights anisotropy of the systems.
The isotropic nature of complex 1 allows us to simultaneously fit83 the χMT(T) and M(B, T) data employing an isotropic exchange interaction operating between the CuII and GdIII ions. The fitting procedure was carried out employing PHI.83 The Hamiltonian, hence, has the following form:
| Ĥ = −2JŜGd·ŜCu + μBB(gGdŜGd + gCuŜCu) | (1) |
To probe the Single Molecule Magnet (SMM) characteristic of the anisotropic complexes, AC studies were conducted. Nonetheless, no frequency-dependent AC signal was detected for the complexes in the temperature range of the study at zero field or upon application of an HDC field, and hence, none of the complexes is an SMM.
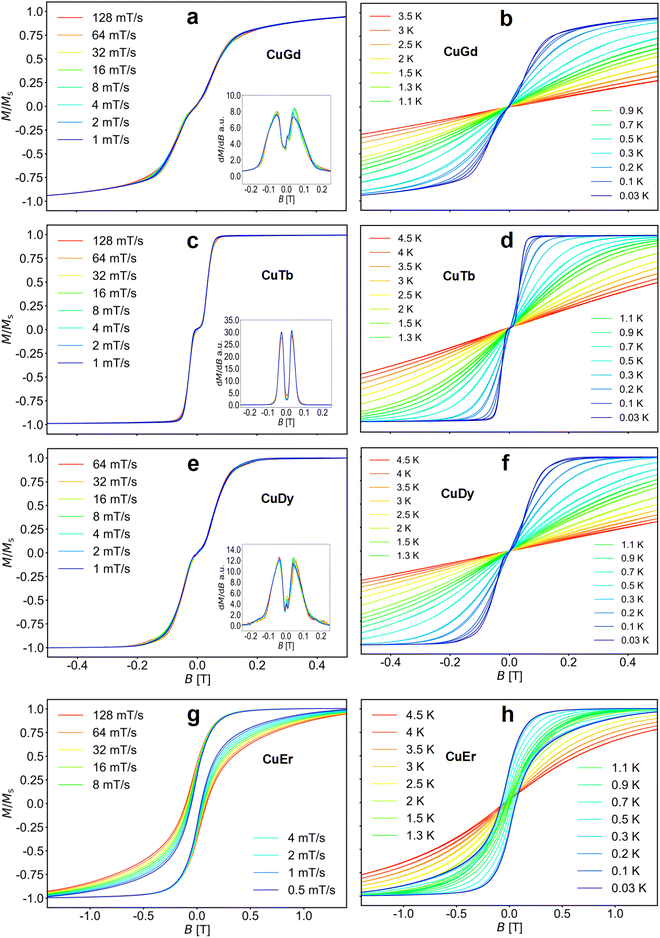
Fig. 3 (left panel) shows the M(B) curves obtained for a single crystal at 30 mK temperature and different sweep rates of the magnetic field, while the right panel shows the temperature dependence of the M(B) loops up to about 4.5 K.
The loops for complexes 1–3 are nearly closed, highlighting fast relaxation. Moreover, the sweep rate independent transitions indicate QTM. Note that samples 1, 2 and 3 show a flat M(B) about zero field (S-shaped loops), a signature of antiferromagnetic coupling.86–89 This is clearly observed in the derivatives shown in the insets of Fig. 3. Upon increasing the temperature, the QTM transitions broaden, while the small hysteresis opening diminishes. At 100 mK bath temperature and above, the antiferromagnetic plateau near zero field in 1–3 is averaged out or disappears. In contrast, the loops for 4 are open up to ∼1 K, indicating slower relaxation.
As observed in the SQUID studies, 3d metals typically couple to the neighbouring Ln ferromagnetically,37,81,82 hence the antiferromagnetic arrangement could be of inter-molecular origin. Considering the inner nature of 4f orbitals and the shortest Ln⋯Ln and Cu⋯Cu distances, the most probable intermolecular interaction is between Cu⋯Cu intermolecular contacts. To assess the strength of the interactions in complexes 1–3, we directly extract the interaction from the μ-SQUID M(B) loops through the mean exchange field Hex = −2JexmS/gμB, where Jex is the interaction, mS is the spin for CuII (S = ½), g = 2.0 and μB is the Bohr magneton. Considering that the crossing for 1 occurs at ±0.101 T, Jex = −0.38 cm−1. For 2 and 3, Jex values of −0.22 and −0.31 cm−1 were obtained, for the crossings at ±0.058 and ±0.082 T, respectively. Considering the shortest Cu⋯Cu distance in the crystal structure, we find that the strongest dipolar interaction is −0.034 cm−1, which is ten times smaller than the Jex, hence, the intermolecular exchange might be operative. Due to the lack of S-shaped loops in 4, no Jex can be determined for this complex.
Theoretical calculations
To understand the magnetic characteristics of studied compounds, DFT calculations were performed for 1–4 with ORCA, and more advanced ab initio calculations for 2–4 employing OpenMolcas (see methods section) were carried out.First, the isotropic exchange parameter J (using definition Ĥ = −2J(Ŝ1·Ŝ2)) was evaluated using the broken-symmetry DFT calculations by comparing the energies of high-spin (HS) and broken-symmetry (BS) spin states, Δ = εBS − εHS, with two approaches defined by Ruiz and Yamaguchi as:
| JR = 2Δ/[(S1 + S2)(S1 + S2 + 1)] | (2) |
| JY = 2Δ/[S2HS − S2BS] | (3) |
Herein, three different DFT functionals were used: a hybrid functional PBE0 and hybrid meta-GGA functionals M06-2X and TPSSh. Such functionals are among those usually applied for the calculations of magnetic exchange for 3d–3d/3d–4f/4f–4f complexes.90–93 First, intramolecular interactions were evaluated for all Cu–Ln complexes, as summarized in Table 1, and the BS-DFT spin densities are shown in Fig. S5.†
| J R/JY (cm−1) of Cu–Gd in 1 | J R/JY (cm−1) of Cu–Tb in 2 | J R/JY (cm−1) of Cu–Dy in 3 | J R/JY (cm−1) of Cu–Er in 4 | |
|---|---|---|---|---|
| PBE0 | 0.81/2.32 | 0.93/2.44 | 1.68/4.03 | 3.69/7.38 |
| M06-2X | 0.69/1.97 | 0.75/1.96 | 0.74/1.78 | 0.83/1.67 |
| TPSSh | 0.75/2.15 | 1.21/3.18 | 4.78/11.48 | 1.25/2.49 |
Evidently, all three DFT functionals suggest ferromagnetic exchange in the presented complexes, which is in accordance with the analysis of the experimental magnetic data. The closest match to the fitted value JCuGd = 2.29 cm−1 is found for the PBE0 functional (JY = 2.32 cm−1). Additionally, the possible intermolecular magnetic interactions were also investigated for complex 1, as the formation of the supramolecular dimer of dinuclear complexes is found in the solid state by close inspection of the crystal structure. Herein, all interactions were evaluated as listed in Table 2, and the BS-DFT spin densities are shown in Fig. S6.†
| J R/JY (cm−1) of Cu–Cu′ | J R/JY (cm−1) of Cu–Gd′ | J R/JY (cm−1) of Gd–Gd′ | |
|---|---|---|---|
| PBE0 | −0.33/−0.67 | 0.09/0.26 | −0.01/−0.01 |
| M06-2X | −0.26/−0.52 | 0.13/0.37 | 0.02/0.02 |
| TPSSh | −0.23/−0.45 | −0.03/−0.09 | −0.02/−0.02 |
The BS-DFT calculations revealed the weak antiferromagnetic exchange for the Cu–Cu′ interactions (d(Cu–Cu′) = 6.343 Å) and very weak interactions for Cu–Gd′ of ferromagnetic nature (PBE0 and M06-2X) or antiferromagnetic nature (TPSSh). The Gd–Gd′ interactions seem to be negligible due to the large interatomic distance, d(Gd–Gd′) = 9.506 Å. As all reported compounds are isostructural, we can conclude that intermolecular magnetic interactions of similar magnitude are also present in 2–4.
Next, CASSCF calculations are discussed. The single ion properties for 2–4 account for the lack of SMM behaviour in the AC studies. For 2, the ligand field splits the states into singlets, being consistent with the absence of an energy barrier to the relaxation of this system. For 3, a ground doublet with g-values gx = 0.0252, gy = 0.0427, and gz = 18.2423 is observed, while the first excited state is found to be at 73 cm−1. In the case of 4, g-values for the ground doublet are found to be gx = 1.1647, gy = 2.9271, and gz = 14.1239, while the first excited state lies at 35 cm−1. The electronic characteristics of DyIII and ErIII single ions can be rationalized by considering the electron density of the lanthanide. The largest mJ state for DyIII, with an oblate electron density, is best stabilized by an axial ligand field. The g-values and separation of the ground state and the first excited state obtained from the CASSCF calculations suggest a slightly axial ligand field for the DyIII ion in 2. In contrast, the g-values for the ErIII ion are not axial and the wavefunctions are rather mixed, arising due to the prolate electron density of ErIII, which is better stabilized by an equatorial ligand field. As can be inferred, although the DyIII results show that the ligand field is axial, it does not provide enough axiality to make the system an SMM. In contrast, for ErIII, the same ligand field is not suited to stabilize an anisotropic ground state.
At this stage, the CASSCF calculations allow us to have insight into the crystal field parameters of the complexes, and hence, it is possible to quantify the interaction operating between the Cu–Ln pairs.94,95 Fitting of χMT(T) and M(B, T) was carried out employing the Lines model83,95, implemented in PHI,83 with the formula:
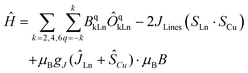 | (4) |
With the full picture at hand (i.e., magnetic data and CASSCF calculations), we can understand the dynamic magnetic properties of 2–4. Magnetic AC susceptibility measurements show no SMM behaviour for any of the complexes, while μ-SQUID loops show a very narrow opening for 2 and 3. In contrast, a larger opening of the loops is observed for 4 (up to near ∼1 K). CASSCF calculations for the single-lanthanide ions show that the ground states are rather scrambled (3 and 4) and/or with a relatively small separation between the ground doublet and the first excited state (2 and 4). The lack of SMM characteristics can therefore be ascribed to the non-Ising nature of the lanthanide ions. The μ-SQUID loops for 2 and 3, besides displaying rather narrow loops, also highlight the existence of antiferromagnetic coupling, which can be ascribed to the intermolecular interactions. Since no out-of-phase component was observed for 4 in the AC studies and the CASSCF results show that the ErIII ion also is characterized by a non-Ising doublet, 4 could not be an SMM. Therefore, the opening of the loop observed for 4 could be of intermolecular ordering and not of single-molecule origin. This fact can also be supported by the ferromagnetic intermolecular interaction obtained by simultaneous fitting of the χMT(T) and M(B) data (vide supra). Our findings in terms of the nature and magnitude of the 3d/4f interactions are in good agreement with previous reports.37,53,85,93 Unfortunately, the complexity of the systems, i.e., ligand field, geometry, and intra/intermolecular interactions, and the highly sensitive nature of the relaxation dynamics of the lanthanides preclude further magneto-structural correlations.
Conclusions
In the present work, we have synthesized four new heterometallic Cu⋯Ln complexes from an in situ reaction of a compartmental ligand and the corresponding lanthanide nitrate salts, yielding four isostructural and isomorphous systems. We find the geometry of the CuII centre to be square pyramidal, while LnIII possesses a muffin-like geometry with Cs symmetry. Magnetic studies show a ferromagnetic coupling between CuII and its respective LnIII ions in all complexes. Single crystal sub-Kelvin μ-SQUID magnetic measurements highlight that complexes 1–3 show fast relaxation, while a slow relaxation process is observed for complex 4. Furthermore, in complexes 1–3, the presence of a weak antiferromagnetic coupling is directly observed as a plateau near zero field in the M(B) curves measured by μ-SQUID. Simulation of χMT(T) and M(B, T) allows us to assess the magnitude and nature of the interactions operating in the complexes. We find an overall ferromagnetic intramolecular interaction in all systems and a weak intermolecular antiferromagnetic interaction. The antiferromagnetic coupling can be explained by considering the intermolecular Cu⋯Cu distance in the crystal structure, as supported by BS-DFT calculations. Finally, CASSCF calculations for the single-lanthanide ions showed that the ground states are rather scrambled (3 and 4) and/or with a relatively small separation between the ground doublet and the first excited state (2 and 4). The lack of SMM characteristics can therefore be ascribed to the non-Ising nature of the lanthanide ions, and further modification of the ligand environment or exchange of the 3d metal ion may prevent it. In this work, we show a general route by which interactions in 3d–4f complexes can be revealed through SQUID, μ-SQUID magnetometry, BS-DFT and CASSCF calculations.Author contributions
A. P. conceived and designed the project and also conducted the synthesis of the complexes together with the analysis and interpretation of X-ray crystallographic data. N. J. performed general characterization studies of the compounds. P. B. collected and processed single-crystal X-ray diffraction data. S. P. and W. W. collected, processed, and interpreted the μ-SQUID results. G. N. collected and processed the SQUID data. R. H. carried out the DFT calculations and data interpretation. E. M.-P. carried out the CASSCF calculations and performed the SQUID data simulations. The manuscript was written by A. P., S. P. and E. M. -P. with input from all authors. All authors have approved the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
A. P. gratefully acknowledges the financial support of this work by the CSIR, New Delhi, India (Sanction No. 01/3118/23/EMR-II dated 08.07.23). E. M.-P. is thankful for the support from the Panamanian National System of Investigators (SNI, SENACYT). P. B. gratefully acknowledges the financial support for this work by the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 and LA/P/0006/2020, financed by national funds through the FCT/MCTES (PIDDAC). We acknowledge the DFG-CRC 1573 “4f for the future”. W. W. acknowledges the A. v. Humboldt Foundation and the ERC grant MoQuOS No. 741276. R. H. acknowledges the financial support from the institutional sources of the Department of Inorganic Chemistry, Palacký University Olomouc, Czech Republic.References
- K. Griffiths and G. E. Kostakis, Dalton Trans., 2018, 47, 12011–12034 RSC.
- L. Aboshyan-Sorgho, C. Besnard, P. Pattison, K. R. Kittilstved, A. Aebischer, J. C. G. Bünzli, A. Hauser and C. Piguet, Angew. Chem., Int. Ed., 2011, 50, 4108–4112 CrossRef CAS PubMed.
- X. F. Li, Y. B. Huang and R. Cao, Cryst. Growth Des., 2012, 12, 3549–3556 CrossRef CAS.
- M. Andruh, J. P. Costes, C. Diaz and S. Gao, Inorg. Chem., 2009, 48, 3342–3359 CrossRef CAS PubMed.
- B.-K. Ling, Y.-Q. Zhai, P.-B. Jin, H.-F. Ding, X.-F. Zhang, Y. Lv, Z. Fu, J. Deng, M. Schulze, W. Wernsdorfer and Y.-Z. Zheng, Matter, 2022, 5, 3485–3498 CrossRef CAS.
- L. R. Piquera and E. C. Sañudo, Dalton Trans., 2015, 44, 8771–8780 RSC.
- Z.-W. An, Y.-Q. Gao, S.-M. Xu, W. Zhang and M.-X. Yao, Cryst. Growth Des., 2023, 23, 1412–1421 CrossRef CAS.
- X.-L. Li, F.-Y. Min, C. Wang, S.-Y. Lin, Z. Liu and J. Tang, Inorg. Chem., 2015, 54, 4337–4344 CrossRef CAS PubMed.
- F.-X. Shen, K. Pramanik, P. Brandão, Y.-Q. Zhang, N. C. Jana, X.-Y. Wang and A. Panja, Dalton Trans., 2020, 49, 14169–14179 RSC.
- K. Pramanik, Y.-C. Sun, P. Brandão, N. C. Jana, X.-Y. Wang and A. Panja, New J. Chem., 2022, 46, 11722–11733 RSC.
- A. Swain, T. Sharma and G. Rajaraman, Chem. Commun., 2023, 59, 3206–3228 RSC.
- D. Chauhan, K. R. Vignesh, A. Swain, S. K. Langley, K. S. Murray, M. Shanmugam and G. Rajaraman, Cryst. Growth Des., 2023, 23, 197–206 CrossRef CAS.
- H. Wang, S. Liu, L. Wei, G. Deng, H. Zhu, S. Chen, J. Yuan and L. Jia, Cryst. Growth Des., 2023, 23, 7432–7439 CrossRef CAS.
- M. N. Akhtar, M. A. AlDamen, C. D. McMillen, A. Escuer and J. Mayans, Inorg. Chem., 2021, 60, 9302–9308 CrossRef CAS PubMed.
- A. Bencini, C. Benelli, A. Caneschi, R. L. Carlin, A. Dei and D. Gatteschi, J. Am. Chem. Soc., 1985, 107, 8128–8136 CrossRef CAS.
- M. Ryazanov, V. Nikiforov, F. Lloret, M. Julve, N. Kuzmina and A. Gleizes, Inorg. Chem., 2002, 41, 1816–1823 CrossRef CAS PubMed.
- O. Margeat, P. G. Lacroix, J. P. Costes, B. Donnadieu, C. Lepetit and K. Nakatani, Inorg. Chem., 2004, 43, 4743–4750 CrossRef CAS PubMed.
- J.-P. Costes, F. Dahan and A. Dupuis, Inorg. Chem., 2000, 39, 165–168 CrossRef CAS PubMed.
- F. He, M.-L. Tong and X.-M. Chen, Inorg. Chem., 2005, 44, 8285–8292 CrossRef CAS PubMed.
- J.-P. Costes, F. Dahan, A. Dupuis and J.-P. Laurent, New J. Chem., 1998, 22, 1525–1529 RSC.
- T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972–9008 RSC.
- S. Osa, T. Kido, N. Matsumoto, N. Re, A. Pochaba and J. Mrozinski, J. Am. Chem. Soc., 2004, 126, 420–421 CrossRef CAS PubMed.
- A. Rauguth, A. Kredel, L. M. Carrella and E. Rentschler, Inorg. Chem., 2021, 60, 14031–14037 CrossRef CAS PubMed.
- A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Coord. Chem. Rev., 2018, 367, 163–216 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press on Demand, 2006 Search PubMed.
- F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119–3129 RSC.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- E. Moreno-Pineda and W. Wernsdorfer, Nat. Rev. Phys., 2021, 3, 645–659 CrossRef CAS.
- M. Andruh, Dalton Trans., 2015, 44, 16633–16653 RSC.
- J. Mayans, Q. Saez, M. Font-Bardiabc and A. Escuer, Dalton Trans., 2019, 48, 641–652 RSC.
- A. Vráblová, M. Tomás, L. R. Falvello, Ľ. Dlháň, J. Titiš, J. Černák and R. Boča, Dalton Trans., 2019, 48, 13943–13952 RSC.
- R. Modak, Y. Sikdar, C. J. Gómez-García, S. Benmansour, S. Chatterjee and S. Goswami, Chem. – Asian J., 2021, 16, 666–677 CrossRef CAS PubMed.
- A. Dey, P. Bag, P. Kalita and V. Chandrasekhar, Coord. Chem. Rev., 2021, 432, 213707–213775 CrossRef CAS.
- M. Towatari, K. Nishi, T. Fujinami, N. Matsumoto, Y. Sunatsuki, M. Kojima, N. Mochida, T. Ishida, N. Re and J. Mrozinski, Inorg. Chem., 2013, 52, 6160–6178 CrossRef CAS PubMed.
- F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Chem. – Eur. J., 2007, 13, 1602–1609 CrossRef PubMed.
- L. B. L. Escobar, G. P. Guedes, S. Soriano, R. A. A. Cassaro, J. Marbey, S. Hill, M. A. Novak, M. Andruh and M. G. F. Vaz, Inorg. Chem., 2018, 57, 326–334 CrossRef CAS PubMed.
- E. Moreno Pineda, N. F. Chilton, F. Tuna, R. E. P. Winpenny and E. J. L. McInnes, Inorg. Chem., 2015, 54, 5930–5941 CrossRef CAS PubMed.
- L. Sorace, C. Sangregorio, A. Figuerola, C. Benelli and D. Gatteschi, Chem. – Eur. J., 2009, 15, 1377–1388 CrossRef CAS PubMed.
- K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2015, 289–290, 74–122 CrossRef CAS.
- H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33 CrossRef CAS.
- A. Dey, J. Acharya and V. Chandrasekhar, Chem. – Asian J., 2019, 14, 4433–4453 CrossRef CAS PubMed.
- G. Brunet, D. A. Safin, J. Jover, E. Ruiz and M. Murugesu, J. Mater. Chem. C, 2017, 5, 835–841 RSC.
- A. Panja, Z. Jagličić, R. Herchel, P. Brandão, K. Pramanik and N. C. Jana, New J. Chem., 2022, 46, 5627–5637 RSC.
- A. Panja, Z. Jagličić, R. Herchel, P. Brandão, K. Pramanik and N. C. Jana, New J. Chem., 2022, 46, 13546–13557 RSC.
- A. Panja, Z. Jagličić, R. Herchel, P. Brandão and N. C. Jana, New J. Chem., 2022, 46, 18751–18763 RSC.
- K. Pramanik, Z. Jagličić, R. Herchel, P. Brandão, N. C. Jana and A. Panja, Dalton Trans., 2023, 52, 1241–1256 RSC.
- G. Novitchi, W. Wernsdorfer, L. F. Chibotaru, J. P. Costes, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2009, 48, 1614–1619 CrossRef CAS PubMed.
- R. Watanabe, K. Fujiwara, A. Okazawa, G. Tanaka, S. Yoshii, H. Nojiri and T. Ishida, Chem. Commun., 2011, 47, 2110–2112 RSC.
- T. Ishida, R. Watanabe, K. Fujiwara, A. Okazawa, N. Kojima, G. Tanaka, S. Yoshii and H. Nojiri, Dalton Trans., 2012, 41, 13609–13619 RSC.
- F. J. Kettles, V. A. Milway, F. Tuna, R. Valiente, L. H. Thomas, W. Wernsdorfer, S. T. Ochsenbein and M. Murrie, Inorg. Chem., 2014, 53, 8970–8978 CrossRef CAS PubMed.
- Y. Ida, S. Ghosh, A. Ghosh, H. Nojiri and T. Ishida, Inorg. Chem., 2015, 54, 9543–9555 CrossRef CAS.
- J. Cirera and E. Ruiz, C. R. Chim., 2008, 11, 1227–1234 CrossRef CAS.
- J.-P. Costes, F. Dahan, A. Dupuis and J.-P. Laurent, Inorg. Chem., 1997, 36, 3429–3433 CrossRef CAS PubMed.
- S. Wang, X. Yang, J. Qian, Q. Li, Z. Chen, L. Zhang, S. Huang, C. Wang and R. A. Jones, Dalton Trans., 2017, 46, 1748–1752 RSC.
- M. Biswas, E. C. Sañudo and D. Ray, Inorg. Chem., 2021, 60, 11129–11139 CrossRef CAS PubMed.
- S. Akine, T. Matsumoto, T. Taniguchi and T. Nabeshima, Inorg. Chem., 2005, 44, 3270–3274 CrossRef CAS PubMed.
- T. Kido, S. Nagasato, Y. Sunatsuki and N. Matsumoto, Chem. Commun., 2000, 2113–2114 RSC.
- G. Rajaraman, F. Totti, A. Bencini, A. Caneschi, R. Sessoli and D. Gatteschi, Dalton Trans., 2009, 3153–3161 RSC.
- T. Shimada, A. Okazawa, N. Kojima, S. Yoshii, H. Nojiri and T. Ishida, Inorg. Chem., 2011, 50, 10555–10557 CrossRef CAS PubMed.
- J.-P. Costes, C. Duhayon, S. Mallet-Ladeira, S. Shova and L. Vendier, Chem. – Eur. J., 2016, 22, 2171–2180 CrossRef CAS PubMed.
- T. Rajeshkumar, H. V. Annadata, M. Evangelisti, S. K. Langley, N. F. Chilton, K. S. Murray and G. Rajaraman, Inorg. Chem., 2015, 54, 1661–1670 CrossRef CAS PubMed.
- H. Ohmori, A. Matsumoto and M. Masui, J. Chem. Soc., Perkin Trans. 2, 1980, 347–357 RSC.
- G. M. Sheldrick, SADABS, University of Göttingen, Germany, 1996 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. Fdez. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. A. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117–214142 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS PubMed.
- P. O. Widmark, P. A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306 CrossRef CAS.
- P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- D. Aravena, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2016, 12, 1148–1156 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. E. P. Winpenny, Chem. Soc. Rev., 1998, 27, 447–452 RSC.
- E. M. Pineda, F. Tuna, Y.-Z. Zheng, R. E. P. Winpenny and E. J. McInnes, Inorg. Chem., 2013, 52, 13702–13707 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- M. Andruh, I. Ramade, E. Codjovi, O. Guillou, O. Kahn and J. C. Trombe, J. Am. Chem. Soc., 1993, 115, 1822–1829 CrossRef CAS.
- J.-P. Costes, S. Shova and W. Wernsdorfer, Dalton Trans., 2008, 1843–1849 RSC.
- W. Wernsdorfer, Supercond. Sci. Technol., 2009, 22, 064013 CrossRef.
- M. Dolai, E. Moreno-Pineda, W. Wernsdorfer, M. Ali and A. Ghosh, J. Phys. Chem. A, 2021, 125, 8230–8237 CrossRef CAS PubMed.
- E. Moreno-Pineda, G. Taran, W. Wernsdorfer and M. Ruben, Chem. Sci., 2019, 10, 5138–5145 RSC.
- E. M. Pineda, Y. Lan, O. Fuhr, W. Wernsdorfer and M. Ruben, Chem. Sci., 2017, 8, 1178–1185 RSC.
- N. C. Jana, M. Jagodič, P. Brandão, M. Patra, R. Herchel, Z. Jagličić and A. Panja, RSC Adv., 2023, 13, 11311–11323 RSC.
- B. Dutta, T. Guizouarn, F. Pointillart, K. Kotrle, R. Herchel and D. Ray, Dalton Trans., 2023, 52, 10402–10414 RSC.
- A. Bhanja, L. Smythe, R. Herchel, I. Nemec, M. Murrie and D. Ray, Dalton Trans., 2021, 50, 5023–5035 RSC.
- K. Kotrle, I. Nemec, J. Moncol, E. Čižmár and R. Herchel, Dalton Trans., 2021, 50, 13883–13893 RSC.
- S. K. Langley, L. Ungur, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. – Eur. J., 2011, 17, 9209–9218 CrossRef CAS PubMed.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977–2984 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data, CASSCF simulation details, and the derivative (dM/dB)-field angle map in complex 2. CCDC 2299767–2299770. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt03557c |
| This journal is © The Royal Society of Chemistry 2024 |