Open Access Article
Open Access ArticleA density functional theory analysis of the C–H activation reactivity of iron(IV)-oxo complexes with an ‘O’ substituted tetramethylcyclam macrocycle†
Lovleen
Kaur
 and
Debasish
Mandal
and
Debasish
Mandal
 *
*
Department of Chemistry and Biochemistry, Thapar Institute of Engineering and Technology, Patiala-147004, Punjab, India. E-mail: debasish.mandal@thapar.edu
First published on 2nd April 2024
Abstract
In this article, we present a meticulous computational study to foresee the effect of an oxygen-rich macrocycle on the reactivity for C–H activation. For this study, a widely studied nonheme Fe(IV)O molecule with a TMC (1,4,8,11-tetramethyl 1,4,8,11-tetraazacyclotetradecane) macrocycle that is equatorially attached to four nitrogen atoms (designated as N4) and acetonitrile as an axial ligand has been taken into account. For the goal of hetero-substitution, step-by-step replacement of the N4 framework with O atoms, i.e., N4, N3O1, N2O2, N1O3, and O4 systems, has been considered, and dihydroanthracene (DHA) has been used as the substrate. In order to neutralise the system and prevent the self-interaction error in DFT, triflate counterions have also been included in the calculations. The study of the energetics of these C–H bond activation reactions and the potential energy surfaces mapped therefore reveal that the initial hydrogen abstraction, which is the rate-determining step, follows the two-state reactivity (TSR) pattern, which means that the originally excited quintet state falls lower in the transition state and the product. The reaction follows the hydrogen atom transfer (HAT) mechanism, as indicated by the spin density studies. The results revealed a fascinating reactivity order, in which the reactivity increases with the enrichment of the oxygen atom in the equatorial position, namely the order follows N4 < N3O1 < N2O2 < N1O3 < O4. The impacts of oxygen substitution on quantum mechanical tunneling and the H/D kinetic isotope effect have also been investigated. When analysing the causes of this reactivity pattern, a number of variables have been identified, including the reactant-like transition structure, spin density distribution, distortion energy, and energies of the electron acceptor orbital, i.e., the energy of the LUMO (σ*z2), which validate the obtained outcome. Our results also show very good agreement with earlier combined experimental and theoretical studies considering TMC and TMCO-type complexes. The DFT predictions reported here will undoubtedly encourage experimental research in this biomimetic field, as they provide an alternative with higher reactivity in which heteroatoms can be substituted for the traditional nitrogen atom.
Introduction
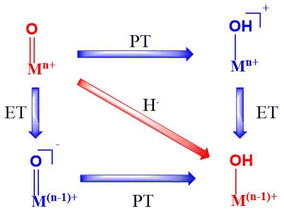
Metal-oxo species of transition metal series are vastly studied, with the earlier members studied more prominently than the later ones owing to the oxo wall and the high-valence Fe(IV)O intermediates being studied in depth widely.1–12 These complexes have been successfully presented in many articles wherein they act as active oxidants in the catalytic cycles of mononuclear non-heme and heme enzymes.13–15 Multiple studies have also been conducted towards understanding the structural and electronic parameters of these metal-oxo complexes to get an idea how they drive towards better reactivity by accessing the mechanisms involved. For example, several octahedral/trigonal bipyramidal geometries have been explored wherein both S = 1 (triplet) and S = 2 (quintet) ground spin states have been taken into account.16,17 It has been proven that spin states of Fe(IV) ions are an important governing factor affecting the catalytic activity of Fe(IV)O complexes. Studies in the last decade revealed that many changes have been projected in the coordination sphere directly in the form of axial as well as equatorial ligands, while other changes on the secondary level caused by manipulation of the ligand architecture have also been proven to have a significant effect on the mechanistic pathways.18,19 Other factors such as the oxidative capabilities of different redox states have also gained attention with a larger oxidation state enhancing the reactivity owing to the electrophilicity and reduction potential.20,21 Multiple DFT and experimental studies have been performed to explore and enhance the C–H activation processes carried out by such complexes, in which the reactivity is significantly influenced by the thermodynamics of bond formation (O–H) and breakage (C–H). These reactions proceed mostly with simultaneous transfer of electrons and protons (HAT or cPCET mechanism), which has been studied from time to time.22–24 Here we see how the transfer of an electron and a proton together as a true H atom is referred to as hydrogen atom transfer, but when they travel differently, it is called proton coupled electron transfer. However, it has also been established that in contrast to these mechanisms, proton and electron transfer can take place stepwise25,26 wherein the transfer involves two steps. These involve PT followed by ET (basic mechanism) or ET followed by PT (oxidative mechanism) as summed in Scheme 1 herein. There might even be asynchronicity involved with the TS consisting of either more electron or proton transfer.PT signifies proton transfer whereas ET is electron transfer. Also, the red arrow shows synchronous behaviour and purple the asynchronous. Such mechanisms have a significant role in some cases wherein the otherwise lower oxidation potential is balanced by factors such as the basicity of the metal oxo complexes (via PT followed by ET).27–30
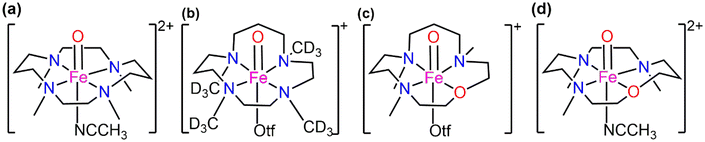
The developments in this field have given considerable momentum to both the understanding and the application of the Fe(IV)-oxo chemistry in homogeneous catalytic oxidation. Now, let's take into contemplation the well-known fact that the biological Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxidants in the (IV) oxidation state of the iron atom usually consist of O-based ligands (weak field in nature), e.g., carboxylate, water located cis to the oxo donor (Scheme 2a).31,32
O oxidants in the (IV) oxidation state of the iron atom usually consist of O-based ligands (weak field in nature), e.g., carboxylate, water located cis to the oxo donor (Scheme 2a).31,32
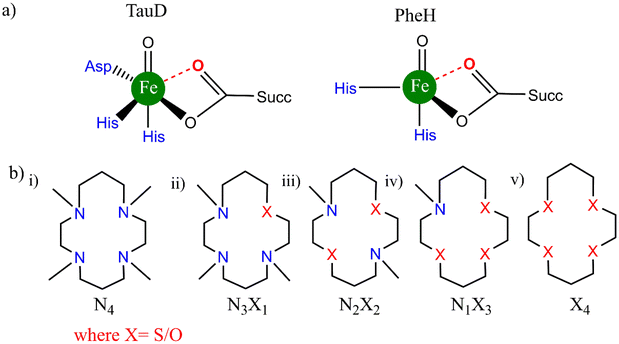 | ||
| Scheme 2 Structures of (a) biological enzymes taurine:αKG dioxygenase and phenylalanine hydroxylase and (b) bioinspired TMC complexes with equatorial substitution. | ||
In our previous work in this field of hetero-substitution, inspired by the study of Ray and co-workers, we highlighted how alterations made in the primary coordination sphere of TMC like complexes in a sequential order (using S) of equatorial ligands resulted in better reactivity trends for the C–H activation process.33 We successfully established that hetero-substitution led to lower reaction barriers and hence opened the door to the use of alternative atoms in the vastly studied ferryl processes.34 In a combined experimental and computational study performed by Prez et al., substitution of the N–CH3 donor in TMC and TMCN macrocycles was studied to depict how this O substitution led to better reactivity patterns. The details of the structures are presented in Scheme 3. Other than the N/O donor atom, there is also a significant difference in the structure between traditional TMC (Scheme 3a) and TMCO (Scheme 3c). The propylene and ethylene linkers are in adjacent positions in TMCO; however, they are in alternate positions in TMC.35 The axial ligands are also different. In TMCN, CD3 substituents on the donor N atoms are attached equatorially in place of CH3 (Scheme 3b).
This encouraged us to investigate the effects on C–H activation reactivity after substituting oxygen for the equatorial donor atom nitrogen. For this purpose, anti-geometric isomers (anti-position of methyl groups w.r.t the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit) of the base molecule with the same axial ligand have been used. The most investigated TMC (Scheme 3a) macrocycle has been selected as the base compound which makes the TMCO complex as presented in Scheme 3d. The primary goal here is to determine whether oxygen-substituted iron-oxo TMC complexes may offer us a better C–H activation catalyst and whether these improvements will happen in a sequential manner. Dihydroanthracene (DHA) is used as a C–H bond source and the reaction has been modelled in the presence of the solvent acetonitrile. Reactivity studies have been performed on both lower (S = 1) and higher (S = 2) spin states. The interplay of various other factors has also been taken into consideration which include-spin density on the abstractor atoms, frontier orbitals and deformation energies to obtain the transition states. Mulliken charges and spin have been carefully analysed guiding us to the correct identification of the electronic states. Effects of N, O-substituted macrocycles on quantum mechanical tunneling and the H/D kinetic isotope effect have also been analysed.36
O unit) of the base molecule with the same axial ligand have been used. The most investigated TMC (Scheme 3a) macrocycle has been selected as the base compound which makes the TMCO complex as presented in Scheme 3d. The primary goal here is to determine whether oxygen-substituted iron-oxo TMC complexes may offer us a better C–H activation catalyst and whether these improvements will happen in a sequential manner. Dihydroanthracene (DHA) is used as a C–H bond source and the reaction has been modelled in the presence of the solvent acetonitrile. Reactivity studies have been performed on both lower (S = 1) and higher (S = 2) spin states. The interplay of various other factors has also been taken into consideration which include-spin density on the abstractor atoms, frontier orbitals and deformation energies to obtain the transition states. Mulliken charges and spin have been carefully analysed guiding us to the correct identification of the electronic states. Effects of N, O-substituted macrocycles on quantum mechanical tunneling and the H/D kinetic isotope effect have also been analysed.36
Computational details
The DFT method has been used to carry out geometry optimization for all the species wherein the popular B3LYP functional (Becke's three-parameter exchange with Lee, Yang, and Parr's correlation functional) has come to practice.37–39 Several independent studies support this functional for the C–H activation reaction catalysed by this type of complex, and hence it is a significant benchmark.40,41 For the study of spin state gaps we have further used the functionals TPSSH and M06-L as presented in Table S7.† For the basis set we have taken (i) LANL2DZ with ECP for Fe and Pople's double zeta 6-31G* for all the other atoms, namely C, H, N, O, F and S marked as B1 for convenience.42,43 The effect of acetonitrile solvent has been computed during optimization using the self-consistent reaction field i.e., the SCRF and SMD model.44,45 Further single-point calculations have also been performed for energy refinement using (ii) Def2tzvpp for all atoms marked as B2 and (iii) 6-311++G(2d,2p) for all atoms and ECP containing SDD for iron marked as B3. The same solvent model as for B1 has also been implemented in B2 and B3. Triflate (CF3SO3−) counterions are poised at the bottom parts of the axial ligands to make the system neutral. The use of solvents with counterions usually diminishes the secondary interactions by neutralising the charges.46 Frequency calculations are very detrimental for validating the nature of the optimized structures wherein one imaginary frequency indicates the transition states (TS), and have been performed at the B1 level of theory. The zero-point vibrational energy (ZPVE) and thermal and entropic corrections to the Gibbs free energy at T = 298 K (25 °C) have been evaluated for valid determination of the potential energy surface. Intrinsic reaction coordinate (IRC) calculations have also been carried out to further verify if the TS are connecting to the proper minima as required.47 This entire DFT study has been performed using Gaussian 1648 program packages, and for the generation as well as visualisation of natural orbitals, Chemcraft software49 has been used. For rate, isotope effect and quantum mechanical tunneling studies have been performed using KiSThelP software.50 The kinetics calculations have been performed using the following equation:51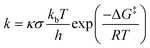 | (1) |
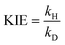 | (2) |
For calculating the reduction of the activation barrier, we have used the following equation where R is the universal gas constant and T is the absolute temperature
ΔΔE‡tun = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ(T) κ(T) | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β, the following equation has been used.57
β, the following equation has been used.57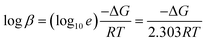 | (4) |
| ΔG = G(ML) + 4 × G(H2O) − G{M(H2O)4} − G(L) | (5) |
Distortion energies for the transition state have been calculated using the following equation:
| ΔE‡dist = (E‡R + E‡S) − (ER − ES) | (6) |
Results
At first, we searched for the potential for production of each of the five Fe(IV)O complexes by figuring out their stability constants, which are represented by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β in eqn (4). Since the constant shows how the ligation of the individual TMC complexes (with varied donor atoms) to the Fe
β in eqn (4). Since the constant shows how the ligation of the individual TMC complexes (with varied donor atoms) to the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit would affect the free energy of formation, higher values of the constant indicate more favourable complex formation. In all five complexes, stability constant values were determined to be approximately 28.2. Kirby et al. in a study of a few U(VI) complexes showed comparable values of log
O unit would affect the free energy of formation, higher values of the constant indicate more favourable complex formation. In all five complexes, stability constant values were determined to be approximately 28.2. Kirby et al. in a study of a few U(VI) complexes showed comparable values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β.57 It is also observed in their case that the calculated values are overestimated with respect to the experimentally observed ones. Here, we are unable to adequately support the absolute values of log
β.57 It is also observed in their case that the calculated values are overestimated with respect to the experimentally observed ones. Here, we are unable to adequately support the absolute values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β because there is a dearth of literature on stability constants for Fe(IV)O. Aside from the absolute value, however, we can declare with confidence that the O-substituted TMC macrocycle can ligate with Fe(IV)O in a manner similar to that of the most popular N4 TMC frameworks. The optimized geometries of the quintet oxidants with important parameters are presented in Fig. 1.
β because there is a dearth of literature on stability constants for Fe(IV)O. Aside from the absolute value, however, we can declare with confidence that the O-substituted TMC macrocycle can ligate with Fe(IV)O in a manner similar to that of the most popular N4 TMC frameworks. The optimized geometries of the quintet oxidants with important parameters are presented in Fig. 1.
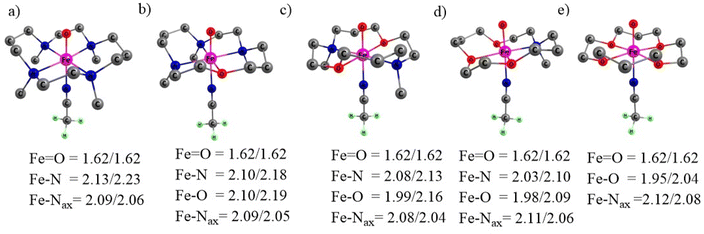 | ||
| Fig. 1 The optimized oxidants with geometrical parameters with S = 1/S = 2, wherein distances are in Å (a) N4, (b) N3O1, (c) N2O2, (d) N1O3 and (e) O4. Hydrogen atoms are omitted for clarity. | ||
While the average Fe–N/Fe–O distance (equatorially linked) decreased progressively, the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and Fe–Nax bond lengths (axially connected) are almost the same in all complexes.
O and Fe–Nax bond lengths (axially connected) are almost the same in all complexes.
Spin state reactivity
In general, the four unpaired electrons in Fe(IV) can be occupied in a variety of ways, resulting in two distinct spin states, S = 1 and S = 2. Thus, the hydrogen atom transfer mechanism can occur in either or both states58 and the electron transfer pathways are presented in Fig. 2.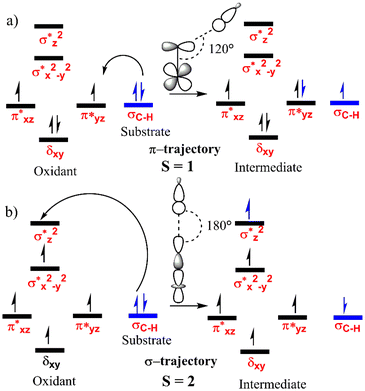 | ||
| Fig. 2 The general electron transfer mechanism for the HAT catalysed by the Fe(IV)O complexes for spin states (a) S = 1 and (b) S = 2. | ||
The panel a of Fig. 2 shows the low spin i.e. triplet state pathway where a β electron from the σC–H bond moves to one of the π* orbitals of Fe. This is referred to as the π pathway/trajectory since the transfer takes place to the π* orbital.59 As depicted, the orientation of the substrate occurs at an Fe–O–H angle of ∼120°. The panel b shows the high spin path i.e. the quintet pathway where one α electron from the σC–H bond of the DHA shifts to the σ*z2 anti-bonding orbital of Fe. Here, as DHA approaches the oxidant through the upper side with an Fe–O–H angle of ∼180°, this pathway is named the σ pathway/trajectory.
Reactivity pattern
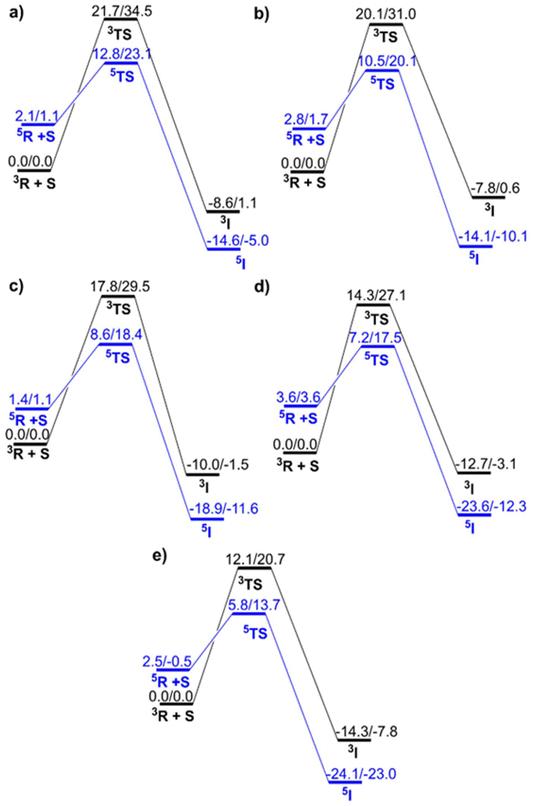
Reactants in the quintet state typically have higher energy than reactants in the triplet state for Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexes; however, this is reversed in the transition state and product, leading to the Two-State-Reactivity (TSR) phenomenon. Fig. 3 depicts all the relevant potential energy surfaces for the rate determining step of the C–H activation process catalysed by all five complexes.
O complexes; however, this is reversed in the transition state and product, leading to the Two-State-Reactivity (TSR) phenomenon. Fig. 3 depicts all the relevant potential energy surfaces for the rate determining step of the C–H activation process catalysed by all five complexes.
S = 1 is observed as the ground state in all oxidants, and the spin state energy gaps (ΔEQ–T) are 2.1, 2.8, 1.4, 3.6, and 2.5 for N4, N3O1, N2O2, N1O3, and O4, respectively. As a manifestation of exchange enhanced reactivity,60 TSR is observed here.61–64
In this instance an interesting reactivity pattern is observed. The C–H activation barrier for catalysis by five different oxidants is observed to decrease in a sequential manner with the increasing amount of oxygen substitution in the TMC macrocycle. Regardless of the choice of the basis set or thermodynamic parameters used, such as free energy or ZPE corrected energy, the reactivity pattern remains consistent. In the B2 level of theory the barrier of activation values kept decreasing as 12.82 (23.14) (N4) > 10.50 (20.06) (N3O1) > 8.59 (18.38) (N2O2) > 7.19 (17.52) (N1O3) > 5.79 (13.73) (O4) wherein the values in the brackets indicate free energies. The free energy trend at B3 appeared to be 20.90 for N4, 15.80 for N3O1, 14.76 for N2O2, 13.16 for N1O3 and 12.24 for O4. Even on comparing the values for triplet states of all the complexes, respectively, we observed the same trend of reactivity i.e., N4 < N3O1 < N2O2 < N1O3 < O4. By comparing the energies and free energies of the intermediates (Fe(III)OH⋯˙R), specifically in the quintet state, it is found that substituting nitrogen with oxygen in the macrocycle results in increased exothermicity of the reaction. This may be attributed to the reduction in energy of the dz2 orbital, which decreases sequentially with each O-replacement. However, this replacement had no substantial effect on the energy of the dx2−y2 orbital; therefore, the ΔEQ–T in the reactant remained essentially unchanged. All these data have been presented in Table S1.† This led us to divulge into the contributing cause of this kind of fascinating pattern. As the spin state gaps are identical in all the complexes and S = 1 is the ground state for reactants, we observed a crossover to the S = 2 surface during TSR, and this led us to take into consideration factors other than the triplet–quintet gap which are discussed in detail below.
Spin density
The spin density on the abstractor, i.e., on the oxygen of Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, plays a key role in the reaction dynamics.65 On evaluating these values on the O atom of the ferryl group in the TS we observed a sequential increase from 0.28 (N4) to 0.30 (N3O1) to 0.33 (N2O2) to 0.35 (N1O3) to 0.40 (O4). In the plot in Fig. 4, we notice a sufficiently linear connection (R2 = 0.93) between the spin density on the abstractor and the energy of activation.
O, plays a key role in the reaction dynamics.65 On evaluating these values on the O atom of the ferryl group in the TS we observed a sequential increase from 0.28 (N4) to 0.30 (N3O1) to 0.33 (N2O2) to 0.35 (N1O3) to 0.40 (O4). In the plot in Fig. 4, we notice a sufficiently linear connection (R2 = 0.93) between the spin density on the abstractor and the energy of activation.
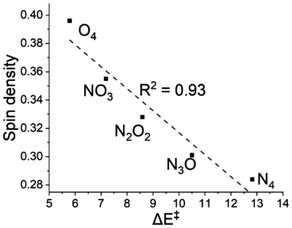 | ||
Fig. 4 A plot of activation energy (ΔE‡) versus spin density at the ‘O’ of the Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit in the S = 2 transition state. O unit in the S = 2 transition state. | ||
LUMO energies
The acceptor orbital's energy has a significant impact on the reactivity of electron transfer processes. In the S = 2 state of these oxidants, the electron acceptor orbital (σ*z2) is the lowest unoccupied molecular orbital (LUMO), and its lower energy values make the electron transfer from the substrate easier. Therefore, the trend −3.56 (N4) to −3.58 (N3O1) to −3.96 (N2O2) to −4.24 (N1O3) to −4.60 (O4) showed that the process of accepting electrons from DHA became more convenient as we continued to replace N atoms with O. This is one of the prominent reasons for the increased reactivity with this hetero-substitution.33,34 As depicted in Fig. 5, the linear relationship between activation energy and LUMO energy provides insight into reactivity.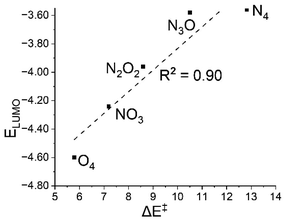 | ||
| Fig. 5 A plot of activation energy (ΔE‡) versus the energy of the LUMO i.e., the electron acceptor orbital (ELUMO) of the oxidants at the S = 2 state. | ||
The lowering tendency in LUMO energy could have resulted from oxygen having a weaker field effect than nitrogen, which in turn stabilises the anti-bonding acceptor orbital. This can be explained on the basis of charge transfer. We performed NBO and Mulliken population analyses to see how on moving from N4 to O4 the charge transferred from the ligands attached to the metal centre. As more and more charges were transferred, the trend at the Fe atoms was 0.55 (N4) to 0.61 (N3O1) to 0.64 (N2O2) to 0.73 (N1O3) to 0.81 (O4), and it is safe to say that the ligand field kept on weakening sequentially resulting in a more electrophilic metal centre and hence more reactivity.
Distortion energies
To further validate our results, we then used eqn (6) from the Computational details section to determine the distortion energies (ΔE‡dist) of the oxidants and substrate in order to reach the transition states. A plot of ΔE‡dist and the energy of activation is presented in Fig. 6.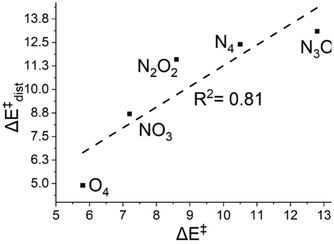 | ||
| Fig. 6 A plot of activation energy (ΔE‡, in kcal mol−1) versus the distortion energies (ΔE‡dist, in kcal mol−1) of the oxidants at the S = 2 state. | ||
Fig. 6 demonstrates a consistent decrease in ΔE‡dist, with the greatest value of 13.1 in N4; other values are 12.4 for N3O1, 11.6 and 8.7 for N2O2 and N1O3, respectively, and 4.9 for O4. Lower distortion energies in the oxygen-substituted complexes show how the distortion undergone is minimum in these cases and hence the formation of the transition state is more favourable.
Our findings also show good consistency with earlier research in related complexes, which published theoretical calculations and experimentally validated investigations for TMC and TMCO complexes (Scheme 3a and c). The B3LYP/TDZP estimated free energy of activation for the cyclohexene substrate indicates that the TMCO complex was more favourable than the TMC-N4 by 6.3 kcal mol−1.35 Here for the DHA substrate we found a similar value, 5.1 kcal mol−1, in the B3 level of theory.
Quantum chemical tunneling
We were also curious to look for the impact of ‘O’ substitution on quantum mechanical tunneling. The data related to the tunneling calculation of the H-abstraction reaction catalysed by all five complexes are presented in Table 1.| Complex | k H | k D | κ H | κ D | KIEECK | ΔΔE‡tun | ΔE − ΔΔE‡tun |
|---|---|---|---|---|---|---|---|
| a The value in parentheses is the experimental value.66 | |||||||
| N4 | 8.12 × 10−25 | 6.48 × 10−26 | 6.61 | 2.96 | 12.5 (10)a | 1.12 | 11.7 |
| N3O | 3.44 × 10−23 | 4.38 × 10−24 | 3.04 | 2.03 | 7.9 | 0.66 | 9.8 |
| N2O2 | 2.20 × 10−22 | 4.15 × 10−23 | 2.05 | 1.64 | 5.3 | 0.42 | 8.2 |
| NO3 | 2.17 × 10−20 | 6.55 × 10−21 | 1.19 | 1.64 | 3.3 | 0.10 | 7.1 |
| O4 | 3.65 × 10−20 | 1.82 × 10−20 | 1.03 | 1.02 | 2.0 | 0.01 | 5.8 |
Standard TMC complexes (N4) have a tunneling corrected H/D kinetic isotope effect of 12.5, which is in good accord with an earlier empirically reported value of 10.66 It's interesting to note that when ‘O’ is substituted on TMC, the transmission coefficient and KIE fall progressively. The values of the tunneling adjusted KIE are 12.5 (N4), 7.9 (N3O1), 5.3 (N2O2), 3.3 (N1O3), and 2.0 (O4) as shown in column 6 of Table 1.
It is revealed that the imaginary frequency of the transition states, which regulates the potential energy surface's curvature, is the cause of this pattern. Higher tunneling is insinuated by a narrower curvature, which is implied by a higher imaginary frequency value.40Fig. 7 presents the transition state structures with significant geometrical features and imaginary frequencies.
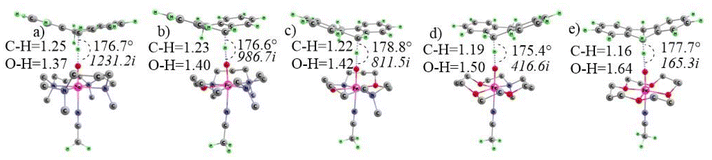 | ||
| Fig. 7 Quintet TS with their imaginary frequencies for (a) N4, (b) N3O1, (c) N2O2, (d) N1O3 and (e) O4 macrocyclic ligands with C–H (breaking) and O–H (forming) bond lengths. | ||
The imaginary frequency value for N4 is 1231.2i, and it decreases steadily to 986.7i for N3O1, 811.5i for N2O2 and 416.6i for O4 and 165.3i for N1O3. In the context of breaking C–H and forming O–H bond parameters in the transition state it is clear that the transition state for N4 is most symmetric. The C–H bond keeps becoming shorter from N4 to O4, and oppositely, the O–H bond distances keep increasing, making the TS product-like in prior cases but reactant-like in the latter.
So, the decreasing frequencies with the substitution taking place hint at the role of quantum tunneling since it's a well-known fact that the mechanism of QM tunneling (quantum mechanical tunneling) relies on the path function, and potential energy surfaces (PES) depend on the imaginary frequencies. Higher imaginary frequencies indicate a sharper PES, i.e., an atom has to tunnel through a shorter distance making the phenomenon more favourable. The tunneling coefficients for H and D isotope counterparts with Eckart corrected values of KIE are reported herein. We have also calculated the tunneling corrected barrier. When switching from N4 to O4, the calculated natural charges on Fe in the S = 2 oxidant are nearly equal with oxygen replacement, i.e., 0.95, 0.94, 0.93, 0.95, and 0.97. It follows that anti-electrophilicity has no influence on tunneling in this situation.40
Although the reduction of the activation barrier by tunneling (column 7 in Table 1) is higher in N4 (due to the higher transmission coefficient), the overall effective barrier (column 8 in Table 1) is not able to alter the earlier reactivity pattern obtained from classical thermodynamics.
Conclusions
This computational study has been devoted to investigating the reactivity of the oxygen substituted iron(IV)-oxo N4 macrocycle in order to design a better catalyst for C–H activation. A well-known TMC compound, [Fe(IV)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(TMC-N4)(CH3CN)]2+, has been taken into consideration for base compounds. Additionally, the method of sequentially replacing the equatorial N atoms with O atoms results in the formation of four additional compounds with frameworks consisting of N4, N3O1, N2O2, N1O3, and O4. The computed values of the stability constants support the formation of these complexes, which proved to be as beneficial as the main compound N4. The hydrogen atom transfer from dihydroanthracene, i.e., the rate determining step of the C–H activation, has been investigated in both triplet and quintet spin states. Due to the presence of exchange enhanced reactivity and the two-state-reactivity phenomenon, S = 2 was found to be more reactive in all five cases. An interesting reactivity trend is observed, namely, the C–H activation reactivity gradually increases with the enrichment of ‘O’ in TMC macrocycles, i.e., N4 < N3O1 < N2O2 < N1O3, and O4, irrespective of the computed levels of theories. The increased reactivity in the substituted compounds may be to some extent explained by the TS being reactant-like for the oxygen substituted TMC, as shown by the length of the breaking and forming bonds. This is further reflected in the distortion energy pattern, where the substituted TMC complexes require progressively less energy. Given that the spin state gap remains consistent across all complexes, it is not the primary determining factor in this scenario. Additionally, the energy of the electron acceptor orbital, or LUMO energy, which progressively drops with the number of oxygen-enriched macrocycles, was likewise connected with the reactivity pattern. The weak ligand field on moving from N4 to O4 is evident from the charge transfer values. An interesting pattern was also observed in the case of quantum mechanical tunneling (QMT) and H/D KIE, which continually decreases with transformation from N4 to O4. This might be explained by the broad H-transfer curvature as predicted by the low imaginary frequencies in the transition states. The barrier reduction amount by QMT was not significant enough to alter the classical reactivity trend. Our results are also in line with the previous studies conducted on TMC like complexes. Finally, these studies if carried out experimentally will make a path for alternative complexes other than typical N complexes and hence lead to new choices in this bioinorganic field.
O(TMC-N4)(CH3CN)]2+, has been taken into consideration for base compounds. Additionally, the method of sequentially replacing the equatorial N atoms with O atoms results in the formation of four additional compounds with frameworks consisting of N4, N3O1, N2O2, N1O3, and O4. The computed values of the stability constants support the formation of these complexes, which proved to be as beneficial as the main compound N4. The hydrogen atom transfer from dihydroanthracene, i.e., the rate determining step of the C–H activation, has been investigated in both triplet and quintet spin states. Due to the presence of exchange enhanced reactivity and the two-state-reactivity phenomenon, S = 2 was found to be more reactive in all five cases. An interesting reactivity trend is observed, namely, the C–H activation reactivity gradually increases with the enrichment of ‘O’ in TMC macrocycles, i.e., N4 < N3O1 < N2O2 < N1O3, and O4, irrespective of the computed levels of theories. The increased reactivity in the substituted compounds may be to some extent explained by the TS being reactant-like for the oxygen substituted TMC, as shown by the length of the breaking and forming bonds. This is further reflected in the distortion energy pattern, where the substituted TMC complexes require progressively less energy. Given that the spin state gap remains consistent across all complexes, it is not the primary determining factor in this scenario. Additionally, the energy of the electron acceptor orbital, or LUMO energy, which progressively drops with the number of oxygen-enriched macrocycles, was likewise connected with the reactivity pattern. The weak ligand field on moving from N4 to O4 is evident from the charge transfer values. An interesting pattern was also observed in the case of quantum mechanical tunneling (QMT) and H/D KIE, which continually decreases with transformation from N4 to O4. This might be explained by the broad H-transfer curvature as predicted by the low imaginary frequencies in the transition states. The barrier reduction amount by QMT was not significant enough to alter the classical reactivity trend. Our results are also in line with the previous studies conducted on TMC like complexes. Finally, these studies if carried out experimentally will make a path for alternative complexes other than typical N complexes and hence lead to new choices in this bioinorganic field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. Mandal is very grateful to the Department of Science and Technology, Government of India, for providing the INSPIRE Faculty Fellowship (DST/INSPIRE/04/2016/001948) and for a Thapar Institute of Engineering and Technology SEED grant (TU/DORSP/57/7278).References
- V. A. Larson, B. Battistella, K. Ray, N. Lehnert and W. Nam, Nat. Rev. Chem., 2020, 4, 404–419 CrossRef CAS PubMed.
- H. Hirao, F. Li, L. Que and K. Morokuma, Inorg. Chem., 2011, 50, 6637–6648 CrossRef CAS PubMed.
- H. Schwarz and S. Shaik, Metal-Oxo and Metal-Peroxo Species in Catalytic Oxidations, 2000 Search PubMed.
- T. Z. H. Gani and H. J. Kulik, ACS Catal., 2018, 8, 975–986 CrossRef CAS.
- J. England, J. O. Bigelow, K. M. Van Heuvelen, E. R. Farquhar, M. Martinho, K. K. Meier, J. R. Frisch, E. Münck and L. Que, Chem. Sci., 2014, 5, 1204–1215 RSC.
- W. Nam, Y. M. Lee and S. Fukuzumi, Acc. Chem. Res., 2014, 47, 1146–1154 CrossRef CAS PubMed.
- K. Rydel-Ciszek, React. Kinet., Mech. Catal., 2021, 133, 579–600 CrossRef CAS.
- A. N. Biswas, M. Puri, K. K. Meier, W. N. Oloo, G. T. Rohde, E. L. Bominaar, E. Münck and L. Que, J. Am. Chem. Soc., 2015, 137, 2428–2431 CrossRef CAS PubMed.
- Y. Wang and K. Han, J. Biol. Inorg. Chem., 2010, 15, 351–359 CrossRef CAS PubMed.
- S. P. de Visser, M. G. Quesne, B. Martin, P. Comba and U. Ryde, Chem. Commun., 2014, 50, 262–282 RSC.
- E. Masferrer-Rius, M. Borrell, M. Lutz, M. Costas and R. J. M. Klein Gebbink, Adv. Synth. Catal., 2021, 363, 3783–3795 CrossRef CAS.
- C. A. Joseph and M. J. Maroney, Chem. Commun., 2007, 3338–3349 RSC.
- M. Sallmann, S. Kumar, P. Chernev, J. Nehrkorn, A. Schnegg, D. Kumar, H. Dau, C. Limberg and S. P. De Visser, Chem. – Eur. J., 2015, 21, 7470–7479 CrossRef CAS PubMed.
- A. J. Johansson, M. R. A. Blomberg and P. E. M. Siegbahn, J. Phys. Chem. C, 2007, 111, 12397–12406 CrossRef CAS.
- W. Nam, Acc. Chem. Res., 2007, 40, 522–531 CrossRef CAS PubMed.
- S. Impeng, S. Siwaipram, S. Bureekaew and M. Probst, Phys. Chem. Chem. Phys., 2017, 19, 3782–3791 RSC.
- K. Warm, A. Paskin, U. Kuhlmann, E. Bill, M. Swart, M. Haumann, H. Dau, P. Hildebrandt and K. Ray, Angew. Chem., Int. Ed., 2021, 60, 6752–6756 CrossRef CAS PubMed.
- H. Park and D. Lee, Chem. – Eur. J., 2020, 26, 5916–5926 CrossRef CAS PubMed.
- C. V. Sastri, J. Lee, K. Oh, J. L. Yoon, J. Lee, T. A. Jackson, K. Ray, H. Hirao, W. Shin, J. A. Halfen, J. Kim, L. Que, S. Shaik and W. Nam, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19181–19186 CrossRef CAS PubMed.
- R. Kumar, B. Pandey, A. Sen, M. Ansari, S. Sharma and G. Rajaraman, Coord. Chem. Rev., 2020, 419 Search PubMed.
- A. Ansari, A. Kaushik and G. Rajaraman, J. Am. Chem. Soc., 2013, 135, 4235–4249 CrossRef CAS PubMed.
- M. Mandal, C. E. Elwell, C. J. Bouchey, T. J. Zerk, W. B. Tolman and C. J. Cramer, J. Am. Chem. Soc., 2019, 141, 17236–17244 CrossRef CAS PubMed.
- J. E. M. N. Klein and G. Knizia, Angew. Chem., Int. Ed., 2018, 57, 11913–11917 CrossRef CAS PubMed.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS PubMed.
- D. Usharani, D. C. Lacy, A. S. Borovik and S. Shaik, J. Am. Chem. Soc., 2013, 135, 17090–17104 CrossRef CAS PubMed.
- M. K. Goetz and J. S. Anderson, J. Am. Chem. Soc., 2019, 141, 4051–4062 CrossRef CAS PubMed.
- T. H. Yosca, J. Rittle, C. M. Krest, E. L. Onderko, A. Silakov, J. C. Calixto, R. K. Behan and M. T. Green, Science, 2013, 342, 825–829 CrossRef CAS PubMed.
- M. T. Green, J. H. Dawson and H. B. Gray, Science, 2004, 304, 1653–1656 CrossRef CAS PubMed.
- P. J. Donoghue, J. Tehranchi, C. J. Cramer, R. Sarangi, E. I. Solomon and W. B. Tolman, J. Am. Chem. Soc., 2011, 133, 17602–17605 CrossRef CAS PubMed.
- D. Dhar, G. M. Yee, T. F. Markle, J. M. Mayer and W. B. Tolman, Chem. Sci., 2017, 8, 1075–1085 RSC.
- N. I. Burzlaff, P. J. Rutledge, I. J. Clifton, C. M. H. Hensgens, M. Pickford, R. M. Adlington, P. L. Roach and J. E. Baldwin, Nature, 1999, 401, 721–724 CrossRef CAS PubMed.
- P. L. Roach, I. J. Clifton, C. M. H. Hensgens, N. Shibata, C. J. Schofield, J. Hajdu and J. E. Baldwin, Nature, 1997, 387, 827–830 CrossRef CAS PubMed.
- J. Deutscher, P. Gerschel, K. Warm, U. Kuhlmann, S. Mebs, M. Haumann, H. Dau, P. Hildebrandt, U. P. Apfel and K. Ray, Chem. Commun., 2021, 57, 2947–2950 RSC.
- L. Kaur and D. Mandal, Inorg. Chem., 2022, 61, 14582–14590 CrossRef CAS PubMed.
- I. Monte Pérez, X. Engelmann, Y. M. Lee, M. Yoo, E. Kumaran, E. R. Farquhar, E. Bill, J. England, W. Nam, M. Swart and K. Ray, Angew. Chem., Int. Ed., 2017, 56, 14384–14388 CrossRef PubMed.
- A. Katoch and D. Mandal, Dalton Trans., 2022, 51, 11641–11649 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS.
- A. Altun, J. Breidung, F. Neese and W. Thiel, J. Chem. Theory Comput., 2014, 10, 3807–3820 CrossRef CAS PubMed.
- J. E. M. N. Klein, D. Mandal, W. M. Ching, D. Mallick, L. Que and S. Shaik, J. Am. Chem. Soc., 2017, 139, 18705–18713 CrossRef CAS PubMed.
- D. Mandal, D. Mallick and S. Shaik, Acc. Chem. Res., 2018, 51, 107–117 CrossRef CAS PubMed.
- Y. Yang, M. N. Weaver and K. M. Merz, J. Phys. Chem. A, 2009, 113, 9843–9851 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. V. Marenich, R. M. Olson, C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 2011–2033 CrossRef CAS PubMed.
- D. Janardanan, D. Usharani, H. Chen and S. Shaik, J. Phys. Chem. Lett., 2011, 2, 2610–2617 CrossRef CAS.
- S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258–269 CrossRef CAS.
- E. B. Bauer, Isr. J. Chem., 2017, 57, 1131–1150 CrossRef CAS.
- J. P. Cerón-Carrasco and D. Jacquemin, Phys. Chem. Chem. Phys., 2013, 15, 4548–4553 RSC.
- S. Canneaux, F. Bohr and E. Hénon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 63–71 CrossRef.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- D. K. Maity, R. L. Bell and T. N. Truong, J. Am. Chem. Soc., 2000, 122, 897–906 CrossRef CAS.
- F. Zhang and T. S. Dibble, Phys. Chem. Chem. Phys., 2011, 13, 17969–17977 RSC.
- A. G. Vandeputte, M. K. Sabbe, M. F. Reyniers, V. Van Speybroeck, M. Waroquier and G. B. Marin, J. Phys. Chem. A, 2007, 111, 11771–11786 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1991, 95, 5853–5860 CrossRef CAS.
- M. E. Kirby, A. Simperler, S. Krevor, D. J. Weiss and J. L. Sonnenberg, J. Phys. Chem. A, 2018, 122, 8007–8019 CrossRef CAS PubMed.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Phys. Chem. A, 2011, 115, 2367–2377 CrossRef CAS PubMed.
- S. A. Wilson, J. Chen, S. Hong, Y. M. Lee, M. Clémancey, R. Garcia-Serres, T. Nomura, T. Ogura, J. M. Latour, B. Hedman, K. O. Hodgson, W. Nam and E. I. Solomon, J. Am. Chem. Soc., 2012, 134, 11791–11806 CrossRef CAS PubMed.
- D. Janardanan, Y. Wang, P. Schyman, L. Que and S. Shaik, Angew. Chem., 2010, 122, 3414–3417 CrossRef.
- D. Mandal, R. Ramanan, D. Usharani, D. Janardanan, B. Wang and S. Shaik, J. Am. Chem. Soc., 2015, 137, 722–733 CrossRef CAS PubMed.
- C. Geng, S. Ye and F. Neese, Angew. Chem., Int. Ed., 2010, 49, 5717–5720 CrossRef CAS PubMed.
- S. P. De Visser, J. Am. Chem. Soc., 2006, 128, 15809–15818 CrossRef CAS PubMed.
- S. Ye, C. Y. Geng, S. Shaik and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 8017–8030 RSC.
- J. England, J. Prakash, M. A. Cranswick, D. Mandal, Y. Guo, E. Münck, S. Shaik and L. Que, Inorg. Chem., 2015, 54, 7828–7839 CrossRef CAS PubMed.
- C. V. Sastri, J. Lee, K. Oh, J. L. Yoon, J. Lee, T. A. Jackson, K. Ray, H. Hirao, W. Shin, J. A. Halfen, J. Kim, L. Que, S. Shaik and W. Nam, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19181–19186 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full citation of Gaussian 16, relative energy tables, Mulliken spin and charges, distortion energies, LUMO values for reactants, and optimized Cartesian coordinates for all the stationary points. See DOI: https://doi.org/10.1039/d4dt00063c |
| This journal is © The Royal Society of Chemistry 2024 |