Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rotational order–disorder and spin crossover behaviour in a neutral iron(II) complex based on asymmetrically substituted large planar ionogenic ligand†
Maksym
Seredyuk
 *abc,
Kateryna
Znovjyak
*abc,
Kateryna
Znovjyak
 a,
Francisco Javier
Valverde-Muñoz
a,
Francisco Javier
Valverde-Muñoz
 b,
M. Carmen
Muñoz
b,
M. Carmen
Muñoz
 d,
Igor O.
Fritsky
a and
José Antonio
Real
d,
Igor O.
Fritsky
a and
José Antonio
Real
 *b
*b
aDepartment of Chemistry, Taras Shevchenko National University of Kyiv, 64/13, Volodymyrska Street, 01601 Kyiv, Ukraine. E-mail: maksym.seredyuk@knu.ua
bInstituto de Ciencia Molecular, Departamento de Química Inorgánica, Universidad de Valencia, 46980 Paterna, Valencia, Spain. E-mail: jose.a.real@uv.es
cEnamine Ltd., Winston Churchill Str. 78, 02094 Kyiv, Ukraine
dDepartamento de Física Aplicada, Universitat Politècnica de València, Camino de Vera s/n, E-46022, Valencia, Spain
First published on 17th April 2024
Abstract
Octahedrally coordinated spin crossover (SCO) FeII complexes represent an important class of switchable molecular materials. This study presents the synthesis and characterisation of a novel complex, [FeII(ppt-2Fph)2]0·2MeOH, where ppt-2Fph is a new asymmetric ionogenic tridentate planar ligand 2-(5-(2-fluorophenyl)-4H-1,2,4-triazol-3-yl)-6-(1H-pyrazol-1-yl)pyridine. The complex exhibits a hysteretic thermally induced SCO transition at 285 K on cooling and at 293 K on heating, as well as light induced excited spin state trapping (LIESST) at lower temperatures with a relaxation T(LIESST) temperature of 73 K. Single crystal analysis in both spin states shows that the compound undergoes an unusual partial (25%) reversible order–disorder of the asymmetrically substituted phenyl group coupled to the thermal SCO. The highly cooperative SCO transition, analysed by structural energy framework analysis at the B3LYP/6-31G(d,p) theory level, revealed the co-existence of stabilising and destabilising energy variations in the lattice. The observed antagonism of intermolecular interactions and synchronous rotational disorder, which contributes to the overall entropy change, is suggested to be at the origin of the cooperative SCO transition.
Introduction
Octahedrally coordinated FeII spin crossover (SCO) complexes are well-known switchable molecular materials that have attracted much attention for their potential applications in displays, sensors, information storage,1 thermal management purposes,2 and spintronics3 among others. In the SCO complexes, the FeII centres reversibly switch between the diamagnetic LS (t62ge0g, S = 0) and the paramagnetic HS (t42ge2g, S = 2) electronic states triggered by changes in temperature and/or pressure, by light irradiation and even by interaction with analytes. The SCO behaviour is associated with dramatic changes in the magnetic, optical and dielectric properties of the material.4 Furthermore, the transfer of electrons between the eg and t2g orbitals is accompanied by remarkable changes in the FeII–ligand bond lengths (about 0.2 Å on average for FeII–N bonds) and angles. In the solid state, these structural changes are propagated throughout the crystal by elastic interactions. Constructive interactions between SCO centres give rise to cooperative and even hysteretic behaviour, which confers bistability and hence memory to the SCO materials.5,6 Exceptionally wide stable thermal hysteresis has been observed independently of the synthetic approach used, polymeric7 or supramolecular.8In the search for new bistable SCO materials based on the supramolecular approach, where cooperativity is achieved through effective, although usually elusive intermolecular interactions, we have recently reported on the synthesis and characterization of the mononuclear FeII SCO neutral complex [FeII(ppt-3MeOph)2]0·nMeOH (3MeO·nMeOH) where ppt-3MeOph is the asymmetric ionogenic tridentate planar ligand 2-(5-(3-methoxyphenyl)-4H-1,2,4-triazol-3-yl)-6-(1H-pyrazol-1-yl)pyridine (Scheme 1). The solvates n = 2 and ≈1.4 are isostructural (orthorhombic Pbcn). The former is LS at 300 K but undergoes a gradual and complete SCO in the interval 300–400 K with TSCO = 365 K due to the desolvation. The loss of ca. 0.6 molecules of MeOH makes the SCO much more cooperative, TSCO = 296 K without hysteresis. However, heating the complex above 550 K favours the complete loss of solvent (n = 0) and provokes a transition to the monoclinic P21/c phase which exhibits an exceptional SCO behaviour featuring a stable 105 K wide hysteresis loop (TSCO ≈ 307 K). More importantly, the supramolecular mechanism facilitating this large over-stabilization of both HS and LS states has been elucidated stemming from the steric effect induced by flipping of the 3MeO functional group between the bent and extended conformations (“supramolecular latch”) and the changes that this causes in the trigonal distortion of the [FeIIN6] octahedron of adjacent complexes.8c
Given the interesting results obtained from this complex and following the strategy of synthesising new neutral FeII SCO complexes derived from new asymmetrically substituted large planar ionogenic ligands, we have decided to systematically investigate the influence of specific substituents as a way to test the lability of the resulting crystal packings and their susceptibility to induce phase transitions and appealing cooperative SCO phenomenologies.9 In this context, we report here on the synthesis, crystal structures, magnetic, photomagnetic and calorimetric properties of the system [FeII(ppt-2Fph)2]0·nMeOH (2F) where ppt-2Fph is the new ligand 2-(5-(2-fluorophenyl)-4H-1,2,4-triazol-3-yl)-6-(1H-pyrazol-1-yl)pyridine.
Magnetic and photomagnetic properties
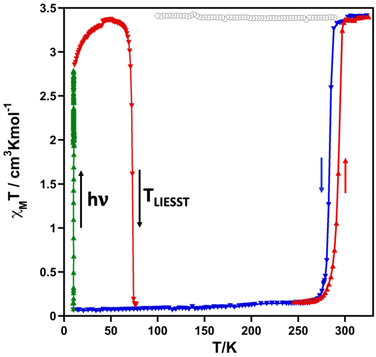
The magnetic properties of the methanolate (2F) and the desolvated complex (2Fdes) in the form of the product χMT versus T, where χM is the molar magnetic susceptibility measured at 1 K min−1 and T is the temperature, are shown in Fig. 1. At 325 K, the χMT value of 2F is 3.40 cm3 K mol−1 and decreases slightly down to 3.33 cm3 K mol−1 upon cooling to 290 K but drops abruptly from this temperature down to 0.15 cm3 K mol−1 at 267 K. Both extreme values are consistent with the HS and LS state of the FeII ion, respectively. In the heating mode, the χMT versus T profile does not match the cooling mode defining a hysteresis ca. 8 K wide. The characteristic temperatures, T↓c and T↑c of the cooperative spin transition calculated as the maximum of the ∂(χMT)/∂T vs. T function are 285 K and 293 K (〈Tc〉 = 289 K), respectively. The desolvated form 2Fdes is paramagnetic at all temperatures with an almost constant χMT value of 3.40 cm3 K mol−1.The photogeneration of the metastable HS* state from the LS state, the so-called light induced excited spin state trapping (LIESST) experiment,10 was performed at 10 K irradiating a microcrystalline sample of 2F with green light (λ = 532 nm). The sample undergoes quantitative (100%) LIESST effect with χMT saturating to a value of ca. 2.80 cm3 K mol−1. Subsequently, the light was switched off and the temperature increased at a rate of 0.3 K min−1 inducing a gradual increase in χMT reaching a maximum value of 3.36 cm3 K mol−1 in the interval of 10–47 K. This increase in χMT reflects the thermal population of different microstates originating from the zero-field splitting of the HS* state. Above 47 K, χMT decreases rapidly upon heating until it joins the SCO thermal curve at ca. 76 K, indicating that the metastable HS* state has relaxed back to the stable LS state. The corresponding TLIESST temperatures, evaluated as ∂(χMT)/∂T,11 is 73 K.
It was demonstrated that a linear correlation between the SCO equilibrium temperature T1/2 and TLIESST generally holds for different types of FeII complexes. In particular, for complexes with tridentate ligands, the two physical quantities can be related by the empirical formula: TLIESST = T0 − 0.3T1/2, where T0 ≈ 150 K.12 The calculated value T0 = TLIESST + 0.3T1/2 for 2F is close to this, being equal to ca. 160 K.
Calorimetric properties
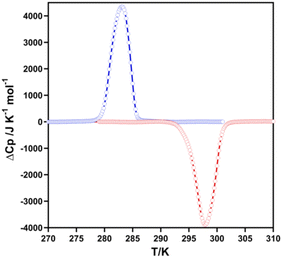
The thermal dependence of the excess heat capacity at constant pressure, ΔCp, for 2F was monitored through differential scanning calorimetric (DSC) measurements recorded at 10 K min−1 (see Fig. 2). The average enthalpy ΔH and entropy variations ΔS (=ΔH/Tc) (being Tc the temperature at the maximum/minimum of ΔCpvs. T plot) associated with the exo- and endothermic peaks are, respectively, 15.8 kJ mol−1 and 56.0 J K−1 mol−1. These ΔH and ΔS values are consistent with the occurrence of a cooperative complete SCO.13 The Tavc = (T↓c + T↑c)/2 = 291 K obtained from DSC data agree reasonably well with that, 289 K, obtained from magnetic measurements. However, as expected, the hysteresis is ca. 7 K wider due to the much larger temperature scan-rate usually employed for the DSC measurements.Crystal structure
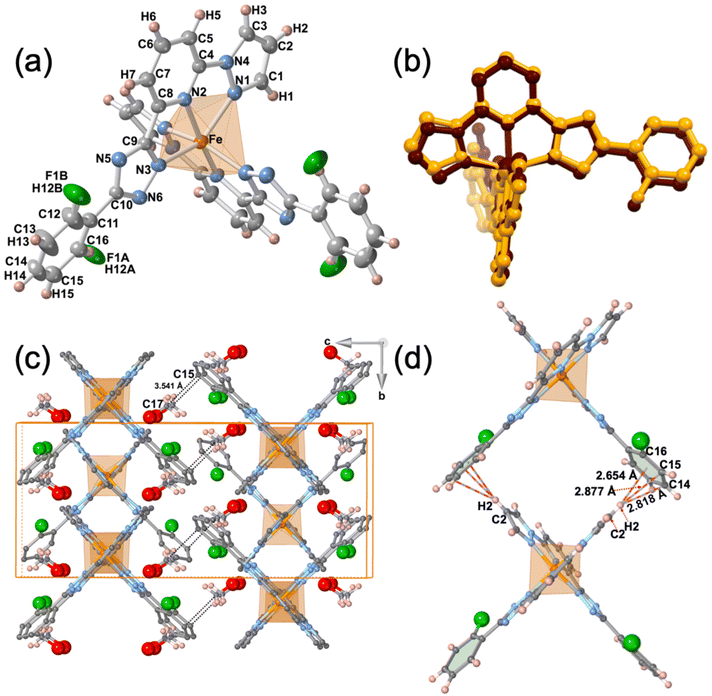
The single crystal structure of 2F was measured at 293 and 220 K in the HS and LS states, respectively. At both temperatures, the crystal adopts the orthorhombic Pbcn space group. Relevant crystallographic data are summarised in Table S1,† and Table 1 collates the relevant bond lengths and angles concerning the [FeIIN6] octahedral site. In the LS state the octahedron is axially compressed with pyridine moiety bond lengths Fe–N2 equal to 1.913(4) Å, while pyrazole Fe–N1 and triazole Fe–N3 bonds are significantly larger (see Fig. 3a). The average bond length 〈Fe–N〉av = 1.955 Å at 220 K is consistent with the LS state observed from magnetic and calorimetric data. At 293 K, the [FeIIN6] sites expand anisotropically becoming much more distorted involving with 〈Fe–N〉av an increment of 0.212 Å reaching a value characteristic, 2.167 Å, of the FeII ion in the HS state. This volume expansion of coordination polyhedron (VCP) is accompanied by noticeable reversible changes in the internal Fe-pptr (Ni–Fe–Nj) bond angles involving the N1/N2, N1/N3 and N2/N3 atoms which decrease by 6.99°, 11.82° and 4.81° when moving to the HS state. Other significant changes involve the Ni–Fe–Nj* angles defined between the two equivalent ligands N2/N2* [−6° (HS)], N2/N3* [+8.75° (HS)] and N3/N3* [+7.7° (HS)]. Indeed, the angular distortion of the [FeN6] from the ideal octahedron, defined as the sum of the angular deviation of the 12 cis angles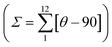 , is considerably larger in the HS, 146.8°, than in the LS state, 89.8°. The same is observed for the trigonal distortion value,
, is considerably larger in the HS, 146.8°, than in the LS state, 89.8°. The same is observed for the trigonal distortion value, 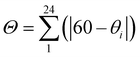 , θi being the angle generated by superposition of two opposite faces of the octahedron, which increases from 314.59° (LS) up to 492.77° (HS). The continuous shape measure index14 in the two spin states, calculated for the octahedral polyhedron geometry [CShM(Oh)], varies from 2.246 to 5.282.
, θi being the angle generated by superposition of two opposite faces of the octahedron, which increases from 314.59° (LS) up to 492.77° (HS). The continuous shape measure index14 in the two spin states, calculated for the octahedral polyhedron geometry [CShM(Oh)], varies from 2.246 to 5.282.
| LS (220 K) | HS (293 K) | Δ(HS − LS) | |
|---|---|---|---|
| Bond lengths/Å | |||
| Fe–N1 | 1.974(4) | 2.235(6) | +0.261 |
| Fe–N2 | 1.913(4) | 2.136(6) | +0.223 |
| Fe–N3 | 1.978(5) | 2.129(6) | +0.151 |
| 〈Fe–N〉av | 1.955 | 2.167 | +0.212 |
| Bond angles/° | |||
| N1–Fe–N2 | 79.67(18) | 72.68(18) | −6.99 |
| N1–Fe–N3 | 159.64(18) | 147.82(18) | −11.82 |
| N2–Fe–N3 | 79.98(18) | 75.17(19) | −4.81 |
| N1–Fe–N1* | 89.8(3) | 88.9(3) | −0.90 |
| N2–Fe–N1* | 95.84(19) | 98.30(18) | +2.46 |
| N1–Fe–N3* | 92.81(18) | 94.4(2) | +1.59 |
| N2–Fe–N2* | 173.7(3) | 167.7(3) | −6 |
| N2–Fe–N3* | 104.49(18) | 113.24(19) | +8.75 |
| N3–Fe–N3* | 91.8(3) | 99.5(3) | +7.7 |
| V CP | 9.62 Å3 | 12.413 Å3 | +2.79 Å3 |
| α | 85.96 | 87.94 | +1.98° |
| Σ | 89.0 | 146.8 | +57.8° |
| Θ | 314.59 | 492.77 | +178.18° |
| CShM(Oh) | 2.25 | 5.28 | +3.03 |
The dihedral angle, α, between the average planes defined by the pyrazole–pyridine–triazole rings of the two ligands is 85.96° in the LS state and due to a scissor-like movement increases by ca. 2.0° when moving to the HS state. Furthermore, in the HS state the F atom is disordered in two positions characterized by 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 occupational probabilities but this disorder disappears in the LS state.
25 occupational probabilities but this disorder disappears in the LS state.
The minimized overlay of the LS and HS molecules visualizing the difference of the molecular shape arising from the above structural transformations is shown in Fig. 3b.
The crystal packing can be described as linear chains of complexes running along b direction. In a chain, the complexes are organised in such a way that the H2 atom of the two pyrazole rings belonging to one complex, point towards the centroids of the two 2-fluorobenzene rings belonging to the next complex, being the separation between them 2.654 (LS)/2.950 (HS) Å. This supramolecular organisation defines wide square windows and generates short contacts [d(C2–H2⋯C14) = 2.819 (LS) Å, d(C2–H2⋯C15) = 2.877 (LS)/2.805 (HS) Å and d(C2–H2⋯C16) = 2.845 (HS) Å] between adjacent complexes, being the separation between two consecutive Fe centres 10.401 (HS)/10.705 (LS) Å (see Fig. 3d). It should be noted that the increase of separation, along b direction, between the FeII centres in the LS state is correlated with the decrease of the dihedral angle θ in the LS. The chains stack along a separated by a/2 = 6.525 (HS)/6.387 (LS) Å and are shifted along b half-way the distance between two consecutive Fe centres (5.200 (HS)/5.352 (LS) Å) defining supramolecular layers parallel to ab running along c. Consequently, each complex belonging to a chain fits in the hollow space generated by the square windows of the adjacent chain, partially filling them. This fact determines the shortest Fe⋯Fe separation within each layer (8.344 (HS)/8.334 (LS) Å). Obviously, the shortest Fe⋯Fe separation between adjacent layers, 12.629 (LS)/12.836 (HS) Å is markedly larger and consequently no significant contacts are found between the corresponding complexes.
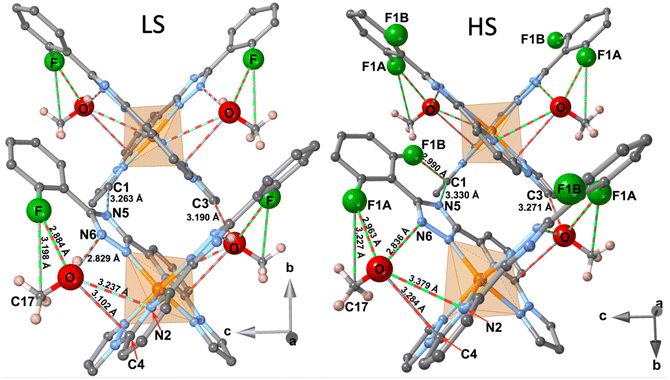
The space within the layers is partially filled by the MeOH molecules, which are located in two equivalent sites placed between the two almost orthogonally oriented ligands of the same complex (Fig. 4), and interact with them showing relatively short contacts in the LS state with the F-phenyl [d(F⋯O) = 2.884 Å, d(F⋯C17) = 3.198 Å] and the pyridine [d(O⋯N2) = 3.237 Å, d(O⋯C4) = 3.102 Å] moieties. Furthermore, in the LS state a strong hydrogen bond d(O–H⋯N6) = 2.829 Å, is formed between the MeOH molecule and the triazole ring. Within each layer, adjacent complexes belonging to two consecutive chains show two short contacts, one involving the N5 atom of the triazole moiety of one complex and the C1 atom of the pyrazole ring of the adjacent molecule [d(N5⋯C1) = 3.263 Å]. The second contact is mediated by the O atom of the MeOH [d(C3⋯O) = 3.190 Å]. Obviously, all these contacts are slightly larger in the HS state than in the LS state (Fig. 4). Only the MeOH molecules of one layer show a relatively short distance to the F-benzene ring of the adjacent layer d(C15⋯C17) = 3.541 Å in the LS state.
As mentioned above, the F atom of the benzene ring is completely ordered in a unique position in the LS state, but in the HS state occupies two positions, F1A (towards FeII) and F1B (away from FeII) (Fig. 4), with occupation factors of 75% and 25%, respectively. The F1A and F atoms in the HS and LS states are equivalent. Interestingly, for a given complex the F1B site in the HS strongly interacts with the C1 atom of the pyrazole moiety of the adjacent complex, being the separation d(F1B⋯C1) = 2.990 Å well below the sum of the corresponding van der Waals radii.
Upon desolvation, the compound becomes non-SCO due to the changes in crystal packing, as can be seen from the comparison of the XRD patterns (Fig. S1†) and the derived cell parameters (Table S2†). The new phase retains the orthorhombic symmetry of the lattice, but the volume of the cell decreases due to the loss of methanol molecules [Vcell(2Fdes) = 3089.6 Å3vs. Vcell(2F293K) = 3401.5 Å3]. The cell parameter b, which corresponds to the periodicity of the molecules in the supramolecular chains discussed above, is the most affected, decreasing by almost 2 Å due to the loss of methanol. This indicates a strong scissor-like distortion of the molecule (i.e., an increase in the dihedral angle α beyond that observed for the HS phase), justifying the trapping of the HS state of the FeII ions down to low temperatures. The transition to the more regular molecular geometry typical of the LS state appears to be hindered by the reduced cell volume and less free space in the lattice.
Energy framework analysis
Energy framework analysis is a convenient visual tool for analysing the interaction energy within molecular crystal structures and correlating with the SCO properties arising from these structures.15 The method assumes the representation of intermolecular interactions in the form of cylindrical bonds between the centroids of neighbouring molecules, the radius of the cylinder being proportional to the value of the interaction energy, which takes into account the contributions of electrostatic, polarisation, dispersion and exchange-repulsion interactions calculated by quantum mechanical methods on the basis of a suitable molecular wave functions. Although originally created to understand the mechanical properties of crystals, energy framework analysis has found its application in SCO research as well.First of all, the interaction energy of the two sublattices in the HS state phase was analysed, corresponding to the two conformations of the molecules, where the F-atom is oriented towards or away from the FeII ion. Counterintuitively at first sight, the intermolecular interaction energies are very close in both cases, differing by up to 2.5 kJ mol−1 in favor of “away” configuration (see Table S3†). In contrast, the binding energy with methanol molecule reaches the energy difference of 5.2 kJ mol−1 in favour of the “towards” geometry due the additional bond F⋯H–O absent in the “away” configuration (see Table S4†). In total, both bond energy gains and losses due to the flipping phenyl moiety are close to cancelling each other out. Presumably, the entropic factor drives the disorder of sterically close fluorine and hydrogen atoms, which are weakly constrained by low binding energy in the looser HS lattice having more free space for rotation compared to the LS lattice. It should also be noted that the above consideration of the separate pure sublattices is for discussion purposes only. The “away” configuration has only 25% population and random distribution in the lattice, i.e. per one “away” molecule there are three “towards” molecules. For the sake of simplicity, only the pure “towards” configuration of molecules will be considered further.
The Energy Difference Framework (EDF) analysis of the HS and LS “towards” configuration lattices allows the mapping of changes in interactions with the immediate neighbourhood, taking into account the full set of intermolecular interactions. This contrasts with the classical approach, which considers only the strongest interaction below van der Waals radii. The EDF enables identification of the molecule–molecule contacts that is the most affected on transformation and provides insight into the pathways of the SCO cooperativity.8c,16 The constructed EDF of 2F features a three-dimensional character, with larger amplitudes of stabilising (negative) and destabilising (positive) of the intermolecular changes localised within the supramolecular layers formed by stacking molecules (Fig. 5a and Table S5†). The interactions between the layers also have opposite sign but are weaker, which we attribute to the larger distance between the molecules and the absence of strongly interacting groups at the molecular periphery.
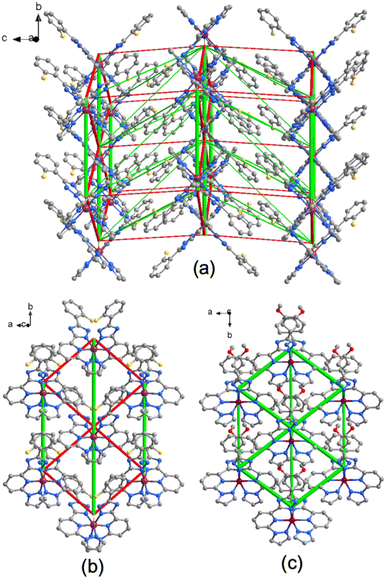 | ||
| Fig. 5 (a) EDF of compound 2F, constructed using the values from the Table S5,† column “ΔE(total)(LS − HS),” and superimposed on a fragment of the LS phase crystal lattice. The red cylinders correspond to weakening interactions, the green cylinders to the strengthening interactions. Tube size is scaled proportionally to the absolute value of the interaction energy, cut-off is 0.5 kJ mol−1; (b) and (c) comparison of EDFs within the supramolecular layer corresponding the compound 2F and 3MeO. Tube size scale is the same in both figures. | ||
As the next step, we have plotted the EDF of only the supramolecular layer showing the strongest interactions and compared to the same of the reported earlier 3MeO·∼1.4MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8c (Fig. 5b and c). While for 2F, which exhibits SCO hysteresis, the interactions are opposite in sign and close to equilibrium (−4.3 and +3.1 kJ mol−1), for 3MeO·∼1.4MeOH, which in non-hysteretic, they are both stabilising across the SCO transition region (−5.1 and −3.5 kJ mol−1). In this context, the simultaneous presence of significant stabilising and destabilising lattice energy changes is attributed to more cooperative SCO transitions, whereas smaller changes are associated with less cooperative SCO transitions as it was demonstrated in reported studies.16 Correspondingly, the hysteretic behaviour of 2F is attributed to the presence of balanced energy changes (stabilising and destabilising), in contrast to 3MeO·∼1.4MeOH, whose EDF consists mainly of the unbalanced stabilising interactions.
8c (Fig. 5b and c). While for 2F, which exhibits SCO hysteresis, the interactions are opposite in sign and close to equilibrium (−4.3 and +3.1 kJ mol−1), for 3MeO·∼1.4MeOH, which in non-hysteretic, they are both stabilising across the SCO transition region (−5.1 and −3.5 kJ mol−1). In this context, the simultaneous presence of significant stabilising and destabilising lattice energy changes is attributed to more cooperative SCO transitions, whereas smaller changes are associated with less cooperative SCO transitions as it was demonstrated in reported studies.16 Correspondingly, the hysteretic behaviour of 2F is attributed to the presence of balanced energy changes (stabilising and destabilising), in contrast to 3MeO·∼1.4MeOH, whose EDF consists mainly of the unbalanced stabilising interactions.
Discussion and conclusions
Following our strategy of investigating new FeII SCO neutral complexes based on asymmetrically substituted large planar ionogenic ligands, here we have described the synthesis and characterization of the second member of this series, compound 2F. This complex is essentially isostructural with 3MeO·nMeOH previously reported,8c which only differ from the substitution of the 2-fluorophenyl (2Fph) group by the 3-methoxyphenyl (3MeOph) group in the triazole ring of the pyridine–pyrazole–triazole-based tridentate chelate ligand. The MeOH molecules, similarly located in both compounds, interact via hydrogen bonding with the triazole and pyridine rings in both cases. However, the fact that the 2Fph and 3MeOph moieties have opposite orientation (180°) with respect to each other argues in favour of the fact that the number of intermolecular interactions between the MeOH molecule and the ligands is larger for the F-derivative. More precisely, the 2Fph group is orientated in such a way that the F-atom interacts with the CH3OH molecule (d(F⋯O) = 2.884 Å (LS)) in contrast to the methoxy derivative in which an equivalent interaction cannot exist (see figure in Table S4†). These differences seem to be reflected on the SCO behaviour which is much more cooperative for the homologous fluoro-derivative than that of the methoxy-derivative. Surprisingly, the partial loss of MeOH, that leads to the formation of a solvate with ∼1.4 molecules of MeOH, in the methoxy derivative stabilizes a different solvate phase whose cooperative SCO behaviour (TSCO = 296 K) is remarkably similar, but without hysteresis, to that of the fluoro-derivative here reported. Indeed, the crystal structure of this new solvate phase is closely related to that of the parent one and that of the fluoro derivative. However, the complete loss of the MeOH and an additional phase transition affords a crystallographically different phase for the methoxy derivative which exhibits a SCO with a 105 K wide hysteresis centred at 307 K. This fact strongly differs from the desolvated form of the fluoro-derivative which is HS at all temperatures.Coming back again to 2F, this compound illustrates an interesting example of an order–disorder transition involving the flipping between two possible opposite rotational orientations of the 2-fluorophenyl ring. Indeed, in the LS state only one orientation is observed and, as mentioned above, it is involved in several intermolecular contacts with the CH3OH molecule. However, in the HS state, 25% of these 2-fluorophenyl groups turn 180° and adopt the opposite orientation, which corresponds to that of the homologous methoxy derivative. This change eliminates the interaction of the F atom with the CH3OH molecule and stabilises a contact with the C1–H1 atoms of the pyrazole ring [d(F1B⋯C1) = 2.990 Å and d(F1B⋯H1) = 2.398 Å] of the neighbouring molecule belonging to the same layer (Fig. 4).
The interplay between order–disorder and spin crossover phenomena has been subject of attention since long ago. The possible influence of order–disorder of the counterion in the SCO of the complex [FeII(2-methyl-1,10-phenanthroline)3](ClO4)2 was first suggested from Mössbauer data.17 This fact became more evident in a subsequent study of the complex [FeII(2,2′-bi-2-imidazoline)3](ClO4)2,18 and then later for cationic complexes of the [Fe(2,6-di(pyrazol-1-yl)pyridine)2]2+ family.19
The influence of orientational order–disorder of solvents included in the lattice on the SCO was also discussed quite early for the complexes [FeII(2-picolylamine)3]Cl2·EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 and [FeII(cis-1,2-bis(diphenylphosphino)ethylene)]X2·2S with S = (CH3)2CO and X = Cl,21 and CHCl3 and X = Br.22 Particular interest arouse from the two-step character of the SCO behaviour of the 2-picolylamine derivative for which detailed investigations concluded that this singular behaviour is due to the onset of an intermediate superstructure phase, coupled to two successive order–disorder phase transitions.23 More recently the occurrence of concerted order–disorder in both the anion and solvents in the same SCO complex has also been analyzed.24
20 and [FeII(cis-1,2-bis(diphenylphosphino)ethylene)]X2·2S with S = (CH3)2CO and X = Cl,21 and CHCl3 and X = Br.22 Particular interest arouse from the two-step character of the SCO behaviour of the 2-picolylamine derivative for which detailed investigations concluded that this singular behaviour is due to the onset of an intermediate superstructure phase, coupled to two successive order–disorder phase transitions.23 More recently the occurrence of concerted order–disorder in both the anion and solvents in the same SCO complex has also been analyzed.24
Order–disorder phenomena originated in the ligands coordinated to the FeII SCO centres was first discussed for [Fe(DAPP)(abpt)](ClO4)2 [DAPP = [bis(3-aminopropyl)(2-pyridylmethyl)amine], abpt = 4-amino-3,5-bis(pyridin-2-yl)-1,2,4-triazole]. In this complex one methylene group is 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 disordered in the two possible positions of a half-boat conformation in the HS state and becomes fully ordered in the LS state.25 A similar observation was recently reported for some complexes formulated [FeII(L)trans-(NCS)2] where L are tetradentate ligands obtained by reaction of N-substituted 1,2,3-triazolecarbaldehyde with 1,3-propanediamine or 2,2-dimethyl-1,3-diaminopropane.16b In the complex cis-[FeII(NCSe)2(DDE)2] with DDE = N2,N2,N4,N4-tetraethyl-N6,N6-di(pyridin-2-yl)-1,3,5-triazine-2,4,6-triamine,26 a crystallographic phase transition occurs induced by ordering of the dangling ethyl moieties of the DDE ligand when the complex moves from the HS to the LS state. Interestingly, order–disorder in the butyl chains of the complex [Fe(n-Bu-im)3tren](PF6)2 ((n-Bu-im)3(tren) = n-butylimidazoltris(2-ethylamino)amine) controls the relaxation dynamics of the photo-induced HS state to the LS state at low temperatures.27 It is important to remark that in all these precedent examples, the aliphatic moieties of the ligands are involved in the order–disorder transition. This explains why aliphatic functionalization of SCO complexes is a fruitful approach to explore the influence of conformational changes on the SCO behaviour, even in absence of order–disorder events.28 Exception to the generalization given above is the order–disorder concerted with SCO observed for the coordinated dicyanamide anion in the {[Fe(bztpen)]2[μ-N(CN)2]}(PF6)3·nH2O (bztpen = N-benzyl-N,N′,N′-tris(2-pyridylmethyl)ethylenediamine) and {Fe(abpt)2[N(CN)2]2} (abpt = 4-amino-3,5-bis(pyridin-2-yl)-1,2,4-triazole) dinuclear29 and mononuclear30 SCO complexes, respectively. In this context, as far as we are aware the results here reported describe the first example of order–disorder transition involving the flipping of an aromatic ring.
50 disordered in the two possible positions of a half-boat conformation in the HS state and becomes fully ordered in the LS state.25 A similar observation was recently reported for some complexes formulated [FeII(L)trans-(NCS)2] where L are tetradentate ligands obtained by reaction of N-substituted 1,2,3-triazolecarbaldehyde with 1,3-propanediamine or 2,2-dimethyl-1,3-diaminopropane.16b In the complex cis-[FeII(NCSe)2(DDE)2] with DDE = N2,N2,N4,N4-tetraethyl-N6,N6-di(pyridin-2-yl)-1,3,5-triazine-2,4,6-triamine,26 a crystallographic phase transition occurs induced by ordering of the dangling ethyl moieties of the DDE ligand when the complex moves from the HS to the LS state. Interestingly, order–disorder in the butyl chains of the complex [Fe(n-Bu-im)3tren](PF6)2 ((n-Bu-im)3(tren) = n-butylimidazoltris(2-ethylamino)amine) controls the relaxation dynamics of the photo-induced HS state to the LS state at low temperatures.27 It is important to remark that in all these precedent examples, the aliphatic moieties of the ligands are involved in the order–disorder transition. This explains why aliphatic functionalization of SCO complexes is a fruitful approach to explore the influence of conformational changes on the SCO behaviour, even in absence of order–disorder events.28 Exception to the generalization given above is the order–disorder concerted with SCO observed for the coordinated dicyanamide anion in the {[Fe(bztpen)]2[μ-N(CN)2]}(PF6)3·nH2O (bztpen = N-benzyl-N,N′,N′-tris(2-pyridylmethyl)ethylenediamine) and {Fe(abpt)2[N(CN)2]2} (abpt = 4-amino-3,5-bis(pyridin-2-yl)-1,2,4-triazole) dinuclear29 and mononuclear30 SCO complexes, respectively. In this context, as far as we are aware the results here reported describe the first example of order–disorder transition involving the flipping of an aromatic ring.
In conclusion, a new FeII complex based on an ionogenic ligand is described which generates a moderate ligand field favouring a SCO transition near room temperature and a relatively high LIESST relaxation temperature. The energy framework analysis highlights the importance of stabilizing and destabilizing interactions in achieving cooperative transition and hysteresis. An additional factor promoting cooperativity may be the rotational order–disorder transition involving the flipping of the 2-fluorophenyl ring in the aromatic ligand, which adds a novel dimension to the study of SCO materials. The results presented here provide a basis for future exploration of similar asymmetrically substituted ligands and their impact on the properties of FeII SCO complexes. This knowledge is crucial for advancing the design and development of molecular materials with enhanced switchable properties for technological applications.
Experimental
Materials
All chemicals were purchased from commercial suppliers and used without further purification (Merck).Synthesis of ligand
The ligand ppt-2Fph was synthesised by the Suzuki cross-coupling reaction from the commercially available precursors according to the previously reported method.8cSynthesis of complexes
2F ([Fe(ppt-2Fph)]0·2MeOH) was produced by layering in standard test tube. The layering sequence was as follows: the bottom layer contains a solution of [Fe(ppt-2Fph)](BF4)2 prepared by dissolving ppt-2Fph (100 mg, 0.314 mmol) and Fe(BF4)2·6H2O (55 mg, 0.163 mmol) in boiling acetone, to which chloroform (5 ml) was then added. The middle layer was a methanol–chloroform mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) (10 ml) which was covered by a layer of methanol (10 ml), to which 100 μl of NEt3 was added dropwise. The tube was sealed, and yellow plate-like single crystals appeared in 2 weeks (yield ca. 60%). Elemental analysis calcd for C34H28F2FeN12O2: C, 55.90; H, 3.86; N, 23.01. Found: C, 55.81; H, 3.77; N, 23.13.
10) (10 ml) which was covered by a layer of methanol (10 ml), to which 100 μl of NEt3 was added dropwise. The tube was sealed, and yellow plate-like single crystals appeared in 2 weeks (yield ca. 60%). Elemental analysis calcd for C34H28F2FeN12O2: C, 55.90; H, 3.86; N, 23.01. Found: C, 55.81; H, 3.77; N, 23.13.
2Fdes [Fe(ppt-2Fph)]0 was prepared by a short heating 2F up to 400 K or by leaving the crystalline 2F in air for 30 minutes. Elemental analysis calcd for C32H20F2FeN12: C, 57.67; H, 3.02; N, 25.22. Found: C, 57.55; H, 3.12; N, 25.17.
Physical characterization
Variable-temperature magnetic susceptibility data (15–20 mg) were recorded on a sample consisting of single crystals at a rate of 1 K min−1 between 10–400 K using a Quantum Design MPMS2 SQUID susceptometer operating at 1 T magnet. The LIESST experiments were performed at 10 K in a commercial sample holder (Quantum Design Fiber Optic Sample Holder), wherein a quartz bucket containing ca. 1 mg of a sample was held against the end of a quartz fiber coupled with a red laser (633 nm, 15 mW cm−1). After reaching the saturation of susceptibility, the sample was heated up at the rate 0.3 K min−1. The raw data were corrected for a diamagnetic background arising from the sample holder. The resulting magnetic signal was calibrated by scaling to match values with those of bulk sample. Differential scanning calorimetric (DSC) measurements were performed on a sample consisting of single crystals on a Mettler Toledo TGA/SDTA 821e under a nitrogen atmosphere with a rate of 10 K min−1. The raw data were analyzed with the Netzsch Proteus software with an overall accuracy of 0.2 K in the temperature and 2% in the heat flow. Elemental CHN analysis was performed after combustion at 850 °C using IR detection and gravimetry by means of a PerkinElmer 2400 series II device. Single crystal X-ray diffraction data of 2F were collected on a Nonius Kappa-CCD single crystal diffractometer using graphite monochromated Mo Kα radiation (λ = 0.71073 Å). A multi-scan absorption correction was performed. The structures were solved by direct methods using SHELXS-2014 and refined by full-matrix least squares on F2 using SHELXL-2014.31 Non-hydrogen atoms were refined anisotropically and hydrogen atoms were placed in calculated positions refined using idealized geometries (riding model) and assigned fixed isotropic displacement parameters. CCDC files, 2330746 and 2330747† contain the supplementary crystallographic data for this paper. Powder X-ray diffraction measurements were performed on a PANalytical Empyrean X-ray powder diffractometer (monochromatic Cu Kα radiation) equipped with a PIXcel detector operating at 40 mA and 45 kV. XRD data for 2Fdes were collected in the 5–40° (2θ) angular range with a step size of 0.013° and using a 0.5 mm glass capillary and soller slits of 0.02° and a divergence slit of 1/4°. Energy framework analysis calculation were performed by using CrystalExplorer21.15b Electrostatic potential and intermolecular interaction energies, which were partitioned into electrostatic, polarization, dispersion and repulsion energy components, were calculated based on the B3LYP/6-31G(d,p) wave functions that were obtained by using the structural data from the corresponding CIF files. The obtained interaction energies were further utilized to map the network of energy frameworks across different pairs.Author contributions
Conceptualization: M. S.; experimental investigation: M. S. and K. Z.; instrumental measurements and formal analysis: M. S., K. Z., F. J. V.-M., M. C. M. and I. O. F.; data processing and visualization: M. S., K. Z. and J. A. R.; writing of the original draft: M. S., K. Z. and J. A. R.; writing – review & editing: all authors; supervision, project administration, and funding acquisition: M. S. and J. A. R. The manuscript was written through contributions of all the authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish Ministerio de Ciencia e Innovación (grant PID2019-106147GB-I00 funded by MCIN/AEI/10.13039/501100011033), Unidad de Excelencia María de Maeztu (CEX2019-000919-M) and Ministry of Education and Science of Ukraine (grants 22BF037-03, 22BF037-04 and 24BF037-03).References
- (a) O. Kahn, C. Kröber and C. Jay, Adv. Mater., 1992, 4, 718–728 CrossRef CAS; (b) O. Kahn and J. Martinez, Science, 1998, 279, 44–48 CrossRef CAS; (c) J. F. Létard, P. Guionneau and L. Goux-Capes, Top. Curr. Chem., 2004, 235, 221–249 CrossRef.
- (a) P. Von Ranke, B. Alho, R. Ribas, E. Nobrega, A. Caldas, V. De Sousa, M. Colaço, L. F. Marques, D. L. Rocco and P. Ribeiro, Phys. Rev. B, 2018, 98, 224408 CrossRef CAS; (b) S. P. Vallone, A. N. Tantillo, A. M. dos Santos, J. J. Molaison, R. Kulmaczewski, A. Chapoy, P. Ahmadi, M. A. Halcrow and K. G. Sandeman, Adv. Mater., 2019, 31, 1807334 CrossRef PubMed; (c) K. Ridier, Y. Zhang, M. Piedrahita-Bello, C. M. Quintero, L. Salmon, G. Molnár, C. Bergaud and A. Bousseksou, Adv. Mater., 2020, 32, 2000987 CrossRef CAS PubMed; (d) C. Ferlay and O. Ceysson, EP3095831A1, 2016; (e) E. Resines-Urien, M. Á. G. García-Tuñón, M. García-Hernández, J. A. Rodríguez-Velamazán, A. Espinosa and J. S. Costa, Adv. Sci., 2022, 9, 2202253 CrossRef PubMed.
- (a) K. S. Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176–205 CrossRef; (b) G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 1703862 CrossRef PubMed; (c) K. S. Kumar and M. Ruben, Angew. Chem., Int. Ed., 2021, 60, 7502–7521 CrossRef CAS PubMed; (d) M. Gruber and R. Berndt, Magnetochemistry, 2020, 6, 1–26 CrossRef; (e) A. Bellec, J. Lagoute and V. Repain, C. R. Chim., 2018, 21, 1287–1299 CrossRef CAS.
- (a) S. Bonhommeau, P. G. Lacroix, D. Talaga, A. Bousseksou, M. Seredyuk, I. O. Fritsky and V. Rodriguez, J. Phys. Chem. C, 2012, 116, 11251–11255 CrossRef CAS; (b) K. Sun, J.-P. Xue, Z.-S. Yao and J. Tao, Dalton Trans., 2022, 51, 16044–16054 RSC; (c) F.-F. Yan, D. Liu, R. Cai, L. Zhao, P.-D. Mao, H.-Y. Sun, Y.-S. Meng and T. Liu, Dalton Trans., 2023, 52, 18206–18213 RSC.
- (a) E. König, Struct. Bonding, 1991, 76, 51–152 CrossRef; (b) P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054 CrossRef; (c) J. A. Real, A. B. Gaspar, V. Niel and M. C. Muñoz, Coord. Chem. Rev., 2003, 236, 121–141 CrossRef CAS; (d) Top. Curr. Chem, ed. P. Gütlich and G. Goodwin, 2004, vol. 233–235 Search PubMed; (e) J. A. Real, A. B. Gaspar and M. C. Muñoz, Dalton Trans., 2005, 2062–2079 RSC; (f) A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313 RSC; (g) Spin-Crossover Materials: Properties and Applications, ed. M. A. Halcrow, John Wiley & Sons Ltd, Chichester, 2013 Search PubMed; (h) M. A. Halcrow, Chem. Lett., 2014, 43, 1178–1188 CrossRef CAS; (i) M. Shatruk, H. Phan, B. A. Chrisostomo and A. Suleimenova, Coord. Chem. Rev., 2015, 289–290, 62–73 CrossRef CAS; (j) N. Ortega-Villar, M. C. Muñoz and J. Real, Magnetochemistry, 2016, 2, 16 CrossRef; (k) M. Paez-Espejo, M. Sy and K. Boukheddaden, J. Am. Chem. Soc., 2016, 138, 3202–3210 CrossRef CAS PubMed.
- Spin crossover phenomenon, ed. A. Bousseksou, C. R. Chimie, 2018, vol. 21, pp. 1055–1299 Search PubMed.
- M. Grzywa, R. Röβ-Ohlenroth, C. Muschielok, H. Oberhofer, A. Błachowski, J. Żukrowski, D. Vieweg, H.-A. K. von Nidda and D. Volkmer, Inorg. Chem., 2020, 59, 10501–10511 CrossRef CAS PubMed.
- (a) B. Weber, W. Bauer and J. Obel, Angew. Chem., Int. Ed., 2008, 47, 10098–10101 CrossRef CAS PubMed; (b) K. Senthil Kumar, B. Heinrich, S. Vela, E. Moreno-Pineda, C. Bailly and M. Ruben, Dalton Trans., 2019, 48, 3825–3830 RSC; (c) M. Seredyuk, K. Znovjyak, F. J. Valverde-Muñoz, I. da Silva, M. C. Muñoz, Y. S. Moroz and J. A. Real, J. Am. Chem. Soc., 2022, 144, 14297–14309 CrossRef CAS PubMed.
- (a) K. Znovjyak, I. O. Fritsky, T. Y. Sliva, V. M. Amirkhanov, S. O. Malinkin, S. Shova and M. Seredyuk, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2023, 79, 962–966 CrossRef CAS PubMed; (b) K. Znovjyak, M. Seredyuk, I. O. Fritsky, T. Y. Sliva, V. M. Amirkhanov, S. O. Malinkin and S. Shova, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2022, 78, 1173–1177 CrossRef; (c) K. Znovjyak, I. O. Fritsky, T. Y. Sliva, V. M. Amirkhanov, S. O. Malinkin, S. Shova and M. Seredyuk, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2022, 78, 1138–1142 CrossRef CAS PubMed; (d) K. Znovjyak, I. O. Fritsky, T. Y. Sliva, V. M. Amirkhanov, S. O. Malinkin, S. Shova and M. Seredyuk, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2022, 78, 1107–1112 CrossRef CAS PubMed.
- S. Decurtins, P. Gütlich, C. P. Köhler, H. Spiering and A. Hauser, Chem. Phys. Lett., 1984, 105, 1–4 CrossRef CAS.
- J. F. Létard, P. Guionneau, L. Rabardel, J. A. K. Howard, A. E. Goeta, D. Chasseau and O. Kahn, Inorg. Chem., 1998, 37, 4432–4441 CrossRef PubMed.
- J.-F. Létard, G. Chastanet, P. Guionneau and C. Desplanches, Spin-Crossover Materials, John Wiley & Sons Ltd, 2013, pp. 475–506 Search PubMed.
- M. Sorai, M. Nakano and Y. Miyazaki, Chem. Rev., 2006, 106, 976–1031 CrossRef CAS PubMed.
- L. J. Kershaw Cook, R. Mohammed, G. Sherborne, T. D. Roberts, S. Alvarez and M. A. Halcrow, Coord. Chem. Rev., 2015, 289, 2–12 CrossRef.
- (a) M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2015, 51, 3735–3738 RSC; (b) P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- (a) M. G. Reeves, E. Tailleur, P. A. Wood, M. Marchivie, G. Chastanet, P. Guionneau and S. Parsons, Chem. Sci., 2021, 12, 1007–1015 RSC; (b) M. Seredyuk, K. Znovjyak, F. J. Valverde-Muñoz, M. C. Muñoz, V. M. Amirkhanov, I. O. Fritsky and J. A. Real, Inorg. Chem., 2023, 62, 9044–9053 CrossRef CAS PubMed.
- J. Fleisch, P. Gütlich, K. M. Hasselbach and W. Müller, Inorg. Chem., 1976, 15, 958–961 CrossRef CAS.
- E. König, G. Ritter, S. K. Kulshreshtha and S. M. Nelson, Inorg. Chem., 1982, 21, 3022–3029 CrossRef.
- (a) J. M. Holland, J. A. McAllister, Z. B. Lu, C. A. Kilner, M. Thornton-Pett and M. A. Halcrow, Chem. Commun., 2001, 577–578 RSC; (b) V. A. Money, J. Elhaik, I. R. Evans, M. A. Halcrow and J. A. K. Howard, Dalton Trans., 2004, 65–69 RSC; (c) H. Shepherd, G. Tonge, L. Hatcher, M. Bryant, J. Knichal, P. Raithby, M. Halcrow, R. Kulmaczewski, K. Gagnon and S. Teat, Magnetochemistry, 2016, 2, 9 CrossRef.
- (a) M. Mikami, M. Konno and Y. Saito, Chem. Phys. Lett., 1979, 63, 566–569 CrossRef CAS; (b) B. A. Katz and C. E. Strouse, J. Am. Chem. Soc., 1979, 101, 6214–6221 CrossRef CAS.
- E. König, G. Ritter, S. K. Kulshreshtha, J. Waigel and L. Sacconi, Inorg. Chem., 1984, 23, 1241–1246 CrossRef.
- C. C. Wu, J. Jung, P. K. Gantzel, P. Gütlich and D. N. Hendrickson, Inorg. Chem., 1997, 36, 5339–5347 CrossRef CAS.
- (a) D. Chernyshov, M. Hostettler, K. W. Törnroos and H. B. Bürgi, Angew. Chem., Int. Ed., 2003, 42, 3825–3830 CrossRef CAS PubMed; (b) N. Huby, L. Guerin, E. Collet, L. Toupet, J. C. Ameline, H. Cailleau, T. Roisnel, T. Tayagaki and K. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 020101 CrossRef.
- G. A. Craig, J. Sánchez Costa, O. Roubeau, S. J. Teat and G. Aromí, Chem. – Eur. J., 2011, 17, 3120–3127 CrossRef CAS PubMed.
- G. S. Matouzenko, A. Bousseksou, S. A. Borshch, M. Perrin, S. Zein, L. Salmon, G. Molnar and S. Lecocq, Inorg. Chem., 2004, 43, 227–236 CrossRef CAS PubMed.
- T. M. Ross, B. Moubaraki, K. S. Wallwork, S. R. Batten and K. S. Murray, Dalton Trans., 2011, 40, 10147 RSC.
- T. Delgado, A. Tissot, L. Guénée, A. Hauser, F. J. Valverde-Muñoz, M. Seredyuk, J. A. Real, S. Pillet, E.-E. Bendeif and C. Besnard, J. Am. Chem. Soc., 2018, 140, 12870–12876 CrossRef CAS PubMed.
- (a) S. Schlamp, B. Weber, A. D. Naik and Y. Garcia, Chem. Commun., 2011, 47, 7152 RSC; (b) M. Seredyuk, M. C. Muñoz, M. Castro, T. Romero-Morcillo, A. B. Gaspar and J. A. Real, Chem. – Eur. J., 2013, 19, 6591–6596 CrossRef CAS PubMed; (c) T. Fujinami, K. Nishi, D. Hamada, K. Murakami, N. Matsumoto, S. Iijima, M. Kojima and Y. Sunatsuki, Inorg. Chem., 2015, 54, 7291–7300 CrossRef CAS PubMed; (d) D. Rosario-Amorin, P. Dechambenoit, A. Bentaleb, M. Rouzières, C. Mathonière and R. Clérac, J. Am. Chem. Soc., 2018, 140, 98–101 CrossRef CAS PubMed; (e) A. Kashiro, K. Some, Y. Kobayashi and T. Ishida, Inorg. Chem., 2019, 58, 7672–7676 CrossRef CAS PubMed.
- N. Ortega-Villar, A. L. Thompson, M. C. Muñoz, V. M. Ugalde-Saldivar, A. E. Goeta, R. Moreno-Esparza and J. A. Real, Chem. – Eur. J., 2005, 11, 5721–5734 CrossRef CAS PubMed.
- C. F. Sheu, S. Pillet, Y. C. Lin, S. M. Chen, I. J. Hsu, C. Lecomte and Y. Wang, Inorg. Chem., 2008, 47, 10866–10874 CrossRef CAS PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2330746 and 2330747. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00368c |
| This journal is © The Royal Society of Chemistry 2024 |