Open Access Article
Open Access ArticlePbV2O6 under compression: near zero-linear compressibility and pressure-induced change in vanadium coordination†
Josu
Sánchez Martín
 *a,
Julio
Pellicer-Porres
*a,
Julio
Pellicer-Porres
 a,
Robin
Turnbull
a,
Robin
Turnbull
 a,
Daniel
Díaz-Anichtchenko
a,
Daniel
Díaz-Anichtchenko
 a,
Simone
Anzellini
a,
Simone
Anzellini
 a,
Akun
Liang
a,
Akun
Liang
 ab,
Catalin
Popescu
ab,
Catalin
Popescu
 c,
Marco
Bettinelli
c,
Marco
Bettinelli
 d,
Plácida
Rodríguez-Hernández
d,
Plácida
Rodríguez-Hernández
 e,
Alfonso
Muñoz
e,
Alfonso
Muñoz
 e and
Daniel
Errandonea
e and
Daniel
Errandonea
 a
a
aDepartamento de Física Aplicada-ICMUV, Universidad de Valencia, Dr. Moliner 50, 46100 Valencia, Burjassot, Spain. E-mail: Josu.Sanchez@uv.es
bCentre for Science at Extreme Conditions and School of Physics and Astronomy, University of Edinburgh, EH9 3FD Edinburgh, UK
cCELLS-ALBA Synchrotron Light Facility, Cerdanyola del Vallès, 08290 Barcelona, Spain
dLaboratorio Materiali Luminescenti, Dipartimento di Biotecnologie, Università di Verona, and INSTM, UdR Verona, Strada Le Grazie 15, 37134 Verona, Italy
eDepartamento de Física, MALTA-Consolider Team, Instituto de Materiales y Nanotecnología, Universidad de La Laguna, San Cristóbal de La Laguna, E-38200 Tenerife, Spain
First published on 19th June 2024
Abstract
This study presents evidence that lead metavanadate, PbV2O6, is a material with zero-linear compressibility, which maintains its crystal size in one crystallographic direction even under external pressures of up to 20 GPa. The orthorhombic polymorph of PbV2O6 (space group Pnma) was studied up to 20 GPa using synchrotron powder X-ray diffraction, Raman spectroscopy, and density-functional theory simulations to investigate its structural and vibrational evolution under compression. Up to this pressure we find no evidence of any structural phase transitions by any diagnostic technique, however, a progressive transformation of the coordination polyhedron of vanadium atoms is revealed which results in the zero-linear compressibility. High-pressure Raman experiments enabled the identification and symmetry assignation of all 54 zone-centre Raman-active modes as well as the calculation of their respective pressure coefficients. Three independent high-pressure powder X-ray diffraction experiments were performed using different pressure-transmitting media (Ne, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–ethanol mixture, and silicone oil). The results show a high anisotropic behaviour in the linear compressibility of the crystallographic axes. The PbV2O6 bulk modulus of 86.1(9) GPa was determined using a third-order Birch-Murnaghan equation of state. The experimental results are supported by ab initio density-functional theory calculations, which provide vibrational patterns, unit-cell parameters, and atomic positions. These calculations also reveal that, unlike MgV2O6 and ZnV2O6, the band gap of PbV2O6 closes with pressure at a rate of −54 meV GPa−1 due to the contribution of the Pb 6s orbital to the top of the valence band.
1 methanol–ethanol mixture, and silicone oil). The results show a high anisotropic behaviour in the linear compressibility of the crystallographic axes. The PbV2O6 bulk modulus of 86.1(9) GPa was determined using a third-order Birch-Murnaghan equation of state. The experimental results are supported by ab initio density-functional theory calculations, which provide vibrational patterns, unit-cell parameters, and atomic positions. These calculations also reveal that, unlike MgV2O6 and ZnV2O6, the band gap of PbV2O6 closes with pressure at a rate of −54 meV GPa−1 due to the contribution of the Pb 6s orbital to the top of the valence band.
I. Introduction
The family of metavanadate compounds (MV2O6, where M is a divalent atom) exhibits a rich polymorphism, even for each individual M element.1 The structures that have been most extensively studied are the brannerite-type (space group C2/m),1–3 the columbite-type (space group Pbcn)4,5 and the NiV2O6-type (space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ).2,6 It is worth noting that for larger cations, such as Sr, Ba, Hg, or Pb, the metavanadates have orthorhombic structures that differ from those above mentioned.1
).2,6 It is worth noting that for larger cations, such as Sr, Ba, Hg, or Pb, the metavanadates have orthorhombic structures that differ from those above mentioned.1
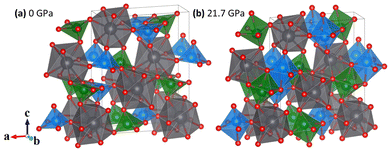
Lead metavanadate (PbV2O6) is known for its magnetic properties7 and for its use as a catalyst in photoelectrochemical water splitting.8 PbV2O6 has various polymorphs at ambient conditions and normally crystallizes in an orthorhombic structure described by space group Pnma, as shown in Fig. 1(a), with a = 9.771(10), b = 3.684(4), c = 12.713(13) Å, and Z = 4.9 In the crystal structure, all atoms are at 4c Wyckoff positions, with V atoms occupying two different positions, V1 and V2. Each V atom is coordinated by 5 oxygen atoms, forming square-based VO5 pyramids. In the Pnma crystal structure of PbV2O6, these VO5 square pyramids share edges to form zig-zag chains parallel to the crystallographic b-axis. The alternating pyramids of V1 and V2 are shown in blue and green respectively in Fig. 1(a). The V–O distances within the two VO5 polyhedra range from 1.610(15) Å to 2.063(15) Å. The next V–O distance is 2.907(14) Å for V1 and 2.619(15) Å for V2. Previous studies have described the structure as being formed by VO6 octahedra,9 as in Fig. 1(b). However, due to the long interatomic distance of the largest V–O distance, it cannot be considered a proper bond. Instead, it is more actually described as a secondary intermolecular bond, which could be easily modified under compression.10
We will demonstrate here that VO6 configuration is only achieved under compression. Each VO5 polyhedron corner-shares via oxygen atoms with the PbO9 distorted triangular dodecahedra. Each one of the nine oxygen atoms in the PbO9 polyhedron comes from a different VO5 pyramid. The PbO9 polyhedron has eight Pb–O bonds with distances from 2.562(12) Å to 2.703(10) Å plus a long bond with a distance of 2.996(15) Å. The PbO9 polyhedra form Pb2O16 dimers via edge sharing. In addition to the stable polymorph of PbV2O6, two metastable polymorphs can be synthesized via quenching of the melt: PbV2O6(II), which has the brannerite-type structure,11 and PbV2O6(III) which crystallizes in an orthorhombic structure (space group C222) and is isostructural to SrV2O6.12
Metavanadates exhibit a wide variety of polymorphs, each with distinct a behaviour under high-pressure (HP), which has attracted the interest of various research groups. Even though they present different crystal structures and vanadium coordination compared to the square pyramid VO5 coordination of PbV2O6, to put our research in context, it is worth taking a look to the whole picture of what has been done in this vanadate family. For instance, SrV2O6 and BaV2O6 (orthorhombic space group C222) undergo phase transitions at about 4 GPa, followed by amorphization between 9 and 10 GPa.13 At pressures above 19 GPa, the brannerite-type MgV2O6 undergoes a phase transition to a structure described by space group C2,14 while the columbite-type remains stable up to 22 GPa.15 For ZnV2O6, a density-functional theory (DFT) study was conducted considering twelve different potential polymorphs up to 30 GPa, finding that only four of them do not have imaginary phonons, and that under compression the brannerite-type might have a transition first to the columbite-type structure at 5 GPa, and then to the monoclinic ThTi2O6-type structure at 15 GPa.16 This same brannerite-type ZnV2O6 was subsequently studied by X-ray diffraction, contradicting the DFT predictions and finding a phase transition to a monoclinic structure (space group C2) at 16.6 GPa.17,18
This work presents a combined experimental and computational study of PbV2O6 up to 20 GPa, including vibrational and structural analysis. Raman spectroscopy was used to determine the frequency and symmetry assignment of all 54 vibrational modes under both ambient and HP conditions. Additionally, powder X-ray diffraction (XRD) data were collected using three different pressure-transmitting media (PTM) in order to determine the unit-cell parameters as a function of pressure. The results indicate that PbV2O6 remains in the low-pressure orthorhombic phase under compression up to 20 GPa. However, we also found evidence of a pressure-induced change in the coordination environment of vanadium. From the XRD data, we have calculated the bulk modulus (B0) and the linear compressibilities of the three crystallographic axes. We found that PbV2O6 has a zero linear compressibility along the b-axis, making it suitable for a wide range of potential applications in complex extreme environments. DFT calculations support all mentioned measurements. They also add the expected infrared (IR) active modes and their pressure coefficients, which have not yet been reported in the literature. The DFT simulations also provide information on the band structure and pressure dependence of the band-gap energy.
II. Methods
A. Synthesis
Orthorhombic PbV2O6 was synthesized via a solid-state reaction.9 High-purity PbO (99.9% Alfa Aesar) and V2O5 (Carlo Erba 99%) were mixed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio and transferred to a Pt crucible with a tightly fitting lid. The mixture was heated in a horizontal furnace in an air atmosphere, starting from room temperature and increasing at a constant rate to 650 °C for one hour, and then maintained at this temperature for 15 minutes. The furnace was then switched off and allowed to cool down to 220 °C. Subsequently, the crucible was removed from the furnace and left to cool to room temperature. The resulting sample was extracted mechanically from the container and washed with doubly distilled water. The obtained powder exhibited a brown-black colour. The orthorhombic crystal structure of PbV2O6 was confirmed by powder XRD.
1 stoichiometric ratio and transferred to a Pt crucible with a tightly fitting lid. The mixture was heated in a horizontal furnace in an air atmosphere, starting from room temperature and increasing at a constant rate to 650 °C for one hour, and then maintained at this temperature for 15 minutes. The furnace was then switched off and allowed to cool down to 220 °C. Subsequently, the crucible was removed from the furnace and left to cool to room temperature. The resulting sample was extracted mechanically from the container and washed with doubly distilled water. The obtained powder exhibited a brown-black colour. The orthorhombic crystal structure of PbV2O6 was confirmed by powder XRD.
B. Details of high-pressure experiments
Raman spectra were acquired in the backscattering geometry using a 632.8 nm He–Ne laser and a Jobin–Yvon spectrometer combined with a thermoelectric-cooled multichannel CCD detector with a spectral resolution of 2 cm−1. OptiGrate Volume Bragg gratings were used to be able to filter the laser from around 10 cm−1. A low laser power of around 2 mW was used to avoid damaging the sample due to heating. The samples were loaded into a diamond-anvil cell (DAC) equipped with low fluorescence diamonds of 350 μm of culet, along with a ruby chip and a stainless-steel gasket. Sample and ruby were embedded in Ne pressure-transmitting medium (PTM) to ensure good hydrostatic conditions.19 The pressure inside the DAC was determined using the ruby luminescence method following the calibration of ref. 20. The Raman mode fitting was performed with MATLAB21 assuming a Pseudo-Voigt peak profile.We performed three sets of HP powder XRD measurements using the same DAC as in the Raman experiment, where the PTM loaded was different in each run: Ne, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–ethanol mixture (ME), and silicone oil (SilOil). All XRD experiments were conducted at the MSPD beamline of the ALBA synchrotron22 using a monochromatic beam of wavelength 0.4246 Å (Ne and ME) and 0.4642 Å (SilOil). The use of different PTM was motivated to check the influence of non-hydrostatic stresses in the behaviour of PbV2O6 under compression. The X-ray beam was focused down to a 20 μm × 20 μm full width at half maximum (FWHM). A Rayonix charge-coupled device detector was used to collect the XRD patterns, with a sample-to-detector distance of 300 (Ne and ME) or 280 mm (SilOil), calibrated following standard procedure using the XRD pattern obtained from LaB6 standard. The pressure was determined using the XRD reflections and the equation of state (EOS) of Cu23 with a precision of ±0.1 GPa. The collected XRD were transformed into one-dimensional patterns using DIOPTAS24 and the structural analysis was performed with PowderCell.25
1 methanol–ethanol mixture (ME), and silicone oil (SilOil). All XRD experiments were conducted at the MSPD beamline of the ALBA synchrotron22 using a monochromatic beam of wavelength 0.4246 Å (Ne and ME) and 0.4642 Å (SilOil). The use of different PTM was motivated to check the influence of non-hydrostatic stresses in the behaviour of PbV2O6 under compression. The X-ray beam was focused down to a 20 μm × 20 μm full width at half maximum (FWHM). A Rayonix charge-coupled device detector was used to collect the XRD patterns, with a sample-to-detector distance of 300 (Ne and ME) or 280 mm (SilOil), calibrated following standard procedure using the XRD pattern obtained from LaB6 standard. The pressure was determined using the XRD reflections and the equation of state (EOS) of Cu23 with a precision of ±0.1 GPa. The collected XRD were transformed into one-dimensional patterns using DIOPTAS24 and the structural analysis was performed with PowderCell.25
C. Ab initio density-functional theory calculations
In this study, zero-temperature simulations were performed with the well-known plane-wave pseudopotential method in the framework of the density-functional theory26 implemented in the Vienna Ab initio Simulation Package, VASP.27 The projector augmented wave (PAW) pseudopotentials28,29 provided in the VASP pseudopotentials database were used, and the exchange–correlation term was described by the generalized gradient approximation (GGA), using the AM0530,31 functional. The Brillouin zone k-points sampling was performed with a Monkhorst–Pack32 sampling of 4 × 8 × 4 for the primitive cell. A plane-wave basis set with an energy cutoff of 600 eV was employed to ensure accurate and highly converged results. All degrees of freedom, lattice parameters, and internal atomic parameters were fully relaxed with self-consistent convergence criteria of 10−6 eV, below 0.003 eV Å−1, and 0.1 GPa, for the total energy, atomic forces, and stress tensor deviation from a diagonal hydrostatic form, respectively. From our simulations, we obtain a set of volume, energy, and pressure data that can be fitted with a Birch–Murnaghan33 equation of state. To analyse the vibrational characteristics, the Phonopy package34 was utilized. The normal mode frequencies and associated eigenvectors were determined at the Γ-point.III. Results and discussion
A. High pressure Raman spectroscopy
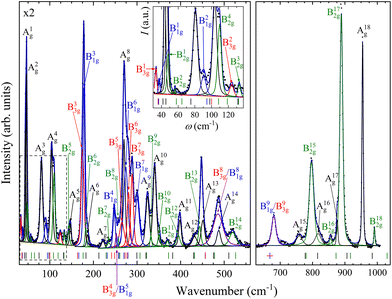
With four molecules in the primitive unit cell, PbV2O6 has a total of 108 vibrational modes. Symmetry analysis shows that all 54 even modes are Raman active,35ΓRaman = 18Ag + 9B1g + 18B2g + 9B3g. By utilizing the information provided by the DFT calculations and the pressure-dependent evolution of modes of the Raman spectra, we have identified the 54 Raman-active modes along with their corresponding symmetries at ambient conditions, as shown in Fig. 2. The figure shows that the symmetry of the modes is mostly distributed in pairs with the same ordering number (superscript). For example, the A4g and B42g modes are close together, as are the B31g and B33g modes. Several B1g and B3g overlap (identified with violet colour in Fig. 2), in which case a single Raman peak is assigned to both modes. Comparing Ag and B2g modes, the intensity of Ag modes is usually larger. Small or partially hidden modes, such as B22g or A14g, are fitted in Fig. 2 as they were properly found in spectra under compression, as their contribution increased in intensity, or they were no longer overlapped by other modes.Regarding the evolution of the Raman spectra under compression, all modes were observed to shift towards higher wavenumbers with increasing pressure, as shown in Fig. 3. No evidence of phase transition was detected in Raman experiments. From this analysis only 48 out of the 52 modes could be followed under compression due to mode overlap. As pressure was increased two interesting phenomena were observed. Firstly, a significant increase in the intensity of the modes above 800 cm−1 occurs starting from 3.9(1) GPa. These modes involve significant stretching movements of the V–O bonds.4,16,36 Therefore, it is not surprising that they will be affected by changes the coordination polyhedron of V that we determined based on XRD experiments and DFT calculations. This observation is discussed in detail in section III.B. Secondly, the intensity of the Raman signal decreases with increasing pressure from 14.5(1) GPa up to the maximum pressure achieved, 19.0(1) GPa, making impossible to distinguish some of the weaker modes from the background. We consider that this phenomenon could be related to absorption of the excitation laser by the sample37 caused by the decrease of the band-gap energy of PbV2O6 under compression. The band-gap energy at ambient pressure is 2.6 eV (ref. 8) and it is a well-known effect that in lead oxides the bandgap closes under compression at a rate between −43 and −72 meV GPa−1.38–40 According to our DFT calculations in PbV2O6 the band gap closes linearly with a rate of −54 meV GPa−1. Therefore, it would not be surprising that near 14.5 GPa the band-gap energy would be around 1.95 eV (683 nm), below the energy of the excitation laser, with the consequent decrease of Raman intensity. This hypothesis is consistent with the fact that the observed signal loss is reversible. The aforementioned pressure induced shift of the Raman modes and increase in intensity of the V–O vibrational modes above 3.9(1) GPa are also totally reversible upon decompression. Comparing PbV2O6 to other metavanadates, it shares the same stability range as the brannerite-type MgV2O6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and ZnV2O6,17,18 which suggest that these structures are more stable than those of SrV2O6 and BaV2O6.13 The difference in pressure stabilities could be related to the more open structural framework of the alkaline rare-earth metavanadates. However, the experiments on SrV2O6 and BaV2O6 should be repeated. For example, the Raman modes reported in ref. 13 become overly broad at low pressures, suggesting a possible bridging of sample between the diamond anvils, which could largely reduce transition pressures41 and trigger amorphization.
14 and ZnV2O6,17,18 which suggest that these structures are more stable than those of SrV2O6 and BaV2O6.13 The difference in pressure stabilities could be related to the more open structural framework of the alkaline rare-earth metavanadates. However, the experiments on SrV2O6 and BaV2O6 should be repeated. For example, the Raman modes reported in ref. 13 become overly broad at low pressures, suggesting a possible bridging of sample between the diamond anvils, which could largely reduce transition pressures41 and trigger amorphization.
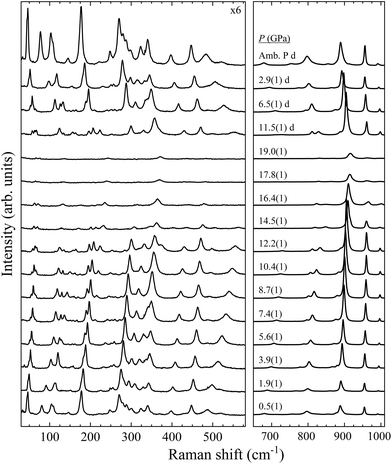 | ||
| Fig. 3 High pressure PbV2O6 Raman spectra at selected pressures. The numbers next to the spectra indicate the pressure in GPa. Spectra acquired on decompression are marked with the letter “d”. | ||
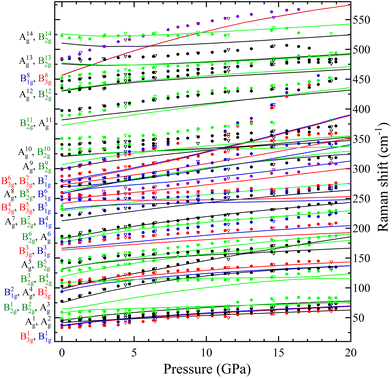
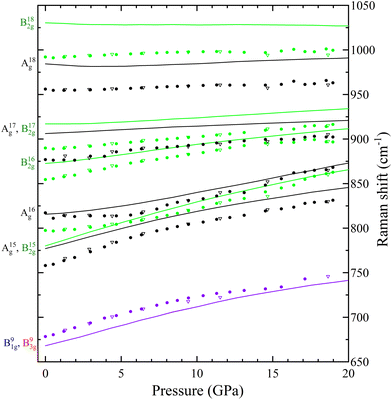
In Table S1 of the ESI† we report the wavenumbers of all Raman-active modes at ambient conditions and their pressure coefficients obtained from experiments and calculations. The level of agreement between the experiments and calculations is relatively high. In the case of the pressure coefficients, a few modes (B11g, B22g, B41g, A9g, B92g, and B112g) have differing values, but they are low intensity peaks which are difficult to follow under pressure. A8g represents the only exception, being easily measured but presenting less than half of the expected pressure coefficient. Furthermore, we show in Fig. 4 and 5 the evolution of all experimentally measured modes along with results from DFT calculations. In Fig. 4 it can be seen a change in the behaviour of the B71g and B73g modes around 11–12 GPa. These are bending vibrations of V–O bonds. It is not surprising that changes in the V coordination would affect their pressure dependence. DFT was key for assigning the symmetry of Raman modes enabling comparison not only of the ambient pressure values, but also of the pressure evolution and the mode crossings. We did not detect any Raman mode of the impurities mentioned in section III.B.
The DFT calculations also provided the forty-two infrared (IR) active modes, all with B1u, B2u, and B3u symmetry, which is the same symmetry of the three acoustic modes. There are nine remaining modes with Au symmetry which are silent. The wavenumbers and pressure coefficients of the IR active modes in ambient conditions are given in Table S2.†
B. High pressure X-ray diffraction
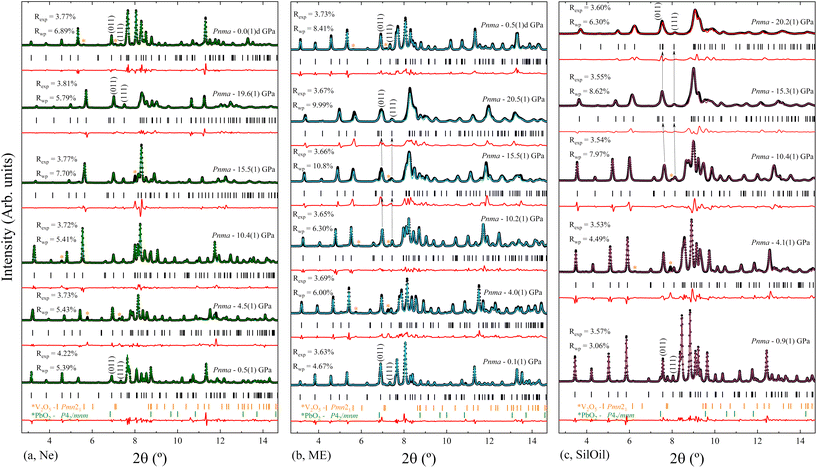
Three independent HP powder XRD experiments were performed on PbV2O6 using three different pressure transmitting media (Ne, ME, and SilOil), reaching a maximum pressure of around 20 GPa in all three runs. Due the influence of preferred orientation effects in the XRD patterns, the Le Bail refinement technique42 was used to analyse the data from all the XRD experiments. The Le Bail fits are shown in Fig. 6 for each PTM at selected pressures. The orthorhombic ambient-pressure structure was successfully fitted in all diffractograms, but additional weak peaks were also detected which have been assigned to rutile-type β-PbO2 (space group P42/mnm) and V2O5 (space group Pmn21). As the peaks of the impurities did not overlap significantly with the peaks from the sample, their presence does not affect the analysis. Additionally, we also observed that the impurity peaks gradually disappeared as pressure was increased and were absent during decompression (see Fig. 6a and b). The disappearance of the V2O5 peaks may be attributed to its well-known pressure-induced irreversible amorphization.43 In the case of β-PbO2, it is known that no phase transition occurs up to 20 GPa.44 However, XRD peaks have been found to broaden due to a pressure-induced disorder of the crystal structure.44 This phenomenon could account for the disappearance of the weak peaks associated with the β-PbO2 impurities.In all three experiments, XRD patterns are consistent with the ambient-pressure orthorhombic structure of PbV2O6 described by space group Pnma, as shown in Fig. 6 where we include R-values from the fits. In the case of the ME and SilOil experiments the peak matching above 15 GPa is not as good as in the other experiments probably due to the influence of non-hydrostatic stresses. Interestingly, during the experiment performed using ME as PTM, we noticed a significant and counterintuitive observation. Beyond 10 GPa, there are XRD reflections, particularly those with a Miller index where k ≠ 0, that evolve with pressure to lower angles. For instance, the arrows over the (011) and (111) reflections in Fig. 6b show this effect. This shift in diffraction peaks towards lower angles indicates an increase in interplanar spacing under sample compression, contrary to the usual observation of a pressure-induced decrease in interplanar spacing. This effect motivated us to repeat the experiment using different PTM to check if the observed phenomenon could be related to non-hydrostatic effects, which begin to develop in ME at 10 GPa.19 Therefore, we performed subsequent experiments using Ne, a quasi-hydrostatic PTM in the pressure range of experiments, and SilOil, a PTM where non-hydrostatic contributions develop beyond 4 GPa.19,45 These results confirmed the influence of non-hydrostatic stresses in the HP behaviour of PbV2O6. Fig. 6a shows that in the Ne experiment, all peaks move towards higher angles with increasing pressure. In contrast, in the SilOil experiment (Fig. 6c), the peaks move towards lower angles, as in the ME experiment (Fig. 6b). As explained below, the counterintuitive shift of the diffraction peaks with a Miller index of k ≠ 0 is due to an artificial expansion of the b-axis caused by the Poisson effect. This is consistent with the structural framework of the PbV2O6 crystal structure. Fig. 1 shows that the b-axis is the shortest of the three axes and that polyhedral chains are aligned along this axis. Consequently, the b-axis is expected to be the least compressible. Under non-hydrostatic conditions, the expansion of this axis is due to deviatoric stresses along the perpendicular directions.46
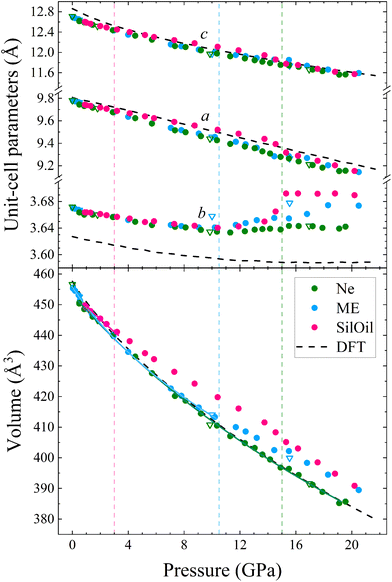
The unit-cell lattice parameters and volume of PbV2O6 were obtained from the XRD data of three experiments conducted from ambient conditions up to 20 GPa. The results are shown in Fig. 7 together with results from DFT calculations. These calculations agree with experiments at ambient pressure, with only a 1% underestimation of the parameter b. These data sets were used to compute the linear compressibility and the P–V equation of state (EOS) for the room-temperature isotherm. Fig. 7 clearly shows the effect of deviatoric stresses on the structure of PbV2O6. According to Ne experiments and DFT calculations the parameters a and c are considerably more compressible than the parameter b. In addition, there is a decrease of the compressibility of b at 15 GPa, with the slope becoming nearly zero beyond this pressure. In both ME and SilOil experiments, a change in the sign of the slope of the pressure dependence of the parameter b occurs at 10 GPa, with b increasing under compression for higher pressures. This phenomenon is more pronounced in the SilOil experiment. Additionally, in the SilOil experiment, the compressibility of the parameter a also decreases at 3 GPa, becoming smaller than the compressibility observed in the other two experiments. The pressure dependence of the volume reveals more noticeable changes, as the results from the SilOil (ME) experiment differ from those obtained from the Ne experiment and DFT simulations at 3.2(1) GPa. These pressures coincide with those where the two PTM become non-hydrostatic.19 This indicates that PbV2O6, and likely related compounds, is significantly affected by non-hydrostatic stresses.
To analyse the pressure dependence of the volume, we determined a P–V EOS using DFT calculations and data from each experiment conducted within the hydrostatic range of the PTM. We used a second-order Birch-Murnaghan EOS33 employing the EosFit7 software.47 The second order nature of the EOS was confirmed from the Eulerian strain-normalized pressure dependence of the data (see Fig. S1 in the ESI†).48 The EOS parameters are summarized in Table 1. Overall, the experimental and calculated results show exceptional agreement, particularly for the Ne run, in which the PbV2O6 bulk modulus was determined to be 86.1(9) GPa. Other published metavanadates exhibit significantly higher bulk moduli, including 188(5) GPa for MgV2O6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and 147(2) GPa for ZnV2O6,18 which crystallize in the brannerite-type structure. This difference may be connected to the fact that the Pb–O bonds, which are more compressible than the Mg–O and Zn–O bonds. These bonds are expected to dominate the volume change of the metavanadates.18 This hypothesis is consistent with the fact that the sequence of bulk moduli PbV2O6 < ZnV2O6 < MgV2O6 is the same as in the compounds PbO < ZnO < MgO.49–51
14 and 147(2) GPa for ZnV2O6,18 which crystallize in the brannerite-type structure. This difference may be connected to the fact that the Pb–O bonds, which are more compressible than the Mg–O and Zn–O bonds. These bonds are expected to dominate the volume change of the metavanadates.18 This hypothesis is consistent with the fact that the sequence of bulk moduli PbV2O6 < ZnV2O6 < MgV2O6 is the same as in the compounds PbO < ZnO < MgO.49–51
| PbV2O6 | V 0 (Å3) | B 0 (GPa) |
|---|---|---|
| Ne PTM up to 19.6(1) GPa | 453.4(5) | 86.1(9) |
| ME PTM up to 10.2(1) GPa | 454.7(4) | 85.6(16) |
| Silicon oil PTM up to 3.2(1) GPa | 454.1(4) | 98(5) |
| DFT calculations up to 21.7 GPa | 455.70(19) | 82.6(4) |
The linear isothermal compressibility for all crystallographic axes of the orthorhombic structure was obtained using the online PASCal tool.52 Data up to 1.5 GPa was used to guarantee hydrostatic conditions for all PTM used. The obtained linear compressibilities at 0 GPa are κa = 4.0(5) × 10−3 GPa−1, κb = 1.6(2) × 10−3 GPa−1 and κc = 8.0(7) × 10−3 GPa−1 according to the experiments and κa = 2.87(4) × 10−3 GPa−1, κb = 1.12(2) × 10−3 GPa−1 and κc = 8.20(7) × 10−3 GPa−1 from the DFT results. As expected, the b axis is less compressible than the other two unit-cell axes, showing a near zero linear compressibility, with is similar to that of diamond, 0.7 × 10−3 GPa−1,53 and comparable to that of Li2Ti(IO3)6, the record zero-linear compressibility material.54 This makes PbV2O6 an excellent candidate for shock-resistant and protection coatings for components of aviation working under extreme conditions.55
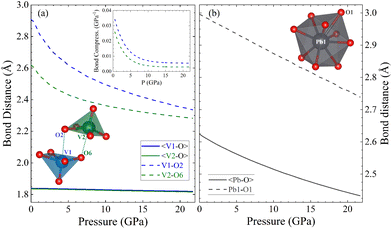
Since calculations show a good agreement with experiments results regarding the pressure dependence of unit-cell parameters and phonon frequencies, and Rietveld refinements could not be performed due to preferred orientations effects, we used the DFT calculated atom positions to analyse the evolution of the constituent polyhedra and corresponding bond lengths in the crystal structure under pressure. Such approach has been successfully used in the past for understanding related ternary oxides.56 To analyse the pressure-evolution of the polyhedral units, we compare the intermolecular V–O bond which connects neighbouring VO5 polyhedra (dashed line in Fig. 8) with the average V–O bond length within the VO5 unit, and the longest Pb–O bond of the PbO9 polyhedron with the average Pb–O bond length within the same polyhedron. The results are shown in Fig. 8. As shown in Fig. 8(a), the intermolecular V–O bonds (dashed lines) are highly compressible, with the average bond distance within the VO5 polyhedra remaining essentially unchanged under pressure. The second observation is consistent with the fact that V–O covalent bonds are highly incompressible.57 The first observation shows that the intermolecular V–O bond attains compressibilities comparable to that of covalent bonds between 5 and 10 GPa (see inset in Fig. 8(a)).58 The development of the sixth V–O bond is supported by the calculated electron-localization function shown in Fig. S2 in the ESI.† The determination of the nature of this bond requests the performance of crystal orbital Hamilton population calculations which is beyond the scope of this study. The formation of a sixth V–O bond leads to the conversion of all the VO5 pyramids into VO6 octahedra, thereby forming rigid columns of edge-sharing VO6 octahedra along the b-direction (see Fig. 1(b)). This rigid column of VO6 octahedra is what makes the b-axis incompressible beyond 15 GPa. Regarding the PbO9 polyhedron, we found that the longest Pb–O bond is equally as compressible as the others in the polyhedron (see Fig. 8(b)). Fig. 8 shows that the Pb–O bonds are much more compressible than the V–O bonds. In contrast, the long and weak sixth V–O bond is much more compressible up to 5 GPa, where the compressibility becomes similar to that of Pb–O bonds. The compressibility of the sixth V–O bond is shown in the inset of Fig. 8(a). At low-pressure, its values are comparable to the compressibility of weak halogen bonds.59 The pressure dependence of the long V–O bond resembles an exponential decay, with the compressibility becoming nearly identical to that of Pb–O bonds (4.5 × 10−3 GPa−1) around 5 GPa. This observation supports the idea that, under ambient conditions, vanadium atoms form rigid VO5 polyhedra which are linked to each other via weak secondary V–O bonds. The compressibility and behaviour of this bond support the formation of a sixth V–O bond at around 5 GPa. This phenomenon is consistent with the increase in signal of the Raman-active modes at similar pressures, which we believe it is related to the configurational changes of the coordination polyhedra of vanadium and behaviour of this bond support the formation of a sixth V–O bond at around 5 GPa. This phenomenon is consistent with the increase in signal of the Raman-active modes at similar pressures, which we believe it is related to the configurational changes of the coordination polyhedra of vanadium.
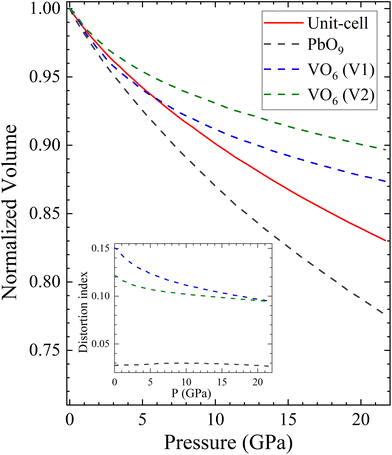
To conclude this section, we will use polyhedral compressibility to better understand pressure-induced changes in the volume. Fig. 9 shows the normalized volume of the unit-cell compared with the normalized volume of different polyhedra, with VO6 octahedra considered for all pressures. The figure indicates that the PbO9 polyhedra undergo the majority of the volume reduction, particularly from 5 GPa onwards. In addition, the PbO9 distortion index, calculated using the formula proposed by Baur,60 is shown in the inset of Fig. 9. It demonstrates that the shape of PbO9 polyhedra remains regular under compression. In contrast, the VO6 octahedra gain symmetry as pressure increases, despite being slightly compressible due to the decrease in the long V–O distance. This confirms the hypothesis that the compressibility of PbV2O6 is determined by the Pb polyhedron.
C. Band structure and band gap
In Fig. 10 we report the calculated band structure of PbV2O6 at 0 and 20 GPa and the corresponding electronic density of states. At 0 GPa, the valence band maximum is at the Γ-point of the Brillouin zone (BZ), which the conduction band has three nearly degenerate minima. The lowest is at the Y point of the BZ, and the other two are at Γ and T. The calculated band-gap energy is 1.98 eV, which underestimates the bandgap by 0.6 eV according to ref. 9, which is typical of the GGA when using the PBEsol functional. The electronic density of states indicates that the states at the top of the valence band mainly originate from the O 2p orbitals, with a non-negligible contribution of Pb 6s orbitals. The bottom of the conduction bands mainly consists of contributions from the V 3d and O 2p orbitals, with the V 3d orbital contributing the most. The contribution of Pb 6s states to the valence band explains why PbV2O6 has a bandgap 0.5 eV smaller than that of MgV2O6 and ZnV2O6,16,18 where the states near the Fermi level are only contributed to by the V 3d and O 2p orbitals. This behaviour has also been observed in other ternary oxides when Pb is the divalent cation instead of Cd, Zn, or an alkaline-earth metal.38–40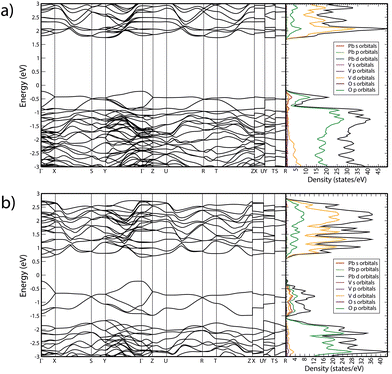 | ||
| Fig. 10 Calculated band structure and electronic density of states of PbV2O6 at (a) 0 GPa and (b) 20 GPa. | ||
As pressure increase, several changes are observed. Firstly, the bandgap closes, reaching a value of 0.88 eV at 20 GPa. This closure follows a linear dependence with pressure, with a slope −54 meV GPa−1. Additionally, there is a noticeable change in the topology of the band structure, which becomes more dispersive. Consequently, at 20 GPa, PbV2O6 becomes a direct gap material with the bandgap located at the Γ point of the BZ. At this pressure, the conduction band has two additional minima close in energy to the minimum at the Γ point, located at the T and Z points. The closing of the bandgap is due to the enhancement of the contribution of Pb 6s states to the top of the valence band, which is a distinctive feature of the presence of lead atoms. This contrasts with the behaviour of MgV2O6 and ZnV2O6,16,17 where the bandgap is determined by V 3d and O 2p states, and it is little affected by pressure. To conclude we would like to add that the closing of the band-gap predicted by DFT (and supported by the decrease of Raman signal) could not be confirmed by absorbance measurements because we have a powder sample, and such studies request single crystals. We hope our predictions will trigger the synthesis of PbV2O6 single crystal and the performance of HP optical-absorption experiments.
IV. Conclusions
The study investigated the structural and vibrational evolution of PbV2O6 under compression up to 20 GPa using synchrotron powder X-ray diffraction, Raman spectroscopy and density-functional theory simulations. The ambient pressure orthorhombic structure (space group Pnma) remained stable over the whole pressure range; however, it exhibited a zero-linear compressibility along the b-axis comparable to that of diamond. The study determined the wavenumbers and symmetries of 54 zone-centre Raman-active modes at ambient conditions, which were previously uncharacterized. Subsequently 48 of these modes were studied under compression in order to determine their respective pressure coefficients. HP angle dispersive powder XRD analysis was performed using three different PTM (Ne, ME, and SilOil) determined that PbV2O6 is highly affected by non-hydrostatic effects. The linear compressibility of each axis and EOS parameters, including bulk moduli, are reported. All experimental results were supported by DFT calculations, finding exceptional agreement among all sets of data. The DFT simulations also provide information on the pressure dependence of IR modes and the electronic band structure of PbV2O6, offering more insight into the behaviour of the vanadium–oxygen bond behaviour under pressure. An analysis of bond distances reveals that compression leads to a transformation of the coordination environment of vanadium. At approximately 5 GPa, a secondary intermolecular V–O bond is transformed into an intermolecular bond. This results in the conversion of the VO5 pyramids into edge sharing VO6 octahedra, which are aligned along the b axis. This phenomenon explains the exceptionally low compressibility observed in that crystallographic direction in PbV2O6. Finally, it was found that pressure causes a significant decrease in the band gap due. This is due to the contribution of Pb 6s states to the bottom of the conduction band.Author contributions
J. Sánchez-Martín and J. Pellicer-Porres were involved in the HP Raman experiments. J. Sánchez-Martín, R. Turnbull, D. Díaz-Anichtchenko, S. Anzellini, A. Liang, C. Popescu and D. Errandonea were involved in the HP XRD measurements. J. Sánchez-Martín, J. Pellicer-Porres, and D. Errandonea were involved in the data analysis. M. Bettinelli was involved in the sample synthesis. P. Rodríguez-Hernández and A. Muñoz were involved in the DFT calculations. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
All relevant data are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Spanish Research Agency (AEI) and Spanish Ministry of Science, Investigation, and Universities (MCIU) under grant PID2019-106383GB-41/43, PID2022-138076NB-C41/C44, MALTA Consolider Team Network (RED2022-134388-T) (https://doi.org/10.13039/501100011033). This work was also supported by the Generalitat Valenciana under Grant No. PROMETEO CIPROM/2021/075-GREENMAT and MFA/2022/007. This study forms part of the Advanced Materials program and is supported by MCIU with funding from European Union Next Generation EU (PRTR-C17.I1) and by the Generalitat Valenciana. J. S.-M. acknowledges the Spanish Ministry of Science, Innovation and Universities for the PRE2020-092198 fellowship. R. T. acknowledges funding from the Generalitat Valenciana for Postdoctoral Fellowship No. CIAPOS/2021/20. S. A. thanks the Generalitat Valenciana for the CIDEGENT Grant No. CIDEXG/2022/6. The authors thank ALBA synchrotron for providing beam time for the HP XRD experiments (Proposals 2021085226 and 2022085940).References
- P. Garnier and D. Weigel, J. Solid State Chem., 1983, 47, 16 CrossRef CAS.
- H. Müller-Buschbaum and M. Kobel, J. Alloys Compd., 1991, 176, 39 CrossRef.
- M. S. Islam, H. Kabir, Y. Inagaki and A. R. Sarker, J. Alloys Compd., 2020, 829, 154499 CrossRef CAS.
- J. P. Peña, P. Bouvier, M. Hneda, C. Goujon and O. Isnard, J. Phys. Chem. Solids, 2021, 154, 110034 CrossRef.
- M. Gondrand, A. Collomb, J. C. Joubert and R. D. Shannon, J. Solid State Chem., 1974, 11, 1 CrossRef CAS.
- G. M. Clark and A. N. Pick, J. Therm. Anal., 1975, 7, 289 CrossRef CAS.
- E. Agostinelli, P. Filaci, D. Fiokani, A. Montenero and M. Bettinelli, J. Non-Cryst. Solids, 1986, 84, 329 CrossRef CAS.
- S. S. Kalanur, Y. J. Lee and H. Seo, ACS Appl. Mater. Interfaces, 2021, 13, 25906 CrossRef CAS PubMed.
- B. D. Jordan and C. Calvo, Can. J. Chem., 1974, 52, 2701 CrossRef CAS.
- R. Turnbull, J. Sánchez-Martín, R. Oliva, J. Ibáñez, C. Popescu, P. Rodríguez-Hernández, A. Muñoz, G. Nénert, D. Vie and D. Errandonea, Phys. Rev. Mater., 2023, 7, 084606 CrossRef CAS.
- G. Calestani, G. D. Andreetti and A. Montenero, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 177 Search PubMed.
- G. Calestani, G. D. Andreetti and A. Montenero, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 179 CrossRef.
- Y. Li, R. Tang, N. Li, H. Li, X. Zhao, P. Zhu and X. Wang, J. Appl. Phys., 2015, 118, 035902 CrossRef.
- R. L. Tang, Y. Li, Q. Tao, N. N. Li, H. Li, D. D. Han, P. W. Zhu and X. Wang, Chin. Phys. B, 2013, 22, 066202 CrossRef.
- R. Tang, Y. Li, S. Xie, N. Li, J. Chen, C. Gao, P. Zhu and X. Wang, Sci. Rep., 2016, 6, 38566 CrossRef CAS PubMed.
- A. Beltrán, L. Gracia and J. Andrés, J. Phys. Chem. C, 2019, 123, 3239 CrossRef.
- D. Díaz-Anichtchenko, D. Santamaría-Perez, T. Marqueño, J. Pellicer-Porres, J. Ruiz-Fuertes, R. Ribes, J. Ibáñez, S. N. Achary, C. Popescu and D. Errandonea, J. Alloys Compd., 2020, 837, 155505 CrossRef.
- R. Tang, Y. Li, N. Li, D. Han, H. Li, Y. Zhao, C. Gao, P. Zhu and X. Wang, J. Phys. Chem. C, 2014, 118, 10560 CrossRef CAS.
- S. Klotz, J. C. Chervin, P. Munsch and G. Le Marchand, J. Phys. D: Appl. Phys., 2009, 42, 7 CrossRef.
- A. D. Chijioke, W. J. Nellis, A. Soldatov and I. F. Silvera, J. Appl. Phys., 2005, 98, 114905 CrossRef.
- D. J. Higham and N. J. Higham, MATLAB Guide, Siam, 2016 Search PubMed.
- F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360 CrossRef CAS.
- A. Dewaele, P. Loubeyre and M. Mezouar, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094112 CrossRef.
- C. Prescher and V. B. Prakapenka, High Pressure Res., 2015, 35, 223 CrossRef CAS.
- W. Kraus and G. Nolze, J. Appl. Crystallogr., 1996, 29, 301 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 86 CrossRef PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. E. Mattsson, R. Armiento, J. Paier, G. Kresse, J. M. Wills and T. R. Mattsson, J. Chem. Phys., 2008, 128, 084714 CrossRef PubMed.
- R. Armiento and A. E. Mattsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085108 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- F. Birch, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- E. Kroumova, M. I. Aroyo, J. M. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phil. Transit., 2003, 76, 155 CAS.
- J. Sánchez-Martín, J. Pellicer-Porres, A. Liang, J. Ibáñez, R. Oliva, C. Popescu, Z. He, P. Rodríguez-Hernández, A. Muñoz and D. Errandonea, J. Phys. Chem. C, 2023, 127, 21684 CrossRef PubMed.
- L. M. Uriarte, L. J. Bonales, J. Dubessy, A. Lobato, V. G. Baonza and M. Cáceres, Microchem. J., 2018, 139, 134 CrossRef CAS.
- D. Errandonea, E. Bandiello, A. Segura, J. J. Hamlin, M. B. Maple, P. Rodriguez-Hernandez and A. Muñoz, J. Alloys Compd., 2014, 587, 14 CrossRef CAS.
- V. Monteseguro, J. Ruiz-Fuertes, J. Contreras-García, P. Rodríguez-Hernández, A. Muñoz and D. Errandonea, Appl. Phys. Lett., 2019, 115, 012102 CrossRef.
- D. Errandonea, D. Martínez-García, R. Lacomba-Perales, J. Ruiz-Fuertes and A. Segura, Appl. Phys. Lett., 2006, 89, 091913 CrossRef.
- D. Errandonea, A. Muñoz and J. Gonzalez-Platas, J. Appl. Phys., 2014, 115, 216101 CrossRef.
- A. Le Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447 CrossRef CAS.
- Y. Zou and H. Zhang, J. Alloys Compd., 2019, 790, 164 CrossRef CAS.
- B. Kalkan, B. K. Godwal, J. Yan and R. Jeanloz, Phys. Rev. B, 2022, 105, 064111 CrossRef CAS.
- D. Errandonea, Y. Meng, M. Somayazulu and D. Häusermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 355, 116 CrossRef CAS.
- J. Zhao, R. J. Angel and N. L. Ross, J. Appl. Crystallogr., 2010, 43, 743 CrossRef CAS.
- J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49, 1377 CrossRef CAS.
- R. J. Angel, Rev. Mineral. Geochem., 2000, 41, 35 CrossRef.
- H. Giefers and F. Porsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 400, 53 CrossRef CAS.
- J. Shanker, S. S. Kushwah and P. Kumar, Phys. B, 1997, 233, 78 CrossRef CAS.
- C. Fan, Q. Wang, L. Li, S. Zhang, Y. Zhu, X. Zhang, M. Ma, R. Liu and W. Wang, Appl. Phys. Lett., 2008, 92, 101917 CrossRef.
- M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, JOSS, 2023, 8, 5556 CrossRef.
- F. Occelli, P. Loubeyre and R. Letoullec, Nat. Mater, 2003, 2, 151 CrossRef CAS PubMed.
- D. Jiang, T. Wen, H. Song, Z. Jiang, C. Li, K. Liu, W. Yang, H. K. Mao and Y. Wang, CCS Chem., 2022, 4, 3246 CrossRef CAS.
- N. C. Burtch, J. Heinen, T. D. Bennett, D. Dubbeldam and M. D. Allendorf, Adv. Mater., 2018, 30, 1704124 CrossRef PubMed.
- O. Gomis, B. Lavina, P. Rodríguez-Hernández, A. Muñoz, R. Errandonea, D. Errandonea and M. Bettinelli, J. Phys.: Condens. Matter, 2017, 29, 095401 CrossRef CAS PubMed.
- D. Errandonea and A. B. Garg, Prog. Mater. Sci., 2018, 97, 123 CrossRef CAS.
- I. Loa, A. Grzechnik, U. Schwarz, K. Syassen, M. Hanfland and R. K. Kremer, J. Alloys Compd., 2001, 317–318, 103–108 CrossRef CAS.
- A. Liang, R. Turnbull and D. Errandonea, Prog. Mater. Sci., 2023, 136, 101092 CrossRef CAS.
- W. H. Baur, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1195 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01321b |
| This journal is © The Royal Society of Chemistry 2024 |