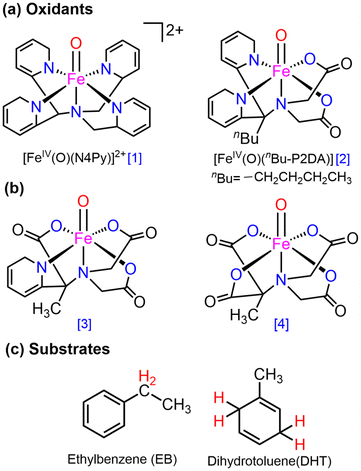
Open Access Article
Open Access ArticleImpact of carboxylate ligation on the C–H activation reactivity of a non-heme Fe(IV)O complex: a computational investigation†
Akanksha
Katoch
and
Debasish
Mandal
 *
*
Department of Chemistry and Biochemistry, Thapar Institute of Engineering and Technology, Patiala-147001, Punjab, India. E-mail: debasish.mandal@thapar.edu
First published on 26th August 2024
Abstract
A comprehensive DFT investigation has been presented to predict how a carboxylate-rich macrocycle would affect the reactivity of a non-heme Fe(IV)O complex towards C–H activation. The popular non-heme iron oxo complex [FeIV(O)(N4Py)]2+, (N4Py = N,N-(bis(2-pyridyl)methyl)N-bis(2-pyridylmethyl)amine) (1), has been selected here as the primary compound. It is transformed to the compound [FeIV(O)(nBu-P2DA)], where nBu-P2DA = N-(1′,1′-bis(2-pyridyl)pentyl)iminodiacetate (2) after the replacement of two pyridine donors of N4Py with carboxylate groups. Two other complexes, namely 3 and 4, have been predicted sequentially substituting nitrogen with the carboxylate groups. Ethylbenzene and dihydrotoluene were chosen as substrates. In terms of C–H activation reactivity, an interesting pattern emerges: as the carboxylate group becomes more equatorially enriched, the reactivity increases, following the trend 1 < 2 < 3 < 4. This also aligns with available experimental reports related to complexes 1 and 2. Fe(IV)O complexes exhibit two-state reactivity (triplet and quintet), whereas the quintet state is more favourable due to the stabilization of the transition states through exchange interactions involving a greater number of unpaired electrons. A detailed analysis of the factors influencing reactivity has been performed, including distortion energy (which decreases for the transition state with the addition of carboxylate groups), the triplet–quintet oxidant energy gap (which consistently decreases as carboxylate group enrichment increases), steric factors, and quantum mechanical tunneling. This investigation provides a detailed explanation of the observed outcomes and predicts the higher reactivity of carboxylate-enriched Fe(IV)O complexes. After potential experimental verification, this could lead to the development of new, optimal catalysts for C–H activation.
Introduction
Currently, synthetic iron(IV)-oxo complexes, which serve as bio-inspired models for active mononuclear non-heme iron enzymes, are gaining interest for their potential in catalyzing C–H activation reactions.1–9 These oxygen-activating metalloenzymes are involved in vital metabolic activities, toxin inactivation, DNA repair, and more. The structural and electronic characteristics of their metal-binding active sites are significantly influenced by relatively weak field carboxylate ligation which facilitates a diverse array of oxidative transformations.10–13 The 2-His-1-carboxylate facial triad14–18 has been mostly identified as the associated structural motif for the active sites of these enzymes such as (i) α-ketoglutarate (α-KG) dependent-taurine dioxygenase (TauD), (ii) 1-aminocyclopropane-1-carboxylic acid oxidases (ACCO), and (iii) phenylalanine hydroxylase (PheH), a pterin-dependent hydroxylase as presented in Fig. 1.19–31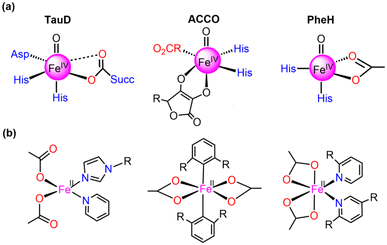 | ||
| Fig. 1 Structures of (a) 2-His-1-carboxylate facial triad superfamily of non-heme iron enzymes and (b) mononuclear Fe(II) carboxylate ligated complexes. | ||
Numerous mononuclear Fe(II) complexes linked with two carboxylate donors have also been extensively characterised (in Fig. 1).32–39 In line with this, McDonald et al.40 synthesized the macrocycle BuP2DA by substituting the two pyridine donors N4Py with carboxylate. They also demonstrated that the C–H activation reactivity of the Fe(IV)O–BuP2DA complex was found to be 6-fold larger than that of the N4Py counterpart. Several investigations have shown that enrichment with oxygen or sulfur donors in the macrocycle, in addition to carboxylate, increases the reactivity of Fe(IV)O compared to nitrogen.41,42 Que and co-workers43 reported that the reactivity of the Fe(IV)O unit is increased by the presence of a trans-carboxylate ligand in comparison to a neutral acetonitrile ligand. While considerable research has been dedicated to the mechanistic insights and reactivity of carboxylate-ligated Fe-oxo complexes,44 there remains a dearth of comprehensive investigations concerning other crucial reactivity-regulating factors, including steric, electronic, hydrogen tunneling, and so forth.
Here, the main objective is to ascertain whether carboxylate-substituted iron-oxo complexes may provide us with an improved C–H activation reactivity and how well these enhancements would occur sequentially. For this purpose, two alternative macrocyclic ligand frameworks were selected. In Fig. 2a, a non-heme iron oxo complex consisting of four nitrogen atoms and comprising the equatorially connected macrocyclic framework [FeIV(O)(N4Py)]2+, (N4Py = N,N-(bis(2-pyridyl)methyl)N-bis(2-pyridylmethyl)amine) (1), has been taken as a primary compound, as previously reported.40 By substituting two pyridine donors of the N4Py ligand with carboxylate ligands in the equatorial plane namely, [FeIV(O)(nBu-P2DA)], where nBu-P2DA = N-(1′,1′-bis(2-pyridyl)pentyl)iminodiacetate (2), the influence of carboxylate ligated substitution on reactivity catalysed by the HAT mechanism was investigated.40 Furthermore, this investigation has been broadened by incorporating derivative compounds (3 and 4, as illustrated in Fig. 2b), which are produced by successively substituting N with the carboxylate group.
As the source of the C–H bond, two distinct substrates, such as ethylbenzene (EB) and dihydrotoluene (DHT), are employed. Numerous potential factors could influence the reactivity such as the possible spin-state pathway, deformation energy to acquire the transition states, the triplet–quintet energy gap, and so forth, which have been extensively investigated. Quantum mechanical tunneling and the H/D kinetic isotope effect45,46 have also been examined in the context of carboxylate-ligated macrocycles.
Computational details
The DFT-B3LYP methodologies, which have been implemented in Gaussian 16,47 were utilised to perform all computations related to optimization, frequency, thermochemistry etc. The B3LYP functional developed by Lee–Yang–Parr is successfully employed in many organometallic reactions.48–58 The following basis sets are utilised here: (i) LANL2DZ59 basis and ECP for Fe and Pople's double zeta 6-31G*60 for all other atoms, which are conveniently termed B1 for the presentation. To validate the transition states, vibrational frequency calculations were performed; the presence of an imaginary frequency signifies the transition state, while the absence of such frequencies indicates minima. At 298 K (25 °C), the thermal and entropic corrections to the Gibbs free energy were carried out.Additional single-point calculations were accomplished to refine the energy using (ii) 6-311++G(2d,2p) for all atoms and SDD-ECP61 for Fe, classified as B2. The implicit impact of the solvent acetonitrile (CH3CN) was evaluated by utilisation of the self-consistent reaction field (SCRF)62 approach in conjunction with Truhlar's solvation model density approximation (SMD). Using the perchlorate (ClO4−) counterions, the systems’ overall positive charge was neutralised to resolve unwanted self-interaction problems in DFT.63 The determination of the percentage of concealed volumes and available capacity was accomplished by using the SambVca 2.1 software.64 With the aid of spin densities, Mulliken charges, and natural spin orbitals, the electronic state was precisely identified. The Chemcraft software was employed to perform image rendering, result depiction, and analysis.65 For the purpose of result discussion, zero-point corrected energy at the B2 level is predominantly used, unless otherwise specified.
Using the KiSThelP2019 software,66 the kinetic isotope effect (KIE) and quantum mechanical tunneling have been performed. Eqn (1) illustrates how the rate constants were calculated via Eyring's transition state theory.67
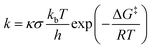 | (1) |
Here, the transmission coefficient and reaction symmetry are designated by κ and σ, respectively. A one-dimensional (1-D) asymmetric Eckart approach, which has become prevalent in a variety of transfer or migration of H-processes,45,46,68–70 was used to assess the tunneling. The subsequent equation generates the effect of the transmission coefficient on the barrier of activation.
ΔΔE‡tun = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ(T) κ(T) | (2) |
This equation denotes the quantitative reduction of an activation barrier resulting from tunneling (ΔΔE‡tun), the universal gas constant (R), and absolute temperature (T).
To prove quantum mechanical tunneling, all reactions’ (H/D) KIEs were determined. The KIE computations used the frequency of stationary states and their deuterium-replaced counterparts, calculated after tunneling influence using eqn (3).
| KIETC = (κH/κD)·KIEEY | (3) |
The transmission coefficients of hydrogen are symbolised by κH while its deuterated isotopomers are represented by κD. The tunneling contribution for a reaction can be contributed using the following eqn (4):71
| %tunneling = 100[(κEckart − 1)/κEckart] | (4) |
Furthermore, distortion energies have been evaluated for the transition state, defined by the following equation:
| ΔE‡dist = (E‡R + E‡S) − (ER − ES) | (5) |
The substrate and reactant equivalents are signified by S and R, in their structure of the transition state. Here, E(S) and E(R) are defined as the energies of the substrate and reactant in their undistorted state, whereas E‡(S) and E‡(R) are the single-point energies of the separated substrate and oxidant fragments in the transition state.
Results and discussion
Spin state preferences and two-state reactivity (TSR)
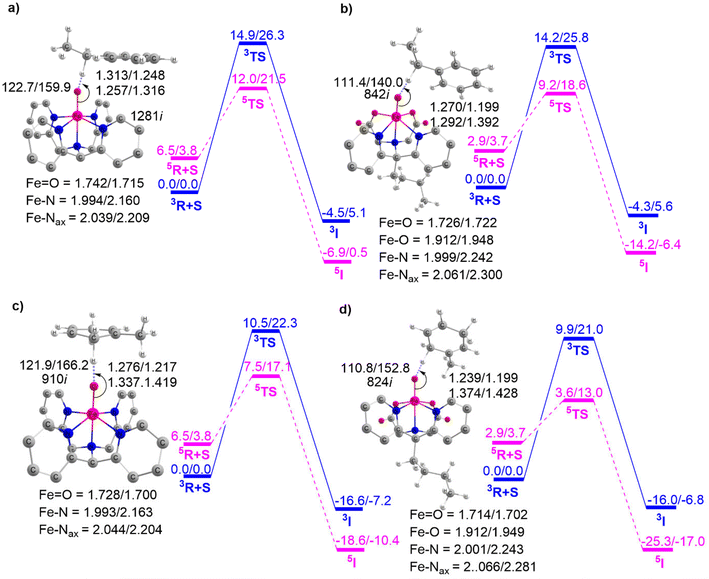
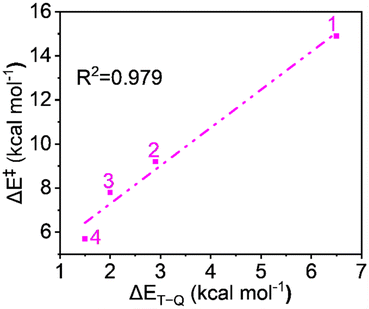
Complexes of Fe(IV)O may manifest two close-lying spin states: the triplet state (S = 1, two unpaired electrons) and quintet state (S = 2, four unpaired electrons). The same was observed in this study (Table S1†), with S = 1 representing the ground state and S = 2 implying the higher energy state. The ΔET–Q for complex 1 was 6.5 kcal mol−1, which was reduced to approximately 2.9, 2.0, and 1.5 kcal mol−1, in complexes 2, 3, and 4 respectively (in Fig. 3). This is expected because replacing a nitrogen-containing pyridine group with an oxygen-containing carboxylate group weakens the ligand field, making the high-spin state more accessible. As compared to the other Fe(IV)O complexes that exhibit the TSR,53 here, also ΔET–Q was found to be smaller, hence it may possess the ability to access the quintet state. Consequently, we have computed both triplet and quintet reaction pathways.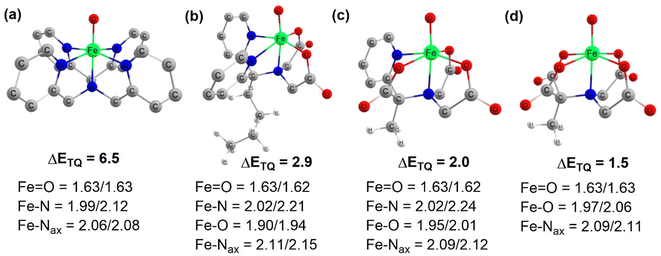 | ||
| Fig. 3 Optimized geometries with geometry parameters (distances are in Å), and ΔET–Q (in kcal mol−1) (a) 1 (b) 2 (c) 3 (d) 4 for both triplet/quintet spin states at the B1 level of theory. | ||
The sequential addition of carboxylate groups had minimal impact on the geometries of the oxidants, as illustrated in Fig. 3. There are no significant alterations in the parameters, as the bond lengths of the axially connected Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and Fe–Nax are nearly identical across all four oxidants.
O and Fe–Nax are nearly identical across all four oxidants.
Electron shift diagram
In the C–H activation reaction, the abstraction of hydrogen occurs with the movement of one electron from the substrate to the acceptor orbital, which may be either the anti-bonding orbital π* (for S = 1) or σ*z2 (S = 2) of the Fe(IV)oxo complex as presented in Fig. 4.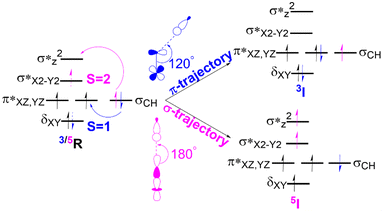 | ||
| Fig. 4 The electron transfer diagram for spin states S = 1 (blue) and S = 2 (pink) during hydrogen atom transfer facilitated by Fe(IV)O complexes. | ||
In the triplet state (S = 1), the π trajectory, with a Fe–O–H angle of about 120°, involves the transfer of a β-electron to the acceptor orbital (π*) of the Fe-oxo moiety (shown in blue). Conversely, in the quintet state (S = 2), the transfer of an α-electron via the σ route to the acceptor orbital (σ*z2) is depicted by the pink arrow, with a preferred Fe–O–H angle of around 180°. This study also follows the exchange-enhanced reactivity (EER)72 as the transition state on the quintet surface has lower energy than that on the triplet surface due to increased exchange interactions (the S = 2 transition state has more unpaired electrons than the S = 1 state). Consequently, during the reaction, the quintet state exhibits a more stable intermediate as it crosses the triplet state.
Reactivity analysis
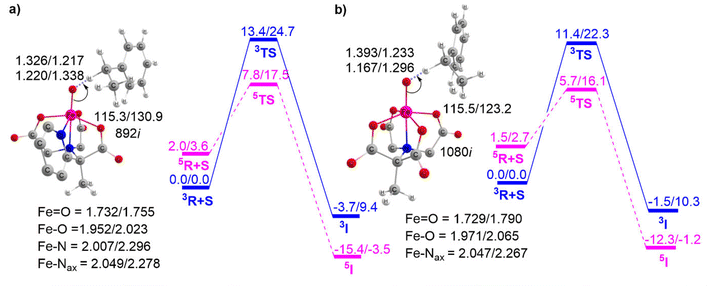
This section outlines the comparison of the HAT reactivity between complexes 1 and 2 with EB and DHT. The corresponding potential energy surface is presented in Fig. 5.As previously mentioned, the PES shows the TSR pattern for these Fe(IV)O complex-catalyzed HAT reactions. Fig. 5a and b indicate that the H-abstraction from EB catalyzed by complex 1 has an activation barrier of approximately 12.0 kcal mol−1. This value is considerably higher compared to the identical reaction catalyzed by complex 2, which has an activation barrier of 9.2 kcal mol−1. This clearly demonstrates that the Fe(IV)O complex BuP2DA ligand has a greater catalytic potential than the macrocycle N4Py. We then proceed to discuss Fig. 5c and d which provide the potential energy surface for the HAT reaction of complexes 1 and 2 with a different substrate DHT.
These figures again demonstrate the higher reactivity of BuP2DA over N4Py, regardless of the substrate. The activation barrier for DHT catalyzed by complex 1 is 7.5 kcal mol−1, while for complex 2 it is 3.6 kcal mol−1. Furthermore, the facts about the C–H activation reactivity concerning the substrate's bond dissociation energy (BDE) will also be amplified by the substrates EB and DHT. The C–H activation barriers of EB catalysed by complexes 1 and 2 are 12.0 and 9.2 kcal mol−1, respectively, which are significantly higher than the activation barrier of the same complexes with DHT 7.5 kcal mol−1 and 3.6 kcal mol−1. This finding is anticipated as EB has higher bond dissociation energy (85.4 kcal mol−1) compared to DHT (77 kcal mol−1).73,74 The computed BDE values for EB and DHT, 84.2 kcal mol−1 and 75.2 kcal mol−1, respectively, are also in close proximity to the previously reported experimental BDE values.
To further demonstrate the effect of sequential carboxylate ligation at the equatorial position, the potential energy surfaces for H-abstraction from EB catalyzed by complexes 3 and 4 are illustrated in Fig. 6.
Fig. 5 and 6 clearly show that enhancing carboxylate ligation at the equatorial position of the Fe(IV)O complexes provides the sequential reduction of the energy of activation. The corresponding pattern is as follows: 1 (12.0 kcal mol−1) < 2 (9.2 kcal mol−1) < 3 (7.8 kcal mol−1) < 4 (5.7 kcal mol−1). We can now investigate the factors that provide this new finding of increased C–H activation reactivity in carboxylate-ligated Fe-oxo complexes.
Steric factor
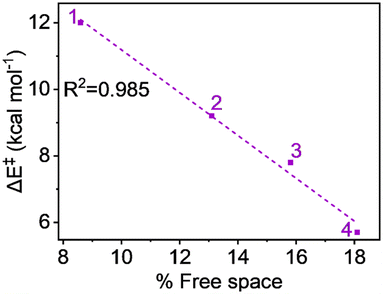
The free space related to the H-atom abstractor (Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) being accessible to the substrates is detailed in Table S3, available in the ESI.† The free space values—8.6%, 13.1%, 15.8%, and 18.1% for complexes 1, 2, 3, and 4, respectively—suggest that the sequential addition of ligand carboxylate groups at the equatorial position increases the accessibility of the abstractor to the substrate. Fig. 7's plot of activation energy against the percentage of free space shows a strong linear relationship, with an R2 value close to unity (0.985). This indicates with certainty that the steric factor can enhance reactivity in line with the increase in carboxylate groups.
O) being accessible to the substrates is detailed in Table S3, available in the ESI.† The free space values—8.6%, 13.1%, 15.8%, and 18.1% for complexes 1, 2, 3, and 4, respectively—suggest that the sequential addition of ligand carboxylate groups at the equatorial position increases the accessibility of the abstractor to the substrate. Fig. 7's plot of activation energy against the percentage of free space shows a strong linear relationship, with an R2 value close to unity (0.985). This indicates with certainty that the steric factor can enhance reactivity in line with the increase in carboxylate groups.
Distortion energy
Next, we analyse the distortion energy required to reach the transition states, as this significantly contributes to the activation energy. The corresponding values have been collected in Table 1.| Reaction | Spin states | ΔS | ΔO | ΔE‡dis |
|---|---|---|---|---|
| 1 + EB | S = 1 | 13.1 | 5.2 | 18.4 |
| S = 2 | 8.4 | 6.0 | 14.4 | |
| 2 + EB | S = 1 | 10.2 | 4.0 | 14.2 |
| S = 2 | 5.1 | 6.1 | 11.2 | |
| 3 + EB | S = 1 | 7.8 | 4.2 | 12.0 |
| S = 2 | 2.5 | 6.9 | 9.4 | |
| 4 + EB | S = 1 | 6.1 | 4.1 | 10.2 |
| S = 2 | 1.4 | 5.6 | 7.0 |
The values demonstrate that the distortion energy for complex 1 is 14.4 kcal mol−1 and it decreases sequentially for 2 (11.2 kcal mol−1), 3 (9.4 kcal mol−1), and 4 (7.0 kcal mol−1) complexes. Notably, the deformation energy of the oxidant is not significant, whereas the substrate distortion mainly contributes to the total distortion energy, decreasing progressively from complex 1 to complex 4. The distortion energy values also show an excellent correlation with the pattern of energy of activation of the reaction. The plot in Fig. 8 shows a remarkable linear correlation between the activation energy and distortion energy, with an R2 value close to unity. We can therefore conclude that the qualitative control of reactivity can be attributed to the distortion energy.
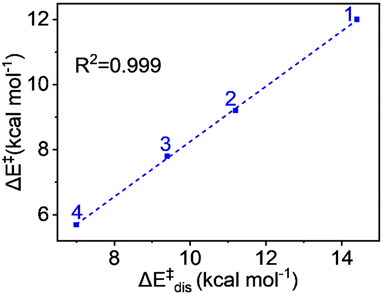 | ||
| Fig. 8 Plot of activation energy (ΔE‡) vs. distortion energy (ΔE‡dis) for the S = 2 pathway for all complexes. | ||
Electrophilicity of the central metal Fe
The hydrogen atom transfer mechanism essentially involves an electron transfer process from the substrate to the central metal ion. Therefore, it is appropriate to examine the atomic charge on Fe, as it directly reflects the electrophilicity of the metal within the ligand framework of complexes 1 to 4 and relates to the reaction barrier. The natural charges, computed using the NBO method, show a continuous increase with carboxylate ligation as follows: 0.841, 0.861, 0.884, and 0.894 from 1 to 4, respectively. This trend is logical because oxygen, being more electronegative than nitrogen, attracts more electron density from the metal. A plot of charge versus activation barrier, shown in Fig. 9, also provides a linear correlation, indicating that the metal's electrophilicity may control the reactivity.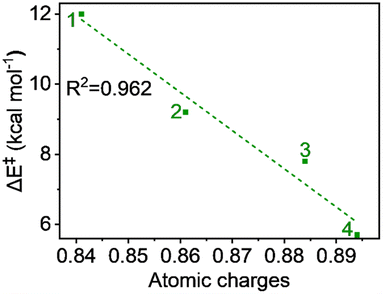 | ||
| Fig. 9 Plot of activation energy (ΔE‡) vs. atomic charges (in au) for the S = 2 pathway for all complexes. | ||
Triplet–quintet energy difference
Since the reaction follows the two-state reactivity (TSR) model, the spin inversion probability is significant and plays a crucial role in understanding surface crossing phenomena. The probability of spin inversion is influenced by the energy gap (ΔET–Q) between the S = 1 ground state and the S = 2 excited state oxidants. Smaller ΔET–Q values generally increase the probability of spin inversion because the spin states are closer in energy, making transitions more feasible. The outcome indicates that the ΔET–Q values continuously decrease from 1 to 4 due to carboxylate ligation as follows: 6.5, 2.9, 2.0, and 1.5 kcal mol−1 for 1 to 4, respectively, which facilitates a higher probability of spin inversion. Fig. 10 shows the plot of the energy of activation and the energy gap between spin states shows quite a linear correlation with R2 = 0.979, which supports the TSR model's prediction that the spin inversion probability increases with decreasing energy gaps, aligning with the observed data.From the aforementioned discussion, it is evident that all reactivity-controlling factors contribute to the increased reactivity of the carboxylate-rich complexes, providing a comprehensive explanation for the overall reactivity.
Quantum mechanical tunneling
As several studies42,45,46,55–58,75 have reported that hydrogen tunneling can be an important factor in metal-oxo-catalyzed C–H activation, we have conducted similar computations here, with the results presented in Table 2.| Reactions | Spin state | ν ‡H | κ H | κ D | KIEEck (298 K) | ΔΔE‡tun | ΔE‡/ΔG | (ΔE‡/ΔG) − ΔΔE‡tun | %Tunneling |
|---|---|---|---|---|---|---|---|---|---|
| a KIE in the parenthesis are computed at 313 K to compare with experiment.75 | |||||||||
| 1 + EB | S = 1 | 1832 | 154.27 | 12.17 | 66.0 (44)a | 3.0 | 14.9/26.3 | 11.9/23.3 | 98.5 |
| S = 2 | 1281 | 7.33 | 3.16 | 11.6 | 1.2 | 12.0/21.5 | 10.8/20.3 | 91.5 | |
| 2 + EB | S = 1 | 1571 | 22.57 | 5.23 | 22.4 | 1.8 | 14.2/25.8 | 12.4/24 | 95.6 |
| S = 2 | 842 | 2.16 | 1.74 | 4.6 | 0.5 | 9.2/18.6 | 8.7/18.1 | 78.3 | |
| 3 + EB | S = 1 | 1854 | 102.36 | 11.69 | 52.5 | 2.7 | 13.4/24.7 | 10.7/22 | 98.1 |
| S = 2 | 892 | 2.41 | 1.76 | 6.3 | 0.5 | 7.8/17.5 | 7.3/17 | 84.1 | |
| 4 + EB | S = 1 | 1801 | 67.14 | 10.06 | 46.1 | 2.5 | 11.4/22.3 | 8.9/19.8 | 97.8 |
| S = 2 | 1080 | 3.42 | 2.09 | 9.9 | 0.7 | 5.7/16.1 | 5/15.4 | 89.9 | |
| 1 + DHT | S = 1 | 1677 | 45.71 | 7.38 | 34.1 | 2.3 | 10.5/22.3 | 8.2/20 | 97.1 |
| S = 2 | 910 | 2.40 | 1.81 | 5.7 | 0.5 | 7.5/17.1 | 7/16.6 | 82.5 | |
| 2 + DHT | S = 1 | 1282 | 5.77 | 2.85 | 10.5 | 1.0 | 9.9/21.0 | 8.9/20 | 90.5 |
| S = 2 | 824 | 1.93 | 1.64 | 4.6 | 0.4 | 3.6/13.0 | 3.2/12.6 | 78.3 | |
The experimentally reported KIE (for 1 + EB) is approximately 45 at 313 K, which closely matches our calculated KIE (44) when considering the S = 1 pathway. It is important to note that the kinetic isotope effect can also indicate the reactive spin state,46,53,75 suggesting that the reaction of EB with 1 likely proceeds via the S = 1 state. Energetically, both pathways appear almost degenerate after tunneling correction (ΔE‡ = 11.9 and 10.8 kcal mol−1 for the S = 1 and S = 2 paths, respectively). This prediction is consistent with earlier research.46 For other reactions, we have no data for comparison, but the tunneling-corrected barrier for the S = 2 pathway appears significantly lower compared to the S = 1 pathway, suggesting that the reactive state is likely S = 2. Considering the tunneling-corrected activation energy (ΔE − ΔΔE‡tun) presented in column 8 of Table 2, it is clear that the reactivity pattern remains consistent with the classical trend as discussed earlier, regardless of the spin state considered for 1 + EB. The experimental observation of higher reactivity in complex 2 compared to complex 1 is also replicated here, along with a suitable explanation.
The % tunneling results in Table 2 also demonstrate a significant contribution of tunneling to the C–H activation reactivity facilitated by the Fe-oxo complexes. Notably, tunneling accounts for over 98% of the total reactions, except for 2 + EB and 2 + DHT, where it still accounts for over 78%.
Conclusion
Several significant conclusions can be drawn from this extensive DFT investigation, including insights into the C–H activation reactivity of the non-heme Fe(IV)O complex linked with a carboxylate-rich macrocycle. In this study, four Fe(IV)O oxidants were examined, starting with the macrocycle N4Py ligand and sequentially replacing pyridine groups with carboxylates to produce three additional oxidants. The complexes of oxidant 2, containing the nBu-P2DA macrocyclic ligand, were previously synthesized and exhibited higher reactivity than complex 1. Two more oxidants (3 and 4) were designed by further replacing pyridine with carboxylate groups.Regarding the C–H activation reactivity, a noteworthy pattern is observed: 1 < 2 < 3 < 4, indicating that reactivity increases with the addition of equatorially enriched carboxylate groups. These findings are in excellent agreement with available experimental results for complexes 1 and 2. Several important insights into this reactivity pattern were identified, including: spin inversion probability: accessibility of the S = 2 state decreases with carboxylate enrichment, free space for the abstractor: increases in carboxylate-rich macrocyclic complexes, deformation energies: consistently decrease from 1 to 4 and electrophilicity of the metal center. Hydrogen tunneling contributes in each case but does not significantly influence the observed reactivity pattern. This investigation establishes that enhancing the carboxylate content on C–H activation reactivity should encourage the bioinorganic community to synthesize more oxidants with carboxylate-rich ligated macrocyclic compounds.
Data availability
The data supporting this article has been included as part of the ESI.†Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Dr Mandal is very much grateful to the Department of Science and Technology, Government of India, for providing the INSPIRE Faculty Fellowship (DST/INSPIRE/04/2016/001948).References
- C. Krebs, D. G. Fujimori, C. T. Walsh and J. M. Bollinger, Acc. Chem. Res., 2007, 40, 484–492 CrossRef CAS PubMed.
- L. Que, Acc. Chem. Res., 2007, 40, 493–500 CrossRef CAS PubMed.
- W. Nam, Acc. Chem. Res., 2007, 40, 522–531 CrossRef CAS PubMed.
- D. C. Lacy, R. Gupta, K. L. Stone, J. Greaves, J. W. Ziller, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2010, 132, 12188–12190 CrossRef CAS PubMed.
- W. Nam, Y. M. Lee and S. Fukuzumi, Acc. Chem. Res., 2014, 47, 1146–1154 CrossRef CAS PubMed.
- W. N. Oloo and L. Que, Acc. Chem. Res., 2015, 48, 2612–2621 CrossRef CAS PubMed.
- A. S. Borovik, Chem. Soc. Rev., 2011, 40, 1870–1874 RSC.
- L. Ji, A. Franke, M. Brindell, M. Oszajca, A. Zahl and R. Van Eldik, Chem. – Eur. J., 2014, 20, 14437–14450 CrossRef CAS PubMed.
- X. Shan and L. Que, J. Inorg. Biochem., 2006, 100, 421–433 CrossRef CAS.
- R. H. Holm, P. Kennepohl and E. I. Solomon, Chem. Rev., 1996, 96, 2239–2314 CrossRef CAS PubMed.
- E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S.-K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y.-S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235–349 CrossRef CAS.
- M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986 CrossRef CAS PubMed.
- L. Que and R. Y. N. Ho, Chem. Rev., 1996, 96, 2607–2624 CrossRef CAS PubMed.
- E. L. Hegg and L. Que, Eur. J. Biochem., 1997, 250, 625–629 CrossRef CAS.
- L. Que, Nat. Struct. Biol., 2000, 7, 182–184 CrossRef CAS.
- K. D. Koehntop, J. P. Emerson and L. Que, J. Biol. Inorg. Chem., 2005, 10, 87–93 CrossRef CAS PubMed.
- P. C. A. Bruijnincx, G. van Koten and R. J. M. Klein Gebbink, Chem. Soc. Rev., 2008, 37, 2716–2744 RSC.
- S. Kal and L. Que, J. Biol. Inorg. Chem., 2017, 22, 339–365 CrossRef CAS PubMed.
- J. M. Bollinger Jr, J. C. Price, L. M. Hoffart, E. W. Barr and C. Krebs, Eur. J. Inorg. Chem., 2005, 4245–4254 CrossRef.
- J. M. Bollinger Jr and C. Krebs, J. Inorg. Biochem., 2006, 100, 586–605 CrossRef.
- J. N. Barlow, Z. Zhang, P. John, J. E. Baldwin and C. J. Schofield, Biochemistry, 1997, 36, 3563–3569 CrossRef CAS.
- G. Capitani, E. Hohenester, L. Feng, P. Storici, J. F. Kirsch and J. N. Jansonius, J. Mol. Biol., 1999, 294, 745–756 CrossRef CAS PubMed.
- O. A. Andersen, T. Flatmark and E. Hough, J. Mol. Biol., 2001, 34, 279–291 CrossRef PubMed.
- J. C. Price, E. W. Barr, B. Tirupati, J. M. Bollinger and C. Krebs, Biochemistry, 2003, 42, 7497–7508 CrossRef CAS.
- J. C. Price, E. W. Barr, T. E. Glass, C. Krebs and J. M. Bollinger, J. Am. Chem. Soc., 2003, 125, 13008–13009 CrossRef CAS PubMed.
- P. J. Riggs-Gelasco, J. C. Price, R. B. Guyer, J. H. Brehm, E. W. Barr, J. M. Bollinger and C. Krebs, J. Am. Chem. Soc., 2004, 126, 8108–8109 CrossRef CAS PubMed.
- J. C. Price, E. W. Barr, L. M. Hoffart, C. Krebs and J. M. Bollinger, Biochemistry, 2005, 44, 8138–8147 CrossRef CAS PubMed.
- S. Sinnecker, N. Svensen, E. W. Barr, S. Ye, J. M. Bollinger, F. Neese and C. Krebs, J. Am. Chem. Soc., 2007, 129, 6168–6179 CrossRef CAS PubMed.
- L. M. Hoffart, E. W. Barr, R. B. Guyer, J. M. Bollinger and C. Krebs, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14738–14743 CrossRef CAS PubMed.
- D. P. Galonic, E. W. Barr, C. T. Walsh, J. M. Bollinger and C. Krebs, Nat. Chem. Biol., 2007, 3, 113–116 CrossRef CAS PubMed.
- D. G. Fujimori, E. W. Barr, M. L. Matthews, G. M. Koch, J. R. Yonce, C. T. Walsh, J. M. Bollinger, C. Krebs and P. J. Riggs-Gelasco, J. Am. Chem. Soc., 2007, 129, 13408–13409 CrossRef CAS PubMed.
- J. R. Hagadorn, L. Que and W. B. Tolman, Inorg. Chem., 2000, 39, 6086–6090 CrossRef CAS PubMed.
- J. R. Hagadorn, L. Que and W. B. Tolman, J. Am. Chem. Soc., 1998, 120, 13531–13532 CrossRef CAS PubMed.
- J. R. Hagadorn, L. Que, W. B. Tolman, I. Prisecaru and E. Münck, J. Am. Chem. Soc., 1999, 121, 9760–9761 CrossRef CAS.
- A. Beck, B. Weibert and N. Burzlaff, Eur. J. Inorg. Chem., 2001, 521–527 CrossRef CAS.
- A. Beck, A. Barth, E. Hubner and N. Burzlaff, Inorg. Chem., 2003, 42, 7182–7188 CrossRef CAS PubMed.
- S. J. Friese, B. E. Kucera, L. Que and W. B. Tolman, Inorg. Chem., 2006, 45, 8003–8005 CrossRef CAS PubMed.
- P. C. A. Bruijnincx, M. Lutz, A. L. Spek, W. R. Hagen, B. M. Weckhuysen, G. Van Koten and R. J. M. K. Gebbink, J. Am. Chem. Soc., 2007, 129, 2275–2286 CrossRef CAS PubMed.
- S. Friedle, E. Reisner and S. J. Lippard, Chem. Soc. Rev., 2010, 39, 2768–2779 RSC.
- A. R. McDonald, Y. Guo, V. V. Vu, E. L. Bominaar, E. Münck and L. Que, Chem. Sci., 2012, 3, 1680–1693 RSC.
- I. Monte-Pérez, X. Engelmann, Y. M. Lee, M. Yoo, E. Kumaran, E. R. Farquhar, E. Bill, J. England, W. Nam, M. Swart and K. Ray, Angew. Chem., Int. Ed., 2017, 56, 14384–14388 CrossRef PubMed.
- L. Kaur and D. Mandal, Dalton Trans., 2024, 53, 7527–7535 RSC.
- J. U. Rohde and L. Que, Angew. Chem., Int. Ed., 2005, 44, 2255–2258 CrossRef CAS PubMed.
- P. J. Cappillino, J. S. McNally, F. Wang and J. P. Caradonna, J. Chem. Soc., Dalton Trans., 2012, 41, 474–483 RSC.
- D. Mandal, R. Ramanan, D. Usharani, D. Janardanan, B. Wang and S. Shaik, J. Am. Chem. Soc., 2015, 137, 722–733 CrossRef CAS PubMed.
- D. Mandal and S. Shaik, J. Am. Chem. Soc., 2016, 138, 2094–2097 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, E. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. Altun, J. Breidung, F. Neese and W. Thiel, J. Chem. Theory Comput., 2014, 10, 3807–3820 CrossRef CAS PubMed.
- Y. Cao, J. A. Valdez-Moreira, S. Hay, J. M. Smith and S. P. de Visser, Chem. – Eur. J., 2023, 29, e202302832 CrossRef PubMed.
- K. Bleher, P. Comba, D. Kass, K. Ray and H. Wadepohl, J. Inorg. Biochem., 2023, 241, 112123 CrossRef CAS PubMed.
- D. Mandal, D. Mallick and S. Shaik, Acc. Chem. Res., 2018, 51, 107–117 CrossRef CAS PubMed.
- C. Wegeberg, M. L. Skavenborg, A. Liberato, J. N. McPherson, W. R. Browne, E. D. Hedegård and C. J. McKenzie, Inorg. Chem., 2021, 60, 1975–1984 CrossRef CAS PubMed.
- A. Katoch and D. Mandal, Dalton Trans., 2022, 51, 11641–11649 RSC.
- A. Katoch and D. Mandal, Dalton Trans., 2024, 53, 2386–2394 RSC.
- L. Kaur and D. Mandal, Inorg. Chem., 2022, 61, 14582–14590 CrossRef CAS PubMed.
- L. Kaur and D. Mandal, Dalton Trans., 2024, 53, 7527–7535 RSC.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923 CrossRef CAS.
- P. Fuentealba, H. Preuss, H. Stoll and L. Von Szentpály, Chem. Phys. Lett., 1982, 89, 418–422 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- D. Janardanan, D. Usharani, H. Chen and S. Shaik, J. Phys. Chem. Lett., 2011, 2, 2610–2617 CrossRef CAS.
- L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872–879 CrossRef CAS PubMed.
- R. A. Massoud and M. A. Makhyoun, J. Struct. Chem., 2019, 60, 882–889 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 63–71 CrossRef.
- D. K. Maity, R. L. Bell and T. N. Truong, J. Am. Chem. Soc., 2000, 122, 897–906 CrossRef CAS.
- F. Zhang and T. S. Dibble, Phys. Chem. Chem. Phys., 2011, 13, 17969–17977 RSC.
- A. G. Vandeputte, M. K. Sabbe, M. F. Reyniers, V. Van Speybroeck, M. Waroquier and G. B. Marin, J. Phys. Chem. A, 2007, 111, 11771–11786 CrossRef CAS PubMed.
- L. Cheng, C. Doubleday and R. Breslow, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4218–4220 CrossRef CAS PubMed.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS PubMed.
- Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, Taylor & Francis, Boca Raton, 2007 Search PubMed.
- A. Barbieri, O. Lanzalunga, A. Lapi and S. Di Stefano, J. Org. Chem., 2019, 84, 13549–13556 CrossRef CAS PubMed.
- E. J. Klinker, Ph.D. Dissertation. Department of Chemistry, University of Minnesota, Minneapolis, MN, 2007.
Footnote |
| † Electronic supplementary information (ESI) available: Relative energy table, bond dissociation energies, calculated %free space data, spin natural orbitals, Mulliken spin and charges, optimized Cartesian coordinates for all the species are available in the ESI. See DOI: https://doi.org/10.1039/d4dt02139h |
| This journal is © The Royal Society of Chemistry 2024 |