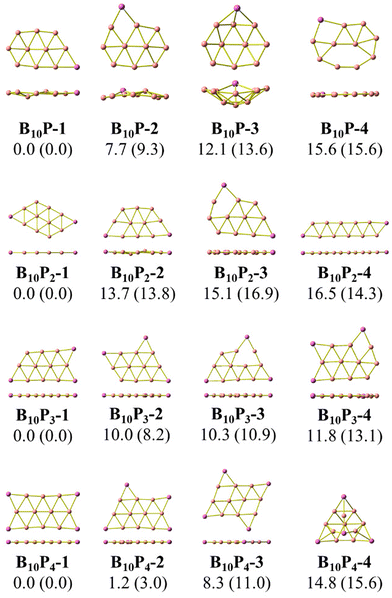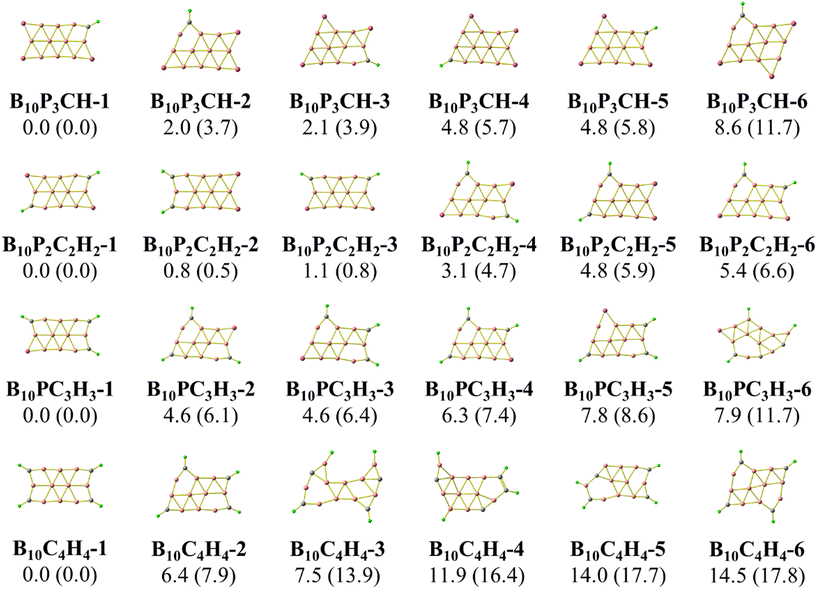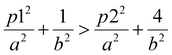Open Access Article
Open Access ArticleTriple-chain boron clusters: lengthening via phosphorus doping and enhancing stability through {P} by {CH} substitution†
Long Van
Duong
 ab,
Nguyen Minh
Tam
ab,
Nguyen Minh
Tam
 c,
Amir
Karton
c,
Amir
Karton
 *d and
Minh Tho
Nguyen
*d and
Minh Tho
Nguyen
 *be
*be
aAtomic Molecular and Optical Physics Research Group, Science and Technology Advanced Institute, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: duongvanlong@vlu.edu.vn
bFaculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
cFaculty of Basic Sciences, University of Phan Thiet, 225 Nguyen Thong, Phan Thiet City, Binh Thuan, Vietnam
dSchool of Science and Technology, University of New England, Armidale, NSW 2351, Australia. E-mail: amir.karton@une.edu.au
eLaboratory for Chemical Computation and Modeling, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: minhtho.nguyen@vlu.edu.vn
First published on 18th October 2024
Abstract
This theoretical study presents novel insights into the doping of boron clusters with an increasing number of dopant atoms, ranging from 1 to 4, that preserve the integrity of the original boron framework. The triple-chain forms of clusters B10 and B16 remain unchanged upon sequential addition of P atoms, showcasing a perfect isolobal substitution of {P} with {CH}. Similarities in the number of delocalized electrons are observed between pure and doped boron clusters, alongside the subsequent substitution of {P} with {CH}. All triple-chain structures exhibit high thermodynamic stability, having low vertical attachment energies and high vertical ionization energies. The lowest-lying isomer of B16P4 has thus a triple-chain shape instead of a tetrahedral Td form as previously reported. While AdNDP analysis confirms the number of globally delocalized electrons, it differs much from a previous interpretation. The magnetic ring current maps support the double aromaticity of triple-chain structures. Electron counting rules established for triple-chain structures are verified. The particle-in-a-rectangular-box model elucidates the relationship between the structure size and electron configuration and aids in understanding the transition from antiaromatic to aromatic configurations. The self-locking phenomenon is crucial for adhering to the triple-chain model and satisfying electron configuration requirements.
1. Introduction
The field of nanocluster science has continuously developed over the past few decades, and the growth mechanisms of the clusters of several elements have gradually emerged. Of the atomic clusters investigated, those formed by the boron atom exhibit the most diverse and non-conventional structural motifs and unpredictable geometry transformations following a small change in the size, net charge, and doping.1 In a series of small pure clusters, going from B3 to B19, they are either planar or quasi-planar (2D)2,3 with a fullerene-like intercalation of the size of B14.4 The size of B20 is renowned for its double ring (DR) tubular structure;5 after which the Bn class returns to the quasi-planar B21 class.6 At larger sizes, there is still an alternating occurrence of the global minima between 2D and 3D structures.7–12 Due to such a geometric diversity of boron clusters, various models of electronic structures have been proposed to rationalize their thermodynamic stability, and in particular their aromatic nature which in part governs their stability. Boron clusters appear to challenge the classical models of chemical bonding, requiring the introduction of numerous new electron count models that also necessitate a redefinition of the aromaticity concept.13,14For small size clusters, the classical Hückel rule proves effective for most planar and quasi-planar structures.15,16 However, for circular structures such as the anion B19−,17,18 or the dianion B202−,19 the Hückel model becomes inadequate; in fact, it failed to rationalize their aromatic character. Instead, the disk aromaticity model19–21 has proved to be more appropriate for the circular disk and even generalizable for a larger class of planar and bowl structures.
Instead of using the 2(N + 1)2 electron count of the Hirsch rule22 or the phenomenological shell model (PSM),23 the hollow cylinder model24,25 provides us with a better understanding of the electronic configuration in tubular structures, especially when the tubes are formed from multiple atomic rings, making the electron picture more evident.21
The ribbon or double-chain motif26–29 has emerged as a distinctive form due to its two boron chains, but because of impurities, often in a negatively charged state, it can now be extended up to a length of 17.0 Å.29 The ribbon model30,31 has subsequently been used to rationalize the aromaticity of ribbon-like structures without necessarily requiring cyclic electron delocalization13 in the structure. Surpassing mass spectrometry experiments for investigating boron ribbons in an anionic state,27 the boron ribbon cluster B2C4H4 was synthesized in a neutral state upon substitution of H atoms with appropriate ligands.32
The structures formed from three boron chains33 are less commonly found, and the electron counting rule of [σ2(n+1)π12(n+1)π22n] was established for rationalizing their aromaticity.34Scheme 1 presents two dianionic structures, B102− and B162−, which represent the triple-chain motif best. The electron configuration of B162− satisfies the [σ2(n+1)π12(n+1)π22n] counting rule with n = 2. Scheme 1 also illustrates the global minima of the anionic and neutral B10−/0 and B16−/0,2,35–37 whose shapes involve a slight geometric deformation from a perfect planarity of the corresponding dianions B102− and B162−, respectively. In this context, a question of interest is whether it is possible to extend the size of boron triple-chain clusters by means of doping. Following multiple attempts to introduce various impurities to the latter, we find that the phosphorus element becomes both a neutralizing impurity and an extending agent. As a matter of fact, the incorporation of P atoms into the above dianionic species not only neutralizes the dianions but also extends the triple-chain form of the resulting B10P4 and B16P4 systems. A similar picture for the evolution of the structural motif of the BxPy clusters remains valid in the isovalent analogues in which each {P} atom is replaced by a {CH} unit (both entities having 5 valence electrons each). The substitution of {P} with {CH} ultimately leads to carborane structures that offer more practical opportunities for synthesis.
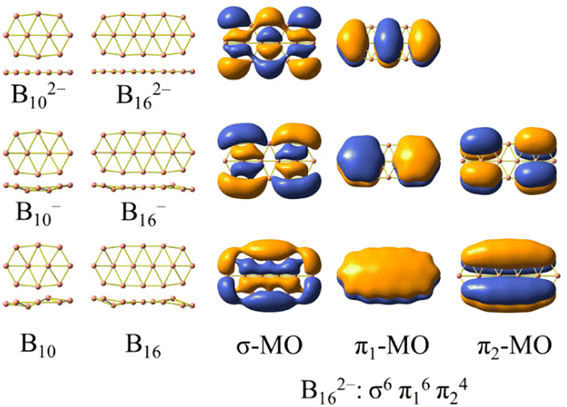 | ||
| Scheme 1 Global minima of boron clusters B102−/−/0 and B162−/−/0 and the electronic configuration of the planar dianion B162− including six σ and ten π orbitals. | ||
The account presented in the next sections aims to contribute to a demonstration of the validity of the [σ2(n+1)π12(n+1)π22n] electron counting rule for this class of triple-chain compounds. Our calculated results point out that the inherent electronic distribution, and thereby the corresponding aromatic character, favours the planar triple-chain form that emerges to be thermodynamically more stable than the more symmetrical tetrahedron or other three-dimensional isomers. This is particularly related to a recent theoretical study which reported that the tetrahedron is the lowest-lying isomer of the B16P4 cluster system.38 In contrast, our results show that the most stable B16P4 isomer exhibits a perfect planar triple-chain geometry.
2. Computational methods
Isomers of each of the clusters considered in this theoretical study were located following full geometry optimizations of over 1000 different initial geometries. These initial geometries were generated using a stochastic search algorithm39 and a genetic algorithm (GA)40 that was implemented by our group.8 Geometries of the initial guess structures were optimized using density functional theory (DFT) with the PBE41 functional, which has recently been benchmarked and found to be suitable for examining the relative energies of clusters containing multiple B atoms,42 and the 6-31G(d)43,44 basis set without subsequent vibrational frequency calculations. The set of isomers with relative energies within 3 eV with respect to the most stable structure is referred to as the seed structure ensemble. Each isomer in the seed structure ensemble was used to generate a series of input for optimization via both the stochastic search algorithm39 and the genetic algorithm (GA).40 After optimizations, the new set of output generated was evaluated to determine whether they belong to the seed structure ensemble. This iterative process continued until no new seed structures were identified.The optimized structures whose total energies were within ∼3 eV from the most stable geometry (the final seed structure ensemble) were then reoptimized using the same PBE functional but with a larger 6-311+G(d)43,44 basis set, along with vibrational frequency calculations in order to ensure the true local minimum character. Zero-point vibrational energy corrections were obtained from the harmonic frequencies without scaling. To identify the global minimum of each system, the electronic energies of a set of ten lowest-lying isomers were subsequently computed using single-point coupled-cluster theory CCSD(T)/6-311+G(d) calculations making use of the PBE/6-311+G(d) optimized geometries. Unrestricted Hartree–Fock (UHF) formalism was used for open-shell systems. All electronic structure calculations were performed using the Gaussian 16 software suite.45
The adaptive natural density partitioning (AdNDP) algorithm,46 as implemented in the Multiwfn software,47 was used to probe the number of globally delocalized electrons. The chemical bonding and aromatic character were assessed through the electron localization function (ELF) maps48,49 using the Dgrid 5.0 package.50
Topological analysis of the electron localization function (ELF) map indicates that a structure with a high bifurcation value on the ELF isosurface displays aromatic characteristics, while that with a low bifurcation value does not exhibit aromaticity. A planar molecule often has aromaticity based on the behavior of its π and σ electrons. Santos et al. demonstrated that ELFπ and ELFσ maps can help classify the aromaticity of these electron types.51 In certain specific cases, σ electrons can distinctly be categorized into localized σ electrons and delocalized σ electrons. At this point, the separation of ELFσ into ELFσl (for localized σ electrons) and ELFσd (for delocalized σ electrons) further clarifies the impact of each electron type on the properties and stability of the structure considered.30,52
Maps of the magnetic current density induced by a perpendicular magnetic field to the planar structure were calculated and visualized using the SYSMOIC53 program; current flows were utilized to indicate the diatropic (clockwise) or paratropic (counterclockwise) nature of the ring current.
3. Results and discussion
3.1. BxPy systems
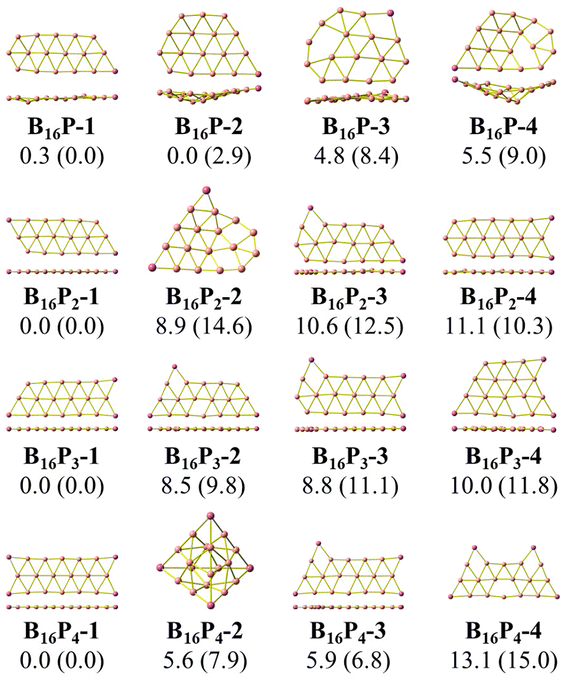
As stated above, we use phosphorus atoms as dopants in two boron systems displayed in Scheme 1. Four phosphorus atoms are thus successively added into the B10 and B16 skeletons. The lowest-lying isomers of the resulting B10Py and B16Py with y = 1, 2, 3 and 4 are presented in Fig. 1 and 2. The relative energy ordering of isomers at 0 K established by (U)CCSD(T) calculations and corrected for zero-point energies (ZPEs) are marked by the labels having increasing numbers of 1, 2, 3, etc…Fig. 1 and 2 illustrate two prominent trends when phosphorus atoms are added into the boron triple-chain structures. Firstly, P atoms are preferentially attached to positions 1, 2, 3 and 4 of four B–B bonds at both ends of the structures, as marked in Scheme 2. The next preferred positions are the B–B bonds denoted as 5, 6, 7 and 8 on the outermost of the two outer B rows.
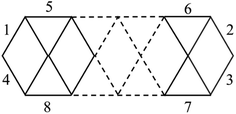 | ||
| Scheme 2 Identification of the preferred binding sites of P atoms into the B–B bonds of the B10+6n triple-chain framework. | ||
The second trend is a rapid flattening of the triple-chain structure following doping, where, upon the second P atom addition, the triple-chain form already becomes perfectly planar, and such a perfect planarity is maintained following doping with the 3rd and 4th P atoms. This is particularly intriguing as it basically differs from a typical observation on boron cluster doping which tends to favour 3D isomers. A recent study conducted by Jin et al.54 reported that the doping of an aluminium atom into the B10 size leads to the most stable 3D isomer in which the Al atom is positioned on the surface of a triple-chain structure, while subsequent lower-lying isomers of AlB10 do not feature any triple-chain framework. Similarly, stable isomers of AlB16 also do not have any triple-chain skeleton.54 A previous study by Mai and co-workers55 indicated that the silicon counterpart of B10P-3 (Fig. 1) is the global minimum of the SiB10 cluster in which the Si atom is attached to one long edge of the triple-chain structure, while the triple-chain framework is not even present in higher-energy isomers. A subsequent study by Mai and co-workers56 also demonstrated that SiB16 has a second lowest-lying isomer in which the Si atom lies in the plane of a triple-chain B16, while the global minimum and other isomers lack a triple-chain skeleton.
With our current knowledge, no previous observation was reported on the doping effect of an element, excluding H, halogens and noble gases, into a small-sized boron cluster whose resulting doped structure retains the original pure boron framework by up to four dopant atoms. The 3D structure that appeared in B10P4 is B10P4-4 which is 14.8 kcal mol−1 higher in energy than the global minimum B10P4-1. In the case of B16P4, the 3D structure bearing the form of a Td tetrahedron B16P4-2 is only 5.6 kcal mol−1 higher than B16P4-1.
The Td tetrahedron P4 is well known for its superior thermodynamic stability,57 which is believed to result from its electron shell satisfying the doubly spherically aromatic count of 2(N + 1)2 with 18σ and 2π electrons.58 Thus, insertion of a B16 unit into the tetrahedral P4 forming the B16P4-2 isomer is highly noteworthy. The existence of both B16P4-1 and B16P4-2 has been recently reported by Gao et al.38 In their study, DFT computations using the PBE0 functional suggested that B16P4-2 (Td) is more stable than B16P4-1, despite the results from TPSSh, or more importantly, CCSD(T) indicates a reversed energy ordering.
In the present study, we find agreement in the energy ordering between the PBE functional and CCSD(T) results, indicating that in the neutral state B16P4-1 is more stable than B16P4-2. Based on PBE functional calculations, B16P4-1 is more stable than B16P4-2 by 27 kcal mol−1 in the anionic state. Consequently, it is more likely that the B16P4-1 can experimentally be detected.
Our present result disagrees with a previous report by Gao et al.,38 which concluded that the Td structure of B16P4-2 is the most stable isomer. These authors38 also relied on the adaptive natural density partitioning (AdNDP) analysis to explain the stability of B16P4-2. In addition, the low-lying B16P4-3 and B16P4-4 isomers were missed in their study. To have another look at these conflicting results, we replicate the analysis made in ref. 38, the details of which are given in the ESI file.†
3.2. BxPyCzHz systems
The concept of “isolobal analogy”, meaning “similar lobes”, developed by Hoffmann59 proved to be helpful in designing novel molecules based on stable molecular structures, and numerous molecules have been discovered using this approach.60,61 Considering the fact that a {P} atom is not only isovalent but also isolobal to a {CH} fragment, we now carry out a sequential substitution of {P} atoms by {CH} units, and the corresponding lowest-lying isomers are presented in Fig. 3 and 4. Furthermore, in the anionic state, the triple chain of BxPyCzHz retains the global minima, as illustrated in Fig. S2 and S3 (ESI file†).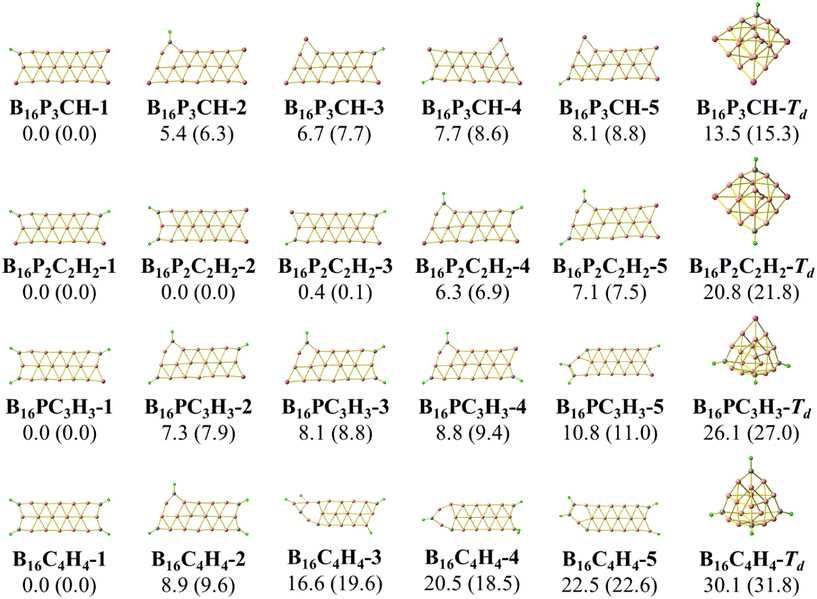 | ||
| Fig. 4 Optimized geometries of the lowest-lying B16PyCzHz isomers with y = 3, 2, 1 and 0, and z = 4 − y. Relative energies, given in kcal mol−1, are obtained from PBE/6-311+G(d) + ZPE computations. | ||
Calculated results indicate the emergence of several stable isomers with a close relative energy (RE) as a consequence of the multiple permutations of positions between {P} and {CH}. The 1-4-isomer is the isomer with {P} or {CH} bonds at the 1, 2, 3 and 4 positions as shown in Scheme 2, and the 5-(2-4)-isomer is that with {P} or {CH} bonds at the 2, 3, 4 and 5 positions. Even more interestingly, we observe a gradual increase in the RE of the most stable isomer (1-4-isomer) as compared to the 5-(2-4)-isomer. This RE increases from 3.0 to 7.9 kcal mol−1 going from B10P4 to B10C4H4. From B16P4 to B16C4H4, the RE increases from 6.8 to 9.6 kcal mol−1, and eventually the triple-chain B16C4H4-1 exhibits a higher likelihood for experimental synthesis with a minimal occurrence of other isomers. The recent synthesis of the ribbon-like carborane B4C2R4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 constitutes a stimulation for a promising generation of these triple-chain carboranes BxC4H4, which in turn could facilitate the synthesis of BxPyCzHz structures in a reversed manner.
32 constitutes a stimulation for a promising generation of these triple-chain carboranes BxC4H4, which in turn could facilitate the synthesis of BxPyCzHz structures in a reversed manner.
The isomers derived from the Td structure of B16PxCyHy presented in Fig. 4 emphasize a rapid increase in the REs between both triple-chain and Td forms when {P} is sequentially substituted by {CH}. This is analogous to the transition from the 3D to the 2D form observed in the tetrahedral P4 when {P} is successively replaced by {CH} forming C4H4.62,63
3.3. Stability trend
The vertical attachment energy (VAE) and the vertical ionization energy (VIE) are defined as:| VAE = E(X0) − E(X−) | (1) |
| VIE = E(X0) − E(X+) | (2) |
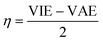 | (3) |
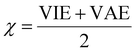 | (4) |
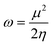 | (5) |
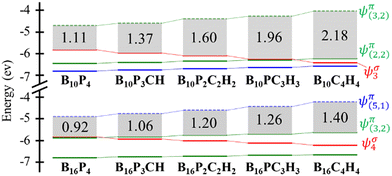
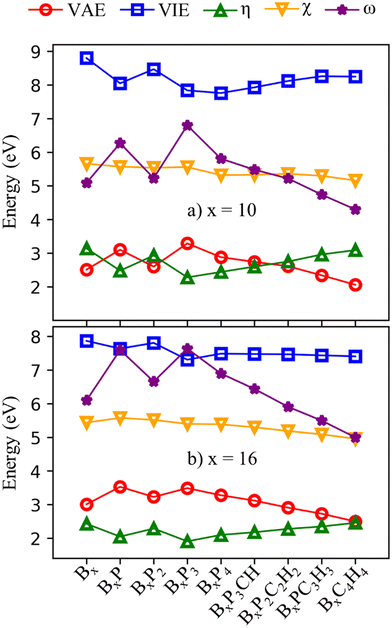
The frontier orbital HOMO–LUMO gaps (HLGs) of BxPyCzHz are presented in Fig. 5, whereas the VAE, VIE, η, χ and ω values are plotted in the graphs shown in Fig. 6, and given in Tables S1 and S2 of the ESI file.†
The HLG and η values point toward increasing structural stability as their values increase, whereas ω indicates that stability increases as its values fall. A high VIE suggests that the structure tightly holds its electrons, whereas a low VAE indicates a stabilized neutral state. Therefore, a high VIE and low VAE values show the stability of a structure in its neutral state. Overall, while the HLG, VAE and η values of B16PyCzHz are lower than those of B10PyCzHz, VIE and ω of B16PyCzHz are higher than that of B10PyCzHz; B10PyCzHz thus have greater stabilization as compared to B16PyCzHz.
Initially, when P is doped into Bx, the values of HLG, VAE, VIP, η and ω vary according to parity; closed-shell systems are more kinetically stable than their open-shell counterparts. Considering only the closed-shell systems, their stability decreases upon P addition: Bx is more stabilized than BxP2, and BxP2 is more stable than BxP4. Subsequently, the replacement of {P} with {CH} leads to the opposite effect: the more {P} is replaced by {CH}, the more stable the structure becomes.
The electronegativity (χ) of a molecule refers to its ability to attract electrons towards itself. The electronegativity of structures considered here exhibits less variability as compared to the aforementioned parameters with the lowest value being 5.0 eV for B16C4H4 and the highest value being 5.7 eV for B10.
3.4. Chemical bonding
The AdNDP method is often employed with the aim of verifying the nature of the MOs in the species considered. The set of σ bonds of the B162− dianion, which was assigned from AdNDP analysis carried out by Sergeeva et al.,37 suggests that B162− has eight σ delocalized electrons leading to its σ antiaromatic character, according to the classical (4n) electron count. Our subsequent study,34 which was a thorough analysis of the σ-out-of-plane contributions to the molecular magnetizability, revealed that B162− rather exhibits σ aromaticity with the sum of magnetic components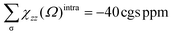 . Our present AdNDP analysis is summarized in Fig. 7 whereas the corresponding MOs are shown in Scheme 1. The ring current maps for σ electrons of B162− displayed in Fig. S8 (ESI file†) also confirm the σ aromatic character of this dianion.
. Our present AdNDP analysis is summarized in Fig. 7 whereas the corresponding MOs are shown in Scheme 1. The ring current maps for σ electrons of B162− displayed in Fig. S8 (ESI file†) also confirm the σ aromatic character of this dianion.
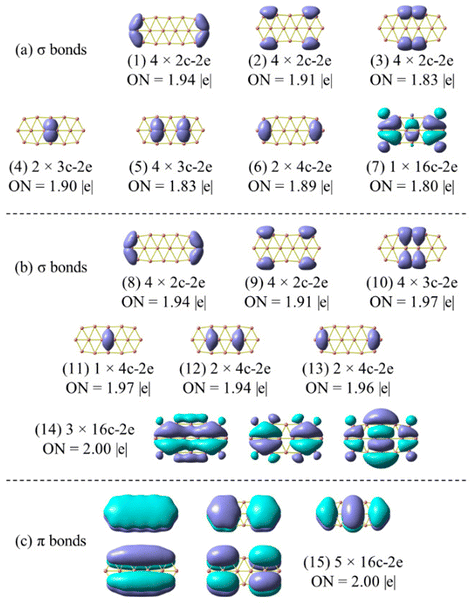 | ||
| Fig. 7 Chemical bonding pattern of the B162− dianion based on AdNDP analysis. Occupation numbers (ONs) are indicated. (a) is the set of σ bonds obtained by replicating Sergeeva's results (ref. 37) excluding bond (7); (b) is the set of σ bonds obtained by the method employed in this study, and (c) represents a set of π bonds, applicable to both (a) and (b). | ||
In view of such a significant discrepancy, we conducted the AdNDP analysis again, and our recent results are presented in Fig. 7a, corresponding to the σ bonding framework of B162−. The set of eighteen σ bonds from (1) to (6) are well reproduced, similar to those reported by Sergeeva et al.,37 despite a slight discrepancy in the occupation numbers (ONs) that are rather not significant due to the utilization of different theoretical methods. It is noteworthy that after collecting eighteen σ bonds (cf. (1–6) in Fig. 7a) and five π bonds (Fig. 7c), a significant amount of residual valence electrons remains sufficient to be considered as a bond. Indeed, a σ 16c–2e bond (7) is obtained from this set of residual valence electrons with an ON value of 1.80 |e|, demonstrating its delocalized nature. This points out that the analysis reported in ref. 37 is not appropriate, thereby prompting us to repeat it by setting the occupation threshold to 1.9 |e| to first identify the bonds with ON values being larger than 1.9 |e|.
The σ bond framework as depicted in Fig. 7b reveals that the four 2c–2e σ bonds (3) turn out to be four 3c–3e σ bonds (10) with ON values now exceeding 1.9 electrons, the six σ 3c–2e bonds (4–5) turn out to be only three σ 4c–2e σ 3c–2e bonds (12–13), and finally, the set of remaining residual valence electrons comprises three globally delocalized σ bonds with shapes analogous to those of the σ delocalized MOs indicated in Scheme 1 (or Fig. S4a in the ESI file†).
The π bond framework also contains five globally delocalized π bonds whose shapes are akin to the π MOs as indicated in Scheme 1. Overall, the B162− dianion truly comprises 3 globally delocalized σ MOs and 5 π MOs as illustrated in Scheme 1. The remaining σ electrons include localized (2c–2e) electrons and restricted delocalized (nc–2e) electrons with n = 3 or 4. Such a chemical bonding pattern, which is similar to those of the B222−, B10P4, B10C4H4, B16P4 and B16C4H4 systems, is presented in Fig. S5, S6 and S7 (ESI file†), and demonstrates the assignment of the MOs pictured in Fig. 8 and Fig. S4 (ESI file†) as globally delocalized MOs are entirely justified.
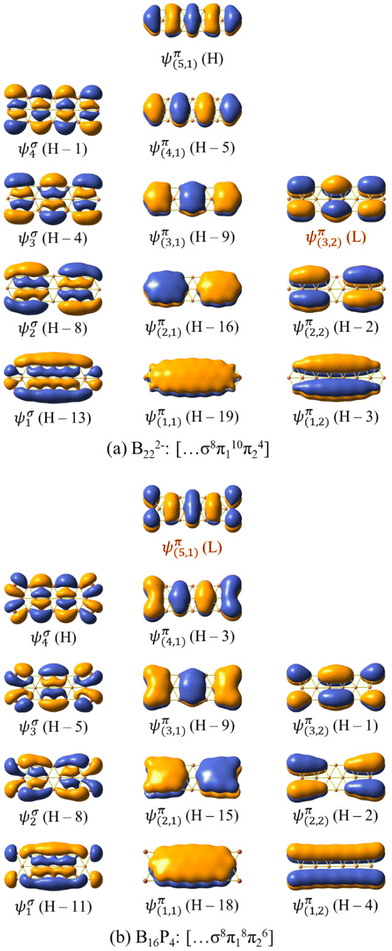 | ||
| Fig. 8 The σ delocalized and π MOs of (a) B222− and (b) B16P4. H and L stand for the HOMO and LUMO, respectively. | ||
The electron counting rule of [σ2(n+1)π12(n+1)π22n] which has been proposed in our previous studies,34 appears to be suitable for rationalizing the aromatic character of the triple-chain B102− and B162−, and the antiaromaticity of the perfectly planar triple-chain B222−.
It should be reiterated again that this electron counting rule stems from consideration of the π electrons of the triple-chain structure as freely moving within a rectangular potential well with infinitely high potential at the boundaries. The corresponding Schrödinger equation for a particle moving in a rectangular box is a well-known basic concept found in many textbooks of quantum chemistry. Its eigenvalues are presented in eqn (6) that express the energy levels:
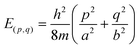 | (6) |
The σ and π MOs of both B162− and B222− as well as those of the doped B10P4 and B16P4 are shown in Fig. 8 and Fig. S4 (ESI file†). Here, the electron configuration [σ6π16π24] of B10P4 coincides with that of B162− and indicates that B10P4 achieves triple-chain aromaticity.
The B222− dianion exhibits triple-chain antiaromatic characteristics due to the electron configuration of [σ8π110π24]. Interestingly, there is a permutation between the two wavefunctions ψπ(5,1) and ψπ(3,2), where ψπ(5,1) is the HOMO in B222− and becomes the LUMO in B16P4, and ψπ(3,2) is the LUMO in B222− and becomes the HOMO−1 in B16P4. This leads to fulfilment of the electron counting rule of [σ8π18π26] for B16P4. According to this triple-chain model, both B10P4 and B16P4 behave as triple-chain aromatic species.
Each of the B222− and B16P4 species exhibits 14 π electrons and thus appears to be aromatic according to the classical (4n + 2) rule with n = 3. As pointed out in our previous study34 and as also demonstrated by the π ring current maps illustrated in Fig. 9, while B222− turns out to be a π antiaromatic species, B16P4 is a π aromatic one. Thus, the classical (4n + 2) electron counting rule does not account for the aromaticity of a triple-chain structure, whereas the [π12(n+1)π22n] electron count represents the more suitable rule related to the triple-chain aromaticity, albeit its representation is somewhat more complex.
The (4n + 2) rule tends to lead us to associate these electrons with one non-degenerate level and n doubly degenerate levels of energy. However, many related structures are characterized with an electron count satisfying the (4n + 2) rule but they do not have any degenerate energy level, such as the oligoacenes. Several recently discovered structures exhibit aromatic properties and are explained by having electron spectra similar to that of naphthalene (C10H8)37,67 or anthracene (C14H10).68 Such a comparison is only partially correct, because while the π electron configuration of boron clusters can be compared to those of hydrocarbons on the basis of the similarity between the π-MO shapes and the number of π electrons, the boron clusters have in addition a set of σ delocalized electrons that do not exist in hydrocarbons. Accordingly, it appears better to avoid an explanation for the aromaticity of boron clusters using the classical (4n + 2) electron counting rule. Indeed, the electron configurations of oligoacenes including naphthalene, anthracene and tetracene that are presented in Fig. S11 (ESI file†) demonstrate well that they follow the [π12(n+1)π22n] rule. In summary, the stability of boron clusters often needs to be understood considering both sets of π and σ characteristics, whereas hydrocarbons only involve their π electrons.
Two additional issues need some further attention, namely, why triple-chain structures need to satisfy the [π12(n+1)π22n] rule, and how a cluster structure can satisfy this rule. Answers for both issues have been presented in our previous study,34 but here, taking the doping effect into account, we would again demonstrate that the above rationalization is entirely valid.
The initial answer can be found through the relationship between the electron localization function (ELF) maps and bond lengths of structures as depicted in Fig. 10 and S10 (ESI file†). Both ELFσd and ELFπ maps represent the ELFs originating from both sets of globally σ and π delocalized electrons. In these figures, the structures are highlighted with purple and yellow rhombuses. Purple rhombuses correspond to locations where multiple interactions of ELFσd and ELFπ basins are present, resulting in shorter edge lengths and diagonals as compared to the edges and diagonals of the yellow rhombuses.
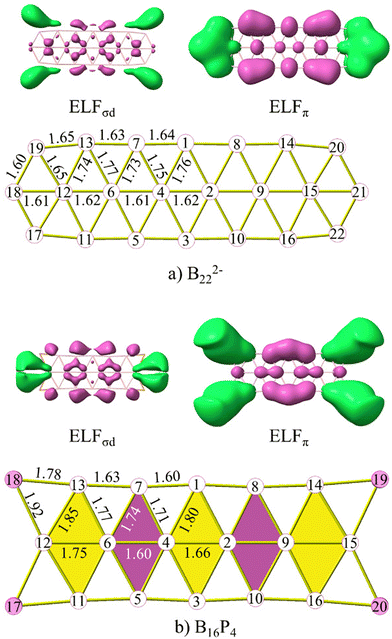 | ||
| Fig. 10 The ELFσd, ELFπ, and the structures of (a) B222− and (b) B16P4. Bond lengths are given in angstrom. | ||
The first observation is that in ELFσl (cf. Fig. S9, ESI file†), which is similar to what has been observed in ribbon-like,30 double ring,52 or triple ring24 structures, the basins of attraction are only observed for bonds within the same row (sr-bond), not connecting rows (cr-bond), except for the bonds at the ends of each structure. Therefore, the common resulting characteristic is that the lengths of sr-bonds are shorter than those of cr-bonds. The ELFπ basins also indicate that they enhance more the bonding of sr-bonds than that of the cr-bonds. Within the same row, the bonds where ELFπ basins are present tend to have shorter distances than those of the same type without ELFπ basins.
The B2–B4 bond length (cf. Fig. S10 ESI file† for atom labels) corresponds to the shortest B–B bond that amounts to 1.54, 1.61 and 1.60 Å in B162−, B10P4 and B10C4H4, respectively. The B4–B6 (B2–B9) bonds are the smallest diagonals within the yellow rhombus adjacent to the central purple rhombus. The deviation between B4–B6 and B2–B4 in B162−, B10P4 and B10C4H4 amounts to 0.09, 0.17 and 0.24 Å, respectively. This significant difference is analogous to the presence of the ELFπ basin in the B2–B4 bond while such a basin is absent in the B4–B6 bond. In B162−, the B6–B16 bond distance is 1.6 Å, and it is also shorter than the neighbouring B4–B6 bond for the same reason. Thus, ELFσd, in turn, tends to show an enhancement of the cr-bonds.
An interesting observation from these results is that the rhombuses with small diagonals that are enhanced continue to be reinforced by ELFσd, while the rhombuses with small diagonals that are not enhanced are not reinforced by ELFσd. We present herewith the clearest observation of this trend. The B6–B7 bond in B162− is still influenced by ELFσd, resulting in a bond length of 1.80 Å. However, in B10P4 it is no longer affected by ELFσd, and this bond length is then increased to 1.85 Å. In B10C4H4 the latter distance further increases to 1.91 Å. The B6–B7 bond in B10P4 corresponds to the B12–B13 bond in B16P4 and B10C4H4 whose respective bond lengths amount to 1.85 and 1.90 Å.
There is an alternating arrangement of domains, coloured as purple and yellow rhombuses, in the triple-chain structure when it achieves aromaticity (cf.Fig. 10). Indeed, such alternation does not exist in B222− and therefore the B222− dianion is considered as a π antiaromatic species.
Although both B16P4 and B222− have the same number of σ and π electrons, only B16P4 is aromatic. The enhanced and non-enhanced rhombuses observed in B16P4 indicate that the triple-chain aromaticity requires its electrons to be distributed in such a way that there is an alternating arrangement of rhombuses in the structure, as described above. This alternation also appears in triple-chain hydrocarbons as previously presented for the ribbon clusters.34
The alternation between enhanced and non-enhanced regions in triple-chain structures34 or ribbon structures30 challenges the common notion of bond length equalization69 for an aromatic structure (such as in the case of benzene). This challenge is further reinforced when the B222− structure, which exhibits even more bond length equalization, is now identified as a π antiaromatic species.
In the ELFσd and ELFπ maps (cf.Fig. 10), large anomalous basins have appeared that are highlighted in green. Due to the insignificant difference between the bonds affected by these basins in B162− as compared to the adjacent bonds, the role of these basins was not mentioned in our previous study.34 Because of the strong influence of impurities, the roles of these basins become more apparent. The significantly shorter bond length of P12–B7 (C12–B7) as compared to P12–B6 (C12–B6) in B10P4 (B10C4H4) or P18–B13 (C18–B13) compared to P18–B12 (C18–B12) in B16P4 (B16C4H4) suggests a self-locking phenomenon akin to the ribbon model.30 Indeed, these B–P (or B–C) bonds that are anomalously short with respect to their normal lengths, and are located at the four corners of the rectangular structure, indicate that the aromatic motif in an triple-chain model self-adjusts to the particle in a rectangular box (PIARB) model, which has infinite potential at the boundary, making it the most suitable electron configuration possible.
Although they have the same number of π electrons, the correspondence between the antiaromatic B222− to the aromatic B16P4 clearly demonstrates the significance of the triple-chain model. In B222−, the ψπ(5,1) level is occupied and the ψπ(3,2) level is unoccupied, whereas in B16P4 the ψπ(3,2) level is occupied and the ψπ(4,1) level is unoccupied (cf.Fig. 8). That means, if the ψπ(p2,2) level is the molecular orbital with p2 being the highest quantum number for the π2 group, then the energy level of ψπ(p2+2,2) must be higher than that of ψπ(p2,2), and the structure must have enough π electrons for the ψπ(p2+1,1) level to be fully occupied. If we set p1 = p2 + 2 and according to eqn (6), the above condition implies:
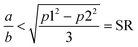 | (7) |
In a recent study, a small and simple Python code snippet was written to determine the dimensions a and b of the rectangle in which the π electrons move freely,42 in which the root mean square error (RMSE) index was calculated for determining the accuracy of the model (eqn (8)):
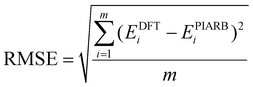 | (8) |
Applying this code, the results for the structures C10H8, B162−, B10P4 and B10C4H4 for 10 π electron systems and C14H10, B222−, B16P4 and B16C4H4 for 14 π electron systems are provided in Table 1. With the RMSE < 0.01 for all systems considered in Table 1, the π electrons appear to follow the PIARB model.
| Species | a (Å) | b (Å) | a/b | SR | RMSE |
|---|---|---|---|---|---|
| C10H8 | 9.21 | 6.52 | 1.41 | 2.00 | 0.0052 |
| B162− | 10.61 | 5.75 | 1.85 | 2.00 | 0.0022 |
| B10P4 | 10.27 | 6.90 | 1.49 | 2.00 | 0.0065 |
| B10C4H4 | 10.34 | 6.97 | 1.48 | 2.00 | 0.0052 |
| C14H10 | 11.98 | 6.57 | 1.82 | 2.31 | 0.0057 |
| B222− | 13.84 | 5.78 | 2.39 | 2.31 | 0.0021 |
| B16P4 | 13.55 | 6.54 | 2.07 | 2.31 | 0.0056 |
| B16C4H4 | 13.56 | 6.55 | 2.07 | 2.31 | 0.0044 |
The heteromolecular compounds with an RMSE being twice as large as that of the pure boron triple-chain clusters indicate the presence of the phenomenological shell model (PSM)23 on the electron spectrum, but it remains non-significant. As the triple-chain size increases, the number of π electrons also increases, proportional to the a/b ratio and SR. However, the ratio a/b is found to increase more rapidly than the SR, leading a/b to approach the SR or even exceed the SR as in B222−. Substitution of a {B62−} unit with a {P4} atom does not only decrease the length a but also increases the width b of the triple-chain form, thereby reducing the a/b ratio. In other words, there is no significant change in the variation of a and b following substitution of {P} with {CH}.
As the triple-chain size increases, the levels ψπ(p2,2) and ψπ(p2+2,1) in the oligoacenes approach each other more closely, meaning that the frontier orbital (HOMO–LUMO) energy gap (HLG) decreases, thereby increasing the multi-reference nature of the molecule and reducing its kinetic stability.70–72 The perfect planarity of B22X4 with X = {P} or {CH} is also due to an electron configuration satisfying the [σ2(n+1)π12(n+1)π22n] rule, but the HLG amounts to only 0.13 and 0.31 eV for B22P4 and B22C4H4, respectively, leading to the appearance of imaginary frequencies for high symmetry structures. Therefore, these clusters are not further discussed in the present work. Furthermore, in boron-based clusters, σ electrons can also serve as the HOMO as seen in B16P4 or the LUMO as in the B15− anion,42 thus making the prediction of the size of the HLG as well as their aromatic character and stability even more challenging.
For a broader perspective on the effect of substitution of {P} with {CH}, the energy diagrams of the structures studied are presented in Fig. 5. At a rapid glance, substitution of {P} with {CH} leads to an increase in HLG, corresponding to enhanced kinetic stability as indicated above. The increase in HLG stems from two opposing processes resulting from the substitution, namely the downward shift of σ MOs and the upward shift of π MOs. This phenomenon is observed more distinctly in B10PyCzHz as compared to B16PyCzHz. In B10PyCzHz, this displacement leads to a rearrangement of the HOMO and HOMO−1 cross positions in B10PC3H3. Therefore, under strict consideration, only B10P4, B10P3CH and B10P2C2H2 are deemed to be isolobal, while the entire set of B10PyCzHz structures are better considered as isovalent.
In B16PyCzHz, the ψσ4 level becomes HOMO−1 in B16PC3H3 and continues to shift downwards with increasing substitution of {P} with {CH}. Therefore, all B16PyCzHz isomers are considered as isolobal, except for B16P4. Both the HOMO and LUMO of B16PyCzHz, except for B16P4, are π MOs, and their energy levels increase. Consequently, the increase in HLG for B16PyCzHz is much slower as compared to that of B10PyCzHz. The increase in HLG for B16PyCzHz is also facilitated by a faster increase in the energy levels of LUMO (antibonding) as compared to HOMO (bonding).
With their π aromaticity, the triple-chain BxPyCzHz that are analogues of the aromatic oligoacenes and further enhanced by intrinsic σ aromaticity, along with a wide range of HLG spectra spanning from 1.1 to 2.2 eV, offer a diverse selection for experimental studies, with tailored applications according to specific purpose on triple-chain boron clusters. To emphasize further that boron triple-chain structures are not entirely analogous to acenes, the UV-Vis spectra of boron triple-chain compounds and oligoacenes displayed in Fig. S12 and S13,† with identical π electron configurations are presented in Fig. S10 (ESI file†). These electronic spectra demonstrate that triple-chain boron compounds exhibit the ability to absorb light across a broad range in the visible region, whereas oligoacenes mainly absorb light within a much narrower range and exhibit a pronounced blue-shift in the ultraviolet region.
4. Concluding remarks
The results obtained in the present theoretical study offer us a case of doped boron clusters in which the original boron framework remains largely unchanged as the number of phosphorus dopant atoms goes from 1 to 4. Indeed, both B10 and B16 host systems maintain their triple-chain form following sequential addition of P atoms. Furthermore, our calculated results indicate a perfect isovalent/isolobal substitution of {P} with {CH}. The similarity in the number of delocalized electrons formed between the triple-chain form of the pure boron Bn2− and the doped Bn−6P4 clusters and in those formed by the substitution of {P} with {CH} thereafter are intriguing. A remarkable effect of P substitution is neutralization of both dianionic hosts. In each series, the triple-row form remains by far the global minimum, ensuring a high likelihood of its experimental detection.This study does not diminish the significance of AdNDP in the analysis of chemical bonding in molecules. However, the subjective nature of AdNDP can lead to user-dependent results. Relying solely on AdNDP analysis can result in a significant misunderstanding of the chemical bonding involved. Therefore, it is essential to employ additional methods to verify the AdNDP findings.
The number of globally delocalized σ and π electrons present in these clusters and the magnetic ring current maps contribute to the verification that BxPyCzHz triple-chain structures exhibit double aromaticity.
While the electron counting rule for the double-chain and ribbon species is [σ2(n+1)π2n], the electron counting rule of [σ2(n+1)π12(n+1)π22n] is established in the present study for the triple-chain form. The latter is first introduced for the dianions B102− and B162−, and following doping, it is confirmed to be accurate for B10P4 and B16P4 through a similarity in electron configuration between the dianions and the doped derivatives. It can also be verified going from the configuration of [σ8π110π24] in B222− to that of [σ8π18π26] in B16P4.
The model of a particle moving in a rectangular box proved to be effective in elucidating the relationship between the size of a structure and its electron configuration, thereby explaining the transition from an antiaromatic configuration of B222− to an aromatic configuration of B16P4. The model of a particle moving in a rectangular box also helps us rationalize the decrease in the frontier orbital energy gap (HLG) of oligoacenes as their size increases.
The electron localization function (ELF) maps and their relationship with different types of bond lengths highlight the self-locking phenomenon as a crucial point for a cluster structure to adhere to the triple-chain model and the [σ2(n+1)π12(n+1)π22n] electron configuration to satisfy the regions of enhanced rhombuses and alternately non-enhanced rhombus areas.
All structures considered have vertical attachment energies (VAEs) smaller than 4 eV and vertical ionization energies (VIEs) larger than 7 eV. The substitution of a {P} atom with a {CH} unit indeed enhances the thermodynamic stability of the boron triple-chain form, which helps facilitate its laboratory synthesis and open avenues for a new class of materials with versatile electronic properties. The calculated UV-Vis spectrum also suggests its potential application as a semi-conductor.
Data availability
AdNDP analysis for the Td tetrahedron B16P4-3 isomer and triple-chain structures; the σ delocalized and π-MOs of triple-chain structures and π-MOs of some oligoacenes; the σ and π ring current maps of triple-chain structures; ELFσl, ELFσd, and ELFπ of triple-chain structures; the predicted electronic absorption spectrum of triple-chain and some oligoacenes; and tables of the HOMO–LUMO gap (HLG), VIE, VAE, hardness (η), electronegativity (χ) and electrophilicity (ω) of triple-chain structures.The quantum chemical program Gaussian 16 has been used. The reference to this program is given in the list of references. The datasets supporting this article are uploaded as part of the ESI file† that also includes the Cartesian coordinates of the optimized geometries and information on their electronic structures.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
LVD and MTN are grateful to Van Lang University. This work was undertaken with the assistance of resources to AK from the National Computational Infrastructure (NCI), which is supported by the Australian Government.References
- J. Barroso, S. Pan and G. Merino, Chem. Soc. Rev., 2022, 51, 1098–1123 RSC
.
- T. B. Tai, D. J. Grant, M. T. Nguyen and D. A. Dixon, J. Phys. Chem. A, 2010, 114, 994–1007 CrossRef CAS PubMed
.
- B. J. Nagare, S. Chavan and V. Bambole, Comput. Theor. Chem., 2018, 1125, 54–62 CrossRef CAS
.
- L. Cheng, J. Chem. Phys., 2012, 136, 104301 CrossRef PubMed
.
- B. Kiran, S. Bulusu, H.-J. H.-J. Zhai, S. Yoo, X. C. Zeng and L.-S. L.-S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961–964 CrossRef CAS PubMed
.
- R. Casillas, T. Baruah and R. R. Zope, Chem. Phys. Lett., 2013, 557, 15–18 CrossRef CAS
.
- T. B. B. Tai and M. T. T. Nguyen, Phys. Chem. Chem. Phys., 2015, 17, 13672–13679 RSC
.
- H. T. Pham, L. Van Duong, B. Q. Pham and M. T. Nguyen, Chem. Phys. Lett., 2013, 577, 32–37 CrossRef CAS
.
- X. Wu, L. Sai, S. Zhou, P. Zhou, M. Chen, M. Springborg and J. Zhao, Phys. Chem. Chem. Phys., 2020, 22, 12959–12966 RSC
.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, Nanoscale, 2014, 6, 11692–11696 RSC
.
- T. B. Tai and M. T. Nguyen, Nanoscale, 2015, 7, 3316–3317 RSC
.
- A. B. Rahane and V. Kumar, Nanoscale, 2015, 7, 4055–4062 RSC
.
- G. Merino, M. Solà, I. Fernandez, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. Cossio, M. A. Petrukhina, J. Wu, J. Wu and A. Restrepo, Chem. Sci., 2023, 21, 1–9 Search PubMed
.
- H. Ottosson, Chem. Sci., 2023, 14, 5542–5544 RSC
.
- A. E. Kuznetsov and A. I. Boldyrev, Struct. Chem., 2002, 13, 141–148 CrossRef CAS
.
- Q. S. Li and H. W. Jin, J. Phys. Chem. A, 2002, 106, 7042–7047 CrossRef CAS
.
- W. Huang, A. P. Sergeeva, H.-J. Zhai, B. B. Averkiev, L.-S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206 CrossRef CAS PubMed
.
- J. O. C. Jiménez-Halla, R. Islas, T. Heine and G. Merino, Angew. Chem., Int. Ed., 2010, 49, 5668–5671 CrossRef PubMed
.
- T. B. Tai, R. W. A. Havenith, J. L. Teunissen, A. R. Dok, S. D. Hallaert, M. T. Nguyen and A. Ceulemans, Inorg. Chem., 2013, 52, 10595–10600 CrossRef CAS PubMed
.
- T. B. Tai, L. Van Duong, H. T. Pham, D. T. T. Mai and M. T. Nguyen, Chem. Commun., 2014, 50, 1558–1560 RSC
.
-
L. Van Duong and M. T. Nguyen, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2023 Search PubMed
.
- A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., 2000, 39, 3915–3917 CrossRef CAS
.
- P. K. Chattaraj and T. Höltzl, Aromat. Met. Clusters, 2018, 281–306 Search PubMed
.
- L. V. Duong, H. T. Pham, N. M. Tam and M. T. Nguyen, Phys. Chem. Chem. Phys., 2014, 16, 19470–19478 RSC
.
- H. T. Pham, L. V. Duong and M. T. Nguyen, J. Phys. Chem. C, 2014, 118, 24181–24187 CrossRef CAS
.
- D.-Z. Li, Q. Chen, Y.-B. Wu, H.-G. Lu and S.-D. Li, Phys. Chem. Chem. Phys., 2012, 14, 14769 RSC
.
- H.-J. Zhai, Q. Chen, H. Bai, H.-G. Lu, W.-L. Li, S.-D. Li and L.-S. Wang, J. Chem. Phys., 2013, 139, 174301 CrossRef PubMed
.
- H. Bai, B. Bai, L. Zhang, W. Huang, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2017, 19, 31655–31665 RSC
.
- H. Bai, Q. Chen, C. Q. Miao, Y. W. Mu, Y. B. Wu, H. G. Lu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2013, 15, 18872–18880 RSC
.
- L. V. Duong and M. T. Nguyen, Phys. Chem. Chem. Phys., 2017, 19, 14913–14918 RSC
.
- L. Van Duong, N. N. Tri, N. P. Hung and M. T. Nguyen, J. Phys. Chem. A, 2022, 126, 3101–3109 CrossRef PubMed
.
- W. Lu, D. C. H. Do and R. Kinjo, Nat. Commun., 2020, 11, 3370 CrossRef PubMed
.
- A. G. Arvanitidis, K. Z. Lim, R. W. A. Havenith and A. Ceulemans, Int. J. Quantum Chem., 2018, 118, 25575 CrossRef
.
- L. Van Duong, D. T. T. Mai, M. P. Pham-Ho and M. T. Nguyen, Phys. Chem. Chem. Phys., 2019, 21, 13030–13039 RSC
.
- H.-J. Zhai, B. Kiran, J. Li and L.-S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS PubMed
.
- T. B. Tai, N. M. Tam and M. T. Nguyen, Chem. Phys. Lett., 2012, 530, 71–76 CrossRef CAS
.
- A. P. Sergeeva, D. Y. Zubarev, H.-J. Zhai, A. I. Boldyrev and L.-S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246 CrossRef CAS PubMed
.
- C.-Y. Gao, Q.-Q. Yan, Q. Chen, Y.-W. Mu and S.-D. Li, J. Cluster Sci., 2024, 35, 1375–1380 CrossRef CAS
.
- M. A. Addicoat and G. F. Metha, J. Comput. Chem., 2009, 30, 57–64 CrossRef CAS PubMed
.
-
J. H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, MIT Press, 1992 Search PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- Y. A. Jeilani, L. Van Duong, O. M. S. Al Qahtani and M. T. Nguyen, Phys. Chem. Chem. Phys., 2024, 26, 11347–11359 RSC
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT
.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- L. Rincon, R. Almeida, J. E. Alvarellos, D. Garcia-Aldea, A. Hasmy and C. Gonzalez, J. Chem. Soc., Dalton Trans., 2009, 3328–3333 RSC
.
- A. Savin, B. Silvi, F. Coionna and F. Colonna, Can. J. Chem., 1996, 74, 1088–1096 CrossRef CAS
.
- M. Kohout, DGrid, version 5.0, Dresden, 2017.
- J. C. Santos, W. Tiznado, R. Contreras and P. Fuentealba, J. Chem. Phys., 2004, 120, 1670–1673 CrossRef CAS PubMed
.
- L. V. Duong and M. T. Nguyen, Chem. Phys. Lett., 2017, 685, 377–384 CrossRef CAS
.
- G. Monaco, F. F. Summa and R. Zanasi, J. Chem. Inf. Model., 2021, 61, 270–283 CrossRef CAS PubMed
.
- S. Jin, B. Chen, X. Kuang, C. Lu, W. Sun, X. Xia and G. L. Gutsev, J. Phys. Chem. C, 2019, 123, 6276–6283 CrossRef CAS
.
- D. T. T. Mai, L. V. Duong, T. B. Tai and M. T. Nguyen, J. Phys. Chem. A, 2016, 120, 3623–3633 CrossRef CAS PubMed
.
- D. T. T. Mai, L. V. Duong, M. P. Pham-Ho and M. T. Nguyen, J. Phys. Chem. C, 2020, 124, 6770–6783 CrossRef
.
- R. O. Jones, G. Ganteför, S. Hunsicker and P. Pieperhoff, J. Chem. Phys., 1995, 103, 9549–9562 CrossRef CAS
.
- A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., Int. Ed., 2001, 40, 2834–2838 CrossRef CAS PubMed
.
- M. Elian, M. M. L. Chen, D. Michael, P. Mingos and R. Hoffmann, Inorg. Chem., 1976, 15, 1148–1155 CrossRef CAS
.
- K. H. Reddy, D. Usharani, J. F. Nixon and E. D. Jemmis, Chem. – Eur. J., 2011, 17, 9142–9152 CrossRef CAS PubMed
.
- C. Heinl, E. Peresypkina, G. Balázs, E. Mädl, A. V. Virovets and M. Scheer, Chem. – Eur. J., 2021, 27, 7542–7548 CAS
.
- R. Haunschild and G. Frenking, Mol. Phys., 2009, 107, 911–922 CAS
.
- A. S. Ivanov, K. V. Bozhenko and A. I. Boldyrev, J. Chem. Theory Comput., 2012, 8, 135–140 CrossRef CAS PubMed
.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CAS
.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CAS
.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CAS
.
- A. P. Sergeeva, B. B. Averkiev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2011, 134, 224304 Search PubMed
.
- A. P. P. Sergeeva, Z. A. A. Piazza, C. Romanescu, W.-L. L. Li, A. I. I. Boldyrev and L.-S. S. Wang, J. Am. Chem. Soc., 2012, 134, 18065–18073 CAS
.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842 CrossRef CAS PubMed
.
- C. A. Bauer, A. Hansen and S. Grimme, Chem. – Eur. J., 2017, 23, 6150–6164 CAS
.
- R. Nieman, J. R. Carvalho, B. Jayee, A. Hansen, A. J. A. Aquino, M. Kertesz and H. Lischka, Phys. Chem. Chem. Phys., 2023, 25, 27380–27393 CAS
.
- A. Pérez-Guardiola, M. E. Sandoval-Salinas, D. Casanova, E. San-Fabián, A. J. Pérez-Jiménez and J. C. Sancho-García, Phys. Chem. Chem. Phys., 2018, 20, 7112–7124 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt02251c |
| This journal is © The Royal Society of Chemistry 2024 |