Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Al(III) and Ga(III) triflate complexes as solvate ionic liquids: speciation and application as soluble and recyclable Lewis acidic catalysts†
Justyna
Więcławik
 a,
Alina
Brzęczek-Szafran
a,
Alina
Brzęczek-Szafran
 a,
Sebastian
Jurczyk
b,
Karolina
Matuszek
a,
Sebastian
Jurczyk
b,
Karolina
Matuszek
 c,
Małgorzata
Swadźba-Kwaśny
c,
Małgorzata
Swadźba-Kwaśny
 *d and
Anna
Chrobok
*d and
Anna
Chrobok
 *a
*a
aDepartment of Organic Chemical Technology and Petrochemistry, Faculty of Chemistry, Silesian University of Technology, Bolesława Krzywoustego 4, 44-100 Gliwice, Poland. E-mail: anna.chrobok@polsl.pl
bInstitute for Engineering of Polymer Materials and Dyes, Lukasiewicz Research Network, Sklodowskiej-Curie 55, PL-87100 Torun, Poland
cAddress School of Chemistry, Monash University, Clayton, Victoria 3800, Australia
dThe QUILL Research Centre, School of Chemistry and Chemical Engineering, Queen's University of Belfast, David Keir Building, Stranmillis Road, Belfast BT9 5AG, UK. E-mail: m.swadzba-kwasny@qub.ac.uk
First published on 4th October 2024
Abstract
This work reports on the first solvate ionic liquids (SILs) based on aluminium(III) and gallium(III) triflates, M(OTf)3, and triglyme (G3). Liquid-phase speciation of these new SILs was studied by multinuclear NMR spectroscopy. Across the compositional range of G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M(OTf)3 mixtures, both metals were found to be in a hexacoordinate environment, with both G3 and [OTf]− ligands present in the first coordination sphere, and apparently exchanging through a dynamic equilibrium. The Lewis acidity was quantified by the Gutmann acceptor number (AN) and compared to the performance of SILs as Lewis acidic catalysts in model [3 + 3] cycloadditions. Despite saturated coordination, AN values were relatively high, reaching AN = ca. 71–83 for Al-SILs and ca. 80–93 for Ga-SILs, corroborating the labile nature of the metal–ligand bonding. In a model catalytic reaction, SILs were fully soluble in the reaction mixtures, in contrast to the corresponding triflate salts. The catalytic performance of SILs exceeded that of the corresponding triflate salts, and Ga-SILs were more active than Al-SILs, in agreement with AN measurements. In conclusion, the new Group 13 SILs can be considered as soluble and catalytically active forms of their corresponding metal triflates, with potential uses in catalysis.
M(OTf)3 mixtures, both metals were found to be in a hexacoordinate environment, with both G3 and [OTf]− ligands present in the first coordination sphere, and apparently exchanging through a dynamic equilibrium. The Lewis acidity was quantified by the Gutmann acceptor number (AN) and compared to the performance of SILs as Lewis acidic catalysts in model [3 + 3] cycloadditions. Despite saturated coordination, AN values were relatively high, reaching AN = ca. 71–83 for Al-SILs and ca. 80–93 for Ga-SILs, corroborating the labile nature of the metal–ligand bonding. In a model catalytic reaction, SILs were fully soluble in the reaction mixtures, in contrast to the corresponding triflate salts. The catalytic performance of SILs exceeded that of the corresponding triflate salts, and Ga-SILs were more active than Al-SILs, in agreement with AN measurements. In conclusion, the new Group 13 SILs can be considered as soluble and catalytically active forms of their corresponding metal triflates, with potential uses in catalysis.
Introduction
The concept of functional liquids, in which a metal cation was solvated by L-type ligands, was first introduced by Angell in 1965.1 He described hydrates, such as Ca(NO3)2·4H2O, as a “new class of molten salt mixtures”, recognising that solvating the metal cation generates low-melting hydrates with high conductivities, potentially useful as electrolytes.2 In contrast to molten salts, however, the thermal stability of such “molten salt mixtures” was limited by the aqua ligand.A similar approach was used in the design of liquid coordination complexes (LCCs), in which metal halides were combined with sub-equimolar quantities of organic L-donors, e.g. AlCl3 and acetamide, or GaCl3 and trioctylphosphine oxide.3,4 LCCs (Fig. 1b), developed as less expensive and more tuneable alternatives to chlorometallate ionic liquids (Fig. 1a), were subsequently demonstrated to be Lewis acidic catalysts in an array of reactions: oligomerisation of olefins,5 Diels–Alder cycloaddition,4 and Friedel–Crafts alkylation,6 as well as co-catalysts in heterogeneous catalysis through solid catalysts with ionic liquid layer (SCILL).7 However, most reported LCCs, like conventional chlorometallate ionic liquids, are highly corrosive due to their high chloride content.
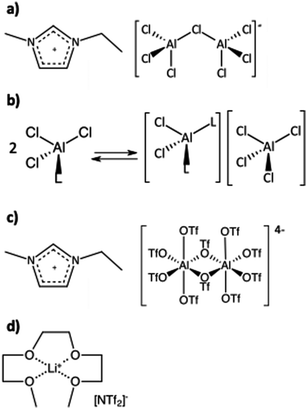 | ||
| Fig. 1 Examples of the structures of metal-containing ionic liquids: (a) chlorometallate ionic liquid, (b) liquid coordination complex (LCC),3 (c) trifloaluminate ionic liquid,8 and (d) solvate ionic liquid.14 | ||
Salts of Lewis acidic metals (M = Al, Ga, and Ln) and trifluoromethanesulfonic acid (known as triflates, OTf) are stable in aqueous media, chloride-free and catalytically active at low concentrations.8,9 However, they suffer from poor solubility in most solvents.10,11 In an attempt to enhance their solubility, we have developed triflometallate ionic liquids, synthesised by the reaction of triflate ionic liquids and Group 13 triflates (Fig. 1c).12 While catalytically active, these ILs are extremely viscous and very expensive. Seeking further alternatives, we have decided to explore the concept of solvate ionic liquids (SILs).
Watanabe and co-workers developed SILs,13–16 exemplified by equimolar mixtures of Li[NTf2] and triglyme (G3), or tetraglyme (G4), for energy storage applications (Fig. 1d). Mandai et al.14 provided formalised criteria for “good” SILs, which behave like ionic liquids, not like solutions of salts in molecular solvents (they are solvent-in-salt systems, not salt-in-solvent). Such SILs combine flexible polydentate ligands, solvating a Group 1 or 2 metal, and weakly basic anions, such as bis(trifluoromethanesulfonate)imide, [NTf2]−. This design yields long-lived robust cations: alkali metals solvated by glyme. “Good” SILs are relatively simple to synthesise, thermally stable, electrically conductive and non-flammable, and therefore make very good electrolytes.17–24
Since SILs have been developed in the context of energy storage applications, their uses in catalysis are scarce.25 Eyckens et al. used SILs in Diels–Alder and [2 + 2] cycloadditions, reporting that higher yields (up to 94%) and improved reaction safety can be achieved by replacing a solution of lithium salt in a molecular solvent with [Li(G3)][NTf2] or [Li(G4)][NTf2], in the formation of oxetanone.26 Obregón-Zúñiga et al. found improved yield and selectivity in an asymmetric aldol reaction in the presence of SILs, also [Li(G3)][NTf2] or [Li(G4)][NTf2], due to their involvement in the catalytically active supramolecular aggregate formation.27 Other uses include Kabachnik–Fields reactions,28 stereo- and regioselective ring opening of epoxides,29 and catalytic additives for curing epoxy systems.30 Importantly for this work, all catalytic studies to date have been focussed on Li-based SILs, a weak Lewis acid. Although SILs based on Na, K, Mg and Al are known, they have only been used in energy storage applications.31,32
In this contribution, we combined our expertise in the design and study of Lewis acidic LCCs and ILs with the potential offered by the solvate ionic liquid design to report a series of solvate ionic liquids based on triflate salts of aluminium and gallium and triglyme (G3). We delved into the speciation of these materials using multinuclear NMR spectroscopy and probed their acidity with the Gutmann acceptor number (AN). Our investigation revealed intricate speciation patterns and strong Lewis acidity of these new Group 13 SILs, demonstrated directly through a catalytic application in a model [3 + 3] cycloaddition reaction. The study highlights notable differences in the coordination chemistry and Lewis acidity of Al-SILs and Ga-SILs, providing new insights into the chemistry of Group 13 metals.
Experimental
Materials
Aluminium(III) trifluoromethanesulfonate (99.9%), triethylene glycol dimethyl ether (99%), triethylphosphine oxide (97%), decane (99%), isoprene (99%, contains <1000 ppm p-tert-butylcatechol as an inhibitor), 2.0 M trimethylaluminum solution in toluene, and anhydrous toluene (99.8%) were all purchased from Sigma Aldrich and used as received. Phosphoric(V) acid (85% in D2O) was also purchased from Sigma Aldrich. 2,4-Dimethylphenol (99%) and gallium(III) trifluoromethanesulfonate (99%) were purchased from Thermo Fisher Scientific. The synthesis of Al(NTf2)3 is described in the ESI.†General procedure for the synthesis of SILs
The SILs were synthesized in a glovebox under an inert argon atmosphere (<0.6 ppm O2 and H2O). The triglyme (G3) and appropriate metal salt M(OTf)3 (Al(OTf)3 or Ga(OTf)3) were weighed into a vial at various molar ratios from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 10
1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (χM(OTf)3 = 0.09–0.33). The mixture was allowed to react in a glovebox (40–45 °C, 3 h), and then the heat was turned off and the mixture was further stirred overnight.
1 (χM(OTf)3 = 0.09–0.33). The mixture was allowed to react in a glovebox (40–45 °C, 3 h), and then the heat was turned off and the mixture was further stirred overnight.
The same procedure was used for Al(NTf2)3 and G3, with χAl(NTf2)3 = 0.09–0.50.
Multinuclear NMR spectroscopy
All NMR spectra (1H, 13C, 19F, 27Al, 31P and 71Ga) were recorded using a Bruker Avance DPX 400 MHz spectrometer. All samples were studied at 297 K, neat using a DMSO-d6 or D2O filled, sealed capillary as an external lock. In the case of 27Al NMR, a solution of Al(NO3)3 hydrate in D2O was used as an external reference. In 71Ga NMR spectroscopy, a solution of Ga(NO3)3 hydrate in D2O was used as an external reference and in 19F NMR, fluorobenzene in acetone-d6 was used as an external reference.Acceptor number determination
Every ionic liquid was sampled into three different NMR tubes, to which triethylphophine oxide (TEPO) was added at the following concentrations: 1 wt%, 2 wt% and 3 wt%. An 85% phosphoric(V) acid solution in D2O enclosed in a capillary was used as the external standard. After TEPO dissolved in the ionic liquid, the 31P NMR spectra were recorded at room temperature and at 161.89 MHz using an Agilent 400 MHz spectrometer. The measured 31P NMR chemical shift for each ionic liquid-TEPO concentration arrangement was extrapolated to infinite dilution of TEPO, δinf. The referential value was the TEPO chemical shift in hexane extrapolated to infinite dilution, δinf hex = 0 ppm. For each ionic liquid, the acceptor number was calculated based on the formula: AN = 2.348·δinf, as described in the literature.33,34General procedure for [3 + 3] cycloaddition
All reactions were carried out under a protective atmosphere of argon. The catalyst (1–5 mol% per 1.00 mol of isoprene) was placed in a flask. Then 0.98 g of 2,4-dimethylphenol (8 mmol) and 0.27 g of isoprene (4 mmol) were added along with 0.10 g (0.7 mmol) of decane as an internal standard. The reaction was carried out using a magnetic stirrer at various temperatures (20–40 °C). The progress of the reaction was monitored by gas chromatography. GC analysis was performed in anhydrous hexane stored over molecular sieves.Results and discussion
Design of Group 13 SILs
Initial screening experiments included three Group 13 salts: aluminium trifluoromethanesulfonate, Al(OTf)3, gallium(III) trifluoromethanesulfonate, Ga(OTf)3, and aluminium bis(trifluoromethane)sulfonimide, Al(NTf2)3, combined with triethylene glycol dimethyl ether (triglyme, G3).Considering that non-coordinating anions were reported to be the best candidates for generating “good” SILs, mixtures of Al(NTf2)3 and G3 were tested first. Combinations with high loadings of the metal salt, χAl(NTf2)3 = 0.33 and 0.51, where χAl(NTf2)3 is the molar ratio of Al(NTf2)3, were homogeneous and extremely viscous liquids. Decreasing the molar fraction of Al(NTf2)3 resulted in apparent autocatalytic decomposition: the mixtures darkened and a dark-brown insoluble solid precipitated from the liquid glyme. This explained the lack of literature data on Al(NTf2)3 and glyme mixtures, while there are several papers on Al(OTf)3 and diglyme,35–37 and on AlCl3 and glymes.38–40
Subsequently, mixtures of G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al(OTf)3 and G3
Al(OTf)3 and G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga(OTf)3 were tested. Initially, it was anticipated that homogeneous compounds could be synthesised from equimolar reactant ratios, χM(OTf)3 = 0.50 (Fig. 2a). However, both G3
Ga(OTf)3 were tested. Initially, it was anticipated that homogeneous compounds could be synthesised from equimolar reactant ratios, χM(OTf)3 = 0.50 (Fig. 2a). However, both G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al(OTf)3 and G3
Al(OTf)3 and G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga(OTf)3 systems formed homogeneous liquids from very low metal triflate loadings, up to χM(OTf)3 = 0.33, which is equivalent to two moles of G3 per mole of M(OTf)3. This suggested the possible formation of both ionic and charge-neutral complexes (exemplified in Fig. 2b), but also significantly more complex species, with either triflates or glymes acting as bridging ligands. Notably, while high metal concentrations (χM(OTf)3 = 0.33, 0.25) are expected to display SIL-like behaviour, low metal loadings (χM(OTf)3 = 0.09, 0.10, etc.) are expected to behave like solutions of metal salts in an organic solvent.
Ga(OTf)3 systems formed homogeneous liquids from very low metal triflate loadings, up to χM(OTf)3 = 0.33, which is equivalent to two moles of G3 per mole of M(OTf)3. This suggested the possible formation of both ionic and charge-neutral complexes (exemplified in Fig. 2b), but also significantly more complex species, with either triflates or glymes acting as bridging ligands. Notably, while high metal concentrations (χM(OTf)3 = 0.33, 0.25) are expected to display SIL-like behaviour, low metal loadings (χM(OTf)3 = 0.09, 0.10, etc.) are expected to behave like solutions of metal salts in an organic solvent.
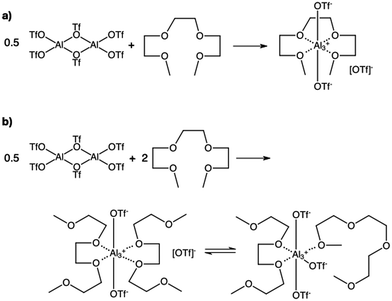 | ||
| Fig. 2 Hypothetical speciation of Al-SILs synthesised at (a) χM(OTf)3 = 0.50 (reaction did not proceed to completion) and (b) χM(OTf)3 = 0.33 (reaction gave a homogeneous liquid). | ||
The apparent viscosity and yellow/orange colour of the formed SILs decreased with decreasing metal loading (Table 1).
| Metal | χ M(OTf)3 | G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M(OTf)3 molar ratio M(OTf)3 molar ratio |
Physical state | AN |
|---|---|---|---|---|
| Al | 0.33 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Very viscous, yellow liquid | 70.9–82.7 |
| 0.25 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Viscous, light yellow liquid | 70.8–82.7 | |
| 0.20 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Pale yellow liquid | 70.7–82.7 | |
| 0.17 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Pale yellow liquid | 70.7–82.6 | |
| 0.14 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Pale yellow liquid | 71.0–82.6 | |
| 0.13 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yellow hue liquid | 71.4–82.6 | |
| 0.11 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yellow hue liquid | 71.2–82.7 | |
| 0.10 | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yellow hue liquid | 71.1–82.5 | |
| 0.09 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Yellow hue liquid | 70.7–82.6 | |
| Ga | 0.33 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Very viscous, orange liquid | 79.6–92.4 |
| 0.25 | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Viscous, light orange liquid | 81.6–92.3 | |
| 0.20 | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Pale orange liquid | 80.4–92.3 | |
| 0.17 | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Pale orange liquid | 80.3–93.4 | |
| 0.14 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Pale orange liquid | 80.3–92.8 | |
| 0.13 | 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Orange hue liquid | 79.9–92.6 | |
| 0.11 | 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Orange hue liquid | 79.6–93.4 | |
| 0.10 | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Orange hue liquid | 80.0–93.5 | |
| 0.09 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Orange hue liquid | 80.1–93.3 | |
| — | — | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (neat G3) 0 (neat G3) |
Colourless liquid | 9.6 |
Acidity measurement with the Gutmann acceptor number
There are several scales currently used to measure Lewis acidity by different research groups; each relies on a probe that interacts with a Lewis acid, and experimental or computational methods are used to quantify the strength of the interaction. Computational methods have gained increasing popularity, but they require detailed information on the structure of the investigated species to accurately perform electronic structure computations and optimise the geometry (Global Electrophilicity Index – GEI)41 or evaluate enthalpy changes associated with fluoride/hydride coordination (Fluoride Ion Affinity – FIA, and Hydride Ion Affinity – HIA).42 Spectroscopic methods, proposed by Gutmann and Childs, are based on NMR spectroscopic probes. They offer less fundamental insights, but they can be used without knowing the speciation, and in some cases, they were successfully used to corroborate speciation studies.43,44 Since the Gutmann acceptor number (AN) has been commonly used to measure the acidity of Lewis acidic ionic liquids,4,12,45 including solvate ionic liquids,26 it has been selected for this study.Following a standard procedure,4,12,33,34,46 AN values were determined from 31P NMR chemical shifts of an NMR probe, a weakly basic hard nucleophile, triethylphosphine oxide (TEPO). The probe was dissolved in G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M(OTf)3 ionic liquids, across the available compositional range, χM(OTf)3 = 0.09–0.33.
M(OTf)3 ionic liquids, across the available compositional range, χM(OTf)3 = 0.09–0.33.
In all cases, there were several distinguishable signals, situated within a narrow range of ca. 8 ppm (Fig. 3). This was in contrast to AN measurements for chlorometallate ionic liquids, characterised by a single 31P NMR signal,45 but similar to LCCs, in which multiple Lewis acidic complexes (or multiple potential modes of TEPO coordination) are reflected in several 31P NMR signals in AN measurements.3 In all cases, the pattern of signals was the same. There were three high-intensity signals: two relatively sharp and deshielded peaks, and one broader signal shifted upfield by ca. 5 ppm, in addition to at least two low intensity peaks. This suggests the existence of several Lewis acidic species capable of interacting with TEPO. The pattern of the 31P NMR signals was broadly the same for Ga-SILs and Al-SILs, but the signals for Ga-SILs were deshielded by ca. 5 ppm with respect to those for Al-SILs, indicating a stronger interaction of TEPO (higher Lewis acidity) of Ga-SILs.
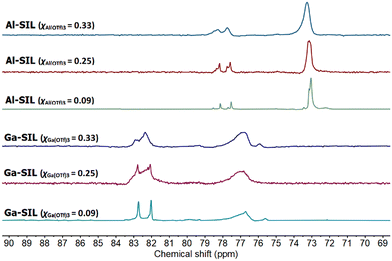 | ||
| Fig. 3 31P NMR comparison Al-SILs and Ga-SILs, studied across three compositions: χM(OTf)3 = 0.33, 0.25 and 0.09. | ||
For the purpose of numerical quantification of Lewis acidity, instead of single AN values, a range of values were reported for each ionic liquid: ANAl-SILs = 70.7–82.7; ANGa-SILs = 79.6–93.5 (Table 1). On comparing these results with the literature, it can be seen that the Lewis acidity of Al-SILs, χAl(OTf)3 = 0.33 and 0.25 (AN = 70.8–82.7), was higher than that of 1-octyl-3-methylimidazolium trifloaluminate ionic liquids, [C8mim][OTf]-Al(OTf)3, with the same molar ratio of aluminium triflate, χAl(OTf)3 = 0.33 and 0.25 (AN = 64.9–69.3),12 but lower than the AN values of archetypal chloroaluminate ionic liquids (AN = 83.3–101.9)4,45,47 or AlCl3 (AN = 85.6–87.0).4 The Lewis acidity of Ga-SILs (AN = 79.6–93.5) was higher than that of Al-SILs, approaching the Lewis acidity of chlorogallate ionic liquids [C8mim]Cl-GaCl3 with an excess of gallium chloride, χGaCl3 > 0.5 (AN = 87.7–107.3).4 Chlorogallate ionic liquids with a sub-stoichiometric loading of gallium chloride (χGaCl3 = 0.33) were only mildly acidic, with AN = 21.7.45
These results led to two questions: whether the difference in measured AN values translates into a difference in catalytic performance, and how is Lewis acidity related to speciation, considering that in chlorometallate ILs there was a clear and direct link between anionic speciation and AN values.4,45
Speciation of Group 13 SILs
In contrast to Li-based SILs, very little is known about the speciation of Al-based SILs. A single FT-IR spectroscopic study of Al(OTf)3 and diglyme mixtures, across a range of concentrations: χAl(OTf)3 = 0.286, 0.130, 0.029 and 0.0015, suggested the presence of free triflate anions in the two most diluted samples, and the prevalence of Al-OTf coordination in the more concentrated samples.35In this work, speciation of SILs was studied as a function of composition using multinuclear 1H, 13C, 27Al or 71Ga NMR spectroscopy. All SILs were studied neat; in NMR spectroscopy, a capillary with D2O was used as a lock and external reference.
The 1H NMR spectrum of neat triglyme (G3) was compared to the 1H NMR spectra of G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M(OTf)3 systems (Fig. 4). Signals corresponding to neat glyme, originating from both methylene and methyl groups (δH = 3.9–4.2 ppm), were less shielded than the corresponding signals in SILs (δH = 3.0–3.5 ppm), indicating the coordination of oxygens to the metal centre in SILs.48–50 Upon increasing the concentration of M(OTf)3 in glyme, from χM(OTf)3 = 0.09 to 0.33, the signals moved gradually downfield, as more oxygens were coordinated to aluminium at any given time. Even for very low concentrations of metal salts (χM(OTf)3 = 0.09), no signals corresponding to free glyme were visible.
M(OTf)3 systems (Fig. 4). Signals corresponding to neat glyme, originating from both methylene and methyl groups (δH = 3.9–4.2 ppm), were less shielded than the corresponding signals in SILs (δH = 3.0–3.5 ppm), indicating the coordination of oxygens to the metal centre in SILs.48–50 Upon increasing the concentration of M(OTf)3 in glyme, from χM(OTf)3 = 0.09 to 0.33, the signals moved gradually downfield, as more oxygens were coordinated to aluminium at any given time. Even for very low concentrations of metal salts (χM(OTf)3 = 0.09), no signals corresponding to free glyme were visible.
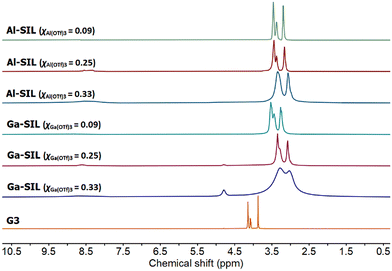 | ||
| Fig. 4 1H NMR spectra of neat glyme, G3, and solvate ionic liquids based on Al(OTf)3 or Ga(OTf)3, studied across three compositions: χM(OTf)3 = 0.33, 0.25 and 0.09. | ||
The 13C NMR spectra of neat glyme and selected SILs (Fig. 5) present a slightly different image: in all SILs, the signals corresponding to methylene carbon atoms (δ13C = 66–72 ppm) are deshielded when compared to neat glyme (δ13C = 70–72 ppm), but no changes are observed for the methyl group signals in neat glyme and in SILs (δ13C = 58 ppm). The same observation was made by Aldous and co-workers in their study of SILs based on Li[NTf2] and several glymes.49 Quartets in the 13C NMR spectra of SILs, arising from CF3 groups in triflates, are found at δ13C = ca. 119.5 ppm, which correspond to bound anions.51,52
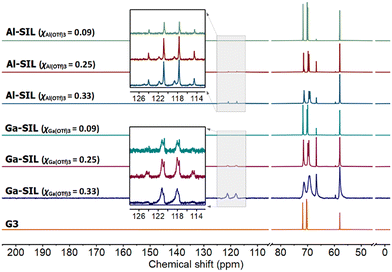 | ||
| Fig. 5 13C NMR spectra of neat glyme, G3, and solvate ionic liquids based on Al(OTf)3 or Ga(OTf)3, studied across three compositions: χM(OTf)3 = 0.33, 0.25 and 0.09. | ||
27Al NMR spectra, recorded for Al-containing SILs (Fig. 6), all featured a group of signals between −13 and 0 ppm corresponding to six-coordinate Al species, in an oxygen coordination environment.53 Multiple signals suggest the co-existence of several coordination environments of aluminium, in a manner resembling the coordination environment of trifloaluminate ionic liquids.12 There were no signals corresponding to tetrahedral (40–140 ppm), or pentacoordinate (25–60 ppm) aluminium environments,54–58 which is unsurprising given the excess of O-donors available in each sample. The very broad signal at ca. 75 ppm has been attributed to the residual signal from NMR probe (instrument artefact).12
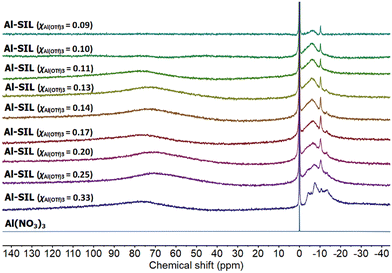 | ||
| Fig. 6 27Al NMR spectra of Al(NO3)3 in D2O, and a full series of Al-SIL compositions, χAl(OTf)3 = 0.33–0.09. | ||
Ga-SILs (χGa(OTf)3 = 0.33–0.09) were studied by 71Ga NMR spectroscopy (Fig. 7). Most spectra were flat, with signals indistinguishable from the baseline; this is commonly found in gallium-based ionic liquids with low-symmetry anions.59 It can be attributed to fast quadrupolar relaxation in these low-symmetry environments, combined with rapid exchanges between several species (as indicated by 1H NMR spectroscopy), all of which would contribute to the signal broadening. In the most concentrated samples (χGa(OTf)3 = 0.33, 0.25 and possibly 0.20), a signal at −50 ppm was detected, attributable to the octahedral environment of gallium (−50 to 50 ppm).60
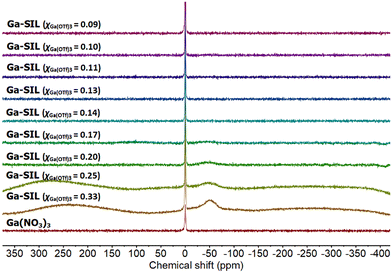 | ||
| Fig. 7 71Ga NMR spectrum of Ga(NO3)3 in D2O and a full series of Ga-SIL compositions, χGa(OTf)3 = 0.33–0.09. | ||
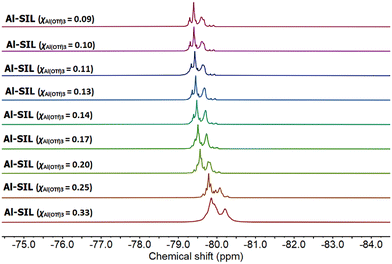
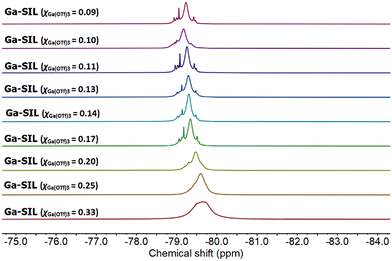
Finally, both Al-SILs and Ga-SILs were studied by 19F NMR spectroscopy across their entire compositional range (χM(OTf)3 = 0.33–0.09). The 19F NMR spectra of Al-SILs exhibited multiple signals within the chemical shift range of −79.2 to −80.2 ppm (Fig. 8), while 19F NMR signals for Ga-SILs were slightly more shielded on average, −78.9 to −79.6 ppm (Fig. 9). To our knowledge, these are the most complicated patterns of 19F NMR signals from triflate anions reported in the IL literature.
1,3-Dialkylimidazolium ILs with free [OTf]− anions, dissolved in a deuterated NMR solvent, all had single sharp 19F NMR signals within −76 to −79 ppm.61 Al-coordinated triflates in triflometallate ILs featured several merged 19F NMR signals, centred around −79 ppm, with minimal downfield shift with increasing χAl(OTf)3, whereas the parent metal-free IL, 1-octyl-3-methylimidazolium triflate, measured neat, had a singlet at −80.2 ppm.12
In this work, all 19F NMR signals shifted upfield with increasing χM(OTf)3, although the pattern of signals did not change significantly with the composition (aside from broadening due to viscosity change). It is understood that speciation of the metal remains constant across the compositional range (hence the pattern of signals remains constant), but their solvent environment changes (hence the solvent-induced change in the chemical shift). Namely, at χM(OTf)3 = 0.33, the neat sample is the neat solvate ionic liquid, composed of Al or Ga coordinated by glymes and triflate anions – a “good” SIL, with strong coulombic interactions. In the neat χM(OTf)3 = 0.09 composition, there are the same triflate anions, and the same coordination complexes of Al or Ga, but they are diluted with excess glyme, acting as a solvent. This change of solvent, from a neat ionic liquid to a solution of ionic liquid in glyme, results in a change in the chemical shift. In both Al-SILs and Ga-SILs, this transition from solution to the SIL environment is observable for χM(OTf)3 ≥ 0.20.
In conclusion, NMR spectroscopy points to both aluminium and gallium having octahedral coordination, with both [OTf]− and G3 ligands coordinated to the metal centre. It can be certainly stated that there is no single well-defined species in any sample, but there are multiple octahedral complexes, each characterised by a number of [OTf]− anions and specific numbers/hapticities of G3 ligands around the metal centre.
On comparing the 19F NMR spectra of Al-SILs (Fig. 8) and Ga-SILs (Fig. 9), further conclusions could be cautiously proposed. Firstly, although there are multiple species, both in Al-SIL and in Ga-SIL, they do not seem to change as a function of χM(OTf)3 in either system. Rather, it could be envisaged that the χM(OTf)3 = 0.33 composition is the concentrated SIL and adding more glyme (towards χM(OTf)3 = 0.09) dilutes the metal species without affecting their coordination environments. AN measurements corroborate this hypothesis, as the range of AN values appears constant for each family of SILs (Table 1). Secondly, the 19F NMR spectra of Al-SILs and Ga-SILs are markedly different; there seems to be an additional deshielded signal in the Al-SIL spectra, which reaches −80.2 ppm for χAl(OTf)3 = 0.33 (more ionic nature, viz. Fig. 2b). In Ga-SILs, all triflates appear to be bound, suggesting that the equilibrium in Fig. 2b is right-shifted for gallium.
Notably, in all samples, there is an excess of O-donors with respect to metal centres. Although no free glymes were detected by 1H or 13C NMR spectroscopy, it must be assumed that dynamic exchange of glyme ligands occurs.
Thermogravimetric analysis
The thermal stability of the solvate ionic liquids was studied by thermogravimetric analysis (TGA). TG curves are available in Fig. S1 and S2 in the ESI.† In contrast to their thermally stable precursors, glyme (Td = 167 °C), Al(OTf)3 (Td = 221 °C) and Ga(OTf)3 (Td = 182 °C), the thermal stability of the investigated systems was much lower with Td5% = 127 °C for Al-SILs and Td5% = 105 °C Ga-SILs, respectively. This unfortunately limits the span of operative conditions for these glymes, but also suggests that the metal centre is highly Lewis acidic, effectively catalysing the decomposition of the glyme at a much lower temperature.Catalytic performance in a [3 + 3] cycloaddition reaction
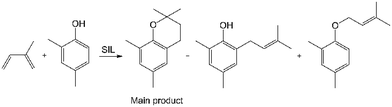
A [3 + 3] cycloaddition was selected as a test reaction for the catalytic activity of the new SILs. The yield and selectivity of products in this reaction depend strongly both on the activity of the Lewis acidic catalyst and on the reaction conditions, which makes it sensitive to subtle changes and therefore a good model to distinguish between catalysts.62,63The synthesis of chromane from 2,4-dimethylphenol and isoprene (Scheme 1) was chosen as a model [3 + 3] cycloaddition. Chromane is a part of a structure of more complicated compounds, including various forms of vitamin E and flavonoids,64 which makes it a common synthetic target. The reaction is typically catalysed by metal triflates, promoting high selectivity towards chromane (main product, Scheme 1).65
All reactions were carried out solventless, at 35 °C, using liquid reactants (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of isoprene
2 molar ratio of isoprene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,4-dimethylphenol). Conversion of 2,4-dimethylphenol was monitored using GC, and each reaction was carried out until a plateau of conversion was reached. All SILs formed homogeneous solutions when added to the reaction mixture, whereas their corresponding solid metal triflates, studied as comparators, were suspended in the reaction mixture.
2,4-dimethylphenol). Conversion of 2,4-dimethylphenol was monitored using GC, and each reaction was carried out until a plateau of conversion was reached. All SILs formed homogeneous solutions when added to the reaction mixture, whereas their corresponding solid metal triflates, studied as comparators, were suspended in the reaction mixture.
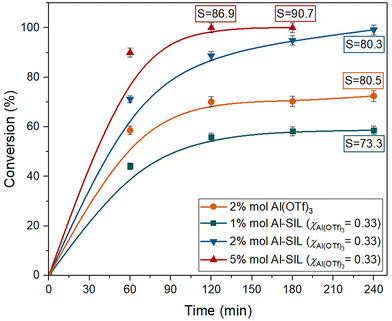
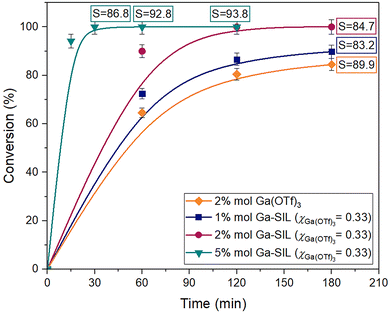
The catalytic performance of Al(OTf)3, at 2 mol% loading of aluminium with respect to isoprene, was compared to Al-SIL (χAl(OTf)3 = 0.33), at 1, 2 and 5 mol% (Fig. 10). While the conversion for 2 mol% of Al(OTf)3 reached a plateau at ca. 70%, the same loading of Al-SIL (χAl(OTf)3 = 0.33) gave ca. 99% conversion after 240 min, with the same selectivity to chromane of ca. 80%. Increasing the Al-SIL loading to 5 mol% resulted in improved reaction kinetics and selectivity; it gave full substrate conversion within 120 min, with selectivity reaching a maximum of 90.7% after 180 min. Decreasing the Al-SIL loading to 1 mol% had the opposite effect, with performance lower than that of the benchmark catalyst, i.e. 2 mol% of Al(OTf)3.
In a series of analogous experiments, the performance of Ga(OTf)3, at 2 mol% loading, was compared to Ga-SIL (χGa(OTf)3 = 0.33), at 1, 2 and 5 mol% loadings (Fig. 11). The reaction catalysed with 2 mol% of Ga(OTf)3 reached ca. 91% conversion after 240 min, with selectivity approaching 90%, whereas the same loading of Ga-SIL (χGa(OTf)3 = 0.33) gave full conversion after only 30 min. The extended reaction time increased the selectivity, from 86.8% after 30 min to 93.8% after 120 min.
Both gallium triflate and Ga-SIL significantly outperformed their aluminium-based analogues, in keeping with higher AN values recorded for Ga-SIL (Table 1). The Ga-SIL (χGa(OTf)3 = 0.33, loading 2 mol%) gave full conversion in 120 min, whereas the analogous Al-SIL required 240 min.
The best outcomes, in terms of conversion and selectivity, achieved with each tested catalyst, are given in Table 2, along with the corresponding experimental conditions. Both Al-SIL and Ga-SIL outperformed their corresponding triflates at the same loadings of 2 mol%. Inferior reaction rates in M(OTf)3-catalysed reactions could be attributed to poor mass transport, as the triflate salts were suspended rather than dissolved. However, for both M(OTf)3 catalysts, conversions reached plateau values, whereas SILs enabled both full conversions and higher selectivities to chromane, which cannot be attributed solely to mass transfer. We therefore concluded that altering coordination around the metal centres, from triflate-only to mixed glyme/triflate complexes, had the dual benefit of (i) increased solubility in the organic phase and (ii) increased catalytic activity.
| No. | Catalyst | χ M(OTf)3 | Catalyst loading (mol%) | Time (min) | Conversion (%) | Selectivity (%) |
|---|---|---|---|---|---|---|
| Reaction conditions: 2,4-dimethylphenol (8 mmol), isoprene (4 mmol), 1000 rpm, T = 35 °C, amount of catalyst calculated in relation to isoprene. | ||||||
| 1 | Al(OTf)3 | 1.00 | 2 | 180 | 70.3 | 80.3 |
| 2 | Al-SIL | 0.33 | 2 | 240 | 99.2 | 80.3 |
| 3 | Al-SIL | 0.33 | 5 | 180 | 100.0 | 90.7 |
| 4 | Al-SIL | 0.09 | 5 | 240 | 64.0 | 70.9 |
| 5 | Ga(OTf)3 | 1.00 | 2 | 240 | 91.4 | 83.2 |
| 6 | Ga-SIL | 0.33 | 2 | 120 | 100.0 | 82.8 |
| 7 | Ga-SIL | 0.33 | 5 | 120 | 100.0 | 93.8 |
| 8 | Ga-SIL | 0.09 | 5 | 240 | 92.6 | 84.3 |
Following this reasoning, it was concluded that further altering of the coordination environment of Al(III) and Ga(III), from triflate to glyme ligands, could be beneficial. To test this hypothesis, both SILs were tested at χM(OTf)3 = 0.09, with a vastly increased concentration of G3 with respect to metal. However, even at 5 mol% loading, the χM(OTf)3 = 0.09 SILs produced inferior results (Table 2, entries 4 and 8), when compared to χM(OTf)3 = 0.33 SILs (Table 2, entries 2, 3, 6 and 7). Most likely, liquids at χM(OTf)3 = 0.09 are merely solutions of SILs of certain fixed compositions in the excess of glyme; upon addition to the reaction mixture, excess glyme is simply washed away and acts as a dilutant to the system, decreasing the overall concentration of reactants.
The recyclability of the best-performing SIL, Ga-SIL (χGa(OTf)3 = 0.33), was tested by extracting the residual substrate and product with anhydrous hexane, after which the phase-separated catalyst layer was isolated, washed twice with hexene, concentrated and used in the next reaction cycle. Full conversion of the substrate was achieved over 4 consecutive reaction cycles, with selectivities above 90% (Table 3).
| Cycle no. | Conversion (%) | Selectivity (%) |
|---|---|---|
| Reaction conditions: 2,4-dimethylphenol (12–16 mmol), isoprene (6–8 mmol), 1000 rpm, T = 35 °C, 5 mol% of Ga-SIL (χGa(OTf)3 = 0.33) (amount of catalyst calculated in relation to isoprene), 120 min. | ||
| 1 | 100.0 | 93.8 |
| 2 | 100.0 | 94.0 |
| 3 | 100.0 | 92.6 |
| 4 | 100.0 | 91.5 |
In conclusion, the G3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga(OTf)3, χGa(OTf)3 = 0.33 SIL was found to be an excellent catalyst for the synthesis of chromane, giving full conversion of isoprene within 2 h, with selectivity towards 2,2-dimethyl-6,8-dimethylchromane reaching 93.8%, slightly higher than those of previously reported catalytic systems, ranging from 80% to 92%.12,66,67 The catalytic performance of Al-SILs and Ga-SILs has followed the AN trend.
Ga(OTf)3, χGa(OTf)3 = 0.33 SIL was found to be an excellent catalyst for the synthesis of chromane, giving full conversion of isoprene within 2 h, with selectivity towards 2,2-dimethyl-6,8-dimethylchromane reaching 93.8%, slightly higher than those of previously reported catalytic systems, ranging from 80% to 92%.12,66,67 The catalytic performance of Al-SILs and Ga-SILs has followed the AN trend.
Conclusions
New solvate ionic liquids based on aluminium(III) and gallium(III) triflates, and G3 have been synthesised, characterised and used as Lewis acidic catalysts for the synthesis of chromane. Both triflate salts dissolved in G3 at low concentrations (χM(OTf)3 = 0.09) and formed homogeneous liquids up to a metal triflate loading of χM(OTf)3 = 0.33. It was found that both metals were octahedral across the entire compositional range, and both G3 and [OTf]− were included in the first coordination sphere of the metal.From multinuclear NMR spectroscopic experiments, it appeared that the coordination environment remained similar across the compositional range, for each of the two metals. Furthermore, it was suggested that speciation of Al-SILs was different from that of Ga-SILs, potentially with more free triflate in the former. AN values (an experimental measure of Lewis acidity) were constant for each SIL family, across the entire compositional range: ca. 71–83 for Al-SILs and ca. 80–93 for Ga-SILs. These values lie within a relatively high acidity range, despite a fully occupied coordination shell.
The catalytic activity of SILs was tested in a model [3 + 3] cycloaddition, yielding 2,2-dimethyl-2,4-dimethylchromane. Both families of SILs were fully dissolved in the reaction mixtures, in contrast to the parent metal triflates, and their catalytic activity has been enhanced when compared at the same metal loading. The catalytic performance was aligned with AN measurements, with Ga-SILs outperforming Al-SILs. The best catalyst (Ga-SIL χM(OTf)3 = 0.33) gave full substrate conversion and a high selectivity of 93.8% after 2 h at 35 °C, and could be recycled four times, retaining consistently high conversion and selectivity.
Given the notorious difficulties in dissolving metal triflates, converting them to SILs may offer a broadly-applicable and robust approach to generate well-soluble metal triflate catalysts; this strategy is likely applicable beyond Group 13, to rare earth triflates and transition metal triflates. Further detailed studies on the structure and applications of Group 13 SILs are currently ongoing in our group.
Author contributions
Justyna Więcławik: data curation, formal analysis, investigation, methodology, validation, visualization and writing – original draft; Alina Brzęczek-Szafran: conceptualisation, formal analysis, methodology, visualization, writing – original draft, and writing – review & editing; Sebastian Jurczyk: formal analysis and methodology; Karolina Matuszek: methodology, validation, and writing – review & editing; Małgorzata Swadźba-Kwaśny: conceptualisation, funding acquisition, supervision, writing – original draft, and writing – review & editing; Anna Chrobok: conceptualisation, funding acquisition, supervision, writing – original draft, and writing – review & editing.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from the National Science Centre, Poland (grant no. UMO-2020/39/B/ST8/00693) is gratefully acknowledged. The authors also express gratitude to the Polish National Agency for Academic Exchange (under the Academic International Partnerships Program, grant agreement PPI/APM/2018/1/00004) for financial support of the internship at The QUILL Research Centre, Queen's University Belfast, which enabled a part of the speciation study, the Polish National Agency for Academic Exchange and grant agreement BPI/PST/2021/1/00039 for enabling scientific discussions in a project funded within the Strategic Partnerships program that helped us interpret a phenomenon described above.Notes and references
- C. A. Angell, J. Electrochem. Soc., 1965, 112, 1224 CrossRef.
- C. Austen Angell, Y. Ansari and Z. Zhao, Faraday Discuss., 2012, 154, 9–27 RSC.
- F. Coleman, G. Srinivasan and M. Swadźba-Kwaśny, Angew. Chem., Int. Ed., 2013, 52, 12582–12586 CrossRef PubMed.
- J. M. Hogg, L. C. Brown, K. Matuszek, P. Latos, A. Chrobok and M. Swadźba-Kwaśny, Dalton Trans., 2017, 46, 11561–11574 RSC.
- J. M. Hogg, F. Coleman, A. Ferrer-Ugalde, M. P. Atkins and M. Swadźba-Kwaśny, Green Chem., 2015, 17, 1831–1841 RSC.
- K. Matuszek, A. Chrobok, J. M. Hogg, F. Coleman and M. Swadźba-Kwaśny, Green Chem., 2015, 17, 4255–4262 RSC.
- M. Lijewski, J. M. Hogg, M. Swadźba-Kwaśny, P. Wasserscheid and M. Haumann, RSC Adv., 2017, 7, 27558–27563 RSC.
- S. Kobayashi, M. Sugiura, H. Kitagawa and W. W. L. Lam, Chem. Rev., 2002, 102, 2227–2302 CrossRef CAS PubMed.
- L. Massi, J. F. Gal and E. Duñach, ChemPlusChem, 2022, 87, e202200037 CrossRef CAS.
- G. A. Olah, O. Farooq, S. M. F. Farnia and J. A. Olah, J. Am. Chem. Soc., 1988, 110, 2560–2565 CrossRef CAS.
- M. Distaso and E. Quaranta, Tetrahedron, 2004, 60, 1531–1539 CrossRef CAS.
- P. Latos, A. Culkin, N. Barteczko, S. Boncel, S. Jurczyk, L. C. Brown, P. Nockemann, A. Chrobok and M. Swadźba-Kwaśny, Front. Chem., 2018, 6, 1–15 CrossRef.
- T. Tamura, T. Hachida, K. Yoshida, N. Tachikawa, K. Dokko and M. Watanabe, J. Power Sources, 2010, 195, 6095–6100 CrossRef CAS.
- T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 8761–8772 RSC.
- T. Mandai, K. Yoshida, S. Tsuzuki, R. Nozawa, H. Masu, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2015, 119, 1523–1534 CrossRef.
- T. Tamura, K. Yoshida, T. Hachida, M. Tsuchiya, M. Nakamura, Y. Kazue, N. Tachikawa, K. Dokko and M. Watanabe, Chem. Lett., 2010, 39, 753–755 CrossRef.
- C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, H. Moon, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2014, 118, 5144–5153 CrossRef PubMed.
- C. Zhang, A. Yamazaki, J. Murai, J. W. Park, T. Mandai, K. Ueno, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 17362–17373 CrossRef.
- H. Hirayama, N. Tachikawa, K. Yoshii, M. Watanabe and Y. Katayama, Electrochemistry, 2015, 83, 824–827 CrossRef.
- K. Ueno, J. Murai, K. Ikeda, S. Tsuzuki, M. Tsuchiya, R. Tatara, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2016, 120, 15792–15802 CrossRef.
- M. Watanabe, K. Dokko, K. Ueno and M. L. Thomas, Bull. Chem. Soc. Jpn., 2018, 91, 1660–1682 CrossRef.
- Z. Yu, C. Fang, J. Huang, B. G. Sumpter and R. Qiao, ACS Appl. Mater. Interfaces, 2018, 10, 32151–32161 CrossRef.
- S. Terada, K. Ikeda, K. Ueno, K. Dokko and M. Watanabe, Aust. J. Chem., 2019, 72, 70–80 CrossRef.
- S. Wei, Z. Li, K. Kimura, S. Inoue, L. Pandini, D. Di Lecce, Y. Tominaga and J. Hassoun, Electrochim. Acta, 2019, 306, 85–95 CrossRef.
- D. J. Eyckens and L. C. Henderson, Front. Chem., 2019, 7, 1–15 CrossRef PubMed.
- D. J. Eyckens, M. E. Champion, B. L. Fox, P. Yoganantharajah, Y. Gibert, T. Welton and L. C. Henderson, Eur. J. Org. Chem., 2016, 2016, 913–917 CrossRef.
- A. Obregón-Zúñiga, M. Milán and E. Juaristi, Org. Lett., 2017, 19, 1108–1111 CrossRef.
- D. J. Eyckens and L. C. Henderson, RSC Adv., 2017, 7, 27900–27904 RSC.
- S. Di Pietro, V. Bordoni, A. Mezzetta, C. Chiappe, G. Signore, L. Guazzelli and V. Di Bussolo, Molecules, 2019, 24, 1–9 CrossRef PubMed.
- N. Hameed, D. J. Eyckens, B. M. Long, N. V. Salim, J. C. Capricho, L. Servinis, M. De Souza, M. D. Perus, R. J. Varley and L. C. Henderson, ACS Appl. Polym. Mater., 2020, 2, 2651–2657 CrossRef.
- T. Mandai, K. Dokko and M. Watanabe, Chem. Rec., 2019, 19, 708–722 CrossRef PubMed.
- Z. Ma, M. Forsyth, D. R. MacFarlane and M. Kar, Green Energy Environ., 2019, 4, 146–153 CrossRef.
- K. Matuszek, A. Chrobok, F. Coleman, K. R. Seddon and M. Swadźba-Kwaśny, Green Chem., 2014, 16, 3463–3471 RSC.
- A. Brzęczek-Szafran, J. Więcławik, N. Barteczko, A. Szelwicka, E. Byrne, A. Kolanowska, M. Swadźba-Kwaśny and A. Chrobok, Green Chem., 2021, 23, 4421–4429 RSC.
- L. D. Reed, A. Arteaga and E. J. Menke, J. Phys. Chem. B, 2015, 119, 12677–12681 CrossRef PubMed.
- L. D. Reed, S. N. Ortiz, M. Xiong and E. J. Menke, Chem. Commun., 2015, 51, 14397–14400 RSC.
- S. Gu, Y. Haoyi, Y. Yuan, Y. Gao, N. Zhu, F. Wu, Y. Bai and C. Wu, Energy Mater. Adv., 2022, 1, 1–10 Search PubMed.
- A. Kitada, K. Nakamura, K. Fukami and K. Murase, Electrochemistry, 2014, 82, 946–948 CrossRef.
- A. Kitada, K. Nakamura, K. Fukami and K. Murase, Electrochim. Acta, 2016, 211, 561–567 CrossRef.
- Z. Zhang, A. Kitada, S. Gao, K. Fukami, N. Tsuji, Z. Yao and K. Murase, ACS Appl. Mater. Interfaces, 2020, 12, 43289–43298 CrossRef PubMed.
- A. R. Jupp, T. C. Johnstone and D. W. Stephan, Dalton Trans., 2018, 47, 7029–7035 RSC.
- P. Erdmann, J. Leitner, J. Schwarz and L. Greb, ChemPhysChem, 2020, 21, 987–994 CrossRef.
- J. Estager, P. Nockemann, K. R. Seddon, M. Swadźba-Kwaśny and S. Tyrrell, Inorg. Chem., 2011, 50, 5258–5271 CrossRef PubMed.
- M. Currie, J. Estager, P. Licence, S. Men, P. Nockemann, K. R. Seddon, M. Swadźba-Kwaśny and C. Terrade, Inorg. Chem., 2013, 52, 1710–1721 CrossRef PubMed.
- J. Estager, A. A. Oliferenko, K. R. Seddon and M. Swadźba-Kwaśny, Dalton Trans., 2010, 39, 11375–11382 RSC.
- K. Matuszek, S. Coffie, A. Chrobok and M. Swadźba-Kwaśny, Catal. Sci. Technol., 2017, 7, 1045–1049 RSC.
- M. Sakhalkar, R. P. Choudhury, V. Bhakthavatsalam, S. V. Lande, J. Pradhan and S. Chandra, J. Mol. Struct., 2020, 1222, 128936 CrossRef.
- N. Peddagopu, P. Rossi, C. Bonaccorso, A. Bartasyte, P. Paoli and G. Malandrino, Dalton Trans., 2020, 49, 1002–1006 RSC.
- J. J. Black, A. Dolan, J. B. Harper and L. Aldous, Phys. Chem. Chem. Phys., 2018, 20, 16558–16567 RSC.
- S. Sun, Y. Niu, Q. Xu, Z. Sun and X. Wei, RSC Adv., 2015, 5, 46564–46567 RSC.
- L. L. Tolstikova, A. V. Bel'Skikh and B. A. Shainyan, Russ. J. Org. Chem., 2010, 46, 383–388 CrossRef.
- P. Latos, A. Wolny, J. Zdarta, F. Ciesielczyk, S. Jurczyk, T. Jesionowski and A. Chrobok, Environ. Technol. Innovation, 2023, 31, 103164 CrossRef.
- M. M. Finnegan, S. J. Rettig and C. Orvig, J. Am. Chem. Soc., 1986, 108, 5033–5035 CrossRef.
- G. A. Olah, O. Farooq, S. M. F. Farnia, M. R. Bruce, F. L. Clouet, P. R. Morton, G. K. S. Prakash, R. C. Stevens, R. Bau, K. Lammertsma, S. Suzer and L. Andrews, J. Am. Chem. Soc., 1988, 110, 3231–3238 CrossRef.
- D. A. Atwood, Coord. Chem. Rev., 1998, 176, 407–430 CrossRef.
- M. Choi, K. Matsunaga, F. Oba and I. Tanaka, J. Phys. Chem. C, 2009, 113, 3869–3873 CrossRef CAS.
- A. W. Apblett, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd, 2012 Search PubMed.
- K. N. Tayade, M. Mishra, K. Munusamy and R. S. Somani, Catal. Sci. Technol., 2015, 5, 2427–2440 RSC.
- K. R. Seddon, G. Srinivasan, M. Swadźba-Kwaśny and A. R. Wilson, Phys. Chem. Chem. Phys., 2013, 15, 4518–4526 RSC.
- Z. L. Ma, K. M. Wentz, B. A. Hammann, I. Y. Chang, M. K. Kamunde-Devonish, P. H. Y. Cheong, D. W. Johnson, V. V. Terskikh and S. E. Hayes, Chem. Mater., 2014, 26, 4978–4983 CrossRef CAS.
- N. V. Ignat'ev, P. Barthen, A. Kucheryna, H. Willner and P. Sartori, Molecules, 2012, 17, 5319–5338 CrossRef.
- P. Quadrelli, Modern applications of cycloaddition chemistry, Elsevier, 2019 Search PubMed.
- J. Deng, X. N. Wang and R. P. Hsung, in Wiley Blackwell 6, Wiley Blackwell, 2014, vol. 9781118299, pp. 283–354 Search PubMed.
- C. Schneider, Mol. Nutr. Food Res., 2005, 49, 7–30 CrossRef PubMed.
- S. W. Youn and J. I. Eom, J. Org. Chem., 2006, 71, 6705–6707 CrossRef PubMed.
- Y. Yamamoto and K. Itonaga, Org. Lett., 2009, 11, 717–720 CrossRef PubMed.
- T. T. Dang, F. Boeck and L. Hintermann, J. Org. Chem., 2011, 76, 9353–9361 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Referenced data S1 and S2, detailed experimental information and TGA thermal curves. See DOI: https://doi.org/10.1039/d4dt02314e |
| This journal is © The Royal Society of Chemistry 2024 |