Open Access Article
Open Access ArticleProbe molecular diffusivity in single ternary inorganic–organic microdroplets via interfacial ozonolysis of thiosulfate†
Tzu-Chiao
Hung
a,
Feng-Yu
Lin
a,
Shao-Hung
Hsu
a,
Toshio
Kasai
ab and
Yuan-Pin
Chang
 *ac
*ac
aDepartment of Chemistry, National Sun Yat-sen University, Kaohsiung 80424, Taiwan. E-mail: ypchang@mail.nsysu.edu.tw
bDivision of Precision Engineering and Applied Physics, Graduate School of Engineering, Osaka University, Suita, Osaka, Japan
cAerosol Science Research Center, National Sun Yat-sen University, Kaohsiung 80424, Taiwan
First published on 14th October 2024
Abstract
In this study, aqueous sodium thiosulfate microdroplets mixed with glucose or sucrose are used as a model system of ternary inorganic–organic aerosols. The interfacial ozone oxidation of thiosulfate, which has been characterized in our previous work [J. Phys. Chem. C, 2023, 127, 6248], is exploited via aerosol optical tweezers to determine the bulk diffusivity of thiosulfate in such inorganic–organic microdroplets under variable conditions of RH and inorganic–organic mass ratio. A kinetic multilayer model of aerosol surface and bulk chemistry (KM-SUB) is also utilized to retrieve the bulk diffusivity of thiosulfate from the kinetics measurement results. The kinetics results at relatively high RHs show that the observed reaction time scale increases when lowering RH, and the magnitude of thiosulfate diffusion coefficients is between Stokes–Einstein predictions for binary sodium thiosulfate–water systems and binary organic–water systems, indicating the dominant diffusion kinetics of thiosulfate in viscous fluid matrices of homogeneously mixed inorganics and organics. However, when RH is below 30% for glucose or 40% for sucrose, the kinetics results exhibit incomplete thiosulfate depletion upon prolonged ozone exposure, indicating the co-existence of two distinctly fast and slow diffusion components of thiosulfate. The diffusion coefficients of undepleted thiosulfates become similar to the SE predictions of binary organic–water systems, and they are a few orders of magnitude smaller than those of rapidly depleted thiosulfates. According to the literature, such a diffusion limitation may be attributed to an ion–molecule effect which may lead to the formation of inorganic–organic microgels in aerosols at atmospherically relevant RHs. The results of this work suggest that the cooperative effects of inorganics and organics can play a potential role in the reaction kinetics of atmospheric inorganic–organic aerosols.
Environmental significanceThis study investigates bulk diffusivity in inorganic–organic microdroplets as a model of atmospheric aerosols, elucidating potential influences of ion–molecule interactions on the reaction kinetics of atmospheric aerosols. By examining the diffusivity of thiosulfates in microdroplets composed of sodium thiosulfate and organics such as glucose or sucrose, the results demonstrate how the diffusion of thiosulfates subjected to these interactions can be significantly restricted. This limitation leads to incomplete depletions of thiosulfates in aerosol particles upon prolonged ozone exposure times and the co-existence of multiple thiosulfate diffusion coefficients, particularly at lower relative humidity. Such findings emphasize the need to consider these ion–molecule interactions in atmospheric models to better predict the environmental and climatic impacts of atmospheric aerosols, as well as their reaction kinetics. |
Introduction
Atmospheric aerosol particles are often mixtures of water, inorganic and organic species,1–7 and their physicochemical properties and chemistry can highly depend on the individual and cooperative influences of chemical species inside such complex compositions. Among the physicochemical properties of aerosols, molecule diffusion plays a fundamental role in the multiphase chemistry and condensed phase mass transport of aerosols.1,8–10 When assuming a valid Stokes–Einstein (SE) relationship, the bulk diffusivity in an aerosol particle can be estimated from its viscosity. The viscosity of aerosols is usually used to indicate the phase state of aerosols, and there have been numerous well-established techniques for determining its magnitude.8 The recent studies by Rovelli et al. and Song et al. determined the viscosities for several ternary (aqueous) inorganic–organic aerosol systems as a benchmark model for atmospheric aerosols, such as the ternary mixtures of sucrose and inorganic salts.11,12 Their results show that the water-activity-dependent viscosities for these ternary inorganic–sucrose mixtures are between those for binary sucrose–water systems and binary inorganic–water systems, agreeing with the bulk-phase predictions which only take into account the individual contributions of chemical species.11–14 However, the recent studies by Richards et al. found that some ternary inorganic–organic systems mixing with divalent ions can have enhanced viscosities which can be significantly larger than those of binary organic–water systems, probably because of cooperative interactions between divalent ions and organic molecules.1,15 This finding implies the non-negligible role of intermolecular interactions in the properties and chemistry of mixed inorganic–organic systems.1,15It should also be noted that the intermolecular interaction is often used to rationalize the observed failure of the SE equation in the case of small molecules diffusing through a matrix of large organic molecules, such as water diffusion in sucrose and secondary organic aerosols.16–25 Thus, in spite of the approximation via the SE equation, it is also desirable to directly determine molecular diffusivity in aerosol particles. Recently, several research groups have exploited the techniques of trapping aerosol particles coupled with various spectroscopy-based methods to determine molecular diffusion in single microdroplets.26 Davies and Wilson utilized the methods of H2O/D2O exchange and aerosol optical tweezers (AOTs) to deduce the water diffusion coefficients in optically trapped microdroplets.10 Nadler et al. also utilized this isotope tracer method while combining with electrodynamic balance to perform the water diffusion measurements of levitated microdroplets.27 Preston et al. determined water diffusivity directly via precision measurement of the frequency-dependent radius response from optically trapped microdroplets, when exposed to oscillations of relative humidity (RH).28 Krieger et al. utilized electrodynamic balance coupled with high-resolution Mie resonance spectroscopy to determine the diffusivities of CO2 and H2O from their mass transport processes in levitated microdroplets.21,22 Marshall et al. exploited the ozonolysis of maleic acid aerosol particles via AOTs to determine the bulk diffusivities of ozone and maleic acid.19,29 Following a similar strategy, Hsu et al. recently demonstrated that the surface ozone oxidation kinetics of sodium thiosulfate microdroplets mixing with sucrose can be exploited to probe the bulk diffusivity of thiosulfates.30 Besides the translational diffusion investigated in the above studies, Miura et al. utilized AOTs and polarized Raman spectroscopy to determine the vibrational and rotational relaxation (diffusion) times which were retrieved from the Fourier transformation of molecular Raman bands.31,32
In this work, we focused on investigating the diffusivity of inorganic ions in ternary organic–inorganic microdroplets via reaction kinetics. We utilized sodium thiosulfate (STS), Na2S2O3, as the model of inorganic salts, and glucose (monosaccharide) or sucrose (disaccharide) as a proxy of soluble organic compounds in atmospheric aerosols. Glucose and sucrose are the typical species of free saccharides in atmospheric aerosols,5 and their aqueous mixtures have been exploited as benchmark systems among laboratory investigations associated with atmospheric aerosols.1,10–12,14–16,19,20,23,25,27,29 This work exploited the interfacial oxidation reaction kinetics of S2O32− with gaseous O3 in ternary aqueous STS microdroplets mixing with glucose or sucrose as simplified models of mixed organic–inorganic aerosols to determine the diffusivities of S2O32− in aerosol bulks under variable conditions of RH and chemical composition. This multiphase reaction has been investigated in detail in several previous studies of atmospheric aerosol chemistry.30,34–36 The kinetics measurements of this reaction in single levitated microdroplets were performed with AOTs integrated with Raman spectroscopy, and a kinetic model dedicated to aerosol kinetics was also employed to retrieve the diffusion coefficients of S2O32− from the kinetics results. Based on these results, the observed dependence of S2O32− diffusivity on RH and chemical composition, as well as their implications for atmospheric aerosols, will be addressed in this report.
Experimental description
The AOT apparatus used in this work has been described in detail elsewhere,30,37,38 and, therefore, it is only briefly described here. A continuous-wave laser emitting at 532 nm was utilized as a trapping and Raman excitation laser. For optimizing the efficiency of optical trapping, the laser beam was expanded using a pair of convex lenses as a telescope, and then it was guided into an inverted microscope. After being directed upwardly by a beamsplitter, the laser beam was focused by a high numerical aperture objective into an aerosol trapping chamber mounted on the stage of the microscope. When a suspending microdroplet was optically trapped at the focus spot of the trapping laser, the Raman scattering of the trapped microdroplet was created simultaneously by the same laser, which had a power of a few mW after passing the objective. This Raman scattering light was then collected by the same objective, and then it was imaged onto the entrance slit of a Raman spectrometer. The integrated time for acquiring time-resolved Raman spectra was 1.2 seconds, and the spectral resolution was about a couple of cm−1, determined from the FWHMs of observed whisper gallery modes (WGMs).When carrying out optical trapping experiments, a dense flow of aqueous aerosols (2 to 6 μm in diameter)38 produced by a medical nebulizer was injected into the trapping chamber for several minutes, until a single microdroplet was optically trapped. The RH in the trapping chamber was maintained from 20% to over 80% via flow of mixed dry and humidified nitrogen, and it was monitored using a humidity sensor (accuracy: 3.5%) attached to the chamber. Gaseous ozone was produced from discharging pure oxygen in an ozone generator, and this gas mixture of O2 and O3 was further diluted with dry nitrogen in a container. When performing the kinetics measurements, the premixed gas flow of O2, O3 and N2 with a flow rate of several sccm was combined with the RH regulated nitrogen gas flow with a flow rate of a few hundred sccm, before injecting into the trapping chamber. The partial pressure of ozone in the mixed gaseous flow was on-line monitored via its UV absorption peak at 250 nm. The sample solutions filled in the medical nebulizer were prepared at several mass ratios, for example, STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (glucose or sucrose)
(glucose or sucrose)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water = 5
water = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15, 4
15, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15, 3
15, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 and 2
15 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15. Such a water-to-solute stoichiometry ratio allows for a low viscosity of the sample solution and thus efficient generation of aerosols from the medical nebulizer. It should be noted that the equilibrium water contents of microdroplets at given RHs are not equivalent to the above water-to-solute stoichiometries for sample solutions filled in the medical nebulizer. The choice of the above STS
15. Such a water-to-solute stoichiometry ratio allows for a low viscosity of the sample solution and thus efficient generation of aerosols from the medical nebulizer. It should be noted that the equilibrium water contents of microdroplets at given RHs are not equivalent to the above water-to-solute stoichiometries for sample solutions filled in the medical nebulizer. The choice of the above STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (glucose or sucrose) mass ratios is similar to those applied in the literature.11,29 However, this work did not further use a STS
(glucose or sucrose) mass ratios is similar to those applied in the literature.11,29 However, this work did not further use a STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (glucose or sucrose) mass ratio of 1
(glucose or sucrose) mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, as the low concentration of STS in microdroplets with this mass ratio resulted in the weak Raman intensities of S2O32−, making any further kinetic measurement unfeasible.
5, as the low concentration of STS in microdroplets with this mass ratio resulted in the weak Raman intensities of S2O32−, making any further kinetic measurement unfeasible.
Kinetic modelling
To simulate the observed ozone oxidation kinetics of S2O32− in microdroplets, the present work used the kinetic multilayer model of aerosol surface and bulk chemistry (KM-SUB), which can provide time- and depth-resolved numerical calculations of mass transport and chemical reactions in spherical particles and thin films.39–42 The KM-SUB model utilizes the rate equations derived under the Pöschl–Rudich–Ammann framework43 to take into account the following surface and bulk processes of volatile species, such as O3, and involatile species, such as S2O32−, in an aerosol particle: gas-phase and bulk-phase diffusion, surface adsorption and desorption, surface-bulk exchange, and chemical reactions at the air–water interface and in the aerosol bulk of the particle.29,30 Since the interfacial and bulk reactions of S2O32− + O3 were characterized in our previous work and literature,30,33 the data-model comparison in the present work further allows for retrieving the bulk diffusivity of S2O32− in microdroplets. Note that to simplify KM-SUB employed in the present work, the reaction of S2O32− and O3 is assumed to be a bimolecular reaction, and the reaction products are assumed to have the same physical properties as the S2O32− reactant.30 The reaction scheme provided in the next section can support this assumption. Also for simplicity, any secondary chemistry and the evaporation of any volatile product are not included in KM-SUB. The rate equations implemented in KM-SUB for such a reaction system of S2O32− and O3 in aerosol microdroplets have been summarized in our recent work.30 Finally, it should also be noted that the model used in the present work assumes a constant droplet radius during the reaction process, and the typical percentage changes of the aerosol radius (about 2 to 5%) and aerosol volume (about 6 to 15%) that existed in kinetics measurements were taken into account in the error analysis instead. The representative data (Expt. 59) in Table S5† show that its radius change during the reaction process is only 50 nm or around 2% with respect to the radius (3.3 μm).Tables 1 and 2 list the key input parameters of KM-SUB for the present work, as well as their further details. According to Table 1, most of the KM-SUB input parameters can be fixed using literature values, experimental data and laboratory conditions. The thickness of each bulk layer in KM-SUB is set to 1 nm. For the input parameters associated with the chemical reaction, our previous work30 has determined the bimolecular surface reaction rate coefficient of the S2O32− + O3 reaction, kSLR, when implementing the literature value from Kanofsky and Sima33 as the bimolecular bulk reaction rate coefficient of the same reaction, kBR, in KM-SUB, as shown in Table 1. It should be noted that this kSLR provided in our previous work is inversely proportional to the desorption lifetime of O3, τd, utilized in KM-SUB.30 Such coupling is because in the framework of KM-SUB, the oxidation kinetics of surface S2O32−via surface-adsorbed O3 depends on the product of τd and kSLR.30 The choice of τd = 2 × 10−7 s in our studies has the same order of magnitude as those converged in recent kinetic studies of ozonolysis,44,45 while the range of τd among various literature studies could potentially span over several orders of magnitude.30,44,46 Nevertheless, any model run performed in this work exhibits no sensitivity to the order of magnitude of τd, ranging from 10−11 s to 10−7 s, since the requisite coupling of τd and kSLR in KM-SUB secures essentially the same aerosol reaction kinetics.30
| Symbol | Unit | Meaning | Value |
|---|---|---|---|
| a Adopted from the parameter set applied by Hsu et al. (ref. 30). b Droplet ionic strength I is defined as: I = 3[S2O32−]b,0. c See Tables S3 and S4 for individual values. d From Kanofsky and Sima (ref. 33). e δ = 0.8 nm. | |||
| α s,0 | Surface accommodation coefficient of O3 | 0.05a | |
| τ d | s | Desorption lifetime of O3 | 2 × 10−7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| k SLR | cm2 s−1 | Bimolecular surface reaction coefficient | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(kSLR) = log 10(kSLR) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(1.5 × 10−10) + 0.017Ia,b,c 10(1.5 × 10−10) + 0.017Ia,b,c |
| k BR | cm3 s−1 | Bimolecular bulk reaction rate coefficient | 1.2 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,d a,d |
| K sol | mol cm−3 atm−1 | Partitioning coefficient of O3 | 10−6 to 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
| [O3]g | cm−3 | Gas-phase number concentration of O3 | ∼4 × 1014 on averagec |
| r | μm | Particle radius | ∼3 on averagec |
| σ | cm2 | Effective molecular cross section of O3 | 1.52 × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| ω | cm s−1 | Mean thermal velocity of gaseous O3 | 3.6 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| [S2O32−]b,0 | cm−3 | Initial bulk number concentration of S2O32− | RH >80%: (∼1 to ∼2) × 1021; RH = ∼20%: (∼2 to ∼7) × 1021![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
| [S2O32−]ss,0 | cm−2 | Initial surface number concentration of S2O32− | δ[S2O32−]b,0e |
Table 2 lists the KM-SUB input parameters which remain adjustable for fitting the experimental results. Table 2 also introduces two types of fitting scenarios for retrieving the molecular diffusivities from the kinetics measurement results. For the first fitting scenario, i.e., Scenario 1, the bulk diffusion coefficient of S2O32−, Db,T, is the only adjustable parameter for capturing the observed reaction time scale. Our previous study30 found that, while the reaction of S2O32− in viscous microdroplets with gaseous O3 mostly occurs at air–water interfaces, the diffusion of S2O32− from aerosol bulks to aerosol surfaces can also play a key role in determining its reaction time scale.30 On the other hand, any dissolved O3 near the surface is mostly depleted by S2O32− prior diffusing into inner aerosol bulks, and thus such aerosol reaction kinetics is not sensitive to the bulk-phase diffusivity of O3.30 For the convenience of data analysis, the bulk-phase diffusion coefficient for O3,Db,O, is coupled to Db,Tvia the SE equation,30 as specified in Table 2. Finally, the justification of Scenario 1, where Db,T is the only adjustable parameter, will be provided in the discussion section.
| Symbol | Meaning | Boundaries | Scenario 1 | Scenario 2 |
|---|---|---|---|---|
| a Coupled to Db,T (Scenario 1) or Db,T,fast (Scenario 2) via the SE equation. b See Tables S3 and S4 for individual values. c Coupled via the equations specified in “Boundaries”. | ||||
| D b,T | Bulk diffusion coefficient for all S2O32− | 10−15–10−5 cm2 s−1 | Adjustable | N. A. |
| D b,T,fast | Bulk diffusion coefficient for faster diffusing S2O32− | 10−12–10−10 cm2 s−1 | N. A. | Adjustable |
| D b,T,slow | Bulk diffusion coefficient for slower diffusing S2O32− | <10−13 cm2 s−1 | N. A. | Adjustable |
| D b,O | Bulk diffusion coefficient of O3 | 10−15–10−5 cm2 s−1 | Fixeda | Fixeda |
| [S2O32−]0 | Initial concentration of all S2O32− | 1021−1022 cm−3 | Fixedb | Fixedb |
| [S2O32−]fast,0 | Initial concentration of faster diffusing S2O32− | [S2O32−]0 ≥ [S2O32−]fast,0 ≥ 0 | N. A. | Adjustablec |
| [S2O32−]slow,0 | Initial concentration of slower diffusing S2O32− | [S2O32−]slow,0 = [S2O32−]0 – [S2O32−]fast,0 | N. A. | Adjustablec |
On the other hand, the second fitting scenario in Table 2, i.e., Scenario 2, is dedicated for the following case: the diffusion of S2O32− in a microdroplet exhibits two distinct time scales which are phenomenologically associated with two distinct bulk-phase diffusion coefficients, i.e., Db,T,fast and Db,T,slow, and the initial concentrations of S2O32− associated with them are [S2O32−]fast,0 and [S2O32−]slow,0, respectively. It is further assumed that these two types of S2O32− do not exchange and interact with each other. Before subjecting to a reaction with O3, the spatial distributions of [S2O32−]fast,0 and [S2O32−]slow,0 are assumed to be homogeneous, and their sum is fixed to that of total S2O32−, i.e., [S2O32−]fast,0 + [S2O32−]slow,0 = [S2O32−]0. As a result, in Scenario 2, Db,T,fast, Db,T,slow, and the ratio between [S2O32−]fast,0 and [S2O32−]slow,0 are three independent and adjustable parameters. The applications of the above two fitting scenarios to analyse the kinetics measurement results will be discussed in detail in the following sections.
Results and discussion
Raman spectroscopy of optically trapped microdroplets
According to our previous study on the ozonolysis of binary STS–water microdroplets,30 the reaction scheme of the S2O32−(aq) + O3 reaction and the secondary chemistry of main products in a neutral aqueous solution are listed as follows:30,47| S2O32− + O3 → SO42− + SO2 | (1) |
| 2S2O32− + O3 + H2O → S4O62− + O2 + 2OH− | (2) |
| SO2 + H2O ⇄ SO2·H2O ⇄ SO32− + 2H+ | (3) |
| S4O62− + SO32− ⇄ S3O62− + S2O32− | (4) |
Fig. 1 shows the representative Raman spectra of ternary (aqueous) STS–sucrose microdroplets before and after O3 exposure. The molecular Raman bands observed prior to the reaction can be readily assigned to the reactant S2O32− and prototype organic species, i.e., sucrose or glucose,48–51 and those that appeared after the reaction can be assigned to the reaction products specified in the above reaction scheme, such as SO42−, S3O62− and S4O62−.30,49,51–53 When lowering RHs, several Raman peaks of S2O32−(aq) exhibit spectral shifts of a few cm−1, indicating the supersaturation of aqueous STS in microdroplets.54 For example, the 996 cm−1 band of S2O32−(aq), i.e., νsym(S–O),51 observed at over 80% RH could shift to around 1005–1010 cm−1 at 20% RH, such as those of STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 5
sucrose 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4
1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures shown in Fig. S1.† It should be noted that the observed Raman shifts of this νsym(S–O) band are still significantly smaller than that in the solid phase (∼1017 cm−1),48 indicating no crystallization of STS in microdroplets in the present work.
2 mixtures shown in Fig. S1.† It should be noted that the observed Raman shifts of this νsym(S–O) band are still significantly smaller than that in the solid phase (∼1017 cm−1),48 indicating no crystallization of STS in microdroplets in the present work.
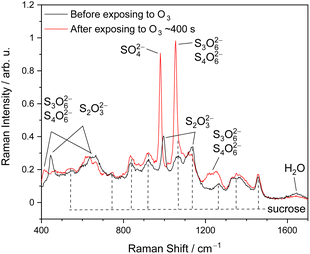 | ||
Fig. 1 Representative Raman spectra of optically trapped microdroplets containing ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mixtures in a 3 sucrose mixtures in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mass ratio (Expt. 32 in Table S1† (ESI)) before (black data) and after (red data) the reaction with O3 at 84% RH, as well as the assignments of sucrose, reactant thiosulfate and reaction products. 3 mass ratio (Expt. 32 in Table S1† (ESI)) before (black data) and after (red data) the reaction with O3 at 84% RH, as well as the assignments of sucrose, reactant thiosulfate and reaction products. | ||
In addition to identifying species, molecular Raman spectroscopy was also utilized to determine the absolute concentrations of STS, sucrose and glucose, as provided in Tables S1 and S2.† Such information was further utilized for the determination of aerosol ionic strengths and Henry's law coefficients prior to the reaction,30 as provided in Tables S1–S4.† It should also be noted that during the reaction, the droplet pH is regulated by reactions (2) and (3).30 Based on no identification of any Raman band of HSO−4 and the simulations of bulk-phase kinetics in our previous work,30 the lower limit of droplet pH after the reaction is estimated to be around 3. Thus, any potential decomposition of S2O32− caused by high acidity is not expected to occur here.30 The decomposition of concentrated S2O32− due to high acidity (pH ≈ 0) should take only a couple of minutes.30 However, the present work did not observe any decomposition of S2O32− in microdroplets prior to O3 exposure, indicating no existence of this high aerosol acidity. Under the condition of high alkalinity (pOH ≈ 0), while S2O32− should remain stable,47,55 S4O62− could decompose to S3O62− and S2O32−.30,55 According to the bulk-phase kinetics simulations of our previous study,30 such high alkalinity could be created by reaction (2) with concentrated S2O32−, subsequently leading to the conversion of S4O62− into S3O62−. It should be noted that the empirical relationship of kSLR with [S2O32−]b,0 listed in Table 1 has included the effect of this secondary chemistry.30
In addition to spontaneous Raman scatterings described above, an optically trapped microdroplet could also emit cavity-enhanced Raman scattering (CERS).9 The wavelengths of CERS are the same as those of the WGMs within the molecular Raman bands of the microdroplet, and the intensities of CERS are further amplified by stimulated Raman scatterings inside the microdroplet as a spherical cavity.56–58 The CERS signals observed in the present work were analyzed via Mie resonance fitting (MRFIT),59 and the droplet radius for the microdroplet of interest could be retrieved with an accuracy of a few nanometers. Table S5† provides several representative examples of such analysis for the data of this work. When there is no observable CERS signal, the droplet radius was determined via brightfield imaging. The typical radius of droplets studied in this work is about 3 μm, as shown in Tables S1 and S2.† Finally, it should be noted that the type of MRFIT utilized in the present work is dedicated to a homogeneous sphere. Since the observed CERS signals can always be assigned by such MRFIT with reasonably small fitting errors, see Table S5,† the present work indicates that there is no formation of phase separation, such as a core–shell structure or partial engulfment, in the microdroplets under the experimental conditions of the present work. According to the literature, the penetration depth of WGMs from the interface is ∼r/m, where r and m are the radius and refractive index of the particle, respectively.57 For the case of this work, the value of m at wavelengths of observed WGMs is around 1.4 (see Table S5†), indicating that the penetration depth is equivalent to ∼0.7r. Thus, for any microdroplet containing an aqueous inorganic core and an organic shell in this work, when the ratio between the volumes of its core and shell is larger than ∼0.03, its CERS signals should be subject to the influence of this core–shell structure. Indeed, the mass ratio between inorganics (STS) and organics (sucrose or glucose) prepared in this work is fixed in the range between 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, which is much larger than 0.03, justifying the above reasoning for the nonexistence of a core–shell structure due to no corresponding signature in the observed CERS signals.
4, which is much larger than 0.03, justifying the above reasoning for the nonexistence of a core–shell structure due to no corresponding signature in the observed CERS signals.
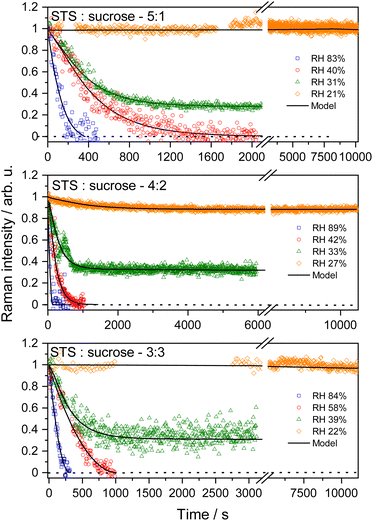
Kinetics measurements of the S2O32− + O3 reaction in microdroplets
Fig. 2 shows the representative kinetics measurement results of ozone oxidation of ternary STS–sucrose microdroplets at different RHs and STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mass ratios. For all mass ratios of STS and organics used in this work, the decay rates of S2O32− integrated Raman intensities at higher RHs are faster than those at lower RHs. Such RH dependence of the reaction time scale can be tentatively attributed to diffusion-limited kinetics and RH-dependent aerosol viscosity, as a higher content of organics (sucrose or glucose) at lower RH can lead to a larger aerosol viscosity and thus a smaller bulk diffusivity in microdroplets.19,29,30
sucrose mass ratios. For all mass ratios of STS and organics used in this work, the decay rates of S2O32− integrated Raman intensities at higher RHs are faster than those at lower RHs. Such RH dependence of the reaction time scale can be tentatively attributed to diffusion-limited kinetics and RH-dependent aerosol viscosity, as a higher content of organics (sucrose or glucose) at lower RH can lead to a larger aerosol viscosity and thus a smaller bulk diffusivity in microdroplets.19,29,30
It should be noted that at relatively high RHs, all S2O32− in microdroplets can be completely depleted by O3, such as those at RH above 40% in Fig. 2. However, the time profiles at relatively low RHs can exhibit the incomplete decays of S2O32−, such as the data of green triangle symbols in Fig. 2. This feature of incomplete decay exhibits a fast initial depletion of S2O32− within 1000 seconds followed by a significantly slower decay at prolonged O3 exposure times, such as over a few thousands of seconds. Finally, when performing the kinetics measurements at even lower RHs, such as those at RH below 25% in Fig. 2, most of S2O32− in microdroplets remain intact with very little depletion, even at O3 exposure times around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 seconds. Besides no decay of reactant Raman bands, the Raman spectra also show the negligible formation of any product, supporting the observations of no S2O32− depletion via ozone oxidation.
000 seconds. Besides no decay of reactant Raman bands, the Raman spectra also show the negligible formation of any product, supporting the observations of no S2O32− depletion via ozone oxidation.
Fig. S2† shows the time evolutions of integrated Raman intensities assigned to products SO42− and S3O62−/S4O62−, from three representative kinetics measurements associated with rapid and prolonged complete depletions and incomplete depletion of S2O32− Raman intensities via O3 exposure. When the Raman intensities of S2O32− started to decrease due to O3 exposure from 0 second, those of products increased accordingly due to reactions (1)–(4). It should be noted that when the decays of S2O32− Raman intensities stopped, the increases of the product signals also stopped correspondingly, no matter for the case of complete S2O32− depletion, such as Fig. S2(a) and (b),† or for the case of incomplete S2O32− depletion, such as Fig. S2(c).† For the latter case, the observed stop of product formation can also support previous assignments of incomplete S2O32− depletion.
Estimating diffusivities in ternary STS–sucrose mixtures
As the diffusion-limited kinetics dominates the S2O32− + O3 reaction in viscous microdroplets, we compared the kinetics data with the KM-SUB model simulation results to retrieve the bulk diffusivity of reactant S2O32− in each microdroplet. For kinetics data exhibiting complete depletions of S2O32−, employing Scenario 1 can yield reasonable model fit results, such as those of RH above 40% in Fig. 2. Since Db,T is the only adjustable parameter in Scenario 1, this good agreement indicates that all S2O32− in each microdroplet have the same bulk diffusivity. All fitted Db,Tvia Scenario 1 for ternary STS–sucrose mixtures are listed in Table S3,† and they are also plotted as a function of RH in Fig. 3. According to Fig. 3, most Db,T determined at above 80% RH are in the range of 10−7 to 10−6 cm2 s−1, and those in the range of ∼40% and ∼70% RH decrease to the range of 10−11 to 10−10 cm2 s−1 due to higher sucrose contents and thus larger droplet viscosity at lower RHs. Fig. 3 also shows that all these values for ternary STS–sucrose mixtures are in between the SE predictions for binary STS–water systems and for binary sucrose–water systems.12,60,61 This trend also agrees with the general feature of ternary inorganic–organic mixtures observed in several previous studies.11,12,16 The dependence of aerosol viscosity on the inorganic–organic mass ratio was also observed in the literature.11 However, Db,T in the present work seems not to exhibit any significant dependence on the STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mass ratio, as shown in Fig. 3. This observation of no apparent compositional dependence may be attributed to the sensitivity of the methodology applied in the present work. According to the statistics and fitting error bars of data shown in Fig. 3, the sensitivity to diffusion coefficient of S2O32− is around one order of magnitude, and such sensitivity may not allow for distinguishing any marginal difference between Db,T of different STS
sucrose mass ratio, as shown in Fig. 3. This observation of no apparent compositional dependence may be attributed to the sensitivity of the methodology applied in the present work. According to the statistics and fitting error bars of data shown in Fig. 3, the sensitivity to diffusion coefficient of S2O32− is around one order of magnitude, and such sensitivity may not allow for distinguishing any marginal difference between Db,T of different STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mass ratios in the range of RH applied in this work.
sucrose mass ratios in the range of RH applied in this work.
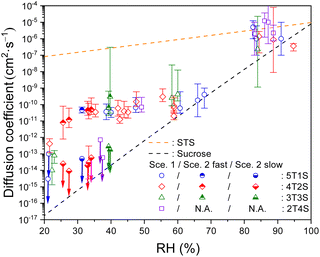 | ||
Fig. 3 Bulk diffusion coefficients of S2O32− (symbols) in ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose microdroplets at different RHs, as well as the SE predictions for a binary STS–water system and for a binary sucrose–water system (lines). 5T1S (blue circles), 4T2S (red diamonds), 3T3S (green triangle) and 2T4S (purple square): ternary STS sucrose microdroplets at different RHs, as well as the SE predictions for a binary STS–water system and for a binary sucrose–water system (lines). 5T1S (blue circles), 4T2S (red diamonds), 3T3S (green triangle) and 2T4S (purple square): ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mixtures in mass ratios of 5 sucrose mixtures in mass ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4 1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 3 2, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2 3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively. Hollow symbols: Db,T, retrieved via Scenario 1. Hollow symbols marked with downward arrows: upper limits of Db,T, retrieved via Scenario 1. Top-filled symbols: Db,T,fast, retrieved via Scenario 2. Bottom-filled symbols marked with downward arrows: upper limits of Db,T,slow, retrieved via Scenario 2. For clarity, the error bars of RH (∼3.5%) are not plotted here. The error bars of diffusion coefficients represent the fitting errors for each kinetics data. See Tables S3 and S4† for the full details of diffusion coefficients. 4, respectively. Hollow symbols: Db,T, retrieved via Scenario 1. Hollow symbols marked with downward arrows: upper limits of Db,T, retrieved via Scenario 1. Top-filled symbols: Db,T,fast, retrieved via Scenario 2. Bottom-filled symbols marked with downward arrows: upper limits of Db,T,slow, retrieved via Scenario 2. For clarity, the error bars of RH (∼3.5%) are not plotted here. The error bars of diffusion coefficients represent the fitting errors for each kinetics data. See Tables S3 and S4† for the full details of diffusion coefficients. | ||
For the kinetics data exhibiting two distinctly fast and slow decays of S2O32−, Scenario 2 was employed to capture both reaction time scales, Db,T,fast and Db,T,slow, as well as their concentration contributions, [S2O32−]fast,0 and [S2O32−]slow,0, respectively. The model fit results of Scenario 2 can have a good agreement with these kinetics data, such as those (triangle symbols) shown in Fig. 2. Note that the relatively slow decay components of S2O32− can remain intact for over several thousand seconds, and it becomes not trivial to pin down the magnitude of its diffusion coefficient (Db,T,slow) with the experimental times available in this work. Thus, this work only provides the upper limits of Db,T,slow, which are represented by symbols with downward arrows in Fig. 3 and 5. It should be noted that for such labelling, only the symbol itself represents the magnitude of the upper limit and the arrow itself just represents no determination of the lower limit. However, the length of each arrow does not have any meaning. Fig. 3 plots each pair of Db,T,fast (top-filled symbols) and the upper limit of Db,T,slow (bottom-filled symbols with arrows) retrieved from each kinetics data of STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 5
sucrose 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 3
2 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixtures via Scenario 2, and Table S4† summarizes these values in detail. According to Fig. 3, the magnitude of Db,T,fast is in the range of 10−11 to 10−10 cm2 s−1, and the upper limit of Db,T,slow is in general below 10−12 cm2 s−1, indicating that the differences between Db,T,fast and Db,T,slow are at least two orders of magnitude. Also according to Fig. 3, the co-existence of two distinct decay components in the kinetics data only appears at RH between 25% and 40%. Finally, when RH is below 25% for STS
3 mixtures via Scenario 2, and Table S4† summarizes these values in detail. According to Fig. 3, the magnitude of Db,T,fast is in the range of 10−11 to 10−10 cm2 s−1, and the upper limit of Db,T,slow is in general below 10−12 cm2 s−1, indicating that the differences between Db,T,fast and Db,T,slow are at least two orders of magnitude. Also according to Fig. 3, the co-existence of two distinct decay components in the kinetics data only appears at RH between 25% and 40%. Finally, when RH is below 25% for STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 5
sucrose 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 3
2 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixtures or below 40% for the 2
3 mixtures or below 40% for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 mixture, their kinetics data exhibit very little depletion of S2O32− during the available observation times of this work. For such a case, the present work employed Scenario 1 to estimate the upper limits of Db,T for these data.
4 mixture, their kinetics data exhibit very little depletion of S2O32− during the available observation times of this work. For such a case, the present work employed Scenario 1 to estimate the upper limits of Db,T for these data.
Fig. 4 plots the concentration ratio between the relatively fast diffusing S2O32− ([S2O32−]fast,0) and the total S2O32− ([S2O32−]0) in each single microdroplet, i.e., ϕfast, as a function of RH. In the range of 30% to 40% RH, ϕfast for STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 5
sucrose 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 3
2 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixtures is in between 0.4 and 0.7, indicating the co-existence of both slow and fast components. When lowering RH to around 27%, ϕfast for the STS:sucrose 4
3 mixtures is in between 0.4 and 0.7, indicating the co-existence of both slow and fast components. When lowering RH to around 27%, ϕfast for the STS:sucrose 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture decreases to a negligible value, such as 0.1, indicating a significant reduction of the fast S2O32− component at lower RHs. It should be noted that besides the results of Scenario 2, several representative results retrieved via Scenario 1 are also implemented as shown in Fig. 4 in terms of two limiting cases, i.e., ϕfast = 1 and 0. For the former case, i.e., ϕfast = 1 or [S2O32−]fast,0 = [S2O32−]0, it corresponds to the kinetic data with Db,T in the range of 10−11 to 10−10 cm2 s−1. For the latter case, i.e., ϕfast = 0 or [S2O32−]slow,0 = [S2O32−]0, it corresponds to the kinetic data with Db,T smaller than 10−12 cm2 s−1. When taking into account the results of both Scenarios 1 and 2, ϕfast of each mass ratio seems to exhibit a drastic change between 0 and 1 around a specific RH like a turning point, as shown in Fig. 4. When comparing Fig. 3 and 4, such a change in ϕfast is also associated with a distinct change in S2O32− diffusivity over 2 orders of magnitude. As shown in Fig. 4, the RH-dependent ϕfast for each mass ratio is phenomenologically fitted using a growth curve. These fit curves for individual mass ratios indicate that the ternary mixture with more sucrose has the turning point of ϕfast at a higher RH. For example, such RH for the STS
2 mixture decreases to a negligible value, such as 0.1, indicating a significant reduction of the fast S2O32− component at lower RHs. It should be noted that besides the results of Scenario 2, several representative results retrieved via Scenario 1 are also implemented as shown in Fig. 4 in terms of two limiting cases, i.e., ϕfast = 1 and 0. For the former case, i.e., ϕfast = 1 or [S2O32−]fast,0 = [S2O32−]0, it corresponds to the kinetic data with Db,T in the range of 10−11 to 10−10 cm2 s−1. For the latter case, i.e., ϕfast = 0 or [S2O32−]slow,0 = [S2O32−]0, it corresponds to the kinetic data with Db,T smaller than 10−12 cm2 s−1. When taking into account the results of both Scenarios 1 and 2, ϕfast of each mass ratio seems to exhibit a drastic change between 0 and 1 around a specific RH like a turning point, as shown in Fig. 4. When comparing Fig. 3 and 4, such a change in ϕfast is also associated with a distinct change in S2O32− diffusivity over 2 orders of magnitude. As shown in Fig. 4, the RH-dependent ϕfast for each mass ratio is phenomenologically fitted using a growth curve. These fit curves for individual mass ratios indicate that the ternary mixture with more sucrose has the turning point of ϕfast at a higher RH. For example, such RH for the STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 2
sucrose 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 mixture, i.e., ∼43%, is around 10% larger than that for the STS
4 mixture, i.e., ∼43%, is around 10% larger than that for the STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 4
sucrose 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixture, i.e., ∼33%. Fig. 4 also shows that the fit curves for nearly all kinds of mixtures reproduce the sharp changes of ϕfast retrieved from the data, whereas the fit curve for the STS
2 mixture, i.e., ∼33%. Fig. 4 also shows that the fit curves for nearly all kinds of mixtures reproduce the sharp changes of ϕfast retrieved from the data, whereas the fit curve for the STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 3
sucrose 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture appears relatively smooth. This difference could be due to not enough data for the STS
3 mixture appears relatively smooth. This difference could be due to not enough data for the STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 3
sucrose 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture around its turning point RH, leading to ambiguity in determining the shape of the fit curve around its turning point. Finally, the RH dependences of ϕfast (see Fig. 4) do not resemble those of spectral positions of the S2O32−νsym(S–O) Raman band (see Fig. S1†). In particular, while the values of ϕfast for STS
3 mixture around its turning point RH, leading to ambiguity in determining the shape of the fit curve around its turning point. Finally, the RH dependences of ϕfast (see Fig. 4) do not resemble those of spectral positions of the S2O32−νsym(S–O) Raman band (see Fig. S1†). In particular, while the values of ϕfast for STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 3
sucrose 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2
3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 mixtures exhibit sharp changes in the RH range of ∼25% to ∼40%, their Raman shifts of the S2O32−νsym(S–O) band in this RH range remain the same as that of dilute STS solution. Since the supersaturation state of STS correlates with the spectral drift of the S2O32−νsym(S–O) Raman band, the disagreement between the RH dependences of ϕfast and this Raman shift implies that the observed changes of ϕfast should not be attributed to supersaturation of STS.
4 mixtures exhibit sharp changes in the RH range of ∼25% to ∼40%, their Raman shifts of the S2O32−νsym(S–O) band in this RH range remain the same as that of dilute STS solution. Since the supersaturation state of STS correlates with the spectral drift of the S2O32−νsym(S–O) Raman band, the disagreement between the RH dependences of ϕfast and this Raman shift implies that the observed changes of ϕfast should not be attributed to supersaturation of STS.
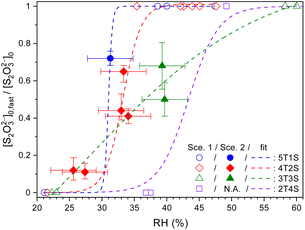 | ||
Fig. 4 Ratios between the fast component to total thiosulfates (ϕfast = [S2O32−]fast,0/[S2O32−]0) in ternary aqueous STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mixtures of different mass ratios plotted as a function of RH, as well as phenomenological fits (lines). 5T1S, 4T2S, 3T3S and 2T4S: ternary STS sucrose mixtures of different mass ratios plotted as a function of RH, as well as phenomenological fits (lines). 5T1S, 4T2S, 3T3S and 2T4S: ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose mixtures in mass ratios of 5 sucrose mixtures in mass ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4 1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 3 2, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2 3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively. Hollow symbols: data analysed using Scenario 1. Filled symbols: data analysed using Scenario 2. The error bars of ϕfast represent the fitting errors of [S2O32−]fast,0 for each kinetic data. See Table S4† for the full details of [S2O32−]fast,0. 4, respectively. Hollow symbols: data analysed using Scenario 1. Filled symbols: data analysed using Scenario 2. The error bars of ϕfast represent the fitting errors of [S2O32−]fast,0 for each kinetic data. See Table S4† for the full details of [S2O32−]fast,0. | ||
Estimating diffusivities in ternary STS–glucose mixtures
To further elucidate the effect of organic species, the present work also determined the bulk diffusivity of S2O32−in microdroplets consisting of aqueous STS mixing with glucose. Fig. 5 plots the diffusion coefficients of S2O32−determined in such a ternary system at different RHs and mass ratios. The values of Db,T determined at above 90% RH are in the order of 10−6 to 10−5 cm2 s−1, and those determined in the range of 30% to 40% RH decrease to the order of 10−11 to 10−10 cm2 s−1 due to higher glucose content and thus higher droplet viscosity at lower RHs. Similar to the case of sucrose, the magnitude of Db,T in ternary STS–glucose mixtures is also in between the SE predictions for binary STS–water systems and for binary glucose–water systems,60–62 as shown in Fig. 5. It should be noted that for this ternary system at RH between 23% and 30%, the present work also observed the feature of incomplete S2O32−depletion where the difference between the reaction time scales of fast and slow decay components can be at least two orders of magnitude. According to Fig. 5, the diffusion coefficients for fast diffusing S2O32−(Db,T,fast) still remain around 10−11 to 10−10 cm2 s−1, while those for slow diffusing S2O32−(Db,T,slow) are below 10−12 cm2 s−1. When the RH is below 23%, the kinetics data exhibit very little depletion of S2O32−. The present work employed Scenario 1 to estimate the upper limits of Db,T, and the values are below 10−13 cm2 s−1, as shown in Fig. 5.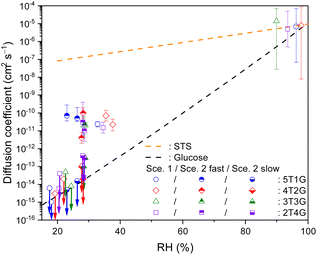 | ||
Fig. 5 Bulk diffusion coefficients of S2O32− (symbols) in ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose microdroplets at different RHs, as well as the SE predictions for binary STS–water systems and for binary glucose–water systems (lines). 5T1G (blue circles), 4T2G (red diamonds), 3T3G (green triangles) and 2T4G (purple squares): ternary STS glucose microdroplets at different RHs, as well as the SE predictions for binary STS–water systems and for binary glucose–water systems (lines). 5T1G (blue circles), 4T2G (red diamonds), 3T3G (green triangles) and 2T4G (purple squares): ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mixtures in mass ratios of 5 glucose mixtures in mass ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4 1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 3 2, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2 3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively. Hollow symbols: Db,T, retrieved via Scenario 1. Hollow symbols marked with downward arrows: upper limits of Db,T, retrieved via Scenario 1. Top-filled symbols: Db,T,fast, retrieved via Scenario 2. Bottom-filled symbols marked with downward arrows: upper limits of Db,T,slow, retrieved via Scenario 2. For clarity, the error bars of RH (∼3.5%) are not plotted here. The error bars of diffusion coefficients represent the fitting errors for each kinetics data. See Tables S3 and S4† for the full details of diffusion coefficients. 4, respectively. Hollow symbols: Db,T, retrieved via Scenario 1. Hollow symbols marked with downward arrows: upper limits of Db,T, retrieved via Scenario 1. Top-filled symbols: Db,T,fast, retrieved via Scenario 2. Bottom-filled symbols marked with downward arrows: upper limits of Db,T,slow, retrieved via Scenario 2. For clarity, the error bars of RH (∼3.5%) are not plotted here. The error bars of diffusion coefficients represent the fitting errors for each kinetics data. See Tables S3 and S4† for the full details of diffusion coefficients. | ||
Fig. 6 plots the values of ϕfast, i.e., [S2O32−]fast,0/[S2O32−]0, for ternary STS–glucose mixtures at different RHs. In the range of ∼23% to ∼30% RH, the value of ϕfast is in between 0.2 and 0.7, indicating the co-existence of both fast and slow decay components. The values of ϕfast below and above this RH range are tentatively assigned to 0 and 1, respectively, because their observed kinetics are associated with the dominance of single decay/diffusing components, such as slow (Db,T ≪ 10−13 cm2 s−1) and fast (Db,T = 10−11 to 10−10 cm2 s−1) ones, respectively. As a result, Fig. 6 shows that ϕfast of most mass ratios have drastic changes between 0 and 1 at specific RHs, similar to the trends shown in Fig. 4. These results in Fig. 6 are also phenomenologically fitted via the growth curve. The fit curves of ϕfast for different mass ratios exhibit no significant difference, when taking into account the accuracy of the RH sensor (3.5%).
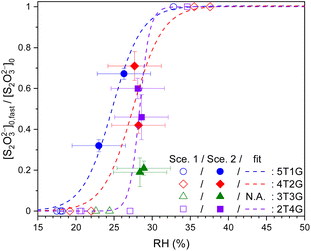 | ||
Fig. 6 Ratios between fast components to total thiosulfates (ϕfast = [S2O32−]fast,0/[S2O32−]0) in ternary aqueous STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose mixtures of different mass ratios (blue circle 5T1G, red diamond 4T2G, green triangle 3T3G and purple square 2T4G) plotted as a function of RH, as well as phenomenological fits (lines). 5T1G, 4T2G, 3T3G and 2T4G: ternary aqueous STS and glucose mixtures in mass ratios of 5 glucose mixtures of different mass ratios (blue circle 5T1G, red diamond 4T2G, green triangle 3T3G and purple square 2T4G) plotted as a function of RH, as well as phenomenological fits (lines). 5T1G, 4T2G, 3T3G and 2T4G: ternary aqueous STS and glucose mixtures in mass ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4 1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 3 2, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 2 3 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, respectively. Hollow symbols: data analysed using Scenario 1. Filled symbols: data analysed using Scenario 2. The error bars of fast ratios represent the fitting errors of [S2O32−]fast,0 for each kinetic data. See Table S4† for the full details of [S2O32−]fast,0. 4, respectively. Hollow symbols: data analysed using Scenario 1. Filled symbols: data analysed using Scenario 2. The error bars of fast ratios represent the fitting errors of [S2O32−]fast,0 for each kinetic data. See Table S4† for the full details of [S2O32−]fast,0. | ||
Diffusion-limited kinetics in ternary STS–organic mixtures
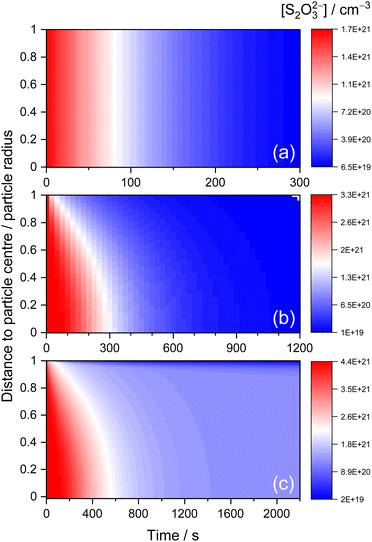
The above KM-SUB model simulation results allow for further understanding of the observed aerosol kinetics. Fig. 7 exhibits the simulated time-dependent radial distribution of [S2O32−] in aerosol bulks for STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 5
sucrose 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures at RH 83%, 40% and 31%, as three representative cases of diffusion-limited kinetics associated with rapid complete depletion, prolonged complete depletion and partial depletion of S2O32−, respectively. For the case of RH 83%, where Db,T is in the order of 10−6 cm2 s−1, Fig. 7(a) shows that this fast bulk diffusion of S2O32− leads to a homogeneous spatial distribution of [S2O32−] during the depletion of S2O32−via surface O3. For the case of RH 40%, where Db,T is in the order of 10−11 cm2 s−1, Fig. 7(b) shows that this relatively slow bulk diffusion of S2O32− leads to an inhomogeneous spatial distribution of [S2O32−] where [S2O32−] at the particle centre is a few times larger than [S2O32−] near the surface. Such a diffusion gradient of concentration inside aerosol bulks has also been revealed by several studies on aerosol kinetics.29,63 For the case of RH 31%, which exhibits the inhibited depletion of S2O32−, Fig. 7(c) shows that some of the S2O32− anions associated with Db,T,fast = ∼10−11 cm2 s−1 exhibit the diffusion gradient, before these S2O32− anions diminish completely after around 1000 s. On the other hand, some of the S2O32− anions associated with Db,T,slow = ∼10−14 cm2 s−1 remain intact over 2000 s, as shown in Fig. 7(c), while S2O32− anions near the surface gradually decay due to penetration of surface O3.
1 mixtures at RH 83%, 40% and 31%, as three representative cases of diffusion-limited kinetics associated with rapid complete depletion, prolonged complete depletion and partial depletion of S2O32−, respectively. For the case of RH 83%, where Db,T is in the order of 10−6 cm2 s−1, Fig. 7(a) shows that this fast bulk diffusion of S2O32− leads to a homogeneous spatial distribution of [S2O32−] during the depletion of S2O32−via surface O3. For the case of RH 40%, where Db,T is in the order of 10−11 cm2 s−1, Fig. 7(b) shows that this relatively slow bulk diffusion of S2O32− leads to an inhomogeneous spatial distribution of [S2O32−] where [S2O32−] at the particle centre is a few times larger than [S2O32−] near the surface. Such a diffusion gradient of concentration inside aerosol bulks has also been revealed by several studies on aerosol kinetics.29,63 For the case of RH 31%, which exhibits the inhibited depletion of S2O32−, Fig. 7(c) shows that some of the S2O32− anions associated with Db,T,fast = ∼10−11 cm2 s−1 exhibit the diffusion gradient, before these S2O32− anions diminish completely after around 1000 s. On the other hand, some of the S2O32− anions associated with Db,T,slow = ∼10−14 cm2 s−1 remain intact over 2000 s, as shown in Fig. 7(c), while S2O32− anions near the surface gradually decay due to penetration of surface O3.
According to the literature, the existence of concentration gradients inside aerosol bulks could be verified via excellent agreement between observed time evolution of Raman signals and kinetic simulation results.10 To compare with the kinetics measurement results of AOT, the simulated radial distribution of [S2O32−] was converted into radial-averaged [S2O32−], i.e., the sum of [S2O32−] at each radial layer along the radial direction. For the present work, since the beam cross section for the Raman excitation laser (∼0.3 μm) is significantly smaller than the size of the microdroplet (∼3 μm), it is assumed that the observed Raman intensities should resemble the radial-averaged simulation results.10 For the case of the concentration gradient in aerosol bulks (see Fig. 7(b)), Fig. S3(b) and (c)† show that the radial-averaged simulation results can exhibit excellent agreement with the shapes of observed Raman intensity time profiles. To justify this assumption of radial averaging, Fig. S3(b) and (c)† also show the volume-averaged simulation results, i.e., the sum of the product of [S2O32−] and volume at each radial layer along the radial direction. However, as shown in Fig. S3(b) and (c),† they cannot completely reproduce the shapes of the experimental results. Besides the data compared in Fig. S3(b) and (c),† the present work also found that the other kinetic data associated with diffusion gradients, such as those fitted with diffusion coefficients below 10−10 cm2 s−1, also have better agreements with radial-averaged simulation results than with volume-averaged ones. Finally, for the case of homogeneously mixed [S2O32−] in aerosol bulks, such as Fig. 7(a), the assumptions of radial and volume averaging should become irrelevant.10 Indeed, Fig. S3(a)† shows that the observed Raman intensity time profile agrees with both the radial-averaged and volume-averaged simulation results which are essentially the same for this case.
Besides the bulk diffusivity of S2O32−, Db,T, the possibility of adjusting other KM-SUB input parameters to capture the observed negative dependence between the reaction time scale and ambient RH is also discussed here. According to the previous study by Hsu et al.,30 the reaction time scale of S2O32−in microdroplets via interfacial ozonolysis mainly depends on the surface reaction rate coefficient (kSLR), the surface ozone concentration and bulk diffusivity of S2O32−. Firstly, if the increase in the observed reaction time scale when decreasing RH is attributed to the decrease of kSLR, this means that kSLR increases with RH. For example, Fig. S4(a) and (b)† show that the fitted values of kSLR for the data of STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 4
sucrose 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures at RH 89% and RH 42% are 3.2 × 10−10 cm2 s−1 and 1.1 × 10−10 cm2 s−1, respectively, when fixing Db,T to 1 × 10−5 cm2 s−1 and only allowing kSLR adjustable. This fitting result yields a positive dependence of kSLR on RH. However, Hsu et al.30 found that kSLR actually should increase when decreasing RH, because of its positive dependence on droplet ionic strength and the negative dependence of droplet ionic strength on RH. As a result, such RH dependence of kSLR from the literature disagrees with the above fitting results (Fig. S4†) and thus rules out the necessity of allowing kSLR adjustable in the present work.
2 mixtures at RH 89% and RH 42% are 3.2 × 10−10 cm2 s−1 and 1.1 × 10−10 cm2 s−1, respectively, when fixing Db,T to 1 × 10−5 cm2 s−1 and only allowing kSLR adjustable. This fitting result yields a positive dependence of kSLR on RH. However, Hsu et al.30 found that kSLR actually should increase when decreasing RH, because of its positive dependence on droplet ionic strength and the negative dependence of droplet ionic strength on RH. As a result, such RH dependence of kSLR from the literature disagrees with the above fitting results (Fig. S4†) and thus rules out the necessity of allowing kSLR adjustable in the present work.
Secondly, it may be possible that the increase in the reaction time scale when decreasing RHs is attributed to the decrease in the surface O3 concentration. Since the concentration of surface O3 depends on [O3]g, αs,0 and τd,30 its decrease is associated with the decreases of αs,0 or/and τd when fixing [O3]g. For the case of the surface accommodation coefficient of O3, i.e., αs,0, Fig. S5(a) and (b)† show that the fitted values of αs,0 for the data of STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 4
sucrose 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures at RH 89% and RH 42% are 8.0 × 10−2and 1.6 × 10−2, respectively, when fixing Db,T to 1 × 10−5 cm2 s−1 and only allowing αs,0 adjustable. This fitting result yields a positive dependence of αs,0 on RH. However, according to the literature, O3 has a stronger preference for accommodating on air–organic interfaces than on air–water interfaces, because of its hydrophobic nature.64 Furthermore, for a microdroplet containing aqueous organics, decreasing RH should increase its organic content. This means that according to the literature, αs,0 for microdroplets containing aqueous organics is less likely to decrease when decreasing RH. And, therefore, the above fitting results of adjusting αs,0 (Fig. S5†) are not supported by the literature, ruling out the necessity of allowing αs,0 to be adjustable in the present work.
2 mixtures at RH 89% and RH 42% are 8.0 × 10−2and 1.6 × 10−2, respectively, when fixing Db,T to 1 × 10−5 cm2 s−1 and only allowing αs,0 adjustable. This fitting result yields a positive dependence of αs,0 on RH. However, according to the literature, O3 has a stronger preference for accommodating on air–organic interfaces than on air–water interfaces, because of its hydrophobic nature.64 Furthermore, for a microdroplet containing aqueous organics, decreasing RH should increase its organic content. This means that according to the literature, αs,0 for microdroplets containing aqueous organics is less likely to decrease when decreasing RH. And, therefore, the above fitting results of adjusting αs,0 (Fig. S5†) are not supported by the literature, ruling out the necessity of allowing αs,0 to be adjustable in the present work.
Thirdly, for the case of O3 desorption time, i.e., τd, Fig. S6(a) and (b)† show that the fitted values of τd for the data of STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 4
sucrose 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mixtures at RH 89% and RH 42% are 3.5 × 10−7 s and 6.5 × 10−8 s, respectively, when fixing Db,T to 1 × 10−5 cm2 s−1 and only allowing τd adjustable. This fitting result yields a positive dependence of τd on RH. However, like the properties of αs,0, since O3 is expected to have more intermolecular interactions with organics than with water, it is less likely that its desorption time, τd, for microdroplets of aqueous organics is shorter at lower RHs, disagreeing with the above fitting results (Fig. S6†). As a result, the present work indicates that such disagreement rules out the necessity of adjusting τd. On the other hand, adjusting Db,T to capture the RH dependence of observed reaction time scales leads to the positive dependence of Db,T on RH, as described above (Fig. 3 and 5), and this slowing of diffusion at low RHs can be attributed to enrichment of organic content which can effectively inhibit the diffusion of S2O32−. Since only the adjustment of diffusivity can provide a more reasonable explanation to our data than the adjustments of other parameters, this work attributes the observed prolongation of reaction time scales to diffusion-limited kinetics. This conclusion also justifies the usage of Scenario 1, i.e., Db,T is the only adjustable parameter. Finally, while fixing kSLR, αs,0 and τd parameters in the model simulations of the present work, i.e., Scenarios 1 and 2, is justified by the above model simulation results and corresponding discussions, they could also be regarded as sensitivity simulations for these parameters.
2 mixtures at RH 89% and RH 42% are 3.5 × 10−7 s and 6.5 × 10−8 s, respectively, when fixing Db,T to 1 × 10−5 cm2 s−1 and only allowing τd adjustable. This fitting result yields a positive dependence of τd on RH. However, like the properties of αs,0, since O3 is expected to have more intermolecular interactions with organics than with water, it is less likely that its desorption time, τd, for microdroplets of aqueous organics is shorter at lower RHs, disagreeing with the above fitting results (Fig. S6†). As a result, the present work indicates that such disagreement rules out the necessity of adjusting τd. On the other hand, adjusting Db,T to capture the RH dependence of observed reaction time scales leads to the positive dependence of Db,T on RH, as described above (Fig. 3 and 5), and this slowing of diffusion at low RHs can be attributed to enrichment of organic content which can effectively inhibit the diffusion of S2O32−. Since only the adjustment of diffusivity can provide a more reasonable explanation to our data than the adjustments of other parameters, this work attributes the observed prolongation of reaction time scales to diffusion-limited kinetics. This conclusion also justifies the usage of Scenario 1, i.e., Db,T is the only adjustable parameter. Finally, while fixing kSLR, αs,0 and τd parameters in the model simulations of the present work, i.e., Scenarios 1 and 2, is justified by the above model simulation results and corresponding discussions, they could also be regarded as sensitivity simulations for these parameters.
Morphology and phase state of aerosol particles
The aerosol particles consisting of water, inorganic and organic components could have several types of morphologies, such as dry particles, homogeneous wet particles and phase-separated particles, and the types of phase separations include liquid–liquid phase separation and partial engulfment.65,66 According to the literature, the elemental O: C ratios for organic species in aerosol particles can be used as an indicator to predict the morphology of aerosols. This means that the particles containing organic species with O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C < 0.56 should be subjected to phase separation, and those with O
C < 0.56 should be subjected to phase separation, and those with O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C > 0.80 are homogeneously mixed.67,68 For the present work, since the O
C > 0.80 are homogeneously mixed.67,68 For the present work, since the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios for glucose and sucrose are 1.0 and 0.9, respectively, the microdroplets containing STS and these organics are expected to be homogeneously mixed. Indeed, for our cases of aqueous STS mixing with sucrose at RH above 40% or with glucose at RH above 30%, this tentative classification of homogeneous mixture can be justified by following observations. Firstly, the observed reaction kinetics of S2O32−in each microdroplet can be adequately captured using the aerosol kinetic model with single diffusion coefficients for S2O32−. Secondly, the magnitudes of the retrieved S2O32−diffusion coefficients are in between the SE predictions for binary STS–water systems and binary organic–water systems, as shown in Fig. 3 and 5, implying homogeneous mixing between STS and organics. Thirdly, as discussed before, the observed spectral positions for Raman bands of S2O32−(Fig. S1†) indicate that STS remains in a supersaturated aqueous phase without any phase transformation to a solid phase.
C ratios for glucose and sucrose are 1.0 and 0.9, respectively, the microdroplets containing STS and these organics are expected to be homogeneously mixed. Indeed, for our cases of aqueous STS mixing with sucrose at RH above 40% or with glucose at RH above 30%, this tentative classification of homogeneous mixture can be justified by following observations. Firstly, the observed reaction kinetics of S2O32−in each microdroplet can be adequately captured using the aerosol kinetic model with single diffusion coefficients for S2O32−. Secondly, the magnitudes of the retrieved S2O32−diffusion coefficients are in between the SE predictions for binary STS–water systems and binary organic–water systems, as shown in Fig. 3 and 5, implying homogeneous mixing between STS and organics. Thirdly, as discussed before, the observed spectral positions for Raman bands of S2O32−(Fig. S1†) indicate that STS remains in a supersaturated aqueous phase without any phase transformation to a solid phase.
However, for our cases of aqueous STS mixing with sucrose at RH between 25% and 40% and aqueous STS mixing with glucose at RH between 23% and 30%, the observed co-existence of both fast and slow diffusing components of S2O32−in each single microdroplet cannot be rationalized in terms of kinetics in homogeneous mixtures. While the morphology of phase separation and its effect on molecular diffusivity have been utilized to rationalize the observation of incomplete PAH depletion in multiphase PAH ozonolysis,69 this mechanism will not be able to rationalize our observation of differing diffusivities satisfactorily. When the morphology of liquid–liquid phase separation occurs, the aerosol particles composed of aqueous inorganic and organic species may have a core–shell structure where the aqueous inorganic-rich and organic-rich phases become the inner core and the shell of coating, respectively. For a particle with such a core–shell structure, the diffusion through the entire depth of the organic-rich shell should be the rate-determining step for bulk S2O32−diffusing to the particle surface, and thus the time scale for most bulk S2O32−reacting with surface O3 should be more or less similar, disagreeing with our observation. On the other hand, the morphology of partial engulfment is also associated with the separation of aqueous inorganic-rich and organic-rich phases, and both phases in a partially engulfed particle could expose to gaseous O3 simultaneously, potentially leading to two distinct reaction timescales. Since the inorganic and organic species are separated, the diffusivity of S2O32−in the aqueous inorganic-rich phase should be similar to that in the binary STS–water system. However, this prediction does not agree with the observation of the present work, as the observed diffusivities of fast S2O32−components are always in between those of binary STS–water systems and binary organic–water systems (see Fig. 3 and 5). Finally, the CERS assignments for our kinetics data indicate the morphology of a homogeneous sphere. For the case of Expt. 10, i.e., the ternary STS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 5
sucrose 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture at RH 31%, while its kinetics data exhibit the co-existence of two distinct S2O32−diffusivities, its CERS assignments provided in Table S5† confirm its morphology of a homogeneous sphere prior to the reaction. In summary, neither a core–shell structure nor partial engulfment can rationalize the observations in the present work.
1 mixture at RH 31%, while its kinetics data exhibit the co-existence of two distinct S2O32−diffusivities, its CERS assignments provided in Table S5† confirm its morphology of a homogeneous sphere prior to the reaction. In summary, neither a core–shell structure nor partial engulfment can rationalize the observations in the present work.
Beside the morphology of aerosol particles, the intermolecular interactions between inorganic and organic species can also affect the molecular diffusivities in aerosol particles via formation of a microgel.10 It has been suggested that lowering RH and thus reducing water content in aerosol particles can prompt the formation of molecular clusters between organic molecules and divalent inorganic ions, such as Ca2+, Mg2+ and SO42−, by means of their ion–molecule intermolecular interactions, and these clusters could further aggregate as a kind of microstructure, such as a microgel, in aerosol particles.1,10,15 For the present work, S2O32−investigated here can also be classified as divalent anions. Thus, if localized formation of such an inorganic–organic microgel also exists in the microdroplets in this work, the observed slow components of S2O32−could be tentatively assigned to those bound in the network of this microgel via ion–molecular interaction. On the other hand, the observed fast components of S2O32−could be assigned to those remaining as isolated species in a viscous fluid. According to the results of the present work (see Fig. 3 and 5), the diffusivity of S2O32−confined in inorganic–organic microgels could be at least two orders of magnitude smaller than those remaining as isolated species. The observed co-existence of both fast and slow diffusing S2O32−in microdroplets can be regarded as a kind of two-phase amorphous state where both the locally formed microgels and the fluid matrix co-exist.10 The sharp RH dependence of ϕfast may imply a phase-changing process associated with the gel formation, while it is not trivial to rationalize such observation by means of conventional theory. According to the literature, the change of diffusivity due to gel formation in binary mixtures could be rationalized via percolation theory, which is often used to predict the effective diffusion coefficient in a mixed system of two media with two different diffusivities.10,24 However, this theory used in the literature is dedicated to binary systems, and it may not be applicable to more complicated ternary systems, such as those studied in the present work. Furthermore, this theory does not predict the simultaneous existences of two effective diffusion coefficients, as well as their population ratio. The main limitation of the present work to predict ϕfast and also its RH dependence is the lack of further understanding of intermolecular interactions between S2O32−and sucrose/glucose from a molecular level, as such understanding allows for retrieving the macroscopic properties required by theory, such as the distribution of pore sizes in this ternary system. A lot of experimental and theoretical efforts are still required for this purpose.
Finally, while the viscosity of the binary sucrose–water system is larger than that of the binary glucose–water system, the magnitudes of S2O32−diffusivity in ternary STS–glucose and STS–sucrose mixtures are similar, see Fig. 3 and 5. The trends of RH-dependent ϕfast (see Fig. 4 and 6) for glucose and sucrose are also similar. It should be noted that glucose and sucrose essentially have the same functional groups, besides their distinct differences in molecular weight and size. Such comparison suggests that the functional groups of organics would play a more major role in determining the properties of the inorganic–organic microgel/gel proposed in the present work, while the molecular weight or size of organics seems to play a rather minor role.
Atmospheric implications
Since atmospheric aerosols can consist of inorganic and organic compounds, their individual and cooperative influences on the properties and chemistry of aerosols have been one of the main topics in aerosol chemistry. One of their cooperative influences is the morphology of phase separation. Numerous studies have demonstrated that this morphology can significantly affect the kinetics of the chemical reaction and mass transport in aerosols,69–80 and a recent review has summarized these findings.66 Recently, the studies by Richards et al. demonstrated that the interactions between inorganic ions and organic molecules can cause various profound influences on the properties and phases of aerosols, such as the enhancement of aerosol viscosity and the RH-dependent gel phase transition.1,15 The present work demonstrates that besides the morphology of phase separation, the intermolecular interaction should also affect the reaction kinetics of aerosols via limiting the bulk diffusivities of chemical species. This means that such interaction facilitates the diffusion limitation of reactant ions via clustering with organics in organic–inorganic microgels and thus significantly prolongs their reaction time scale in aerosol particles with less water content. The magnitude of such organic–inorganic interaction highly depends on the properties of inorganic and organic compounds. It has been suggested that divalent inorganic ions and oxygenated organic molecules can create the most significant cooperative ion–molecule interactions.1,15In the present work, S2O32−is utilized as a model system to represent atmospheric divalent anions, such as SO42−. Glucose and sucrose represent atmospherically relevant oxygenated organic compounds with relatively low and high molecular weights, respectively. The present work found that at relatively high RHs, the S2O32−diffusivity in ternary STS–organic microdroplets remains in between the SE predictions for binary STS–water systems and for binary organic–water systems, agreeing with the general expectation for the viscosities of ternary organic–inorganic mixtures.11,12,16 However, when RH is below 30% or 40% for glucose or sucrose, respectively, the diffusivity of some S2O32−in ternary STS–organic microdroplets decreases at least over two orders of magnitude and becomes rather similar to the SE prediction for binary aqueous organics. Richards et al. also observed a similar trend in the RH-dependent viscosity of ternary (NH4)2SO4-gluconic acid microdroplets.1 In their case, the viscosities of ternary (NH4)2SO4-gluconic acid microdroplets at RH above 15% remain 1 to 2 orders of magnitude smaller than those of binary gluconic acid–water systems. When RH is below 15%, the viscosities of ternary (NH4)2SO4-gluconic acid microdroplets become equal to or even significantly larger than those of binary gluconic acid–water systems, indicating the formation of a gel. These results imply that atmospheric sulfates could also have a similar influence on the phase state of atmospheric organic–inorganic aerosols.
Besides the present work, several previous studies which performed water diffusion measurements for single aerosol microdroplets via the H2O/D2O isotope exchange method have also observed a similar kinetic limitation on the water diffusivity in microdroplets of several binary inorganic–water, binary organic–water or ternary organic–inorganic–water systems as the model systems of atmospheric aerosols, and they attributed such a diffusion limitation of water to the formation of microgel/gel or molecular clusters.10,27,81 Davies and Wilson demonstrated that the gel formation in binary MgSO4-water microdroplets can result in a drastic decrease of water diffusivity by several orders of magnitude, and such a drastic change of water diffusivity highly depends on RH due to the RH-dependent transition of the gel phase state.10 For the cases of binary citric acid-water microdroplets, Nadler et al. observed incomplete H2O/D2O exchanges at RH below 15%, indicating the kinetic inhibition of water diffusion.27 The diffusion coefficients for diffusion-uninhibited water have a good agreement with the literature, i.e., Vignes-type parameterization dedicated for water diffusion in binary mixtures.10,27 However, the percentage of diffusion-inhibited water increases from 0% at RH 15% to 40% at RH 7%, implying a RH-dependent formation of organized molecular structures with confined water. They assumed that such a molecular structure formed in supersaturated microdroplets can be attributed to molecular clusters between citric acid and water or even the aggregation of these clusters. A recent study by Tong et al. also observed the incomplete H2O/D2O exchanges in ternary (NH4)2SO4-organics microdroplets at RH 60%.81 While in each microdroplet, the diffusion coefficient for around 1/2 to 3/4 of water molecules is around 10−12 to 10−11 cm2 s−1, which is similar to those in viscous fluids, the rest of the water molecules are subject to a significant kinetic inhibition of diffusion. It should be noted that the organic compounds used in their study, such as oleic acid, diethyl-L-tartrate and 1,2,6-hexanetriol, have relatively low O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios, and thus they facilitate phase separation in aerosol particles. The authors attributed the incomplete H2O/D2O exchange diffusion to the potential existence of molecule clusters in inorganic-rich phases as the cores of phase-separated microdroplets, while the organic-rich phases as the shells of phase-separated microdroplets determine the diffusion time scale of isolated water diffusing from the cores to the surfaces of microdroplets.
C ratios, and thus they facilitate phase separation in aerosol particles. The authors attributed the incomplete H2O/D2O exchange diffusion to the potential existence of molecule clusters in inorganic-rich phases as the cores of phase-separated microdroplets, while the organic-rich phases as the shells of phase-separated microdroplets determine the diffusion time scale of isolated water diffusing from the cores to the surfaces of microdroplets.
In addition to considering the composition, it is also worthwhile to briefly discuss how the findings from this study can be applied to atmospheric aerosols of various sizes. For the limiting case where interfacial reactions dominate the reactive uptakes of aerosol particles, such as in the ozonolysis of binary aqueous STS microdroplets, the uptake coefficient is independent of the particle radius.30,82,83 However, in more general cases involving coupled interfacial and bulk kinetics, such as the ozonolysis of binary aqueous nitrite microdroplets, the uptake coefficient increases with the particle radius, when the particle radius is within the order of sub μm. Furthermore, when the particle radius increases beyond a couple of μm, the uptake coefficient decreases with the particle radius.44,83 This size dependence of the uptake coefficient can be attributed to bulk kinetics which contributes the effects of the bulk-phase reaction and bulk diffusivity.44,83 In the case of this work, since the organic content in ternary inorganic–organic microdroplets, as well as inorganic–organic intermolecular interactions, can inhibit the bulk diffusivities of reactants and thus raise the contribution of bulk kinetics, it is expected that the uptake coefficient of such microdroplets will exhibit similar size dependence as that for coupled interfacial and bulk kinetics, i.e., the negative size dependence of the uptake coefficient for aerosol particles with sizes larger than μm.
In summary, the results of the laboratory measurements described above indicate a rather ubiquitous existence of the diffusion limitation associated with the formation of microstructures via intermolecular interaction in aerosol particles consisting of inorganics or/and organics. Furthermore, the results of the present work demonstrate that the reaction kinetics of inorganic ions in inorganic–organic aerosols under atmospherically relevant conditions can be affected by their limited diffusion due to their ion–molecule interactions with organic molecules. Thus, besides the formation of phase separation or a glass phase in aerosols,66,84 the ion–molecule effect may also play a role in the reaction kinetics of atmospheric aerosols, demanding a further understanding of such an effect in determining the reactivity of aerosols with more complex mixtures.1
Conclusions
In this work, we exploited the interfacial ozone oxidation kinetics of ternary STS–organic microdroplets via AOTs to probe the bulk diffusivity of S2O32− as a proxy of atmospheric divalent anions at different RHs and inorganic–organic mass ratios. We also utilized a multiphase kinetics model dedicated to aerosol reactions to retrieve the diffusion coefficients of S2O32− from the kinetics measurement results via data-model comparison. The experimental results show that when RH is above a specific threshold, such as ∼30% or ∼40% for glucose or sucrose as organics, respectively, all S2O32− ions in each ternary STS–organic microdroplet can be completely depleted via oxidation with surface O3 at droplet interfaces. The observed reaction time scale increases when decreasing RH and thus increasing the organic content, indicating that the diffusion of S2O32− in STS–organic fluid matrices also plays a key role in the observed aerosol reaction kinetics. The magnitude of S2O32− diffusion coefficients retrieved from the kinetics results is in between the SE predictions for binary STS–water systems and for binary organic–water systems, agreeing with the typical prediction for ternary inorganic–organic mixtures. However, when RH is below the specific RH described above, the kinetics results exhibit not only fast decay but also slow decay in parts of S2O32−, which are assigned to fast and slow diffusing S2O32− in the corresponding kinetic simulation, respectively. While the magnitude of diffusion coefficients for fast diffusing S2O32− is still in between the SE predictions for the binary STS–water system and for the binary organic–water system, that for slow diffusing S2O32− resembles the SE prediction of the binary organic–water system. The results also show that the concentration ratio of fast and slow diffusing S2O32− has a sharp RH dependence. Based on these findings and the literature, the diffusion limitation/inhibition of S2O32− could be attributed to the formation of microstructures with S2O32− and organics. On the other hand, such assignment of the aerosol reaction pathway could also confirm the potential influence of ion–molecule interactions on the reaction kinetics of aerosols.Finally, to further understand the influence of ion–molecule effects on the aerosol reaction kinetics, future studies include the measurements of aerosol reaction kinetics in more complex mixtures, such as exploiting various organic species with different functional groups, and also in the mixtures of salts with divalent cations, such as CaS2O3 and MgS2O3. According to the literature described above, not only Ca2+ but also Mg2+ can lead to gel formation or enhanced viscosity.1,10 To further justify the existence of ion–molecule microstructures, as well as their influences, it may also be possible to carry out the H2O/D2O isotope exchange method to determine the water diffusivity in the ternary STS–organic microdroplets. Furthermore, the measurement focusing on compositional dependence of water diffusivity could serve as a complementary study, clarifying if the intermolecular interaction or methodology of diffusivity measurement also plays a role in the insensitivity of S2O32− diffusivity to the STS–organic mass ratio observed in the present work.
Data availability
Data for this article, including integrated Raman intensity time profiles of thiosulfate of all Expt. numbers and Raman spectra in Fig. 1 are available to download at https://zenodo.org/records/11396132, as well as DOI: https://10.5281/zenodo.11396131. The kinetic model simulation results plotted in Fig. 3–6 have been included as part of the ESI.† The code of the kinetic model (KM-SUB) used in this work has been provided in ref. 40.Author contributions
Y.-P. C., T.-C. H., F.-Y. L. and S.-H. H. designed the experiments. T.-C. H., F.-Y. L. and S.-H. H. performed the AOT experiments. Y.-P. C., T.-C. H. and F.-Y. L. carried out the data analysis. Y.-P. C. and T. K. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ministry of Science and Technology, Taiwan (MOST109-2113-M-110-010-, MOST110-2113-M-110-019- and MOST111-2113-M-110-001-), NSYSU-KMU joint research project (NSYSUKMU 108-I002) and National Science and Technology Council, Taiwan (NSTC112-2113-M-110-011- and NSTC113-2113-M-110-005-). We are also thankful for very kind support from the Aerosol Science Research Center, NSYSU, Taiwan. We thank Prof. Shiraiwa for allowing the usage of KM-SUB in our publications. Finally, we are thankful for the very helpful comments from Prof. C.-M. Chiang, Prof. Jim. J.-M. Lin, Prof. C.-H. Yang and anonymous reviewers of this manuscript.Notes and references
- D. S. Richards, K. L. Trobaugh, J. Hajek-Herrera, C. L. Price, C. S. Sheldon, J. F. Davies and R. D. Davis, Sci. Adv., 2020, 6, eabb5643 CrossRef CAS PubMed.
- A. P. Ault and J. L. Axson, Anal. Chem., 2017, 89, 430–452 CrossRef CAS PubMed.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- B. A. Nault, D. S. Jo, B. C. McDonald, P. Campuzano-Jost, D. A. Day, W. Hu, J. C. Schroder, J. Allan, D. R. Blake, M. R. Canagaratna, H. Coe, M. M. Coggon, P. F. DeCarlo, G. S. Diskin, R. Dunmore, F. Flocke, A. Fried, J. B. Gilman, G. Gkatzelis, J. F. Hamilton, T. F. Hanisco, P. L. Hayes, D. K. Henze, A. Hodzic, J. Hopkins, M. Hu, L. G. Huey, B. T. Jobson, W. C. Kuster, A. Lewis, M. Li, J. Liao, M. O. Nawaz, I. B. Pollack, J. Peischl, B. Rappenglück, C. E. Reeves, D. Richter, J. M. Roberts, T. B. Ryerson, M. Shao, J. M. Sommers, J. Walega, C. Warneke, P. Weibring, G. M. Wolfe, D. E. Young, B. Yuan, Q. Zhang, J. A. de Gouw and J. L. Jimenez, Atmos. Chem. Phys., 2021, 21, 11201–11224 CrossRef CAS.
- R. E. Cochran, O. Laskina, J. V. Trueblood, A. D. Estillore, H. S. Morris, T. Jayarathne, C. M. Sultana, C. Lee, P. Lin, J. Laskin, A. Laskin, J. A. Dowling, Z. Qin, C. D. Cappa, T. H. Bertram, A. V. Tivanski, E. A. Stone, K. A. Prather and V. H. Grassian, Chem, 2017, 2, 655–667 CAS.
- S. M. Kruse and J. H. Slade, J. Phys. Chem. A, 2023, 127, 4724–4733 CrossRef CAS PubMed.
- V. F. McNeill, G. M. Wolfe and J. A. Thornton, J. Phys. Chem. A, 2007, 111, 1073–1083 CrossRef CAS PubMed.
- J. P. Reid, A. K. Bertram, D. O. Topping, A. Laskin, S. T. Martin, M. D. Petters, F. D. Pope and G. Rovelli, Nat. Commun., 2018, 9, 956 CrossRef PubMed.
- A. Rafferty and T. C. Preston, Phys. Chem. Chem. Phys., 2018, 20, 17038–17047 RSC.
- J. F. Davies and K. R. Wilson, Anal. Chem., 2016, 88, 2361–2366 CrossRef CAS PubMed.
- G. Rovelli, Y. C. Song, A. M. Maclean, D. O. Topping, A. K. Bertram and J. P. Reid, Anal. Chem., 2019, 91, 5074–5082 CrossRef CAS PubMed.
- Y. C. Song, J. Lilek, J. B. Lee, M. N. Chan, Z. Wu, A. Zuend and M. Song, Atmos. Chem. Phys., 2021, 21, 10215–10228 CrossRef CAS.
- J. Lilek and A. Zuend, Atmos. Chem. Phys., 2022, 22, 3203–3233 CrossRef CAS.
- A. Marsh, S. S. Petters, N. E. Rothfuss, G. Rovelli, Y. C. Song, J. P. Reid and M. D. Petters, Phys. Chem. Chem. Phys., 2018, 20, 15086–15097 RSC.
- D. S. Richards, K. L. Trobaugh, J. Hajek-Herrera and R. D. Davis, Anal. Chem., 2020, 92, 3086–3094 CrossRef CAS PubMed.
- R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, Chem. Sci., 2013, 4, 2597–2604 RSC.
- H. C. Price, J. Mattsson, Y. Zhang, A. K. Bertram, J. F. Davies, J. W. Grayson, S. T. Martin, D. O'Sullivan, J. P. Reid, A. M. J. Rickards and B. J. Murray, Chem. Sci., 2015, 6, 4876–4883 RSC.
- L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Proc. Natl. Acad. Sci. U.S.A., 2013, 110, 8014–8019 CrossRef CAS PubMed.
- F. H. Marshall, R. E. H. Miles, Y. C. Song, P. B. Ohm, R. M. Power, J. P. Reid and C. S. Dutcher, Chem. Sci., 2016, 7, 1298–1308 RSC.
- H. C. Price, B. J. Murray, J. Mattsson, D. O'Sullivan, T. W. Wilson, K. J. Baustian and L. G. Benning, Atmos. Chem. Phys., 2014, 14, 3817–3830 CrossRef.
- B. Zobrist, V. Soonsin, B. P. Luo, U. K. Krieger, C. Marcolli, T. Peter and T. Koop, Phys. Chem. Chem. Phys., 2011, 13, 3514–3526 RSC.
- J. Dou, B. Luo, T. Peter, P. A. Alpert, P. Corral Arroyo, M. Ammann and U. K. Krieger, J. Phys. Chem. Lett., 2019, 10, 4484–4489 CrossRef CAS PubMed.
- Y. C. Song, S. Ingram, R. E. Arbon, D. O. Topping, D. R. Glowacki and J. P. Reid, Chem. Sci., 2020, 11, 2999–3006 RSC.
- M. Shiraiwa, M. Ammann, T. Koop and U. Poschl, Proc. Natl. Acad. Sci. U.S.A., 2011, 108, 11003–11008 CrossRef CAS PubMed.
- V. Molinero and W. A. Goddard 3rd, Phys. Rev. Lett., 2005, 95, 045701 CrossRef PubMed.
- Y. P. Chang, Y. Devi and C. H. Chen, Chem.–Asian J., 2021, 16, 1644–1660 CrossRef CAS PubMed.
- K. A. Nadler, P. Kim, D. L. Huang, W. Xiong and R. E. Continetti, Phys. Chem. Chem. Phys., 2019, 21, 15062–15071 RSC.
- T. C. Preston, J. F. Davies and K. R. Wilson, Phys. Chem. Chem. Phys., 2017, 19, 3922–3931 RSC.
- F. H. Marshall, T. Berkemeier, M. Shiraiwa, L. Nandy, P. B. Ohm, C. S. Dutcher and J. P. Reid, Phys. Chem. Chem. Phys., 2018, 20, 15560–15573 RSC.
- S.-H. Hsu, F.-Y. Lin, G. G. Huang and Y.-P. Chang, J. Phys. Chem. C, 2023, 127, 6248–6261 CrossRef CAS.
- A. Miura, R. Nakajima, S. Abe and N. Kitamura, J. Phys. Chem. A, 2020, 124, 9035–9043 CrossRef CAS PubMed.
- R. Nakajima, A. Miura, S. Abe and N. Kitamura, Anal. Chem., 2021, 93, 5218–5224 CrossRef CAS PubMed.
- J. R. Kanofsky and P. D. Sima, Arch. Biochem. Biophys., 1995, 316, 52–62 CrossRef CAS PubMed.
- B. Müller and M. R. Heal, Phys. Chem. Chem. Phys., 2002, 4, 3365–3369 RSC.
- S. Enami, C. D. Vecitis, J. Cheng, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. A, 2007, 111, 13032–13037 CrossRef CAS PubMed.
- R. G. Utter, J. B. Burkholder, C. J. Howard and A. R. Ravishankara, J. Phys. Chem., 2002, 96, 4973–4979 CrossRef.
- Y. P. Chang, S. J. Wu, M. S. Lin, C. Y. Chiang and G. G. Huang, Phys. Chem. Chem. Phys., 2021, 23, 10108–10117 RSC.
- J. R. Li and Y. P. Chang, J. Chin. Chem. Soc., 2023, 70, 1390–1398 CrossRef CAS.
- T. Berkemeier, S. S. Steimer, U. K. Krieger, T. Peter, U. Pöschl, M. Ammann and M. Shiraiwa, Phys. Chem. Chem. Phys., 2016, 18, 12662–12674 RSC.
- A. K. Hua, P. S. J. Lakey and M. Shiraiwa, J. Chem. Educ., 2022, 99, 1246–1254 CrossRef CAS.
- M. Shiraiwa, C. Pfrang and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 3673–3691 CrossRef CAS.
- T. Berkemeier, A. J. Huisman, M. Ammann, M. Shiraiwa, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2013, 13, 6663–6686 CrossRef.
- U. Pöschl, Y. Rudich and M. Ammann, Atmos. Chem. Phys., 2007, 7, 5989–6023 CrossRef.
- M. D. Willis and K. R. Wilson, J. Phys. Chem. A, 2022, 126, 4991–5010 CrossRef CAS PubMed.
- T. Berkemeier, A. Mishra, C. Mattei, A. J. Huisman, U. K. Krieger and U. Pöschl, ACS Earth Space Chem., 2021, 5, 3313–3323 CrossRef CAS.
- M. Roeselová, P. Jungwirth, D. J. Tobias and R. B. Gerber, J. Phys. Chem. B, 2003, 107, 12690–12699 CrossRef.
- M. Takizawa, A. Okuwaki and T. Okabe, Bull. Chem. Soc. Jpn., 1973, 46, 3785–3789 CrossRef CAS.
- J. A. Haigh, P. J. Hendra, A. J. Rowlands, I. A. Degen and G. A. Newman, Spectrochim. Acta, Part A, 1993, 49, 723–725 CrossRef.
- S. Sato, S. Higuchi and S. Tanaka, Appl. Spectrosc., 1985, 39, 822–827 CrossRef CAS.
- R. Goodacre, B. S. Radovic and E. Anklam, Appl. Spectrosc., 2002, 56, 521–527 CrossRef CAS.
- E. A. Nicol, J. Y. Baron, J. Mirza, J. J. Leitch, Y. Choi and J. Lipkowski, J. Solid State Electrochem., 2013, 18, 1469–1484 CrossRef.
- H. Gerding and K. Eriks, Recl. Trav. Chim. Pays-Bas, 1950, 69, 724–728 CrossRef CAS.
- B. Meyer and M. Ospina, Phosphorus, Sulfur, Silicon Relat. Elem., 2006, 14, 23–36 CrossRef.
- H.-J. Tong, J. P. Reid, J.-L. Dong and Y.-H. Zhang, J. Phys. Chem. A, 2010, 114, 12237–12243 CrossRef CAS PubMed.
- E. Rolia and C. L. Chakrabarti, Environ. Sci. Technol., 1982, 16, 852–857 CrossRef CAS PubMed.
- R. J. Hopkins, L. Mitchem, A. D. Ward and J. P. Reid, Phys. Chem. Chem. Phys., 2004, 6, 4924 RSC.
- R. Symes, R. M. Sayer and J. P. Reid, Phys. Chem. Chem. Phys., 2004, 6, 474–487 RSC.
- J. P. Reid, H. Meresman, L. Mitchem and R. Symes, Int. Rev. Phys. Chem., 2007, 26, 139–192 Search PubMed.
- T. C. Preston and J. P. Reid, J. Opt. Soc. Am. A, 2015, 32, 2210 CrossRef PubMed.
- S. Mahiuddin and K. Ismail, Fluid Phase Equil., 1996, 123, 231–243 CAS.
- J. Buffle, Z. Zhang and K. Startchev, Environ. Sci. Technol., 2007, 41, 7609–7620 CrossRef CAS PubMed.
- Y. C. Song, A. E. Haddrell, B. R. Bzdek, J. P. Reid, T. Bannan, D. O. Topping, C. Percival and C. Cai, J. Phys. Chem. A, 2016, 120, 8123–8137 CrossRef CAS PubMed.
- G. D. Smith, E. Woods, T. Baer and R. E. Miller, J. Phys. Chem. A, 2003, 107, 9582–9587 CrossRef CAS.
- W. Li, C. Y. Pak, X. Wang and Y.-L. S. Tse, J. Phys. Chem. C, 2019, 123, 18924–18931 CrossRef CAS.
- M. A. Freedman, Acc. Chem. Res., 2020, 53, 1102–1110 CrossRef CAS PubMed.
- K. A. Wokosin, E. L. Schell and J. A. Faust, Environ. Sci.: Atmos., 2022, 2, 775–828 Search PubMed.
- Y. You, M. L. Smith, M. Song, S. T. Martin and A. K. Bertram, Int. Rev. Phys. Chem., 2014, 33, 43–77 Search PubMed.
- M. A. Freedman, Chem. Soc. Rev., 2017, 46, 7694–7705 RSC.
- S. Zhou, B. C. H. Hwang, P. S. J. Lakey, A. Zuend, J. P. D. Abbatt and M. Shiraiwa, Proc. Natl. Acad. Sci. U.S.A., 2019, 116, 11658–11663 CrossRef CAS PubMed.
- M. Riva, Y. Chen, Y. Zhang, Z. Lei, N. E. Olson, H. C. Boyer, S. Narayan, L. D. Yee, H. S. Green, T. Cui, Z. Zhang, K. Baumann, M. Fort, E. Edgerton, S. H. Budisulistiorini, C. A. Rose, I. O. Ribeiro, E. O. RL, E. O. Dos Santos, C. M. D. Machado, S. Szopa, Y. Zhao, E. G. Alves, S. S. de Sa, W. Hu, E. M. Knipping, S. L. Shaw, S. Duvoisin Junior, R. A. F. de Souza, B. B. Palm, J. L. Jimenez, M. Glasius, A. H. Goldstein, H. O. T. Pye, A. Gold, B. J. Turpin, W. Vizuete, S. T. Martin, J. A. Thornton, C. S. Dutcher, A. P. Ault and J. D. Surratt, Environ. Sci. Technol., 2019, 53, 8682–8694 CrossRef CAS PubMed.
- G. T. Drozd, J. L. Woo and V. F. McNeill, Atmos. Chem. Phys., 2013, 13, 8255–8263 CrossRef.
- Y. Zhang, Y. Chen, A. T. Lambe, N. E. Olson, Z. Lei, R. L. Craig, Z. Zhang, A. Gold, T. B. Onasch, J. T. Jayne, D. R. Worsnop, C. J. Gaston, J. A. Thornton, W. Vizuete, A. P. Ault and J. D. Surratt, Environ. Sci. Technol. Lett., 2018, 5, 167–174 CrossRef CAS.
- Y. Zhang, Y. Chen, Z. Lei, N. E. Olson, M. Riva, A. R. Koss, Z. Zhang, A. Gold, J. T. Jayne, D. R. Worsnop, T. B. Onasch, J. H. Kroll, B. J. Turpin, A. P. Ault and J. D. Surratt, ACS Earth Space Chem., 2019, 3, 2646–2658 CrossRef CAS.
- J. F. Davies, R. E. H. Miles, A. E. Haddrell and J. P. Reid, Proc. Natl. Acad. Sci. U.S.A., 2013, 110, 8807–8812 CrossRef CAS PubMed.
- C. R. Ruehl and K. R. Wilson, J. Phys. Chem. A, 2014, 118, 3952–3966 CrossRef CAS PubMed.
- W. Li, X. Teng, X. Chen, L. Liu, L. Xu, J. Zhang, Y. Wang, Y. Zhang and Z. Shi, Environ. Sci. Technol., 2021, 55, 16339–16346 CrossRef CAS PubMed.
- E. F. Mikhailov, M. L. Pöhlker, K. Reinmuth-Selzle, S. S. Vlasenko, O. O. Krüger, J. Fröhlich-Nowoisky, C. Pöhlker, O. A. Ivanova, A. A. Kiselev, L. A. Kremper and U. Pöschl, Atmos. Chem. Phys., 2021, 21, 6999–7022 CrossRef CAS.
- A. Milsom, A. M. Squires, B. Woden, N. J. Terrill, A. D. Ward and C. Pfrang, Faraday Discuss., 2021, 226, 364–381 RSC.
- J. A. Faust and J. P. D. Abbatt, J. Phys. Chem. A, 2019, 123, 2114–2124 CrossRef CAS PubMed.
- J. A. Thornton and J. P. Abbatt, J. Phys. Chem. A, 2005, 109, 10004–10012 CrossRef CAS PubMed.
- Y.-K. Tong, Z. Wu, M. Hu and A. Ye, Atmos. Chem. Phys., 2024, 24, 2937–2950 CrossRef CAS.
- G. D. Smith, E. Woods, C. L. DeForest, T. Baer and R. E. Miller, J. Phys. Chem. A, 2002, 106, 8085–8095 CrossRef CAS.
- K. R. Wilson, A. M. Prophet and M. D. Willis, J. Phys. Chem. A, 2022, 126, 7291–7308 CrossRef CAS PubMed.
- B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ea00072b |
| This journal is © The Royal Society of Chemistry 2024 |