Increasing the Earth's albedo: the Köhler equation at sea
Received
30th May 2024
, Accepted 14th August 2024
First published on 23rd August 2024
Abstract
Increasing marine haze and clouds has been considered as a possible means of increasing the Earth's albedo. This would reduce solar heating and global warming, counteracting the effects of the anthropogenic increase in greenhouse gases. One proposed method of doing so would inject small droplets of seawater or condensation nuclei into the marine boundary layer, creating artificial haze and cloud. The equilibrium size of such droplets is described by the Köhler equation that includes the vapor pressure reduction attributable to the solute according to Raoult's law and the vapor pressure increase of a small droplet as a result of surface tension according to Kelvin. Here we apply this classic result to small droplets in the marine boundary layer, where the partial pressure of water vapor is less than the equilibrium vapor pressure because it is in equilibrium with the saline ocean. We calculate the equilibrium size of a droplet containing dissolved ions and find that the radius of a droplet of seawater shrinks greatly before it achieves equilibrium.
Environmental significance
Increasing the Earth's albedo by nucleating clouds or injecting seawater aerosols into the atmosphere has been proposed to counteract global warming produced by anthropogenic greenhouse gases. The equilibrium sizes of these aerosols are determined by evaporation and condensation of atmospheric water vapor.
|
1 Introduction
Marine cloud-brightening by injection of seawater aerosols as condensation nuclei was proposed1–3 to increase the Earth's albedo (fraction of incident sunlight reflected back to space) to counteract the warming effects of anthropogenic greenhouse gases. Here I review the properties of saline water droplets in equilibrium with the oceanic boundary layer that is itself in equilibrium with the ocean. Köhler's classic equation describes the vapor pressure of a small droplet, increased by surface tension and decreased by the presence of a solute. The equilibrium size of such a droplet depends on the ambient vapor density. I apply those results to droplets, initially with the salinity of seawater as would be produced by its atomization, coming to equilibrium in the boundary layer over the ocean surface in which the partial pressure of water vapor is in equilibrium with the saline ocean and less than the equilibrium vapor pressure of pure water.4
This work is only concerned with the region very close to the ocean surface, not with subsequent enhancement of marine clouds at higher altitudes.5–9 While the general physical principles have long been known,10,11 here I express their interaction in simple and transparent analytic results. I do not consider the effects of possible surfactants12 because they are poorly characterized and vary greatly from place to place. In application to albedo modification, water could be drawn from below the ocean surface and would have little surfactant content.
2 Köhler's equation
Köhler's equation for the vapor pressure p(r) of a droplet of radius r of fluid with molecular number density n and surface tension σ, containing N solute atoms, ions or molecules5–7,13 may be written| | 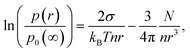 | (1) |
where p0(∞) is the vapor pressure of a flat surface of the pure liquid. This result is based on Raoult's law10 for the equilibrium partial pressure pi of a component i that has a pure component, liquid state equilibrium vapor pressure p0 over a solution in which i constitutes a mole fraction xiand Kelvin's law11| | 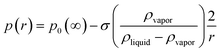 | (3) |
for the reduction of vapor pressure by curvature of the surface of a spherical drop of radius r and that these small corrections are additive. It neglects non-ideal properties of the solution and any dependence of σ on the solute (all good approximations for dilute solutions). N must include the van't Hoff factor, the number of dissociated ions per molecule, which is close to 2 for dilute solutions of ocean salts.
3 Köhler's equation at sea
For droplets in the atmospheric sea-surface equilibrium boundary layer in equilibrium with slightly undersaturated water vapor, the application of Köhler's equation requires consideration of the undersaturation. Substituting p(r) = p(∞) = (1 − ε)p0(∞) in the left hand side of eqn (1) and approximating ln(1 − ε) ≈ −ε yields a cubic equation for the equilibrium radius r:| | 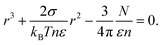 | (4) |
We take T = 293 K, n = 3.35 × 1028 m−3 and σ = 0.07 N m−1.
Application of Raoult's law (eqn (2)) to the vapor pressure p(∞) of a flat surface of seawater indicates that p(∞) = 0.9796p0(∞); we define the undersaturation ε = 1 − p(∞)/p0(∞) = 1–0.9796 = 0.0204.
4 Nucleation
4.1 Minimum N and r
The first two terms in eqn (4) are positive while the third term, ∝ N, is negative. This sets a lower bound on the values of N for which a solution is possible. This bound is not zero because the minimum meaningful rmin ≈ 0.1 nm (for a smaller droplet σ is not well defined). For small r the cubic term may be neglected in comparison to the quadratic term, yielding| | 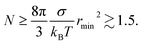 | (5) |
Although the formalism indicates that for some values of the parameters there is a meaningful minimum N that permits formation of a stable droplet, for droplets large enough to justify the use of continuum theory this minimum (eqn (5)) is so small as to be irrelevant. It is meaningful to solve eqn (4) for r(N) or N(r) when r ≫ 0.1 nm and N ≫ 2.
4.2 Equilibrium droplet size
The cubic eqn (4) may be solved explicitly for r(N), giving the equilibrium radius of a drop nucleated by a particle containing N nonvolatile solute atoms, ions or molecules. The cumbersome algebraic solution is shown graphically in Fig. 1. A droplet with radius r < r(N) will condense additional water vapor until r = r(N). A droplet with r > r(N) will evaporate until r = r(N).
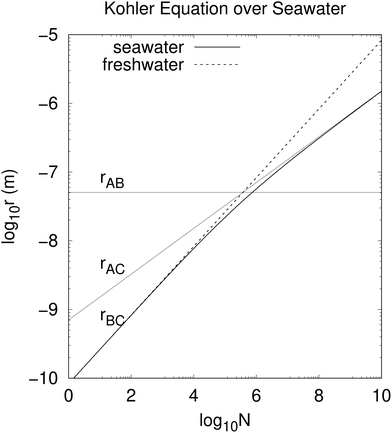 |
| | Fig. 1 Relation between equilibrium droplet radius r and number of solute ions N, evaluated in the marine atmospheric equilibrium boundary layer. The air is slightly undersaturated in water vapor compared to air over pure water because of ocean salinity. At smaller N and r the quadratic (surface tension) term in eqn (4) dominates and r ∝ N1/2, while at larger N and r the cubic (undersaturation) term dominates and r ∝ N1/3. The cross-over between these regimes occurs for r ≈ rAB ≈ 50 nm and N ≈ 5 × 105 (eqn (6)). rBC is identical to r(N) for fresh water. | |
There are three cross-overs in eqn (4), values of r when two terms are equal. The cubic term (in r) equals the quadratic term when
| | 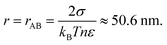 | (6) |
Each of these terms act to make the droplet evaporate, but for
r >
rAB subsaturation is more important that surface tension. If there is sufficient solute these effects may be overcome and a droplet condenses further water vapor. To simplify the algebra we consider these terms separately.
The cubic term in r in eqn (4) equals the negative term when
| | 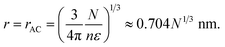 | (7) |
When
r >
rAC subsaturation overcomes the effect of the solute and the droplet shrinks. If
r <
rAB surface tension also contributes to evaporation. If
r <
rAC the solute is more important and the droplet will condense additional water vapor unless
r <
rAB, in which case surface tension must also be considered.
The term quadratic in r equals the negative term when
| | 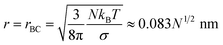 | (8) |
When
r >
rBC the droplet will shrink, while for
r <
rBC the droplet will condense additional water vapor, unless
r >
rAC. If
r >
rAC subsaturation makes the droplet shrink, even without the contributing effect of surface tension.
Very small droplets (those with r ≪ 100 nm) are ineffective scatterers of light, so we now consider the regime in which the quadratic term in eqn (4) may be neglected in comparison to the cubic term (r ≫ rAB ≈ 50 nm). Neglecting the quadratic term, we find
| | 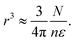 | (9) |
Then the number of water molecules in the droplet
| | 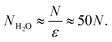 | (10) |
Condensation of seawater multiplies the volume of the aerosol by a factor 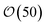 and multiplies its scattering by another large factor. This latter factor is proportional to the square of the volume in the Rayleigh scattering regime applicable to very small droplets (r ≲ 100 nm), and to the 2/3 power of the volume in the geometrical optics regime applicable to larger droplets (r ≳ 1000 nm)14.
and multiplies its scattering by another large factor. This latter factor is proportional to the square of the volume in the Rayleigh scattering regime applicable to very small droplets (r ≲ 100 nm), and to the 2/3 power of the volume in the geometrical optics regime applicable to larger droplets (r ≳ 1000 nm)14.
5 Seawater droplets
Rather than injecting small soluble particles to nucleate droplets from water vapor in the marine equilibrium boundary layer, it is possible to inject small droplets of seawater, available in unlimited quantity at sea. Such a particle will have a higher vapor pressure than the sea itself because of its surface curvature. Equate the vapor pressure in a droplet of seawater that has shrunken by evaporation from an initial radius r0 (containing N = 4πnεr03/3 solute ions) to a radius r to the partial pressure of water over the ocean:| | 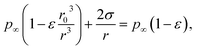 | (11) |
where p∞ ≈ 1.7 × 103 Pa is the vapor pressure of a flat surface of pure water at 15 °C. Defining a characteristic radius| | 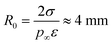 | (12) |
leads to the cubic equation
In the relevant regime r ≪ R0 (larger droplets fall rapidly as rain) and the cubic term may be neglected, leading to the approximation
| | 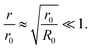 | (14) |
The increase in vapor pressure attributable to surface tension is balanced for the shrinking droplet by the decrease resulting from increasing salinity. The Raoult (solute) decrease grows faster with decreasing radius than does the Kelvin (surface tension) increase, and the droplet comes to an equilibrium radius that is much smaller than its initial radius.
The solution of eqn (4) and is shown in Fig. 2. In fact, shrinkage is limited by the breakdown of Raoult's law when the solution becomes concentrated. r/r0 cannot be less than 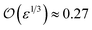 ; the result is a particle of moist salt or highly concentrated brine containing all the originally dissolved salt but little or none of the original water. Shrinkage stops because the increase in vapor pressure as a result of reduced radius is balanced by the (more rapidly growing) decrease as a result of growing salinity.
; the result is a particle of moist salt or highly concentrated brine containing all the originally dissolved salt but little or none of the original water. Shrinkage stops because the increase in vapor pressure as a result of reduced radius is balanced by the (more rapidly growing) decrease as a result of growing salinity.
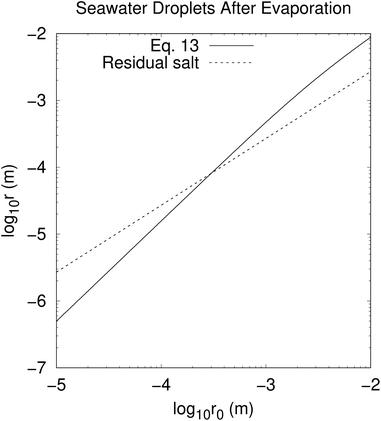 |
| | Fig. 2 Equilibrium radius r of seawater drop of original radius r0 in oceanic equilibrium boundary layer according to eqn (13). Dashed line (r = 0.27r0) shows where Raoult's law breaks down because the droplet becomes concentrated brine or moist salt; values of r lying below this line are unphysical. This may be dealt with a modified Raoult's law,15 but without the simple result shown here. | |
6 Conclusions
Increasing the Earth's albedo by stimulating cloud formation has been proposed1–3 as a method of counteracting the global warming produced by anthropogenic greenhouse gases. Condensation of water vapor on a saline nucleus multiplies its mass, volume and optical scattering by large factors. The ready availability of seawater makes its atomization a feasible means of producing cloud condensation nuclei, but the increased vapor pressure of small seawater droplets makes them shrink by large factors in radius (and by the cube of that factor in mass and volume) as they come into equilibrium with the ambient water vapor in the surface equilibrium boundary layer. The processes discussed here must be allowed for when considering seawater droplets as a surface source of cloud condensation nuclei that may grow into effective scatterers at higher altitude. This applies to naturally produced droplets (ocean spray produced by spindrift and bubble collapse at the ocean surface) as well as to those that might be produced artificially.
Using atomized seawater as cloud condensation nuclei differs from the mechanism producing ship tracks from dry products of combustion, whose physical chemistry must differ from and be more complicated than that of salt. While seawater droplets do have well-defined “dry radii” (the radius of a dry salt particle containing their salt content), they can never become that small because the decrease of their vapor pressure as they shrink stops evaporation at the equilibrium radii given by eqn (4) and (13) and shown in the figures. A significant consequency of the evaporative shrinkage of an injected seawater droplet is that its gravitational sink rate is reduced, facilitating its entrainment by turbulent flow in the marine boundary layer, and therefore its transport to altitudes at which supersaturation may make it grow sufficiently to become an effective scatterer of sunlight.
Saline water droplets may be produced in great numbers by flow of bulk seawater through a nozzle or a wire grid. They may be subsequently lofted in the turbulent marine boundary layer to altitudes at which adiabatic cooling has rendered the air supersaturated. Further growth may make them effective scatterers of sunlight.5–9,15 This resembles the mechanism by which cloud seeding may stimulate rainfall from clouds supersaturated by evaporation of small droplets, although in the marine case supersaturation results from adiabatic cooling of rising air rather than by evaporation of smaller droplets (Ostwald ripening). This further growth involves turbulent mixing in the marine boundary layer, a complex process beyond the scope of this paper.
7 Open research
This theoretical study generated no data.
Data availability
This theoretical paper did not use any data and did not produce any new data.
Author contributions
The single author conceived and carried out the research and wrote the paper.
Conflicts of interest
There are no conflicts of interest.
Acknowledgments
I thank Matthew Alford and Baylor Fox-Kemper for useful discussions.
Notes and references
- J. Latham, Nature, 1990, 347, 339–340 CrossRef.
- J. Latham, Atmos. Sci. Lett., 2002, 3, 52–58 CrossRef.
- J. Latham, K. Bower, T. Choularton, H. Coe, P. Connolly, G. Cooper, T. Craft, J. Foster, A. Gadian, L. Galbraith, H. Iacovides, D. Johnston, B. Lawader, B. Leslie, J. Meyer, A. Naukermans, B. Ormond, B. Parkes, P. Rasch, J. Rush, S. Salter, T. Stevenson, H. Wang, Q. Wang and R. Wood, Philos. Trans. R. Soc., A, 2012, 370, 4217–4262 CrossRef PubMed.
- F. J. Millero, R. Feistel, D. G. Wright and T. J. McDougall, Deep Sea Res., Part I, 2008, 55, 50–72 CrossRef.
-
M. K. Yau and R. R. Rogers, A Short Course in Cloud Physics, Elsevier, Amsterdam, edn. 3rd, 1989 Search PubMed.
-
K. C. Young, Microphysical Processes in Clouds, Oxford U. Press, Oxford, 1993 Search PubMed.
-
J. M. Wallace and P. V. Hobbs, Atmospheric Science: an Introductory Survey, Elsevier, Amsterdam, edn. 2nd, 2006 Search PubMed.
- R. A. Houze, Int. Geophys., 2014, 104, 47–76 Search PubMed.
- K. N. Fossum, J. Ovadnevaite, D. Ceburnis, J. Preiß, J. R. Snifer, R.-J. Huang, A. Zuend and C. O'Dowd, npj Clim. Atmos. Sci., 2020, 3, 14 CrossRef CAS.
-
L. D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon, London, 1958, p. 279 Search PubMed.
-
A. B. Pippard, The Elements of Chemical Thermodynamics, Cambridge U. Press, Cambridge, 1966, p. 111 Search PubMed.
- W. D. Garrett, J. Geophys. Res., 1968, 73, 5145–5150 CrossRef CAS.
-
M. H. P. Ambaum, Thermal Physics of the Atmosphere, Wiley-Blackwell, Chichester, West Sussex, UK, 2010 Search PubMed.
-
H. C. van de Hulst, Light Scattering by Small Particles, Dover, New York, 1981 Search PubMed.
- M. D. Petters and S. M. Kreidenweis, Atmos. Chem. Phys., 2007, 7, 1961–1971 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
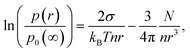
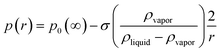
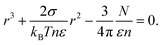
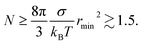

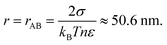
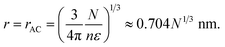
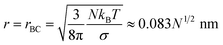
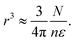
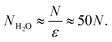
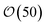 and multiplies its scattering by another large factor. This latter factor is proportional to the square of the volume in the Rayleigh scattering regime applicable to very small droplets (r ≲ 100 nm), and to the 2/3 power of the volume in the geometrical optics regime applicable to larger droplets (r ≳ 1000 nm)14.
and multiplies its scattering by another large factor. This latter factor is proportional to the square of the volume in the Rayleigh scattering regime applicable to very small droplets (r ≲ 100 nm), and to the 2/3 power of the volume in the geometrical optics regime applicable to larger droplets (r ≳ 1000 nm)14.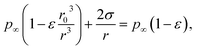
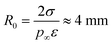
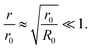
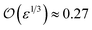 ; the result is a particle of moist salt or highly concentrated brine containing all the originally dissolved salt but little or none of the original water. Shrinkage stops because the increase in vapor pressure as a result of reduced radius is balanced by the (more rapidly growing) decrease as a result of growing salinity.
; the result is a particle of moist salt or highly concentrated brine containing all the originally dissolved salt but little or none of the original water. Shrinkage stops because the increase in vapor pressure as a result of reduced radius is balanced by the (more rapidly growing) decrease as a result of growing salinity.
