Influence of contouring the lithium metal/solid electrolyte interface on the critical current for dendrites

Abstract

Contouring or structuring of the lithium/ceramic electrolyte interface and therefore increasing its surface area has been considered as a possible strategy to increase the charging current in solid-state batteries without lithium dendrite formation and short-circuit. By coupling together lithium deposition kinetics and the me chanics of lithium creep within calculations of the current distribution at the interface, and leveraging a model for lithium dendrite growth, we show that efforts to avoid dendrites on charging by increasing the interfacial surface area come with significant limitations associated with the topography of rough surfaces. These limitations are sufficiently severe such that it is very unlikely contouring could increase charging currents while avoiding dendrites and short-circuit to the levels required. For example, we show a sinusoidal surface topography can only raise the charging current before dendrites occur by approx. 50% over a flat interface.

---

Broader context

Unlocking the potential of the lithium metal anode for solid-state batteries is key to realising solid state batteries with energy densities exceeding lithium-ion batteries used today. However, on charging such solid-state cells they suffer from lithium dendrite growth, leading to short-circuits and cell failure. This is one of the biggest problems facing solid state batteries. Increasing the surface area between the lithium metal anode and solid electrolyte by contouring the interface could lower the local current densities compared with a flat interface, helping to avoid dendrite growth. Herein, we used 3D printing to form contoured solid electrolytes with different topographies, peak separations and heights. We find the limitations due to inhomogeneous current distribution across the contoured (rough) surface quickly outweighs the benefit of increasing surface area between the lithium metal anode and solid electrolyte. Only a 50% improvement in critical charging current before dendrites occur can be achieved compared with a flat interface. As a result, contouring is unlikely to solve the dendrite problem in lithium anode solid state batteries.

Introduction

Solid-state batteries with a lithium metal anode and solid ceramic electrolyte could increase the energy density of lithium batteries compared with those used today.^1–10 On charging (lithium plating) at rates of several mA cm⁻², lithium dendrites (filaments) penetrate the solid electrolyte, leading to short-circuit and cell failure.^11–20 The critical current for dendrites is typically defined as the geometrical current density – the current per unit cross sectional area of the cell – at and above which dendrites penetrate the solid electrolyte.^21–26 However, dendrites are driven by the local current density at the lithium/electrolyte interface.^27,28 For a perfectly planar interface, the geometrical and local current densities equate. Contouring or roughening the Li/electrolyte interface increases the interfacial area, which reduces the ratio of the average local current density for a given geometrical current density below unity. To explore the effect of interfacial topography on the critical current for dendrites, several authors have deliberately increased the interfacial area by a variety of methods including polishing and laser cutting.^29–33 Some groups have reported increases in the critical current for dendrites,^29,31 whereas others pointed out that surface roughness can cause instability of Li deposition at the Li/electrolyte interface.^34–36 Explanations have invoked the current density distribution across the contoured interface or variations in the local equivalent stress state of Li metal near the interface.³¹

Here we consider the different factors that influence the critical current for dendrite formation when the Li/electrolyte interface is periodically contoured. Employing 3D printing to form a contoured solid electrolyte surface, we found that 3D bisinusoidal (commonly known as “egg-box”) interfacial shapes have the highest critical current for dendrites compared to other periodic topographies, specifically square pyramids and frustums of square pyramids. Using egg-box interfaces with different combinations of peak height and peak separation, we show that it is necessary to include the interfacial reaction kinetics of lithium deposition and the stress arising from lithium flow in the mechanistic picture. By examining how the local kinetics of lithium deposition and flow-induced surface stress/pressure are distributed across the interface, and by linking these distributions to a model for lithium dendrite growth,³⁷ we rationalise how the critical current for dendrites varies with the topography of the contoured Li/electrolyte interfaces. Contouring increases the critical current for dendrite formation by increasing the interfacial surface area, but the increase is almost entirely suppressed by kinetic effects, severely limiting the extent to which the critical current can be increased by contouring. For example, a sinusoidal surface topography can only raise the charging current without dendrites by approx. 50% compared with a flat interface. It is very unlikely that contouring or shaping of the metal/solid electrolyte interface will solve the problem of increasing the charging current of solid-state batteries with a lithium metal anode without dendrite penetration.

Results and discussion

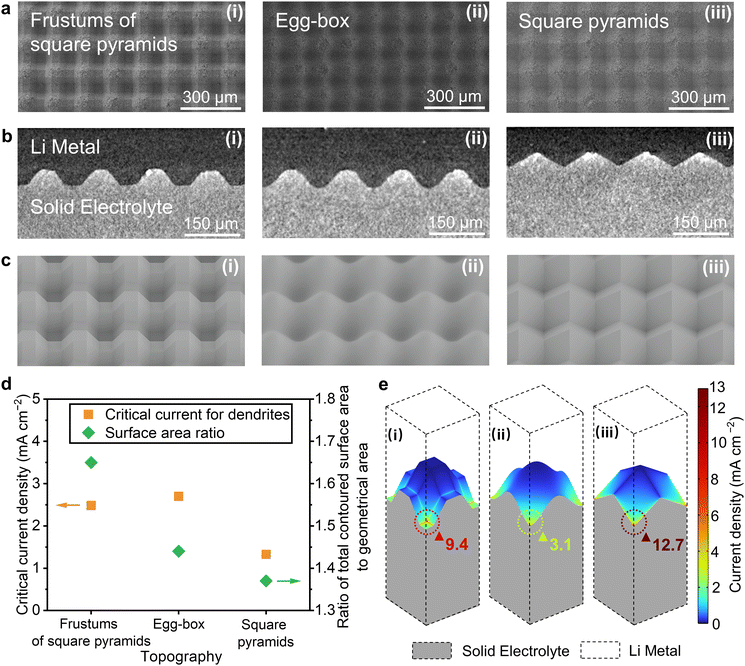
Argyrodite solid electrolytes (Li₆PS₅Cl) with differently contoured surfaces were prepared by 3D printing as described in Methods. In summary, polymer templates were printed representing three regular repeating patterns with equal periodicity in both in-plane directions perpendicular to the axis of the cell, frustums of square pyramids, egg-box, and square pyramids. Argyrodite powder was placed between two pieces of the polymer template and pressure applied to imprint the contoured surface onto both sides of solid electrolyte, Fig. S1a (ESI†). The templates were then removed and replaced with lithium metal. Lithium metal was also used for the reference electrode. The three-electrode cell is shown in Fig. S1b (ESI†).

Scanning electron microscopy (SEM) images showing the top-down planar view of the solid electrolyte with frustums of square pyramids, egg-box, and square pyramidal contoured surfaces before applying the Li metal and X-ray computed tomography (XCT) virtual cross-sectional views of the interface with the lithium metal in place are shown in Fig. 1a and b respectively. Fig. 1c shows simulations of the frustums of square pyramids, egg-box and square pyramidal contoured surfaces from an off-axis angle. The critical current for dendrites was determined by the voltage drop (2 mV) during plating, as described in Methods and Fig. S4 (ESI†), for each of the three differently contoured topographies shown in Fig. 1d. The voltage drops due to greater Li/solid electrolyte interfacial area and hence lower polarisation when dendrites penetrate the ceramic. It is also worth noting that the critical current for dendrites can be lower after long-term cycling due to voiding on stripping.²¹ Here we are considering the intrinsic limits due to contouring, as observed on the first plating. All the cells were measured under stack pressure of 7 MPa. Upon contact with a lithium metal anode, the thickness of interphase formed between Li₆PS₅Cl and lithium metal would typically reach at most 250 nm.^38,39 A thin interphase would not contribute to any major inhomogeneity compare to the feature sizes of contoured surfaces, e.g. 900 to 10 μm. All the trapezoid waves, cosine waves and triangle waves in the cross sections of the frustums of square pyramids, egg-box, and square pyramids respectively, have the same peak height (H) of 25 μm and peak separation (S) of 150 μm, abbreviated as H25S150. Also plotted in Fig. 1d are the ratios of the total surface area of the Li/electrolyte interface to the geometrical area (area of cell cross-section), from which it is apparent that the variation of critical current for dendrites cannot be explained solely by changes in the surface area at the interface (surface roughness).

Fig. 1 Experimentally determined critical currents for dendrites and calculated local currents for different interfacial topographies. (a) Top-down view from SEM of (i) Frustums of square pyramids (ii) Egg-box (iii) Square pyramidal surfaces with the same peak separation of 150 μm and peak height of 25 μm. (b) XCT virtual cross-sections of (i) Frustums of square pyramids (trapezoidal waves) (ii) Egg-box (cosine waves) (iii) Square pyramidal (triangle waves) surfaces. (c) 3D simulated illustrations of (i) Frustums of square pyramids (ii) Egg-box (iii) Square pyramidal surfaces from an off-axis angle. (d) Experimentally determined critical current densities and surface area ratios for the three topographies. (e) Distribution of local current density normal to surface calculated without including interfacial kinetics or mechanical considerations for (i) Frustums of square pyramids (ii) Egg-box (iii) Square pyramidal, at the Li/electrolyte interface for 1 mA cm⁻² geometrical current density with colour scale bar at right. The values for the maximum local current densities for each geometry are shown.

The calculated current density distributions across the interfaces for each of the three contoured topographies are shown in Fig. 1e. This is the current distribution due to the contoured shape of the interface alone, and is found by treating the electrolyte as a resistor with constant potential boundary conditions at the interfaces where it contacts Li – i.e., assuming that there is no interfacial resistance. The detailed calculation is described in S2 (ESI†). Local current densities scale with the geometrical current density and the former can be substantially higher than the latter. A geometrical current density of 1 mA cm⁻² was used for the calculations in Fig. 1e. Currents are greatest at the bottoms of the troughs as viewed in Fig. 1e (i.e., at the farthest protrusions of Li metal into the Argyrodite) in each case. The maximum local current densities vary widely with contour type, emphasizing that local currents are highly morphology dependent, even on periodic surfaces with identical peak heights and peak separations. Importantly, the locations where local current density is highest represent the most likely sites for dendrite initiation, i.e. the local currents at these locations determine the values of the critical current for dendrites.⁴⁰ The general observed trend in the critical currents for dendrites across contour types loosely correlates with the trend in these current maxima, but the large numerical difference between the simulated maxima for the frustums of square pyramids and egg-box surfaces is not reflected in the critical current for dendrites, suggesting that the current-distribution calculations in Fig. 1e do not suffice to explain how contour topography affects the critical current for dendrites.

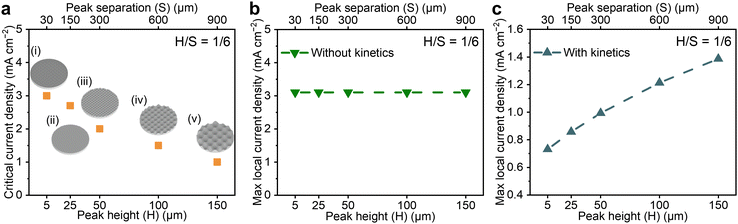
To investigate how changes in the dimensions of structural features affect the critical current for dendrites, a series of egg-box contoured surfaces were prepared in which the height and separation of the peaks were varied systematically. The experimentally determined critical currents for dendrites for simultaneously varying peak heights (H) and separations (S) that maintain a fixed ratio of peak height to separation (H/S) are presented in Fig. 2a. The current distribution across the interface is invariant when H and S are changed at a fixed H/S, as reflected in the calculated local current maxima being invariant as shown in Fig. 2b. However, the experimentally determined critical currents for dendrites do vary for different combinations of peak height and peak separation with the same H/S, in accord with the observation that the current distribution in Fig. 1e cannot solely explain how the critical current for dendrites varies.

Fig. 2 Experimentally determined critical currents for dendrites and calculated maximum currents for egg-box contoured surfaces with the same ratio of peak height (H) to separation (S). (a) Experimentally determined critical current densities for dendrites for all five constant H/S ratio surfaces (orange squares), the 3D simulated surfaces for each are also shown in grey (i) H5S30 (ii) H25S150 (iii) H50S300 (iv) H100S600 (v) H150S900. (b) Calculated maximum (max) local current density without including Li deposition kinetics for all five constant H/S ratio surfaces for 1 mA cm⁻² geometrical current density. (c) Calculated maximum (max) local current density including Li deposition kinetics for all five constant H/S ratio surfaces for 1 mA cm⁻² geometrical current density.

The current density distributions across the interface in Fig. 1e and Fig. 2b do not account for the kinetics of lithium deposition, which generally lead to surface overpotential.⁴¹ A linearized kinetic expression based on Butler–Volmer kinetics was coupled into the model to calculate how this affects the current density distribution across the Li/electrolyte interface, see S2 (ESI†) for details. The local current density distribution including the effect of kinetics was calculated for a geometrical current density of 1 mA cm⁻². The calculated maxima extracted for the different surfaces are shown in Fig. 2c. By including the kinetics of Li deposition in the calculation of current distribution, the maximum local current density increases with an increase in the peak height and separation at a fixed H/S ratio. The increase in this maximum local current implies a decrease in the critical current for dendrites, in accord with the trend seen in Fig. 2a. It has been suggested that the intrinsic kinetics of Li deposition at the interface can be very fast.^42–44 However, where interfacial kinetics are finite they play an important role in determining the local current density distribution, and therefore how the critical current for dendrites varies for contoured surfaces with constant H/S ratio.

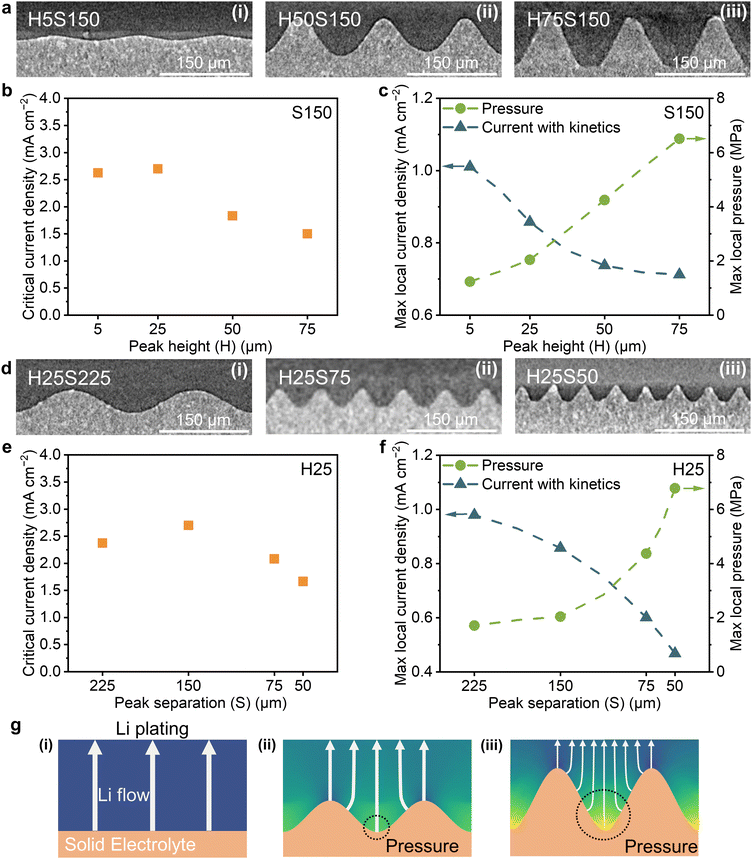
Varying the H/S ratio impacts the current density distribution. Fig. 3 presents experimentally determined critical currents for dendrites as well as the calculated maximum current density for a series of egg-box surfaces with varying H/S, specifically with varying peak heights at a fixed separation of 150 μm (Fig. 3a–c) and varying peak separations at a fixed peak height of 25 μm (Fig. 3d–f). As the peak height increases at fixed peak separation or peak separation decreases at fixed peak height (i.e., as the H/S ratio increases at constant S or H), the experimental critical currents for dendrites pass through a maximum and then start to decrease. As shown in Table S1 (ESI†), the interfacial area for an egg-box interface increases monotonically as its H/S ratio increases, further proving that a simple surface area scaling cannot explain the trend of critical current for dendrites. From the modelling results in Fig. 3c and f, the maximum local current density, including the effect of kinetics, decreases with increasing peak height at fixed separation and with decreasing peak separation at fixed height (increasing H/S ratio). Therefore, although including the effect of kinetics at the Li/electrolyte interface can explain the constant H/S case, there are still other factors that influence the critical currents for dendrites.

Fig. 3 Experimentally determined critical currents for dendrites and calculated maximum local current densities and pressures for egg-box surfaces varying either peak height or separation. (a) XCT virtual cross-sections of egg-box surfaces varying in peak heights (H) at a fixed separation (S) of 150 μm (i) H5S150 (ii) H50S150 (iii) H75S150. (b) Experimentally determined critical current densities for dendrites for surfaces with varying peak height at constant peak separation (150 μm). (c) Calculated maximum (max) local current density including kinetics and maximum (max) local pressure for 1 mA cm⁻² geometrical current density and constant peak separation surfaces. The max means the highest magnitude of local current density and pressure at the interface. (d) XCT virtual cross-sections of egg-box surfaces varying in peak separation (S) at a fixed height (H) of 25 μm (i) H25S225 (ii) H25S75 (iii) H25S50. (e), Experimentally determined critical current densities for dendrites for surfaces with varying peak separation at constant peak height (25 μm). (f), Calculated maximum (max) local current density including kinetics and maximum (max) local pressure for 1 mA cm⁻² geometrical current density and constant peak height surfaces. (g), Schematics of lithium plating at (i) a planar surface (ii) an egg-box contoured surface with a low H/S ratio (iii) an egg-box contoured surface with a high H/S ratio, showing how pressure increases in troughs with increased peak height.

During charging, the deposition of Li builds pressure at the interface because of the viscoplasticity of Li metal.^45–47 The pressures at different points across the interface are determined by the local current density distribution (including the effect of interfacial kinetics), which expresses the rate of lithium metal deposition locally, and its consequent creeping flow away from the interface.⁴⁸ Unlike the planar geometry, the uneven current density distribution on a contoured surface can lead to local pressure accumulation, Fig. 3g, which can reduce the critical current for dendrites below the expected value. Using the current density distribution including the effect of interfacial kinetics, a momentum balance that includes the creep power law for lithium metal^49–51 was solved to determine the pressure distribution at the Li/electrolyte interface, see S2 (ESI†) for calculation details. The maximum local excess pressure, i.e., the interfacial pressure minus the stack pressure, was calculated for 1 mA cm⁻² geometrical current density and is shown in Fig. 3c and f.

In principle, the mechanical state of the interface and its electrokinetics are coupled. Monroe and Newman showed how interfacial pressure impacts the interfacial resistance at deforming electrochemical interfaces.⁴¹ This coupling was considered here in an iterative calculation, in which the mechanical and electrical models were solved simultaneously (S2, ESI†). The iterative calculation (see Fig. S2, ESI†) showed that the kinetic current density was changed by less than 1% when coupled to interfacial pressure, so the interfacial resistance was assumed to remain constant and independent of pressure in further modelling.

As shown in Fig. 3c and f, maximum local pressure increases with increasing peak height at fixed peak separation, and with decreasing peak separation at fixed height (i.e. increasing H/S ratio). Increasing the H/S ratio also increases the interfacial surface area, reducing the average local current density across the interface and as a result reducing the maximum local current density. Although the resultant maximum rate of lithium plating is also lower, the sharper geometry associated with a higher H/S ratio (higher peaks and/or lower peak separation) constrains the creep of the plated lithium metal. Steeper peaks (higher H/S ratio) direct the plated lithium towards the troughs in the solid electrolyte (where the Li protrudes most into the electrolyte), since lithium plating only occurs in the direction normal to the contoured surface. The creeping lithium flow concentrates at and pressurises the bottoms of the troughs, as illustrated in Fig. 3g(ii) and (iii). The opposing effects of lower maximum local current density and higher maximum local pressure with increasing H/S are in accord with the maximum observed in the critical current for dendrites when increasing the H/S ratio, Fig. 3(b) and (e). Any method of increasing the interfacial surface area in an attempt to increase critical current for dendrites will come with inherently limiting mechanical and electrical effects due to the topography of rougher surfaces, which will eventually dominate thus limiting the current density for dendrites.

A recent dendrite propagation model explored the growth of dendrites within the ceramic electrolyte, taking account of surface tension, inhomogeneities and crack dimensions and in particular the correlation between the interfacial pressure and the current density required for a dendrite to grow cracks within a solid electrolyte (i_g).³⁷ By invoking this relationship, the effect of the current density and pressure distributions across the contoured surfaces on dendrite growth can be evaluated quantitatively. As shown above, the maximum local current density, including the effect of interfacial kinetics, and maximum interfacial pressure occur at the same location on the contoured surface (tip of the Li protrusions into the solid electrolyte), illustrated in Fig. S3 (ESI†). The magnitude of the local pressure is, of course, dependent on the local current and the creep properties of lithium. When the local current and consequent local pressure are sufficiently high, the crack will lengthen, and this process is associated with a specific geometrical current density. The model is described in S2 (ESI†).

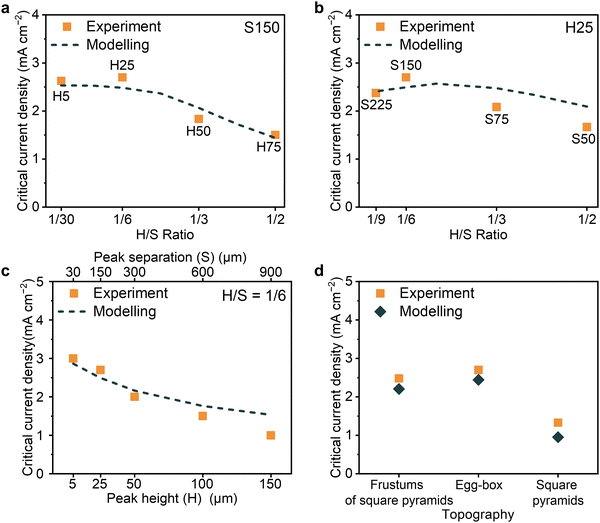
Results are summarised in Fig. 4. The dashed lines in Fig. 4a–c represent the calculated geometrical current densities for dendrite growth, showing how they vary with changes in peak height and peak separation of the contoured surface. The calculated trends follow the experimentally determined values. Comparing the frustums of square pyramids, egg-box and square pyramidal surfaces, the trend in the calculated geometrical current density for dendrite growth agrees with the experimental results, showing the egg-box topography being the best (Fig. 4d). It is important to note that the calculated values in Fig. 4 are just trends and do not reflect the absolute values of the currents required for dendrite growth. Predicting critical currents would require knowledge of the dendritic crack dimensions for each case at the position of the maximum local current and pressure. However, the trends of the calculate and experimental values are in accord.

Fig. 4 Trends in the calculated geometrical currents for dendrite growth compared with experimental values. (a)–(d) Comparing the experimental data with the modelling trends from the dendrite growth model for constant peak separation (S) (a), constant peak height (H) (b), constant H/S ratio (c) and three different topographies (d).

Conclusion

3D printing was used to create contoured surfaces on the solid electrolyte, Li₆PS₅Cl, enabling the investigation of how contouring influences the critical current for dendrite growth at the Li/electrolyte interface. It is important to consider the current distribution, interfacial kinetics of Li deposition and the Li creep that results in pressure variation across the contoured surface in order to understands how contouring affects the critical current for dendrite growth. Frustums of square pyramids, egg-box and square pyramidal were examined. The egg-box surface exhibits higher critical currents than the frustums of square pyramids and square pyramidal surfaces. The influence of changing the feature sizes of egg-box surfaces, i.e. the height and separation of the peaks, were considered. Increasing the peak height at a constant peak separation or decreasing the peak separation at a constant peak height can lead to an initially increasing and then decreasing trend for the critical current. This can be qualitatively explained by the calculated decreasing maximum current including kinetics but increasing local pressure. By invoking a model that relates interfacial pressure and the current for dendrite growth, the overall trends in geometrical current density for dendrite growth were calculated and compared with experimental values. While contouring the lithium/solid electrolyte interface raises the critical current for dendrites by increasing the surface area, the extent of such an increase in critical current is severely limited due to kinetic effects. As a result, contouring or otherwise roughening the interface is unlike to solve the problem of charging solid state cells with a lithium anode while avoiding dendrites at the required current densities.

Methods

Preparation of contoured Li₆PS₅Cl solid electrolytes

The 3D templates were printed using a high-resolution 3D printer (Nanoscribe Photonic Professional GT). The printing configuration of Dip-in laser lithography was selected with a 25×/0.8 (objective/numerical aperture) lens. All the procedures for creating printing job files and detailed design of 3D templates are given in S1 (ESI†). After printing, the templates were washed with propylene glycol monomethyl ether acetate (≥99.5%, Sigma-Aldrich) and isopropanol (≥99.5%, Sigma-Aldrich), then vacuum dried overnight before use in the argon-filled glovebox, where all subsequent procedures were carried out. As illustrated in Fig. S1a (ESI†), Li₆PS₅Cl (AMPCERA) ultra-fine (D50 ∼ 1 μm) powder was loaded into the die between two 3D templates. 400 MPa uniaxial pressure was applied to imprint the contoured surface onto both sides of the Li₆PS₅Cl disc while densifying the electrolyte to a thickness of approximately 1 mm. The 3D templates were removed from both sides of the Li₆PS₅Cl disc after pressing. The contoured Li₆PS₅Cl disc was then heat-treated in a furnace at 300 °C for 30 min. The sintered and contoured Li₆PS₅Cl disc was assembled into the electrochemical cell.

Cell assembly

The three-electrode cells were assembled inside a glove box using Li metal for the working, counter and reference electrodes, as shown in Fig. S1b (ESI†). Two 2-mm-diameter Li discs were punched out from Li foil. The Li discs were concentrically pressed onto both sides of the Li₆PS₅Cl disc, acting as the working and counter electrodes. A 0.5 mm diameter Li reference electrode was placed near the working electrode. The three-electrode cells were vacuum sealed into pouch cells. All the cells were heat-treated under 80 °C and 7 MPa before any electrochemical measurement to aid intimate interfacial contact.

Measurements of the critical current for dendrites

Electrochemical measurements were conducted using the Gamry 1010E. The stack pressure was 7 MPa. Critical currents were determined by first plating at 0.5 mA cm⁻² and stripping at 0.2 mA cm⁻² under capacity of 0.2 mA h cm⁻². For the following cycles, the plating current was increased in 0.5 mA cm⁻² steps each cycle, but the stripping current remained at 0.2 mA cm⁻². The critical current for dendrites was determined when the voltage dropped by 2 mV, as shown in Fig. S4a (ESI†). This voltage drop accords with the presence of a dendrite crack as observed by XCT in Fig. S4b (ESI†).

Scanning electron microscope

The contoured Li₆PS₅Cl discs were transferred to a Zeiss Merlin scanning electron microscope using an air-tight transfer device (Gatan) enabling examination of the contoured Li₆PS₅Cl surfaces.

X-ray computed tomography

X-ray CT data were collected using a Zeiss Xradia 610 Versa X-ray microscope. For each tomogram, 3201 projections were taken over 360°. The tomogram data were reconstructed using the Zeiss Reconstructor Scout-and-Scan Control System program with the pixel size of 2 μm.

Author contributions

S. Z. contributed to all aspects of the research. S. Z. performed the preparation of electrolyte disc and cell assembly. B. H. and Z. N. carried out the XCT. S. Z., Z. G., G. L. and C. W. M. conducted the modelling. S. Z., X. G. and D. S.-J. performed the SEM experiment. S. Z. and M. J. performed 3D printing. S. Z., B. H., Z. G, X. G., D. S.-J., D. L. R. M., G. L., C. W. M. and P. G. B. discussed the data. All authors contributed to the interpretation of data. S. Z., D. S.-J., D. L. R. M, C. W. M. and P. G. B. wrote the manuscript, with contributions and revisions from all authors. The project was supervised by P. G. B.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. G. B. is indebted to the Faraday Institution (FIRG026), the Engineering and Physical Sciences Research Council (EP/M009521/1), and the Henry Royce Institute for Advanced Materials for financial support (EP/R00661X/1, EP/S019367/1, and EP/R010145/1). The authors acknowledge use of characterisation facilities within the David Cockayne Centre for Electron Microscopy, Department of Materials, University of Oxford, alongside financial support provided by the Henry Royce Institute (Grant ref EP/R010145/1). The X-ray tomography facilities were funded by EPSRC Grant [EP/M02833X/1] “University of Oxford: experimental equipment upgrade”.

References

1. J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141.
2. A. Banerjee, X. F. Wang, C. C. Fang, E. A. Wu and Y. S. Meng, Chem. Rev., 2020, 120, 6878–6933.
3. R. S. Chen, Q. H. Li, X. Q. Yu, L. Q. Chen and H. Li, Chem. Rev., 2020, 120, 6820–6877.
4. L. Ye and X. Li, Nature, 2021, 593, 218–222.
5. W. Yan, Z. Mu, Z. Wang, Y. Huang, D. Wu, P. Lu, J. Lu, J. Xu, Y. Wu, T. Ma, M. Yang, X. Zhu, Y. Xia, S. Shi, L. Chen, H. Li and F. Wu, Nat. Energy, 2023, 2023, 1–14.
6. Y. G. Lee, S. Fujiki, C. Jung, N. Suzuki, N. Yashiro, R. Omoda, D. S. Ko, T. Shiratsuchi, T. Sugimoto, S. Ryu, J. H. Ku, T. Watanabe, Y. Park, Y. Aihara, D. Im and I. T. Han, Nat. Energy, 2020, 5, 299–308.
7. Y. C. Yin, J. T. Yang, J. Da Luo, G. X. Lu, Z. Huang, J. P. Wang, P. Li, F. Li, Y. C. Wu, T. Tian, Y. F. Meng, H. S. Mo, Y. H. Song, J. N. Yang, L. Z. Feng, T. Ma, W. Wen, K. Gong, L. J. Wang, H. X. Ju, Y. Xiao, Z. Li, X. Tao and H. Bin Yao, Nature, 2023, 616, 77–83.
8. S. Randau, D. A. Weber, O. Kötz, R. Koerver, P. Braun, A. Weber, E. Ivers-Tiffée, T. Adermann, J. Kulisch, W. G. Zeier, F. H. Richter and J. Janek, Nat. Energy, 2020, 5, 259–270.
9. L. Zhou, T.-T. Zuo, C. Y. Kwok, S. Y. Kim, A. Assoud, Q. Zhang, J. Janek and L. F. Nazar, Nat. Energy, 2022, 7, 83–93.
10. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030.
11. V. Reisecker, F. Flatscher, L. Porz, C. Fincher, J. Todt, I. Hanghofer, V. Hennige, M. Linares-Moreau, P. Falcaro, S. Ganschow, S. Wenner, Y.-M. Chiang, J. Keckes, J. Fleig and D. Rettenwander, Nat. Commun., 2023, 14, 2432.
12. E. Kazyak, R. Garcia-Mendez, W. S. LePage, A. Sharafi, A. L. Davis, A. J. Sanchez, K. H. Chen, C. Haslam, J. Sakamoto and N. P. Dasgupta, Matter, 2020, 2, 1025–1048.
13. J. Doux, H. Nguyen, D. H. S. Tan, A. Banerjee, X. Wang, E. A. Wu, C. Jo, H. Yang and Y. S. Meng, Adv. Energy Mater., 2020, 10, 1903253.
14. J. Janek and W. G. Zeier, Nat. Energy, 2023, 8, 230–240.
15. Y. Chen, Z. Wang, X. Li, X. Yao, C. Wang, Y. Li, W. Xue, D. Yu, S. Y. Kim, F. Yang, A. Kushima, G. Zhang, H. Huang, N. Wu, Y. W. Mai, J. B. Goodenough and J. Li, Nature, 2020, 578, 251–255.
16. G. McConohy, X. Xu, T. Cui, E. Barks, S. Wang, E. Kaeli, C. Melamed, X. W. Gu and W. C. Chueh, Nat. Energy, 2023, 8, 241–250.
17. J. A. Lewis, F. J. Q. Cortes, Y. Liu, J. C. Miers, A. Verma, B. S. Vishnugopi, J. Tippens, D. Prakash, T. S. Marchese, S. Y. Han, C. Lee, P. P. Shetty, H. W. Lee, P. Shevchenko, F. De Carlo, C. Saldana, P. P. Mukherjee and M. T. McDowell, Nat. Mater., 2021, 20, 503–510.
18. M. B. Dixit, B. S. Vishugopi, W. Zaman, P. Kenesei, J.-S. Park, J. Almer, P. P. Mukherjee and K. B. Hatzell, Nat. Mater., 2022, 21, 1298–1305.
19. F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187–196.
20. X. Liu, R. Garcia-Mendez, A. R. Lupini, Y. Cheng, Z. D. Hood, F. Han, A. Sharafi, J. C. Idrobo, N. J. Dudney, C. Wang, C. Ma, J. Sakamoto and M. Chi, Nat. Mater., 2021, 20, 1485–1490.
21. J. Kasemchainan, S. Zekoll, D. Spencer Jolly, Z. Ning, G. O. Hartley, J. Marrow and P. G. Bruce, Nat. Mater., 2019, 18, 1105–1111.
22. H. Wan, Z. Wang, S. Liu, B. Zhang, X. He, W. Zhang and C. Wang, Nat. Energy, 2023, 8, 473–481.
23. Z. Ning, D. S. Jolly, G. Li, R. De Meyere, S. D. Pu, Y. Chen, J. Kasemchainan, J. Ihli, C. Gong, B. Liu, D. L. R. Melvin, A. Bonnin, O. Magdysyuk, P. Adamson, G. O. Hartley, C. W. Monroe, T. J. Marrow and P. G. Bruce, Nat. Mater., 2021, 20, 1121–1129.
24. X. Gao, Y. N. Zhou, D. Han, J. Zhou, D. Zhou, W. Tang and J. B. Goodenough, Joule, 2020, 4, 1864–1879.
25. M. Otoyama, M. Suyama, C. Hotehama, H. Kowada, Y. Takeda, K. Ito, A. Sakuda, M. Tatsumisago and A. Hayashi, ACS Appl. Mater. Interfaces, 2021, 13, 5000–5007.
26. C. Wang, T. Deng, X. Fan, M. Zheng, R. Yu, Q. Lu, H. Duan, H. Huang, C. Wang and X. Sun, Joule, 2022, 6, 1770–1781.
27. V. Raj, V. Venturi, V. R. Kankanallu, B. Kuiri, V. Viswanathan and N. P. B. Aetukuri, Nat. Mater., 2022, 21, 1050–1056.
28. G. T. Hitz, D. W. McOwen, L. Zhang, Z. Ma, Z. Fu, Y. Wen, Y. Gong, J. Dai, T. R. Hamann, L. Hu and E. D. Wachsman, Mater. Today, 2019, 22, 50–57.
29. R. H. Basappa, T. Ito and H. Yamada, J. Electrochem. Soc., 2017, 164, A666.
30. L. Porz, T. Swamy, B. W. Sheldon, D. Rettenwander, T. Frömling, H. L. Thaman, S. Berendts, R. Uecker, W. C. Carter and Y.-M. Chiang, Adv. Energy Mater., 2017, 7, 1701003.
31. R. Xu, F. Liu, Y. Ye, H. Chen, R. R. Yang, Y. Ma, W. Huang, J. Wan and Y. Cui, Adv. Mater., 2021, 33, 2104009.
32. D. W. McOwen, S. Xu, Y. Gong, Y. Wen, G. L. Godbey, J. E. Gritton, T. R. Hamann, J. Dai, G. T. Hitz, L. Hu, E. D. Wachsman, D. W. McOwen, S. Xu, Y. Gong, Y. Wen, G. L. Godbey, J. E. Gritton, T. R. Hamann, J. Dai, G. T. Hitz, L. Hu and E. D. Wachsman, Adv. Mater., 2018, 30, 1707132.
33. M. K. Jangid, A. L. Davis, D. W. Liao and N. P. Dasgupta, ACS Energy Lett., 2023, 15, 2522–2531.
34. Q. Tu, L. Barroso-Luque, T. Shi and G. Ceder, Cell Rep. Phys. Sci., 2020, 1, 100106.
35. X. Zhang, Q. J. Wang, K. L. Harrison, S. A. Roberts and S. J. Harris, Cell Rep. Phys. Sci., 2020, 1, 100012.
36. D. K. Singh, A. Henss, B. Mogwitz, A. Gautam, J. Horn, T. Krauskopf, S. Burkhardt, J. Sann, F. H. Richter and J. Janek, Cell Rep. Phys. Sci., 2022, 0, 101043.
37. Z. Ning, G. Li, D. L. R. Melvin, Y. Chen, J. Bu, D. Spencer-Jolly, J. Liu, B. Hu, X. Gao, J. Perera, C. Gong, S. D. Pu, S. Zhang, B. Liu, G. O. Hartley, A. J. Bodey, R. I. Todd, P. S. Grant, D. E. J. Armstrong, T. J. Marrow, C. W. Monroe and P. G. Bruce, Nature, 2023, 618, 287–293.
38. S. Wenzel, S. J. Sedlmaier, C. Dietrich, W. G. Zeier and J. Janek, Solid State Ionics, 2018, 318, 102–112.
39. S. K. Otto, L. M. Riegger, T. Fuchs, S. Kayser, P. Schweitzer, S. Burkhardt, A. Henss and J. Janek, Adv. Mater. Interfaces, 2022, 9, 2102387.
40. R. Choudhury, M. Wang and J. Sakamoto, J. Electrochem. Soc., 2020, 167, 140501.
41. C. Monroe and J. Newman, J. Electrochem. Soc., 2004, 151, A880.
42. A. Sharafi, E. Kazyak, A. L. Davis, S. Yu, T. Thompson, D. J. Siegel, N. P. Dasgupta and J. Sakamoto, Chem. Mater., 2017, 29, 7961–7968.
43. T. Krauskopf, B. Mogwitz, H. Hartmann, D. K. Singh, W. G. Zeier and J. Janek, Adv. Energy Mater., 2020, 10, 2000945.
44. D. K. Singh, T. Fuchs, C. Krempaszky, B. Mogwitz and J. Janek, Adv. Sci., 2023, 10, 2302521.
45. X. Xu, Y. Liu, O. O. Kapitanova, Z. Song, J. Sun, S. Xiong, X. Xu, Y. Liu, O. O. Kapitanova, Z. Song, J. Sun and S. Xiong, Adv. Mater., 2022, 34, 2207232.
46. C. D. Fincher, D. Ojeda, Y. Zhang, G. M. Pharr and M. Pharr, Acta Mater., 2020, 186, 215–222.
47. L. Barroso-Luque, Q. Tu and G. Ceder, J. Electrochem. Soc., 2020, 167, 020534.
48. T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291.
49. W. S. LePage, Y. Chen, E. Kazyak, K.-H. Chen, A. J. Sanchez, A. Poli, E. M. Arruda, M. D. Thouless and N. P. Dasgupta, J. Electrochem. Soc., 2019, 166, A89.
50. A. Masias, N. Felten, R. Garcia-Mendez, J. Wolfenstine and J. Sakamoto, J. Mater. Sci., 2019, 54, 2585–2600.
51. Y. Wang and Y. T. Cheng, Scr. Mater., 2017, 130, 191–195.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee03322h

---