Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermal battery cost scaling analysis: minimizing the cost per kW h†
Jordan D.
Kocher
 a,
Jason
Woods
a,
Jason
Woods
 b,
Adewale
Odukomaiya
b,
Adewale
Odukomaiya
 b,
Allison
Mahvi
b,
Allison
Mahvi
 bc and
Shannon K.
Yee
bc and
Shannon K.
Yee
 *ab
*ab
aGeorge W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, USA. E-mail: shannon.yee@me.gatech.edu
bNational Renewable Energy Laboratory, Golden, CO, USA
cDepartment of Mechanical Engineering, University of Wisconsin, Madison, WI, USA
First published on 13th February 2024
Abstract
Thermal energy storage technologies have many applications, from grid-scale energy storage to building space cooling and heating storage. When packaged into a device, these “thermal batteries” contain a storage material, heat exchangers to supply and extract the stored heat, and insulation to prevent the stored heat from escaping. Energy can be stored through sensible, latent, or thermochemical heat, with latent heat “phase change materials” (PCMs) being among the most common. While much ongoing work focuses on reducing the cost of either the PCM, the heat exchangers, or the insulation, herein we evaluate the cost scaling analysis wholistically to consider the entire system cost. We show how costs scale with certain characteristic lengths and the tradeoffs thereof. Our analytical framework reveals that the optimal PCM thickness (which minimizes the $ per kW h cost of the thermal battery) is often on the order of cm and depends exactly on the PCM properties and operational parameters. For example, improving the thermal conductivity of n-tetradecane by adding graphite filler reduces the thermal battery cost from $155 per kW h to $69 per kW h, and further improving the properties (density and latent heat) to the Department of Energy aspirational target reduces the thermal battery cost to $24 per kW h (for a C-rate of C/4). Our methodology applies to thermal storage systems of many geometries, requiring only knowledge of how the geometry affects the device state of charge. We provide a cost regime map with three regions: one in which the PCM cost dominates, one in which the heat exchanger costs dominate, and one in which insulation costs dominate. From the regime map, we also derive figures-of-merit for PCM thermal storage materials corresponding to the three different cost-dominant regimes.
Broader contextBuildings account for nearly 40% of all U.S. energy use. Both heating (space and water heating) and cooling (space cooling and refrigeration) are the two largest end uses of building energy, and air conditioning energy consumption is projected to grow faster than any other use. To achieve a more environmentally and economically sustainable future, thermal management in the built environment must become more efficient and less expensive. However, thermal management is often needed when it is least efficient. For example, air conditioning is needed during the hottest part of the day, but that is also when it is least efficient. Ideally, the air conditioner would be run at night, when cooling cycles are efficient and electricity is cheap. This mismatch can be overcome with “thermal batteries”, in which a material stores heat (or cooling) and later discharges it to the thermal load. This can be used not only for thermal management in the built environment, but also for energy storage in power plants. However, existing thermal batteries are expensive, hindering their adoption. In this work, we develop a framework to optimize system design and select storage materials that minimize thermal battery cost. |
Introduction
Energy storage technologies have the potential to reduce operational costs, improve energy efficiency, and provide environmental benefits when employed in various applications. Grid-scale energy storage1–4 enables energy generated by intermittent renewable energy sources to be delivered on-demand; energy can be stored when renewable energy is abundant and used when renewable energy is scarce. Well-explored grid-scale storage technologies include pumped hydro,5 compressed air,6 mechanical flywheel,7 electrochemical batteries,8 and thermal batteries.9,10 Amy et al. described a thermal battery that could achieve a far lower cost than traditional electrochemical batteries, highlighting the potential of thermal batteries as cost effective methods of energy storage.11Thermal batteries are useful not only for grid scale energy storage, but also for thermal load shifting in buildings.10,12–21 To keep occupants comfortable, a building in a hot climate must be cooled, with the most cooling being necessary during the hottest part of the day, which is the time when the cooling system will be least efficient. In addition, the hottest part of the day often is when electricity is most expensive due to peak-hour electricity pricing. Conversely, the cooling system will be most efficient and cost-effective at night when the outside temperature and electricity costs are lowest. The inverse scenario occurs when a building is in a cold climate and must be heated; a heat pump is most efficient when the outside temperature is high but needed most when the outside temperature is low. A thermal battery alleviates this issue, allowing heat (or cold) to be stored when the heat pump or refrigeration system is efficient and discharged on-demand.
The three main thermal storage media are sensible storage materials, phase change materials (PCMs), and thermochemical storage materials (TCMs).17 Sensible materials22,23 store energy entirely through the sensible heat that accompanies a change in temperature. These materials have low energy densities, which limits their cost-effectiveness. PCMs24–28 store only a small portion of their energy through sensible heat, with most of their storage capacity coming from the latent heat associated with phase change (often solidification or melting). As such, PCMs have far higher energy densities than sensible storage materials. TCMs29–33 store most of their energy through endothermic or exothermic chemical reactions, giving them even higher densities than PCMs. However, TCMs currently suffer from stability/cyclability issues32 and TCM thermal batteries have not yet been widely deployed. In existing thermal batteries, PCMs are often used, due to the high energy density associated with phase change and the ability to discharge heat at a steady temperature for long durations.24,25,34 As such, this work focuses mostly on PCMs, but we also extend our analysis to sensible storage in the ESI† (Note 12). Additionally, we provide a discussion of what can be done to apply our analysis to TCMs in future works.
Currently, ongoing research and development focuses on creating better thermal energy storage materials with higher volumetric energy densities at lower costs. However, a thermal battery (system) will always have a higher cost than the cost of the storage material alone, due to the existence of heat exchangers, insulation, and other system components. To date, much of the thermal storage literature discusses storage material cost,35–37 but few present a comprehensive analysis of system cost. The works that do focus on system cost do not often analyze the optimal geometry to minimize cost, nor do they discuss how the storage material properties affect the optimal geometry and impact cost.11,17 A cost scaling analysis is a powerful tool to: (i) quantify the individual contributions to the overall cost of a system, (ii) understand how these contributions scale with geometric parameters, and (iii) minimize the cost of the system through optimization. This type of analysis is lacking within the body of thermal storage literature and would serve as a powerful tool in the push for thermal storage systems that can serve as a cost-effective means of energy storage across different scales of both storage time and capacity.
In this paper, we present a cost scaling analysis of phase change thermal batteries. This cost scaling methods has previously been applied to other technologies, such as thermoelectrics.38 We provide a broadly applicable technique for the minimization of the $ per kW h cost of a thermal battery system, based on optimization of the geometry, in particular the characteristic length scales. We also show how the heat exchanger and insulation costs scale with these characteristic lengths, and how these lengths affect the battery efficiency, all of which affect the system cost. Finally, we present a regime map with three different regimes: one in which the storage material costs dominate, one in which heat exchanger costs dominate, and one in which insulation costs dominate. We then present the thermal storage material figures-of-merit for each regime.
Thermal battery state of charge limitations
An important parameter in the operation of a thermal battery is the state of charge (SOC). Recently, Woods et al. provided a framework that illustrates the analogy between electrochemical batteries and thermal energy storage devices.24 At a given instant, the electrochemical battery has some SOC, which is the fraction of the total energy capacity that is currently stored within the battery. Due to internal resistance losses, the electrochemical battery supplies power at a lower voltage than the open circuit voltage, and the supply voltage drops as the battery is discharged. Eventually, the supply voltage reaches some cutoff voltage, at which point the battery can no longer supply the required power, even though there is still some charge within the battery.Woods et al. showed that PCM thermal batteries exhibit a similar behavior.20,24 Consider a thermal battery that must provide heat transfer at a constant rate. The supply temperature drops (for hot storage) or increases (for cold storage) as the thermal battery is discharged because internal thermal resistances increase during discharge (e.g., the liquid region grows during melting of a phase change material). Eventually, the supply temperature reaches a cutoff temperature (Tcutoff), which is the temperature that the thermal load is not allowed to exceed. Notably, the thermal storage material has some “charge” left within it when the load reaches the cutoff temperature; in other words, it could still provide some heat transfer to the load. However, it would not be able to provide that heat transfer without either the temperature of the load exceeding Tcutoff (which is not allowed) or the rate of heat transfer dropping below the prescribed constant value (which is also not allowed). This results in a portion of the thermal battery's storage capacity being inaccessible during discharge at a constant rate, a phenomenon described by Woods et al. in their seminal “thermal Ragone” work.24
Woods et al. showed that several parameters affect the thermal capacity that can be extracted from the battery before the cutoff temperature is reached; we call the fraction of thermal capacity that is extracted before cutoff ΔSOC. We define ΔSOC as the enthalpy change during discharge (from a fully frozen state at some average temperature below melting to a partially or fully melted state at some average temperature below the cutoff temperature) divided by the total storage capacity (from fully frozen and uniform at the charged temperature to fully melted and uniform at the cutoff temperature); this is illustrated for cold storage in Note 14 (ESI†). Quantities that affect ΔSOC include operational parameters like the cutoff temperature and the rate at which the battery is discharged (i.e., C-rate), material properties like the PCM thermal conductivity and latent heat, and geometric parameters like the PCM thickness. Woods et al. found that ΔSOC decreases with increasing PCM thickness,24 but this also increases the storage capacity, making the heat exchangers’ contribution to system cost less significant. This presents the opportunity to minimize the thermal battery cost as a function of the PCM thickness.16
In our analysis, the limitations on SOC (and therefore cost) result from the constraint that the thermal battery must discharge at a constant power. Contrary to discharging, we assume that charging does not need to occur at a constant power and that there is plenty of time to allow the storage material to reach a uniform temperature during charging. This significantly reduces the consequences that the charging process has on system cost. The few aspects of the charging and storage processes that do affect cost (e.g., subcooling and storage time) are discussed in Note 1 (ESI†).
Development of the $ per kW h cost metric
A complete thermal storage system will include costs of the storage device (e.g., storage material, heat exchangers, insulation, etc.), costs of the system that connects the thermal battery to the load (pumps, heat transfer fluid, etc.),11 and labor costs to fabricate and install the system. This study focuses on the costs of the storage device itself (i.e., the thermal battery), which we refer to as G, in units of $ per kW h. Though we focus on latent heat thermal storage, we also present an analysis of sensible heat thermal storage in Note 12 (ESI†).Common to phase change thermal storage devices is the presence of a PCM, heat exchangers (to allow the PCM to exchange heat with the thermal load), and insulation (to prevent the PCM from losing its capacity during storage); other components may exist in certain systems, but these three elements are always present in (latent heat) thermal batteries. The cost of the PCM scales with the PCM volume (VPCM) and density (ρPCM), with the proportionality constant being the PCM cost per unit mass, cPCM [$ per kg].
Heat exchanger costs generally scale with the heat transfer coefficient (UHX) and the surface area of the heat exchanger (AHX),39 giving a proportionality constant cHX in units [$ per W per K]. If other costs scale with the heat exchanger area (for example, a sealant then needs to be applied to the heat exchanger), then these costs can be lumped into cHX by first dividing them by UHX. If the insulation material is fixed (i.e., the thermal conductivity is fixed) the insulation costs scale with the R-value 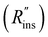 , since the R-value is equal to insulation thickness divided by thermal conductivity, and the insulated surface area (Ains), with a material-dependent proportionality constant cins in [$ per m4 per K per W]. The insulated surface area is also the external surface area of the device, and there will likely be other costs that scale with this external area, such as the cost of the tank or device housing. As with the heat exchanger, these areal costs can be lumped into cins by dividing them by
, since the R-value is equal to insulation thickness divided by thermal conductivity, and the insulated surface area (Ains), with a material-dependent proportionality constant cins in [$ per m4 per K per W]. The insulated surface area is also the external surface area of the device, and there will likely be other costs that scale with this external area, such as the cost of the tank or device housing. As with the heat exchanger, these areal costs can be lumped into cins by dividing them by 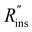 . The sum of all of these component costs gives the total system cost C [$]:
. The sum of all of these component costs gives the total system cost C [$]:
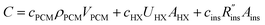 | (1) |
The cost of a thermal battery, G, in [$ per kW h] can be written as the system cost C [$], divided by the thermal storage capacity [kW h]. The total capacity of the PCM is VPCMSPCM, where SPCM is the volumetric energy density of the PCM. However, as explained by Woods et al., not all of the PCM capacity can be discharged at the desired power.24 As such, the usable capacity of the thermal battery is the product of the total PCM capacity and the SOC that can be accessed during discharge.
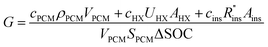 | (2) |
Upon algebraic rearrangement to create dimensionless groups, a pre-factor emerges, 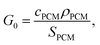 which represents the PCM cost per unit thermal storage [$ per kW h] and is the innate cost-scaling (pre-factor) for thermal storage. What this means is that the thermal battery system cost (G) will always be greater than the PCM cost (G0) due to the presence of other components (heat exchangers, insulation, etc.). In this work, SPCM includes the PCM latent capacity and the sensible capacity of the phase in which the PCM is stored (e.g., the solid phase for cold storage).
which represents the PCM cost per unit thermal storage [$ per kW h] and is the innate cost-scaling (pre-factor) for thermal storage. What this means is that the thermal battery system cost (G) will always be greater than the PCM cost (G0) due to the presence of other components (heat exchangers, insulation, etc.). In this work, SPCM includes the PCM latent capacity and the sensible capacity of the phase in which the PCM is stored (e.g., the solid phase for cold storage).
The expression for G has some costs factors that scale with PCM volume and others that scale with certain areas. The ratios of the volume to these areas are characteristic lengths. The first characteristic length appears in the equation for heat transfer to the PCM from the heat exchanger (LC = VPCM/AHX [m]). Lc is simply the PCM volume divided by the interfacial surface area between the heat exchanger and PCM. For a rectangular slab of PCM, Lc reduces to the thickness of the PCM slab. The second characteristic length appears in the equation for the heat transfer between the PCM and the surroundings, which occurs through the insulation (LS = VPCM/Ains [m]). Ls is simply the ratio of the PCM volume to the surface area of the PCM that must be insulated. There are also two “cost lengths” that arise as ratios of the cost proportionality constants: LHX and Lins. LHX is the areal heat exchanger cost [$ per m2] divided by the PCM volumetric costs [$ per m3] (LHX = cHXUHX/(cPCMρPCM)), giving units of [m]. The latter is the areal insulation cost [$ per m2] divided by the volumetric costs [$ per m3] 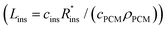 , also with units of [m]. These are not physical lengths within in the system, but they do have units of length (hence the term “cost length”). Using these characteristic lengths, as well as the pre-factor G0, the thermal battery cost can be written as dimensionless groups:
, also with units of [m]. These are not physical lengths within in the system, but they do have units of length (hence the term “cost length”). Using these characteristic lengths, as well as the pre-factor G0, the thermal battery cost can be written as dimensionless groups:
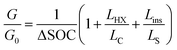 | (3) |
In the expression for G/G0, the cost scaling factors are LHX/Lc, and Lins/Ls. The first (unity) term is the PCM material cost scaling factor, LHX/Lc is the heat exchanger cost scaling factor, and Lins/Ls is the insulation cost scaling factor. While LHX is the heat exchanger cost per unit area [$ per m2] divided by the PCM cost per unit volume [$ per m3], LHX/Lc is the heat exchanger cost [$] divided by the PCM cost [$], such that LHX/Lc is dimensionless. As such, a value of LHX/Lc = 1 means that the PCM and heat exchanger are equally contributing to the total device cost. Other normalizations and dimensionless groups can exist; however, we find this approach to be the most intuitive given the prevailing emphasis on the PCM material cost. This particular nondimensionalization is also useful for several reasons. First, the storage material cost per unit storage capacity (G0) is widely reported for many thermal storage materials and serves as the minimum value that the system cost can take. Then, G/G0 serves as the storage material cost multiplier that yields system cost; a value of G/G0 far greater than one indicates that the thermal battery cost is dominated not by the storage material but by the other components. Finally, nondimensionalizing the cost in this way allows for a direct comparison between thermal batteries that utilize storage materials with similar G0 values, elucidating the effect that other material properties (e.g., thermal conductivity of the storage material) have on system cost (Table 1).
| Quantity | Units | Description |
|---|---|---|
| L c | m | PCM volume per heat exchanger surface area |
| L s | m | PCM volume per device external surface area that must be insulated |
| L HX | m | Heat exchanger cost per unit area, divided by PCM cost per unit volume |
| L HX/Lc | Unitless | Heat exchanger cost, divided by PCM cost |
| L ins | m | Insulation cost per unit area, divided by PCM cost per unit volume |
| L ins/Ls | Unitless | Insulation cost, divided by PCM cost |
| G | $ per kW h | Thermal battery cost per unit usable storage capacity |
| G 0 | $ per kW h | PCM cost per unit total storage capacity |
| G/G0 | Unitless | Dimensionless thermal battery cost |
Determining the fractional SOC as a function of system geometry
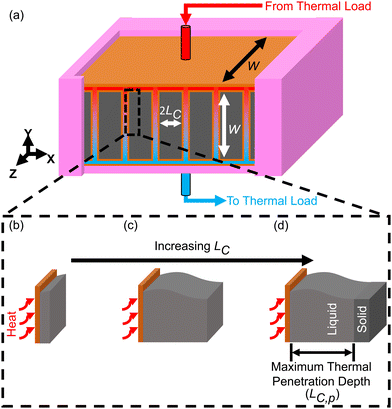
It is important to understand the effect that ΔSOC has on the thermal battery system cost. Upon observation of eqn (3), it might initially seem wise to maximize ΔSOC. However, according to Woods et al., this is achieved by making the PCM layer as thin as possible.24 This results in very little PCM for a given heat exchanger size. This in turn drives up the $ per kW h cost of the thermal battery because the heat exchangers, while necessary components, contribute to system cost without contributing to the thermal storage capacity. Ideally, the heat exchangers would not contribute to the system cost at all (LHX/Lc = 0). It might then seem wise to add as much PCM to the thermal battery as possible, as this would give more storage capacity without increasing the heat exchanger size. However, if the amount of PCM is very large, then by the time the cutoff temperature is reached, the heat transfer will not have penetrated through the entire PCM. This is illustrated for a rectangular thermal battery in Fig. 1. In Fig. 1b, the PCM slab is thin and melts entirely by the time cutoff is reached. In Fig. 1c, the slab is thicker, but the melting front still propagates all the way through the PCM before cutoff is reached. In Fig. 1d, the melting front does not reach the edge of the PCM slab by the time cutoff is reached, so a portion of the PCM thermal storage capacity is entirely unused. In Fig. 1b the PCM slab is thinner than the maximum thermal penetration depth, while in Fig. 1d the PCM is thicker than the thermal penetration depth. In a real thermal battery, ΔSOC would be slightly higher for the thin slab in Fig. 1b than for the thicker slab in Fig. 1c, because the temperature drop across the slab is smaller in Fig. 1b (allowing more of the sensible capacity to be discharged). However, in our simplified analysis, we neglect the sensible capacity of the liquid phase, so both Fig. 1b and c would have a ΔSOC of unity (assuming no losses during the storage period).In this work, we focus mainly on a thermal battery with the geometry illustrated in Fig. 1. For this geometry, we derive ΔSOC as a function of Lc and Ls in Note 1 (ESI†), and we derive the maximum thermal penetration depth (Lc,p) as a function of the material properties (such as latent heat of melting) and the operation parameters (such as the cutoff temperature) in Note 2 (ESI†). The expression for Lc,p is provided in eqn (4).
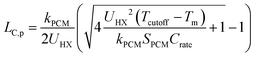 | (4) |
In thermal batteries, ΔSOC takes on a value less than unity due to losses that occur during discharge (as discussed above) and losses that occur during storage. One important approximation that was made is that the sensible capacity of the liquid phase is negligible; this was necessary to obtain a simple analytical expression for ΔSOC that is used later in the paper to derive PCM figures-of-merit. In Note 5 (ESI†), we show that this approximation has little effect on the general results of the heat transfer and cost analyses. In eqn (4), kPCM is the thermal conductivity of the phase through which heat is propagating during discharge. For cold storage (as depicted in Fig. 1), the thermal resistance occurs through the liquid phase, so kPCM is the thermal conductivity of the liquid PCM. For hot storage, kPCM is the thermal conductivity of the solid phase (we show that this is the case in Note 2, ESI†).
The relevance of the thermal penetration depth is not unique to the geometry in Fig. 1. Latent heat thermal batteries of other geometries (such as the cylindrical geometry analyzed in Note 11, ESI†) and sensible heat thermal batteries (such as the one analyzed in Note 12, ESI†) also have thermal penetration depths, beyond which a negligible amount of heat has penetrated at the time cutoff is reached. Any material beyond this thickness goes unused and its thermal storage capacity is wasted. This constrains the thermal battery design and places an upper bound on the thermal storage material thickness. As we will demonstrate through the following analysis, the cost-optimized design will have a thermal storage material thickness (LC) somewhere between zero and this thermal penetration depth (Lc,p). If the storage material is costly, the optimal thickness will be closer to zero; whereas, if the heat exchanger is costly (which is often the case), the optimal thickness will be equal to the thermal penetration depth. The heat exchanger is deemed costly relative to the PCM if LHX/Lc,p ≫ 1, while the PCM is deemed costly relative to the heat exchanger if LHX/Lc,p ≪ 1.
In Note 1 (ESI†), we find that the optimal value of Ls would be infinitely large. However, for a thermal battery with a finite capacity, LS is constrained to some maximum value, LS,max, which we derive in Note 4 (ESI†). The insulation is deemed costly when compared to the PCM if Lins/LS,max ≫ 1, while the PCM is deemed costly relative to the insulation if Lins/LS,max ≪ 1.
Results
$ per kW h minimization of thermal batteries
For the thermal battery depicted in Fig. 1, the effect of PCM thickness (LC) on system cost is illustrated in Fig. 2, using the same n-tetradecane/graphite PCM that Woods et al.24 considered in their work. James et al.16 considered an areal heat exchanger cost of $39 per m2 based on the cost of aluminum in microchannel heat exchangers, but this did not consider additional costs (manifolds, brazing, etc.). As such, we considered a baseline heat exchanger areal cost of $50 per m2 in most of our analyses. For the insulation, we considered fiberglass (Note 6 contains the relevant cost and thermal resistance values, ESI.†). The vertical axes of the plots in Fig. 2 corresponds to dimensionless cost (G/G0). The horizontal axes correspond to the characteristic length of thermal discharge (LC), which is also the PCM thickness. We provide curves for different thermal conductivities and latent heats of fusion.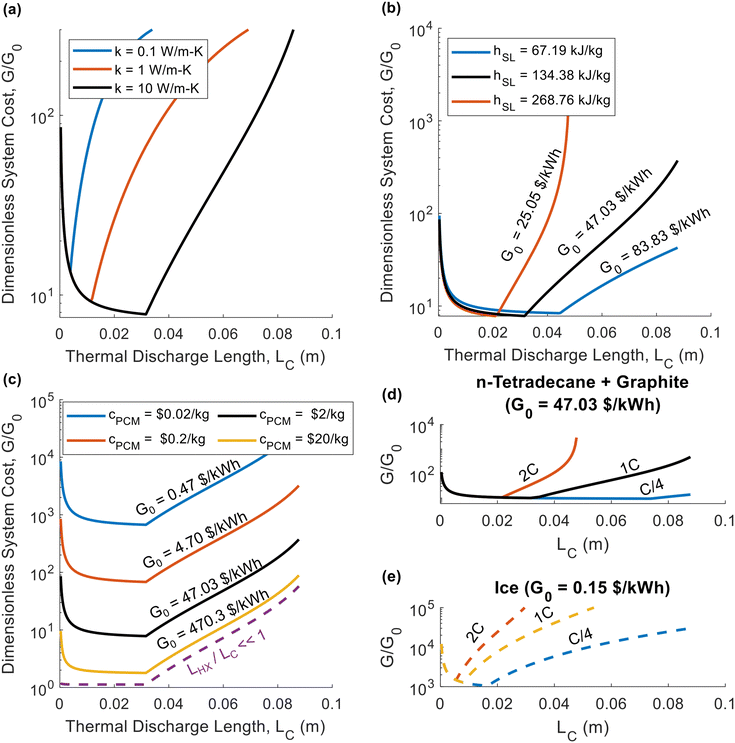 | ||
| Fig. 2 Plots of the dimensionless thermal battery system cost (G/G0) as a function thermal discharge length (LC), with curves for different thermal conductivities (a), different latent heats (b), different PCM costs (c), and different C-rates (d) and (e). The baseline properties in (a)–(d) are k = 10 W m−1 K−1, hSL = 167.98 kJ kg−1, cPCM = $2 per kg, and Crate = 1 h−1, with the black curve in all four plots representing the baseline case. The properties in (a)–(d) correspond to n-tetradecane with graphite additive, while (e) corresponds to ice. A full list of the material properties used in this analysis are given in Note 13 (ESI†). In all plots the system was sized such that LS = 0.01 m (an arbitrary value of LS that is smaller than LS,max for the entire range of LC values considered). | ||
In Fig. 2a, the system cost is plotted as a function of PCM thickness for three different thermal conductivity values, with all other properties held constant. High thermal conductivity is known to be desirable for thermal storage materials,26,40 and Fig. 2a illustrates its benefits to system cost. By increasing the thermal conductivity, the minimum achievable system cost is reduced. The mechanism by which an increase in thermal conductivity reduces system cost is that a higher thermal conductivity results in a greater thermal penetration depth. This allows the heat to propagate further into the PCM by the time cutoff is reached, allowing more PCM to be used in the thermal battery, thereby increasing the storage capacity and reducing the contribution to the system cost from the heat exchangers. In Fig. 2a, all three curves have the same G0 value of $47.03 per kW h, since thermal conductivity does not explicitly affect G0 (materials with higher thermal conductivities are likely to be more expensive, but for simplicity we kept the PCM cost constant in Fig. 2).
In Fig. 2b, we again plot the dimensionless system cost as a function of PCM thickness, this time with different curves for different latent heats. Upon initial observation, it may seem as though the latent heat has no effect on system cost, because the minima stay at roughly the same G/G0 value. However, it is important to recognize that G/G0 is the dimensionless system cost, and the [$ per kW h] system cost (G) is found by multiplying the dimensionless cost (G/G0) by the PCM cost (G0). Then, observing that G0 decreases with increasing latent heat, it is clear that a greater latent heat reduces system cost. Meanwhile, in Fig. 2c, the decreasing the PCM cost increases the dimensionless cost but decreases G0, such that the system cost (G) remains approximately constant (as it is dominated by the heat exchanger cost). The one exception is for cPCM = $10 per kg, as this is a high enough PCM cost to cause G to increase, since the PCM begins to dominate system cost at this high cPCM. If cPCM were high enough that LHX/LC ≪ 1, the dimensionless cost collapses onto the dashed purple line in Fig. 2c, at which point the minimum achievable system cost is simply G0.
In Fig. 2d, we plot the dimensionless thermal battery cost for n-tetradecane with graphite filler at different C-rates; we provide a similar plot for ice in Fig. 2e. The optimal PCM thickness is smaller for ice than for n-tetradecane + graphite, due to the low thermal conductivity of ice. Because these two PCMs have different G0 values, the dimensionless cost cannot be directly compared; we compare them on the basis of G in Fig. 3. Fig. 2d and e indicate that the system cost increases with C-rate. Because the C-rate is the rate at which the thermal battery is discharged, the thermal power density of the storage material is PPCM [kW m−3] = SPCMCrate. A higher C-rate means that the battery is being discharged at a higher power (i.e., greater rate of heat transfer), which reduces the thermal resistance at cutoff. A lower cutoff resistance also decreases the optimal PCM thickness (LC), which is why the minimum system cost increases with C-rate.
The minima of the curves in Fig. 2 occur at exactly LC = LC,p (the PCM thickness equals the thermal penetration depth). The thermal penetration depth will always be the optimal PCM thickness when the heat exchanger cost far outweighs the PCM cost (LHX/LC,p ≫ 1), which is often the case in real-world thermal batteries. The other extreme occurs when the heat exchanger is free (LHX/LC = 0), in which case there is no incentive to add as much PCM as possible, and ΔSOC should be maximized by making the PCM as thin as possible (LC → 0). If both the heat exchanger and PCM costs are on the same order of magnitude, the optimal PCM thickness will be somewhere between zero and the thermal penetration depth; we give results for this scenario in Note 9 (ESI†), providing plots similar to those in Fig. 2 but with a lower heat exchanger cost. However, it should be noted that when heat exchanger and PCM costs are on the same order of magnitude, our simple analytical model for ΔSOC will not accurately predict the optimal value of LC. This occurs because we neglect the sensible heat of the liquid phase in our analytical model, and the capacity from the liquid phase sensible heat is more important when the PCM is expensive. Therefore, in Note 9 (ESI†) we use the numerical model developed by Woods et al.24 to find ΔSOC.
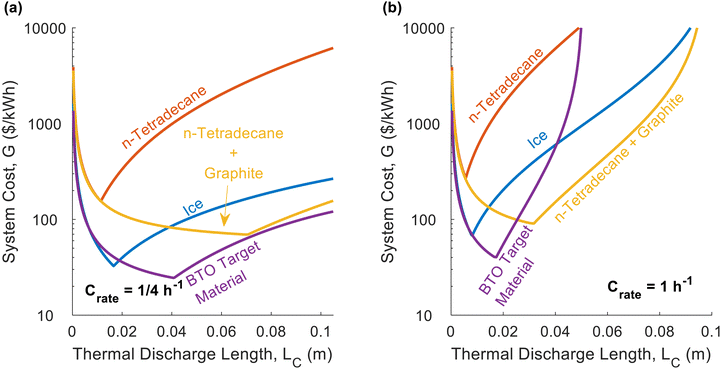
While Fig. 2 explored the effects that material properties have on dimensionless cost, in Fig. 3 we plot the total thermal battery cost, G, for different real PCMs. The exact values of the material properties, cost values, and operational parameters are given in Note 13 (ESI†). Pure n-tetradecane performs the worst, due to its low thermal conductivity, low latent heat, and high cost. At the lower C-rate of C/4, pure ice (low thermal conductivity) outperforms the n-tetradecane with graphite, because the thermal conductivity is less important at low C-rates and the ice has a much lower G0 value than the n-tetradecane with graphite. However, at the higher C-rate of 1C, pure ice and n-tetradecane with graphite are closer in cost. The higher thermal conductivity of the n-tetradecane with graphite provides as much value as the high energy density and low cost of ice because the heat exchanger cost becomes more important at higher C-rates. The BTO target material is an aspirational material with properties defined by the Department of Energy's Building Technologies Office (BTO)41 and performs better than all of the other PCMs for both C-rates. The target thermal conductivity was not dictated by BTO, so for Fig. 3 we chose a value of 10 W m−1 K−1. However, in one of the figures below (Fig. 5), we consider a lower thermal conductivity of 1 W m−1 K−1 for the BTO target, which results in a significantly higher cost (roughly 2× the cost in Fig. 3a). This highlights the importance of also dictating an appropriate thermal conductivity when setting aspirational targets for storage materials.
In Fig. 2 and 3, the effect of LS on system cost was not considered. As such, we provide a contour plot of the dimensionless cost of an n-tetradecane + graphite thermal battery in Fig. 4 with LC and LS as the two principal axes. This serves as a cost design field that illustrates how to minimize the thermal battery cost as a function of LC and LS (which themselves are functions of the system geometry). From Fig. 4, the minimum nondimensional cost is 2.5, which occurs when LC = 0.033 m and LS = 0.13 m. This dimensionless cost means that the total system cost is 150% greater than the PCM cost, which is the lowest possible value for the given PCM, heat exchangers, and insulation. In physically relevant quantities, the minimum system cost is $95.03 per kW h, which is obtained by making the thickness of the PCM layers (LC) equal to 3.33 cm, the number of layers (N) equal to 23, and the width of the layers (W) equal to 79.15 cm. The derivation of the optimal N and W is detailed in the ESI† (Note 4). When N and W take on their optimal values, LS is maximized, which minimizes the heat lost from the thermal battery during storage.
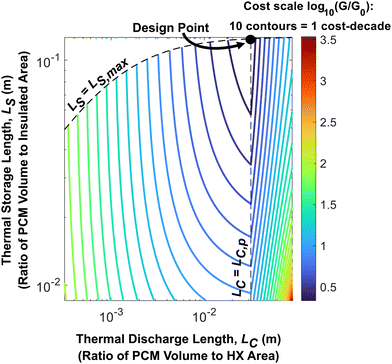 | ||
| Fig. 4 Cost-design field for an n-tetradecane PCM thermal battery. The contour lines represent constant values of log10(G/G0). The plot was generated for n-tetradecane/graphite composite PCM; the material properties of this PCM and the operational parameters considered in this analysis are given in Note 13 (ESI†). The dashed vertical line corresponds to the maximum thermal penetration depth, LC,p; when the PCM thickness is equal to this value, the device cost is minimized. The dashed curve along the top of the contour plot is the maximum possible value of LS for a given LC. This maximum LS is determined by the storage capacity of the PCM within the thermal battery; for this example, the system thermal storage capacity is 21.1 kW h. | ||
Regime map and thermal battery figures of merit
A regime map can be created with Lins/LS and LHX/LC as the axes, shown in Fig. 5. Based on the functional form of G/G0, the cost scaling factor of the volumetric costs is unity, while the axes of Fig. 5 correspond to the other two cost scaling factors. When both Lins/LS ≪ 1 and LHX/LC ≪ 1, the volumetric costs dominate the device cost. When Lins/LS ≫ 1 and Lins/LS ≫ LHX/LC, the insulation costs dominate. Finally, when LHX/LC ≫ 1 and LHX/LC ≫ Lins/LS, the heat exchanger costs dominate. In each of these regimes, the minimum device cost can be found by assuming the two non-dominant cost scaling factors are negligible. Also, when LC/LC,p and LS/LS,max, then ΔSOC ≈ 1. From the minimum device cost in each regime, a figure-of-merit (FOM) can be determined by extracting the group of PCM material properties that would minimize G. These various cost minima and system optimization goals can help influence the design of thermal batteries to operate most cost effectively. The different points correspond to different C-rates (e.g., C/4 is a C-rate of ¼ h−1), which are listed in the legend below the plot, and different material properties, which are listed in Note 13 (ESI†). Changing operational parameters (cutoff temperature, C-rate, etc.) or material properties causes the points to move on the plot.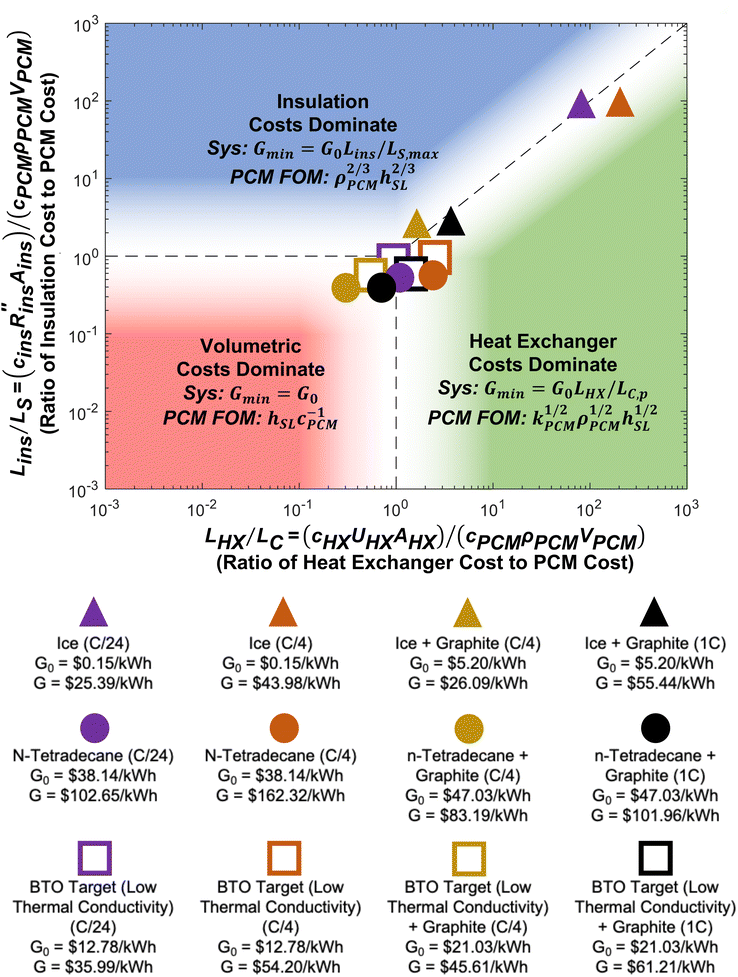 | ||
| Fig. 5 Regime map of dominating costs for thermal batteries. The plot shows three different regimes in which one particular cost dominates: the volumetric costs, such as the PCM (bottom left), the external areal costs, such as the insulation (top), and the heat exchanger costs (right). Each regime corresponds to a particular cost scaling factor being at least an order-of-magnitude greater than the other two cost scaling factors. In each regime, the minimum device cost is found by assuming the non-dominant costs are zero. Then, a PCM figure-of-merit (FOM) is the group of PCM properties that minimizes the device cost in a particular regime. The filled shapes represent real materials, while the open shapes represent targets. The material properties and operational parameters associated with each data point are listed in Note 13 (ESI†). | ||
In the volumetric cost dominated regime, the minimum system cost is G0, and the group of PCM material properties that would minimize this is SPCM/(cPCMρPCM) = hSL/cPCM, with units of [kW h per $]. In the insulation cost dominated regime, the minimum system cost is G0Lins/LS,max. By evaluating the expression for G when LS/LS,max (which occurs when the device is designed to minimize the external surface area of the system for a given amount of PCM), the group of PCM material properties that would minimize this cost is (ρPCMhSL)n, with units of [kW h m−3]n, however, the scaling here is slightly weaker with an exponent of only n = 2/3. Finally, the heat exchanger cost dominated regime has a minimum system cost of G0LHX/LC,p. After evaluating this expression for LC,p, the group of PCM properties that minimizes this cost is (kPCMρPCMhSL)m, with units of [kW h m−4 K−1]m, and the scaling here is even weaker with an exponent of m = 1/2.
Note that the heat exchanger cost dominant FOM can be rewritten as 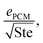 where ePCM is the thermal effusivity of the PCM and Ste is the Stefan number of the PCM. Notably, this FOM is similar to the one derived by Shamberger for the cooling capacity of PCMs,26 though Shamberger derived his for a fixed temperature boundary condition, as opposed to a fixed heat flux. As a result, the denominator of Shamberger's FOM is erf(λ2) (where λ2 is the solution to the Stefan problem transcendental equation), as opposed to our FOM, which has a denominator of
where ePCM is the thermal effusivity of the PCM and Ste is the Stefan number of the PCM. Notably, this FOM is similar to the one derived by Shamberger for the cooling capacity of PCMs,26 though Shamberger derived his for a fixed temperature boundary condition, as opposed to a fixed heat flux. As a result, the denominator of Shamberger's FOM is erf(λ2) (where λ2 is the solution to the Stefan problem transcendental equation), as opposed to our FOM, which has a denominator of 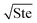 . For PCMs with small Ste (as is desired for thermal storage and as was assumed in our derivations),
. For PCMs with small Ste (as is desired for thermal storage and as was assumed in our derivations), 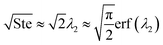 (as explained by Jiji42). Therefore, our FOM for the heat exchanger dominated regime is equivalent to Shamberger's FOM for most practical PCMs. In Note 10 (ESI†), we provide plots to illustrate how changing material properties will cause the thermal battery to move from one cost regime to another and how a particular material will affect the system cost while it is in one regime but have no effect in a different regime. For sensible heat thermal batteries, the FOMs are the same as they are for latent heat thermal batteries, except that the enthalpy of melting (hSL) is replaced with the specific heat capacity (cp); see Note 12 (ESI†) for derivations and a regime map.
(as explained by Jiji42). Therefore, our FOM for the heat exchanger dominated regime is equivalent to Shamberger's FOM for most practical PCMs. In Note 10 (ESI†), we provide plots to illustrate how changing material properties will cause the thermal battery to move from one cost regime to another and how a particular material will affect the system cost while it is in one regime but have no effect in a different regime. For sensible heat thermal batteries, the FOMs are the same as they are for latent heat thermal batteries, except that the enthalpy of melting (hSL) is replaced with the specific heat capacity (cp); see Note 12 (ESI†) for derivations and a regime map.
For 7 of the 12 data points in Fig. 5, the heat exchanger is the most expensive component of the thermal battery. This reveals the need for cheaper heat exchanger designs and materials. Increasing the thermal conductivity of the PCMs (by adding conductive filler) moves the points closer to the volumetric regime where PCM costs dominate. However, even when the thermal conductivity is high and the C-rate is low, none of the thermal batteries reach the point where heat exchanger cost is negligible (LHX/LC ≤ 0.1), emphasizing the pervasive need for better heat exchangers.
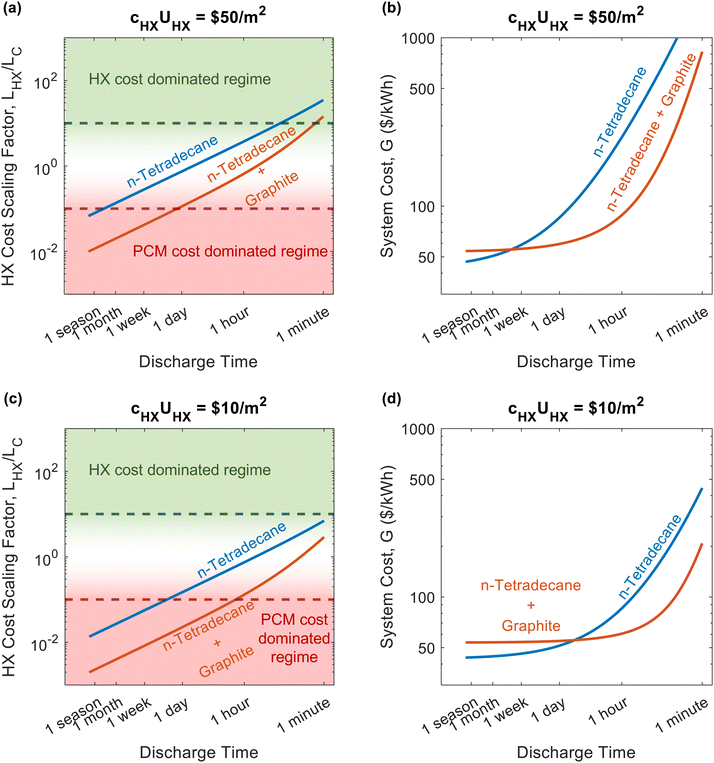
To further explore the effect of C-rate on thermal battery design, we created Fig. 6a, which plots the heat exchanger cost scaling factor as a function of discharge time (the reciprocal of C-rate). We give results for n-tetradecane and n-tetradecane with graphite filler. We also plotted the thermal battery cost in Fig. 6b to show which material would results in a less expensive thermal battery at the different discharge timescales. Shorter timescales (less than 1 hour) will be heavily dominated by the heat exchanger cost. When heat exchanger costs are significant, highly conductive PCMs are preferable, even if this increases the PCM $ per kW h cost (G0). The PCM with graphite filler becomes dominated by PCM costs at timescales of 1.5 days. Meanwhile, the PCM without graphite filler does not reach the PCM cost dominated regime until the discharge time is on the order of a season (3 months). At long discharge timescales (>1.5 weeks), inexpensive, energy dense PCMs are preferable, making the pure PCM favorable over the graphite filled PCM. Fig. 6c and d plot the same quantities but with a hypothetical heat exchanger that has the same conductance but one fifth the cost, which shifts the point at which the pure n-tetradecane becomes the favorable material. This motivates the need for cheaper heat exchangers, as they would lead to less expensive thermal batteries that utilize cheap, energy dense PCMs without thermally conductive filler.
Fig. 6 also highlights the importance of the PCM figures-of-merit. When both systems (pure n-tetradecane and n-tetradecane with graphite) are in or near the PCM cost dominated regime, the material with the greater hSL/cPCM will achieve the lower thermal battery system cost, which is the pure n-tetradecane. Meanwhile, when both PCMs are in the heat exchanger cost dominated regime, the material with the greater (kPCMρPCMhSL)1/2 will achieve the lower thermal battery cost, which is the n-tetradecane with graphite.
We note that our simple analytical solution for ΔSOC assumes that losses during discharge are negligible, which is a good approximation for the higher C-rates (≥C/24) on which we primarily focused in this work. However, it will be less accurate at the lower C-rates considered in Fig. 6. As such, in Fig. 6 we assumed that the insulation is free and enough is used that losses are negligible over any discharge timescale. A more complex expression (or numerical approximation) for ΔSOC would be required to accurately account for storage losses and is beyond the scope of this work, though the general trends for the HX cost scaling factor would remain similar to what is presented in Fig. 6. We also note that both the cost of graphite and areal heat exchanger cost can vary significantly from one vendor to another; as such, we provide results for different graphite and heat exchanger costs in Notes 7 and 8 (ESI†), respectively.
Case study: residential HVAC thermal battery
To demonstrate the use of our cost scaling method, we provide a case study for thermal storage used in a residential building. Consider a house with a 3 ton air conditioner, and the owners are on an electricity plan with 4 peak hours and would like to forgo running their air conditioner during those entire 4 hours. The storage system must be able to provide a constant 3 tons (10.6 kW) of cooling, with a C-rate of 1/4 h−1, giving a total storage capacity of Cap = 42.4 kW h. An aluminum heat exchanger with an areal cost of $50 per m2 and conductance of 570 W m−2 K−1 is selected. The system cost is to be compared for three different PCMs: n-tetradecane (G0 = $38.14 per kW h), n-tetradecane + graphite (G0 = $47.03 per kW h1), and ice (G0 = $0.15 per kW h); the thermophysical properties for these three PCMs are listed in Note 13 (ESI†). The insulation resistance is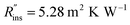 , with an insulation cost of Cins = $23.1 per W per m4 per K.
, with an insulation cost of Cins = $23.1 per W per m4 per K.
For n-tetradecane, the optimal PCM thickness is 1.14 cm, the optimal device width is 80.60 cm, and the optimal number of PCM layers is 65, giving heat exchanger and insulation cost scaling factors of 2.61 and 0.57, respectively. Meanwhile, n-tetradecane + graphite has an optimal PCM thickness of 7.05 cm, optimal device width of 76.57 cm, and 11 as the optimal number of layers, yielding a heat exchanger cost scaling factor of 0.36 and insulation cost scaling factor of 0.45. When n-tetradecane is used, the system cost is dominated by the heat exchanger, owing to the poor PCM thermal conductivity. By adding graphite, the energy density of the PCM decreases slightly, but the thermal battery cost decreases significantly (from 161.47 to 84.21 $ per kW h) because the increase in thermal conductivity allows for a much greater PCM thickness. Finally, ice has an optimal PCM thickness of 1.66 cm, optimal device width of 61.00 cm, and optimal layer number of 35. This gives a heat exchanger cost scaling factor of 201.11 and insulation cost scaling factor of 82.41. The large cost scaling factors might initially seem to imply that the ice system is more expensive, but when multiplying the factors by the G0 value for ice, it becomes clear that ice is the cheapest option ($43.59 per kW h1 system cost for ice).
One can also consider the effect that changing the heat exchanger material has on the system cost. Assume that a new heat exchanger material reduces the areal cost by 80% (giving a value of $10 per m2) and also reduces the conductance by 80% (to a value of 114 W m−2 K−1). With ice as the storage material, the optimal PCM thickness is reduced to 1.47 cm, but the system cost drops to $19.80 per kW h because of the cheaper heat exchanger, indicating that the cheaper heat exchanger is the better option. Further reducing the areal cost and conductance to 2% of their original values yields an even lower system cost of $15.84 per kW h, but reducing the areal cost and conductance even further to 0.2% of their original values yields a higher system cost of $24.61 per kW h. This emphasizes the importance of performing the cost scaling analysis not only for different thermal storage materials but also for different heat exchanger options as well. It should be noted that in this example we assumed that the heat exchanger conductance and areal cost are linearly related, but this might not always be the case.
Conclusions
From grid-scale storage to building thermal management, thermal batteries are promising energy storage devices. Just as electrochemical batteries can provide electricity until some cutoff voltage is reached, thermal batteries can provide heat (or cooling) until a cutoff temperature is reached. Woods et al. showed that the fraction of total heat that can be accessed from a thermal battery is a function of the device geometry.24 Complementing this finding, we present a cost scaling analysis of thermal batteries, demonstrating how the system can minimize the [$ per kW h] cost. We present a universal cost framework for thermal batteries that can be used to optimize the system on a [$ per kW h] cost basis. This equation is a function of two independent characteristic lengths, one of which relates to the thickness of the PCM layers and the other relates to the device cross-sectional area and number of PCM layers.We show that, when the sensible capacity is small relative to the latent capacity, the optimal PCM thickness is the thickness that results in the PCM just completing the melting process as the cutoff temperature is reached (the maximum thermal penetration depth), which is often on the order of cm (for kPCM < 10 W m−1 K−1) or tens of cm (for kPCM > 10 W m−1 K−1). If the PCM thickness is less than this optimal value, then more heat exchanger area is required for a given amount of PCM, without a significant increase in the SOC that can be accessed from the thermal battery. Conversely, if the PCM thickness is greater than the optimal value, then too much capacity is left within the device when the cutoff temperature is reached, reducing the usable capacity of the device and increasing the [$ per kW h] cost. For example, in Fig. 3a, we analyze a thermal battery that would have a cost of $155 per kW h when n-tetradecane is used as the storage material. When the thermal conductivity of the storage material is increased by adding graphite filler, the thermal battery cost decreases to $69 per kW h. Further improving the density and latent heat to the DOE BTO target values reduces the thermal battery cost to $24 per kW h.
Additionally, the characteristic length of heat loss through the insulation should be maximized to minimize the overall device cost. However, for a fixed capacity, this characteristic length cannot take on any value, and the maximum possible value is given in eqn (S8) of the ESI.† When the device geometry is designed such that the two characteristic lengths take on their optimal values, the device cost will be minimized. The analysis in Note 9 (ESI†) reveals that the optimal PCM thickness can be somewhat smaller than the maximum melting front penetration depth is sensible capacity is non-negligible (in which case our analytical approximation is not applicable). However, the optimal thickness will never be greater than the maximum penetration depth.
A regime map was drawn with the heat exchanger cost scaling factor on the horizontal axis and the insulation cost scaling factor on the vertical axis. Three regimes exist on the map: (i) PCM costs dominate, (ii) heat exchanger costs dominate, (iii) insulation costs dominate. Each regime has a different functional form for the minimum achievable device cost, along with different PCM material figures-of-merit. The most intuitive regime is the PCM cost dominant regime. In this regime, the material figure-of-merit is simply the [$ per kW h] cost of the PCM (G0). However, heat exchangers are often the dominating expense, so many thermal batteries reside in the heat exchanger cost dominant regime instead. In this regime, reducing the [$ per kW h] cost of the PCM will do very little to reduce the [$ per kW h] cost of the thermal battery, since the heat exchanger dominates the battery's cost. Instead, the figure-of-merit for this regime, which includes the PCM thermal conductivity and latent heat, should be maximized. This would allow a greater amount of PCM to be added to the battery for a given heat exchanger area, increasing the battery capacity without increasing the cost, thereby reducing the [$ per kW h] battery cost.
The general expression we provide for the dimensionless cost, G/G0, applies to many types of thermal batteries (eqn (3)). However, the functional form of ΔSOC will depend on the particular thermal battery design. Our analysis was conducted for the geometry in Fig. 1, using a simple, analytical expression for the SOC of such a device. We used a simple expression for ΔSOC for the sake of brevity and to illustrate general trends and opportunities for optimization. Our simple analytical approximation serves to broadly demonstrate the opportunity for optimization of thermal batteries through design of the device. This framework helps elucidate what is important to reduce cost (e.g., cost scaling) for thermal batteries. We similarly analyze ΔSOC for another geometry (Note 11, ESI†) and sensible storage materials (Note 12) in the ESI.†
For the more complex thermal battery designs that would be encountered in the real world, numerical models and simulations would likely be required to accurately determine ΔSOC as a function of PCM geometry. In these simulations, the simple analytical model that we present for ΔSOC can serve as a starting point for the PCM length scale, reducing the computational time needed to find the optimal geometry. Once ΔSOC is obtained, eqn (3) can still be used to determine the system cost. Likewise, when analyzing a thermochemical storage system, a different analysis than the one presented in this paper would be required to find ΔSOC as a function of TCM geometry (whether the analysis is analytical or numerical), but then our eqn (3) can be used to optimize for cost. The exponents within the PCM figures of merit will change with the system geometry, which means that systems with complex geometries will scale with PCM properties in the exact same way as the geometry in Fig. 1. However, while the exponents will change, the appearance of different properties within the different cost regimes will remain the same (i.e., thermal conductivity will appear in the HX-dominated regime, latent heat will appear in all three regimes, etc.). We show that this is the case with the cylindrical geometry in the ESI† (Note 11).
Author contributions
J. D. K. and S. K. Y. conceptualized the work and developed the cost scaling equation. J. D. K. derived the simplified analytical solution for state of charge and maximum thermal penetration depth, performed the analysis and wrote the original draft. J. W., A. O., and A. M. provided feedback on data visualization, material properties, costs, and operational parameters. J. D. K., S. K. Y., J. W., A. O., and A. M. reviewed and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. D. K. would like to acknowledge funding from the IBUILD Graduate Research Fellowship. This research was performed under an appointment to the Building Technologies Office (BTO) IBUILD-Graduate Research Fellowship administered by the Oak Ridge Institute for Science and Education (ORISE) and managed by Oak Ridge National Laboratory (ORNL) for the U.S. Department of Energy (DOE). ORISE is managed by Oak Ridge Associated Universities (ORAU). All opinions expressed in this paper are the author's and do not necessarily reflect the policies and views of DOE, EERE, BTO, ORISE, ORAU or ORNL. This work was authored in part by the National Renewable Energy Laboratory (NREL), operated by Alliance for Sustainable Energy, LLC, for the US DOE under contract no. DE-AC36-08GO28308, with support from the US DOE Building Technologies Office. The views expressed in the article do not necessarily represent the views of the DOE or the US Government. We thank Sven Mumme from the DOE Building Technologies Office for his support and feedback on the concepts discussed in this work.Notes and references
- G. F. Frate, L. Ferrari and U. Desideri, Renewable Energy, 2021, 163, 1754–1772 CrossRef.
- I. Chernyakhovskiy, T. Bowen, C. Gokhale-Welch and O. Zinaman, USAID Energy Storage Decision Guide for Policymakers, 2021 Search PubMed.
- A. G. Olabi, C. Onumaegbu, T. Wilberforce, M. Ramadan, M. A. Abdelkareem and A. H. Al-Alami, Energy, 2021, 214, 118987 CrossRef CAS.
- S. Koohi-Fayegh and M. A. Rosen, J. Energy Storage, 2020, 27, 101047 CrossRef.
- S. Rehman, L. M. Al-Hadhrami and Md. M. Alam, Renewable Sustainable Energy Rev., 2015, 44, 586–598 CrossRef.
- M. Budt, D. Wolf, R. Span and J. Yan, Appl. Energy, 2016, 170, 250–268 CrossRef.
- A. G. Olabi, T. Wilberforce, M. A. Abdelkareem and M. Ramadan, Energies, 2021, 14, 2159 CrossRef.
- Innovation landscape brief: utility-scale batteries, IRENA, 2019.
- D. Enescu, G. Chicco, R. Porumb and G. Seritan, Energies, 2020, 13, 340 CrossRef.
- I. Sarbu and C. Sebarchievici, Sustainability, 2018, 10, 191 CrossRef.
- C. Amy, H. R. Seyf, M. A. Steiner, D. J. Friedman and A. Henry, Energy Environ. Sci., 2019, 12, 334–343 RSC.
- A. Sevault, F. Vullum-Bruer and O. L. Tranås, Reference Module in Earth Systems and Environmental Sciences, Elsevier, 2020 Search PubMed.
- J. Woods, M. Brandt and P. Tabares-Velasco, Synergies Between Building-Sited Batteries and Thermal Energy Storage, National Renewable Energy Lab. (NREL), Golden, CO (United States), 2023 Search PubMed.
- M. Brandt, J. Woods and P. C. Tabares-Velasco, J. Energy Storage, 2022, 50, 104216 CrossRef.
- R. Huang, A. Mahvi, W. Odukomaiya, A. Goyal and J. Woods, Energy Convers. Manage., 2022, 263, 115692 CrossRef.
- N. James, A. Mahvi and J. Woods, J. Energy Storage, 2022, 56, 105875 CrossRef.
- A. Odukomaiya, J. Woods, N. James, S. Kaur, K. R. Gluesenkamp, N. Kumar, S. Mumme, R. Jackson and R. Prasher, Energy Environ. Sci., 2021, 14, 5315–5329 RSC.
- W. Parker, A. Odukomaiya, J. Thornton and J. Woods, Sol. Energy, 2023, 249, 684–693 CrossRef.
- A. Mahvi, E. Kozubal and J. Woods, Performance of a Hybrid HVAC-Integrated Thermal Storage Device, National Renewable Energy Lab. (NREL), Golden, CO (United States), 2021 Search PubMed.
- A. Mahvi, K. P. Shete, A. Odukomaiya and J. Woods, J. Energy Storage, 2022, 55, 105514 CrossRef.
- A. Bulk, A. Odukomaiya, E. Simmons and J. Woods, J. Therm. Sci., 2023, 32, 1213–1226 CrossRef CAS.
- L. F. Cabeza, in Thermal Energy Storage: Materials, Devices, Systems and Applications, ed. Y. Ding, Royal Society of Chemistry, London, 2021, ch. 3, pp. 42–54 Search PubMed.
- B. Koçak, A. I. Fernandez and H. Paksoy, Sol. Energy, 2020, 209, 135–169 CrossRef.
- J. Woods, A. Mahvi, A. Goyal, E. Kozubal, A. Odukomaiya and R. Jackson, Nat. Energy, 2021, 6, 295–302 CrossRef.
- W. Fu, X. Yan, Y. Gurumukhi, V. S. Garimella, W. P. King and N. Miljkovic, Nat. Energy, 2022, 7, 270–280 CrossRef CAS.
- P. J. Shamberger, J. Heat Transfer, 2015, 138(2), 024502 CrossRef.
- W. Aftab, A. Usman, J. Shi, K. Yuan, M. Qin and R. Zou, Energy Environ. Sci., 2021, 14, 4268–4291 RSC.
- H. Jouhara, A. Żabnieńska-Góra, N. Khordehgah, D. Ahmad and T. Lipinski, Int. J. Thermofluids, 2020, 5–6, 100039 CrossRef CAS.
- G. Sadeghi, Energy Storage Mater., 2022, 46, 192–222 CrossRef.
- J. Romaní, J. Gasia, A. Solé, H. Takasu, Y. Kato and L. F. Cabeza, Appl. Energy, 2019, 235, 954–962 CrossRef.
- W. Li, J. J. Klemeš, Q. Wang and M. Zeng, Renewable Sustainable Energy Rev., 2022, 154, 111846 CrossRef CAS.
- W. Li, M. Zeng and Q. Wang, Sol. Energy Mater. Sol. Cells, 2020, 210, 110509 CrossRef CAS.
- X. Chen, Z. Zhang, C. Qi, X. Ling and H. Peng, Energy Convers. Manage., 2018, 177, 792–815 CrossRef CAS.
- P. J. Shamberger, Nat. Energy, 2021, 6, 221–222 CrossRef.
- J. Hirschey, N. Kumar, T. Turnaoglu, K. R. Gluesenkamp and S. Graham, Review of Low-Cost Organic and Inorganic Phase Change Materials with Phase Change Temperature between 0 °C and 65 °C, Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), 2021 Search PubMed.
- N. Kumar, J. Hirschey, T. J. LaClair, K. R. Gluesenkamp and S. Graham, J. Energy Storage, 2019, 24, 100794 CrossRef.
- Y. Li, N. Kumar, J. Hirschey, D. O. Akamo, K. Li, T. Tugba, M. Goswami, R. Orlando, T. J. LaClair, S. Graham and K. R. Gluesenkamp, Composites, Part B, 2022, 233, 109621 CrossRef CAS.
- S. K. Yee, S. LeBlanc, K. E. Goodson and C. Dames, Energy Environ. Sci., 2013, 6, 2561–2571 RSC.
- R. K. Shah and D. P. Sekulić, Fundamentals of heat exchanger design, John Wiley & Sons, Hoboken, NJ, 2003 Search PubMed.
- J. A. Tomko, A. Pena-Francesch, H. Jung, M. Tyagi, B. D. Allen, M. C. Demirel and P. E. Hopkins, Nat. Nanotechnol., 2018, 13, 959–964 CrossRef CAS PubMed.
- Buildings Energy Efficiency Frontiers and Innovation Technologies (BENEFIT) DE-FOA-0002090, US Department of Energy, Office of Energy Efficiency and Renewable Energy, 2019 Search PubMed.
- L. M. Jiji, Heat conduction, Springer, Berlin Heidelberg, 3 edn, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee03594h |
| This journal is © The Royal Society of Chemistry 2024 |