Open Access Article
Open Access ArticleStructural and transport properties of battery electrolytes at sub-zero temperatures†
Nikhil
Rampal
 *ab,
Stephen E.
Weitzner
*ab,
Stephen E.
Weitzner
 *ab,
Seongkoo
Cho
*ab,
Seongkoo
Cho
 ab,
Christine A.
Orme
ab,
Marcus A.
Worsley
ab,
Christine A.
Orme
ab,
Marcus A.
Worsley
 ab and
Liwen F.
Wan
ab and
Liwen F.
Wan
 *ab
*ab
aMaterials Science Division, Lawrence Livermore National Laboratory, Livermore, California 94550, USA. E-mail: rampal1@llnl.gov; weitzner1@llnl.gov; wan6@llnl.gov
bLaboratory for Energy Applications for the Future (LEAF), Lawrence Livermore National Laboratory, Livermore, California 94550, USA
First published on 13th September 2024
Abstract
Lithium-ion batteries (LIBs) have become a core portable energy storage technology due to their high energy density, longevity, and affordability. Nevertheless, their use in low-temperature environments is challenging due to significant Li-metal plating and dendrite growth, sluggish Li-ion desolvation kinetics, and suppressed Li-ion transport. In this study, we employ classical molecular dynamics simulations to provide a mechanistic understanding of the impact of temperature- and concentration-effects on the ionic conductivity of a prototypical battery electrolyte, lithium hexafluorophosphate in ethylene carbonate (LiPF6/EC). We further investigate the interplay between temperature and ionic speciation via a graph-based clustering analysis that resolves species–specific ionic conductivity contributions. Using these findings, we formulate two fundamental design principles governing electrolyte performance: one for ambient temperature and another for low-temperature conditions. The modeling framework outlined in this work provides a foundation for identifying design principles that can be used to rationally improve the low-temperature performance of LIBs.
Broader contextThere is a critical need for accelerated development of next-generation energy storage devices that can operate under extreme conditions, such as low temperatures, for the grid, EV, space exploration, and defense applications. One of the critical challenges is identifying appropriate electrolyte formulations to balance several microscopic factors that may collectively affect the overall performance of the electrolyte. Unfortunately, current research primarily relies on chemical intuition but needs clear strategies and established design metrics, which significantly impedes the exploration of the vast molecular database. Our work aims to address this issue by identifying design principles that would allow for rational design of high-performing electrolytes for low-temperature operations. Using the findings in this study, we formulated two fundamental design principles governing electrolyte performance: one for ambient temperature and another for low-temperature conditions. The approach discussed in this study offers insightful guidelines for developing next-generation lithium-ion batteries with optimized performance under extreme conditions. |
As the world transitions from traditional fossil energy sources to renewable energies, the demand for durable and cost-effective Li-ion batteries (LIBs) continues to grow. Unfortunately, current commercial LIBs exhibit degraded performance at low temperatures, creating pressing challenges for large-scale civil applications, such as electric vehicle and grid operations in harsh environments, as well as utilization in defense systems, space exploration, and subsea operations. Recently, the customization of specific solute–solvent chemistries within the electrolyte has garnered attention as a means to optimize the performance of low temperature LIBs. The performance of LIBs suffers significantly at low temperatures due to a complex interplay of factors affecting their internal processes.1–3 As temperatures drop, the electrolyte viscosity increases, which decreases ion mobility. At the same time, lower temperatures shift the equilibrium within the electrolyte, which alters the charge carrying species, the transference numbers, the electrolyte conductivity, and the electrolyte stability. Collectively, these inhibited processes result in an increase in bulk electrolyte resistance.
Presently, the ability to rationally design high-performance low-temperature battery electrolytes is a pressing challenge that requires a holistic understanding of battery materials compatibility, their respective intrinsic stability under extreme operating conditions, as well as detailed insights into the microscopic factors that promote rapid Li-ion transport through the bulk electrolyte. In recent years, attempts have been made to address low temperature performance. For example, Liu et al.4 explored the addition of solvent additives such as dimethyl carbonate (DMC), ethyl methyl carbonate (EMC), and diethyl carbonate (DEC) in an effort to suppress the kinetic barrier for Li-ion desolvation under low-temperature conditions. Wang et al.5 showed that the use of salt mixtures (high-entropy electrolytes) lead to enhanced ionic conductivity and broad temperature stability by virtue of the increased configurational entropy and diversified solvation structures present in the electrolyte. In addition, these compositional adjustments to the electrolyte are frequently made using chemical intuition but lack clear strategies and established design metrics specifically geared towards improving low-temperature performance. For informed design, a mechanistic understanding of the processes occurring within the electrolyte is imperative. This entails systematic investigation of these electrolytes' fundamental structural and transport properties with the goal of elucidating the interplay between speciation, diffusivity, and ionic conductivities, and their deviations from ideality. This understanding will enable the identification of specific challenges, opportunities, and informed design principles, guiding the foundational development of electrolytes with enhanced properties to address the unique challenges posed at low temperatures.
To achieve this goal, atomistic-scale simulations can play a pivotal role in providing detailed insights into the behavior of electrolytes at the molecular level. Quantum level6–9 and Classical MD simulations10,11 have been performed to understand the structural12–15 and transport properties16–18 of various electrolytes. In one such study, Ringsby et al.19 examined the transport phenomena in low temperature electrolytes using classical MD simulations. They attribute poor low-temperature performance to solvent viscosity, rather than ion aggregation or cation transference numbers (t+). In addition, they report t+ > 1 throughout the temperature range, contrary to experimental observations.20 Holoubek et al.21 made an effort to correlate the local ionic configuration/speciation in the electrolyte to overall reactivity. They postulated that contact ion pairs (CIP) will provide greater stability than the solvent-separated ion pairs (SSIP), leading to lower interfacial charge transfer resistance. This study underscores the significance of ionic speciation and its impact on both bulk and interfacial charge transfer resistances.
Though the aforementioned studies independently elucidated properties that effect low-temperature performance, there are key knowledge gaps that still need to be addressed to formulate meaningful descriptors used to screen electrolytes. Some of these gaps include rationalizing correlations between ionic speciation and transport, providing a quantitative atomic-scale description of the ionic conductivity and understanding the origins and mechanisms of solvent transport at sub-zero conditions. Therefore, in this study, we aim to fill in these knowledge gaps and derive design principles using a prototypical battery electrolyte, lithium hexafluorophosphate in ethylene carbonate (LiPF6/EC). Though this electrolyte is solid at room temperature, this system was selected because of its compositional simplicity, and therefore serves as a representative model. Within this framework, we provide a straightforward comparative approach for screening electrolytes by identifying descriptors that readily screen based on bulk electrolyte transport. In addition, we highlight the microscopic origins of ionic conductivity by calculating the ionic speciation based on both temperature and concentration, and by deconvoluting it into its species–specific contributions. This enables a more comprehensive comparison of species that contribute to overall battery performance over a wide range of temperature and concentration. Finally, we correlate solvent properties with overall electrolyte performance by calculating the electrolyte viscosity, lifetimes of EC within the Li-ion solvation shell and t+. Bridging these gaps leads to formulation of two key design principles: at room temperature, the prominence of ionic speciation influences overall electrolyte performance, emphasizing the importance of maximizing the number of highly mobile charge carriers. Contrarily, at low temperatures, despite a large population of Li-ion species, the rate-limiting processes that govern overall electrolyte performance are dominated by solvent transport and the electrolyte viscosity. The validity of our modeling framework and design principles is extended to a realistic battery electrolyte that is known to be liquid at room temperature (1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (3
EMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7)). This understanding and framework can be extended to other electrolyte systems to screen and engineer optimal compositions of electrolytes. The improved understanding resulting from this study will enhance our predictive capability in designing more robust battery electrolytes for lower-temperature (sub-zero) applications.
7)). This understanding and framework can be extended to other electrolyte systems to screen and engineer optimal compositions of electrolytes. The improved understanding resulting from this study will enhance our predictive capability in designing more robust battery electrolytes for lower-temperature (sub-zero) applications.
Results and discussion
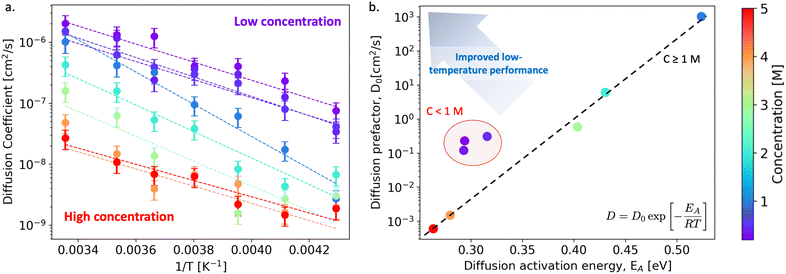
We begin our discussion by examining the impact of electrolyte concentration and temperature on Li-ion transport in bulk LiPF6/EC electrolytes. This data is summarized in Fig. 1(a), which shows the variation of Li-ion diffusion coefficient with respect to inverse temperature as the electrolyte concentration ranges between 0.2–5 M and for temperatures between 233–298 K (−40 to +25 °C). As expected, we observe that the Li-ion diffusion coefficient decreases with decreasing temperature for each electrolyte composition. However, the rate at which the diffusion coefficient decreases is not a linear response to electrolyte concentration. To quantify these differences, we fit the diffusivity data to an Arrhenius relation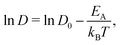 | (1) |
Inspecting the data in Fig. 1(b) more closely, we observe a non-trivial dependence of Li-ion diffusivity on electrolyte concentration that indicates certain concentrations outperform others in terms of their low-temperature performance. Specifically, we find that at low electrolyte concentrations (0.2–0.5 M), the Arrhenius descriptors are clustered (D0 = 0.1–1 cm2 s−1, EA = 0.28–0.34 eV), yet at higher concentrations, the diffusion prefactor appears to exhibit an exponential dependence on the activation energy, decreasing with increased electrolyte concentration. The highest diffusivity and largest activation energy occurs for the 1 M case (D0 = 103 cm2 s−1, EA = 0.55 eV) which highlights its optimal performance at room temperature but degraded properties at low temperatures. Moreover, at concentrations larger than 1 M, we find that while EA decreases with increasing concentration, the exponential dependence of D0 on EA indicates suppressed overall diffusivity to a point that these electrolytes would no longer be suitable for practical applications. To highlight this relationship, a trend line is included in Fig. 1(b). Although the low concentration electrolytes are shifted from the trend line towards the target top-left corner of the property map, the low charge carrier concentration may also limit their effective transport properties. In addition, we've characterized the mode of diffusion as a function of concentration and temperature in Fig. S18, ESI.†
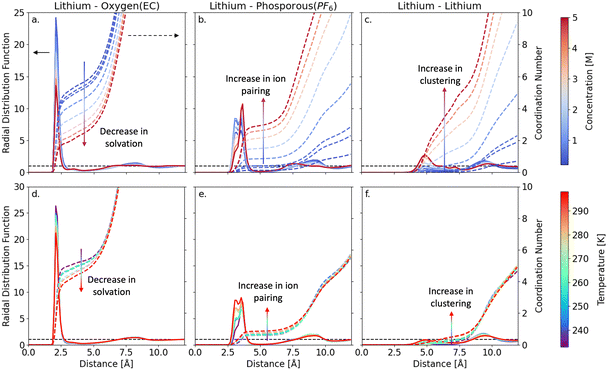
It is widely acknowledged that Li-ion diffusivity through the electrolyte is closely linked to the bulk ionic speciation. Consequently, in the following section, we aim to provide comprehensive understanding of the interplay between electrolyte composition, temperature, and ionic speciation and collectively their impact on Li-ion transport behavior and discuss key design principles that can be derived from these assessments. In Fig. 2(a)–(c), we present radial distribution functions (RDFs) gij(r) and integrated RDFs nij(r) for a series of LiPF6 concentrations at room temperature. At low concentrations (<1 M), Li-ions are coordinated with 5–6 EC molecules (nLi–OEC = 5.47) within their first solvation shells (3.15 Å). However, as the concentration increases, nLi–OEC decreases towards 2 at 5 M, with notable signatures of ion pairing and extended cluster formation. Specifically, the number of PF6 anions that coordinate with Li-ions (nLi–PF6) increases from 0.14 at 1 M concentration to 2.94 at 5 M concentration, at which point they exhibit a higher population than EC in the first solvation shell of Li-ions. Moreover, as evidenced by the vanishing double peak feature at ∼3 Å with increasing concentration in Fig. 2(b), several different types of cation–anion pairing structures emerge within these electrolyte. At lower concentrations, the double peak structure is prevalent due to the low anion (PF6−) concentration in the Li-ion solvation shell, which allows Li-ions to bind to PF6 anions in a bidentate mode. At higher concentrations, a decrease in RDF peak intensity is observed, which can be attributed to the increase in steric effects and ion–ion competition that stabilize the Li–PF6 bond to a monodentate binding mode. For further details, see Fig. S3, ESI† and the surrounding discussion in Section S3, ESI.† Finally, in Fig. 2(c), we observe that the onset of ion clustering is closely coupled with cation–anion pairing. At low concentrations (<1 M), Li–Li coordination is observed in relation to concentration change (nLi–Li = 0.64), signifying the absence of cluster formation. However, at concentrations beyond 1 M, both Li–Li and Li–P coordination increases signaling the onset of ion pairing and extended ion cluster formation. The coordination numbers for ion pairing increase with increasing concentration and ultimately peak at the largest concentration sampled (5 M) with values of nLi–PF6 = 2.94 and nLi–Li = 3.04. As anticipated, this trend shows that extended clusters form as the electrolyte passes through its saturation limit (1.72 M) indicating the origin of particle nucleation. Hence, the suppression of Li-ion transport at higher concentrations (Fig. 1) can be attributed to changes in the ionic speciation. Qualitatively, these results suggest that at higher concentrations, higher proportions of ionic aggregates form, thereby reducing the number of highly mobile solvated Li-ions and increasing the number of larger Li-containing species that exhibit lower mobility. A detailed quantitative comparison of diffusion characteristics of these clusters is shown in Section S4, ESI† (Fig. S4, ESI†).
Using a similar approach, we also assess the effect of temperature on electrolyte structure and ionic speciation for a 1 M LiPF6/EC electrolyte in Fig. 2(d)–(f). As the temperature increases from 233–298 K, the Li–OEC coordination number (nLi–OEC) decreases from 5.4 to 4.7, as shown in Fig. 2(d). In addition, there is a subtle change in the Li–PF6 ion pair coordination number (nLi–PF6) from 0.63 to 0.84, indicating that ion pairing is mildly favored at higher temperatures. The latter is also corroborated in the Li–P RDF at 3.8 Å (Fig. 2(e)), which transitions from a single- to a double-peak feature as temperature increases, revealing the impact of temperature on the competition between EC and PF6 ions within the first solvation shell of Li-ions. Similarly, we find that the effect of temperature on clustering is also negligible, as the Li–Li coordination number (nLi–Li) ranges from 0.22–0.48 (233–298 K). These slight changes in coordination environments are likely due to reduced thermal motion at lower temperatures, which at room temperature corresponds to 1 kBT in energy (2.479 kJ mol−1). Collectively, these results show that the LiPF6/EC electrolyte structure and ionic speciation is more sensitive to changes in electrolyte concentration than temperature. However, as the Li-ion diffusivity for the 1 M electrolyte changes ∼3 orders of magnitude between −40 to +25 °C, it is evident that the subtle structural changes observed in the temperature-dependent RDFs alone cannot fully account for the large suppression in transport behavior.
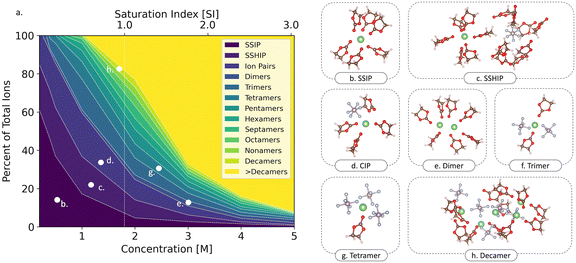
To gain more insight, we now consider a more quantitative analysis of the impacts of temperature and concentration on the ionic speciation of the LiPF6/EC electrolytes. Fig. 3(a) shows the average speciation as a fraction of total ion population as a function of electrolyte concentration at a fixed temperature of 298.15 K. At lower concentrations (<1 M), the solution is composed predominately of solvated ions pairs (Li+ and PF6−) denoted as solvent-separated ion pairs (SSIP – Fig. 3(b)), solvent-shared ion pairs (SSHIP – Fig. 3(c)), and a small population of neutral contact ion pairs (CIP – Fig. 3(d)). Specifically, at 0.2 M, ∼60% and ∼20% of the Li-ions exist as SSIP and SSHIPs, respectively. As the electrolyte concentration increases, we find that the degree of ion pairing also increases. This trend persists until the concentration reaches 1 M, wherein the total number of free ions (SSIP + SSHIP) reaches a maximum relative to all other concentrations considered. We additionally find that at 1 M, the total number of SSHIPs exceeds that of the SSIPs and the electrolyte exhibits a greater proportion of SSHIPs relative to all other concentrations. The importance of this observation will be discussed in the following sections. At the LiPF6/EC saturation limit (1.72 M), as shown by the vertical dashed line in Fig. 3(a), the ionic speciation within the electrolyte becomes highly diversified, with Li-containing species ranging in size from solvated ion pairs (SSIPs and SSHIPs) to clusters larger than decamers (Li5 (PF6)5, Fig. 3(h)). Here, ∼20% of the Li+ and PF6− ions are fully solvated (SSIP and SSHIP), while the remaining ions are involved in ion pairs or larger clusters. And as anticipated, under supersaturated conditions (>1.72 M22), we observe a marked increase in ionic clustering, for which >80% of the ions within the solution aggregate into clusters, suggesting the onset of particle nucleation. Notably, at concentrations of 4 and 5 M, ions in the SSIP, SSHIP, and CIP configurations become negligible, with the majority (>85%) forming large clusters. An in-depth statistical description of the types of solvation structures and aggregates observed at various concentrations is shown in Fig. S5 (ESI†) and the temperature-dependent speciation in Fig. S6 (ESI†).
In addition, we explore the coupled effect of ion mobility and ion speciation by using the transference numbers (t+) as a potential descriptor to screen electrolytes. Herein, we utilize the traditional Nernst–Einstein (ion mobility) and its variant cluster-Nernst–Einstein (ion mobility and speciation) expression.23 At low concentrations (<1 M), the t+ are similar using the two approaches. However, at high concentrations (>3 M), using the former leads to positive t+ values across all temperature and concentration ranges. Whereas, using the latter originates in t+ < 0 (negative t+ values), shown in Fig. S7 (ESI†). A detailed discussion is shown in Section S7, ESI.† The origins of negative values are due to the negatively-charged aggregates that speciate at high concentrations and low temperatures, resulting in overall negative electrophoretic mobility. This phenomenon is primarily attributed to the assumptions inherent in the classical nature of Nernst–Einstein expression.23 This can be potentially used to address the disparity between the experimentally-observed and simulation-calculated transference numbers in other electrolyte systems.19
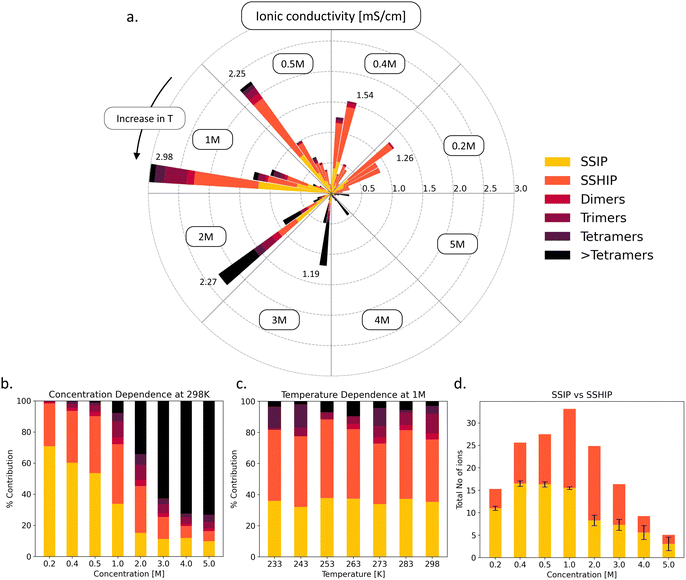
In order to make informed decisions regarding the electrolyte performance at low-temperature, it is imperative that we provide information on the ionic species that drive ionic conductivity. In Fig. 4(a), we present a comprehensive overview of ionic conductivity across various concentrations and temperatures, with a breakdown highlighting conductivity specific to different species present in the electrolyte. At temperatures below 265 K, regardless of concentration, the ionic conductivity remains consistently low, below 0.5 mS cm−1. However, temperatures above 265 K result in moderate conductivity, falling within the 0.5–1.5 mS cm−1 range for low electrolyte concentrations (<1 M). The highest conductivity is observed at 298 K across all concentrations, ranging from 1.27 mS cm−1 for 0.2 M to a maximum at 2.98 mS cm−1 for the 1 M electrolyte concentration. Similar to what was observed for the Li-ion diffusivity (Fig. 1), we find that beyond 1 M, conductivity gradually decreases, reaching 0.29 mS cm−1 at 5 M concentration. Fig. 4(b) and (c) examines the distribution of different species that contribute to the conductivity and their dependencies on salt concentration and temperature. At low electrolyte concentrations (<0.5 M), the majority of ionic conductivity (over 95%) arises from fully solvent-separated ion pairs (SSIP) and solvent-shared ion pairs (SSHIP). At 1 M concentration, which corresponds to peak ionic conductivity of 2.98 mS cm−1, contributions from SSIP and SSHIPs account for 35% and 40% of the overall conductivity, respectively, up to 75% of the total. The remaining conductivity stems from higher-order species like trimers and tetramers. As the concentration increases further (>1 M), the contribution from SSIPs and SSHIPs diminishes, while larger species, such as dimers and trimers, become increasingly significant. At 4 and 5 M electrolyte concentrations, species larger than tetramers dominate (>65%) the overall ionic conductivity, leading to ionic conductivities of 0.44 and 0.29 mS cm−1. This shift is primarily attributed to limited availability and slower transport of charge carriers (Li+) when they are part of larger clusters or aggregates (Fig. S8, ESI†).
To further understand the origins of enhanced conductivity, we examined the total population of SSIPs and SSHIPs as a primary descriptor of conductivity, depicted in Fig. 4(d). As the electrolyte concentration increases from 0.2 M to 1 M, we observe a gradual increase in the number of SSIPs compared to SSHIPs. Specifically, at 1 M concentration, there is an inflection point, where the number of SSHIPs surpasses the number of SSIPs, with the maximum ionic conductivity (2.98 mS cm−1). In addition, we also observe the highest number of SSHIPs. For concentrations >1 M, the population of SSHIPs and SSIPs starts to decline due to a tendency for the ions to form clusters and larger-sized aggregates. This explains why we observe high ionic conductivity at room temperature for the model 1 M LiPF6/EC electrolyte. Also, these charge carriers (SSIP or SSHIP) exhibit fast diffusion across the electrolyte solution (shown in S4 and S8, ESI†). This is reflected at 1 M concentration, where the net average diffusion will be much higher when we maximize the number of ions/clusters that are most diffusive. Beyond 1 M concentration, clustering is observed, and since these clusters are bulkier than SSIP/SSHIPs, they are less diffusive. However, it does not explain why we observe a large temperature-dependent drop in Li-ion diffusivity at 1 M concentration (represented by largest EA in Fig. 1). This drop in diffusivity cannot be explained from an ionic speciation viewpoint since the population of SSIPs and SSHIPs remains consistent across different temperatures (Fig. S9, ESI†). However, in comparison to other concentrations, the solvent (EC) diffusion (Fig. S10, ESI†) and solvent lifetimes within the Li-ion solvation shell (Fig. S11, ESI†) exhibit the largest change over the temperature range. This is quantitatively represented by the large activation barriers for these two processes shown in Table S2 (ESI†) and Table S3 (ESI†). In addition, there is a distinct correlation between the activation barriers of Li-ion diffusion (ELiDiffA), solvent diffusion (ESolDiffA), and solvent lifetimes (ESolLifeA), that are all maximum at 1 M electrolyte concentration. In short, our results show that the large drop in Li-ion diffusivity can be attributed to the large drop in solvent lifetime and diffusivity, which is detailed in Section S12 (ESI†) (Fig. S12, ESI†)
To investigate potential factors dictating the performance of low-temperature electrolytes, we computed the viscosity (η) of the electrolyte and analyzed its response to changes in concentration and temperature, shown in Fig. S13 (ESI†). As the concentration increases, the viscosity of the electrolyte increases. This is due to larger-sized clusters being formed that make the electrolyte much more viscous. Concurrently, as the temperature decreases, we observe a similar trend, where the viscosity tends to increase. These results have been summarized in the form of a Walden plot in Fig. S14 (ESI†). Here, we observe a non-linear change over the concentration and temperature range, thus explaining the reduction in the model electrolyte's low-temperature performance, especially at high electrolyte concentrations.
Clearly, in the low-temperature regime, descriptors that go beyond ionic speciation are required to explain overall performance. These include solvent properties such a solvent viscosity/diffusion and the coupled effect of the ionic speciation and transport using the t+. From this study, we are able to rationalize two key design principles: at room temperature, the prominence of ionic speciation influences overall electrolyte performance, emphasizing the importance of maximizing the number of highly mobile charge carriers. Contrarily, at low temperatures, despite a large population of ionic species, the rate-limiting processes that govern overall electrolyte performance are dominated by solvent transport and the electrolyte viscosity. This understanding and framework can be extended to other electrolyte systems to screen and engineer optimal compositions of electrolytes. The improved understanding resulting from this study will enhance our predictive capability in designing more robust battery electrolytes for lower-temperature (sub-zero) applications.
Conclusions
This work reports progress on understanding the microscopic factors that promote rapid Li-ion transport through bulk electrolytes, wherein we have analyzed the impact of temperature and concentration effects on the structural and transport properties of bulk LiPF6/EC battery electrolytes using classical molecular dynamics simulations. Our simulations reveal that the diffusivity of Li-ions in these electrolytes follows an approximate Arrhenius-like relation, enabling simple and direct comparisons of bulk electrolyte transport behavior through the comparison of effective Arrhenius model prefactors and activation energies. Within this framework, electrolytes with improved low-temperature bulk Li-ion transport can be readily identified as those that exhibit large diffusion prefactors and low activation energies, providing a straightforward comparative approach for screening applications. Structural changes were assessed by calculating radial distribution functions and coordination numbers between Li-ions and other electrolyte species. This analysis revealed the tendency for ion pairing and extended cluster formation to occur at lower temperatures and for higher concentration electrolytes, helping to explain in part the observed decrease in Li-ion diffusivity for nearly-saturated and super-saturated electrolytes. The ionic speciation of these electrolytes was subsequently studied quantitatively, providing key insights into the partitioning of free Li-ions in the form of solvent-separated ion pairs (SSIPs), solvent-shared ion pairs (SSHIPs), neutral contact ion pairs (CIPs), and bound Li-ions in the form of higher order ionic clusters. Leveraging on this information, the ionic conductivities of the LiPF6/EC electrolytes were resolved in terms of each species' individual contribution. This analysis revealed the importance of maintaining high proportions of solvated, single Li-ions within the electrolyte as the overall conductivity appears to be strongly correlated to the total number of SSIPs and SSHIPs in the electrolyte. However, as the operating temperatures drop, overall electrolyte performance is dominated by solvent transport and the electrolyte viscosity.Extension of design principles to 1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) EMC (3
EMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 7)
7)
With the aim of identifying design principles to enable rational design of low-temperature battery electrolytes, we have intentionally studied the model electrolyte LiPF6 in EC given its compositional simplicity. However, this electrolyte is not practical due to its high melting temperature. To highlight the transferability of the design principles identified in this study, we have additionally considered a more realistic electrolyte 1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (3
EMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7), which has a considerably lower melting point, enabling <0 °C operation.19,24 To assess the applicability of the first design principle, we show in Fig. S17 (ESI†) that the number of mobile charge carriers (SSIP + SSHIP) is maximized at 1 M concentration which, as anticipated, coincides with the maximum ionic conductivity (S16, ESI†). Furthermore, our second design principle states the low temperature performance is governed by solvent transport and viscosity. For 1 M LiPF6 in EC
7), which has a considerably lower melting point, enabling <0 °C operation.19,24 To assess the applicability of the first design principle, we show in Fig. S17 (ESI†) that the number of mobile charge carriers (SSIP + SSHIP) is maximized at 1 M concentration which, as anticipated, coincides with the maximum ionic conductivity (S16, ESI†). Furthermore, our second design principle states the low temperature performance is governed by solvent transport and viscosity. For 1 M LiPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (3
EMC (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7), Ringsby et al.19 reported temperature-dependent viscosity that was measured using an electromagnetically spinning viscometer. One of the key conclusions they drew from their findings was that “the dominant factor influencing low-temperature transport is solvent viscosity, rather than ion aggregation or cation transference number”, which strongly supports our second design principle. While this is only a cursory examination of the transferability of the design principles, we find the agreement to be encouraging. Future work will focus on expanding our analysis for realistic electrolytes to better understand their low-temperature performance limitations and rationally explore strategies for remediation.
7), Ringsby et al.19 reported temperature-dependent viscosity that was measured using an electromagnetically spinning viscometer. One of the key conclusions they drew from their findings was that “the dominant factor influencing low-temperature transport is solvent viscosity, rather than ion aggregation or cation transference number”, which strongly supports our second design principle. While this is only a cursory examination of the transferability of the design principles, we find the agreement to be encouraging. Future work will focus on expanding our analysis for realistic electrolytes to better understand their low-temperature performance limitations and rationally explore strategies for remediation.
Implications for bulk electrolyte resistance
The implications for bulk electrolyte resistance and low-temperature battery electrolyte discovery is two fold. From a structural standpoint, ion clustering can have both positive and negative effects on battery performance. Ion clustering can stabilize the electrolyte, reducing the risk of unwanted side reactions.25 However, excessive clustering can lower the population of mobile ions, thereby reducing battery capacity and efficiency. Additionally, uncontrolled clustering may increase solution viscosity and contribute to the electrolyte degradation, potentially leading to cell failure.26 This is particularly vital at low temperatures, where ion transport kinetics face significant constraints, necessitating optimization of charge carrier availability within the electrolyte. From a transport standpoint, these findings underscore the importance of selecting the right concentration and temperature conditions for the electrolyte. Designing electrolytes with tunable concentration profiles that align with the observed trends in diffusion activation barriers and prefactors can lead to more efficient and high-performance batteries in the low-temperature regime. This includes engineering electrolytes that limit aggregate formation, which would otherwise lead to suppressed lithium-ion diffusion and viscosity. Excessive electrolyte concentration is often accompanied by the formation of negatively charged clusters, that results in negative electrophoretic mobility (t+ < 0). Designing electrolytes that promote the generation of more positively charged clusters (t+ ≫ 1) can result in enhanced Li-ion transport and conductivity. Transport of these negatively charged clusters can cause large concentration overpotentials, thereby, limiting the operating voltage and inducing Li plating, causing relatively short battery lifetimes.Implications for interfacial charge transfer resistance
Though this manuscript addresses a critical piece of the puzzle, that is, the structural and transport properties of the bulk electrolyte, a more holistic approach of coupling the electrolyte with other components is required to understand the overall performance at low temperatures. Although, this entails integration of theory (including interfacial systems) and experiments to understand key factors that go beyond the electrolyte, we can tease out important design principles based on ionic speciation that factor both bulk and interfacial charge transfer resistances based on Holoubek et al.21 In the model system studied here, the population of CIPs is maximized at 1 M concentration. Following this hypothesis, we can speculate that at this concentration, we would minimize interfacial charge transfer resistance. Coincidentally, the number of SSIPs are also maximized at 1 M. Therefore, not only are we minimizing the interfacial charge transfer resistances, but we are also minimizing the bulk resistances by maximizing bulk ionic conductivity. Hence, examining the lithium solvation, pairing, and extended clustering through this analysis demonstrates the intricate interplay of concentration and temperature effects on electrolyte structure. In battery systems where interfacial charge transfer resistance is the rate-limiting step rather than solution resistance, it will be beneficial to tune the speciation to favor CIPs, although these species do not contribute to the bulk conductivity. In contrast, when solution resistance dominates, as often occurs at low temperatures, then a more effective strategy would be to tune the solvent viscosity.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344 and was supported by Laboratory Directed Research and Development funding under project number 23-SI-002.References
- A. Gupta and A. Manthiram, Adv. Energy Mater., 2020, 10, 2001972 CrossRef CAS PubMed.
- N. Zhang, T. Deng, S. Zhang, C. Wang, L. Chen, C. Wang and X. Fan, Adv. Mater., 2022, 34, 2107899 CrossRef CAS PubMed.
- S. Zhang, K. Xu and T. Jow, J. Power Sources, 2003, 115, 137–140 CrossRef CAS.
- B. Liu, Q. Li, M. H. Engelhard, Y. He, X. Zhang, D. Mei, C. Wang, J.-G. Zhang and W. Xu, ACS Appl. Mater. Interfaces, 2019, 11, 21496–21505 CrossRef CAS PubMed.
- Q. Wang, C. Zhao, J. Wang, Z. Yao, S. Wang, S. G. H. Kumar, S. Ganapathy, S. Eustace, X. Bai and B. Li, et al. , Nat. Commun., 2023, 14, 440 CrossRef CAS PubMed.
- P. Wróbel, P. Kubisiak and A. Eilmes, J. Phys. Chem. B, 2021, 125, 1248–1258 CrossRef.
- P. Ganesh, D.-e Jiang and P. Kent, J. Phys. Chem. B, 2011, 115, 3085–3090 CrossRef CAS PubMed.
- P. Ganesh, P. Kent and D.-E. Jiang, J. Phys. Chem. C, 2012, 116, 24476–24481 CrossRef CAS.
- M. T. Ong, H. Bhatia, A. G. Gyulassy, E. W. Draeger, V. Pascucci, P.-T. Bremer, V. Lordi and J. E. Pask, J. Phys. Chem. C, 2017, 121, 6589–6595 CrossRef CAS.
- A. Mallarapu, V. S. Bharadwaj and S. Santhanagopalan, J. Mater. Chem. A, 2021, 9, 4858–4869 RSC.
- A. Khetan, H. R. Arjmandi, V. Pande, H. Pitsch and V. Viswanathan, J. Phys. Chem. C, 2018, 122, 8094–8101 CrossRef CAS.
- E. Duboué-Dijon, P. E. Mason, H. E. Fischer and P. Jungwirth, J. Phys. Chem. B, 2017, 122, 3296–3306 CrossRef.
- N. Rampal, H.-W. Wang, D. Biriukov, A. B. Brady, J. C. Neuefeind, M. Předota and A. G. Stack, J. Mol. Liq., 2021, 340, 116898 CrossRef CAS.
- D. Biriukov, H.-W. Wang, N. Rampal, C. Tempra, P. Kula, J. C. Neuefeind, A. G. Stack and M. Předota, J. Chem. Phys., 2022, 156(19), 194505 CrossRef CAS PubMed.
- Z. Yu, N. P. Balsara, O. Borodin, A. A. Gewirth, N. T. Hahn, E. J. Maginn, K. A. Persson, V. Srinivasan, M. F. Toney and K. Xu, et al. , ACS Energy Lett., 2021, 7, 461–470 CrossRef.
- M. I. Chaudhari, J. R. Nair, L. R. Pratt, F. A. Soto, P. B. Balbuena and S. B. Rempe, J. Chem. Theory Comput., 2016, 12, 5709–5718 CrossRef CAS PubMed.
- O. Borodin, L. Suo, M. Gobet, X. Ren, F. Wang, A. Faraone, J. Peng, M. Olguin, M. Schroeder and M. S. Ding, et al. , ACS Nano, 2017, 11, 10462–10471 CrossRef CAS.
- Y. Zhang, I. Bier and V. Viswanathan, ACS Energy Lett., 2022, 7, 4061–4070 CrossRef CAS.
- A. J. Ringsby, K. D. Fong, J. Self, H. K. Bergstrom, B. D. McCloskey and K. A. Persson, J. Electrochem. Soc., 2021, 168, 080501 CrossRef CAS.
- J. Landesfeind and H. A. Gasteiger, J. Electrochem. Soc., 2019, 166, A3079–A3097 CrossRef.
- J. Holoubek, H. Liu, Z. Wu, Y. Yin, X. Xing, G. Cai, S. Yu, H. Zhou, T. A. Pascal and Z. Chen, et al. , Nat. Energy, 2021, 6, 303–313 CrossRef CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- A. France-Lanord and J. C. Grossman, Phys. Rev. Lett., 2019, 122, 136001 CrossRef CAS PubMed.
- E. Logan, E. M. Tonita, K. Gering, J. Li, X. Ma, L. Beaulieu and J. Dahn, J. Electrochem. Soc., 2018, 165, A21 CrossRef CAS.
- S. Choudhury and S. Choudhury, Rational Design of Nanostructured Polymer Electrolytes and Solid-Liquid Interphases for Lithium Batteries, 2019, pp. 199–227 Search PubMed.
- M. McEldrew, Z. A. Goodwin, S. Bi, A. A. Kornyshev and M. Z. Bazant, J. Electrochem. Soc., 2021, 168, 050514 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee01437e |
| This journal is © The Royal Society of Chemistry 2024 |