Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A “seat-squatting” strategy via lithium substitution to suppress Fe-migration in Na layered oxide cathodes†
Yaoshen
Niu
 ab,
Zilin
Hu
a,
Huican
Mao
*c,
Lin
Zhou
a,
Liguang
Wang
ab,
Zilin
Hu
a,
Huican
Mao
*c,
Lin
Zhou
a,
Liguang
Wang
 d,
Xiaobing
Lou
e,
Bo
Zhang
f,
Dongdong
Xiao
a,
Yang
Yang
d,
Xiaobing
Lou
e,
Bo
Zhang
f,
Dongdong
Xiao
a,
Yang
Yang
 a,
Feixiang
Ding
a,
Xiaohui
Rong
*g,
Juping
Xu
h,
Wen
Yin
a,
Feixiang
Ding
a,
Xiaohui
Rong
*g,
Juping
Xu
h,
Wen
Yin
 h,
Nian
Zhang
i,
Zhiwei
Li
f,
Yaxiang
Lu
h,
Nian
Zhang
i,
Zhiwei
Li
f,
Yaxiang
Lu
 a,
Bingwen
Hu
a,
Bingwen
Hu
 e,
Jun
Lu
d,
Ju
Li
e,
Jun
Lu
d,
Ju
Li
 *j and
Yong-Sheng
Hu
*j and
Yong-Sheng
Hu
 *a
*a
aKey Laboratory for Renewable Energy, Beijing Key Laboratory for New Energy Materials and Devices, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, The College of Materials Sciences and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100190, China. E-mail: yshu@iphy.ac.cn
bFrontier Institute of Science and Technology, Xi’an Jiaotong University, Xi’an 710049, China
cDepartment of Energy Storage Science and Engineering, School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China. E-mail: hcmao@ustb.edu.cn
dChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL, USA
eShanghai Key Laboratory of Magnetic Resonance, State Key Laboratory of Precision Spectroscopy, School of Physics and Electronic Science, East China Normal University, Shanghai 200241, P. R. China
fKey Lab for Magnetism and Magnetic Materials of the Ministry of Education, Lanzhou University, Lanzhou 730000, China
gYangtze River Delta Physics Research Center Co. Ltd, Liyang, 213300, China. E-mail: rongxiaohui@ioply.cn
hSpallation Neutron Source Science Center, Dongguan 523803, China
iState Key Laboratory of Functional Materials for Informatics, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, People's Republic of China
jDepartment of Nuclear Science and Engineering and Department of Materials Science and Engineering, MIT, Cambridge, MA 02139, USA. E-mail: liju@mit.edu
First published on 20th September 2024
Abstract
Na-ion batteries (NIBs) are emerging as a promising alternative to Li-ion batteries (LIBs). To align with sustainability principles, the design of electrode materials must incorporate considerations for abundant and environmentally friendly elements, such as redox-active Fe. Despite its appeal, the enduring challenge of Fe migration in layered cathodes remains inadequately addressed over decades. Here, we propose a “seat-squatting” strategy via Li-substitution to fundamentally suppress Fe migration. Li is strategically introduced to migrate first, occupying available migration sites without inducing structural damage and effectively raising the activation energy for Fe migration. Experimental and theoretical validation using O3-Na0.83Li0.17Fe0.33Mn0.5O2 (NaLFM) demonstrates a robust suppression of irreversible Fe migration. As a result, the NaLFM cathode delivers enhanced structural and electrochemical cycling stability. This work illustrates a compelling strategy to curb irreversible Fe migration in NIBs, offering a pathway for the development of stable and cost-effective layered oxides based on Fe redox centers.
Broader contextTransition metal-based cathode materials play a pivotal role in advancing rechargeable battery technologies, particularly for applications in electric vehicles and grid-scale energy storage systems. Among these, Fe, abundant in Earth's crust, stands out for its potential in enhancing the cost competitiveness of batteries. While LiFePO4 has been widely adopted, the emergence of Na-ion batteries (NIBs) presents an opportunity to leverage Fe's advantages further. However, Fe-containing cathodes in NIBs face challenges such as Jahn–Teller distortion and migration issues, compromising their performance and durability. Despite efforts to understand Fe migration, existing strategies often prioritize reducing Fe content or resort to costly element substitutions, undermining the goal of maximizing Fe utilization. Addressing this gap, our study introduces a novel ‘seat-squatting’ strategy through lithium substitution to fundamentally suppress Fe migration in NIB cathodes. Through computational simulations and experimental validation, we demonstrate that Li incorporation within the cathode structure effectively impedes Fe migration, leading to enhanced structural stability and battery performance. Our findings highlight the potential of this approach in enabling the development of stable and cost-effective Fe-based cathode materials for next-generation NIBs, paving the way for sustainable energy storage solutions. |
Introduction
The abundance of Fe, a multi-valent transition metal, in Earth's crust makes it ideal for rechargeable batteries. LiFePO4, for example, is a popular cathode material for use in electric vehicles and grid-scale energy storage systems due to its exceptional performance and low cost.1,2 Na-ion batteries (NIBs) have emerged as contenders to replace lithium-ion batteries (LIB), inheriting many of the desirable traits of LIBs.3–5 To maximize cost competitiveness, it is desirable to increase the concentration of Fe as the redox center in NIB cathodes.6,7 However, Fe-containing layered cathodes typically exhibit a Jahn–Teller (J–T) distortion and migration issues, which can jeopardize the layered structure, leading to reduced capacity and cycle life.8–13 Consequently, the development of effective NIB cathodes hinges on finding strategies to impede iron migration.It is intriguing that, despite the numerous reports on NIB cathodes, the research on Fe migration has primarily focused on confirming its existence, with limited efforts invested in developing effective mitigation strategies.8,12,14,15 Among the existing literature, computational studies have pinpointed that local Fe enrichment and the Jahn–Teller (J–T) effect of Fe4+O6 are the key factors triggering Fe migration.16–18 Conversely, other studies have centered on reducing Fe content through substitution to minimize structural damage arising from Fe migration.19–28 This approach represents a reversal of priorities, as NIB cathodes should ideally maximize Fe utilization, rather than resorting to the use of more expensive elements like Ni and Co for substitution. Boivin et al. recently reported that Mg substitution can enhance the oxidation degree of Fe3+, effectively limiting the amount of Fe3+ that can migrate at high voltages. Furthermore, the reversible migration of Mg can delay the P–O phase transition, thereby suppressing Fe migration.29 However, this method has its limitations, including the instability of Fe4+ and its susceptibility to being reduced to Fe3+ by the electrolyte.8 Moreover, the limited mobility of Mg does not provide a long-term solution.30
In this study, we introduce a facial “seat-squatting” strategy by Li-substitution to fundamentally suppress Fe migration. Our density functional theory (DFT) calculations demonstrate that the inclusion of smaller Li within the Na layer significantly increases the activation energy for Fe migration. To validate our hypothesis, we synthesized O3-Na0.83Li0.17Fe0.33Mn0.5O2 (NaLFM) and compared it with our previously reported O3-Na0.83Mg0.33Fe0.17Mn0.5O2 (NaMFM), which contains half the Fe content yet experiences Fe migration.30 A comprehensive analysis, combining operando X-ray diffraction (XRD), 57Fe-Mössbauer spectroscopy (Fe-MS), and 7Li solid-state nuclear magnetic resonance (ssNMR) experiments, unequivocally demonstrates the effective suppression of the irreversible migration of Fe from an octahedral site in the transition metal (TM) layer to a tetrahedral site in the Na layer during deep desodiation in NaLFM. This suppression is accompanied by excellent structural stability. Our proposed strategy is substantiated by nudged elastic band (NEB) calculations. The O3-NaLFM exhibits a higher half-cell reversible capacity of ∼220 mA h g−1 at 10 mA g−1, and the NaLFM/hard carbon full cell delivers an impressive specific energy of up to 270 W h kg−1 (total mass of cathode and anode active materials) with 93% and 85% capacity retention after 100 and 200 cycles, respectively. Our work underscores the potential of Li's “seat-squatting” effect for NIBs, providing an effective means to suppress irreversible Fe migration. This strategy opens the door to the development of more stable and cost-effective layered oxides based on Fe redox centers through the “seat-squatting” approach.
Results
Design criteria for the “seat-squatting” strategy
In this work, we have pursued a “seat-squatting” strategy, and the objective is to identify an element that can migrate more readily than Fe but, critically, without causing significant structural damage. In essence, we seek an element with similar ionic radii but a lower valence than the transition-metal cations, thereby increasing the activation energy required for Fe migration and, in turn, addressing the challenge of Fe migration.Studies have shown that LiTM (Li in transition metal layer) in Li-rich materials migrates to the alkali layer during charging, and, under specific local conditions, Li migration can occur without encountering an activation barrier.31 Furthermore, investigations into NIBs have uncovered instances of reversible LiTM migration between the transition metal (TM) layer and the Na layer.32,33 Drawing inspiration from these findings, we posit that Li may be the ideal candidate to implement the “seat-squatting” strategy. Specifically, Li is more readily incorporated into the TM sites due to its small ionic radius.34 Additionally, the migration of Li is not expected to cause significant alterations to the original structure, primarily due to its smaller radius and +1 valence.33,35 Moreover, reversible hopping of lithium ions between TM layers and Na layers at high voltages can effectively stabilize the host structure after a high-level sodium deintercalation process.34,36–40
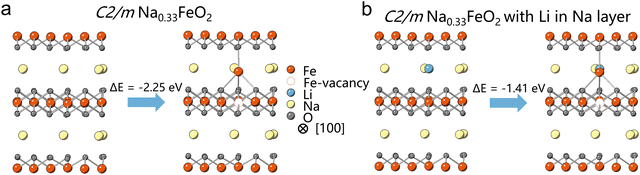
To explore the “seat-squatting effect” of Li+, we conducted initial energy calculations on C2/m Na0.33FeO2 and Li-substituted Na0.33FeO2 systems, where Li+ was introduced at the tetrahedral site of the Na layer.16 Our calculations indicate that the energy barrier for Fe migration from an octahedral site in the TM layer to a tetrahedral site in the Na layer of Na0.33FeO2 is lower than that of Li-substituted Na0.33FeO2 (Fig. 1 and Fig. S1, ESI†). This suggests that Li+ occupying the tetrahedral site in the Na layer can raise the energy barrier for Fe migration, implying that LiTM may have the capability to impede Fe migration in layered oxides like NaFeO2. Our energy calculations have thus established the feasibility of the “seat-squatting” strategy, motivating us to extend our hypothesis to experimental scenarios.
 | ||
| Fig. 1 Energy calculation of Fe-migration's energy barrier on (a) C2/m Na0.33FeO2 and (b) Li-substituted Na0.33FeO2. | ||
Lithium occupancy
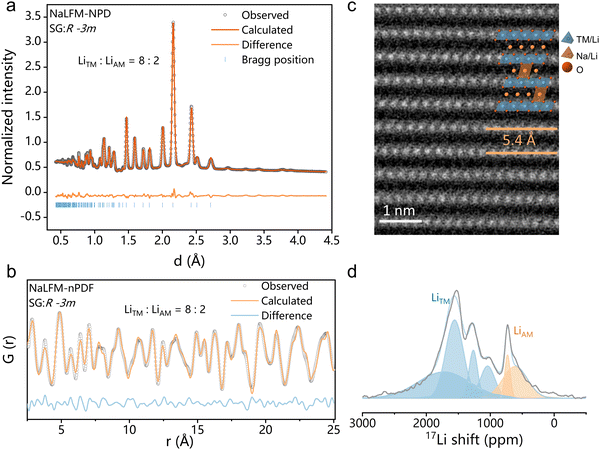
The crystal structure of NaLFM was analyzed by neutron powder diffraction (NPD) and neutron pair distribution function (nPDF) measurements and refined using the Rietveld method. As shown in Fig. 2(a), the NPD patterns perfectly match the O3-type NaFeO2 structure with a space group (SG) of R![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m. The NPD refinement yielded a chemical composition of Na0.83Li0.17Fe0.33Mn0.5O2, which aligns with the results obtained from inductively coupled plasma optical emission spectroscopy (Na0.84Li0.16Fe0.34Mn0.52O2), as presented in Table S1 (ESI†). The nPDF results for NaLFM, illustrated in Fig. 2(b), were refined using the O3 structure as the model, and the outcomes are consistent with those from the NPD patterns. The refinement resulted in an Rw value of 17.753%, as listed in Table S3 (ESI†). The refined lattice parameters for the NaLFM sample are a = 2.9445 Å and c = 16.3372 Å, signifying that the distance between neighboring transition metal (TM) layers is ∼5.45 Å. This value corresponds to the measurement from the HAADF-STEM image (Fig. 2(c)). The results of both NPD and nPDF Rietveld refinements (Table S3, ESI†) reveal that ∼80% of Li ions occupy the TM sites, while the remaining 20% of Li ions are located in the alkali metal (AM) sites within NaLFM. These findings are strongly supported by the resonance observed at ∼650 ppm, corresponding to the presence of Li in the AM sites, as indicated by 7Li solid-state pj-MATPASS magic-angle spinning (MAS) nuclear magnetic resonance (NMR) spectroscopy (Fig. 2(d)). To emphasize the Li distribution, the molecular formula of NaLFM will be referred to as Na0.83Li0.035[Li0.132Fe0.33Mn0.5]O2, where the Li elements inside the square brackets represent those located in the TM layers, and the Li element outside the square brackets corresponds to those situated in the AM layers. Fig. S3 (ESI†) displays the EDS mapping results of NaLFM, while Fig. S4 (ESI†) shows the EELS mapping of Li. These analyses reveal the homogeneous distribution of Na, Li, Fe, Mn, and O ions within the particles. The SEM image (Fig. S5, ESI†) demonstrates that the sample mainly consists of micrometric platelets, displaying a lamellar structure commonly observed in layered O3 cathode materials.30 The surface appears clean and smooth, indicating good crystallization of the particles. The crystal structure of NaMFM is shown in Fig. S2 and Table S2 (ESI†).
m. The NPD refinement yielded a chemical composition of Na0.83Li0.17Fe0.33Mn0.5O2, which aligns with the results obtained from inductively coupled plasma optical emission spectroscopy (Na0.84Li0.16Fe0.34Mn0.52O2), as presented in Table S1 (ESI†). The nPDF results for NaLFM, illustrated in Fig. 2(b), were refined using the O3 structure as the model, and the outcomes are consistent with those from the NPD patterns. The refinement resulted in an Rw value of 17.753%, as listed in Table S3 (ESI†). The refined lattice parameters for the NaLFM sample are a = 2.9445 Å and c = 16.3372 Å, signifying that the distance between neighboring transition metal (TM) layers is ∼5.45 Å. This value corresponds to the measurement from the HAADF-STEM image (Fig. 2(c)). The results of both NPD and nPDF Rietveld refinements (Table S3, ESI†) reveal that ∼80% of Li ions occupy the TM sites, while the remaining 20% of Li ions are located in the alkali metal (AM) sites within NaLFM. These findings are strongly supported by the resonance observed at ∼650 ppm, corresponding to the presence of Li in the AM sites, as indicated by 7Li solid-state pj-MATPASS magic-angle spinning (MAS) nuclear magnetic resonance (NMR) spectroscopy (Fig. 2(d)). To emphasize the Li distribution, the molecular formula of NaLFM will be referred to as Na0.83Li0.035[Li0.132Fe0.33Mn0.5]O2, where the Li elements inside the square brackets represent those located in the TM layers, and the Li element outside the square brackets corresponds to those situated in the AM layers. Fig. S3 (ESI†) displays the EDS mapping results of NaLFM, while Fig. S4 (ESI†) shows the EELS mapping of Li. These analyses reveal the homogeneous distribution of Na, Li, Fe, Mn, and O ions within the particles. The SEM image (Fig. S5, ESI†) demonstrates that the sample mainly consists of micrometric platelets, displaying a lamellar structure commonly observed in layered O3 cathode materials.30 The surface appears clean and smooth, indicating good crystallization of the particles. The crystal structure of NaMFM is shown in Fig. S2 and Table S2 (ESI†).
Electrochemistry and redox mechanisms
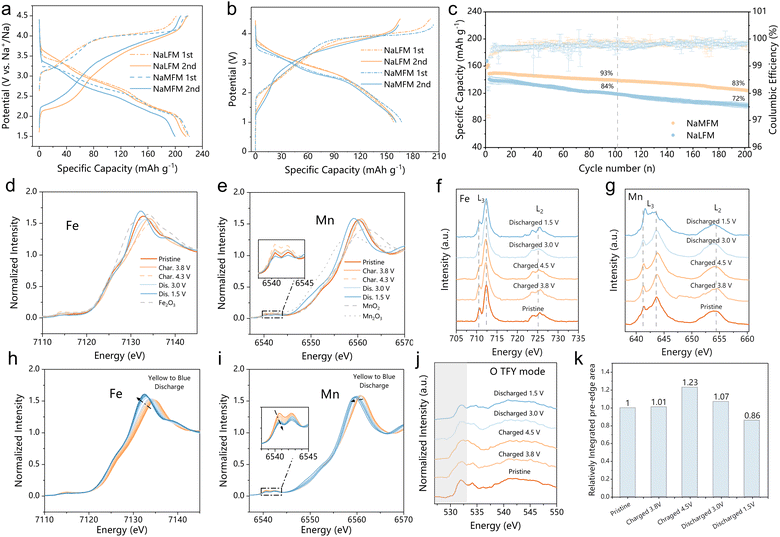
Electrochemical analyses were performed in both half-cells (Fig. 3(a) and Fig. S6, ESI†) and in full-cells (Fig. 3(b) and (c)) using hard carbon as the negative electrode (see Fig. S7 for hard carbon profile, ESI†). In the half-cell setup, the initial two galvanostatic charge/discharge profiles of NaLFM and NaMFM cathodes were examined at a current density of 10 mA g−1 within a voltage range of 1.5–4.5 V (Fig. 3(a)). Both cathodes displayed a characteristic voltage plateau during the initial charge, resulting in a capacity of approximately 200 mA h g−1, corresponding to the removal of about 0.8 Na+ ions per formula unit. While the discharge capacities were similar, the discharge profiles of NaLFM and NaMFM revealed subtle differences. Notably, NaMFM exhibited higher polarization during charge and discharge, indicating a more significant energy penalty during the deintercalation/intercalation process. Additionally, NaMFM experienced pronounced capacity decay after the second discharge due to irreversible phase changes caused by Fe migration during initial charging (Fig. S6, ESI†).30 The NaLFM thus delivers much better capacity retention than NaMFM after 50 cycles. To evaluate materials in practical applications and mitigate the impact of the unstable solid–electrolyte interface (SEI) on the Na anode, full-cell tests using a hard carbon negative electrode were conducted. The voltage versus specific capacity profiles for NaLFM and NaMFM full cells over the initial two cycles at a current of 10 mA g−1 are shown in Fig. 3(b), illustrating capacity loss and increased polarization in the case of NaMFM. NaLFM cathodes demonstrated enhanced cycling performance, retaining 93% and 85% of their capacities after 100 and 200 cycles, respectively, compared to NaMFM cathodes, which retained 85.5% after 100 cycles and 72% after 200 cycles (Fig. 3(c)). Furthermore, NaLFM electrodes exhibited higher and more stable energy efficiency than NaMFM electrodes (Fig. S8, ESI†). These results highlight the effectiveness of Li substitution in inhibiting Fe migration, preserving structural integrity, and providing NaLFM with excellent electrochemical performance during Na+ intercalation/deintercalation.To elucidate changes in the electronic structure and local environment of NaLFM, K-edge X-ray absorption near edge structure (XANES) and soft X-ray absorption structural (sXAS) spectra were obtained at Fe- and Mn-L2,3 edges in total electron yield (TEY) modes at various charge/discharge states in the first cycle. Fig. 3(d) and (e) show the normalized Fe and Mn K-edge XANES spectra at different charge and discharge states. The Fe K-edge shift indicates a valence change from +3 to a higher value, in line with the observed shift in the Fe L-edges (Fig. 3(f)). In contrast, the Mn K-edge showed minimal changes, signifying distortions in the MnO6 octahedra rather than variations in the oxidation state.41,42Fig. 3(g) demonstrates that the Mn L-edge sXAS remains unchanged during 1st charging, indicating the maintenance of Mn ions in their Mn4+ states upon Na+ deintercalation. Upon discharging to 1.5 V, both Mn K-edge and Mn L3-edge peaks shifted to lower energy regions compared to the fresh electrode, implying a reduction in Mn valence. The Fe K-edge and L-edge shifts exhibited high reversibility throughout the charge–discharge process.
Operando X-ray absorption spectroscopy (XAS) was employed to investigate changes in the electronic structure of Fe and Mn during the first discharge of NaLFM. As the voltage decreased to 2.6 V (Fig. 3(h) and (j)), the Fe K-edge shifted to lower energy by 3.8 eV, implying a reduction of Fe. Further discharge to 1.5 V showed negligible changes in the Fe XANES spectra, suggesting no further reduction at this voltage region. In contrast, operando Mn K-edge XANES spectra (Fig. 3(j)) exhibited significantly different behavior. Mn ion oxidation states remained stable until 2.6 V, beyond which they gradually reduced, as indicated by the decreased half-height of the lower energy pre-edge (Fig. S10, ESI†). Notably, we used the half-height of a lower energy peak located at the Mn K pre-edge of the standard manganese-based compounds for this study, due to Mn K-edge spectrum's inherent complexity, direct differentiation of Mn ion oxidation states through absorption edge shifting is difficult.41,43 This particular peak was chosen as an indicator due to its strong linear correlation (correlation coefficient of 0.9, as shown in Fig. S11, ESI†) with the valence state of Mn, thus serving as a reliable means to assess Mn oxidation states. These findings suggest that Fe and Mn alternately contribute to capacity during the first discharge, with oxygen reduction also playing a role in charge compensation, as evident from the transfer of nearly 0.46 electrons above 2.6 V (approximately 125 mA h g−1), whereas Fe can only provide a maximum of 0.33 electrons (approximately 90 mA h g−1).
O K-edge spectra were measured in total electron yield (TEY, probing up to ∼5 nm) modes and total fluorescence yield (TFY, probing up to ∼100 nm) of sXAS to explore the involvement of oxygen redox in charge compensation (Fig. S12 (ESI†) and Fig. 3(j)). Na2CO3 had a peak of 533.5 eV in the O–K edge spectra, which vanished during charging and reappeared at 1.5 V in both TEY and TFY modes.44 The peaks observed at 529.5 and 532 eV correspond to the unoccupied Fe/Mn 3d-O 2p t2g and eg* hybridized states, respectively. Upon charging from OCV to 4.5 V, the density of unoccupied states just above the Fermi level increased continuously, whereas during the reverse discharge, the density of unoccupied states declined continuously, suggesting the reduction of O anions. The integrated area under the O K-edge pre-edge (528 to 533 eV) at different stages during the first cycle was compared in the TFY mode (Fig. 3(k)). The pre-edge peak area increased while charging, demonstrating an increase in O 2p holes and the average effective charge, indicating oxygen's charge compensation role. During discharge, the integrated area of the pre-edge peak decreased, suggesting the high reversibility of oxygen anion-redox in NaLFM. The O K-edge sXAS spectra demonstrated that NaLFM exhibited reversible oxygen anion-redox throughout the voltage range during charge and discharge, thus together with TM redox, making this a hybrid anion- and cation-redox (HACR) cathode.45 Furthermore, the effect of Li substitution in active anion-redox reactions (ARR) was investigated further using density of states (DOS) calculations (Fig. S13, ESI†). The results revealed that Li-substituted samples have a higher anionic redox activity of O2−/O−.
Lithium substitution suppresses Fe migration
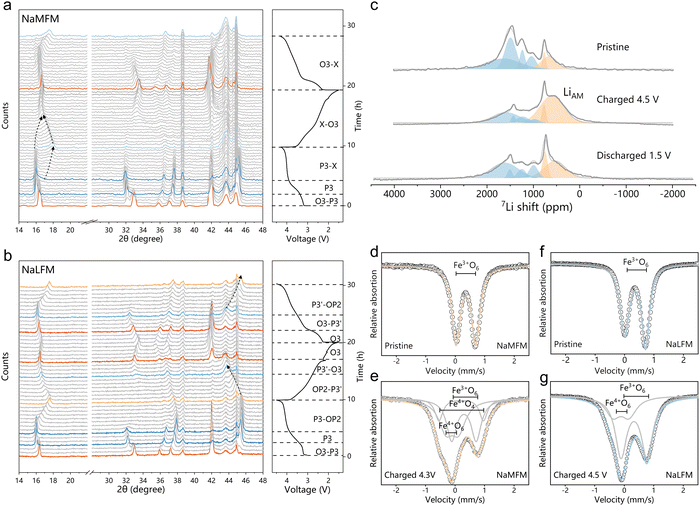
To investigate the impact of Li+ on structural changes in Na-half cells, we conducted operando XRD analysis on both NaMFM and NaLFM (Fig. 4(a) and (b)). Up to 3.8 V, NaMFM and NaLFM display nearly parallel phase evolution. However, beyond 3.8 V, more complex structural transitions occur in NaMFM compared to the more straightforward evolution in NaLFM. In the case of NaMFM cycled beyond 3.8 V, a distinctive peak emerges around 17° and shifts to a higher angle as Na is removed. This indicates a reduction in the c lattice parameter, and all of the peaks are broadened as Na is removed. As we previously reported, this phase is assigned to the “X” phase, comprising P3 and the fully desodiated O1 phase with Fe migration.30 Fe migration significantly reduces the unit-cell volume,which is detrimental to the cycle stability. In contrast, NaLFM shows a smoother transition from P3 to OP2 over the same voltage range. The P3(00l) peaks shift to higher angles with slightly reduced intensity. Importantly, most P3-associated peaks remain after charging, indicating fewer O-type stacking faults in the OP2 phase. We attribute the structural failure and capacity loss to volume contraction and crystallinity loss due to Fe migration. Here, the large amount of P3 phase retention in the material means that the O-type stacking faults available for Fe migration are reduced, thereby limiting the migration of Fe. Moreover, the preserved crystallinity and lower c-axis contraction suggest better structural reversibility. This suggests that Li's easier migration plays a key role in dampening the effects of Na removal and blocking Fe migration, resulting in a gentler phase transition for NaLFM during charging.To verify our hypotheses and gain a comprehensive understanding of Li and Fe migration during Na (de)intercalation, we performed ex situ7Li pj-MATPASS NMR and 57Fe-Mössbauer spectroscopy. Fig. 4(c) illustrates changes in Li's local environment during Na (de)intercalation. We observe two major resonance clusters: one centered around 1000–1750 ppm representing Li sites in the transition metal layer (LiTM), and the splitting into four lines at 1712 ppm (LiTM1), 1544 ppm (LiTM2), 1250 ppm (LiTM3) and 1300 ppm (LiTM4) probably stem from the varied Fe:Mn ratio of surrounding TMO6 (TM = Fe,Mn) octahedron.46 In addition, the minor resonance at ∼650 ppm is assigned to Li sites in the AM layer, and the splitting into two lines at 719 ppm (LiAM1), 610 ppm (LiAM2).33,47 As charging progresses, the LiTM peak decreases, while the broad peak at ∼610 ppm, assigned to migrated Li+ in the AM plane (LiAM2), grows.31,36,48 The LiAM2 could be attributed to Li+ ions in the O-type layers of the high-voltage “OP2” phase (potentially occupying both octahedral and tetrahedral sites49), a formation corroborated by operando XRD characterizations. The out-of-plane migration of Li ions is largely reversible, as the LiAM2 peak fades away upon discharge and the LiTM peak regains dominance.
Fig. 4(d) and (e) presents the 57Fe-Mössbauer spectroscopy of NaMFM and NaLFM samples at different charge states, with fitted parameters listed in Table 1. The pristine samples exhibit similar spectra with an isomer shift of ∼0.36 mm s−1 and a quadrupolar splitting of ∼0.70 mm s−1, indicative of high-spin Fe3+ in an octahedral environment. Charged materials are fitted with three components. The main component represents Fe3+O6 in an octahedral environment with a lower isomer shift (∼0.30 mm s−1) and a larger quadrupolar splitting (∼0.85 mm s−1) than its pristine counterpart. The former is due to the covalency of the M–O bond increasing upon deintercalation, which increases the electron density at iron nuclei,50 the latter is due to the distorted local environment.51 Due to the non-centrosymmetry of its ligand environment, the second component with an isomer shift of 0.20 mm s−1 and a high quadrupolar splitting of 1.5 mm s−1 is assigned to Fe3+O4 (tetrahedral coordination).12 The third component, with an isomer shift close to zero and a quadrupolar splitting of ∼0.5 mm s−1, aligns with Fe4+O6 in layered oxides.
| Component | IS (mm s−1) | QS (mm s−1) | Area (%) | ||
|---|---|---|---|---|---|
| NaMFM | Pristine | Fe3+O6 | 0.3628 | 0.6665 | 100 |
| Charged 4.3 V | Fe3+O6 | 0.3019 | 0.8260 | 42.19 | |
| Fe4+O6 | −0.0943 | 0.4287 | 38.92 | ||
| Fe3+O4 | 0.2081 | 1.5110 | 18.89 | ||
| NaLFM | Pristine | Fe3+O6 | 0.3630 | 0.7114 | 100 |
| Charged 4.5 V | Fe3+O6 | 0.3309 | 0.8817 | 70.53 | |
| Fe4+O6 | −0.1114 | 0.5491 | 29.47 | ||
| Fe3+O4 | — | — | 0 |
Comparing fully charged NaMFM and NaLFM samples, NaMFM exhibits clear Fe migration, while NaLFM does not. Combined with the 7Li pj-MATPASS NMR results, all the phenomena strongly suggested that Li, who is more easily able to migrate than Fe, has grabbed the migratable site from Fe during charge, thereby inhibiting the migration of Fe. Furthermore, Li ion out-of-plane migration is mostly reversible, resulting in gentler structural changes. Additionally, migrated Li atoms during charging release repulsive forces between neighboring oxygen layers, anchoring the adjacent TM layer to prevent further P to O transformations and minimize volume changes.
Discussion
“Seat-squatting” mechanism
In the investigation of Fe and Li migration behaviors in the O-type layers of the high-voltage “OP2” phase in de-sodiated NaLFM, we employed computational methods, specifically the bond-valence (BV)38,39 and nudged elastic band (NEB) methods,40,41 as outlined in the Methods section. Initially, the BV-based method was utilized to identify potential ionic transportation channels. As depicted in Fig. 5(a), the calculated isosurfaces of potential energies in de-sodiated NaLFM illustrate continuous networks for Li and Fe ions, delineating migration pathways that connect Fe and Li ions from an octahedral site in the TM layer to a tetrahedral site in the Na layer.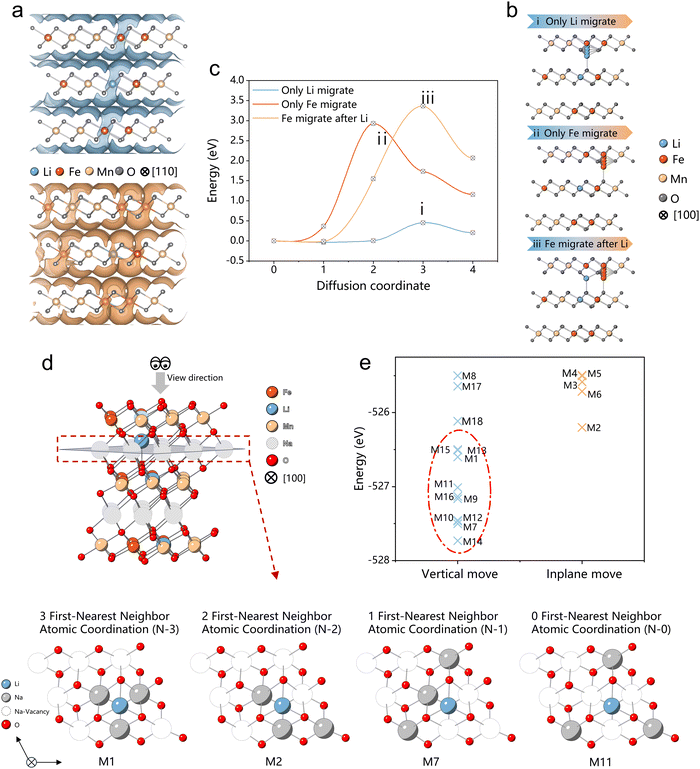 | ||
| Fig. 5 Theoretical calculations (a) bond-valence (BV) calculation of migration channels for Li and Fe ions, (b) illustration of three different migration scenarios for nudged elastic band (NEB) calculations, and the (c) corresponding activation energy. (d) The Illustration example of four different Na arrangement scenarios (N-3, N-2, N-1, and N-0) for Na0.33Li0.17Fe0.33Mn0.5O2, along with additional N-3, N-2, N-1, and N-0 configurations as depicted in Fig. S13 (ESI†). The 9 Na ions in the Na layer are divided into two groups based on their proximity to the Li ion: the first-nearest neighbor positions, containing three Na ions, and the non-first-nearest neighbor positions, comprising six Na ions. N-3/N-2/N-1/N-0 configurations require three/two/one/zero Na ions to be positioned at the first-nearest neighbor positions of the Li ion, while the remaining Na ions are situated at non-first-nearest neighbor positions. (e) Calculated total energies of 18 configurations for Na0.33Li0.17Fe0.33Mn0.5O2, with a total of 18 unique configurations calculated out of all 84 non-symmetry-equivalent configurations. | ||
To delve deeper into the kinetic properties uncovered by the BV method, we conducted NEB calculations to determine activation energies for the aforementioned hopping pathway of Fe and Li ions. The calculated barrier shapes and corresponding activation energies for Fe and Li ions are depicted in Fig. 5(b) and (c). Our computations reveal that the activation energy of Li+ (0.45 eV) is significantly lower than that of Fe3+ (3.0 eV), indicating that Li+ is more prone to migration than Fe3+. Furthermore, once Li+ migrates to the tetrahedral site in the Na layer, the activation energy for Fe3+ to migrate increases by 0.5 eV, making it more challenging for Fe3+ to move. Additionally, as the number of Li ions occupying tetrahedral sites increases, the available tetrahedral sites in the Na layer decrease, further impeding Fe migration. Our theoretical calculations confirm that Li ions impede Fe migration, thereby enhancing the performance of Na-ion cathodes.
Li reversibility
Upon the release of Na ions, Li ions migrate from the octahedral center of the transition metal layer to the tetrahedral center of the Na ion layer, effectively impeding the migration of transition metal Fe ions. A pivotal question arises: can these Li ions undergo reversible migration back to the transition metal layer during the discharge process, and if so, to what extent? To address this inquiry, we conducted theoretical calculations. To simulate the migrated Li's behavior during the discharge process, we meticulously selected and analyzed 18 typical Na ion configurations for Na0.33Li0.17Fe0.33Mn0.5O2, as depicted in Fig. S16 (ESI†). These 18 configurations were further categorized into four structure types based on the number of Na ions occupying the Li's first-nearest neighbor positions: 3 first-nearest neighbor (N-3), 2 first-nearest neighbor (N-2), 1 first-nearest neighbor (N-1), and 0 first-nearest neighbor (N-0) atomic coordination.Following structure optimization, it was observed that all N-3, N-1, and N-0 configurations exhibited a tendency for Li ions to reoccupy the octahedral positions within the transition metal (TM) layer, while only one structural type, N-2, demonstrated a propensity for Li ions to remain within the Na layer. The calculation results underscore that, during the discharging process, the arrangement of Na ion configurations, linked to the Coulombic repulsion magnitude, plays a pivotal role in determining the reversibility of Li ions. Among the aforementioned Na ion configurations, the lower energy configurations were associated with N-3, N-1, and N-0, while N-2 configurations exhibited higher energy levels (Fig. 5(e)). This observation suggests that, in the context of the discharging process, the formation of N-3, N-1, and N-0 configurations is more favorable, thereby facilitating the reversible migration of Li ions between the TM layer and Na layer.
Based on our experimental and computational findings, Li has proven to play a pivotal role in effectively suppressing Fe migration in the cathode. Moreover, the migration of Li exhibits a remarkably high degree of reversibility. Additionally, regarding the small fraction of Li that remains in the sodium (Na) layer, it can continue to serve as a pillar to back-stop the inter layer gliding. However, this approach is not without inherent challenges that require attention. For example, the small amount of migrated Li residue may be depleted upon Na deintercalation in very-high voltage regions (refer to ICP results in Table S4, ESI†), and Li migration may also result in oxygen loss,35 limiting the cycle life somewhat at very high charging voltages.
In this study, we propose a simple yet potent approach to restrain Fe migration in the cathode, leveraging Li's natural ability to inhibit Fe migration in layered oxides undergoing O-type phase transitions. For practical applications, since Li acts as an inert dopant and does not contribute to capacity, the optimal Li/Fe ratio needs to be optimized based on the specific composition to achieve an ideal balance among cost, capacity, and cycling stability. Therefore, when designing layered cathode materials using the cost-effective Fe as the redox center, pairing it with Li is an excellent choice, as not a lot of Li is needed to stabilize the heavily desodiated structure.
Conclusion
Our proposed “seat-squatting” strategy to mitigate Fe migration, which involves utilizing the more mobile Li ions to precede Fe migration, thereby occupying the available migration sites and increasing the activation energy for Fe migration, was validated through theoretical calculations and detailed experiments. This approach fundamentally suppresses Fe migration and improves the performance of the NIB cathode material.The O3-type NaLFM has shown a remarkable full cell specific capacity of ∼170 mA h g−1 and excellent cycling stability, maintaining 85% of its initial capacity after 200 cycles. In contrast to O3-NaMFM, our experimental results indicate that there is no Fe migration in the O3-NaLFM system, even though its Fe content is twice that of the control material O3-NaMFM, as confirmed by operando XRD and 57Fe-Mössbauer spectroscopy. Solid-state 7Li NMR experiments also demonstrate the reversibility of Li migration. Our experiments suggest that the “seat-squatting” effect of Li effectively suppresses Fe migration. Furthermore, BV and DFT calculations theoretically support our findings, indicating that Li is more likely to migrate than Fe and that Fe migration becomes more difficult after Li migration.
In this work, we proposed a simple yet effective strategy to solve the long-standing issue of Fe migration, thereby redirecting the research emphasis of layered Na-ion battery cathodes back to Fe as the redox center and paving the way for the development of high-performance and cost-effective Na-ion cathodes.
Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in N-methyl-2-pyrrolidone onto an Al foil. The loading mass of active material in each electrode pellet of 10.0 mm in diameter was 3–4.0 mg cm−2. HC anodes were prepared by spreading a slurry consisting of hard carbon (HC), sodium alginate binder, and acetylene black (92
1 in N-methyl-2-pyrrolidone onto an Al foil. The loading mass of active material in each electrode pellet of 10.0 mm in diameter was 3–4.0 mg cm−2. HC anodes were prepared by spreading a slurry consisting of hard carbon (HC), sodium alginate binder, and acetylene black (92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) on Al foil for full cells, with approximately 2.5 mg cm−2 of active anodes. After drying at 100 °C under vacuum for 12 hours, the electrodes were fabricated into CR2032 coin-type cells in an argon-filled glove box (H2O, O2 < 0.1 ppm). Glass fibers and sodium metal/HC were used as separators and counter/reference electrodes, respectively. 1 M NaClO4 in propylene carbonate (PC) with fluoroethylene carbonate (FEC, 2% in volume) was used as the electrolyte. Charge and discharge measurements were conducted on the Land CT2001A battery test system (Wuhan, China) at various voltage windows. The full cells were charged and discharged in the voltage range of 1.0–4.3 V and 1.0–4.5 V with an N/P ratio of 1.1. For all experiments, at least three coin cells were used, an average discharge capacity reported, and the standard deviation among cells used as error bars in the relevant figures.
4) on Al foil for full cells, with approximately 2.5 mg cm−2 of active anodes. After drying at 100 °C under vacuum for 12 hours, the electrodes were fabricated into CR2032 coin-type cells in an argon-filled glove box (H2O, O2 < 0.1 ppm). Glass fibers and sodium metal/HC were used as separators and counter/reference electrodes, respectively. 1 M NaClO4 in propylene carbonate (PC) with fluoroethylene carbonate (FEC, 2% in volume) was used as the electrolyte. Charge and discharge measurements were conducted on the Land CT2001A battery test system (Wuhan, China) at various voltage windows. The full cells were charged and discharged in the voltage range of 1.0–4.3 V and 1.0–4.5 V with an N/P ratio of 1.1. For all experiments, at least three coin cells were used, an average discharge capacity reported, and the standard deviation among cells used as error bars in the relevant figures.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for 2D pj-MATPASS experiment and thus each spectrum takes about 12 hours to acquire. All the 7Li shifts were calibrated with respect to 1 M LiCl solution (0 ppm). Transmission Mössbauer spectra (MS) at room temperature were recorded using a conventional spectrometer working in constant acceleration mode with a γ-ray source of 25 mCi 57Co (Rh) vibrating at room temperature. The drive velocity was calibrated using sodium nitroprusside (SNP) powder and the isomer shifts (IS) quoted in this work are relative to that of the α-Fe foil at room temperature. All the MS data were analyzed with the MossWinn 4.0 program.56 All the samples were transferred under proper protection in any of the above tests.
000 for 2D pj-MATPASS experiment and thus each spectrum takes about 12 hours to acquire. All the 7Li shifts were calibrated with respect to 1 M LiCl solution (0 ppm). Transmission Mössbauer spectra (MS) at room temperature were recorded using a conventional spectrometer working in constant acceleration mode with a γ-ray source of 25 mCi 57Co (Rh) vibrating at room temperature. The drive velocity was calibrated using sodium nitroprusside (SNP) powder and the isomer shifts (IS) quoted in this work are relative to that of the α-Fe foil at room temperature. All the MS data were analyzed with the MossWinn 4.0 program.56 All the samples were transferred under proper protection in any of the above tests.
The operando X-ray diffraction (XRD) signals were collected on an X’Pert Pro MPD X-ray diffractometer (D8 Advance with a LynxEye_XEdetector, Bruker) with Cu Kα1 radiation (λ = 1.5405 Å) and metal aluminum (Al) metal as the window of a specially designed electrochemical cell. Polytetrafluoroethylene (PTFE) was used as the binder of the current-collector-free electrode. The cell was cycled between 1.5 and 4.5 V vs. Na+/Na at a current density of 10 mA g−1.
First-principles calculations
In this work, all density functional theory (DFT) calculations were carried out using the Vienna ab initio simulation package (VASP) code.57,58 The exchange–correlation effect is described via the generalized gradient approximation (GGA)59 with the form of Perdew–Burke–Ernzerhof (PBE).60 Hubbard U potential correction was applied to take into account the electronic correlation effects of transition-metal 3d electrons in Fe (4.9 eV) and Mn (5.0 eV) ions.61 The DFT calculations employed an energy cutoff of 500 eV. Ions were fully relaxed in the optimization with the energy and force convergence criterion of 10−6 eV and 0.02 eV Å−1, respectively. The quasi-empirical bond-valence (BV) method62,63 was carried out to obtain the possible ionic transportation channels. The migration energy barriers of Li and Fe ions were obtained with the nudged elastic band (NEB) method.64,65For the Na0.33FeO2 system, the calculations were based on a supercell obtained by expanding the conventional cell NaFeO2 (C2/m) by a factor of 2 × 3 × 2, which includes 8 Na, 24 Fe, and 48 O atoms.
In the case of de-sodiated NaLFM, the calculations were carried out using a 3 × 3 × 1 supercell of the R-3m NaFeO2, which contained 3 Li, 9 Fe, 15 Mn, and 54 O atoms. Li et al. reported that the energy required for Fe migration from the transition-metal (TM) layer into the Na layer drops significantly when Fe clusters together.17 Consequently, we constructed a configuration of local Fe clusters in the TM layer, where the Li atom was surrounded by three adjacent Fe atoms and three Mn atoms. In NEB calculations, we adopted the local Fe-clusters configuration with the lowest energy to obtain the activation energies of Fe and Li ions.
In the calculations of density of states, for NaFe0.5Mn0.5O2, Na0.83Fe0.5Mn0.5O2 and Na0.83Li0.17Fe0.33Mn0.5O2, the calculations were based on the supercell obtained by 2 × 3 × 1 expansion of the conventional cell O3-NaFeO2 (R![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m), including 18 Na, 9 Fe, 9 Mn, 36 O atoms, and 15 Na, 9 Fe, 9 Mn, 36 O atoms, and 15 Na, 3 Li, 6 Fe, 9 Mn, 36 O atoms, respectively. For Na0.5Fe0.5Mn0.5O2 and Na0.5Li0.17Fe0.33Mn0.5O2, the calculations were based on the supercell obtained by 2 × 3 × 1 expansion of the conventional cell P3-NaxCoO2 (R3m), including 9 Na, 9 Fe, 9 Mn, 36 O atoms, and 9 Na, 3 Li, 6 Fe, 9 Mn, 36 O atoms, respectively. For the calculations of density of states, Gaussian smearing was employed with ISMEAR = 0 and SIGMA = 0.05.
m), including 18 Na, 9 Fe, 9 Mn, 36 O atoms, and 15 Na, 9 Fe, 9 Mn, 36 O atoms, and 15 Na, 3 Li, 6 Fe, 9 Mn, 36 O atoms, respectively. For Na0.5Fe0.5Mn0.5O2 and Na0.5Li0.17Fe0.33Mn0.5O2, the calculations were based on the supercell obtained by 2 × 3 × 1 expansion of the conventional cell P3-NaxCoO2 (R3m), including 9 Na, 9 Fe, 9 Mn, 36 O atoms, and 9 Na, 3 Li, 6 Fe, 9 Mn, 36 O atoms, respectively. For the calculations of density of states, Gaussian smearing was employed with ISMEAR = 0 and SIGMA = 0.05.
In the calculations of structure optimization and static enengy for Na0.44Li0.17Fe0.33Mn0.5O2, Na0.33Li0.17Fe0.33Mn0.5O2 and Na0.22Li0.17Fe0.33Mn0.5O2, we constructed the 3 × 3 × 1 supercell based on O3-NaFeO2 (R![[3 with combining overline]](https://www.rsc.org/images/entities/char_0033_0305.gif) m). In these configurations, Li ions were strategically placed at the tetrahedral centers of the Na layer, whereas Na ions were randomly distributed at the octahedral positions within the Na layer.
m). In these configurations, Li ions were strategically placed at the tetrahedral centers of the Na layer, whereas Na ions were randomly distributed at the octahedral positions within the Na layer.
Author contributions
Y-S. H. and X. R. conceived the project. J. L. and Y. N. developed the theory. Y. N. and Z. H. synthesized the materials and conducted the electrochemical measurements. X. D. conducted the STEM measurements. Y. N., Y. Y. and J. X. conducted NPD and nPDF measurements. Y. N. and L. Z. assembled and tested full cells. H. M. conducted theoretical calculations. X. L. and B. H. conducted 7Li-ssNMR measurements. B. Z. and Z. L. conducted Fe-MS measurements. L. W., N. Z. F. D, and Y. N. conducted XAS measurements. Y. N. analyzed the data. Y. N., H. M., J. L., and Y-S. H. wrote the paper. All authors discussed and contributed to the writing.Data availability
Data supporting the findings in the present work are available in the manuscript and ESI.†Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the National Key R&D Program of China (2022YFB3807800), National Natural Science Foundation (NSFC) of China (52122214 and 52002394) and the Jiangsu Provincial Carbon Peak and Neutrality Innovation Program (Industry Tackling on Prospect and Key Technology), China (Grant No. BE2022002-5). J. L. acknowledges support from Honda Research Institute USA, Inc. Y. N. acknowledges and thanks the beloved Chu Sun for the ToC comic drawing.References
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef.
- P. G. Bruce, B. Scrosati and J.-M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930–2946 CrossRef PubMed.
- H. Pan, Y.-S. Hu and L. Chen, Energy Environ. Sci., 2013, 6, 2338 RSC.
- C. Zhao, Q. Wang, Z. Yao, J. Wang, B. Sánchez-Lengeling, F. Ding, X. Qi, Y. Lu, X. Bai, B. Li, H. Li, A. Aspuru-Guzik, X. Huang, C. Delmas, M. Wagemaker, L. Chen and Y.-S. Hu, Science, 2020, 370, 708–711 CrossRef PubMed.
- R. Usiskin, Y. Lu, J. Popovic, M. Law, P. Balaya, Y.-S. Hu and J. Maier, Nat. Rev. Mater., 2021, 6, 1020–1035 CrossRef.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517 CrossRef.
- Y. Takeda, J. Akagi, A. Edagawa, M. Inagaki and S. Naka, Mater. Res. Bull., 1980, 15, 1167–1172 CrossRef.
- E. Lee, D. E. Brown, E. E. Alp, Y. Ren, J. Lu, J.-J. Woo and C. S. Johnson, Chem. Mater., 2015, 27, 6755–6764 CrossRef.
- J. C. Kim, D. Kwon, J. H. Yang, H. Kim, S. Bo, L. Wu, H. Kim, D. Seo, T. Shi, J. Wang, Y. Zhu and G. Ceder, Adv. Energy Mater., 2020, 10, 2001151 CrossRef.
- J. W. Somerville, A. Sobkowiak, N. Tapia-Ruiz, J. Billaud, J. G. Lozano, R. A. House, L. C. Gallington, T. Ericsson, L. Häggström, M. R. Roberts, U. Maitra and P. G. Bruce, Energy Environ. Sci., 2019, 12, 2223–2232 RSC.
- B. Mortemard de Boisse, J.-H. Cheng, D. Carlier, M. Guignard, C.-J. Pan, S. Bordère, D. Filimonov, C. Drathen, E. Suard, B.-J. Hwang, A. Wattiaux and C. Delmas, J. Mater. Chem. A, 2015, 3, 10976–10989 RSC.
- E. Talaie, V. Duffort, H. L. Smith, B. Fultz and L. F. Nazar, Energy Environ. Sci., 2015, 8, 2512–2523 RSC.
- N. Sharma, E. Gonzalo, J. C. Pramudita, M. H. Han, H. E. A. Brand, J. N. Hart, W. K. Pang, Z. Guo and T. Rojo, Adv. Funct. Mater., 2015, 25, 4994–5005 CrossRef.
- J. Xu, Z. Han, K. Jiang, P. Bai, Y. Liang, X. Zhang, P. Wang, S. Guo and H. Zhou, Small, 2020, 16, 1904388 CrossRef.
- D. Saurel, B. Silván, E. C. Gonzalo, J. X. Lian and J. Carrasco, ECS Meet. Abstr., 2020, MA2020-02, 101 CrossRef.
- Y. Li, Y. Gao, X. Wang, X. Shen, Q. Kong, R. Yu, G. Lu, Z. Wang and L. Chen, Nano Energy, 2018, 47, 519–526 CrossRef.
- X. Li, Y. Wang, D. Wu, L. Liu, S.-H. Bo and G. Ceder, Chem. Mater., 2016, 28, 6575–6583 CrossRef.
- X. Chen, S. Hwang, R. Chisnell, Y. Wang, F. Wu, S. Kim, J. W. Lynn, D. Su and X. Li, Adv. Funct. Mater., 2018, 28, 1803896 CrossRef.
- D. D. Yuan, Y. X. Wang, Y. L. Cao, X. P. Ai and H. X. Yang, ACS Appl. Mater. Interfaces, 2015, 7, 8585–8591 CrossRef PubMed.
- H. Yoshida, N. Yabuuchi and S. Komaba, Electrochem. Commun., 2013, 34, 60–63 CrossRef CAS.
- J.-L. Yue, W.-W. Yin, M.-H. Cao, S. Zulipiya, Y.-N. Zhou and Z.-W. Fu, Chem. Commun., 2015, 51, 15712–15715 RSC.
- J. Wang, X. He, D. Zhou, F. Schappacher, X. Zhang, H. Liu, M. C. Stan, X. Cao, R. Kloepsch, M. S. Sofy, G. Schumacher and J. Li, J. Mater. Chem. A, 2020, 4, 3431–3437 RSC.
- S. Gençtürk, D. Uzun and S. Yeşilot, Ionics, 2020, 26, 223–231 CrossRef.
- L. Yang, X. Li, J. Liu, S. Xiong, X. Ma, P. Liu, J. Bai, W. Xu, Y. Tang, Y.-Y. Hu, M. Liu and H. Chen, J. Am. Chem. Soc., 2019, 141, 6680–6689 CrossRef PubMed.
- M.-H. Cao, Y. Wang, Z. Shadike, J.-L. Yue, E. Hu, S.-M. Bak, Y.-N. Zhou, X.-Q. Yang and Z.-W. Fu, J. Mater. Chem. A, 1980, 5, 5442–5448 RSC.
- S. Xu, J. Wu, E. Hu, Q. Li, J. Zhang, Y. Wang, E. Stavitski, L. Jiang, X. Rong, X. Yu, W. Yang, X.-Q. Yang, L. Chen and Y.-S. Hu, J. Mater. Chem. A, 2018, 6, 20795–20803 RSC.
- N. Yabuuchi, M. Yano, H. Yoshida, S. Kuze and S. Komaba, J. Electrochem. Soc., 2013, 160, A3131–A3137 CrossRef CAS.
- I. Abate, S. Y. Kim, C. D. Pemmaraju, M. F. Toney, W. Yang, T. P. Devereaux, W. C. Chueh and L. F. Nazar, Angew. Chem., Int. Ed., 2021, 60, 10880–10887 CrossRef CAS.
- E. Boivin, R. A. House, J.-J. Marie and P. G. Bruce, Adv. Energy Mater., 2022, 12, 2200702 CrossRef CAS.
- Y. Niu, Z. Hu, B. Zhang, D. Xiao, H. Mao, L. Zhou, F. Ding, Y. Liu, Y. Yang, J. Xu, W. Yin, N. Zhang, Z. Li, X. Yu, H. Hu, Y. Lu, X. Rong, J. Li and Y. Hu, Adv. Energy Mater., 2023, 13, 2300746 CrossRef CAS.
- C. P. Grey, W.-S. Yoon, J. Reed and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A290 CrossRef CAS.
- H. Liu, C. Zhao, Q. Qiu, B. Hu, F. Geng, J. Li, W. Tong, B. Hu and C. Li, J. Phys. Chem. Lett., 2021, 12, 8740–8748 CrossRef CAS.
- C. Zhao, C. Li, H. Liu, Q. Qiu, F. Geng, M. Shen, W. Tong, J. Li and B. Hu, J. Am. Chem. Soc., 2021, 143, 18652–18664 CrossRef CAS.
- Z. Wu, Y. Ni, S. Tan, E. Hu, L. He, J. Liu, M. Hou, P. Jiao, K. Zhang, F. Cheng and J. Chen, J. Am. Chem. Soc., 2023, 145, 9596–9606 CrossRef CAS.
- R. A. House, U. Maitra, L. Jin, J. G. Lozano, J. W. Somerville, N. H. Rees, A. J. Naylor, L. C. Duda, F. Massel, A. V. Chadwick, S. Ramos, D. M. Pickup, D. E. McNally, X. Lu, T. Schmitt, M. R. Roberts and P. G. Bruce, Chem. Mater., 2019, 31, 3293–3300 CrossRef CAS.
- J. Xu, D. H. Lee, R. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269 CrossRef CAS.
- C. Zhao, Z. Yao, Q. Wang, H. Li, J. Wang, M. Liu, S. Ganapathy, Y. Lu, J. Cabana, B. Li, X. Bai, A. Aspuru-Guzik, M. Wagemaker, L. Chen and Y.-S. Hu, J. Am. Chem. Soc., 2020, 142, 5742–5750 CrossRef CAS.
- Q. Wang, D. Zhou, C. Zhao, J. Wang, H. Guo, L. Wang, Z. Yao, D. Wong, G. Schuck, X. Bai, J. Lu and M. Wagemaker, Nat. Sustainable, 2024, 7, 338–347 CrossRef.
- X. Yang, S. Wang, H. Li, J. Tseng, Z. Wu, S. Indris, H. Ehrenberg, X. Guo and W. Hua, Electron, 2024, 2, e18 CrossRef.
- J. E. Wang, H. Kim, Y. H. Jung, D. K. Kim and D. J. Kim, Small, 2021, 17, 2100146 CrossRef CAS.
- A. Ito, Y. Sato, T. Sanada, M. Hatano, H. Horie and Y. Ohsawa, J. Power Sources, 2011, 196, 6828–6834 CrossRef.
- K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edström, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Nat. Chem., 2016, 8, 684–691 CrossRef PubMed.
- L. Wang, A. Dai, W. Xu, S. Lee, W. Cha, R. Harder, T. Liu, Y. Ren, G. Yin, P. Zuo, J. Wang, J. Lu and J. Wang, J. Am. Chem. Soc., 2020, 142, 14966–14973 CrossRef.
- E. Hu, X. Yu, R. Lin, X. Bi, J. Lu, S. Bak, K.-W. Nam, H. L. Xin, C. Jaye, D. A. Fischer, K. Amine and X.-Q. Yang, Nat. Energy, 2018, 3, 690–698 CrossRef.
- Y. Dong and J. Li, Chem. Rev., 2023, 123, 811–833 CrossRef PubMed.
- R. J. Clément, J. Xu, D. S. Middlemiss, J. Alvarado, C. Ma, Y. S. Meng and C. P. Grey, J. Mater. Chem. A, 2017, 5, 4129–4143 RSC.
- C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512 CrossRef PubMed.
- J. Cabana, N. A. Chernova, J. Xiao, M. Roppolo, K. A. Aldi, M. S. Whittingham and C. P. Grey, Inorg. Chem., 2013, 52, 8540–8550 CrossRef.
- M. C. Tucker, J. A. Reimer and E. J. Cairns, J. Electrochem. Soc., 2001, 148, A951 CrossRef.
- G. Prado, L. Fournès and C. Delmas, J. Solid State Chem., 2001, 159, 103–112 CrossRef.
- D. Darbar, N. Muralidharan, R. P. Hermann, J. Nanda and I. Bhattacharya, Electrochim. Acta, 2021, 380, 138156 CrossRef.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- P. Juhás, J. N. Louwen, L. van Eijck, E. T. C. Vogt and S. J. L. Billinge, J. Appl. Crystallogr., 2018, 51, 1492–1497 CrossRef.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- Z. Klencsár, AIP Conf. Proc., 2014, 1622, 30–39 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 54, 11169–11186 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121 CrossRef.
- R. Xiao, H. Li and L. Chen, Sci. Rep., 2011, 5, 14227 CrossRef.
- S. Adams and R. P. Rao, Phys. Status Solidi A, 2011, 208, 1746–1753 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef.
- S. Smidstrup, A. Pedersen, K. Stokbro and H. Jónsson, J. Chem. Phys., 2014, 140, 214106 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee01867b |
| This journal is © The Royal Society of Chemistry 2024 |