Open Access Article
Open Access ArticleRevealing the role of redox reaction selectivity and mass transfer in current–voltage predictions for ensembles of photocatalysts†
Luisa
Barrera‡
 a,
Bradley W.
Layne
a,
Bradley W.
Layne
 b,
Zejie
Chen
b,
Zejie
Chen
 b,
Kenta
Watanabe
b,
Kenta
Watanabe
 cd,
Akihiko
Kudo
c,
Daniel V.
Esposito
cd,
Akihiko
Kudo
c,
Daniel V.
Esposito
 e,
Shane
Ardo
e,
Shane
Ardo
 bfg and
Rohini
Bala Chandran
bfg and
Rohini
Bala Chandran
 *a
*a
aDepartment of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA. E-mail: rbchan@umich.edu
bDepartment of Chemistry, University of California Irvine, Irvine, CA 92697, USA
cDepartment of Applied Chemistry, Faculty of Science, Tokyo University of Science, Tokyo 162-8601, Japan
dDepartment of Chemical Science and Engineering, School of Materials and Chemical Technology, Tokyo Institute of Technology, Nagatsuta-cho, Midori-ku, Yokohama 226-8501, Japan
eDepartment of Chemical Engineering, Columbia University, New York, NY 10027, USA
fDepartment of Chemical & Biomolecular Engineering, University of California Irvine, Irvine, CA 92697, USA
gDepartment of Materials Science & Engineering, University of California Irvine, Irvine, CA 92697, USA
First published on 10th September 2024
Abstract
Photocatalysts are conceptually simple reaction units where nanoscale semiconductors integrated with catalysts drive a pair of redox reactions on illumination. However, the proximity of reaction sites performing cathodic and anodic reactions poses dire challenges to realize large light-to-fuel conversion efficiencies. In this study, a powerful, yet straightforward, equivalent-circuit detail-balance modeling framework is developed and applied to evaluate the performance of photocatalytic systems featuring multiple light absorbers. Specifically, low bandgap iridium-doped strontium titanate is modeled as a Z-scheme photocatalyst to achieve desirable hydrogen evolution and iron-based redox shuttle oxidation reactions. Our model has unique capabilities to simulate competing redox reactions and address mass-transfer limitations. In a significant departure from state-of-the-art circuit models, our study develops tools to perform load-line analyses by incorporating a net electrochemical load curve that includes both desired and competing redox reactions. Consequently, reaction selectivity is predicted from equivalent circuit models for photocatalytic and photoelectrochemical systems. Our investigation into ensembles comprised of multiple, semi-transparent light absorbers reveals their potential to outperform a single, optically thick light absorber, particularly when operated under mass-transfer-limited conditions. However, this outcome hinges on minimizing mass-transfer rates of select redox species to prevent undesired reactions of hydrogen oxidation and/or redox shuttle reduction. Our findings demonstrate that reaction selectivity can be achieved by tuning asymmetry in redox species mass-transfer even with perfectly symmetric electrocatalytic charge-transfer coefficients. The influences of various kinetic, mass-transfer, and thermodynamic parameters are explored to offer crucial insights for synthesis of the next-generation of photocatalysts and selective coatings, and reactor designs.
Broader contextIn global pursuit of net-zero carbon emissions, a significant emphasis is placed on green hydrogen from water and renewable resources. Hydrogen is versatile as an energy carrier and a storage medium and has enormous potential to decarbonize industrial sectors. The U.S. Department of Energy Hydrogen Shot Initiative aims to lower the production cost of green hydrogen to less than $1 per kilogram by 2030. Presently, electrolytic technologies that harness renewable electricity to produce hydrogen and oxygen by splitting water are experiencing rapid development and commercialization. However, formidable cost and stability barriers persist. Alternatively, sunlight-driven, photocatalytic hydrogen production with metal oxide semiconductors has immense potential to be cost-effective but faces efficiency hurdles. Most photocatalytic systems are operative at less than 10% solar-to-hydrogen efficiencies. To overcome this hurdle, there is a crucial need for the development of rigorous, yet simple, models that link fundamental material properties, kinetics, and mass transfer behavior with performance characterized by solar-to-hydrogen efficiencies. An often-overlooked aspect in state-of-the-art models is the undesired reactions due to (electro)chemical recombination of products formed, which negatively influence efficiency. Addressing this will be crucial to surpass 10% solar-to-hydrogen conversion efficiencies, and towards meeting the Hydrogen Shot cost target. |
1. Introduction
Nanoscale-semiconductor-mediated redox reactions powered by sunlight form the basis of photocatalysis.1,2 Such systems enable the conversion of abundant, yet intermittent and diffuse, sunlight into storable and transportable chemical fuels,3–6 including hydrogen,7–14 carbon monoxide for synthesis gas15–21 and methanol,20–27 by using water and carbon dioxide as feedstock. Photocatalytic oxidation reactions also have extensive applications, for example, to treat organic contaminants in water28–30 and air,30,31 and to effect methane transformations,32–38 albeit often only increasing reaction rates and not storing free-energy compared to the fuel-forming photocatalytic systems. Recently, the field of photocatalysis has expanded significantly to include synthesis of commodity chemicals and pharmaceuticals using molecular dye sensitizers.39–42 This study develops an equivalent-circuit, detailed-balance modeling framework particularly focusing on modeling competing redox reactions, and ensemble effects from multiple light absorbers to predict solar-to-fuel energy conversion efficiencies in photocatalytic systems.On a photocatalyst surface, each photogenerated pair of charge carriers that do not recombine will drive at least one reduction and one oxidation reaction to maintain charge neutrality. Herein, we focus on photocatalytic hydrogen evolution, H+ + e− → 1/2H2, coupled to an oxidation reaction, represented as D+/D (D → D+ + e−) (Fig. 1(a)), which commonly includes D+/D species of O2/H2O, Fe(III)/Fe(II), or I−/IO3− (with reaction stoichiometries and water/protonic species excluded for simplicity). While the hydrogen evolution reaction (HER) is the desired reduction reaction from conduction-band states, undesired reduction of D+ is both thermodynamically, and often kinetically, favored, serving as a shunt and attenuating desired redox reactivity (Fig. 1(b)). The same effects hold for desirable oxidation of D by valence-band states in comparison to undesired H2 oxidation. Such undesired redox reactions, i.e. D+ reduction and H2 oxidation, have been observed experimentally in photocatalytic systems, even in cases when metallic cocatalysts are incorporated with the intention of catalyzing desired redox reactions.43–46 The challenge of reaction selectivity is most stark in two-step/dual-compartment Z-scheme photocatalysis with soluble redox shuttles that typically involve reversible D+/D redox species that relay electrons between light absorbers that drive both the oxygen evolution reaction (OER) and the HER.12,47 Z-scheme reactors are important to consider as they facilitate intrinsic spatial separation of H2 and O2 to promote safe operation by mitigating an explosive mixture of gases that are likely to be formed when water splitting efficiencies are large. Additionally, prior48,49 and our team's recent technoeconomic analyses50,51 suggest that low-cost materials and suspension reactor design concepts could be cost-competitive with steam methane reforming for H2 production when solar-to-hydrogen efficiency is larger than 10%. Therefore, there is a critical need to predict reaction selectivity and determine how performance is influenced by redox shuttle kinetic parameters. Additionally, photocatalyst-particle-based reactor architectures, either as suspensions12,47 or photocatalyst sheets,11,52 are more likely to be subject to mass-transfer limitations due to one, or all, of the following factors: (i) ineffective stirring/mixing on the reactor scale; (ii) small redox shuttle species concentrations that are restricted either due to their strong parasitic absorption of visible light or limited solubility; and (iii) small redox shuttle diffusivities, especially for large molecules like quinones12 and inorganic coordination compounds like those based on cobalt.53
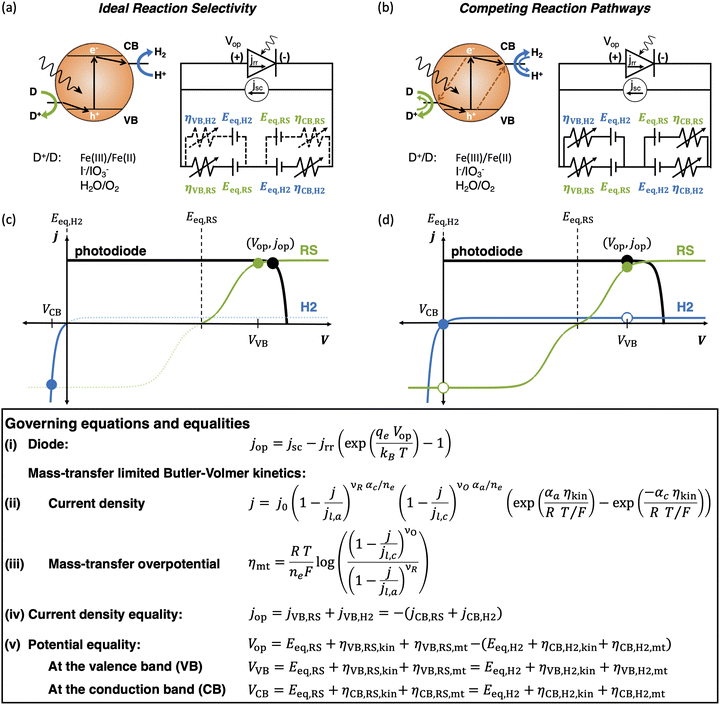 | ||
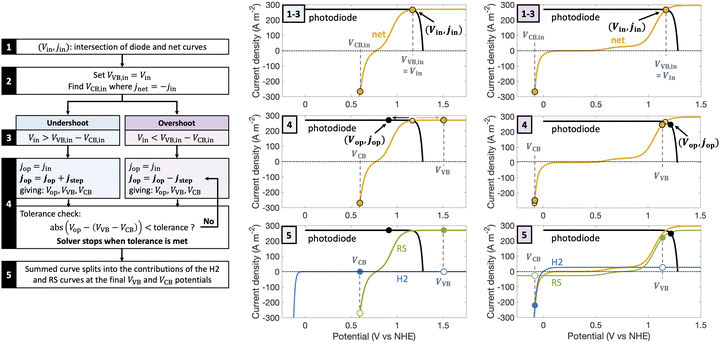
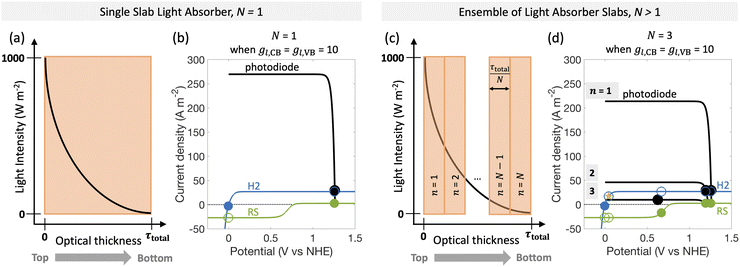
| Fig. 1 Comparison of the current state-of-the-art models (left column) and the approach used herein (right column). Single-particle-level reaction schematic and equivalent circuit diagram for (a) the ideal scenario, where only the desirable redox reactions for reduction (H+/H2) occur from conduction band (CB) states and for oxidation (D+/D) occur from valence band (VB) states, with ignored competing redox reactions shown by dashed lines; D+/D is representative of reduced/oxidized aqueous redox shuttle species, where for simplicity the mass-balancing H2O and H+ species are not indicated; (b) the more realistic scenario where competing redox reactions occur in parallel with desired redox reactions. Kinetic and mass-transfer resistances are accounted for at both the VB and the CB, and the sum of these components is represented as a variable resistor in the circuit. Load-line analyses of the photodiode power curve (black) with the load curves (green for the redox shuttle, RS, and blue for the hydrogen, H2, redox reactions) (c) when only desired redox reactions are implemented (ignored competing reactions indicated by dashed lines) and (d) when competing reactions are considered as well, where desired redox reaction currents are shown as filled circles and competing undesired redox reaction currents are shown as open circles. (d) The high proclivity of competing redox shuttle reduction as compared to the desired H2 evolution at CB, whereas H2 oxidation is constrained by solubility limits at the VB. Operating point is indicated by the black marker on the photodiode power curve, while satisfying current and potential equalities (eqn (iv) and (v) in the inset). Key governing equations are included in the inset below for: (i) the current–voltage (jop, Vop) relationship for a semiconductor modeled as an ideal photodiode; (ii) kinetic, ηkin, and (iii) mass-transfer, ηmt, overpotentials as a function of the limiting anodic and cathodic current densities respectively, jl,a and jl,c, and other kinetic parameters (j0, αa, αc); and (iv) current and (v) potential equality in series and parallel circuit elements respectively. A nomenclature of all symbols is provided in the ESI.† | ||
Modeling tools that are analogous to detailed-balance efficiency predictions in photovoltaic cells already exist for photovoltaic-electrolyzer, photoelectrochemical, and photocatalytic systems.13,54–60 Most of these models pair the current–voltage behavior of an ideal photodiode with electrochemical loads due to reaction kinetics and ohmic/solution resistance.56,58 Many of the studies have also looked at the behavior of multiple semiconductor diodes connected electrically in series, tandem or multijunction set-ups,13,56–58 with recent studies extending modeling capabilities to account for different configurations including thinning of semiconductors for better photocurrent matching59,60 and our own work on electrochemically mediated tandem solar water splitting systems, which did not consider competing redox reactions and ensemble effects.13 Even with such comprehensive predictive tools and foundational knowledge in the literature, all studies outside of our recent work have unanimously discounted the effects of competing, parallel redox reaction pathways (Fig. 1).12,61 Recently, we modeled Z-scheme photocatalysis from a suspension of particles that coupled light absorption, photodiode power production, diffusive transport, and electrochemical reactions. However, the influences of competing reactions were conservatively modeled with a simplified calculation of driving forces for competing reactions based on using the same operating potential that was derived from the assumption of perfect selectivity.12 We also modeled competing reactions for conduction-band states for photoelectrochemical NO3− reduction, but did not include these considerations for valence-band states, and only considered a single, optically thick light absorber.61 This latter aspect is significant, because photocatalyst suspension reactors12,13,47,53,62,63 and particulate photocatalyst sheets10,11,14,52,64,65 include an ensemble of light absorbers, suggesting that detailed-balance models to simulate them should include this effect as well. To this end, we recently developed a modeling framework to predict the performance of an array of optically thin semiconductor light absorbers driving solar water splitting.66,67 However, that study did not rigorously model the effects of competing redox reactions and mass-transfer limitations.
Motivated by the outlined knowledge gaps, our study extends the equivalent-circuit modeling approach, modifying it to be more applicable for photocatalytic reactor concepts. As such, we included competing redox reactions and interdependent effects of kinetics, mass transfer, and light transport on selectivity and solar-to-chemical efficiencies for a varying number of planar slabs of semiconductor light absorbers. Model predictions are applied to compare and interpret experimental data for photocatalytic particle suspension reactors for water splitting. Our model includes multiple light absorbers that undergo several physical processes that depend on materials' thermodynamic and kinetic parameters, while factoring in reaction selectivity and mass-transfer limitations. A significant contribution is the development of a new circuit-based modeling approach that accounts for all possible electrochemical load curves together with photodiode power curves and applies this framework for an ensemble of light absorbers. Predictions of selectivity, and the inclusion of mass-transfer effects, are unique distinctions and a deviation from state-of-the-art models that are tailored toward efficiency predictions for externally biased and/or membrane-containing wireless photoelectrochemical electrodes, where perfect reaction selectivity is assumed.68–72 Even though our study specifically focuses on performance predictions for Z-scheme photocatalytic solar water splitting systems,6,12,13 the approach developed herein is more broadly applicable to understand and predict performance limits for photocatalytic and photoelectrochemical systems alike.
2. Theory and experimental
2.1. Photodiode modeling
The current–potential behavior of the semiconductor light absorber was modeled using the Shockley–Queisser detailed-balance analysis,73 and this was comprehensively explained in prior work (eqn (S1)–(S5), ESI†).13,55–57,73 To enable performance predictions that are material agnostic and to facilitate a wide range of parameter explorations and sensitivity studies, additional assumptions were made:(i) Ideal photodiode behavior, where the short-circuit photocurrent density, jsc (Fig. 1(i)), is obtained by assuming a step-function for the absorption onset at the bandgap, a prescribed fraction of incident photons, dictated by the absorptance, is absorbed by the light absorber (eqn (S2), ESI†), and each absorbed photon generates a single electron–hole pair.
(ii) Equilibrium radiative recombination current density, jrr (Fig. 1(i)), that arises from thermal emission to the surrounding medium at 298.15 K was modeled; for the sake of simplicity inter-absorber photon recycling was not modeled.
(iii) Interfaces between the light absorber and water and air are modeled to be transparent, and without any reflections; spectral optical properties for absorption and emission were not included.
All light absorbers are modeled as planar slabs with intensity variations modeled only along the direction of the incident light. No absorption of incident light was assumed to be taking place in the surrounding electrolyte, as competition from redox shuttle species in solution has been specifically addressed in prior work.12 The short-circuit photocurrent density of the nth light absorber, jsc,n, is dictated by its absorptance and the incident light intensity (eqn (S2), ESI†), which was assumed to be the air mass 1.5 global (AM1.5G) solar spectrum and normal to the plane of the light absorbers.74 The semiconductor assumed to be a narrow bandgap photocatalyst (1.55 eV corresponding to Ir-doped SrTiO3)75 was fixed throughout the study, as bandgap effects have been well captured in prior work.12,13,61 Optical thickness, τ, is a non-dimensional length scale dictated by the absorption coefficient and the geometric thickness of a slab and characterizes the extent of absorption – the absorptance increases as the optical thickness increases, i.e., A = 1 − exp(−τ); optical thickness is equivalent to the Napierian absorbance.76 While we model a varying number of light absorbers, the total absorptance and optical thickness are constrained to be the same for all cases, Atotal = 0.99 and τtotal = 4.61. This is achieved by modifying the optical thickness of individual light absorbers to be inversely proportional to the number of light absorbers (eqn (S4), ESI†), i.e., the same total mass and volume of the semiconductor material is considered irrespective of the number of light absorbers modeled. The absorption coefficient was intentionally made spectrally independent to allow the absorptance and optical thickness to remain well-controlled variables that are material-agnostic.
The equilibrium radiative recombination current density, jrr (Fig. 1(i)), was modeled by considering multiple scenarios. For the base case that is applied for most of the results presented, jrr is computed from the blackbody emission spectrum that is scaled by the same absorptance that was used to calculate jsc,n (eqn (S2) and (S5), ESI†). This is consistent with the Shockley–Queisser formulation and accounts for (re)absorption of radiative intensity within the volume of the semiconductor slab, i.e., we include intra-absorber photon recycling.73,77,78 Therefore, for this baseline case, while the equilibrium radiative recombination current density, jrr,n, remains the same for every light absorber, the short-circuit photocurrent density jsc,n (eqn (S2), ESI†) decreases with increasing light absorber number due to exponentially decreasing incident solar light intensity (Fig. 6). This baseline case was compared against scenarios where the theoretical maximum for radiative recombination was modeled (eqn (S6), ESI†) that assumes homogenous emission without any attenuation within the volume of the semiconductor slab. Additionally, to model scenarios where other recombination mechanisms are at play, such as non-radiative recombination mechanisms, we considered three other cases where the recombination current density is arbitrarily made 10, 100, and 1000 times larger than the theoretical maximum value for the radiative recombination current density (Fig. S1, ESI†). Overall, the baseline case with idealized diode behavior was chosen to highlight the effects of mass-transport and kinetic parameters on the system performance. Introducing non-idealities such as a non-unity ideality factor for the diode, imperfect internal quantum yields for charge-separation, and more mechanistic details on non-radiative recombination of the generated charge-carriers will lead to a reduction in the predicted solar-to-chemical efficiencies (and external quantum yields), however we anticipate predicted trends to remain qualitatively still the same.
2.2. Electrochemical reactions and mass-transfer
For the electrochemical loads in the circuit (Fig. 1(ii) and (iii)), concentration and kinetic overpotentials have been accounted based on the assumption of unity activity of all redox species in the bulk.79 Relative areas for each redox reaction were assumed to be the same, such that current densities and currents exhibit identical outcomes. While the concentration overpotential accounts for concentration differences between the surface of a cocatalyst and the bulk solution, the kinetic overpotential is influenced by the electrocatalytic parameters of exchange current density, charge-transfer coefficient, and surface concentration of redox species. This surface species concentration is dictated by the ratio of the operating current density to the respective limiting current density (eqn (S7), ESI†). Table S1 (ESI†) summarizes all modeling parameters considered. Many factors influence the limiting current density, including the mass-transfer behavior, as dictated by the concentration boundary layer thickness, species diffusivity, and bulk species concentration. To broadly consider these interconnected factors, limiting current densities of individual species were varied over several orders of magnitude to traverse different operating regimes. The limiting current density for the desired anodic reaction of the redox shuttle (D → D+ + e−), jl,RS,a, was varied with respect to the short-circuit photocurrent density of the light absorber (factors of 1 × 10−2 to 1). We model uniform limiting currents across all the light absorbers for the ensemble case, which is representative of fast mixing of all species concentrations in the reactor volume. However, these limiting currents will be influenced by the spatially dependent rates of reactant/product consumption/formation calculated from the load line analyses performed (Section 2.4), and this should be considered in future work.Asymmetry factors gl were introduced to compare the limiting current densities of the competing reactions to the desired redox shuttle oxidation current density. This asymmetry factor is defined for both the valence and conduction band states to respectively quantify the extent of competing H2 oxidation (gl,VB = jl,H2,a/jl,RS,a) and the competing redox shuttle reduction (gl,CB = |jl,RS,c|/jl,RS,a) as compared to the desired redox shuttle oxidation. Cathodic current density for H2 evolution was reasonably defined to be much larger than the short-circuit photocurrent density of the photodiode (jl,H2,c/jsc = −1000). In addition to the limiting current densities, the exchange current density (j0,RS = 1 × 10−5−1 × 10−3 A m−2) and the asymmetry in the charge transfer coefficients (αa,RS = 0.01–0.99, where αc,RS + αa,RS = 1) for the redox shuttle reaction were also parametrized. H2 evolution was modeled based on established kinetic parameters for Pt cocatalysts, with j0,H2 = 10 A m−2 and αa,H2 = αc,H2 = 1 for all cases, unless otherwise indicated.80–82
2.3. Performance metrics
Solar-to-chemical (STC) efficiency (eqn (1)) is obtained to convert the incident sunlight at 1 Sun irradiance (1000 W m−2) to a chemical power density stored in the net H2 formed at the conduction band (CB) and valence band (VB).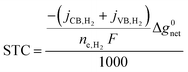 | (1) |
To provide results that are agnostic to the standard potential of the net reaction, we also calculate the apparent quantum yield (AQY) of converting the absorbed photon flux to a H2 flux as in eqn (2):
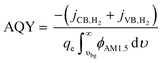 | (2) |
A reaction selectivity (Srxn) is computed based on the molar reaction rates of the desired products as compared to the total rate of desirable and competing redox reactions at both the valence and the conduction bands (eqn (3)).
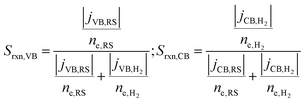 | (3) |
2.4. Load-line analysis
Fig. 2 is a graphical illustration of the procedure used to determine operating potential and current density for a light absorber and the corresponding current densities for individual redox species reactions at the valence band (VB) and the conduction band (CB). A net electrochemical load curve is first obtained that combines the polarization (j–V) behavior of the individual redox species – (Fe(III)/Fe(II) and H+/H2 in Fig. 2). This net electrochemical load curve dictates the operating point of the photodiode (Fig. 2), from which the individual j–V pairs for the redox species are obtained based on the two constraints of current and potential equalities (eqn (S8) and (S9), ESI†).The intersection point of the photodiode power curve and load curve (Vin, jin) was used as the starting point for the solver.83 From this step, VVB is set equal to Vin, and VCB is computed such that the conduction band operates at the same magnitude of current density as jin but with a negative value; subplots for steps 1–3 in Fig. 2 show representative intersection curves for the same light absorber but with two different electrochemical load curves. At this point, if the operating potential is not equal to the difference between the valence and the conduction band potentials, i.e., VVB − VCB = Vin was not satisfied, the operating point on the photodiode was shifted in a stepwise manner until the governing potential and current density equalities are satisfied (step 4 in Fig. 2). The direction of the shift depends on whether the initial guess underestimates (“undershoot”) or overestimates (“overshoot”) the potentials where the constraint is satisfied. Depending on this, the operating current density was either increased or decreased in a step-wise manner, with the steps in current density, jstep, proportioned to be small compared to either the intersection current density, jin, or the difference between jin and the maximum current density that can be sustained by the system, jmax. This iterative process is done until VVB and VCB satisfy the constraints for the operating potential within a tolerance of 10−5. Tolerance is here defined as the difference between the left-hand and right-hand sides of eqn (S9) (ESI†). From the converged solutions for the operating point (Vop and jop in Fig. 2 subplots for step 5) of the light absorber and the valence and conduction band potentials (VVB and VCB), we can determine the corresponding split in the current densities between parallel reactions.
This approach of performing load-line analysis was verified against previously reported data to obtain a solar-to-hydrogen conversion efficiency of 18% for a single, optically thick light absorber driving O2 and H2 evolution with assumptions of perfect selectivity at both the valence and conduction bands.13,58,61
2.5. Varying model parameters to traverse different operating regimes
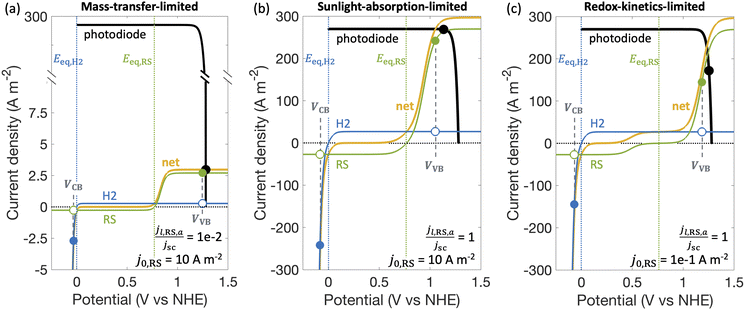
Fig. 3 shows different regimes of operation depending on the limiting current densities and the electrocatalytic parameters (Table S1, ESI†) modeled by considering Fe(III)/Fe(II) as the redox shuttle paired with the H2 evolution for a single, optically thick light absorber. The limiting current densities are treated as variables, ranging over several orders of magnitude, to cover different operating regimes. In the mass-transfer-limited regime (Fig. 3(a)), the minimum limiting current density amongst the desired redox reactions, in this case for Fe(II) oxidation, jl,RS,a, is much smaller compared to the short-circuit photocurrent density, jsc, (jl,RS,a/jsc = 1 × 10−2 in Fig. 3(a)), meaning that operating current densities are restricted to being less than jl,RS,a. In the sunlight-absorption-limited regime (i.e., jl,RS,a/jsc ≥ 1) (Fig. 3(b)), operating current densities are restricted to being less than the short-circuit current, which is influenced by the bandgap, optical absorptance, and the incident spectrum (eqn (S2), ESI†). The kinetic parameters for the redox reactions can further restrict the operating current densities in this sunlight-limited regime (Fig. 3(c)). Compared to Fig. 3(b) that modeled an exchange current density for the redox shuttle reactions of j0,RS = 10 A m−2, Fig. 3(c) modeled a smaller value of j0,RS = 0.1 A m−2, which leads to a larger kinetic overpotential for the Fe(II) oxidation reaction and therefore further restrains the operating current density.2.6. Experimental measurements with photocatalytic particles
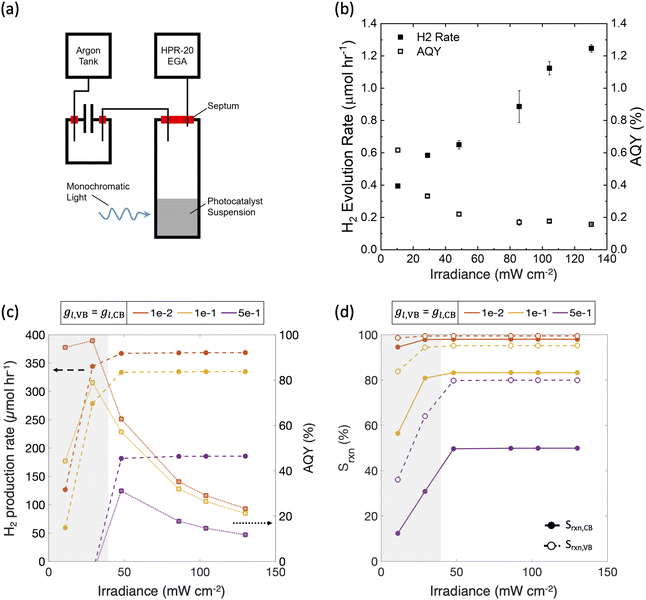
Model predictions were compared against and used to interpret experimental data with suspensions of photocatalytic particles. SrTiO3 nanoparticles doped with Ir and containing Ir cocatalysts were synthesized using a previously reported procedure.84 The photocatalytic activity of these nanoparticles (2 mg) suspended in 1 mL of an aqueous CH3OH solution (10%, v/v) was determined by continuously sampling the headspace above the solution using a mass spectrometer/residual gas analyzer (Hiden Analytical, HPR-20 EGA) via a previously reported protocol.75 Nanoparticle suspensions were prepared using ultrahigh-purity deionized water (>18 MOhm cm, Millipore Sigma, Milli-Q Reference Water Purification System) and were dispersed using an analog vortex mixer (VWR) and placed into a 1 cm pathlength cuvette (FireflySci Cuvette Shop, Type 41 Macro Cuvette with Screw Cap (OG 41FLUV10)) before CH3OH (Fisher Chemical, Optima™ LC/MS Grade) was added. The cuvette was housed in a custom 3D-printed white holder to maximize absorptance and was stirred with a 3 × 8 mm PTFE-coated rare earth magnetic stir bar (2mag-USA, Power Bar 8 PI 01108) driven by a cuvette stirring system at 1200 rpm (2mag-USA, 2mag cuvetteMIXdrive 1, 2mag MIXcontrol eco Control Unit). Argon (99.999% ultrahigh purity) was used as a carrier gas and a 405 nm laser diode (Thorlabs, L405G1) was used as the illumination source, whose power was varied from 11–130 mW. At every illumination power, except the smallest power of 11 mW, two trials were performed to assess material stability under repeated illumination. A known volume of molecular hydrogen (99.999% ultrahigh purity) was injected at the end of the experiment using a 10 μL gastight syringe (Hamilton, 1701N) to calibrate the m/z = 2 signal for calculation of the H2 evolution rate and the apparent quantum yield.To compare model predictions with these measurements, a single optically thick slab (N = 1) was modeled with calibrated input parameters. The total absorptance, Atotal, was fixed at 99% (eqn (4)), which is reasonable based on the near-zero transmittance measured for the suspension at an incident wavelength of 405 nm. Incident photon flux was varied from 11–130 mW cm−2 based on a 1 cm2 projected area for the laser power source in the experimental set up. Based on these parameters, the short-circuit current density (eqn (S2), ESI†) ranges from 36–424 A m−2. Limiting current density for methanol oxidation (jl,RS,a) is on the order of 100 A m−2, based on: (i) a conservatively assumed diffusion boundary layer thickness of 100 μm in particle suspensions, where the mixing is expected to be somewhat ineffective even with stirring because of the small reactor volumes, (ii) a methanol concentration of 2.5 M, (iii) 2 holes per mole of methanol being oxidized, and (iv) a bulk diffusivity of 10−10 m2 s−1 for methanol. All these estimates translate to the ratio of the desired oxidation reaction limiting current to the short-circuit current density of the photodiode, jl,RS,a/jsc, ranging between 0.1–10 corresponding to the experimental variations in the incident laser power. The standard state potential for methanol oxidation is assumed to be the same value modeled for Fe(III)/Fe(II) (0.77 V) as a simplification. Additionally, for the sake of computational tractability and conservative estimates, we model a single optically thick slab (N = 1), however ensemble calculations (N ≥ 1) were performed for the smallest and the largest incident photon fluxes.
3. Results and discussion
3.1. Influences of redox shuttle kinetics on selectivity – single slab light absorber
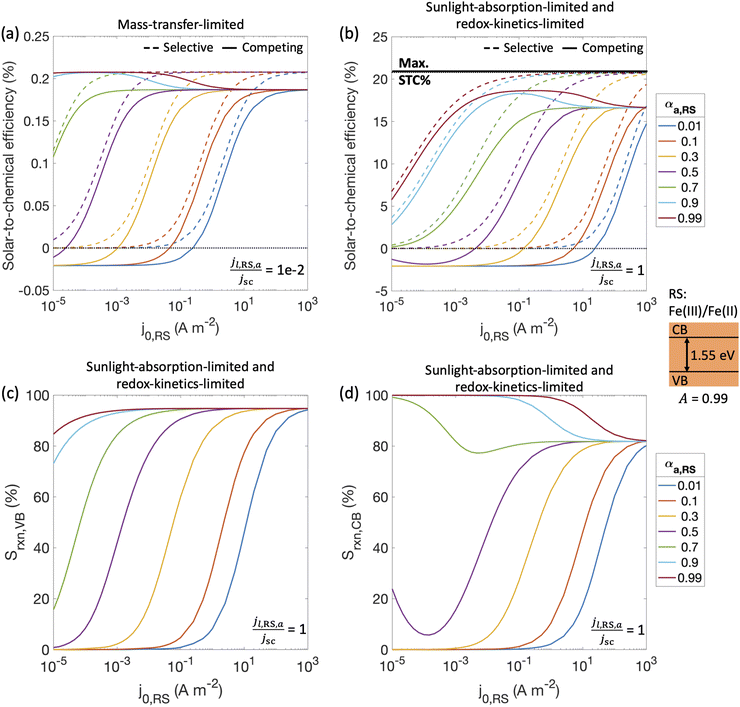
With a better understanding of the three possible limiting regimes in Fig. 3, we examined further the influence of electrocatalytic parameters for the cases of perfectly selective versus competing reactions for the mass-transfer-limited regime (Fig. 4(a)) and the sunlight-absorption-limited regime (Fig. 4(b)). When competing reactions were modeled, the competing reactions were assumed to occur at an order-of-magnitude smaller limiting current density as compared to the desired redox reactions. i.e., the asymmetry factors in the limiting current densities (gl,VB and gl,CB) were assumed to be 0.1.STC efficiencies decrease when competing reaction pathways were modeled as compared to ideally selective reactions (Fig. 4(a) and (b)). This illustrates the substantial driving forces for the competing reactions for both Fe(III)/Fe(II) and H+/H2 species. Notably, when the desirable oxidation of Fe(II) at the valence band becomes slow (e.g. due to small exchange current density and anodic charge-transfer coefficient for the Fe(III)/Fe(II) reaction), the valence band more effectively oxidizes H2 resulting in decreased STC efficiencies. At the slowest rates of Fe(II) oxidation examined, H2 oxidation at the valence band occurs more rapidly than H2 evolution at the conduction band, resulting in net H2 consumption and negative STC efficiencies. Conditions in the mass-transfer-limited regime (Fig. 4(a)) illustrate the dramatic effect of the limiting redox shuttle oxidation (Fe(II) → Fe(III)) rates on the STC efficiencies. While the maximum STC efficiency proportionally decreases with the extent of mass-transfer limitation, i.e. jl,RS,a/jsc, the overall trends with respect to the electrocatalytic parameters are similar to those observed for the sunlight-absorption-limited regime (Fig. 4(b)). For large exchange current densities, irrespective of the value of the charge-transfer coefficient, the STC efficiency approaches 0.21% for jl,RS,a/jsc = 1 × 10−2 (Fig. 4(a)) and 18.64% for jl,RS,a/jsc = 1 (Fig. 4(b)). To put these values in perspective, the STC efficiency corresponding to the scenario with ideal reaction selectivity, and infinitely fast kinetics and mass transfer is projected to be a maximum value of 20.79%, where the net current density to produce H2 is nearly equal to the short-circuit current density (i.e., |jCB,H2| = 99.999% jsc). Note that this efficiency is larger than typically reported maximum solar- to-hydrogen conversion efficiency of ∼18% for a single light absorber, which is computed for a net water splitting reaction to produce H2 and O2 with a minimum required potential of 1.23 V under standard conditions. In contrast, we model H2 evolution paired with Fe(II) oxidation to Fe(III), and this has a much smaller thermodynamic potential of 0.77 V, which results in a larger upper limit for the solar-to-fuel efficiency.
Trends for STC efficiency with respect to electrocatalytic parameters are generally similar whether ideally selective or competing reactions were modeled – larger values for the redox shuttle exchange current density, j0,RS, and anodic charge-transfer coefficient, αa,RS, result in larger STC efficiencies for both mass-transfer-limited and sunlight-absorption-limited regimes ((Fig. 4(a) and (b)). This is because of the associated decrease in the kinetic overpotentials for the desirable Fe(II) oxidation at the valence band. However, when competing reactions are considered, select values of αa,RS result in an optimal exchange current density that maximizes STC efficiencies. This is because of the balance between the gains from the increased rates of the desired redox shuttle reactions (Fe(II) oxidation) with the losses from the undesired redox shuttle reactions (Fe(III) reduction).
The trends in reaction selectivity in Fig. 4(c) and (d) at the conduction and valence bands help further explain trends in STC efficiency when competing reactions were modeled in the sunlight-absorption-limited regime (Fig. 4(b)). Selectivity trends are similar for the mass-transfer-limited regime (Fig. 4(a), and hence not shown. For small values of j0,RS and αa,RS examined, selectivity towards both the desired Fe(II) redox shuttle oxidation and H2 evolution, Srxn,VB and Srxn,CB respectively, is small and near-zero, which results in the low STC efficiencies obtained under these conditions. With an increase in the j0,RS, selectivity toward desirable oxidation of the Fe(II) redox shuttle increases monotonically and reaches a maximum of ∼95% (Fig. 4(c)), which restricts the maximum STC efficiency observed to 18.64% (Fig. 4(b)). The balance contribution is from mass-transfer-limited hydrogen oxidation, which is small in value due to the limited solubility of H2 in water (0.78 mM in equilibrium with 1 atm H2 at 300 K). However, reaction selectivity toward H2 evolution, Srxn,CB, exhibits different trends, especially when αa,RS ≤ 0.7, where it initially decreases with increasing j0,RS, but subsequently increases. This trend is explained by the combined behaviors of the RS reaction at both the conduction and valence bands: for small j0,RS values, both RS oxidation and reduction reactions are kinetically limited (Fig. S2(b), ESI†); as j0,RS approaches 1 × 10−4 A m−2, the competing RS reaction at the conduction band increases whereas the desired RS oxidation at the valence band remains kinetically limited, resulting in the decrease in Srxn,CB (Fig. S2(c), ESI†); for j0,RS > 1 × 10−4 A m−2, the RS reaction at the conduction band becomes mass-transfer limited, but the valence band remains kinetically limited (Fig. S2(d), ESI†). When αa,RS > 0.7 the selectivity towards H2 production decreases from 100% with an increase in j0,RS (Fig. 4(d)), because of the increase in the rate of the competing Fe(III) reduction. For large values of j0,RS, selectivity for H2 evolution at the conduction band approaches the same value irrespective of αa,RS, because the competing reduction of the Fe(III) species is limited by mass transfer at this point (Fig. 3(a)).
Overall, the STC efficiency is dictated by the product of the reaction selectivity at the valence and conduction bands, which leads to an optimal range of j0,RS for select αa,RS values; for αa,RS = 0.99, Fig. 4(b) shows an optimal range for j0,RS between 1 × 10−2 – 1 A m−2. Although the STC efficiency magnitudes in Fig. 4 are dependent on many model-specific parameters, the trends in these efficiencies are more critical and revealing of the influences of competing redox shuttle reactions and kinetic parameters. Fig. S3 (ESI†) shows that these trends are preserved even when we computed an external/apparent quantum yield (eqn (2)), which is a ratio of the flux of charge-carriers utilized for H2 production compared to an incident flux of photons on the light absorber.
3.2. Influences of the redox shuttle reduction potential – single slab light absorber
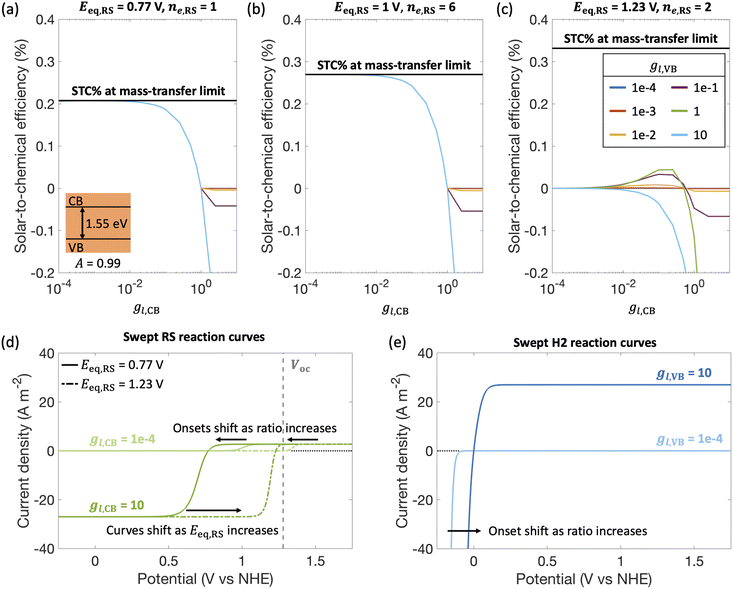
By fixing the kinetic parameters for the redox shuttle (j0,RS = 10 A m−2, αa,RS = 0.5), we illustrate the influences of considering different redox shuttles by varying their reduction potentials, Eeq,RS and correspondingly the number of electrons involved. For example, Eeq,RS = 0.77 V, 1 V and 1.23 V vs. NHE is representative of Fe(III)/Fe(II), I−/IO3− and H2O/O2 redox shuttles, respectively. Moreover, the redox shuttle potential has been previously shown to influence optimal solar-to-hydrogen efficiencies in Z-scheme solar water splitting systems.13Fig. 5 illustrates that the reduction potential of the redox shuttle not only impacts the magnitudes of the STC efficiency, but also the extent to which the asymmetry in mass-transfer rates (gl,VB and gl,CB) affects the performance. For all cases (Fig. 5(a)–(c)), as the reduction potential of the redox shuttle increases, the maximum STC efficiency decreases, with a more significant drop from Eeq,RS = 1 V to 1.23 V (Fig. 5(b) and (c)). With the increase in Eeq,RS, the operating potential shifts towards the open-circuit potential (1.26 V, Fig. 5(d)) of the light absorber, which decreases the operating current density and therefore the STC efficiency. For a small enough Eeq,RS, as compared to the open-circuit potential (Fig. 5(a) and (b)), the STC efficiency generally decreases with an increase in the asymmetry factor for redox shuttle reduction (gl,CB), and levels off when the STC efficiency becomes limited by H2 oxidation at the valence band. As expected, as the asymmetry factor for H2 oxidation, gl,CB, increases, the STC efficiency monotonically decreases. However, when Eeq,RS increases, an optimum exists for both asymmetry factors, except when gl,VB = 10. This is due to the tradeoffs in the enhanced reaction rates for the desired reactions with the increase in mass-transfer rates of competing redox reactions. As the asymmetry factor increases, the surface concentrations of corresponding redox species increase (eqn (S7), ESI†), which enhances reaction rates and consequently lowers the onset potential. For instance, with increasing limiting current density for redox shuttle reduction (i.e., gl,CB), the onset potential for RS oxidation decreases by 200 mV when gl,CB increases from 1 × 10−4 to 1 × 10−1 for Eeq,RS = 1.23 V in Fig. 5(d). Similarly, increasing the limiting current density for redox shuttle oxidation (i.e., gl,VB) results in a shift in the anodic potential by up to 100 mV (Fig. 5(e)). These gains in reaction rates (and lower onset potentials) bear more significance when the redox shuttle reduction potential approaches the open-circuit potential of the photodiode, where the operating currents are low. However, when gl,VB becomes 10, STC monotonically declines with gl,CB due to increased losses from H2 oxidation.
3.3. Influences of mass-transfer asymmetry in ensembles of light absorbers
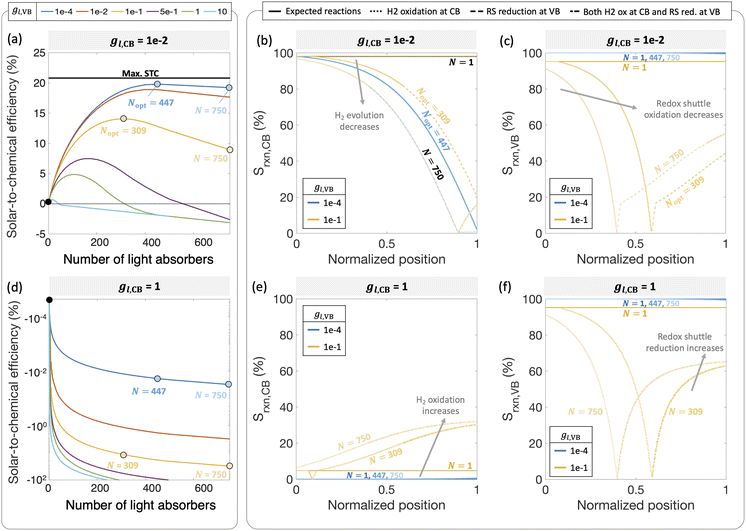
Fig. 6 predicts the performance for an ensemble of light absorbers in the mass-transfer-limited regime (jl,RS,a/jsc,N=1 = 1 × 10−2, Fig. 3(a), Fig. 4(a)), where the gains of multiple, optically thin light absorbers (N > 1) are expected to be larger compared to a single, optically thick light absorber (N = 1). Fig. 6(a) and (c) illustrate the qualitative differences in intensity profiles between these two cases, while Fig. 6(b) and (d) show corresponding differences in the load line analyses. Because the incident photon flux from sunlight exponentially decreases as per the Beer–Lambert law, the light absorbers at the bottom become increasingly limited by the incident photon flux as the number of light absorbers increases. Therefore, even though a single light absorber slab (N = 1) is mass-transfer-limited (Fig. 6(b)), as N increases, the slabs near the bottom will become sunlight-absorption-limited (Fig. 6(d)).Fig. 7 reveals that two distinct trends emerge for how the ensemble influences STC efficiency dependent on the asymmetry factor for redox shuttle reduction (gl,CB). While for small values of gl,CB ≤ 1 × 10−2 (Fig. 7(a)), there is an optimum number of light absorbers, for large values of gl,CB ≥ 1 × 10−1 (Fig. 7(d) shows gl,CB = 1), increasing the number of light absorbers results in monotonically decreasing STC efficiencies. For the case of gl,CB ≤ 1 × 10−2 (Fig. 7(a)), at the optimal point, the multiplicative gain from positive STC efficiencies produced per light absorber is balanced by those in the bottom driving the competing redox shuttle reduction reactions. At these optimal points, even though the top light absorber is mass-transfer-limited, most of the light absorbers (>75%) in the bottom are sunlight-absorption-limited. Fig. 7(b) and (c) further illustrate the ensemble influences on the reaction selectivity. As the number of light absorbers increases, the bottom light absorbers are sunlight-absorption-limited and operate with a much smaller open-circuit potential, which favors competing reactions. This effect is amplified when larger radiative recombination current densities are assumed, and results in overall smaller STC efficiencies being reached (Fig. S1, ESI†). Together with the asymmetry factors, the smaller open-circuit potentials influence how reaction selectivity varies from the top to the bottom for both H2 evolution, Srxn,CB (Fig. 7(b)) and redox shuttle oxidation, Srxn,VB (Fig. 7(c)). For small asymmetry factors, while mass-transfer limits STC values for a single light absorber, N = 1, reaction selectivity becomes the limiting factor as N increases. An ensemble with N = 447 is the optimal number of light absorbers that maximizes STC efficiency for gl,CB = 1 × 10−2 and gl,VB = 1 × 10−4. For this case, the H2 evolution selectivity at the conduction band, Srxn,CB, progressively decreases from the top to the bottom, as the decrease in the open-circuit potential favors the competing redox shuttle reduction. Because the asymmetry factor in mass-transfer rates for H2 oxidation, gl,VB, is very small, redox shuttle oxidation selectivity at the valence band, Srxn,VB, is unaffected and nearly 100%. When gl,VB increases from 1 × 10−4 to 1 × 10−1 (Fig. 7(a)), the optimal number of light absorbers is N = 309. While the reaction selectivity towards H2 production, Srxn,CB, still monotonically decreases from the top to the bottom, Srxn,VB initially declines to a value of 0, and then counterintuitively increases in the bottom half of the light absorbers. This increase in Srxn,VB is because of the increasing contributions from the competing redox shuttle reduction in addition to H2 oxidation at the valence band states (Fig. S4(d)–(f) (ESI†) shows similar outcomes for N = 750). Redox shuttle reduction translates to an increase in the selectivity, Srxn,VB, because it is defined based on the magnitude of the current density towards redox shuttle species reactions, irrespective of whether it is oxidation or reduction (eqn (2)). Selectivity further worsens at any location as the number of light absorbers increases beyond the optimal value to N = 750. Fig. S4 (ESI†) maps different points from the top to the bottom on the selectivity plots with the load-line analyses to further illustrate the individual reactions occurring at the valence and the conduction bands. When there are a larger number of light absorbers that are vertically stacked, the light absorbers at the very bottom are so severely sunlight-absorption limited that a complete reversal happens with only undesired redox reactions taking place at both the valence and conduction bands. Fig. S4(f), ESI† shows that for the very last light absorber (i.e., n = 750), the net reaction is H2 oxidation simultaneous with redox shuttle reduction on the photocatalyst.
When the asymmetry factor in mass-transfer rates for redox shuttle reduction increases, gl,CB ≥ 1 × 10−1, the STC efficiency decreases with increasing number of light absorbers even for the lowest gl,VB modeled (Fig. 7(d)). Selectivity trends depicted in Fig. 7(e) and (f) provide further insights indicating that largely H2 oxidation occurs at the conduction band at all spatial positions. Similar to Fig. 7(c), redox shuttle reduction also becomes a competing reaction at the valence band for the light absorbers in the bottom half of the reactor (Fig. 7(f)). This amplified extent of H2 oxidation, balanced by redox shuttle reduction, occurring at both the valence and conduction bands, results in increasingly large negative STC efficiencies as the number of light absorbers increases in the ensemble.
Fig. 7 considered effects of the relative rates of mass-transfer for the desired and undesired redox reactions, but with fixed kinetic parameters for the H2 and the RS species (H2: j0,H2 = 10 A m−2 and αa,H2 = αc,H2 = 1; redox shuttle: j0,RS = 10 A m−2 and αa,RS = 0.5). These baseline values are selected based on commonly reported exchange current densities and charge-transfer coefficients for these reactions. In this mass-transfer-limited regime, if the kinetic parameters were varied, similar to that in Fig. 4 for the single slab, we still expect the trends to remain intact for the dependence of STC efficiency on the number of light absorbers, however magnitudes and the optimal points will shift. These parametric explorations with the ensemble can also be conducted for the scenario where the topmost light absorber is not mass-transfer-limited but operative in the sunlight-absorption-limited regime with jl,RS,a/jsc,N=1 ≥ 1 (Fig. 10). Under these conditions, the trends of the STC with respect to the number of light absorbers could be different, and the effects of the asymmetry parameters for mass-transfer are expected to be more subdued. While outside the scope of the current study, to quantitatively identify decisive factors for selectivity at the ensemble level, more extensive parametric explorations and sensitivity analyses should be performed.
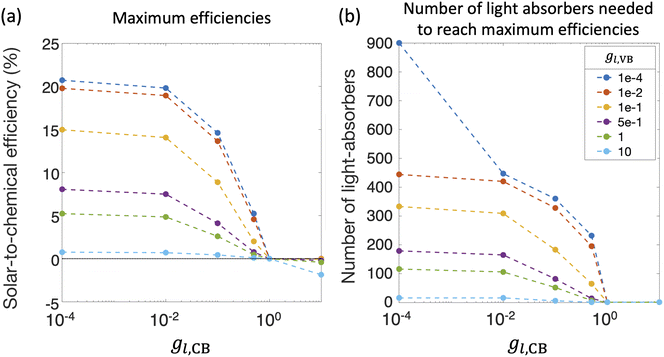
Fig. 8(a) and (b) compile optimal STC efficiencies and the corresponding number of light absorbers as a function of asymmetry factors in mass-transfer rates for redox shuttle reduction and H2 oxidation (gl,CB and gl,VB). For the specific kinetic parameters modeled, asymmetry factors larger than 1 × 10−2 substantially penalize the STC efficiencies as the competing redox shuttle reduction and H2 oxidation dominate over the desired reactions. For any value of gl,VB, when gl,CB = 1, all STC efficiencies converge to 0 because all light absorbers are implementing equal mass-transfer limited rates of the desired redox shuttle oxidation and redox shuttle reduction. Generally, the STC efficiency is strongly influenced by the greater of the two asymmetry factors, which has implications that it is equally important to develop strategies to restrict mass transfer of both H2 and the oxidized redox shuttle species (Fe(III) in this case) to the reaction sites. As the asymmetry factors increase, the optimal number of light absorbers to maximize efficiency rapidly decreases to N = 1, indicating that all light absorbers other than the first are implementing H2 oxidation more than H2 evolution. For the smallest asymmetry factor modeled for the limiting current density of H2 oxidation (gl,VB = 1 × 10−4), a notable change in the optimal number of light absorbers occurs, from 900 to 447, when gl,CB increases from 1 × 10−4 to 1 × 10−2. This is because such a small asymmetry factor in mass-transfer rates for redox shuttle reduction, gl,CB = 1 × 10−4, facilitates continued operation within the mass-transfer-limited regime, such that the benefits from additional light absorbers still occurs even at N = 900.
3.4. Implications of model predictions and comparisons with measurements
Our results and interpretations of the optimal effect of the number of light absorbers are broadly relevant for nano- and micro-scale individual and ensembles of photocatalysts, including particle-suspension reactors,12,47 photocatalytic sheets of particles11,52 and other structured ensemble systems such as nanowire arrays.85,86 Analogous to the ensembles of planar slabs considered in this study, where each absorber is subject to different short-circuit and operating current densities (Fig. 6), every particle in a particle-suspension reactor will yield different rates of desired and undesired chemical reactions, even notwithstanding transport effects, depending upon its spatial position, size, and distribution in the reactor.The absorptance dependence on the optical thickness for individual and ensembles can be defined specific to the system. For instance, the absorptance-optical thickness relationship for a homogeneous suspension of small, non-scattering particles is given by eqn (4) and (5),12,75
| Atotal = Asuspension = 1 − exp(−τsuspension) | (4) |
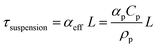 | (5) |
In our current study, the total absorptance was fixed at 99% irrespective of the number of planar slabs in the ensemble. When the number of light absorbers is larger than 1 (N > 1), improved and better load matching occurs, especially in the mass-transfer limited regime, to yield better performance from multiplicative gains. For particle-suspensions with a fixed total suspension absorptance (eqn (5)), this effect can analogously arise from: (i) an optimal particle diameter and/or (ii) a spatially varying particle concentration distribution that optimizes the solar-to-chemical efficiency. However, there could be convoluted effects at the ensemble-scale especially when the particle size is considered as a design variable. The internal quantum yields, dictated by charge-separation efficiencies at the individual particle-scale,75 and aggregation of particles in a suspension are both strongly particle-size dependent,87,88 and could dominate performance in a real suspension reactor.
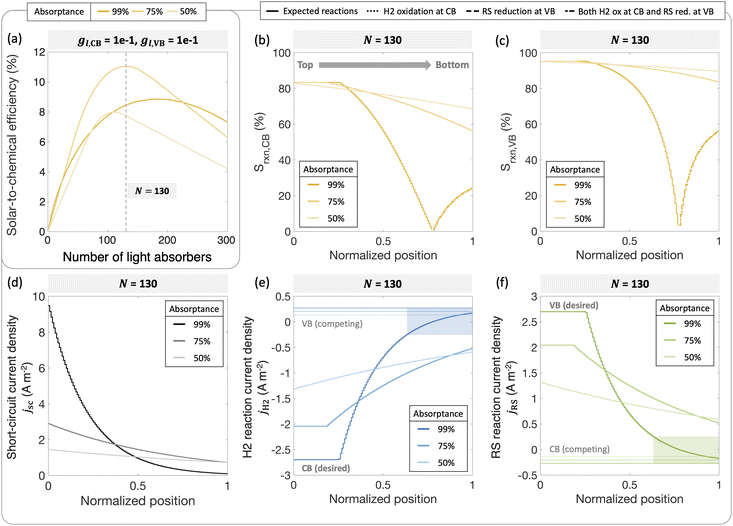
To further illustrate the applicability of the models developed, we apply and compare model predictions to both previously reported and new experimental data to interpret trends in H2 evolution rates and efficiencies (apparent quantum yield) with (a) varying particle concentration and (b) incident photon flux. In recent work, Lin et al. experimentally demonstrated that with a C2O3/Pt/IrO2/Sm2Ti2O5S2 photocatalyst, increasing loadings resulted in an optimal H2 evolution rate of 1.333 g L−1.88 In our models varying particle concentration translates to varying the total absorptance of the suspension (eqn (4) and (5)). This approach is applied to predict photocatalytic H2 production in the presence of a redox shuttle as a function of the total absorptance for Atotal = 50%, 75% and 99%.
Fig. 9 shows that a maximum solar-to-chemical efficiency is obtained for a total ensemble absorptance of 75%. This is somewhat analogous to an optimal particle concentration that maximizes solar-to-chemical efficiency in the experimental data. At a total suspension absorptance of Atotal = 50%, representing a low concentration of particles in the solution, the solar-to-chemical efficiencies are relatively lower even with high selectivity values (Fig. 9(b) and (c)) because the desired reaction rates are limited by the absorption of incident photons. However, for the highest absorptance modeled of Atotal = 99%, indicative of a large concentration of particles, the solar-to-chemical efficiencies are limited by the reaction selectivity (Fig. 9(b) and (c)). For this case, even though the particles in the upper quartile (normalized position ≤0.25) of the reactor are driving H2 evolution at the largest current densities of the three cases modeled (Fig. 9(d)), and operate with high selectivity (Fig. 9(b) and (c)), the particles in the lower quartile of the reactor (normalized position ≥0.75) paint a different picture. Specifically, the change in the selectivity slopes (Fig. 9(b) and (c)) is due to the complete reversal of redox reactions taking place at both the conduction and valence bands – i.e., H2 oxidation and redox shuttle reduction occur at the conduction band, whereas redox shuttle reduction and H2 oxidation occur at the valence band. This reversal occurs because the absorbers at the bottom are severely light-limited, resulting in very low open-circuit and operating potentials, leading to competing, thermodynamically downhill reactions instead of the desired chemical reactions. The shaded areas in Fig. 9(e) and (f) indicate normalized depths within the suspension reactor, where the desired reactions reach current densities smaller than the competing reactions, and this occurs only for the highest absorptance of Atotal = 99%.
Overall, an absorptance of 75% and equivalently, an optimal particle concentration best balances the efficiency of light absorption and the reaction selectivity, resulting in an optimal efficiency. An underlying assumption is that the suspension operates at the optimal efficiency at any absorptance modeled, which need not be the case. While reflection losses due to scattering by particle agglomerates can also increase with an increase in the particle concentration, our model predictions show that the spatial distribution of photocurrents within the reactor volume will also significantly influence reaction selectivity and performance. Therefore, having the ability to tune, both the magnitude and the spatial distribution of photon absorption in a photocatalytic reactor will be useful towards performance optimization.
Fig. 10 shows that model predictions qualitatively compare well with experimental measurements. The incident photon flux was varied in a suspension of Ir-doped SrTiO3 particles for H2 evolution in the presence of 10 v/v% CH3OH, which acts as a hole scavenger. Fig. 10(b) shows that experimentally, while the measured H2 production rate increases with the input power, it is not a proportional rise. Therefore, there is a monotonically decreasing trend of the measured apparent quantum yield (AQY), which is indicative of performance limitations arising from factors other than light absorption. Fig. 10(c) shows model predictions for the H2 production rates and the apparent quantum yields with calibrated input parameters for the experimental measurements (Section 2.6). As the incident flux of photons increases, the H2 production rate initially increases, but levels-off thereafter due to increasingly mass-transfer-limited CH3OH oxidation. Correspondingly, the AQY also monotonically decreases and is qualitatively consistent with the experimental data after a threshold incident flux of 30 mW cm−2. Even though the absolute magnitudes for the predictions are significantly larger than the experimentally measured performance, the qualitative trends are the same. Fig. 10(d) shows that the reaction selectivity at both the conduction and valence bands initially increases with the incident photon flux but plateaus when the desired reaction rates transition from light absorption to mass transport limitations. At the low incident photon flux, reaction selectivity is negatively influenced due to the reduced operating potentials from the limited light absorption. Calculations performed with an ensemble of optically thin slabs (N > 1) also predict that the optimal AQY decreases from the smallest (11 mW cm−2) to the largest (130 mW cm−2) incident flux modeled, although the extent of reduction with incident flux is smaller than in Fig. 10 with N = 1. At the smallest incident flux, the photocatalytic suspension is light-absorption-limited (Fig. 3(b)), and therefore N = 1 leads to the maximum AQY value. Whereas, for fluxes larger than 30 mW cm−2, mass-transfer limitations become more dominant (Fig. 3(a)), where cases with N > 1 will lead to higher efficiencies and AQY values (similar to Fig. 7 and Fig. 9) than the N = 1 case.
Similar to Fig. 7 and 8, as the asymmetry factors – gl,VB and gl,CB – modeled for mass-transfer limited reaction rates increase, the performance decreases. Although there can be uncertainty in what the specific values are for these asymmetry factors, for the concerned experiments, the mass-transfer-limited rates of the competing reactions, and therefore the asymmetry factors, at both the conduction and valence bands are expected to be small. This is because, unlike a reversible redox shuttle such as Fe(III)/Fe(II), methanol is a hole scavenger that will more selectively oxidize, and H2 oxidation rates are limited by the small concentration of the dissolved H2 (∼1 mM). Therefore, a dominant factor attributed to the discrepancy between the measured and the predicted AQY magnitudes is likely from the assumptions of idealized photodiode behavior, and perfect charge-separation of the generated carriers. Consistent with this expectation, in our recent work, Zutter et al. demonstrate severe penalties in charge-carrier separation quantum yields for Rh-doped SrTiO3 photocatalytic particles.75
Overall, Fig. 9 and 10 reinforce the value of applying a simple, tractable circuit-based model to help interpret and explain experimental data by interrogating the effects of many materials, thermodynamic, kinetic, and reactor design/operation parameters. These results illustrate that to fully reap the benefits of an ensemble of optically thin photo absorbers, the incident light profile on every absorber needs to be tuned to best match the electrochemical loads dictated by kinetics and mass-transfer rates. The idealizing assumptions made in the detailed balance formulation and assuming perfect charge-separation make it challenging to directly compare predictions against measurements, but provide powerful guidelines and capabilities to identify and isolate key parameters that influence performance.
3.5. Perspectives and insights to increase photocatalytic solar-to-chemical efficiency
A main finding from our study is that altering the relative mass transfer rates of competing redox species can boost reaction selectivity even with symmetric kinetic parameters for electrocatalysis (i.e., αa = αc) for reversible reactions. When the products of the desired reactions (e.g., dissolved H2 and oxidized redox shuttle species in this study) have significantly smaller mass-transfer rates compared to the reactants, they result in smaller mass-transfer asymmetry factors – gl,VB and gl,CB. This asymmetry depends on many factors that influence mass-transfer-limited current densities of the reactant and product species, including: (i) concentrations in the bulk solution, (ii) diffusivity, and (iii) the transport/mixing conditions. This improves STC efficiencies should especially for ensembles of photocatalysts that are otherwise limited to low efficiencies per light absorber (Fig. 7(a)). Notably, the optimal efficiency achieved with ensembles of light absorbers with low enough mass-transfer asymmetry factors (gl,VB < 1 × 10−2 and gl,VB ≤ 1 × 10−2) nearly matches the maximum efficiency predicted assuming ideally selective reactions and infinitely fast kinetics and mass transfer with a single, optically thick, light absorber (Fig. 4(b)). Therefore, we demonstrate that the design and development of functional interfaces to selectively tune and control species mass transfer to reaction sites, such that competing reactions are minimized, can play an outsized role to enhance STC efficiencies in photocatalytic systems. While this feature has been experimentally demonstrated in prior work with selectively permeable and thin oxide coatings in electrocatalysis89–91 and photocatalysis,92–94 our study quantitatively demonstrates the influences of mass-transfer asymmetry on efficiency and selectivity. These predictions are well-suited to be combined with measured or simulated structure-function-property relationships for selective coatings to develop guidelines for designing coatings that optimize the STC efficiencies of photocatalytic systems.89,95Additionally, from a reactor design and operation standpoint, mass-transfer asymmetry can be achieved more effectively with flow as compared to static/batch reactors. Transport asymmetry can also arise from having gaseous products, e.g., H2 and O2, that are sparingly soluble in water, which can bubble out of that solution and away from reaction sites, precluding back reactions. Redox reactions with the soluble and reversible redox shuttles will not have this advantage. In flow reactors, reactants are continuously delivered simultaneous with the product species being swept away from reaction sites, which can intrinsically introduce mass-transfer asymmetry in the desired direction. In contrast, for batch reactors the product species accumulates over time, leading to higher rates of (electro)chemical recombination of the product(s) formed. For instance, in the recently reported photocatalytic co-production of H2 and O2 with an impressively large 9% solar-to-hydrogen efficiency,96 periodic degassing/vacuuming was performed during stability tests over many cycles to prevent recombination of the H2 and O2 formed.97 While flow systems are widely used in electrolyzers, fuel cells, and photoelectrochemical systems, they are much less common in photocatalysis for H2 production. Future research should consider and further investigate this design question to quantitatively assess tradeoffs between efficiency and parasitic energy costs for pumping.
Our Fig. 8 predictions underscore the potential for avoiding significant efficiency and selectivity penalties when mass-transfer asymmetry factors are smaller than 1 × 10−2. Notably, considerable improvements are projected even with a tenfold reduction from symmetric mass-transfer rates particularly for the redox shuttle. While the redox shuttle conveniently physically separates the H2 and O2 production sites, the onus of performance is in-part transferred to engineering and optimizing mass transfer. This points to the need for further research focusing on developing and testing functional interfaces capable of tuning species transport to and from photocatalytic reaction sites. Overall, to unlock the next frontier of efficiency gains in photocatalytic H2 production, mass-transfer considerations are critical, together with optical/band-gap engineering, materials stability, and reactor-scale design/testing.
4. Conclusion
We have developed and adapted a powerful, yet simple, equivalent-circuit modeling framework for photocatalytic and (photo)electrochemical systems with multiple light absorbers with unique capabilities to model competing redox reactions and mass-transfer limitations. Notably, we predict reaction selectivity by performing load-line analyses of a photodiode power curve with the incorporation of a net electrochemical load curve that accounts for both the desired and the competing redox reactions. These electrochemical load curves account for not only kinetic but also mass-transfer overpotentials, which enables us to draw insights on the influences of different operating regimes limited by sunlight absorption, redox species mass-transfer, and electrochemical kinetics. This model is applied to evaluate the performance of a narrow bandgap (1.55 eV) photocatalyst – Ir-doped SrTiO3 – that evolves hydrogen together with oxidation of an aqueous redox shuttle for applications like Z-scheme solar water splitting with particulate photocatalysts. Models are developed to predict the solar-to-chemical efficiencies of a single, optically thick and an ensemble of optically thin light absorbers, with physical interpretations and insights to maximize reaction selectivity and efficiency.For a single, optically thick light absorber evolving hydrogen with oxidation of Fe(II) salt, larger solar-to-chemical efficiencies are predicted in the sunlight-absorption-limited regime, with optimal exchange current densities and asymmetric charge-transfer coefficients. The relative difference in the predicted efficiencies with and without modeling the competing redox reactions can be large, highlighting the need to account for undesired redox reactions, which includes hydrogen oxidation and Fe(III) reduction. When mass transfer becomes more limiting than the light absorption, the solar-to-chemical efficiency scales proportional with the limiting current densities of the desired reactions. Different redox shuttles (Fe(III)/Fe(II), I−/IO3− and H2O/O2) were modeled with the H2-evolving photocatalyst to demonstrate that the maximum attainable solar-to-chemical efficiencies generally decrease with increasing reduction potentials. For small redox shuttle reduction potentials, the efficiency monotonically decreases with an increase in the mass-transfer asymmetry factor, which compares the mass-transfer rates of the undesired to those of the desired reactions. However, this trend changes as the redox shuttle potential becomes more comparable to the open circuit potential of the photodiode (e.g., H2O/O2). Optimal mass-transfer asymmetry factors balance increased rates of the desired reactions with the increased surface concentrations for the competing redox reactions.
For an ensemble comprising of multiple, semi-transparent, and optically thin light absorbers, model predictions reveal their potential to outperform a single, optically thick light absorber, only when operated in mass-transfer-limited regime. However, to reap these projected benefits that stem from multiplicative gains from the different light absorbers, it is critical to minimize limiting currents of the undesired redox reactions as compared to the desired redox reactions. When the mass-transfer rates of the reactants for the competing redox reactions are 100-fold smaller than the desired reactions, i.e., mass-transfer asymmetry factors that are less than 1 × 10−2, an optimum number of planar slabs of light absorbers maximize efficiency. Even under these optimal conditions, a large fraction of the light absorbers in the bottom are driving competing reactions. When the mass-transfer-limited rates of the competing redox reactions match or become larger than the desired reaction rates, H2 oxidation predominates at both the valence and conduction band states. This translates to worse performance with every additional light absorber in the ensemble.
A unique finding from this study is that even with perfectly symmetric kinetic driving forces for the desired and the competing reactions, tuning the asymmetry in the limiting current densities of desired and competing redox reactions can achieve similar outcomes as having a single, optically thick, ideal light absorber with rapid mass-transfer and ideally selective kinetics. This discovery reveals that achieving selectivity need not solely depend on surface kinetics, and that manipulating redox species mass-transfer, for example with selective coatings, can help achieve reaction selectivity. Even a tenfold reduction in the mass-transfer rates of the competing reactions of the redox shuttle is projected to lead to significant performance benefits. The model developed is computationally tractable to explore the influences of various thermodynamic, kinetic and transport parameters, and the results have been further interpreted with experimental data in suspension reactors to provide important insights and guidance to advance next generation photocatalysts, selective coatings, and reactor designs.
Author contributions
Bala Chandran, Barrera, and Ardo – conceptualization; Bala Chandran and Barrera – data analyses and algorithm for code development; Barrera – coding, result generation, and plots; Bala Chandran, Barrera, and Esposito – mass-transfer and limiting current formulations; Layne and Chen – photocatalysis experimental measurements and related plots shown in Fig. 10; Wantanabe and Kudo – synthesis and characterization of Ir-doped SrTiO3 with an Ir cocatalyst for data shown in Fig. 10; and Bala Chandran and Barrera –manuscript writing, editing, and revisions.Data availability
All the datasets in the figures for the main manuscript and the code developed in this study are uploaded on Zenodo (https://10.0.20.161/zenodo.13800069).Conflicts of interest
There are no conflics to declare.Acknowledgements
The authors acknowledge financial support provided by the U.S. Department of Energy, Fuel Cell Technologies Office through the DE-EE0008838 award for study conceptualization, model development and debugging, all early simulations and data analyses. Publication-ready simulation data and figures, and manuscript revisions including experimental data collection were supported as part of Ensembles of Photosynthetic Nanoreactors (EPN), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science under Award Number DE-SC0023431. We also additionally acknowledge helpful discussions with Robert Stinson and Will Stinson from Columbia University to help formulate mass-transfer limited current densities.References
- A. J. Bard, J. Phys. Chem., 1982, 86, 172–177 CrossRef CAS.
- M. X. Tan, P. E. Laibinis, S. T. Nguyen, J. M. Kesselman, C. E. Stanton and N. S. Lewis, in Progress in Inorganic Chemistry, ed. K. D. Karlin, 1994, vol. 41, pp. 21–144 Search PubMed.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- M. T. Spitler, M. A. Modestino, T. G. Deutsch, C. X. Xiang, J. R. Durrant, D. V. Esposito, S. Haussener, S. Maldonado, I. D. Sharp, B. A. Parkinson, D. S. Ginley, F. A. Houle, T. Hannappel, N. R. Neale, D. G. Nocera and P. C. McIntyre, Sustainable Energy Fuels, 2020, 4, 985–995 RSC.
- G. Segev, J. Kibsgaard, C. Hahn, Z. J. Xu, W. H. Cheng, T. G. Deutsch, C. Xiang, J. Z. Zhang, L. Hammarström, D. G. Nocera, A. Z. Weber, P. Agbo, T. Hisatomi, F. E. Osterloh, K. Domen, F. F. Abdi, S. Haussener, D. J. Miller, S. Ardo, P. C. McIntyre, T. Hannappel, S. Hu, H. Atwater, J. M. Gregoire, M. Z. Ertem, I. D. Sharp, K. S. Choi, J. S. Lee, O. Ishitani, J. W. Ager, R. R. Prabhakar, A. T. Bell, S. W. Boettcher, K. Vincent, K. Takanabe, V. Artero, R. Napier, B. R. Cuenya, M. T. M. Koper, R. Van De Krol and F. Houle, J. Phys. D: Appl. Phys., 2022, 55, 1–52 CrossRef.
- S. Ardo, D. Fernandez Rivas, M. A. Modestino, V. Schulze Greiving, F. F. Abdi, E. Alarcon Llado, V. Artero, K. Ayers, C. Battaglia, J. P. Becker, D. Bederak, A. Berger, F. Buda, E. Chinello, B. Dam, V. Di Palma, T. Edvinsson, K. Fujii, H. Gardeniers, H. Geerlings, S. M. Hashemi, S. Haussener, F. Houle, J. Huskens, B. D. James, K. Konrad, A. Kudo, P. P. Kunturu, D. Lohse, B. Mei, E. L. Miller, G. F. Moore, J. Muller, K. L. Orchard, T. E. Rosser, F. H. Saadi, J. W. Schüttauf, B. Seger, S. W. Sheehan, W. A. Smith, J. Spurgeon, M. H. Tang, R. Van De Krol, P. C. K. Vesborg and P. Westerik, Energy Environ. Sci., 2018, 11, 2768–2783 RSC.
- A. J. Bard and M. A. Fox, Acc. Chem. Res., 1995, 28, 141–145 CrossRef CAS.
- T. Takata, J. Jiang, Y. Sakata, M. Nakabayashi, N. Shibata, V. Nandal, K. Seki, T. Hisatomi and K. Domen, Nature, 2020, 581, 411–414 CrossRef CAS PubMed.
- Z. Wang, C. Li and K. Domen, Chem. Soc. Rev., 2019, 48, 2109–2125 RSC.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef CAS.
- H. Nishiyama, T. Yamada, M. Nakabayashi, Y. Maehara, M. Yamaguchi, Y. Kuromiya, Y. Nagatsuma, H. Tokudome, S. Akiyama, T. Watanabe, R. Narushima, S. Okunaka, N. Shibata, T. Takata, T. Hisatomi and K. Domen, Nature, 2021, 598, 304–307 CrossRef CAS PubMed.
- R. Bala Chandran, S. Breen, Y. Shao, S. Ardo and A. Z. Weber, Energy Environ. Sci., 2018, 11, 115–135 RSC.
- S. Keene, R. Bala Chandran and S. Ardo, Energy Environ. Sci., 2019, 12, 261–272 RSC.
- Y. Goto, T. Hisatomi, Q. Wang, T. Higashi, K. Ishikiriyama, T. Maeda, Y. Sakata, S. Okunaka, H. Tokudome, M. Katayama, S. Akiyama, H. Nishiyama, Y. Inoue, T. Takewaki, T. Setoyama, T. Minegishi, T. Takata, T. Yamada and K. Domen, Joule, 2018, 2, 509–520 CrossRef CAS.
- A. Iwase, S. Yoshino, T. Takayama, Y. H. Ng, R. Amal and A. Kudo, J. Am. Chem. Soc., 2016, 138, 10260–10264 CrossRef CAS PubMed.
- Z. Li, Y. Yang, J. Tian, J. Li, G. Chen, L. Zhou, Y. Sun and Y. Qiu, ChemSusChem, 2022, 15, 1–10 Search PubMed.
- P. G. Alsabeh, A. Rosas-Hernández, E. Barsch, H. Junge, R. Ludwig and M. Beller, Catal. Sci. Technol., 2016, 6, 3623–3630 RSC.
- D. K. Chauhan, N. Sharma and K. Kailasam, Mater. Adv., 2022, 3, 5274–5298 RSC.
- Z. Fu, X. Wang, A. M. Gardner, X. Wang, S. Y. Chong, G. Neri, A. J. Cowan, L. Liu, X. Li, A. Vogel, R. Clowes, M. Bilton, L. Chen, R. S. Sprick and A. I. Cooper, Chem. Sci., 2020, 11, 543–550 RSC.
- J. L. White, M. F. Baruch, J. E. Pander, Y. Hu, I. C. Fortmeyer, J. E. Park, T. Zhang, K. Liao, J. Gu, Y. Yan, T. W. Shaw, E. Abelev and A. B. Bocarsly, Chem. Rev., 2015, 115, 12888–12935 CrossRef CAS PubMed.
- V. N. Nguyen and L. Blum, Chem. Ing. Tech., 2015, 87, 354–375 CrossRef CAS.
- A. D. Tjandra and J. Huang, Chin. Chem. Lett., 2018, 29, 734–746 CrossRef CAS.
- P. Prabhu, V. Jose and J. M. Lee, Adv. Funct. Mater., 2020, 30, 1–32 CrossRef.
- W. Zhang, A. R. Mohamed and W. J. Ong, Angew. Chem., Int. Ed., 2020, 59, 22894–22915 CrossRef CAS PubMed.
- M. Bellardita, V. Loddo, F. Parrino and L. Palmisano, ChemPhotoChem, 2021, 5, 767–791 CrossRef CAS.
- D. Adekoya, M. Tahir and N. A. S. Amin, Renewable Sustainable Energy Rev., 2019, 116, 109389 CrossRef CAS.
- S. C. Roy, O. K. Varghese, M. Paulose and C. A. Grimes, ACS Nano, 2010, 4, 1259–1278 CrossRef CAS PubMed.
- D. Bahnemann, Sol. Energy, 2004, 77, 445–459 CrossRef CAS.
- N. Wang, X. Zhang, Y. Wang, W. Yu and H. L. W. Chan, Lab Chip, 2014, 14, 1074–1082 RSC.
- X. Zhang, J. Wang, X. X. Dong and Y. K. Lv, Chemosphere, 2020, 242, 125144 CrossRef CAS PubMed.
- S. Escobedo and H. de Lasa, Catalysts, 2020, 10, 966 CrossRef CAS.
- Q. Li, Y. Ouyang, H. Li, L. Wang and J. Zeng, Angew. Chem., Int. Ed., 2022, 61, 1–27 Search PubMed.
- M. S. A. Sher Shah, C. Oh, H. Park, Y. J. Hwang, M. Ma and J. H. Park, Adv. Sci., 2020, 7, 2001946 CrossRef CAS PubMed.
- D. Hu, V. V. Ordomsky and A. Y. Khodakov, Appl. Catal., B, 2021, 286, 119913 CrossRef CAS.
- S. Navarro-Jaén, M. Virginie, J. Bonin, M. Robert, R. Wojcieszak and A. Y. Khodakov, Nat. Rev. Chem., 2021, 5, 564–579 CrossRef PubMed.
- L. Yuliati and H. Yoshida, Chem. Soc. Rev., 2008, 37, 1592 RSC.
- J. Xie, R. Jin, A. Li, Y. Bi, Q. Ruan, Y. Deng, Y. Zhang, S. Yao, G. Sankar, D. Ma and J. Tang, Nat. Catal., 2018, 1, 889–896 CrossRef CAS.
- X. Li, C. Wang and J. Tang, Nat. Rev. Mater., 2022, 7, 617–632 CrossRef CAS.
- C. Sambiagio and T. Noël, Trends Chem., 2020, 2, 92–106 CrossRef CAS.
- M. Oelgemöller, Chem. Rev., 2016, 116, 9664–9682 CrossRef PubMed.
- G. Chen, G. I. N. Waterhouse, R. Shi, J. Zhao, Z. Li, L. Wu, C. Tung and T. Zhang, Angew. Chem., 2019, 131, 17690–17715 CrossRef.
- M. H. Shaw, J. Twilton and D. W. C. MacMillan, J. Org. Chem., 2016, 81, 6898–6926 CrossRef CAS PubMed.
- H. Kato, Y. Sasaki, N. Shirakura and A. Kudo, J. Mater. Chem. A, 2013, 1, 12327 RSC.
- Y. Qi, S. Chen, J. Cui, Z. Wang, F. Zhang and C. Li, Appl. Catal., B, 2018, 224, 579–585 CrossRef CAS.
- C. Bie, L. Wang and J. Yu, Chem, 2022, 8, 1567–1574 CAS.
- Y. Sasaki, A. Iwase, H. Kato and A. Kudo, J. Catal., 2008, 259, 133–137 CrossRef CAS.
- D. M. Fabian, S. Hu, N. Singh, F. A. Houle, T. Hisatomi, K. Domen, F. E. Osterloh and S. Ardo, Energy Environ. Sci., 2015, 8, 2825–2850 RSC.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 RSC.
- B. D. James, G. N. Baum, J. Perez and K. N. Baum, Technoeconomic Analysis of Photoelectrochemical (PEC) Hydrogen Production, 2009 Search PubMed.
- B. D. James, D. A. Desantis, J. M. Huya-Kouadio, C. Houchins, Y. Acevedo and G. Saur, DOE Hydrogen Program, Annual Merit Review and Peer Evaluation Meeting Search PubMed.
- B. D. James, J. M. Huya-Kouadio, C. Houchins, Y. Acevedo, K. Mcnamara and G. Saur, DOE Hydrogen Program, Annual Merit Review and Peer Evaluation Meeting Search PubMed.
- Q. Wang, T. Hisatomi, Y. Suzuki, Z. Pan, J. Seo, M. Katayama, T. Minegishi, H. Nishiyama, T. Takata, K. Seki, A. Kudo, T. Yamada and K. Domen, J. Am. Chem. Soc., 2017, 139, 1675–1683 CrossRef CAS PubMed.
- Y. Sasaki, H. Kato and A. Kudo, J. Am. Chem. Soc., 2013, 135, 5441–5449 CrossRef CAS PubMed.
- Y. Surendranath, D. K. Bediako and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15617–15621 CrossRef CAS PubMed.
- M. R. Shaner, K. T. Fountaine and H. J. Lewerenz, Appl. Phys. Lett., 2013, 103(143905), 1–4 Search PubMed.
- M. T. Winkler, C. R. Cox, D. G. Nocera and T. Buonassisi, Proc. Natl. Acad. Sci. U. S. A., 2013, 1–7 CAS.
- K. T. Fountaine, H. J. Lewerenz and H. A. Atwater, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- S. Hu, C. Xiang, S. Haussener, A. D. Berger and N. S. Lewis, Energy Environ. Sci., 2013, 6, 2984–2993 RSC.
- B. Seger, O. Hansen and P. C. K. Vesborg, Sol. RRL, 2017, 1, 1600013 Search PubMed.
- I. Holmes-Gentle and K. Hellgardt, Sci. Rep., 2018, 8, 1–9 CAS.
- L. Barrera and R. Bala Chandran, ACS Sustainable Chem. Eng., 2021, 9, 3688–3701 CrossRef CAS.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 RSC.
- S. Nandy, S. A. Savant and S. Haussener, Chem. Sci., 2021, 12, 9866–9884 RSC.
- Z. Wang, T. Hisatomi, R. Li, K. Sayama, G. Liu, K. Domen, C. Li and L. Wang, Joule, 2021, 5, 344–359 CrossRef CAS.
- Q. Wang, T. Hisatomi, Q. Jia, H. Tokudome, M. Zhong, C. Wang, Z. Pan, T. Takata, M. Nakabayashi, N. Shibata, Y. Li, I. D. Sharp, A. Kudo, T. Yamada and K. Domen, Nat. Mater., 2016, 15, 611–615 CrossRef CAS PubMed.
- S. Ardo, S. T. Keene and G. S. Phun, US 2020/0140293A1, 2020.
- S. T. Keene, Detailed Balance Modeling of Novel Solar Fuels Designs, PhD thesis, University of California, Irvine, 2018 Search PubMed.
- E. Verlage, S. Hu, R. Liu, R. J. R. Jones, K. Sun, C. Xiang, N. S. Lewis and H. A. Atwater, Energy Environ. Sci., 2015, 8, 3166–3172 RSC.
- K. Sun, R. Liu, Y. Chen, E. Verlage, N. S. Lewis and C. Xiang, Adv. Energy Mater., 2016, 6, 1600379 CrossRef.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 RSC.
- C. Xiang, A. Z. Weber, S. Ardo, A. Berger, Y. Chen, R. Coridan, K. T. Fountaine, S. Haussener, S. Hu, R. Liu, N. S. Lewis, M. A. Modestino, M. M. Shaner, M. R. Singh, J. C. Stevens, K. Sun and K. Walczak, Angew. Chem., Int. Ed., 2016, 55, 12974–12988 CrossRef CAS PubMed.
- M. R. Singh, K. Papadantonakis, C. Xiang and N. S. Lewis, Energy Environ. Sci., 2015, 8, 2760–2767 RSC.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- ASTM G173-03(2012), ASTM International, 2013, 03, pp. 1–21.
- B. Zutter, Z. Chen, L. Barrera, W. Gaieck, A. S. Lapp, K. Watanabe, A. Kudo, D. V. Esposito, R. Bala Chandran, S. Ardo and A. A. Talin, ACS Nano, 2023, 17, 9405–9414 CrossRef CAS PubMed.
- International Union of Pure and Applied Chemistry - Physical Chemistry Division, Quantities, Units and Symbols in Physical Chemistry, Second, 1993.
- A. Martí, J. L. Balenzategui and R. F. Reyna, J. Appl. Phys., 1997, 82, 4067–4075 CrossRef.
- R. Brenes, M. Laitz, J. Jean, D. W. Dequilettes and V. Bulović, Phys. Rev. Appl., 2019, 12, 014017 CrossRef CAS.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems, 3rd edn, 2004 Search PubMed.
- B. E. Conway and L. Rai, J. Electroanal. Chem., 1986, 198, 149–175 CrossRef CAS.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39, 163–184 CrossRef CAS.
- K. C. Neyerlin, W. Gu, J. Jorne and H. A. Gasteiger, J. Electrochem. Soc., 2007, 154, B631 CrossRef CAS.
- NS, Curve Intersections, MATLAB Central File Exchange, 2022 Search PubMed , https://www.mathworks.com/matlabcentral/fileexchange/22441-curve-intersections.
- S. Suzuki, H. Matsumoto, A. Iwase and A. Kudo, Chem. Commun., 2018, 54, 10606–10609 RSC.
- G. Wang, H. Wang, Y. Ling, Y. Tang, X. Yang, R. C. Fitzmorris, C. Wang, J. Z. Zhang and Y. Li, Nano Lett., 2011, 11, 3026–3033 CrossRef CAS PubMed.
- Y. Ji, L. Yang, X. Ren, G. Cui, X. Xiong and X. Sun, ACS Sustainable Chem. Eng., 2018, 6, 9555–9559 CrossRef CAS.
- M. Kobayashi, F. Juillerat, P. Galletto, P. Bowen and M. Borkovec, Langmuir, 2005, 21, 5761–5769 CrossRef CAS PubMed.
- L. Lin, Y. Ma, J. J. M. Vequizo, M. Nakabayashi, C. Gu, X. Tao, H. Yoshida, Y. Pihosh, Y. Nishina, A. Yamakata, N. Shibata, T. Hisatomi, T. Takata and K. Domen, Nat. Commun., 2024, 15, 397 CrossRef CAS PubMed.
- M. E. S. Beatty, E. I. Gillette, A. T. Haley and D. V. Esposito, ACS Appl. Energy Mater., 2020, 3, 12338–12350 CrossRef CAS.
- D. V. Esposito, ACS Catal., 2018, 8, 457–465 CrossRef CAS.
- A. A. Bhardwaj, J. G. Vos, M. E. S. Beatty, A. F. Baxter, M. T. M. Koper, N. Y. Yip and D. V. Esposito, ACS Catal., 2021, 11, 1316–1330 CrossRef CAS.
- K. Maeda, N. Sakamoto, T. Ikeda, H. Ohtsuka, A. Xiong, D. Lu, M. Kanehara, T. Teranishi and K. Domen, Chem. – Eur. J., 2010, 16, 7750–7759 CrossRef CAS PubMed.
- S. Nandy, T. Hisatomi, M. Nakabayashi, H. Li, X. Wang, N. Shibata, T. Takata and K. Domen, Joule, 2023, 7, 1641–1651 CrossRef CAS.
- T. Suguro, F. Kishimoto, N. Kariya, T. Fukui, M. Nakabayashi, N. Shibata, T. Takata, K. Domen and K. Takanabe, Nat. Commun., 2022, 13, 5698 CrossRef CAS PubMed.
- F. Aydin, M. F. C. Andrade, R. S. Stinson, A. Zagalskaya, D. Schwalbe-Koda, Z. Chen, S. Sharma, A. Maiti, D. V. Esposito, S. Ardo, T. A. Pham and T. Ogitsu, ACS Appl. Mater. Interfaces, 2023, 15, 17814–17824 CrossRef CAS PubMed.
- P. Zhou, I. A. Navid, Y. Ma, Y. Xiao, P. Wang, Z. Ye, B. Zhou, K. Sun and Z. Mi, Nature, 2023, 613, 66–70 CrossRef CAS PubMed.
- H. Jung and J. W. Ager, Joule, 2023, 7, 459–461 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee02005g |
| ‡ Current address: School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30308, USA. |
| This journal is © The Royal Society of Chemistry 2024 |