Open Access Article
Open Access ArticleTailoring the Wadsley–Roth crystallographic shear structures for high-power lithium-ion batteries†
Panpan
Jing‡
ab,
Mengting
Liu‡
bc,
Hsin-Pei
Ho
d,
Yifan
Ma
e,
Weibo
Hua
 c,
Haohui
Li
a,
Nan
Guo
a,
Yong
Ding
b,
Weilin
Zhang
c,
Haohui
Li
a,
Nan
Guo
a,
Yong
Ding
b,
Weilin
Zhang
 b,
Hailong
Chen
b,
Hailong
Chen
 e,
Bote
Zhao
e,
Bote
Zhao
 *bf,
Jenghan
Wang
*d and
Meilin
Liu
*bf,
Jenghan
Wang
*d and
Meilin
Liu
 *b
*b
aSchool of Materials Science and Engineering, Shaanxi Key Laboratory of Green Preparation and Functionalization for Inorganic Materials, Shaanxi University of Science & Technology, Xi’an, Shaanxi Province 710021, China
bSchool of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA. E-mail: meilin.liu@mse.gatech.edu
cSchool of Chemical Engineering and Technology, Center of Nanomaterials for Renewable Energy, State Key Laboratory of Electrical Insulation and Power Equipment, School of Electrical Engineering, Xi’an Jiaotong University, Xi’an, Shaanxi 710049, China
dDepartment of Chemistry, National Taiwan Normal University, Taipei, 116, Taiwan. E-mail: jenghan@ntnu.edu.tw
eThe Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
fSchool of Environment and Energy, South China University of Technology, Guangzhou, 510006, China. E-mail: botezhao@scut.edu.cn
First published on 6th August 2024
Abstract
Exploring a universal strategy to increase Li-ion storage capacity and ionic conductivity while maintaining a robust crystal framework is a significant challenge for advancing Wadsley–Roth shear phases as promising anodes for high-power lithium-ion batteries. Here we report a potent cation-engineering driven crystallographic shear structure tailoring strategy, demonstrated through a novel titanium niobium tungsten oxide (TNWO). This is a significant model containing inspiring domains with tetrahedron, tetrahedron-free and large-size blocks in the lattice. Theoretical calculations reveal that the TNWO model, featuring the partial absence of a [WO4] tetrahedron and intrinsic multiple cation features, not only exhibits enhanced electronic conductivity and alleviated Li+ adsorbed structural distortion, but also facilitates both horizontal inter-block type and vertical-tunnel type Li+ diffusions, accompanied by sufficient redox reactions. Accordingly, it offers 1.48 Li+ per metal atom along with a high Li+ diffusion coefficient of 10−12 cm−2 s−1 and remarkable structural stability, featuring a reversible spatial phase transition. Additionally, through modification of surface anisotropy, dimensional uniformity and electronic conductivity of individual TNWO particles, a composite anode demonstrates ultrahigh rate capability (103.7 mA h g−1 at 15 A g−1) and excellent cycling stability (capacity retention of 80% at 5 A g−1 over 4900 cycles). This work is believed to have opened a new avenue for tailoring shear structures and creating unprecedented phases to transcend the existing Wadsley–Roth niobium-based oxide system for next-generation high-power lithium-ion batteries.
Broader contextDevelopment of advanced lithium-ion batteries (LIBs) is driven by the growing demand for higher energy density, faster charging rates, higher power output, and longer operational life. Wadsley-Roth shear phase materials have emerged as promising anode candidates for high-power and fast-charging LIBs. However, their commercialization is hindered by limited conductivities and unfavorable structural distortions within the host material. Tailoring the intrinsic crystallographic shear structures is believed to be the most effective strategy to improve their performance. Our work focuses on a titanium niobium tungsten oxide (TNWO), which features tailored crystallographic domains with distinct shear planes, highlighting its potential as an optimized anode. The unit created in the TNWO material, comprising 27 metal ions, represents the largest block, suggesting the feasibility of constructing super-large blocks to enhance diffusion kinetics. In addition to providing fast Li+ storage capability, our proposed strategy of tailoring crystallographic shear structures through cation-engineering can be extended to other Wadsley-Roth oxide systems, offering opportunities for designing new shear phases of niobium-based materials for high-power LIBs. |
Introduction
Lithium-ion batteries (LIBs) have found widespread applications in consumer electronics, electrified transportation, and even power grids. However, they are facing significant challenges in meeting the rapidly rising market demand for safety, fast-charging capability, and long calendar life.1–3 Upon significant research and technical progress over the past three decades, the specific energy of commercial LIBs with a graphite anode has nearly approached its limit at 350 W h kg−1. However, the charging speed and power output of contemporary traction LIBs, which are closely associated with the anodes, still do not fully alleviate market's expectation.4–6 Commercial graphite anodes have a theoretical capacity of 372 mA h g−1, but their Li+ intercalation dynamics are severely restricted by high tortuosity and anisotropic insertion/extraction behavior.7,8 The low operating potential (below 0.2 V vs. Li/Li+) results in organic electrolyte degradation, solid electrolyte interphase (SEI) formation, and unintended lithium plating or dendrite formation, leading to serious irreversible capacity loss, thermal runaway, and safety risk during high-rate charging.7 Spinel Li4Ti5O12, known as a “zero-strain” anode, operates within a safe working potential (∼1.55 V vs. Li+/Li), thereby avoiding the formation of the SEI and lithium dendrites, making it a considered safe anode.9 Unfortunately, its theoretical capacity of only 175 mA h g−1 is less than half that of graphite, compromising the battery's energy density.10,11As an extensive group of Wadsley–Roth block phases, also referred to crystallographic shear structures, niobium-based materials including titanium niobium oxides (Ti–Nb–O) and niobium tungsten oxides (Nb–W–O) have recently emerged as exhilarating anodic candidates for secure and fast LIB applications.12–22 They have been demonstrated to offer high working potentials (∼1.6 V vs. Li+/Li), variable theoretical capacities (200–400 mA h g−1), rich and reversible redox chemistries (Nb5+/Nb4+/Nb3+, W6+/W5+ and Ti4+/Ti3+), as well as open frameworks with interconnected Li+ diffusion tunnels. Nevertheless, the intrinsic limited conductivities and significant host structural distortions remain thorny issues that need to be addressed before they can serve as ideal materials for practical high-power LIBs.13,14 To date, acceptable strategies applied to improve their Li+ storage performance have mainly focused on pore construction,13,23 size miniaturization14,24 and chemical regulation.25 However, there have been few investigations into tailoring their intrinsic crystallographic shear structures.
Typically, both Ti–Nb–O and Nb–W–O compounds with crystallographic shear structures consist of corner-sharing [MO6] (M = Nb, Ti or W) octahedrons arranged in ReO3-type blocks. Every four nearest blocks of Nb–W–O compounds (Nb14W3O44, Nb16W5O55 and Nb18W8O69)18–20 are linked by an [WO4] tetrahedron through corner-sharing, while the tetrahedral characteristic has not been found in some Ti–Nb–O compounds, including TiNb2O713 and Ti2Nb10O2916 (Fig. S1, ESI†). Theoretical calculations have indicated that the Li+ activation energies of the tetrahedral sites are very different from that of octahedron sites within the blocks, where it is hard for Li+ to hop between the tetrahedral sites and block sites.26,27 While the crystallographic shear planes formed by edge-sharing between adjacent blocks can stabilize the host structures against severe distortion during Li+ insertion, they may also prevent the Li+ cross hoping from one block to another block. Compared to the Ti–Nb–O compounds, on the other hand, the Nb–W–O compounds usually have larger block sizes with more [MO6] octahedrons, resulting in more isotropic vertical Li+ diffusion tunnels formed by the horizontal cavities of every four octahedrons within a block. Moreover, the block size of Nb–W–O compounds increases as the atomic ratio of Nb to W decreases. Therefore, manipulating the existing or creating new crystallographic shear structures containing the large block dimension characteristic of Nb–W–O compounds and the tetrahedron-free characteristic of Ti–Nb–O compounds holds unprecedented implications for niobium-based oxides in LIBs.
To this end, we propose a cation-engineering driven crystallographic shear structural tailoring strategy, exemplified by a novel titanium niobium tungsten oxide (TNWO) model, which incorporates abundant distinguish domains with tetrahedron, tetrahedron-free and large-size blocks within the lattice. As an anode for LIBs, the TNWO model exhibits a significant number of intrinsic Li+ storage sites with high structural stability, a Li+ diffusion coefficient of 10−13–10−12 cm−2 s−1, and high reversible spatial phase transition. Moreover, when combined with size reduction, dimensional uniformity and segmented surficial carbon coating, the TNWO composite anode demonstrates ultrahigh rate capability (103.7 mA h g−1 at 15 A g−1) and excellent cycling lifespan (with a high retention of ∼80% and an extremely low fading rate of ∼0.004% per cycle at 5 A g−1 over 4900 cycles). These performances surpass those of recently reported niobium tungsten oxides. To gain a deep understanding of this new model from perspective, systematic analyses involving microstructure determination, electrochemical measurements, and theoretical computations were conducted. These analyses open up significant opportunities to tailor Wadsley–Roth shear structures and design new block phases for future high-power LIB applications.
Results and discussion
Crystal structure of TNWO bulk powders
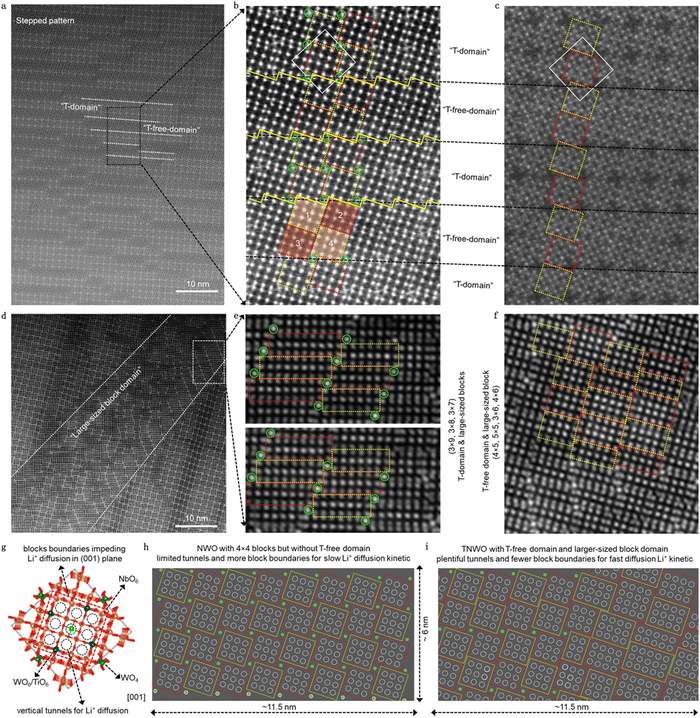
The designed TNWO bulk powders were synthesized using a solid-state reaction (ESI†), resulting in irregular and oversized particles with size ranging from 5 to 10 μm (Fig. S2, ESI†). Aberration-corrected high-angle annular dark field scanning transmission electron microscopy (HAADF-STEM) was used to analyze the local cation arrangement in the TNWO grains along the [001] direction (Fig. S3, ESI†). As depicted in Fig. 1a and b, the observed bright dots corresponding to metal cations are periodically arranged in standard 4 × 4 blocks (enclosed by yellow and red dashed boxes), with the exception of isolated ones (marked by green circles). Under the annular bright field (ABF), the bridge oxygen atoms between every two metal cations within the blocks are clearly observed (Fig. 1c). In each block, every metal cation (Mn+) occupies the center of six oxygen anions (O2−) to form a [MO6] octahedron, connected with each other through corner-sharing. Additionally, each isolated Mn+ located at the outer corners of the blocks bonds with four O2− anions to form a [MO4] tetrahedron. However, these blocks and tetrahedrons align in two kinds of order domains as expected, resulting in a distinctive step-shaped pattern. One is the normal “T-domain” (i.e. domain with tetrahedrons) of typical Nb–W–O compounds, where every four nearest blocks (two yellow ones and two red ones) are linked by one tetrahedron (green) through corner-sharing in the ab-plane. The two ipsilateral blocks (one yellow and one red) with 1/2 octahedral offset in the c-axis are linked through edge-sharing. These blocks extend along the c-axis to form columns, with the tetrahedral columns serving as the 2-fold rotation axis of the domain. In contrast, the other is the “T-free-domain” (i.e. tetrahedron-free domain) of typical Ti–Nb–O compounds, where the tetrahedral sites for Mn+ are absent, resulting in the blocks being linked directly through edge-sharing. Consequently, the blocks marked as “3” and “4” shift to align with those marked as “1” and “2”, respectively. The T-domains and T-free domains exhibit slight variations in “thickness”, measured in units of the side length of a 4 × 4 block in the ab-plane. These domains are alternately stacked with typical zigzag boundaries (Fig. 1b, indicated by yellow solid lines), which serve as shear planes and represent intrinsic features of the T-domain. Moreover, an extraordinary domain with an area of several hundred square nanometers emerges in the lattice, as depicted in Fig. 1d. Within this domain, Mn+ are organized not only into 4 × 4 blocks, each containing 9 vertical tunnels for Li+ diffusion (marked as black dotted circles along the [001] direction in Fig. 1g), but also into 3 × 6, 4 × 5, 4 × 6, 5 × 5, 3 × 7, 3 × 8, and even the 3 × 9 blocks (Fig. 1e and f). These blocks possess varying numbers of vertical tunnels: 10, 12, 15, 16, 12, 14, and 16, respectively. Notably, the 3 × 9 blocks represent the largest structural units, containing the highest numbers (27) of Mn+ among the recently reported niobium-based oxides with crystallographic shear structures (Table S1, ESI†).13,15,18,20,26Despite the complex domain configuration observed in the new TNWO material lattice, its high-energy synchrotron X-ray diffraction (XRD) pattern can be accurately indexed to a single phase of the space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) . This indexing is achieved without any redundant peaks of impurities, using the tetragonal crystallographic Nb14W3O44 as a reference (ICSD 23801) (Fig. S4, ESI†). The Rietveld refinement indicates that its lattice parameters (a = b = 21.000 Å and c = 3.821(1) Å) are very close to that of standard NWO (a = b = 21.020 Å and c = 3.824 Å).19,24 In addition to the given W6+ (green balls) in [WO4] coordination (Fig. 1g), the new Ti4+ and the remaining W6+ (blue balls) preferentially occupy identical octahedral sites at two of the eight block-edge-centers in a 4 × 4 block, as supported by the following information: (i) the presence of Nb5+, W6+, and Ti4+ in the TNWO powders was confirmed by XPS spectra and EDS mapping (Fig. S5 and S6, ESI†), with a stoichiometry of Nb5+
. This indexing is achieved without any redundant peaks of impurities, using the tetragonal crystallographic Nb14W3O44 as a reference (ICSD 23801) (Fig. S4, ESI†). The Rietveld refinement indicates that its lattice parameters (a = b = 21.000 Å and c = 3.821(1) Å) are very close to that of standard NWO (a = b = 21.020 Å and c = 3.824 Å).19,24 In addition to the given W6+ (green balls) in [WO4] coordination (Fig. 1g), the new Ti4+ and the remaining W6+ (blue balls) preferentially occupy identical octahedral sites at two of the eight block-edge-centers in a 4 × 4 block, as supported by the following information: (i) the presence of Nb5+, W6+, and Ti4+ in the TNWO powders was confirmed by XPS spectra and EDS mapping (Fig. S5 and S6, ESI†), with a stoichiometry of Nb5+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (W6+ + Ti4+) = 26
(W6+ + Ti4+) = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (4 + 1) ≈ 14
(4 + 1) ≈ 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.7 established at the preparation, which is lower than the ratio (Nb5+
2.7 established at the preparation, which is lower than the ratio (Nb5+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W6+ = 14
W6+ = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) for the standard NWO; (ii) Ti4+ (6.05 Å) and W6+ (6.0 Å) exhibit quite similar ionic radii; and (iii) the Ti–O bonds of [TiO6] octahedrons are detected using Raman spectra at ∼540 cm−1 (Fig. S7, ESI†). The cation occupancy pattern in the new TNWO differs significantly from that of NWO, where W6+ prefers to occupy two of the block-central octahedral sites and all tetrahedral sites (Fig. S8d, ESI†). This pattern was initially elucidated by Koçer et al. based on DFT calculations of total energies26 and by Cheetham and Allen using neutron powder diffraction analysis.26,28 While it was recognized that cation occupancy in the block depends on the electrostatic interactions related to lattice potential, cation occupancies in niobium-based shear phases are typically disordered to some extent. Synthesis conditions, such as temperature and stoichiometry, can affect the lattice potential. In niobium-based oxide materials, Nb5+ and low-valent Ti4+ typically form [MO6] octahedron blocks, while Nb5+ and high-valent W6+ can incorporate both [MO6] octahedral and [WO4] tetrahedral motifs. Compared to existing literature on NWO compositions annealed at 1200 °C, the appearance of T-domains and T-free domains, as well as the cation occupancy observed in the TNWO material, may be attributed to the lower sintering temperature (1100 °C) in an open atmosphere, slight excess of low-valent Ti4+, and the non-stoichiometry between cations and O2− anions. For comparison, a pure Nb14W3O44 (NWO) bulk material with only T-domains of standard 4 × 4 blocks of corner-shearing [MO6] octahedrons with WO4 tetrahedrons was also prepared using the same method (Fig. S8, ESI†).
3) for the standard NWO; (ii) Ti4+ (6.05 Å) and W6+ (6.0 Å) exhibit quite similar ionic radii; and (iii) the Ti–O bonds of [TiO6] octahedrons are detected using Raman spectra at ∼540 cm−1 (Fig. S7, ESI†). The cation occupancy pattern in the new TNWO differs significantly from that of NWO, where W6+ prefers to occupy two of the block-central octahedral sites and all tetrahedral sites (Fig. S8d, ESI†). This pattern was initially elucidated by Koçer et al. based on DFT calculations of total energies26 and by Cheetham and Allen using neutron powder diffraction analysis.26,28 While it was recognized that cation occupancy in the block depends on the electrostatic interactions related to lattice potential, cation occupancies in niobium-based shear phases are typically disordered to some extent. Synthesis conditions, such as temperature and stoichiometry, can affect the lattice potential. In niobium-based oxide materials, Nb5+ and low-valent Ti4+ typically form [MO6] octahedron blocks, while Nb5+ and high-valent W6+ can incorporate both [MO6] octahedral and [WO4] tetrahedral motifs. Compared to existing literature on NWO compositions annealed at 1200 °C, the appearance of T-domains and T-free domains, as well as the cation occupancy observed in the TNWO material, may be attributed to the lower sintering temperature (1100 °C) in an open atmosphere, slight excess of low-valent Ti4+, and the non-stoichiometry between cations and O2− anions. For comparison, a pure Nb14W3O44 (NWO) bulk material with only T-domains of standard 4 × 4 blocks of corner-shearing [MO6] octahedrons with WO4 tetrahedrons was also prepared using the same method (Fig. S8, ESI†).
As a niobium-based shear phase, it is understood that the Li+ available sites are located within the horizontal window of the block facets, while the fastest diffusion tunnels are oriented vertically to the block facets.27,29 Using a typical 4 × 4 block with tetrahedra at the corners as a prototype (Fig. 1g), there are 9 available cavities or vertical tunnels for Li+ diffusion. Based on these observations, we constructed two structure schemes of the same size (11.5 nm × 6 nm) in the [001] projection for comparison: one for the standard NWO (Fig. 1h) and the other for the new TNWO (Fig. 1i). The white dashed circles within blocks represent either horizontal cavities or vertical tunnels. Clearly, in the “T-free-domain” of the TNWO scheme, every set of four nearest neighbor blocks in the plane featuring 36 cavities/tunnels occupies a smaller planar area than the NWO scheme. In the entire plane of 69 nm2, the TNWO structure boasts 328 of cavities/tunnels, significantly more than 288 in the NWO structure. This results in a theoretical increase of 13.8% in Li+ adsorption sites and diffusion paths. O2− anions act as bridges between contact octahedra within a block and are the main binding sites for Li+. In the “T-free-domain”, the distance between frontier O2− anions of two adjacent blocks is shorter than that in the “T-domain”. This suggests that Li+ diffusion between blocks in the “T-free-domain” may encounter a lower barrier, potentially influenced by Ti4+, which will be further investigated through theoretical investigations. As a result, the new TNWO material, with its T-free-domain and large-size block domain, ensures an abundance of Li+ available sites, diffusion tunnels, and lower diffusion energy barriers.
Theoretical calculations of Li+ storage kinetics and stability
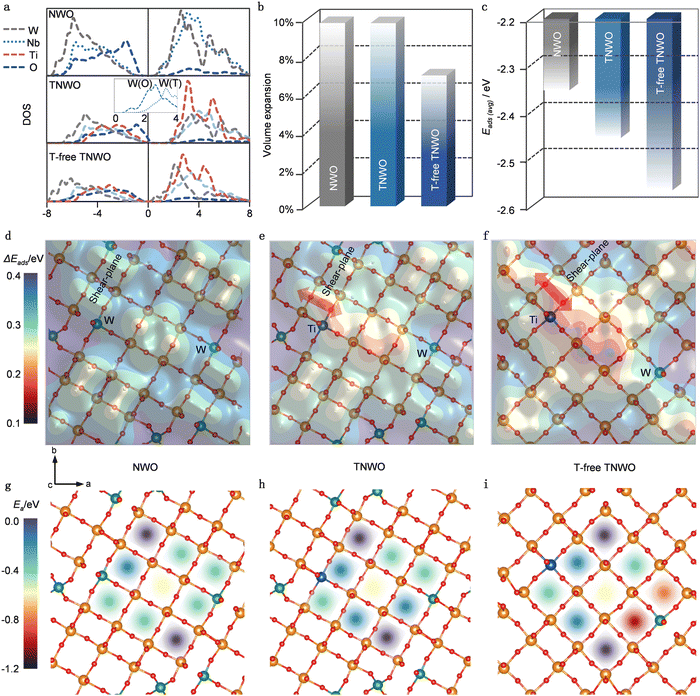
Given the distinctive crystal features of the T-domain, the T-free-domain and the presence of multiple cations in the new TNWO material, we employed density functional theory (DFT) calculation to predict its Li+ storage behaviors. Owing to the limitations on computational complexity, typical NWO, TNWO and T-free-TNWO models were separately constructed using Nb28W6O88, Nb28W5Ti1O88, and Nb30W1Ti1O80 supercells, respectively. These models were optimized based on standard Nb14W3O44 and Ti-substituted Nb14W3O44 with/without WO4 tetrahedrons (Fig. S9a, ESI†). All models feature octahedron corner-sharing 4 × 4 blocks connected along share planes of edge-sharing octahedra. It is important to note that both the NWO and TNWO models include tetrahedrons (T) to fill the voids at the corners. In the TNWO model, W6+ occupies the T sites, while the remaining W6+ and Ti4+ in both TNWO and T-free TNWO models occupy boundary octahedron sites. The Li+ adsorption sites in these models can be classified as pocket, vertical window and horizontal window sites (Fig. S9b, ESI†). As mentioned earlier, Li+ tends to diffuse along the vertical tunnels formed by the horizontal windows along the [001] direction (Fig. S9c, ESI†).27,29We firstly analyzed the density of states (DOS) to examine the electronic conductivities of these models (Fig. 2a). In all models, the metallic (Nb, W, and Ti) d bands mainly contribute to the conduction bands above the Fermi levels, while the O p bands play major roles in the valence bands. However, the inset in the middle plot shows that the W6+ in tetrahedral sites (W(T), dotted line) has a higher energetic d band than that in octahedral sites (W(O), dashed line). As a result, both the NWO and TNWO models exhibit obvious band gaps of ∼1 eV, while the T-free TNWO model has a lower energetic d band and a significantly narrowed band gap due to the partial absence of [WO4] tetrahedra. Thus, the T-free TNWO model exhibits higher electronic conductivity than the other two models. Secondly, we thoroughly examined the energy and structures of Li+ adsorption on these models. The volume changes and averaged adsorption energy (Eads(avg)) are compared when Li+ are fully adsorbed on the pocket and window sites (Fig. 2b and c). Detailed analysis of the evolution of each lattice parameter reveals that all three models experience the largest expansion along the c-axis (Fig. S10, ESI†). Structurally, both NWO and TNWO models with T features of relatively looser structure exhibit larger volume expansions than the T-free-TNWO model upon full Li+ adsorption. Energetically, Li+ adsorption induces electronic donation to t2g orbitals of [MO6] octahedrons (the lowest unoccupied orbitals).30,31 Lower-valent Ti4+ has less filled t2g orbitals of [TiO6] octahedrons (than those of [NbO6] and [WO6] octahedrons with higher valent Nb5+ and W6+), which can better stabilize the donated electrons and promote Li+ adsorption. Both the TNWO and T-free-TNWO models, which include Ti4+, have stronger Eads(avg) than the NWO model. It is known that minimizing volume expansion leads to minimal structural distortion during the Li+ storage, while stronger Eads(avg) maximizes lithiation. Thus, the T-free-TNWO model demonstrates the highest reversibility and the largest discharge/charge capacity.
Moreover, we extensively examined single Li+ adsorption on each pocket and vertical window sites to elucidate Li+ diffusion in the ab-plane. It is well known that Li+ adsorption energy (Eads), which has been widely employed to investigate the Li+ insertion processes and clarify the complex Li+ filling sequence, plays an important role in the Li+ diffusion mechanism.26,27,30 The regions with stronger Eads values have higher Li+ concentration, while those with weaker Eads values have lower ones. The concentration gradient between those regions further promotes the Li+ diffusion kinetics. To assess Eads variation (i.e. ΔEads) on each site, we referenced their Eads values to the lowest one Eads(lowest), defining ΔEads = Eads − Eads(lowest). Contour plots illustrating the distribution of ΔEads on the three models are shown in Fig. 2d–f. Detailed definitions of each site are provided in Fig. S9a (ESI) and plotted in Fig. S11 (ESI†). Remarkably, the ΔEads is also influenced by the structural and electronic effects. Structurally, vertical window sites situated at the center of blocks and certain pocket sites linking between blocks have stronger Eads; this is because the central vertical window sites provide more space to disperse the donated electrons, while the pocket sites contain more O2− ions to bond with Li+ ions, thereby promoting adsorption. Electronically, low-valent Ti4+ and [TiO6] with less filled t2g orbitals can better facilitate adsorption, while the high-valent W6+ and [WO6] tend to resist it. Additionally, the electronic effect outweighs the structural effect. Both the TNWO and T-free-TNWO models demonstrate significantly stronger ΔEads distributions around their Ti4+ sites, indicating enhanced adsorption, while the NWO model without Ti4+ exhibits a more uniform and lower ΔEads. As a result, Eads with uneven distributions in TNWO and T-free TNWO models can induce larger concentration gradients to promote Li+ diffusion (Fig. 2e and f). Also, the stronger ΔEads distribution around the Ti4+ sites situated between blocks induces greater Li+ concentration gradient to facilitate inter-block Li+ diffusion as indicated by the red arrows in the ab-plane. In contrast, evenly distributed Eads in the NWO model has smaller concentration gradient and slow Li+ diffusion (Fig. 2d). Finally, we examined the Li+ diffusion through the vertical tunnels along the c-axis, which serve as the main diffusion path in shear-structure niobium-based oxides.27,29 The activation barriers (Ea) along all 9 tunnels within a 4 × 4 block of the three models are plotted (Fig. 2g–i). The energetic analysis reveals that the diffusion tunnel at the center of the block has lower Ea (∼0.2 eV, indicated by the yellow shadow), while those in the corners have higher ones (∼0.4 eV, indicated by the purple shadow). Also, both the NWO and TNWO models with [WO4] tetrahedrons have similar diffusion barriers. However, the T-free-TNWO model shows a different pattern with lower diffusion barriers. The two diffusion tunnels neighboring the [WO6] octahedral sites have the lowest Ea (<0.15, indicated by the red and orange shadows) because the [WO6] octahedron with high-valent W6+ has weaker binding with Li+. Consequently, the T-free-TNWO model utilizes this weak binding to boost the Li+ diffusion along the vertical tunnels, resulting in faster discharge/charge kinetics.
Therefore, our DFT calculations reveal that both atomistic and electronic structures play decisive roles in determining the overall electrochemical performance of the new TNWO material with the unique crystallographic domains. In the T-domains, high-valent Nb5+ and W6+ are the key elements of the large block structures, with some W6+ bonding with four O2− anions to form [WO4] tetrahedrons and fill the voids of the block-corners. However, the partial absence of tetrahedrons in the T-free domains not only enhances the electronic conductivity but also reduces distortion of the Li+ adsorbed host structure and lowers the diffusion barrier, thus promoting stability and kinetics. Electronically, low-valent Ti4+ in [TiO6] units located at the block edge enhances Li+ adsorption energy and facilitates Li+ hoping within pocket sites to achieve inter-block diffusion within the ab-plane. High-valent W6+ in [WO6] units further reduces activation barriers to boost Li+ diffusion along the vertical tunnels. Nevertheless, both the atomistic and electronic structure effects for the TNWO material can only optimize Li+ storage performance when the most ideal metallic cation configurations are present.
Electrochemical performance evaluation
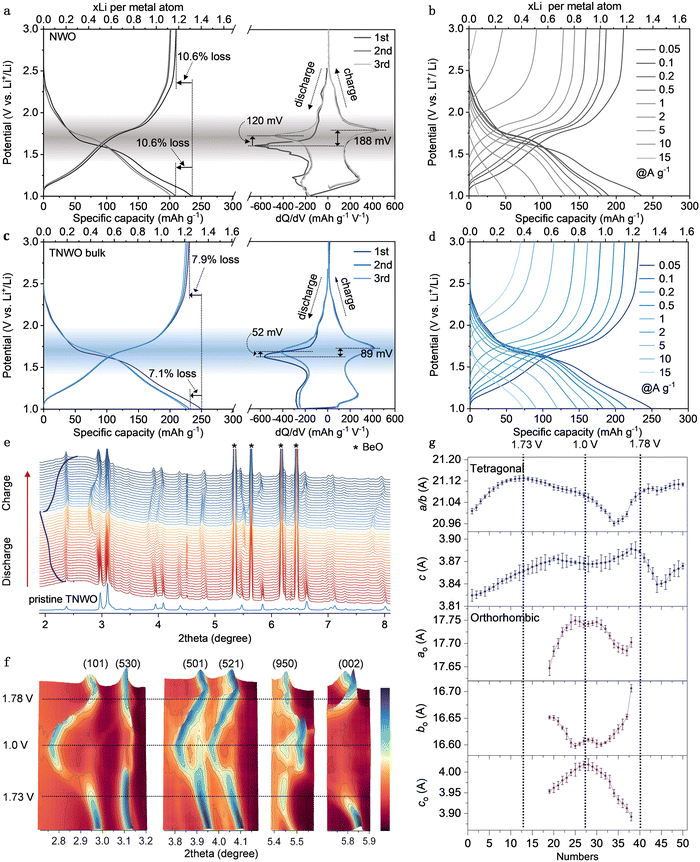
R2032 coin type half-cells were assembled to evaluate the electrochemical performances of the TNWO materials in the potential range of 3.0 to 1.0 V vs. Li metal electrode. The optimal metallic cation stoichiometry of the TNWO bulk was determined based on the powder XRD patterns and rate-capability for Li+ storage (Fig. S12, ESI†). The lithiation/delithiation processes of the TNWO and NWO bulk anodes follow three regions, which can be identified via the galvanostatic charge–discharge (GCD) curves with varying slopes and derived dQ/dV plots or cyclic voltammetry (CV) curves with featured redox reaction peaks (Fig. 3a, c and Fig. S13, ESI†). Such behaviors have been previously reported in many crystallographic niobium-based shear materials, such as Ti2Nb10O29,14 Nb16W5O55,18 Nb18W8O69,20 and H–Nb2O5.32 The Li+-(de)intercalation in the 1st and 3rd regions (1.9 to 3.0 V and 1.0 to 1.45 V) with fast voltage drops/swells is considered as a solid-solution reaction, where the host phase in the 1st region remains unchanged. In contrast, the 2nd region (1.45 to 1.9 V) exhibits long oblique plateaus in the GCD curves and sharp redox reaction peaks in the dQ/dV plots, indicating a two-phase coexistence reaction. The detailed structural features of the second phases have been scarcely clarified despite abundant efforts made by researchers. In our case, the electrochemical reactions occurring in the entire regions can be successively attributed to the redox couples of W6+/W5+ and Ti4+/Ti3+ due to their limited atomic concentrations and higher redox potentials of 2.5 to 1.95 V,14,24 as well as all Nb5+/Nb4+ redox reactions (1.9 to 1.45 V) and partial Nb4+/Nb3+ redox couples (1.45 to 1.0 V).14,19 Although the average working voltage of ∼ 1.56 V is slightly higher than that of the Li4Ti5O12 anode (Fig. S14, ESI†), the TNWO anode delivered a much larger initial discharge/charge capacity of ∼249.8/230.1 mA h g−1 with a high coulombic efficiency (CE) of ∼92.1% at a current density of 0.05 A g−1. Moreover, 92.7% of the capacity can be retained in the subsequent cycles. The voltage polarization for the Nb5+/Nb4+ redox couple during the Li+ insertion–extraction is only ∼89 mV, with a reduction voltage shifting from the 1st to 2nd discharge of approximately 52 mV. In comparison, the NWO anode showed a larger voltage polarization of 188 mV and a voltage shift of 120 mV, resulting in a lower initial CE of 90% and capacity retention of 88.7%. As observed by the initial GCD curves (Fig. 3b and c) and derivative dQ/dV plots (Fig. S15, ESI†) at each current density ranging from 0.05 to 15 A g−1, both anodes maintained their (de)lithiation behaviors, accompanied by the expected decrease in OCVs and specific capacities. However, the NWO bulk anode suffered a significant OCV decay of 868 mV, decreasing from 2.535 to 1.667 V throughout the process. Additionally, the potentials for the reduction of Nb5+ to Nb4+ and the oxidation of Nb4+ to Nb5+ shifted by 450 and 520 mV, respectively. The specific capacity experienced a significant decline from 243 mA h g−1 (1.31 Li+ per metal atom) for the initial discharge at 0.05 A g−1 to only 48 mA h g−1 (0.26 Li+ per metal atom) at 15 A g−1. In contrast, the TNWO bulk anode demonstrated a smaller OCV decay of 750 mV and reduction/oxidation potential shifts (430 and 480 mV). The reversible capacities at each current density were 249.8, 215.9, 200.7, 183.0, 164.5, 147.1, 120.4, 91.1, and 74.2 mA h g−1, respectively. Notably, a capacity of 0.38 Li+ per metal atom was achieved at 15 A g−1. Undoubtedly, the impressive performance of the TNWO anode can be attributed to the abundant Li+ available adsorption sites along with an increased diffusion coefficient (Fig. 4b) and decreased resistance (Fig. 4c).To unveil the crystal structural evolution of the TNWO and NWO hosts during Li+ (de)intercalations, operando high-energy synchrotron XRD and ex situ powder XRD patterns were recorded throughout their initial discharge/charge cycle. The patterns with discontinuous evolutions of a few characteristic diffraction peaks clearly evidence that both anodes underwent a reversible phase transition (Fig. 3e, f and Fig. S16, ESI†). For the NWO anode, this transition commenced at ∼1.75 V during the discharge stage and completed after 1.75 V during the charge stage (Fig. S16, ESI†). This result is different from some previous reports on the NWO anode, including bulk materials and nanomaterials.19,24 Regarding the new TNWO anode, apart from some extremely strong peaks of the BeO module used in the testing device, all reflections that appeared on the operando patterns are well-indexed to the tetragonal TNWO (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ) during the initial sloping region for Li+ intercalation from OCV (2.73 V) to ∼1.73 V (Fig. 3e and f). No new reflections corresponding to other phases were observed. Rietveld refinement results similarly indicate that the host existed solely in its original tetragonal phase (Fig. 3g), indicating that the reduction reactions of limited W6+ → W5+ and Ti4+ → Ti3+ during the 1st sloping region did not cause a phase transition in the TNWO anode. Echoed by a shift of the Bragg position to lower angles and weakening of the intensity, the tetragonal lattice parameters of both a(b) and c gradually extended, consistent with the DFT calculations.
) during the initial sloping region for Li+ intercalation from OCV (2.73 V) to ∼1.73 V (Fig. 3e and f). No new reflections corresponding to other phases were observed. Rietveld refinement results similarly indicate that the host existed solely in its original tetragonal phase (Fig. 3g), indicating that the reduction reactions of limited W6+ → W5+ and Ti4+ → Ti3+ during the 1st sloping region did not cause a phase transition in the TNWO anode. Echoed by a shift of the Bragg position to lower angles and weakening of the intensity, the tetragonal lattice parameters of both a(b) and c gradually extended, consistent with the DFT calculations.
In comparison, while the parameter c exhibits a linear rise, the parameter a(b) extends notably at first and then stabilizes. This suggests that the Li+ insertion initially occurs within the given vertical tunnels within blocks along the c-axis, followed by diffusion in the ab-plane. This behavior is also evident in the shift of the characteristic reflections. For example, consider the peak at 5.83° indexed to the (002) plane, as shown in contour plots. Initially, the peak slightly shifts to lower angles, similar to other peaks, and then shifts more intensely. As lithiation progresses from the oblique plateau (1.73–1.45 V) to the 2nd sloping region (1.45–1.0 V), accompanied by the reduction of Nb5+ to Nb4+ and further to Nb3+, although the tetragonal phase persists in the TNWO host, some reflections of (101), (530), (521), and (002) planes are significantly weakened in intensity or even disappear. Instead, new reflections corresponding to an orthorhombic crystal structure (Pbcm) are detected. The transition from the tetragonal phase to the orthorhombic phase is likely ascribed to the anisotropy of Li+ diffusion in the ab-plane and the asynchronous change in crystal lattice dimensions. While the parameter a(b) begins to shrink and c continues to increase, nearing a constant value in the tetragonal phase and aligning with DFT computational predictions (Fig. S10, ESI†), the parameters of the orthorhombic phase undergo more dramatic changes at the same time. Moreover, both parameters ao and co rapidly increased, while bo changed in the opposite direction (the subscript “o” represents orthorhombic). Due to the two-phase coexistence state observed in the TNWO host, the detailed mechanism of Li+ diffusion is likely to be very complex, and we can only hypothesize a reasonable one as above. During the charging process, the lattice parameters of the orthorhombic phase recovered reversibly as Li+ were de-intercalated from the host, although changes also occurred in the tetragonal phase. The complete disappearance of the orthorhombic phase, undetectable in the corresponding XRD patterns, only occurred when the cell was charged to a voltage above 1.78 V, coinciding with the oxidation of all Nb3+ and Nb4+ to Nb5+. However, the unique changes of parameters suggest that the Li+ extracted from the tetragonal phase may follow a new route rather than the original intercalation pathway. Comparisons of reflections and refined lattice parameters between the fully charge state with a voltage reaching 3.0 V and the initial states before discharge reveal that both lattice parameters a(b) and c of the TNWO host slightly increased, but the corresponding unit cell volume expansion was only ∼2%. Therefore, the novel TNWO material can serve as a stable anode for Li+ storage despite undergoing phase-changes and a complex Li+ (de)intercalation mechanism.
Modification of TNWO bulk powders
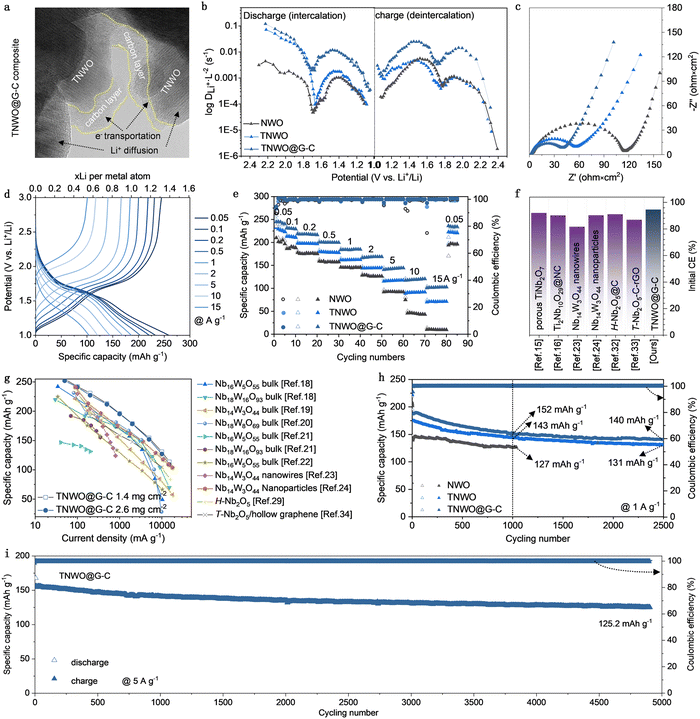
In order to further boost the practical electrochemical performance of the TNWO material in LIBs, certain modifications are necessary to eliminate intrinsic surface anisotropy, improve dimensional uniformity, and increase electronic conductivity of particles. In this work, the TNWO bulk powders were subject to ball-milling with a trace amount of graphene sheets followed by amorphous carbon coating (ESI†). The procedure is straightforward. Compared to pristine TNWO bulk powders, the final TNWO@G–C composite consists of smaller granular particles (∼1 μm) (Fig. S17a, ESI†). We found that the ball-milling without graphene additives can also refine the TNWO powders, but the particles tend to separate, and the size distribution is not as uniform as in the case with graphene (Fig. S17b, ESI†). The graphene-assisted-ball-milling technique proves to be a feasible method for refining bulk materials and ensuring dimensional homogeneity. The resulting thin amorphous carbon layer, with a thickness of only 5–10 nm, is segmentedly coated on the surface of the TNWO particles (Fig. 4a and Fig. S18, ESI†). Moreover, the carbon thin layer adequately infiltrates into the TNWO grain boundary, forming an evident conductive interface. This approach is preferable to full carbon coating, which may increase the diffusion barrier of desolvated Li+ from electrolyte into the active particles, preventing the Li+ storage performance, especially at high rates (Fig. S19, ESI†). The XRD pattern and Raman spectrum further confirm the refined grain size feature of TNWO and the presence of carbonaceous components in the TNWO@G–C composite, as evidenced by the broadened diffraction peaks and the appearance of a new apparent D-band (∼1348 cm−1) and G-band (∼1571 cm−1) (Fig. S20, ESI†). Moreover, the unchanged positions of diffraction peaks and chemical bond vibrational modes, compared with the original bulk material, indicate that the TNWO particles in the composite retain the phase structure and chemistry. The total mass ratio of graphene and carbon coating is measured to be only ∼5.65 wt% (Fig. S20c, ESI†).According to the galvanostatic intermittent titration technique (GITT) test, the TNWO@G–C composite anode exhibits reduced iR drop values at the beginning of each current pulse compared to both TNWO and NWO bulk anodes (Fig. S21, ESI†). This decrease suggests lowered polarization and enhanced Li+ diffusion kinetics (Fig. 4b). The Li+ diffusivity of the composite anode was nearly 20 to 50 times higher than that of the NWO bulk in the plateau range and remained consistently high throughout further cycling (Fig. S22, ESI†). Additionally, the composite anode showed significantly smaller charge transfer resistance than the TNWO bulk anode, as revealed by electrochemical impedance spectroscopy (EIS) (Fig. 4c). At a current density of 0.05 A g−1, the composite anode demonstrated superior Li+ storage capacities of ∼259.0/244.8 mA h g−1 (equivalent to 1.41/1.33 Li+ per metal ion), an initial CE of 94.5%, and over 95% capacity retention in subsequent cycles (Fig. S23, ESI†). Based on the CV curves recorded at sweep rates ranging from 0.3 to 2.5 mV s−1 and the corresponding fitted slope values of the log(current)–log(sweep rate) plots for the cathodic and anodic branches (Fig. S24, ESI†), both the TNWO bulk and TNWO@G–C composite anodes exhibited considerable pseudo-capacitive Li+ intercalation behavior. However, the capacitive contributions to the total capacities of the TNWO@G–C composite anode (ranging from 81.42% to 96.9%) were significantly enhanced compared to the TNWO bulk anode (ranging from 75.41% to 95.16%). Owing to the improved Li+ diffusion kinetics, the composite anode exhibited enhanced rate-capability with significantly reduced OCV dropping and redox peak potential shift of 610 and 364 mV, respectively (Fig. 4d and e and Fig. S15c, ESI†). The average reversible capacities at each current density (0.05–15 A g−1) were about 259.0, 233.0, 221.0, 203.0, 186.1, 168.9, 144.3, 120.8, and 103.7 mA h g−1, respectively, with nearly 100% of CEs. The number of Li+ per cations reached up to 0.56, even at 15 A g−1, which is twice that of the NWO bulk anode. Among the various niobium-based anodes reported, including those endowed with porous features, carbon modifications, or nanostructures,13,14,23,24,32,33 as well as near all niobium–tungsten oxides at all scales to date,18–24,29,34 both the high initial CE and rate performance of the TNWO@G–C composite anode stand out as the state-of-the-art (Fig. 4f and g).
During long-term cycling, both the TNWO@G–C composite and TNWO bulk anodes exhibited considerable capacity endurance. Their reversible capacities, respectively delivered at 1 A g−1 after 1000 cycles, were 152 and 143 mA h g−1, much higher than 134 mA h g−1 for the NWO bulk anode (Fig. 4h). Even after 2500 cycles, the TNWO@G–C composite anode maintained a capacity of ∼ 140 mA h g−1. Most impressively, the composite anode can be continuously discharged–charged with stable performance at 5 A g−1 for more than 4900 cycles (Fig. 4i and Fig. S25, ESI†), with a high retention of ∼80% and an extremely low fading rate of ∼0.004% per cycle. Additionally, each discharge or charge process took less than 4 min. Consequently, the excellent rate-capability and long cycling endurance endow the TNWO@G–C composite with enormous application potential for advancing high-power LIB applications.
Conclusions
In summary, we have successfully developed a new strategy for engineering Wadsley–Roth shear structures aimed at enhancing fast-charging speed and extending lifespan of LIB applications. This brand-new crystallographic tailoring strategy has led to the creation of a novel TNWO material characterized by a lattice featuring rich domains with T, T-free and large-size blocks. With its intrinsic abundant Li+ storage sites exhibiting high structural stability, a high Li+ diffusion coefficient, and significant reversible spatial phase transition, the new TNWO material holds great promise as an anode material. Drawing on multi-scale regulations from the bulk lattice to particle dimensions and surface characteristics, we engineered a TNWO@G–C composite using a solid-state reaction method, graphene-assisted ball milling, and segmented surficial carbon coating. The TNWO@G–C composite demonstrates exceptional performance, boasting ultrahigh rate capability (103.7 mA h g−1 at 15 A g−1) and excellent cycling stability (achieving a high retention of ∼80% and an extremely low fading rate of ∼0.004% per cycle at 2 A g−1 over 4900 cycles) as an anode of LIBs.Author contributions
P. P. J. and M. T. L. contributed equally to this work. M. L. L. conceived the project. B. T. Z. and M. L. L. supervised the research. P. P. Jing designed and performed all the experiments of materials preparation, materials characterization, electrochemical test, and analysed most of the experimental data with the help of M. T. L., H. H. L., N. G., B. T. Z., W. B. H., Y. F. M. and W. L. Z. Y. F. M., W. B. H. and H. L. C. contributed to collecting and analyzing the synchrotron XRD patterns. Y. D. performed the STEM test. H.-P. H. and J. H. W. performed computational studies and analyzed the computational data. P. P. J., M. T. Liu, J. H. W. and B. T. Z. discussed the results and wrote the manuscript. M. L. L. revised the manuscript.Data availability statement
All data supporting the finding of this paper are available in the main text and in its ESI.† Also, they are available from the corresponding author on reasonable request.Conflicts of interest
There are no any conflicts to declare.Acknowledgements
This work was supported by CBMM, a Hightower Endowment to the Georgia Tech Foundation, and a fellowship from the China Scholarship Council (201808615040).References
- A. Masias, J. Marcicki and W. A. Paxton, ACS Energy Lett., 2021, 6, 621–630 CrossRef CAS.
- G. Zhou, H. Chen and Y. Cui, Nat. Energy, 2022, 7, 312–319 CrossRef CAS.
- W. Li, J.-H. Wang, L. Yang, Y. Li, H.-Y. Yen, J. Chen, L. He, Z. Liu, P. Yang, Z. Guo and M. Liu, Adv. Mater., 2024, 36, 2314054 CrossRef CAS PubMed.
- C.-Y. Wang, T. Liu, X.-G. Yang, S. Ge, N. V. Stanley, E. S. Rountree, Y. Leng and B. D. McCarthy, Nature, 2022 DOI:10.1038/s41586-022-05281-0.
- M. Weiss, R. Ruess, J. Kasnatscheew, Y. Levartovsky, N. R. Levy, P. Minnmann, L. Stolz, T. Waldmann, M. Wohlfahrt-Mehrens, D. Aurbach, M. Winter, Y. Ein-Eli and J. Janek, Adv. Energy Mater., 2021, 11, 2101126 CrossRef CAS.
- Y. Liu, Y. Zhu and Y. Cui, Nat. Energy, 2019, 4, 540–550 CrossRef.
- H. Zhang, Y. Yang, D. Ren, L. Wang and X. He, Energy Storage Mater., 2021, 36, 147–170 CrossRef.
- J. Billaud, F. Bouville, T. Magrini, C. Villevieille and A. R. Studart, Nat. Energy, 2016, 1, 16097 CrossRef CAS.
- B. Zhao, X. Deng, R. Ran, M. Liu and Z. Shao, Adv. Energy Mater., 2016, 6, 1500924 CrossRef.
- T. Yuan, Z. Tan, C. Ma, J. Yang, Z.-F. Ma and S. Zheng, Adv. Energy Mater., 2017, 7, 1601625 CrossRef.
- M. M. Thackeray and K. Amine, Nat. Energy, 2021, 6, 683 CrossRef CAS.
- J.-T. Han, Y.-H. Huang and J. B. Goodenough, Chem. Mater., 2011, 23, 2027–2029 CrossRef CAS.
- B. Guo, X. Yu, X.-G. Sun, M. Chi, Z.-A. Qiao, J. Liu, Y.-S. Hu, X.-Q. Yang, J. B. Goodenough and S. Dai, Energy Environ. Sci., 2014, 7, 2220–2226 RSC.
- T. Yuan, S. Luo, L. Soule, J.-H. Wang, Y. Wang, D. Sun, B. Zhao, W. Li, J. Yang, S. Zheng and M. Liu, Mater. Today, 2021, 45, 8–19 CrossRef CAS.
- Y. Yang and J. Zhao, Adv. Sci., 2021, 8, 2004855 CrossRef CAS PubMed.
- J. Liu, P. Jing, L. Zheng, N. Guo, C. Liu and H. Wang, Chem. Eng. J., 2024, 482, 148866 CrossRef CAS.
- X. Ding, F. Meng, Q. Zhou, X. Li, H. Kuai and X. Xiong, Nano Energy, 2024, 121, 109188 CrossRef CAS.
- K. J. Griffith, K. M. Wiaderek, G. Cibin, L. E. Marbella and C. P. Grey, Nature, 2018, 559, 556–563 CrossRef CAS PubMed.
- Y. Yang, H. Zhu, J. Xiao, H. Geng, Y. Zhang, J. Zhao, G. Li, X. L. Wang, C. C. Li and Q. Liu, Adv. Mater., 2020, 32, e1905295 CrossRef PubMed.
- K. J. Griffith and C. P. Grey, Chem. Mater., 2020, 32, 3860–3868 CrossRef CAS.
- A. S. Lakhnot, T. Gupta, Y. Singh, P. Hundekar, R. Jain, F. Han and N. Koratkar, Energy Storage Mater., 2020, 27, 506–513 CrossRef.
- Y. Xu, J. Feng, H. Ma, J. Zhu, X. Zhang, J. Lang, S. Yang and X. Yan, Adv. Funct. Mater., 2022, 32, 2112223 CrossRef CAS.
- L. Yan, J. Shu, C. Li, X. Cheng, H. Zhu, H. Yu, C. Zhang, Y. Zheng, Y. Xie and Z. Guo, Energy Storage Mater., 2019, 16, 535–544 CrossRef.
- C. Guo, Z. Liu, K. Han, L. Zhang, X. Ding, X. Wang and L. Mai, Small, 2022, 18, e2107365 CrossRef PubMed.
- R. Tao, T. Zhang, S. Tan, C. J. Jafta, C. Li, J. Liang, X.-G. Sun, T. Wang, J. Fan, Z. Lu, C. A. Bridges, X. Suo, C.-L. Do-Thanh and S. Dai, Adv. Energy Mater., 2022, 12, 2200519 CrossRef CAS.
- C. P. Kocer, K. J. Griffith, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2019, 141, 15121–15134 CrossRef CAS PubMed.
- C. P. Koçer, K. J. Griffith, C. P. Grey and A. J. Morris, Chem. Mater., 2020, 32, 3980–3989 CrossRef PubMed.
- A. K. Cheetham and N. C. Allen, J. Chem. Soc., Chem. Commun., 1983, 1370–1372, 10.1039/C39830001370,.
- T. Li, G. Nam, K. Liu, J.-H. Wang, B. Zhao, Y. Ding, L. Soule, M. Avdeev, Z. Luo, W. Zhang, T. Yuan, P. Jing, M. G. Kim, Y. Song and M. Liu, Energy Environ. Sci., 2022, 154, 254–264 RSC.
- M. Saber, M. B. Preefer, S. K. Kolli, W. Zhang, G. Laurita, B. Dunn, R. Seshadri and A. Van der Ven, Chem. Mater., 2021, 33, 7755–7766 CrossRef CAS.
- T. Li, S. Huang, N. Kane, J.-H. Wang, Z. Luo, W. Zhang, G. Nam, B. Zhao, Y. Qi and M. Liu, ACS Energy Lett., 2023, 8, 3131–3140 CrossRef CAS.
- Z. Song, H. Li, W. Liu, H. Zhang, J. Yan, Y. Tang, J. Huang, H. Zhang and X. Li, Adv. Mater., 2020, 32, 2001001 CrossRef CAS PubMed.
- P. Jing, K. Liu, L. Soule, J. Wang, T. Li, B. Zhao and M. Liu, Nano Energy, 2021, 89, 106398 CrossRef CAS.
- H. Sun, L. Mei, J. Liang, Z. Zhao, C. Lee, H. Fei, M. Ding, J. Lau, M. Li, C. Wang, X. Xu, G. Hao, B. Papandrea, I. Shakir, B. Dunn, Y. Huang and X. Duan, Science, 2017, 356, 599–604 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee02293a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |