Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hot carrier organic solar cells†
Priya
Viji
,
Constantin
Tormann
,
Clemens
Göhler
 and
Martijn
Kemerink
and
Martijn
Kemerink
 *
*
Institute for Molecular Systems Engineering and Advanced Materials, Heidelberg University, Im Neuenheimer Feld 225, Heidelberg 69120, Germany. E-mail: martijn.kemerink@uni-heidelberg.de
First published on 4th October 2024
Abstract
Hot-carrier solar cells use the photon excess energy, that is, the energy exceeding the absorber bandgap, to do additional work. These devices have the potential to beat the upper limit for the photovoltaic power conversion efficiency set by near-equilibrium thermodynamics. However, since their conceptual inception in 1982, no experimental realization that works under normal operational conditions has been demonstrated, mostly due to the fast thermalization of photo-generated charges in typical semiconductor materials. Here, we use noise spectroscopy in combination with numerical modelling to show that common bulk heterojunction organic solar cells actually work as hot-carrier devices. Due to static energetic disorder, thermalization of photo-generated electrons and holes in the global density of states is slow compared to the charge carrier lifetime, leading to thermal populations of localized charge carriers that have an electronic temperature exceeding the lattice temperature. Since charge extraction takes place in a high-lying, narrow energy window around the transport energy, the latter takes the role of an energy filter. For common disorder values, this leads to enhancements in open circuit voltage of up to ∼0.2 V. We show that this enhancement can be understood as a thermovoltage that is proportional to the temperature difference between the lattice and the charge populations and that comes on top of the near-equilibrium quasi-Fermi level splitting.
Broader contextOne of the major efficiency limiting factors in conventional solar cells is thermalization losses, which refer to all photon energies in excess of the absorber bandgap being lost due to photogenerated charges quickly reaching thermal equilibrium. A conceptually simple way to harvest this excess energy was proposed by Ross and Nozik in 1982, and it relies on (i) slowing down thermalization to achieve ‘hot’ populations of electrons and holes and (ii) selectively extracting charges from these populations at energies exceeding the bandgap. Making this concept work under practical conditions has proven an unsurmountable hurdle, mostly due to the fast thermalization of photo-generated charges in typical semiconductor materials like silicon. Here, we use noise spectroscopy in combination with numerical modelling to show that the electronic temperature of photo-generated charges in organic solar cells under standard operational conditions far exceeds the lattice temperature and that these devices, in stark contrast to all other (inorganic and hybrid) solar cells, actually work as hot-carrier devices as envisioned by Ross and Nozik. Our results show a new way to realize hot-carrier solar cells and indicate a need to rethink how energy losses in organic solar cells are understood and, accordingly, can be minimized. |
Introduction
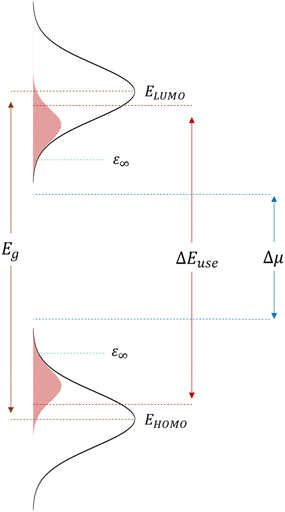
In their 1982 seminal paper, Ross and Nozik introduced the concept of harnessing excess energy from photo-absorption that could mitigate thermalization losses and, therefore, surpass the detailed balanced limit.1 They coined the term “hot-carrier” solar cells (HCSCs) for a device in which photo-excited charges thermally equilibrate among themselves but are extracted before reaching an equilibrium with the lattice. These HCSCs can potentially achieve power conversion efficiencies up to 66% for a single bandgap absorber, which is to be contrasted with the near-equilibrium Shockley–Queisser limit of about 30% for a single junction and 68% for a multi-junction solar cell consisting of an infinite number of layers. Despite the conceptualization almost half a century ago, experimental realization of such a device that works around room temperature and with reasonable illumination intensities is essentially non-existent.2 The main difficulties are the fast, ∼1 ps, time scale of thermalization of photo-generated charges by phonon emission in typical inorganic semiconductors like silicon, in combination with the difficulty to construct an efficient energy-selective contact.3–5 The crucial role of the latter is to selectively extract hot charges while blocking cold charges.For a device working as described above and as illustrated in Fig. 1, from which ‘hot’ charges, i.e., charges that are not thermalized to the band edge, are extracted via a utilization pathway at energy ΔEuse, which sits well above the semiconductor bandgap (and absorption onset) Egap, Ross and Nozik derived for the open-circuit voltage VOC
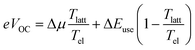 | (1) |
The focus of the HCSC community's search for a suitable absorber has predominantly centered on inorganic materials such as GaAs,2 halide perovskites,6,7 and hybrid perovskites.8 These materials have shown hot carrier cooling lifetimes in the order of a few 100 picoseconds to a few nanoseconds, which is slow in the context of inorganic semiconductors but still insufficient in comparison to competing processes. Despite much longer thermalization timescales of up to tens of μs,9 organic semiconductors were, somewhat surprisingly, never considered for HCSC applications. This could stem from the apparent success of near-equilibrium models to explain a range of experiments, most notably the value of the open-circuit voltage and the overall shape of the current–voltage characteristics.10–12 In addition, energetic disorder in organics is generally understood to be an additional source of energy losses, running counter to the goal of HCSCs: full thermalization in a Gaussian density of states (DOS) with a typical width σDOS = 50–90 meV would amount to energy losses of 0.1–0.3 eV.13,14
Although transient absorption spectroscopy can be employed to determine carrier temperatures and decay times in perovskite-based systems,7,8,15–17 determining the electronic temperature directly from the shape of transient or static optical spectra is impossible in organics due to broadening by static disorder.18 Nevertheless, experimental signatures of non-thermalized charges in organic solar cells have been seen through time-dependent mobilities, faster-than-equilibrium extraction,14 and non-thermalized populations of charge transfer (CT) states under steady-state illumination.19 Moreover, it was argued that the reciprocity relations, which underlie the near-equilibrium treatment of VOC may not hold in organic solar cells.20
To avoid confusion, it must be pointed out that thermalization in energetically disordered organic semiconductors, that is, the typical materials used to make state-of-the-art organic photovoltaic (OPV) devices,21,22 occurs as a two-step process. The first is a fast, mostly onsite, thermalization to the lattice temperature by coupling to molecular vibrations. This is equivalent to cooling by phonon emission in inorganic semiconductors and produces, in a timeframe of ∼0.1 ps, a localized polaron.23,24 Despite being ‘locally cold’, this polaron is typically not created at the equilibrium energy of the global density of localized states but much above it. For a Gaussian DOS and low charge carrier densities, as typical for good OPV devices, the equilibrium energy sits at εeq = −σDOS2/kBT, while charges are, on average, excited at the DOS center at ε = 0. It is the ‘global’ thermalization process, by hopping through intermediate sites, towards this equilibrium energy that is slow and is one of the crucial ingredients that make general OPV to hot carrier devices.25,26
In this letter, we utilize Johnson thermometry through cross-correlated current noise spectroscopy to measure the temperature of the charge carrier populations in two representative bulk heterojunction OPV systems, PM6:Y6 and P3HT:PCBM, under operational conditions. In stark contrast to their inorganic counterpart, exemplified by a commercial silicon PV device, the charge distributions in the organic solar cells are almost twice as hot as the lattice. We confirm our experimental results by performing kinetic Monte Carlo (kMC) simulations of typical OPV devices. The simulations quantitatively confirm that the static disorder in the organic material causes the high electronic temperature and, concomitantly, the enhanced noise signals. We then connect this finding to the Ross–Nozik model and demonstrate that the open-circuit voltage can be described by eqn (1), using independently determined parameters.
Results and discussion
We used cross-correlated current noise spectroscopy to measure the thermal noise and, thereby, the temperatures associated with the electronic charge distributions in the device under test (DUT) using the setup shown in Fig. 2a. The setup and methodology, which corrects for noise arising from cross-talk between the transimpedance amplifiers over the DUT resistance, were tested on commercial resistors and doped organic thin films, as discussed in the Supplementary Text S1, S2 and S5 (ESI†). Over a wide resistance range, electronic temperatures equal to the lattice temperature were found.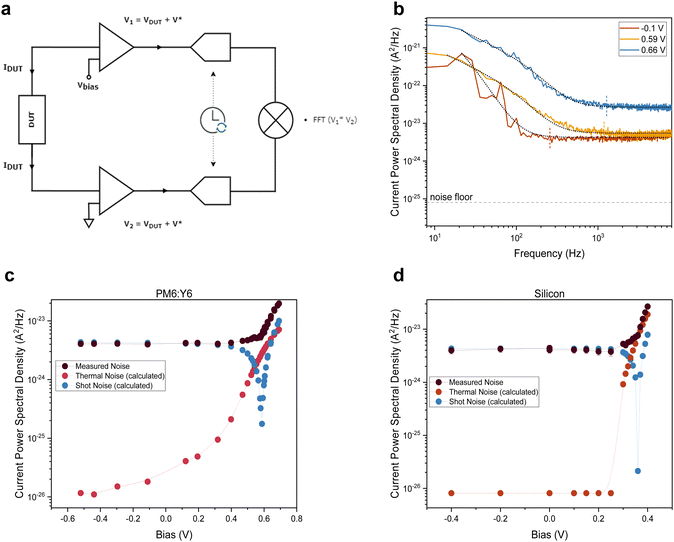 | ||
| Fig. 2 Noise spectroscopy setup and measurements. (a) Cross-correlation noise spectroscopy setup. The two terminals of the device under test (DUT) are connected to the inputs of two synchronized lock-in amplifiers through transimpedance amplifiers. The lock-in outputs are cross-correlated to suppress instrument noise. (b) Noise spectra from an illuminated PM6:Y6 solar cell at room temperature for different biases. The dashed vertical line indicates the beginning of the white spectra, and the black dotted line is a fit to eqn (2). (c) and (d) Noise after cross-talk correction vs. bias voltage for sub-1 Sun illuminated PM6:Y6 and silicon PV devices, respectively, with thermal and shot noise values calculated assuming the electronic temperature equals the lattice temperature and a Fano factor F = 1. | ||
Experiments were performed on two different, prototypical organic bulk heterojunction systems, the classical polymer–fullerene system P3HT:PCBM and the state-of-the-art PM6:Y6 system. In addition, a commercial inorganic silicon photodiode was tested. Exemplary measurement data of an organic PV device are shown in Fig. 2b and comprise 1/f-noise, characterized by an exponent α, shot noise, that is proportional to the product of the current I and the Fano factor F, in addition to the thermal (Johnson) noise that depends on the electronic temperature Tel and device resistance R.
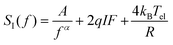 | (2) |
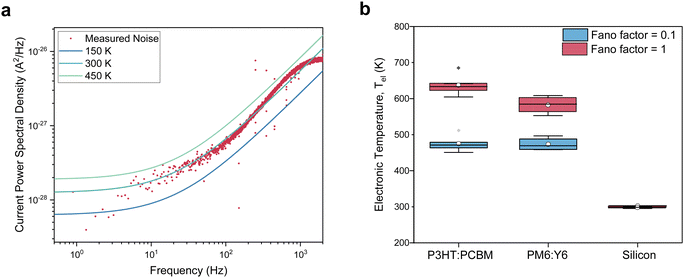
Noise measurements of illuminated solar cells were taken at different bias voltages, including at short- and open-circuit; Fig. 2c and d plots the resulting plateau values (black symbols), along with estimates of the shot and thermal noise, assuming F = 1, Tel = Tlatt and calculating R from the slope of the IV-curve, i.e. R(V) = (dI(V)/dV)−1. Focussing on the region around open-circuit, where the shot noise contribution is negligible, highlights a marked difference between the organic (Fig. 2c) and inorganic (Fig. 2d) devices. While for the silicon PV cell, the measured noise coincides with the estimated noise, the PM6:Y6 solar cell shows a significantly higher (Johnson) noise than expected for electronic distributions in equilibrium with the lattice. Noise measurements performed on the same organic solar cells in the dark confirm that, without illumination, charges are in equilibrium with the lattice and give an electronic temperature of ∼300 K, cf.Fig. 3a. The upswing in noise spectral density towards higher frequencies is due to the capacitive contribution to the conductance that is relatively large in the absence of photo-generated charges (Supplementary Text S3, ESI†). We also ensured that the signals for the organic devices were not due to heating of the lattice by the illumination (Fig. S2, ESI†). Similar measurements of noise with varying bias voltages were also performed on the P3HT:PCBM solar cell and are shown in Fig. S9c and d (ESI†).
Converting the raw noise data from Fig. 2c and d to effective temperatures using eqn (2) requires knowledge of the Fano factor, which accounts for correlations in the transport in the device and reduces the actual shot noise.27 Unfortunately, no previous work has been done to determine the Fano factor in a three-dimensional system of the type at hand.28 Using numerically exact kinetic Monte Carlo simulations, we estimate the Fano factor to be between 0.1 and 1 and recognize that it depends on temperature and electric field, as further discussed in the Supplementary Text S4 (ESI†). Hence, a Fano factor determined in the dark or under short-circuit conditions would not be applicable at open-circuit. After subtracting the shot noise and cross-talk contributions, we measure an electronic temperature between 450 and 650 K for the two organic systems. The charge carrier temperatures in silicon were found to be ∼305 K. In all cases, the lattice temperature was maintained at room temperature, i.e. 295 K. As such, Fig. 3b provides an upper limit for the electronic temperature at F = 1, while F = 0.1 provides a lower limit; the (unlikely) scenario in which F < 0.1 would not significantly decrease the temperatures further, as discussed in the Supplementary Text S4 (ESI†). Having established that charge carrier populations in operational OPV devices have, in stark contrast to silicon, a temperature that lies significantly above that of the lattice does, in itself, not imply that OPV devices operate as HCSCs in the way proposed by Ross and Nozik. To demonstrate this, we will use kinetic Monte Carlo (kMC) simulations to first show that, indeed, the enhanced electronic temperatures are due to the ‘global’ thermalization of photo-generated charges in a disorder-broadened DOS and, subsequently, that the so-called transport energy εtr takes the role of the energy filter, as schematically shown in Fig. 4c.
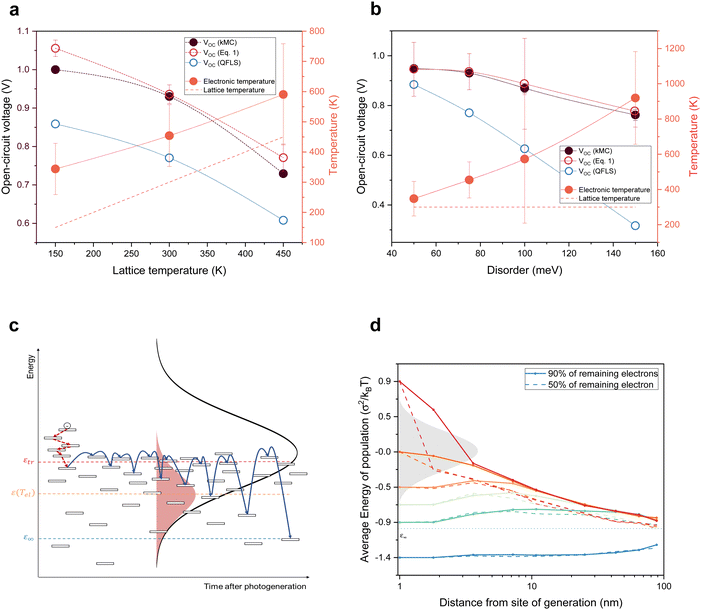 | ||
| Fig. 4 Implications of electronic temperatures higher than the lattice temperature and the role of excess photon energy. (a) and (b) Calculated open-circuit voltages for different lattice temperatures for σDOS = 75 meV (a) and different disorders for Tlatt = 300 K (b) for the near-equilibrium model, kMC and the hot-carrier model. The open red circles indicate the open-circuit voltage values from eqn (1), using the quasi-Fermi level splitting (open blue circles) and electronic temperature Tel (orange circles) as the input. The orange dashed lines show the lattice temperature. (c) Schematics of charge transport in a disordered organic semiconductor. (d) Average energy of the carriers remaining after 10% (solid lines) and 50% (dashed lines) of the charges are extracted as a function of extraction distance for different excitation energies. | ||
The kMC method is an established way to simulate the extremely complex reality of large numbers of excitons and charges moving and interacting in the active layer of a macroscopic operational device. It does so by assigning probabilities to all possible events in a simulation box of finite size, here typically 30 × 30 × 55 sites, each with a random energy drawn from the Gaussian DOS. Using the calculated rates as weighting factors for each possible event (exciton generation and recombination, charge hopping, injection and extraction), a single event is randomly chosen and executed, after which the procedure is repeated. The method was previously used to reproduce a number of experiments on OPV devices, including full IV curves of PM6:Y6 bulk heterojunctions (BHJs) at different temperatures and ternary BHJs with and without composition gradients and non-equilibrium effects on recombination;13,29,30 further details are given in the Supplementary Text S6 (ESI†).
Building on our previous work, in which we used the kMC method to simulate IV-curves of OPV devices,29 we extended the kMC model to simultaneously calculate current noise. Subsequently, a similar analysis to that used for the experiments was conducted to extract the electronic temperature under open-circuit conditions (Supplementary Note S7, ESI†). The results are shown by black circles in Fig. 4a for different lattice temperatures and Fig. 4b for different energetic disorders, measured by the width σDOS of the Gaussian density of states. In contrast to the experiments, the kMC simulations allow one to compare the noise temperature to the actual electronic temperature as determined by fitting σDOS2/kBTel to the mean energy of the photo-generated charge carriers (cf. Supplementary Text S8, ESI†). Fig. S12 (ESI†) shows that the electronic temperature is consistent with the noise temperature of photo-generated charges.
As intuitively expected, Fig. 4a shows that the closer the system is to a band-like model, that is, the smaller σDOS, the closer the electronic temperature is to the lattice. However, even for the smallest disorder considered, 50 meV, a finite difference remains. Since disorder values reported for OPV materials typically fall in the range of 60–90 meV, the results presented here should apply to the vast majority of OPV devices.21 This is also the reason why the two model systems that we used, P3HT:PCBM and PM6:Y6, give rise to similar electronic temperatures despite having very different device performance. The reason for the trends in Fig. 4a and b is that with increasing disorder or decreasing temperature, charges need an exponentially longer time to relax to global equilibrium as defined by the equilibrium energy.25,26 The slowdown can, in turn, be understood via the concept of a ‘transport energy’, as illustrated in Fig. 4c. The transport energy εtr is easily defined as the most likely energy that charges hop to in order to contribute to the charge transport. It was shown by Baranovskii et al. that for a broad class of strongly energy-dependent DOS, including, but not limited to, Gaussians, the width of the transport path (in energy space) is narrow and that its center does not depend on the initial energy of the hopping charge.31 Hence, by the definition of the transport energy, charges that have partially thermalized to an energy ε (εtr > ε >εeq) need to be thermally excited to the transport energy to become mobile and have the possibility to find a lower energy. The associated waiting time scales with exp((εtr − ε)/kBT), explaining the slowdown of the thermalization process with time and increasing disorder (see Fig. 4c and Fig. S3, ESI†).
In the context of organic solar cells, the importance of the transport energy is that photo-generated charges are extracted at energies close to εtr, thus acting as an energy filter. In contrast to the Ross/Nozik idea (Fig. 1), this filter does not only sit at the contacts but is present throughout the device and is the result of the peculiarities of hopping transport in energetically disordered media. We used our kMC simulations to confirm the above and to determine the position of the transport energy εtr ≈ −σDOS2/2kBT, relative to the center of the DOS (see Supplementary Text S9, ESI†). Accordingly, ΔEuse in eqn (1) is taken as the difference between the electron and hole transport energies, ΔEuse = εetr − εhtr. The parameter Δμ in eqn (1) is the quasi-Fermi level splitting in the device, as seen from the perspective of an observer at Tel, and is determined by the difference in the Fermi energies of electrons and holes, i.e. Δμ = εeF − εhF. This is extracted directly from the kMC simulations (blue circles in Fig. 4a and b). Thus, with Tel determined from noise simulations (orange dots in Fig. 4a and b), along with ΔEuse and Δμ, we can compute the non-equilibrium VOC using eqn (1) (open red circles), which coincides with the VOC as read from the IV-curves obtained from the kMC simulations (filled black circles). The fact that the VOC values from eqn (1) almost exactly coincide with the VOC values from the kMC model is the main result of this letter. This shows that ‘common’ organic solar cells are hot carrier solar cells.
Realizing that the difference between the transport energy and the Fermi energy over the electronic temperature is nothing but the entropy carried by a moving charge or, equivalently, the Seebeck coefficient32,33 allows us to rewrite eqn (1) as
| eVOC = Δμ + 2S (Tel − Tlatt), | (3) |
Hot-carrier contributions notwithstanding, state-of-the-art OPV devices, having PCEs just below 20%, do so far not beat the Shockley–Queisser limit for a single, disorder-free absorber with a rectangular absorption onset (PCE = 30%).22 The reason is that disorder constitutes a loss channel, even if it is mitigated by hot-carrier effects. Still, the question arises whether these insights can be used to make more effective OPVs. Intuitively, one might imagine that optically exciting the system with more energetic photons, producing electron–hole pairs with higher excess energies, or making the active layer thinner, giving charges less time to equilibrate, would increase the electronic temperature and, in turn, the open-circuit voltage. To this end, we calculated the average energy of photo-generated charges as a function of the distance between the generation and extraction point for different excitation energies. By plotting the mean energy after 10% (solid lines in Fig. 4d) and 50% (dashed lines) of the charges are extracted, we obtain a measure of the temperature of the remaining populations; details of this calculation are given in the Supplementary Text S13 (ESI†).
The data in Fig. 4d confirm the previous result from Melianas et al. that any excess energy above the center of the DOS is lost within a few nm.14 Excitations below the DOS center, but above the equilibrium energy, are longer lived, with transients converging after several tens of nm. Hence, one might expect minor VOC increases for device thicknesses L below twice this distance (since the mean extraction distance is ∼L/2). Unfortunately, at these thicknesses, VOC actually drops due to incomplete absorption and charges diffusing to the wrong contact.13 Nevertheless, Fig. 4d suggests that a rather efficient OPV device can be made by exploiting the fact that high-energy excitations actually do not significantly contribute to the enhanced electronic temperature because they quickly lose their excess energy. Hence, exciting the system with low-excess energy photons that predominantly excite electrons and holes in the lower half of the DOS will hardly change the electronic temperature and hence the VOC enhancement. For this to work, one needs a system where the energies of the first excited singlet state (S1) and the charge transfer (CT) state are similar, which is the case for low driving force systems like PM6:Y6.37,38 A simple estimate suggests that for a narrow excitation band around the S1 absorption maximum at ∼1.4 eV, a PCE around 40% should be possible. Explicit kMC simulations confirm this simple estimate and, as discussed in the Supplementary Text S14 (ESI†), show that narrow-band illumination around the transport energy further improves the device performance; only for even lower excitation energies, the lack of excess energy reduces both free charge generation and VOC. While this is not immediately applicable to single-junction devices harvesting white (sun)light, it does offer new perspectives for organic multi-junction solar cells or applications where more narrow-band light is harvested, including smart windows or indoor PVs.
Conclusions
In summary, we measured the temperature of the charge carrier populations in operational organic solar cells by noise spectroscopy. The experiments prove that, for two representative model systems, the electronic temperature under illumination is almost twice that of the lattice, while the electronic temperature in an operational commercial silicon solar cell is equal to that of the lattice. Using kinetic Monte Carlo simulations, we reproduce the high noise temperature and confirm its relation to an enhanced electronic temperature. Building on the established theory for disordered semiconductors, we show that the hotness of the electron and hole populations is due to the slow thermalization in a broadened density of localized states, requiring increasingly difficult re-excitation to a relatively narrow transport energy, which thereby takes the role of an energy filter. With that, the charge and energy transport in an operational organic solar cell can be one-on-one mapped on the hot carrier solar cell concept by Ross and Nozik. Taking the electronic temperature and extraction energies as input, we quantitatively reproduce the enhancement of the open-circuit voltage over its equilibrium value. These findings demonstrate that typical organic solar cells, including the current state-of-the-art, are hot carrier solar cells. While the ultimate goal of an HCSC is to surpass the detailed balance limit, this work is a step towards this goal in demonstrating the importance of hot-carrier effects in OSCs, and in particular their contributions to VOC.Since organic solar cells have so far almost uniquely been optimized on the basis of loss analyses assuming near-equilibrium,39 the notion that charge carrier populations are actually hot, and that this hotness contributes to VOC, not only necessitates a rethink but also greatly widens the scope of strategies to further improve these devices.40,41 First, and most straightforward, our work suggests noise spectroscopy as a probe for energetic disorder, the reduction of which should, hot carrier effects notwithstanding, lead to higher VOC as shown in Fig. 4b. Second, and more interesting, the connection between the Seebeck effect and VOC (eqn (3)) offers a novel way towards high-performance OPV devices. Techniques from the seemingly unrelated field of organic thermoelectrics, such as DOS engineering42,43 and morphology control,44 could be used to enhance the S of the blend of organic materials that form the active layer of the OPV device.
Beyond organic PVs, we expect our findings to inspire new avenues towards high-efficiency harvesting of solar energy.
Author contributions
P. V. performed the noise experiments; P. V. and C. G. fabricated the samples and performed the sample characterization; P. V. and C. T. performed the numerical simulations; P. V., C. T. and M. K. wrote the manuscript; M. K. conceived the idea and supervised the project. All authors contributed to the data analysis and conceptualization.Data availability
The data supporting this article have been included as part of the manuscript and its ESI.†Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work has been funded by the German Research Foundation under Germany's Excellence Strategy (2082/1 – 390761711, C.T.). M. K. thanks the Carl Zeiss Foundation for financial support. We are grateful to Olle Inganäs and Dieter Neher for discussions and critical reading of the manuscript and Sebastian Klein for noise floor characterization.References
- R. T. Ross and A. J. Nozik, J. Appl. Phys., 1982, 53, 3813–3818 CrossRef CAS.
- D. T. Nguyen, L. Lombez, F. Gibelli, S. Boyer-Richard, A. Le Corre, O. Durand and J. F. Guillemoles, Nat. Energy, 2018, 3, 236–242 CrossRef CAS.
- G. Conibeer, S. Shrestha, S. Huang, R. Patterson, H. Xia, Y. Feng, P. Zhang, N. Gupta, M. Tayebjee, S. Smyth, Y. Liao, S. Lin, P. Wang, X. Dai and S. Chung, Sol. Energy Mater. Sol. Cells, 2015, 135, 124–129 CrossRef CAS.
- S. Kahmann and M. A. Loi, J. Mater. Chem. C, 2019, 7, 2471–2486 RSC.
- D. König, K. Casalenuovo, Y. Takeda, G. Conibeer, J. F. Guillemoles, R. Patterson, L. M. Huang and M. A. Green, Phys. E, 2010, 42, 2862–2866 CrossRef.
- M. Li, J. Fu, Q. Xu and T. C. Sum, Adv. Mater., 2019, 31, 1802486 CrossRef CAS PubMed.
- Y. Yang, D. P. Ostrowski, R. M. France, K. Zhu, J. Van De Lagemaat, J. M. Luther and M. C. Beard, Nat. Photonics, 2016, 10, 53–59 CrossRef CAS.
- Z. Guo, Y. Wan, M. Yang, J. Snaider, K. Zhu and L. Huang, Science, 2017, 356, 59–62 CrossRef CAS PubMed.
- A. Melianas and M. Kemerink, Adv. Mater., 2019, 31, 1806004 CrossRef PubMed.
- U. Rau, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085303 CrossRef.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Nat. Mater., 2009, 8, 904–909 CrossRef CAS PubMed.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125204 CrossRef.
- T. Upreti, S. Wilken, H. Zhang and M. Kemerink, J. Phys. Chem. Lett., 2021, 12, 9874–9881 CrossRef CAS PubMed.
- A. Melianas, F. Etzold, T. J. Savenije, F. Laquai, O. Inganäs and M. Kemerink, Nat. Commun., 2015, 6, 8778 CrossRef CAS PubMed.
- M. Li, J. Fu, Q. Xu and T. C. Sum, Adv. Mater., 2019, 31, 1802486 CrossRef CAS PubMed.
- L. Dai, J. Ye and N. C. Greenham, Light: Sci. Appl., 2023, 12, 208 CrossRef CAS PubMed.
- M. B. Price, J. Butkus, T. C. Jellicoe, A. Sadhanala, A. Briane, J. E. Halpert, K. Broch, J. M. Hodgkiss, R. H. Friend and F. Deschler, Nat. Commun., 2015, 6, 8420 CrossRef CAS PubMed.
- N. Felekidis, A. Melianas and M. Kemerink, J. Phys. Chem. Lett., 2020, 11, 3563–3570 CrossRef CAS PubMed.
- A. N. Brigeman, M. A. Fusella, B. P. Rand and N. C. Giebink, Phys. Rev. Appl., 2018, 10, 034034 CrossRef CAS.
- D. Scheunemann, C. Göhler, C. Tormann, K. Vandewal and M. Kemerink, Adv. Electron. Mater., 2023, 9, 2300293 CrossRef CAS.
- S. M. Hosseini, S. Wilken, B. Sun, F. Huang, S. Y. Jeong, H. Y. Woo, V. Coropceanu and S. Shoaee, Adv. Energy Mater., 2023, 13, 2203576 CrossRef CAS.
- L. Zhu, M. Zhang, J. Xu, C. Li, J. Yan, G. Zhou, W. Zhong, T. Hao, J. Song, X. Xue, Z. Zhou, R. Zeng, H. Zhu, C. C. Chen, R. C. I. MacKenzie, Y. Zou, J. Nelson, Y. Zhang, Y. Sun and F. Liu, Nat. Mater., 2022, 21, 656–663 CrossRef CAS PubMed.
- P. A. Lane, P. D. Cunningham, J. S. Melinger, O. Esenturk and E. J. Heilweil, Nat. Commun., 2015, 6, 7558 CrossRef CAS PubMed.
- V. Abramavicius, V. Pranculis, A. Melianas, O. Inganäs, V. Gulbinas and D. Abramavicius, Sci. Rep., 2016, 6, 32914 CrossRef CAS PubMed.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef.
- S. D. Baranovskii, Phys. Status Solidi B, 2014, 251, 487–525 CrossRef CAS.
- U. Fano, Phys. Rev., 1947, 72, 26–29 CrossRef CAS.
- Y. A. Kinkhabwala, V. A. Sverdlov, A. N. Korotkov and K. K. Likharev, J. Phys.: Condens. Matter, 2006, 18, 1999 CrossRef CAS PubMed.
- S. Wilken, T. Upreti, A. Melianas, S. Dahlström, G. Persson, E. Olsson, R. Österbacka and M. Kemerink, Sol. RRL, 2020, 4, 2000029 CrossRef CAS.
- G. Zuo, S. Shoaee, M. Kemerink and D. Neher, Phys. Rev. Appl., 2021, 16, 034027 CrossRef CAS.
- S. D. Baranovskii, T. Faber, F. Hensel and P. Thomas, J. Phys.: Condens. Matter, 1997, 9, 2699 CrossRef CAS.
- H. Fritzsche, Solid State Commun., 1971, 9, 1813–1815 CrossRef CAS.
- D. Scheunemann and M. Kemerink, Thermoelectric properties of doped organic semiconductors, Elsevier, 2021 Search PubMed.
- I. Konovalov and V. Emelianov, Energy Sci. Eng., 2017, 5, 113–122 CrossRef CAS.
- J. F. Sierra, I. Neumann, M. V. Costache and S. O. Valenzuela, Nano Lett., 2015, 15, 4000–4005 CrossRef CAS PubMed.
- P. Wu, Y. Xiong, L. Sun, G. Xie and L. Xu, Org. Electron., 2018, 55, 90–96 CrossRef CAS.
- J. Liu, S. Chen, D. Qian, B. Gautam, G. Yang, J. Zhao, J. Bergqvist, F. Zhang, W. Ma, H. Ade, O. Inganäs, K. Gundogdu, F. Gao and H. Yan, Nat. Energy, 2016, 1, 16089 CrossRef CAS.
- L. Perdigón-Toro, H. Zhang, A. Markina, J. Yuan, S. M. Hosseini, C. M. Wolff, G. Zuo, M. Stolterfoht, Y. Zou, F. Gao, D. Andrienko, S. Shoaee and D. Neher, Adv. Mater., 2020, 32, 1906763 CrossRef PubMed.
- D. Qian, Z. Zheng, H. Yao, W. Tress, T. R. Hopper, S. Chen, S. Li, J. Liu, S. Chen, J. Zhang, X. K. Liu, B. Gao, L. Ouyang, Y. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganäs, V. Coropceanu, J. L. Bredas, H. Yan, J. Hou, F. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS PubMed.
- O. Andersson and M. Kemerink, Sol. RRL, 2020, 4, 2000400 CrossRef CAS.
- T. Upreti, C. Tormann and M. Kemerink, J. Phys. Chem. Lett., 2022, 13, 6514–6519 CrossRef CAS PubMed.
- G. Zuo, H. Abdalla and M. Kemerink, Adv. Electron. Mater., 2019, 5, 1800821 CrossRef CAS.
- O. Zapata-Arteaga, S. Marina, G. Zuo, K. Xu, B. Dörling, L. Alberto Pérez, J. Sebastián Reparaz, J. Martín, M. Kemerink, M. Campoy-Quiles, O. Zapata-Arteaga, K. Xu, B. Dörling, L. A. Pérez, J. S. Reparaz, M. Campoy-Quiles, S. Marina, J. Martín and G. Zuo, Adv. Energy Mater., 2022, 2104076 CrossRef CAS.
- D. Scheunemann, V. Vijayakumar, H. Zeng, P. Durand, N. Leclerc, M. Brinkmann and M. Kemerink, Adv. Electron. Mater., 2020, 6, 2000218 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee02612h |
| This journal is © The Royal Society of Chemistry 2024 |