Quantitative structure–activity relationships for the reaction kinetics of trace organic contaminants with one-electron oxidants†
Received
1st August 2023
, Accepted 21st November 2023
First published on 5th December 2023
Abstract
Understanding the reactivity between trace organic contaminants (TrOCs) and radicals involved in advanced oxidation processes (AOPs) is necessary for a good process design, but the experimentally determined rate constants (k values) are not sufficient for numerous artificial TrOCs. Thus, the development of quantitative structure–activity relationships (QSARs) for predicting k values may be an effective way to address this limitation. In this work, we developed QSARs for the reactions of TrOCs with AOP-related one-electron oxidants. Specifically, 15 QSARs using Hammett constants and 8 cross-correlations were developed based on the k values of over 400 reactions between TrOCs (most contain electron-rich moieties, such as phenol, aniline, and alkoxy benzene) and 5 one-electron oxidants (SO4˙−, Br˙, Br2˙−, Cl2˙−, and CO3˙−). Overall, the developed QSARs show a good predictive performance with 94% (237/251, for Hammett constant-based QSARs) and 80% (218/274, for cross-correlations) of the k values predicted within a factor of 3. All the Hammett constant-based QSARs show negative slope values and all cross-correlations show positive relationships, suggesting all 5 one-electron oxidants mainly share similar electrophilic mechanisms with the TrOCs highlighted in this work. Previous QSAR studies on the k values of one-electron oxidants were compared and integrated into their model analysis. Furthermore, k values predicted herein from the QSARs were used to evaluate the degradation of TrOCs during UV/persulfate and UV/chlorine treatment in multiple wastewater matrices, which were demonstrated to be useful. Finally, remarks on the use of the developed QSARs were presented.
Environmental significance
Chemical water quality is critical to human and environmental health. Therefore, AOPs exploiting powerful oxidizing radicals have been widely employed for the removal of trace organic contaminants (TrOCs) in water and wastewater treatment. Although, tens of thousands of potential TrOCs are continuously manufactured and identified, their reactivities toward radicals can be hardly determined via experimental approaches. Therefore, alternative strategies are needed to predict the fate of endless contaminants in water. In this work, 23 QSARs based on accessible descriptors were developed to predict the reaction kinetics of TrOCs with 5 one-electron oxidants (SO4˙−, Cl2˙−, Br˙, Br2˙−, and CO3˙−) and compared with previous QSAR studies. The reaction mechanisms involved were interpreted based on the analysis of the reaction kinetics and QSAR performance. This information improves the understanding of the radical chemistry of AOPs applied in multiple wastewater matrices.
|
1. Introduction
Trace organic contaminants (TrOCs), such as pharmaceuticals and endocrine-disrupting chemicals are increasingly detected in municipal wastewater effluents and drinking water sources.1–3 These TrOCs are continuously released into waters through human activities, posing a great threat to the ecosystem.1–5 Advanced oxidation processes (AOPs) exploiting powerful oxidizing ˙OH (E0(˙OH/OH−) = 1.9 V vs. NHE and E0 (˙OH, H+/H2O) = 2.7 V vs. NHE) have been increasingly applied for the remediation of recalcitrant TrOCs in water.5–12 Alternative strategies, such as persulfate-based AOPs and chlorine photolysis employing powerful sulfate radicals (SO4˙−, 2.4 V)12 and chlorine radicals (e.g., Cl˙ (2.4 V)),12 respectively, have also gained significant interest.10,11,13,14 Moreover, these primary radicals react rapidly with trace background inorganic anions (e.g., bicarbonate ions) in real-world AOP applications to form various secondary radicals (eqn (1)–(9)),15–21 such as halogen radicals (Cl2˙− (2.1 V), Br˙ (2.0 V) and Br2˙− (1.6 V)) and carbonate radicals (CO3˙− (1.6 V)).12 These secondary radicals often have higher concentrations than the primary radicals in AOPs, which is mainly due to their lower quenching rate constants with the water background matrix (e.g., ions and dissolved organic matter).18,22,23 For example, the steady-state concentrations of dihalide and carbonate radicals (∼10−9–10−13 M) were 1–4 orders of magnitude higher than that of ˙OH (∼10−14 M) during the UV/chlorine treatment of secondary effluents.24 Due to their high abundance, these secondary radicals may also significantly contribute to the degradation of TrOCs depending on their reaction rate constants.23,25–27| | | ˙OH + Br− ⇌ BrOH˙−, kforward = 1.1 × 1010 M−1 s−1, kbackward = 3.3 × 107 s−1 | (1) |
| | | BrOH˙− ⇌ Br˙ + OH−, kforward = 4.2 × 106 s−1, kbackward = 1.3 × 1010 M−1 s−1 | (2) |
| | | ˙OH + HCO3−/CO32− → CO3˙− + H2O/ HO−, k = 8.5 × 106 M−1 s−1/3.9 × 108 M−1 s−1 | (3) |
| | | SO4˙− + Cl−/Br− → Cl˙/Br˙ + SO42−, k = 3.2 × 108 M−1 s−1/3.5 × 109 M−1 s−1 | (4) |
| | | SO4˙− + HCO3−/CO32− → CO3˙− + HSO4−/SO42−, k = 2.8 × 106 M−1 s−1/4.1 × 106 M−1 s−1 | (5) |
| | | Cl˙ + Cl− ⇌ Cl2˙−, kforward = 8.5 × 109 M−1 s−1, kbackward = 6.0 × 104 s−1 | (6) |
| | | Br˙ + Br− ⇌ Br2˙−, kforward = 1.2 × 1010 M−1 s−1, kbackward = 1.9 × 104 s−1 | (7) |
| | | Cl˙ + HCO3−/CO32− → CO3˙− + HCl/Cl−, k = 2.2 × 108 M−1 s−1/5.0 × 108 M−1 s−1 | (8) |
| | | HClO/ClO− + hv → ˙OH/O˙− + Cl˙ | (9) |
The quantitative reactivities (i.e., second-order rate constants, k values) of oxidants toward TrOCs are crucial to predict the transformation efficiency of TrOCs during AOPs.24,25,28,29 In the last two decades, the k values of a wide range of TrOCs toward radicals were determined via multiple approaches, such as transient absorption spectroscopy, steady-state competition kinetics, and complex kinetic modeling.30–40 These k values of TrOCs usually show high reactivity and low selectivity for ˙OH and Cl˙ (both ∼109–1010 M−1 s−1), but higher selectivity for SO4˙− (107–1010 M−1 s−1), Br˙ (<108–1010 M−1 s−1), Br2˙− (<105–109 M−1 s−1), Cl2˙− (<106–109 M−1 s−1) and CO3˙− (<105–109 M−1 s−1).35–39 Although all these radicals can react with TrOCs via various pathways such as one-electron transfer, radical addition, and hydrogen abstraction, the main reaction mechanism of the latter five radicals (i.e., SO4˙−, Br˙, Br2˙−, Cl2˙− and CO3˙−) is one-electron transfer.18,32,38,39 Other reaction routes may also occur but often play minor roles. These radicals undergoing the one-electron transfer mechanism is named as a one-electron oxidant.41–43 Due to the constant emergence of thousands of TrOCs, the k values of one-electron oxidants with TrOCs remain largely unavailable in the literature.
Due to the high selectivity of the k values of one-electron oxidants and their structure dependence, quantitative structure–activity relationships (QSARs) can be established between the k values and structural descriptors of the reactants.44–47 QSARs serve as quick and low-cost tools in predicting unavailable k values, which benefit from predicting the degradation of TrOCs in AOPs free of laborious experiments.45,48 Furthermore, the different performances of QSARs provide mechanistic information on the reactions of radicals with TrOCs, helping to understand the fate of TrOCs during AOPs and other radical-involved chemical processes.34,45,48 Thus far, many QSAR studies focus on predicting the k values of TrOCs toward chemical oxidants (e.g., ozone, free chlorine, chlorine dioxide, and Fe(VI))45,49–51 and ˙OH,45,49,52–56 while studies covering the reaction of TrOCs with one-electron oxidants are limited. Table 1 summarizes the reported QSARs for predicting the k values of AOP-related radicals. For example, Hammett constant-based QSARs for the CO3˙− oxidation of simple mono-substituted benzenes, phenolates, and anilines have been developed, but many emerging TrOCs are not included.46 Alkoxyl benzenes are common structures of many environmental chemicals such as biomass, lignin, and β-blocker pharmaceuticals;38,57 however, there are only limited QSARs targeting this class of compounds. Moreover, our group recently developed QSARs for Cl2˙−, Br˙, and Br2˙− with aromatics using Hammett σ+ values.38,39 Nevertheless, an update with expanded datasets is necessary for these QSARs, where different scales of Hammett constants (σ, σ+, and σ−) should be tested to give a more comprehensive understanding. Overall, the current lack of up-to-date, user-friendly, and validation-tested QSARs between one-electron radicals and TrOCs in the literature encouraged us to perform this study.
Table 1 QSARs for predicting the k values of AOP-related radicals in the literature
| Compounds |
Radicals |
QSAR descriptors |
Statistical indicator values |
Data points |
Ref. |
| Aromatic compounds |
˙OH |
MW, piPC09, Mor02e, Mor26p, EHOMO |
R
2 = 0.735, Q2 = 0.686 |
78 |
54
|
| Organic micropollutants |
˙OH |
DBE, WPSA, IP |
R
2 = 0.832, QLOO2 = 0.78, QBOOT2 = 0.82 |
83 |
49
|
| Fluoroquinolones and sulfonamides |
˙OH |
C-006, qC+, μ |
R
adj
2 = 0.805, RMSEtr = 0.228, QLOO2 = 0.778, QBOOT2 = 0.770 |
60 |
53
|
|
R
ext
2 = 0.820, RMSEext = 0.197, Qext2 = 0.816 |
| Trace organic contaminants |
SO4˙− |
#O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, ELUMO − EHOMO C, ELUMO − EHOMO |
R
2 = 0.866, QLOO2 = 0.86, QBOOT2 = 0.87, AMB = 0.73 |
85 |
34
|
|
R
ext
2 = 0.89, Qext2 = 0.89 |
| Mono-substituted benzene, p-substituted phenolates, p-substituted anilines |
CO3˙− |
Hammett σ+ |
R
benzene
2 = 0.96, Rphenolates2 = 0.99, Ranilines2 = 0.98 |
7, 8, 7 |
46
|
| Anilines, phenolates and phenylureas |
CO3˙− |
Hammett σ+ |
R
anilines
2 = 0.898, Rphenolates2 = 0.840, Rphenylureas2 = 0.650 |
9, 8, 12 |
33
|
| Substituted benzoic compounds |
Cl˙, Cl2˙−, ClO˙ |
Hammett σ |
R
Cl˙
2 = 0.976, RCl2˙−2 = 0.938, RClO˙2 = 0.821 |
6, 6, 6 |
93
|
|
p-Substituted phenols |
Cl2˙− |
Hammett σ |
R
Cl2˙−
2 = 0.947 |
6 |
82
|
| Organic compounds (phenols, alkoxy benzenes and anilines) |
Cl2˙− |
Hammett σ+ |
R
phenols
2 = 0.924, RAB2 = 0.951, Ranilines2 = 0.881 |
15, 9, 7 |
38
|
| Organic compounds (phenols, phenolates, alkoxy benzenes and anilines) |
Br˙, Br2˙− |
Hammett σ+ |
R
phenols,Br˙
2 = 0.903, RAB,Br˙2 = 0.929, Ranilines,Br˙2 = 0.825 |
13, 8, 8 |
39
|
|
R
phenols,Br2˙−
2 = 0.964, RAB,Br2˙−2 = 0.945, Ranilines,Br2˙−2 = 0.936 |
16, 9, 7 |
|
R
phenolates,Br2˙−
2 = 0.845 |
15 |
Thus, the main objective of this work was to develop QSARs for the reaction kinetics of TrOCs with SO4˙−, Br˙, Br2˙−, Cl2˙− and CO3˙−. A total of 23 QSARs was developed employing either Hammett constants as descriptors or cross-correlations between k values for two radicals. The predictive performances and reaction mechanisms involved were discussed, which were compared with established QSARs in the literature. The k values predicted by the QSARs here were used to evaluate the TrOC degradation in both UV/persulfate and UV/chlorine AOP in real secondary effluents. Finally, the basic principles of using the developed QSARs were proposed.
2. Materials and methods
2.1 Source and selection of k values
The second-order reaction rate constants (k values) of SO4˙−, Cl2˙−, Br˙, Br2˙− and CO3˙− were derived from the literature16,36,37,39,40 and NIST kinetic database,58 and a complete list of references is provided in the ESI.† Aromatic compounds are the main object of this study. Phenol, aniline, and alkoxy benzene (anisole) were selected as the parent moieties in the development of the Hammett constant-based QSARs. These moieties are commonly found in the molecular structures of TrOCs and likely serve as the main reaction sites in oxidation reactions due to their high electron density.23,47,59–61 Among the three parent moieties, phenols undergo acid–base speciation, resulting in dramatically higher k values for phenolates.23 In this case, the k values of phenols and phenolates were treated separately, and thus readers can calculate the k values at a specific pH by including pKa values. For phenolic compounds, only k values measured at a pH < (pKa − 3) were chosen as the k of the undissociated phenols. This can ensure the neglected interference of phenolate due to the difference in k values between phenol and phenolate being no more than 2 orders of magnitude for selected radicals. Also, the k values measured at a pH > (pKa + 1) were chosen as the k of the phenolates. We excluded k values obtained from complex kinetic modeling and that exceeding the diffusion-controlled limits (∼1.5 × 1010 M−1 s−1, estimated based on the Smoluchowski equation).62,63 When multiple k values for the same reaction were reported in the literature, the average value was calculated and used. This data collection of experimental k values was employed for both the Hammett constant-based QSARs and cross-correlations. Moreover, the cross-correlations used a larger database than the Hammett constant-based QSARs. Besides the compounds involved in the Hammett constant-based QSARs (i.e., phenols, anilines, and alkoxy benzenes), TrOCs with multiple reactive sites (e.g., sulfonamides) and amines were also involved in the cross-correlations.
2.2 Descriptor variables
In this study, the Hammett σ constant was used as the descriptor in the development and analysis of QSARs. It is one of the most widely used empirical parameters accounting for the substituent effects in aromatic compounds.64–67 These constants quantitatively characterize the electronic effects of aromatic substituents, where positive values represent electron-withdrawing substituents and negative values represent electron-donating substituents.67–69 However, Hammett σ constants fail to characterize reactions where resonance effects are expected to have a major impact. Therefore, Hammett σ+ and σ− constants were further proposed, which are optimized scales of the σ constants considering the resonance effects of substituents.64,70 In comparison to the σ scale, the σ+ scale usually gives a better fit when dealing with electron-donating substituents (e.g., –OH, –OCH3, and –NH2 groups), while the latter σ− scale performs better in electron-withdrawing substituents (e.g., –NO2 and –CN groups). Moreover, each scale has the corresponding σo, σm, and σp values representing substituents in the ortho-, meta-, and para-positions, respectively, in the parent structure (e.g., –OH group of phenols). These are summed to produce ∑σo,m,p, ∑σo,m,p+ and ∑σo,m,p− to account for the effects of all substituents on different locations of the aromatic ring.
Most of these Hammett constants were obtained from literature.64,65 When a particular constant was not available, an approximated value was used via two empirical relationships to account for the ortho effects (σo+ = 0.66σp+, σo− = σp−).64,65,71 All three σ scales (σ, σ+ and σ−) were examined to find the best correlations in the development of QSARs. In the case of TrOCs with complex substituents, their σ constants are often unavailable in the literature. Given that the electronic effect of the substituents is determined by the atoms adjacent to the reaction center but not the remote ones,69,70 structural approximations can be applied to estimate the Hammett constants for compounds with complicated structures. Structure approximations similar to Lee and von Gunten's work were used to keep consistency.45 For example, oxytetracycline can be approximated to 2-hydroxy-2-(hydroxymethyl) ethenylbenzene. Details of all the applied structural approximations are shown in ESI, Tables S3–S17.† For the compounds bearing more than one aromatic ring, we summed the σ values of the different substitutes for each aromatic ring and chose the ring having the lowest ∑σ value for developing the QSARs. This is because an aromatic ring with higher electron density (lower ∑σ values) likely serves as the main reactive site and dominates the rate constants.
2.3 Linear correlations
The OriginPro 2021 (version 9.8.0.200) software was used for the analysis and development of the QSARs. All the k values were logarithmically transformed and plotted with the summed Hammett σ constants (∑σo,m,p, ∑σo,m,p+ and ∑σo,m,p−). Then they were fitted to a linear regression in the form of log(k) = y0 + ρ × ∑σo,m,p, where y0 and ρ are the intercept and slope of the linear regression. All three σ scales (σ, σ+ and σ−, respectively) were tested to determine the best-correlated one based on the coefficient of correlation (i.e., R2). Moreover, the cross-correlations between the k values for the reactions of every two radicals were also investigated. In this case, two sets of k values were logarithmically transformed and plotted, and then fitted to a linear regression in the form of log(k1) = y0 + ρ × log(k2). Details of the QSAR analysis and results are provided in ESI, Tables S3–S26.†
2.4 Validation of developed QSARs
Validation of QSAR models is necessary to check their robustness and predictive capacity. In this study, all k values were used for model development with no k values to run external tests because there were not enough data points available for most datasets. The internal validation was performed by the leave-one-out (LOO) method, in which one compound in the data set was removed and a QSAR model is constructed and used to predict the k value of the removed compound. This process was repeated for each compound in the data set. The analysis yielded QLOO2, the coefficient of correlation, to determine the expected error of future predictions. Its value ranged from 0 to 1. In the LOO validation method, Q2 > 0.5 indicates a robust and predictive model. In this study, the LOO internal validation was performed by the Caret Package in R. For the 23 developed models, QLOO2 ranged from 0.53 to 0.94, indicating a good predictive performance. Additionally, the residual plot for all data was plotted. A random scatter plot was observed, which indicated that the regression model was appropriate for the data. The residual plot is shown in ESI, Table S2.†
3. Results and discussion
The Hammett constant-based QSARs are presented for the reaction of 5 one-electron oxidants (i.e., SO4˙−, Br˙, Br2˙−, Cl2˙−, and CO3˙−) with the parent moieties in the order of phenol, phenolate, aniline, alkoxy benzene, followed by their cross-correlations. All the developed QSARs are summarized in Table 2. All the Hammett constant-based QSARs show negative slope values, suggesting an electrophilic reaction (i.e., oxidation reaction) mechanism. The magnitude of the slope reflects the overall sensitivity of the reaction toward substituent variations, and the intercept (i.e., unsubstituted moiety) reflects the overall reactivity between radicals and TrOCs. For a specific radical, it is common that the sensitivity toward substituent variations (i.e., slope) decreases with an increase in the intercept.
Table 2 A summary of the developed QSARs
| Eqn no. |
Compound class |
Radicals |
QSAR equationsa |
nb |
R
2
|
RMSEd |
Q
LOO
2
|
RMSELOOf |
|
In QSAR equations, values in parentheses are 95% confidence intervals.
n is the number of data points.
R
2 is the coefficient of correlation.
RMSE is the root mean square error and calculated as RMSE = (SS/n)1/2 where SS is the sum-of-squares of the distance of the linear regression from the data points and n is the number of data points.
Q
LOO
2 is the coefficient of correlation resulted from leave-one-out cross-validation.
RMSELOO is the root mean square error resulted from leave-one-out cross-validation.
|
| (10) |
Phenols |
Br˙ |
log(kPhOH) = 9.99 (±0.02) − 0.39 (±0.05) ∑σo,m,p− |
16 |
0.84 |
0.07 |
0.80 |
0.09 |
| (11) |
Br2˙− |
log(kPhOH) = 7.31 (±0.09) − 0.87 (±0.15) ∑σo,m,p+ |
33 |
0.81 |
0.28 |
0.80 |
0.33 |
| (12) |
Cl2˙− |
log(kPhOH) = 8.40 (±0.04) − 0.68 (±0.11) ∑σo,m,p+ |
27 |
0.78 |
0.19 |
0.67 |
0.23 |
| (13) |
CO3˙− |
log(kPhOH) = 7.75 (±0.15) − 2.93 (±0.53) ∑σo,m,p |
11 |
0.75 |
0.26 |
0.66 |
0.31 |
| (14) |
Phenolates |
Br2˙− |
log(kPhO−) = 8.58 (±0.03) − 0.55 (±0.07) ∑σo,m,p− |
22 |
0.78 |
0.17 |
0.72 |
0.19 |
| (15) |
CO3˙− |
log(kPhO−) = 8.55 (±0.06) − 0.92 (±0.12) ∑σo,m,p− |
33 |
0.71 |
0.32 |
0.67 |
0.37 |
| (16) |
Anilines |
Br˙ |
log(kArNH2) = 10.13 (±0.02) − 0.37 (±0.06) ∑σo,m,p+ |
8 |
0.88 |
0.06 |
0.75 |
0.09 |
| (17) |
Br2˙− |
log(kArNH2) = 8.26 (±0.08) − 0.59 (±0.14) ∑σo,m,p− |
9 |
0.77 |
0.17 |
0.68 |
0.20 |
| (18) |
Cl2˙− |
log(kArNH2) = 8.80 (±0.06) − 0.61 (±0.12) ∑σo,m,p+ |
10 |
0.76 |
0.15 |
0.53 |
0.22 |
| (19) |
CO3˙− |
log(kArNH2) = 8.72 (±0.05) − 0.81 (±0.09) ∑σo,m,p+ |
13 |
0.90 |
0.11 |
0.81 |
0.15 |
| (20) |
Alkoxy benzenes |
SO4˙− |
log(kAB) = 9.56 (±0.05) − 0.51 (±0.09) ∑σo,m,p− |
21 |
0.82 |
0.17 |
0.71 |
0.24 |
| (21) |
Br˙ |
log(kAB) = 9.84 (±0.05) − 0.86 (±0.07) ∑σo,m,p |
10 |
0.84 |
0.12 |
0.79 |
0.15 |
| (22) |
Br2˙− |
log(kAB) = 7.04 (±0.15) − 1.10 (±0.15) ∑σo,m,p+ |
16 |
0.86 |
0.36 |
0.79 |
0.44 |
| (23) |
Cl2˙− |
log(kAB) = 8.26 (±0.04) − 0.84 (±0.07) ∑σo,m,p+ |
11 |
0.96 |
0.11 |
0.94 |
0.14 |
| (24) |
CO3˙− |
log(kAB) = 5.95 (±0.17) − 1.52 (±0.24) ∑σo,m,p+ |
11 |
0.79 |
0.33 |
0.67 |
0.42 |
| (25) |
Organic compounds |
SO4˙−/Cl2˙− |
log(kCl2˙−) = −0.77 (±0.79) + 0.98 (±0.13) log(kSO4˙−) |
31 |
0.82 |
0.42 |
0.79 |
0.44 |
| (26) |
SO4˙−/CO3˙− |
log(kCO3˙−) = −1.70 (±1.15) + 0.96 (±0.10) log(kSO4˙−) |
28 |
0.68 |
0.48 |
0.64 |
0.48 |
| (27) |
SO4˙−/Br˙ |
log(kBr˙) = 5.22 (±0.73) + 0.50 (±0.11) log(kSO4˙−) |
26 |
0.66 |
0.30 |
0.56 |
0.33 |
| (28) |
SO4˙−/Br2˙− |
log(kBr2˙−) = −0.60 (±1.05) + 0.89 (±0.12) log(kSO4˙−) |
23 |
0.80 |
0.39 |
0.76 |
0.42 |
| (29) |
Cl2˙−/CO3˙− |
log(kCO3˙−) = −0.92 (±1.28) + 1.05 (±0.13) log(kCl2˙−) |
25 |
0.63 |
0.45 |
0.56 |
0.52 |
| (30) |
Cl2˙−/Br˙ |
log(kBr˙) = 7.17 (±0.40) + 0.33 (±0.06) log(kCl2˙−) |
34 |
0.62 |
0.16 |
0.55 |
0.22 |
| (31) |
Cl2˙−/Br2˙− |
log(kBr2˙−) = −2.43 (±1.02) + 1.19 (±0.10) log(kCl2˙−) |
37 |
0.71 |
0.40 |
0.67 |
0.43 |
| (32) |
Br˙/Br2˙− |
log(kBr2˙−) = −5.55 (±0.93) + 1.34 (±0.10) log(kBr˙) |
70 |
0.75 |
0.41 |
0.73 |
0.43 |
3.1 Undissociated phenols and phenolates
The k values of phenolic compounds with 5 one-electron oxidants cover 4 orders of magnitude ranging from 106 to 1010 M−1 s−1. For undissociated phenols, four QSARs for Cl2˙−, Br˙, Br2˙− and CO3˙− were successfully developed, but failed for SO4˙− although all three σ scales were tested (Table S28†). The collected 23 SO4˙−k values for phenols are quite high and vary only within a relatively narrow range of 109 to 1010 M−1 s−1, which is the primary cause of the failure in the QSAR development given that a wider range of k values is needed for models. Instead, a decent prediction could be achieved by using the average k value of 5.52 × 109 M−1 s−1 as the predicted k value of SO4˙− with all phenols, in which case all 23 k values were predicted within a factor of 1/3–3 (Table S28†). In addition, the cross-correlation-based models could also be applied to predict the SO4˙−k values (R2 = 0.66–0.82, eqn (25)–(28)). For the four developed QSARs for phenols, their intercepts follow the ascending order of Br2˙− (7.31) < CO3˙− (7.75) < Cl2˙− (8.40) < Br˙ (9.99), while their slopes follow the ascending order of CO3˙− (−2.93) < Br2˙− (−0.87) < Cl2˙− (−0.68) < Br˙ (−0.39). Fig. 1 shows all four developed QSARs toward phenols. In the case of phenolates toward SO4˙−, Br˙ and Cl2˙−, limited k values are available and also fall in a narrow range (approaching the diffusion limit), and thus only two QSARs for Br2˙− and CO3˙− were developed (Fig. 2).
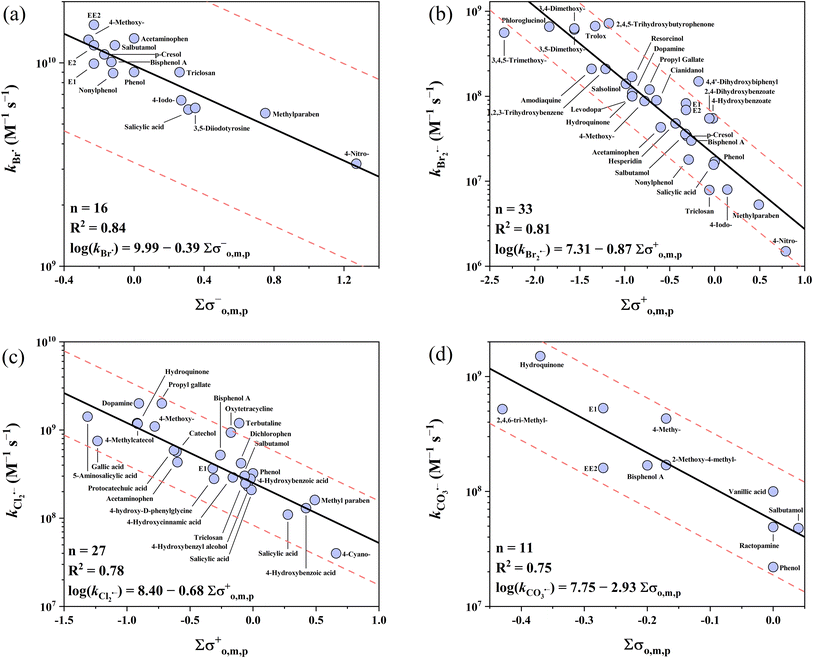 |
| | Fig. 1 Correlations between the second-order rate constants (k) for the reactions of phenols with (a) Br˙, (b) Br2˙−, (c) Cl2˙−, and (d) CO3˙−vs. ∑σo,m,p−, ∑σo,m,p+, ∑σo,m,p+, and ∑σo,m,p, respectively. The solid lines represent the fitted linear relationships and the dashed lines represent the predicted error ranges of a factor of 1/3 and 3, respectively. | |
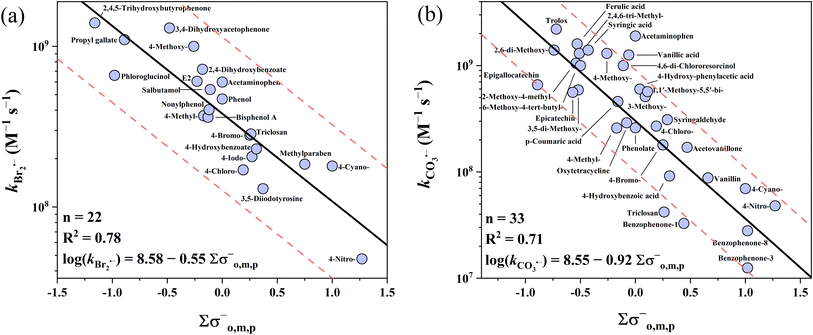 |
| | Fig. 2 Correlations between the second-order rate constants (k) for the reactions of phenolates with (a) Br2˙−, (b) CO3˙−vs. ∑σo,m,p−, and ∑σo,m,p−, respectively. The solid line represents the fitted linear relationship and the dashed lines represent the predicted error ranges of a factor of 1/3 and 3, respectively. | |
3.1.1 Undissociated phenols vs. Br˙ and Br2˙−.
Br˙ has the highest k values with the phenols of the four radicals. The collected k values are in the range of 109 to 1010 M−1 s−1 (n = 16). The σo,m,p− scale is the best descriptor variable with an R2 of 0.84. All the k values of Br˙ were predicted within a factor of 1.4. Recently, von Gunten's group investigated the reaction kinetics of Br˙ with numerous organics (e.g., aromatics, amines) and developed QSARs between the k values of Br˙ and theoretically calculated free energies of activation for single-electron transfer (ΔGactSET).72 Compared to the QSARs by von Gunten's group, the Hammett constant-based QSARs developed here show a better predictive performance. It should be noted that the electron transfer pathway dominates the reactions of Br˙ with aromatics,22,39,72,73 which is different from Cl˙ (i.e., addition on aromatic ring often occurred).38,74,75 In comparison, Br2˙− has the lowest k values with phenols among the 5 radicals. The reported k values range across 2 orders of magnitude from 106 to 108 M−1 s−1 (n = 33). For Br2˙−, the best correlation was obtained when applying the σo,m,p+ scale with an R2 of 0.81. Also, 30 out of 33 (91%) k values of Br2˙− were predicted within a factor of 1/3–3. Among them, 4,4′-dihydroxybiphenyl was underestimated by a factor of 5.1, which is probably due to its two symmetrical phenol moieties. Recently, Lei et al. determined the k values of Br2˙− with substantial micropollutants and developed QSARs between the k values and Hammett σo,m,p+ values.39 The updated QSARs in this work show no significant difference from the QSARs from Lei et al. due to the use of a similar database (Table 1).
3.1.2 Undissociated phenols vs. Cl2˙−.
The k values of phenols with Cl2˙− range across 2 orders of magnitude from 107 to 109 M−1 s−1 (n = 29) and show the second highest k values with phenols after Br˙. Most of the k values (27/29) can be used to develop the QSARs and the σo,m,p+ scale yields the best correlation with an R2 of 0.78. All 27 k values of Cl2˙− were predicted within a factor of 2.8. As exceptions, the k values of 4,4′-thiodiphenol and ioxynil are significantly higher than the prediction line, given that organic sulfur can also serve as a reactive site.76,77 Organic intermediates bearing a sulfur-chlorine three-electron bond are quickly formed in these reactions,78–80 with rate constants that are much higher than that of phenols.40,81 Compared to previous QSARs of Cl2˙− with only para-substituted phenols using σ constants as descriptors,82 the R2 is lower (0.78 in this work vs. 0.95 in the literature) though more data are involved in this work. Given that descriptors mainly account for the electronic effects of substituents, Hammett constants have limitations in determining the steric hindrance effects. Thereby, Hammett constant-based QSARs for para-substituted compounds often have a better predictive performance than multi-substituted ones, as evident by the reactions of Cl2˙− with phenols, as mentioned above. Moreover, for CO3˙− reactions with phenolates, the use of only para-substituted phenolates (σ+, R2 = 0.99) also shows a better predictive performance than this work (σ−, R2 = 0.71).46
3.1.3 Undissociated phenols vs. CO3˙−.
The k values of CO3˙− with phenols range across 2 orders of magnitude from 107 to 109 M−1 s−1 (n = 11). The overall k values of phenols with CO3˙− are ∼1–2 order of magnitude lower than that of phenols with Cl2˙−. The σo,m,p scale is the best descriptor variable with an R2 of 0.75. All 11k values of CO3˙− were predicted within a factor of 2.6.
3.1.4 Phenolates vs. Br2˙− and CO3˙−.
The collected k values of Br2˙− range from 107 to 109 M−1 s−1 (n = 22). These k values of phenolates are ∼1–2 orders of magnitude higher than that of the corresponding phenols, resulting from the greater electron-donating capacity of the –O group (σp+ = −2.3) than the OH group (σp+ = −0.92).64 The best correlation was obtained when applying the σo,m,p− scale with an R2 of 0.78. All 22 k values of Br2˙− were predicted within a factor of 2.0. In the case of CO3˙−, its k values with phenolates range across 2 orders of magnitude from 107 to 109 M−1 s−1 (n = 33). Similar to Br2˙−, the k values of CO3˙− with phenolates are ∼1–2 orders of magnitude higher than that of the corresponding phenols. The σo,m,p− scale is the best descriptor variable with an R2 of 0.71. Also, 27 out of the 33 (82%) k values of CO3˙− were predicted within a factor of 1/3–3. The k values for 4 complex compounds (e.g., epigallocatechin with Mw > 300 Da) were overestimated by a factor of over 3, which may because the simplified structural approximation may ignore potential reactive sites (Table S8†). This implies the limitations of structural approximation in predicting the reaction kinetics of complicated structural compounds. Based on the intercept and slope, it can be inferred that CO3˙− shows similar reactivity toward phenolates compared to Br2˙− (intercept: 8.55 vs. 8.58), while CO3˙− is more selective (slope: −0.92 (CO3˙−) vs. −0.55 (Br2˙−)).
3.2 Anilines
Anilines have the highest k values of the three electron-rich moieties examined (except phenolates). The reported k values range across 4 orders of magnitude from 107 to 1011 M−1 s−1. The k values for sulfonamides were excluded in the developed QSARs because (1) the circumneutral pKa values of sulfonamide-NH result in the uncertainty in their speciation83,84 and (2) potential reactive sites other than the aniline ring (e.g., the oxazole ring in sulfamethoxazole). As an alternative, the average k values of sulfonamides can be used for a rough prediction with acceptable errors (see below). Among the five radicals, four QSARs for Cl2˙−, Br˙, Br2˙− and CO3˙− were developed for anilines, except for SO4˙−. On the one hand, the high k values of SO4˙− with anilines are effectively diffusion controlled. On the other hand, some reported k values of SO4˙− with sulfonamides reach ∼1011 M−1 s−1, significantly exceeding the diffusion-controlled limits.85–90 This unexpected data may be due to the involvement of other reaction routes (e.g., direct photolysis) in the kinetic methods.36 For the 4 developed QSARs, the intercepts follow the ascending order of Br2˙− (8.26) < CO3˙− (8.72) < Cl2˙− (8.80) < Br˙ (10.13), while the slopes follow the ascending order of CO3˙− (−0.81) < Cl2˙− (−0.61) < Br2˙− (−0.59) < Br˙ (−0.37). All the developed QSARs toward anilines are shown in Fig. 3.
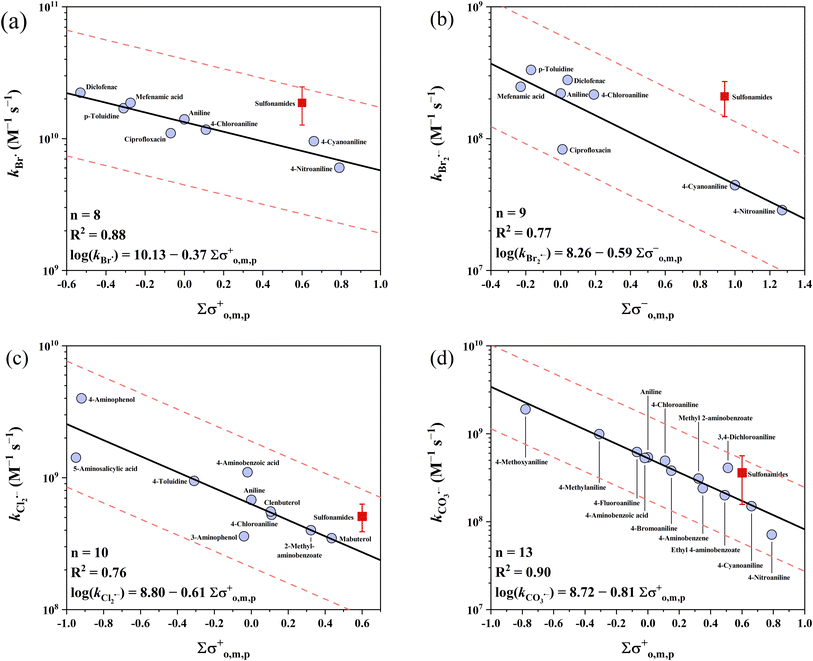 |
| | Fig. 3 Correlations between the second-order rate constants (k) for the reactions of anilines with (a) Br˙, (b) Br2˙−, (c) Cl2˙−, and (d) CO3˙−vs. ∑σo,m,p+, ∑σo,m,p−, ∑σo,m,p+, and ∑σo,m,p+, respectively. The red symbols represent the mean rate constants of sulfonamides, which are not included in the QSARs. The solid lines represent the fitted linear relationships and the dashed lines represent the predicted error ranges of a factor of 1/3 and 3, respectively. | |
3.2.1 Anilines vs. Br˙ and Br2˙−.
Br˙ has the highest k values with anilines among the four radicals. The majority of the k values of anilines with Br˙ (n = 13) are higher than 1 × 1010 M−1 s−1, with two exceptions of 4-nitroaniline and 4-cyanoaniline. For the other 8 k values of Br˙ (except for sulfonamides), the σo,m,p+ scale is the best descriptor with an R2 of 0.88 and all the k values were predicted within a factor of 1.3. Lei et al. developed a QSAR for k values of Br˙ with anilines using σo,m,p+ constants, while including unsuitable sulfonamides, which probably resulted in their slightly lower predictive performance (R2 = 0.825).39 In contrast to the highest reactivity of Br˙, Br2˙− has the lowest k values with anilines for all the radicals examined. The reported k values range from 107 to 108 M−1 s−1 (n = 14). The best correlation was obtained when applying σo,m,p− with an R2 of 0.77, and all these 9 k values of Br2˙− were predicted within a factor of 2.2.
3.2.2 Anilines vs. Cl2˙− and CO3˙−.
Cl2˙− has the second highest reactivity toward anilines after Br˙, with k values ranging from 108 to 109 M−1 s−1 (n = 18). For the 10 k values of Cl2˙− (except for sulfonamides), σo,m,p+ yielded the best correlation with an R2 of 0.76 and all were predicted within a factor of 1.9. The k values of CO3˙− are slightly lower than that of Cl2˙−, ranging across 2 orders of magnitude from 107 to 109 M−1 s−1 (n = 23). The average value of 3.60 × 108 M−1 s−1 can be used as the predicted k value for all reactions of CO3˙− with sulfonamides, where all 10 k values were predicted within a factor of 2.9. For the other 13 k values, the σo,m,p+ scale is the best descriptor variable with an R2 of 0.90. All 13 k values of CO3˙− were predicted within a factor of 2.1.
3.3 Alkoxy benzenes
Alkoxy benzenes show the lowest reactivity among the three electron-rich parent moieties, with k values covering 5 orders of magnitude ranging from 105 to 1010 M−1 s−1. Five QSARs were developed for the reactions of all 5 radicals with alkoxy benzenes. The intercepts follow the ascending order of CO3˙− (5.95) < Br2˙− (7.04) < Cl2˙− (8.26) < SO4˙− (9.56) < Br˙ (9.84), while the slopes follow the ascending order of CO3˙− (−1.52) < Br2˙− (−1.10) < Br˙ (−0.86) < Cl2˙− (−0.84) < SO4˙− (−0.51). All the developed QSARs toward alkoxy benzenes are shown in Fig. 4.
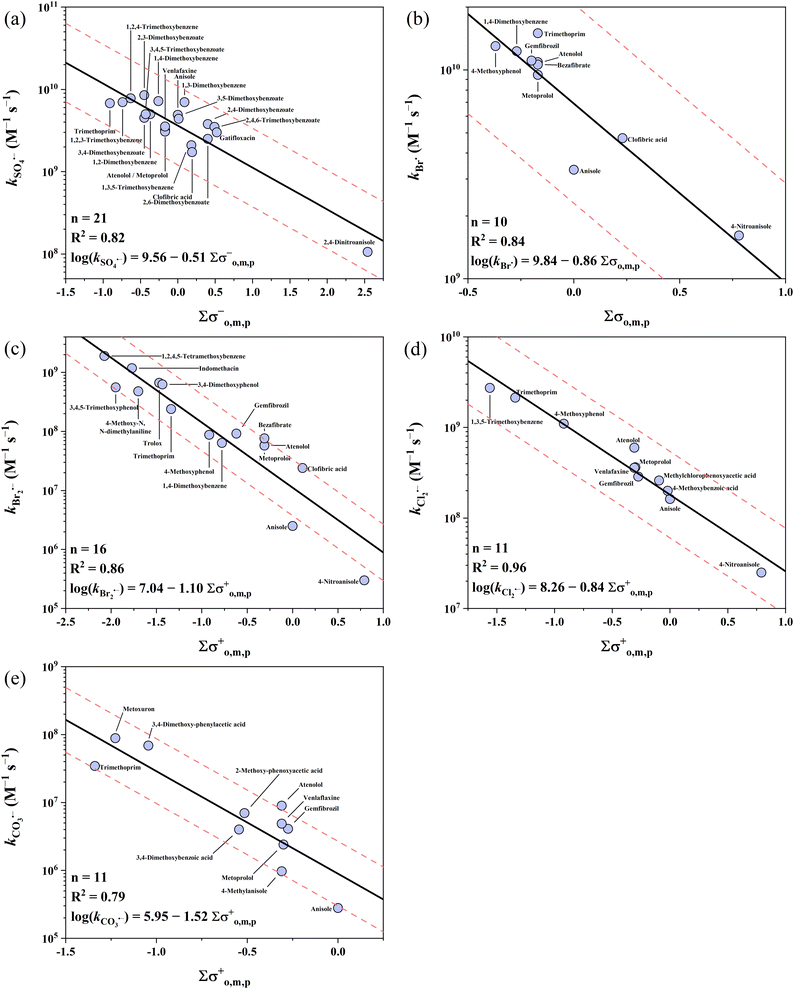 |
| | Fig. 4 Correlations between the second-order rate (k) for the reactions of alkoxy benzenes with (a) SO4˙−, (b) Br˙, (c) Br2˙−, (d) Cl2˙−, and (e) CO3˙−vs. ∑σo,m,p−, ∑σo,m,p, ∑σo,m,p+, ∑σo,m,p+, and ∑σo,m,p+, respectively. The solid lines represent the fitted linear relationships and the dashed lines represent the predicted error ranges of a factor of 1/3 and 3, respectively. Symbols of atenolol, metoprolol and clofibric acid are not mentioned in (a) due to space limitation. | |
3.3.1 Alkoxy benzenes vs. SO4˙−.
Almost all the k values for alkoxy benzenes with SO4˙− are in the range of ∼109 M−1 s−1 with one exception of 2,4-dinitro anisole (n = 21), which has the lowest k value of 1.06 × 108 M−1 s−1 due to the strong electron-withdrawing capacity of the –NO2 group.36 The best correlation was obtained when applying the σo,m,p− scale with an R2 of 0.82, and all the k values were predicted within a factor of 2.2. Xiao et al. developed QSARs for SO4˙− with organics using computational molecular descriptors and found that the k values can be predicted using the combination of O/C ratio and ELUMO and EHOMO gap (ELUMO − EHOMO), that is, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 26.8 − 3.97 × O/C − 0.746 × (ELUMO − EHOMO) with an R2 of 0.86.34 However, this cannot be directly compared with our Hammett constant-based QSARs given that its database is quite different. Here, we performed a comparison of the QSARs developed with Hammett constants and computational descriptors using the same database, that is, the reactions of SO4˙− with alkoxy benzenes. The computational descriptors from Xiao's work and k values in our database were used to develop the QSAR of alkoxy benzenes, which resulted in a tentative relationship (ln
k = 26.8 − 3.97 × O/C − 0.746 × (ELUMO − EHOMO) with an R2 of 0.86.34 However, this cannot be directly compared with our Hammett constant-based QSARs given that its database is quite different. Here, we performed a comparison of the QSARs developed with Hammett constants and computational descriptors using the same database, that is, the reactions of SO4˙− with alkoxy benzenes. The computational descriptors from Xiao's work and k values in our database were used to develop the QSAR of alkoxy benzenes, which resulted in a tentative relationship (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 29.9 − 5.79 × O/C − 1.02 × (ELUMO − EHOMO), R2 = 0.52, p < 0.05, details in Table S32†). It was found that the predictive performance was much lower than using the QSAR model developed in this work using the Hammett constant (R2 = 0.82). This highlights the importance of using the appropriate descriptors in developing QSARs.
k = 29.9 − 5.79 × O/C − 1.02 × (ELUMO − EHOMO), R2 = 0.52, p < 0.05, details in Table S32†). It was found that the predictive performance was much lower than using the QSAR model developed in this work using the Hammett constant (R2 = 0.82). This highlights the importance of using the appropriate descriptors in developing QSARs.
3.3.2 Alkoxy benzenes vs. Br˙ and Br2˙−.
Br˙ has the highest k values with alkoxy benzenes among the five radicals, which are marginally higher than that of SO4˙−. The k values range from 109 to 1010 M−1 s−1 (n = 10). The best correlation was obtained when applying the σo,m,p scale with an R2 of 0.84. All the k values of Br˙ were predicted within a factor of 2.1. In comparison, Br2˙− has the lowest k values with alkoxy benzenes among the five radicals examined. The reported k values range across 4 orders of magnitude from 105 to 109 M−1 s−1 (n = 16). The best correlation for Br2˙− was obtained when applying the σo,m,p+ scale with an R2 of 0.86. Also, 13 out of 16 (81%) k values of Br2˙− were predicted within a factor of 1/3–3. This is an update of the previous QSARs of Br˙ and Br2˙− with more kinetic data input,39 which shows a comparable predictive performance.
3.3.3 Alkoxy benzenes vs. Cl2˙−.
The k values of Cl2˙− range across 3 orders of magnitude from 107 to 109 M−1 s−1 (n = 11), which are ∼1–2 orders of magnitude lower than that of SO4˙− and Br˙. The k value of 1,3,5-trimethoxybenzene is significantly higher than the predicted line, which may be due to the underestimated electron-donating capacity of the meta –OCH3 group using the reported σm+ (0.05). Replacing σm+ with σp+ (−0.78) resulted in a satisfactory prediction performance within a factor <1.4. For the other 10 k values, the σo,m,p+ scale was the best descriptor variable with an R2 of 0.96 and all of them were predicted within a factor of 1.9.
3.3.4 Alkoxy benzenes vs. CO3˙−.
Collected k values of CO3˙− range across 4 orders of magnitude from 105 to 109 M−1 s−1 (n = 29). However, a major amount of them (18 out of 29) are both alkoxy benzenes and phenolates (bearing –O− group), whose k values (107 to 109 M−1 s−1) are much higher than the other 11 k values (105 to 107 M−1 s−1). These phenolates were excluded in developing QSARs because the –O− group (σp+ = −2.30) has a much stronger electron-donating capacity and determines the reactivity. Therefore, these k values can be well-predicted as phenolates using eqn (15). For the other 11 k values, the σo,m,p+ scale produces a correlation with an R2 of 0.79.
3.4 Cross-correlations and holistic comparison
The aforementioned Hammett constant-based QSARs can well predict the k values when the Hammett constants are known and the compounds belong to phenol, aniline or alkoxy benzenes. As an alternative, cross-correlations may be developed between the k values of two radicals given that these five radicals mainly undergo similar reaction mechanisms with TrOCs (i.e., one-electron transfer).18,38,39 Aromatic and amino TrOCs were used to develop the cross-correlations, which have a larger kinetic database than the Hammett constant-based QSARs. These two types TrOCs provide abundant k values with wide ranges, which is essential to develop models. Moreover, the k values of both types of TrOCs are affected by the conjugate/induction electric effects of the groups adjacent to the reactive site, which are also involved in the cross-correlations in previous QSAR works.45 The electron-poor compounds and saturated carbon skeleton were not included due to their low reactivity and potential other reaction mechanism (some radicals can even hardly oxidize them).91
Fig. 5 shows the 8 developed cross-correlations. Eqn (25)–(32) represent the correlations between the k values of SO4˙−vs. Cl2˙−, SO4˙−vs. CO3˙−, SO4˙−vs. Br˙, SO4˙−vs. Br2˙−, Cl2˙−vs. CO3˙−, Cl2˙−vs. Br˙, Cl2˙−vs. Br2˙− and Br˙ vs. Br2˙−, respectively. All cross-correlations show a positive slope, suggesting that these five radicals share similar electrophilic reaction mechanisms. In terms of predictive performance, 22 out of 31 (71%), 19 out of 28 (68%), 23 out of 26 (88%), 18 out of 23 (78%), 16 out of 25 (64%), 34 out of 34 (100%), 32 out of 37 (86%) and 54 out of 70 (77%) k values were predicted within a factor of 1/3–3 by eqn (25)–(32), respectively. This predictive performance is noticeably lower than that of the Hammett constant-based QSARs. For example, 161 out of 274 (59%) k values were predicted within a factor of 1/2–2 by the 8 cross-correlations, while 207 out of 251 (82%) were predicted within a factor of 1/2–2 by the 15 Hammett constant-based QSARs. Therefore, the developed cross-correlations serve as an alternative to Hammett constant-based QSARs, but their application range is restricted within aromatic and amino TrOCs.
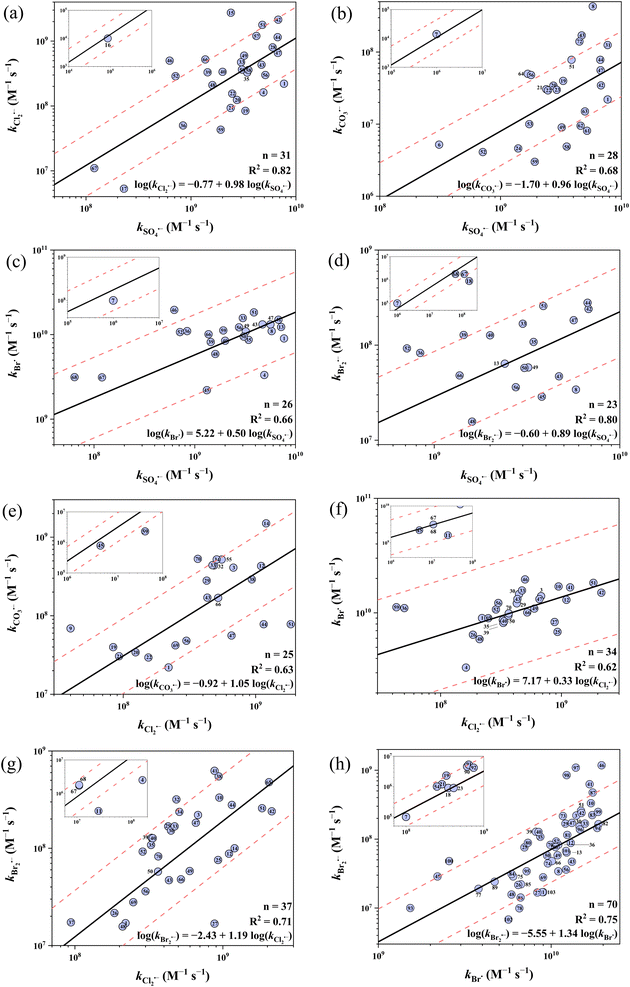 |
| | Fig. 5 Cross-correlations for organic compounds between (a) log(kSO4˙−) and log(kCl2˙−), (b) log(kSO4˙−) and log(kCO3˙−), (c) log(kSO4˙−) and log(kBr˙), (d) log(kSO4˙−) and log(kBr2˙−), (e) log(kCl2˙−) and log(kCO3˙−), (f) log(kCl2˙−) and log(kBr˙), (g) log(kCl2˙−) and log(kBr2˙−), (h) log(kBr˙) and log(kBr2˙−). The solid lines represent the fitted linear relationships and the dashed lines represent the predicted error ranges of a factor of 1/3 and 3, respectively. Symbols are numbered rather than named due to space limitation, see ESI, Table S18† for the full list of compounds and their corresponding numbers. | |
Overall, the predictive performance of QSARs in this work is generally higher than previous QSARs based on computed molecular descriptors, although smaller datasets were applied here (Table 1). For example, the average absolute model bias (AMB) signifies the predictive power of the developed QSARs (smaller indicates better predictivity), which is calculated by averaging the absolute deviation between the predicted and observed k values.92 The AMB of the QSAR for the oxidation of TrOCs by SO4˙− developed by Xiao et al. is 0.73,34 while that of the developed in this study is 0.55 (details in ESI, Table S2†). QSARs for CO3˙− with phenols and alkoxy benzenes were newly developed. The QSARs for Cl2˙−, Br˙ and Br2˙− improved on the works by Lei et al.38,39 with updated and expanded datasets, the removal of inappropriate compounds (e.g., sulfonamides), and all three scales of Hammett σ were tested. The updated QSARs showed a comparable good predictive performance (over 95% k values predicted within a factor of 1/3–3) and underwent internal validation.
3.5 Environmental applications and remarks on QSARs
One of the main objectives of acquiring the k values of TrOCs toward numerous radicals is to predict their fate in municipal water treatment systems. Therefore, the k values predicted using the QSARs here were employed to evaluate the elimination of various TrOCs in both UV/PDS and UV/chlorine treatment in wastewater effluents (UV/PDS: pH = 8.23, [DOC] = 4.78 mgC L−1, [CO32−] = 0.33 mgC L−1, [HCO3−] = 10.61 mgC L−1, [Cl−] = 103.66 mg L−1, [Br−] = 0.46 mg L−1; UV/chlorine: pH = 7.0, [DOC] = 3.5 mgC L−1, [HCO3−] = 1.3 mM, [Cl−] = 2.92 mM, [Br−] = 5.75 μM).24,38 The first-order decay rates of TrOCs can be calculated using the following simplified kinetic model (eqn (33)):| | 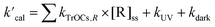 | (33) |
where 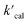 is the calculated pseudo-first-order degradation rate of TrOCs, kTrOCs,R is the second-order rate constant of the radicals with TrOCs, [R]ss is the steady-state concentrations of radicals from kinetic modelling using the Kintecus software,28kUV is the pseudo-first-order photolysis rate of TrOCs, and kdark is the pseudo-first-order dark oxidation rate of TrOCs by PDS or chlorine, which are shown in the literature and Table S27.†24,38 The kOH˙ and kCl˙ were collected from the work by Lei et al.,38 while the kSO4˙−, kCO3˙−, kBr˙, kBr2˙− and kCl2˙− values were predicted using the QSARs developed in this work (either Hammett constant-based QSARs or cross-correlations, details in Table S27†). Then
is the calculated pseudo-first-order degradation rate of TrOCs, kTrOCs,R is the second-order rate constant of the radicals with TrOCs, [R]ss is the steady-state concentrations of radicals from kinetic modelling using the Kintecus software,28kUV is the pseudo-first-order photolysis rate of TrOCs, and kdark is the pseudo-first-order dark oxidation rate of TrOCs by PDS or chlorine, which are shown in the literature and Table S27.†24,38 The kOH˙ and kCl˙ were collected from the work by Lei et al.,38 while the kSO4˙−, kCO3˙−, kBr˙, kBr2˙− and kCl2˙− values were predicted using the QSARs developed in this work (either Hammett constant-based QSARs or cross-correlations, details in Table S27†). Then  was compared with the experimental k′
was compared with the experimental k′ 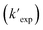 from the literature.24,38 As shown in Fig. 6a, this model showed a good performance in predicting the degradation of TrOCs. Most of the pseudo-first-order degradation rates (16 out of 18) were predicted within a factor of 1/3–3. Fig. 6b shows the contribution of various radicals and UV + dark oxidation to the degradation of TrOCs. It implies that secondary radicals (CO3˙−, Cl2˙− and Br2˙−, etc.) have significant contributions to the degradation of selected TrOCs. Especially for electron-rich TrOCs such as trimethoprim and ractopamine, where CO3˙− contributes over half of their degradation in both AOPs. This result stresses the importance of obtaining k values for secondary radical reactions in AOPs.
from the literature.24,38 As shown in Fig. 6a, this model showed a good performance in predicting the degradation of TrOCs. Most of the pseudo-first-order degradation rates (16 out of 18) were predicted within a factor of 1/3–3. Fig. 6b shows the contribution of various radicals and UV + dark oxidation to the degradation of TrOCs. It implies that secondary radicals (CO3˙−, Cl2˙− and Br2˙−, etc.) have significant contributions to the degradation of selected TrOCs. Especially for electron-rich TrOCs such as trimethoprim and ractopamine, where CO3˙− contributes over half of their degradation in both AOPs. This result stresses the importance of obtaining k values for secondary radical reactions in AOPs.
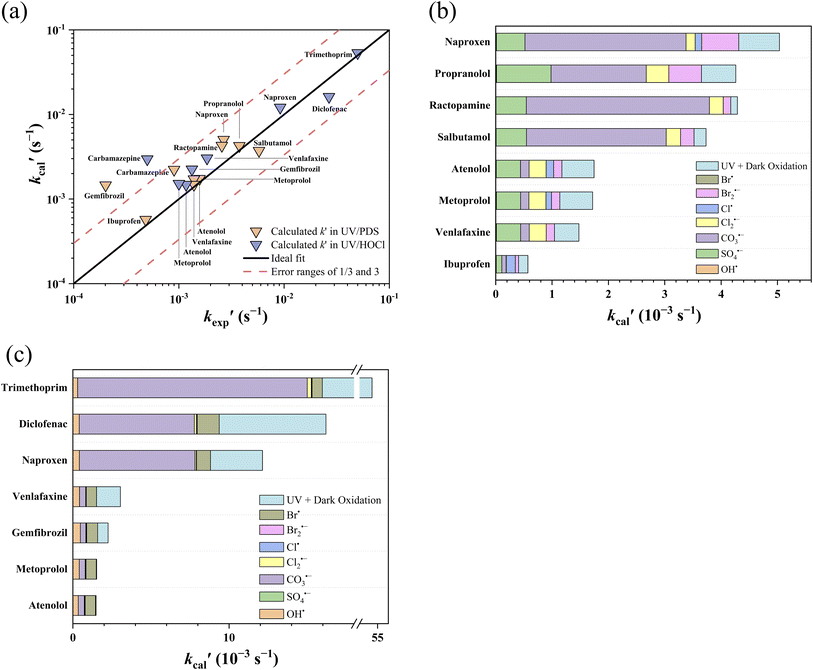 |
| | Fig. 6 (a) Relationships between the experimental pseudo-first-order degradation rate of TrOCs 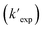 and calculated pseudo first-order degradation rate and calculated pseudo first-order degradation rate 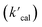 in the UV/chlorine and UV/PDS treatment of typical wastewater effluents (Table S27†). The contribution of TrOC degradation from various radicals and UV + dark oxidation during (b) UV/PDS and (c) UV/chlorine treatment. in the UV/chlorine and UV/PDS treatment of typical wastewater effluents (Table S27†). The contribution of TrOC degradation from various radicals and UV + dark oxidation during (b) UV/PDS and (c) UV/chlorine treatment. | |
Overall, by using the established QSARs to acquire k values and radical levels from kinetic modeling, one may predict the degradation of TrOCs without tedious experiments. It should be noted that the effects of the water parameters (e.g., pH) should be carefully considered in engineered applications of AOPs. For example, in Fig. 6, the k values of atenolol and metoprolol are predicted as alkoxy benzene due to the structural approximation. This may be a stopgap given that the amine group (pKa ∼11) may become the reactive site at higher pH. Moreover, one should apply the appropriate models for protonated and deprotonated species (e.g., phenol vs. phenolate) at different pH. Finally, some remarks on the usage of the developed QSARs in this work are suggested as follows. (1) Hammett constant-based QSARs should be the prior choice whenever possible because they have significantly higher accuracy over cross-correlation-based models. (2) When one compound has multiple substituent groups, the substituent groups having the strongest electron-donating capacity (i.e., –O− ≈ –NH2 > –OH > –OCH3) is better to serve as the parent structure in QSARs (e.g., take 4-methoxyaniline as an aniline but not anisole in QSARs). (3) Cross-correlations have a specific application range (e.g., aromatics and amines in this work). (4) Be aware of the errors introduced by structural approximation given that additional reactive sites may be overlooked via this approach. (5) QSARs should only serve as an alternative when reliable experimental k values are not available.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Financial support from the National Natural Science Foundation of China (22176225), the National Postdoctoral Program for Innovative Talents (BX20220305), Guangdong Basic and Applied Basic Research Foundation (2021A1515010389) and the China Postdoctoral Science Foundation (2022M723200) is gratefully acknowledged.
References
- R. P. Schwarzenbach, B. I. Escher, K. Fenner, T. B. Hofstetter, C. A. Johnson, U. von Gunten and B. Wehrli, The Challenge of Micropollutants in Aquatic Systems, Science, 2006, 313(5790), 1072–1077, DOI:10.1126/science.1127291.
- P. Westerhoff, Y. Yoon, S. Snyder and E. Wert, Fate of Endocrine-Disruptor, Pharmaceutical, and Personal Care Product Chemicals during Simulated Drinking Water Treatment Processes, Environ. Sci. Technol., 2005, 39(17), 6649–6663, DOI:10.1021/es0484799.
- Y. Luo, W. Guo, H. H. Ngo, L. D. Nghiem, F. I. Hai, J. Zhang, S. Liang and X. C. Wang, A review on the occurrence of micropollutants in the aquatic environment and their fate and removal during wastewater treatment, Sci. Total Environ., 2014, 473–474, 619–641, DOI:10.1016/j.scitotenv.2013.12.065.
- W.-W. Li, H.-Q. Yu and B. E. Rittmann, Chemistry: Reuse water pollutants, Nature, 2015, 528(7580), 29–31, DOI:10.1038/528029a.
- U. von Gunten, Oxidation Processes in Water Treatment: Are We on Track?, Environ. Sci. Technol., 2018, 52(9), 5062–5075, DOI:10.1021/acs.est.8b00586.
- Y. Deng and R. Zhao, Advanced oxidation processes (AOPs) in wastewater treatment, Curr. Pollut. Rep., 2015, 1, 167–176, DOI:10.1007/s40726-015-0015-z.
- D. B. Miklos, R. Hartl, P. Michel, K. G. Linden, J. E. Drewes and U. Hübner, UV/H2O2 process stability and pilot-scale validation for trace organic chemical removal from wastewater treatment plant effluents, Water Res., 2018, 136, 169–179, DOI:10.1016/j.watres.2018.02.044.
- Z. Yang, J. Qian, C. Shan, H. Li, Y. Yin and B. Pan, Toward Selective Oxidation of Contaminants in Aqueous Systems, Environ. Sci. Technol., 2021, 55(21), 14494–14514, DOI:10.1021/acs.est.1c05862.
- Y. Lee, D. Gerrity, M. Lee, S. Gamage, A. Pisarenko, R. A. Trenholm, S. Canonica, S. A. Snyder and U. von Gunten, Organic Contaminant Abatement in Reclaimed Water by UV/H2O2 and a Combined Process Consisting of O3/H2O2 Followed by UV/H2O2: Prediction of Abatement Efficiency, Energy Consumption, and Byproduct Formation, Environ. Sci. Technol., 2016, 50(7), 3809–3819, DOI:10.1021/acs.est.5b04904.
- J. Lee, U. von Gunten and J. H. Kim, Persulfate-Based Advanced Oxidation: Critical Assessment of Opportunities and Roadblocks, Environ. Sci. Technol., 2020, 54(6), 3064–3081, DOI:10.1021/acs.est.9b07082.
- K. Guo, Z. Wu, C. Chen and J. Fang, UV/Chlorine Process: An Efficient Advanced Oxidation Process with Multiple Radicals and Functions in Water Treatment, Acc. Chem. Res., 2022, 55(3), 286–297, DOI:10.1021/acs.accounts.1c00269.
- D. A. Armstrong, R. E. Huie, W. H. Koppenol, S. V. Lymar, G. Merényi, P. Neta, B. Ruscic, D. M. Stanbury, S. Steenken and P. Wardman, Standard electrode potentials involving radicals in aqueous solution: inorganic radicals (IUPAC Technical Report), Pure Appl. Chem., 2015, 87(11–12), 1139–1150, DOI:10.1515/pac-2014-0502.
- W.-D. Oh, Z. Dong and T.-T. Lim, Generation of Sulfate Radical through Heterogeneous Catalysis for Organic Contaminants Removal: Current Development, Challenges and Prospects, Appl. Catal., B, 2016, 194, 169–201, DOI:10.1016/j.apcatb.2016.04.003.
- Y. Yeom, J. Han, X. Zhang, C. Shang, T. Zhang, X. Li, X. Duan and D. D. Dionysiou, A review on the degradation efficiency, DBP formation, and toxicity variation in the UV/chlorine treatment of micropollutants, Chem. Eng. J., 2021, 424(15), 130053, DOI:10.1016/j.cej.2021.130053.
- P. Wardman, Reduction Potentials of One-Electron Couples Involving Free Radicals in
Aqueous Solution, J. Phys. Chem. Ref. Data, 1989, 17(2), 1637–1755, DOI:10.1063/1.555805.
- C. Chen, Z. Wu, S. Zheng, L. Wang, X. Niu and J. Fang, Comparative Study for Interactions of Sulfate Radical and Hydroxyl Radical with Phenol in the Presence of Nitrite, Environ. Sci. Technol., 2020, 54(13), 8455–8463, DOI:10.1021/acs.est.0c02377.
- G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, Critical Review of Rate Constants for Reactions of Hydrated Electrons, Hydrogen Atoms and Hydroxyl Radicals (˙OH/O˙–) in Aqueous Solution, J. Phys. Chem. Ref. Data, 1988, 17(2), 513–886, DOI:10.1063/1.555805.
- P. Neta, R. E. Huie and A. B. Ross, Rate Constants for Reactions of Inorganic Radicals in Aqueous Solution, J. Phys. Chem. Ref. Data, 1988, 17(3), 1027–1284, DOI:10.1063/1.555808.
- J. L. Wang and S. Z. Wang, Reactive Species in Advanced Oxidation Processes: Formation, Identification and Reaction Mechanism, Chem. Eng. J., 2020, 401, 126158, DOI:10.1016/j.cej.2020.126158.
- I. Lampre, J.-L. Marignier, M. Mirdamadi-Esfahani, P. Pernot, P. Archirel and M. Mostafavi, Oxidation of Bromide Ions by Hydroxyl Radicals: Spectral Characterization of the Intermediate BrOH˙–, J. Phys. Chem. A, 2013, 117(5), 877–887, DOI:10.1021/jp310759u.
- G. V. Buxton, M. Bydder, G. A. Salmon and J. E. Williams, The Reactivity of Chlorine Atoms in Aqueous Solution Part III. The Reactions of Cl˙ with Solutes, Phys. Chem. Chem. Phys., 2000, 2(2), 237–245, 10.1039/a907133d.
- Y. Lei, X. Lei, P. Westerhoff, X. Tong, J. Ren, Y. Zhou, S. Cheng, G. Ouyang and X. Yang, Bromine Radical (Br˙ and Br2˙–) Reactivity with Dissolved Organic Matter and Brominated Organic Byproduct Formation, Environ. Sci. Technol., 2022, 56(8), 5189–5199, DOI:10.1021/acs.est.2c00549.
- X. Yang, F. L. Rosario-Ortiz, Y. Lei, Y. Pan, X. Lei and P. Westerhoff, Multiple Roles of Dissolved Organic Matter in Advanced Oxidation Processes, Environ. Sci. Technol., 2022, 56(16), 11111–11131, DOI:10.1021/acs.est.2c01017.
- K. Guo, Z. Wu, S. Yan, B. Yao, W. Song, Z. Hua, X. Zhang, X. Kong, X. Li and J. Fang, Comparison of the UV/Chlorine and UV/H2O2 Processes in the Degradation of PPCPs in Simulated Drinking Water and Wastewater: Kinetics, Radical Mechanism and Energy Requirements, Water Res., 2018, 147, 184–194, DOI:10.1016/j.watres.2018.08.048.
- L. Lian, B. Yao, S. Hou, J. Fang, S. Yan and W. Song, Kinetic Study of Hydroxyl and Sulfate Radical-Mediated Oxidation of Pharmaceuticals in Wastewater Effluents, Environ. Sci. Technol., 2017, 51(5), 2954–2962, DOI:10.1021/acs.est.6b05536.
- W. Li, T. Jain, K. Ishida and H. Liu, A Mechanistic Understanding of the Degradation of Trace Organic Contaminants by UV/Hydrogen Peroxide, UV/Persulfate and UV/Free Chlorine for Water Reuse, Environ. Sci.: Water Res. Technol., 2017, 3(1), 128–138, 10.1039/C6EW00242K.
- K. Zhang and K. M. Parker, Halogen Radical Oxidants in Natural and Engineered Aquatic Systems, Environ. Sci. Technol., 2018, 52(17), 9579–9594, DOI:10.1021/acs.est.8b02219.
- K. Guo, Z. Wu, C. Shang, B. Yao, S. Hou, X. Yang, W. Song and J. Fang, Radical Chemistry and Structural Relationships of PPCP Degradation by UV/Chlorine Treatment in Simulated Drinking Water, Environ. Sci. Technol., 2017, 51(18), 10431–10439, DOI:10.1021/acs.est.7b02059.
- Y. Lee and U. Von Gunten, Advances in predicting organic contaminant abatement during ozonation of municipal wastewater effluent: Reaction kinetics, transformation products, and changes of biological effects, Environ. Sci.: Water Res. Technol., 2016, 2(3), 421–442, 10.1039/c6ew00025h.
- M. C. Dodd, M.-O. Buffle and U. von Gunten, Oxidation of Antibacterial Molecules by Aqueous Ozone: Moiety-Specific Reaction Kinetics and Application to Ozone-Based Wastewater Treatment, Environ. Sci. Technol., 2006, 40(6), 1969–1977, DOI:10.1021/es051369x.
- W. Song, W. Chen, W. J. Cooper, J. Greaves and G. E. Miller, Free-radical destruction of beta-lactam antibiotics in aqueous solution, J. Phys. Chem. A, 2008, 112(32), 7411–7417, DOI:10.1021/jp803229a.
- W. Song, W. J. Cooper, S. P. Mezyk, J. Greaves and B. M. Peake, Free Radical Destruction of β-Blockers in Aqueous Solution, Environ. Sci. Technol., 2008, 42(4), 1256–1261, DOI:10.1021/es702245n.
- S. Canonica, T. Kohn, M. Mac, F. J. Real, J. Wirz and U. von Gunten, Photosensitizer Method to Determine Rate Constants for the Reaction of Carbonate Radical with Organic Compounds, Environ. Sci. Technol., 2005, 39(23), 9182–9188, DOI:10.1021/es051236b.
- R. Xiao, T. Ye, Z. Wei, S. Luo, Z. Yang and R. Spinney, Quantitative Structure–Activity Relationship (QSAR) for the Oxidation of Trace Organic Contaminants by Sulfate Radical, Environ. Sci. Technol., 2015, 49(22), 13394–13402, DOI:10.1021/acs.est.5b03078.
- L. Wojnárovits, T. Tóth and E. Takács, Critical Evaluation of Rate Coefficients for Hydroxyl Radical Reactions with Antibiotics: A Review, Crit. Rev. Environ. Sci. Technol., 2018, 48(6), 575–613, DOI:10.1080/10643389.2018.1463066.
- L. Wojnárovits and E. Takács, Rate Constants of Sulfate Radical Anion Reactions with Organic Molecules: A Review, Chemosphere, 2019, 220, 1014–1032, DOI:10.1016/j.chemosphere.2018.12.156.
- L. Wojnárovits, T. Tóth and E. Takács, Rate Constants of Carbonate Radical Anion Reactions with Molecules of Environmental Interest in Aqueous Solution: A Review, Sci. Total Environ., 2020, 717, 137219, DOI:10.1016/j.scitotenv.2020.137219.
- Y. Lei, S. Cheng, N. Luo, X. Yang and T. An, Rate Constants and Mechanisms of the Reactions of Cl˙ and Cl2˙– with Trace Organic Contaminants, Environ. Sci. Technol., 2019, 53(19), 11170–11182, DOI:10.1021/acs.est.9b02462.
- Y. Lei, X. Lei, Y. Yu, K. Li, Z. Li, S. Cheng, G. Ouyang and X. Yang, Rate Constants and Mechanisms for Reactions of Bromine Radicals with Trace Organic Contaminants, Environ. Sci. Technol., 2021, 55(15), 10502–10513, DOI:10.1021/acs.est.1c02313.
- L. Wojnarovits and E. Takacs, Rate constants of dichloride radical anion reactions with molecules of environmental interest in aqueous solution: a review, Environ. Sci. Pollut. Res. Int., 2021, 28(31), 41552–41575, DOI:10.1007/s11356-021-14453-w.
- M. Roder, G. Földiák and L. Wojnárovits, Electron transfer from cresols to N3, BrO2, ClO2, NO2 and SO−4 radicals: correlation between rate constants and one-electron reduction potentials, Radiat. Phys. Chem., 1999, 55(5), 515–519, DOI:10.1016/S0969-806X(99)00240-6.
- L. Szabó, T. Tóth, E. Takács and L. Wojnárovits, One-Electron Oxidation of Molecules with Aromatic and Thioether Functions: Cl2˙–/Br2˙– and ˙OH Induced Oxidation of Penicillins Studied by Pulse Radiolysis, J. Photochem. Photobiol., A, 2016, 326, 50–59, DOI:10.1016/j.jphotochem.2016.04.025.
- X. Lei, J. Guan, Y. Lei, L. Yao, P. Westerhoff and X. Yang, One-Electron Oxidant-Induced Transformations of Aromatic Alcohol to Ketone Moieties in Dissolved Organic Matter Increase Trichloromethane Formation, Environ. Sci. Technol., 2022, 57, 18597–18606, DOI:10.1021/acs.est.2c06425.
- M. Ren, S. Sun, Y. Wu, Y. Shi, Z. J. Wang, H. Cao and Y. Xie, The structure-activity relationship of aromatic compounds in advanced oxidation processes: a review, Chemosphere, 2022, 296, 134071, DOI:10.1016/j.chemosphere.2022.134071.
- Y. Lee and U. von Gunten, Quantitative Structure–Activity Relationships (QSARs) for the Transformation of Organic Micropollutants during Oxidative Water Treatment, Water Res., 2012, 46(19), 6177–6195, DOI:10.1016/j.watres.2012.06.006.
- S. Canonica and P. G. Tratnyek, Quantitative structure-activity relationships for oxidation reactions of organic chemicals in water, Environ. Toxicol. Chem., 2003, 22(8), 1743–1754, DOI:10.1897/01-237.
- T. M. Krygowski, K. Ejsmont, B. T. Stepień, M. K. Cyrański, J. Poater and M. Sola, Relation between the substituent effect and aromaticity, J. Org. Chem., 2004, 69(20), 6634–6640, DOI:10.1021/jo0492113.
- P. R. Tentscher, M. Lee and U. von Gunten, Micropollutant Oxidation Studied by Quantum Chemical Computations: Methodology and Applications to Thermodynamics, Kinetics, and Reaction Mechanisms, Acc. Chem. Res., 2019, 52(3), 605–614, DOI:10.1021/acs.accounts.8b00610.
- S. Sudhakaran and G. L. Amy, QSAR models for oxidation of organic micropollutants in water based on ozone and hydroxyl radical rate constants and their chemical classification, Water Res., 2013, 47(3), 1111–1122, DOI:10.1016/j.watres.2012.11.033.
- W. Yang, Y. Tang, L. Liu, X. Peng, Y. Zhong, Y. Chen and Y. Huang, Chemical behaviors and toxic effects of ametryn during the UV/chlorine process, Chemosphere, 2020, 240, 124941, DOI:10.1016/j.chemosphere.2019.124941.
- H. Lei and S. A. Snyder, 3D QSPR models for the removal of trace organic contaminants by ozone and free chlorine, Water Res., 2007, 41(18), 4051–4060, DOI:10.1016/j.watres.2007.05.010.
- B. Wols and D. Vries, On a QSAR approach for the prediction of priority compound degradation by water treatment processes, Water Sci. Technol., 2012, 66(7), 1446–1453, DOI:10.2166/wst.2012.328.
- X. Luo, X. Wei, J. Chen, Q. Xie, X. Yang and W. J. Peijnenburg, Rate constants of hydroxyl radicals reaction with different dissociation species of fluoroquinolones and sulfonamides: Combined experimental and QSAR studies, Water Res., 2019, 166, 115083, DOI:10.1016/j.watres.2019.115083.
- H. Kušić, B. Rasulev, D. Leszczynska, J. Leszczynski and N. Koprivanac, Prediction of rate constants for radical degradation of aromatic pollutants in water matrix: A QSAR study, Chemosphere, 2009, 75(8), 1128–1134, DOI:10.1016/j.chemosphere.2009.01.019.
- L. F. Delgado, P. Charles, K. Glucina and C. Morlay, QSAR-like models: a potential tool for the selection of PhACs and EDCs for monitoring purposes in drinking water treatment systems–a review, Water Res., 2012, 46(19), 6196–6209, DOI:10.1016/j.watres.2012.08.016.
- L. Wojnárovits and E. Takács, Structure dependence of the rate coefficients of hydroxyl radical+ aromatic molecule reaction, Radiat. Phys. Chem., 2013, 87, 82–87, DOI:10.1016/j.radphyschem.2013.02.036.
- C. Liu, D. Chen and X. e. Chen, Atmospheric Reactivity of Methoxyphenols: A Review, Environ. Sci. Technol., 2022, 56(5), 2897–2916, DOI:10.1021/acs.est.1c06535.
- O. B. Zusman, M. L. Kummel, J. M. De la Rosa and Y. G. Mishael, Dissolved Organic Matter Adsorption from Surface Waters by Granular Composites versus Granular Activated Carbon Columns: An Applicable Approach, Water Res., 2020, 181, 115920, DOI:10.1016/j.watres.2020.115920.
- W. Duan, F. Meng, H. Cui, Y. Lin, G. Wang and J. Wu, Ecotoxicity of phenol and cresols to aquatic organisms: A review, Ecotoxicol. Environ. Saf., 2018, 157, 441–456, DOI:10.1016/j.ecoenv.2018.03.089.
- S. Mohammadi, A. Kargari, H. Sanaeepur, K. Abbassian, A. Najafi and E. Mofarrah, Phenol removal from industrial wastewaters: a short review, Desalin. Water Treat., 2015, 53(8), 2215–2234, DOI:10.1080/19443994.2014.883327.
- N. K. Chaturvedi, Comparison of available treatment techniques for hazardous aniline-based
organic contaminants, Appl. Water Sci., 2022, 12(7), 173, DOI:10.1007/s13201-022-01695-3.
- M. K. Dail and S. P. Mezyk, Hydroxyl-Radical-Induced Degradative Oxidation of β-Lactam Antibiotics in Water: Absolute Rate Constant Measurements, J. Phys. Chem. A, 2010, 114(32), 8391–8395, DOI:10.1021/jp104509t.
- K. Sarang, T. Otto, K. Rudzinski, T. Schaefer, I. Grgić, K. Nestorowicz, H. Herrmann and R. Szmigielski, Reaction Kinetics of Green Leaf Volatiles with Sulfate, Hydroxyl, and Nitrate Radicals in Tropospheric Aqueous Phase, Environ. Sci. Technol., 2021, 55(20), 13666–13676, DOI:10.1021/acs.est.1c03276.
- C. Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91(2), 165–195, DOI:10.1021/cr00002a004.
-
C. Hansch, A. Leo and D. Hoekman, Exploring QSAR: hydrophobic, electronic, and steric constants, American Chemical Society, Washington, DC, 1995, vol. 2 Search PubMed.
- H. Szatylowicz, A. Jezuita and T. M. Krygowski, On the relations between aromaticity and substituent effect, Struct. Chem., 2019, 30, 1529–1548, DOI:10.1007/s11224-019-01360.
-
C. D. Johnson, The Hammett Equation, CUP Archive, 1973 Search PubMed.
- A. Baker and A. Shulgin, Intramolecular hydrogen bonding. II. The determination of Hammett sigma constants by intramolecular hydrogen bonding in Schiff's bases, J. Am. Chem. Soc., 1959, 81(7), 1523–1529, DOI:10.1021/ja01516a001.
-
D. D. Perrin, B. Dempsey and E. P. Serjeant, pKa prediction for organic acids and bases, pKa Prediction for Organic Acids and Bases, 1981 Search PubMed.
- Y. Yukawa and Y. Tsuno, Resonance effect in Hammett relationship. II. Sigma constants in electrophilic reactions and their intercorrelation, Bull. Chem. Soc. Jpn., 1959, 32(9), 965–971, DOI:10.1246/bcsj.32.965.
- M. Jonsson, J. Lind, T. E. Eriksen and G. Merényi, O–H bond strengths and one-electron reduction potentials of multisubstituted phenols and phenoxyl radicals. Predictions using free energy relationships, J. Chem. Soc., Perkin Trans. 2, 1993,(9), 1567–1568, 10.1039/P29930001567.
- S. Lim, B. Barrios, D. Minakata and U. von Gunten, Reactivity of Bromine Radical with Dissolved Organic Matter Moieties and Monochloramine: Effect on Bromate Formation during Ozonation, Environ. Sci. Technol., 2023, 57, 18658–18667, DOI:10.1021/acs.est.2c07694.
- J. C. Scaiano, M. Barra, M. Krzywinski, R. Sinta and G. Calabrese, Laser Flash Photolysis Determination of Absolute Rate Constants for Reactions of Bromine Atoms in Solution, J. Am. Chem. Soc., 1993, 115(18), 8340–8344, DOI:10.1021/ja00071a048.
- D. O. Mártire, J. A. Rosso, S. Bertolotti, G. C. L. Roux, A. M. Braun and M. C. Gonzalez, Kinetic Study of the Reactions of Chlorine Atoms and Cl2˙– Radical Anions in Aqueous Solutions. II. Toluene, Benzoic Acid, and Chlorobenzene†, J. Phys. Chem. A, 2001, 105(22), 5385–5392, DOI:10.1021/jp004630z.
- M. L. Alegre, M. Gerones, J. A. Rosso, S. G. Bertolotti, A. M. Braun, D. O. Martire and M. C. Gonzalez, Kinetic Study of the Reactions of Chlorine Atoms and Cl2˙– Radical Anions in Aqueous Solutions. 1. Reaction with Benzene, J. Phys. Chem. A, 2000, 104, 3117–3125, DOI:10.1021/jp9929768.
- H. Mohan and J. P. Mittal, Pulse radiolysis investigations on electron-transfer reactions in aqueous solutions of substituted alkyl sulfides, J. Chem. Soc., Perkin Trans. 2, 1992,(2), 207–212, 10.1039/P29920000207.
- G. Dey, D. Naik, K. Kishore and P. Moorthy, Pulse radiolysis study of some substituted thiophenols in aqueous solutions, Radiat. Phys. Chem., 1999, 54(1), 19–27, DOI:10.1016/S0969-806X(98)00200-X.
- M. Bonifačić and K.-D. Asmus, Stabilization of Oxidized Sulphur Centres by Halide Ions. Formation and Properties of R2S∴X Radicals in Aqueous Solutions, J. Chem. Soc., Perkin Trans. 2, 1980, 5, 758–762, 10.1039/P29800000758.
- H. Mohan and J. Mittal, Electron transfer reactions in aqueous solutions of 2, 2′-thiodiethanol: A pulse radiolysis study, Int. J. Radiat. Appl. Instrum., Part C, 1991, 38(1), 45–50, DOI:10.1016/1359-0197(91)90043-2.
- H. Mohan, Intra-and inter-molecular electron transfer reactions in 3, 3′-thiodipropionic acid, J. Chem. Soc., Perkin Trans. 2, 1990,(11), 1821–1824, 10.1039/P29900001821.
- H. Mohan and J. Mittal, Spectral, kinetics, and redox properties of the transients formed on one-electron oxidation of 4, 4′-thiodiphenol: A pulse radiolysis study, Int. J. Chem. Kinet., 1999, 31(9), 603–610, DOI:10.1002/(SICI)1097-4601(1999)31:9<603::AID-KIN2>3.0.CO;2-B.
- K. Hasegawa and P. Neta, Rate Constants and Mechanisms of Reaction of Cl2˙– Radicals, J. Phys. Chem., 1978, 82(8), 854–857, DOI:10.1021/j100497a003.
- P. R. Tentscher, S. N. Eustis, K. McNeill and J. S. Arey, Aqueous oxidation of sulfonamide antibiotics: aromatic nucleophilic substitution of an aniline radical cation, Chemistry, 2013, 19(34), 11216–11223, DOI:10.1002/chem.201204005.
- Z. Qiang and C. Adams, Potentiometric Determination of Acid Dissociation Constants (pKa) for Human and Veterinary Antibiotics, Water Res., 2004, 38(12), 2874–2890, DOI:10.1016/j.watres.2004.03.017.
- R. Zhang, Y. Yang, C. H. Huang, L. Zhao and P. Sun, Kinetics and modeling of sulfonamide antibiotic degradation in wastewater and human urine by UV/H2O2 and UV/PDS, Water Res., 2016, 103, 283–292, DOI:10.1016/j.watres.2016.07.037.
- R. Zhang, P. Sun, T. H. Boyer, L. Zhao and C. H. Huang, Degradation of pharmaceuticals and metabolite in synthetic human urine by UV, UV/H2O2, and UV/PDS, Environ. Sci. Technol., 2015, 49(5), 3056–3066, DOI:10.1021/es504799n.
- M. M. Ahmed, S. Barbati, P. Doumenq and S. Chiron, Sulfate radical anion oxidation of diclofenac and sulfamethoxazole for water decontamination, Chem. Eng. J., 2012, 197, 440–447, DOI:10.1016/j.cej.2012.05.040.
- Y. Wu, Y. Shi, H. Chen, J. Zhao and W. Dong, Activation of persulfate by magnetite: Implications for the degradation of low concentration sulfamethoxazole, Process Saf. Environ. Prot., 2018, 116, 468–476, DOI:10.1016/j.psep.2018.03.020.
- S. Sabharwal, K. Kishore and P. Moorthy, Pulse radiolysis study of oxidation reactions of sulphacetamide in aqueous solutions, Radiat. Phys. Chem., 1994, 44(5), 499–506, DOI:10.1016/0969-806X(94)90047-7.
- A. Acosta-Rangel, M. Sánchez-Polo, A. Polo, J. Rivera-Utrilla and M. Berber-Mendoza, Sulfonamides degradation assisted by UV, UV/H2O2 and UV/K2S2O8: Efficiency, mechanism and byproducts cytotoxicity, J. Environ. Manage., 2018, 225, 224–231, DOI:10.1016/j.jenvman.2018.06.097.
- F. Wicktor, A. Donati, H. Herrmann and R. Zellner, Laser Based Spectroscopic and Kinetic Investigations of Reactions of the Cl atom with Oxygenated Hydrocarbons in Aqueous Solution, Phys. Chem. Chem. Phys., 2003, 5(12), 2562–2572, 10.1039/b212666d.
- R. Xiao, J. A. Arnot and M. MacLeod, Towards an improved understanding of processes controlling absorption efficiency and biomagnification of organic chemicals by fish, Chemosphere, 2015, 138, 89–95, DOI:10.1016/j.chemosphere.2015.05.053.
- S. Zhou, W. Zhang, J. Sun, S. Zhu, K. Li, X. Meng, J. Luo, Z. Shi, D. Zhou and J. C. Crittenden, Oxidation Mechanisms of the UV/Free Chlorine Process: Kinetic Modeling and Quantitative Structure Activity Relationships, Environ. Sci. Technol., 2019, 53(8), 4335–4345, DOI:10.1021/acs.est.8b06896.
Footnote |
| † Electronic supplementary information (ESI) available: Details of chemical compounds, reaction rate constants, Hammett σ constants, calculation and correlation of QSARs, structural approximations, prediction of QSARs, calculation on predicting the TrOC elimination in UV/PDS and UV/chlorine AOPs (Excel file). See DOI: https://doi.org/10.1039/d3em00329a |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab and
Xin
Yang
*ab and
Xin
Yang
 *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, ELUMO − EHOMO
C, ELUMO − EHOMO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 26.8 − 3.97 × O/C − 0.746 × (ELUMO − EHOMO) with an R2 of 0.86.34 However, this cannot be directly compared with our Hammett constant-based QSARs given that its database is quite different. Here, we performed a comparison of the QSARs developed with Hammett constants and computational descriptors using the same database, that is, the reactions of SO4˙− with alkoxy benzenes. The computational descriptors from Xiao's work and k values in our database were used to develop the QSAR of alkoxy benzenes, which resulted in a tentative relationship (ln
k = 26.8 − 3.97 × O/C − 0.746 × (ELUMO − EHOMO) with an R2 of 0.86.34 However, this cannot be directly compared with our Hammett constant-based QSARs given that its database is quite different. Here, we performed a comparison of the QSARs developed with Hammett constants and computational descriptors using the same database, that is, the reactions of SO4˙− with alkoxy benzenes. The computational descriptors from Xiao's work and k values in our database were used to develop the QSAR of alkoxy benzenes, which resulted in a tentative relationship (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 29.9 − 5.79 × O/C − 1.02 × (ELUMO − EHOMO), R2 = 0.52, p < 0.05, details in Table S32†). It was found that the predictive performance was much lower than using the QSAR model developed in this work using the Hammett constant (R2 = 0.82). This highlights the importance of using the appropriate descriptors in developing QSARs.
k = 29.9 − 5.79 × O/C − 1.02 × (ELUMO − EHOMO), R2 = 0.52, p < 0.05, details in Table S32†). It was found that the predictive performance was much lower than using the QSAR model developed in this work using the Hammett constant (R2 = 0.82). This highlights the importance of using the appropriate descriptors in developing QSARs.

 is the calculated pseudo-first-order degradation rate of TrOCs, kTrOCs,R is the second-order rate constant of the radicals with TrOCs, [R]ss is the steady-state concentrations of radicals from kinetic modelling using the Kintecus software,28kUV is the pseudo-first-order photolysis rate of TrOCs, and kdark is the pseudo-first-order dark oxidation rate of TrOCs by PDS or chlorine, which are shown in the literature and Table S27.†24,38 The kOH˙ and kCl˙ were collected from the work by Lei et al.,38 while the kSO4˙−, kCO3˙−, kBr˙, kBr2˙− and kCl2˙− values were predicted using the QSARs developed in this work (either Hammett constant-based QSARs or cross-correlations, details in Table S27†). Then
is the calculated pseudo-first-order degradation rate of TrOCs, kTrOCs,R is the second-order rate constant of the radicals with TrOCs, [R]ss is the steady-state concentrations of radicals from kinetic modelling using the Kintecus software,28kUV is the pseudo-first-order photolysis rate of TrOCs, and kdark is the pseudo-first-order dark oxidation rate of TrOCs by PDS or chlorine, which are shown in the literature and Table S27.†24,38 The kOH˙ and kCl˙ were collected from the work by Lei et al.,38 while the kSO4˙−, kCO3˙−, kBr˙, kBr2˙− and kCl2˙− values were predicted using the QSARs developed in this work (either Hammett constant-based QSARs or cross-correlations, details in Table S27†). Then  was compared with the experimental k′
was compared with the experimental k′  from the literature.24,38 As shown in Fig. 6a, this model showed a good performance in predicting the degradation of TrOCs. Most of the pseudo-first-order degradation rates (16 out of 18) were predicted within a factor of 1/3–3. Fig. 6b shows the contribution of various radicals and UV + dark oxidation to the degradation of TrOCs. It implies that secondary radicals (CO3˙−, Cl2˙− and Br2˙−, etc.) have significant contributions to the degradation of selected TrOCs. Especially for electron-rich TrOCs such as trimethoprim and ractopamine, where CO3˙− contributes over half of their degradation in both AOPs. This result stresses the importance of obtaining k values for secondary radical reactions in AOPs.
from the literature.24,38 As shown in Fig. 6a, this model showed a good performance in predicting the degradation of TrOCs. Most of the pseudo-first-order degradation rates (16 out of 18) were predicted within a factor of 1/3–3. Fig. 6b shows the contribution of various radicals and UV + dark oxidation to the degradation of TrOCs. It implies that secondary radicals (CO3˙−, Cl2˙− and Br2˙−, etc.) have significant contributions to the degradation of selected TrOCs. Especially for electron-rich TrOCs such as trimethoprim and ractopamine, where CO3˙− contributes over half of their degradation in both AOPs. This result stresses the importance of obtaining k values for secondary radical reactions in AOPs.

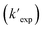 and calculated pseudo first-order degradation rate
and calculated pseudo first-order degradation rate 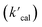 in the UV/chlorine and UV/PDS treatment of typical wastewater effluents (Table S27†). The contribution of TrOC degradation from various radicals and UV + dark oxidation during (b) UV/PDS and (c) UV/chlorine treatment.
in the UV/chlorine and UV/PDS treatment of typical wastewater effluents (Table S27†). The contribution of TrOC degradation from various radicals and UV + dark oxidation during (b) UV/PDS and (c) UV/chlorine treatment.



