Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic study of isoprene hydroxy hydroperoxide radicals reacting with sulphur dioxide and their global-scale impact on sulphate formation†
Hiroo
Hata
 *a and
Kenichi
Tonokura
*a and
Kenichi
Tonokura
 b
b
aResearch Institute of Science for Safety and Sustainability, National Institute of Advanced Industrial Science and Technology (AIST), 16-1 Onogawa, Tsukuba, Ibaraki 305-8569, Japan. E-mail: hata-hiroo@aist.go.jp; Tel: +81-80-2212-2713
bDepartment of Environment Systems, Graduate School of Frontier Sciences, The University of Tokyo, Kashiwano-ha, Kashiwa, Chiba 277-8563, Japan
First published on 10th June 2024
Abstract
Isoprene is the most relevant volatile organic compound emitted during the biosynthesis of metabolism processes. The oxidation of isoprene by a hydroxy radical (OH) is one of the main consumption schemes that generate six isomers of isoprene hydroxy hydroperoxide radicals (ISOPOOs). In this study, the rate constants of ISOPOOs + sulphur dioxide (SO2) reactions that eventually generate sulphur trioxide (SO3), the precursor of sulphate aerosol (SO42−(p)), are determined using microcanonical kinetic theories coupled with molecular structures and energies estimated by quantum chemical calculations. The results show that the reaction rates range from 10−27 to 10−20 cm3 molecule−1 s−1, depending on the atmospheric temperature and structure of the six ISOPOO isomers. The effect of SO3 formation from SO2 oxidation by ISOPOOs on the atmosphere is evaluated by a global chemical transport model, along with the rate constants obtained from microcanonical kinetic theories. The results show that SO3 formation is enhanced in regions with high SO2 or low nitrogen oxide (NO), such as China, the Middle East, and Amazon rainforests. However, the production rates of SO3 formation by ISOPOOs + SO2 reactions are eight orders of magnitude lower than that from the OH + SO2 reaction. This is indicative of SO42−(p) formation from the direct oxidation of SO2 by ISOPOOs, which is almost negligible in the atmosphere. The results of this study entail a detailed analysis of SO3 formation from gas-phase reactions of isoprene-derived products.
Environmental significanceThis study discusses the impact of six isomers of isoprene hydroxy hydroperoxide radicals (ISOPOOs) on the global-scale formation of sulphate aerosol (SO42−(p)). The rate constants of ISOPOOs + SO2 and subsequent reactions are estimated using microcanonical kinetic theory (transition-state theory and RRKM/Master equation theory) coupled with quantum chemical calculations. The obtained rate constants are incorporated into a global chemical transport model, GEOS-Chem, to evaluate the effects of ISOPOOs on sulphur trioxide (SO3), a precursor of SO42−(p). The obtained results suggest that the direct oxidation of SO2 by ISOPOOs contributes maximally 10−6 % of gas-phase SO3 formation in the high-isoprene regions, indicating the negligible contribution of ISOPOOs to the direct oxidation of SO2 for forming SO42−(p) on a global scale. |
Introduction
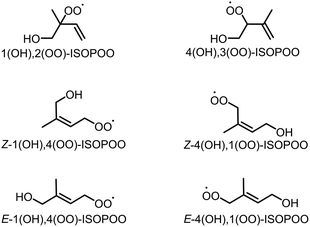
Isoprene (C5H8) is a biogenic volatile organic compound (BVOC) emitted to the atmosphere during the biosynthesis of metabolic processes.1–3 Isoprene contains two carbon–carbon double bonds, and its reactivity enables the high-production potential of tropospheric ozone (O3) and secondary organic aerosol (SOA).4,5 Globally, isoprene dominates ∼60% of the total VOC emissions that are condensed in forests and vegetated areas such as the Amazon.6–8 Fig. S1 of the ESI† shows typical pathways for the oxidation of isoprene by O3 and hydroxy radical (OH).9 The oxidation of isoprene by O3, shown in Fig. S1(a),† produces Criegee intermediates (CIs) that finally form sulphate aerosols (SO42−(p)) by the oxidation of sulphur dioxide (SO2), the nuclei of particulate matter,10–15 However, the contribution of the CIs-to-SO42−(p) formation is negligible compared to that of OH.9 Conversely, the oxidation of isoprene by OH forms six isomers of isoprene hydroxy hydroperoxide radicals (ISOPOOs) as shown in Fig. 1, which then form isoprene epoxydiols (IEPOXs) as shown in Fig. S1(b).†16–19 Thereafter, owing to low volatility and the water-soluble chemical structure from the two hydroxyl groups of IEPOXs, SOA is eventually generated. Several studies have reported the importance of in-cloud oxidation of bisulphate (HSO3−) by the reaction of ISOPOOHs (formed by the hydroperoxyl radical (HO2) + ISOPOOs reactions described in Fig. S1(b)†) to form SO42−(p).20–22Notably, the formation pathways of SOA and SO42− shown in Fig. S1(b) and (c)† can proceed under low NO conditions owing to the high reactivity of NO and HO2 with organic peroxide radicals (RO2) including ISOPOOs.23–26 Some of the ISOPOOs hold ring structures formed by the intramolecular hydrogen bond of the hydroxy (–OH) and peroxyl radical (–OO) groups, which cause unimolecular isomerization due to hydrogen shift from –OH to –OO.27,28 Wennberg et al. reviewed and summarized ISOPOO reactions,29 with their pathways already considered in atmospheric chemical mechanisms. Unlike other atmospheric oxidants such as OH, nitrate radical (NO3) or RO2 including ISOPOOs are relatively stable in the atmosphere and can accumulate to high concentrations in oxidation systems.30 Thus, to the best of our knowledge, limited studies have focused on the direct oxidation of SO2 by ISOPOOs, with low expected rates of oxidation estimated by Kurtén et al. who conducted the theoretical calculation of the reaction of SO2 with four peroxide radicals; HO2, methyl peroxide (CH3OO), ethyl peroxide (C2H5OO) and hydroxymethyl peroxide (CH3(OH)OO).31 Nevertheless, isoprene is the most relevant BVOC in the atmosphere, and owing to the high global concentrations of isoprene and isoprene-derived intermediates, acknowledgement of the contributions of ISOPOOs to the oxidation and formation of SO2 and SO42−(p), respectively, is significant.
In this study, the direct oxidation rate constants of SO2 obtained from the six isomers of ISOPOOs, shown in Fig. 1 (1(OH),2(OO)-ISOPOO, 4(OH),3(OO)-ISOPOO, Z-1(OH),4(OO)-ISOPOO, Z-4(OH),1(OO)-ISOPOO, E-1(OH),4(OO)-ISOPOO, and E-4(OH),1(OO)-ISOPOO), are determined using the transition state theory. The estimated rate constants are incorporated into the chemical mechanism of the global chemical transport model to evaluate the effect of SO2 oxidation by ISOPOOs on the global scale SO3 formation. The results of this study are expected to contribute towards a quantitative understanding of direct oxidation of SO2 by ISOPOOs in the atmosphere.
Methodology
Kinetic analysis
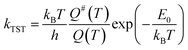 | (1) |
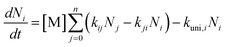 | (2) |
Global chemical transport modelling
The Goddard Earth observing system chemistry model (GEOS-Chem (v14.2.3))50 was used to evaluate the global impact of the reactions between ISOPOOs and SO2. For this study, a grid resolution of 2 × 2.5° (latitude × longitude) with 72 vertical layers holding the ground surface to the stratosphere was selected. The modern-era retrospective analysis for research and applications version 2 (MERRA2) was used as the meteorological input.51 For emission inventories, emissions database for community emissions data system (CEDSv2) was used for anthropogenic emissions,52 hemispheric transport of air pollution (HTAPv3) was used for ship emissions,53 monthly-mean data of Aviation Emissions Inventory (AEIC2019) was used for aircraft emissions,54 global fire emissions database (GFED) was used for biomass burning,55 and the model of emissions of gases and aerosols from nature (MEGAN) was used for BVOC emissions.56 The targeted period spanned from 1st July 2018 to 31st December 2019. The following six-month period was treated as a spin-off period, while the second year of 2019 was treated as the analysis term. The branching ratio and related reactions of the six isomers of ISOPOOs were modified using the full-chemistry module of the kinetic pre-processor (KPP) that controlled the chemical reactions of GEOS-Chem; the details are described in the subsequent section.Results
Optimised structures and diagnostic values for the ISOPOO and SO2 reactions
The globally optimised structures of the six ISOPOO isomers are shown in Fig. S3† and the detailed cartesian coordinates are listed in Tables S1 to S6 of the ESI.† Compounds 1,2-, 4,3-, Z-1,4- and Z-4,1-ISOPOOs adopted a ring structure due to the formation of intramolecular hydrogen bonds between –OH and –OO. E-1,4-ISOPOO also formed a ring structure, but the distance between –OH and –OO was large, enabling SO2 to form a complex with E-1,4-ISOPOO, as shown in Fig. S4 and Tables S7 and S8 of the ESI.†E-4,1-ISOPOO had a straight chain structure. Peeters et al. conducted the optimization and energetical calculations of the six isomers of ISOPOOs using quantum chemical calculations (CCSD(T)/aug-cc-pVTZ//M06-2X/6-311++G(3df,2p)).57 The obtained optimized structures of ISOPOOs well represented the results obtained by Peeters et al. The initial reactions of ISOPOOs + SO2 led to intermediate products of ISOPOOSO2s through the transition states of TS1, followed by the unimolecular decomposition of ISOPOOSO2s to form SO3 and alkoxy radicals (ISOPOs). The calculated structures of TS1 and TS2, ISOPOOs, ISOPOs, SO2 and SO3 are presented in Fig. S5 to S9 and Tables S9 to S34 of the ESI,† respectively.Evaluation of the extra-tight d function of sulphur-containing molecules
Table 1 shows the total atomization energy (TAE) and zero-point energy (ZPE) of aug-cc-pVTZ and aug-cc-pV(T+d)Z obtained by M06-2X and CCSD(T) calculations. The values of the vibrational frequencies, rotational constants, electronic state and point group, spin contamination and T1-diagnostic for the targeted molecules are listed in Tables S35–S48, S49–S50, S51, S52–S55 and S56–S57†respectively. For all species, the calculations that applied a basis set with extra-tight d functions showed a ∼10 kcal mol−1 decrease in the TAE compared to the values for a normal basis set. Contrarily, all ZPE values obtained from the results of the extra-tight d function were ∼0.1 to 0.2 kcal mol−1 higher than those of a normal basis-set. The reference TAE values of SO2 and SO3 were reported to be 258.3 and 343.7 kcal mol−1 respectively, and when compared to M06-2X and CCSD(T) for the two basis sets, the value of M06-2X was closer to the experimental results than that of CCSD(T). All the sulphur-included ISOPOO species demonstrated ∼10 to 20 kcal mol−1 more stability when introducing the basis set encompassing the extra-tight d function. To the best of our knowledge, no experimental values of the TAE have been reported for sulphur-containing ISOPOO species; therefore, it is hard to verify which basis sets are effective. Nevertheless, several studies have suggested the effectiveness of kinetic analyses that were conducted based on the basis-set results of the extra-tight d function (CCSD(T)/aug-cc-pV(T+d)Z//M06-2X/aug-cc-pV(T+d)Z).| Molecule | M06-2X | CCSD(T) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| D 0 | D 0_d | Diff | ZPE | ZPE_d | Diff | D 0 | D 0_d | Diff | |
| SO2 | 237.6 | 247.4 | 9.713 | 4.559 | 4.645 | 0.08597 | 231.5 | 240.4 | 8.896 |
| SO3 | 313.0 | 327.8 | 14.85 | 7.899 | 8.087 | 0.1883 | 302.7 | 316.8 | 14.07 |
| 1,2-TS1 | 1746 | 1756 | 10.14 | 92.61 | 92.70 | 0.08722 | 1705 | 1715 | 9.516 |
| 4,3-TS1 | 1745 | 1755 | 10.16 | 92.90 | 93.01 | 0.1086 | 1704 | 1713 | 9.528 |
| E-1,4-TS1 | 1747 | 1757 | 9.896 | 93.41 | 93.47 | 0.06212 | 1705 | 1714 | 9.295 |
| E-4,1-TS1 | 1744 | 1754 | 10.10 | 93.01 | 93.10 | 0.08346 | 1702 | 1711 | 9.468 |
| Z-1,4-TS1 | 1745 | 1755 | 10.16 | 93.38 | 93.45 | 0.07216 | 1702 | 1712 | 9.542 |
| Z-4,1-TS1 | 1744 | 1754 | 10.11 | 93.32 | 93.43 | 0.1117 | 1702 | 1711 | 9.475 |
| 1,2-ISOPOOSO2 | 1749 | 1760 | 11.10 | 93.68 | 93.83 | 0.1569 | 1707 | 1718 | 10.69 |
| 4,3-ISOPOOSO2 | 1747 | 1759 | 11.15 | 93.94 | 94.08 | 0.1450 | 1706 | 1716 | 10.75 |
| E-1,4-ISOPOOSO2 | 1750 | 1761 | 10.94 | 94.48 | 94.68 | 0.1958 | 1707 | 1718 | 10.57 |
| E-4,1-ISOPOOSO2 | 1746 | 1757 | 11.09 | 94.04 | 94.21 | 0.1688 | 1704 | 1715 | 10.70 |
| Z-1,4-ISOPOOSO2 | 1747 | 1759 | 11.07 | 94.35 | 94.54 | 0.1839 | 1705 | 1715 | 10.67 |
| Z-4,1-ISOPOOSO2 | 1747 | 1758 | 11.07 | 94.35 | 94.54 | 0.1945 | 1704 | 1715 | 10.67 |
| 1,2-TS2 | 1736 | 1749 | 12.44 | 92.29 | 92.47 | 0.1770 | 1698 | 1710 | 11.87 |
| 4,3-TS2 | 1736 | 1749 | 12.48 | 92.49 | 92.62 | 0.1299 | 1697 | 1709 | 11.90 |
| E-1,4-TS2 | 1737 | 1750 | 12.31 | 92.74 | 92.90 | 0.1562 | 1697 | 1709 | 11.74 |
| E-4,1-TS2 | 1720 | 1732 | 11.93 | 91.77 | 91.96 | 0.1945 | 1675 | 1685 | 10.02 |
| Z-1,4-TS2 | 1737 | 1749 | 12.33 | 92.82 | 93.01 | 0.1908 | 1697 | 1708 | 11.75 |
| Z-4,1-TS2 | 1734 | 1747 | 12.41 | 92.96 | 93.13 | 0.1719 | 1695 | 1707 | 11.79 |
| E-1,4-complex1 | 1762 | 1771 | 9.467 | 93.37 | 93.39 | 0.02259 | 1720 | 1728 | 8.707 |
| E-1,4-complex2 | 1779 | 1794 | 14.99 | 92.98 | 93.20 | 0.2115 | 1735 | 1749 | 14.31 |
Diagnostics of the electronic states of ISOPOO-related species
According to Tables S52–S55,† the open-shell radicals (S = 0.5) of the M06-2X calculations show almost no spin contamination after annihilation of the effect (the value could be S(S+1) = 0.75 when no spin contamination occurs). On the other hand, the CCSD(T) calculations exhibit weak spin contamination for the TS2 species. Additionally, only E-4,1-TS2 show the high value of 1.38 after annihilation. According to Tables S56 and S57 of the ESI,† all species with the exception of the TS2s meet the required T1-diagnostic value for single-reference methods,58 approximately ranging from less than 0.02 to 0.03. In terms of the TS2s apart from E-4,1-isomer shows a value lesser than 0.033, which meets the criterion of the T1-diagnostic value for open-shell calculations,58 and almost no multireference characteristic is expected. The results of the high-spin contamination and the high T1-diagnostic value imply that E-4,1-TS2 has strong multireference characteristics and the single-point energy can be estimated by multireference wave function methods such as the Complete Active Space Second Order Perturbation Theory (CASPT2).59 Nevertheless, further calculations were not conducted for E-4,1-TS2 in this study, because the total reaction rate of E-4,1-ISOPOO + SO2 to form SO3 and the total existence ratio of E-4,1-ISOPOO in the atmosphere were expected to be low, which is discussed in the later section. A detailed analysis of the multireference characteristics will be conducted as future work.Potential energy diagram of the reaction of ISOPOO + SO2
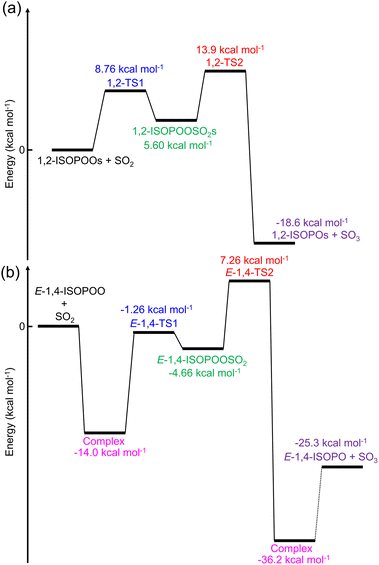
The potential energy diagram of the entire reaction initiated by 1,2-ISOPOO and SO2 is shown in Fig. 2(a), and that by 4,3-, Z-1,4-, Z-4,1- and E-4,1-ISOPOOs are shown in Fig. S10 to S13 of the ESI.† According to Fig. 2(a) and S10 to S13,† the barrier heights for the formation of TS1 by ISOPOOs, barring E-1,4-ISOPOO, ranged from 7.9 to 9.1 kcal mol−1. From Fig. 2(b), E-1,4-ISOPOO held a complex with SO2, which stabilized the total energy of the reactant system to 14.0 kcal mol−1. The barrier height from complex to TS1 rose to 12.7 kcal mol−1. Thus, ISOPOOs, barring E-1,4-ISOPOO, reacted with SO2; however, in terms of E-4,1-ISOPOO, the barrier height of TS2 was significantly higher than that of the other ISOPOOs, and less decomposition to SO3 was expected. The barrier height of TS1 for the reaction of E-1,4-ISOPOO and SO2 was ∼4 kcal mol−1 higher than that of other ISOPOOs owing to the formation of the complex, and the reaction was expected to be very slow. The entire reaction was exothermic. Detailed kinetics are presented in the following section.Results of kinetic calculations
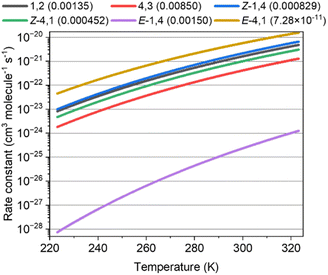
Fig. 3 shows the rate constants calculated for the ISOPOOs + SO2 reaction and the branching ratio (η) of ISOPOOSO2s to form SO3, which were obtained by RRKM/ME calculation. The parameters of the rate constants in Arrhenius form are listed in Table S58 of the ESI.†E-1,4-ISOPOO showed 5 orders of lower magnitude for the SO2 reaction at 298 K than that of other isomers, which ranged from ∼10−22 to 10−21 cm3 molecule−1 s−1 in standard conditions (T = 298 K). Kurtén et al. suggested almost the same kinetic values, 5 × 10−21 cm3 molecule−1 s−1 or less for the reactions of organic peroxides and SO2 of which the value was consistent with the ISOPOOs results obtained in this study.31 As aforementioned, the barrier height of the E-1,4-ISOPOO reacting with SO2 was approximately 4 kcal mol−1 higher than that of the other isomers, leading to lower rate constants for the E-1,4-ISOPOO + SO2 reaction. The branching ratios, η, required to form SO3 by the unimolecular reactions of ISOPOOSO2s, generated from ISOPOOs + SO2 reactions, are described in parenthesis in Fig. 3. All the values of the unimolecular reactions were recorded at the conditions of 298 K and 1atm. The values of η, barring E-4,1-ISOPOO, ranged from ∼0.0005 to 0.009; thus, maximally only 1% of ISOPOOSO2s decomposed to SO3 and ISOPO, while the remaining ISOPOOSO2s reproduced ISOPOO and SO2 by a reverse reaction due to high energy barrier of TS2, as shown in Fig. 2. The value of η of E-4,1-ISOPOO was more than approximately 7 orders of magnitude lower than that of the other isomers, implying no complete generation of SO3 from E-4,1-ISOPOO. Thus, both E-1,4- and E-4,1-ISOPOOs were less relevant to form SO3 owing to the lower rate constant of the reaction with SO2 for E-1,4-ISOPOO and lower η value for E-1,4-ISOPOO.Global-scale impact of ISOPOOs and SO2 reactions on the formation of sulphates
Detail of the reaction mechanisms incorporated into the global chemical transport model
The impact of the ISOPOOs + SO2 reactions on SO3 formation was estimated using GEOS-Chem. Since the rate constants of the ISOPOOs + SO2 reactions were low, direct incorporation of the kinetic parameters of these reactions resulted in reaching the limit of numerical error of GEOS-Chem. For this reason, we estimated the impact of the reactions via an indirect method, i.e., by calculating the concentration of ISOPOOs and then multiplying the concentration of SO2 by the rate constants in each grid to obtain the rate of SO3 formation. For the estimations, the reactions related to E-1,4- and E-4,1-ISOPOOs were excluded because these two reactions were expected to be highly slower than the remaining reactions, according to the kinetic parameters described in Fig. 3. The reactions for the production of ISOPOOs from isoprene oxidation by OH were modified in this study. KPP defines ISOPOOs as IHOO1 and IHOO4, corresponding to 1(OH)–ISOPOOs and 4(OH)–ISOPOOs, which cannot be distinguished by the six geometric isomers shown in Fig. 1. In this study, IHOO1 and IHOO4 were divided into three isomers, each with a branching ratio as proposed in a previous study (1,2-ISOPOO: 0.479, 4,3-ISOPOO: 0.259, Z-1,4-ISOPOO: 0.049, Z-4,1-ISOPOO: 0.063, E-1,4-ISOPOO: 0.102, E-4,1-ISOPOO: 0.048).29 All other IHOO1 and IHOO4-related reactions were substituted by the corresponding six geometric isomers.Results of global chemical transport modelling
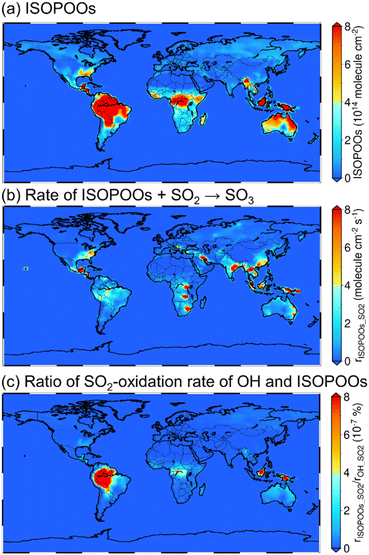
The annual mean tropospheric column concentrations of (a) total concentration of the six isomers of ISOPOO (molecule cm−2), (b) rate of SO3 formation from ISOPOOs + SO2 reactions (rISOPOO_SO2 = ηkISOPOO_SO2[ISOPOOs][SO2] where η is the branching ratio of ISOPOOSO2s to form SO3 and kISOPOO_SO2 is the rate constant of ISOPOOs + SO2 reactions; molecule cm−2 s−1) and (c) ratio of the rISOPOO_SO2 to the rate of SO3 formation from OH + SO2 (rOH_SO2) (%) are shown in Fig. 4. Here, OH was chosen to compare the rate of SO2 oxidation because OH is the most relevant oxidiser of SO2 in the atmosphere, which accounts for around 50% of total SO2 oxidation.9,60 The annual mean tropospheric column concentrations of isoprene, SO2, NO and HO2 are described in Fig. S14 to S17 of the ESI,† respectively. According to Fig. 4(a) and S14,† the distribution of ISOPOOs is condensed in high-isoprene regions such as the Amazon rainforests, Central Africa and Australia. On the other hand, according to Fig. 4(b), rISOPOO_SO2 is high not only in the high-isoprene regions, but also in highly polluted regions such as China, India, Middle Eastern regions and the north to middle regions of the American continent due to high SO2 concentrations in those regions. Finally, according to Fig. 4(c), the ratio of rISOPOO_SO2/rOH_SO2 is maximally ∼10−6% in the Amazon rainforests and Southeast Asian countries, which indicates that SO3 formation from the ISOPOOs + SO2 reactions is almost negligible, and that the reactions may not contribute to SO42−(p) formation in the real atmosphere. The reason for the negligible contribution of the ISOPOOs + SO2 reactions towards SO3 formation is the low ISOPOOs concentrations caused by the scavengers of ISOPOOs such as NO, HO2 and other organic peroxy radicals, and by the low-rate constants of entire reaction paths. Isoprene is the most popular VOC on a global scale, and ISOPOOs are the most relevant organic peroxy radicals generated from isoprene and OH reaction. However, according to the results of this study, the direct oxidation of SO2 by ISOPOOs is almost negligible. This indicates that other organic peroxy radicals generated by the different VOCs may also not contribute to SO3 and SO42−(p) formations in the global-scale atmosphere.Summary
The reaction kinetics of six isomers of ISOPOOs and SO2 are evaluated using microcanonical kinetic calculations coupled with quantum chemical calculations. The results show that the reaction barriers of five isomers, 1,2-, 4,3-, Z-1,4-, Z-4,1- and E-4,1-ISOPOOs, are sufficient to form intermediate products, ISOPOOSO2s, with rate constants ranging from ∼10−27 to ∼10−20 cm3 molecule−1 s−1. The branching ratio of ISOPOOSO2s to form SO3 by unimolecular decomposition is estimated as maximally as 0.0085, implying the expected formulation of only a small amount of SO3. Furthermore, the contribution of E-1,4- and E-4,1-ISOPOOs to sulphate aerosol formation is expected to be almost negligible owing to the low-rate constant of ISOPOOSO2 (E-1,4-ISPOO) formation and the low branching ratio of SO3 (E-4,1-ISOPOO) formation. The results of the global chemical transport modelling suggest that the rates of the ISOPOOs + SO2 reactions are relatively higher in high-SO2 and high-isoprene regions. Nevertheless, the contribution of the ISOPOOs + SO2 reactions to form SO3 was estimated to be eight orders of magnitude lower than that from the OH + SO2 reactions, which indicated negligible effects of ISOPOOs to SO42−(p) formation in the real atmosphere.Author contributions
Hiroo Hata proposed the research concept, conducted kinetic analysis and global-chemical transport modelling, wrote the draft paper, and Kenichi Tonokura supervised and checked the work for accuracy.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by a Grant-in-Aid for Scientific Research (C) and (B) from the Japan Society for the Promotion of Science (JSPS; Grant Number JP21K12286 and JP24K03088). We are grateful to the handling editor and the anonymous reviewers who raised suggestions and provided clarity to on behalf of this study.References
- T. D. Sharkey, A. E. Wiberley and A. R. Donohue, Isoprene emission from plants: why and how, Ann. Bot., 2008, 101, 5–18 CrossRef CAS PubMed.
- B. A. Logan, R. K. Monson and M. J. Potosnak, Biochemistry and physiology of foliar isoprene production, Trends Plant Sci., 2000, 5(11), 477–481 CrossRef CAS PubMed.
- L. Cappellin, F. Loreto, F. Biasioli, P. Pastore and K. McKinney, A mechanism for biogenic production and emission of MEK from MVK decoupled from isoprene biosynthesis, Atmos. Chem. Phys., 2019, 19, 3125–3135 CrossRef CAS.
- A. G. Carlton, C. Wiedinmyer and J. H. Kroll, A review of Secondary Organic Aerosol (SOA) formation from isoprene, Atmos. Chem. Phys., 2009, 9, 4987–5005 CrossRef CAS.
- J. C. Acosta Navarro, S. Smolander, H. Struthers, E. Zorita, A. M. Ekman, J. O. Kaplan, A. Guenther, A. Arneth and I. Riipinen, Global emissions of terpenoid VOCs from terrestrial vegetation in the last millennium, J. Geophys. Res.: Atmos., 2014, 119(11), 6867–6885 CrossRef CAS PubMed.
- K. Sindelarova, C. Granier, I. Bouarar, A. Guenther, S. Tilmes, T. Stavrakou, J.-F. Müller, U. Kuhn, P. Stefani and W. Knorr, Global data set of biogenic VOC emissions calculated by the MEGAN model over the last 30 years, Atmos. Chem. Phys., 2014, 14, 9317–9341 CrossRef.
- R. von Kuhlmann, M. G. Lawrence, U. Pöschl and P. J. Crutzen, Sensitivities in global scale modeling of isoprene, Atmos. Chem. Phys., 2004, 4, 1–17 CrossRef CAS.
- E. V. Avzianova and P. A. Ariya, Temperature-dependent kinetic study for ozonolysis of selected tropospheric alkenes, Int. J. Chem. Kinet., 2002, 34(12), 678–684 CrossRef CAS.
- H. Hata, S. Hoshino, M. Fujita and K. Tonokura, Atmospheric impact of isoprene-derived Criegee intermediates and isoprene hydroxy hydroperoxide on sulfate aerosol formation in the Asian region, Atmos. Environ.: X, 2023, 20, 100226 CAS.
- G. T. Drozd, T. Kurtén, N. M. Donahue and M. I. Lester, Unimolecular decay of the dimethyl-substituted Criegee intermediate in alkene ozonolysis: decay time scales and the importance of tunneling, J. Phys. Chem. A, 2017, 121(32), 6036–6045 CrossRef CAS PubMed.
- J. P. Hakala and N. M. Donahue, Pressure-dependent Criegee intermediate stabilization from alkene ozonolysis, J. Phys. Chem. A, 2016, 120(14), 2173–2178 CrossRef CAS PubMed.
- M. J. Newland, A. R. Rickard, M. S. Alam, L. Vereecken, A. Muñoz, M. Ródenas and W. J. Bloss, Kinetics of stabilised Criegee intermediates derived from alkene ozonolysis: reactions with SO2, H2O and decomposition under boundary layer conditions, Phys. Chem. Chem. Phys., 2015, 17, 4076–4088 RSC.
- M. J. Newland, B. S. Nelson, A. Muñoz, M. Ródenas, T. Vera, J. Tárrega and A. R. Rickard, Trends in stabilisation of Criegee intermediates from alkene ozonolysis, Phys. Chem. Chem. Phys., 2020, 22, 13698–13706 RSC.
- A. R. Cox, M. Ammann, N. J. Crowley, H. Herrmann, E. M. Jenkin, F. V. McNeill, A. Mellouki, J. Troe and J. T. Wallington, Evaluated kinetic and photochemical data for atmospheric chemistry, Atmos. Chem. Phys., 2020, 20, 13497–13519 CrossRef.
- H. K. Bates, D. J. Crounse, M. J. St. Clair, B. N. Bennett, B. T. Nguyen, H. J. Seinfeld, M. B. Stoltz and O. P. Wennberg, Gas phase production and loss of isoprene epoxydiols, J. Phys. Chem. A, 2014, 118(7), 1237–1246 CrossRef PubMed.
- S. H. Budisulistiorini, A. Nenes, A. G. Carlton, J. D. Surratt, V. F. McNeill and H. O. T. Pye, Simulating aqueous-phase isoprene-epoxydiol (IEPOX) secondary organic aerosol production during the 2013 Southern Oxidant and Aerosol Study (SOAS), Environ. Sci. Technol., 2017, 51(9), 5026–5034 CrossRef CAS PubMed.
- M. N. Chan, J. D. Surratt, M. Claeys, E. S. Edgerton, R. L. Tanner, S. L. Shaw, M. Zheng, E. M. Knipping, N. C. Eddingsaas, P. O. Wennberg and J. H. Seinfeld, Characterization and Quantification of isoprene-derived epoxydiols in ambient aerosol in the Southeastern United States, Environ. Sci. Technol., 2010, 44(12), 4590–4596 CrossRef CAS PubMed.
- T. B. Nguyen, M. M. Coggon, K. H. Bates, X. Zhang, R. H. Schwantes, K. A. Schilling, C. L. Loza, R. C. Flagan, P. O. Wennberg and J. H. Seinfeld, Organic aerosol formation from the reactive uptake of isoprene epoxydiols (IEPOX) onto non-acidified inorganic seeds, Atmos. Chem. Phys., 2014, 14, 3497–3510 CrossRef.
- E. Dovrou, J. C. Rivera-Rios, K. H. Bates and F. N. Keutsch, Sulphate formation via cloud processing from isoprene hydroxyl hydroperoxides (ISOPOOH), Environ. Sci. Technol., 2019, 53, 12476–12484 CrossRef CAS PubMed.
- E. Dovrou, K. H. Bates, J. C. Rivera-Rios, J. L. Cox, J. D. Shutter and F. N. Keutsch, Towards a chemical mechanism of the oxidation of aqueous sulphur dioxide via isoprene hydroxyl hydroperoxides (ISOPOOH), Atmos. Chem. Phys., 2021, 21(11), 8999–9008 CrossRef CAS.
- T. Fang, P. S. J. Lakey, J. C. Rivera-Rios, F. N. Keutsch and M. Shiraiwa, Aqueous-phase decomposition of isoprene hydroxy hydroperoxide and hydroxyl radical formation by Fenton-like reactions with iron ions, J. Phys. Chem. A, 2020, 124(25), 5230–5236 CrossRef CAS PubMed.
- A. P. Teng, J. D. Crounse and P. O. Wennberg, Isoprene peroxy radical dynamics, J. Am. Chem. Soc., 2017, 139(15), 5367–5377 CrossRef CAS PubMed.
- A. M. Miller, L. Y. Yeung, A. C. Kiep and M. J. Elrod, Overall rate constant measurements of the reactions of alkene-derived hydroxyalkylperoxy radicals with nitric oxide, Phys. Chem. Chem. Phys., 2004, 6, 3402–3407 RSC.
- D. Zhang, R. Zhang and S. W. North, Experimental study of NO reaction with isoprene hydroxyalkyl peroxy radicals, J. Phys. Chem. A, 2003, 107, 11013–11019 CrossRef CAS.
- P. Stevens, D. L'Esperance, B. Chuong and G. Martin, Measurements of the kinetics of the OH-initiated oxidation of isoprene: radical Propagation in the OH + isoprene + O2 + NO reaction system, Int. J. Chem. Kinet., 1999, 31, 637–643 CrossRef CAS.
- D. Stone, L. K. Whalley and D. E. Heard, Tropospheric OH and HO2 radicals: field measurements and model comparisons, Chem. Soc. Rev., 2012, 41, 6348–6404 RSC.
- G. da Silva, C. Graham and Z. F. Wang, Unimolecular β-hydroxyperoxy radical decomposition with OH recycling in the photochemical oxidation of isoprene, Environ. Sci. Technol., 2010, 44, 250–256 CrossRef CAS PubMed.
- M. E. Jenkin, J. C. Youg and A. R. Rickard, The MCM v3.3.1 degradation scheme for isoprene, Atmos. Chem. Phys., 2015, 15, 11433–11459 CrossRef CAS.
- P. O. Wennberg, K. H. Bates, J. D. Crounse, L. G. Dodson, R. C. McVay, L. A. Mertens, T. B. Nguyen, E. Praske, R. H. Schwantes, M. D. Smarte, J. M. St Clair, A. P. Teng, X. Zhang and J. H. Seinfeld, Gas-phase reactions of isoprene and its major oxidation products, Chem. Rev., 2018, 118, 3337–3390 CrossRef CAS PubMed.
- M. J. Goldman, W. H. Green and J. H. Kroll, Chemistry of simple organic peroxy radicals under atmospheric through combustion conditions: role of temperature, pressure, and NOx level, J. Phys. Chem. A, 2021, 125(48), 10303–10314 CrossRef CAS PubMed.
- T. Kurtén, R. J. Lane, S. Jørgensen and G. H. Kjaergaard, A computational study of the oxidation of SO2 to SO3 by gas-phase organic oxidants, J. Phys. Chem. A, 2011, 115(31), 8669–8681 CrossRef PubMed.
- M. J. Frisch; G. W. Trucks; H. B. Schlegel; G. E. Scuseria; M. A. Robb; J. R. Cheeseman; G. Scalmani; V. Barone; G. A. Petersson; H. Nakatsuji; X. Li; M. Caricato; A. V. Marenich; J. Bloino; B. G. Janesko; R. Gomperts; B. Mennucci; H. P. Hratchian; J. V. Ortiz; A. F. Izmaylov; J. L. Sonnenberg; D. Williams-Young; F. Ding; F. Lipparini; F. Egidi; J. Goings; B. Peng; A. Petrone; T. Henderson; D. Ranasinghe; V. G. Zakrzewski; J. Gao; N. Rega; G. Zheng; W. Liang; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; K. Throssell; J. A. Montgomery Jr; J. E. Peralta; F. Ogliaro; M. J. Bearpark; J. J. Heyd; E. N. Brothers; K. N. Kudin; V. N. Staroverov; T. A. Keith; R. Kobayashi; J. Normand; K. Raghavachari; A. P. Rendell; J. C. Burant; S. S. Iyengar; J. Tomasi; M. Cossi; J. M. Millam; M. Klene; C. Adamo; R. Cammi; J. W. Ochterski; R. L. Martin; K. Morokuma; O. Farkas; J. B. Foresman and D. J. Fox, Gaussian16, Revision C. 01, Gaussian, Inc., Wallingford CT 2016 Search PubMed.
- M. Walker, A. J. A. Harvey, A. Sen and H. E. C. Dessent, Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M6 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen-bonding interactions, J. Phys. Chem. A, 2013, 117(47), 12590–12600 CrossRef CAS PubMed.
- F. J. Stanton, Why CCSD(T) works: a different perspective, Chem. Phys. Lett., 1997, 281(1–3), 130–134 CrossRef.
- D. R. Bell and K. A. Wilson, SO3 revisited: Impact of tight d augmented correlation consistent basis sets on atomization energy and structure, Chem. Phys. Lett., 2004, 394(1–3), 105–109 CrossRef.
- L. J. M. Marti, A fully ab initio quartic force field of spectroscopic quality for SO3, Spectrochim. Acta, 1999, 55(3), 709–718 CrossRef.
- A. P. Denis, Basis set requirements for sulfur compounds in density functional theory: a comparison between correlation-consistent, polarized-consistent, and People-type basis sets, J. Chem. Theory Comput., 2005, 1(5), 900–907 CrossRef PubMed.
- X. N. Wang and K. A. Wilson, Density functional theory and the correlation consistent basis sets: the tight d effect of HSO and HOS, J. Phys. Chem. A, 2005, 109(32), 7187–7196 CrossRef PubMed.
- P. B. Pritchard, D. Altarawy, B. Didier, D. T. Gibson and L. T. Windus, New Basis Set Exchange: an open, up-to-date resource for the molecular sciences community, J. Chem. Inf. Model., 2019, 59(11), 4814–4820 CrossRef PubMed.
- J. T. Lee and R. P. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36(S23), 199–207 CrossRef.
- C. Gonzales and H. B. Schlegel, Reaction path following in mass-weighted internal coordinates, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, Computational thermochemistry: scale factor databases and scale factors for vibrational frequencies obtained from electronic model chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current status of transition-state theory, J. Phys. Chem., 1996, 100(31), 12771–12800 CrossRef CAS.
- A. Miyoshi, GPOP software, rev. 2022.01.20ml, available from the author. See http://akrmys.com/gpop/ Search PubMed.
- R. L. Brown, A method of calculating tunneling corrections for Eckart potential barriers, J. Res. Natl. Bur. Stand., 1997, 86(4), 357–359 CrossRef PubMed.
- A. M. Dean and H.-H. Carstensen, Chapter 4 The kinetics of pressure-dependent reactions, Compr. Chem. Kinet., 2007, 42, 101–184 Search PubMed.
- A. Miyoshi, SSUMES software, rev. 2018.06.14m5, available from the author. See http://akrmys.com/ssumes/ Search PubMed.
- J. Troe, Theory of thermal unimolecular reactions at low-pressures. I. Solutions of the master equation, J. Chem. Phys., 1977, 66, 4745–4757 CrossRef CAS.
- H. Hippler, J. Troe and H. J. Wendelken, Collisional deactivation of vibrationally highly excited polyatomic molecules. III. Direct observations for substituted cycloheptatrienes, J. Chem. Phys., 1983, 78, 6718–6724 CrossRef CAS.
- GEOS-chem (GC Classic) 14.1.1, DOI:10.5281/zenodo.7696651.
- R. Gelaro, W. McCarty, M. J. Suárez, R. Todling, A. Molod, L. Takacs, C. A. Randles, A. Darmenov, M. G. Bosilovich, R. Reichle, K. Wargan, L. Coy, R. Cullather, C. Draper, S. Akella, V. Buchard, A. Conaty, A. M. da Silva, W. Gu, G.-K. Kim, R. Koster, R. Lucchesi, D. Merkova, J. E. Nielsen, G. Partyka, S. Pawson, W. Putman, M. Rienecker, S. D. Schubert, M. Sienkiewicz and B. Zhao, The Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2), J. Clim., 2017, 30(14), 5419–5454 CrossRef PubMed.
- E. E. McDuffie, S. J. Smith, P. O'Rourke, K. Tibrewal, C. Venkataraman, E. A. Marais, B. Zheng, M. Crippa, M. Brauer and R. V. Martin, A global anthropogenic emission inventory of atmospheric pollutants from sector- and fuel-specific sources (1970-2017): an application of the Community Emissions Data System (CEDS), Earth Syst. Sci. Data, 2020, 12, 3413–3442 CrossRef.
- G. Janssens-Maenhout, M. Crippa, D. Guizzardi, F. Dentener, M. Muntean, G. Pouliot, T. Keating, Q. Zhang, J. Kurokawa, R. Wankmüller, H. Denier van der Gon, J. J. P. Kuenen, Z. Klimont, G. Frost, S. Darras, B. Koffi and M. Li, HTAP_v2.2: a mosaic of regional and global emission grid maps for 2008 and 2010 to study hemispheric transport of air pollution, Atmos. Chem. Phys., 2015, 15, 11411–11432 CrossRef CAS.
- V. V. Pham, J. Tang, S. Alam, C. Lokan and H. A. Abbass, Aviation emission inventory development and analysis, Environ. Model. Softw., 2010, 25(12), 1738–1753 CrossRef.
- G. R. van der Werf, J. T. Randerson, L. Giglio, T. T. van Leeuwen, Y. Chen, B. M. Rogers, M. Mu, M. J. E. van Marle, D. C. Morton, G. J. Collatz, R. J. Yokelson and P. S. Kasibhatla, Global fire emissions estimates during 1997–2016, Earth Syst. Sci. Data, 2017, 9(2), 697–720 CrossRef.
- A. B. Guenther, X. Jiang, C. L. Heald, T. Sakulyanontvittaya, T. Duhl, L. K. Emmons and X. Wang, The Model of Emissions of Gases and Aerosols from Nature version 2.1 (MEGAN2.1): an extended and updated framework for modeling biogenic emissions, Geosci. Model Dev., 2012, 5, 1471–1492 CrossRef.
- J. Peeters, J. F. Müller, T. Stavrakou and V. S. Nguyen, Hydroxyl radical recycling in isoprene oxidation driven by hydrogen bonding and hydrogen tunneling: the upgraded LIM1 mechanism, J. Phys. Chem. A, 2014, 118, 8625–8643 CrossRef CAS PubMed.
- G. Manonmani, L. Sandhiya and K. Senthilkumar, Reaction of Criegee Intermediates with SO2 – A possible route for sulfurous acid formation in the atmosphere, ACS Earth Space Chem., 2023, 7(10), 1890–1904 CrossRef CAS.
- P. Pulay, A perspective on the CASPT2 method, Int. J. Quantum Chem., 2011, 111(13), 3273–3279 CrossRef CAS.
- S. Hattori, Y. Iizuka, B. Alexander, S. Ishino, K. Fujita, S. Zhai, T. Sherwen, N. Oshima, R. Uemura, A. Yamada, N. Suzuki, S. Matoba, A. Tsuruta, J. Savarino and N. Yoshida, Isotopic evidence for acidity-driven enhancement of sulfate formation after SO2 emission control, Sci. Adv., 2021, 7(19), eabd4610 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4em00232f |
| This journal is © The Royal Society of Chemistry 2024 |