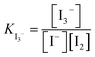Open Access Article
Open Access ArticleSolvent-dependent iodide interactions in LiO2 electrolytes – a molecular dynamics study†
Erlendur
Jónsson
 *,
Astrid H.
Berge
*,
Astrid H.
Berge
 ,
Clare P.
Grey
,
Clare P.
Grey
 and
Israel
Temprano
and
Israel
Temprano
 *
*
Yusuf Hamied Department of Chemistry, University of Cambridge, UK. E-mail: ej311@cam.ac.uk; it251@cam.ac.uk
First published on 18th August 2023
Abstract
Iodide-based redox mediation in Li–O2 batteries is regarded as a promising system due to its relatively high round-trip efficiency, compared to alternative systems. Here we explore the role of electrolyte composition in the solvation of I−, which has been shown to be critical for the efficient operation of this redox mediator, using a molecular dynamics approach. A combinatorial exploration of I− and H2O concentrations was performed, for a fixed concentration of Li+, across a series of glymes, with increasing chain length (mono- to tetraglyme). The resulting radial distribution functions show that shorter glymes allow for a closer packing of the I− redox mediator. Furthermore, increasing the I− concentration also reduces the solvation of Li+ in the glymes, especially in G2. The presence of water further pulls the I− and Li+ together. With increasing water content, its presence in the iodide's coordination shell increases markedly – an effect most pronounced for monoglyme. Competition between Li+ and I− for the coordination of water is modulated by the different solvents as they perturb the local coordination shell of these important complexes, with longer chain lengths being less affected by increases in water concentrations.
Introduction
The electrochemical behaviour of the iodide/triiodide/iodine redox system (I−/I3−/I2) has been extensively studied for nearly a century due to its relevance in a large number of applications, particularly related to its mild reducing properties.1 In the context of electrochemical energy-related production and storage, this redox couple is of special interest for the development of dye-sensitised solar cells (DSSCs),2,3 and it has been recently studied as redox mediator in Li–O2 batteries (LOBs).4–9The I−/I3−/I2 redox system can be described as a complex iodide (I−) oxidation process to iodine (I2), with an intermediate recombination process to generate polyiodide species such as I5−, I7−, or I9−, although in practice only I3− is of importance in most applications, as that is the dominant species that can be observed:
| 2I− ⇌ I2 + 2e− |
| I− + I2 ⇌ I3− |
The equilibrium constant of triiodide formation (KI3−) is typically high in the organic solvents used in electrolytes in DSSCs and LOBs,10 and therefore in practice, this complex redox system becomes a de-facto I−/I3− redox couple. This makes iodide a practical redox mediator as I2 is highly reactive and volatile.
It has been known for a long time that the electrochemical behaviour of halogen couples depends strongly on the electrolytic solvent,1 with more polarizable halogens being more susceptible to this effect. This is highly relevant for applications where the redox potential of the mediator determines the energy efficiency of the process, such as in DSSCs and LOBs. Pande and Viswanathan11 discussed this effect in reference to redox mediators for LOBs, arguing that, since the Gibbs free energy of a particular species in solution (ΔGsol) is primarily dependent on the interactions in its first solvation shell, these interactions ought to influence the equilibrium of redox pairs differently depending on their nature. The solvation of I− has been explored experimentally with UV/Vis and NMR, where strong effects from concentration and solvent choice were seen.12
The I−/I3−/I2 redox system has been characterized extensively in a range of conventional solvents, most notably water13–15 and acetonitrile.16–21 Recently, several studies have investigated the effect of an electrolyte's physicochemical parameters (solvent acceptor/donor number, salt concentration, etc.) on the measured redox potentials of the I−/I3− redox pair10,22,23 and their influence on its capacity to mediate the decomposition of various discharge products in LOBs.6,12,24 During LOB discharge, O2 gets reduced and precipitates as a Li oxide, such as Li2O2, i.e. an oxygen reduction reaction (ORR). During charging, oxygen gets oxidised and is released as O2 back into the atmosphere, i.e. an oxygen evolution reaction (OER). Redox mediators aid in these reactions by transporting electrons to/from electrode, from/to the discharge product.
It is by now well established that adding water to iodide-mediated electrolytes, either as an additive or from ambient air, can switch the dominant product from Li2O2 to LiOH.9 This change would enable a moisture-tolerant Li–air battery (LAB), allowing for the use of air instead of pure O2, while also stabilising the electrolyte, as Li2O2 is reactive towards solvents.25
Amongst the more promising and studied solvents in the metal–air-battery literature are the glymes, a series of solvents based on dimethyl ethers of poly(ethylene glycol) – the simplest is known as dimethoxyethane (DME) or monoglyme (G1). Here, we study the glyme series: ethylene glycol dimethyl ether (monoglyme, G1), diethylene glycol dimethyl ether (diglyme, G2), triethylene glycol dimethyl ether (triglyme, G3) and tetraethylene glycol dimethyl ether (tetraglyme, G4), as seen in Fig. 1. They will be referred to by G1, G2, G3 and G4 from this point. At very high salt concentrations, the glymes have been studied due to their propensity to form solvate ionic liquids,26 including with the I−/I3− redox couple.27
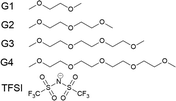 | ||
| Fig. 1 The glyme series, going from monoglyme (G1) to tetraglyme (G4), and TFSI, the electrolyte anion. | ||
Whilst some prior computational studies have looked at the diffusion of O2 and other atmospheric gases using molecular dynamics,28–30 in this work, we look at the influence of various parameters on the solvation of relevant species in solution, linking this to the efficiency of I−/I3− as a redox mediator for glyme-based LOB systems.
To simplify the role of Li+ in this study, its concentration is kept fixed at 400 mM, whilst the concentration of the two anions, I− and TFSI, are varied. This concentration is chosen due to the low experimental solubility of LiI in some of the glymes studied. The chosen counter-anion is bis(trifluoromethylsulfonyl) imide (TFSI, also shown in Fig. 1), a common counter anion in the literature.
Experimental
Molecular dynamics
The molecular boxes were constructed with Packmol31 and minimised before starting the molecular dynamics (MD) procedure. Each MD run was started with a 0.1 ns NVT equilibration, which was followed by NPT equilibrations (Berendsen for 1 ns, then Parrinello–Rahman for 1 ns – this combination was chosen for simulation stability after testing). The thermostat was set to 298 K with a time constant of 1 ps and the barostats were set to 1 atm, with a time constant of 2.5 ps. The production runs used the NVT ensemble and ran for 10 ns, with data stored every 2500 steps. In each case, a time step of 1 fs was used. Cutoffs were set at 1.2 nm, both for van der Waals and electrostatics (which used the particle mesh Ewald solver).The Gromacs software package was used for all simulations.32 The forcefield chosen was the all-atom optimized potentials for liquid simulations (OPlS-AA) for the glymes (with additional torsional parameters33), Li+, and I−, with the simple point-charge (SPC) H2O model. C–H bonds used constraints. The TFSI models used the parameters of Canongia Lopes and Pádua.34 This is similar to our previous work.12
The simulations used the first four glymes, i.e. G1, G2, G3 and G4 (Fig. 1). [Li+] is kept at a constant 400 mM in all of the systems. The counter anions are varied, with a series of [I−] (which we will use for naming): 50, 100, 200, 300 and 400 mM. The [TFSI] is 350, 300, 200, 100 and 0 mM in these respective systems to ensure a charge balance. Water concentration was set at dry, 1k, 5k and 20k ppm. Table 1 in the ESI† shows the number of molecules in each case. After running the simulations, the built-in analysis tools of Gromacs were used to generate radial distribution functions and their coordination numbers (CNs). Each individual radial distribution function and their CN plot are found in the ESI,† with the collated and derived plots shown in the main matter. An example of the CN between I− and I− can be seen in Fig. 2 for the dry case. To simplify the presentation of the data, we opted to extract a CN at a fixed distance, chosen for I−–I− as 5 Å (each figure will note the chosen plateau) due to the plateau seen in Fig. 2. The extracted CNs are then plotted as a function of iodide concentration, as seen in Fig. 3a.
Results
The key parameter in the electrochemical behaviour of the I−/I3− redox couple is the I−–I− interaction,10,12 as it proceeds via the I3−-mechanism (3I− ↔ I3− + 2e−), hence requiring at least some interactions between multiple iodides in solution. Thus, we initially investigated how the coordination number of I− to I− develops as a function of solvent choice and [I−].Comparison of the I−–I− interactions, as [I−] increases across the different solvents, can be carried out by analysing the coordination numbers (CNs) of I− to I−, as seen in Fig. 2. For all [I−] studied, a plateau can be observed between 5 and 7 Å. Thus, this point (5 Å) can be used to provide a more tractable visualisation of how the coordination evolves over the compositional range of interest (Fig. 3a).
At the lowest [I−] studied (50 mM), both G2 and G3 show a very small CN with I− at 5 Å, while G1 and G4 CN values only start at larger distances (yellow and purple traces in Fig. 2a) than for G2 and G3. It must be noted that at 50 mM I−, there are only 20 I− atoms in the system; thus, I−–I− comparisons at low [I−] should be considered to have large error bars. At 100 mM, the I−–I− CN in both G2 and G3 decreases, while in G1 and G4 it increases. Notably, all values are lower than the ca. 0.2 of G3 at 50 mM. At 200 mM [I−], a small increase in the CN can be observed for all but G4, which slightly decreases.
At 300 mM [I−], there is a noticeable increase in the I−–I− CN in all of the glymes. G2 shows the largest change, with a CN of about 0.3. Going to 400 mM [LiI], G2 increases even more. G1 also increases notably, while there is only a small increase for G4 and G3.
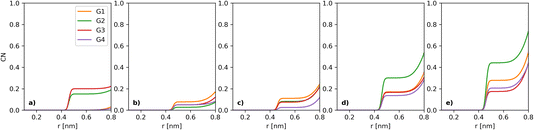
Fig. 3 shows the evolution of the coordination shell of I− over [I−] for key constituents: I− (at 5 Å), Li+ (at 3 Å), TFSI (at 4.5 Å) and O (solvent) (at 5 Å). The previously discussed I−–I− tends to become less prominent upon using the same y-scale for all the components shown here. For I−–Li+ (Fig. 3b), there is a small non-uniform variation, with CN close to 1. Thus, one can expect that Li+ will be found in the local environment of I−, while the reverse statement about the local environment of Li+ is only true at the highest [I−] (as seen in section 2.7 of the ESI†). For I−–TFSI (Fig. 3c), there is a gentle decrease as [I−] goes up, which is to be expected, as [TFSI] goes down simultaneously. The I−–O-solvent (Fig. 3d) values have a gentle downwards slope. It is also interesting that the CN between I− and O-solvent is somewhat similar across the different glymes. Thus, despite the bulkiness of the longer-chain glymes, they are able to effectively solvate the I− ion.
Water effect
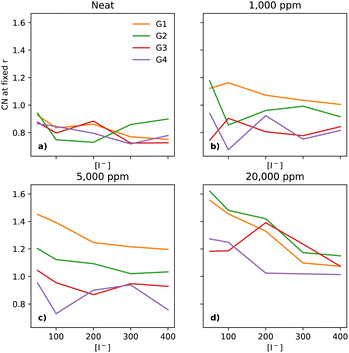
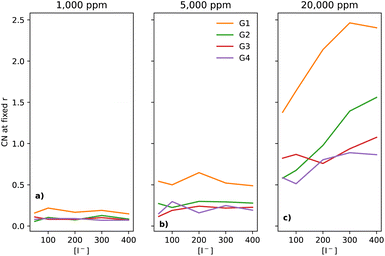
In electrolytes with 1000 ppm of water (Fig. 4b), there is a substantial increase in the I−–I− CNs. This is very noticeable with G1, which now has a CN spanning from 0.1 to 0.8, which increases monotonically across the range of [I−].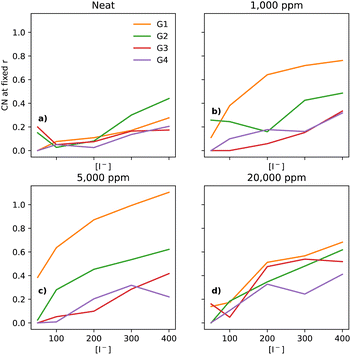 | ||
| Fig. 4 CNs of I− to I− at a fixed distance of 5 Å, for the four different glymes (G1 = yellow, G2 = green, G3 = red, G4 = purple) studied here, across the four different water concentrations (from left to right: (a) dry, (b) 1k, (c) 5k, and (d) 20k ppm of water). Note that (a) is a subset of the data shown in Fig. 3. | ||
At 5000 ppm of water (Fig. 4c), the effect on G1 is far stronger than at 1000 ppm. There is also an increase in I−–I− CN for G2. Increases for the G3 and G4 are minor, as compared to the 1000 ppm case.
At 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm of water (Fig. 4d), the I−–I− CN drops substantially for G1, while staying quite similar for G2. The CN for G3 increases substantially. There is also a modest increase for G4. Broadly speaking, higher [I−] leads, unsurprisingly, to a higher CN between I−–I−.
000 ppm of water (Fig. 4d), the I−–I− CN drops substantially for G1, while staying quite similar for G2. The CN for G3 increases substantially. There is also a modest increase for G4. Broadly speaking, higher [I−] leads, unsurprisingly, to a higher CN between I−–I−.
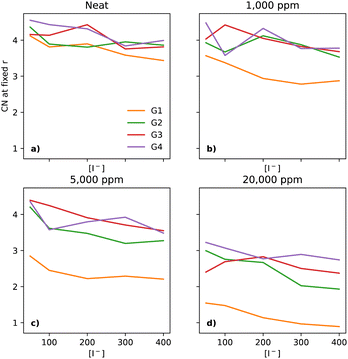
The interactions between I− and Li+ occur at shorter distances, as expected due to the attractive charges, which is evidenced by a plateau in the CNs at 3 Å (section ESI 2.6†). As the [Li+] is constant throughout the compositional range, there should be a small decrease in the CN, at the distance of 3 Å, as a function of [I−], as the I−/Li+ ratio becomes smaller. Interestingly, that behaviour is not seen in dry electrolytes, which have a somewhat narrow distribution of CNs across the glymes (emphasised in Fig. 5a, where the y-axis is expanded as compared to Fig. 3b).
Neat electrolytes display some variation upon increasing the [I−], however without a clear trend (Fig. 5a). Upon the addition of water, the I−–Li+ CNs undergo changes, as water pulls these ions together. The trend is clear at the start with G1 at 1000 ppm (Fig. 5b), with a smaller effect for G2, and no effect for G3 and G4.
At 5000 ppm, G1 and G2 still show a strong effect due to the increase in water (Fig. 5c), with G3 showing a small effect, unlike G4. Interestingly, there seems to be a weak downwards trend for G1 as [I−] increases. At 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm (Fig. 5d), all four solvents show a more tight organisation of I− and Li+ in the electrolyte than in neat electrolytes, with the same small downwards trend as seen for G1 at 5000 ppm.
000 ppm (Fig. 5d), all four solvents show a more tight organisation of I− and Li+ in the electrolyte than in neat electrolytes, with the same small downwards trend as seen for G1 at 5000 ppm.
The I−–H2O interaction is used here to measure how easily the I− can participate in formation of LiOH during the ORR, as it is well established that water-containing I-mediated electrolytes promote LiOH formation under certain conditions. Fig. 6 shows the CNs of I− to H2O with increasing water concentrations. For the 1000 ppm case (Fig. 6a), there is very little change as [I−] increases, across all four glymes. G1 has a slightly higher CN than the other glymes. At 5000 ppm (Fig. 6b), while all glymes have a higher I−–H2O CN than for the 1000 ppm case, that of G1 continues to be considerably higher than those of G2 and G3. Notably, the CN stays relatively flat across the [I−] range. Interestingly, at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm (Fig. 6c), the I−-concentration has a clear effect on the CN of I− to the H of H2O for the two shorter chain glymes. For G1, the CN increases nearly monotonically (the CN at 300 mM is slightly higher than for 400 mM). The CN for G2 increases over the [I−] range, while for G3 and G4 the CN stays flatter.
000 ppm (Fig. 6c), the I−-concentration has a clear effect on the CN of I− to the H of H2O for the two shorter chain glymes. For G1, the CN increases nearly monotonically (the CN at 300 mM is slightly higher than for 400 mM). The CN for G2 increases over the [I−] range, while for G3 and G4 the CN stays flatter.
Finally, we look at how I− interacts with the solvent O atoms of the solvents chosen (Fig. 7). In neat electrolytes, there is a downwards trend as the [I−] increases (Fig. 7a). The shortest glyme, G1, has in most cases the lowest CN. As water gets introduced to the system, the CN of I−–O-solvent drops significantly for G1 even at 1000 ppm of water (Fig. 7b), whereas G2 to G4 are slightly changed, but not in a systematic manner. Further increasing the water concentration to 5000 ppm (Fig. 7c) leads to a lower CN in the case of G1 and G2. There is also a very small decrease for G3 (more easily visualised in Fig. 7 of the ESI†). At 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm of water (Fig. 7d), all four glymes demonstrate a substantial decrease in CN, with G1 showing the lowest numbers.
000 ppm of water (Fig. 7d), all four glymes demonstrate a substantial decrease in CN, with G1 showing the lowest numbers.
Li+ coordination shell
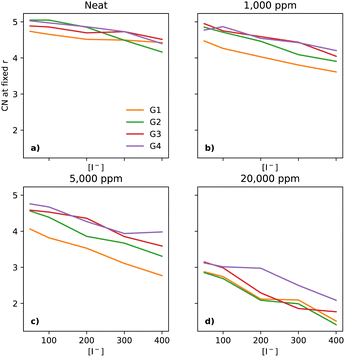
As Li+ is also a fundamental part of the key reactions of the LOBs and its local environment affects the reaction pathways, one must also take a look at its solvation environment. In Fig. 8a, there is a notable decrease in the CN between Li+ and O (of the glyme solvent) as [I−] increases. The trend is quite similar across the glymes in neat electrolytes. However, upon the addition of water, there are substantial changes. At 1000 ppm (Fig. 8b), the CN in G1 is distinctly lower than in the other glymes. At 5000 ppm (Fig. 8c), G1 continues to have the lowest CN; however, G2 is now distinct from G3 and G4. At 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm of water (Fig. 8d), the four glymes now overlap heavily, with the lowest values of CN seen at the highest [I−], showing that I− perturbs the solvation shell of Li+ differently to TFSI, in effect pulling Li+ out of the glymes.
000 ppm of water (Fig. 8d), the four glymes now overlap heavily, with the lowest values of CN seen at the highest [I−], showing that I− perturbs the solvation shell of Li+ differently to TFSI, in effect pulling Li+ out of the glymes.
Discussion
The overall picture that arises from the MD simulations on glyme-base electrolytes indicates that shorter glymes allow for a closer packing of the I− redox mediator. As the key reactions involve the interplay of I−, Li+ and water, figuring out the appropriate ratios and understanding how these may vary depending on the solvent is paramount for the development of iodide-mediated systems. As [I−] increases, I− should be more accessible to I− for facilitating the I− → I3− process; however, as the I−–I− CNs show, the change is small, despite increasing [I−] eightfold for the neat electrolyte (Fig. 3). Considering that there are 20 I− atoms in the 50 mM systems, any future work that looks closely at the low [I−] limit should consider running multiple independent simulations to ensure that I−–I− comparisons can be made with greater confidence at low [I−]. However, it is notable that Li+ seems to be less solvated by the glymes with increasing [I−] (Fig. 8), showing that Li+ should be more readily accessible. Higher concentrations of I− are not practical due to the limited solubility of LiI, especially in G2, and the increased incidence of shuttling effects.9 While this work did not explore the role of increasing [Li+], we have previously explored that question at a fixed [I−] concentration,12 where we noted that at very high [LiTFSI] the long range structuring of I−–I− was apparent in neat G4 electrolytes. The effect of changing solvent in the neat system shows that G1 does have a slightly greater effect on the I−–I− and I−–O (solvent) structuring, while for I−–Li+, G2 has a small effect (Fig. 5a).Water is clearly a key driver for modulation of the solvent shell around both Li+ and I−. Considering that water is a highly polar solvent, it is not very surprising that the ions show a strong response to its presence. We have previously reported this phenomenon affecting the electrochemistry of LiOH-based LOBs.6 With increasing water concentration, its role seems to be enhanced, pulling I− and Li+ closer together (Fig. 5), as the glyme solvent is being pushed out of the first solvation shell of these ions (Fig. 7 and 8). This effect is stronger for the shorter chain glymes, which is congruent with previous studies of Li–glyme35,36 and Na–glyme37 interactions, where a stronger binding is expected for longer-chain glymes due to the crown-ether-like coordination around the Li+/Na+. This effect might also have a kinetic component, as unravelling crown-ether-like solvation complexes should be a multistep process, wherein every step will have some competition between the anions, water and the oxygens of the glyme molecule in question.
As an interesting counterpoint to the small [I−] effect seen in the interaction between I− and water (Fig. 6), the interaction of Li+ with the O of the solvents (Fig. 8) shows far stronger I−-concentration effects, along with an increasing effect with increasing [H2O]. Thus, the glymes get pushed out of the solvation shell of Li+ by both I− and H2O. However, there seems to be a critical ratio for the I− to see strong interactions between I− and H2O. It also shows that the shorter glymes are more affected by these interactions. Unfortunately, the shortest glyme, G1, is a very volatile solvent, unlike the other glymes,38 which might make it impractical in LOBs due to exposure to the open cathode.
The electrolyte's solvation environments have been noted to have a considerable effect on the redox chemistry of LOBs. The donor (DN) and acceptor (AN) numbers are one metric of solute/solvent interactions. These metrics have been used to guide the choice of redox mediator in the LOB literature11 due to how they affect the efficiency of the overall redox mediation. It was also noted that the AN is more important for tuning the I−/I3−, as the AN is a measure of Lewis acidity, which can describe how well anions interact with the solvent.
In G4-based electrolytes, it was noted that increasing the Li+ concentration did not affect the apparent AN, unlike in DMSO.12 DNs are a measure of Lewis basicity, which is correlated with the solvation energy of the Li+ and the solvent. The glymes studied here are low-DN solvents, though it has been noted that a high DN can be beneficial,39 assuming a sensible choice of salt.40
It may be conceptually easier to look at the solvation directly, rather than using the DN/AN, considering how the electrolyte composition is varied here, as it is known that the local environment changes the I−/I3− redox, e.g. through solvent choice.10,23 For example, increasing the solvation energy of Li+ and O2− can increase the potential of the reaction.41 Thus, the oxidising power of the I−/I3− couple can be modified by changing the solvation environment.22 This can be exploited to change the reaction mechanism by using additives that modify the solvation of I−. For example, adding an ionic-liquid cation has been observed to increase the I−/I3− redox potential in G4-based electrolytes, driving the OER instead of iodate formation.24 The overall results here show that modifying the electrolyte composition does affect the local environment of the I−. Thus, using the shorter glymes will allow for more control of the solvation, though it has been noted that G2 should be a better chelator of Na+ than G1.37 Coupled with how strongly the water concentration affects the local environment, this gives us another means of controlling the reactions of the system.
Striking the balance of how much exploration of the compositional space of electrolytes should be done is going to be challenging, especially as we have not been able to identify a direct trend that gives a clear predictor that would simplify the selection of electrolyte components. However, based on prior work, there do seem to be a number of local maxima of higher performance, whether the focus is on the solvent choice37 or I−/H2O ratio.6,42 Some work has gone into exploring solvent choice and I−/H2O ratio simultaneously,12 but always for a subset of the compositional variables; e.g., this paper has a fixed amount of Li+ to reduce the complexity. Thus, we believe that optimising these electrolytes will simultaneously be challenging but might bear fruit.
Future work on these systems would benefit from the inclusion of I3− and/or O2 in the simulations, due to their role in the electrochemistry of the I−-mediated Li–air batteries. While it was not explored here, modulating the local environment can affect the redox properties of the I−/I3− couple,10,24 and alternative salts can be used to change the relative stabilities of intermediaries.40 However, such simulations would require the use of polarisable force fields, which are not readily available. A very ambitious approach would be to use ab initio MD simulations to explore these systems’ reactions (such as side reactions with 1O2), as the classical force field used here cannot be applied to reactions. However, while such an approach could give the deepest insight, it would be prohibitively expensive to explore the full range of compositions that we explored here. Thus, future simulation work might incorporate some ab initio simulations and create force fields through machine learning.
Another direction for future work would be to incorporate electrodes into the simulations. This would give insight into the layering behaviour of the electrolyte, i.e. probe the double layer, and how that will be modulated by the composition of the electrolyte and the magnitude/sign of the applied voltage. It is expected that electrodes would impose an ordering on the electrolyte (especially the ones that would be used in a simulation with periodic boundary conditions). Upon applying a potential, ions would adsorb on the surface, allowing for more structuring of the electrolyte. Recent work from multiple groups has resulted in MD codes43–45 that allow for simulations where the electrodes have a constant potential, giving us new tools for the future.
Conclusions
Our results show that electrolytes using I− as a redox mediator can contain quite distinct local environments of iodide. This suggests that careful selection of solvent, salt and water concentration is needed, in order to optimise its performance, especially for tuning the I−/I3− equilibrium redox potential.However, the interplay between these components is complex, as while water does increase I−–I− interactions (a requirement for I3− formation), it can encapsulate I−. The short-chain-length glymes allow for a greater interaction between the reactive species in the electrolyte. It is also possible to tune their properties through careful choice of salt/water content, thus modifying the electrolyte's redox properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by an EC H2020 ERC Advanced Investigator Grant for Prof. Dame Clare Grey, Project No. 835073. Via our membership to the UK's HEC Materials Chemistry Consortium, which is funded by the EPSRC (EP/L000202, EP/R029431), this work used the ARCHER UK National Supercomputing Service (https://www.archer.ac.uk).References
- K. J. Hanson and C. W. Tobias, Electrochemistry of Iodide in Propylene Carbonate: I. Cyclic Voltammetry Monitored by Optical Spectroscopy, J. Electrochem. Soc., 1987, 134(9), 2204–2210 CrossRef CAS.
- G. Boschloo and A. Hagfeldt, Characteristics of the Iodide/Triiodide Redox Mediator in Dye-Sensitized Solar Cells, Acc. Chem. Res., 2009, 42(11), 1819–1826 CrossRef CAS PubMed.
- L. Bay, K. West, B. Wintherjensen and T. Jacobsen, Electrochemical reaction rates in a dye-sensitised solar cell—the iodide/tri-iodide redox system, Sol. Energy Mater. Sol. Cells, 2006, 90(3), 341–351 CrossRef CAS.
- T. Liu, M. Leskes, W. Yu, A. J. Moore, L. Zhou and P. M. Bayley, et al., Cycling Li-O2 batteries via LiOH formation and decomposition, Science, 2015, 350(6260), 530–533 CrossRef CAS.
- C. M. Burke, R. Black, I. R. Kochetkov, V. Giordani, D. Addison and L. F. Nazar, et al., Implications of 4 e– oxygen reduction via iodide redox mediation in Li–O2 batteries, ACS Energy Lett., 2016, 1(4), 747–756 CrossRef CAS.
- T. Liu, G. Kim, E. Jónsson, E. Castillo-Martínez, I. Temprano and Y. Shao, et al., Understanding LiOH formation in a Li-O2 battery with LiI and H2O additives, ACS Catal., 2019, 9(1), 66 CrossRef CAS.
- W. J. Kwak, H. Kim, H. G. Jung, D. Aurbach and Y. K. Sun, Review—A Comparative Evaluation of Redox Mediators for Li-O2 Batteries: A Critical Review, J. Electrochem. Soc., 2018, 165(10), A2274–A2293 CrossRef CAS.
- W. J. Kwak, S. D. Rosy, C. Xia, H. Kim and L. R. Johnson, et al., Lithium–Oxygen Batteries and Related Systems: Potential, Status, and Future, Chem. Rev., 2020, 120(14), 6626–6683 CrossRef CAS.
- Z. Gao, I. Temprano, J. Lei, L. Tang, J. Li and C. P. Grey, et al., Recent Progress in Developing a LiOH-Based Reversible Nonaqueous Lithium–Air Battery, Adv. Mater., 2023, 35(1), 2201384 CrossRef CAS.
- C. L. Bentley, A. M. Bond, A. F. Hollenkamp, P. J. Mahon and J. Zhang, Voltammetric Determination of the Iodide/Iodine Formal Potential and Triiodide Stability Constant in Conventional and Ionic Liquid Media, J. Phys. Chem. C, 2015, 119(39), 22392–22403 CrossRef CAS.
- V. Pande and V. Viswanathan, Criteria and Considerations for the Selection of Redox Mediators in Nonaqueous Li–O2 Batteries, ACS Energy Lett., 2017, 2(1), 60–63 CrossRef CAS.
- E. Jónsson, J. H. J. Ellison, E. Wang, V. Kunz, T. Liu and I. Temprano, et al., On the Solvation of Redox Mediators and Implications for their Reactivity in Li-Air Batteries, J. Electrochem. Soc., 2021, 168(3), 030529 CrossRef.
- L. M. Dané, L. J. J. Janssen and J. G. Hoogland, The iodine/iodide redox couple at a platinum electrode, Electrochim. Acta, 1968, 13(3), 507–518 CrossRef.
- S. Swathirajan and S. Bruckenstein, Ring-disk electrode studies of the open-circuit dissolution of iodine films formed during the anodic oxidation of iodide on platinum, J. Electroanal. Chem. Interfacial Electrochem., 1981, 125(1), 63–71 CrossRef CAS.
- S. Swathirajan and S. Bruckenstein, The anodic behavior of iodide at platinum in the presence of an iodine film under potentiostatic steady-state and hydrodynamic modulation conditions, J. Electroanal. Chem. Interfacial Electrochem., 1983, 143(1–2), 167–178 CrossRef CAS.
- A. I. Popov and D. H. Geske, Studies on the Chemistry of Halogen and of Polyhalides. XIII. Voltammetry of Iodine Species in Acetonitrile, J. Am. Chem. Soc., 1958, 80(6), 1340–1352 CrossRef CAS.
- I. V. Nelson and R. T. Iwamoto, Voltammetric evaluation of the stability of trichloride, tribromide, and triiodide ions in nitromethane, acetone, and acetonitrile, J. Electroanal. Chem., 1964, 7(3), 218–221 CAS.
- G. Dryhurst and P. J. Elving, Electrooxidation of halides at pyrolytic graphite electrode in aqueous and acetonitrile solutions, Anal. Chem., 1967, 39(6), 606–615 CrossRef CAS.
- V. A. Macagno, M. C. Giordano and A. J. Arvía, Kinetics and mechanisms of electrochemical reactions on platinum with solutions of iodine-sodium iodide in acetonitrile, Electrochim. Acta, 1969, 14(4), 335–357 CrossRef CAS.
- L. Sereno, V. A. Macagno and M. C. Giordano, Electrochemical behaviour of the chloride/chlorine system at platinum electrodes in acetonitrile solutions, Electrochim. Acta, 1972, 17(3), 561–575 CrossRef CAS.
- F. Magno, G. A. Mazzocchin and G. Bontempelli, Electrochemical behaviour of the bromide ion at a platinum electrode in acetonitrile solvent, J. Electroanal. Chem. Interfacial Electrochem., 1973, 47(3), 461–468 CrossRef CAS.
- G. Leverick, M. Tułodziecki, R. Tatara, F. Bardé and Y. Shao-Horn, Solvent-Dependent Oxidizing Power of LiI Redox Couples for Li-O2 Batteries, Joule, 2019, 3(4), 1106–1126 CrossRef CAS.
- A. Nakanishi, M. L. Thomas, H. M. Kwon, Y. Kobayashi, R. Tatara and K. Ueno, et al., Electrolyte Composition in Li/O2 Batteries with LiI Redox Mediators: Solvation Effects on Redox Potentials and Implications for Redox Shuttling, J. Phys. Chem. C, 2018, 122(3), 1522–1534 CrossRef CAS.
- I. Temprano, T. Liu, E. Petrucco, J. H. J. Ellison, G. Kim and E. Jónsson, et al., Toward Reversible and Moisture-Tolerant Aprotic Lithium-Air Batteries, Joule, 2020, 4(11), 2501–2520 CrossRef CAS.
- R. Younesi, M. Hahlin, F. Björefors, P. Johansson and K. Edström, Li–O2 battery degradation by lithium peroxide (Li2O2): A model study, Chem. Mater., 2013, 25(1), 77–84 CrossRef CAS.
- K. Shimizu, A. A. Freitas, R. Atkin, G. G. Warr, P. A. FitzGerald and H. Doi, et al., Structural and aggregate analyses of (Li salt + glyme) mixtures: The complex nature of solvate ionic liquids, Phys. Chem. Chem. Phys., 2015, 17(34), 22321–22335 RSC.
- K. Shigenobu, A. Nakanishi, K. Ueno, K. Dokko and M. Watanabe, Glyme–Li salt equimolar molten solvates with iodide/triiodide redox anions, RSC Adv., 2019, 9(39), 22668–22675 RSC.
- A. Schürmann, R. Haas, M. Murat, N. Kuritz, M. Balaish and Y. Ein-Eli, et al., Diffusivity and Solubility of Oxygen in Solvents for Metal/Oxygen Batteries: A Combined Theoretical and Experimental Study, J. Electrochem. Soc., 2018, 165(13), A3095–A3099 CrossRef.
- R. Haas, M. Murat, M. Weiss, J. Janek, A. Natan and D. Schröder, Understanding the Transport of Atmospheric Gases in Liquid Electrolytes for Lithium–Air Batteries, J. Electrochem. Soc., 2021, 168(7), 070504 CrossRef CAS.
- N. Kuritz, M. Murat, M. Balaish, Y. Ein-Eli and A. Natan, PFC and triglyme for Li–Air batteries: A molecular dynamics study, J. Phys. Chem. B, 2016, 120(13), 3370–3377 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30(13), 2157–2164 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith and B. Hess, et al., GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- P. M. Anderson and M. R. Wilson, Developing a force field for simulation of poly(ethylene oxide) based upon ab initio calculations of 1,2-dimethoxyethane, Mol. Phys., 2005, 103(1), 89–97 CrossRef CAS.
- J. N. Canongia Lopes and A. A. H. Pádua, Molecular force field for ionic liquids composed of triflate or bistriflylimide anions, J. Phys. Chem. B, 2004, 108(43), 16893–16898 CrossRef.
- M. Callsen, K. Sodeyama, Z. Futera, Y. Tateyama and I. Hamada, The Solvation Structure of Lithium Ions in an Ether Based Electrolyte Solution from First-Principles Molecular Dynamics, J. Phys. Chem. B, 2017, 121, 180–188 CrossRef CAS.
- Y. Sun and I. Hamada, Insight into the Solvation Structure of Tetraglyme-Based Electrolytes via First-Principles Molecular Dynamics Simulation, J. Phys. Chem. B, 2018, 122(43), 10014–10022 CrossRef CAS.
- N. Ortiz Vitoriano, I. R. de Larramendi, R. L. Sacci, I. Lozano, C. A. Bridges and O. Arcelus, et al., Goldilocks and the three glymes: How Na+ solvation controls Na-O2 battery cycling, Energy Storage Mater., 2020, 29, 235–245 CrossRef.
- S. Tang and H. Zhao, Glymes as versatile solvents for chemical reactions and processes: from the laboratory to industry, RSC Adv., 2014, 4(22), 11251 RSC.
- D. Sharon, D. Hirsberg, M. Salama, M. Afri, A. A. Frimer and M. Noked, et al., Mechanistic role of Li+ dissociation level in aprotic Li–O2 battery, ACS Appl. Mater. Interfaces, 2016, 8(8), 5300–5307 CrossRef CAS.
- C. M. Burke, V. Pande, A. Khetan, V. Viswanathan and B. D. McCloskey, Enhancing electrochemical intermediate solvation through electrolyte anion selection to increase nonaqueous Li–O2 battery capacity, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(30), 9293–9298 CrossRef CAS PubMed.
- D. G. Kwabi, V. S. Bryantsev, T. P. Batcho, D. M. Itkis, C. V. Thompson and Y. Shao-Horn, Experimental and computational analysis of the solvent-dependent O2/Li+-O2− redox couple: Standard potentials, coupling strength, and implications for lithium-oxygen batteries, Angew. Chem., Int. Ed., 2016, 128(9), 3181–3186 CrossRef.
- M. Tułodziecki, G. M. Leverick, C. V. Amanchukwu, Y. Katayama, D. G. Kwabi and F. Bardé, et al., The role of iodide in the formation of lithium hydroxide in lithium–oxygen batteries, Energy Environ. Sci., 2017, 10(8), 1828–1842 RSC.
- L. Scalfi, M. Salanne and B. Rotenberg, Molecular Simulation of Electrode-Solution Interfaces, Annu. Rev. Phys. Chem., 2021, 72(1), 189–212 CrossRef CAS.
- A. Coretti, C. Bacon, R. Berthin, A. Serva, L. Scalfi and I. Chubak, et al., MetalWalls: Simulating electrochemical interfaces between polarizable electrolytes and metallic electrodes, J. Chem. Phys., 2022, 157(18), 184801 CrossRef CAS.
- L. J. V. Ahrens-Iwers, M. Janssen, S. R. Tee and R. H. Meißner, ELECTRODE: An electrochemistry package for atomistic simulations, J. Chem. Phys., 2022, 157(8), 084801 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00090g |
| This journal is © The Royal Society of Chemistry 2024 |