Open Access Article
Open Access ArticleBiological lipid hydration: distinct mechanisms of interfacial water alignment and charge screening for model lipid membranes
Clara-Magdalena
Saak†
 a,
Lisa B.
Dreier†
bc,
Kevin
Machel
b,
Mischa
Bonn
a,
Lisa B.
Dreier†
bc,
Kevin
Machel
b,
Mischa
Bonn
 b and
Ellen H. G.
Backus
b and
Ellen H. G.
Backus
 *ab
*ab
aFaculty of Chemistry, Institute of Physical Chemistry, University of Vienna, Währingerstrasse 42, 1090, Vienna, Austria. E-mail: ellen.backus@univie.ac.at
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128, Mainz, Germany
cGraduate School of Materials Science in Mainz, Staudingerweg 9, 55128, Mainz, Germany
First published on 7th July 2023
Abstract
Studying lipid monolayers as model biological membranes, we demonstrate that water molecules interfacing with different model membranes can display preferential orientation for two distinct reasons: due to charges on the membrane, and due to large dipole fields resulting from zwitterionic headgroups. This preferential water orientation caused by the charge or the dipolar field can be effectively neutralized to net-zero water orientation by introducing monolayer counter-charges (i.e. lipids with oppositely charged headgroups). Following the Gouy–Chapman model, the effect of monolayer surface charge on water orientation is furthermore strongly dependent on the electrolyte concentration and thus on the counterions in solution. In contrast, the effect of ions in the subphase on the dipolar alignment of water is zero. As a result, the capability of monolayer counter-charges to null the effect of dipolar orientation is strongly electrolyte-dependent. Notably, the different effects are additive for mixed charged/zwitterionic lipid systems occurring in nature. Specifically, for an E. coli lipid membrane extract consisting of both zwitterionic and negatively charged lipids, the water orientation can be explained by the sum of the constituents. Our results can be quantitatively reproduced using Gouy–Chapman theory, revealing the relatively straightforward electrostatic effects on the hydration of complex membrane interfaces.
1 Introduction
Lipids are the main structural components of biological membranes. The formation of these membranes is mainly driven by the interaction of amphiphilic lipid molecules with the water molecules in the surrounding aqueous phase.1,2 The self-assembly of lipids into membranes originates from the hydrophobic alkyl tails grouping together and dehydrating – thereby forming an interface between hydrophilic and hydrophobic regions. In addition to hydrophobic interactions, hydrophilic interactions between the polar headgroups and water play an essential role in membrane formation and function. Indeed, details of the hydrated polar headgroup of the lipid, either zwitterionic or negatively charged in most biological membranes at physiological pH,3,4 are essential for determining membrane properties. As the interface between biological membranes and the surrounding water molecules constitutes a platform where many biological reactions occur, the structure and charge density of said interface is of great importance.5 The charge density of the membrane surfaces will influence the properties of water in the interfacial region.6 This, in turn, may have a significant trickle-down influence on important biochemical processes which take place on membranes, such as protein folding7,8 or the transport of ions and metabolites across the membrane.9–11To better understand the environment in which these processes take place and the impact that the properties of the membrane interface itself may have on them, it is crucial to understand not only the effective charge of the membrane under physiological conditions, but also the structure of the aqueous phase around it. The latter has been shown to influence the effective viscosity and dynamics of water in intracellular media.12
Due to the experimental challenge of working with soft aqueous interfaces, our molecular-level structural understanding of biological membranes, the effective charge, and its impact on the structure of the aqueous subphase has been limited. The properties of the membrane itself may impact water structure in its proximity, both through the hydration shell structure of the solvated headgroups and – arguably to an even larger extent – through its net charge.
While the extent to which charged interfaces affect water structure has been extensively studied for mineral/liquid interfaces, the soft and malleable nature of the lipid/water interface, as well as the wide variety of charge architecture in the lipid headgroup, make it very challenging to straightforwardly transfer findings between these systems. The lipids in, e.g., inter- and intracellular membranes can contain headgroups of varying charge and charge density and multiple charges within one lipid. While the first approach to assigning an average charge to these systems is, without doubt, a helpful entry point, it has been shown that especially zwitterionic lipids, which are net neutral, still have the ability to strongly impact water structure close to the headgroup.13 This is because the strong and localized field between the positive and negative charge leads to the formation of a small population of water molecules – intercalating with the headgroups – that are highly ordered.13
As such, the specific charge architecture of lipid headgroups and the resulting differences in the behavior of the water molecules hydrating these headgroups need to be considered when describing the lipid membrane's influence on the structure of water.
For example, simple charged lipids, which carry 1 or 2 units of negative charge on their headgroup, can be considered to form a simple charged interface, similar to some solid/liquid interfaces. The Coulomb potential extending into the liquid will thus induce reorientation of the water molecules according to their dipole. Moreover, this potential also polarises the water molecules. These Coulomb potentials can reach quite deep into the aqueous interfacial region; however, they decay exponentially and are also strongly screened by ions and other charges that may be present. Their influence on water structure is thus highly sensitive to the composition of the aqueous phase, but can be described and predicted reasonably well using existing theories.14
In the case of multiple charges of opposing polarity in, for example, zwitterionic lipids, the behavior may be more complex, as the hydrating water molecules will experience strong and highly localized fields generated by these charges.13 This will lead to a tightly bound hydration shell, in which water molecules are highly oriented by the charges in the headgroup. It is also probable that this local field effect will be less sensitive to screening by ions near the lipid. This population of water molecules is likely relatively small – as it is possibly a fraction of the hydration shell – but will display pronounced and persistent structural alignment with the headgroup.
Another critical factor for biochemical processes influenced by membrane charges is the local distribution of other solutes contained within the aqueous phase, such as ions or smaller organic molecules. A significant charge density at the interface will increase the propensity of ions or charged molecules of opposite charge to approach the interface. This interaction between charged solutes and the charged membrane interface leads to the formation of a Stern and diffuse layer,14 in which the orientation and structure of water can strongly deviate from that in the bulk due to the resulting surface potential. The spatial extent of non-bulk orientation is known to strongly depend on the ion concentration in the aqueous phase, as these charges may screen the field generated by the lipid headgroups.15–17
Different membranes are known to exhibit different compositions and different surface charge densities. It is not a priori clear how these properties, each influencing the water orientation, will interact for complex membranes composed of both charged and zwitterionic lipids and for subphases with different concentrations of ions. Here we systematically study the effect of surface charge and salinity on the interfacial water orientation by studying the constituents of complex membranes isolated and combined under low salinity and physiological conditions. The current study aims to determine if the effects are simply additive or if cooperativity plays a role.
Since biologically relevant membranes are complex composite systems made up of many different lipids, we will first study the behaviour of three individual lipids representing headgroups of different charge architecture, namely the negatively charged PG, positively charged TAP, and zwitterionic, but net-neutral, PC (see Fig. 1 and Experimental section below). Subsequently, we compare the properties of these mono-lipidic systems with the model organic monolayer of Escherichia Coli (E. coli) extract to investigate to what degree the composite system mirrors the properties determined for the individual lipids. We use E. coli as a model system, as it is one of the most widely studied model organisms18,19 in various fields. The inner leaflet of the E. coli plasma membrane mainly consists of zwitterionic and negatively charged phospholipids,20 and the polar lipid extract of the E. coli membrane is often used as a model system for studying bacterial cell membranes.20–22 The influence of the ions present in the subphase will allow insight into the charge screening and resulting surface potential of the monolayer and, thus, the mechanism through which these lipids impact water structure.
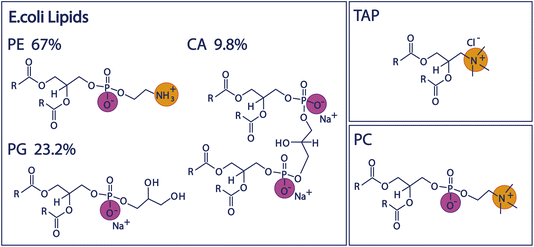 | ||
| Fig. 1 Chemical structures of the lipid headgroups contained in the E. coli polar extract as well as the structures of the positively charged TAP lipid and the zwitterionic PC lipid. | ||
The interfacial water orientation can be measured by sum-frequency-generation (SFG) spectroscopy, a surface-sensitive vibrational technique. The amplitude of the observed water vibrational band can be correlated with the charge-induced orientation of the water molecules near an interface. Briefly, SFG relies upon light generation at the sum-frequency of two incident beams. Since this is a second-order nonlinear optical process, it can only occur in non-centrosymmetric media. The centrosymmetry of the bulk is inherently broken at the interface, making SFG a surface-specific technique. In the case of vibrational SFG, employed in this study, one of the incident beams is in the IR range, whereas the second beam is in the visible range. When the wavelength of the incident IR beam is in resonance with a molecular vibrational transition, the SFG process becomes resonantly enhanced, thereby providing a vibrational spectrum of the surface region. The material response probed in the SFG process is the second-order nonlinear susceptibility, which scales not only with the number density of SFG active molecules ni in the ensemble, but also with the projection of the transition dipole onto the surface normal dav – which is linked to their respective orientation.
| ISFG ∝ |χ(2)|2 ∝ |ni·dav|2 | (1) |
In the case of the lipid monolayers studied here, a large SFG signal could therefore be attributed to either a high number density of oriented molecules in the surface region and/or a high degree of orientational order of the molecules making up the surface. For charged surfaces, another contribution has to be considered, namely the χ(3) signal generated by a combination of the fields of the two incident beams and the surface potential ϕ0 generated by the surface charge, which may additionally polarise the water molecules. The observed SFG intensity is, therefore, also related to the charge density at the surface – and the resulting surface potential ϕ0 – as well as the interaction of any ions and water molecules in proximity to the charged surface on a molecular scale.16,17,23 Including this contribution, the SFG intensity is more accurately described as follows:
| ISFG ∝ |χ(2) + χ(3)·ϕ0|2 ∝ |χ(2)eff|2 | (2) |
Since the third-order χ(3) contribution is not subject to the same selection rules as the χ(2) contribution, and can be generated in centrosymmetric media as well, it can already be the dominant contribution in the SFG spectrum at moderate surface charges. However, the χ(3) contribution can be screened effectively by ions in the aqueous phase, since the surface potential is inversely proportional to the ionic strength I of the aqueous phase,15–17,23,24 mathematically described by:
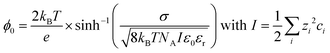 | (3) |
With kB being the Boltzmann constant, T the temperature, e the elementary charge, σ the surface charge density, NA Avogadro's constant, ε0 the vacuum permittivity, and εr the relative permittivity of the subphase. The ionic strength I is determined by the square of the charge number zi of the specific ion multiplied by the concentration of that ion in the bulk ci, summed over all ions i.
The χ(3)-term of eqn (2) can be expanded by an interference term, which accounts for the interference between SFG radiation generated from different depths inside the Stern and diffuse layers constituting the electric double layer (EDL). However, for salt concentrations above 1 mM this EDL is very thin, and this interference term becomes 1. As in the current study we work at ion concentrations of 10 mM and above, the interference term has the value of 1.16,25
We study the effect of charge and dipolar field on the water orientation by studying the OH-stretch SFG signal of water molecules in contact with a purely negatively charged 1,2-dipalmitoyl-phosphatidylglycerol (PG) monolayer, a purely positively charged 1,2-dipalmitoyl-3-trimethylammonium-propane (TAP) monolayer, and a zwitterionic 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (PC) monolayer as a function of salinity. Subsequently, we increase the complexity of the system and study the polar lipid extract of E. coli, mainly consisting of lipids with three different headgroups, namely the zwitterionic phosphoethanolamine (PE), the negatively charged phosphatidylglycerol (PG) and the doubly negatively charged cardiolipin (CA). The ratio of these three different headgroups in the extract is 67% PE, 23.2% PG and 9.8% CA, as determined by the supplier (see below). Moreover, different combinations of the negatively charged and zwitterionic lipids with the positively charged lipid TAP are studied. The chemical structure of the various lipids is depicted in Fig. 1.
2 Experimental
2.1 Sample preparation and environment
All lipids were obtained in powder form from Avanti Polar Lipids and were used without further purification: 16:0 TAP (890870), 16:0 PC (850355), 16:0 PG (840455), and E. coli polar extract (100600). The lipids were dissolved in a mixture of chloroform (stabilized with Amylene, >99%; Thermo Fischer Scientific) and methanol (99.8%; VWR Chemicals) with a ratio of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, yielding a lipid concentration of 4.3 × 10−4 M. As the polar E. coli extract in its powder form is unstable to oxygen, the parent solution was prepared under an inert N2 atmosphere.
1, yielding a lipid concentration of 4.3 × 10−4 M. As the polar E. coli extract in its powder form is unstable to oxygen, the parent solution was prepared under an inert N2 atmosphere.
Since we aim to study the monolayers in a stepwise approach toward physiological conditions, we study the monolayers on subphases of increasing salinity, namely 10 mM NaCl, 100 mM NaCl and 150 mM NaCl solutions and 150 mM phosphate-buffered saline (PBS, ionic strength 171 mM). NaCl and PBS were purchased from Sigma Aldrich; NaCl was heated to 600 °C under ambient conditions for 6 h to remove impurities. The aqueous solutions were prepared by dissolving NaCl or PBS buffer in ultrapure Water (MilliQ, 18.2 MΩ resistivity) at the desired concentration. In the case of PBS, one PBS tablet was dissolved in 200 mL of ultrapure water, resulting in the following ion concentrations in the solution: 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.8 mM KH2PO4. For this composition, we determine the ionic strength of PBS to be 171 mM, assuming that most phosphate groups remain protonated in the solution.
For the charge titration experiments, the lipid solutions were mixed at different ratios before being deposited onto the subphase (20 mL) using a microliter syringe. After deposition, the monolayers were left to equilibrate for 5 min. All experiments were performed at a constant area per molecule of 78 Å2, corresponding to a surface pressure of roughly 15 mN m−1 for the pure E. coli monolayer. All SFG experiments were performed on a rotating trough to prevent local heating effects.26
2.2 Sum-frequency generation
SFG spectroscopy has previously been described in detail elsewhere.27,28 In this study, SFG experiments were performed with a pulsed Ti:sapphire regenerative amplifier that generated 800 nm pulses with a pulse duration of 40 fs and a repetition rate of 1 kHz. A part of the output was used to pump an optical parametric amplifier with a difference frequency generation (DFG) stage to generate a broad IR pulse. The narrowband (around 15 cm−1 FWHM) VIS pulse was generated by passing another part of the laser output through a Fabry–Perot etalon. Both beams were then focused onto the sample surface and overlapped in time and space. The generated SFG signal was collimated, focused onto a grating spectrometer and detected with an electron multiplied charge-coupled device (CCD) camera. The polarization of both the IR and VIS beams can be tuned by a combination of polarisers and half-wave plates. All SFG spectra shown here were collected in ssp polarisation (s-polarised SFG, s-polarised VIS and p-polarised IR) and normalized to the non-resonant signal of z-cut quartz. All SFG spectra obtained in this study were acquired in the CH/OH-stretch window of the vibrational spectrum, i.e. the region between 2700 and 3600 cm−1.3 Results and discussion
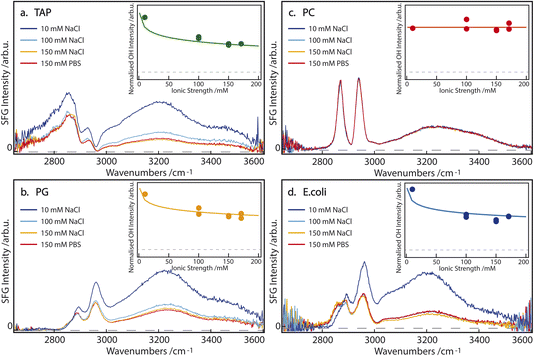
SFG spectra of pure TAP, PG, PC, and E. coli monolayers, on subphases containing 10, 100, and 150 mM NaCl, as well as 150 mM PBS, are depicted in Fig. 2. The narrow bands of the spectrum between 2800 and 3000 cm−1 originate from CH-stretch vibrations of the alkyl tails of the lipids, while the broad double feature extending from 3000 to 3600 cm−1 arises from the hydrogen-bonded OH-stretch vibrations of water molecules below the lipid monolayer, as well as from the OH groups contained in certain lipid headgroups. A more detailed peak assignment can be found in Table 1.| Assignment | Sign | Frequency ω [cm−1] | Width 2Γ [cm−1] |
|---|---|---|---|
| CH3 bend overtone | − | 2735–2760 | 45–60 |
| CH2 symmetric | − | 2845–2855 | 20–30 |
| CH3 symmetric | − | 2870–2875 | 20–25 |
| CH2 fermi | − | 2890–2905 | 40–45 |
| CH3 fermi | − | 2930–2935 | 20–40 |
| CH3 asymmetric | + | 2950–2960 | 20–35 |
| OH symmetric 1 | ± | 2180–3220 | 280–310 |
| OH symmetric 2 | ± | 3420–3480 | 190–260 |
In agreement with the literature,15–17 the intensity of the OH-stretch band for the singly positively charged TAP and singly negatively charged PG lipids decreases with increasing salinity of the subphase (Fig. 2a and b). This indicates that the ions in the subphase effectively screen the cumulative surface charge of the monolayer, thereby reducing the surface potential and, consequently, the χ(3) contribution to the overall SFG signal, as explained above in eqn (2) and (3). The difference in the spectral shape, especially between 2900 and 3050 cm−1, can be explained by the opposite charge of the lipid headgroups. As is predicted from the net charge and previously observed in the literature,29 the sign of the χ(2) contribution to the OH-stretch band, and thus the orientation of the water molecules, flips when comparing negatively (PG) and positively (TAP) charged lipids. However, the signal corresponding to the CH3 asymmetric-stretch vibration of the end of the lipid tails appears at approximately 2950 cm−1 and is known to have a positive χ(2) for an aqueous subphase, irrespective of the headgroup. This band thus interferes, either constructively or destructively, with the OH-stretch signal, depending on the net orientation of the interfacial water molecules and the resulting sign of χ(2) of the water signal. The interference between the CH3 asymmetric stretch of the lipid tails and the OH stretch of the oriented water molecules, therefore, acts as an indicator for the sign of χ(2) of the interfacial water groups. Specifically, in the case of positively charged aqueous surfaces, such as the TAP monolayer (Fig. 2a), this interference is destructive and results in a prominent dip in the SFG spectrum, which is not observed at negatively charged aqueous surfaces, such as the PG monolayer (Fig. 2b).
In contrast, the SFG spectrum of monolayers containing the zwitterionic PC lipids, and in particular the OH-stretch area, is not affected by the salinity of the subphase at all (Fig. 2c). This clearly shows that screening does not impact the dipole-induced water orientation, originating from the negative and positive charge present in the lipid headgroup. This observation can be traced to the assumption that ions are unlikely to incorporate into the hydration shell of the headgroup. This observation of salt-independence confirms the conclusion drawn in ref. 13, that in zwitterionic headgroups, the relative position of the phosphate and the choline moieties determines the water orientation. Additionally, the spectral shape of the OH-stretch band is also different in the case of PC compared to PG and TAP: the double feature of the band is less pronounced and the band at higher wavenumbers appears to be slightly redshifted. This supports the previously outlined assumption that the water population for zwitterionic lipids is not the same as for charged lipids.
From these experiments, we can already highlight the following points: firstly, charged lipids, and their resulting cumulative surface charge, are effectively screened by ions in the subphase. Secondly, the intermolecular dipole of the zwitterionic lipid headgroup induces a net orientation in the water molecules, which is completely unaffected by the addition of salt. We attribute this to the pronounced short-range ordering of water in the hydration shell of the zwitterionic headgroup.
If we now turn to the composite E. coli monolayer, we still see a clear dependence of the OH-stretch area on the salinity of the subphase, specifically between 10 and 100 mM NaCl (Fig. 2d). However, the area of the OH-stretch band is stable at higher salt concentrations, i.e. 100 to 150 mM NaCl and 150 mM PBS. Since the E. coli monolayer is comprised of both zwitterionic (PE) and charged lipids (PG an CA), its behavior bears a resemblance to both cases: at low to intermediate subphase salinity (10–100 mM NaCl) the increased ionic strength of the subphase effectively screens the molecular charge of PG and CA, thereby reducing the surface potential and the degree of water orientation these lipids may induce. However, at larger ionic concentrations in the subphase (≥100 mM), the persistent water OH-stretch band is attributed to the persistent water orientation induced by the zwitterionic PE lipids. Qualitatively, the E. coli monolayer can therefore be described as a composite case, with the properties of the charged lipids dominating at low subphase salinity, and those of the zwitterionic lipids becoming increasingly apparent at high salinity. Although the zwitterionic lipid PE has a small difference in the headgroup structure compared to PC (Fig. 1), the water SFG spectra have been shown to be very similar30 and, as such, very likely the water structure is too. Additionally, we observe a difference in the shape of the low-wavenumber flank of the CH region (between 2800 and 2850 cm−1) for the E. coli monolayer on a 10 mM NaCl subphase, which has been attributed to the change in the amplitude of the OH-stretch band and the resulting changes in the interference between the bands. These results show that the impact of a membrane's apparent charge, as related to the specific architecture of the charge distribution, will play a significant role in the resulting water orientation, even under physiological conditions.
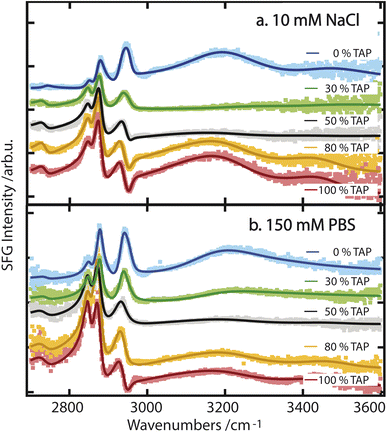
While these results allow for a qualitative understanding of the processes that drive water orientation at these monolayers, we aim to obtain a deeper understanding of how charge impacts water structure. To this end, we perform lipid titration experiments, as previously outlined by Dreier et al.27 These experiments involve replacing, in defined increments, a fraction of the lipids covering the surface with lipids of the opposing charge, thereby varying the net charge from, e.g., net negative to net positive. As can be seen in Fig. 3a and b for a subphase of 10 mM NaCl and 150 mM PBS, respectively, the combined OH-stretch band, between 3000 and 3600 cm−1, is quite pronounced in the case of the pure negatively charged E. coli lipid monolayer (blue spectrum). When positively charged TAP is added to the monolayer – decreasing the net charge – the area of the OH band decreases (green and grey spectra) until it reaches a minimum, from which its area increases again (orange and red spectra) with increasing TAP fraction as the monolayer becomes positively charged.
As the net negative charge of the monolayer is reduced and finally switched to a net positively charged monolayer, the orientation of the interfacial water molecules is expected to decrease correspondingly and eventually flip (from hydrogen towards the monolayer to hydrogen towards the bulk). This reorientation of the interfacial water molecules will result in a positive/negative sign of the nonlinear response in the OH-stretch region for a positive/negative monolayer.29 In contrast, the orientation of the hydrophobic lipid tails is independent of the charge of the headgroup, as their orientation is primarily determined by the hydrophobic effect. Therefore, the sign of χ(2) of the CH-stretch bands has to be the same for all lipids. Thus, the flip in the nonlinear response of the water signal causes a difference in the interference between 2900 and 3000 cm−1 as mentioned above, and is indeed clearly visible by comparing the blue/green spectra with the orange/red ones in Fig. 3. We can therefore conclude that the successive addition of positively charged TAP to the negatively charged E. coli lipid monolayer decreases the overall negative charge, as expected. This results in a corresponding decrease in the orientation of the water molecules, as observed through the resulting decrease in the OH-stretch band amplitude generated by the aqueous phase. When sufficient positively charged TAP headgroups are present to neutralize the net charge of the monolayer, resulting in a neutral surface, the water signal passes through a minimum, which we refer to as a crossing point here. By comparing Fig. 3a and b, it is clear that this crossing point appears at a higher amount of added TAP for the 150 mM PBS case. This can be explained by the screening effect of the ions on the TAP lipids, effectively partially neutralizing the monolayer. As such, at higher ionic strength, more TAP has to be added to achieve the point of zero water orientation. Upon further increasing the relative fraction of TAP in the mixture, the net charge of the surface becomes more positive, and the amplitude of the water signal increases again. This reflects the growing positive charge of the monolayer and the resulting orientation of the water molecules in the subphase. As the water molecules are now oriented in the opposite direction (with the oxygen facing toward the lipid layer), we now observe a dip in the spectra below 3000 cm−1 due to the destructive interference with the CH3 asymmetric-stretch vibration of the lipid tails, as mentioned above. To build on this qualitative understanding of the structural changes that occur across the lipid titration, we now evaluate the water orientation close to the monolayers in a more quantitative manner.
In order to trace the changes in the OH-stretch band, we take the sum of the fitted An parameters of the two OH-stretch bands OH1 and OH2 (see Table 1) and evaluate their evolution as a function of %TAP in the monolayer, as can be seen in Fig. 4. To obtain the amplitude of the OH bands, we use a commonly used model to fit SFG spectra based on a sum of complex Lorentzian lines, assuming that the χ(2) and χ(3) components can be combined into an effective χ(2) as described in eqn (2). The fit function is:
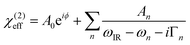 | (4) |
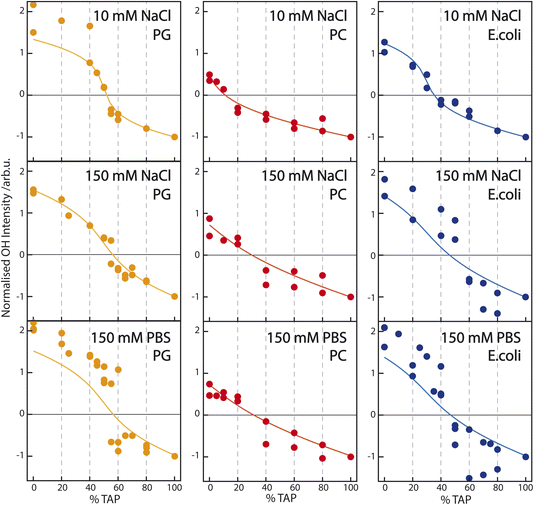 | ||
| Fig. 4 Sum of the fit parameter An corresponding to the two water resonances OH1 and OH2 (see Table 1) – normalized to the OH-stretch area at pure TAP – as a function of increasing TAP fraction for PG/TAP (orange), PC/TAP (red), and E. coli/TAP (blue) mixed monolayers on a subphase containing (top) 10 mM NaCl, (middle) 150 mM NaCl, and (bottom) PBS buffer. The corresponding model (solid line) is based on the Gouy–Chapman model described in the Introduction and assumes the observed SFG signal to be a combination of a constant χ(2) and a surface-potential-dependent χ(3) contribution. | ||
The titration curves for PG are only weakly affected by the nature of the subphase. The zero crossing, indicating the point of zero water orientation, is slightly above 50% TAP on 10 mM NaCl, increasing to just below 60% for 150 mM NaCl and PBS. The charge-screening effects for PG and TAP are, therefore, very similar. In comparison, for PC the zero crossing shifts to higher TAP concentration much more with increasing ionic strength of the subphase, due to the screening of the positive charge of the TAP lipids by the negative ions in the subphase. The higher the ionic strength, the larger the screening effect, and more TAP has to be added to neutralize the water orientation induced by the dipolar alignment of the water molecules in the PC headgroup. The titration curve of E. coli shows qualitatively the same result: more TAP is needed to obtain the point of zero water orientation upon increasing ionic strength.
To quantify how the contributions to water alignment – charge-induced alignment, dipole-induced alignment, and charge screening – influence each other, the data are modeled with the Gouy–Chapman model described in the Introduction. In the modeling, we assume that the OH-stretch amplitude of the water molecules in the case of a TAP monolayer is dominated by χ(3); we set the χ(2) component in eqn (2) to zero. According to this equation, the SFG amplitude is then proportional to ϕ0, which is calculated following eqn (3). The resulting curve, using a charge density of 0.205 C m−2 given by our working conditions of an area per lipid molecule of 78 Å2, as a function of ionic strength is depicted in the inset of Fig. 2a. The data points in the same inset are obtained by fitting the SFG spectra from the main panel of the figure, as described above. Besides a scaling factor, no adjustable parameters are used to model the experimental data, and good agreement is achieved. For the PG curve in Fig. 2b, we add a small χ(2) component as well, which will be explained in more detail below. As no salt dependence is observed for the zwitterionic lipid PC, the SFG spectrum is fully dominated by the χ(2) contribution. As E. coli consists of a mixture of zwitterionic, charged, and doubly-charged lipids, both a χ(2) and χ(3) contribution are used to model the experimental data in Fig. 2d. The charge density at an area per lipid molecule of 78 Å2 is given by considering that E. coli consists of 67% PE (zwitterionic), 23.2% PG (singly charged) and 9.8% CA (doubly charged), resulting in a surface charge density of −0.087 C m−2.
To model the titration curves of Fig. 4, we use the Gouy–Chapman model to calculate the ϕ0 at a given TAP fraction by considering that the charge density changes linearly between the charge density for the pure PG (−0.205 C m−2), pure PC (0 C m−2), or pure E. coli monolayer (−0.087 C m−2) at 0% TAP and the charge density at 100% TAP. The calculation is repeated for the three different ionic strengths. For the PC/TAP titration (red curves in the middle panel of Fig. 4), we assume that the TAP lipids contribute to the total SFG amplitude as χ(3)ϕ0, while the PC lipids contribute with solely a χ(2) component linearly scaling with the fraction of PC present in the mixture. The thus obtained curves are normalized as in the experiment to −1 at 100% TAP. To describe the variation of the curves with ionic strength, we only change the ionic strength I in eqn (3), and we keep the values of χ(2) and χ(3) constant. This simple model describes the data remarkably well. For the PG/TAP titration, a similar procedure is followed, except that PG has a χ(2) and χ(3) contribution. If no χ(2) contribution is included, the difference in absolute intensity at 100% PG (left side of the titration curve) and 100% TAP (right side of the titration curve) could not be explained, as we assume that the χ(3) term should be equal for PG and TAP, as it is coming from the bulk. Moreover, the small χ(2) contribution is also responsible for the small shift of the zero-crossing with increasing ionic strength. The ratio between the χ(2) and χ(3) contributions for PG is the same in the inset of Fig. 2b and the orange curves in Fig. 4. This straightforward model also describes the titration curves for PG well. For the E. coli lipid membrane extract, the mixed lipid contributions are described with a sum of χ(2) and χ(3) components. The ratio of χ(2) and χ(3) is constant for varying ionic strength; the ionic strength is only changing ϕ0 and thereby the SFG amplitude. The resulting model curves are depicted in orange in Fig. 4. Also, for this complex lipid mixture, the model describes the subphase-dependent crossing of the x-axis very well.
Combining both Fig. 2 and 4, it is clear that the Gouy–Chapman model, taking charge screening into account, can explain the observed trends very well. As mentioned, we model the data by assuming zero χ(2) contribution for the TAP lipids. Of course, we could equally well describe the titration data, including a χ(2) contribution for TAP and a subsequent change in the χ(2) contribution for PG, PC, and E. coli. The dependence of the modeled amplitude of the SFG data vs. concentration (insets Fig. 2) is not sensitive enough to exclude a small χ(2) contribution to the TAP curve. In our previous publication,33 we additionally invoked counterion condensation to explain the leveling off of the water signals for highly charged monolayers. Within the signal-to-noise of the current dataset, this additional effect does not have to be invoked to account for the data.
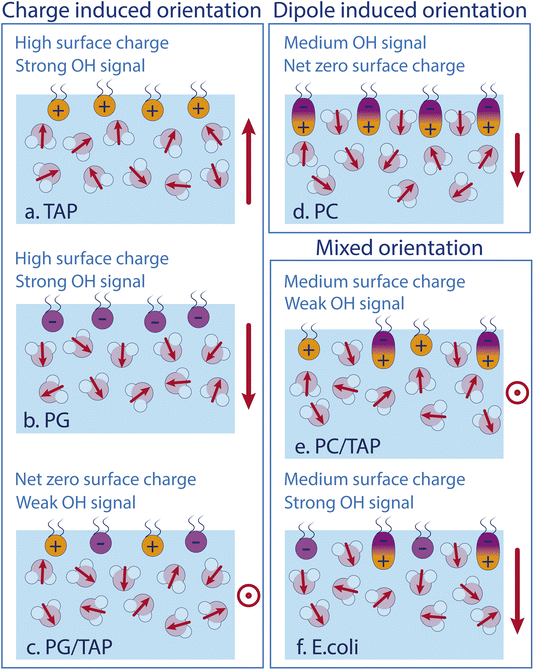
As the model describes all experimental data very well, we conclude that the water SFG signal and, as such, the average orientation of water molecules in the close proximity of a lipid layer, can be described by the effect of each constituent of the monolayer itself. Fig. 5 schematically depicts the different effects. Positively and negatively charged lipids orient the water molecules by their charges, with the oxygen or hydrogen, respectively, pointing towards the lipids. The charge-induced surface potential even breaks the symmetry over nm length scales, so that the SFG signal does not come from just one interfacial layer. This charge-induced effect can be screened by increasing the ionic strengths of the subphase. Interestingly, the ionic strength of the subphase has no effect on the water alignment for zwitterionic lipids, which is explained by the dipole alignment of water molecules between the opposite charges in the headgroup (see Fig. 5d). For zwitterionic lipids with the negative charge above the positive charge, the water orientation has the same direction as for negative lipids and the lipid ‘appears’ to be negatively charged (see Fig. 5b and d). A mixed PG/TAP monolayer with 50% TAP results in a zero water signal in SFG and, as such, on average a zero water orientation, but each lipid could still orient certain water molecules (Fig. 5c). ‘Neutralising’ the water orientation caused by zwitterionic lipids (Fig. 5e), occurs at a TAP concentration significantly smaller than 50%, as the apparent charge is not as high as for a pure negatively charged lipid monolayer. With increasing ionic strength in the subphase, more TAP has to be added to achieve a net-zero water orientation, as the charge of a TAP molecule becomes more screened with increasing ionic strength. The alignment of water molecules underneath a complex lipid monolayer like E. coli can be very well described as a simple sum of its constituents – we find no indications for cooperative or collective effects.
4 Conclusion
In this study of lipid hydration in model membrane lipid monolayers, we have shown that there are two distinct mechanisms leading to lipid-induced orientation of water molecules: monopolar (charge-induced) and dipolar (zwitterionic) water alignment. We probe the water alignment using nonlinear vibrational spectroscopy. Charges give rise to a so-called χ(3) contribution, whereas dipolar alignment gives rise to a χ(2) contribution to the water response. The two contributions can be separated by their strong dependence (monopole, χ(3)) vs. absence of dependence (dipole, χ(2)) on electrolyte concentration. The electrolyte can screen the monopolar but not the dipolar field. The response of water to an E. coli lipid extract, consisting of a mixed monolayer of charged and zwitterionic lipids, can be very well approximated by a sum of the separate contributions, despite the system's complexity.Author contributions
The conception and design of this study was carried out by L. B. D., E. H. G. B., and M. B. Experiments and acquisition of the presented data were performed by L. B. D., C. M. S., and K. M. The experimental results were analyzed by L. B. D., C. M. S., E. H. G. B., and K. M. All authors contributed to the interpretation of the experimental results as well as the writing and editing of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
C. M. S. acknowledges funding through the REWIRE program at the University of Vienna under the EU Horizon 2020 program, Marie Sklodowska-Curie Grant Agreement No. 847693.References
- J. Fraxedas, Water at Interfaces, CRC Press, 1st edn, 2014 Search PubMed.
- Membrane Biophysics, ed. H. Wang and G. Li, Springer, Singapore, 2018 Search PubMed.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS PubMed.
- M. Pekker and M. Shneider, J. Phys. Chem. Biophys., 2015, 5, 1000177 Search PubMed.
- Membrane Hydration, ed. E. A. Disalvo, Springer International Publishing, Cham, 2015, vol. 71 Search PubMed.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Phys. Rev. Lett., 2011, 107, 166102 CrossRef.
- S. M. Butterfield and H. A. Lashuel, Angew. Chem., Int. Ed., 2010, 49, 5628–5654 CrossRef CAS.
- M. Boström, V. Deniz and B. W. Ninham, J. Phys. Chem. B, 2006, 110, 9645–9649 CrossRef.
- M. L. Berkowitz, D. L. Bostick and S. Pandit, Chem. Rev., 2006, 106, 1527–1539 CrossRef CAS PubMed.
- K. Gawrisch, D. Ruston, J. Zimmerberg, V. Parsegian, R. Rand and N. Fuller, Biophys. J., 1992, 61, 1213–1223 CrossRef CAS PubMed.
- J. Milhaud, Biochim. Biophys. Acta, Biomembr., 2004, 1663, 19–51 CrossRef CAS.
- P. Ball, Proc. Natl. Acad. Sci., 2017, 114, 13327–13335 CrossRef CAS.
- L. B. Dreier, A. Wolde-Kidan, D. J. Bonthuis, R. R. Netz, E. H. Backus and M. Bonn, J. Phys. Chem. Lett., 2019, 10, 6355–6359 CrossRef CAS PubMed.
- G. Gonella, E. H. G. Backus, Y. Nagata, D. J. Bonthuis, P. Loche, A. Schlaich, R. R. Netz, A. Kühnle, I. T. McCrum, M. T. M. Koper, M. Wolf, B. Winter, G. Meijer, R. K. Campen and M. Bonn, Nat. Rev. Chem., 2021, 5, 466–485 CrossRef CAS.
- K. C. Jena, P. A. Covert and D. K. Hore, J. Phys. Chem. Lett., 2011, 2, 1056–1061 CrossRef CAS.
- G. Gonella, C. Lütgebaucks, A. G. F. de Beer and S. Roke, J. Phys. Chem. C, 2016, 120, 9165–9173 CrossRef CAS.
- Y.-C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Phys. Rev. Lett., 2016, 116, 016101 CrossRef PubMed.
- M. Papanastasiou, G. Orfanoudaki, M. Koukaki, N. Kountourakis, M. F. Sardis, M. Aivaliotis, S. Karamanou and A. Economou, Mol. Cell. Proteomics, 2013, 12, 599–610 CrossRef CAS.
- H. Cypionka, Grundlagen der Mikrobiologie, Springer, Berlin, Heidelberg, 2010 Search PubMed.
- L. Soblosky, A. Ramamoorthy and Z. Chen, Chem. Phys. Lipids, 2015, 187, 20–33 CrossRef CAS PubMed.
- T. Berry, D. Dutta, R. Chen, A. Leong, H. Wang, W. A. Donald, M. Parviz, B. Cornell, M. Willcox, N. Kumar and C. G. Cranfield, Langmuir, 2018, 34, 11586–11592 CrossRef CAS PubMed.
- H. M. Britt, C. A. García-Herrero, P. W. Denny, J. A. Mosely and J. M. Sanderson, Chem. Sci., 2019, 10, 674–680 RSC.
- J. Schaefer, G. Gonella, M. Bonn and E. H. G. Backus, Phys. Chem. Chem. Phys., 2017, 19, 16875–16880 RSC.
- P. Ober, J. Hunger, S. H. Kolbinger, E. H. G. Backus and M. Bonn, Angew. Chem., Int. Ed., 2022, 61, e202207017 CrossRef CAS.
- S. Sun, J. Schaefer, E. H. G. Backus and M. Bonn, J. Chem. Phys., 2019, 151, 230901 CrossRef PubMed.
- E. H. G. Backus, D. Bonn, S. Cantin, S. Roke and M. Bonn, J. Phys. Chem. B, 2012, 116, 2703–2712 CrossRef CAS PubMed.
- L. B. Dreier, Y. Nagata, H. Lutz, G. Gonella, J. Hunger, E. H. G. Backus and M. Bonn, Sci. Adv., 2018, 4, eaap7415 CrossRef.
- S. Hosseinpour, F. Tang, F. Wang, R. A. Livingstone, S. J. Schlegel, T. Ohto, M. Bonn, Y. Nagata and E. H. G. Backus, J. Phys. Chem. Lett., 2017, 8, 2195–2199 CrossRef CAS.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Chem. Phys., 2009, 130, 204704 CrossRef.
- D. Maltseva, G. Gonella, J.-M. Ruysschaert and M. Bonn, J. Chem. Phys., 2022, 156, 234706 CrossRef CAS.
- E. H. G. Backus, J. M. Kuiper, J. B. F. N. Engberts, B. Poolman and M. Bonn, J. Phys. Chem. B, 2011, 115, 2294–2302 CrossRef CAS.
- J. F. D. Liljeblad, V. Bulone, M. W. Rutland and C. M. Johnson, J. Phys. Chem. C, 2011, 115, 10617–10629 CrossRef CAS.
- L. B. Dreier, M. Bonn and E. H. G. Backus, J. Phys. Chem. B, 2019, 123, 1085–1089 CrossRef CAS.
Footnote |
| † Authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |