Open Access Article
Open Access ArticleVibrational energy transfer in ammonia–helium collisions
Jérôme
Loreau
 *a and
Ad
van der Avoird
*a and
Ad
van der Avoird
 b
b
aKU Leuven, Department of Chemistry, B-3001 Leuven, Belgium. E-mail: jerome.loreau@kuleuven.be
bInstitute for Molecules and Materials, Radboud University, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands
First published on 28th February 2024
Abstract
While the rotational energy transfer of ammonia by rare gas atoms and hydrogen molecules has been the focus of many studies, little is known about its vibrational relaxation, even though transitions involving the umbrella bending mode have been observed in many astrophysical environments. Here we explore the vibrational relaxation of the umbrella mode of ammonia induced by collisions with helium atoms by means of the close-coupling method on an ab initio potential energy surface. We compute cross sections up to kinetic energies of 1500 cm−1 and rate coefficients up to a temperature of 300 K for vibrational, rotational, and inversion transitions involving the lowest two vibrational states. We show that vibrational relaxation is much less efficient than rotation–inversion relaxation, although the rate coefficients for vibrational relaxation strongly increase with the temperature. We also observe important differences for vibrationally-elastic transitions within the lowest two vibrational states, i.e., for rotation–inversion transitions. These are a direct consequence of the difference in the tunnelling splitting of the lowest inversion levels.
1 Introduction
Ammonia is one of the most widely observed molecules in space. Although the observed rovibrational spectra can be used to derive physical properties of astrophysical media such as the local temperature, these spectra often display deviations from the local thermodynamic equilibrium (LTE) assumption, and their interpretation thus requires the knowledge of the rate coefficients for collisional excitation by dominant colliders in space, i.e., He atoms or H2 molecules. In this context a large number of theoretical studies have focused on computing rate coefficients corresponding to the rotation–inversion collisional excitation of ammonia by helium atoms1–3 or H2 molecules,4–6 including hyperfine excitation.7 Experimentally, ammonia can be considered a prototypical polyatomic molecule for the investigations of inelastic collisions. As such, the rotation–inversion scattering properties of (deuterated) ammonia with He or H2 have been widely explored using molecular beams with quantum state selection.8–13 Simulations of rotational cooling of NH3 in a helium buffer gas cell have also been carried out based on state-to-state cross sections.14,15Despite this, little is known about the vibrational collisional excitation of ammonia, even though transitions involving the umbrella bending mode have been observed in many astrophysical environments, including circumstellar envelopes of various evolved stars,16,17 protostars and star-forming regions,18,19 and protoplanetary disks.20 In astronomical observations, rovibrational transitions of ammonia usually involve the first excited level of the umbrella mode ν2, at wavelengths centered around 10.5 μm, although observations of rotation–inversion transitions within the first excited vibrational state have also been reported. LTE conditions cannot be assumed for vibrational levels, and radiative transfer calculations taking into account the effect of collisions must be carried out to interpret observations.21
In the past few years, there has been an increased interest in the development and application of theoretical methods to treat vibrational energy transfer in inelastic collisions involving polyatomic molecules.22 Such developments are needed in an astrochemical context, with the recent launch of the James Webb Space Telescope JWST that provides a new window to observe the universe in the infrared. Up to now, quantum scattering calculations of the vibrational excitation of polyatomic molecules have been limited to collisions with helium atoms, which have been performed for CH3,23 HCN,24 C3,25 CO2,26 as well as for the torsional motion of CH3OH,27 and to the excitation of H2O by H2.28–30 In a previous paper31 we examined rotation–inversion transitions of NH3 in collisions with rare gas atoms, including He, by performing quantum scattering calculations that describe the umbrella motion of ammonia explicitly. This is a form of vibrational excitation, although it occurs at an energy scale much lower than usual for vibrational modes. The computational requirements of these quantum calculations are high but they are crucial to benchmark more efficient but approximate methods.
Here we extend our previous study by exploring the vibrational excitation and relaxation of the first excited state of the umbrella mode of ammonia induced by collisions with helium atoms, by means of the close-coupling method on an ab initio potential energy surface. In Section 2 we briefly review the theoretical approach used in our calculations. In Section 3 we calculate cross sections for kinetic energies up to 1500 cm−1 and rate coefficients up to temperatures of 300 K for vibrational transitions involving the lowest two ν2 states, as well as for rotation–inversion transitions within these vibrational states. For the latter, we show that the splitting of the lowest two inversion vibrational levels due to tunnelling leads to a dependence of the cross section upon the vibrational state. Finally, we compare our results for rotation–inversion transitions in the ground vibrational state to data from the literature. We summarize our findings in Section 4.
2 Methods
The methods have been described extensively in two previous papers,31,32 and we only recall their main features here. The potential energy surface (PES) for the collision was calculated at the coupled-cluster level with single and double excitations and a perturbative treatment of triple excitations [CCSD(T)] with the AVQZ basis set on all atoms in the long-range, while in the short range the explicitly-correlated variant CCSD(T)-F12 was used, with the same basis set. The four-dimensional PES V(R, θ, ϕ, ρ) depends on three spherical coordinates (R, θ, ϕ) that define the position of the He atom with respect to the center of mass of NH3, as well as on the umbrella angle ρ. 4180 ab initio points were computed and fitted to an expansion in spherical harmonics.The scattering calculations are performed by means of the quantum-mechanical close-coupling (CC) method.
The Hamiltonian of the NH3–He scattering complex, including the umbrella coordinate, can be written as
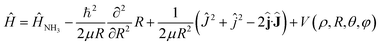 | (1) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) where
where ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) is the relative angular momentum.
is the relative angular momentum.
Ĥ NH3 is the Hamiltonian describing ammonia, given by the sum of three terms:
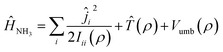 | (2) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (ρ) is the kinetic operator corresponding to the inversion motion, and Vumb(ρ) is a double well potential with two equivalent equilibrium angles ρ = 112.1° and ρ = 67.9°. The double well leads to a splitting of the first two vibrational states, ν2 = 0 and ν2 = 1, into doublets with a splitting of 0.79 cm−1 in the ground state and 35.2 cm−1 in the excited state. The potential Vumb(ρ) is parametrized analytically and fitted to reproduce the energy of these lowest four states, as well as the average ν2 = 0 → 1 transition energy of 949.9 cm−1. The expressions for these operators can be found in ref. 31 and 32.
(ρ) is the kinetic operator corresponding to the inversion motion, and Vumb(ρ) is a double well potential with two equivalent equilibrium angles ρ = 112.1° and ρ = 67.9°. The double well leads to a splitting of the first two vibrational states, ν2 = 0 and ν2 = 1, into doublets with a splitting of 0.79 cm−1 in the ground state and 35.2 cm−1 in the excited state. The potential Vumb(ρ) is parametrized analytically and fitted to reproduce the energy of these lowest four states, as well as the average ν2 = 0 → 1 transition energy of 949.9 cm−1. The expressions for these operators can be found in ref. 31 and 32.
In the CC method, the total wave function is expanded as a sum of products of radial, angular, and vibrational functions. The first four vibrational wavefunctions ϕ±v(ρ), corresponding to the symmetric (+) and antisymmetric (−) umbrella tunnelling components of the vibrational states ν2 = 0 (ϕ+0(ρ) and ϕ−0(ρ)) and ν2 = 1 (ϕ+1(ρ) and ϕ−1(ρ)), were obtained by solving the one-dimensional Schrödinger equation for the umbrella motion. Such an approach was previously used to interpret high resolution IR spectroscopic experiments of the NH3–rare gas complexes in the ν2 region.33
The inelastic scattering cross sections are then calculated by solving the coupled equations with the Hamiltonian (1) in the basis of rovibrational states. The scattering rate coefficients are obtained by averaging the cross sections over a Maxwell–Boltzmann distribution of velocities,
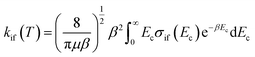 | (3) |
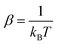 and kB, T and μ denote the Boltzmann constant, the kinetic temperature and the NH3–He reduced mass, respectively.
and kB, T and μ denote the Boltzmann constant, the kinetic temperature and the NH3–He reduced mass, respectively.
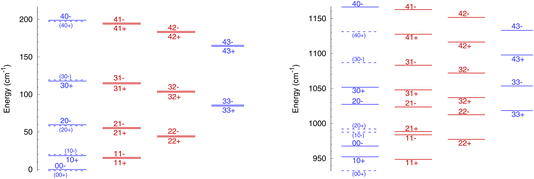
The rotational energy levels of NH3 are denoted as jk±, where k is the projection of the angular momentum j on the symmetry axis of the molecule. Due to nuclear spin statistics, NH3 occurs as ortho-NH3 (for k = 3n, where n is an integer) and para-NH3 (for k = 3n ± 1) that cannot be interconverted through inelastic collisions, and for k = 0 half of the levels are forbidden. The lowest levels (up to j = 4 and k = 3) are shown in Fig. 1 for ν2 = 0 and for ν2 = 1. The variation in rotational structures is a consequence of the large difference in the splitting in ν2 = 0 and ν2 = 1 and can be expected to impact the dynamics of NH3–He collisions.
The coupled equations were solved by means of the renormalized Numerov propagator for all initial states of NH3 up to j = 4 and for kinetic energies in the range 0.01–1500 cm−1. For energies below 50 cm−1, the radial grid consists of 444 points between 4 a0 to 80 a0, while for energies above 50 cm−1 the grid extends from 4 a0 to 40 a0 with 211 points. The maximum value of the total angular momentum J needed to obtain convergence of the inelastic cross sections depends on the collision energy and is Jmax = 70 at the highest energy considered. The size of the rotational basis set was truncated at jmax = 14.
3 Results
3.1 Rotation–inversion transitions
Cross sections and rate coefficients for rotation–inversion transitions in the ground vibrational state are available in the literature. The reference rate coefficients for astrophysical applications have been computed by Machin and Roueff2 and cover temperatures up to 300 K. These data were obtained from quantum scattering calculations on a PES constructed by Hodges and Wheatley by fitting to scaled perturbation theory calculations.34 This PES is qualitatively similar to the one used in the present work, although the two PESs lead to large differences in the resonance structure of the cross sections, as discussed in ref. 32 for the 11− → 11+ transition. Another difference concerns the way the inversion is taken into account. In the work of Machin and Roueff,2 the ground tunnelling states are approximated as symmetric or antisymmetric linear combinations of delta functions localized at the equilibrium angles, which allows a calculation of rotation–inversion cross sections without the need for a potential dependent on the umbrella angle. The same approach has been used for all quantum scattering calculations performed so far on NH3–H2 as well.5,6,12 The impact of using a Hamiltonian for ammonia that depends explicitly on the umbrella coordinate on rotation–inversion transitions was discussed in ref. 31 and 32 for the 11− → 11+ transition of experimental interest, and found to be small except at low energies.Our calculations for other transitions involving levels of NH3 up to j = 4 confirm these observations. In Fig. 2 we compare the behaviour of the collisional relaxation rate coefficient for two transitions, jk± = 10+ → 00− in ortho-NH3 and 11− → 11+ in para-NH3. At low temperature the differences can be as large as 50% but decrease with increasing temperatures, indicating that the largest discrepancies originate from the low energy regime. These differences can be attributed to the quality of the underlying PESs on which the scattering calculations are performed. We further tested the impact of the explicit treatment of the umbrella motion for other rotation–inversion transitions in the ground vibrational state and found a small impact overall. Treating the first excited vibrational state requires at least four tunnelling functions. Including two more umbrella functions, for a total of six, leads to small differences on the cross sections (on the order of 5%).
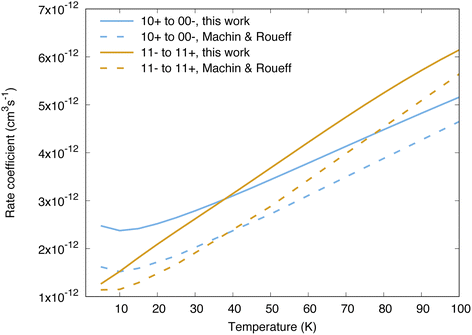 | ||
| Fig. 2 Comparison between the reference rate coefficients of ref. 2 and those calculated in the present work, for the transitions 10+ → 00− and 11− → 11+. | ||
It is also instructive to compare the rotation–inversion cross sections and rate coefficients in ν2 = 1 to those in ν2 = 0. It is often assumed, both by experimentalists as well as in non-LTE astrochemical models, that the scattering cross section or rate coefficient for a given rotational transition is the same within any vibrational level of a molecule excited by an atom or a molecule, which implies that the vibrational and rotational motions are decoupled. This assumption has been verified through computations, e.g., for H2O–H2 inelastic collisions.28 In the case of NH3, the situation is more complex because of the splitting of the inversion levels and the fact that the splitting is dramatically different in the ground state (0.79 cm−1) and in the excited state (35.2 cm−1), as illustrated in Fig. 1.
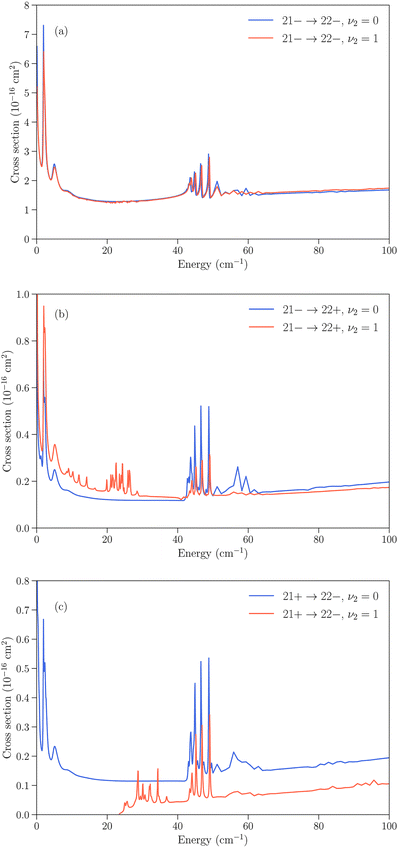
Several cases can then arise. The simplest is when an inelastic collision conserves the inversion symmetry (transitions jk+ → j′k′+ or jk− → j′k′−). Since the inversion splitting is almost independent of the quantum numbers j and k, the energy gap between the initial and final rotation–inversion state is identical in ν2 = 0 and ν2 = 1 and these transitions have cross sections that are similar. This is illustrated in panel (a) of Fig. 3 for the transition 21− → 22−.
The second case concerns relaxation in transitions jk− → j′k′+, i.e. from an initial antisymmetric inversion level to a final symmetric level. Given that the splitting in ν2 = 1 is much larger than in ν2 = 0, a relaxation transition from the upper (−) inversion component of an initial rotational state to the lower (+) inversion component of a final rotational state corresponds to a larger energy gap in ν2 = 1 compared to ν2 = 0. As a consequence, the cross sections for those transitions are usually larger in ν2 = 0 than in ν2 = 1. This is illustrated in panel (b) of Fig. 3 for the transition 21− → 22+. We note that for an excitation with an initial antisymmetric inversion level (jk− → j′k′+), the converse is usually true as the energy gap is smaller in ν2 = 1 compared to ν2 = 0.
The third case is for relaxation in transitions jk+ → j′k′− where the situation is reversed, with a larger energy gap in ν2 = 0 than in ν2 = 1, and an associated cross section that is usually larger for rotation–inversion transitions in ν2 = 1 than in ν2 = 0. For an excitation with an initial symmetric inversion level (jk+ → j′k′−), the converse is true.
Finally, the dependence of the rotational structure on ν2 leads to cases where transitions are exothermic in one vibrational state but endothermic in the other. An example is provided by the jk± = 21+ → 22− transition, which is a relaxation in ν2 = 0 but an excitation in ν2 = 1, with a threshold of about 23 cm−1. This leads to large differences in the low energy regime, as can be seen in panel (c) of Fig. 3.
All the transitions illustrated in Fig. 3 display a resonance structure arising from quasi-bound states of the complex. The resonances at kinetic energies around 2 cm−1 and in the range 40–50 cm−1 are seen for all final states and can be associated with the initial jk = 22 state, while the resonance structure between those energies depends on the final state. It can also be noted that transitions that conserve the symmetry of the umbrella state (+ ↔ + and − ↔ −) tend to have larger cross sections than transitions that change the umbrella state (+ ↔ −).31,32
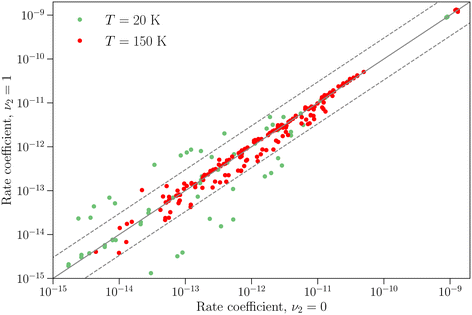
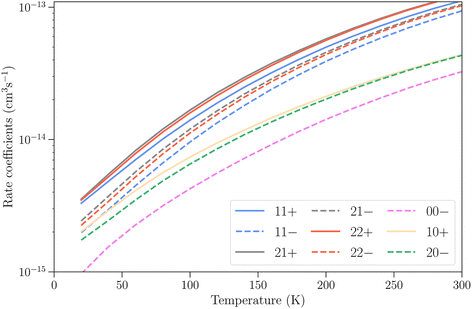
The differences between the rotation–inversion rate coefficients in ν2 = 0 and ν2 = 1 can also be illustrated by considering the rate coefficients instead of the cross sections. Fig. 4 displays a comparison of the rate coefficients for all transitions (excitation and relaxation) starting from all initial levels j = 0–2 to all final levels in the range j′ = 0–5 at a temperature of 20 K and 150 K. The rate coefficients for transitions that conserve the inversion symmetry are almost identical in the two vibrational states (this includes the elastic rate coefficients, with magnitudes of order 10−9 cm3 s−1). For the other cases discussed above the discrepancy is usually smaller than a factor of 3, but it can reach an order of magnitude at low temperature for weak transitions. The discrepancy is smaller at higher temperature since the difference in rotational structure in the two vibrational states becomes less and less important as the kinetic energy increases.
3.2 Vibrational relaxation cross sections
We now turn to vibrationally-inelastic transitions, i.e. transitions ν2 = 1 → 0. An important question concerns the magnitude of the corresponding cross sections (or rate coefficients), compared to vibrationally-elastic transitions. Vibrational relaxation cross sections are expected to be much smaller than rotational relaxation cross sections, given the large difference between the vibrational transition energy (∼950 cm−1) and the depth of the NH3–He PES (∼35 cm−1), but the extent remains to be quantified.In Fig. 5 we show the cross sections for the 21− → 22− and 21− → 22+ transitions for these two cases. The vibrational relaxation cross sections are seen to be on the order of 105 times smaller than the vibrationally-elastic transitions, making vibrational energy transfer seemingly very inefficient for NH3–He collisions. The same propensity to conserve the symmetry of the umbrella state is observed as for vibrationally-elastic cross sections. The resonance structures discussed above are also seen for the vibrational relaxation cross sections, although the magnitude of the resonances is smaller.
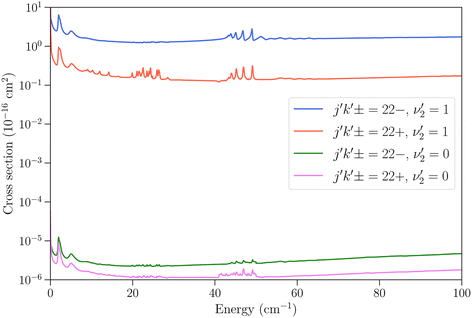 | ||
Fig. 5 Cross sections as function of kinetic energy for the transitions with initial state jk± = 21− in ν2 = 1 and final states 22− and 22+ with  (vibrationally-elastic) and (vibrationally-elastic) and  (vibrationally-inelastic). (vibrationally-inelastic). | ||
In Fig. 6 we examine the vibrational relaxation cross sections in more detail for the initial state 11− in ν2 = 1 and all final states j = 1–3 in ν2 = 0 for para-NH3. For all final states we observe again a larger cross section for transitions that conserve the inversion symmetry. The cross sections increase strongly with kinetic energy, as was also observed for CH3–He collisions,23 although for NH3–He collisions the growth observed here is not linear.
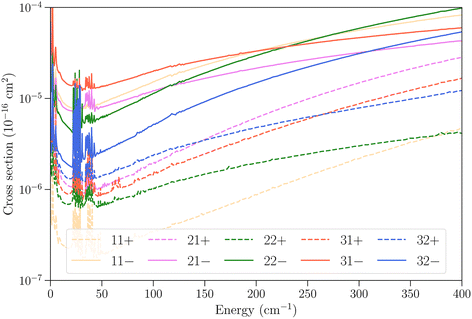 | ||
Fig. 6 Cross sections as function of kinetic energy for the vibrational relaxation transitions with initial state jk± = 11− in ν2 = 1 and various final states in  . . | ||
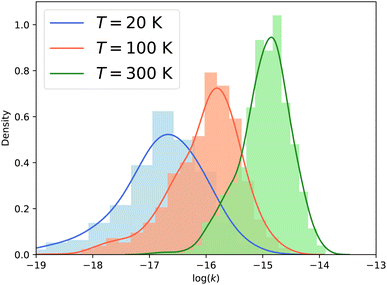
Fig. 7 presents the distribution of the vibrational relaxation rate coefficients for all initial states with j ≤ 3 in ν2 = 1 and all final states j′ ≤ 10 in ν2 = 0. At low temperature (20 K), the vibrational relaxation rate coefficients are on the order of 10−18 to 10−16 cm3 s−1, while the rotation–inversion rate coefficients are typically on the order of 10−12 to 10−11 cm3 s−1. However, the rate coefficients increase quickly with increasing temperature as a result of the growth of the cross sections discussed above. At 300 K the vibrational relaxation rate coefficients are on the order of 10−16 to 10−14 cm3 s−1, corresponding to an increase of two orders of magnitude compared to the values at a temperature of 20 K. It would be interesting to investigate the behaviour of the rate coefficients at higher temperatures, especially for astrochemical applications. Given the magnitude of the rate coefficients, and the large number of rotational states in the ground vibrational level that are open, vibrational relaxation could be efficient in warm astrophysical environments, although the state-to-state rate coefficients are several orders of magnitude smaller than the vibrationally-elastic ones. This will require the use of different scattering methodology, such as that presented in ref. 26, since the fully quantum-mechanical CC calculations performed here become intractable at the higher energies required to obtain converged rate coefficients above 300 K.
Finally, we present in Fig. 8 the total vibrational relaxation rate coefficients for all initial rotation–inversion states with j = 0–2 summed over all final states. The total rate coefficients vary from 10−15 cm3 s−1 at T = 20 K and increase up to 10−13 cm3 s−1 at T = 300 K for initial rotation–inversion states in para-NH3, corresponding to the increase with temperature discussed earlier at the state-to-state level. For a given initial rotational level, the total vibrational relaxation rate coefficients are slightly larger for symmetric inversion levels than for antisymmetric ones. The rate coefficients for levels 21+ and 22+ or 21− and 22− are virtually identical, but larger than those for 11+ and 11− respectively. Moreover, they are larger for para-NH3 than for ortho-NH3 by a factor of about 2. This difference originates from the difference in the number of final rotation–inversion states available in ν2 = 0 for vibrational relaxation, which is roughly twice as large for para-NH3 than for ortho-NH3.
4 Conclusions and outlook
In the present paper we have presented a study of vibration–rotation–inversion transitions in NH3 induced by collisions with He atoms by considering the umbrella inversion vibrational mode of ammonia. We obtained cross sections for collision energies up to 1500 cm−1, and rate coefficients for temperatures up to 300 K. The calculations relied on an accurate four-dimensional PES used in quantum-mechanical scattering calculations. Important differences were found with reference data for the inelastic rate coefficients in the ground vibrational state, which were attributed to the use of a more recent PES. There are also large differences between pure rotation–inversion cross sections within the ground vibrational state or the first vibrational excited state. These follow from the difference in the inversion splitting in the ground and excited umbrella vibrational levels. For transitions that conserve the inversion symmetry, rotation–inversion cross sections are virtually identical in the two vibrational levels.The vibrational relaxation cross sections are about five orders of magnitude smaller than the vibrationally-elastic cross sections at low energy, and the same observation is made for the rate coefficients at low temperature (below 50 K). However, vibrational relaxation cross sections display a strong increase as function of collision energy. The rate coefficients for vibrationally-inelastic transitions are therefore much larger at high temperature, with a typical increase of more than two orders of magnitude between 20 K and 300 K, while the vibrationally-elastic rate coefficients increase much less rapidly. It thus appears that vibrational relaxation of NH3 by He atoms can be quite efficient at high temperature, given the large number of rotation–inversion states that are populated through inelastic collisions.
The results presented here are however limited in several respects. First, we only considered initial rotational levels of NH3 with j < 5. In order to use these rate coefficients in a non-LTE radiative transfer model, many more initial states would need to be considered. Secondly, the temperature was limited to 300 K, which is unlikely to be high enough for applications to warm astrophysical environments. This limitation is due to a combination of factors. First, the PES used here needs to be completed by adding points in the short range to be used for high energy collisions (above 3000 cm−1 of total energy). Second, at high energy there are too many open rotational levels, so that the rotational basis used in the close-coupling expansion becomes too large for the current available computational resources. A promising approach to generate data sets of rate coefficients for astrophysical applications would be to employ approximate methods such as those presented in ref. 26, which allow a drastic reduction of the computational requirements. On the other hand, highly accurate quantum-mechanical calculations such as presented here are still purposeful to benchmark approximate methods. Vibrational relaxation from the second excited state of the umbrella mode could also be treated by the same methods. Since the second excited state is above the inversion barrier, the state-to-state rate coefficients can be expected to be completely different from those in the first two vibrational states.
Finally, the vibrational relaxation by collisions with H2 molecules should also be investigated. It is expected to be more favorable than for He since relaxation can then also occur to excited rotational states of H2, which has been shown to be much more efficient than for H2 (j = 0) in the case of H2O.29,30
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Milena Rohrs and Gerrit Groenenboom for useful discussions. J. L. acknowledges support from KU Leuven through grant no. C14/22/082. The calculations presented in this work were performed on the VSC clusters (Flemish Supercomputer Center), funded by the Research Foundation Flanders (FWO) and the Flemish Government.Notes and references
- S. Green, J. Chem. Phys., 1976, 64, 3463 CrossRef CAS.
- L. Machin and E. Roueff, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 1519 CrossRef CAS.
- B. Yang and P. C. Stancil, Eur. Phys. J. D, 2008, 47, 351 CrossRef CAS.
- G. Danby, D. R. Flower, P. Valiron, E. Kochanski, L. Kurdi and G. H. F. Diercksen, J. Phys. B: At. Mol. Phys., 1987, 20, 1039 CrossRef CAS.
- S. Maret, A. Faure, E. Scifoni and L. Wiesenfeld, Mon. Not. R. Astron. Soc., 2009, 399, 425 CrossRef CAS.
- S. Demes, F. Lique, J. Loreau and A. Faure, Mon. Not. R. Astron. Soc., 2023, 524, 2368–2378 CrossRef CAS.
- J. Loreau, A. Faure, F. Lique, S. Demes and P. J. Dagdigian, Mon. Not. R. Astron. Soc., 2023, 526, 3213 CrossRef CAS.
- J. Schleipen and J. ter Meulen, Chem. Phys., 1991, 156, 479 CrossRef CAS.
- F. Pirani, L. Roncaratti, L. Belpassi, F. Tarantelli and D. Cappelletti, J. Chem. Phys., 2011, 135, 194301 CrossRef PubMed.
- O. Tkac, A. K. Saha, J. Onvlee, C.-H. Yang, G. Sarma, C. K. Bishwakarma, S. Y. T. van de Meerakker, A. van der Avoird, D. H. Parker and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2014, 16, 477–488 RSC.
- O. Tkac, A. K. Saha, J. Loreau, Q. Ma, P. J. Dagdigian, D. H. Parker, A. van der Avoird and A. J. Orr-Ewing, Mol. Phys., 2015, 113, 3925 CrossRef CAS.
- Q. Ma, A. van der Avoird, J. Loreau, M. Alexander, S. Y. T. van de Meerakker and P. J. Dagdigian, J. Chem. Phys., 2015, 143, 044312 CrossRef PubMed.
- Z. Gao, J. Loreau, A. van der Avoird and S. Y. T. van de Meerakker, Phys. Chem. Chem. Phys., 2019, 21, 14033 RSC.
- O. Schullian, J. Loreau, N. Vaeck, A. van der Avoird, B. R. Heazlewood, C. J. Rennick and T. P. Softley, Mol. Phys., 2015, 113, 3972 CrossRef CAS.
- M. J. Doppelbauer, O. Schullian, J. Loreau, N. Vaeck, A. van der Avoird, C. J. Rennick, T. P. Softley and B. R. Heazlewood, J. Chem. Phys., 2017, 146, 044302 CrossRef PubMed.
- J. D. Monnier, W. C. Danchi, D. S. Hale, P. G. Tuthill and C. H. Townes, Astrophys. J., 2000, 543, 868–879 CrossRef CAS.
- K. T. Wong, K. M. Menten, T. Kamiński, F. Wyrowski, J. H. Lacy and T. K. Greathouse, Astron. Astrophys., 2018, 612, A48 CrossRef.
- C. Knez, J. H. Lacy, N. J. Evans, E. F. van Dishoeck and M. J. Richter, Astrophys. J., 2009, 696, 471 CrossRef CAS.
- J. C. Barentine and J. H. Lacy, Astrophys. J., 2012, 757, 111 CrossRef.
- J. R. Najita, J. S. Carr, S. D. Brittain, J. H. Lacy, M. J. Richter and G. W. Doppmann, Astrophys. J., 2021, 908, 171 CrossRef CAS.
- J. H. Lacy, Astrophys. J., 2013, 765, 130 CrossRef.
- T. Selim, A. van der Avoird and G. C. Groenenboom, J. Chem. Phys., 2022, 157, 064105 CrossRef CAS PubMed.
- Q. Ma, P. J. Dagdigian and M. H. Alexander, J. Chem. Phys., 2013, 138, 104317 CrossRef PubMed.
- T. Stoecklin, O. Denis-Alpizar, P. Halvick and M.-L. Dubernet, J. Chem. Phys., 2013, 139, 124317 CrossRef PubMed.
- T. Stoecklin, O. Denis-Alpizar and P. Halvick, Mon. Not. R. Astron. Soc., 2015, 449, 3420–3425 CrossRef CAS.
- T. Selim, A. van der Avoird and G. C. Groenenboom, J. Chem. Phys., 2023, 159, 164310 CrossRef CAS PubMed.
- D. Rabli and D. R. Flower, Mon. Not. R. Astron. Soc., 2011, 411, 2093–2098 CrossRef CAS.
- T. Stoecklin, O. Denis-Alpizar, A. Clergerie, P. Halvick, A. Faure and Y. Scribano, J. Phys. Chem. A, 2019, 123, 5704–5712 CrossRef CAS PubMed.
- L. Wiesenfeld, J. Chem. Phys., 2021, 155, 071104 CrossRef CAS PubMed.
- R.-M. Garcia-Vazquez, A. Faure and T. Stoecklin, ChemPhysChem, 2024, 25, e202300698 CrossRef CAS PubMed.
- J. Loreau and A. van der Avoird, J. Chem. Phys., 2015, 143, 184303 CrossRef CAS PubMed.
- K. B. Gubbels, S. Y. T. van de Meerakker, G. C. Groenenboom, G. Meijer and A. van der Avoird, J. Chem. Phys., 2012, 136, 074301 CrossRef PubMed.
- Y. Belkhodja, J. Loreau, A. van der Avoird, Y. Berger and P. Asselin, Phys. Chem. Chem. Phys., 2021, 23, 10864 RSC.
- M. P. Hodges and R. J. Wheatley, J. Chem. Phys., 2001, 114, 8836 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |