Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reaction dynamics of S(3P) with 1,3-butadiene and isoprene: crossed-beam scattering, low-temperature flow experiments, and high-level electronic structure calculations†
Jinxin
Lang
a,
Casey D.
Foley
a,
Shameemah
Thawoos
a,
Abbas
Behzadfar
a,
Yanan
Liu
a,
Judit
Zádor
 *b and
Arthur G.
Suits
*b and
Arthur G.
Suits
 *a
*a
aDepartment of Chemistry, University of Missouri, Columbia, MO 65211, USA. E-mail: suitsa@missouri.edu
bCombustion Research Facility, Sandia National Laboratories, Livermore, California 94551, USA. E-mail: jzador@sandia.gov
First published on 7th February 2024
Abstract
Sulfur atoms serve as key players in diverse chemical processes, from astrochemistry at very low temperature to combustion at high temperature. Building upon our prior findings, showing cyclization to thiophenes following the reaction of ground-state sulfur atoms with dienes, we here extend this investigation to include many additional reaction products, guided by detailed theoretical predictions. The outcomes highlight the complex formation of products during intersystem crossing (ISC) to the singlet surfaces. Here, we employed crossed-beam velocity map imaging and high-level ab initio methods to explore the reaction of S(3P) with 1,3-butadiene and isoprene under single-collision conditions and in low-temperature flows. For the butadiene reaction, our experimental results show the formation of thiophene via H2 loss, a 2H-thiophenyl radical through H loss, and thioketene through ethene loss at a slightly higher collision energy compared to previous observations. Complementary Chirped-Pulse Fourier-Transform mmWave spectroscopy (CP-FTmmW) measurements in a uniform flow confirmed the formation of thioketene in the reaction at 20 K. For the isoprene reaction, we observed analogous products along with the 2H-thiophenyl radical arising from methyl loss and C3H4S (loss of ethene or H2 + acetylene). CP-FTmmW detected the formation of thioformaldehyde via loss of 1,3-butadiene, again in the 20 K flow. Coupled-cluster calculations on the pathways found by the automated kinetic workflow code KinBot support these findings and indicate ISC to the singlet surface, leading to the generation of various long-lived intermediates, including 5-membered heterocycles.
Introduction
Scattering studies of the reaction dynamics of small molecules provide important insights that have shaped our understanding of chemical behavior over many decades.1–4 Current studies of simple systems in new domains at low temperature5–8 and involving excited states9–12 remain an important ongoing frontier of exploration. For such systems, quantum-state-specific state preparation and detection afford deep insight into molecular interactions. Analogous studies involving more complex molecules rarely, if ever, feature state-to-state measurements.13,14 Instead, they bring new challenges in product detection, while at the same time delivering new rewards: recent advances from such studies include evidence of roaming dynamics in bimolecular interactions,15 deep insight into mechanisms of PAH formation,16 unexpected intersystem crossing (ISC),17–19 and cyclization to aromatics under single-collision conditions.20 Much has been achieved using the venerable crossed-molecular-beam technique with a rotatable mass spectrometer detector. Recently, imaging methods have come to play an important role, and as we will show here, broadband rotational spectroscopy21–24 adds a new dimension of product detection that is complementary to these more established methods. Another key aspect for interpretation of such studies is the tremendous advances in theoretical and computational kinetics methods for treating complex systems.25–27 Pertinent to this work, advances made in automated theoretical calculations are fundamental, especially the ones that can propose, locate, and characterize reaction pathways.28–33 Put together with the large computing power available to researchers, workflow codes can capture chemical complexity for mid-size molecules in unprecedented detail and in much shorter time than ever before.34 This puts the theory–experiment duality in many areas of elementary reaction research on a more equal footing. For example, theorists, equipped with the right tools, are much more likely to propose important but unobserved reaction products, inspiring further experimental work. In the following pages, we illustrate these notions with studies of the reaction of a ground-state sulfur atom with 1,3-butadiene and isoprene, building on our recent study.35Sulfur-atom reactions are of considerable current interest, with SO2 injection into the stratosphere being considered to reduce Earth’s albedo,36 while at the same it has recently been shown that UV photodissociation of SO2 gives S(3P) + O2 as a direct product channel.37 The consequences of this are obvious topics of concern. There is keen interest in sulfur reactions for astrochemistry as well: organic sulfur compounds including thiophenes have recently been detected on Mars,38 and it is now believed that sulfur chemistry contributes to haze formation in CO2-rich exoplanet atmospheres, which can interfere with observations.39 The fundamental dynamics of sulfur-atom reactions are thus of significant interest.
Oxygen-atom reactions with complex polyatomic co-reactants have exemplified the capabilities of the traditional crossed-beam method, in work beginning with that of Roger Grice40 and Y. T. Lee,41 and culminating in extensive studies from Casavecchia and coworkers.42,43 Imaging studies from our group have been applied to larger target molecules as well.44,45 In contrast, the detailed dynamics of sulfur-atom reactions have gained far less scrutiny, with one obvious reason being the importance of oxygen-atom reactions in combustion. Crossed-beam studies of sulfur-atom reactions have largely focused on S(1D), with particular interest directed to its reaction with molecular hydrogen and its isotopologues.46–51 This system serves as an illustration of insertion dynamics analogous to that of O(1D): in both cases, the insertion and exit to products are barrierless, and although both involve deep wells, for oxygen the reaction exoergicity is 28% of the well depth, while for sulfur it is only 7%.52 This clearly signals the importance of a long-lived intermediate in the latter case, and this is borne out by the forward–backward symmetric angular distributions seen in experiment and widely confirmed by theory.46 Furthermore, spin–orbit interaction is thrice larger for the heavier sulfur atom, and nonadiabatic effects induced thereby have been invoked to account for nonstatistical branching between SD and SH products in the S(1D) + HD reaction.50 The importance of this substantial spin–orbit interaction will also come into play in the work presented here. Crossed-beam and low-temperature kinetics of S(1D) reaction with methane,53 ethylene54 and other hydrocarbons have also recently appeared, with dynamics governed by insertion, just as for H2.
However, until our recent report,35 which we expand upon here, there had been no crossed-beam studies of ground-state sulfur atom reactions. Reactions of both S(1D) and S(3P) with a wide range of target species were studied over many years by Gunning and Strausz in a cell environment, first with mass spectrometric examination of the end products following distillation,55 and subsequently augmented with gas chromatography.56 They showed that S(1D) reaction with olefins chiefly proceeds by insertion, giving thiols, while S(3P) and possibly S(1D) give thiiranes.57 In reaction with 1,3-butadiene (13BD), they showed that S(3P) gives thiophene + H2 and an addition product, vinyl thiacyclopropane (VTCP), with the yield of the former channel determined to be 9% under their conditions.56 However, these high-pressure conditions and end-product analysis cannot ensure primary reaction pathways are being examined.
As noted above, we recently reported direct formation of thiophene and the resonantly stabilized 2H-thiophen-5-yl (2HT) radical under single-collision conditions from the crossed-beam reaction of S(3P) with 13BD at a collision energy of 13.6 kcal mol−1. The experimental results were interpreted with the aid of high-level automated electronic structure explorations of the triplet and singlet potential energy surfaces (PESs) by KinBot29,58 along with statistical calculations. Theory suggests the reaction proceeds by ISC to the singlet surface, giving the following pathways and branching:
 | (1) |
The velocity map imaging59 experiments, as in the present work, employed ionization by a fluorine excimer laser at 157 nm, which can sensitively detect products with ionization energies below the 7.9 eV photon energy (generally C3 or larger radicals or metal-containing species).45 This, along with the fact that the scattered 2HT product was confined by momentum conservation to velocities very near the center of mass, gave us the ability to detect channel (3) despite the minor branching. Thiophene (1) was detected weakly using a focused laser, likely by 1 + 1 ionization, and the translational energy distribution showed evidence of the substantial exit barrier predicted by theory.
We also reported preliminary results for the related reaction S(3P) + isoprene (2-methyl-1,3-butadiene). In that case, we detected radical products at mass 99 u (H loss) and 85 u (methyl loss). We identified the former as 2H-3-methyl-thiophen-5yl (2H3MT) or 2H-4-methyl-thiophen-5yl (2H5MT) radicals (or both), while the 85 u product was identified as the same 2HT radical produced in the 13BD reaction.
In the present report, we delve more deeply into these reactions, exploring the range of products in both systems now using a combination of crossed-beam reactions at relatively high collision energies with measurements in a Laval flow60 thermalized at 20 K using Chirped-Pulse Fourier-Transform mmWave spectroscopy (CP-FTmmW).21 This latter approach, which we term CPUF for Chirped-Pulse/Uniform Flow,24,61,62 provides complementary detection for several product channels and confirms, certainly for those, that the reactions have little or no barrier. For the S(3P) + 13BD reactions, we employ beams seeded entirely in H2, giving a slightly higher collision energy and ensuring the complete absence of S(1D). Here, we also employ a forward convolution analysis that includes the beam velocity spreads, which permits a more accurate determination of the translational energy release for the slowly recoiling fragments. We also provide a much deeper look into the complex S(3P) + isoprene potential energy surfaces, focusing on the singlet surface.
Experimental
Crossed-beam
The gas-phase reaction of atomic sulfur (3P) with 1,3-butadiene (13BD) and isoprene (2-methyl-1,3-butadiene, Sigma-Aldrich, 99%) was carried out under single-collision conditions in a crossed-molecular-beam apparatus, as described previously.63 A supersonic beam of sulfur atoms was generated by the 193 nm photodissociation (GAM ArF excimer laser, 30 mJ per pulse) of CS2 (Sigma-Aldrich, 99%) seeded at 12% in a mix of 12% H2/helium for the isoprene reaction, and in pure H2 for the 13BD reaction. H2 is used to quench the S(1D) via the fast reaction, giving SH + H.64 Given the largely temperature-independent rates reported and our high density, we estimate the first order decay rate for S(1D) under our conditions to be >105 μs−1.The 193 nm beam was focused by a cylindrical lens onto a 10 mm long, 1 mm inner diameter quartz capillary directly extended from the pulsed valve. The sulfur beam is crossed perpendicularly with the hydrocarbon supersonic beam seeded in helium with a backing pressure of 4 bar. The two supersonic beams were released by piezoelectric stack actuator pulsed valves operating at a repletion rate of 10 Hz and a pulse width of 35 μs. The reactively scattered products were ionized by a loosely focused F2 excimer laser at 157 nm (GAM, ∼1 mJ per pulse, 7.9 eV). Ions were subsequently accelerated by a dc slice ion optics assembly65 and projected onto a dual microchannel plate (MCP) detector coupled with a phosphor screen. The back MCP was gated to only select the center slice of the scattered product ions with specific m/z. Images were recorded using a CCD camera and collected with our own NuAcq software.
The images were analyzed using the forward convolution approach, as described previously,12 although here we include modeling of the beam velocity spreads as well. In this case, we project the signal along one axis, much like a Doppler profile, and compare it to a simulation using a trial velocity distribution. This approach has the advantage that the background signal is distributed uniformly in velocity space rather than growing linearly with velocity, as in a direct inversion of the image. In the implementation of this approach, we used sections of the images in some cases and symmetrized the profiles to avoid a beam background and increase the signal-to-noise.
Chirped-pulse Fourier-transform mmWave spectroscopy in a uniform flow (CPUF)
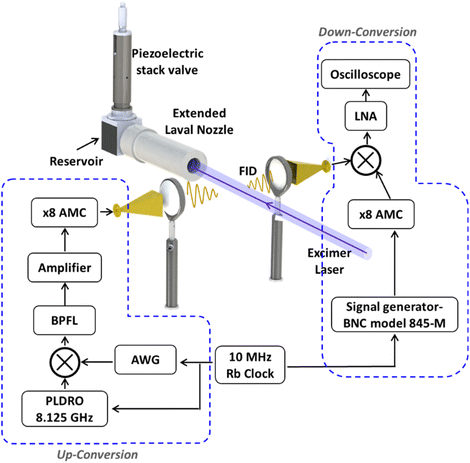
Determination of the products of the reactions of S(3P) with 1,3-butadiene (13BD) and 2-methyl-1,3-butadiene (isoprene) via rotational spectroscopy was performed using the CPUF experimental setup (Fig. 1). A detailed account of the apparatus has been presented elsewhere; in our current approach the reaction is performed using an extended Laval nozzle.62 The extended Laval nozzle creates a uniform flow within the nozzle, which is then followed by a shock-free secondary expansion. The secondary expansion gives a low-density, cold underexpanded jet, which is ideal for CP-FTmmW detection. The experimental setup utilizes a pulsed Laval flow generated using a home-built high-throughput piezoelectric stack valve.66 The valve operates to fill a reservoir with a capacity of approximately 20 cm3 up to a pressure of 360 torr at a 1 Hz repetition rate and stays open for 3.5 ms. S(3P) was produced by photolyzing CS2 with a 193 nm excimer laser, as in the crossed-beam reaction described above. The excimer laser is aligned along the axis of the flow and has a fluence of approximately 50 mJ cm−2. The reactants, 13BD (≥99%), isoprene (99%) and CS2 (≥99.9%), were purchased from Sigma-Aldrich. Reagent-grade CO2 (used to quench and react with any S(1D)) and helium were purchased from Airgas. All chemicals are used without further purification. The reactants were introduced into the flow using a combination of flow controllers.Premixes of ∼16% 13BD in helium and ∼5% CS2 in helium were prepared in separate mixing bottles. The premixes were further diluted, and a mix of ∼0.05% 13BD and ∼0.70% CS2 with less than 1% CO2 was introduced into the flow using flow controllers (Alicat MCS-type). Similarly, for the reaction with isoprene, a controlled amount of ∼0.20% isoprene and ∼1.50% CS2 was introduced into the flow by passing a high-pressure (∼120 psi) flow of helium gas through two separate reservoirs containing the respective chemicals. The reservoir containing CS2 was maintained at room temperature, whereas the reservoir containing isoprene was kept in an ice bath. The outputs from these reservoirs were further diluted and mixed with ∼1% CO2 before introducing into the flow.
Various configurations of the mmWave spectrometer have been employed and described elsewhere and a brief overview of the present setup used is provided here. An 8.125 GHz phase-locked dielectric resonator oscillator (PLDRO, Narda-MITEQ) was utilized as the up-conversion local oscillator (LO). The signals from an arbitrary waveform generator (AWG7082C, Tektronix) were then mixed with the LO using a double balanced mixer (Marki M10418LC). The frequency sum output of the mixer was then filtered through a bandpass filter and then sent through a low noise amplifying (LNA) stage and subsequently to an active multiplier chain (AMC, QuinStar Technology, QMM-751020080) where the frequency was multiplied by a factor of 8. The output of the AMC was broadcasted into the pulsed Laval flow in bursts of 1 μs frequency chirps at 5 μs intervals for a total of 250 μs. The free induction decay (FID) of the polarized sample is collected through a receiving horn and down-converted, amplified, and fed into an oscilloscope for time-domain averaging.
Computational methods
We used our gas-phase kinetics workflow code, KinBot28,29,58 to explore the triplet and singlet PESs for the S + 13BD and S + isoprene systems systematically. The details of the S + 13BD calculations can be found in our previous work, where we explored this reaction at the CCSD(T)-F12a/cc-pVTZ-F12//ωB97X-D/6-311++G(d,p) level of theory. KinBot drives all electronic structure calculations automatically for tasks including the exploration of the reaction pathways and conformational searches, with the possibility to control many other parameters of the search and electronic structure calculations. KinBot invokes generalized reaction templates, which generate many saddle-point guesses that are then refined and verified using intrinsic reaction coordinate calculations (IRCs) before including them in the reaction network.The pathway exploration and conformational search was carried out for both surfaces at the L1 = B3LYP/6-31+G* level. Rovibrational properties were refined at the L2 = ωB97X-D/6-311++G** level, and electronic energies at the L3 = CCSD(T)-F12a/cc-pVDZ-F12 level. On the triplet surface, there are four distinct initial adducts, as S(3P) can add to any one of the sp2 carbon atoms. Since these adducts are not necessarily connected via saddle points in the energy range of interest, we started the exploration on the triplet PES in more than one well until all of them were included. On the singlet PES, we started the search in 2-methyl-2-vinylthiirane, the singlet species that arises from one of the terminal S-atom adducts on the triplet PES upon ISC. Because of the challenges such complex PESs pose, we improved our search algorithm. Instead of simply using the L1 barrier heights to decide whether to include a channel or not, we set two thresholds. The first threshold was set at L1, and the second at L2. All saddles below the L1 threshold were reoptimized at L2, but we only considered species below the L2 threshold in the reaction network. Hence, we eliminated the significant uncertainty of our L1 theory in this case. This is important, because the barrier height ladder is very dense (i.e., there are hundreds of saddle points within 10–20 kcal mol−1 of each other), and errors at the L1 level can lead to somewhat arbitrary inclusion or exclusion of channels. Our L2 threshold was set to 63 kcal mol−1 above the starting species, and the L1 threshold was set to be 5 kcal mol−1 higher. Moreover, we allowed an additional 10 kcal mol−1 to include barrierless reactions at the L1 level, because barrierless reactions typically have a significant entropic advantage compared to reactions with a barrier.
The L1 and L2 energies and optimizations were carried out using the Gaussian 16 suite,67 while the L3 calculations were carried out using Molpro 2022.68 The PESs were visualized using our PESViewer code.69
Results and discussion
S(3P) + 1,3-butadiene
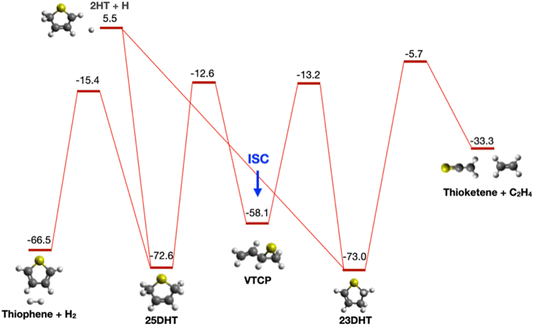
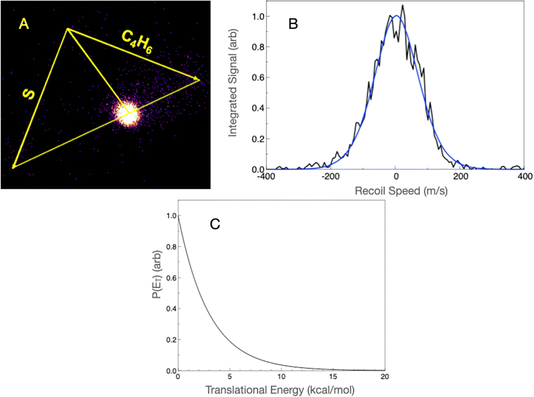
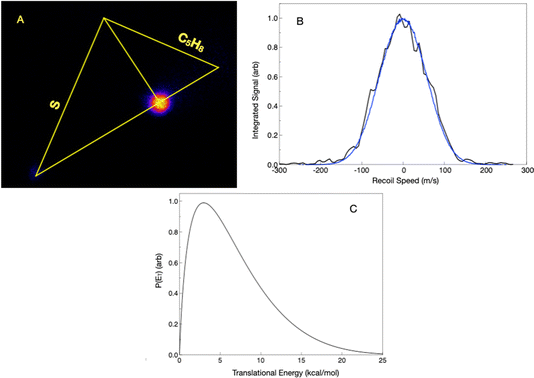
We first present the S(3P) + 13BD reaction, which we previously examined in some detail, now including results from low-temperature measurements in a uniform flow. Theoretical investigation found that the only path to products on the triplet surface led to the H-loss radical 2HT, with a bottleneck saddle point 9.3 kcal mol−1 above the entrance, contrasting with a barrierless path to a triplet terminal adduct at −16.1 kcal mol−1. We concluded that formation of bimolecular products on the triplet surface was unlikely and ascribed the detected products to efficient ISC from the terminal adduct. Fig. 2 shows the key stationary points on the singlet potential energy surface identified in the previous study. ISC from the triplet terminal adduct brings the system to the VTCP minimum, as shown. From there, the system can isomerize to deep minima corresponding to 2,5- or 2,3-dihydrothiophene (25DHT and 23DHT, respectively) over barriers about 13 kcal mol−1 below the entrance channel. Hydrogen-atom loss from either adduct can form the detected 2HT radical 5.5 kcal mol−1 above the reactant energy. 25DHT can eliminate H2 to form thiophene over a barrier of 57.2 kcal mol−1 (15.4 kcal mol−1 below the entrance channel). The exit barrier in that case is 51.1 kcal mol−1. In addition to forming the 2HT radical via H loss, 23DHT can rearrange to 34 DHT (not shown), ultimately eliminating ethene to form thioketene over a barrier of 5.7 kcal mol−1 below the entrance channel. The exit barrier in this case is 27.6 kcal mol−1. Theory suggested branching strongly favoring the formation of thiophene + H2 (80.5%) over thioketene + ethene (19.3%) and 2HT + H (0.2%).Here, we re-examine the S(3P) + 13BD reaction at a slightly higher collision energy, 13.1 kcal mol−1, than in the previous study and under improved conditions. The calculated ionization energy of the 2HT radical is 6.3 eV, well below the 7.9 eV photon energy. We readily detected a product at mass 85 u using an unfocused laser and attributed it to the 2HT radical. In the present work, we use a forward convolution analysis approach that includes the beam velocity spreads, as discussed in the Experimental section. The scattering image, projected velocity distribution, and associated translational energy distribution are shown in Fig. 3. The latter, peaking near zero, is consistent with the barrierless dissociation to radicals, as is the maximum translational energy of ∼15 kcal mol−1. The average translational energy release is 3.0 kcal mol−1. We believe our sensitivity to this minor channel arises from the sensitive single-photon ionization detection, combined with the fact that the heavy product is confined to a very small velocity region around the center of mass.
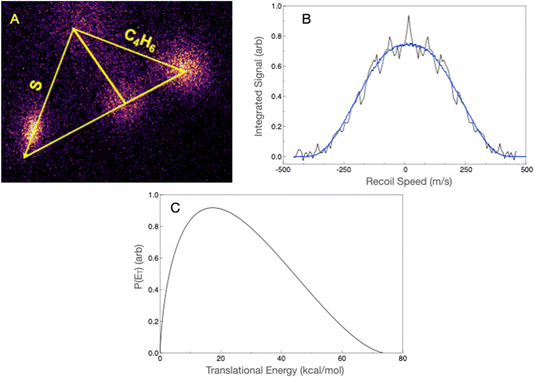
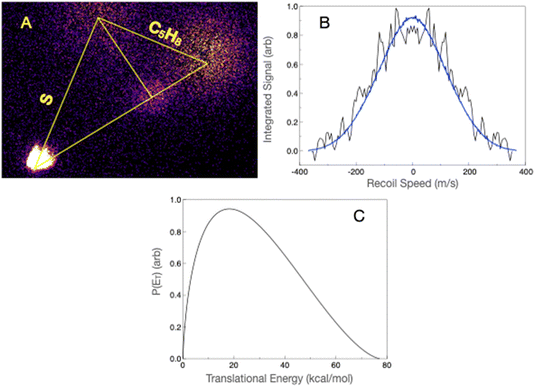
Although the dominant thiophene product has an ionization energy above the 7.9 eV probe photon energy, we were able to detect it by focusing the probe laser, as we have shown for other systems in the past.70,71 The scattering image at mass 84 u is shown in Fig. 4A. Although there is considerable interference from the ionization of the reactant molecules giving a substantial background, we were able to isolate the scattering signal and obtain the translational energy distribution using the forward convolution strategy. This is shown in Fig. 4B, along with the result of the forward convolution. The latter then yields the translational energy distribution shown in Fig. 4C. The translational energy distribution shows a peak at ∼20 kcal mol−1 and extends to 75 kcal mol−1, consistent with the theoretically predicted exit barrier and exoergicity. The average translational energy release is 26.9 kcal mol−1, which is 38% of the available energy.
Although we could weakly detect the reactive scattering leading to the predicted thioketene product suggested by theory at mass 58 u, the signal-to-noise was inadequate for obtaining translational energy distributions. However, we could detect this product from the S(3P) + 13BD reaction in the 20 K flow of the CPUF apparatus. Under these conditions, the products are rotationally (and, to a more limited extent, vibrationally) cooled in the flow for detection by rotational spectroscopy. We searched here only for the closed-shell products, as we have no data on the rotational spectra of the radicals, and the branching to open-shell products is likely too low to detect. The thioketene product was readily detected on the 70,7–60,6 transition at 78.424 GHz, as shown in Fig. 5.72 The photolysis is initiated by firing the excimer laser 13 μs after the first chirp. The delay from laser initiation to detection represents the time it takes for products to propagate from the nozzle to the detection region. This result shows that thioketene is formed in the reaction at 20 K, consistent with the potential surface shown in Fig. 2, which shows no barrier above the reactant energy en route to products. We then searched unsuccessfully for thiophene, which is predicted to dominate branching at zero collision energy by 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Simply on the basis of linestrength and the 20 K rotational partition function, we would expect the thiophene signal to be nearly 50 times larger than that of thioketene. However, given the large exoergicity and the much hotter expected internal energy distribution for thiophene vs. thioketene, we believe the non-detection of thiophene in the low-temperature experiment is due to the large difference in the vibrational partition function.
1. Simply on the basis of linestrength and the 20 K rotational partition function, we would expect the thiophene signal to be nearly 50 times larger than that of thioketene. However, given the large exoergicity and the much hotter expected internal energy distribution for thiophene vs. thioketene, we believe the non-detection of thiophene in the low-temperature experiment is due to the large difference in the vibrational partition function.
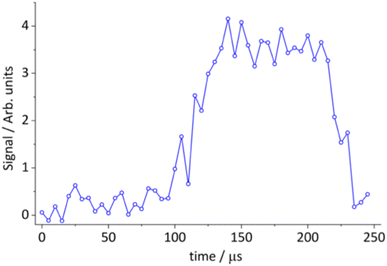 | ||
| Fig. 5 Time-dependent integrated line intensity of the thioketene 70,7–60,6 transition at 78.424 GHz, from the reaction of S(3P) + 1,3-BD → thioketene (C2H2S) + ethene (C2H4). | ||
S(3P) + isoprene
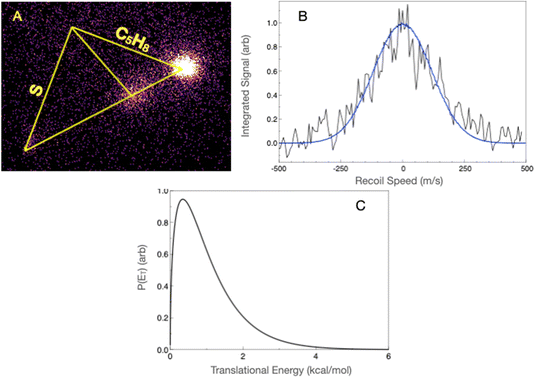
For the isoprene reaction, we also show complementary results obtained in crossed beams at high collision energy, along with results in the low-temperature flow with detection by rotational spectroscopy.In the crossed-beam experiment, we detect products at masses 99 (H loss), 98 (H2 loss), 85 (CH3 loss), and 72 (ethene loss). We have re-measured the radical products at masses 99 and 85 under somewhat improved conditions, but at a similar collision energy to before, now using the forward convolution analysis. Fig. 6A shows the H-loss image, along with the most probable Newton diagram superimposed, while Fig. 6B shows the projected distribution and fit, and Fig. 6C shows the translational energy distribution. The scattered product is highly localized at the center of mass velocity. The translational energy distribution peaks at ∼3 kcal mol−1 and extends to ∼20 kcal mol−1, with an average translational energy release of 6.6 kcal mol−1. The translational energy limit is somewhat higher than the calculated limit of the available energy, as discussed further below. Fig. 7A shows the methyl-loss image obtained at 85 u. For both H loss and methyl loss, the signals are very strong and obtained without focusing the probe laser, hence the excellent signal-to-noise. We obtained the methyl-loss translational energy distribution by direct inversion of the image, as in this case the signals are very strong and the beam velocity spreads make little contribution to the image. The translational energy distribution (Fig. 7B) peaks at zero and extends to ∼20 kcal mol−1, consistent with the available energy given the 4.3 kcal mol−1 calculated exoergicity. We note that in the previous paper we referred incorrectly to bottleneck saddlepoints as reaction exoergicities; these energies are summarized below and in greater detail in the interactive PES in the ESI.†
In the present investigation, we also detected mass 72 u without focusing the probe laser. The image is shown in Fig. 8A, with the translational energy distribution given in Fig. 8B. The latter shows a translational energy distribution peaking at zero and only extending to 3 kcal mol−1. There are several unusual aspects of this product. The mass suggests a closed-shell product, or at least an even number of electrons, but the facile ionization at 7.9 eV and the translational energy distribution that peaks at zero and extends only to 3 kcal mol−1would both suggest a radical product. We discuss the possible product assignment in the context of the PES below.
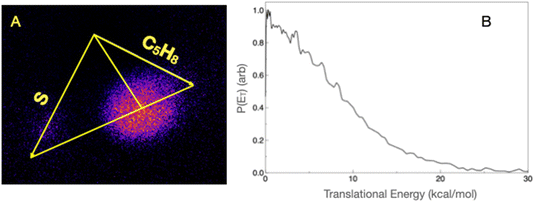
We now consider the closed-shell products detected with the focused probe laser. Loss of molecular hydrogen could lead to mass 98 u – methyl thiophene in analogy to the 13BD case above, as well as several other possibilities. Indeed, we detect this product in the crossed-beam reaction, as shown in Fig. 9A. Owing to the challenging background with the focused laser, we again use the forward convolution approach to simulate the 1-D projection of the image. The projection, fit, and resulting translational energy distribution are shown in Fig. 9B and C. The translational energy distribution is broad, peaking near 20 but extending to 70 kcal mol−1. The average translational energy release is 26.0 kcal mol−1, which is 34% of the available energy, assuming the product is methyl thiophene. This leaves 50 kcal mol−1 in the internal energy of the products, most of which is likely to be in the vibration in the methyl thiophene product, given the larger density of states.
We also searched for a range of possible products using the CPUF apparatus. In this case, we readily detected thioformaldehyde on the 21,1–11,0 transition at 69.747 GHz.72 The result, shown in Fig. 10, shows rapid reaction to thioformaldehyde, even at 20 K. We also searched unsuccessfully for thioketene and methyl thiophene. Non-detection of the latter species again may be attributed to the large vibrational energy in the product and the unfavorable vibrational partition function.
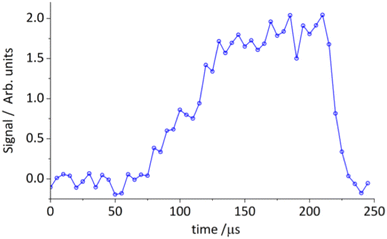 | ||
| Fig. 10 Time-dependent integrated line intensity of thioformaldehyde 21,1–11,0 at 69.747 GHz from the reaction of S(3P) + isoprene → thioformaldehyde (H2CS) + C4H6. | ||
S + isoprene PESs
In the previous paper, we only provided a few key aspects of the S(3P) + isoprene PESs, so the results of our deeper investigation are presented here. Addition of the S atom on the triplet PES to the central carbon atoms of isoprene can yield 2-thyil-isoprene or 3-thyil-isoprene. We found that the only potentially open channel under the experimental conditions is their interconversion; see Fig. S1.† The main reason for this simplicity is that these central adduct wells are very shallow (−1.1 and −2.1 kcal mol−1, respectively), just as when S adds to the central carbons of 13BD.In contrast, the terminal triplet adduct 1-thyil-isoprene is 16.8 kcal mol−1 below the reactants (cf. 16.1 kcal mol−1 for the S + 13BD adduct), opening the possibility for a larger number of reactions. Indeed, we explored a plethora of pathways with KinBot. However, in the case of 13BD, we found that ISC is the most likely fate for the initial terminal adduct, owing to its well depth, the strong spin–orbit coupling, and the relatively high and tight transition states leading out from this well. The presence of the methyl group is unlikely to alter the propensity for ISC, and because the exit channels from the initial adduct in this case also have relatively high barriers, as shown in Fig. S2,† we conclude that ISC is the dominant mechanism for further reactions for this terminal adduct as well. Finally, the potential well of the other terminal adduct, the 4-thyil-isoprene radical, is 14.9 kcal mol−1 deep. It has a low (0.8 kcal mol−1 relative to the reactants) barrier for an internal H-atom transfer via a six-member ring (see Fig. S3†), but the steps after that are energetically blocked. Here, we also assume that ISC dominates and happens largely in the region of the initial adduct.
While ISC is often modeled using a formalism borrowed from transition-state theory, it is important to keep in mind that minimum energy crossing points (MECPs) are not saddle points, and do not form dynamical bottle necks the same way saddles do.73 As a consequence, dynamical effects can be important and can alter the identity of the species appearing immediately after crossing.74 Nevertheless, in the case of 13BD, our short trajectory calculations have shown that such dynamical effects are negligible for our system, and by far the most likely initial species to emerge on the singlet PES is simply VTCP, a species with a three-membered ring incorporating the S atom. Again, we assume that the presence of the methyl group does not significantly change the nature of the crossing; hence, we simply consider two initial singlet species: 2-methyl-2-vinylthiirane and 2-(prop-1-en-2-yl)thiirane, which directly originate from the two terminal adducts. The two wells are within 1 kcal mol−1 of each other on the singlet surface.
Limiting the search on the triplet surface using the energy of the entrance yields relatively few viable reaction pathways. However, once the system crosses to the singlet surface, there is very significantly more energy available for chemical reactions: 2-methyl-2-vinylthiirane is 58.7 kcal mol−1 below the S(3P) + isoprene triplet entrance channel (cf. 58.1 kcal mol−1 for the analogous VTCP in the case of S(3P) + 13BD). Considering that the experiments are carried out in a largely collisionless environment, many reaction channels became potentially viable. As a consequence, KinBot identified 130 wells and 104 bimolecular products using the prescribed energy range. The complete PES can be viewed in the ESI† in an interactive format. Here, a simplified version of the PES is presented, akin to Fig. 2. We analyzed the graph that represents the wells, bimolecular products, and saddles on the singlet surface using a systematic graph-search algorithm, as implemented in our PESViewer package,69 to find the bottleneck barriers between 2-methyl-2-vinylthiirane and the bimolecular products. We searched the network up to a depth of 10 to find the pathways with the lowest overall barrier, and recorded that barrier height as the bottleneck.
Fig. 11 shows the low-energy pathways and their bottleneck energies, starting from 2-methyl-2-vinylthiirane. This is the slightly lower energy direct product upon ISC. Moreover, the same search from the other initial singlet species, 2-(prop-1-en-2-yl)thiirane, yields identical or higher bottleneck energies. The products are grouped by their masses for clarity. For reactions with barriers, only bottlenecks below the triplet entrance are shown. For barrierless reactions, we show channels up to 7.3 kcal mol−1. In the following we discuss the assignment of the possible detected products, generally in order of decreasing stability.
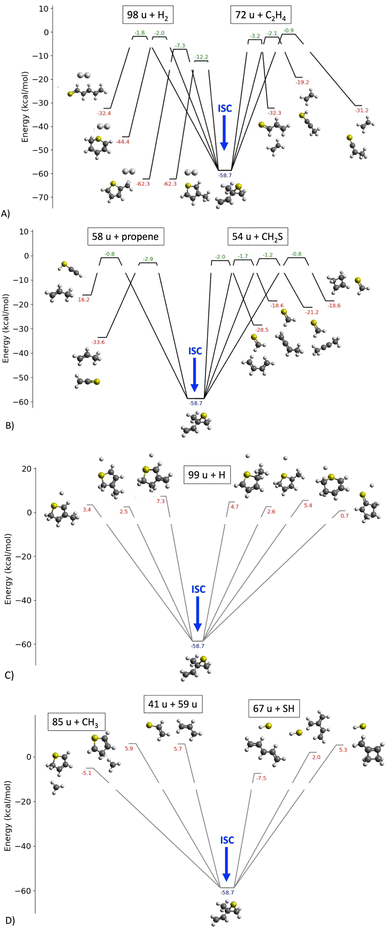 | ||
| Fig. 11 Low-energy pathways forming bimolecular products on the singlet surface reached in the S(3P) + isoprene reaction. The barriers shown are the bottlenecks (emphasized by the broken lines of the pathways); the reactions leading to the products consist typically of many elementary steps. The energies are shown relative to the triplet entrance. The full network of intermediates and saddles can be seen in the ESI† in an interactive plot. (A) Channels producing 98 u + H2 (left) and 72 u + C2H4 (right) product pairs. (B) Channels producing 58 u + propene (left) and 54 u + CH2S (right) product pairs. (C) Products likely formed in barrierless channels where all other prior barriers are submerged, yielding 99 u + H product pairs. (D) Products likely formed in barrierless channels where all other prior barriers are submerged, yielding 85 u + CH3 (left), 41 u + 59 u (center) and 67 u + SH (right) product pairs. | ||
There are four channels to form H2, two of them being the lowest-energy exit channels (−12.2 and −7.3 kcal mol−1 barriers), forming methyl thiophenes, which are also by far the most stable products. All other products are formed via significantly higher bottleneck energies, −2.0 kcal mol−1 and above. We thus ascribe our H2-loss product at 98 u to 2- or 3-methyl thiophene. The translational energy distribution in Fig. 9C, peaking at 20 and extending to 75 kcal mol−1, is consistent with the available energy and the ∼50 kcal mol−1 exit barrier for this process given in the ESI.† While the low barriers suggest that the methyl thiophene isomers are the dominant products, it is not possible to carry out further ordering of the rest of the products without more detailed kinetic calculations, because the entropic contributions can differ significantly for the various channels. In the following we only provide a qualitative interpretation for the rest of the products.
Mass 72 u, which is also observed experimentally, was found to be formed as a coproduct of ethene. The chemical identity of 72 u could be thioacrolein, methyl thioketene, or CH3CCSH. The lowest barrier among these, at −3.2 kcal mol−1, leads ultimately to thioacrolein. This product also has the lowest ionization energy (8.3 eV), more in accord with our ability to detect it without the lens. Although Fig. 11A shows a bottleneck saddlepoint at −3.2 kcal mol−1, this is not the direct saddle leading to thioacrolein + ethene. The precursor to formation of thioacrolein is in fact thiocyclohex-2-ene, which has a deep minimum at −72.5 kcal mol−1, as shown in the ESI.† That final TS leading to thioacrolein + ethene is at −18.2 kcal mol−1, suggesting an exit barrier of 14.0 kcal mol−1.
A likely product at 58 u is thioketene, formed with propene. This shows a bottleneck at −2.9 kcal mol−1 and can be formed from several immediate precursors. We detected this mass weakly with the focused laser, as we did previously in the 13BD reaction, but the signal was too weak to obtain reliable translational energy distributions. We successfully detected it in the 13BD reaction in the cold flow, as shown in Fig. 5. Attempts to detect it in the flow from the isoprene reaction were unsuccessful, likely owing to competition from many other available product channels.
Mass 54 u, thioformaldehyde, can be formed with many possible co-products, as shown in Fig. 11B. All show bottlenecks from −2.0 to −0.8 kcal mol−1. We do not detect this product in the imaging experiment, but it is readily seen unambiguously in the 20 K flow shown in Fig. 10. A favorable line-strength and lower rotational partition function aid in this detection. In all of these product groups, we can see that the thermodynamically most favored products also have the lowest barriers; however, for the reasons mentioned above and due to the uncertainties in the calculated energies, we can only hypothesize that these thermodynamically favored products are also the kinetically most favored ones.
Finally, there is a range of products that can be formed via a series of steps where all barriers are submerged relative to the final product energies, and where the last, dissociative step is likely barrierless. It is important to stress that KinBot does not rigorously test if a reaction is barrierless. Rather, for each species it proposes homolytic scission processes, and if the resulting products are below the energy threshold and no barriers are found leading to them, they are flagged as barrierless. Nevertheless, the proposed reactions in this case all happen to be radical + radical reactions, which are likely formed in barrierless or near barrierless processes.
There are seven H-loss reactions shown in Fig. 11C corresponding to the experimental results in Fig. 6. These range in energy from 0.7 to 7.3 kcal mol−1. Interestingly, of these, cyclopentanethione-2-yl is the lowest in energy, rather than the thiophenyl radical. However, calculations suggest a higher adiabatic ionization energy for this product, out of the range of our probe laser for this species. Moreover, the product ion is a thiirane structure, so there is negligible Franck–Condon overlap. It is likely that the H-loss product we detect includes at least the two methyl substituted analogues of the 2HT radical. We note that the translational energy distribution extends a bit beyond the limit calculated for these radicals. We do not have a ready explanation for this, although one possibility is that this endoergic channel is favored by the higher collision energy events. Given an estimated 15% spread in the collision energy, from our previous determination of the microcanonical rates we estimate a fourfold increase in the rate as the collision energy is increased from 14 to 16.1 kcal mol−1. Thus, the high energy tail of the collision energy distribution could be responsible for the tail of the translational energy distribution.
There are two channels that eliminate methyl, but only one of these is favorable, with a bottleneck at −5.1 kcal mol−1. This pathway is clearly responsible for the detected 85 u product shown in Fig. 7. This is further supported by the translational energy distribution that extends to ∼20 kcal mol−1, consistent with the available energy for that product.
There are three pathways that form an SH radical in conjunction with mass 67 u, with the channel giving vinyl propargyl likely an important one. However, attempts to detect either this product or the SH product was unsuccessful owing to overwhelming signals from the beams. There is also a pathway that forms CH2CHS + propargyl, but at 5.7 kcal mol−1 this is deemed unlikely.
Concluding remarks
These results highlight the challenges of studying the elementary reaction dynamics of complex polyatomic systems and the need for complementary detection techniques. The critical role of theory for such systems is also clear – without it, little sense could be made of the experimental results. As noted above, for the isoprene reaction (a 14-atom system) at conditions relevant to our experiments, the automated KinBot system identifies 130 wells and 104 product channels, and locates the bottlenecks en route to products as well. It is difficult to imagine sorting through this with chemical intuition alone.Using ionization with the fluorine excimer laser at 157 nm, we have excellent sensitivity to the radical products. Closed-shell products in some cases are accessible but challenging, although many are out of reach. The CPUF experiment identifies some key products not seen in the scattering experiment, and perhaps more importantly confirms reaction at 20 K, supporting the overall mechanism involving ISC to the singlet surface. It is interesting to consider possible alternative probe techniques that could be used to fill in some of the missing products and help gain quantitative branching information. The traditional crossed-beam approach with a rotatable electron impact mass spectrometer detector has the advantage of greater universality, but faces challenges with fragmentation of many of these product masses into others that could make identification difficult. The use of low-energy electron ionization can surely help with that.75 There are also kinematic constraints that give these methods excellent sensitivity for slowly recoiling products, but might make it difficult to see products with large recoil velocity, such as the methyl thiophenes here. Nevertheless, there is surely much to be gained by applying these methods to the subject reactions as well. Finally, the use of tunable vacuum ultraviolet radiation as a probe in a crossed-beam configuration76,77 or for multichannel kinetics measurements78 could afford additional advantages for identifying products and branching in these and related reactions. One message of this work is clearly that no single detection strategy is likely to provide the whole story for such complex systems, and much is to be gained from a multi-faceted approach.
The present results extend our previous observations of cyclization to thiophenes for the reaction of ground-state sulfur atoms with the conjugated dienes 13BD and isoprene, and highlight the rich array of products formed following ISC to the singlet surfaces in the case of isoprene. From 13BD, we detect the H-loss radical 2HT and the H2-loss product thiophene, and in the low-temperature flow we detect the predicted thioketene product. For the reaction with isoprene, we detect H-loss and methyl-loss radicals, and closed-shell products including 2- and 3-methyl thiophene and thioacrolein. In the 20 K flow we detect thioformaldehyde. Potentially important channels we do not identify here include the H-abstraction pathway, which is likely quite significant but obscured by beam interference, and the lowest-energy H-loss product, which is a cyclopentathionyl radical. It would also be interesting (but challenging) to identify the relative branching among the possible C4H6 isomers that accompany production of thioformaldehyde. There are significant astrochemical implications of this work as well. Direct reaction of S(3P) produced by UV photodissociation of SO2 with olefins could make thiophenes, as detected on Mars.38 Sulfur processing in icy grains is invoked to account for the “missing sulfur”, as these grains are warmed in the approach to a protostar79,80 and reactions such as these will be relevant. To-date, sulfur has not been detected on Titan,81 but if it is bound into larger species and incorporated into aerosols, it may have eluded detection. It will be of interest to explore the consequences of including reactions such as those presented here into the appropriate models.
Data availability
Data supporting the results presented here are included in the manuscript and ESI,† or available from the authors upon reasonable request.Author contributions
AGS conceived the experiment and directed the experimental investigation. JZ conceived the theoretical approaches and performed the theoretical investigation. JL conducted the crossed-beam investigation with support from CDF and YL. ST conducted the CPUF investigations with support from AB.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Science, Geoscience and Bioscience of the U.S. Department of Energy (DOE). The contract no. for Missouri is DE-SC0017130. Sandia National Laboratories is a multimission laboratory managed and operated by the National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. DOE National Nuclear Security Administration under contract DE-NA0003525. This article has been co-authored by an employee of National Technology & Engineering Solutions of Sandia, LLC under contract no. DE-NA0003525 with the U.S. DOE. The employee owns right, title and interest in and to the article and is responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan: https://www.energy.gov/downloads/doe-public-access-plan.Notes and references
- Y. T. Lee, Science, 1987, 236, 793–798 CrossRef CAS PubMed.
- K. Liu, Annu. Rev. Phys. Chem., 2001, 52, 139–164 CrossRef CAS PubMed.
- J. Z. Zhang and W. H. Miller, J. Chem. Phys., 1989, 91, 1528–1547 CrossRef CAS.
- H. Pan, K. Liu, A. Caracciolo and P. Casavecchia, Chem. Soc. Rev., 2017, 46, 7517–7547 RSC.
- B. R. Heazlewood and T. P. Softley, Nat. Rev. Chem, 2021, 5, 125–140 CrossRef CAS PubMed.
- M. Kirste, X. Wang, H. C. Schewe, G. Meijer, K. Liu, A. van der Avoird, L. M. Janssen, K. B. Gubbels, G. C. Groenenboom and S. Y. van de Meerakker, Science, 2012, 338, 1060–1063 CrossRef CAS PubMed.
- S. Y. Van De Meerakker, H. L. Bethlem and G. Meijer, Nat. Phys., 2008, 4, 595–602 Search PubMed.
- T. de Jongh, M. Besemer, Q. Shuai, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. van de Meerakker, Science, 2020, 368, 626–630 CrossRef CAS PubMed.
- C. Amarasinghe, H. Li, C. A. Perera, M. Besemer, J. Zuo, C. Xie, A. van der Avoird, G. C. Groenenboom, H. Guo and J. Kłos, Nat. Chem., 2020, 12, 528–534 CrossRef CAS PubMed.
- C. A. Perera, C. Amarasinghe, H. Guo and A. G. Suits, Phys. Chem. Chem. Phys., 2023, 25, 22595–22606 RSC.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 358, 356–359 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. Croft, J. Zuo, H. Guo, N. Balakrishnan and F. J. Aoiz, Phys. Rev. Lett., 2023, 130, 033002 CrossRef CAS PubMed.
- H. Li and A. G. Suits, Phys. Chem. Chem. Phys., 2020, 22, 11126–11138 RSC.
- P. Casavecchia, Rep. Prog. Phys., 2000, 63, 355 CrossRef CAS.
- B. Joalland, Y. Shi, A. Kamasah, A. G. Suits and A. M. Mebel, Nat. Commun., 2014, 5, 4064 CrossRef CAS PubMed.
- R. I. Kaiser, D. S. Parker and A. M. Mebel, Annu. Rev. Phys. Chem., 2015, 66, 43–67 CrossRef CAS PubMed.
- H. Li, A. Kamasah, S. Matsika and A. G. Suits, Nat. Chem., 2019, 11, 123–128 CrossRef CAS PubMed.
- K. Ramasesha, J. D. Savee, J. Zádor and D. L. Osborn, J. Phys. Chem. A, 2021, 125, 9785–9801 CrossRef CAS PubMed.
- P. Recio, S. Alessandrini, G. Vanuzzo, G. Pannacci, A. Baggioli, D. Marchione, A. Caracciolo, V. J. Murray, P. Casavecchia, N. Balucani, C. Cavallotti, C. Puzzarini and V. Barone, Nat. Chem., 2022, 14, 1405–1412 CrossRef CAS PubMed.
- B. M. Jones, F. Zhang, R. I. Kaiser, A. Jamal, A. M. Mebel, M. A. Cordiner and S. B. Charnley, Proc. Natl. Acad. Sci. U.S.A., 2011, 108, 452–457 CrossRef CAS PubMed.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- G. B. Park and R. W. Field, J. Chem. Phys., 2016, 144, 200901 CrossRef PubMed.
- K. Prozument, G. B. Park, R. G. Shaver, A. K. Vasiliou, J. M. Oldham, D. E. David, J. S. Muenter, J. F. Stanton, A. G. Suits and G. B. Ellison, Phys. Chem. Chem. Phys., 2014, 16, 15739–15751 RSC.
- C. Abeysekera, B. Joalland, N. Ariyasingha, L. N. Zack, I. R. Sims, R. W. Field and A. G. Suits, J. Phys. Chem. Lett., 2015, 6, 1599–1604 CrossRef CAS PubMed.
- J. A. Pople, Rev. Mod. Phys., 1999, 71, 1267 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, 2000, vol. 15, pp. 1–86 Search PubMed.
- S. J. Klippenstein, Proc. Combust. Inst., 2017, 36, 77–111 CrossRef CAS.
- J. Zádor, C. Martí, R. Van de Vijver, S. L. Johansen, Y. Yang, H. A. Michelsen and H. N. Najm, J. Phys. Chem. A, 2023, 127, 565–588 CrossRef PubMed.
- R. Van de Vijver and J. Zádor, Comput. Phys. Commun., 2020, 248, 106947 CrossRef CAS.
- A. L. Dewyer and P. M. Zimmerman, Org. Biomol. Chem., 2017, 15, 501–504 RSC.
- A. L. Dewyer, A. J. Arguelles and P. M. Zimmerman, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1354 CrossRef.
- S. Maeda, Y. Harabuchi, M. Takagi, T. Taketsugu and K. Morokuma, Chem. Rec., 2016, 16, 2232–2248 CrossRef CAS PubMed.
- C. A. Grambow, L. Pattanaik and W. H. Green, Sci. Data, 2020, 7, 137 CrossRef CAS PubMed.
- C. Martí, H. A. Michelsen, H. N. Najm and J. Zádor, J. Phys. Chem. A, 2023, 127, 1941–1959 CrossRef PubMed.
- H. Li, J. Lang, C. D. Foley, J. Zádor and A. G. Suits, J. Phys. Chem. Lett., 2023, 14, 7611–7617 CrossRef CAS PubMed.
- P. J. Crutzen, Clim. Change, 2006, 77, 211 CrossRef CAS.
- D. Rösch, Y. Xu, H. Guo, X. Hu and D. L. Osborn, J. Phys. Chem. Lett., 2023, 14, 3084–3091 CrossRef PubMed.
- J. L. Eigenbrode, R. E. Summons, A. Steele, C. Freissinet, M. Millan, R. Navarro-González, B. Sutter, A. C. McAdam, H. B. Franz and D. P. Glavin, Science, 2018, 360, 1096–1101 CrossRef CAS PubMed.
- C. He, S. M. Hörst, N. K. Lewis, X. Yu, J. I. Moses, P. McGuiggan, M. S. Marley, E. M.-R. Kempton, S. E. Moran and C. V. Morley, Nat. Astron., 2020, 4, 986–993 CrossRef.
- R. Grice, Acc. Chem. Res., 1981, 14, 37–42 CrossRef CAS.
- A. Schmoltner, P. Chu, R. Brudzynski and Y. T. Lee, J. Chem. Phys., 1989, 91, 6926–6936 CrossRef CAS.
- P. Casavecchia, F. Leonori and N. Balucani, Int. Rev. Phys. Chem., 2015, 34, 161–204 Search PubMed.
- C. Cavallotti, A. Della Libera, C.-W. Zhou, P. Recio, A. Caracciolo, N. Balucani and P. Casavecchia, Faraday Discuss., 2022, 238, 161–182 RSC.
- R. L. Gross, X. Liu and A. G. Suits, Chem. Phys. Lett., 2003, 376, 710–716 CrossRef CAS.
- X. Liu, R. L. Gross and A. G. Suits, J. Chem. Phys., 2002, 116, 5341–5344 CrossRef CAS.
- S.-H. Lee and K. Liu, J. Phys. Chem. A, 1998, 102, 8637–8640 CrossRef CAS.
- S.-H. Lee and K. Liu, Chem. Phys. Lett., 1998, 290, 323–328 CrossRef CAS.
- A. Chang and S. Lin, Chem. Phys. Lett., 2000, 320, 161–168 CrossRef CAS.
- L. Bañares, F. Aoiz, P. Honvault and J.-M. Launay, J. Phys. Chem. A, 2004, 108, 1616–1628 CrossRef.
- B. Maiti, G. C. Schatz and G. Lendvay, J. Phys. Chem. A, 2004, 108, 8772–8781 CrossRef CAS.
- S. Ying Lin and H. Guo, J. Chem. Phys., 2005, 122, 074304 CrossRef PubMed.
- X. Liu, J. J. Lin, S. Harich, G. C. Schatz and X. Yang, Science, 2000, 289, 1536–1538 CrossRef CAS PubMed.
- C. Berteloite, S. D. Le Picard, I. R. Sims, M. Rosi, F. Leonori, R. Petrucci, N. Balucani, X. Wang and P. Casavecchia, Phys. Chem. Chem. Phys., 2011, 13, 8485–8501 RSC.
- F. Leonori, R. Petrucci, N. Balucani, P. Casavecchia, M. Rosi, D. Skouteris, C. Berteloite, S. D. Le Picard, A. Canosa and I. R. Sims, J. Phys. Chem. A, 2009, 113, 15328–15345 CrossRef CAS PubMed.
- O. P. Strausz and H. E. Gunning, J. Am. Chem. Soc., 1962, 84, 4080–4083 CrossRef CAS.
- K. Sidhu, E. Lown, O. Strausz and H. Gunning, J. Am. Chem. Soc., 1966, 88, 254–263 CrossRef CAS.
- E. Lown, E. Dedio, O. Strausz and H. Gunning, J. Am. Chem. Soc., 1967, 89, 1056–1062 CrossRef CAS.
- R. Van De Vijver, A. L. Dewyer, C. Martí and J. Zádor, 2019, https://github.com/zadorlab/KinBot, accessed 2023-12-15.
- A. T. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- I. Sims, J. Queffelec, A. Defrance, C. Rebrion-Rowe, D. Travers, B. Rowe and I. Smith, J. Chem. Phys., 1992, 97, 8798–8800 CrossRef CAS.
- N. Dias, R. M. Gurusinghe, B. M. Broderick, T. J. Millar and A. G. Suits, Astrophys. J., 2023, 944, 77 CrossRef.
- S. Thawoos, N. Suas-David, R. M. Gurusinghe, M. Edlin, A. Behzadfar, J. Lang and A. G. Suits, J. Chem. Phys., 2023, 159, 214201 CrossRef CAS PubMed.
- B. Joalland, Y. Shi, A. D. Estillore, A. Kamasah, A. M. Mebel and A. G. Suits, J. Phys. Chem. A, 2014, 118, 9281–9295 CrossRef CAS PubMed.
- C. Berteloite, M. Lara, A. Bergeat, S. D. Le Picard, F. Dayou, K. M. Hickson, A. Canosa, C. Naulin, J.-M. Launay and I. R. Sims, Phys. Rev. Lett., 2010, 105, 203201 CrossRef PubMed.
- D. Townsend, M. P. Minitti and A. G. Suits, Rev. Sci. Instrum., 2003, 74, 2530–2539 CrossRef CAS.
- C. Abeysekera, B. Joalland, Y. Shi, A. Kamasah, J. M. Oldham and A. G. Suits, Rev. Sci. Instrum., 2014, 85, 116107 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, J. Baker, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll and M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges and T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O’Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, P. Pulay, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk and T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, see https://www.molpro.net.
- R. Van de Vijver, C. Martí and J. Zádor, https://github.com/zadorlab/PESViewer2023.
- H. Li, D. Troya and A. G. Suits, J. Chem. Phys., 2020, 153, 014302 CrossRef CAS PubMed.
- A. D. Estillore, L. M. Visger-Kiefer, T. A. Ghani and A. G. Suits, Phys. Chem. Chem. Phys., 2011, 13, 8433–8440 RSC.
- H. S. P. Müller, S. Thorwirth, D. A. Roth and G. Winnewisser, Astron. Astrophys., 2001, 370, L49–L52 CrossRef.
- J. N. Harvey, Phys. Chem. Chem. Phys., 2007, 9, 331–343 RSC.
- X. Li, A. W. Jasper, J. Zádor, J. A. Miller and S. J. Klippenstein, Proc. Combust. Inst., 2017, 36, 219–227 CrossRef CAS.
- P. Casavecchia, F. Leonori, N. Balucani, R. Petrucci, G. Capozza and E. Segoloni, Phys. Chem. Chem. Phys., 2009, 11, 46–65 RSC.
- D. A. Blank, N. Hemmi, A. G. Suits and Y. T. Lee, Chem. Phys., 1998, 231, 261–278 CrossRef CAS.
- C.-H. Chin, W.-K. Chen, W.-J. Huang, Y.-C. Lin and S.-H. Lee, J. Phys. Chem. A, 2012, 116, 7615–7622 CrossRef CAS PubMed.
- J. D. Savee, E. Papajak, B. Rotavera, H. Huang, A. J. Eskola, O. Welz, L. Sheps, C. A. Taatjes, J. Zádor and D. L. Osborn, Science, 2015, 347, 643–646 CrossRef CAS PubMed.
- J. C. Laas and P. Caselli, Astron. Astrophys., 2019, 624, A108 CrossRef CAS.
- T. H. Vidal, J.-C. Loison, A. Y. Jaziri, M. Ruaud, P. Gratier and V. Wakelam, Mon. Not. R. Astron. Soc., 2017, 469, 435–447 CrossRef CAS.
- V. Vuitton, R. Yelle, S. Klippenstein, S. Hörst and P. Lavvas, Icarus, 2019, 324, 120–197 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Exploration and characterization of the S(3P) + isoprene PES. Interactive S(3P) + isoprene PES. See DOI: https://doi.org/10.1039/d4fd00009a |
| This journal is © The Royal Society of Chemistry 2024 |