Open Access Article
Open Access ArticleIon transport in polymerized ionic liquids: a comparison of polycation and polyanion systems
Javad
Jeddi
a,
Jukka
Niskanen
b,
Benoît H.
Lessard
 *cd and
Joshua
Sangoro
*cd and
Joshua
Sangoro
 *a
*a
aDepartment of Chemical and Biomolecular Engineering Ohio State University, Columbus, Ohio 43210, USA. E-mail: sangoro.1@osu.edu
bDepartment of Chemical and Metallurgical Engineering, Aalto University, Kemistintie 1, 02150 Espoo, Finland
cDepartment of Chemical and Biological Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, Ontario K1N 6N5, Canada. E-mail: benoit.lessard@uottawa.ca
dSchool of Electrical Engineering and Computer Science, University of Ottawa, 800 King Edward Ave, Ottawa, ON K1N 6N5, Canada
First published on 17th May 2024
Abstract
The correlation among chemical structure, mesoscale structure, and ion transport in 1,2,3-triazole-based polymerized ionic liquids (polyILs) featuring comparable polycation and polyanion backbones is investigated by wide-angle X-ray scattering (WAXS), differential scanning calorimetry, and broadband dielectric spectroscopy (BDS). Above the glass transition temperature, Tg, higher ionic conductivity is observed in polycation polyILs compared to their polyanion counterparts, and ion conduction is enhanced by increasing the counterion volume in both polycation or polyanion polyILs. Below Tg, polyanions show lower activation energy associated with ion conduction. However, the validity of the Barton–Nakajima–Namikawa relation indicates that hopping conduction is the dominant charge transport mechanism in all the polyILs studied. While a significant transition from a Vogel–Fulcher–Tammann to Arrhenius type of thermal activation is observed below Tg, the decoupling index, often used to quantify the extent to which segmental dynamics and ion conduction are correlated, remains unaltered for the polyILs studied, suggesting that this index may not be a general parameter to characterize charge transport in polymerized ionic liquids. Furthermore, detailed analyses of the WAXS results indicate that both the mobile ion type and the structure of the pendant groups control mesoscale organization. These findings are discussed within the framework of recent models, which account for the subtle interplay between electrostatic and elastic forces in determining ion transport in polyILs. The findings demonstrate the intricate balance between the chemical structure and interactions in polyILs that determine ion conduction in this class of polymer electrolytes.
Polymerized ionic liquids (polyILs) are a new class of polymer electrolytes combining promising ion conduction, electrochemical stability, and thermal stability of ionic liquids (ILs) with the mechanical properties of polymers for different applications such as solar cells, lithium-ion rechargeable batteries, fuel cells, actuators, electrochromic devices, and electronic transistors.1–10 The ionic conductivity, one of the most important properties of polyILs, is sensitive to different factors such as the chemical structure of the cation and anion, length, and type of spacer between the polymer backbone and chemically bonded ion, molecular architecture, degree of polymerization, and ion density.11–22 In contrast to molecular ILs, the ionic conductivity of polyILs drops by several orders of magnitude upon polymerization, limiting their use in many applications.3 Previous studies of polyILs have mainly focused on attempts to understand ion transport mechanisms in systems where the cations are tethered to the polymeric chain.3,18,22,23 One of the key findings is that ionic conduction in polyILs is decoupled from segmental dynamics in contrast to the well-studied polyethylene oxide (PEO) based polymer electrolytes.23–26 The decoupling is usually highlighted by a transition of the dc ionic conductivity from Vogel–Fulcher–Tammann (VFT) to Arrhenius type of thermal activation below the glass transition temperature, Tg. For many practical applications such as Li-ion batteries, anionic polyILs are more relevant yet these systems have not been well studied. The extent to which the insights from cationic polyILs apply to their anionic counterparts remains an open question.
One of the peculiar characteristics of organic ionic salts such as ionic liquids and polyILs is the tendency to form distinct structural features due to the mesoscopic organization of ionic, polar, and non-polar moieties.27–30 Wide-angle X-ray scattering is instrumental in examining the structure of amorphous ionic liquids and polyILs.30,31 In the polyILs based on alkyl-imidazolium cations, different morphologies of polar and nonpolar domains can form, and the backbone-to-backbone correlation peak is observed to shift to lower q values with increasing alkyl chain length. These structural features significantly influence ion transport in polycation polyILs.22,30,32 However, it is unclear if such structural signatures exist and influence charge transport in polyILs with anions tethered on the polymer backbones.
In this study, four model 1,2,3-triazole-based polyILs with either polycation or polyanion backbones comprising comparable chemical structures, are investigated to understand the impact of mobile ion types and chemical structure of the backbone on the correlation between mesoscopic organization and ionic conductivity. A combination of broadband dielectric spectroscopy (BDS) and X-ray scattering techniques are employed to elucidate the effects of the chemistry of anionic and cationic backbone structures and ion dynamics. It is found that a subtle interplay between the chemical structure and interactions in polyILs determines the ion conduction in both classes of polyILs.
The model 1,2,3-triazole-based polymerized ionic liquids (polyILs) studied in this work include poly(1-(4-vinyl benzyl)-1H-1,2,3-triazole-4-yl)methanesulfonate) with 1-butyl-3-methyl-imidazolium (C4MIm+) and Na+ as the cations (PVB-SO3C4MIm and PVB-SO3Na), poly(4-butyl-3-methyl-1-(4-vinyl benzyl)-1H-1,2,3-triazol-3-ium chloride) (PVB-MeCl), and poly(4-butyl-3-methyl-1-(4-vinylbenzyl)-1H-1,2,3-triazol-3-ium TFSI) (PVB-MeTFSI). These systems were synthesized using a copper-catalyzed azidealkyne cycloaddition (CuAAC) ‘click’ reaction as reported previously.33 The thermal properties were characterized using differential scanning calorimetry (DSC). DSC measurements of polyIL samples were carried out using a TA Instruments DSC2500 unit calibrated with indium (temperature and enthalpy) and sapphire (heat capacity). The samples were dried in a vacuum oven at 350 K for 24 hours before sealing in the Tzero aluminum hermetic pans. Standard heat–cool–heat cycles at 10 K min−1 were applied to determine the glass transition temperatures, Tgs. The Tg was considered as the midpoint of the step in the second heating cycle.
A Novocontrol High-Resolution Alpha Dielectric Analyzer equipped with a Quatro Cryosystem for temperature control was employed for the BDS measurements in the frequency range 0.1–107 Hz. The samples were prepared by thermomechanically pressing between two Teflon sheets to obtain a film of about 10 mm in diameter. The films were sandwiched between two polished brass electrodes in a parallel plate configuration. The sample thickness was kept constant at 100 μm using silica spacers, then annealed at 350 K for 24 h in a vacuum oven to remove moisture before starting the BDS measurements. In the dielectric analyzer, the samples were further annealed at 375 K under dry nitrogen gas while the dielectric response was continuously monitored until a plateau in the real part of the complex dielectric function versus time at various frequency points, was reached. The Quatro Cryosystem was employed to control the temperature of the samples within ±0.1 K accuracy of the set point.
The X-ray scattering experiments were conducted in the transmission mode using a Xenocs Xeuss 3.0 X-ray scattering instrument equipped with a Cu Kα 50 kV Xenocs Genix ULD SL X-ray source (λ = 1.5418 Å) at room temperature. Pressed sample films (100 μm) were dried in a vacuum oven at 350 K for 24 h before starting the measurement to minimize the moisture effect on the results. The two-dimensional scattering patterns were registered in a PILATUS3 R 300K detector from Dectris, Ltd. The scattered intensity was obtained as a function of the scattering vector q = (4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/λ, where 2θ is the scattering angle through azimuthal averages of the 2D data in the given angular range.
θ)/λ, where 2θ is the scattering angle through azimuthal averages of the 2D data in the given angular range.
The chemical structures and molecular properties of the polyILs investigated in this work are shown in Fig. 1 and Table 1, respectively. Fig. 2 shows the differential scanning calorimetry (DSC) thermograph of the polyILs studied in the current work. PVB-MeTFSI shows the lowest Tg among all systems investigated and this result can be understood at a qualitative level. The glass transition temperature, Tg, of polyILs is thought to be controlled by cooperative dynamics determined by intermolecular interactions, which can be influenced by free volume or packing effects, coulombic interactions between anions and cations, and molecular weight.30 For the TFSI− anion, the charge delocalization between S–N–S bonds along with steric hindrances from sulfonyl and trifluoromethane groups, results in the reduction of the strength of coulombic interactions with the triazolium cation, leading to a lower Tg.22,34,35 However, the high charge density of the Cl− anion results in stronger ionic interactions with the triazolium cation, leading to the higher Tg of PVB-MeCl. Based on similar arguments, the higher Tg values of the polyanions compared to their polycation counterparts can be rationalized. In both polyanion and polycation systems, larger counterions result in lower Tg. This observation is consistent with previous studies that explored the counterion charge density in determining Tg of the polyILs.4 However, rationalization of the higher Tg in the polyanions requires a more in-depth study of the structure, as discussed later based on the wide-angle X-ray scattering (WAXS) results.
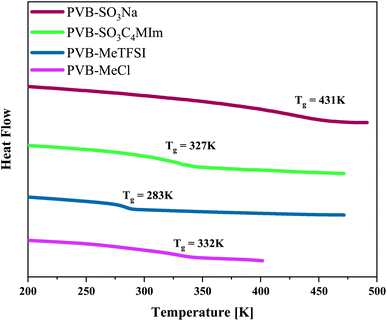 | ||
| Fig. 2 Differential scanning calorimetry thermograph of the polymerized ionic liquids investigated in the current work. | ||
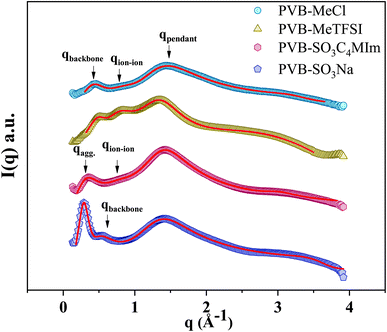
Fig. 3 shows the wide-angle X-ray scattering (WAXS) spectra presented in terms of the intensity versus scattering vector (q). The characteristic X-ray scattering peaks for the cationic polyILs indicate the rich mesoscale organization associated with polar, non-polar, and ionic moieties.30,36–39 Through a combination of molecular dynamics simulations and X-ray scattering experiments to analyze the mesoscopic structure in polyILs, three general structural features corresponding to the backbone-to-backbone (low q), ion–ion (intermediate q), and pendant group (high q) correlation distances have been identified.19,22,30,32,36,40,41
To quantitatively determine the peak position, asymmetric Lorentzian functions, 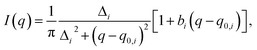 are used to fit the X-ray scattering data.42,43 This equation represents an asymmetric distribution with the center at q0 = 2π/d, a full-width at half maximum (FWHM) of Δ, and an asymmetric parameter b. The fit parameters yield characteristic correlation lengths, presented in Table 2.
are used to fit the X-ray scattering data.42,43 This equation represents an asymmetric distribution with the center at q0 = 2π/d, a full-width at half maximum (FWHM) of Δ, and an asymmetric parameter b. The fit parameters yield characteristic correlation lengths, presented in Table 2.
| PVB-MeCl | PVB-MeTFSI | PVB-SO3C4MIm | PVB-SO3Na | |
|---|---|---|---|---|
| d backbone (Å) | 14.85 ± 0.1 | 12.69 ± 0.1 | — | 13.68 ± 0.1 |
| d ion (Å) | 7.22 ± 0.2 | 8.16 ± 0.2 | 8.24 ± 0.2 | — |
| d pendant (Å) | 4.65 ± 0.1 | 4.67 ± 0.1 | 4.51 ± 0.1 | 4.65 ± 0.1 |
Despite the similarity of WAXS spectra of polyanion and polycation samples, there are some unique differences. The low-q and intermediate-q peaks of PVB-SO3Na appear at lower q in comparison with polycations. The sharp low-q peak of PVB-SO3Na corresponds to the center-to-center spacing between ion aggregates (daggregate), which is associated with the characteristic length scale of 21.7 Å.44–47 The intermediate-q peak of correlation distance 13.7 Å may be related to the backbone-to-backbone distance, which is comparable to the polycation counterparts. On the other hand, the broad low-q peak of PVB-SO3C4MIm that appears in the q = 0.31 Å−1, daggregate = 20.3 Å, may be due to the merging of the backbone-to-backbone and ion aggregate peaks. The second intermediate-q peak of PVB-SO3C4MIm shows a correlation length scale of 8.24 Å, corresponding to the ion–ion correlation.
The length of the fully stretched pendant groups of polyanion and polycation polyILs were estimated to be 12.25 and 12.5 Å using the open-source Avogadro software. Thus, idealized, fully stretched, non-interdigitated systems should yield nearly double backbone-to-backbone correlation distances. Although this is a crude estimate, some insights may be gleaned from these values. The comparable pendant group sizes of the polycation and polyanion polyILs agree with dbackbone values from WAXS, implying interdigitation of the pendant groups. However, the association of SO3− and the free cations at the end of the pendant group, likely results in large aggregates while the butyl pendant group of the polycations presumably disrupts the ion aggregate formation.48–50 These ion aggregates can act as physical cross-linking points resulting in the segmental dynamics restriction and higher Tg in polyanions.
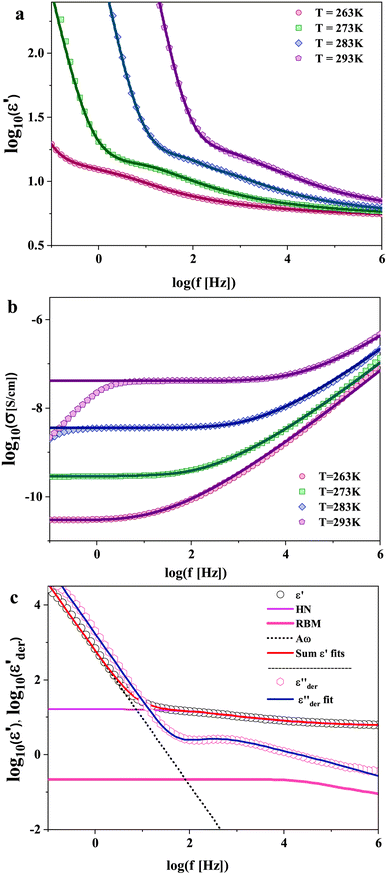
The dielectric spectra of PVB-MeTFSI at different temperatures are shown in Fig. 4. A combination of the empirical Havriliak–Negami (HN) and the random barrier model (RBM) functions were used to describe the dielectric spectra:51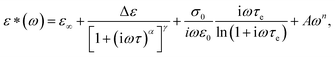 where Δε is the dielectric relaxation strength, τHN is the relaxation time, α and γ are symmetric and asymmetric stretching parameters of the HN function in the first term. The second term represents the RBM part where σ0 is the dc ionic conductivity, τe is the characteristic charge transport time, ε0 is the vacuum permittivity, and ε∞ is the limiting high-frequency permittivity. The Aωn term is used to account for electrode polarization. The empirical HN model describes the orientational polarization effects associated with ion conduction.18,19 On the other hand, the RBM model accounts for charge transport. Within the RBM framework, ion hopping occurs by overcoming the spatially randomly distributed energy barriers.52 Above Tg, the counterion diffusion in the polyILs is coupled to some degree to the segmental dynamics or α-relaxation. However, the dielectric relaxations in this spectral range are not detectable due to the dominant contributions of the ionic conductivity to ε′′. To suppress the dc conductivity contributions, the derivative representation of the imaginary part of the complex dielectric function, defined as
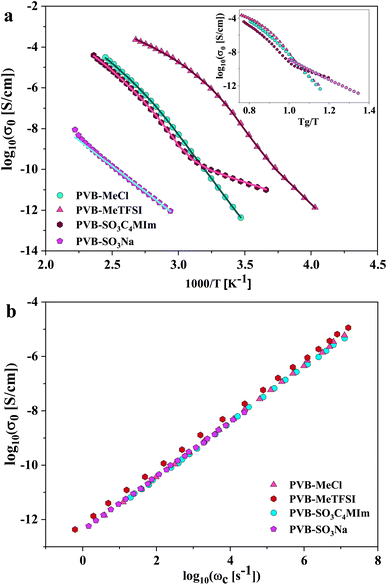
where Δε is the dielectric relaxation strength, τHN is the relaxation time, α and γ are symmetric and asymmetric stretching parameters of the HN function in the first term. The second term represents the RBM part where σ0 is the dc ionic conductivity, τe is the characteristic charge transport time, ε0 is the vacuum permittivity, and ε∞ is the limiting high-frequency permittivity. The Aωn term is used to account for electrode polarization. The empirical HN model describes the orientational polarization effects associated with ion conduction.18,19 On the other hand, the RBM model accounts for charge transport. Within the RBM framework, ion hopping occurs by overcoming the spatially randomly distributed energy barriers.52 Above Tg, the counterion diffusion in the polyILs is coupled to some degree to the segmental dynamics or α-relaxation. However, the dielectric relaxations in this spectral range are not detectable due to the dominant contributions of the ionic conductivity to ε′′. To suppress the dc conductivity contributions, the derivative representation of the imaginary part of the complex dielectric function, defined as 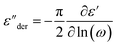 based on the Kramers–Kronig relation, is used. Fig. 5a shows variation in the dc ionic conductivity with the inverse temperature. The high dc conductivity of PVB-MeTFSI and PVBSO3C4MIm compared to their counterparts correlates with their lower Tg. The bulky structure of the counterions likely lowers the charge density and coulombic interaction strengths, resulting in faster segmental dynamics of the polymer backbone. To analyze the results at comparable timescales, the dc conductivity is plotted versus Tg-normalized temperature. Above Tg (Tg/T < 1), the conductivity of PVB-MeTFSI is slightly higher while PVBSO3C4MIm has the lowest conductivity.
based on the Kramers–Kronig relation, is used. Fig. 5a shows variation in the dc ionic conductivity with the inverse temperature. The high dc conductivity of PVB-MeTFSI and PVBSO3C4MIm compared to their counterparts correlates with their lower Tg. The bulky structure of the counterions likely lowers the charge density and coulombic interaction strengths, resulting in faster segmental dynamics of the polymer backbone. To analyze the results at comparable timescales, the dc conductivity is plotted versus Tg-normalized temperature. Above Tg (Tg/T < 1), the conductivity of PVB-MeTFSI is slightly higher while PVBSO3C4MIm has the lowest conductivity.
This suggests that above Tg, ion transport is more effective in the PVB-MeTFSI at the same value of Tg/T. However, we could not study the σdc conductivity of PVB-SO3Na above Tg due to the possibility of sample degradation at higher temperatures. The temperature dependence of σ0 above Tg can be represented by the Vogel–Fulcher–Tammann (VFT) equation 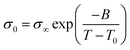 , where B, σ∞, and T0 are fitting parameters (Table 3), below Tg, the Arrhenius equation is employed. Fig. 5b shows the variation of the dc conductivity versus ωc(=1/τe) which follows the empirical Barton, Nakajima, and Namikawa (BNN) relation.51 The BNN relation correlates the dc conductivity to the dielectric relaxation strength through σ0 = pε0Δεωc, where p is a dimensionless empirical number, σ0 is the apparent dc conductivity, Δε is the dielectric relaxation strength, and ωc is from the RBM. Fig. 5b suggests that the underlying mechanisms of ion conduction and dielectric relaxation in polyanion and polycation polyILs are similar.21
, where B, σ∞, and T0 are fitting parameters (Table 3), below Tg, the Arrhenius equation is employed. Fig. 5b shows the variation of the dc conductivity versus ωc(=1/τe) which follows the empirical Barton, Nakajima, and Namikawa (BNN) relation.51 The BNN relation correlates the dc conductivity to the dielectric relaxation strength through σ0 = pε0Δεωc, where p is a dimensionless empirical number, σ0 is the apparent dc conductivity, Δε is the dielectric relaxation strength, and ωc is from the RBM. Fig. 5b suggests that the underlying mechanisms of ion conduction and dielectric relaxation in polyanion and polycation polyILs are similar.21
| Sample | σ ∞ | B | T 0 | E σ (kJ mol−1) | Decoupling index (m) |
|---|---|---|---|---|---|
| PVB-MeCl | 64 | 2927 | 207 | 165 ± 1 | 6.7 |
| PVB-MeTFSI | 0.24 | 1013 | 227 | 123 ± 1 | 6.7 |
| PVB-SO3-C4MIm | 18 | 2702 | 217 | 43 ± 1 | 5.9 |
| PVB-SO3Na | — | — | — | 95 ± 1 | 6.1 |
The degree of decoupling, m, determined at Tg using m = 15 + log10(σ0), was proposed to quantify the coupling between segmental and ion conduction.53 The extent of decoupling of the ion conduction from segmental dynamics is dictated by the backbone and pendant group stiffness.54 The close decoupling indices suggest that the chain stiffness of polycations and polyanions are comparable. In the current study, the effect of the counterions of either the cation or anion on the degree of decoupling is negligible (see Table 3), indicating that m is likely controlled by the backbone structure. However, a close examination of the remarkable differences below Tg implies that m may not be an appropriate parameter for characterizing ion transport in polyILs.
The Eσ values can be calculated from the temperature dependence of ionic conductivity below the Tg using the Arrhenius equation 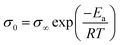 , where σ∞ is a pre-exponential factor and R is the universal gas constant. More accurate estimates are obtained by the fitting data in a broad range of temperatures by combining the VFT and Arrhenius equations. Despite the comparable decoupling indices, polyanion polyILs show lower ion conduction activation energy, Eσ, than their polycation counterparts. Moreover, smaller counterions result in higher Eσ in polycation and polyanion polyILs. Deeper insights into the ion conduction properties of the polyILs can be gleaned by attempting to find correlations between their ion transport properties below Tg and their chemical structure.
, where σ∞ is a pre-exponential factor and R is the universal gas constant. More accurate estimates are obtained by the fitting data in a broad range of temperatures by combining the VFT and Arrhenius equations. Despite the comparable decoupling indices, polyanion polyILs show lower ion conduction activation energy, Eσ, than their polycation counterparts. Moreover, smaller counterions result in higher Eσ in polycation and polyanion polyILs. Deeper insights into the ion conduction properties of the polyILs can be gleaned by attempting to find correlations between their ion transport properties below Tg and their chemical structure.
In the polyanion systems, the strong coulombic interactions within the ion aggregates result in slower segmental dynamics, as reflected by the Tg values. Below Tg, polyanion systems show lower ion activation energy than their polycation counterparts. This result is presumably associated with the percolation of the ion aggregates. We conjecture that the larger characteristic lengths associated with the ion aggregates of the polyanions lead to frustrations in the packing of the polymeric chains and form percolated ion paths resulting in facilitated ion mobility below Tg. On the other hand, the interdigitation of butyl pendant groups leads to better-packed structures and steric hindrances that limit the available sites for ion hopping as reflected by the higher Eσ.
The counterion size is another factor that controls the Eσ. The overall effect of the counterion size and charge density on the Eσ can be interpreted using the Anderson–Stuart Model. Within the framework of this model, the activation energy is given by:55,56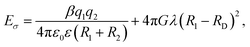 where the first term describes the coulombic interactions between mobile ions with charge, q1 and radius R1, and counterions with charge q2 and radius R2. ε0 and ε are vacuum permittivity and medium static dielectric permittivity, and β is the Madelung constant. The second term defines the elastic contribution of the ion jump process. The G term is the shear modulus, RD is the radius of free volume for ion hopping, and λ is the ion jump length. In the polycation systems, it is observed that the Eσ of PVB-MeCl is higher than PVB-MeTFSI. The small size of Cl− results in stronger coulombic interactions with the triazolium ring. So, according to this model, the coulombic term dominates the Eσ. It was previously shown that the elastic modulus of polyILs increases with the ionic volume of the counteranion.57 However, the lower Eσ of PVB-MeTFSI correspond to the weaker coulombic interactions of the large TFSI− and backbone despite higher shear modulus.
where the first term describes the coulombic interactions between mobile ions with charge, q1 and radius R1, and counterions with charge q2 and radius R2. ε0 and ε are vacuum permittivity and medium static dielectric permittivity, and β is the Madelung constant. The second term defines the elastic contribution of the ion jump process. The G term is the shear modulus, RD is the radius of free volume for ion hopping, and λ is the ion jump length. In the polycation systems, it is observed that the Eσ of PVB-MeCl is higher than PVB-MeTFSI. The small size of Cl− results in stronger coulombic interactions with the triazolium ring. So, according to this model, the coulombic term dominates the Eσ. It was previously shown that the elastic modulus of polyILs increases with the ionic volume of the counteranion.57 However, the lower Eσ of PVB-MeTFSI correspond to the weaker coulombic interactions of the large TFSI− and backbone despite higher shear modulus.
The higher Eσ of PVB-SO3Na than PVB-SO3C4MIm can also be understood using the Anderson–Stuart Model. The strong coulombic interaction of the Na+ and polyanion backbone enhances Eσ. On the other hand, C4MIm+ can increase the shear modulus and decrease the coulombic interaction. The low Eσ indicates the effect of the weaker coulombic interaction dominates the higher shear modulus role in controlling ion conduction activation energy. This microscopic understanding of ion dynamics in polymerized ionic liquids will be valuable in designing solid polymer electrolytes. These results suggest that a subtle counterbalance between electrostatic and elastic forces determines the overall ionic conduction. A rational design of polyILs for practical applications should involve carefully selecting the target ionic groups that optimize the total contribution of these forces in a wide range of temperatures.
In summary, differential scanning calorimetry (DSC), broadband dielectric spectroscopy (BDS), and wide-angle X-ray scattering (WAXS) were employed to understand the correlation between chemical structure, nanoscale organization, and ion transport properties of 1,2,3-triazole based polymerized ionic liquids. Above Tg, polycation polyILs showed higher ion conduction compared to anionic backbone counterparts due to the coupling of the ion conduction and segmental dynamics. Below Tg, polyanions show lower Eσ of ion conduction than their polycation counterpart. The strong coulombic interactions between the backbone and the counterions result in higher Eσ while increasing the volume of the counterion leads to higher shear modulus and reduction of the Eσ, qualitatively consistent with the Anderson–Stuart model. The findings of this work provide insights into the rational design of solid electrolytes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation for financial support through the Division of Materials Research award DMR-2327018. We thank the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery grant RGPIN 2020-04079 (B. H. L.), the Canada Research Chairs Program 950-230724 (B. H. L.).References
- H. Ohno, Design of Ion Conductive Polymers Based on Ionic Liquids, Macromol. Symp., 2007, 249–250, 551–556 CrossRef.
- H. Ohno, M. Yoshizawa and W. Ogihara, Development of new class of ion conductive polymers based on ionic liquids, Electrochim. Acta, 2004, 50, 255–261 CrossRef CAS.
- J. R. Sangoro, C. Iacob, A. Agapov, Y. Wang, S. Berdzinski, H. Rexhausen, V. Strehmel, C. Friedrich, A. Sokolov and F. Kremer, Decoupling of ionic conductivity from structural dynamics in polymerized ionic liquids, Soft Matter, 2014, 10, 3536–3540 RSC.
- D. Mecerreyes, Polymeric ionic liquids: Broadening the properties and applications of polyelectrolytes, Prog. Polym. Sci., 2011, 36, 1629–1648 CrossRef CAS.
- B. Yang, G. Yang, Y.-M. Zhang and S. X.-A. Zhang, Recent advances in poly (ionic liquid) s for electrochromic devices, J. Mater. Chem. C, 2021, 9, 4730–4741 RSC.
- M. N. Tousignant, M. Ourabi, J. Niskanen, B. Mirka, W. J. Bodnaryk, A. Adronov and B. H. Lessard, Poly (ionic liquid) dielectric for high performing P-and N-type single walled carbon nanotube transistors, Flexible Printed Electron., 2022, 7, 034004 CrossRef CAS.
- N. J. Dallaire, B. Mirka, J. G. Manion, W. J. Bodnaryk, D. Fong, A. Adronov, K. Hinzer and B. H. Lessard, Conjugated wrapping polymer influences on photoexcitation of single-walled carbon nanotube-based thin film transistors, J. Mater. Chem. C, 2023, 11, 9161–9171 RSC.
- A. J. Peltekoff, S. Brixi, J. Niskanen and B. H. Lessard, Ionic liquid containing block copolymer dielectrics: designing for high-frequency capacitance, low-voltage operation, and fast switching speeds, JACS Au, 2021, 1, 1044–1056 CrossRef CAS PubMed.
- A. J. Peltekoff, V. E. Hiller, G. P. Lopinski, O. A. Melville and B. H. Lessard, Unipolar polymerized ionic liquid copolymers as high-capacitance electrolyte gates for n-type transistors, ACS Appl. Polym. Mater., 2019, 1, 3210–3221 CrossRef CAS.
- J. Niskanen, M. N. Tousignant, A. J. Peltekoff and B. H. Lessard, Poly (ethylene glycol)-Based Poly (ionic liquid) Block Copolymers through 1, 2, 3-Triazole Click Reactions, ACS Appl. Polym. Mater., 2022, 4, 1559–1564 CrossRef CAS.
- Z. Zhang, N. Marioni, H. S. Sachar and V. Ganesan, Polymer Architecture-Induced Trade-off between Conductivities and Transference Numbers in Salt-Doped Polymeric Ionic Liquids, ACS Macro Lett., 2023, 12, 1351–1357 CrossRef CAS PubMed.
- M. Cotessat, D. Flachard, D. Nosov, E. I. Lozinskaya, D. O. Ponkratov, D. F. Schmidt, E. Drockenmuller and A. S. Shaplov, Effects of repeat unit charge density on the physical and electrochemical properties of novel heterocationic poly (ionic liquid) s, New J. Chem., 2021, 45, 53–65 RSC.
- J. R. Keith, N. J. Rebello, B. J. Cowen and V. Ganesan, Influence of counterion structure on conductivity of polymerized ionic liquids, ACS Macro Lett., 2019, 8, 387–392 CrossRef CAS PubMed.
- C. M. Evans, C. R. Bridges, G. E. Sanoja, J. Bartels and R. A. Segalman, Role of tethered ion placement on polymerized ionic liquid structure and conductivity: pendant versus backbone charge placement, ACS Macro Lett., 2016, 5, 925–930 CrossRef CAS PubMed.
- Y. Fu, V. Bocharova, M. Ma, A. P. Sokolov, B. G. Sumpter and R. Kumar, Effects of counterion size and backbone rigidity on the dynamics of ionic polymer melts and glasses, Phys. Chem. Chem. Phys., 2017, 19, 27442–27451 RSC.
- F. Fan, W. Wang, A. P. Holt, H. Feng, D. Uhrig, X. Lu, T. Hong, Y. Wang, N.-G. Kang and J. Mays, others Effect of molecular weight on the ion transport mechanism in polymerized ionic liquids, Macromolecules, 2016, 49, 4557–4570 CrossRef CAS.
- F. Fan, Y. Wang, T. Hong, M. F. Heres, T. Saito and A. P. Sokolov, Ion conduction in polymerized ionic liquids with different pendant groups, Macromolecules, 2015, 48, 4461–4470 CrossRef CAS.
- M. A. Harris, M. F. Heres, J. Coote, A. Wenda, V. Strehmel, G. E. Stein and J. Sangoro, Ion transport and interfacial dynamics in disordered block copolymers of ammonium-based polymerized ionic liquids, Macromolecules, 2018, 51, 3477–3486 CrossRef CAS.
- M. Heres, T. Cosby, E. U. Mapesa, H. Liu, S. Berdzinski, V. Strehmel, M. Dadmun, S. J. Paddison and J. Sangoro, Ion transport in glassy polymerized ionic liquids: Unraveling the impact of the molecular structure, Macromolecules, 2019, 52, 88–95 CrossRef CAS.
- E. U. Mapesa, M. Chen, M. F. Heres, M. A. Harris, T. Kinsey, Y. Wang, T. E. Long, B. S. Lokitz and J. R. Sangoro, Charge transport in imidazolium-based homo-and triblock poly (ionic liquid) s, Macromolecules, 2019, 52, 620–628 CrossRef CAS.
- U. H. Choi, Y. Ye, D. Salas de la Cruz, W. Liu, K. I. Winey, Y. A. Elabd, J. Runt and R. H. Colby, Dielectric and viscoelastic responses of imidazolium-based ionomers with different counterions and side chain lengths, Macromolecules, 2014, 47, 777–790 CrossRef CAS.
- C. Iacob, A. Matsumoto, M. Brennan, H. Liu, S. J. Paddison, O. Urakawa, T. Inoue, J. Sangoro and J. Runt, Polymerized ionic liquids: Correlation of ionic conductivity with nanoscale morphology and counterion volume, ACS Macro Lett., 2017, 6, 941–946 CrossRef CAS PubMed.
- V. Bocharova and A. P. Sokolov, Perspectives for polymer electrolytes: a view from fundamentals of ionic conductivity, Macromolecules, 2020, 53, 4141–4157 CrossRef CAS.
- C. Imrie, M. Ingram and G. McHattie, Ion transport in glassy polymer electrolytes, J. Phys. Chem. B, 1999, 103, 4132–4138 CrossRef CAS.
- J. Bartels, G. E. Sanoja, C. M. Evans, R. A. Segalman and M. E. Helgeson, Decoupling mechanical and conductive dynamics of polymeric ionic liquids via a trivalent anion additive, Macromolecules, 2017, 50, 8979–8987 CrossRef CAS.
- S. Cheng, Z. Wojnarowska, J. Sangoro and M. Paluch, Ion dynamics in pendant and backbone polymerized ionic liquids: A view from high-pressure dielectric experiments and free-volume model, Phys. Rev. E, 2022, 105, 054502 CrossRef CAS PubMed.
- O. Russina, A. Triolo, L. Gontrani and R. Caminiti, Mesoscopic structural heterogeneities in room-temperature ionic liquids, J. Phys. Chem. Lett., 2012, 3, 27–33 CrossRef CAS.
- O. Russina, F. L. Celso, M. Di Michiel, S. Passerini, G. Appetecchi, F. Castiglione, A. Mele, R. Caminiti and A. Triolo, Evidences of fluorinated nano-domains in room temperature ionic liquids with perfluoroalkylsulfonylimide anions, Faraday Discuss., 2013, 499, 167 Search PubMed.
- L. Gontrani, P. Ballirano, F. Leonelli and R. Caminiti, X-ray diffraction studies of ionic liquids: from spectra to structure and back, The Structure of Ionic Liquids, 2014, pp. 1–37 Search PubMed.
- D. S.-D. la Cruz, M. D. Green, Y. Ye, Y. A. Elabd, T. E. Long and K. I. Winey, Correlating backbone-to-backbone distance to ionic conductivity in amorphous polymerized ionic liquids, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 338–346 CrossRef.
- A. Triolo, O. Russina, H.-J. Bleif and E. Di Cola, Nanoscale segregation in room temperature ionic liquids, J. Phys. Chem. B, 2007, 111, 4641–4644 CrossRef CAS PubMed.
- S. Li, J. L. Bañuelos, J. Guo, L. Anovitz, G. Rother, R. W. Shaw, P. C. Hillesheim, S. Dai, G. A. Baker and P. T. Cummings, Alkyl chain length and temperature effects on structural properties of pyrrolidinium-based ionic liquids: a combined atomistic simulation and small-angle X-ray scattering study, J. Phys. Chem. Lett., 2012, 3, 125–130 CrossRef CAS.
- J. Niskanen, M. N. Tousignant, A. J. Peltekoff and B. H. Lessard, 1, 2, 3-Triazole based poly (ionic liquids) as solid dielectric materials, Polymer, 2021, 212, 123144 CrossRef CAS.
- J. Leys, R. N. Rajesh, P. C. Menon, C. Glorieux, S. Longuemart, P. Nockemann, M. Pellens and K. Binnemans, Influence of the anion on the electrical conductivity and glass formation of 1-butyl-3-methylimidazolium ionic liquids, J. Chem. Phys., 2010, 133, 034503 CrossRef PubMed.
- A. Pipertzis, G. Papamokos, M. Mühlinghaus, M. Mezger, U. Scherf and G. Floudas, What determines the glass temperature and dc-conductivity in imidazolium-polymerized ionic liquids with a polythiophene backbone?, Macromolecules, 2020, 53, 3535–3550 CrossRef CAS.
- H. Liu and S. J. Paddison, Direct comparison of atomistic molecular dynamics simulations and X-ray scattering of polymerized ionic liquids, ACS Macro Lett., 2016, 5, 537–543 CrossRef CAS PubMed.
- C. F. Buitrago, J. E. Jenkins, K. L. Opper, B. S. Aitken, K. B. Wagener, T. M. Alam and K. I. Winey, Room temperature morphologies of precise acid-and ion-containing polyethylenes, Macromolecules, 2013, 46, 9003–9012 CrossRef CAS.
- M. E. Seitz, C. D. Chan, K. L. Opper, T. W. Baughman, K. B. Wagener and K. I. Winey, Nanoscale morphology in precisely sequenced poly (ethylene-co-acrylic acid) zinc ionomers, J. Am. Chem. Soc., 2010, 132, 8165–8174 CrossRef CAS PubMed.
- H. V. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, What is the origin of the prepeak in the X-ray scattering of imidazolium-based room-temperature ionic liquids?, J. Phys. Chem. B, 2010, 114, 16838–16846 CrossRef CAS PubMed.
- J. C. Araque, J. J. Hettige and C. J. Margulis, Modern room temperature ionic liquids, a simple guide to understanding their structure and how it may relate to dynamics, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- K. M. Beers and N. P. Balsara, Design of Cluster-free Polymer Electrolyte Membranes and Implications on Proton Conductivity, ACS Macro Lett., 2012, 1, 1155–1160 CrossRef CAS PubMed.
- H. Weiss, J. Mars, H. Li, G. Kircher, O. Ivanova, A. Feoktystov, O. Soltwedel, M. Bier and M. Mezger, Mesoscopic correlation functions in heterogeneous ionic liquids, J. Phys. Chem. B, 2017, 121, 620–629 CrossRef CAS PubMed.
- D. Pontoni, M. DiMichiel and M. Deutsch, Nanoscale Structure in Short-Chain Ionic Liquids, ChemPhysChem, 2020, 21, 1887–1897 CrossRef CAS PubMed.
- B. A. Paren, N. Nguyen, V. Ballance, D. T. Hallinan, J. G. Kennemur and K. I. Winey, Superionic Li-ion transport in a single-ion conducting polymer blend electrolyte, Macromolecules, 2022, 55, 4692–4702 CrossRef CAS.
- E. G. Sorte, B. A. Paren, C. G. Rodriguez, C. Fujimoto, C. Poirier, L. J. Abbott, N. A. Lynd, K. I. Winey, A. L. Frischknecht and T. M. Alam, Impact of hydration and sulfonation on the morphology and ionic conductivity of sulfonated poly (phenylene) proton exchange membranes, Macromolecules, 2019, 52, 857–876 CrossRef CAS.
- Z. Zhang, C. Liu, X. Cao, J.-H. H. Wang, Q. Chen and R. H. Colby, Morphological evolution of ionomer/plasticizer mixtures during a transition from ionomer to polyelectrolyte, Macromolecules, 2017, 50, 963–971 CrossRef CAS.
- B. A. Paren, B. A. Thurston, W. J. Neary, A. Kendrick, J. G. Kennemur, M. J. Stevens, A. L. Frischknecht and K. I. Winey, Percolated ionic aggregate morphologies and decoupled ion transport in precise sulfonated polymers synthesized by ring-opening metathesis polymerization, Macromolecules, 2020, 53, 8960–8973 CrossRef CAS.
- A. Agrawal, D. Perahia and G. S. Grest, Cluster morphology-polymer dynamics correlations in sulfonated polystyrene melts: computational study, Phys. Rev. Lett., 2016, 116, 158001 CrossRef PubMed.
- S. Kang and M. J. Park, 100th Anniversary of Macromolecular Science Viewpoint: Block Copolymers with Tethered Acid Groups: Challenges and Opportunities, ACS Macro Lett., 2020, 9, 1527–1541 CrossRef CAS PubMed.
- J. Park, A. Staiger, S. Mecking and K. I. Winey, Structure–Property Relationships in Single-Ion Conducting Multiblock Copolymers: A Phase Diagram and Ionic Conductivities, Macromolecules, 2021, 54, 4269–4279 CrossRef CAS.
- F. Kremer and A. Schönhals, Broadband Dielectric Spectroscopy, Springer Science & Business Media, 2002 Search PubMed.
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Fundamental questions relating to ion conduction in disordered solids, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- C. Austen Angell, Concepts and conflicts in polymer electrolytes: The search for ion mobility, Electrochim. Acta, 2019, 313, 205–210 CrossRef CAS.
- Z. Wojnarowska, H. Feng, Y. Fu, S. Cheng, B. Carroll, R. Kumar, V. N. Novikov, A. M. Kisliuk, T. Saito, N.-G. Kang and Others, Effect of chain rigidity on the decoupling of ion motion from segmental relaxation in polymerized ionic liquids: Ambient and elevated pressure studies, Macromolecules, 2017, 50, 6710–6721 CrossRef CAS.
- O. Anderson and D. Stuart, Calculation of activation energy of ionic conductivity in silica glasses by classical methods, J. Am. Ceram. Soc., 1954, 37, 573–580 CrossRef CAS.
- K. Kumbhakar, T. D. Pham, K.-K. Lee, K. Kwak and M. Cho, Dielectric Relaxation Spectroscopy for the Characterization of Ion Transport in Solid Polymer Electrolytes in Li-ion Cells, Electrochim. Acta, 2023, 462, 142759 CrossRef CAS.
- A. Matsumoto, C. Iacob, T. Noda, O. Urakawa, J. Runt and T. Inoue, Introducing large counteranions enhances the elastic modulus of imidazolium-based polymerized ionic liquids, Macromolecules, 2018, 51, 4129–4142 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |