 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The EFG Rosetta Stone: translating between DFT calculations and solid state NMR experiments†
Javier Valenzuela Reina a,
Federico Civaia
a,
Federico Civaia a,
Angela F. Harper
a,
Angela F. Harper a,
Christoph Scheurera and
Simone S. Köcher
a,
Christoph Scheurera and
Simone S. Köcher *ab
*ab
aFritz-Haber Institute of the Max Planck Society, Berlin, Germany
bInstitut für Energie und Klimaforschung (IEK-9), Forschungszentrum Jülich GmbH, Jülich, Germany. E-mail: s.koecher@fz-juelich.de
First published on 13th May 2024
Abstract
We present a comprehensive study on the best practices for integrating first principles simulations in experimental quadrupolar solid-state nuclear magnetic resonance (SS-NMR), exploiting the synergies between theory and experiment for achieving the optimal interpretation of both. Most high performance materials (HPMs), such as battery electrodes, exhibit complex SS-NMR spectra due to dynamic effects or amorphous phases. NMR crystallography for such challenging materials requires reliable, accurate, efficient computational methods for calculating NMR observables from first principles for the transfer between theoretical material structure models and the interpretation of their experimental SS-NMR spectra. NMR-active nuclei within HPMs are routinely probed by their chemical shielding anisotropy (CSA). However, several nuclear isotopes of interest, e.g. 7Li and 27Al, have a nuclear quadrupole and experience additional interactions with the surrounding electric field gradient (EFG). The quadrupolar interaction is a valuable source of information about atomistic structure, and in particular, local symmetry, complementing the CSA. As such, there is a range of different methods and codes to choose from for calculating EFGs, from all-electron to plane wave methods. We benchmark the accuracy of different simulation strategies for computing the EFG tensor of quadrupolar nuclei with plane wave density functional theory (DFT) and study the impact of the material structure as well as the details of the simulation strategy. Especially for small nuclei with few electrons, such as 7Li, we show that the choice of physical approximations and simulation parameters has a large effect on the transferability of the simulation results. To the best of our knowledge, we present the first comprehensive reference scale and literature survey for 7Li quadrupolar couplings. The results allow us to establish practical guidelines for developing the best simulation strategy for correlating DFT to experimental data extracting the maximum benefit and information from both, thereby advancing further research into HPMs.
1 Introduction
Properties, functionality, and longevity of solid state high performance materials (HPMs) depend critically on their atomistic structure. In order to improve and tailor a material's properties, an understanding of its underlying structure is therefore essential. Solid-state nuclear magnetic resonance (SS-NMR) spectroscopy stands as a pivotal analytical tool in the study of inorganic, organic, and hybrid materials, irrespective of their crystalline or amorphous nature.5 The technique's inherent sensitivity to local atomic environments, coupled with its non-destructive approach, renders it indispensable for probing the intricate structural details of various materials.6 Advanced SS-NMR experiments also probe atom dynamics and even allow for in situ and operando studies.7However, most HPMs, such as battery electrodes or catalysts, exhibit complex, ambiguous SS-NMR spectra due to dynamic effects or amorphous phases. NMR crystallography for such challenging materials requires reliable, accurate, and efficient computational methods for calculating NMR observables from first principles for the transfer between theoretical models of a material and the unambiguous interpretation and analysis of its experimental SS-NMR spectra.8–10 Furthermore, as the field turns towards predicting NMR spectra using machine learning and surrogate models which take training data from computed NMR quantities, the accuracy of the underlying first-principles computed observables is often considered as a baseline for extrapolation. Therefore, it is critical to provide a reference to the actual experimental values, to avoid compounding errors during the training process.11
The local atomistic structure of HPMs is often studied by probing the chemical shielding anisotropy (CSA) of their NMR-active nuclei.8–10,12–14 The interpretation of the chemical shifts of diamagnetic compounds in SS-NMR experiments with first-principles calculations of the CSA tensors is already well established.10,12,15,16 However, several nuclear isotopes of interest, e.g. 7Li, and 27Al, also have a nuclear quadrupole and therefore experience additional interactions with the surrounding electric field gradient (EFG), which are another valuable source of information complementing the CSA.17 While the isotropic chemical shielding is an indirect probe for the ability of the local electron density to shield the nucleus in an applied magnetic field,18–20 the quadrupolar coupling is exceptionally sensitive to the symmetry of the electron density distribution and hence a powerful probe for local atomistic environments, structural motifs, and distortions.21,22 The calculation of quadrupolar coupling also requires less computational effort, since it is based on the ground state electronic structure and does not rely on response theory.23 But the quadrupolar coupling manifests as complex features in experimental NMR spectra, such as broadened lines or satellite peaks, hence making theoretical simulations indispensable for reliable interpretation and analysis.2,21,24 There are several examples in the literature which show that experimental quadrupolar parameters in combination with density functional theory (DFT) simulations can be leveraged to perform structure refinement,25,26 force-field validation27,28 as well as dynamic29 and structural investigation30,31 in complex materials.
In the present work, we study the 7Li and 27Al nuclei in detail, since both nuclei play a critical role in high performance energy storage materials, such as solid state electrolytes, state-of-the-art electrodes, and stabilizing coatings.32–34 We apply pseudopotential (PP) plane wave DFT codes to calculate the quadrupolar observables in a series of diamagnetic, ionic, Li and Al crystalline compounds and include an extensive literature survey of experimentally determined quadrupolar properties. We chose to limit our study to diamagnetic compounds, as paramagnetic systems require spin-polarized DFT calculations and often yield less accurate experimental results due to fast relaxation and pronounced broadening.35 The comparison of our simulations with experimental values from literature provides a reference scale and a comprehensive benchmark of the accuracy of the simulation and its dependence on various parameters we tested. Furthermore, we assess the implications of various approximations applied during the computational process.
2 Methods
2.1 The EFG tensor
For NMR-active nuclei with a nuclear spin I > 1/2, the nuclear electric quadrupole moment Q interacts with the local EFG tensor, V, which leads to an additional splitting of energy levels in an external magnetic field beyond the Zeeman effect.36–39 The second-rank, traceless, symmetric EFG tensor describes the gradient of the electric field at the nucleus depending on the surrounding charge distribution as the spatial second derivative of the electrostatic potential V(x)40
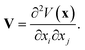 | (1) |
More commonly studied quadrupolar coupling observables are determined by the three eigenvalues Vii of the EFG tensor, which are ordered according to44
| |Vzz| > |Vyy| > |Vxx|. | (2) |
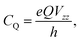 | (3) |
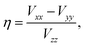 | (4) |
| Isotope | I | Q/fm2 |
|---|---|---|
| 7Li | 3/2 | −4.01 |
| 27Al | 5/2 | 14.66 |
2.2 Calculation of EFG tensors
First approaches to correlate experimental NMR observables with specific structural information or motifs started shortly after the invention of NMR spectroscopy. The first correlation and increment schemes were empirical in nature and targeted indirect spin–spin coupling46,47 and chemical shielding48–52 mostly restricted to organic molecules. The first ab initio calculations of tensorial NMR properties based on the electronic structure near the nucleus relied on local basis sets and were hence technically challenging for the simulation of extended solids.19,20,53,54Crystalline and semi-crystalline (e.g. defected, disordered) solid materials are most commonly described in periodic boundary conditions (PBC) utilizing Bloch plane waves55 to take advantage of the translational symmetry.56,57 PPs approximate the electron density in the nuclear region by an effective core potential and thereby increase the efficiency of plane wave calculations significantly. However, the concept of PPs approximating the core region is diametrically opposed to simulating NMR observables, which capture interactions of the nuclear spin or quadrupolar moment with the local electron density near the nucleus. Only the introduction of the projected augmented wave (PAW)58 and the gauge-including projector augmented-wave (GIPAW)59 methods finally allowed for the simulation of NMR properties of solids in the computationally efficient PP-PBC picture. The PAW formalism reconstructs the electron density in the core region from the optimized pseudo-electron density, while GIPAW adds translational invariance of the magnetic field gauge.17
Since NMR parameters are highly sensitive to the electronic structure, any simulation parameter that influences the converged electron density near the nucleus has an impact on the accuracy of the NMR parameter prediction. In particular, small atoms, such as Li, with a small number of electrons, where the distinction between core region and valence electrons becomes vague, are expected to be susceptible to modifications in the electronic structure calculations.
One of the factors which is known to affect the resulting NMR parameter predictions is the atomistic geometry.60,61 Depending on the material and the method (X-ray diffraction (XRD), neutron scattering), the experimentally determined structure might not be accurate. Hence, first-principles geometry relaxations are sometimes recommended.9,60
In this work, we test several simulation parameters and their impact on the accuracy of the resulting quadrupolar coupling. In order to study the effects of geometry, we compare EFG simulations with the unmodified empirical experimental input structures (empir.), optimized structures with fixed experimental lattice vectors and relaxed atomic positions (fixed cell), and fully optimized structures with both relaxed atomic positions and lattice vectors (opt.). While empir. structures determined by XRD usually fail to give reliable positions for light atoms such as hydrogen, a full DFT structure relaxation yields equilibrium structures at 0 K. Fixed cell structures maintain the room temperature lattice constants adopted from empir. structures, while optimizing atomic positions and in particular equilibrating the coordinates of light atoms.
In addition, we test the influence of exchange–correlation (xc) functionals4,62–64 (LDA,65 PBE,66 PBEsol,67 PW91,68 RSCAN69), PPs, as well as cell size on the accuracy of the quadrupolar coupling computation and establish a reference scale correlating the results with experimental values from literature.
A similar study was previously conducted for CSA of 7Li,15 however for 7Li quadrupolar CQ and η parameters, available literature is significantly sparser. In order to describe the amount of information available for all of the data in our survey, we have classified the 7Li and 27Al compounds into two groups according to the extent of information available.
Group 1: Crystal structure and experimental values for CQ and/or η are available, but not necessarily from the same reference.
Group 2: Crystal structure and the full EFG tensor (direction cosines) are available.
As has been previously reported, the accuracy of the nuclear electric quadrupole moment Q is also critical for comparing experimental and computational CQ values.70,71 But since the Q values for 27Al and 7Li (c.f. Table 1) have not changed by more than 1% since 2008,72,73 we neglect this discussion here.
2.3 Computational details
The structures of the Li and Al compounds were extracted from the Materials Project database,74 the Cambridge Structural Database (CSD)75 or from the cited references.21,41–43,76–106The EFG calculations and geometry optimizations with CASTEP v23.1107,108 are converged with respect to the basis set cut-off energy and the Monkhorst Pack k-point grid. The convergence threshold is set to a variation of less than 5% for CQ as well as η. For the geometry optimizations, an energy tolerance of 2.0 × 10−5 eV per atom, a maximum force of 0.05 eV Å−1, and a stress tolerance of 0.1 GPa per atom are employed. Cut-off energy and k-point grid are adopted from the EFG calculations. The same procedure is followed for the calculations with Quantum ESPRESSO 7.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109,110 (QE), using the same convergence criteria. Further computational details are presented in the ESI.†
109,110 (QE), using the same convergence criteria. Further computational details are presented in the ESI.†
3 Results
3.1 27Al NMR
27Al is one of the best-known and most widely studied quadrupolar nuclei in SS-NMR, both theoretically and experimentally. There is extensive experimental data available in the literature for its quadrupolar observables, both CQ and even η.111 However, to the best of our knowledge, experimental data on its full EFG tensors is rather sparse. Here, we discuss a set of 13 Al compounds of Group 1 and two of Group 2.Since Al is rather oxophilic, it is preferentially coordinated by oxygen in octahedral AlO6 environments, which suggests a small to negligible quadrupolar coupling due to the high local symmetry. But the large nuclear electric quadrupole moment Q amplifies even a small Vzz, which might arise from small distortions or a less symmetric crystal space group, to a sizable CQ.112
Testing the impact of the xc-functional on the calculated CQ and η with CASTEP shows that the highly ionic Al compounds studied here are well described by both LDA,65 GGA (PBE,66 PBEsol,67 PW9168), and meta-GGA (RSCAN69) functionals. The standard deviation of CQ and η with respect to the applied xc-functional is on the order of 3% and 9%, respectively. The impact of the xc-functional is thus deemed negligible and further calculations are all conducted with PBE.66
Similarly, simulations based on the different crystal geometries empir., fixed cell, and opt. derived with CASTEP only yield standard deviations on the order of 6% and 15% for CQ and η, respectively. Overall, the fixed cell structures provide the best agreement with experimental reference values. The opt. structures yield the least reliable predictions, since PBE66 is well known to overestimate interatomic bond lengths113 and hence allows the cell volume to extend and distort. Lattice parameters of crystalline materials determined experimentally with high confidence are regularly available in literature or databases, discouraging the use of the opt. structures in this case.114 Since the effect of DFT relaxation, either fixed cell or opt., is minimal, all further calculations are performed with fixed cell structures.
The power of PBC is that they represent an infinitely large defect-free model of a crystalline solid by exploiting the translational symmetry of the Bloch plane waves.55 Calculations in PBC are usually conducted on the smallest possible unit cell (primitive cell) and expected to yield the same results as a supercell. However, previous studies have shown that cell symmetry and supercell effects can cause numerical errors depending on the implementation of the PBC, grids, and the charge augmentation.15,115 Hence, the CASTEP EFG calculations are repeated with 2 × 2 × 2 supercells producing identical results and ruling out any supercell effects in the case of Al.
Al is a third period element with three valence electrons in the 3s and 3p orbitals. The ten electrons of the first and second period orbitals can be considered core orbitals. Correspondingly, the default CASTEP PP (C19) includes those electrons in the effective core potential and only treats the three valence electrons explicitly. The same discrimination is made in the Quantum ESPRESSO PP utilized in this work. Tests using a CASTEP hard PP with eleven electrons being treated explicitly yield a minor decline in agreement with experiment by 0.17 MHz for CQ, whereas η remains unaffected. Details can be found in the ESI Table S3.†
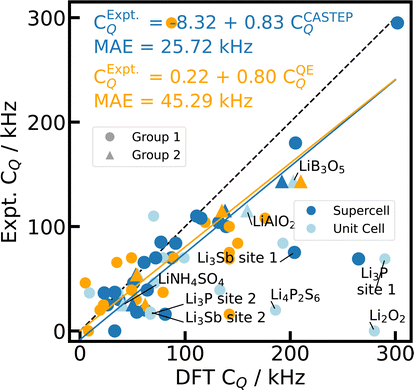
In general, the simulations with PBE,66 fixed cell geometry, and default PP yield a good agreement with experimental 27Al CQ values both for CASTEP and Quantum ESPRESSO calculations as shown in Fig. 1 with a mean absolute error of the linear fit (MAE) of 0.90 MHz (18%) and 1.14 MHz (24%), respectively. Distinct outliers are found for θ-Al2O3,98 κ-Al2O3,78 and AlVO479 (c.f. ESI†), which feature Al on multiple inequivalent crystallographic positions. For κ-Al2O3 and AlVO4, comparison of the literature references78,79,81,116 with the structural data derived from CSD75 does not allow for an unambiguous assignment of the different crystallographic positions or reveal inconsistencies between different references. Therefore, we neglect κ-Al2O3 and AlVO4 here.
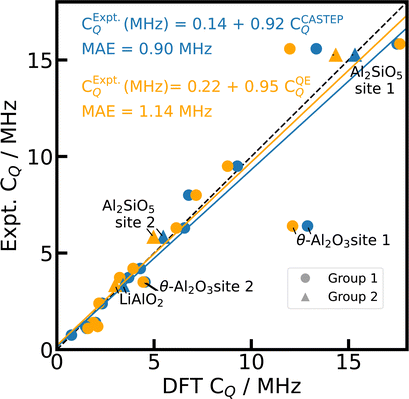 | ||
| Fig. 1 Reference scale for 27Al CQ. The 27Al CQ values for 15 Al-containing compounds are simulated with PBE, fixed cell geometries, default PP, and unit cells using CASTEP (blue) and Quantum ESPRESSO (orange). The experimental values from literature can be found in ESI Table S3.† κ-Al2O3 and AlVO4 are omitted (see text). The dashed diagonal line indicates the limit of ideal correlation. | ||
In comparison to the reference scale for 27Al CQ, the correlation between DFT and experimental values of 27Al η is considerably less accurate, especially for the mentioned outliers (c.f. ESI†), with a MAE of 0.13 and 0.16 (c.f. Fig. 2) for CASTEP and Quantum ESPRESSO, respectively. The asymmetry of η is even more sensitive to the local charge distribution and its symmetry than CQ as a result of its dependence on all the three components of the EFG tensor (eqn (4)), leading to a more pronounced error propagation of inaccuracies in the electron density. When correlating the individual principal components of the EFG tensor with values derived from experimental CQ and η values (ESI Fig. S3†), the larger deviation of η is reflected in the larger errors of Vyy, in particular for the outlier θ-Al2O3.
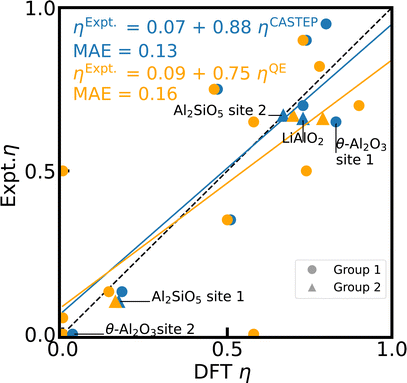 | ||
| Fig. 2 Reference scale for 27Al η. The 27Al η values for 15 Al-containing compounds are simulated with PBE, fixed cell geometries, default PP, and unit cells using CASTEP (blue) and Quantum ESPRESSO (orange). The experimental values from literature can be found in ESI Table S3.† κ-Al2O3 and AlVO4 are omitted (see text). The dashed diagonal line indicates the limit of ideal correlation. | ||
For 27Al, we found full experimental EFG tensors for both Al2SiO5 and γ-LiAlO2 in the literature43,117 (Group 2), which provide us with the unique opportunity to not only evaluate the accuracy of the calculated magnitude CQ and shape η of the EFG tensor, but also its orientation with respect to the crystal lattice. The experimental references provide the so-called direction cosines of the EFG tensor for each magnetically inequivalent 27Al site, which can be correlated to the eigenvectors of the EFG tensor. Fig. 3 depicts the comparison of experimental and theoretical direction cosines (red and orange for Al2SiO5 and pink for γ-LiAlO2). The DFT simulations can reproduce the experimental values with an average error of 5%, and show especially good agreement for γ-LiAlO2, which actually outperforms the previous DFT results,97,118 hence predicting the orientation of the EFG tensor with excellent accuracy.
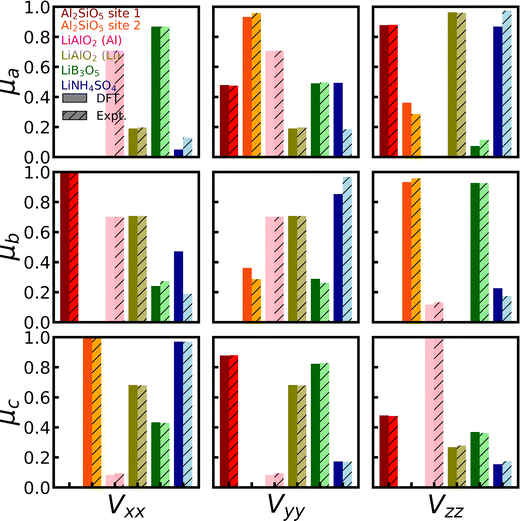 | ||
| Fig. 3 Orientation of EFG tensors for 7Li and 27Al. The experimentally determined direction cosines of LiB3O5,41 LiNH4SO4,42 Al2SiO5,43 and γ-LiAlO297 are compared with full EFG tensors calculated with CASTEP, PBE, fixed cell geometry, default PP, and supercells (for 7Li) and unit cells (for 27Al). The direction cosines give the projection of each EFG eigenvector Vi on each lattice vector μj of the studied material. | ||
The reliable prediction of quadrupolar observables for 27Al with good accuracy independent of xc-functional, geometry relaxation, PP, and supercell effect verifies the plane wave, PP method with GIPAW as a robust and useful approach for calculating solid state EFGs. The quantitatively close agreement between CASTEP and Quantum ESPRESSO results proves the reliability of the method independent of the implementation, for 27Al.
3.2 7Li NMR
Although 7Li and its quadrupolar couplings are not as well studied as 27Al, quadrupolar 7Li SS-NMR plays a crucial role in materials research for Li ion batteries, where Li is the charge carrier.34 A multitude of different NMR experiments is available that probe the local atomistic structure of 7Li as well as its dynamics by addressing either CSA or quadrupolar interactions.91 Operando experiments even allow for tracking charge transport through batteries while cycling.119In contrast to 27Al, the nuclear electric quadrupole moment Q for 7Li is an order of magnitude smaller, and Li has only three electrons. A small number of electrons presents a challenge when using a Li PP, which divides the electrons into core and valence electrons as well as the electron density in a core and an interstitial region. For the three electrons of Li, this distinction becomes ambiguous. Furthermore, the number of experimental 7Li CQ, and in particular η and explicit EFG tensors components for crystalline, ionic, diamagnetic Li compounds available in the literature is limited. In the following, we discuss a set of 23 Li compounds, of which 20 belong to Group 1, and three to Group 2. However, the availability of data for η is extremely sparse.
As already observed for 27Al, the impact of the xc-functional is negligible for these ionic compounds with standard deviations of 1% and 3% for CASTEP-based CQ and η, respectively. PBE66 is chosen as the default xc-functional for all further analyses (c.f. Fig. 4).
 | ||
| Fig. 4 Reference scale for 7Li CQ. The 7Li CQ values for 23 Li-containing compounds are calculated with PBE, fixed cell geometries, using CASTEP for unit cells (light blue), 2 × 2 × 2 supercells (blue), and Quantum ESPRESSO (orange) with the default PP in each case. The experimental values from literature can be found in ESI Table S4.† The dashed diagonal line indicates the limit of ideal correlation. Outliers including Li3P and Li3Sb are labelled and described further in the text. The data point for Li3N [site 1] (CQ = 582 kHz, ESI Table S4†) is beyond the depicted range, but is included in the regression analysis. | ||
Similarly, the details of geometry relaxation are largely irrelevant with a standard deviation of 3% (CQ) and 10% (η) for empir., fixed cell, and opt. geometries simulated with CASTEP. However, there is one significant exception, LiNH4SO4.42 With the experimental crystal structure adopted from CSD,75 the calculated η is off by more than factor 3 for the unit cell and gets even worse for the supercell (data not shown). Closer inspection of the crystal structure reveals rather different N–H bond lengths in the NH4+ units, which do not correspond to the structure visualized in ref. 42. Neither the fixed cell nor the opt. structures improve the accuracy notably with respect to the experimental reference of η. Only a DFT fixed cell relaxation with a relaxed symmetry tolerance allows the N–H bonds to equilibrate, yielding a considerably better agreement with experiment and in particular an improvement by the supercell effect (c.f. Fig. 5).
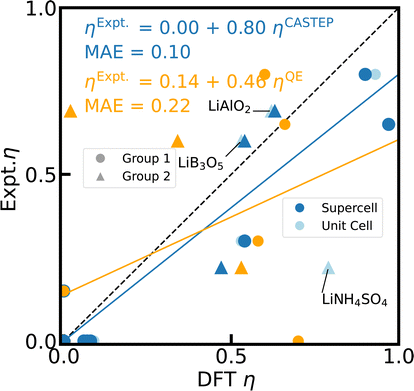 | ||
| Fig. 5 Reference scale for 7Li η. The 7Li η values for 23 Li-containing compounds are calculated with PBE, fixed cell geometries, using CASTEP for unit cells (light blue), 2 × 2 × 2 supercells (blue), and Quantum ESPRESSO (orange) with the default PP in each case. For 15 of those compounds, the experimental values from literature can be found in ESI Table S4.† The dashed diagonal line indicates the limit of ideal correlation. Outliers including LiNH4SO4 are labelled and described further in the text. | ||
Other striking outliers in the CQ correlation (Fig. 4) can be identified as the hexagonal, layered Li pnictide Li3P and its homologous Li3Sb90 (hex-Li3Pn). The calculated CQ values of the different crystallographic sites are qualitatively correct, matching the Li in the Li–pnictogen layer (P, Sb) with the larger CQ value and the Li in the pure Li interlayer with the smaller CQ constant. However, the overestimation by DFT simulations amounts to factor 3 to 5. Both Li3P and Li3Sb are well-known Li ion conductors, facilitating fast ionic mobility through the pure Li layer, which is known to result in a smaller experimentally observable quadrupolar coupling constant reduced by partial motional averaging.15,120 Li3N is also known as a good Li ion conductor, but shows excellent agreement for CQ simulated with CASTEP. Here we study the cubic, layered Li3N phase, rather than one homologous to the hexagonal Li3P and Li3Sb, where Li ion mobility up to 300 K takes place predominantly within the Li–pnictogen layer.121 Including the temperature-dependent influence of ionic mobility on the quadrupolar observables either via the vibrational modes,122 via chemical exchange models,15 or via molecular dynamics12,13,123,124 is beyond the scope of this study.
Even when neglecting the outliers, the correlation of the calculated CQ and η with experimental values (Fig. 4 and 5 in light blue) exhibits a major, systematic overestimation of CQ and distinct discrepancies of η by up to several orders of magnitude for unit cell simulations. CASTEP calculations with 2 × 2 × 2 supercells confirm a significant supercell effect, especially for materials with small CQ and small unit cells. The supercell effect converges rapidly with cell size as test calculations with 3 × 3 × 3 supercells corroborate, showing convergence is already achieved for 2 × 2 × 2. The effect might result from approximations in the charge augmentation of CASTEP that exceed their physical limit125 or from long range interactions not correctly captured by the approximations utilized in the PBC implementation. The supercell effect is not observable in Quantum ESPRESSO.
Despite the correction for the supercell effect by using 2 × 2 × 2 cells, the CASTEP DFT calculations still feature a significant overestimation of CQ by about 20% (12% without hex-Li3Pn) with respect to experimental values. In principle, an inaccurate nuclear electric quadrupole moment Q for deriving CQ from the DFT calculated EFG tensor could explain the discrepancy. However, this overestimation has been observed before21 for 7Li as well as other light nuclei, and is usually attributed to a hypothesis formulated in the 1950s by Sternheimer,126–128 proposing that the polarization of the electronic K-shell induces a secondary quadrupolar moment that shields the nuclear electric quadrupole moment Q. This effect cannot be correctly reproduced within the PP approach. Therefore, the PP-GIPAW calculations tend to overestimate CQ.
In contrast to 27Al, 7Li is a second period element with only three electrons in total. The distinction between core and valence electrons becomes ambiguous for such small elements. The default PP of CASTEP (C19) and the one utilized for Quantum ESPRESSO in this work describe all three electrons explicitly as valence electrons. Nevertheless, there is still a core region defined by the core radius which is pseudized. The larger the core radius, the softer the PP and hence the less computationally demanding are the DFT calculations of the electronic structure, since they converge faster with respect to the number of plane waves. On the other hand, a smaller core radius makes the PP harder, potentially improves the description of the electron density in the vicinity of the core, and presumably is better able to capture the polarization near the nucleus. The impact of the core radius was tested for four Li salts by generating a set of modified pseudopotentials with different core radii.129 The comparison in Fig. 6 shows that reducing the size of the core region can trigger important changes in the predicted EFGs, lowering the calculated CQ with only minor impact on η (c.f. ESI Fig. S2†). Although these results can be interpreted as a reduction in the overestimation of CQ, their reliability requires a more detailed investigation in the Discussion.
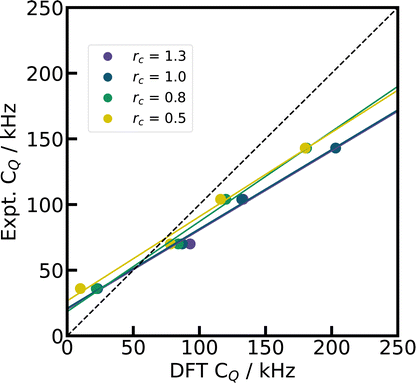 | ||
| Fig. 6 Test with harder CASTEP PP. By changing the core radius rc for the Li PP in CASTEP (default rc = 1.0), we demonstrate the effect of a smaller Li pseudized core region on the simulated CQ for four Li compounds (LiIO3,96 Li2CO3,21 Li2B4O7,87 LiB3O541), with PBE, fixed cell geometries, and supercells. The dashed diagonal line indicates the limit of ideal correlation. | ||
For 7Li, we could also find experimentally determined eigenvalues of the EFG tensors for Li2B4O7, LiNbO3, LiCsB6O10 (Group 1) and LiB3O5 (Group 2)41 (c.f. ESI Table S5†). Together with the principal components Vii derived from the experimental CQ and η, the correlation plot Fig. S4 (ESI)† shows that CASTEP is able to predict these quantities quite reliably. However, the systematic overestimation observed for CQ is naturally reproduced by the notable overestimation of Vzz. But also Vxx and Vyy are overestimated, supporting the hypothesis of a shielded nuclear electric quadrupole moment, which does not become apparent in the η correlation in Fig. 5.
For LiB3O5, LiNH4SO4, and γ-LiAlO2, the full experimental EFG tensors are available in the literature41,42,97,118 (Group 2). Fig. 3 (blue and greens) shows the comparison of the series of tensors. The DFT simulations can reproduce the experimental values with a MAE of 15% of the experimental values, hence predicting the orientation of the EFG tensor with reasonable accuracy. Nevertheless, also for LiB3O5, LiNH4SO4, and γ-LiAlO2, we observe the systematic overestimation of the magnitude CQ as described before.
In contrast to 27Al, the quadrupolar coupling of 7Li proves to be more challenging to simulate reliably with CASTEP. Geometry relaxation and xc-functional once again do not show any significant impact as such, whereas the case of LiNH4SO4 demonstrates clearly the crucial importance of the correct representation of local atomistic structure and symmetry in particular on η. However, the CASTEP implementation of PBC does not prove to be robust to supercell effects, providing inaccurate results for primitive unit cell simulations in particular for small CQ values. Furthermore, the PP approximation appears to reach its limits for 7Li, which presumably results in the systematic overestimation of CQ for 7Li. Nevertheless, considering the linear correlation between experiment and DFT calculated η values, the choice of approximations and computational schemes implemented in CASTEP performs quite well and predicts η with a MAE of 0.10 and a scaling factor of 0.80.
Quantum ESPRESSO and CASTEP are both PP-GIPAW, plane wave DFT codes, describing the electronic structure within the same basis based on the same physical picture and approximations. Our Quantum ESPRESSO simulations follow the workflow described for CASTEP as closely as possible. The xc-functional and the crystal geometries are identical, while the computational settings and convergence parameters are chosen to reflect the CASTEP ones as accurately as possible. While the results for 27Al CQ are almost identical between CASTEP and Quantum ESPRESSO (Fig. 1) and follow a comparable trend for 27Al η (Fig. 2), 7Li reveals major discrepancies.
The default GIPAW-PPs of CASTEP and Quantum ESPRESSO for Li and Al are based on the same assignment of core and valence electrons for each element. Nevertheless, other PP key values such as core radius, number and angular momentum of projectors, local and non-local channels as well as the parameterization are not comparable. For 27Al, transferability between the codes does not suffer despite the different default PPs. The smaller 7Li on the other hand is more sensitive to modifications in the PP. Moreover, the sizable supercell effect demonstrated for 7Li in CASTEP, which is not detectable in Quantum ESPRESSO, proves that the implementations though based on the same physical descriptions are distinctly different. In order to get comparable accuracy and reliability for 7Li EFG calculations in Quantum ESPRESSO, a similar, detailed testing and workflow optimization as described above for CASTEP is necessary but beyond the scope of this work. It is just important to stress that simulation strategies and workflows cannot necessarily be transferred between codes, even if they are based on the same physical principles.
4 Discussion
In recent decades, the PP-GIPAW method has established itself as the standard method for calculating NMR properties for crystalline solid state materials ranging from CSA, indirect spin–spin coupling to quadrupolar coupling.130–132 At first glance, the PP approximation of the electron density in the core region by an effective core potential appears counterintuitive for simulating interactions of nuclear spin with its environment. However, the reconstruction of the all-electron electron density from the converged, pseudized electron density with the GIPAW method has proven to be an efficient and reliable approach to predict nuclear interactions with robust accuracy for a wide range of materials.133,134Our results for 27Al CQ quadrupolar observables and their excellent agreement with experimental references confirm the PP-GIPAW method as a powerful tool for EFG predictions, supporting NMR crystallography as has been shown before.135 While 27Al is one of the most commonly studied quadrupolar nuclei in SS-NMR and well described in the PP picture, our literature survey confirms that 7Li is not as widely studied and challenges the PP approximation. On the one hand, previous benchmarking has shown accurate predictions of 7Li chemical shifts with PP-GIPAW methods.15 On the other hand, the EFG tensor is highly sensitive to small changes and aspherical asymmetries of the electron density near the nucleus,1 since it depends with r−3 on the charge distribution and its symmetry.17 Furthermore, it is known that the polarization of the K-shell electrons in a magnetic field induces a local quadrupolar moment, which counteracts the nuclear electric quadrupole moment Q and yields a reduced effective quadrupole moment.126–128 The K-shell polarization is most pronounced for first and second period elements. In addition, elements on the left side of the periodic table have been reported to struggle with a precise representation of shallow core states in the plane wave basis, where electrons of the shell below the valence shell (n − 1) have semi-core character and need to be described as quasi-valence electrons.1
Several examples show that PP-GIPAW predictions of CQ for 7Li and other light nuclei29,136 suffer from a systematic overestimation.21 Our simulations exceed the experimental CQ by about 20% (12% without hex-Li3Pn) on average, which is well in line with reported overestimation factors for 7Li of 1.20,21 1.15,136 and 1.11.127
Specific modifications of the Li PP and CASTEP test calculations with harder PPs support the hypothesis that the systematic overestimation for 7Li CQ might originate from the inadequate description of the K-shell polarization and/or the semi-core states in the default PP picture. However, harder PPs require much larger plane wave basis sets for convergence and hence increase the computational cost by orders of magnitude. Moreover, development of reliable, transferable, robust, and versatile PPs is an art in itself. Our test Li PPs have not been optimized or tested beyond their convergence with cut-off energy and they have not been benchmarked against other properties such as energies, forces, or band structure, not even against other NMR parameters, e.g. CSA. The harder Li PPs with smaller core regions have only been used to test the hypothesis that a better, i.e. explicit treatment of the electron density close to the nucleus improves the agreement of simulated CQ with experimental values. Modifying PPs to improve agreement with experimental reference values is strongly discouraged, even if it can be physically justified. Instead, linear correlation relationships offer a viable and robust tool to translate between DFT simulated quadrupolar couplings and experimental observables, which is both computationally efficient and transferable to other systems within the limits of the applied methods, settings, and parameters.
The strong sensitivity of the EFG tensor to the local charge distribution is not only expressed in the significance of K-shell polarization and semi-core states, but also in any factor that potentially impacts the accuracy of DFT-derived electronic densities. Several of these factors are computational parameters, which can be converged, such as basis set size, k-point grid, integration grid, convergence threshold etc, and are not discussed here. More general computational settings, which cannot be converged, include xc-functional, crystal geometry, and supercell effects. In order to establish a robust and reliable linear interpolation scheme, these factors need to be studied.
For ionic, diamagnetic 27Al and 7Li compounds, we could show that the xc-functional and geometry relaxation have only minor significance and can be disregarded. However, this observation cannot be generalized. Compounds and elements with more covalent type binding character, hydrogen bonds, or π-orbital interactions might not be adequately represented by LDA or GGA but might benefit from hybrid xc-functionals. Naturally, crystal geometry and the local atomic environment has a major impact on the electron density throughout the material as well as close to nuclei. The observed, negligible impact of geometry relaxation arises from the very accurate, experimental crystal structures, where additional first-principles relaxations do not show any major change in atomic coordinates anyway. The most notable exceptions are materials containing hydrogen, such as LiNH4SO4, since H does not scatter very well and its position cannot be determined reliably with XRD. Hence, fixed cell optimizations have been reported to improve prediction accuracy of DFT-derived NMR properties.114
The supercell effect, which we have introduced above, is a collective term comprising any change in the computed property by simulating supercells or conventional instead of primitive unit cells. Supercell effects might arise from the implementation of integration grids, the treatment of crystal symmetry,15 charge augmentations,125 or any physical approximations applied in the PBC, which might be stretched beyond their limits of validity. Besides, supercell effects might only affect certain elements (e.g. light elements), certain crystal symmetries (e.g. hexagonal) or cells (e.g. small unit cells). Therefore, testing for supercell effects is expedient to rule out any obscure inconsistencies between simulation and experiment.
In general, the PP-GIPAW method is verified as a powerful tool for simulating EFG tensors and quadrupolar observables in periodic solids as demonstrated by the good accuracy of the predicted EFG tensor orientations with respect to the crystal lattice. Even for challenging nuclei such as 7Li, the PP approach can be successfully applied, if certain measures are taken. With careful benchmarking of the nucleus and material class of interest, a transferable interpolation scheme has to be derived, which is only valid for the specified set of method (i.e. software), settings (i.e. xc, basis set and k-point grid convergence), and approximations (i.e. PP, PBC), but can then be utilized for production calculations of unknown, more complex materials.
5 Conclusion
The performance and accuracy of the plane wave PP-GIPAW DFT method for computing quadrupolar couplings has been benchmarked before,31,137 even specifically for 27Al.1,116 In this work, we focus on the less well-studied quadrupolar nucleus 7Li and compare it with the widely known 27Al, including a comprehensive literature survey and summary of the available experimental data. To the best of our knowledge, we report the first EFG reference scale for 7Li.We evaluate the performance of the plane wave PP-GIPAW DFT method, using CASTEP and Quantum ESPRESSO, and investigate not only the magnitude of the quadrupolar coupling CQ, but also the shape of the EFG tensor η as well as its orientation given by the experimental direction cosines. Testing the impact of xc-functional, structure relaxation, PP, and supercell effects on the accuracy of the theoretical prediction, the simulations prove to be robust and reliable for 27Al. 7Li however exceeds the limits of the PP approximation and shows considerable supercell effects in CASTEP. Based on benchmarking well-known reference substances, we propose practical guidelines for establishing a transferable linear correlation scheme for challenging nuclei such as 7Li, which can then be applied to translate between theoretical simulations and experimental results of unknown, complex materials. Using this in depth scrutinised and optimized linear correlation scheme, the simulated CQ and η for both 7Li and 27Al are in good agreement with experiment with an average error on the order of 10% to 20%, while the accuracy of the predicted tensor orientation is excellent.
The PP-GIPAW method competes with all-electron methods, which avoid the PP approximation but are technically more complex for periodic systems and computationally more expensive.3,17 More recently, solid state cluster embedding methods138–141 have been developed for NMR properties, which describe the immediate environment of the nucleus of interest at all-electron level and embed it in layered shells of classical molecular mechanics and point charges to mimic the long range interactions of a bulk material. While methodologically rather complex, the embedding method is very promising, especially for aperiodicities such as defects or disorder and for amorphous solid phases.
Author contributions
Javier Valenzuela Reina: investigation, methodology, writing – original draft, data curation. Federico Civaia: writing – original draft, writing – review and editing. Angela F. Harper: supervision, visualization. Christoph Scheurer: conceptualization, funding acquisition, supervision. Simone S. Köcher: conceptualization, supervision, writing – original draft, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
All the authors would like to thank Prof. Chris Pickard, Prof. Jonathan Yates, Dr Philipp Schleker, and Prof. Dr Josef Granwehr for scientific exchange and valuable discussions. We finally gratefully acknowledge the computational and data resources provided by the Max Planck Computing and Data Facility (MPCDF). AFH would like to acknowledge the support of the Alexander von Humboldt Foundation. JV acknowledges funding by the Bundesministerium für Bildung und Forschung (BMBF) within the Verbundprojekt AdamBatt (FKZ: 03XP0305D). FC and CS would like to acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the cluster of excellence EXC 2089: e-conversion.References
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz and P. Herzig, Phys. Rev. Lett., 1985, 54, 1192–1195 CrossRef CAS PubMed.
- A. R. Ferreira, K. Reuter and C. Scheurer, RSC Adv., 2016, 6, 41015–41024 RSC.
- R. Böhmer, K. R. Jeffrey and M. Vogel, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87–174 CrossRef.
- B. Reif, S. E. Ashbrook, L. Emsley and M. Hong, Nat. Rev. Methods Primers, 2021, 1, 2 CrossRef CAS PubMed.
- L. A. O'Dell and C. I. Ratcliffe, in NMR of Quadrupolar Nuclei in Solid Materials, ed. R. E. Wasylishen, S. E. Ashbrook and S. Wimperis, Wiley, Hoboken, NJ, 1st edn, 2012, pp. 213–232 Search PubMed.
- S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204 RSC.
- R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174–S186 CrossRef CAS PubMed.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS.
- M. C. Venetos, M. Wen and K. A. Persson, J. Phys. Chem. A, 2023, 127, 2388–2398 CrossRef CAS PubMed.
- A. F. Harper, S. P. Emge, P. C. Magusin, C. P. Grey and A. J. Morris, Chem. Sci., 2023, 14, 1155–1167 RSC.
- I. Chubak, L. Scalfi, A. Carof and B. Rotenberg, J. Chem. Theory Comput., 2021, 17, 6006–6017 CrossRef CAS PubMed.
- S. A. Southern and D. L. Bryce, Annu. Rep. NMR Spectrosc., 2021, 102, 1–80 CrossRef CAS.
- S. Köcher, P. Schleker, M. Graf, R.-A. Eichel, K. Reuter, J. Granwehr and C. Scheurer, J. Magn. Reson., 2018, 297, 33–41 CrossRef PubMed.
- C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512 CrossRef CAS PubMed.
- J. W. Zwanziger, in NMR of Quadrupolar Nuclei in Solid Materials, ed. R. E. Wasylishen, S. E. Ashbrook and S. Wimperis, Wiley, Hoboken, NJ, 1st edn, 2012, pp. 199–209 Search PubMed.
- W. Kutzelnigg, in Calculation of NMR and EPR Parameters: Theory and Applications, 2004, pp. 43–82 Search PubMed.
- W. Kutzelnigg, Isr. J. Chem., 1980, 19, 193–200 CrossRef CAS.
- W. Kutzelnigg, U. Fleischer and M. Schindler, in Deuterium and Shift Calculation, NMR Basic Principles and Progress, Springer, Berlin, 1990, vol. 23 Search PubMed.
- M. T. Dunstan, J. M. Griffin, F. Blanc, M. Leskes and C. P. Grey, J. Phys. Chem. C, 2015, 119, 24255–24264 CrossRef CAS.
- S. E. Ashbrook and S. Sneddon, J. Am. Chem. Soc., 2014, 136, 15440–15456 CrossRef CAS PubMed.
- J. R. Yates and C. J. Pickard, in eMagRes, John Wiley & Sons Ltd, 2007 Search PubMed.
- M. M. Islam and T. Bredow, J. Phys. Chem. C, 2016, 120, 7061–7066 CrossRef CAS.
- F. A. Perras and D. L. Bryce, J. Phys. Chem. C, 2012, 116, 19472–19482 CrossRef CAS.
- F. A. Perras, I. Korobkov and D. L. Bryce, CrystEngComm, 2013, 15, 8727–8738 RSC.
- S. T. Holmes and R. W. Schurko, J. Phys. Chem. C, 2018, 122, 1809–1820 CrossRef CAS.
- S. T. Holmes, C. S. Vojvodin and R. W. Schurko, J. Phys. Chem. A, 2020, 124, 10312–10323 CrossRef CAS PubMed.
- J. M. Griffin, A. J. Miller, A. J. Berry, S. Wimperis and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2010, 12, 2989–2998 RSC.
- J. M. Griffin, L. Clark, V. R. Seymour, D. W. Aldous, D. M. Dawson, D. Iuga, R. E. Morris and S. E. Ashbrook, Chem. Sci., 2012, 3, 2293–2300 RSC.
- S. E. Ashbrook, L. L. Pollès, C. J. Pickard, A. J. Berry, S. Wimperis and I. Farnan, Phys. Chem. Chem. Phys., 2007, 9, 1587–1598 RSC.
- S. Stegmaier, R. Schierholz, I. Povstugar, J. Barthel, S. P. Rittmeyer, S. Yu, S. Wengert, S. Rostami, H. Kungl and K. Reuter, et al., Adv. Energy Mater., 2021, 11, 2100707 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- F. Blanc, L. Spencer and G. R. Goward, in NMR of Quadrupolar Nuclei in Solid Materials, ed. R. E. Wasylishen, S. E. Ashbrook and S. Wimperis, Wiley, Hoboken, NJ, 1st edn, 2012 Search PubMed.
- J. Cuny, J. Yates, R. Gautier, E. Furet, E. Le Fur and L. Le Pollès, Magn. Reson. Chem., 2010, 48, S171–S175 CrossRef CAS PubMed.
- P. P. Man, in Encyclopedia of Nuclear Magnetic Resonance, ed. D. M. Grant and R. K. Harris, J. Wiley, Chichester, 1996, pp. 3838–3848 Search PubMed.
- J. D. Memory, Quantum Theory of Magnetic Resonance Parameters, McGraw-Hill, New York, 1968 Search PubMed.
- P. Schwerdtfeger, M. Pernpointner and W. Nazarewicz, in Calculation of NMR and EPR Parameters, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH, Weinheim, 1st edn, 2004, pp. 279–289 Search PubMed.
- K. Schmidt-Rohr and H. W. Spiess, in Multidimensional Solid State NMR and Polymers, Acad. Press, London, 1st edn, 1994, pp. 18–21 Search PubMed.
- A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, Oxford, 1st edn, 1961 Search PubMed.
- A. R. Lim, J. W. Kim and C. S. Yoon, J. Appl. Phys., 2003, 94, 5095–5099 CrossRef CAS.
- A. Lim, S.-E. Park and S.-Y. Jeong, Solid State Commun., 2000, 113, 389–394 CrossRef CAS.
- S. S. Hafner, M. Raymond and S. Ghose, J. Chem. Phys., 1970, 52, 6037–6041 CrossRef CAS.
- R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59–84 CrossRef CAS.
- M. H. Levitt, Spin Dynamics, John Wiley & Sons, 2008 Search PubMed.
- M. Karplus, J. Chem. Phys., 1959, 30, 11–15 CrossRef CAS.
- M. Karplus, J. Am. Chem. Soc., 1963, 85, 2870–2871 CrossRef CAS.
- D. M. Grant and E. G. Paul, J. Am. Chem. Soc., 1964, 86, 2984–2990 CrossRef CAS.
- L. P. Lindeman and J. Q. Adama, Anal. Chem., 1971, 43, 1245–1252 CrossRef CAS.
- W. Bremser, Anal. Chim. Acta, 1978, 103, 355–365 CrossRef CAS.
- A. Ejchart, Org. Magn. Reson., 1980, 13, 368–371 CrossRef CAS.
- Y. A. Shahab and H. A. Al-Wahab, J. Chem. Soc., Perkin Trans. 2, 1988, 255–256 RSC.
- M. Schindler and W. Kutzelnigg, J. Chem. Phys., 1982, 76, 1919–1933 CrossRef CAS.
- M. Schindler and W. Kutzelnigg, J. Am. Chem. Soc., 1983, 105, 1360–1370 CrossRef CAS.
- F. Bloch, Z. Phys., 1929, 52, 555–600 CrossRef.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20 CrossRef CAS PubMed.
- F. Vasconcelos, S. Cristol, J.-F. Paul, L. Montagne, F. Mauri and L. Delevoye, Magn. Reson. Chem., 2010, 48, S142–S150 CrossRef CAS PubMed.
- M. Body, C. Legein, J.-Y. Buzaré, G. Silly, P. Blaha, C. Martineau and F. Calvayrac, J. Phys. Chem. A, 2007, 111, 11873–11884 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235118 CrossRef.
- F. Tran, S. Ehsan and P. Blaha, Phys. Rev. Mater., 2018, 2, 023802 CrossRef CAS.
- R. Laskowski, P. Blaha and F. Tran, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195130 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101 CrossRef PubMed.
- C. Leroy, P. M. Szell and D. L. Bryce, Magn. Reson. Chem., 2019, 57, 265–267 CrossRef CAS PubMed.
- Y. Zhang, S. Mukherjee and E. Oldfield, J. Am. Chem. Soc., 2005, 127, 2370–2371 CrossRef CAS PubMed.
- P. Pyykkö, Mol. Phys., 2008, 106, 1965–1974 CrossRef.
- P. Pyykkö, Mol. Phys., 2018, 116, 1328–1338 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- T. Bräuniger, C. Chandran, U. Wedig and M. Jansen, Z. Anorg. Allg. Chem., 2011, 637, 530–535 CrossRef.
- D. Müller, E. Jahn, G. Ladwig and U. Haubenreisser, Chem. Phys. Lett., 1984, 109, 332–336 CrossRef.
- C. V. Chandran, C. E. A. Kirschhock, S. Radhakrishnan, F. Taulelle, J. A. Martens and E. Breynaert, Chem. Soc. Rev., 2019, 48, 134–156 RSC.
- U. G. Nielsen, A. Boisen, M. Brorson, C. J. H. Jacobsen, H. J. Jakobsen and J. Skibsted, Inorg. Chem., 2002, 41, 6432–6439 CrossRef CAS PubMed.
- J. Skibsted, E. Henderson and H. J. Jakobsen, Inorg. Chem., 1993, 32, 1013–1027 CrossRef CAS.
- B. Ollivier, R. Retoux, P. Lacorre, D. Massiot and G. Férey, J. Mater. Chem., 1997, 7, 1049–1056 RSC.
- R. C. L. Mooney, Acta Crystallogr., 1956, 9, 728–734 CrossRef CAS.
- Y. Muraoka and K. Kihara, Phys. Chem. Miner., 1997, 24, 243–253 CrossRef CAS.
- C. Jacoboni, A. Leble and J. Rousseau, J. Solid State Chem., 1981, 36, 297–304 CrossRef CAS.
- T. M. Gesing and W. Jeitschko, Z. Naturforsch. B, 1995, 50, 196–200 CrossRef CAS.
- A. R. Lim, K. S. Hong, S. H. Choh and S.-Y. Jeong, Solid State Commun., 1997, 103, 693–698 CrossRef CAS.
- A. R. Lim and I. G. Kim, Solid State Nucl. Magn. Reson., 2015, 66–67, 40–44 CrossRef CAS PubMed.
- M. Leskes, N. E. Drewett, L. J. Hardwick, P. G. Bruce, G. R. Goward and C. P. Grey, Angew. Chem., Int. Ed., 2012, 51, 8560–8563 CrossRef CAS PubMed.
- E. Witt, C. V. Chandran and P. Heitjans, Solid State Ionics, 2017, 304, 60–64 CrossRef CAS.
- G. W. Ossman and A. A. Silvidi, J. Chem. Phys., 1971, 54, 979–982 CrossRef CAS.
- O. E. O. Zeman, I. L. Moudrakovski, C. Hartmann, S. Indris and T. Bräuniger, Molecules, 2020, 25, 469 CrossRef CAS PubMed.
- H. Maekawa, S. Kato, K. Kawamura and T. Yokokawa, Am. Mineral., 1997, 82, 1125–1132 CAS.
- H. Eckert, Z. Zhang and J. H. Kennedy, Chem. Mater., 1990, 2, 273–279 CrossRef CAS.
- T. K. Halstead, J. Chem. Phys., 1970, 53, 3427–3435 CrossRef CAS.
- A. R. Lim, J. W. Kim and C. S. Yoon, Solid State Commun., 2002, 123, 505–510 CrossRef CAS.
- T. Minamisono, T. Ohtsubo, Y. Nakayama, S. Fukuda, T. Izumikawa, M. Tanigaki, M. Matsui, S. Takeda, N. Nakamura, M. Fukuda, K. Matsuta and Y. Nojiri, Hyperfine Interact., 1993, 78, 159–163 CrossRef CAS.
- S. Indris, P. Heitjans, R. Uecker and T. Bredow, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245120 CrossRef.
- L. O’Dell, S. Savin, A. Chadwick and M. Smith, Solid State Nucl. Magn. Reson., 2007, 31, 169–173 CrossRef PubMed.
- D. Müller, W. Gessner, A. Samoson, E. Lippmaa and G. Scheler, J. Chem. Soc., Dalton Trans., 1986, 1277–1281 RSC.
- D. Müller, E. Jahn, G. Ladwig and U. Haubenreisser, Chem. Phys. Lett., 1984, 109, 332–336 CrossRef.
- B. Zhou, B. L. Sherriff, J. S. Hartman and G. Wu, Am. Mineral., 2007, 92, 34–43 CrossRef CAS.
- J. F. Hon and P. J. Bray, Phys. Rev., 1958, 110, 624–629 CrossRef CAS.
- G. E. Peterson, P. M. Bridenbaugh and P. Green, J. Chem. Phys., 1967, 46, 4009–4014 CrossRef CAS.
- M. A. Pimenta, P. Echegut, Y. Luspin, G. Hauret, F. Gervais and P. Abélard, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 3361–3368 CrossRef CAS PubMed.
- A. R. Lim, S. H. Choh and S. Y. Jeong, J. Phys.: Condens. Matter, 1996, 8, 4597–4602 CrossRef CAS.
- K. Arbi, J. Rojo and J. Sanz, J. Eur. Ceram. Soc., 2007, 27, 4215–4218 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- S. Sturniolo, T. F. G. Green, R. M. Hanson, M. Zilka, K. Refson, P. Hodgkinson, S. P. Brown and J. R. Yates, Solid State Nucl. Magn. Reson., 2016, 78, 64–70 CrossRef CAS PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- D. Ceresoli, Davide Ceresoli – Pseudopotentials, 2024, https://sites.google.com/site/dceresoli/pseudopotentials Search PubMed.
- D. Freude and J. Haase, Survey of NMR Parameters for Quadrupolar Nuclei in Powder Materials, in Particular for 27Al, 23Na and 17O, 2019, https://dieter-freude.de/quad-nmr/8.pdf.
- N. Wiberg, A. F. Holleman, E. Wiberg and G. Fischer, Lehrbuch der Anorganischen Chemie, De Gruyter, Berlin New York, 102nd edn, 2007 Search PubMed.
- P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- R. K. Harris, E. D. Becker, S. M. C. De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Magn. Reson. Chem., 2008, 46, 582–598 CrossRef CAS PubMed.
- W. Ku, T. Berlijn and C.-C. Lee, Phys. Rev. Lett., 2010, 104, 216401 CrossRef PubMed.
- R. Lizárraga, E. Holmström, S. C. Parker and C. Arrouvel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094201 CrossRef.
- T. Vosegaard, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 123, 51–72 CrossRef CAS PubMed.
- T. Bräuniger, B. Groh, I. L. Moudrakovski and S. Indris, J. Phys. Chem. A, 2016, 120, 7839–7846 CrossRef PubMed.
- X. Li, M. Tang, X. Feng, I. Hung, A. Rose, P.-H. Chien, Z. Gan and Y.-Y. Hu, Chem. Mater., 2017, 29, 8282–8291 CrossRef CAS.
- M. F. Graf, H. Tempel, S. S. Köcher, R. Schierholz, C. Scheurer, H. Kungl, R.-A. Eichel and J. Granwehr, RSC Adv., 2017, 7, 25276–25284 RSC.
- R. Messer, H. Birli and K. Differt, J. Phys. Colloq., 1980, 41, C6–28–C6–31 CrossRef.
- B. Monserrat, R. J. Needs and C. J. Pickard, J. Chem. Phys., 2014, 141, 134113 CrossRef PubMed.
- A. H. Mazurek, Ł. Szeleszczuk and D. M. Pisklak, Int. J. Mol. Sci., 2021, 22, 4378 CrossRef CAS PubMed.
- C. Lei, A. Erlebach, F. Brivio, L. Grajciar, Z. Tošner, C. J. Heard and P. Nachtigall, Chem. Sci., 2023, 14, 9101–9113 RSC.
- J. Yates, personal communication, 2023.
- R. Sternheimer, Phys. Rev., 1950, 80, 102–103 CrossRef CAS.
- R. Sternheimer, Phys. Rev., 1951, 84, 244–253 CrossRef CAS.
- T. P. Das, Phys. Rev., 1956, 102, 733–738 CrossRef CAS.
- C. Pickard, personal communication, 2023.
- S. E. Ashbrook, L. Le Pollès, R. Gautier, C. J. Pickard and R. I. Walton, Phys. Chem. Chem. Phys., 2006, 8, 3423–3431 RSC.
- S. Sen, Mol. Simul., 2008, 34, 1115–1120 CrossRef CAS.
- F. Pourpoint, C. Gervais, L. Bonhomme-Coury, F. Mauri, B. Alonso and C. Bonhomme, C. R. Chim., 2007, 11, 398–406 CrossRef.
- J. D. Hartman, A. Mathews and J. K. Harper, Front. Chem., 2021, 9, 751711 CrossRef CAS PubMed.
- D. V. Dudenko, J. R. Yates, K. D. M. Harris and S. P. Brown, CrystEngComm, 2013, 15, 8797 RSC.
- B. Karasulu, S. P. Emge, M. F. Groh, C. P. Grey and A. J. Morris, J. Am. Chem. Soc., 2020, 142, 3132–3148 CrossRef CAS PubMed.
- G. S. Harbison, J. Magn. Reson., 2015, 257, 24–31 CrossRef CAS PubMed.
- K. Choudhary, J. N. Ansari, I. I. Mazin and K. L. Sauer, Sci. Data, 2020, 7, 362 CrossRef PubMed.
- A. Dittmer, G. L. Stoychev, D. Maganas, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2020, 16, 6950–6967 CrossRef CAS PubMed.
- M. Kick and H. Oberhofer, J. Chem. Phys., 2019, 151, 184114 CrossRef CAS PubMed.
- D. Berger, H. Oberhofer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075308 CrossRef.
- D. Berger, A. J. Logsdail, H. Oberhofer, M. R. Farrow, C. R. A. Catlow, P. Sherwood, A. A. Sokol, V. Blum and K. Reuter, J. Chem. Phys., 2014, 141, 024105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00075g |
| This journal is © The Royal Society of Chemistry 2024 |
