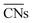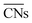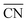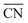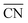Exploration of structure sensitivity of gold nanoparticles in low-temperature CO oxidation†
Received
25th October 2023
, Accepted 24th November 2023
First published on 27th November 2023
Abstract
Gold nanoparticles (NPs) exhibit remarkable catalytic activity in low-temperature CO oxidation and their performance is highly dependent on size and shape. However, the underlying mechanism isn't fully understood yet. Herein, we combine density functional theory calculations, a multiscale structure reconstruction model, and kinetic Monte Carlo simulations to investigate the activity and structure sensitivity of Au NPs under different reaction conditions. The results indicate that increasing the partial pressure ratio of O2 to CO leads to the decrease of optimal reaction temperature accompanied with the increase of performance. At low temperatures, the morphology of the NPs evolves to expose a higher proportion of (110) facets to promote the activity significantly. Moreover, the size dependence analysis suggests that O2-rich conditions are favorable for small-sized NPs, while CO-rich conditions favor the large-sized NPs. These findings not only enrich our basic understanding of the structure–reactivity relationship and the origin of structure sensitivity in gold-catalysis, but provide a guide for rational design of Au catalysts.
Keywords: Kinetic Monte Carlo; CO oxidation; Gold catalysis; Nanoparticles.
1 Introduction
Gold nanoparticles (NPs) exhibit extraordinary catalytic activities in various reactions under mild conditions, including CO oxidation,1–3 water-gas shift reaction,4 and partial oxidation of hydrocarbons.5 Among these reactions, CO oxidation is of particular interest because Au NPs can catalyze this reaction at temperatures as low as 203 K.1,2 It is generally agreed that the catalytic properties of Au NPs highly depend on their sizes and shapes.3,6–10 Therefore, substantial efforts have been dedicated to synthesizing and characterizing Au NPs with well-defined shapes and sizes.11–14 However, the situation becomes complicated due to the change in particle morphology under reaction conditions.15,16 It poses a challenge to comprehensively investigate the structure–reactivity relationship taking the reaction-condition-driven particle reshaping into account.
In the past decade, several theoretical models based on density functional theory (DFT)17 have contributed significant atomic-level insights into the structure sensitivity of Au NPs in CO oxidation.18–23 These models were formulated upon small gold clusters or fixed high-symmetrical structures, e.g., a classical truncated octahedral geometry. Due to the neglect of the influence of reaction environments on morphology, their ability to offer a comprehensive understanding of realistic catalytic activity is limited.
In this work, a density functional theory (DFT) based multiscale structural reconstruction (MSR) model24–26 was used to construct the equilibrium structure of Au NPs in the size range of 3–10 nm under varying reaction conditions. Then, kinetic Monte Carlo (KMC) simulations were performed to evaluate the corresponding catalytic performance. This work focused on the investigation of freestanding single crystalline Au NPs, while exploring the effect of twinning27,28 and the support oxide6,18,29 on Au catalysis would be an interesting study in the future. Our results show that the activity is significantly influenced by the structural reconstruction induced by the reaction atmosphere. Furthermore, the size dependency of activity is intricately linked to the reaction conditions.
2 Results and discussion
2.1 Structure–reactivity relation
The shape evolution of 5 nm Au NPs at different temperatures and under changing partial pressure ratios of PO2/PCO (1 bar total pressure) is shown in Fig. 1a. The temperature ranged from 273 to 373 K and PO2/PCO ranged from 1 to 100. The NPs with different shapes are distinguished by the average coordination number of surface atoms 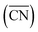 .30 Typical structures with different
.30 Typical structures with different 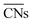 are illustrated in Fig. 1c. In general, when the temperature is higher than 343 K and PO2/PCO is larger than 60, the adsorption of gas on the Au NPs becomes difficult, and the corresponding structure (
are illustrated in Fig. 1c. In general, when the temperature is higher than 343 K and PO2/PCO is larger than 60, the adsorption of gas on the Au NPs becomes difficult, and the corresponding structure (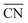 = 8.6) is close to the structure under vacuum (Fig. 1). With a decrease in temperature and O2 partial pressure, the fraction of the (110) facet increases, while the fraction of the (111) facet decreases. This change is attributed to the different coverage evolution on different facets.25 The coverage of CO increases rapidly on the (110) facet due to its stronger adsorption energy (Table S1†), resulting in the rapid decrease of the interface energy of the (110) facet, which further leads to a change of equilibrium morphology. More details can be found in Section 4.2 and our previous works.24–26 The contour plot of TOFs of these NPs under corresponding reaction conditions shows that the catalytic activity is significantly enhanced under low temperature and O2-rich conditions (Fig. 1b). To demonstrate how structure evolution affects the activity clearly, contour lines of
= 8.6) is close to the structure under vacuum (Fig. 1). With a decrease in temperature and O2 partial pressure, the fraction of the (110) facet increases, while the fraction of the (111) facet decreases. This change is attributed to the different coverage evolution on different facets.25 The coverage of CO increases rapidly on the (110) facet due to its stronger adsorption energy (Table S1†), resulting in the rapid decrease of the interface energy of the (110) facet, which further leads to a change of equilibrium morphology. More details can be found in Section 4.2 and our previous works.24–26 The contour plot of TOFs of these NPs under corresponding reaction conditions shows that the catalytic activity is significantly enhanced under low temperature and O2-rich conditions (Fig. 1b). To demonstrate how structure evolution affects the activity clearly, contour lines of 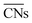 are marked by black dashed curves in Fig. 1b. It can be observed that there is partial overlap between the contour lines of
are marked by black dashed curves in Fig. 1b. It can be observed that there is partial overlap between the contour lines of 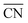 and TOFs, showing the shape-sensitivity of this system. The 110-dominant structures (
and TOFs, showing the shape-sensitivity of this system. The 110-dominant structures (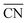 ≤ 7.0) exhibit high activity (TOF ≥ 5.6 × 106 per site per s) when PO2/PCO is higher than 50, while the (111)-dominated structures (
≤ 7.0) exhibit high activity (TOF ≥ 5.6 × 106 per site per s) when PO2/PCO is higher than 50, while the (111)-dominated structures (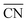 ≥ 8.5) always show low activity (TOF ≤ 1.8 × 106 per site per s).
≥ 8.5) always show low activity (TOF ≤ 1.8 × 106 per site per s).
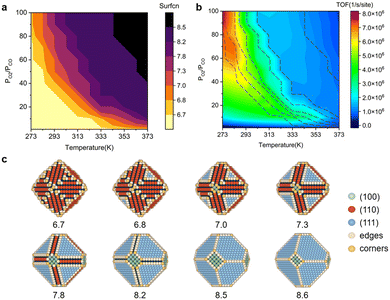 |
| | Fig. 1 (a) Contour plot of  (b) TOFs for 5 nm Au NPs changing with the temperature and partial pressure ratio (Ptotal = 1 bar). Contour lines of (b) TOFs for 5 nm Au NPs changing with the temperature and partial pressure ratio (Ptotal = 1 bar). Contour lines of  are marked by black dashed curves as guides to the eyes; (c) typical structures with different are marked by black dashed curves as guides to the eyes; (c) typical structures with different  . . | |
To disentangle the contribution of morphology changes and reaction conditions to the catalytic activity, Stru-6.7, Stru-7.3, Stru-7.8, and Stru-8.6 were chosen to obtain the fixed-structure contour plots of TOFs (Fig. S3†). Surface site fractions of these four structures are presented in Fig. 2a and their TOFs as a function of temperature were compared under PO2/PCO = 1, 10, and 100, respectively (Fig. 2b–d). It can be observed that a higher proportion of (110) facet sites is generally beneficial for catalytic reactions in our studied conditions, and the TOFs of different structures exhibit similar trends. At PO2/PCO = 1, the TOFs are below 0.8 × 106 per site per s and increase slightly with the increase of temperature for all NPs. At PO2/PCO = 10, the TOFs initially increase and then decrease as the temperature increases. The maximum TOF values are 3.6 × 106 per site per s at 333 K, 3.0 × 106 per site per s at 323 K, 2.0 × 106 per site per s at 323 K, and 1.0 × 106 per site per s at 353 K for Stru-6.7, Stru-7.3, Stru-7.8, and Stru-8.6, respectively. At PO2/PCO = 100, the TOFs of NPs are highest at 273 K ranging from 2.4 × 106 to 7.6 × 106 per site per s and decline at higher temperatures. The results indicate that as PO2/PCO increases, the optimal temperature for the highest TOF decreases. Meanwhile, the value of the highest TOF increases. This is because the binding energy of CO is about 0.45–0.57 eV stronger than that of O2 (Fig. S1†). Therefore, the increase of O2 partial pressure eliminates the risk of CO poisoning at low temperatures and facilitates the adsorption of O2 (Fig. S4†), leading to a higher activity.
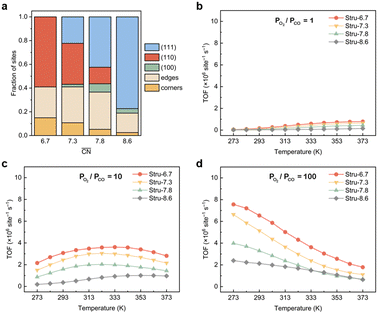 |
| | Fig. 2 (a) Surface site fractions of (111), (110), (100), edges and corners of Au NPs with different 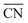 ; TOFs as a function of temperature at Ptotal = 1 bar with PO2/PCO = 1 (b), 10 (c), and 100 (d) for Au NPs with different ; TOFs as a function of temperature at Ptotal = 1 bar with PO2/PCO = 1 (b), 10 (c), and 100 (d) for Au NPs with different 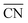 . . | |
2.2 Site-specific activity
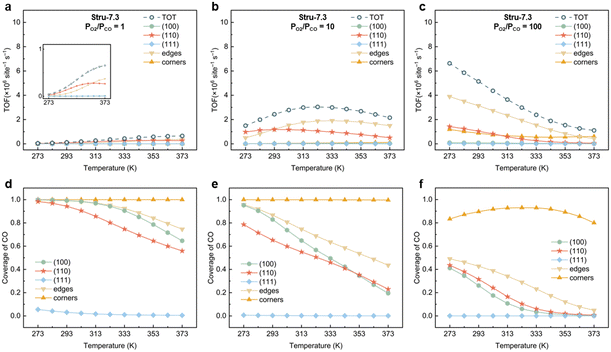
To understand the activity changes in detail, Au NPs with 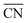 = 7.3, which possess a relatively uniform site distribution, were chosen as an example to show the site-specific contributions to TOFs and CO coverages at atmosphere pressure with PO2/PCO = 1, 10, and 100 (Fig. 3). The plots of the other three structures are displayed in Fig. S5–S7.† Generally, the activities of NPs reach the maximum as their coverage of CO is around 0.60. This results in the decrease of the optimal temperature with the increase of O2 partial pressure. At PO2/PCO = 1 (Fig. 3a and d), the overly adsorbed CO poisoned all sites except the (111) facet at 273 K, causing a very low total TOF (4.2 × 104 per site per s). The increase of temperature alleviates the CO poisoning on (110) facets first, followed by the edges and (100) facet sites, resulting in a monotonic increase in activity. At PO2/PCO = 10 (Fig. 3b and e), the activity of the (110) facet increases first and then declines as the temperature increases. The maximum activity of 1.2 × 106 per site per s is achieved at 293 K, with a CO coverage of 0.65. For edge sites, the optimal temperature is higher (333 K), with a maximum activity of 1.9 × 106 per site per s and a CO coverage of 0.63. At PO2/PCO = 100 (Fig. 3c and f), corner sites are protected from poisoning and maintained relatively stable activity at around 7.2 ± 2.1 × 105 per site per s from 273 to 373 K, whereas the activity of (110) facets declines from 1.4 × 106 to 4.9 × 104 per site per s and the activity of edge sites declines from 3.9 × 106 to 4.2 × 105 per site per s. Overall, the (110) facet and edge sites dominate the reactions except at 373 K with PO2/PCO = 100, in which condition corner sites make the major contributions. The contributions of (100) and (111) to TOFs are negligible under all conditions. Decreasing the temperature and increasing the PO2/PCO promote the reaction and increase the exposure of active (110) facet sites, thereby further enhancing the activity of Au NPs.
= 7.3, which possess a relatively uniform site distribution, were chosen as an example to show the site-specific contributions to TOFs and CO coverages at atmosphere pressure with PO2/PCO = 1, 10, and 100 (Fig. 3). The plots of the other three structures are displayed in Fig. S5–S7.† Generally, the activities of NPs reach the maximum as their coverage of CO is around 0.60. This results in the decrease of the optimal temperature with the increase of O2 partial pressure. At PO2/PCO = 1 (Fig. 3a and d), the overly adsorbed CO poisoned all sites except the (111) facet at 273 K, causing a very low total TOF (4.2 × 104 per site per s). The increase of temperature alleviates the CO poisoning on (110) facets first, followed by the edges and (100) facet sites, resulting in a monotonic increase in activity. At PO2/PCO = 10 (Fig. 3b and e), the activity of the (110) facet increases first and then declines as the temperature increases. The maximum activity of 1.2 × 106 per site per s is achieved at 293 K, with a CO coverage of 0.65. For edge sites, the optimal temperature is higher (333 K), with a maximum activity of 1.9 × 106 per site per s and a CO coverage of 0.63. At PO2/PCO = 100 (Fig. 3c and f), corner sites are protected from poisoning and maintained relatively stable activity at around 7.2 ± 2.1 × 105 per site per s from 273 to 373 K, whereas the activity of (110) facets declines from 1.4 × 106 to 4.9 × 104 per site per s and the activity of edge sites declines from 3.9 × 106 to 4.2 × 105 per site per s. Overall, the (110) facet and edge sites dominate the reactions except at 373 K with PO2/PCO = 100, in which condition corner sites make the major contributions. The contributions of (100) and (111) to TOFs are negligible under all conditions. Decreasing the temperature and increasing the PO2/PCO promote the reaction and increase the exposure of active (110) facet sites, thereby further enhancing the activity of Au NPs.
 |
| | Fig. 3 Site-specific contributions to TOFs and coverages of CO for Au NPs with Stru-7.3 under PO2/PCO = 1 (a, d), 10 (b, e), and 100 (c, f). | |
2.3 Size effect
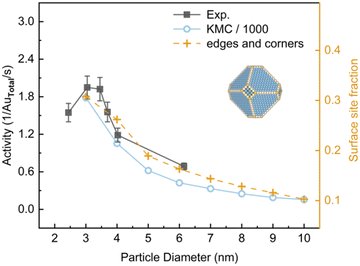
It is suggested that the critical size for finite-size effects of Au is about 2.7 nm.31 To compare with the experiment,3 the activities of Au NPs in the size range of 3–10 nm constructed by the MSR model were investigated at 350 K at a total pressure of 0.053 bar with PO2/PCO = 5 (Fig. 4). In this condition, Au nanoparticles exhibited a classical truncated octahedral geometry. KMC calculations overestimated the activity by approximately 3 orders of magnitude as compared to the experimental results, which arises from the use of the PBE functional and scaling relationship.32 Nevertheless, a similar trend was obtained. Yellow dashed lines in Fig. 4 show the fraction of edges and corners for particle sizes. It suggests that the activity dependence on the particle size under experimental conditions is closely correlated with the fractions of edges and corners. This finding is coincident with previous studies which suggested that the main effect of decreasing the size of Au NPs is the increase of the proportion of low-coordinated Au atoms.7,33,34
 |
| | Fig. 4 The activity for CO oxidation at 350 K under 40 Torr with PO2/PCO = 5 as a function of particle diameter of the Au NPs. Experimental data from ref. 3. Activity is expressed as (product molecules) × (total Au atoms)−1 × s−1. Reaction-condition-dependent structure of 5 nm Au NP is shown in inserts. | |
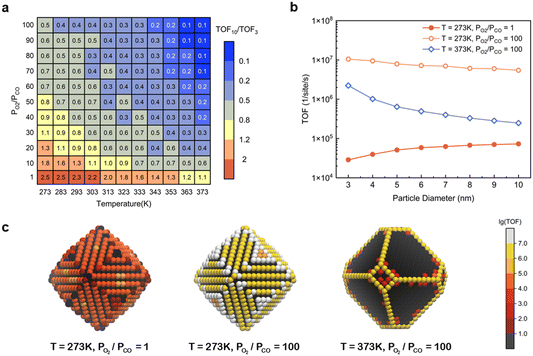
However, as discussed in the preceding sections, at certain temperatures and partial pressure ratios, adsorbates can induce the structural reconstruction of gold nanoparticles, resulting in the exposure of the active (110) surface at atmospheric pressure. Under these conditions, the catalytic activity of Au NPs should exhibit different size dependence. To validate it, the TOFs for Au NPs with reaction-condition-dependent structure in the size range of 3–10 nm were obtained at different temperatures and partial pressure ratios PO2/PCO with the fixed total pressure of 1 bar (Fig. S8†). The size effects were measured by the TOF ratio between 10 nm and 3 nm particles (TOF10/TOF3) and were plotted as a heatmap (Fig. 5a). Three representative size-dependent TOF trends are shown in Fig. 5b, and the corresponding 5 nm particle geometries colored according to the TOF at specific sites are illustrated in Fig. 5c. At high temperature and high PO2/PCO (e.g., T = 373 K, PO2/PCO = 100), only edge and corner sites are active, resulting in a sharp decrease when the diameter increases, similar to Fig. 4. However, at low temperature and low PO2/PCO (e.g., T = 273 K, PO2/PCO = 1), the (110) facet sites are the only active sites, because the edges and corners are poisoned. So, the TOF grows with particle size, similar to the effect for Pt particles.10,35 Notably, at low temperature and high PO2/PCO (e.g., T = 273 K, PO2/PCO = 100), all sites are active. Although the edge and corner sites exhibit higher intrinsic activities, the (110) facet sites also make a large contribution to the total activity owing to the large area, especially for large NPs. This allows the particle to maintain a relatively high activity even at a size of 10 nm, which is about half the activity of a 3 nm particle.
 |
| | Fig. 5 (a) Heatmap of TOF10/TOF3 changing with the temperature and partial pressure ratio with a fixed total pressure of 1 bar; (b) three representative size-dependent TOF trends; (c) 5 nm Au NPs colored according to the TOF at specific sites. | |
From the above results and discussion, we show that when the effect of CO poisoning is strong, the particle activity is unusually proportional to its size. When the particle is not poisoned by CO, its activity increases with the decrease of size. These findings may explain why the optimal active size of Au NPs is around 3 nm.3,9 When the size of the Au NP becomes extremely small (1–2 nm), its interaction with CO will be enhanced due to the finite size effect.31 This could induce the CO poisoning effect and thus inversely reduce the activity.
3 Conclusions
In conclusion, we investigated the CO oxidation over Au NPs with reaction-condition dependent structures at sizes ranging from 3 to 10 nm at different temperatures and partial pressure ratios PO2/PCO with the fixed total pressure of 1 bar. The temperature ranged from 273 to 373 K and PO2/PCO ranged from 1 to 100. The results suggested that with the increase in PO2/PCO, the optimal temperature decreases from 373 to 273 K and the highest TOF increases. This is because the reaction is limited by O2 adsorption. At low temperatures and under O2-rich conditions, all sites exhibit high activity without being poisoned by CO. Also, under these conditions, a higher proportion of (110) facets is exposed induced by adsorbates, making a substantial contribution to total activity together with corners and edges, especially for the large-size particles. This work provides a comprehensive understanding of the structure sensitivity for Au NPs in CO oxidation. Also, it provides a promising way to further catalyst design based on atomic-level understanding.
4 Computational methods
The Langmuir–Hinshelwood mechanism involving the formation of an OCOO intermediate36 was considered to model the Au-catalyzed CO oxidation:| | 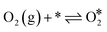 | (R2) |
| | | OCOO* → CO2(g) + O* + * | (R4) |
| | | CO(g) + O* → CO2(g) + * | (R5) |
| | | CO* + * → * + CO* (diffusion) | (R6) |
| | 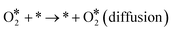 | (R7) |
| | | O* + * → * + O* (diffusion) | (R8) |
Here, an asterisk * stands for a free site in the surface. And the surface species are labelled with superscript asterisks. For simplicity, the reaction product (CO2) was considered to desorb immediately after its formation and the diffusion of the reaction intermediate (OCOO) was neglected.
4.1 Density functional theory
DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP) in the projector-augmented wave (PAW) scheme.37–39 The electronic states were expanded on a plane wave basis with a cutoff of 400 eV. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional was adopted.40 Structures were optimized until all forces were below 0.05 eV Å−1.
Surface tensions under vacuum were extracted41 from the energies of a series of (1 × 1) slab models with increasing layers from 6 to 20. For surface species, (4 × 4), (2 × 2), and (1 × 1) slab models were constructed to calculate adsorption energies and lateral interactions between adsorbates.25 Each model contained 6 atomic layers, where the positions of 2 bottom layers were fixed. The vacuum space of 15 Å was set along the z-axis. The k-point grids42 were set to be (3 × 3 × 1), (6 × 6 × 1), and (10 × 10 × 1) for the (4 × 4), (2 × 2), (1 × 1) slab models, respectively. All calculated results are listed in Tables S1 and S2.†
4.2 MSR model
By combing the Fowler–Guggenheim (F–G) adsorption isotherm43 and Wulff theorem,44 the equilibrium shape of Au NPs under reaction conditions can be constructed based on the interface tension24–26 of three low-index facets ((100), (110), (111)):| | | γinthkl = γhkl + [θCO(ECO − z(wCO−COθCO + wCO−O2θO2)) + θO2(EO2 − z(wCO−O2θCO + wO2−O2θO2))]/Aat | (1) |
Here, γhkl is the surface tension of the (hkl) facet under vacuum, ECO and EO2 are the adsorption energy of CO and O2 on this facet, θ is the coverage of the corresponding adsorbates, z is the number of nearest neighbor sites, w is the lateral interaction between two neighboring adsorbates, and Aat is the surface area per atom. Considering the short lifetime of intermediates, their coverage on the NP during reaction has been neglected. The coverages of CO and O2 on each facet can be derived by solving the following equations, respectively:| | 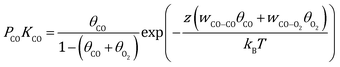 | (2) |
| | 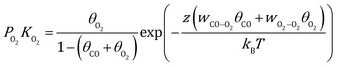 | (3) |
where kB is the Boltzmann constant, and K is the equilibrium constant defined as:| | 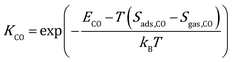 | (4) |
| | 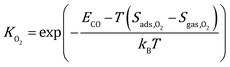 | (5) |
where Sads represents the entropy of the adsorbed species, which is assumed to be negligible. Sgas represents the entropy of gas-phase species, which is obtained from the NIST-JANAF thermochemical tables.45
4.3 Kinetic Monte Carlo
KMC simulation with the direct method (DM)46–48 was adopted to study the catalytic activities of Au NPs under operando conditions. In the DM, the time interval of each KMC step is evaluated by the total rate constant (ktot = ∑kevent):| | 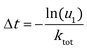 | (6) |
Here u1 is a random number on the interval (0, 1]. The event occurring at this step is chosen with a probability proportional to its rate constant and determined by another random number u2.
The rate constant for adsorption is obtained from collision theory, assuming a zero-activation energy:
| | 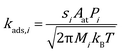 | (7) |
where the subscript
i denotes the species,
M denotes its molecular mass and
s denotes the sticking coefficient. On the facet sites, the sticking coefficient is assumed to be 0.9 for CO and 0.1 for O
2.
49,50 While on edges and corners they are both assumed to be 1.0. To ensure thermodynamic equilibrium, the corresponding desorption rate constant is obtained from
kads,i and equilibrium constant
Ki:
| | 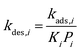 | (8) |
The rate constants for reaction and diffusion events are obtained from transition state theory (TST):
| | 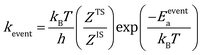 | (9) |
Here, h is the plank's constant. ZTS and ZIS are the partition function of the transition state and initial state, which are assumed to be equal in the simulation. Eeventa is the activation energy. For the reaction 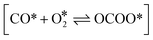 and [OCOO* → CO2(g) + O* + *], the activation energy is evaluated by the BEP relations and scaling relation fitted based on ref. 19–21 and 51–53 (Fig. S1c–e†). For the reaction [CO(g) + O* → CO2(g) + *], the activation energy is assumed to be 0.1 eV following the previous study.21 For diffusion, we increase the diffusion barrier to 0.6 eV for all adsorbates to accelerate KMC simulation while ensuring convergence (Fig. S2†).
and [OCOO* → CO2(g) + O* + *], the activation energy is evaluated by the BEP relations and scaling relation fitted based on ref. 19–21 and 51–53 (Fig. S1c–e†). For the reaction [CO(g) + O* → CO2(g) + *], the activation energy is assumed to be 0.1 eV following the previous study.21 For diffusion, we increase the diffusion barrier to 0.6 eV for all adsorbates to accelerate KMC simulation while ensuring convergence (Fig. S2†).
To ensure the reliability of the results, all KMC simulations were performed for a total of 100 million steps. The turnover frequency (TOF) of the reaction was calculated as the reaction rate per surface site over the last 10 million steps.
Author contributions
Y. G. initiated the project. Y. G. and B. Z. supervised the project. L. Y. and Y. H. performed the calculations. L. Y. performed the simulations and data analysis. L. Y. wrote the original draft. Y. G. and B. Z. revised the manuscript. All authors have given approval to the final version of the manuscript.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
The work is supported by the National Natural Science Foundation of China (12174408), Natural Science Foundation of Shanghai (22JC1404200), and the Foundation of Key Laboratory of Low-Carbon Conversion Science & Engineering, Shanghai Advanced Research Institute, Chinese Academy of Sciences (KLLCCSE-202201Z, SARI, CAS). B. Z. acknowledges the financial support of Key Research Program of Frontier Sciences, CAS, Grant No. ZDBS-LY-7012. All calculations were performed at National Supercomputer Centers in Tianjin, Shanghai and Guangzhou.
References
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Novel gold catalysts for the oxidation of carbon monoxide at a temperature far below 0 °C, Chem. Lett., 1987, 16, 405–408 CrossRef.
- M. Haruta, S. Tsubota, T. Kobayashi, H. Kageyama, M. J. Genet and B. Delmon, Low-temperature oxidation of CO over gold supported on TiO2, α-Fe2O3, and Co3O4, J. Catal., 1993, 144, 175–192 CrossRef CAS.
- M. Valden, X. Lai and D. W. Goodman, Onset of catalytic activity of gold clusters on titania with the appearance of nonmetallic properties, Science, 1998, 281, 1647–1650 CrossRef CAS PubMed.
- D. Andreeva, V. Idakiev, T. Tabakova and A. Andreev, Low-temperature water–gas shift reaction over Au/α-Fe2O3, J. Catal., 1996, 158, 354–355 CrossRef CAS.
- M. D. Hughes, Y.-J. Xu, P. Jenkins, P. McMorn, P. Landon, D. I. Enache, A. F. Carley, G. A. Attard, G. J. Hutchings, F. King, E. H. Stitt, P. Johnston, K. Griffin and C. J. Kiely, Tunable gold catalysts for selective hydrocarbon oxidation under mild conditions, Nature, 2005, 437, 1132–1135 CrossRef CAS PubMed.
- M. Haruta, Size- and support-dependency in the catalysis of gold, Catal. Today, 1997, 36, 153–166 CrossRef CAS.
- N. Lopez, T. Janssens, B. Clausen, Y. Xu, M. Mavrikakis, T. Bligaard and J. Norskov, On the origin of the catalytic activity of gold nanoparticles for low-temperature CO oxidation, J. Catal., 2004, 223, 232–235 CrossRef CAS.
- M. S. Chen and D. W. Goodman, Structure–activity relationships in supported Au catalysts, Catal. Today, 2006, 111, 22–33 CrossRef CAS.
- I. Laoufi, M.-C. Saint-Lager, R. Lazzari, J. Jupille, O. Robach, S. Garaudée, G. Cabailh, P. Dolle, H. Cruguel and A. Bailly, Size and catalytic activity of supported gold nanoparticles: An in operando study during Co oxidation, J. Phys. Chem. C, 2011, 115, 4673–4679 CrossRef CAS.
- S. Cao, F. (Feng) Tao, Y. Tang, Y. Li and J. Yu, Size- and shape-dependent catalytic performances of oxidation and reduction reactions on nanocatalysts, Chem. Soc. Rev., 2016, 45, 4747–4765 RSC.
- Y. Sun and Y. Xia, Shape-controlled synthesis of gold and silver nanoparticles, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed.
- A. R. Tao, S. Habas and P. Yang, Shape control of colloidal metal nanocrystals, Small, 2008, 4, 310–325 CrossRef CAS.
- R. P. Briñas, M. Hu, L. Qian, E. S. Lymar and J. F. Hainfeld, Gold nanoparticle size controlled by polymeric Au(I) thiolate precursor size, J. Am. Chem. Soc., 2007, 130, 975–982 CrossRef PubMed.
- P. Suchomel, L. Kvitek, R. Prucek, A. Panacek, A. Halder, S. Vajda and R. Zboril, Simple size-controlled synthesis of Au nanoparticles and their size-dependent catalytic activity, Sci. Rep., 2018, 8, 4589 CrossRef PubMed.
- T. Uchiyama, H. Yoshida, Y. Kuwauchi, S. Ichikawa, S. Shimada, M. Haruta and S. Takeda, Systematic morphology changes of gold nanoparticles supported on CeO2 during CO oxidation, Angew. Chem., Int. Ed., 2011, 50, 10157–10160 CrossRef CAS PubMed.
- N. Kamiuchi, K. Sun, R. Aso, M. Tane, T. Tamaoka, H. Yoshida and S. Takeda, Self-activated surface dynamics in gold catalysts under reaction environments, Nat. Commun., 2018, 9, 2060 CrossRef PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- T. V. W. Janssens, B. S. Clausen, B. Hvolbæk, H. Falsig, C. H. Christensen, T. Bligaard and J. K. Nørskov, Insights into the reactivity of supported Au nanoparticles: Combining theory and experiments, Top. Catal., 2007, 44, 15–26 CrossRef CAS.
- H. Li, L. Li, A. Pedersen, Y. Gao, N. Khetrapal, H. Jónsson and X. C. Zeng, Magic-number gold nanoclusters with diameters from 1 to 3.5 nm: Relative stability and catalytic activity for CO oxidation, Nano Lett., 2014, 15, 682–688 CrossRef PubMed.
- J. X. Liu, I. A. W. Filot, Y. Su, B. Zijlstra and E. J. M. Hensen, Optimum particle size for gold-catalyzed CO oxidation, J. Phys. Chem. C, 2018, 122, 8327–8340 CrossRef CAS PubMed.
- H. Xu, D. Cheng, Y. Gao and X. C. Zeng, Assessment of catalytic activities of gold nanoclusters with simple structure descriptors, ACS Catal., 2018, 8, 9702–9710 CrossRef CAS.
- F. H. Kaatz, D. Yu. Murzin and A. Bultheel, Coordination-dependent kinetics in the catalysis of gold nanoclusters, ACS Catal., 2021, 11, 9073–9085 CrossRef CAS.
- Y. Gao, N. Shao, Y. Pei, Z. Chen and X. C. Zeng, Catalytic activities of subnanometer gold clusters (Au16–Au18, Au20, and Au27–Au35) for CO oxidation, ACS Nano, 2011, 5, 7818–7829 CrossRef CAS PubMed.
- B. Zhu, Z. Xu, C. Wang and Y. Gao, Shape evolution of metal nanoparticles in water vapor environment, Nano Lett., 2016, 16, 2628–2632 CrossRef CAS PubMed.
- J. Meng, B. Zhu and Y. Gao, Shape evolution of metal nanoparticles in binary gas environment, J. Phys. Chem. C, 2018, 122, 6144–6150 CrossRef CAS.
- B. Zhu, J. Meng, W. Yuan, X. Zhang, H. Yang, Y. Wang and Y. Gao, Reshaping of metal nanoparticles under reaction conditions, Angew. Chem., Int. Ed., 2020, 59, 2171–2180 CrossRef CAS PubMed.
- X. Ma, F. Lin, X. Chen and C. Jin, Unveiling Growth Pathways of Multiply Twinned Gold Nanoparticles by In Situ Liquid Cell Transmission Electron Microscopy, ACS Nano, 2020, 14, 9594–9604 CrossRef CAS PubMed.
- E. yakout El koraychy, C. Roncaglia, D. Nelli, M. Cerbelaud and R. Ferrando, Growth mechanisms from tetrahedral seeds to multiply twinned Au nanoparticles revealed by atomistic simulations, Nanoscale Horiz., 2022, 7, 883–889 RSC.
- D. Widmann and R. J. Behm, Activation of Molecular Oxygen and the Nature of the Active Oxygen Species for CO Oxidation on Oxide Supported Au Catalysts, Acc. Chem. Res., 2014, 47, 740–749 CrossRef CAS PubMed.
- X. Duan, X. Y. Li, B. Zhu and Y. Gao, Identifying the morphology of Pt nanoparticles for the optimal catalytic activity towards CO oxidation, Nanoscale, 2022, 14, 17754–17760 RSC.
- J. Kleis, J. Greeley, N. A. Romero, V. A. Morozov, H. Falsig, A. H. Larsen, J. Lu, J. J. Mortensen, M. Dułak, K. S. Thygesen, J. K. Nørskov and K. W. Jacobsen, Finite size effects in chemical bonding: From small clusters to solids, Catal. Lett., 2011, 141, 1067–1071 CrossRef CAS.
- Y. Yang, T. Shen and X. Xu, Understanding the source of error in first-principles-based micro-kinetic modeling: Density functional theory calculations versus the mean-field approximation, J. Phys. Chem. C, 2023, 127, 9631–9639 CrossRef CAS.
- X. Bokhimi, R. Zanella and A. Morales, Au/rutile catalysts: Effect of support dimensions on the gold crystallite size and the catalytic activity for CO oxidation, J. Phys. Chem. C, 2007, 111, 15210–15216 CrossRef CAS.
- K. Qian, L. Luo, H. Bao, Q. Hua, Z. Jiang and W. Huang, Catalytically active structures of SiO2-supported Au nanoparticles in low-temperature CO oxidation, Catal. Sci. Technol., 2013, 3, 679–687 RSC.
- M. Jørgensen and H. Grönbeck, Scaling relations and kinetic Monte Carlo simulations to bridge the materials gap in heterogeneous catalysis, ACS Catal., 2017, 7, 5054–5061 CrossRef.
- Z. P. Liu, P. Hu and A. Alavi, Catalytic role of gold in gold-based catalysts: A density functional theory study on the CO oxidation on gold, J. Am. Chem. Soc., 2002, 124, 14770–14779 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- V. Fiorentini and M. Methfessel, Extracting convergent surface energies from slab calculations, J. Phys.: Condens. Matter, 1996, 8, 6525–6529 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
-
R. H. Fowler and E. A. Guggenheim, Statistical Thermodynamics, Cambridge University Press, Cambridge, U.K., 1939 Search PubMed.
- G. Wulff, On the question of speed of growth and dissolution of crystal surfaces, Z. Kristallogr. Mineral., 1901, 34, 450–530 Search PubMed.
-
M. W. Chase, NIST-JANAF Thermochemical Tables, American Institute of Physics, 4th edn, 1998 Search PubMed.
-
A. P. J. Jansen, An Introduction to Kinetic Monte Carlo Simulations of Surface Reactions, Springer, Berlin, Heidelberg, 2012 Search PubMed.
- D. T. Gillespie, A general method for numerically simulating the stochastic time evolution of coupled chemical reactions, J. Comput. Phys., 1976, 22, 403–434 CrossRef CAS.
- D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys. Chem., 1977, 81, 2340–2361 CrossRef CAS.
- J. M. Gottfried, K. J. Schmidt, S. L. M. Schroeder and K. Christmann, Adsorption of carbon monoxide on Au(1 1 0)-(1 × 2), Surf. Sci., 2003, 536, 206–224 CrossRef CAS.
- Y. Han, X.-Y. Li, B. Zhu and Y. Gao, Unveiling the Au surface reconstruction in a CO environment by surface dynamics and Ab initio thermodynamics, J. Phys. Chem. A, 2022, 126, 6538–6547 CrossRef CAS PubMed.
- H. Li and J. Ho, Theoretical calculations on the oxidation of CO on Au55, Ag13Au42, Au13Ag42, and Ag55 clusters of nanometer size, J. Phys. Chem. C, 2012, 116, 13196–13201 CrossRef CAS.
- J. L. C. Fajín, A. S. Moura and M. N. D. S. Cordeiro, First-principles-based kinetic Monte Carlo simulations of CO oxidation on catalytic Au(110) and Ag(110) surfaces, Phys. Chem. Chem. Phys., 2021, 23, 14037–14050 RSC.
- W. An, Y. Pei and X. C. Zeng, CO oxidation catalyzed by single-walled helical gold nanotube, Nano Lett., 2007, 8, 195–202 CrossRef PubMed.
|
| This journal is © Institute of Process Engineering of CAS 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ac and
Yi
Gao
*ac and
Yi
Gao
 *acd
*acd
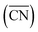 .30 Typical structures with different
.30 Typical structures with different 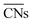 are illustrated in Fig. 1c. In general, when the temperature is higher than 343 K and PO2/PCO is larger than 60, the adsorption of gas on the Au NPs becomes difficult, and the corresponding structure (
are illustrated in Fig. 1c. In general, when the temperature is higher than 343 K and PO2/PCO is larger than 60, the adsorption of gas on the Au NPs becomes difficult, and the corresponding structure (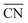 = 8.6) is close to the structure under vacuum (Fig. 1). With a decrease in temperature and O2 partial pressure, the fraction of the (110) facet increases, while the fraction of the (111) facet decreases. This change is attributed to the different coverage evolution on different facets.25 The coverage of CO increases rapidly on the (110) facet due to its stronger adsorption energy (Table S1†), resulting in the rapid decrease of the interface energy of the (110) facet, which further leads to a change of equilibrium morphology. More details can be found in Section 4.2 and our previous works.24–26 The contour plot of TOFs of these NPs under corresponding reaction conditions shows that the catalytic activity is significantly enhanced under low temperature and O2-rich conditions (Fig. 1b). To demonstrate how structure evolution affects the activity clearly, contour lines of
= 8.6) is close to the structure under vacuum (Fig. 1). With a decrease in temperature and O2 partial pressure, the fraction of the (110) facet increases, while the fraction of the (111) facet decreases. This change is attributed to the different coverage evolution on different facets.25 The coverage of CO increases rapidly on the (110) facet due to its stronger adsorption energy (Table S1†), resulting in the rapid decrease of the interface energy of the (110) facet, which further leads to a change of equilibrium morphology. More details can be found in Section 4.2 and our previous works.24–26 The contour plot of TOFs of these NPs under corresponding reaction conditions shows that the catalytic activity is significantly enhanced under low temperature and O2-rich conditions (Fig. 1b). To demonstrate how structure evolution affects the activity clearly, contour lines of 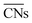 are marked by black dashed curves in Fig. 1b. It can be observed that there is partial overlap between the contour lines of
are marked by black dashed curves in Fig. 1b. It can be observed that there is partial overlap between the contour lines of 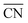 and TOFs, showing the shape-sensitivity of this system. The 110-dominant structures (
and TOFs, showing the shape-sensitivity of this system. The 110-dominant structures (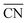 ≤ 7.0) exhibit high activity (TOF ≥ 5.6 × 106 per site per s) when PO2/PCO is higher than 50, while the (111)-dominated structures (
≤ 7.0) exhibit high activity (TOF ≥ 5.6 × 106 per site per s) when PO2/PCO is higher than 50, while the (111)-dominated structures (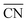 ≥ 8.5) always show low activity (TOF ≤ 1.8 × 106 per site per s).
≥ 8.5) always show low activity (TOF ≤ 1.8 × 106 per site per s).
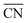 = 7.3, which possess a relatively uniform site distribution, were chosen as an example to show the site-specific contributions to TOFs and CO coverages at atmosphere pressure with PO2/PCO = 1, 10, and 100 (Fig. 3). The plots of the other three structures are displayed in Fig. S5–S7.† Generally, the activities of NPs reach the maximum as their coverage of CO is around 0.60. This results in the decrease of the optimal temperature with the increase of O2 partial pressure. At PO2/PCO = 1 (Fig. 3a and d), the overly adsorbed CO poisoned all sites except the (111) facet at 273 K, causing a very low total TOF (4.2 × 104 per site per s). The increase of temperature alleviates the CO poisoning on (110) facets first, followed by the edges and (100) facet sites, resulting in a monotonic increase in activity. At PO2/PCO = 10 (Fig. 3b and e), the activity of the (110) facet increases first and then declines as the temperature increases. The maximum activity of 1.2 × 106 per site per s is achieved at 293 K, with a CO coverage of 0.65. For edge sites, the optimal temperature is higher (333 K), with a maximum activity of 1.9 × 106 per site per s and a CO coverage of 0.63. At PO2/PCO = 100 (Fig. 3c and f), corner sites are protected from poisoning and maintained relatively stable activity at around 7.2 ± 2.1 × 105 per site per s from 273 to 373 K, whereas the activity of (110) facets declines from 1.4 × 106 to 4.9 × 104 per site per s and the activity of edge sites declines from 3.9 × 106 to 4.2 × 105 per site per s. Overall, the (110) facet and edge sites dominate the reactions except at 373 K with PO2/PCO = 100, in which condition corner sites make the major contributions. The contributions of (100) and (111) to TOFs are negligible under all conditions. Decreasing the temperature and increasing the PO2/PCO promote the reaction and increase the exposure of active (110) facet sites, thereby further enhancing the activity of Au NPs.
= 7.3, which possess a relatively uniform site distribution, were chosen as an example to show the site-specific contributions to TOFs and CO coverages at atmosphere pressure with PO2/PCO = 1, 10, and 100 (Fig. 3). The plots of the other three structures are displayed in Fig. S5–S7.† Generally, the activities of NPs reach the maximum as their coverage of CO is around 0.60. This results in the decrease of the optimal temperature with the increase of O2 partial pressure. At PO2/PCO = 1 (Fig. 3a and d), the overly adsorbed CO poisoned all sites except the (111) facet at 273 K, causing a very low total TOF (4.2 × 104 per site per s). The increase of temperature alleviates the CO poisoning on (110) facets first, followed by the edges and (100) facet sites, resulting in a monotonic increase in activity. At PO2/PCO = 10 (Fig. 3b and e), the activity of the (110) facet increases first and then declines as the temperature increases. The maximum activity of 1.2 × 106 per site per s is achieved at 293 K, with a CO coverage of 0.65. For edge sites, the optimal temperature is higher (333 K), with a maximum activity of 1.9 × 106 per site per s and a CO coverage of 0.63. At PO2/PCO = 100 (Fig. 3c and f), corner sites are protected from poisoning and maintained relatively stable activity at around 7.2 ± 2.1 × 105 per site per s from 273 to 373 K, whereas the activity of (110) facets declines from 1.4 × 106 to 4.9 × 104 per site per s and the activity of edge sites declines from 3.9 × 106 to 4.2 × 105 per site per s. Overall, the (110) facet and edge sites dominate the reactions except at 373 K with PO2/PCO = 100, in which condition corner sites make the major contributions. The contributions of (100) and (111) to TOFs are negligible under all conditions. Decreasing the temperature and increasing the PO2/PCO promote the reaction and increase the exposure of active (110) facet sites, thereby further enhancing the activity of Au NPs.


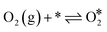
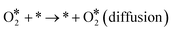
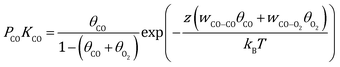
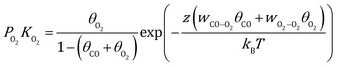
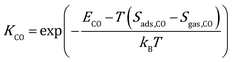
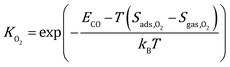
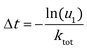
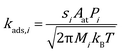
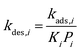
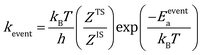
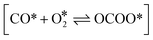 and [OCOO* → CO2(g) + O* + *], the activation energy is evaluated by the BEP relations and scaling relation fitted based on ref. 19–21 and 51–53 (Fig. S1c–e†). For the reaction [CO(g) + O* → CO2(g) + *], the activation energy is assumed to be 0.1 eV following the previous study.21 For diffusion, we increase the diffusion barrier to 0.6 eV for all adsorbates to accelerate KMC simulation while ensuring convergence (Fig. S2†).
and [OCOO* → CO2(g) + O* + *], the activation energy is evaluated by the BEP relations and scaling relation fitted based on ref. 19–21 and 51–53 (Fig. S1c–e†). For the reaction [CO(g) + O* → CO2(g) + *], the activation energy is assumed to be 0.1 eV following the previous study.21 For diffusion, we increase the diffusion barrier to 0.6 eV for all adsorbates to accelerate KMC simulation while ensuring convergence (Fig. S2†).