Empirical evaluation of the TXRF detector field of view – a coffee-ring case study†
Sven
Hampel
 ,
Franziska
Sand
,
Franziska
Sand
 ,
Heiko Sebastian
Till
and
Ursula Elisabeth Adriane
Fittschen
*
,
Heiko Sebastian
Till
and
Ursula Elisabeth Adriane
Fittschen
*
Clausthal University of Technology, Institute of Inorganic and Analytical Chemistry, Arnold-Sommerfeld-Straße 4, Clausthal-Zellerfeld, 38678, Germany. E-mail: ursula.fittschen@tu-clausthal.de
First published on 10th November 2023
Abstract
TXRF is a microanalytical method for trace elemental determination. Common sample preparation comprises drying a sample volume in the microliter range on a hydrophobized reflector. However, such specimens often dry as “coffee-ring”-like deposits. It is reported in the literature that coffee-ring specimens are correlated with poor accuracy. Nonetheless, models suggest that coffee-ring specimens provide the least errors from primary absorption. With picoliter derived specimens, the position dependent analyte signal response can be investigated. Here we study the elemental sensitivities obtained from ring-like deposits prepared by pL-printing with respect to their radius and position relative to the detector field of view (FOV). To understand the influence of a ring-like deposit on the TXRF signal we (a) determined the detector FOV and (b) modelled the declining response with increasing offset and finally (c) designed a multiple ring specimen for experimental validation. The detector FOV was determined from 128 individual micro specimens (Co, Cu, Ga, and Ni) with defined offsets using an in-house-build pL-printer. The 2d Gaussian intensity profile of the FOV exhibits a mean of 26.7 cps−1 ng−1 (Co Kα), offset from the reflector centre by +0.62 mm (x-axis) and +0.28 mm (y-axis). The σ of the intensity profile is located at 2.4 mm (x-axis) and 2.2 mm (y-axis). At a distance of 9.47 mm (x) and 8.71 mm (y) (4σ) from the centre the counts are down to 10%. The local relative sensitivity (e.g., Co Kαoffset normalized to Ga Kαoffset) (RS) corresponded well to the mean RS of all positions (e.g., Co Kαmean normalized to Ga Kαmean). The position-dependent errors in signal intensities were evaluated experimentally with concentric ring structures (Co, Cu, Ga, and Mn) with up to 6 mm distance from the centre. The bias originating from a total spatial separation of the IS and the analyte and location of the IS in the centre and analyte on circles of different radii was determined. A negative bias of 33% was observed for the 2 mm radius circle, 80% for the 4 mm radius and 99% for the 6 mm radius circle. The observation for the two inner circles matches the determined FOV profile.
Introduction
A crucial step in quantitative total reflection X-ray fluorescence analysis (TXRF) is correct sample preparation.1,2 In general, specimens are prepared by depositing microliter droplets on reflectors and subsequent drying.3 Under optimal drying conditions, the drying procedure yields a homogenous film or deposit.4 Depending on the sample type, the drying step can lead to “coffee ring”-like residues.5 Inhomogeneous elemental distribution is a source of determination errors and has been observed by Wellenreuther et al.6 The formation of a “coffee-ring” structure and its influence on the accuracy and uncertainty of suspension assisted TXRF were studied by Fernández-Ruiz.7 Characteristic of “coffee ring” specimens is that most of the material dries in a ring with some offset to the centre and only a minor part of the sample remains in the middle. It has been reported that non-uniform drying leads to bias in elemental determination.8 Nonetheless, model calculations suggest that ring-like deposits are superior to other sample geometries with respect to attenuation of the primary beam.9 Shading effects can occur depending on the morphology of the residues and excitation energy.10 Besides these effects, the position of the residue with respect to the detector field of view (FOV) influences the fluorescence intensity. Even deviations of the relative intensities between Co versus Ga of approx. 10% have been reported.11The magnitude of the offset effect is best studied with specimens of small deposits, which are well-defined in shape, elemental load, and position. Offset effects were studied with residues from microliter droplets by Tabuchi and Tsuji.11 They used 25 individual samples with distances up to 4 mm from the middle of the carrier to cover an area of 8 mm × 8 mm. The residues were formed by drying 10 μL of an aqueous solution at 70 °C. Fast drying prevents large volumes in the microliter range from developing a “coffee ring”-like structure. Surface modification of the substrate and well-controlled drying conditions would be other options for this purpose. The position was controlled using an air blowing technique while drying. The dried sample size was not determined, but offsets from the middle of the carrier while drying were specified in the range of 531–1270 μm. The TXRF measurements were performed with a table-top device equipped with a 7 mm2 silicon drift detector.11 Tsuji et al. expanded their offset effect study with 5 nm thick gold layers (1 mm diameter) at distances up to 8 mm from centre with rotation of the samples in 45° steps. They determined the change of the FOV at four different excitation angles.12
The picoliter approach applied here simplifies the procedure for determining the detector FOV. It allows positioning the deposits more precisely using motorized stages, which allow for independent movement in the x-, y- and z-directions.
The reduction of the volume down to picoliters results in spot-like deposits of defined elemental composition and sizes of 10 to 250 μm in diameter as well as 0.1 to 50 μm in height after a drying time of a few seconds at room temperature (see Fig. S1, ESI† as well as Hampel et al.).13
Residues from picoliter droplets commonly have a well-defined morphology, which has been observed with optical microscopy, atomic force microscopy, and secondary electron microscopy.13–15 Those deposits were used to investigate the physical interactions of the residues with X-rays. Menzel et al. and Fittschen et al. used a colour X-ray camera at BESSY II to illustrate shading of X-rays in TXRF within a picoliter residue pattern.10,16 Macis et al. used a microdrop dispenser with a mean volume of 180 pL to prepare specimens of a reference soil suspended in water onto hydrophilic filters. The dried residues were studied with microXRF with respect to the homogeneity of the fluorescence signal.17 Besides picoliter droplets, nanoliter droplets were used to prepare specimens of TXRF. Evertz et al. used a setup with 15 nL droplet volume for the preparation of patterns and subsequent analysis with TXRF.18 The device was recently used in a round robin test for the preparation of patterns with a nominal mass of 50 ng for TXRF analysis.19 Besides TXRF analysis nanoliter and picoliter droplets were used for sample injection for inductively coupled plasma mass spectrometry by Orlandini v. Niessen et al. in several studies.20–22 The so-far described nanoliter and picoliter printers are either quite expensive or prototypes.
Therefore, Hampel et al. developed an inexpensive picoliter printing device, which produces well-shaped approx. spherical residues from EDTA-stabilized elemental solutions, excellently suited for use in TXRF.13 Since then, the device has been applied to assist in different studies, i.e., Kulow et al. studying coded apertures, which potentially are game-changers in full-field microXRF and Leppin et al. showcasing the potentials of an ultrafast quartz crystal microbalance.23–25
In this work picoliter derived deposits were used to determine the detector FOV, which allows the calculation of the influence of mass accumulated at different radii around the centre. For further experimental evaluation, reference samples with different elements deposited in the centre and three different radii around the centre were prepared from picoliter dried deposits to evaluate the influence of coffee-ring formation on the elemental determination and compare them to the model results. The specimens had either full elemental separation or were prepared with all elements present in each substructure (null bias). From this reference biases in elemental determination arising from spatial separation of the IS and the analytes were determined. The influence of the sample heights according to its position in the X-ray standing wave field and double excitation regime above the reflector was also studied using angle scans.
Materials and methods
Chemicals and materials
For the preparation of the various formulations single element standard solutions of V, Mn, Co, Ni, Cu and Ga (1 g L−1, Roti®Star ICP-standards, Carl Roth, Karlsruhe, Germany), ethylenediaminetetraacetic acid (EDTA) (pro analysi, Rotipuran®, Carl Roth, Karlsruhe, Germany) and ammonia (10% aqueous solution, Carl Roth, Karlsruhe, Germany) were used. All dilutions were prepared with ultra-pure water (>18.2 MΩ cm, Purelab Flex 4, ELGA Veolia, Paris, France). Two C6602A cartridges (droplet volume of 160 pL, HP, Palo Alto, CA, USA) were used to deliver the solutions.26Solutions for inkjet printing
An EDTA-stock solution was prepared by adding 341 mg EDTA and 1.6 mL ammonia solution to 5 mL of water and diluted to a final volume of 40 mL. A four-element standard solution was prepared by adding 1 mL of each single element standard solution, 4 mL EDTA-stock solution, and 2 mL ammonia resulting in a concentration of 100 mg L−1 per element. The four-element standard solution was also diluted with ultra-pure water, resulting in a concentration of 10 mg L−1 per element. Single element solutions of Mn, Co, Cu, and Ga with 100 mg L−1 were prepared analogously.Sample preparation
The cartridges had to be modified for elemental printing according to the procedure from Hampel et al.13 In this process, ink and the sponge were removed, and the ink chamber was cleaned with ultra-pure water. A 3d printed lid with an air hole was applied to the cartridge. All following preparation steps were carried out in a laminar flow box Cruma 870FL (Diantech Solutions S.L., Barcelona, Spain). Four millilitres of the elemental standard solution were filled into the ink chamber, closed with the lid, and the air hole was sealed with tape. Before the actual printing process, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 droplets (≈4.8 μL) were printed three times from each nozzle to clean the nozzle and vent trapped air. A single deposit consisting of a certain number of droplets was printed on a carrier with defined offsets to the middle with various quiet times between droplet spotting. One individual carrier was prepared for each offset. The first series comprised 37 samples covering an area of 100 mm2 with deposits in an offset of up to 5 mm in the x- and 5 mm in the y-direction from the sample carrier centre with distances of 2 mm between deposits in each direction. Each specimen consisted of 100 droplets of the diluted four-element standard solution (10 mg L−1).
000 droplets (≈4.8 μL) were printed three times from each nozzle to clean the nozzle and vent trapped air. A single deposit consisting of a certain number of droplets was printed on a carrier with defined offsets to the middle with various quiet times between droplet spotting. One individual carrier was prepared for each offset. The first series comprised 37 samples covering an area of 100 mm2 with deposits in an offset of up to 5 mm in the x- and 5 mm in the y-direction from the sample carrier centre with distances of 2 mm between deposits in each direction. Each specimen consisted of 100 droplets of the diluted four-element standard solution (10 mg L−1).
The second series included 81 samples with offsets of up to 1.6 mm in both directions and a resolution of 0.4 mm in each direction. Each specimen was made up of 50 droplets of the four-element standard solution (100 mg L−1). After preparation, the printing solution was removed and the cartridge was cleaned with ultra-pure water.
As an example of the influence of the detector FOV a ring structure pattern was printed onto siliconized quartz glass reflectors. Each ring and the centre deposit consisted of an individual element out of the four elements Co, Cu, Ga, and Mn.
The three rings had different distances to the detector FOV centre. The distance between two droplets was set to 200 μm with a quiet time of 1 s (for Co and Ga) and 2.5 s (for Cu and Mn). Each element was printed separately with additional quantification with six repetitions using the same quiet times.
The centred 6 × 6 pattern (Ga) consisted of 288 droplets; the 1st ring (Co) of 76 droplets, the 2nd ring (Cu) of 156 droplets, and the 3rd ring (Mn) of 236 droplets (see Fig. 1). The same elemental solutions were printed as a single residue as well as a 6 × 6 pattern (1 × 1 mm) using the same number of droplets per element with similar droplet numbers (Co: 72, Cu: 144, Ga: 288, and Mn: 252 droplets). A null bias sample was prepared using the same number of droplets and quiet times with all elements at once for each sub-pattern.
Quantification via internal standardization was performed using the same solutions and printing parameters for 304 droplets of each element centred on the reflector (six repetitions), addition of 5 ng V (10 μL of 0.5 mg L−1 V in 1% nitric acid), and subsequent drying under infrared light.
Instruments
The printer was assembled from a Q2299A mount for the cartridge, an Arduino Uno Rev3 (Arduino, New York, NY, USA), and an InkShield by Lewis (Nerd Creation Lab, Everett, WA, USA).27 The Q2299A mount was attached to a Newport 430 linear stage (Newport, Irvine, CA, USA) using two 3D-printed ABS construction parts. The positioning of the carrier was performed by a combination of linear stages X-LSM025A, X-LSM050A, and X-VSR20A (Zaber, Vancouver, BC, Canada). The setup was controlled by software written in Python. The specimens were prepared on poly(methyl methacrylate) discs (PMMA, 30 mm diameter, 3 mm thickness, Formulor, Baden–Baden, Germany) without further modification.Total reflection X-ray fluorescence analysis was performed using a Bruker S4 T-STAR® (Bruker Nano, Berlin, Germany) with an air-cooled X-ray tube (50 kV and 1 mA) with a Mo target (Kα = 17.5 keV). A Peltier-cooled 60 mm2 XFlash® silicon drift detector (SDD) with 400 μm thickness was used. The TXRF prototype device allows the use of focused and non-focused optics for Mo Kα excitation with the possibility of angle-resolved measurements for both monochromators.28–30 Angle calibration of the device was performed by Till (MSc thesis) using the critical angle of five different materials and validated with gold nanoparticles and their respective angle-dependent signal response.31
The lifetime using the focussing monochromator was set to 1000 s for the first series and 600 s for the second series with six repetitions for all samples. Measurements were also performed with a Goebel mirror optic with a parallel beam instead of the focused multilayer monochromator with an incident angle of 0.066°. The lifetime for these measurements was set to 1000 s using the samples of the second series with six repetitions for all samples. Grazing incidence XRF was performed in the angular range from approx. −0.095° to 0.280° (Δθ = 0.006°, lifetime 600 s per position) with the focused beam and from −0.055° to 0.205° (Δθ = 0.005°, lifetime 1000 s per position) for the parallel non-focused beam. The spectral evaluation was performed with PyMCA 5.4.2.32 Optical microscopy was realized with a Nikon Eclipse 80i microscope using a Nikon LV-LH50PC halogen lamp and a Nikon DS-Vi1 digital camera. Data evaluation was performed using Nikon NIS-Elements BR V4.20.01 (Nikon, Tokyo, Japan). Confocal laser scanning microscopy was performed with a Keyence VK-X210 (Keyence, Osaka, Japan).
Results and discussion
Field of view determination
In laboratory based TXRF the beam footprint usually covers the entire area under the detector. Accordingly, the detector FOV is mainly limited by the active size of the semiconductor, the collimator geometry, and the distance to the sample. Naturally, the solid angle captured by the detector from each point in the FOV decreases from the middle to the rim. It can be modelled to estimate the effect of specimen morphology and inhomogeneity on the signal.33 The approach introduced here allows validating modelled detection geometries experimentally and obtaining actual data from synthetic samples of defined dimensions. Here, the picoliter-assisted sample preparation approach is introduced evaluating the decrease of the captured solid angle experimentally.Two series of individual pL specimens were used to determine the FOV
From the first series an overview of the detector FOV was obtained. The second series probed the identified the main area of the FOV in series #1 with a higher spatial resolution. The first series used offsets of up to 5 mm in each direction from the centre of a sample carrier, corresponding to an area of 100 mm2; this large area was investigated with 37 samples. For each offset position, an individual picoliter-derived specimen was prepared. Each residue was composed of Co, Ni, Cu, and Ga, each 160 pg per element, and used to visualize the FOV and determine position-dependent sensitivities (see Fig. S3, ESI†). The diameter of an individual deposit was determined to be about 65 μm for the first series using optical microscopy.The sample with no offset shows the largest net intensity of N(Co Kα) = 4996 ± 139 counts. It drops significantly at 3 mm from the centre (<25% of the max). The intensity at larger offsets was below the limit of quantification (LOQ) given by the concentration ci, the net intensity Ni, and the intensity of the background NBG.
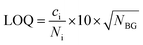 | (1) |
Using the linear interpolation between data points, an asymmetry of the intensity distribution is detected. The uncertainties of the results were obtained by repetitive measurements of the samples (n = 6) and from counting statistics. The SD from repetitive measurements is nearly constant over the whole area with about 100–200 counts for all elements (see Fig. S3 panel B, ESI†). This corresponds to an RSD of 4% for deposits with no offset. The RSD increases significantly at 3 mm from the centre up to 40%. The error from the counting statistics is lower than the error from the repetitive measurements.
TXRF quantification is most commonly performed using an internal standard (IS) and relative sensitivities (RS), meaning the sensitivity of a specific elemental line, e.g., Co Kα over a reference line e.g., Ga Kα. The advantage of using the IS is clear, even though an outer deposit yields less signal, it will do so for both the analyte line and the internal standard, so the RS stays constant. The local RSs were calculated to confirm constant RSs when the IS and analyte are located at the same position in the detector FOV. As the concentrations per element of each residue are the same, the local RS can be expressed as the quotient of the net intensity of the corresponding element by the net intensity of Ga Kα. The mean of the local RS of the five centre positions corresponds to 0.550 ± 0.007 for the 95% confidence interval (95% CI). For Co Kα, the RS in the middle is RS(Co Kα) = 0.550 ± 0.011 (95% CI). Within the experimental error, for positions <3 mm from the middle the RS is not significantly different from the RS in the middle, although the uncertainty increases as well (see Fig. S3 panel D, ESI†). Only at the very edges of the FOV did the RS deviate significantly from the values determined in the middle. The RS for Co Kα decreases to 0.443 ± 0.164 (95% CI) for the sample with −1 mm (x) and +3 mm (y) the largest distance to the maximum net intensity.
In the second series, the centre of the FOV was analysed with a higher resolution to allow for a more accurate description of the area contributing most to the signal. The masses per element were increased to 800 pg per element in the second series to reduce the measurement time. Furthermore, the distance between two residues was decreased to 0.4 mm to gain a better spatial resolution. The area was restricted to 1.6 × 1.6 mm (9 × 9 deposits) to keep the experiment within a reasonable time frame. The shape and size of each residue were analysed using optical microscopy. The residues were found to have all round shape with minor distortions. The diameter of all samples was 91.4 ± 5.7 μm (n = 80). Five samples were found with increased and distorted shape (the shape depends strongly on the substrate as contaminations or scratches induce distorted circle formation with a greater diameter), but with no influence on the intensity during TXRF measurement. Microscopy images of round as well as distorted shaped residues are shown in Fig. S2 (ESI†).
First, the distribution of the net intensity at each position was considered (Fig. S4 panel A, ESI†). Cobalt was chosen, again, to allow a direct comparison to the first series. The overall shape of the area with high intensities corresponds to the shape seen before. The shift to larger offsets is visible, as expected from the first series. The maximum intensity is at an offset of +0.4 mm (x) and +1.2 mm (y) with N(Co) = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 ± 187 counts. A low spread was found regarding the standard deviation of six measurements. The furthest residues show the largest RSDs of up to 19% while for most residues the RSD is well below 5%. The results are in good agreement with the data of the first series (shown in Fig. S3 panel B, ESI†).
880 ± 187 counts. A low spread was found regarding the standard deviation of six measurements. The furthest residues show the largest RSDs of up to 19% while for most residues the RSD is well below 5%. The results are in good agreement with the data of the first series (shown in Fig. S3 panel B, ESI†).
The local RSs are nearly constant over the probed area with a mean of 0.540 ± 0.001 (95% CI). The RSs from the second series seem to be somewhat lower than those from the first series with a mean of 0.550 ± 0.007 (95% CI) considering the whole probed reflector. Using only the inner area of interest both series are not significantly different. The RSs of the second series show three outliers for Cu, because of Cu contamination. Other minor contaminations such as Ti, Fe, and Zn were found on some carriers but occurred randomly. The SD of the local RS for most samples is <0.05.
Merging both series into a single data set
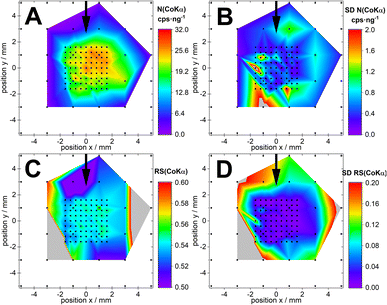
The first series (0.16 ng, 1000 s measurement time) was successfully merged with the second series (0.80 ng, 600 s measurement time). As both data sets used different live times per spectra and different deposited masses per carrier, the data sets were normalized to those values. The normalized intensity and sensitivity distribution of Co Kα are shown in Fig. 2. In general, colour maps show the net intensities of the Co Kα-line, the standard deviation of the net intensities, and the sensitivities at each point relative to the Ga Kα-line. Each black dot represents the position of an individual sample.The normalized intensity of the second series fits well in the middle of the probed area. Overall, the normalized intensities of the second series N(Co Kα) = 21.2 ± 0.3 cps ng−1 (95% CI, n = 486) appear to be somewhat lower than the intensities obtained from the first series at comparable positions with N(Co Kα) = 23.8 ± 1.7 cps ng−1 (95% CI, n = 30). The merged image illustrates the centre offset in the x- and y-direction nicely (Fig. 2, panel A). The merged RS reveals no differences between both series in the middle area as shown in Fig. 2, panel C. Considering the SD of the RS (Fig. 2, panel D), both values are not significantly different.
The normalized data from both series were used to determine the Gaussian-like distribution in Fig. 3.
 | ||
| Fig. 3 Comparison of the normalized intensity profile (panel A) and 2d Gaussian distribution fit of the intensity profile (panel B). | ||
A two-dimensional Gaussian fit using the raw data of Co Kα yields a correlation of R2 = 0.861. The fit results in Table 1 show an offset (x0 and y0) of the Gaussian distribution from the centre of the carrier.
| Parameter | Co Kα | Ni Kα | Cu Kα | Ga Kα | Mean |
|---|---|---|---|---|---|
| A/cps ng−1 | 26.7 ± 0.5 | 34.2 ± 0.6 | 37.8 ± 0.7 | 49.1 ± 0.9 | — |
| x 0/mm | 0.62 ± 0.08 | 0.69 ± 0.09 | 0.72 ± 0.09 | 0.61 ± 0.08 | 0.66 ± 0.09 |
| y 0/mm | 0.28 ± 0.06 | 0.31 ± 0.07 | 0.29 ± 0.07 | 0.27 ± 0.06 | 0.29 ± 0.07 |
| σ(x)/mm | 2.37 ± 0.13 | 2.53 ± 0.14 | 2.57 ± 0.14 | 2.38 ± 0.13 | 2.46 ± 0.10 |
| σ(y)/mm | 2.18 ± 0.11 | 2.34 ± 0.12 | 2.33 ± 0.12 | 2.21 ± 0.11 | 2.27 ± 0.11 |
| 4σ(x)/mm | 9.47 ± 0.50 | 10.12 ± 0.55 | 10.30 ± 0.57 | 9.52 ± 0.50 | 9.85 ± 0.54 |
| 4σ(y)/mm | 8.71 ± 0.42 | 9.36 ± 0.47 | 9.33 ± 0.47 | 8.83 ± 0.43 | 9.06 ± 0.46 |
| R 2/— | 0.861 | 0.842 | 0.841 | 0.861 | — |
The fit delivered a maximum of 26.7 ± 0.5 cps−1 ng−1, a σ of 2.37 ± 0.13 mm in the x-direction, a σ of 2.18 ± 0.11 mm in the y-direction, a basis (4σ) of 9.4 ± 0.50 mm in the x-direction and 8.7 ± 0.42 mm in the y-direction. The latter can be used as an expression of the FOV dimensions. From the fitted data a nearly symmetrical 2d Gaussian distribution is found. The dimensions are comparable between all four elements used (see Table 1). There are slight differences between Co and Ga compared to Ni and Cu, respectively. The differences are in the range of the standard errors of the fit and the confidence intervals overlap.
The data's shape of a 2d Gaussian distribution corresponds to the investigations of Tabuchi and Tsuji, where microliter droplet residues were used.11 Simulations of the detector's solid angle acceptance function by Beckhoff et al. delivered a comparable distribution to the FOV results presented here. However with a plateau of maximum intensity in the detector centre instead of Gaussian distribution.33
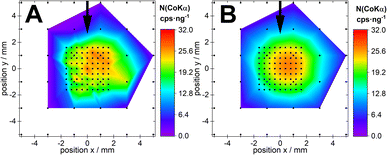
These data were used to optimize the position of the quartz carrier relative to the detector as much as possible. The specimens of the second series were used to redetermine the FOV after the alignment procedure yielding comparable results to the initial set up beside a better match between the centre of the FOV and the centre of the sample carriers.
The normalized intensity and the standard deviations are comparable to the results from before the optimization (see Fig. S6, ESI†).
The local RS and the SD of the local RS are the same within the error of measurement. This indicates long term stability of the specimens.
The previous FOV determinations were obtained from the focussing monochromator. It was somewhat expected that the FOV would have some anisotropy due to the focussed illumination. However only slight distortion of the Gaussian distribution was observed. For the last FOV determination the parallel beam optic (Goebel mirror monochromator) was used instead of the focusing optics (see Fig. S6, ESI†). It is designed for the lowest possible beam divergence. The setup and characterization are shown by Hönicke et al. including two apertures limiting the detector FOV.29 The parallel beam is expected to have a wider footprint and homogeneous illumination. The normalized intensity distribution (Fig. S6, ESI†) shows a reduction of about factor 3 compared to the focusing optics due to the beam intensity outside of the detector FOV. Aside from the reduced intensity the normalized intensity distribution is comparable with the results from the focused monochromator measurements. The SD of the normalized intensity is reduced by about a factor of 2. This is expected as the error comes mostly from the counting statistics. There are a few outliers which are randomly distributed overall specimens. The RS with the Goebel mirror optic is the same as the measurement with the focused beam within the error of measurement. The SD of the RS is also in the same range as before.
Comparing the FOV of the focusing multilayer set up and the parallel beam set up slight differences in size and position could be found (see Fig. 4). Hence, it can be concluded that the focusing has no influence on the FOV in the studied set up.
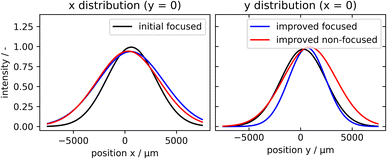 | ||
| Fig. 4 2D Gaussian distribution fits from initial two series and optimized series II for focused and non-focused beams shown for the x- and y-direction, respectively. | ||
Errors measuring inhomogeneous ring-like deposits
From the FOV determined in the previous chapter it can be concluded how parts of the specimen's positions further away from the centre of the FOV contribute less to the recorded signal. Using an internal standard and having a homogeneous distribution of the IS and analyte a negligible error is expected. However, separation of the IS and the analyte may occur between the “coffee ring” and the centre of the specimens as has been observed by Wellenreuther et al. for the hELAC1 protein bound Zn and the IS when prepared on silicon.6 They found an enrichment of the IS elements Ga and Sc in the “coffee ring” compared to Zn.The influence of the elemental location on the signal intensity can be experimentally evaluated using the picoliter printed elemental pattern shown in Fig. 1. Each residue in the respective sub patterns has its own contribution to the intensity yielding a mean intensity for each sub pattern. The mean intensity contribution is given as the FOV factor. The comparison of signal intensity from a single residue, a 6 × 6 pattern (1 × 1 mm), and the ring structures is shown with the TXRF spectra in Fig. 5. The fluorescence lines in the 6 × 6 specimen (covering 1 × 1 mm) versus the single drop have nearly the same intensity, and even a little bit higher. This is unexpected from the two-dimensional Gaussian FOV described in this work and the FOV modelled by Beckhoff et al., which showed a plateau of maximum intensity in the detector centre, might be better suited to describe this particular phenomenon.33
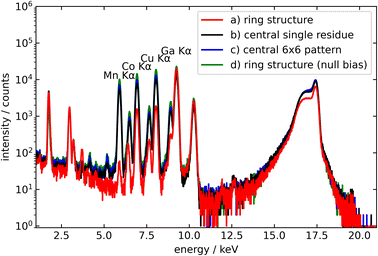 | ||
| Fig. 5 Influence of the position on the signal intensity of a four-element composition as (a) single residue of Ga in the centre with Co (radius 2 mm), Cu (radius 4 mm), and Mn (radius 6 mm) as concentric coffee rings (see Fig. 1), (b) the same elements as single residues at the centre, and (c) the same elements as a 6 × 6 pattern (1 mm × 1 mm). A null bias (d) was added for comparison using the ring structure (a) consisting of all elements in each ring. | ||
However, matrix effects depending on composition and morphology were not considered here. The large one-spot deposit may also suffer more from absorption effects. Together both can explain the intensity increase in the 6 × 6 pattern. If the mass is distributed as ring structures the mean intensity decreases drastically with increasing distance to the centre.
This is evident from the spectra in Fig. 5. The red spectrum represents the concentric ring pattern with the Mn-ring having the largest radius of 6 mm and the lowest signal (1% of the single residue), followed by the Cu-signal (20% of the central residue) which is deposited in a ring with a radius of 4 mm and Co-signal (67% of the single residue) on the 2 mm radius. The null bias sample had no significant intensity decrease as all elements are present homogeneously in each ring and the centre.
Some of the variation is due to the deposited masses which vary slightly between the specimens. Accordingly, the intensities were normalized to the lifetime and the deposited mass (see Table 2) to quantify the reduction of the net intensities (see Table 3).
| Intensity/counts s−1 ng−1 | Ga Kα (centre) | Co Kα (1st ring, 2 mm) | Cu Kα (2nd ring, 4 mm) | Mn Kα (3rd ring, 6 mm) |
|---|---|---|---|---|
| Ring structure (all elements, null bias) | 21.6 ± 1.5 | 11.5 ± 0.8 | 16.3 ± 1.2 | 8.1 ± 0.7 |
| Ring structure | 48.3 ± 1.1 | 15.9 ± 0.4 | 7.1 ± 0.2 | 0.076 ± 0.004 |
| Single residue | 42.0 ± 0.9 | 21.7 ± 0.5 | 32.1 ± 0.7 | 15.6 ± 0.5 |
| 6 × 6 pattern | 44.6 ± 1.0 | 23.6 ± 0.5 | 34.6 ± 0.7 | 17.4 ± 0.6 |
| Ring structure (all elements, null bias) offset corrected | 22.5 ± 1.5 | 12.1 ± 0.9 | 17.0 ± 1.3 | 8.4 ± 0.7 |
| Ring structure offset corrected | 47.8 ± 1.1 | 15.8 ± 0.4 | 7.5 ± 0.2 | 0.10 ± 0.01 |
| Single residue offset corrected | 42.1 ± 0.9 | 21.1 ± 0.5 | 31.2 ± 0.6 | 15.7 ± 0.6 |
| 6 × 6 pattern offset corrected | 43.9 ± 1.0 | 23.2 ± 0.5 | 34.0 ± 0.7 | 17.6 ± 2.3 |
| FOV factors | Ga Kα (centre) | Co Kα (1st ring, 2 mm) | Cu Kα (2nd ring, 4 mm) | Mn Kα (3rd ring, 6 mm) | |
|---|---|---|---|---|---|
| Compared to single residues | Theoretical | 0.979 | 0.714 | 0.254 | 0.046 |
| Experimental | 1.137 | 0.745 | 0.242 | 0.006 | |
| Compared to a 6 × 6 pattern | Theoretical | 0.919 | 0.670 | 0.238 | 0.043 |
| Experimental | 1.088 | 0.678 | 0.222 | 0.007 | |
The mass per element was determined with quantification via the IS with a separate sample series with centred single deposits. In total, 6.1 ng Mn, 1.5 ng Co, 4.2 ng Cu, and 7.2 ng Ga were deposited on the ring structure as well as with the single residue. The masses for the 6 × 6 pattern varied slightly with 6.5 ng Mn, 1.4 ng Co, 3.9 ng Cu, and 7.2 ng Ga. The null bias sample consisted of 17.0 ng Mn, 18.0 ng Co, 18.1 ng Cu, and 17.7 ng Ga.
The normalized results show the same tendencies already visible in the spectra. The 6 × 6 pattern in comparison to a single residue at the centre yields an increase in intensity by 6% to 12%. Approximately the same masses printed as the ring structure experiences drastic reduction of the normalized intensity of up to 99.5% for the Mn ring with about 6 mm distance to the centre, 80% Cu (radius 4 mm) and 33% Co (radius 2 mm). Interestingly, the normalized intensity of Ga which sits as a 6 × 6 pattern in the middle of the concentric rings increases by 15%. The only difference from the 6 × 6 pattern is the absence of other elements. The increase may be explained by lower absorption effects, which occur when Co, Cu and Mn experience secondary excitation from the Ga Kα fluorescence. The discussed specimens were centred on the quartz glass reflectors and according to our FOV determination are slightly off set to the centre of the FOV. To obtain perfectly FOV centred structures another set of specimens was prepared, however not centred on the quartz but with an offset so they are centred in the FOV. The results are shown in Table 2 with the annotation “offset corrected”. For the single residue and the 6 × 6 pattern no significant differences from the initial specimens were found. The ring structure only has significant differences for large distances to the centre improving the intensity of Cu by 6% and for Mn by 32%.
Having determined the signal reduction from a mock-up ring like deposit, it can be evaluated if those can be solely explained by the Gaussian profile determined previously. The null bias sample showed the same relative intensity ratios as the single residue within the error of measurement. The offset corrected specimens were used for the comparison of the Gaussian profiles. Theoretical values are derived by setting the Gaussian mean (centre of FOV) to unity. The expected contributions of each microdeposit at a known distance to the centre are then calculated from the Gaussian distribution in Table 1. As the middle of the specimen has a 6 × 6 pattern the mean FOV factor is slightly less than unity, e.g., 0.979 and 0.919. The experimental FOV factors are derived as a ratio of net intensity in the ring structure and intensity in a single residue and 6 × 6 pattern, respectively (see Table 3).
The determined experimental FOV factors match the theoretical values quite well. The experimental data for Ga yield FOV factors greater than unity due to the printing as a 6 × 6 pattern. This indicates that either the Gaussian model is not entirely true or the deposits suffer less from absorption as discussed previously. The values for Co and Cu match within an error of less than 7%. Only Mn doesn't reach its expected value with a difference of up to 87%. The low sensitivity in combination with the large distance to the detector yields a significant decrease in the experimental values. Absorption of the fluorescence in air is negligible (Mn Kα absorption less than 1%).
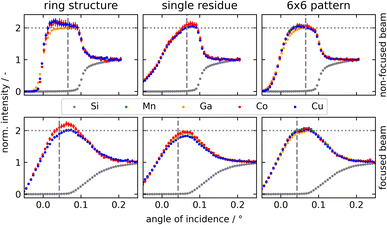
Bias may not only originate from the offset of the deposits but also from its position in the X-ray standing wave field and double excitation regime above the reflector (an influence mainly determined using the heights of the deposit). In TXRF two positions are generally distinguished the film-like deposit (low rise deposit excited by the X-ray standing wave field only) and particle-like deposit (high rise excited by double excitation). The sensitivity of a film-like deposit at the common angle (70% of the critical angle) for TXRF measurement can be about 15–30% higher or lower (depending on the actual height of the deposit) than for a particle-like deposit. As different morphologies of the analyte and IS also influence the net intensity, grazing incidence XRF was performed on all specimens under non-focused and focused beam conditions (see Fig. 6).
The printing conditions were set for the deposition of particular residues due to the height concentration of the elemental solutions and the long quiet time.
The ring structure has small differences between Co and Cu as analytes and Ga as the IS. The net intensity for Mn was too low to obtain reasonable data as the propagated error is quite high. This can be shown for both beam optics. Nevertheless, particular residues were obtained as expected.
Printing all elements as single residues at the centre results in large deviations from the common particular type of shape. The plateau for the quasi-double excitation is reduced towards 0° and below 0° there is a significant increase in intensity. Till et al. reported that height effects have influences on the intensity using Monte Carlo simulation of GIXRF scans. Below 0° high specimens are already illuminated. The quasi-double excitation is reduced as only fractions of the same volume are excited by incident and reflected beams.34 From printing the same mass per element onto an area of 1 × 1 mm (6 × 6 pattern) this effect is expected to be drastically reduced which is visible in Fig. 6.
In general, focused beam optics are robust towards small deviations in the morphology at the given TXRF angle and allow good quantification. Nevertheless, the small differences which are still present have an influence on the experimentally derived FOV factors. This is notably visible for Ga with its deviation from the theoretical values.
Here we have shed light on bias obtained from an extreme, where the elements are separated 100%. The bias to the true amounts is 33% for a 2 mm radius coffee ring, 80% for a 4 mm radius coffee ring, and 99% for a 6 mm radius coffee ring. Real samples will exhibit less severe elemental separations and therefore suffer from a lower bias if at all. This was demonstrated using a null bias sample with the same ring structure where all elements are present in each ring and the centre. Within the error of measurement no significant differences in the relative intensities between all elements were found. Only the normalized intensity is significantly changed according to the signal contribution within the detector FOV.
Conclusions
In this work, we studied the detector's FOV influence on the determination of coffee ring specimens using picoliter residues. The FOV was determined using 128 individual single micro deposit specimens. Each reflector consists of one residue with a defined offset. Combining all results, intensities and RSs over a large area were visualized. The intensity profile of the FOV corresponded to a 2d Gaussian-like distribution with a maximum height of 26.7 cps−1 ng−1 for Co Kα, σs of 2.4 mm (x) and 2.2 mm (y), a basis (4σ) of 9.47 mm (x) and 8.71 mm (y), and offsets from the centre of 0.62 mm (x) and 0.28 mm (y), describing the dimensions of the FOV. Each residue consisted of Co, Ni, Cu, and Ga; therefore for each element, a statement on the intensity distribution and the local RS could be made. The local RSs were found to be constant within the experimental error in the FOV. Position-dependent signal intensities were shown for concentric ring structures compared to single residues and a 6 × 6 pattern (covering 1 × 1 mm) with the same masses. The 6 × 6 pattern in comparison to a single residue at the centre yields an increase in intensity by up to 12%. The 100% separation of the IS and analyte results in a bias of 33% for a 2 mm radius coffee ring, 80% for a 4 mm radius coffee ring, and 99% for a 6 mm radius coffee ring. The reduction is explained by the residues being up to 6 mm off from the FOV centre.The approach introduced here allows not only to validate modelled detection geometries experimentally, but also in the future to obtain actual data from synthetic samples of defined horizontal dimensions (ring-shape, concentric deposits, etc.), defined composition, e.g., gradients from the middle to the rim and potentially also defined vertical morphology, etc. gradients from film-like to particle-like. This will allow learning how these gradients affect TXRF results.
Author contributions
Sven Hampel: conceptualization, methodology, software, validation, formal analysis, investigation, writing – original draft, writing – review & editing, visualization. Franziska Sand: investigation, formal analysis, writing – review & editing. Heiko S. Till: software, formal analysis, writing – review & editing. Ursula E. A. Fittschen: resources, writing – original draft, writing – review & editing, project administration.Conflicts of interest
There are no conflicts to declare.References
- I. de La Calle, N. Cabaleiro, V. Romero, I. Lavilla and C. Bendicho, Sample pretreatment strategies for total reflection X-ray fluorescence analysis: A tutorial review, Spectrochim. Acta, Part B, 2013, 90, 23–54 CrossRef CAS.
- R. Klockenkämper and A. von Bohlen, Total-reflection X-Ray Fluorescence Analysis and Related Methods, Wiley, Hoboken, New Jersey, 2nd edn, 2015 Search PubMed.
- D. Hellin, J. Rip, V. Geens, T. Delande, T. Conard, S. de Gendt and C. Vinckier, Remediation for TXRF saturation effects on microdroplet residues from preconcentration methods on semiconductor wafers, J. Anal. At. Spectrom., 2005, 20, 652–658 RSC.
- L. Fabry, S. Pahlke and L. Kotz, Accurate calibration of TXRF using microdroplet samples, Anal. Bioanal. Chem., 1996, 354, 266–270 CrossRef CAS PubMed.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Capillary flow as the cause of ring stains from dried liquid drops, Nature, 1997, 389, 827–829 CrossRef CAS.
- G. Wellenreuther, U. E. A. Fittschen, M. Achard, A. Faust, X. Kreplin and W. Meyer-Klaucke, Optimizing total reflection X-ray fluorescence for direct trace element quantification in proteins I: Influence of sample homogeneity and reflector type, Spectrochim. Acta, Part B, 2008, 63, 1461–1468 CrossRef.
- R. Fernández-Ruiz, Three empirical cases of the deposition morphology influence in the analytical quality of direct solid suspension measurements by total-reflection X-ray fluorescence, Spectrochim. Acta, Part B, 2009, 64, 672–678 CrossRef.
- B. U. Peschel, U. E. A. Fittschen, G. Pepponi, C. Jokubonis, C. Streli, P. Wobrauschek, G. Falkenberg and J. A. C. Broekaert, Direct analysis of Al2O3 powders by total reflection X-ray fluorescence spectrometry, Anal. Bioanal. Chem., 2005, 382, 1958–1964 CrossRef CAS PubMed.
- C. Horntrich, P. Kregsamer, P. Wobrauschek and C. Streli, Considerations on the ideal sample shape for Total Reflection X-ray Fluorescence Analysis, Spectrochim. Acta, Part B, 2011, 66, 815–821 CrossRef CAS.
- U. E. A. Fittschen, M. Menzel, O. Scharf, M. Radtke, U. Reinholz, G. Buzanich, V. M. Lopez, K. McIntosh, C. Streli and G. J. Havrilla, Observation of X-ray shadings in synchrotron radiation-total reflection X-ray fluorescence using a color X-ray camera, Spectrochim. Acta, Part B, 2014, 99, 179–184 CrossRef CAS.
- Y. Tabuchi and K. Tsuji, TXRF intensity dependence on position of dried residue on sample carrier and TXRF determination of halogen in liquid samples, X-Ray Spectrom., 2016, 45, 197–201 CrossRef CAS.
- K. Tsuji, N. Taniguchi, H. Yamaguchi and T. Matsuyama, Evaluation of analysis volume in total reflection X-ray fluorescence analysis, X-Ray Spectrom., 2023, 52(6), 357–363 CrossRef CAS.
- S. Hampel, F. Sand, D. A. M. Gonzalez, G. Pepponi, G. Helsch, J. Deubener, T. Schirmer, A. Fittschen and U. E. A. Fittschen, Chelate complexed multi-elemental printing performance of a small and cost efficient picoliter droplet printing device for micro preparation, Spectrochim. Acta, Part B, 2023, 106716 CrossRef CAS.
- U. E. A. Fittschen, N. H. Bings, S. Hauschild, S. Förster, A. F. Kiera, E. Karavani, A. Frömsdorf, J. Thiele and G. Falkenberg, Characteristics of picoliter droplet dried residues as standards for direct analysis techniques, Anal. Chem., 2008, 80, 1967–1977 CrossRef CAS PubMed.
- C. M. Sparks, U. E. A. Fittschen and G. J. Havrilla, Picoliter solution deposition for total reflection X-ray fluorescence analysis of semiconductor samples, Spectrochim. Acta, Part B, 2010, 65, 805–811 CrossRef.
- M. Menzel, O. Scharf, S. H. Nowak, M. Radtke, U. Reinholz, P. Hischenhuber, G. Buzanich, A. Meyer, V. Lopez, K. McIntosh, C. Streli, G. J. Havrilla and U. E. A. Fittschen, Shading in TXRF: calculations and experimental validation using a color X-ray camera, J. Anal. At. Spectrom., 2015, 30, 2184–2193 RSC.
- S. Macis, G. Cibin, V. Maggi, G. Baccolo, D. Hampai, B. Delmonte, A. D'Elia and A. Marcelli, Microdrop Deposition Technique: Preparation and Characterization of Diluted Suspended Particulate Samples, Condens. Matter, 2018, 3, 21 CrossRef.
- M. Evertz, T.-N. Kröger, M. Winter and S. Nowak, Total reflection X-ray fluorescence in the field of lithium ion batteries – Elemental detection in Lithium containing electrolytes using nanoliter droplets, Spectrochim. Acta, Part B, 2018, 149, 118–123 CrossRef CAS.
- R. Unterumsberger, B. Beckhoff, A. Gross, H. Stosnach, S. Nowak, Y. P. Stenzel, M. Krämer and A. von Bohlen, A round robin test for total reflection X-ray fluorescence analysis using preselected and well characterized samples, J. Anal. At. Spectrom., 2021, 36, 1933–1945 RSC.
- J. O. Orlandini v Niessen, K. M. Krone and N. H. Bings, Effect of operation conditions of the drop-on-demand aerosol generator on aerosol characteristics: Pseudo-cinematographic and plasma mass spectrometric studies, Spectrochim. Acta, Part B, 2014, 92, 51–59 CrossRef.
- J. O. Orlandini v Niessen, J. H. Petersen, J. N. Schaper and N. H. Bings, Comparison of novel and conventional calibration techniques for the analysis of urine samples using plasma source mass spectrometry combined with a new dual-drop-on-demand aerosol generator, J. Anal. At. Spectrom., 2012, 27, 1234–1244 RSC.
- J. O. Orlandini v Niessen, J. N. Schaper, J. H. Petersen and N. H. Bings, Development and characterization of a thermal inkjet-based aerosol generator for micro-volume sample introduction in analytical atomic spectrometry, J. Anal. At. Spectrom., 2011, 26, 1781–1789 RSC.
- A. Kulow, A. Guilherme Buzanich, U. Reinholz, F. Emmerling, S. Hampel, U. E. A. Fittschen, C. Streli and M. Radtke, Comparison of three reconstruction methods based on deconvolution, iterative algorithm and neural network for X-ray fluorescence imaging with coded aperture optics, J. Anal. At. Spectrom., 2020, 35, 1423–1434 RSC.
- A. Kulow, A. Guilherme Buzanich, U. Reinholz, F. Emmerling, S. Hampel, U. E. A. Fittschen, C. Streli and M. Radtke, Reconstruction and superresolution for coded aperture full-field X-ray fluorescence imaging, Adv. X-Ray Anal., 2021, 65, 57–70 Search PubMed.
- C. Leppin, S. Hampel, F. S. Meyer, A. Langhoff, U. E. A. Fittschen and D. Johannsmann, A Quartz Crystal Microbalance, Which Tracks Four Overtones in Parallel with a Time Resolution of 10 Milliseconds: Application to Inkjet Printing, Sensors, 2020, 20, 5915 CrossRef PubMed.
- HP Inc., HP Extended TIJ 1.0 Print Cartridges Datasheet, 2003 Search PubMed.
- N. C. Lewis, InkShield, https://github.com/NicholasCLewis/InkShield, accessed 8 May 2023.
- V. Szwedowski-Rammert, J. Baumann, C. Schlesiger, U. Waldschläger, A. Gross, B. Kanngießer and I. Mantouvalou, Laboratory based GIXRF and GEXRF spectrometers for multilayer structure investigations, J. Anal. At. Spectrom., 2019, 34, 922–929 RSC.
- P. Hönicke, U. Waldschläger, T. Wiesner, M. Krämer and B. Beckhoff, Towards a calibration of laboratory setups for grazing incidence and total-reflection X-ray fluorescence analysis, Spectrochim. Acta, Part B, 2020, 174, 106009 CrossRef.
- V. Szwedowski-Rammert, P. Hönicke, M. Wu, U. Waldschläger, A. Gross, J. Baumann, G. Goetzke, F. Delmotte, E. Meltchakov, B. Kanngießer, P. Jonnard and I. Mantouvalou, Laboratory grazing-incidence X-ray fluorescence spectroscopy as an analytical tool for the investigation of sub-nanometer CrSc multilayer water window optics, Spectrochim. Acta, Part B, 2020, 174, 105995 CrossRef CAS.
- H. S. Till, Master thesis, Clausthal University of Technology, 2020.
- V. A. Solé, E. Papillon, M. Cotte, P. Walter and J. Susini, A multiplatform code for the analysis of energy-dispersive X-ray fluorescence spectra, Spectrochim. Acta, Part B, 2007, 62, 63–68 CrossRef.
- B. Beckhoff, R. Fliegauf, M. Kolbe, M. Müller, J. Weser and G. Ulm, Reference-free total reflection X-ray fluorescence analysis of semiconductor surfaces with synchrotron radiation, Anal. Chem., 2007, 79, 7873–7882 CrossRef CAS PubMed.
- H. S. Till, A. Gross and U. E. A. Fittschen, in ANAKON 2023, ed. M. Marchetti-Deschmann, E. Rosenberg and V. Weiss, TU Wien, Vienna, 2023 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ja00316g |
| This journal is © The Royal Society of Chemistry 2024 |