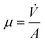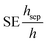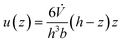Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient numerical modelling of magnetophoresis in millifluidic systems†‡
Johannes
Soika
 *a,
Tobias
Wanninger
a,
Patrick
Muschak
b,
Anja
Schnell
a,
Sebastian P.
Schwaminger
*a,
Tobias
Wanninger
a,
Patrick
Muschak
b,
Anja
Schnell
a,
Sebastian P.
Schwaminger
 bcd,
Sonja
Berensmeier
be and
Markus
Zimmermann
a
bcd,
Sonja
Berensmeier
be and
Markus
Zimmermann
a
aLaboratory for Product Development and Lightweight Design, Tum School of Engineering and Design, Technical University of Munich, Boltzmannstr. 15, 85748 Garching, Germany. E-mail: johannes.soika@tum.de
bChair of Bioseparation Engineering, Tum School of Engineering and Design, Technical University of Munich, Boltzmannstr. 15, 85748 Garching, Germany
cDivision of Medicinal Chemistry, Otto Loewi Research Center, Medical University of Graz, Neue Stiftingtalstraße 6, 8010 Graz, Austria
dBioTechMed-Graz, Mozartgasse 12, 8010 Graz, Austria
eMunich Institute for Integrated Materials, Energy and Process Engineering, Technical University of Munich, Lichtenbergstr. 4a, 85748 Garching, Germany
First published on 18th September 2024
Abstract
Continuous flow magnetophoresis represents a common technique for actively separating particles within a fluid. For separation systems design, accurately predicting particle behaviour helps to characterise system performance, typically measured by the separation efficiency (SE). While finite element method (FEM) simulations offer high accuracy, they demand extensive computational resources. Alternatively, results can be achieved more quickly with simplified numerical models that use analytical descriptions of fluid flow, magnetic fields, and particle movement. In this research, we model a millifluidic system that separates magnetic particles using magnetophoresis. Therefore, we (1) develop a simple numerical model that can simulate continuous flow magnetophoresis for rectangular channels in two and three dimensions, (2) introduce a novel and simple approach to calculate the SE, and (3) quantify the effects of model assumptions in flow profile and dimensions on SE. Our method for estimating SE considers particle flux variation across the channel's cross-section due to the flow profile. The results are compared to an FEM model developed in COMSOL. The obtained three-dimensional simulation model computes results in seconds, around 180 times faster than the FEM approach, while deviating less than 2% from the FEM results. A comparison of the different two-dimensional and three-dimensional models underscores the significant influence of the flow profile and the SE calculation method on the result. The two dimensional models generally overestimate the SE of up to 15% due to their lower peak flow velocity. However, using a constant flow velocity leads to good agreement for high SE due to the overlap of differences in flow profile and SE calculation.
1 Introduction
Magnetic manipulation technologies are used to sort, separate and isolate magnetic or magnetised particles.1 Examples of practical applications are the separation of E. coli bacteria from blood,2 cell sorting in millifluidic devices,3 kidney stone treatment using bare iron oxide,4 magnetic drug delivery,5 separation of yeast cells,6 or immunomagnetically labelled mammalian cells,7 and various other lab-on-a-chip applications.8The underlying phenomenon is magnetophoresis, where magnetic or magnetically labelled particles are set in motion by an externally imposed magnetic field gradient.9 For the separation of bio-molecules (cells, proteins, antibodies, bacteria, DNA, RNA, etc.), the target molecule is labelled with a functionalised magnetic particle, enabling separation through magnetophoresis.10 Magnetic nanoparticles (MNPs), such as iron oxide nanoparticles, exhibit superparamagnetic behaviour when below a certain size threshold. This characteristic implies that MNPs become magnetised in the presence of a magnetic field and lose their magnetisation once the field is removed.11,12 One important parameter is the magnetic susceptibility, which indicates how much a material will become magnetized in an applied magnetic field and therefore significantly affects separation behavior.13 The susceptibility is highly dependent on the magnetic field and the temperature and can be expressed in volume, mass, and molar forms.14 The magnetic field affects magnetic forces and leverages phenomena such as aggregation.15,16
A continuous flow magnetophoretic separator is in essence a fluidic unit – usually a straight channel of different shapes with one or more in- and outlets – to which one or more magnets are attached to the channel walls.17–20 In the realm of magnetophoretic separation system design, achieving an optimal system might seem straightforward. Parametric studies show that minimising volume flux and channel height while maximising magnet forces, magnet strength, and particle concentration increases separation efficiency.18,20 However, the design considerations extend beyond separation efficiency alone. In addition to achieving high separation efficiency, requirements such as minimising test duration or overall separator costs can be crucial.21 These additional considerations may introduce conflicts between design variables. For example, decreasing the fluid flow might enhance separation efficiency but cause longer test duration.
Simulation models are used to evaluate system behaviour when designing the fluidic unit. Generally, the models consist of a fluid description in an Eulerian frame, superposed with the particle's motion in a Lagrangian frame.22 Trajectory simulation can be done by numerical models, employing finite-element-method (FEM) for the fluid and magnet simulation combined with a particle tracing module.23–26 FEM models are capable of considering all three dimensions. Additionally, they can respect various forces and effects, such as particle–particle26 and two-way coupled particle–fluid interactions.24 However, FEM simulations require significant time and a good model design to obtain meaningful results.27
A more simple simulation can be achieved, replacing the FEM calculations with mathematical descriptions of the fluid flow and magnetic field. Analytical approximations exist for simple magnet shapes, for instance, for a cylindrical magnet.28 The fluid is either described with a velocity profile incorporating a no-slip condition at the walls which induces a parabolic profile18,29–33 or with an averaged velocity profile,19,20 characterised by a constant velocity over the channel's cross-section. The simple models are often reduced to two dimensions. Although the simplification to two dimensions decreases the model's complexity and thus leads to rapid simulation results, it comes at the cost of lower resolution of the actual system. Exceptions are given by Barnsley et al.30 and Chen et al.,33 who investigate the separation behaviour of 3D cylindrical channels. Typically, the models consider the magnetic force Fmag and the drag force Fd. Depending on the magnitude, gravity forces, and buoyancy Fg,b might be relevant.26
The separation behaviour demonstrates distinct variations when dealing with rectangular geometries as opposed to cylindrical channels. However, modelling the fluid in rectangular shapes becomes more intricate due to the absence of closed analytical solutions for fluid velocity.22 No simple models have been presented yet to simulate the separation behaviour of 3D rectangular channels.
Table 1 provides an overview of the various simple models and their underlying assumptions regarding the flow model and the relevant forces. A multitude of model combinations have been employed. In particular, there are notable differences in the dimensions and flow profiles. Nevertheless, a comparison of the different simulation assumptions and the deviations between the results has not been conducted.
| Source | Forces | Flow model |
|---|---|---|
| Tan et al.19 | 0 = Fmag + Fd | 2D constant |
| Chong et al.20 | 0 = Fmag + Fd | 2D constant |
| Nandy et al.18 | 0 = Fmag + Fd | 2D parabolic |
| Furlani et al.29 | mẍ = Fmag + Fd | 2D parabolic |
| Gleich et al.31 | 0 = Fmag + Fd + Fg,b | 2D parabolic |
| Sharma et al.32 | 0 = Fmag + Fd + Fg,b | 2D parabolic |
| Barnsley et al.30 | 0 = Fmag + Fd + Fg,b | 3D cylindrical |
| Chen et al.33 | 0 = Fmag + Fd + Fg,b | 3D cylindrical |
The separation efficiency (SE), or capture efficiency, represents the fraction of separated particles compared to the total amount of particles within the fluid.18,20 The assessment of experiments employs direct comparisons between values that are inherently related to the number of particles, such as the concentration of particles before and after the test, namely C0 and C,19 calculated in eqn (1).
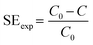 | (1) |
In computational simulations, the models compute which particles are being separated. This information can be used to calculate separation efficiency. Often, the number of trajectories that are separated is compared to the total number of trajectories.18–20 The SE is simply calculated by dividing the height of the last captured particle hsep compared to the channel height h as per eqn (2). This equation only applies if the magnet(s) are attached to one side of the channel only.
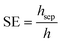 | (2) |
Considering a fully developed viscous flow within a channel and a homogeneous suspension of the MNP, the particle flux through regions close to the wall is significantly smaller than in the channel's centre, where the peak velocity is located. Therefore, simply counting the captured trajectories is not directly related to the amount of captured particles. As a conclusion, eqn (2) is not comparable to eqn (1). Barnsley et al.30 compensate for this discrepancy by considering the particle flux by varying the initial particle distribution, resulting in more trajectories starting at the centre. However, this approach is simulation-intensive as a large number of trajectories have to be simulated in 3D space.
To address the open questions outlined above, we aim to create a simulation model that is both fast and easy to apply, without compromising accuracy. The underlying system is a rectangular channel with a magnet attached to the walls of the channel. The aim is to separate either MNP agglomerates or MNP attached to a bacterium, which could be the case for immunomagnetic separation purposes.34
Therefore, a highly flexible Python-based simulation model is developed that can vary the channel's dimensions, particle properties, volume flux, and magnet configurations. The model is capable of displaying trajectories in three dimensions, helping to understand the separation process.
A novel way of calculating the separation efficiency is derived by considering the different particle fluxes through cross-section areas, that is proportional to the velocity. Integration over the separated flux allows an efficient calculation of the SE, requiring only a few trajectories to evaluate system behaviour.
Table 1 shows various modelling strategies to predict separation efficiency. This paper compares three simulation configurations of the simple model to illustrate and quantify the deviations and compares the results to an FEM model developed in COMSOL.
The paper begins with the necessary mathematical descriptions for fluid and particle dynamics, followed by the development of both a simple numerical model and an FEM model. Subsequently, a novel approach to calculating separation efficiency is introduced. The results of the models are then presented. Comparative analyses are conducted between the FEM model, the 3D and the 2D models. In the final section, the deviations of the models are analysed, and recommendations for utilising different models are provided.
2 Mathematical background
2.1 Particle forces
Forces applied to the magnetic particle are considered for simulating particle motion relative to the fluid. Under certain circumstances, forces can be neglected as they are orders of magnitude smaller than their counterparts, although this depends on the system constraints.26Inertial forces are neglected due to the low mass of particles leading to extremely high accelerations, causing negligible time scales till equilibrium velocity is reached.18A particle experiences a gravitational force resulting from gravitational acceleration and the particle's mass, which is counteracted by buoyancy.26 As gravity and buoyant forces counteract each other, they are represented as one resulting force Fg,b. Eqn (3) presents Fg,b, where g is gravitational acceleration, and ρf and ρp are densities for the fluid and the particle, respectively. Vtot is the total volume of the investigated particle, including diamagnetic volumes. An averaged density can be used for heterogeneous particle agglomerates, e.g., MNP with a bacterium.
| Fg,b = Vtotg(ρp − ρf) | (3) |
The drag force of a sphere in steady-state motion can be modelled using Stokes drag.22,35 The spherical consideration of the particle can serve as a suitable first-order approximation. Eqn (4) presents the Stokes drag Fd where vf and vp are the velocity vectors of the fluid and particle, respectively. The hydraulic drag diameter dp is considered, corresponding to the diameter of the agglomerate, including diamagnetic volumes.
| Fd = 3πηdp(vf − vp) | (4) |
The magnetophoretic force Fmag is determined by eqn (5).36 Particles are attracted along the magnetic field gradient for magnetic susceptibilities of χ > 0, applicable for paramagnetic and ferromagnetic particles. For sufficiently small external fields (∇B < 100 T m−1 (ref. 20)), the magnetisation of magnetic nanoparticles linearly depends on the local magnetic field. However, when magnetisation saturation is reached, it does not further magnetise, as indicated in eqn (6). It is assumed that the susceptibility of the fluid is negligibly small.36Mp,s represents the magnetisation saturation. For example, for iron oxide, this value is 86 A m2 kg−1.37Vmnp is the total volume of the magnetic nanoparticles, excluding the volume of diamagnetic particles.
| Fmag = μ0VmnpK(H·∇)H | (5) |
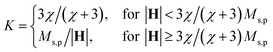 | (6) |
The mentioned forces are commonly used for surrogate modelling of millifluidic systems. Neglecting Brownian forces is justified as they are orders of magnitude smaller than those presented.26,38 However, incorporating additional forces can improve the simulation results. Interaction forces are often neglected. While they may be negligible for low particle concentrations, they are relevant in systems with high concentrations. It is challenging to include interaction forces in simple models. Two-way coupled particle–fluid interactions, so-called particle-induced convection,16 can be observed, speeding up the separation process. Modelling this interactive effect requires FEM solvers and a high simulation effort.24,26 Due to their dipole interactions, particle-particle interactions result in magnetic forces between closely magnetised particles. Additionally, particle collision forces come into play.26
2.2 Fluid models
The fluid flow is described in Eulerian frame.22 A laminar flow is assumed, as the Reynolds number is sufficiently low. Therefore, the velocity in the channel's cross-section directions y and z is zero, vf = (uf, 0, 0)T. A constant stationary velocity is assumed so that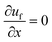 . In the simple models, the most straightforward modelling of the fluid's velocity profile assumes a constant velocity over the channel's cross-section. Eqn (7) represents a velocity uf in the main flow direction independent of the position in the channel's plane perpendicular to the main flow direction. A represents the cross-sectional area, and
. In the simple models, the most straightforward modelling of the fluid's velocity profile assumes a constant velocity over the channel's cross-section. Eqn (7) represents a velocity uf in the main flow direction independent of the position in the channel's plane perpendicular to the main flow direction. A represents the cross-sectional area, and ![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) is the volume flux.
is the volume flux.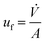 | (7) |
When incorporating viscosity, the Navier–Stokes equation is used to model the velocity profile for pressure-driven, steady-state flow, known as Poiseuille flow.22 Analytical solutions exist for various shapes. Eqn (8) is derived assuming an infinite parallel-plate channel, making the velocity independent of the y-direction. This model equals a 2D parabolic flow profile and fulfils the no-slip condition, assuming a zero velocity at the wall due to viscosity. h represents the channel height.
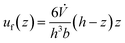 | (8) |
Besides elliptic and circular cross-section shapes, a closed solution of the Poisson equation is unknown, necessitating an approximation of the solution.22 The solution for rectangular geometries is presented in eqn (9), encompassing a pressure gradient as outlined in eqn (10).
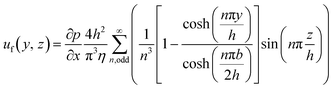 | (9) |
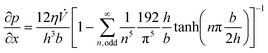 | (10) |
2.3 Superposition of fluid model and particle force model
Considering only the Stokes drag, magnetic force, and gravity and buoyant force,18 the force equilibrium simplifies to 0 = Fmag + Fd + Fg,b. Inserting the eqn (3)–(5), and adding the velocity as in eqn (9), we obtain the eqn (11) for the absolute velocity of a particle.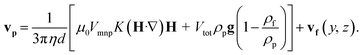 | (11) |
3 Simulation model
3.1 System outline
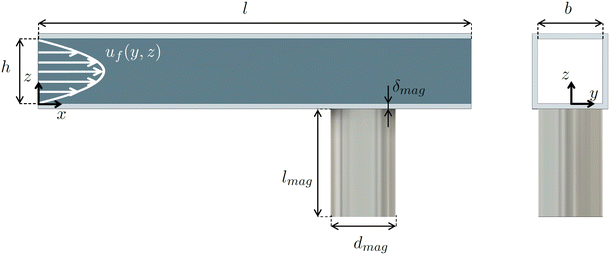
Fig. 1 shows the system under investigation consisting of a fluidic channel and a magnet. As presented in our previous study,21 several design variables can be chosen for the magnetophoretic system design.A cylindrical magnet is considered, with the length lmag, the polarisation Jmag, which depends on the grade of the magnet, and the diameter dmag. Additionally, the position of the magnet can be varied. The model takes the volume of magnetic nanoparticles as an input. The channel dimensions h, b, and l can be chosen, as well as the volume flux. The volume range of the MNPs were chosen according to dynamic light scattering measurements of bare iron oxide nanoparticles in a pH 7 solution in absence of a magnetic field, as described in section S5 of the ESI.‡ The volume corresponds to an agglomerate of many MNPs due to attraction among the MNPs. The volumetric magnetic susceptibility of the bulk MNPs is set to χ = 28, assuming that we are below saturation magnetization.39
Table 2 summarises the design parameters and variables, together with the investigated design space.
| Attribute | Symbol | Value | Value parameter study |
|---|---|---|---|
| Channel height | h | 0.0035 m | [0.00175, 0.00875] m |
| Channel width | b | 0.0035 m | [0.002625, 0.0035] m |
| Channel length | l | 0.015 m | 0.015 m |
| Volume flux |
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif)
|
1 × 10−7 m3 s−1 | [2.5 × 10−8, 2.0 × 10−7] m3 s−1 |
| Volume MNP | V mnp | 4.93 × 10−18 m3 | [0.75 × 10−18, 1.25 × 10−17] m3 s−1 |
| Density MNP | ρ mnp | 5240 kg m−3 | 5240 kg m−3 |
| Mag. susceptibility of MNP | χ | 2.8 | 2.8 |
| Magnet length | l mag | 0.01 m | 0.01 m |
| Magnet diameter | d mag | 0.0035 m | 0.0035 m |
| Magnet polarisation | J mag | 1.5 T | [1.0, 1.5] T |
| Distance magnet to fluid | δ mag | 0.0001 m | 0.0001 m |
| Magnet position x | — | 0.01325 m | 0.01325 m |
| Magnet position y | — | 0.0 m | 0.0 m |
| Magnet position z | — | −0.0051 m | −0.0051 m |
| Viscosity | η | 0.001 Pas | 0.001 Pas |
| Density fluid | ρ f | 997 kg m−3 | 997 kg m−3 |
3.2 Simple numerical model
Different from FEM models, simple numerical models incorporate analytical descriptions for fluid and magnet to predict the particle trajectories.The trajectory from different starting positions within the channel's cross-section is of interest. The magnetic field strength highly depends on the particle's position. The field strength is calculated using the open source Python class Magpylib V 4.2.0,40 which can analytically approximate three-dimensional fields of different magnetic shapes efficiently with minor errors (as long as μr = 1.1, which is the case for neodymium).41
As eqn (11) depends on time and location, a time-step integration scheme is used for computing particle trajectories. The Python function solve_ivp from the scipy.integrate package facilitates the integration of a system of ordinary differential equations, initialised with a starting value (in this context, the particle's initial position at t = 0). Employing the explicit Runge–Kutta method of 5th order with an accuracy of 4th order, the solver concludes its operation if the particle exits the channel, collides with the bottom, or reaches the ceiling (which might occur if gravitational forces act in a direction contrary to the magnetic force). Subsequently, the trajectories of an arbitrary initial particle position can be computed and visualised in three dimensions.
The system is simulated in three dimensions. The 3D model of a rectangular channel uses eqn (9) to model the velocity field inside the channel. For the 2D models, the system remains in three dimensions, but only the x–z plane in the centre of the channel is analysed. Due to the symmetry, particles starting here do not deviate from this plane. Therefore, computational costs for one trajectory in 2D are the same as in 3D. However, in 2D, just one plane is evaluated; thus, the total computational costs are lower in 2D. 3D models use several evaluation planes to obtain a 3D resolution. The more planes are used, the higher the resolution. For the following investigation, six evaluation planes are used. Additional planes do not enhance the accuracy of the calculations but do result in higher computational costs. A convergence study for selecting the number of evaluation planes is provided in section S1 of the ESI.‡
Cooperative effects due to magnetic dipole–dipole interactions have not been considered in the models, as the results of this comparative study are not significantly affected by the inclusion of these effects. This is because the size of the agglomerates would change the same way in all systems, thereby not altering the relative comparisons. However, the effects can be relevant for systems with large particles,16 and thus also occur in this system outline. One approach to account for this effect is to increase the assumed volume of the MNP Vmnp, in the model by a factor N. Chong et al.20 provide an analytical expression that approximates the agglomerate size; however, this approach neglects the effects of time scales, particularly the residence time of the MNP near the magnet, and may predict unrealistically large agglomerate sizes for systems with large initial particle sizes. Alternatively, empirical correlations can be used to adjust the MNP volume, that consider the residence time of the MNPs near the magnet, as demonstrated by Tan et al.19
3.3 FEM-model
An FEM model is compared to the simple models. The COMSOL Multiphysics 6.2 model assistant is used for this purpose.First, two stationary studies are conducted, namely “magnetic fields, no currents” and “laminar flow”. As the Reynolds number is low, a laminar flow can be assumed. To simulate the time-dependent particle motion, the study “particle tracing for fluid flow” is used. The channel is implemented as in Fig. 1, considering a sufficiently long channel to ensure developed flow conditions. A sphere of air is implemented around the system to model the magnetic field. At the channel's inlet, the boundary condition is set to fully developed flow, while the no-slip condition is applied at the channel walls. At the outlet, the pressure boundary condition p0 = 0 Pa is applied. The second stationary study generates a magnetic field within the simulated sphere. The magnet itself is modelled as a remanent flux density of the value of the magnetic polarisation of Table 2. The particles in the time-dependent study are assigned with the values of Table 2. Gravity forces, drag forces, and magnetophoretic forces are activated.
Convergence analysis reveals that a physics-controlled mesh set to “finer”, corresponding to 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374 elements for the setup of Table 2, is a good compromise regarding computation time and accuracy. More information about the FEM Model can be found in the ESI‡ S3.
374 elements for the setup of Table 2, is a good compromise regarding computation time and accuracy. More information about the FEM Model can be found in the ESI‡ S3.
3.4 Novel separation efficiency calculation
Neglecting wall effects, a uniform particle distribution across the channel's cross-section is assumed before entering the magnetic field. Particle flux varies, increasing in faster-velocity regions (e.g., the middle of the channel) and decreasing in slower-velocity regions (e.g., near the walls). Therefore, most particles traverse the middle, with negligible flux close to the walls. With the assumption of equally distributed particles, particle flux is proportional to the fluid's volume flux. The separation height is determined by the initial particle z-position where the last particle is attracted. Increasing the height of the initial position would lead to exiting the channel. The SE for the system is obtained by integrating the velocity profile from the channel bottom to the separation height, yielding the separated volume flux![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) sep.
sep.
For a two-dimensional parabolic flow profile, as defined in eqn (8), the separated volume flux is expressed as
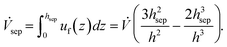 | (12) |
Comparing eqn (12) to the total volume flux, eqn (13) is obtained for the separation efficiency depending only on the separation height hsep and channel height:
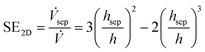 | (13) |
The calculation can be extended to the channel's width in three dimensions, corresponding to the y-direction. To calculate the separation efficiency of a 3D system, eqn (14) can be applied.
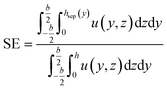 | (14) |
The separation height hsep(y) varies with the y position within the channel, rather than being a constant value. As demonstrated in previous studies,30 the separation height tends to follow a bathtub-shaped curve, with the lowest hsep achieved at the channel's middle and the highest hsep near the walls.
In the provided model, hsep is initially determined by step-wise descending the channel at specific y-positions until the particle gets attracted. Subsequently, a gradient descent-like algorithm converges to a hsep within a few iterations (approximately 15–25). This process is repeated for multiple y-positions. Considering the channel's symmetry, only six distinct y-positions for the starting plane are sufficient. This yields the separation line hsep(y), which is then employed in eqn (14). A maximum of 150 particle trajectories is required to calculate the 3D separation efficiency.
3.5 Model comparison strategy
In the preceding sections, different modelling approaches for the magnetophoretic separation system have been presented, with various configurations that introduce distinct sources of deviation. The potential impact of these configurations on simulation deviations in SE remains uncertain. To address this, the following section compares three specific configurations of the simple model, chosen based on the models documented in the literature summarised in Table 1. The FEM model is added for comparison.The simple models are based on the implemented Python class. They deviate in velocity profile and several evaluation planes, as the 2D models evaluate the centre plane, while the 3D model investigates trajectories apart from this plane. Configuration 1 employs the simplest fluid model, featuring a constant 2D flow profile. Solving eqn (14) for this setup yields a straightforward SE expression: 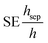 . Configuration 2 assumes a 2D parabolic flow model and computes the SE using eqn (13). Configuration 3 uses the 3D Poiseuille flow model for a rectangular cross-section and calculates the SE as in eqn (14). Configuration 4 is the FEM model for a rectangular channel. Table 3 shows the different model configurations compared in the following section.
. Configuration 2 assumes a 2D parabolic flow model and computes the SE using eqn (13). Configuration 3 uses the 3D Poiseuille flow model for a rectangular cross-section and calculates the SE as in eqn (14). Configuration 4 is the FEM model for a rectangular channel. Table 3 shows the different model configurations compared in the following section.
Two main aspects are compared. First, the behaviour of the trajectories and the separation height is investigated. This gives information about the influence of the flow profile and the resolution of the system. Second, the quantity of interest for channel design, the SE, is compared, quantifying the deviations between the models. Configuration 3 is chosen as the baseline for comparison because it represents the novel 3D approach introduced in this paper. However, other configurations could have been selected as well.
4 Results and discussion
4.1 Results of the simple 3D model
The simple model for a 3D rectangular channel takes around 20–30 seconds to evaluate the SE using an AMD Ryzen 7 6800H processor. However, besides the simulation settings and hardware, the simulation time depends on the SE; for lower SE, more iterations are necessary to compute hsep. The model is able to visualise the trajectories of different initial particle positions. Fig. 2 illustrates the paths of particles released from an equally spaced grid. It is apparent that trajectories close to the wall experience a slight attraction towards the magnet's poles. Moreover, more trajectories at the channel side exhibit attraction, demonstrating that the system does not possess a uniform separation height but rather a distributed one. The trajectories at the bottom get attracted before the magnet, caused by gravitational force and the magnet's far-field influences. The slow velocity at the walls due to the parabolic velocity profile leads to long residence times of the particle within the channel. Fig. S1 in the ESI‡ shows the flow profile in the rectangular channel, calculated with eqn (9).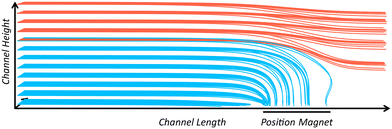 | ||
| Fig. 2 3D trajectories within the channel from a side view. The design variables are defined following Table 2. | ||
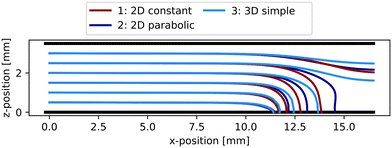
Comparing the trajectories to existing models in literature,18–20,29–33 the models agree on the trajectory path. The deflection is high near the magnet, while the trajectories are barely influenced before and after the magnet. However, the 3D visualisation helps to understand the behaviour of side trajectories, how the particles are bent towards the centre, and especially where trajectories end. This is relevant information, for example, when implementing a sensor for measurement.
4.2 Comparison of the configurations
As outlined in section 3.4, three different simple configurations are developed that deviate mainly in evaluation planes (for 2D: one plane, for 3D: more than one plane) and velocity profiles depending on the level of simplification.| Configuration | Maximum velocity [m s−1] |
|---|---|
| 1: 2D constant | 0.0082 |
| 2: 2D parabolic | 0.0122 |
| 3: 3D simple | 0.0169 |
| 4: 3D FEM | 0.0172 |
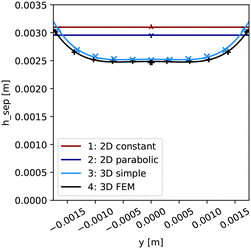
According to these results, an explicit dependency between the maximum velocity, and thus the velocity profile, and the separation height can be observed. The faster the flow profile, the less time the particle has to be attracted, resulting in more particles escaping. In Fig. 4, trajectories of different starting positions are compared among the simple models, showing that the higher the initial positions, the more the final position of the particle deviates. For the second highest starting position, the particle escapes in configuration 3 while the 2D models attract the particle, leading to higher separation heights of the 2D models. The deviation of the end positions between the models is slight for low initial positions.
Overall, it can be concluded that the position-dependent velocity, especially the peak velocity in the parabolic profiles, leads to more particle escape and a lower separation height. The deviation is not constant but initial height-dependent.
![[V with combining dot above]](https://www.rsc.org/images/entities/i_char_0056_0307.gif) , and Bmag have been made. In Fig. 5, the SE of the different configurations is compared for all data points. The dashed line depicts an equal SE as configuration 3. Results above the line indicate an overestimation of the SE, while results below the line imply an underestimation. The results of configuration 4, the FEM model, are plotted as black triangles. The results are slightly below the line. This means that the FEM model predicts a lower SE that the simple 3D model. The deviations are generally below 2%, as shown in section S4 of the ESI.‡
, and Bmag have been made. In Fig. 5, the SE of the different configurations is compared for all data points. The dashed line depicts an equal SE as configuration 3. Results above the line indicate an overestimation of the SE, while results below the line imply an underestimation. The results of configuration 4, the FEM model, are plotted as black triangles. The results are slightly below the line. This means that the FEM model predicts a lower SE that the simple 3D model. The deviations are generally below 2%, as shown in section S4 of the ESI.‡
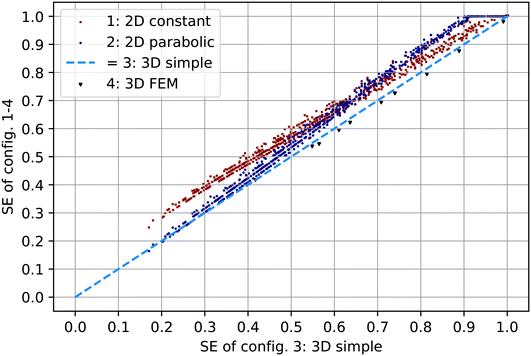 | ||
| Fig. 5 The SE of the 2D models and the FEM model over the simple 3D model. The design variables channel height and width, volume flux, volume of the MNP and polarization of the magnet are varied in accordance with Table 2. The 2D models generally overestimate the SE while the FEM model underestimates the SE compared to 3D rectangular simulations. | ||
The red squared dots represent the outcomes of configuration 2. At low SE, these results align reasonably well with the ones of configuration 3. However, as the SE increases, the deviation reaches a maximum of 15%. The dark blue dots denote SE values derived from configuration 1. This configuration tends to overestimate the SE at lower SE values, while the deviation diminishes at higher SE values.
Different ways for calculating the SE have been presented, as eqn (2) for the literature standard and eqn (14) for the novel calculation developed in this study. Fig. 6 depicts the difference of the SE when calculated according to the novel SE calculation, eqn (13), in comparison to eqn (2). It shows that for small hsep/h, eqn (13) has a lower SE by up to 10%, while for high SE, the deviation is reversed, and the novel calculation is up to 10% higher.
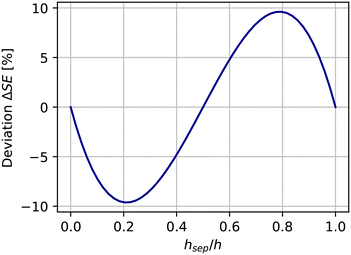 | ||
| Fig. 6 Deviations ΔSE when the particle flux is considered, as in eqn (13), and when the flux is not considered, as in eqn (2). The plot represents this deviation of the 2D parabolic setup. It shows that deviations of up to 10% arise due to the calculation methods. | ||
The plots show that the evaluation method already leads to a deviation of up to 10% for the same system. Combining the deviation with other model influences, such as flow profile and dimensions, further increases the deviation between the model configurations.
Based on the insights from Fig. 3 and 4, it can be summarized that the flow profile and the dimension significantly influences the separation height and the SE. The 3D flow, characterised by the highest velocity in the middle, causes the lowest separation height for these trajectories. The velocity peak generally leads to lower hsep for the 3D model.
However, configuration 1 shows low deviations to the 3D model for high SE. This can be explained by the overlapping influences of velocity profile, which leads to an overestimation of hsep by the 2D model, and SE calculation, which corrects the deviation to lower SE according to Fig. 6. For lower SE, however, the deviations of configuration 1 are high. In this case, the deviations caused by the flow profile are small, as illustrated in Fig. 4. On the other side, the deviations from the SE calculation remains significant, so that it dominates the deviations. Configuration 2 shows good agreement for low SE. For high SE, the difference in trajectories due to the velocity differences leads to a growing difference in SE between configuration 2 and the 3D models.
A variation of the aspect ratio affects the deviations between the configurations, showing that the deviations of the 2D models tends to decrease with increasing aspect ratios 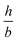 . A detailed analysis of this influence is provided in section S6 of the ESI.‡
. A detailed analysis of this influence is provided in section S6 of the ESI.‡
4.3 Implication for model selection
The primary advantage of the 2D models over the simple 3D model is the faster simulation time caused by the higher number of evaluation planes of the 3D model. The FEM model has a significantly longer simulation duration (see ESI‡ S3) while obtaining similar results of the SE compared to configuration 3. This leads to the following conclusions:• Configuration 1 (2D constant): for high SE, this model setup gives results comparable to the 3D models, but with the advantage of faster simulations, requiring only 2–3 seconds per simulation. It is therefore suitable for conducting extensive parameter studies and investigating system behaviour for high SE. However, at low SE, the absolute error compared to other models is around 15%, leading to very high relative errors ΔSE/SE3D.
• Configuration 2 (2D parabolic): this model shows higher SE deviations from the 3D models as SE increases. However, the relative error generally remains reasonably small, typically less than 15%. The simulation time is comparable to configuration 1, but the deviation is much smaller at low SE. This model is suitable for carrying out parameter studies, with the advantage that relative deviations remain reasonable.
• Configuration 3 (3D rectangular): This model exhibits minimal deviation from the FEM model of less than 2% (ESI‡ S4). The 3D model, with a run time of 20–30 seconds per simulation, remains efficient and suitable for smaller parameter studies. It can account for factors such as magnet shapes that are difficult to incorporate in 2D models. This setup is recommended for detailed analysis and visualisation of particle trajectories and smaller parameter studies.
In summary, choosing a setup for modelling magnetophoretic separation systems requires careful consideration of the influence of assumptions and constraints. When comparing models to experiments, variations in simulation setups may yield different results, influencing the interpretation of experimental deviations. Generally, the models need to be calibrated through experiments to cover the actual conditions. If particle interactions, as highlighted by Tan et al.,19 significantly influence the SE, the simple models lack consideration for these effects. However, there are ways to consider such effects.20 For suitable conditions, such as low particle concentrations, a well-calibrated 3D model is expected to have the highest accuracy and can serve as a reference for interpreting experimental results. The simple 3D model shows minor deviations from the FEM model and can therefore replace the FEM model, as the computation time is significantly smaller. All three models offer sufficient accuracy to grasp the system's behaviour for preliminary design and exploring the design space. It shall be highlighted that configuration 1 obtains its high accuracy for high SE due to the overlap of two counteracting deviations and is thus, by coincidence, precise.
5 Conclusion and outlook
In this study, we develop an efficient simulation model for a rectangular magnetophoretic separation channel with a magnet positioned on one of the channel walls, capable of modelling in 2D and 3D. The 3D model uses analytical descriptions for a rectangular Poiseuilles flow and calculates separation efficiencies in about 20–30 seconds. The 2D models, where one model uses a parabolic velocity profile and one a constant, simulate within two to five seconds. The simulation setup is highly adaptable, allowing changes in channel dimensions, magnet characteristics and position, volume flux and particle properties. For evaluation purposes, a novel method of calculating SE is presented, highlighting the importance of separating the centre of the channel, where particle flux is highest.The results are compared to a FEM model implemented in COMSOL, showing deviations of the simple 3D model of less than 2% in SE, while simulating 180 times faster. The 2D models simulate even faster, however, they tend to overestimate the SE due to two effects. First, the velocity profile, and especially the lower peak velocity leads to more particles separated. Second, the calculation of the SE based on the flow profile, which is directly correlated to the separated particle flux, which leads to further deviations. This leads to deviations up to 15% between the 3D models and the 2D models.
For high SE, however, the results of the 2D model with a constant velocity profile match well with the 3D simulations. This is because the deviation caused by the velocity profile and the SE calculation cancel each other out. In conclusion, this study shows that different model assumptions lead to different results for the SE. The user needs to be aware of these differences when selecting the simulation model for magnetophoretic separator design and when interpreting experimental results.
For further work, the deviation of cylindrical channels can be evaluated, as a variety of 3D models for cylindrical channels are used in literature. The influence of different model assumptions can be expected to be similar to the rectangular models. However, the deviations have not yet been quantified.
Experiments are necessary to calibrate and validate the model's accuracy. Although particle motion equations are well-established, suitability with actual conditions needs examination, as additional effects can occur, such as cooperative magnetophoresis or magnetophoresis-induced convection.16 The assumption of evenly distributed particles in the SE calculation may differ in experimental setups due to wall effects or particle interactions.
Code availability
The code for conducting the simple simulations in 2D and 3D is available at https://github.com/Jo-Soika/magnetophoretic_separation_model.git.Data availability
The data that support the findings of this study are openly available at the following link: https://syncandshare.lrz.de/getlink/fiFKNkEqaWVcgGGDx6wNGL/.Author contributions
J. S. was responsible for the conceptualization, formal analysis and methodology of the study, developed the software, and wrote the original draft of the manuscript. T. W. contributed to the methodology and software development. P. M. was involved in the methodology, formal analysis and contributed to the writing through review and editing. A. S. assisted with the methodology. S. P. S. contributed to the methodology, formal analysis, reviewed and edited the manuscript, and provided supervision. S. B. and M. Z. provided supervision throughout the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support from the Federal Ministry for Economic Affairs and Climate Action (BMWK) of the Federal Republic of Germany, which provided funding for this project under project numbers KK5326001 and KK5231502.References
- A. Dalili, E. Samiei and M. Hoorfar, Analyst, 2018, 144, 87–113 RSC.
- J.-J. Lee, K. J. Jeong, M. Hashimoto, A. H. Kwon, A. Rwei, S. A. Shankarappa, J. H. Tsui and D. S. Kohane, Nano Lett., 2014, 14, 1–5 CrossRef CAS PubMed.
- N. Reiter, J. Auchter, M. Weber, S. Berensmeier and S. P. Schwaminger, Magnetochemistry, 2022, 8, 113 CrossRef CAS.
- S. P. Schwaminger, H. Werner, M. Wengler and S. Srinivasan, Current Directions in Biomedical Engineering, 2022, 8(2), 612–615 CrossRef.
- Y.-L. Liu, D. Chen, P. Shang and D.-C. Yin, J. Controlled Release, 2019, 302, 90–104 CrossRef CAS PubMed.
- J. Zeng, Y. Deng, P. Vedantam, T.-R. Tzeng and X. Xuan, J. Magn. Magn. Mater., 2013, 346, 118–123 CrossRef CAS.
- T. P. Forbes and S. P. Forry, Lab Chip, 2012, 12, 1471–1479 RSC.
- M. Suwa, S. Tsukahara and H. Watarai, Lab Chip, 2023, 23, 1097–1127 RSC.
- M. Zborowski, L. Sun, L. R. Moore, P. Stephen Williams and J. J. Chalmers, J. Magn. Magn. Mater., 1999, 194, 224–230 CrossRef CAS.
- O. Oduwole, D. T. Grob and S. Sheard, J. Magn. Magn. Mater., 2016, 407, 8–12 CrossRef CAS.
- A. Munaz, M. J. A. Shiddiky and N.-T. Nguyen, Biomicrofluidics, 2018, 12, 031501 CrossRef PubMed.
- S. P. Schwaminger, K. Schwarzenberger, J. Gatzemeier, Z. Lei and K. Eckert, ACS Appl. Mater. Interfaces, 2021, 13, 20830–20844 CrossRef CAS PubMed.
- J. Sun, L. Moore, W. Xue, J. Kim, M. Zborowski and J. J. Chalmers, Biotechnol. Bioeng., 2018, 115, 1288–1300 CrossRef CAS PubMed.
- R. Thompson, F. Oldfield, R. Thompson and F. Oldfield, Environmental magnetism, 1986, pp. 21–38 Search PubMed.
- J. S. Andreu, J. Camacho and J. Faraudo, Soft Matter, 2011, 7, 2336 RSC.
- S. S. Leong, Z. Ahmad, S. C. Low, J. Camacho, J. Faraudo and J. Lim, Langmuir, 2020, 36, 8033–8055 CrossRef CAS PubMed.
- N. Pamme, Lab Chip, 2006, 6, 24–38 RSC.
- K. Nandy, S. Chaudhuri, R. Ganguly and I. K. Puri, J. Magn. Magn. Mater., 2008, 320(7), 1398–1405 CrossRef CAS.
- Y. W. Tan, S. S. Leong, J. Lim, W. M. Yeoh and P. Y. Toh, Electrophoresis, 2022, 43, 2234–2249 CrossRef CAS PubMed.
- P. H. Chong, Y. W. Tan, Y. P. Teoh, C. H. Lim, P. Y. Toh, J. Lim and S. S. Leong, J. Supercond. Novel Magn., 2021, 34, 2151–2165 CrossRef CAS.
- J. Soika, P. Wanninger, P. Muschak, S. Schwaminger, S. Berensmeier and M. Zimmermann, Proceedings of the International Design Conference, 2024 Search PubMed.
- H. Bruus, Theoretical Microfluidics, Oxford University Press, 1997 Search PubMed.
- N. Modak, A. Datta and R. Ganguly, J. Phys. D: Appl. Phys., 2010, 43, 485002 CrossRef.
- S. A. Khashan and E. P. Furlani, Microfluid. Nanofluid., 2012, 43(48), 485002 Search PubMed.
- J. Gómez-Pastora, I. H. Karampelas, E. Bringas, E. P. Furlani and I. Ortiz, Sci. Rep., 2019, 9, 7265 CrossRef PubMed.
- P. Pálovics and M. Rencz, Microsyst. Technol., 2022, 28, 1545–1559 CrossRef.
- J. Castillo-León and W. E. Svendsen, Lab-on-a-Chip devices and micro-total analysis systems: a practical guide, Springer, 2014 Search PubMed.
- E. Furlani, S. Reznik and W. Janson, IEEE Trans. Magn., 1994, 30, 2916–2919 Search PubMed.
- E. P. Furlani, J. Phys. D: Appl. Phys., 2007, 40(5), 1313 CrossRef CAS.
- L. C. Barnsley, D. Carugo, M. Aron and E. Stride, Phys. Med. Biol., 2017, 62, 2333–2360 CrossRef CAS PubMed.
- B. Gleich, N. Hellwig, H. Bridell, R. Jurgons, C. Seliger, C. Alexiou, B. Wolf and T. Weyh, IEEE Trans. Nanotechnol., 2007, 6, 164–170 Search PubMed.
- S. Sharma, V. Katiyar and U. Singh, J. Magn. Magn. Mater., 2015, 379, 102–107 CrossRef CAS.
- J. Chen, C. Wang and R. Mo, Chin. Phys. B, 2023, 32, 094302 CrossRef.
- D. W. Inglis, R. Riehn, R. Austin and J. Sturm, Appl. Phys. Lett., 2004, 85, 5093–5095 CrossRef CAS.
- S. Dey, S. Z. Ali and E. Padhi, Proc. R. Soc. A, 2019, 475, 20190277 CrossRef PubMed.
- E. P. Furlani and Y. Sahoo, J. Phys. D: Appl. Phys., 2006, 39, 1724–1732 CrossRef CAS.
- L. Maldonado-Camargo, M. Unni and C. Rinaldi, Biomedical Nanotechnology: Methods and Protocols, Springer, New York, NY, 2017, pp. 47–71 Search PubMed.
- G. Bossis, O. Volkova, S. Lacis and A. Meunier, in Magnetorheology: Fluids, Structures and Rheology, ed. S. Odenbach, Springer Berlin Heidelberg, Berlin, Heidelberg, 2002, pp. 202–230 Search PubMed.
- P. Pálovics, M. Németh and M. Rencz, Energies, 2020, 13, 4871 CrossRef.
- M. Ortner, et al., magpylib, https://magpylib.readthedocs.io/en/latest/ Search PubMed.
- M. Ortner and L. G. C. Bandeira, SoftwareX, 2020, 11, 100466 CrossRef.
Footnotes |
| † Open-access simulation model repository: https://github.com/Jo-Soika/magnetophoretic_separation_model.git |
| ‡ Electronic supplementary information (ESI) available: With further information about the simple model, the FEM and the comparison methodology. See DOI: https://doi.org/10.1039/d4lc00595c |
| This journal is © The Royal Society of Chemistry 2024 |