Optically active defects in carbon nanotubes via chlorination: computational insights

Abstract

Optical and electronic properties resulting from chlorine functionalization of (6,2) single-walled carbon nanotubes (SWCNTs) are explored using density functional theory. P-type doping character is evident from the generation of an unoccupied mid-gap state originating from the sp³-hybridized defect brought by neutral chlorine adducts to the sp²-hybridized lattice of the SWCNT. Such mid-gap states are realized in all binding configurations of chlorine atoms explored in this work, with the energy of the mid-gap state varying depending on the chlorine positions at the nanotube surface. A chlorine pair placed on the same hexagonal SWCNT ring shows the strongest binding to the tube sidewall while reducing the intensity of the main optical E₁₁ band and brings new redshifted, highly optically active transitions. However, the optical intensity of the defect-introduced transitions significantly diminishes with increased distance between bound chlorines and their concentration. Functionalization with negatively charged chlorine ions is less thermodynamically stable compared to neutral chlorination, favoring only monochlorination. With the introduction of a charge, occupied mid-gap states appear near the conduction band resulting in an n-doped system. The lowest-energy, defect-associated transitions of charged systems are more redshifted but nearly optically inactive. Our calculations demonstrate that efficient emission of chlorinated SWCNTs is possible only for neutral chlorine adducts placed on the same carbon ring and at very small concentrations.

---

Introduction

Single-walled carbon nanotubes (SWCNTs) have been widely studied in the last few decades due to their promising chirality-dependent electronic and optical properties¹ that make them useful for a wide range of applications including photovoltaic devices,^2–4 light emitting diodes,^5–8 and sensors.^9–13 Of particular interest is advancing optical properties inherent to pristine nanotubes^14–18 by covalent sidewall functionalization.^19,20 The ability to control the chemistry of the defect has led to new synthetic routes toward functionalization with single-strand DNA (ssDNA)^21–23 wrapping and photochemistry utilizing singlet and triplet state pathways^24,25 as well as with well-established chemistries using diazonium salts, hypochlorite, and ozone functionalization.^26–29 Most commonly, oxygen^30–32 and aryl-containing^{18,21,25,33–38} functional groups have been used in recent studies showing redshifted and enhanced emission of SWCNTs.

Such covalent functionalization results in the creation of defect sites with sp³-hybridization at the sp²-hybridized lattice of the SWCNT.^19,20 This sp³-defect in the nanotube introduces new spatially localized states inside the energy gap of the pristine SWCNT system.^39,40 Upon photoexcitation, highly mobile excitons travel along the pristine lattice until encountering a defect site, where the excitons can either scatter (e.g. auger,^41–44 dark-state redistribution,³⁷etc.) or become trapped by the excitonic potential energy well. Once trapped by the local defect potential, sub-picosecond thermal relaxation from the band-edge to the defect-associated excitonic state occurs,⁴⁵ followed by bright radiative emission enhanced from the pristine SWCNT by the large transition dipole between the defect-associated exciton and the ground state.^31,33,46,47 Additionally, similar to nitrogen-vacancy (NV) centers in diamonds,⁴⁸ a chemical defect in the SWCNT creates suitable conditions for single-photon emission (SPE), namely a quasi-two-level sub-system composed of ground and defect-associated states that are energetically separated from the higher-energy states. SPE in the infrared (IR) and telecommunication frequencies at room temperature has been established in SWCNTs.^6,33,49–51

Halogenation of SWCNTs was also under consideration over the last two decades. SWCNTs have been successfully functionalized with fluorine,^52–55 chlorine,^56–60 and bromine.⁶¹ A typical strategy for chlorination involves treatment with AuCl₃, which results in the generation of an electronically doped system (p-type)^62–65 through the introduction of unoccupied states within the energy gap of the pristine system.⁶⁶ Highly tunable p-type states, for example, are desirable for the fabrication of photovoltaic devices for efficient charge separation upon photo-excitation.^67–69 Multiple strategies of p-type doping have been discussed in the literature, ranging from the single-tube covalent binding of single-strand DNA²¹ to bulk substrate and chemical modification.⁷⁰ Recent investigations revealed that under sonication, halogenated solvents, such as dichloromethane or chloroform commonly employed to prepare SWCNT dispersions, can dope SWCNTs introducing unoccupied mid-gap states and increase the carrier concentration, which positively influences the electrical conductivity but negatively affects the thermopower.⁷¹

Changes to the electronic structure of the SWCNTs have been experimentally shown to be highly dependent on the precise chemical sites of chlorine functionalization on the surface of SWCNTs.⁵⁸ However, the precise species that binds to the SWCNT surface has generated controversy in the SWCNT community and has led to extensive computational studies.^{58,66,72–77} Some proposed mechanisms include the functionalization of individual chlorine atoms⁷⁶ or the adsorption of an entire gold chloride cluster.⁷⁴ Changes to the electronic structure and the p-doping character of SWCNTs exposed to halogen-containing solvents have been explained by non-covalent bonding of halide molecules to SWCNTs, while causing strong interactions between them and the nanotube, inducing some structural changes to the nanotube lattice.⁷² An alternative explanation has suggested covalent attachments of halogen adducts⁷¹ forming sp³-defects in SWCNTs similar to diazonium treated SWCNTs upon sonication in water.⁷⁸ Thus, mechanisms of halide–SWCNT interactions are still under debate. In contrast to extensive studies of the ground state properties, optical response associated with chlorine adducts has not been addressed in previous calculations, except for a very recent report on the optical spectra of fluorinated zigzag (11,0) SWCNTs.⁷⁷ The reported calculations have been mainly done for zigzag or armchair SWCNTs. Chiral SWCNTs typically have much larger primitive unit cells than zigzag nanotubes, which complicates first principle calculations for these systems; meanwhile, most experimental samples mainly include chiral SWCNTs. Thus, the exact mechanisms of chlorine doping of chiral SWCNTs is not completely understood and the ways of controlling the optical properties of SWCNTs via chlorination are still not known.

Here we computationally investigate the effect of chlorination on the electronic structure and optical response of the chiral (6,2) SWCNT. These studies are performed utilizing both a shortened nanotube model (∼3 nm in length) and its longer analog (∼8 nm in length), with both models terminated by methylenes and hydrogens at each end, as illustrated in Fig. 1. Both systems show quantitative similar features in their electronic structure compared to the electronic structure of the infinitely long (6,2) nanotube constructed by using 1D periodic boundary conditions with a 4.5 nm long supercell. Similar trends in the electronic structures and optical spectra allow us to generalize the obtained results for finite-size SWCNT models to the realistic SWCNT samples of more than 100 nm in length. We also compare the neutral and charged SWCNT systems with chlorines placed at various positions and with different concentrations on the SWCNT surface to study different mechanisms of functionalization and their effect on the optical transitions of SWCNTs.

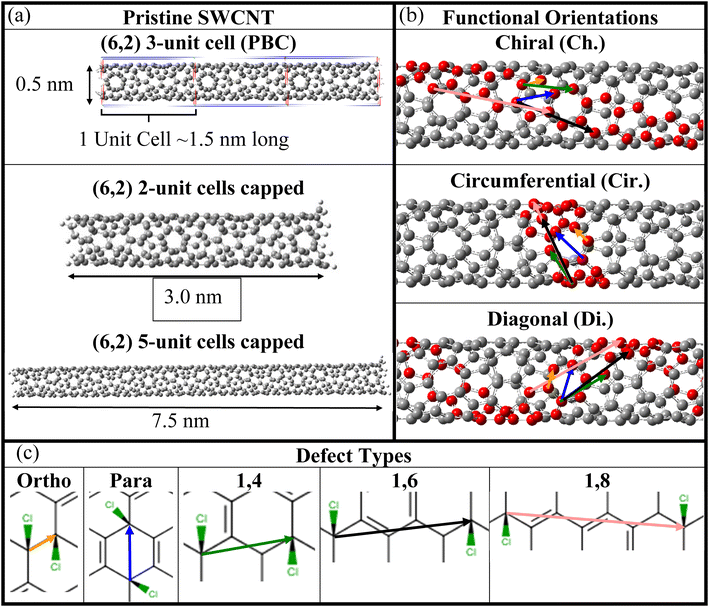Fig. 1 SWCNT atomistic models of pristine and chlorinated (6,2) SWCNTs and the sp³-defect arrangements considered for calculations. (a) Optimized geometries of the pristine SWCNT for various length and simulation environments. (Top) One unit cell, repeated three times for visual clarity, with periodic boundary conditions. (Middle) Two and (bottom) five unit cells in length with the proper capping of the edge atoms to recover the semi-infinite electronic structure of the SWCNT lattice (see Methods). (b) Principal SWCNT directions with respect to the SWCNT main axis, namely along the SWCNT's (top) chiral axis (Ch.), (middle) circumference (Cir.), and (bottom) diagonal (Di.), which, in the notation of other studies, are “+”, “−”, and “++”.¹⁸ (c) Various relative orientations (i.e., defect configurations) of Cl pairs creating a single sp³-defect on the nanotube surface. Ortho (yellow) and para (blue) arrangements have two Cl atoms bound to the same ring, while 1,4 (green), 1,6 (black), and 1,8 (pink) arrangements have two Cl atoms bound to different rings. The coloring of the arrows is repeated for clarity in (b) for the same relative orientations for each SWCNT principle direction.

One of the suggested mechanisms of p-doping of SWCNTs using AuCl₃ complexes is reduction of Ag cation to zero-valent gold followed by subsequent neutralization of the SWCNT by chlorine anions.^62,63 Recent investigations of SWCNTs exposed to halogen-containing solvents under sonication have suggested the defect formation mechanism resulting in p-doping of SWCNTs being similar to the sp³-defect formation in diazonium treated SWCNTs sonicated in water.⁷⁸ These mechanisms of nanotube chlorination are expected to result in neutral chlorine adducts on the SWCNT surface. However, excess carriers in noncovalently electrochemically doped (6,5) SWNTs are also found to give rise to a redshifted absorption band associated with trion states (coupled exciton-to-charge states) similar to defect-related states in (6,5) SWCNTs in which doping is introduced via redox-chemistry using AuCl₃ solution.^64,65 These reports provide further evidence for the confinement and localization of excess charge carriers by impurity potentials. Thus, doping of SWCNTs may include charging together with chemically introduced defects at the nanotube surface. Additionally, some small charge might be accumulated on the SWCNT due to electron transfer processes with an environment. Since the mechanisms of reactions with AuCl₃ and other halide-containing molecules used to introduce p-doping in SWCNTs is not completely understood, we have considered negatively charged systems with a negative one charge supposed to be localized around each chlorine adsorbed to the SWCNT surface in addition to the neutral chlorinated SWCNT models. Such computations of the effect of charge on SWCNTs with Cl adducts taken at different concentrations have not been reported yet for chiral SWCNTs.

Our calculations demonstrate that negatively charged (6,2) SWCNTs with two chlorines contributing to the sp³-defect are less thermodynamically stable compared to similar neutral structures. In contrast, functionalization with a single chlorine is thermodynamically stable only when an extra electron is present in the system. However, the efficient emission of chlorinated SWCNTs is possible only for neutral systems when chlorine adducts are placed close to each other at very small concentrations. These findings provide valuable insights into the photophysical and structural properties of chlorinated chiral SWCNTs, which will be instrumental in guiding new synthesis procedures^21–29 and characterization techniques^{22,36,46,78,79} allowing for chemical control over emission efficiency in SWCNTs.

Results and discussion

Interactions between the SWCNT surface and chlorine adducts

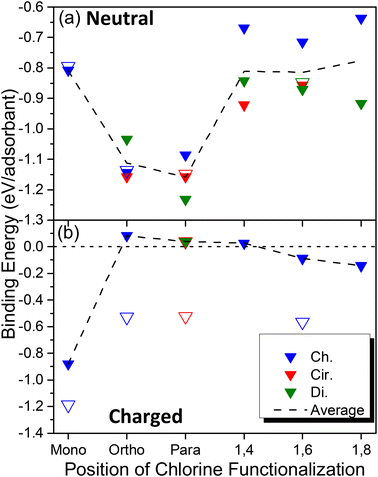
Having provided motivation for this work, we now move to a discussion of thermodynamic driving forces for the covalent binding of one or more chlorine atoms via the calculation of binding energy (see eqn (1) in Methods and Fig. S1†) for a variety of configurations and relative orientations. Fig. 1 depicts various schematics for the SWCNT models used in this study, showcasing the pristine SWCNT models of various lengths and boundary conditions (Fig. 1a), the SWCNT principal directions (Fig. 1b) and the various types of di-chlorinated species (Fig. 1c), all of which showcase significant changes to the local electronic structure in the ground and excited states. We have considered a wide range of functionalization types, including the covalent attachment of two species to a single SWCNT ring, namely at ortho and para positions of the SWCNT ring, as has been done in many previous reports.^{18,38,80–86} Additionally, we have simulated structures where the chlorine atoms are placed on adjacent rings (named 1,4), two rings apart (named 1,6), and three rings apart (named 1,8), as illustrated in Fig. 1c. These styles of covalent attachment are not common in the literature due to the assumption of a highly reactive site on the same SWCNT ring as the first attachment; however, experimental synthesis using chlorination may have the ability to mitigate these fast reactions or, as will be discussed later, when the systems are negatively charged prior to functionalization, an energetically favored chlorine–chlorine separation along the SWCNT axis is found.

The binding energy calculations were performed using properly capped (see Methods), finite-length (6,2) SWCNT models with 2-unit (∼3 nm) and 5-unit cells (∼8 nm). As shown in Fig. 2a, all neutral systems explored show a thermodynamically favorable interaction (i.e., a negative binding energy, vertical axis) between the SWCNT lattice and two chlorine atoms, regardless of their relative binding configuration (horizontal axis, see Fig. 1) and exhibit similar binding energy values and trends between the 2-unit (filled symbols) and 5-unit (open symbols) cell SWCNT models. This indicates that the length of our 2-unit cell SWCNT model is sufficient to represent the trends in binding configurations of neutral chlorinated SWCNTs. Further, the most stable structures are observed when the pair of chlorine atoms is bound to the same ring either in para or in ortho configurations. The binding energies between the two most stable positions, ortho and para, are −1.15 eV and −1.25 eV, respectively. These results are comparable with reported calculations for (6,5) and (11,0) SWCNTs functionalized by different aryl-derivatives in ortho and para positions.⁴⁰ We note that the C–Cl bond length is slightly shorter for ortho (1.83–1.85 Å) than for para (1.86–1.87 Å), as can be seen in Fig. S2 and S3a.† This difference can be rationalized by π-orbital misalignment enforced at the ortho-defect, making it more reactive,^18,38,40 which is reflected in the shortening of C–Cl bonds.

Fig. 2 Binding energy of different defect configurations with varying relative orientation and configuration between the two chlorine atoms for (a) neutral chlorinated SWCNTs and (b) negatively charged (Q = −1 for mono, Q = −2 for all others) chlorinated SWCNTs. Hollow data points represent five unit cell (∼7.5 nm) SWCNT models and filled data points represent two-unit cell (∼3 nm) SWCNT models. Negative binding energy represents increased thermodynamic stability of the chlorine–SWCNT covalent attachment(s).

The binding of a single neutral chlorine atom to the sidewall of the finite (6,2) SWCNT (i.e., mono configuration) is significantly less favorable compared to ortho and para configurations (Fig. 2a). The C–Cl bond length in this case is 1.91 Å (Fig. S3a†) and is the longest observed for any neutral chlorinated system in this study, which directly points toward the thermodynamic instability of the singly chlorinated system. The addition of a single chlorine atom to the SWCNT results in the generation of an unstable, open-shell radical species forcing all carbon atoms in adjacent hexagonal rings to adopt partial sp³-hybridized character (see the LUMO orbital for the mono configuration in Table 1 discussed later), which leads to the increase in relative energy. In this way, binding an additional chlorine atom to one of the adjacent carbon atoms that are electronically preconditioned to form another bond (i.e., with partial sp³-like vacancies that point outward from the SWCNT, see Table 1) becomes more thermodynamically favorable. This conclusion is supported by other DFT calculations of chlorinated (5,5), (9,0) and (10,0) SWCNTs, which also confirmed that the Cl atoms should be adsorbed in pairs.⁵⁸

Table 1 The highest occupied (HOMO) and the lowest unoccupied (LUMO) molecular orbitals of the neutral chlorinated two-unit cell (6,2) SWCNT models are shown for various chlorination schemes. The ground state energy gap is labeled for each system along with a qualitative label of the localization to the chlorine attachments as delocalized, mixed, or localized character for each orbital

Neutral system (HL gap)	HOMO	LUMO
MONO (1.93 eV)
Ortho Cir. (1.84 eV)
Para Di. (1.63 eV)
1,4 Cir. (1.36 eV)
1,6 Di. (1.27 eV)
1,8 Di. (1.25 eV)

---

However, such stabilization is much less pronounced in the cases where two chlorine atoms are bound far away, to separate rings, as is the case with the 1,4, 1,6, and 1,8 configurations (see Fig. 1), compared to ortho and para attachments, which share the same carbon ring. A weaker Cl–SWCNT interaction of 1,4-, 1,6-, and 1,8-functionalization is accompanied by longer C–Cl bond lengths of 1.88–1.90 Å (see Fig. S3†) as well as a smaller degree of lattice distortion in the vicinity of the functional group, resulting in smaller bond length alternations (BLA, see Fig. S3b† and Methods). The values of BLA for the 1,4, 1,6, and 1,8 configurations are comparable to those of a single Cl attachment (Fig. S3b†). Note that in the limit of infinitely separated covalent attachments, all properties of the 1,4, 1,6, and 1,8 schemes should be equivalent to that of the mono-functionalization, as previously discussed for two interacting pairs of covalent attachments which then act as a single pair of covalent attachments.⁸⁰ For chlorines bound to different carbon rings, the binding energy varies dramatically, ranging from −0.95 to −0.65 eV, and appears to be mostly dependent on the direction of functionalization with respect to the SWCNT axis where chiral arrangements (see Fig. 1 for geometries) are generally less stable than circumferential and diagonal arrangements (Fig. 2a).

In contrast, charged systems demonstrate an opposite trend: a single charged chlorine attached to the nanotube (mono, Q = −1) provides the most stable structure (E_b = −0.88 eV), while a pair of charged chlorines (Q = −2) attached at the ortho or para positions result in a drastic reduction in stability, as can be seen in Fig. 2b. When a charge is introduced, mono-functionalization results in a closed-shell system, whereas an open-shell system is generated when a second chlorine anion is bound to the nanotube. This explains the reverse trend for the charged cases. For the shorter 2-unit cell SWCNT models, electrostatic repulsion between chlorine ions eliminates the stability of the functionalized system, resulting in slightly positive binding energies for structures with two chlorine atoms in close proximity to each other. However, this instability is reduced as the distance between chlorine atoms increases, with negative binding energies being seen for 1,6 and 1,8 cases (Fig. 2b).

All charged, di-chlorinated systems, however, are noticeably less stable than either their monochlorinated or neutral counterparts. As a result, for all charged systems, the C–Cl bond lengths are longer than 1.9 Å (Fig. S3c†) and the C–C BLA is smaller than 0.09 Å (Fig. S3d†), showing less degree of their sp³-character compared to their neutral counterparts (Fig. S3b†). A Mulliken charge analysis indicates that the negative charge introduced into the chlorinated systems is shared between the chlorine and the sp³-hybridized carbon atom where functionalization occurs, similar to results for divalent functionalization of (6,5) SWCNTs from previous work.³⁸ The instability generated by the electrostatic repulsion between the negatively charged sp³-carbon and chlorine as well as between chlorines significantly elongates the C–Cl bond lengths compared to neutral structures (Fig. S3c†). For the same reason, the binding energy for the charged chlorine case is heavily dependent on the proximity of the two negative charges along the SWCNT axis, which becomes weakly thermodynamically stabilized for the far-separated chlorines in the 1,6 and 1,8 configurations (Fig. 2b).

The dependence of the Cl–SWCNT binding energy on the Cl–Cl separation is enhanced by the confinement effect of short SWCNT models due to strong electron localization around the defect in our charged 2-unit cell SWCNT model systems. Therefore, unlike the neutral models where Cl–SWCNT interactions are nearly insensitive to the nanotube length, there is a substantial increase in the stability of chlorinated systems when the length of a nanotube is increased for charged cases (Fig. 2b). Comparing 5-unit cell and 2-unit cell SWCNT models, the Cl–SWCNT binding strength increases by about 300 meV and 500 meV for the charged monochlorinated and di-chlorinated cases, respectively. We expect this difference in the binding energy is due to the increased delocalization of the negative charge over several neighboring carbons as the length of the SWCNTs increases, leading to less negative charge on each atom of the SWCNT. Nonetheless, the Cl–SWCNT binding is still weaker by a factor of 1.5–2.0 compared to those of neutral five-unit cell SWCNT systems. As such, it can be concluded that chlorinated SWCNT samples holding a negative charge likely occur at very low concentrations, with predominantly mono-functionalization of the SWCNT by an isolated chloride ion.

The ground state electronic structure of chlorinated SWCNTs

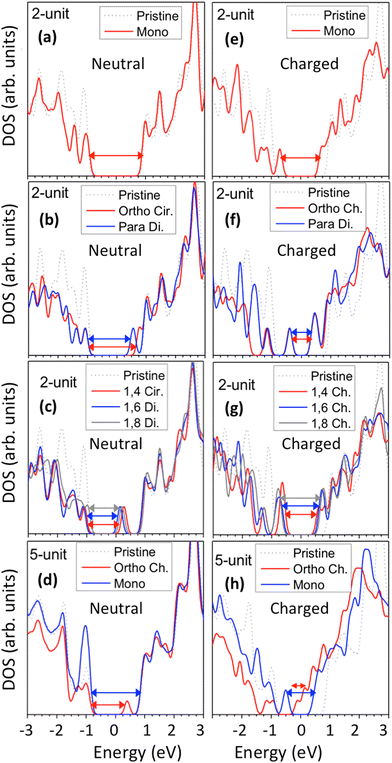
Functionalization of SWCNTs with chlorines results in significant changes to the electronic structure of both charged and neutral systems. As has been previously described for functionalization with aryl groups^39,40 and hydrogen atoms,⁸⁷ the binding of the chlorine atoms to the SWCNT surface results in a reduction of the HOMO–LUMO energy gap due to the introduction of one or more molecular orbitals (MOs) inside the pristine energy gap. These new MOs showcase broken π-conjugation with nodal points in the wavefunction near the sp³-carbons of the lattice. In the pristine system, the frontier MOs show degeneracy due to the high amount of symmetry. Upon functionalization, the degenerate states are shifted away from the energy gap, leaving non-degenerate defect-related HOMO and LUMO states.^18,40 The precise position of these new defect-associated MOs is dependent on the functionalization scheme.

Fig. 3 showcases the ground state electronic density of states (DOS) for the Kohn–Sham MOs. Here, the DOS has been broadened by a Gaussian function of width σ = 0.1 eV to account for experimental conditions that generate finite lifetimes of states, such as the thermal motion induced by the interaction with a bath and disorder. Monochlorination in neutral systems, for both the 2-unit cell (Fig. 3a, solid red line) and the 5-unit cell (Fig. 3d, solid blue line) SWCNT models, negligibly alters the energy gap and the DOS profile, except the peak height at the edge of the valence band. In contrast, binding of a pair of chlorine atoms results in the introduction of a new, unoccupied state inside the energy gap of the pristine system, which can be interpreted as a p-type electronic dopant (Fig. 3b and c). For both ortho and para configurations, these unoccupied states appear closer to the conduction band (Fig. 3b), and increasingly reduce energy gaps for ortho-Ch. and para-Cir. (Fig. S4†). This trend is similar for the longer 5-unit cell SWCNT models, except with a slightly reduced energy gap which follows from the relaxation of the confinement effect (Fig. 3d and S4d†).

Fig. 3 Density of states (DOS) for pristine and chlorine-functionalized (6,2) SWCNTs for (a)–(d) neutral and (e)–(h) charged systems (Q = −1 for mono, Q = −2 for all others). The zero-energy reference is taken as the middle of the HOMO–LUMO gap of the pristine SWCNT, while the energies of functionalized SWCNTs are artificially shifted such that the largest peaks reside deep inside the valence and conduction bands of the pristine SWCNT. The arrows indicate the energy gap of the system.

For 1,4, 1,6 and 1,8 defects, where chlorines bound on different carbon rings of the nanotube, the new unoccupied states are nearly in the middle of the pristine HOMO–LUMO energy gap, resulting in the reduction of the energy gap by a factor of two compared to the pristine SWCNT (Fig. 3c and S4d†). In these far-away chlorine attachments (Fig. 3c), the relative energy of the new mid-gap states is nearly insensitive to the defect configuration, in contrast to the ortho and para cases (Fig. 3b). Similar dependence of the frontier orbital energies on the fluorine separation has been obtained in recent calculations⁷⁷ of (11,0) SWCNT: At large separations of fluorine (like our 1,6, and 1,8 defects), a pair of new mid-gap states are introduced and pushed toward one another and further into the energy gap of the pristine SWCNT. At low axial separation (like para and ortho defects), the mid-gap states become energetically separated, and one is pushed beyond the valance band edge of the pristine SWCNT.⁷⁷ Overall, for all neutral, di-chlorinated models, p-type electronic doping was observed and is expected to provide useful properties beneficial for photo-voltaic devices, chemical sensors, photocatalytic agents, etc. The p-type electronic dopant character of the new MOs is confirmed by the localization of the LUMO around the Cl/sp³-defect. Table 1 showcases the HOMO and LUMO MOs for several representable chlorination schemes for the 2-unit cell (6,2) model, and Fig. S5† depicts the ground state frontier MOs of the 5-unit cell (6,2) model. In all neutral systems, the LUMO is strongly localized around the sp³-defect with a large contribution from chlorines. Fig. S6† depicts the projected DOS onto the SWCNT and chlorine contributions to quantitatively confirm the strong chlorine character of the LUMO in each case. In contrast, the HOMO is delocalized over the SWCNT backbone with negligible contribution from the chlorine sites for the mono, ortho, or para functionalization schemes.

However, for far-away chlorine attachments at different carbon rings – the 1,6 and 1,8 cases – the character of the HOMO changes from delocalized to defect-localized. The 1,4 case shows mixed character of the MO with partial localization to the chlorine attachment sites, which implies a crossing of states in the band structure with increasing chlorine–chlorine separation distance. These results agree with previous calculations of zigzag SWCNTs showing charge transfer from the tube to the Cl adducts.^66,73 Moreover, a similar trend in increasing HOMO localization around the defect with decreasing axial separation between fluorines has been observed in recent calculations of (11,0) SWCNT.⁷⁷ Our calculations show that this trend appears even for non-axial separation in chiral SWCNTs and for varying defect configurations with respect to the nanotube axis and, therefore, generalize results reported in ref. 77.

The effect of functionalization for charged systems is qualitatively different from those of neutral systems. The extra electrons in the charged chlorinated SWCNTs introduce new occupied states inside the energy gap of the pristine SWCNT (Fig. 3e–h) in addition to one or more new unoccupied states. This leads to significantly reduced energy gaps, compared to the pristine model, where the most pronounced reduction is found for the longer 5-unit cell SWCNT systems due to the mitigated confinement effect (Fig. S4c†). For all charged systems, the HOMO is now localized around the defect with a large contribution coming from the chlorine atoms (Table 2 and Fig. S5†). These results illustrate the n-type electronic doping nature of negatively charged systems, where the role (i.e., localization character) of the HOMO and LUMO has been reversed compared to the previous results for the neutral models where p-type doping was present.

Table 2 The highest occupied (HOMO) and the lowest unoccupied (LUMO) molecular orbitals of the charged chlorinated 2-unit cell (6,2) SWCNT models are shown for various chlorination schemes (Q = −1 for Mono, Q = −2 for all others). The ground state energy gap (HL-Gap) is labeled for each system along with a qualitative label of the localization character of the electron density for each orbital as edge or defect localized

Charged system (HL gap)	HOMO	LUMO
MONO (1.42 eV)
Ortho Ch. (0.80 eV)
Para Ch. (0.79 eV)
1,4 Ch. (1.22 eV)
1,6 Ch. (1.35 eV)
1,8 Ch. (1.45 eV)

---

For various defect positions, the longer 5-unit cell SWCNT model exhibits similar edge localization for the charged cases, but somewhat mitigated, compared to the short 2-unit cell models of (6,2) SWCNTs (see Fig. S5† for visualizations of the HOMO/LUMO for the charged ortho circumferential and para chiral functionalization schemes). Due to the strong Coulomb repulsion in the charged cases, the charge is localized on the edges due to the larger spatial separation allowed for those states. The edge-localization is enhanced by a confinement effect, a lack of absolute symmetry of two ends of the finite-size SWCNT models with respect to the defect location, and more shallow shape of the trap potential for some defect configurations, such as strongly separated defects 1,4, 1,6 and 1,8 (Fig. S5†). Overall, such edge-localization of frontier orbitals likely implies that the accumulated charge requires a longer SWCNT model to stabilize the non-edge-localized states due to the strong Coulomb repulsion. However, the low-energy bright states seen in the absorption spectra (to be discussed in Fig. 4 and 5) are the physically meaningful states observed in experiments; they are present in our models regardless of the edge-localized states, which support the feasibility of used models.⁸⁸

Fig. 4 Absorption spectra of neutral chlorinated and pristine (6,2) SWCNTs of (a)–(c) two- (∼3 nm) and (d) 5-unit (∼7.5 nm) cell SWCNT models for a variety of functionalization schemes. The vertical lines represent the oscillator strength of the four lowest-energy optical transitions in each model.

Fig. 5 Absorption spectra of negatively charged chlorinated and pristine (6,2) SWCNTs of (a)–(c) two- (∼3 nm) and (d) 5-unit (∼7.5 nm) cell SWCNT models for a variety of functionalization schemes (Q = −1 for mono, Q = −2 for all others). The vertical lines represent the oscillator strength of the four lowest-energy optical transitions in each model.

These edge-localized states explain the significant changes in the shape and relative energetic alignment of the conduction band edge of charged systems compared to that of the pristine SWCNT (Fig. 3e–h). This also explains the similarity of the conduction band between different functionalization schemes (Fig. 3f and g), since low unoccupied MOs are edge-localized and, thus, insignificantly sensitive to the defect configurations. The reduction of the finite-size effects, moving from the 2- to the 5-unit cell SWCNT models, showcases a significantly reduced energy gap to 90–200 meV for the charged systems in the ortho and para configurations (Fig. 3h and S4c†). Most importantly, this reduction is accompanied by the occupied Cl/defect-related states (Fig. S5†) moving closely to unoccupied states of the conduction band and indicating the n-type electronic doping character for negatively charged SWCNTs with all choices of functionalization schemes for both long 5-unit and short 2-init (6,2) SWCNT models. This contrasts with the p-type doping character of the neutral cases.

Linear optical spectra of chlorinated SWCNTs

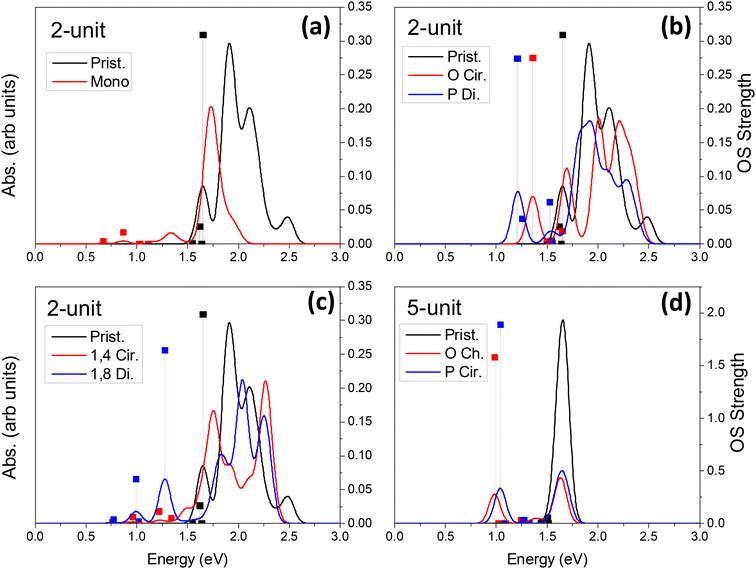
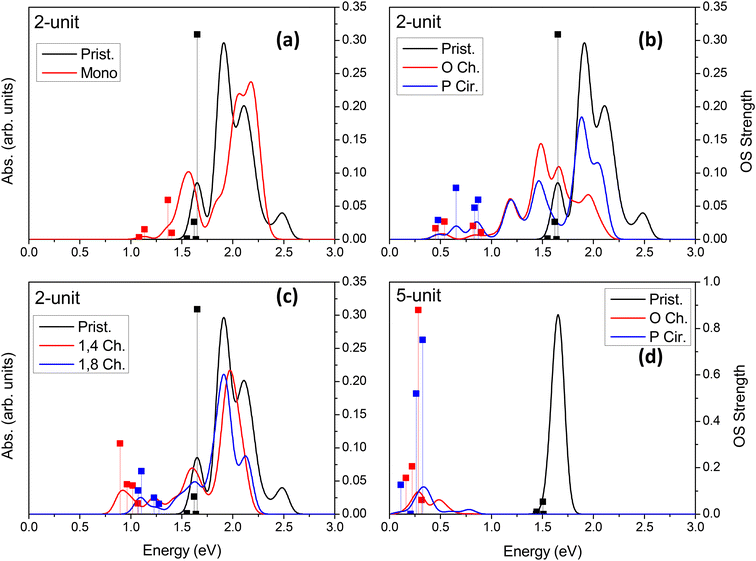
Linear optical^{24,33,34,36,37,46,85,89–91} and vibronic^{22,36,79,92–97} spectroscopy are some of the simplest ways to probe sp³-defect states in SWCNTs. Other methods also exist, such as electro-luminescence,⁹⁸ transmission electron microscopy (TEM),⁹⁹ and atomic force microscopy (AFM).³⁷ Absorption and emission optical spectroscopy, in particular, are the oldest and most widely used methods of detecting the presence and even the spatial location⁷⁸ of individual or groups of covalent defects.^{24,27,36,37,89,90,100} The simulated absorption spectra for neutral and charged chlorinated nanotubes are shown in Fig. 4 and 5, respectively. For both 2-unit cell (Fig. 4b) and 5-unit cell (Fig. 4d) (6,2) SWCNT models with neutral para and ortho functionalization schemes, the lowest-energy optical transition is redshifted and highly optically active, compared to the optically inactive lowest-energy states found in the pristine SWCNT model (black line in Fig. 4b and d). Thus, neutral para or ortho functionalization provides favorable conditions for emission of chlorinated SWCNTs, similar to the observed enhanced emission brought by aryl-based functionalization of SWCNTs having different chiralities and diameters.^{18,21–28,65,89}

When a pair of chlorine atoms are separated from one another (1,4 and 1,8 defects shown in Fig. 4c), the lowest-energy transitions appear even further redshifted and are significantly less optically active. In the limit of infinite separation, i.e., mono scheme, similar absorption features are seen at the same transition energies with even further decreased optical intensity. The reduced optical activity of the defect-associated excitonic states for the cases where the chlorines are separated from one another is rationalized by the stronger localization of the electronic distribution of the frontier orbitals (Table 1), compared to that of the ortho or para cases (Table 1 and Fig. 5), which reduces the transition dipole moment between the ground and the defect-associated excited states. Thus, for application toward light-emitting systems, it is crucial to bind the chlorine atoms to the same carbon ring to maximize the luminescence efficiency of the localized quantum defect. This conclusion agrees with the one obtained from calculations^39,87 of various SWCNTs covalently functionalized by aryl diazonium moieties, which has been recently confirmed experimentally.⁷⁸

For charged systems (Fig. 5), the lowest energy excitonic states also exhibit redshift of their lowest transitions compared to the main pristine E₁₁ band. However, the defect-associated states for the charged ortho and para functionalization schemes become more redshifted (Fig. 5b) than the separated schemes (1,4, and 1,8 defects shown in Fig. 5c) and the infinitely separated scheme (i.e., mono, Fig. 5a). Further, the optical intensity of the lowest-energy transitions for the charged ortho and para models are an order of magnitude smaller compared to the neutral systems, while the charged spatially separated models exhibit roughly the same or slightly higher optical intensity for the lowest-energy transitions compared to the neutral systems. We rationalize that the small increase in oscillator strength for the charged spatially separated defects is partially attributed to the edge localization in the short, 2-unit cell SWCNT models (Table 2), as discussed before, which leads to charge-transfer states that are partially edge-localized. The longer 5-unit cell (6,2) model helps to mitigate these spurious states reducing edge-localization of lowest excitons in charged systems with closely placed chlorine adduct at ortho and para (Fig. S5 and S8†). However, for these charged 5-unit cell models, the defect-associated states are strongly redshifted (Fig. 5d) – beyond the expected decrease in energy stemming from finite-size effects, seen to be ∼0.25 eV in the neutral 5-unit cell (6,2) system (Fig. 4d). These lowest energy transitions in charged 5-unit cell models have non-zero optical activity, although weaker than the neutral ortho or para cases (compare Fig. 5d and 4d).

We visualize the optical transitions (i.e., the excitons) through the real-space projected transition density,^37,80,101 as shown in Fig. S8.† This quantity allows for more precise examination of the localization of the excitons along the SWCNT main axis. Fig. S8† presents the data for the neutral and charged ortho-chiral functionalization of the 5-unit cell (6,2) model. One important observation is that the low-energy states change character between the neutral and charged cases, where the lowest-energy excitation for the neutral case is defect-localized, while it is a highly delocalized pristine-like exciton with a noticeable contribution from edges in the charged cases. This observation can be rationalized by examining the HOMO and LUMO orbitals of Table 1 (and Fig. S5†): the HOMO is localized to the pristine portion of the SWCNT while the LUMO is defect localized. One could imagine that the addition of two electrons simply re-labels the LUMO as the HOMO, while a strong Coulomb repulsion between added charges shifts the electron density to the nanotube's edges. In this case, the lowest-energy electronic transitions involving the frontier orbitals should differ in their character from the neutral case simply because of the re-labeling of the molecular orbitals. This is expected to persist across all SWCNT models as well as between SWCNT chiralities and diameters.

To generalize our results to other SWCNT chiralities, we have calculated several defect configurations of (6,5) SWCNT. Fig. S9† shows the absorption spectra and the excited electron–hole pairs (natural transition orbitals) contributing to the lowest optical transitions for the charged and neutral cases of ortho chiral functionalization of the (6,5) model of 12 nm in length with two chlorines as well as for the neutral pristine (6,5) SWCNT. For the aryl-functionalized (6,5) SWCNT, this defect configuration was calculated to provide the most redshifted defect-related optically bright transition.^40,102 Corrected for confinement errors,¹⁰² this transition is in good agreement with the experimentally observed most redshifted defect-related 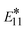emission peak (∼1.09 eV) for aryl-functionalized (6,5) SWCNTs.³⁴ Similar optically active, redshifted defect-related features (∼1.06 eV) have been experimentally detected in p-doped (6,5) SWCNTs, where a low degree of doping is introduced either via redox-chemistry using AuCl₃ solution or electrochemically (noncovalently).^64,65

As can be seen in Fig. S9,† the calculated optical transitions for the neutral chlorinated (6,5) model are similar to those previously calculated for aryl-functionalized (6,5) SWCNTs. Applying the confinement error correction following the procedure from ref. 102, the defect-related state and its splitting from the pristine E₁₁ band for the neutral chlorinated (6,5) model shows good agreement with absorption peaks detected in redox-dopped (6,5) SWCNTs under a small concentration of AuCl₃.^64,65 This similarity is rationalized by localization of the 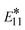exciton mainly on the sp³-defect, with a small contribution from adducts, as we have shown in our previous studies.^38,103 Experimental data from recent investigations of larger diameter SWCNTs exposed to halogen-containing solvents under sonication⁷¹ have suggested the defect formation mechanism resulting in p-doping of these wide-diameter SWCNTs being similar to the sp³-defect formation in diazonium treated smaller diameter (6,5) SWCNTs sonicated in water.⁷⁸ Thus, it seems reasonable to assume that changes in the electronic structure caused by the covalent attachments of various adducts to SWCNTs of different chiralities and diameters have similar nature and, thus, result in similar trends in their photophysical properties, while their quantitative characteristics have to be verified probing response from each SWCNT diameter and chirality.

The charged chlorinated (6,5) model exhibits optically active, low-energy excitons below 0.5 eV along with many dark states contributing from nanotube edges (Fig. S9†), similar to those observed for the charged (6,2) SWCNT model (Fig. 5). However, this strongly redshifted defect-related peak in the charged model deviates from those observed in the electrochemically field-doped (6,5) SWCNT films, which show no noticeable difference between redox- and electrochemically field-doped samples at small concentrations of carriers and defects.^65,104 We explain this discrepancy by the enhanced edge-localization of low-energy excitons due to a strong confinement effect of the charged 12 nm model (Fig. S9b†), which is unlikely present in experimental samples of long SWCNTs (>100 nm in length). Similar to the 8 nm (6,2) model, the edge-localization of low-energy excitons in the 12 nm (6,5) model implies that the accumulated charge requires a longer SWCNT model to stabilize the non-edge-localized states due to the strong Coulomb repulsion. Nonetheless, observed similarities between the lowest-energy peak of the chlorinated and pristine (6,5) charged models (dashed lines in Fig. S9†) point to similar characters of the distributions in the electron density for excess charge carriers in systems with and without covalent defects. This conclusion goes along with detected similar optical features between redox- and electrochemically field-doped samples of (6,5) SWCNts.^64,65,104

In all cases of functionalization scheme and charge, the energy of the main optical band E₁₁ (∼1.5–2.3 eV) roughly coincides with those of the pristine (6,2) SWCNT but is notably reduced in its optical intensity. This trend is the most pronounced for the longer 5-unit systems (Fig. 4d and S10†). In an attempt to understand this modulation of the pristine E₁₁ transition, we performed additional simulations at a higher level of theory. Using infinitely long SWCNTs (with periodic boundary conditions), the vertical excitations and linear absorption rates were computed using the Bethe–Salpeter equation (BSE)^105–109 on the basis of DFT Kohn–Sham states (see ref. 109 for methodological details) for a pristine and a para functionalized SWCNT model (Fig. S10†). Interestingly, the reduced optical activity of the E₁₁ band as a result of functionalization is further verified by these more rigorous simulations, indicating that the effects seen in our shorter, finite-sized models are justified and accurately capture the correct qualitative physics. We rationalize the reduction in the pristine E₁₁ optical transition upon covalent functionalization by the reduction in the orbital symmetry (i.e., degeneracy) in the pristine manifold, effectively reducing the oscillator strength of the bright pristine E₁₁ exciton. A similar decrease in the intensity of the main E₁₁ absorption band has been detected in low and moderately electrochemically and redox-doped films of (6,5) SWCNTs under small concentrations of AuCl₃.^64,65,104

Overall, diluted chlorine functionalization results in several main changes to the optical spectrum and electronic properties. First, there is a significant decrease in intensity of the main E₁₁ band. This is the result of the previously mentioned breaking of degeneracy in the electronic structure of SWCNTs due to surface functionalization (Fig. S4†). Second, there is an introduction of redshifted transitions originating from the sp³-defect whose energy-splitting and optical intensity strongly depend on the relative configuration and spatial separation of functional groups on the SWCNT surface. Third, neutral ortho and para defects provide optically active, lowest-energy transitions, while with increased distance between functional groups the optical intensity of the lowest-lying transitions decreases. Finally, negatively charged models exhibit reduced optical activity and the largest redshift of the low-energy, defect-associated states, but this trend is likely pronounced only in strongly confined SWCNT structures of ∼10 nm in length. While literature reports on computations of charged SWCNTs are limited, excitations in the charged SWCNT models are expected to provide important insights into the optical properties and formation of charged exciton states. For example, trions (singly charged excitons or three-particle states) in SWCNTs have been a topic of recent research and may give rise to a new type of defect-associated states used for their electronic and optical properties.^110–113 These systems are expected to be useful in ultra-long-wavelength emission in nano-structure-fabricated telecommunications devices.

The effect of defect concentration on electronic and optical properties

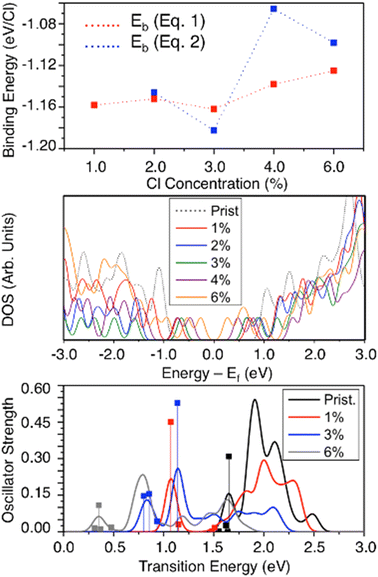
Concentration dependence of covalent functionalization has been the subject of recent interest in both experimental and theoretical research.^{22,36,37,65,80,114} We introduce higher concentrations of SWCNT-bound chlorine atoms in pairs, all of the same-ring para circumferential functionalization scheme for neutral 2-unit cell (6,2) SWCNT model systems. This defect configuration is chosen because it exhibits the brightest, lowest-energy exciton (Fig. 4b) for the system when one defect is introduced. Charged cases with higher concentration are not considered because data for charged mono- and di-chlorinated systems indicate that higher concentrations are unlikely to be stable due to the significant charge build-up on the defect-involved atoms leading to strong electrostatic repulsion upon further functionalization (Fig. 2 and S3†). Increased total charge in the considered SWCNT models may give rise to spurious results due to the strong Coulombic interaction coupled with the finite-length SWCNT, as discussed before (Table 2). Spectroscopic measurements evidence that redox-based doping leads to hard segmentation of the (6,5) SWNTs with intrinsic undoped segments being separated by randomly distributed charge puddles of 3.4–4 nm in width for the low and moderate concentrations of AuCl₃ as well as for electrochemically field-doped samples.^65,104 As such, the calculations of concentration dependence in charged systems require significantly larger than 10 nm length SWCNT models that can accommodate the excess charge, avoiding edge effects.

As observed in Fig. 6(top), the binding energy per chlorine exhibits only a small change as the number of neutral pairs of chlorine atoms is increased from 1% (2 chlorine atoms contributing to a single para sp³-defect) to 6% (12 chlorine atoms contributing to 6 sp³-defects separated by ∼0.5 nm). The thermodynamic stability of the chlorine–SWCNT interaction negligibly changes as the concentration is increased up to 3% (3 defects separated by ∼1 nm) and only reduces slightly as the concentration is further increased from 3 to 6 defects (Fig. 6(top)). We rationalize this result by the strong charge localization around the sp³-defect on the SWCNT, which reduces the sensitivity of the system to added numbers of defects. Based on our calculations, structures with 1–3 defects well distant from the nanotube edges are the most thermodynamically feasible. This agrees with recent experimental work¹¹⁴ where 1 to 3 quantum defects have been estimated as the most common defect concentration introduced by diazonium salt chemistry to (6,5) SWCNTs. However, binding energies are likely sensitive to the relative positioning of chlorine pairs on the SWCNT surface, and the arrangements chosen in this work might vary from the most stable one. Nonetheless, the underlying physics obtained from the concentration dependence of the para-circumferential configuration (Fig. 6(top)) suggests that low to high chlorine concentrations are feasible in experimental samples and may be controlled and manipulated by chemical means.

Fig. 6 Concentration-dependent effects in neutral chlorine functionalizations for the ground and excited electronic states. (Top) Binding energies of chlorine to the nanotube surface with respect to chlorine concentrations. The concentration is introduced by binding multiple chlorine pairs in the para functionalization scheme in the circumferential direction/orientation: two chlorines per 1% concentration. (Middle) The density of states (DOS) for the SWCNT for different chlorine concentrations. The zero-value reference for the X-axis is taken as the middle of the HOMO–LUMO gap (E_f) for each model. (Bottom) Simulated absorption spectra at various chlorine concentrations.

Increasing the number of sp³-defects from 1 to 3 (1–3%) only slightly changes the DOS and the HOMO–LUMO gap of the system (Fig. 6(middle)). However, as the chlorine concentration further increases, the number of mid-gap states contributed from chlorination increases,³⁷ resulting in a dramatically smaller HOMO–LUMO energy gap (∼0.53 eV) as the chlorine concentration increases to 6% (6 sp³-defects). This trend but with more pronounced reduction of the energy gap with increased defect concentration is observed in longer 5-unit-cell models (Fig. S11a and b†). Thus, increasing chlorine concentration effectively increases the p-type electronic doping character of chlorinated SWCNTs. The defect-associated mid-gap states contribute to multiple, redshifted optical transitions (Fig. 6(bottom)), whose energy decreases with the number of defects. The optical activity of these lowest-energy transitions noticeably reduces with increasing defect concentration, with this trend being the most pronounced in longer 5-unit cell models (Fig. S11c†). This optical behavior is rationalized as the result of the extension of the defect-associated exciton across all defect pairs, as has been explored previously for defect–defect interactions in SWCNTs.^37,80 At high defect concentrations, two defects are so close (<1 nm apart) that they form a hybrid defect state that cannot be factorized into the two original defects due to the large wavefunction overlap between several interacting excitons.⁸⁰ These closely spaced defects have been experimentally formed using single strand DNA^21–23,85 to control the spatial separation and defect concentration up to 20 defects per 100 nm of the SWCNT.³⁷ These high-concentration defects exhibit a further increase in the optical redshift compared to few-defect systems,^37,80 which agree with the calculated redshift trend for increased chlorination from 1% to 6% (red and grey lines in Fig. 6(bottom)).

However, recent experimental studies have shown that the defect-related emission energy 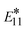remains constant while its intensity and linewidth increase with diazonium salt concentration, at the conditions of 1 to 3 defects per (6,5) SWCNT.¹¹⁴ In contrast, our results demonstrate a small redshift and decrease in the optical intensity for the lowest energy transitions when the number of defects is growing from 1 to 3 defects (red and blue line in Fig. 6(bottom)). This discrepancy can be associated with a strong confinement effect of our finite size SWCNT models, resulting in significantly larger energy splitting between states originating from different interacting defects (∼0.5 nm apart from each other), so that they do not additively contribute to one optical peak, as they likely would for infinitely long systems with a few well-separated non-interacting defects. This confinement effect is well illustrated for a single defect in the (6,2) SWCNT with varying length in Fig. S10.†

The appearance of defect-related low-energy transitions is accompanied by slight changes in the energy of the main bandgap-related E₁₁ transition and its reduced optical intensity as the defect concentration increases, which is an expected extension of the previous discussion regarding Fig. 4 and S8.† This trend agrees well with the experimentally observed reduced intensity of the E₁₁ emission peak in (6,5) SWCNTs with increasing diazonium salt concentration, which is regarded as an approximate measure for defect density.¹¹⁴ For increased concentrations of CuAl₃, the redox-doped (6,5) SWCNTs also show consistent reduction in the intensity of the E₁₁ band with doping concentration,^64,65,104 which correlates with our results. Overall, through the functionalization of additional chlorine atoms, the energy of optical transitions becomes more energetically tunable but less optically active in its main bands, pointing to a trade-off of value when using the concentration of the defects as a strategy for the tuning of such properties for practical optical applications. Additionally, the increase in the number of low-energy states with low optical activity will lead to competitions between radiative emission to the ground state and non-radiative relaxation from defect-associated states. The energetic location of these states is also highly sensitive to the atom-specific location of the many chlorine species in these high concentration schemes.

Conclusions

The structural, electronic, and optical properties of chlorinated (6,2) SWCNTs were examined using DFT and TD-DFT methods for both neutral and negatively charged systems. Neutral systems displayed selective binding with respect to configuration of the chlorine pair, where the system is the most energetically stable when two chlorine atoms are bound to the same ring of the SWCNT sidewall, either in ortho or in para configurations, independent of the length of the SWCNT model. Binding two chlorine atoms to different SWCNT carbon rings with increased chlorine–chlorine distance results in much weaker chlorine–SWCNT binding in which cases elongated C–Cl bond lengths as well as a reduction in sp³-character of C–C bonds near the functionalization can be seen. The reduced chlorine–chlorine interactions at large separation lengths lead to comparable thermodynamic stability as observed for the mono-chlorinated SWCNT, the least stable in this study. Preferential binding of neutral chlorine atoms at two close sites (on the same SWCNT carbon ring) – and therefore avoiding the formation of an open-shell system (monochlorination) – agrees with experimental data showing that a SWCNT radical is extremely short-lived due to high reactivity at the adjacent carbon sites.

In contrast, for negatively charged chlorinated SWCNTs, the chlorine binding energy is the most favorable for mono-chlorinated SWCNTs, since this configuration avoids the formation of an open-shell system, while additional charge dramatically reduces the stability for di-chlorinated SWCNTs, especially when the distance between chlorines is small. Our calculations show that the negative charge introduced into the chlorinated SWCNTs is predominantly localized not only on chlorine but also on the sp³-hybridized carbon atoms, which results in strong Cl–Cl (long-range) and C–Cl (short-range) electrostatic repulsions which destabilize the system. Therefore, we conclude that chloride ions likely bind to SWCNTs only in very low concentrations (effectively mono-chlorinated). In contrast, for neutral systems, the strength of the binding energy per chlorine atom is only slightly reduced with increasing chlorine concentration, since the frontier orbital charge density is mainly localized around the sp³-hybridized carbons where functionalization occurs, rather than on the chlorines themselves. This result confirms that high degrees of neutral chlorination should be feasible in experimental samples and can be used to tune subsequent electronic and optical properties.

The binding of neutral chlorine atoms to the SWCNT results in the introduction of unoccupied mid-gap states, resembling a p-type electronically doped system. As previously demonstrated for aryl-functionalized SWCNTs, the depth of the potential energy felt by the bound electron–hole pair (i.e., exciton) attributed to these defect-associated states is heavily dependent on the relative configuration of the two covalent functionalizations. All explored configuration schemes for the chlorines result in a decrease in the optical intensity of the main E₁₁ native excitonic band, which corresponds to optically active transitions in the pristine SWCNT, while also generating new redshifted, optically active transitions (for the ortho and para schemes) associated with the sp³-hybridization defect. However, increasing the distance between bound chlorines as well as increasing chlorine concentrations strongly reduces the optical intensity of both the pristine-associated E₁₁ and the redshifted, defect-associated transitions. Thus, even moderate concentrations (4–6%) of bound chlorines are expected to quench the emission of chlorinated SWCNTs. The binding of charged chloride ions to the SWCNT sidewall introduces occupied states to the energy gap of the nanotube, resulting in n-type electronic doping character. However, the intensities of redshifted, defect-associated optical transitions are found to be weak or completely inactive. As such, a reduction in the optical activity of low-energy optical bands can serve as a fingerprint of charged species in chlorinated SWCNTs.

Overall, our findings provide valuable insights into the photophysical and structural properties of chlorinated SWCNTs, which can be instrumental in guiding new synthesis procedures and characterization techniques, allowing for chemical control over emission efficiency in SWCNTs. Our quantum chemistry calculations complement experimental efforts in improving optical and electronic performance in these nanomaterials and are important for the fabrication of photovoltaic, lighting, sensor, and quantum information devices.

Methods

Atomistic models

Our ab initio simulations used finite-length (6,2) SWCNT models with two (220 atoms, ∼3 nm) and five (532 atoms, ∼7.5 nm) primitive unit cells in length using the Tubegen¹¹⁵ software. Each end of the finite SWCNT was functionalized with one methylene group attached to the dangling bond along the chiral vector/axes of the SWCNT (see Fig. 1b), with hydrogen atoms placed at all other terminal positions. It has been shown that the electronic structure of finite SWCNT models are sensitive to the number of methylene groups at the SWCNT terminus,⁸⁸ and this particular capping scheme was previously found to eliminate the electronic trap states located predominantly on the ends of the SWCNTs and provides proper scaling relationships between energies of optical features and system length.¹¹⁶ The pristine SWCNTs were then optimized using MOPAC¹¹⁷ software with AM1 (ref. 118) methodology and an STO-3G basis set as previously performed.⁸⁷ Further optimization was then performed using Gaussian09 software¹¹⁹ at the level of the density functional theory (DFT), with all results calculated using the PBE1PBE (also called PBE0) functional with the 6-31G* basis set for 5 nm (6,2) models and the mixed basis set using STO-3G for carbons and 6-31G* for chlorines in 8 nm (6,2) and 12 nm (6,5) SWCNTs.

The optimized (6,2) SWCNTs were functionalized with either one or two chlorine atoms initially placed at a distance of about 1.5 Å from one of the SWCNT carbon atoms to initiate the C–Cl bonding. The optimization of these initial geometries results in one sp³-hybridized defect in the otherwise sp²-hybridized crystal lattice of the SWCNT. As a result of non-zero chiral angle in (6,2) SWCNTs, functionalization with two chlorine atoms generates sp³-defect sites in three distinct orientations with respect to the SWCNT main axis (see Fig. 1b). Unique electronic and optical properties for functionalization along three orientations have been demonstrated in aryl-functionalized (6,5) systems and others.^{18,19,38,40,80,103} Various choices for the relative orientation and configuration of chlorine attachments on the (6,2) SWCNT lattice are presented in Fig. 1b and c. Both ortho and para arrangements with both chlorine atoms located on the same six-membered ring of the SWCNT are considered the most plausible species, from synthetic considerations.⁴⁰Meta configurations were not examined due to their instability.^58,75 The mono attachment (a single chlorine) was also considered, forming an open-shell system.

In addition, we have created structures where two chlorine atoms are separated from each other by four (1,4 defect), six (1,6 defect), and eight (1,8 defect) carbons. This results in defect sites being generated on adjacent rings, two rings apart, and three rings apart, respectively, as illustrated in Fig. 1b and c. Since intermediate steps in SWCNT functionalization with chlorine atoms are expected to involve charge transfer processes, charged systems were considered with both a zero and a negative one charge per chlorine adsorbed to the SWCNT surface, in addition to the neutral systems. In several of the charged systems, geometry optimization revealed the energetically favorable geometries to consist of isolated SWCNTs and chlorine species. The data for these arrangements where functionalization is not expected to occur is excluded from further consideration.

Calculated structural properties

The binding energy of a chlorine adduct to the tube was determined by the following formulas:

ΔE_b = [E_chlorinated − (E_CNT + nE_Cl)]/n, (1)

ΔE_b = [E_chlorinated − (E_{CNT/(n−2)Cl} + 2E_Cl)], (2)

where E_chlorinated is the total energy of the optimized chlorinated SWCNT, E_CNT is the energy of the optimized pristine SWCNT, E_Cl is the energy of a pristine chlorine atom (or an ion), n is the number of chlorine atoms (or ions) in the system, and E_{CNT/(n−2)Cl} is the energy of the chlorinated SWCNT with missed two chlorines forming one defect. Eqn (1) provides an average binding energy of a Cl adduct to the nanotube (see Fig. 2), while eqn (2) provides the energy of a specific Cl-based defect at the nanotube, when more than one defect is introduced to the model (high defect concentrations, see Fig. 6).

To determine the extent to which the sp²-hybridization in the pristine SWCNT lattice is disrupted by the presence of covalently attached chlorines, the bond length alternation (BLA) was defined as the difference between the average bond lengths between carbon atoms of the non-functionalized part of the SWCNT and the average of those bond lengths adjacent to the functionalized carbon atoms in the SWCNT. The shared bond between two defect sites in ortho/para-functionalized configurations is elongated to a higher degree than all other bonds in the system, due to its high sp³-hybridized character, and was therefore excluded from this average. Such analysis of binding energies and geometries enables the characterization of the degree of covalent functionalization for different binding configurations and methodologies.

Ground and excited state electronic structure calculations

To facilitate the selection of methodology, the results for finite-sized, functionalized (6,2) SWCNTs were compared using a number of different functionals and basis sets. Functionals that were tested include PBE,^120,121 PBE0,^120–122 B3LYP,^123–125 and ωB97XD,^126,127 all as constructed by the Gaussian09 software package¹¹⁹ with the 6-31G* basis set. These calculations revealed that the binding energies between chlorine adducts and the SWCNT, the C–Cl bond length, and the C–C BLA obtained by the hybrid PBE0 functional are comparable to those of the more advanced range-separated wB97XD functional with dispersion corrections (Fig. S1 and S2† and Discussion in the ESI†). While ωB97XD is expected to be more accurate for predicting geometries and adduct–SWCNT interactions, it provides unreasonably large band gaps in SWCNTs.^102,103,128 Therefore, we have used the PBE0 functional for all calculations of chlorinated SWCNTs, which shows reasonable performance for both the geometry and the electronic structure of these systems. The PBE0 functional was also used for the subsequent benchmarking of STO-3G,^129,130 6-31G,^131–135 and 6-31G*¹³⁶ basis sets, shown in Fig. S1b and d and S2b and d.† The inclusion of polarization functions to the basis set stabilizes the energy of the system, resulting in a more reasonable C–Cl bond length and increased C–C BLA corresponding to the significant sp³-character of carbon atoms involved in functionalization compared to the 6-31G basis set. Overall, our studies show that the 6-31G* basis set and the PBE0 functional is a sufficient methodology for calculations of chlorinated SWCNTs, which agrees with our conclusions from previous calculations of functionalized SWCNTs.¹⁰³

For analysis of the electronic structure in each case, the density of states (DOS) was generated by broadening the single-particle Kohn–Sham electronic states using a Gaussian function with linewidth σ = 0.1 eV. Optical transitions were generated using linear response time dependent DFT (TD-DFT)^137,138 on the finite-sized models optimized with the PBE0 functional and 6-31G* basis set. The 40 and 20 lowest-energy excited states (i.e., vertical excitations at the Condon geometry) were calculated for the 2- and 5-unit SWCNT models, respectively. To replicate the thermal effects, simulated absorption spectra were generated by broadening the ground-to-excited transitions with finite-width (σ = 0.1 eV) Gaussian functions. Natural transition orbitals (NTOs)¹³⁹ were generated for the lowest energy and the most intense optical transitions to visualize the localization of the electron–hole pair contributing to the first optically active excitonic state associated with the defect of the functionalized SWCNTs.

Author contributions

Braden M. Weight: conceptualization, data curation, methodology, validation, calculations of chlorinated (6,5) models, writing – original draft, writing – review & editing. Brendan J. Gifford: conceptualization, data curation, methodology, validation, writing – original draft. Grace Tiffany: calculations of molecular orbitals and absorption spectra of 5-unit cell chlorinated (6,2) models, writing – review & editing. Elva Henderson: calculations of all data for chlorinated 2-unit cell (6,2) models. Deyan Mihaylov: calculations of chlorinated (6,2) SWCNTs using periodic boundary conditions and applying many bodies perturbation theory. Dmitri Kilin: conceptualization, data curation, writing – review & editing. Svetlana Kilina: resources, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All authors thank the DOE EPSCoR: Building EPSCoR-State/National Laboratory Partnerships (Grant Number: DE-SC0021287) for the financial support of our research. For computational resources authors thank the Center for Computationally Assisted Science and Technology (CCAST) at North Dakota State University, whose computational facilities were enhanced due to the NSF MRI (Grant Number: 2019077). We also acknowledge the National Energy Research Scientific Computing Center (NERSC), supported by the Office of Science of the DOE under Contract Number DE-AC02-05CH11231, for providing computational resources used for a selection of the calculations performed in this work. This study was performed, in part, at the Center for Integrated Nanotechnology (CINT) and Center for Nonlinear Studies (CNLS), U.S. Department of Energy and Office of Basic Energy Sciences user facilities and supported by the Los Alamos National Laboratory (LANL) Directed Research and Development funds (LDRD).

References

1. R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998.
2. S. Cataldo, P. Salice, E. Menna and B. Pignataro, Carbon Nanotubes and Organic Solar Cells, Energy Environ. Sci., 2012, 5(3), 5919–5940,  10.1039/C1EE02276H.
3. B. J. Landi, R. P. Raffaelle, S. L. Castro and S. G. Bailey, Single-Wall Carbon Nanotube–Polymer Solar Cells, Progr. Photovolt.: Res. Appl., 2005, 13(2), 165–172,  DOI:10.1002/pip.604.
4. J. U. Lee, Photovoltaic Effect in Ideal Carbon Nanotube Diodes, Appl. Phys. Lett., 2005, 87(7), 073101,  DOI:10.1063/1.2010598.
5. M. Bansal, R. Srivastava, C. Lal, M. N. Kamalasanan and L. S. Tanwar, Carbon Nanotube-Based Organic Light Emitting Diodes, Nanoscale, 2009, 1(3), 317–330,  10.1039/B9NR00179D.
6. T. Mueller, M. Kinoshita, M. Steiner, V. Perebeinos, A. A. Bol, D. B. Farmer and P. Avouris, Efficient Narrow-Band Light Emission from a Single Carbon Nanotube p–n Diode, Nat. Nanotechnol., 2010, 5(1), 27–31,  DOI:10.1038/nnano.2009.319.
7. S. Wang, Q. Zeng, L. Yang, Z. Zhang, Z. Wang, T. Pei, L. Ding, X. Liang, M. Gao, Y. Li and L.-M. Peng, High-Performance Carbon Nanotube Light-Emitting Diodes with Asymmetric Contacts, Nano Lett., 2011, 11(1), 23–29,  DOI:10.1021/nl101513z.
8. S. Bahena-Garrido, N. Shimoi, D. Abe, T. Hojo, Y. Tanaka and K. Tohji, Plannar Light Source Using a Phosphor Screen with Single-Walled Carbon Nanotubes as Field Emitters, Rev. Sci. Instrum., 2014, 85(10), 104704,  DOI:10.1063/1.4895913.
9. Y. Wang and J. T. W. Yeow, A Review of Carbon Nanotubes-Based Gas Sensors, J. Sens., 2009, 2009, 493904,  DOI:10.1155/2009/493904.
10. W.-D. Zhang and W.-H. Zhang, Carbon Nanotubes as Active Components for Gas Sensors, J. Sens., 2009, 2009, 160698,  DOI:10.1155/2009/160698.
11. J. Li, Y. Lu, Q. Ye, M. Cinke, J. Han and M. Meyyappan, Carbon Nanotube Sensors for Gas and Organic Vapor Detection, Nano Lett., 2003, 3(7), 929–933,  DOI:10.1021/nl034220x.
12. T. Chen, L. Wei, Z. Zhou, D. Shi, J. Wang, J. Zhao, Y. Yu, Y. Wang and Y. Zhang, Highly Enhanced Gas Sensing in Single-Walled Carbon Nanotube-Based Thin-Film Transistor Sensors by Ultraviolet Light Irradiation, Nanoscale Res. Lett., 2012, 7(1), 644,  DOI:10.1186/1556-276X-7-644.
13. S. Dhall, N. Jaggi and R. Nathawat, Functionalized Multiwalled Carbon Nanotubes Based Hydrogen Gas Sensor, Sens. Actuators, A, 2013, 201, 321–327,  DOI:10.1016/j.sna.2013.07.018.
14. F. Wang, G. Dukovic, L. E. Brus and T. F. Heinz, The Optical Resonances in Carbon Nanotubes Arise from Excitons, Science, 2005, 308(5723), 838–841,  DOI:10.1126/science.1110265.
15. R. B. Weisman and S. M. Bachilo, Dependence of Optical Transition Energies on Structure for Single-Walled Carbon Nanotubes in Aqueous Suspension: An Empirical Kataura Plot, Nano Lett., 2003, 3(9), 1235–1238,  DOI:10.1021/nl034428i.
16. J. K. Streit, S. M. Bachilo, S. Ghosh, C.-W. Lin and R. B. Weisman, Directly Measured Optical Absorption Cross Sections for Structure-Selected Single-Walled Carbon Nanotubes, Nano Lett., 2014, 14(3), 1530–1536,  DOI:10.1021/nl404791y.
17. M. J. O'Connell, Band Gap Fluorescence from Individual Single-Walled Carbon Nanotubes, Science, 2002, 297(5581), 593–596,  DOI:10.1126/science.1072631.
18. B. J. Gifford, A. Saha, B. M. Weight, X. He, G. Ao, M. Zheng, H. Htoon, S. Kilina, S. K. Doorn and S. Tretiak, Mod(n-m,3) Dependence of Defect-State Emission Bands in Aryl-Functionalized Carbon Nanotubes, Nano Lett., 2019, 19(12), 8503–8509,  DOI:10.1021/acs.nanolett.9b02926.
19. B. J. Gifford, S. Kilina, H. Htoon, S. K. Doorn and S. Tretiak, Controlling Defect-State Photophysics in Covalently Functionalized Single-Walled Carbon Nanotubes, Acc. Chem. Res., 2020, 53(9), 1791–1801,  DOI:10.1021/acs.accounts.0c00210.
20. J. Zaumseil, Luminescent Defects in Single-Walled Carbon Nanotubes for Applications, Adv. Opt. Mater., 2022, 10(2), 2101576,  DOI:10.1002/adom.202101576.
21. Y. Zheng, S. M. Bachilo and R. B. Weisman, Controlled Patterning of Carbon Nanotube Energy Levels by Covalent DNA Functionalization, ACS Nano, 2019, 13(7), 8222–8228,  DOI:10.1021/acsnano.9b03488.
22. Z. Lin, L. C. Beltran, Z. A. De los Santos, Y. Li, T. Adel, J. A. Fagan, A. R. H. Walker, E. H. Egelman and M. Zheng, DNA-Guided Lattice Remodeling of Carbon Nanotubes, Science, 2022, 377(6605), 535–539,  DOI:10.1126/science.abo4628.
23. Y. Zheng, A. A. Alizadehmojarad, S. M. Bachilo and R. B. Weisman, Guanine-Specific Chemical Reaction Reveals SsDNA Interactions on Carbon Nanotube Surfaces, J. Phys. Chem. Lett., 2022, 2231–2236,  DOI:10.1021/acs.jpclett.2c00030.
24. Y. Zheng, Y. Han, B. M. Weight, Z. Lin, B. J. Gifford, M. Zheng, D. Kilin, S. Kilina, S. K. Doorn, H. Htoon and S. Tretiak, Photochemical Spin-State Control of Binding Configuration for Tailoring Organic Color Center Emission in Carbon Nanotubes, Nat. Commun., 2022, 13(1), 4439,  DOI:10.1038/s41467-022-31921-0.
25. Y. Zheng, S. M. Bachilo and R. B. Weisman, Photoexcited Aromatic Reactants Give Multicolor Carbon Nanotube Fluorescence from Quantum Defects, ACS Nano, 2020, 14(1), 715–723,  DOI:10.1021/acsnano.9b07606.
26. S. Ghosh, S. M. Bachilo, R. A. Simonette, K. M. Beckingham and R. B. Weisman, Oxygen Doping Modifies Near-Infrared Band Gaps in Fluorescent Single-Walled Carbon Nanotubes, Science, 2010, 330(6011), 1656–1659,  DOI:10.1126/science.1196382.
27. H. Kwon, A. Furmanchuk, M. Kim, B. Meany, Y. Guo, G. C. Schatz and Y. Wang, Molecularly Tunable Fluorescent Quantum Defects, J. Am. Chem. Soc., 2016, 138(21), 6878–6885,  DOI:10.1021/jacs.6b03618.
28. X. He, I. Kevlishvili, K. Murcek, P. Liu and A. Star, [2π + 2π] Photocycloaddition of Enones to Single-Walled Carbon Nanotubes Creates Fluorescent Quantum Defects, ACS Nano, 2021, 15(3), 4833–4844,  DOI:10.1021/acsnano.0c09583.
29. C.-W. Lin, S. M. Bachilo, Y. Zheng, U. Tsedev, S. Huang, R. B. Weisman and A. M. Belcher, Creating Fluorescent Quantum Defects in Carbon Nanotubes Using Hypochlorite and Light, Nat. Commun., 2019, 10(1), 2874,  DOI:10.1038/s41467-019-10917-3.
30. S. Ghosh, S. M. Bachilo, R. A. Simonette, K. M. Beckingham and R. B. Weisman, Oxygen Doping Modifies Near-Infrared Band Gaps in Fluorescent Single-Walled Carbon Nanotubes, Science, 2010, 330(6011), 1656–1659,  DOI:10.1126/science.1196382.
31. X. Ma, L. Adamska, H. Yamaguchi, S. E. Yalcin, S. Tretiak, S. K. Doorn and H. Htoon, Electronic Structure and Chemical Nature of Oxygen Dopant States in Carbon Nanotubes, ACS Nano, 2014, 8(10), 10782–10789,  DOI:10.1021/nn504553y.
32. X. Ma, J. K. S. Baldwin, N. F. Hartmann, S. K. Doorn and H. Htoon, Solid-State Approach for Fabrication of Photostable, Oxygen-Doped Carbon Nanotubes, Adv. Funct. Mater., 2015, 25(39), 6157–6164,  DOI:10.1002/adfm.201502580.
33. X. He, N. F. Hartmann, X. Ma, Y. Kim, R. Ihly, J. L. Blackburn, W. Gao, J. Kono, Y. Yomogida and A. Hirano, Tunable Room-Temperature Single-Photon Emission at Telecom Wavelengths from SP-3 Defects in Carbon Nanotubes, Nat. Photonics, 2017, 11, 577–582,  DOI:10.1038/nphoton.2017.119.
34. X. He, B. J. Gifford, N. F. Hartmann, R. Ihly, X. Ma, S. V. Kilina, Y. Luo, K. Shayan, S. Strauf, J. L. Blackburn, S. Tretiak, S. K. Doorn and H. Htoon, Low-Temperature Single Carbon Nanotube Spectroscopy of Sp ³ Quantum Defects, ACS Nano, 2017, 11(11), 10785–10796,  DOI:10.1021/acsnano.7b03022.
35. T. Shiraki, T. Shiraishi, G. Juhász and N. Nakashima, Emergence of New Red-Shifted Carbon Nanotube Photoluminescence Based on Proximal Doped-Site Design, Sci. Rep., 2016, 6, 28393,  DOI:10.1038/srep28393.
36. Y. Piao, B. Meany, L. R. Powell, N. Valley, H. Kwon, G. C. Schatz and Y. Wang, Brightening of Carbon Nanotube Photoluminescence through the Incorporation of Sp3 Defects, Nat. Chem., 2013, 5(10), 840–845,  DOI:10.1038/nchem.1711.
37. Y. Zheng, B. M. Weight, A. C. Jones, V. Chandrasekaran, B. J. Gifford, S. Tretiak, S. K. Doorn and H. Htoon, Photoluminescence Dynamics Defined by Exciton Trapping Potential of Coupled Defect States in DNA-Functionalized Carbon Nanotubes, ACS Nano, 2021, 15(1), 923–933,  DOI:10.1021/acsnano.0c07544.
38. B. J. Gifford, X. He, M. Kim, H. Kwon, A. Saha, A. E. Sifain, Y. Wang, H. Htoon, S. Kilina, S. K. Doorn and S. Tretiak, Optical Effects of Divalent Functionalization of Carbon Nanotubes, Chem. Mater., 2019, 31(17), 6950–6961,  DOI:10.1021/acs.chemmater.9b01438.
39. J. Ramirez, M. L. Mayo, S. Kilina and S. Tretiak, Electronic Structure and Optical Spectra of Semiconducting Carbon Nanotubes Functionalized by Diazonium Salts, Chem. Phys., 2013, 413, 89–101,  DOI:10.1016/j.chemphys.2012.10.010.
40. B. J. Gifford, S. V. Kilina, H. Htoon, S. K. Doorn and S. Tretiak, Exciton Localization and Optical Emission in Aryl Functionalized Carbon Nanotubes, J. Phys. Chem. C, 2018, 122, 1828–1838,  DOI:10.1021/acs.jpcc.7b09558.
41. K. Hyeon-Deuk and O. V. Prezhdo, Time-Domain Ab Initio Study of Auger and Phonon-Assisted Auger Processes in a Semiconductor Quantum Dot, Nano Lett., 2011, 11(4), 1845–1850,  DOI:10.1021/nl200651p.
42. F. Wang, Y. Wu, M. S. Hybertsen and T. F. Heinz, Auger Recombination of Excitons in One-Dimensional Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(24), 245424,  DOI:10.1103/PhysRevB.73.245424.
43. H. Wang, J. H. Strait, C. Zhang, W. Chan, C. Manolatou, S. Tiwari and F. Rana, Fast Exciton Annihilation by Capture of Electrons or Holes by Defects via Auger Scattering in Monolayer Metal Dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(16), 165411,  DOI:10.1103/PhysRevB.91.165411.
44. K. Hyeon-Deuk, J. Kim and O. V. Prezhdo, Ab Initio Analysis of Auger-Assisted Electron Transfer, J. Phys. Chem. Lett., 2015, 6(2), 244–249,  DOI:10.1021/jz502505m.
45. B. Weight, A. Sifain, B. Gifford, H. Htoon and S. Tretiak, On-the-Fly Non-Adiabatic Dynamics Simulations of Single-Walled Carbon Nanotubes with Covalent Defects, ACS Nano, 2023, 17, 6208–6219,  DOI:10.1021/acsnano.2c08579.
46. M. Kim, L. Adamska, N. F. Hartmann, H. Kwon, J. Liu, K. A. Velizhanin, Y. Piao, L. R. Powell, B. Meany, S. K. Doorn, S. Tretiak and Y. Wang, Fluorescent Carbon Nanotube Defects Manifest Substantial Vibrational Reorganization, J. Phys. Chem. C, 2016, 120(20), 11268–11276,  DOI:10.1021/acs.jpcc.6b02538.
47. N. F. Hartmann, S. E. Yalcin, L. Adamska, E. H. Hároz, X. Ma, S. Tretiak, H. Htoon and S. K. Doorn, Photoluminescence Imaging of Solitary Dopant Sites in Covalently Doped Single-Wall Carbon Nanotubes, Nanoscale, 2015, 7(48), 20521–20530,  10.1039/C5NR06343D.
48. M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup and L. C. L. Hollenberg, The Nitrogen-Vacancy Colour Centre in Diamond, Phys. Rep., 2013, 528(1), 1–45,  DOI:10.1016/j.physrep.2013.02.001.
49. X. Ma, N. F. Hartmann, J. K. S. Baldwin, S. K. Doorn and H. Htoon, Room-Temperature Single-Photon Generation from Solitary Dopants of Carbon Nanotubes, Nat. Nanotechnol., 2015, 10(8), 671–675,  DOI:10.1038/nnano.2015.136.
50. A. Jeantet, Y. Chassagneux, C. Raynaud, P. Roussignol, J. S. Lauret, B. Besga, J. Estève, J. Reichel and C. Voisin, Widely Tunable Single-Photon Source from a Carbon Nanotube in the Purcell Regime, Phys. Rev. Lett., 2016, 116(24), 247402,  DOI:10.1103/PhysRevLett.116.247402.
51. R. Kawabe, H. Takaki, T. Ibi, Y. Maeda, K. Nakagawa and H. Maki, Pure and Efficient Single-Photon Sources by Shortening and Functionalizing Air-Suspended Carbon Nanotubes, ACS Appl. Nano Mater., 2020, 3(1), 682–690,  DOI:10.1021/acsanm.9b02209.
52. A. Hirsch, Functionalization of Single-Walled Carbon Nanotubes, Angew. Chem., Int. Ed., 2002, 41(11), 1853–1859,  DOI:10.1002/1521-3773(20020603)41:11<1853::AID-ANIE1853>3.0.CO;2-N.
53. E. T. Mickelson, C. B. Huffman, A. G. Rinzler, R. E. Smalley, R. H. Hauge and J. L. Margrave, Fluorination of Single-Wall Carbon Nanotubes, Chem. Phys. Lett., 1998, 296(1–2), 188–194,  DOI:10.1016/S0009-2614(98)01026-4.
54. V. N. Khabashesku, W. E. Billups and J. L. Margrave, Fluorination of Single-Wall Carbon Nanotubes and Subsequent Derivatization Reactions, Acc. Chem. Res., 2002, 35(12), 1087–1095,  DOI:10.1021/ar020146y.
55. L. B. Alemany, L. Zhang, L. Zeng, C. L. Edwards and A. R. Barron, Solid-State NMR Analysis of Fluorinated Single-Walled Carbon Nanotubes: Assessing the Extent of Fluorination, Chem. Mater., 2007, 19(4), 735–744,  DOI:10.1021/cm0618906.
56. V. K. Abdelkader, S. Scelfo, C. García-Gallarín, M. L. Godino-Salido, M. Domingo-García, F. J. López-Garzón and M. Pérez-Mendoza, Carbon Tetrachloride Cold Plasma for Extensive Chlorination of Carbon Nanotubes, J. Phys. Chem. C, 2013, 117(32), 16677–16685,  DOI:10.1021/jp404390h.
57. V. K. Abdelkader, M. Domingo-García, M. D. Gutiérrez-Valero, R. López-Garzón, M. Melguizo, C. García-Gallarín, F. J. Lopez-Garzon and M. J. Pérez-Mendoza, Sidewall Chlorination of Carbon Nanotubes by Iodine Trichloride, J. Phys. Chem. C, 2014, 118(5), 2641–2649,  DOI:10.1021/jp411935g.
58. D. Erbahar and S. Berber, Chlorination of Carbon Nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(8), 085426,  DOI:10.1103/PhysRevB.85.085426.
59. I. Pełech, R. Pełech, U. Narkiewicz, D. Moszyński, A. Jędrzejewska and B. Witkowski, Chlorination of Carbon Nanotubes Obtained on the Different Metal Catalysts, J. Nanomater., 2013, 2013, 1–9,  DOI:10.1155/2013/836281.
60. A. O. Osikoya, C. W. Dikio, N. Ayawei, D. Wankasi, A. S. Afolabi and E. D. Dikio, Synthesis, Characterization and Adsorption Studies of Chlorine–Doped Carbon Nanotubes, Adv. Mater. Sci. Appl., 2015, 4(2), 53–62,  DOI:10.5963/AMSA0402003.
61. L. Oliveira, F. Lu, L. Andrews, G. A. Takacs, M. Mehan and T. Debies, UV Photo-Chlorination and -Bromination of Single-Walled Carbon Nanotubes, J. Mater. Res., 2014, 29(2), 239–246,  DOI:10.1557/jmr.2013.382.
62. I. H. Lee, U. J. Kim, H. B. Son, S.-M. Yoon, F. Yao, W. J. Yu, D. L. Duong, J.-Y. Choi, J. M. Kim, E. H. Lee and Y. H. Lee, Hygroscopic Effects on AuCl₃-Doped Carbon Nanotubes, J. Phys. Chem. C, 2010, 114(26), 11618–11622,  DOI:10.1021/jp1036662.
63. S.-M. Yoon, U. J. Kim, A. Benayad, I. H. Lee, H. Son, H.-J. Shin, W. M. Choi, Y. H. Lee, Y. W. Jin, E.-H. Lee, S. Y. Lee, J.-Y. Choi and J. M. Kim, Thermal Conversion of Electronic and Electrical Properties of AuCl₃-Doped Single-Walled Carbon Nanotubes, ACS Nano, 2011, 5(2), 1353–1359,  DOI:10.1021/nn103055u.
64. K. H. Eckstein, F. Hirsch, R. Martel and T. Hertel, Infrared Study of Charge Carrier Confinement in Doped (6,5) Carbon Nanotubes, J. Phys. Chem. C, 2021, 125(10), 5700–5707,  DOI:10.1021/acs.jpcc.1c00123.
65. K. H. Eckstein, F. Oberndorfer, M. M. Achsnich, F. Schöppler and T. Hertel, Quantifying Doping Levels in Carbon Nanotubes by Optical Spectroscopy, J. Phys. Chem. C, 2019, 123(49), 30001–30006,  DOI:10.1021/acs.jpcc.9b08663.
66. H. Pan, Y. P. Feng and J. Y. Lin, Ab Initio Study of F- and Cl-Functionalized Single Wall Carbon Nanotubes, J. Phys.: Condens. Matter, 2006, 18(22), 5175,  DOI:10.1088/0953-8984/18/22/017.
67. A. Kongkanand, R. M. Domínguez and P. V. Kamat, Single Wall Carbon Nanotube Scaffolds for Photoelectrochemical Solar Cells. Capture and Transport of Photogenerated Electrons, Nano Lett., 2007, 7(3), 676–680,  DOI:10.1021/nl0627238.
68. P. Brown, K. Takechi and P. V. Kamat, Single-Walled Carbon Nanotube Scaffolds for Dye-Sensitized Solar Cells, J. Phys. Chem. C, 2008, 112(12), 4776–4782,  DOI:10.1021/jp7107472.
69. D. D. Tune, H. Shirae, V. Lami, R. J. Headrick, M. Pasquali, Y. Vaynzof, S. Noda, E. K. Hobbie and B. S. Flavel, Stability of Chemically Doped Nanotube–Silicon Heterojunction Solar Cells: Role of Oxides at the Carbon–Silicon Interface, ACS Appl. Energy Mater., 2019, 2(8), 5925–5932,  DOI:10.1021/acsaem.9b01050.
70. C. Biswas, S. Y. Lee, T. H. Ly, A. Ghosh, Q. N. Dang and Y. H. Lee, Chemically Doped Random Network Carbon Nanotube p–n Junction Diode for Rectifier, ACS Nano, 2011, 5(12), 9817–9823,  DOI:10.1021/nn203391h.
71. P. Taborowska, G. Stando, M. Sahlman, M. Krzywiecki, M. Lundstrom and D. Janas, Doping of Carbon Nanotubes by Halogenated Solvents, Sci. Rep., 2022, 12, 7004,  DOI:10.1038/s41598-022-11162-3.
72. B. Kumanek, G. Stando, P. Stando, K. Matuszek, K. Z. Milowska and M. Krzywiecki, et al., Enhancing Thermoelectric Properties of Single-Walled Carbon Nanotubes Using Halide Compounds at Room Temperature and Above, Sci. Rep., 2021, 11, 8649,  DOI:10.1038/s41598-021-88079-w.
73. D. L. Duong, I. H. Lee, K. K. Kim, J. Kong, S. M. Lee and Y. H. Lee, Carbon Nanotube Doping Mechanism in a Salt Solution and Hygroscopic Effect: Density Functional Theory, ACS Nano, 2010, 4(9), 5430–5436,  DOI:10.1021/nn1011489.
74. A. Murat, I. Rungger, C. Jin, S. Sanvito and U. Schwingenschlögl, Origin of the P-Type Character of AuCl3 Functionalized Carbon Nanotubes, J. Phys. Chem. C, 2014, 118(6), 3319–3323,  DOI:10.1021/jp4100153.
75. S. Saha, T. C. Dinadayalane, J. S. Murray, D. Leszczynska and J. Leszczynski, Surface Reactivity for Chlorination on Chlorinated (5,5) Armchair SWCNT: A Computational Approach, J. Phys. Chem. C, 2012, 116(42), 22399–22410,  DOI:10.1021/jp307090t.
76. S. M. Kim, K. K. Kim, Y. W. Jo, M. H. Park, S. J. Chae, D. L. Duong, C. W. Yang, J. Kong and Y. H. Lee, Role of Anions in the AuCl3-Doping of Carbon Nanotubes, ACS Nano, 2011, 5(2), 1236–1242,  DOI:10.1021/nn1028532.
77. J. Fortner and Y. Wang, Quantum Coupling of Two Atomic Defects in a Carbon Nanotube Semiconductor, J. Phys. Chem. Lett., 2022, 8908–8913,  DOI:10.1021/acs.jpclett.2c02439.
78. P. Wang, J. Fortner, H. Luo, J. Kaos, X. Wu, H. Qu, F. Chen, Y. Li and Y. Wang, Quantum Defects: What Pairs with the Aryl Group When Bonding to the sp² Carbon Lattice of Single-Wall Carbon Nanotubes?, J. Am. Chem. Soc., 2022, 144(29), 13234–13241,  DOI:10.1021/jacs.2c03846.
79. B. Weight, M. Zheng and S. Tretiak, Signatures of Chemical Dopants in Simulated Resonance Raman Spectroscopy of Carbon Nanotubes, ChemRxiv, 2022, preprint,  DOI:10.26434/chemrxiv-2022-d56f5.
80. B. M. Weight, A. E. Sifain, B. J. Gifford, D. Kilin, S. Kilina and S. Tretiak, Coupling between Emissive Defects on Carbon Nanotubes: Modeling Insights, J. Phys. Chem. Lett., 2021, 12(32), 7846–7853,  DOI:10.1021/acs.jpclett.1c01631.
81. N. J. Hestand and F. C. Spano, Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer, Chem. Rev., 2018, 118(15), 7069–7163,  DOI:10.1021/acs.chemrev.7b00581.
82. N. J. Hestand and F. C. Spano, Molecular Aggregate Photophysics beyond the Kasha Model: Novel Design Principles for Organic Materials, Acc. Chem. Res., 2017, 50(2), 341–350,  DOI:10.1021/acs.accounts.6b00576.
83. M. Kasha, Energy Transfer Mechanisms and the Molecular Exciton Model for Molecular Aggregates, Radiat. Res., 1963, 20(1), 55–70,  DOI:10.2307/3571331.
84. M. Kasha, H. R. Rawls and M. A. El-bayoumi, The Exciton Model in Molecular Spectroscopy, Pure Appl. Chem., 1965, 371–592.
85. Y. Zheng, Y. Kim, A. C. Jones, G. Olinger, E. R. Bittner, S. M. Bachilo, S. K. Doorn, R. B. Weisman, A. Piryatinski and H. Htoon, Quantum Light Emission from Coupled Defect States in DNA-Functionalized Carbon Nanotubes, ACS Nano, 2021, 15(6), 10406–10414,  DOI:10.1021/acsnano.1c02709.
86. B. M. Weight, A. E. Sifain, B. J. Gifford, H. Htoon and S. Tretiak, On-the-Fly Nonadiabatic Dynamics Simulations of Single-Walled Carbon Nanotubes with Covalent Defects, ACS Nano, 2023, 17(7), 6208–6219,  DOI:10.1021/acsnano.2c08579.
87. S. Kilina, J. Ramirez and S. Tretiak, Brightening of the Lowest Exciton in Carbon Nanotubes via Chemical Functionalization, Nano Lett., 2012, 12(5), 2306–2312,  DOI:10.1021/nl300165w.
88. A. Sharma, B. J. Gifford and S. Kilina, Tip Functionalization of Finite Single-Walled Carbon Nanotubes and Its Impact on the Ground and Excited State Electronic Structure, J. Phys. Chem. C, 2017, 121(15), 8601–8612,  DOI:10.1021/acs.jpcc.7b00147.
89. X. He, L. Sun, B. J. Gifford, S. Tretiak, A. Piryatinski, X. Li, H. Htoon and S. K. Doorn, Intrinsic Limits of Defect-State Photoluminescence Dynamics in Functionalized Carbon Nanotubes, Nanoscale, 2019, 11(18), 9125–9132,  10.1039/C9NR02175B.
90. Y. Kim, S. V. Goupalov, B. M. Weight, B. J. Gifford, X. He, A. Saha, M. Kim, G. Ao, Y. Wang, M. Zheng, S. Tretiak, S. K. Doorn and H. Htoon, Hidden Fine Structure of Quantum Defects Revealed by Single Carbon Nanotube Magneto-Photoluminescence, ACS Nano, 2020, 14(3), 3451–3460,  DOI:10.1021/acsnano.9b09548.
91. Y. Kim, K. A. Velizhanin, X. He, I. Sarpkaya, Y. Yomogida, T. Tanaka, H. Kataura, S. K. Doorn and H. Htoon, Photoluminescence Intensity Fluctuations and Temperature-Dependent Decay Dynamics of Individual Carbon Nanotube Sp3 Defects, J. Phys. Chem. Lett., 2019, 10(6), 1423–1430,  DOI:10.1021/acs.jpclett.8b03732.
92. A. Ishibashi and N. Nakashima, Individual Dissolution of Single-Walled Carbon Nanotubes in Aqueous Solutions of Steroid or Sugar Compounds and Their Raman and Near-IR Spectral Properties, Chem. – Eur. J., 2006, 12(29), 7595–7602,  DOI:10.1002/chem.200600326.
93. T. Inaba, Y. Tanaka, S. Konabe and Y. Homma, Effects of Chirality and Defect Density on the Intermediate Frequency Raman Modes of Individually Suspended Single-Walled Carbon Nanotubes, J. Phys. Chem. C, 2018, 122(16), 9184–9190,  DOI:10.1021/acs.jpcc.8b01017.
94. C. Fantini, A. Jorio, M. Souza, L. O. Ladeira, A. G. Souza Filho, R. Saito, G. G. Samsonidze, G. Dresselhaus, M. S. Dresselhaus and M. A. Pimenta, One-Dimensional Character of Combination Modes in the Resonance Raman Scattering of Carbon Nanotubes, Phys. Rev. Lett., 2004, 93(8), 087401,  DOI:10.1103/PhysRevLett.93.087401.
95. C. Fantini, A. Jorio, M. Souza, R. Saito, G. G. Samsonidze, M. S. Dresselhaus and M. A. Pimenta, Steplike Dispersion of the Intermediate-Frequency Raman Modes in Semiconducting and Metallic Carbon Nanotubes, Phys. Rev. B, 2005, 72(8), 085446,  DOI:10.1103/PhysRevB.72.085446.
96. V. Skákalová, J. Maultzsch, Z. Osváth, L. P. Biró and S. Roth, Intermediate Frequency Modes in Raman Spectra of Ar+-Irradiated Single-Wall Carbon Nanotubes, Phys. Status Solidi RRL, 2007, 1(4), 138–140,  DOI:10.1002/pssr.200701069.
97. Z. Luo, F. Papadimitrakopoulos and S. K. Doorn, Intermediate-Frequency Raman Modes for the Lower Optical Transitions of Semiconducting Single-Walled Carbon Nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(20), 205438,  DOI:10.1103/PhysRevB.75.205438.
98. N. F. Zorn, F. J. Berger and J. Zaumseil, Charge Transport in and Electroluminescence from Sp3-Functionalized Carbon Nanotube Networks, ACS Nano, 2021, 15(6), 10451–10463,  DOI:10.1021/acsnano.1c02878.
99. H. Hiura, T. W. Ebbesen, J. Fujita, K. Tanigaki and T. Takada, Role of Sp3 Defect Structures in Graphite and Carbon Nanotubes, Nature, 1994, 367(6459), 148–151,  DOI:10.1038/367148a0.
100. N. Danné, M. Kim, A. G. Godin, H. Kwon, Z. Gao, X. Wu, N. F. Hartmann, S. K. Doorn, B. Lounis, Y. Wang and L. Cognet, Ultrashort Carbon Nanotubes That Fluoresce Brightly in the Near-Infrared, ACS Nano, 2018, 12(6), 6059–6065,  DOI:10.1021/acsnano.8b02307.
101. S. Tretiak, Triplet State Absorption in Carbon Nanotubes: A TD−DFT Study, Nano Lett., 2007, 7(8), 2201–2206,  DOI:10.1021/nl070355h.
102. B. J. Gifford, A. E. Sifain, H. Htoon, S. K. Doorn, S. Kilina and S. Tretiak, Correction Scheme for Comparison of Computed and Experimental Optical Transition Energies in Functionalized Single-Walled Carbon Nanotubes, J. Phys. Chem. Lett., 2018, 9(10), 2460–2468,  DOI:10.1021/acs.jpclett.8b00653.
103. B. M. Weight, B. J. Gifford, S. Tretiak and S. Kilina, Interplay between Electrostatic Properties of Molecular Adducts and Their Positions at Carbon Nanotubes, J. Phys. Chem. C, 2021, 125(8), 4785–4793,  DOI:10.1021/acs.jpcc.0c10157.
104. K. H. Eckstein, H. Hartleb, M. M. Achsnich, F. Schoeppler and T. Hertel, Localized Charges Control Exciton Energetics and Energy Dissipation in Doped Carbon Nanotubes, ACS Nano, 2017, 11, 10401–10408,  DOI:10.1021/acsnano.7b05543.
105. X. Blase, I. Duchemin, D. Jacquemin and P.-F. Loos, The Bethe–Salpeter Equation Formalism: From Physics to Chemistry, J. Phys. Chem. Lett., 2020, 11(17), 7371–7382,  DOI:10.1021/acs.jpclett.0c01875.
106. X. Blase, I. Duchemin and D. Jacquemin, The Bethe–Salpeter Equation in Chemistry: Relations with TD-DFT, Applications and Challenges, Chem. Soc. Rev., 2018, 47(3), 1022–1043,  10.1039/C7CS00049A.
107. L. X. Benedict, A. Puzder, A. J. Williamson, J. C. Grossman, G. Galli, J. E. Klepeis, J.-Y. Raty and O. Pankratov, Calculation of Optical Absorption Spectra of Hydrogenated Si Clusters: Bethe-Salpeter Equation versus Time-Dependent Local-Density Approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(8), 085310,  DOI:10.1103/PhysRevB.68.085310.
108. A. Kryjevski, D. Mihaylov, S. Kilina and D. Kilin, Multiple Exciton Generation in Chiral Carbon Nanotubes: Density Functional Theory Based Computation, J. Chem. Phys., 2017, 147(15), 154106,  DOI:10.1063/1.4997048.
109. A. Kryjevski, D. Mihaylov, B. Gifford and D. Kilin, Singlet Fission in Chiral Carbon Nanotubes: Density Functional Theory Based Computation, J. Chem. Phys., 2017, 147(3), 034106,  DOI:10.1063/1.4992785.
110. H. Kwon, M. Kim, M. Nutz, N. F. Hartmann, V. Perrin, B. Meany, M. S. Hofmann, C. W. Clark, H. Htoon, S. K. Doorn, A. Högele and Y. Wang, Probing Trions at Chemically Tailored Trapping Defects, ACS Cent. Sci., 2019, 5(11), 1786–1794,  DOI:10.1021/acscentsci.9b00707.
111. C. Möhl, A. Graf, F. J. Berger, J. Lüttgens, Y. Zakharko, V. Lumsargis, M. C. Gather and J. Zaumseil, Trion-Polariton Formation in Single-Walled Carbon Nanotube Microcavities, ACS Photonics, 2018, 5(6), 2074–2080,  DOI:10.1021/acsphotonics.7b01549.
112. J. T. Glückert, L. Adamska, W. Schinner, M. S. Hofmann, S. K. Doorn, S. Tretiak and A. Högele, Dipolar and Charged Localized Excitons in Carbon Nanotubes, Phys. Rev. B, 2018, 98(19), 195413,  DOI:10.1103/PhysRevB.98.195413.
113. A. H. Brozena, J. D. Leeds, Y. Zhang, J. T. Fourkas and Y. Wang, Controlled Defects in Semiconducting Carbon Nanotubes Promote Efficient Generation and Luminescence of Trions, ACS Nano, 2014, 8(5), 4239–4247,  DOI:10.1021/nn500894p.
114. C. Ma, C. A. Schrage, J. Gretz, A. Akhtar, L. Sistemich, L. Schnitzler, H. Li, K. Tschulik, B. S. Flavel and S. Kruss, Stochastic Formation of Quantum Defects in Carbon Nanotubes, ACS Nano, 2023, 17(16), 15989–15998,  DOI:10.1021/acsnano.3c04314.
115. J. T. Frey and D. J. Doren, TubeGen 3.4, 2011.
116. S. Kilina and S. Tretiak, Excitonic and Vibrational Properties of Single-Walled Semiconducting Carbon Nanotubes, Adv. Funct. Mater., 2007, 17(17), 3405–3420,  DOI:10.1002/adfm.200700314.
117. J. J. P. Stewart, MOPAC2009, 2008.
118. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, AM1: A New General Purpose Quantum Mechanical Molecular Model, J. Am. Chem. Soc., 1985, 107(13), 3902–3909,  DOI:10.1021/ja00299a024.
119. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009.
120. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
121. J. P. Perdew and K. B. Errata, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
122. C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170,  DOI:10.1063/1.478522.
123. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789,  DOI:10.1103/PhysRevB.37.785.
124. A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100,  DOI:10.1103/PhysRevA.38.3098.
125. A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652,  DOI:10.1063/1.464913.
126. J.-D. Chai and M. Head-Gordon, Systematic Optimization of Long-Range Corrected Hybrid Density Functionals, J. Chem. Phys., 2008, 128(8), 084106,  DOI:10.1063/1.2834918.
127. J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615,  10.1039/b810189b.
128. S. Kilina, E. Badaeva, A. Piryatinski, S. Tretiak, A. Saxena and A. R. Bishop, Bright and Dark Excitons in Semiconductor Carbon Nanotubes: Insights from Electronic Structure Calculations, Phys. Chem. Chem. Phys., 2009, 11, 4113–4123,  10.1039/B818473A.
129. W. J. Hehre, R. F. Stewart and J. A. Pople, Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals, J. Chem. Phys., 1969, 51(6), 2657–2664,  DOI:10.1063/1.1672392.
130. J. B. Collins, P. v. R. Schleyer, J. S. Binkley and J. A. Pople, Self-Consistent Molecular Orbital Methods. XVII. Geometries and Binding Energies of Second-Row Molecules. A Comparison of Three Basis Sets, J. Chem. Phys., 1976, 64, 5142–5151,  DOI:10.1063/1.432189.
131. P. M. W. Gill, B. G. Johnson, J. A. Pople and M. J. Frisch, The Performance of the Becke–Lee–Yang–Parr (B–LYP) Density Functional Theory with Various Basis Sets, Chem. Phys. Lett., 1992, 197(4–5), 499–505,  DOI:10.1016/0009-2614(92)85807-M.
132. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li–F, J. Comput. Chem., 1983, 4(3), 294–301,  DOI:10.1002/jcc.540040303.
133. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions, J. Chem. Phys., 1980, 72(1), 650–654,  DOI:10.1063/1.438955.
134. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56(5), 2257–2261,  DOI:10.1063/1.1677527.
135. R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728,  DOI:10.1063/1.1674902.
136. P. C. Hariharan and J. A. Pople, The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies, Theor. Chim. Acta, 1973, 28(3), 213–222,  DOI:10.1007/BF00533485.
137. R. O. Jones and O. Gunnarsson, The Density Functional Formalism, Its Applications and Prospects, Rev. Mod. Phys., 1989, 61(3), 689–746,  DOI:10.1103/RevModPhys.61.689.
138. A. Hellman, B. Razaznejad and B. I. Lundqvist, Potential-Energy Surfaces for Excited States in Extended Systems, J. Chem. Phys., 2004, 120(10), 4593–4602,  DOI:10.1063/1.1645787.
139. R. L. Martin, Natural Transition Orbitals, J. Chem. Phys., 2003, 118(11), 4775,  DOI:10.1063/1.1558471.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3lf00064h

‡ Both authors contributed equally to this work.

---